- 1National Institute on Alcohol Abuse and Alcoholism, Bethesda, MD, USA
- 2National Institute on Drug Abuse, Bethesda, MD, USA
The temporal dynamics of complex networks such as the Internet are characterized by a power scaling between the temporal mean and dispersion of signals at each network node. Here we tested the hypothesis that the temporal dynamics of the brain networks are characterized by a similar power law. This realization could be useful to assess the effects of randomness and external modulators on the brain network dynamics. Simulated data using a well-stablished random diffusion model allowed us to predict that the temporal dispersion of the amplitude of low frequency fluctuations (ALFF) and that of the local functional connectivity density (lFCD) scale with their temporal means. We tested this hypothesis in open-access resting-state functional magnetic resonance imaging datasets from 66 healthy subjects. A robust power law emerged from the temporal dynamics of ALFF and lFCD metrics, which was insensitive to the methods used for the computation of the metrics. The scaling exponents (ALFF: 0.8 ± 0.1; lFCD: 1.1 ± 0.1; mean ± SD) decreased with age and varied significantly across brain regions; multimodal cortical areas exhibited lower scaling exponents, consistent with a stronger influence of external inputs, than limbic and subcortical regions, which exhibited higher scaling exponents, consistent with a stronger influence of internal randomness. Findings are consistent with the notion that external inputs govern neuronal communication in the brain and that their relative influence differs between brain regions. Further studies will assess the potential of this metric as biomarker to characterize neuropathology.
Introduction
During resting-state functional magnetic resonance imaging (rfMRI) (Biswal et al., 1995) the human brain sequentially engages in a series of diverse free-streaming subject-driven mental states supported by different brain networks (Mason et al., 2007; Doucet et al., 2012; Shirer et al., 2012; Liu and Duyn, 2013; Yang et al., 2014). These complex and time-varying functional operations require a dynamic brain network topology to support the context-dependent coordination of neuronal populations (Allen et al., 2014; Zalesky et al., 2014) and its characterization and measurement could facilitate development of clinical biomarkers in neurology and psychiatry (Hutchison et al., 2013). Thus, the temporal dynamics of the human brain connectome (Chang and Glover, 2010; Sakoğlu et al., 2010) provides a new metric of brain function to assess healthy and disease conditions (Calhoun et al., 2014). However, our lack of understanding of the principles governing network dynamics may preclude the interpretation of the observed dynamics, which increases the within-subjects variability of the functional connectivity metrics (Tomasi et al., 2016a,b). A better understanding of how the collective behavior of neuronal communities contributes to the observable dynamics is crucial for the interpretation of the dynamics of functional connectivity.
Previous studies have shown that temporal mean 〈Si〉, and dispersion, σi, of the activity at a given node are related through a power law across network nodes (Argollo de Menezes and Barabasi, 2004)
where the scaling exponent, b, is a property of the network. Based on theoretical grounds and independent from the topology of the network, b equals either ½ or 1, which reflect a competition between the system's internal collective dynamics and temporal changes in the external environment (Argollo de Menezes and Barabasi, 2004). Specifically, in the absence of external modulation, b = ½, but when external driving forces become dominant, b = 1. For instance, whereas the network of internet routers is characterized by b = ½, the network of highways and the World Wide Web are characterized by b = 1. However, empirical evidence from ecology, where (1) describes the spatiotemporal variability of natural populations, supports the existence of intermediate b-values (Taylor, 1961) suggesting that meaningful temporal dynamic require ½ < b < 1.
Inasmuch as brain networks have scale-free (Barabasi and Albert, 1999; Eguíluz et al., 2005) and small-world (Watts and Strogatz, 1998) properties exhibited by complex networks we hypothesized that the mean and σ of FC properties such as ALFF, the amplitude of the low frequency fluctuations (Yang et al., 2007) or lFCD, the local degree of connectivity (Tomasi and Volkow, 2010) would reveal the characteristic power scaling properties exhibited by other complex networks. Specifically, we hypothesized that the mean and σ would be related by the power law (1) and that different brain networks would exhibit different scaling exponents reflecting differential balance between internal randomness (random firing) and external inputs (non-random firing). We selected functional connectivity (ALFF and lFCD) metrics rather than raw signals because the mean and dispersion values of the BOLD-fMRI signals are not expected to be in agreement with Equation (1).
Methods
To interpret the observed power scaling law (1), we study a simple dynamical model based on random diffusion. Using this model and functional connectivity information extracted from rfMRI datasets, we assessed the validity of Equation (1) in the context of brain functional connectivity. However, since direct application of Equation (1) to the mean and dispersion values of the raw fMRI time series is meaningless (the MRI signal mainly reflects tissue properties such as water density and T1 and T2 relaxation rates, which do not change as a function of time; the BOLD signal is zero-mean by definition), we simulated the temporal dynamics of ALFF and lFCD.
Model
Similar to previous studies (Argollo de Menezes and Barabasi, 2004), to model the signal S(t) we simulated the random diffusion of W walkers (messages) on a network of N nodes described by its adjacency matrix, Aij. Each walker was placed at a randomly chosen network node from which it departed randomly along one of the edges of that node in the next time step. This diffusion process was independently repeated 1,200 times and we recorded the number of incoming visits by various walkers at each network node to compute the time-varying signal at each node, Si(t). Temporal fluctuations in W were used to simulate externally induced modulations in Si(t), which for random networks and scale-free networks results in b = 1 exponent in (1) (Argollo de Menezes and Barabasi, 2004). Thus we varied the number of walkers as a function of time as: W(t) = W + ξ(t), where ξ(t) was a uniformly distributed random variable in the interval [−ΔW, ΔW], with ΔW = k*103 and k = 0,1,2,…, 9, and W = 104.
Simulations
The FreeSurfer gray matter parcellations (wmparc.2.nii) for 7 randomly selected MRI datasets were used to determine imaging voxels in the occipital, cingulate and insular networks (Figure 1A). The occipital network comprised bilateral cuneus, lateral occipital, lingual, and pericalcarine cortices (number of nodes/voxels, N = 8,200 ± 600). The cingulate network comprised bilateral rostral anterior, caudal anterior, isthmus, and posterior cingulate (N = 3,100 ± 400). The insular network comprised the bilateral insula (N = 2,300 ± 100). The Pearson correlation was used to compute correlation matrices reflecting the functional connectivity between voxels within each network for each subject. A correlation threshold R = 0.2 (p < 0.05) was used to compute the corresponding binary adjacency matrices. We implemented the diffusion model described above (Argollo de Menezes and Barabasi, 2004). We assumed the signal is proportional to the rate of incoming messages at each node as a function of time, which was simulated using 1,200 steps.
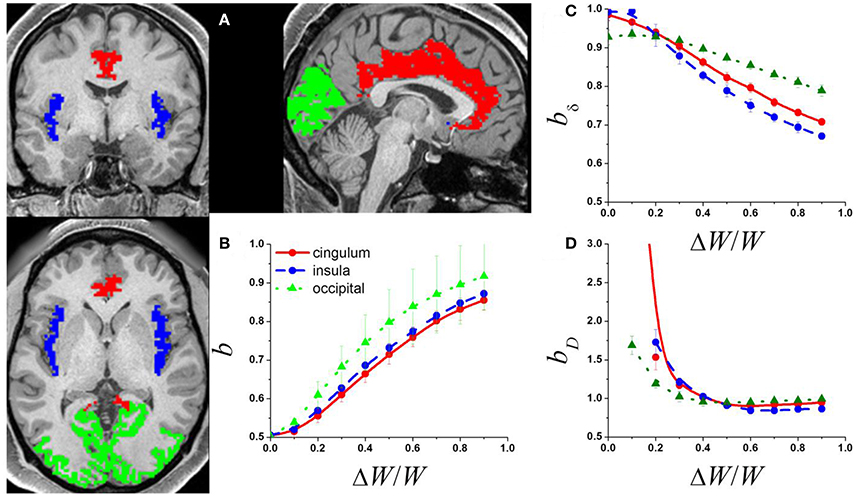
Figure 1. (A) Exemplary single-subject structural data showing occipital (green) cingulate (red) and insular (blue) gray matter networks used to compute the adjacency matrix from the corresponding rfMRI datasets. The adjacency matrices of these networks and a random diffusion model were used to produce simulated signal fluctuations, Si, with variable relative external modulation (ΔW/W) at each network node. The scaling exponent, b, was obtained by linear fitting the temporal mean and dispersion values of 〈Si〉 in a log-log plot. (B) Average b across network nodes and 7 subjects as a function of ΔW/W for the 3 different networks. Scaling exponent as a function of ΔW/W for the 3 different networks for: (C) the amplitude of the signal fluctuations, bδ; and (D) the degree of the functional connectivity, bD (see Methods).
To simulate the dynamics in the amplitude of the signal fluctuations, δi, at each node we segmented the Si(t) data (1,200 time points) into 23 epochs (window length: 100 time points; window shift: 50 time points) using a popular rectangular sliding window approach (Chang and Glover, 2010). The temporal standard deviation of Si(t) during each epoch was used to estimate δi. Degree, Di, the number of links connected to a network node (Rubinov and Sporns, 2010), was computed for each of the 23 epochs of the synthetic Si(t) data using a correlation threshold, R > 0.5 (p < 10−7). The linear model log(σX) = log(a) + blog〈X〉 with 2 freely adjustable parameters: log(a) and b, was used to fit the power law (1) to the temporal mean and dispersion values of the dynamic δ and D metrics (X).
Datasets
To test the predictions of the random diffusion model we analyzed rfMRI datasets drawn from the Human Connectome Project (HCP; http://www.humanconnectome.org/). No experimental activity with any involvement of human subjects took place at the author's institutions. The 66 participants (age: 30 ± 3 years; 32 females; Subject IDs: 100408, 103515, 103818, 105115, 105216, 106319, 110411, 118730, 118932, 119833, 120212, 122317, 123117, 125525, 127933, 128632, 129028, 130013, 131924, 133625, 133827, 133928, 134324, 136833, 137128, 138231, 138534, 140824, 142828, 143325, 144226, 149337, 149539, 150423, 151526, 153429, 156637, 158540, 159239, 159340, 160123, 161731, 162329, 163129, 165840, 167743, 172332, 178950, 182739, 191437, 192439, 192540, 194140, 197550, 199150, 199251, 200614, 201111, 210617, 217429, 249947, 250427, 255639, 304020, 307127, 329440) of the WU-Minn HCP Q1 data release included in this study provided written informed consent according to procedures approved by the IRB at Washington University in St. Louis.
Resting-state (eyes open) functional images were acquired using a gradient-echo-planar (EPI) sequence with multiband factor 8, TR 720 ms, TE 33.1 ms, flip angle 52°, 104 × 90 matrix size, 72 slices, 2 mm isotropic voxels, and 1200 timepoints (Smith et al., 2013; Uğurbil et al., 2013). Scans were repeated twice using different phase encoding directions (LR and RL) on each of two imaging sessions (REST1 and REST2) collected on different days. The “minimal preprocessing” datasets, which include gradient distortion correction, rigid-body realignment, field-map processing, spatial normalization to the stereotactic space of the Montreal Neurological Institute (MNI), high pass filtering (1/2,000 Hz frequency cutoff) (Glasser et al., 2013), independent component analysis-based denoising (Salimi-Khorshidi et al., 2014), and brain masking were used in this study.
Preprocessing
Framewise displacements, FD, computed for every time point from head translations and rotations using a radius of r = 50 mm (Power et al., 2012) did not differ between MRI sessions or phase encoding directions across subjects (p > 0.2, paired t-test; 〈FD〉 = 0.176 ± 0.05 mm). Scrubbing was not implemented to preserve the frequency spectra used for the computation of ALFF. Multilinear regression of head translations and rotations were used to minimize motion related fluctuations in the MRI signals (Tomasi and Volkow, 2010). Standard 0.01–0.08 Hz band-pass filtering was used to minimize physiologic noise of high frequency components.
Dynamic ALFF and lFCD
The average of the power spectrum's square root in the 0.01–0.08 Hz low frequency bandwidth was used to compute the ALFF (Yang et al., 2007). Functional connectivity density mapping was used to compute the lFCD (Tomasi and Volkow, 2010) at three different thresholds R > 0.3, 0.4 and 0.5. A sliding window approach (Chang and Glover, 2010) with two different window lengths (72s and 144s) and two different window shapes (rectangular and Hamming) was used to compute dynamic ALFF and lFCD maps with 2-mm isotropic resolution at two different temporal resolutions (36s and 72s). The window shift was set as half of the window length.
Region-of-Interest (ROI) Analysis
To test the power law (1) we contrasted scaling factors for the simulated signal fluctuations (δ) and degree (D) against those for ALFF and lFCD. Since lFCD has high sensitivity and specificity for gray matter (Tomasi et al., 2016c), the FC metrics were averaged within the anatomical gray matter regions-of-interest for each individual to minimize confounds arising from the variability of the folding patterns of cortical gray matter. Specifically, the FreeSurfer gray matter parcellations (wmparc.2.nii) were used as ROIs to compute the averages of the temporal mean and dispersion values of ALFF(t) and lFCD(t) within 34 cortical and 9 subcortical gray matter regions in each brain hemisphere. A probabilistic atlas for each of the gray matter parcellations was developed by averaging each of the gray matter parcellations across subjects independently, and used to display ROI results (i.e., bALFF or blFCD) in the MNI stereotactic space (Figures 2A, 3A).
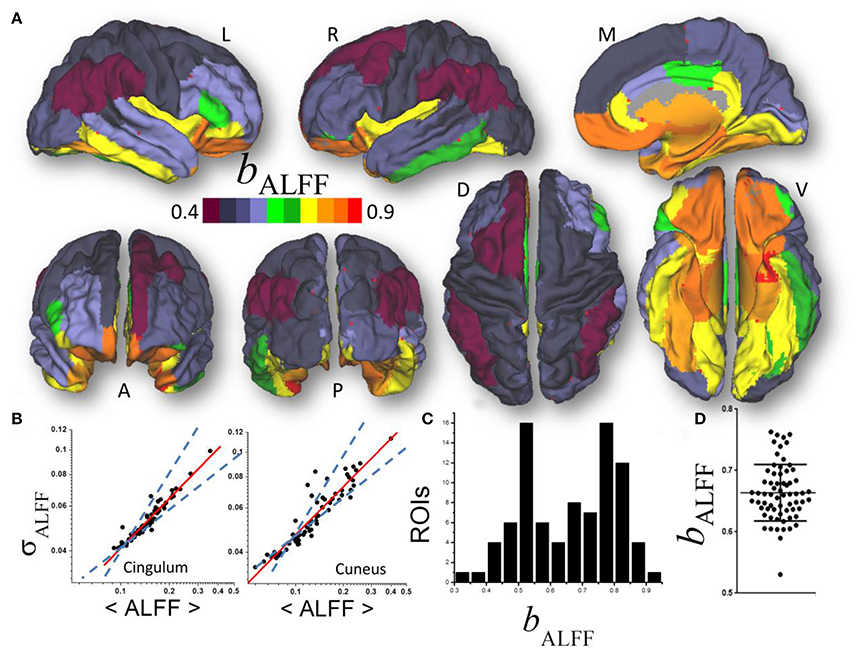
Figure 2. (A) Average scaling exponent (bALFF) for the temporal dynamics of the amplitude of low frequency fluctuations (ALFF) computed across nodes independently for each of the individual anatomical ROIs, superimposed on left (L), right (R), dorsal (D), medial (M), ventral (V) anterior (A), and posterior (P) views of the cerebral surface of the PALS_B12 template. (B) Scatter plots showing the good agreement across 66 subjects (dots) between the power law (1) (red line) and the dynamics of ALFF which is characterized by its temporal mean, 〈ALFF〉, and dispersion, σALFF. Dashed lines are the upper (bδ = 1; pure randomness) and lower (bδ = ½; pure external modulation) limits for the scaling exponent. (C) Frequency count histogram reflecting the probability distribution of bALFF across cortical and subcortical gray matter ROIs. (D) Scatter plot demonstrating the variability of bALFF across 66 young adults.
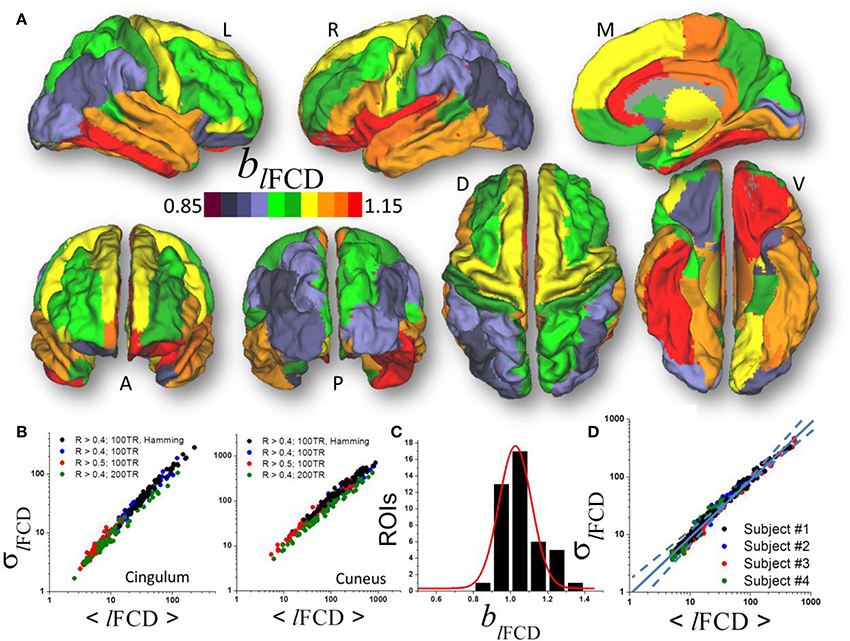
Figure 3. (A) Average scaling exponent (blFCD) for the temporal dynamics of the local functional connectivity density (lFCD) computed across nodes independently for each of the individual anatomical ROIs superimposed on left (L), right (R), dorsal (D), medial (M), ventral (V) anterior (A), and posterior (P) views of the cerebral surface of the PALS_B12 template. (B) Scatter plots across 66 subjects showing the robustness of the power law (1) that reflects the dynamics of lFCD to changes in correlation thresholds, sliding window lengths and shapes. (C) Frequency count histogram reflecting the probability distribution of blFCD across cortical and subcortical gray matter ROIs. (D) Scatter plot demonstrating the moderate differences power law (computed across 86 ROIs) in four typical subjects.
Statistical Methods
The linear model log(σ) = log(a)+blog〈X〉 with 2 free adjustable parameters: log(a) and b, was used to fit the power law (1) to the temporal mean and dispersion values of the dynamic ALFF and lFCD metrics (X). Paired t-test was used to assess within subjects differences in bALFF and blFCD as a function of session, phase encoding direction, correlation threshold, and window length and shape. Two samples t-test and Pearson correlation were used to assess gender and aging effects on bALFF and blFCD.
Results
Simulations
The power law (1) fitted well (R2 > 0.8) the temporal mean and standard deviation values of Si(t) across nodes. The b exponents increased monotonically with ΔW, which is consistent with the notion that internal randomness (diffusion) and external modulation (ΔW) proportionally alter Si(t) in the network (Argollo de Menezes and Barabasi, 2004). Thus, ΔW contributed to the temporal variability of the signal at each network node, gradually increasing b from ½ to 1 in all three brain networks (Figure 1B) as it occurs in other complex networks. Thus, if its magnitude is significant (ΔW ~ ½ 〈W〉), the external modulation can dominate the dynamics of Si(t).
The mean and dispersion values of δi computed across epochs were also in good agreement with the power law (1). Our simulations suggest that, bδ ~ 1, when internal randomness dominates over the external modulations (Figure 1C). However, bδ decreased with the amplitude of the external modulation and was constrained in the interval [0.5, 1]. Similarly, the mean and dispersion values of Di computed across epochs were in good agreement with the power law (1). Our simulations suggest that bD ~ 1 when the external modulation dominates over the internal randomness, but bD increases significantly above 1 when the relative weight of the external modulation decreases (Figure 1D). The power law failed to fit the data when internal randomness dominated over the external modulation (ΔW/W > ½) suggesting lack of association between the mean and dispersion values of D in this regime.
Amplitude of Fluctuations
A linear fit of whole-brain average and dispersion values of ALFF on a log-log plot computed across nodes demonstrated good agreement between Equation (1) and the dynamic amplitude of the signal fluctuations in each of the individual ROI (bALFF = 0.66 ± 0.16, mean ± standard deviation; 28 < t-score <294; P < 1E-37; Figure 2A). Consistent findings emerged from average and dispersion values within anatomical regions, independently for each of the 86 gray matter ROIs (R2 > 0.8; Figures 2B,C). The average scaling exponent was not different for subcortical (cerebellum, thalamus, caudate, putamen, pallidum, hippocampus, amygdala, accumbens and ventral diencephalon; bALFF = 0.78 ± 0.04, mean ± standard error) than for cortical (bALFF = 0.81 ± 0.07) regions (p > 0.4), independent of session, phase encoding direction (LR vs. RL), sliding window length (72s vs. 144s) and shape (rectangular vs. Hamming).
There were no significant differences in bALFF across subcortical regions. However, bALFF varied significantly across cortical regions. Specifically, the scaling exponent was higher for limbic (cingulum, orbitofrontal, parahippocampal and entorhinal) and visual (lingual, fusiform and pericalcarine) areas, the temporal and insular cortices and pars orbitalis (bALFF = 0.89 ± 0.02) than for occipital (cuneus, lateral occipital), parietal (inferior, superior, precuneus, postcentral), language (opercularis, triangularis, supramarginal) and prefrontal (paracentral, precentral, rostral, middle and superior frontal) areas (bALFF = 0.72 ± 0.03; p < 10−9; Figure 2B). The scaling exponent had normal distribution (center bALFF = 0.80; width = 0.16) across the 86 gray matter ROIs (R2 = 0.999, Gaussian fit; Figure 2C).
Significant between-subjects variability in the scaling exponent emerged from the data when we fitted Equation (1) to the mean and dispersion values of ALFF across the 43 ROIs, independently for each individual (bALFF = 0.66 ± 0.05; Figure 2D) and with similar robustness (R2 > 0.96). The scaling exponent slightly decreased with age (slope = −0.03/decade; R = −0.234; p = 0.03, one-tailed). However, there were no significant gender differences (p > 0.77; two-tailed two-sample t-test) in bALFF.
Local Degree
Similar to ALFF, a linear fit of whole-brain average and dispersion values of lFCD on a log-log plot computed across nodes demonstrated good agreement between Equation (1) and the local degree of brain functional connectivity in each of the individual ROI (blFCD = 1.05 ± 0.17, mean ± standard deviation; 43 <t-score <179; P <3E-49; Figure 3A). Average and dispersion values within anatomical regions showed consistent findings with those from the whole-brain analysis (R2 > 0.8; Figure 3B). The average scaling exponent was higher for subcortical (blFCD = 1.23 ± 0.09, mean ± standard error) than for cortical (blFCD = 1.06 ± 0.10) regions (p < 10−3, two-tailed two-sample t-test), independent of the correlation threshold used in the computation of the lFCD (R > 0.3, 0.4, or 0.5), session, phase encoding direction, window length (72s vs. 144s) and shape.
For lFCD, the scaling exponent was higher for limbic (cingulum, orbitofrontal, parahippocampal, and entorhinal), language (opercularis, orbitalis, triangularis), temporal (inferior, middle superior), and frontal (paracentral, superior and pole), insula and fusiform gyrus (blFCD = 1.13 ± 0.07) than for occipital (cuneus, lateral occipital, lingual and pericalcarine), parietal (inferior, superior, precuneus, supramarginal, paracentral, postcentral), prefrontal (precentral, rostral, middle, and superior) and temporal (entorhinal temporal pole, transverse) areas (blFCD = 0.98 ± 0.06; p < 10−6; Figure 3B). Across the 86 gray matter ROIs the scaling exponent had a right-skewed distribution with peak at blFCD = 1.03 and width = 0.17 (R2 = 0.95, Gaussian fit; Figure 3C). Fitting mean and dispersion values of lFCD across the 43 gray matter ROIs, independently for each subject, revealed modest between-subjects variability in the scaling exponent (blFCD = 1.09 ± 0.06; Figure 3D), and blFCD did not show significant age or gender differences (p > 0.23).
In visual areas (pericalcarine, lateral occipital, and cuneus) the standardized scaling factors bz were lower than average and were significantly lower for lFCD than for ALFF (p < 0.0005, t-test; Figure 4, left). In prefrontal regions (middle Frontal, superior frontal, precentral, paracentral, pars opercularis, and caudal anterior cingulate), the lower than average bz was lower for ALFF than for lFCD (p < 0.001). In frontal and temporal poles, entorhinal and lingual cortex showed the higher than average bz was higher for ALFF than for lFCD (p < 0.0001; Figure 4 right). In anterior (rostral) and posterior (isthmus) cingulate, fusiform gyrus and subcortical regions (hippocampus, thalamus and cerebellum) the higher than average bz was higher for lFCD than for ALFF (p < 0.0006).
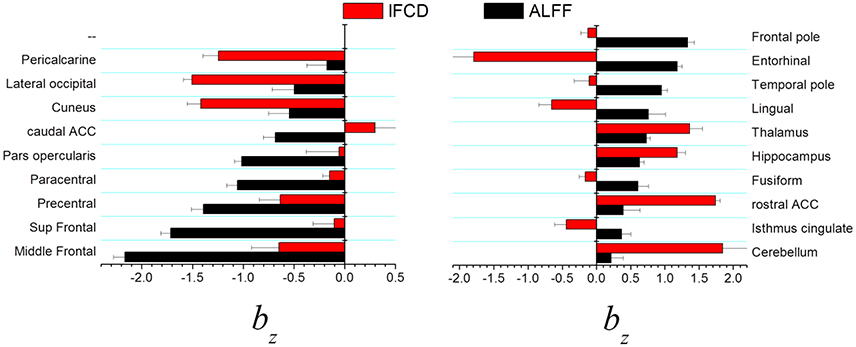
Figure 4. Brain regions showing statistically significant differences in standardized scaling exponents, bz, for ALFF and lFCD at p < 0.001. ACC, anterior cingulate cortex.
Effect of Bandpass Filtering
Given that frequency information may be of interest and that the ICA-FIX denoising procedure can remove a significant fraction of the physiological noise of respiratory origin (Salimi-Khorshidi et al., 2014), we also computed dynamic lFCD measures without 0.01–0.08 Hz bandpass filtering to assess the effect of higher frequencies on the power scaling law (Equation 1). Without bandpass filtering the scaling exponent b of the dynamic lFCD metrics was significantly larger than with bandpass filtering (p < 0.0001; Figure 5), and the agreement between the data and Equation (1) was significantly reduced [R2 = 0.82 (without) and 0.96 (with bandpass filtering)].
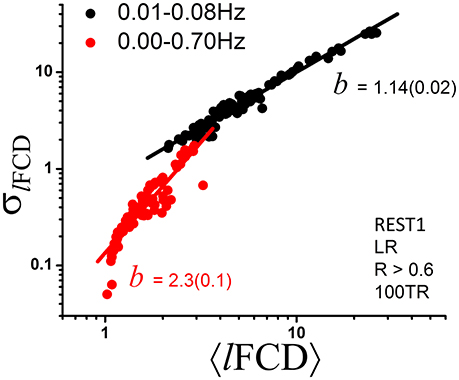
Figure 5. Scatter plot demonstrating the effect of bandpass filtering on the power scaling (Equation 1) of lFCD across ROIs. The fitted slope, b, the scaling factor in Equation (1), is significantly steeper without bandpass filtering (standard errors in parenthesis) suggesting increased level of randomness (see Figure 1D).
Discussion
Here we show for the first time that the mean and the dispersion values of dynamic FC metrics such as ALFF or lFCD are linked by a power law (1). This characteristic of complex networks such as rivers and highways networks, the Internet and the World Wide Web (Argollo de Menezes and Barabasi, 2004), and many biological systems (Taylor, 1961), reflects the competition between the system's internal collective dynamics and changes in the external environment. This strongly suggests that the dynamics of the FC metrics embeds important functional information, a possibility previously highlighted (Hutchison et al., 2013; Calhoun et al., 2014; Rashid et al., 2014; Hutchison and Morton, 2015), which could help in the development of biomarkers of brain function.
Our simulations were based on a random diffusion model previously proposed by Argollo de Menezes and Barabasi to explain the power scaling between the mean and the dispersion of the signals observed in natural and technological networks (Argollo de Menezes and Barabasi, 2004). Whereas the approach by Argollo de Menezes and Barabasi was based on random and scale-free networks (Barabasi and Albert, 1999; Barabási, 2009), the present approach was based on real FC networks directly extracted from in vivo resting fMRI data. The scaling exponents for the brain in the present work are consistent with those obtained previously in random and scale-free networks (Argollo de Menezes and Barabasi, 2004).
Here we extended the random diffusion model in order simulate the amplitude of spontaneous signal fluctuation and the degree of connectivity. Our simulations suggest that under pure randomness (i.e., without external driving forces, ΔW = 0) the mean and the dispersion values of the amplitude of signal fluctuations and degree are associated by power laws with scaling exponents bδ = 1 and bD > 1, respectively. However, under the influence of dynamic external modulations (ΔW/W ~ 1), bδ < 1 and bD = 1 characterize the dynamic behavior of the signal fluctuations and degree. The analysis of variability of resting-state fMRI datasets from the HCP database shows a range of scaling exponents for ALFF (0.5 < bALFF < 1) and for lFCD (1 < blFCD), which is consistent with the presence of dynamic external modulations of brain activity (0.5 < bδ < 1) and the corresponding degree (1 < bD). Overall, our findings are also consistent with the existence of dynamic modulations of brain activity that may reflect orchestrated dynamic neural processing (Yu et al., 2012; Allen et al., 2014; Gonzalez-Castillo et al., 2015).
This is the first study to document differences in scaling exponents between brain regions. Multimodal association areas (opercularis, triangularis, rostral, middle and superior frontal, precentral and paracentral, inferior and superior parietal and precuneus), somatosensory (supramarginal, postcentral) and visual (cuneus, lateral occipital) unimodal association areas showed low scaling exponent both for ALFF (bALFF ~ 0.7) and for lFCD (blFCD ~ 1). These findings suggest that the dynamics of the FC metrics was driven by external inputs (ΔW/W > ½) rather than by internal random processes (ΔW/W <0.5; Figures 1C,D), which is also consistent with the existence of dynamic modulations of resting brain activity (Yu et al., 2012; Allen et al., 2014; Gonzalez-Castillo et al., 2015). The multimodal cortex is highly interconnected with higher-order association areas involved in cognition and motor planning (Goldman-Rakic, 1988). Thus dynamic engagement of functional connectivity hubs in multimodal and unimodal association cortices may explain the low scaling exponent in these regions. On the other hand, limbic and subcortical regions exhibited relatively higher scaling exponents (bALFF ~ 0.8 and blFCD ~ 1.2) suggesting a stronger influence of internal randomness in the resting dynamics of the FC metrics in these regions.
We identify regional differences in the influence of internal randomness for different FC metrics. The direct comparison of standardized measures suggests a weaker influence of randomness in visual areas for lFCD than for ALFF and in prefrontal areas for ALFF than for lFCD, and a stronger influence of randomness in subcortical and limbic regions for lFCD than for ALFF. ALFF and lFCD reflect different network properties. Whereas ALFF is proportional to the BOLD signal fluctuations that reflect neuronal communication (Logothetis et al., 2001), the synchronous fluctuations of local communities measured by lFCD reflects the local degree of connectivity (Tomasi and Volkow, 2010).
The scaling exponent for ALFF, and to a lesser extent for lFCD, showed significant variability (ΔbALFF = 12%; ΔblFCD = 9%) across subjects suggesting that the dynamics of the b has potential as a biomarker for psychiatry and neurology. To illustrate the potential of this metric here we show that even in a relatively small sample (66 subjects) with narrow age range (22–35 years), bALFF is sensitive to aging effects, consistent with previous studies in large samples (~1000 subjects) with wide age range (17–82 years) that documented age-related decreases in FC (Biswal et al., 2010; Tomasi and Volkow, 2012).
The scaling exponent for lFCD increased significantly above 1 when frequencies other than those in the 0.01–0.08 Hz band were not removed from the data. At the same time, the agreement with a power scaling was reduced when Equation (1) was fitted to the data without bandpass filtering. This likely reflects the introduction of additional randomness and is consistent with increased noise level and lack of additional information at higher frequencies than those in the 0.01–0.08 Hz band.
The brain normally operates under certain level of randomness that is important for multiple operation including perception and decision-making. The relevance of internal neuronal noise has been most extensively studied for visual perception (Brascamp et al., 2006; Kim et al., 2006). Theoretical studies have also shown that randomness may influence behavioral responses when there are multiple routes to action and suggested that noise generated by random firing rates of neurons can be used to predict a decision (Rolls, 2012). Since limbic and subcortical regions support automatic, implicit decision making (Floresco et al., 2008; Mitchell, 2015) the higher scaling exponents in these regions suggests an important role of randomness in implicit decision making processes. The sensitivity to randomness of b could be useful for studying psychiatric disorders such as autism, which is associated with increased randomness of endogenous brain oscillations (Lai et al., 2010).
Study Limitations
Note that b = ½ emerges either from diffusion or from flow models, independently of the number of steps in the diffusion model, and from random networks as well as from scale-free networks. This indicates that b = ½ is not a particular property of the random diffusion model, but it is shared by several dynamic processes (Argollo de Menezes and Barabasi, 2004). Our computational resources did not allow demanding whole brain network simulations at 2-mm isotropic resolution (~105 nodes/voxels). Thus, our simulations suggesting that when internal randomness dominates over the external modulations (ΔW/W ~ 0) bδ ~ 1 and bD > 1, but when external modulations dominate over internal randomness (ΔW/W ~ 1) bδ ~ 0.5 and bD ~ 1 are limited to the 3 exemplary networks in this work. However, it is likely that they apply also to the whole brain. Instrumental noise likely resulted in overestimations of intrinsic randomness in subcortical regions for which the 32 channel RF coil used by the HCP has low sensitivity. Since the theoretical model was developed across network nodes, the interpretation of the power law across ROIs and subjects could be considered controversial. Our empirical evidence, however, suggests that the temporal mean and standard deviation values of dynamic functional connectivity metrics also adhere to a power law computed across ROIs or subjects, which are consistent with the power law computed across nodes (i.e., across nodes of each individual ROI, blFCD = 1.05 ± 0.17 mean ± standard deviation; across the 86 gray matter, ROIs blFCD = 1.03 ± 0.17; across 66 subjects, blFCD = 0.98 ± 0.16). This suggests similar effects of randomness and external modulators on power scaling factors computed across network nodes, ROIs or subjects.
Dynamic lFCD is restricted to the local functional connectivity cluster. We did not assess the dynamics of global functional connectivity density (gFCD) because at high spatiotemporal resolution gFCD is extremely demanding and beyond our computational resources. However, this is not a strong limitation because previous studies have shown that the lFCD and gFCD metrics are proportional to one another (Tomasi and Volkow, 2011).
Author Contributions
DT designed the study, carried the analyses and wrote the manuscript. ES developed imaging tools and wrote the manuscript. NV wrote the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Data was provided by the Human Connectome Project (HCP), WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University. This work was accomplished with support from the National Institute on Alcohol Abuse and Alcoholism (Y1AA-3009).
References
Allen, E., Damaraju, E., Plis, S., Erhardt, E., Eichele, T., and Calhoun, V. (2014). Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 24, 663–676. doi: 10.1093/cercor/bhs352
Argollo de Menezes, M., and Barabasi, A. (2004). Fluctuations in network dynamics. Phys. Rev. Lett. 92:028701. doi: 10.1103/PhysRevLett.92.028701
Barabási, A. (2009). Scale-free networks: a decade and beyond. Science 325, 412–413. doi: 10.1126/science.1173299
Barabasi, A., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512. doi: 10.1126/science.286.5439.509
Biswal, B., Mennes, M., Zuo, X., Gohel, S., Kelly, C., Smith, S., et al. (2010). Toward discovery science of human brain function. Proc. Natl. Acad. Sci. U.S.A. 107, 4734–4739. doi: 10.1073/pnas.0911855107
Biswal, B., Yetkin, F. Z., Haughton, V. M., and Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 34, 537–541. doi: 10.1002/mrm.1910340409
Brascamp, J., Van Ee, R., Noest, A., Jacobs, R., and van den Berg, A. (2006). The time course of binocular rivalry reveals a fundamental role of noise. J. Vis. 6, 1244–1256. doi: 10.1167/6.11.8
Calhoun, V., Miller, R., Pearlson, G., and Adali, T. (2014). The chronnectome: time-varying connectivity networks as the next frontier in fMRI data discovery. Neuron 84, 262–274. doi: 10.1016/j.neuron.2014.10.015
Chang, C., and Glover, G. (2010). Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 50, 81–98. doi: 10.1016/j.neuroimage.2009.12.011
Doucet, G., Naveau, M., Petit, L., Zago, L., Crivello, F., Jobard, G., et al. (2012). Patterns of hemodynamic low-frequency oscillations in the brain are modulated by the nature of free thought during rest. Neuroimage 59, 3194–3200. doi: 10.1016/j.neuroimage.2011.11.059
Eguíluz, V., Chialvo, D., Cecchi, G., Baliki, M., and Apkarian, A. (2005). Scale-free brain functional networks. Phys. Rev. Lett. 94:018102. doi: 10.1103/PhysRevLett.94.018102
Floresco, S., St. Onge, J., Ghods-Sharifi, S., and Winstanley, C. (2008). Cortico-limbic-striatal circuits subserving different forms of cost-benefit decision making. Cogn. Affect. Behav. Neurosci. 8, 375–389. doi: 10.3758/CABN.8.4.375
Glasser, M., Sotiropoulos, S., Wilson, J., Coalson, T., Fischl, B., Andersson, J., et al. (2013). The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. doi: 10.1016/j.neuroimage.2013.04.127
Goldman-Rakic, P. (1988). Topography of cognition: parallel distributed networks in primate association cortex. Annu. Rev. Neurosci. 11, 137–156. doi: 10.1146/annurev.ne.11.030188.001033
Gonzalez-Castillo, J., Hoy, C., Handwerker, D., Robinson, M., Buchanan, L., Saad, Z., et al. (2015). Tracking ongoing cognition in individuals using brief, whole-brain functional connectivity patterns. Proc. Natl. Acad. Sci. U.S.A. 112, 8762–7867. doi: 10.1073/pnas.1501242112
Hutchison, R., and Morton, J. (2015). Tracking the brain's functional coupling dynamics over development. J. Neurosci. 35, 6849–6859. doi: 10.1523/JNEUROSCI.4638-14.2015
Hutchison, R., Womelsdorf, T., Allen, E., Bandettini, P., Calhoun, V., Corbetta, M., et al. (2013). Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage 80, 360–378. doi: 10.1016/j.neuroimage.2013.05.079
Kim, Y., Grabowecky, M., and Suzuki, S. (2006). Stochastic resonance in binocular rivalry. Vis. Res. 46, 392–406. doi: 10.1016/j.visres.2005.08.009
Lai, M., Lombardo, M., Chakrabarti, B., Sadek, S., Pasco, G., Wheelwright, S., et al. (2010). A shift to randomness of brain oscillations in people with autism. Biol. Psychiatry 68, 1092–1099. doi: 10.1016/j.biopsych.2010.06.027
Liu, X., and Duyn, J. (2013). Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc. Natl. Acad. Sci. U.S.A. 110, 4392–4397. doi: 10.1073/pnas.1216856110
Logothetis, N., Pauls, J., Augath, M., Trinath, T., and Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature 412, 150–157. doi: 10.1038/35084005
Mason, M., Norton, M., Van Horn, J., Wegner, D., Grafton, S., and Macrae, C. (2007). Wandering minds: the default network and stimulus-independent thought. Science 315, 393–395. doi: 10.1126/science.1131295
Mitchell, A. (2015). The mediodorsal thalamus as a higher order thalamic relay nucleus important for learning and decision-making. Neurosci. Biobehav. Rev. 54, 76–88. doi: 10.1016/j.neubiorev.2015.03.001
Power, J., Barnes, K., Snyder, A., Schlaggar, B., and Petersen, S. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59, 2142–2154. doi: 10.1016/j.neuroimage.2011.10.018
Rashid, B., Damaraju, E., Pearlson, G., and Calhoun, V. (2014). Dynamic connectivity states estimated from resting fMRI Identify differences among Schizophrenia, bipolar disorder, and healthy control subjects. Front. Hum. Neurosci. 8:897. doi: 10.3389/fnhum.2014.00897
Rolls, E. (2012). Willed action, free will, and the stochastic neurodynamics of decision-making. Front. Integr. Neurosci. 6:68. doi: 10.3389/fnint.2012.00068
Rubinov, M., and Sporns, O. (2010). Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069. doi: 10.1016/j.neuroimage.2009.10.003
Sakoğlu, Ü., Pearlson, G. D., Kiehl, K. A., Wang, Y. M., Michael, A. M., and Calhoun, V. D. (2010). A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia. MAGMA 23, 351–366. doi: 10.1007/s10334-010-0197-8
Salimi-Khorshidi, G., Douaud, G., Beckmann, C., Glasser, M., Griffanti, L., and Smith, S. (2014). Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468. doi: 10.1016/j.neuroimage.2013.11.046
Shirer, W., Ryali, S., Rykhlevskaia, E., Menon, V., and Greicius, M. (2012). Decoding subject-driven cognitive states with whole-brain connectivity patterns. Cereb. Cortex 22, 158–165. doi: 10.1093/cercor/bhr099
Smith, S., Beckmann, C., Andersson, J., Auerbach, E., Bijsterbosch, J., Douaud, G., et al. (2013). Resting-state fMRI in the human connectome project. Neuroimage 80, 144–168. doi: 10.1016/j.neuroimage.2013.05.039
Tomasi, D., Shokri-Kojori, E., and Volkow, N. (2016a). Temporal changes in local functional connectivity density reflect the temporal variability of the amplitude of low frequency fluctuations in gray matter. PLoS ONE 11:e0154407. doi: 10.1371/journal.pone.0154407
Tomasi, D., Shokri-Kojori, E., and Volkow, N. (2016b). Temporal evolution of brain functional connectivity metrics: could 7 min of rest be enough? Cereb. Cortex doi: 10.1093/cercor/bhw1227. [Epub ahead of print].
Tomasi, D., Shokri-Kojori, E., and Volkow, N. D. (2016c). High-resolution functional connectivity density: hub locations, sensitivity, specificity, reproducibility, and reliability. Cereb. Cortex 26, 3249–3259. doi: 10.1093/cercor/bhv171
Tomasi, D., and Volkow, N. (2010). Functional connectivity density mapping. Proc. Natl. Acad. Sci. U.S.A. 107, 9885–9890. doi: 10.1073/pnas.1001414107
Tomasi, D., and Volkow, N. (2011). Functional connectivity hubs in the human brain. Neuroimage 57, 908–917. doi: 10.1016/j.neuroimage.2011.05.024
Tomasi, D., and Volkow, N. (2012). Aging and functional brain networks. Mol. Psychiatry 17, 549–558. doi: 10.1038/mp.2011.81
Uğurbil, K., Xu, J., Auerbach, E., Moeller, S., Vu, A., Duarte-Carvajalino, J., et al. (2013). Pushing spatial and temporal resolution for functional and diffusion MRI in the human connectome project. Neuroimage 80, 80–104. doi: 10.1016/j.neuroimage.2013.05.012
Watts, D., and Strogatz, S. (1998). Collective dynamics of 'small-world' networks. Nature 393, 440–442. doi: 10.1038/30918
Yang, H., Long, X., Yang, Y., Yan, H., Zhu, C., Zhou, X., et al. (2007). Amplitude of low frequency fluctuation within visual areas revealed by resting-state functional MRI. Neuroimage 36, 144–152. doi: 10.1016/j.neuroimage.2007.01.054
Yang, Z., Craddock, R. C., Margulies, D. S., Yan, C. G., and Milham, M. P. (2014). Common intrinsic connectivity states among posteromedial cortex subdivisions: insights from analysis of temporal dynamics. Neuroimage 93(Pt 1), 124–137. doi: 10.1016/j.neuroimage.2014.02.014
Yu, Q., Allen, E., Sui, J., Arbabshirani, M., Pearlson, G., and Calhoun, V. (2012). Brain connectivity networks in schizophrenia underlying resting state functional magnetic resonance imaging. Curr. Top. Med. Chem. 12, 2415–2425. doi: 10.2174/156802612805289890
Keywords: FCDM, ALFF, lFCD, functional connectivity (FC), graph theory analysis, brain networks, Taylor's law, numerical simulations
Citation: Tomasi DG, Shokri-Kojori E and Volkow ND (2017) Brain Network Dynamics Adhere to a Power Law. Front. Neurosci. 11:72. doi: 10.3389/fnins.2017.00072
Received: 13 November 2016; Accepted: 31 January 2017;
Published: 14 February 2017.
Edited by:
Xi-Nian Zuo, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Xin Di, New Jersey Institute of Technology, USAMaarten Mennes, Radboud University Nijmegen, Netherlands
Copyright © 2017 Tomasi, Shokri-Kojori and Volkow. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dardo G. Tomasi, dG9tYXNpZGdAbWFpbC5uaWguZ292
 Dardo G. Tomasi
Dardo G. Tomasi Ehsan Shokri-Kojori1
Ehsan Shokri-Kojori1