Abstract
In this study, the stability for a class of sampled-data Takagi-Sugeno (T-S) fuzzy systems with state quantization was investigated. Using the discontinuous Lyapunov-Krasoskii functional (LKF) approach and the free-matrix-based integral inequality bounds processing technique, a stability condition with less conservativeness has been obtained, and the controller of the sampled-data T-S fuzzy system with the quantized state has been designed. Furthermore, based on the results, the sampled-data T-S fuzzy system without the state quantization was also discussed, and the required controller constructed. The results of two simulation examples show that both the maximum sampling intervals, with and without the quantized state for T-S fuzzy systems, are actually superior to the existing results.
1. Introduction
In the real world, most physical systems and processes can be modeled mathematically as complex nonlinear systems. Because some parts of nonlinear systems are always coupled and influence each other, it is difficult to analyze and synthesize these systems. Therefore, establishing an effective and suitable control model to address this issue in nonlinear systems, is significant. In recent years, T-S fuzzy systems has been an effective method to analyze and synthesize nonlinear systems, because of the fact that the T-S fuzzy model is able to transform a complex nonlinear system into several simple linear systems with membership functions, approximating the nonlinear function smoothly with an arbitrary precision in the closed set space, which is ubiquitous in chemical processes, robotics systems, and automatic systems (Tanaka and Wang, 2004). Thus, many results on T-S fuzzy systems, analyzing nonlinear systems, have been reported in terms of various methods, including stability analysis (Lam et al., 2007; Zhao et al., 2009; Zhu et al., 2012, 2018a), controller design (Xia et al., 2010; Wu et al., 2014a,b, 2015; Liu et al., 2016; Wang et al., 2018a; Zhong et al., 2018; Zhao et al., 2019), and fault detection and filter design (Li et al., 2015; Wang et al., 2016, 2017, 2018b; Zhu et al., 2018b), etc.
At the front line of other research, there has been increasing interest in the sampled-data control system, a rapid development of digital and communication technology (Chen and Francis, 2012). The sampled-data control systems involve both continuous-time and discrete-time signals, which make the analysis and synthesis more complicated and challenging. It should be noted that the sampling period is an important issue when analyzing system stability. A larger sampling period can reduce the occupation of the communication channel, and the actuation of the controller and signal transmission. Thus, it is very important to guarantee the stability of the sampled-data system, with a sampling period as large as possible. Over the past several years, sampled-data control systems have drawn much attention (see Hu et al., 2007; Zhu et al., 2012; Shao et al., 2014; Wu et al., 2014a,b, 2015; Liu et al., 2016; Lee and Park, 2017; Wang et al., 2018a and the references therein), and one popular and widely used approach to analyze and synthesize sampled-data systems is the input delay approach, which is based on the representation of the sampled-data system as a continuous-time system with a delayed control input, and does not require the sampling interval to be constant (Fridman et al., 2004; Fridman, 2010; Yang et al., 2014; Li et al., 2015). The authors in Hu et al. (2007) designed a sampled-data controller for networked linear control, and Shao et al. (2014) researched the problem of sampling-interval-dependent stability for sampled-data systems with state quantization. Nevertheless, the results of Hu et al. (2007) and Shao et al. (2014) required the research system to be linear, which is impractical for many applications. Very recently, the problem of stability and stabilization for sampled-data nonlinear fuzzy systems with state quantization was investigated in Liu et al. (2016). Furthermore, the authors in Wang et al. (2018a), designed a dissipativity-based reliable controller for the sampled-data T-S fuzzy system, using the limited Bessel-Legendre inequality proposed in Liu et al. (2017), and a less conservative sufficient stabilization criterion was obtained to guarantee that the sampled-data systems are asymptotically stable. Although there are few results to study the stability of sampled-data T-S fuzzy systems, it is still necessary to decrease the conservativeness of the stability criteria further.
It is well-known that due to the limited capacity and energy consumption in the network system, it is especially important to quantize the sampled-data before transmission. However, most existing studies assume that the data transmission can be performed with infinite precision, and the impact of quantization is always ignored in the network environment. On the other hand, sampling quantization before signal transmission may lead to a limited cycle and chaos. Thus, the study of sampled-data systems with state quantization has attracted significant research attention (Fu and Xie, 2005; Niu et al., 2009; Shao et al., 2014; Liu et al., 2016; Dong et al., 2017a,b). The author in Dong et al. (2017b) studied the reliable control problem for fuzzy systems with state quantization and switched actuator failures. The output feedback control problem of the network control systems with signal quantization and packet loss has been studied in Niu et al. (2009). The stability for sampled-data systems and linear systems with state quantization, have been studied in Dong et al. (2017a), Shao et al. (2014), and Fu and Xie (2005), respectively. Up to now, to the best of authors' knowledge, little attention is given to the issue of quantized sampled-data control for T-S fuzzy systems. Thus, the aim of this work, with a focus on the stability and stabilization problem for sampled-data T-S fuzzy systems with state quantization, is to decrease the conservativeness of the stability criteria even further.
Motivated by that, this work mainly discusses the stability and stabilization control problem for nonlinear T-S fuzzy sampled-data systems with quantized states. By using the discontinuous LKF approach and free-matrix-based integral inequality boundary processing technique, stability conditions with less conservativeness are obtained for T-S fuzzy systems, with sampled-data and quantized states, and the controllers are designed accordingly. Furthermore, the stability of T-S fuzzy sampled-data systems without quantized states is also analyzed utilizing the above theoretical results, and the required sampling data controllers are designed simultaneously. The main contributions of this paper can be summarized as follows: (1) In constructing LKF aspects, it is not necessary that the discontinuous LKF approach applied in this work are positive for all time t, only at the sampling times tk and tk+1, which can broaden the restriction in LKF. (2) In estimating the derivation of LKF, the free-matrix-based integral inequality boundary processing technique is used to provide more freedom in deriving stability for sampled-date T-S fuzzy systems. From two points of view, the conservativeness of stability conditions can be decreased for sampled-data T-S fuzzy systems with and without quantized states effectively through the methods of our design in this work.
Notations. Throughout this paper, I denotes the identity matrix with appropriate dimensions. Sym(A) denotes A + AT. denotes the n dimensional Euclidean space, and is the set of all n × m real matrices. denotes the n dimensional symmetric positive matrices. * denotes the elements below the main diagonal of a symmetric block matrix.
2. Problem Formulation
A class of continuous-time nonlinear systems can be described using the following T-S fuzzy model
The rules of plant i: If θ1(t) is Mi1(t) and … and θn(t) is Min(t), then
where and are the state and control input vectors of the system, respectively. Ai and Bi are any matrices with appropriate dimensions. θ(t) = [θ1(t)⋯θn(t)] is the premise variable; Mij(t) is the fuzzy set, with i = 1, 2, ⋯ , r as the amount of fuzzy rules. Then the above continuous time T-S fuzzy system (Equation 1) can be expressed in the following form
where hi(θ(t)) represents the membership function and satisfies ; , where Mij(θj(t)) is the degree of membership and θj(t) belongs to the fuzzy set of Mij, which has the following properties. For θ(t), ωi(θ(t)) ≥ 0 and , we can determine hi(θ(t)) ≥ 0 (∀i = 1, 2, ⋯ , r) and .
Suppose the control signal is a sequence of holding times generated by a zero-order-holder function.
This paper designs the controller based on the state feedback for T-S fuzzy systems described in (1) and uses the idea of parallel distributed compensation to share the same fuzzy set with the fuzzy model in the premise part of the designed fuzzy controller.
Controller rules j: If θ1(tk) is Mj1(t) and … and θn(tk) is Mjn(t), then
where Kj is the state feedback gain matrix with appropriate dimension, and x(tk) is the discrete measurement value at the sampling time of tk.
The logarithm quantizer is described as
The mth sub-quantizer qm(•) is symmetric, and therefore we have
The quantizer satisfies the following quantization criteria
where ρm and are quantizer density and initial quantization values, respectively. qm(•) is strictly defined as follows
where lm = 1 − ρm/1 + ρm(m = 1, 2, ⋯ , n) is the parameter of the quantizer. When xm(tk) > 0, the following relationship is established
For xm(tk) < 0, the following is satisfied
Therefore, the quantizer can be expressed as
where
Hence, the overall state feedback controller with the quantized state can be designed
Suppose the distance between two consecutive sampling instants belongs to an interval, and then for all k > 0 there exists
where hL and hU are known constants satisfying 0 ≤ hL ≤ hU. Combining Equations (1)–(6), the T-S fuzzy sampled-data system with state quantization can be obtained as follows
The following lemma is important for further analysis.
Lemma 1. Lee and Park (2017) (Free-Matrix-Based Integral Inequality) For given matrices , N1, , the following inequality holds for any continuously differentiable function x(t) in
where
Remark 1. Note that the free-matrix-based integral inequality in Lemma 1 provides more freedom in deriving stability for sampled-date T-S fuzzy systems. So, it provides the possibility of finding a tight bound for . On the other hand, the augmented vector ϕ(α, β) includes instead of , and this avoids appearance of the term (t − tk)ϕ(tk, t) in sampled-data systems, which is actually much easier to handle.
3. Main Result
3.1. Stability Analysis of the Sampled-Data T-S Fuzzy System With State Quantization
In this section, the asymptotic stability conditions of T-S fuzzy systems with state quantization are analyzed.
For the convenience of system analysis and design, we define
where ei is defined as the block entry matrix. Other notations are defined as
Theorem 1. For given scalars hL and hU, satisfying 0 ≤ hL ≤ hU, system (Equation 7) is asymptotically stable, if there are some symmetric positive definite matrices , X1, , ; a diagonal matrix ; any matrices G1, G2, X2, N1, N2 with appropriate dimensions, and for any i ≥ 1 and j ≤ r, the following linear matrix inequalities (LMIs) hold
where
with
and Z1, Z2 have been defined in Lemma 1.
Proof: The novel discontinuous LKF in this work is constructed as follows
where
with
Remark 2. It should be noted that the constructed LKF (Equation 10) of this work is the discontinuous Lyapunov functional, as V3(t) is actually a time-dependent discontinuous term. Moreover, it is not necessary that V1(t) and V2(t) in LKF (Equation 10) are positive for all time t, but only positive at the sampling times tk and tk+1. All this can decrease the conservativeness of stability conditions effectively.
The derivative of V1(t), V2(t), and V3(t) can, respectively, be deduced as
By Lemma 1, we obtain the inequality
Based on the closed-loop system (Equation 7), the following equality holds
and it can be further written as
From Equation (4), for the diagonal matrix D > 0, it holds that
Then combining (Equations 11–16), an upper bound of can be obtained as follows
where
with the following two equalities
Therefore, using Schur Complement, Equations (8) and (9) are equivalent to . This completes the proof.
Additionally, Theorem 1 has provided the stability results for T-S fuzzy sampled-data systems (Equation 7) with state quantization, and, the following Theorem 2 will be given in order to obtain the sampled-data controller.
Theorem 2. For given scalars hL and hU, satisfying 0 ≤ hL ≤ hU, system (Equation 7) is asymptotically stable, if there are some symmetric positive definite matrices , , , ; diagonal matrix ; any matrices G, Tj, , , with appropriate dimensions, and for any i ≥ 1 and j ≤ r, the following LMIs hold
where
with
The gain matrix Kj of the sampled-data controller with state quantization is defined as .
Proof: Define
Equation (8) is pre- and post-multiplied by diag{G, G, G, G, G} and its transpose, respectively. Equation (9) is pre- and post-multiplied by diag{G, G, G, G, G, G, G} and its transpose, respectively. We accordingly obtain Equations (18) and (19). This completes the proof.
Remark 3. Theorems 1 and 2 provide the stability condition and the controller design for the sampled-data T-S fuzzy system with the quantized state, using the discontinuous LKF approach. If we do not consider the impact of the state quantization in system (Equation 7), f(x(tk)) in V2(t) could be eliminated, and the result can be degenerated for the case without the quantized state, which will be discussed in the next section.
Remark 4. In order to obtain less conservativeness sufficient stability condition for sampled-data T-S fuzzy systems with state quantization, some other methods combined with free-matrix-based integral inequality bounds processing technique could be used, such as parameter-dependent LKF and two-sided looped-functional.
3.2. Stability Analysis of Sampled-Data T-S Fuzzy System Without State Quantization
In this section, the impact of the quantized state is not considered, and the T-S fuzzy sampled-data system then becomes
Define
Now, using the same method used in Theorem 1, we have the following Corollary without considering the state quantization.
Corollary 1. For given scalars hL and hU with 0 ≤ hL ≤ hU, the system (Equation 20) is asymptotically stable, if there are some symmetric positive definite matrices , X1, , and any metrics G1, G2, X2, N1, N2 with appropriate dimensions, and for any i ≥ 1 and j ≤ r, the following LMIs hold
where
with
where Z1, Z2, R, ℜ1 and ℜ2 have been defined in Theorem 1.
Furthermore, the following Corollary regarding the sampled-data controllers design can be derived using a similar method used in Theorem 2.
Corollary 2. For given scalars hL and hU with 0 ≤ hL ≤ hU, system (Equation 20) is asymptotically stable, if there exist symmetric positive definite matrices , , , and any matrix G, Tj, , , with appropriate dimensions, and for any 1 ≤ i, and j ≤ r, the following LMIs hold
where
with
where , , , , , , R, and have been defined in Theorem 2, and the gain matrix Kj of the sampled-data controller without state quantization is defined as .
Remark 5. The stability of the sampled-data T-S fuzzy system with and without the quantized state is investigated in Theorem 1 and Corollary 1. And the upper bound of the sampling interval for T-S fuzzy system is larger than the existing results in Lam et al. (2007), Zhu et al. (2012), Wu et al. (2014b), and Liu et al. (2016), which will be proven in further simulation examples.
4. Numerical Examples
This section provides two numerical examples to demonstrate the effectiveness and superiority of the proposed method.
Example 1. The Lorenz system with an input term (Wu et al., 2014b) is given as follows
The Lorenz system (Equation 25) can be represented as a type of T-S fuzzy system (Equation 2) with the following parameters
and the membership functions satisfy and h2(x1(t)) = 1 − h1(x1(t)).
Here we choose a = 10, b = 8/3, c = 28, and d = 25.
Case I: For the case with the quantized state, take the quantizer densities as
and the quantizer parameter is supposed as
Considering the quantized state based on Theorem 2, when ε = 0.1, the allowable maximum sampling period that can ensure the asymptotic stability of system (Equation 1) is 0.0742, which is larger than 0.0503 obtained in Liu et al. (2016) actually, and the corresponding gain matrices are
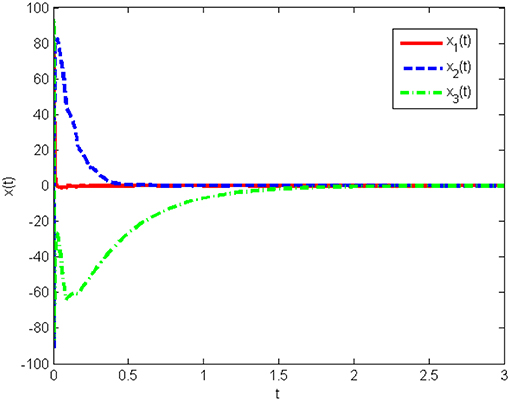
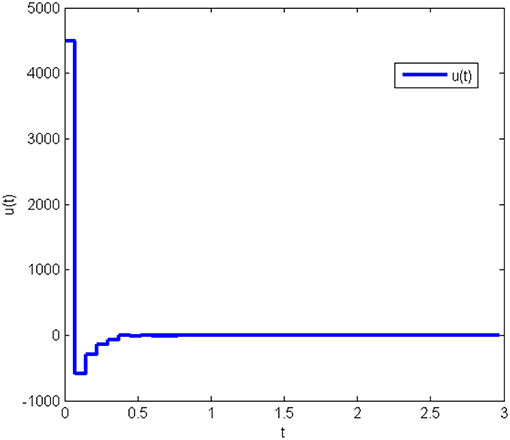
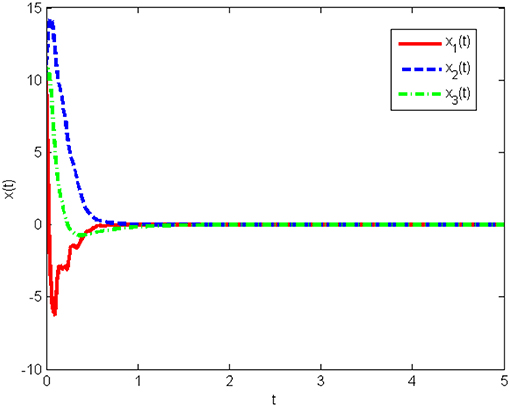
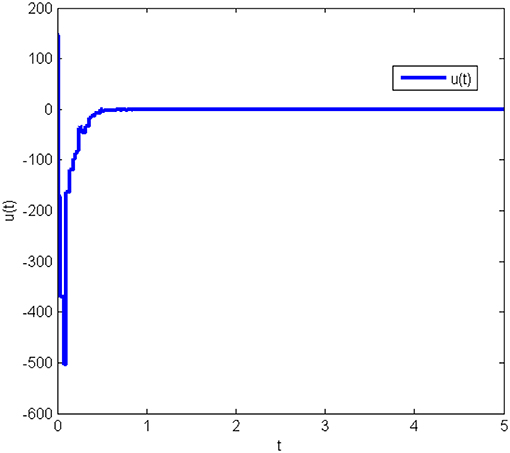
The response curves of system (Equation 25) under the initial condition x(0) = [20 50 80]T with the obtained gain matrices are given in Figure 1, and the control input u(t) is shown in Figure 2. This proves that the Lorenz system (Equation 25) with state quantization under the obtained sampled-data controller, in this work, is asymptotically stable.
Figure 1
Figure 2
Case II: For the case without state quantization, based on Corollary 2, as ε = 0.1, the allowable maximum sampling period ensuring the asymptotic stability of system (Equation 7) is 0.0741. And the allowable upper bounds h for the sampling interval are obtained, listed in Table 1. It can be seen that the upper bound for the sampling interval under the proposed method is larger than those obtained with existing methods in Lam et al. (2007), Zhu et al. (2012), Liu et al. (2016), and Wu et al. (2014b).
Table 1
| Lam et al., 2007 | Zhu et al., 2012 | Wu et al., 2014b | Liu et al., 2016 | Corollary 2 | |
| h | 0.0158 | 0.0270 | 0.0347 | 0.0560 | 0.0741 |
Maximum allowable bounds h without state quantization in Example 1.
Simulation results are provided to verify the effectiveness of the proposed method. When h = 0.0741, by solving LMIs (Equations 23, 24), we can obtain corresponding gain matrices as follows
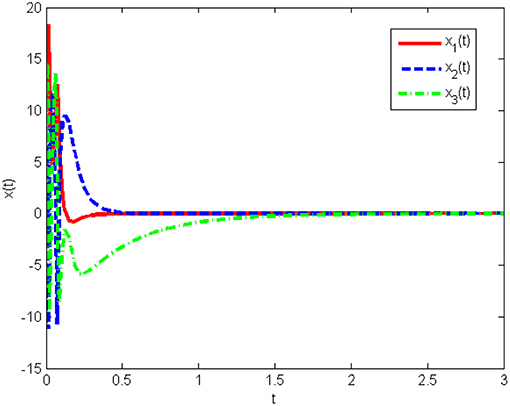
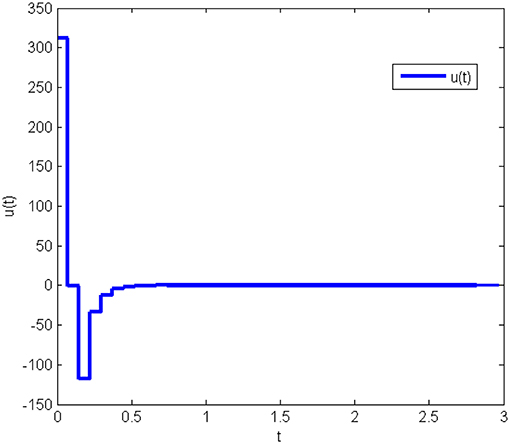
The response curves of the system (Equation 25) with the initial condition x(0) = [10 10 10]T under the obtained gain matrices are given in Figures 3, 4 shows the control input u(t). This proves that the controller obtained in this work is correct and valid.
Figure 3
Figure 4
Example 2. The dynamic of unified chaotic system with an input term (Liu et al., 2016) is given as
Note that the unified chaotic system (Equation 26) with x1(t) ∈ [−d, d] can be represented in the T-S fuzzy system (Equation 2) with
and the membership functions are h1(x1(t)) = (d + x1(t))/2d and h2(x1(t)) = (d − x1(t))/2d, respectively.
Here a = 0.2 and d = 10 are chosen, and two cases with and without state quantization are considered further.
Case I: Taking the same quantizer densities as in Example 1, and using Theorem 2, when ε = 0.01, system (Equation 26) can be asymptotically stable with the maximum sampling period h = 0.0535, which is larger than 0.0424 in Liu et al. (2016). Then, we choose h = 0.02, and by solving LMIs (Equations 18, 19), the corresponding gain matrices can be obtained as follows
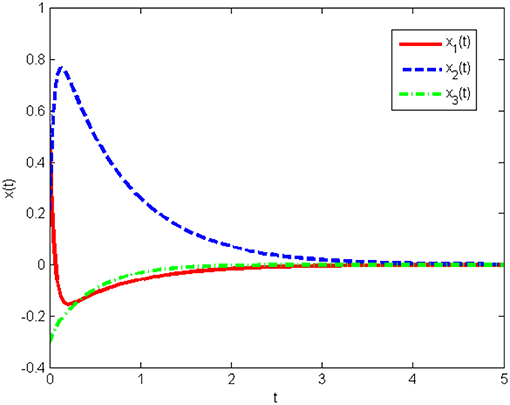
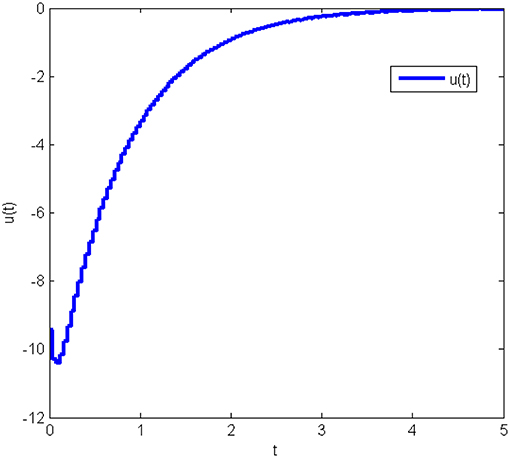
Under the obtained gain matrices and the initial condition x(0) = [10 10 10]T, the state response and control input u(t) for system (Equation 26) are shown in Figures 5, 6, respectively. This proves that the controller obtained in this work is correct and valid.
Figure 5
Figure 6
Case II: The maximum allowable upper bound of the sampling interval h without state quantization under the sampled-data control is listed in Table 2, which shows that the results in Corollary 2 is superior to existing ones.
Table 2
Maximum allowable bounds h without state quantization in Example 2.
When ε = 0.1 and h = 0.04, by solving LMIs (Equations 23, 24), we can obtain the corresponding gain matrices as follows
The response curves of system (Equation 26) with initial condition x(0) = [0.5 0.2 − 0.3]T under the above gain matrices are displayed in Figure 7, and the corresponding control input u(t) is given in Figure 8. This proves that the controller proposed in Corollary 2 can ensure the asymptotic stability of the T-S fuzzy sampled-data system (Equation 26) without state quantization.
Figure 7
Figure 8
5. Conclusions
In this work, we have investigated the stability for a class of nonlinear T-S fuzzy sampled-data systems with state quantification. A new LKF approach has been constructed and a Free-Matrix-Based boundary treatment technique for integral inequalities has been adopted in order to obtain less conservative stability conditions and correspondingly, a controller has been designed. Furthermore, the stability of the T-S fuzzy sampled-data system without quantized states, has also been discussed and sampled-data controllers have been designed accordingly. The experimental results show that the maximum sampling interval for T-S fuzzy sampled-data systems with and without quantized states in our work, are both larger than the results in previous studies. Nevertheless, some other interesting problems that need to be addressed still exist, such as the reliable control design for the sampled-data T-S fuzzy systems with state quantization, and the extension of our developed approaches to the dissipativity-based sampled-data control design, which deserve further investigation.
Statements
Author contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Acknowledgments
This work was supported by the Natural Science Foundation of China under Grant 61503045, 61603121, National Natural Science Foundation of Jilin Province under Grant 20180101333JC.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1
ChenT. W.FrancisB. (2012). Optimal Sampled-Data Control Systems.Berlin: Springer Science, Business Media.
2
DongS.SuH.ShiP. (2017a). Filtering for discrete-time switched fuzzy systems with quantization. IEEE Trans. Fuzzy Syst.25, 1616–1628. 10.1109/TFUZZ.2016.2612699
3
DongS.WuZ.G.ShiP.SuH.LuR. (2017b). Reliable control of fuzzy systems with quantization and switched actuator failures. IEEE Trans. Syst. Man Cybern. Syst.47, 2198–2208. 10.1109/TSMC.2016.2636222
4
FridmanE. (2010). A refined input delay approach to sampled-data control. Automatica46, 421–427. 10.1016/j.automatica.2009.11.017
5
FridmanE.SeuretA.RichardJ. P. (2004). Robust sampled-data stabilization of linear systems: an input delay approach. Automatica40, 1441–1446. 10.1016/j.automatica.2004.03.003
6
FuM.XieL. (2005). The sector bound approach to quantized feedback control. IEEE Trans. Automatic Control50, 1698–1711. 10.1109/TAC.2005.858689
7
HuL. S.BaiT.ShiP.WuZ. M. (2007) Sampled-data control of networked linear control systems. Automatica43, 903-911. 10.1016/j.automatica.2006.11.015
8
LamH. K.LeungF. H. F. (2007). Stabilization of chaotic systems using linear sampled-data controller. Int. J. Bifurcat. Chaos17, 2021–2031. 10.1142/S0218127407018191
9
Lee TaeHPark JuH. (2017). Stability analysis of sampled-Data systems via free-matrix-based time-dependent discontinuous lyapunov approach. IEEE Trans. Automatic Control62, 3653–3657. 10.1109/TAC.2017.2670786
10
LiHGaoYWuLLamH.K. (2015). Fault detection for T-S fuzzy time-delay systems: Delta operator and input-output methods. IEEE Trans. Cybernetic.45, 229–241. 10.1109/TCYB.2014.2323994
11
LiuKSeuretAXiaY. (2017). Stability analysis of systems with time-varying delays via the second-order Bessel-Legendre inequality. Automatica76, 138–142. 10.1016/j.automatica.2016.11.001
12
LiuY.LeeS. M. (2016). Stability and stabilization of Takagi-Sugeno fuzzy systems via sampled-data and state quantized controller. IEEE Trans. Fuzzy Syst.24, 635–644. 10.1109/TFUZZ.2015.2469099
13
NiuY.JiaT.WangX.YangF. (2009). Output feedback control design for NCSs subject to quantization and dropout. Inf. Sci.179, 3804–3813. 10.1016/j.ins.2009.07.006
14
ShaoH.HanQ. LZhangZ.ZhuX. (2014). Sampling-interval-dependent stability for sampled-data systems with state quantization. Int. J. Robust Nonlinear Control24, 2995–3008. 10.1002/rnc.3038
15
TanakaK.WangH. O. (2004). Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach. New York, NY: John Wiley Sons.
16
WangSFengJJiangY. (2016). Input-output method to fault detection for discrete-time fuzzy networked systems with time-varying delay and multiple packet losses. Int. J. Syst. Sci.47, 1495–1513. 10.1080/00207721.2014.938785
17
WangSJiWPangJJiangY. (2018a). Dissipativity-based sampled-data reliable control design for T-S fuzzy system using limited bessel-legendre inequality. IEEE Access6, 73405–73415. 10.1109/access.2018.2882125
18
WangSJiangYLiY. (2018b). Distributed H∞ consensus fault detection for uncertain T-S fuzzy system with time-varying delays over lossy sensor networks. Asian J. Control20, 2171–2184. 10.1002/asjc.1721
19
WangSJiangYLiYLiuD. (2017). Fault detection and control co-design for discrete-time delayed fuzzy networked control systems subject to quantization and multiple packet dropouts. Fuzzy Sets Syst.306, 1–25. 10.1080/00207721.2012.658882
20
WuZShiPSuH. (2014a). Sampled-data fuzzy control of chaotic systems based on a T-S fuzzy model. IEEE Trans. Fuzzy Syst.22, 153–163. 10.1177/0142331217740420
21
WuZ.ShiPSuHLuR. (2015). Dissipativity-based sampled-data fuzzy control design and its application to truck-trailer system. IEEE Trans. Fuzzy Syst.23, 1669–1679. 10.1109/TFUZZ.2014.2374192
22
WuZ. G.ShiP.SuH.ChuJ. (2014b). Sampled-data fuzzy control of chaotic systems based on a T-S fuzzy system model. IEEE Trans. Fuzzy Syst.22, 153–162. 10.1109/TFUZZ.2013.2249520
23
XiaY.YangH.ShiP.FuM. (2010). Constrained infinite-horizon model predictive control for fuzzy-discrete-time systems. IEEE Trans. Fuzzy Syst.18, 429–436. 10.1109/TFUZZ.2010.2043441
24
YangF.ZhangH.WangY. (2014). An enhanced input-delay approach to sampled-data stabilization of T-S fuzzy systems via mixed convex combination. Nonlinear Dynam.75, 501–512. 10.1007/s11071-013-1080-8
25
ZhaoJ.LinC.-M.ChaoF. (2019). Wavelet fuzzy brain emotional learning control system design for MIMO uncertain nonlinear systems. Front. Neurosci.12:918. 10.3389/fnins.2018.00918
26
ZhaoY.GaoH.LamJ.DuB. (2009). Stability and stabilization of delayed T-S fuzzy systems: a delay partitioning approach. IEEE Trans. Fuzzy Syst.17, 750–762. 10.1109/TFUZZ.2008.928598
27
ZhongZ.ZhuY.LamH. K. (2018). Asynchronous piecewise output-feedback control for large-scale fuzzy systems via distributed event-triggering schemes. IEEE Trans. Fuzzy Syst.26, 1688–1703. 10.1109/TFUZZ.2017.2744599
28
ZhuY. ZZhongZ. X.Basin MichaelV.ZhouD. H. (2018a). A descriptor system approach to stability and stabilization of discrete-time switched PWA systems. IEEE Trans. Autom. Control2018, 3456–3463. 10.1109/TAC.2018.2797173
29
ZhuY. ZZhongZ. X.ZhengW. X.ZhouD. H. (2018b). HMM-based H∞ filtering for discrete-time markov jump LPV systems over unreliable communication Channels. IEEE Trans. Syst. Man Cybernetic. Syst.48, 2035–2046. 10.1109/TSMC.2017.2723038
30
ZhuX.ChenB.YueD.WangY. (2012). An improved input delay approach to stabilization of fuzzy systems under variable sampling. IEEE Trans. Fuzzy Syst.20, 330–341. 10.1109/TFUZZ.2011.2174242
Summary
Keywords
stabilization, T-S fuzzy systems, quantization, sampled-data system, discontinuous LKF approach
Citation
Wang S, Chen S, Ji W and Liu K (2019) Quantized Sampled-Data Control for T-S Fuzzy System Using Discontinuous LKF Approach. Front. Neurosci. 13:372. doi: 10.3389/fnins.2019.00372
Received
20 January 2019
Accepted
01 April 2019
Published
24 April 2019
Volume
13 - 2019
Edited by
Yanzheng Zhu, Western Sydney University, Australia
Reviewed by
Bo Zhao, Beijing Normal University, China; Tiao-Yang Cai, Hebei Normal University, China; Junyi Wang, Loughborough University, United Kingdom
Updates
Copyright
© 2019 Wang, Chen, Ji and Liu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Keping Liu liukeping@ccut.edu.cn
This article was submitted to Autonomic Neuroscience, a section of the journal Frontiers in Neuroscience
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.