An Intelligence EEG Signal Recognition Method via Noise Insensitive TSK Fuzzy System Based on Interclass Competitive Learning

Epilepsy is an abnormal function disease of movement, consciousness, and nerve caused by abnormal discharge of brain neurons in the brain. EEG is currently a very important tool in the process of epilepsy research. In this paper, a novel noise-insensitive Takagi–Sugeno–Kang (TSK) fuzzy system based on interclass competitive learning is proposed for EEG signal recognition. First, a possibilistic clustering in Bayesian framework with interclass competitive learning called PCB-ICL is presented to determine antecedent parameters of fuzzy rules. Inherited by the possibilistic c-means clustering, PCB-ICL is noise insensitive. PCB-ICL learns cluster centers of different classes in a competitive relationship. The obtained clustering centers are attracted by the samples of the same class and also excluded by the samples of other classes and pushed away from the heterogeneous data. PCB-ICL uses the Metropolis–Hastings method to obtain the optimal clustering results in an alternating iterative strategy. Thus, the learned antecedent parameters have high interpretability. To further promote the noise insensitivity of rules, the asymmetric expectile term and Ho–Kashyap procedure are adopted to learn the consequent parameters of rules. Based on the above ideas, a TSK fuzzy system is proposed and is called PCB-ICL-TSK. Comprehensive experiments on real-world EEG data reveal that the proposed fuzzy system achieves the robust and effective performance for EEG signal recognition.

Introduction

Epilepsy occurs randomly and may occur multiple times in a day. In the case of epileptic seizures, the patients have a sudden physical convulsions and loss of consciousness, which bring great physical and psychological pain to patients (Ahmadlou and Adeli, 2011; Gummadavelli et al., 2018; Cury et al., 2019). Seizures will lead to brain cell death, affect brain function, and even threaten patients' lives in serious cases. The incidence of epilepsy is high, and the age range is very wide, including children, adolescents, and the elderly, but the incidence of children and adolescents is the highest. Both men and women are likely to have the disease, and men are more likely to have this disease than women. As an important clinical means of monitoring and diagnosing epilepsy, EEG provides a more rapid and stable low-cost and non-invasive technology in monitoring the brain activity of the cerebral cortex. It provides information that other physiological methods cannot provide. The specific waveforms such as spike, sharp, and complex wave can be reflected by EEG. Therefore, the prevention and treatment of epilepsy research for epilepsy patients is of great significance. In the process of diagnosis and treatment of epilepsy, EEG plays an irreplaceable role. Doctors usually judge the condition of patients by observing their EEG.

The traditional way to judge the EEG signal is not only inefficient, but also because of the difference of experts' subjective experience, the automatic detection of EEG signal is still one of the hot issues in biomedical research (Jiang et al., 2017a; Martinez-Vargas et al., 2017; Li et al., 2019). An automatic epilepsy detection method can help doctors improve the accuracy of epilepsy diagnosis and also greatly save time. The research of automatic epilepsy detection is of great value to the prevention, diagnosis, and treatment of epilepsy. At present, epilepsy can be detected by machine learning and data mining. Firstly, the effective feature information is extracted from EEG and preprocessed for data analysis; secondly, the preprocessed EEG data are sent to the classifier for analysis and detection of epileptic and non-epileptic EEG data. In the above implementation process, the key research is to design an effective prediction and discrimination method that can be applied to normal EEG signal and epileptic EEG signal. Many effective methods have been successfully applied to automatic epilepsy detection system, including extreme learning machine (ELM), artificial neural network, Bayesian linear discriminant analysis, support vector machine (SVM), and fuzzy system (Kabir and Zhang, 2016; Qi et al., 2017; Akhavan and Moradi, 2018; Truong et al., 2018; Hossain et al., 2019; Liu et al., 2019; Sreej and Samanta, 2019; Xia et al., 2020). The fuzzy system is a model constructed to deal with the thinking, analysis, reasoning, and decision-making processes in production and practice. It can directly translate natural language into computer language. Due to its ability to process uncertain and ambiguous information, it has a high degree of interpretability and strong learning ability (Juang et al., 2007; Gu et al., 2017a; Jiang et al., 2017b,c; Gu and Wang, 2018). However, the traditional fuzzy system has poor robustness and anti-interference ability, and the classification accuracy is not high in data noise scenarios. But in real life, the classification of noise data is widely used. For example, in actual application scenarios, due to differences in machine advices or scanning technology, such as different rotation angles and noise, the quality of medical images may vary greatly (Siuly and Li, 2015; Hussein et al., 2019; Razzak et al., 2019).

Based on key technology of fuzzy system modeling, this paper proposes a novel noise-insensitive Takagi–Sugeno–Kang (TSK) fuzzy system. How to determine the antecedent and consequent parameters is the key to modeling the noise-insensitive fuzzy system (Takagi and Sugeno, 1985; Jiang et al., 2015). For the antecedent part of fuzzy rules, clustering is one kind of a commonly used strategy, such as fuzzy c-means (FCM) clustering (Bezdek et al., 1984), fuzzy (c + p) clustering (Leski, 2015), Bayesian fuzzy clustering (BFC) (Glenn et al., 2015), and possibilistic c-means (PCM) clustering (Krishnapuram and Keller, 1993). However, FCM, fuzzy (c + p), and BFC are sensitive to noise and will lead to unsatisfactory partition in noisy scenarios. PCM inherits the practicability and flexibility of fuzzy clustering and greatly enhances the clustering performance of data with noise or outliers. However, the unsupervised nature of PCM makes it unable to use the class label information of samples, which easily causes the insufficient fuzzy space partition, thus further affecting the learning of antecedent parameters of fuzzy rules. The principle of antecedent parameter learning using PCM clustering is shown in Figure 1A. PCM clustering is directly used on whole datasets or on samples in each class, and then the antecedent parameters are learned using the obtained clustering results. Then the data samples are simply divided into several clusters, without fully taking advantage of the geometry of data and the label information of samples. In this case, in the data overlapping regions, the distance between clustering centers may be too small or the centers may overlap.

FIGURE 1

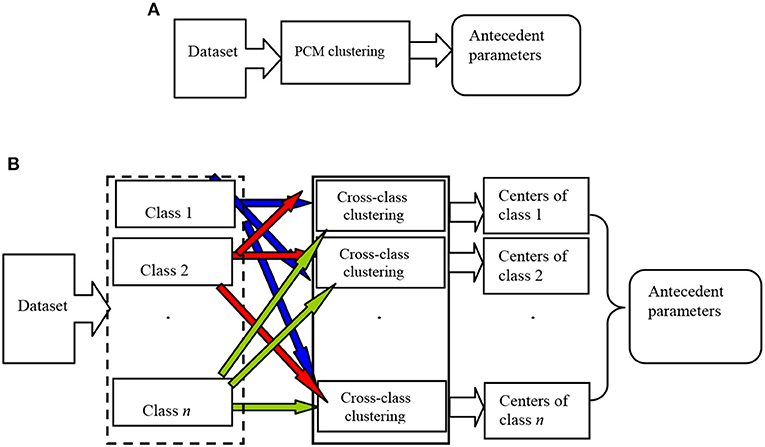
Figure 1. Principle of antecedent parameter learning using PCB-ICL clustering. (A) The principle of antecedent parameter learning using PCM clustering. (B) The principle of antecedent parameter learning using PCB-ICL clustering.

In this paper, we first propose a noise-insensitive possibilistic clustering in Bayesian framework with interclass competitive learning called PCB-ICL. Inherited by PCB, PCB-ICL is noise insensitive; meanwhile, different classes of cluster centers will produce a competitive relationship during the learning process. That is, in the sample overlapping area, the clustering centers are attracted by the samples of the same class and also excluded by the samples of other classes and pushed away from the heterogeneous data. The principle of antecedent parameter learning using PCB-ICL clustering is shown in Figure 1B. PCB-ICL integrates the competitive learning mechanism of clustering centers among different classes in the Bayesian framework. PCB-ICL considers the structure information of samples in the clustering procedure and realizes the competition between clustering centers among different classes. We obtain the antecedent part of fuzzy rules by performing PCB-ICL alternatively on each class samples. Then, a Ho–Kashyap procedure (Leski, 2003) with an asymmetric expectile term (Huang et al., 2014a,b) is adopted to estimate the consequent parameters of fuzzy rules. Due to the statistical characteristics of the asymmetric expectile term, it is insensitive to noise; so the asymmetric expectile term is used to measure the misclassification error. Based on the above idea, the TSK fuzzy system called PCB-ICL-TSK is developed, which learns antecedent parameters by PCB-ICL clustering and consequent parameters by the Ho–Kashyap procedure with an asymmetric expectile term. We apply the proposed algorithm on the Bonn EEG dataset, and the experimental results on several noisy classification tasks demonstrate that PCB-ICL-TSK can achieve satisfactory performance in EEG signal classification. The novelty of our study is as follows. (1) Both the PCB-ICL and Ho–Kashyap procedure with an asymmetric expectile term are insensitive to noise; thus, the obtained antecedent and consequent parameters are noise insensitive. (2) With the Bayesian framework, the clustering results of PCB-ICL are globally optimal. In addition, the competitive relationship strategy between cluster centers enhances the interpretability of the antecedents of fuzzy rules. (3) The experiments on real-word EEG datasets confirm the effectiveness of PCB-ICL-TSK.

The detailed chapters are arranged as follows. Section Backgrounds introduces the TSK fuzzy system and PCM clustering. Section Possibilistic Clustering in Bayesian With Interclass Competitive Learning explores PCB-ICL clustering. Section Noise-Insensitive TSK Fuzzy System via Interclass Competitive Learning explores the noise-insensitive TSK fuzzy system PCB-ICL-TSK. Section Experiment is experiments on noisy EEG data. Section Conclusion is the conclusion.

Backgrounds

Dataset

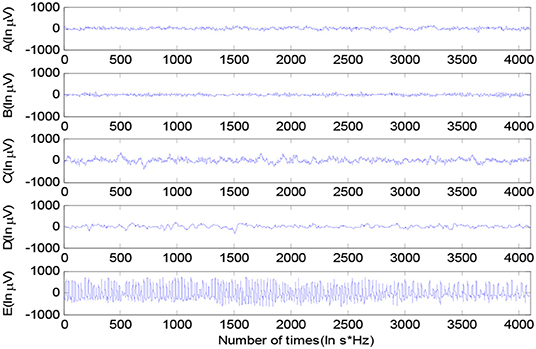
The epileptic EEG in the experiment is the Bonn dataset from Bonn University, Germany (Tzallas et al., 2009). The Bonn EEG dataset consists of five groups of data, namely, A to E, shown in Figure 2. Each group of data contains 100 EEG signal segments of 23.6 s, which were selected from continuous single-channel EEG recordings. The EEG signals were recorded under different conditions with five patients and five healthy volunteers. The basic information of groups A–E is shown in Table 1.

FIGURE 2

Figure 2. The epileptic EEG signals in groups A to E.

TABLE 1

Table 1. The basic information of EEG data groups of A–E.

TSK Fuzzy System

The most commonly used rule in the zero-order TSK fuzzy system can be represented by

Rule R_k: IF x₁ is A_k,1 and x₂ is A_k,2 and … and x_d is A_k,_d,

$\begin{array}{ll}then{f}_k(\text{x})=P_{k,0},(k=1,2,\dots ,K)& (1)\end{array}$

where x₁, x₂, …, x_d are input variables, A_k,_i is a fuzzy subset, and K is the number of fuzzy rules. For an input vector x, the output of the corresponding TSK fuzzy system is represented by

$\begin{array}{ll}{y}_{output}=\frac{{\displaystyle \sum _{k=1}^K}{\mu }_k(\text{x})p_{k,0}^{}}{{\displaystyle \sum _{k=1}^K}{\mu }_k(\text{x})}={\displaystyle \sum _{k=1}^K}{\tilde{\mu }}_k(\text{x})p_{k,0}^{},& (2)\end{array}$

where the fuzzy membership μ_k(x) and the normalized fuzzy membership ${\tilde{\mu }}_k(\text{x})$ is

$\begin{array}{ll}{\mu }_k(\text{x})={\prod }_{i=1}^d{\mu }_{A_{k,i}^{}}(x_i),& (3)\end{array}$

$\begin{array}{ll}{\tilde{\mu }}_k(\text{x})=\frac{{\mu }_k(\text{x})}{{\displaystyle \sum _{k^{{}^{\prime }}=1}^K}{\mu }_{k^{{}^{\prime }}}(\text{x})}.& (4)\end{array}$

For the sample x_i, we can rewrite it by

$\begin{array}{ll}d({\text{x}}_i)={\left[{\tilde{\mu }}_1({\text{x}}_i),{\tilde{\mu }}_2({\text{x}}_i),\dots ,{\tilde{\mu }}_K({\text{x}}_i)\right]}^T,& (5)\end{array}$

Generally, antecedent and consequent parameters of rules are determined separately. A popular way to estimate antecedent parameters is to use a certain fuzzy clustering method (Takagi and Sugeno, 1985; Gu et al., 2017b; Salgado et al., 2017). Then ${\mu }_{A_{k,i}^{}}(x_i)$ can be computed by

$\begin{array}{ll}{\mu }_{A_{k,i}^{}}(x_i)=\text{exp}(-\frac{{(x_i-y_{k,i}^{})}^2}{2{\delta }_{k,i}^{}}),& (6)\end{array}$

where the width parameter δ_k,_i can be obtained by

$\begin{array}{ll}{\delta }_{k,i}^{}=\frac{h·{\displaystyle \sum _{j=1}^N}{u}_{k,j}{(x_{ji}-y_{k,i}^{})}^2}{{\displaystyle \sum _{j=1}^N}{u}_{k,j}},& (7)\end{array}$

where h is the scale parameter and u_k,_j is the fuzzy membership of the jth input sample x_j belonging to the kth cluster.

Then the learning of consequent parameters can be represented by

$\begin{array}{ll}{\displaystyle \underset{\text{p}}{min}}{\displaystyle \sum _{i=1}^N}|l_{i}d{({\text{x}}_i^{})}^T\text{p}-1|& (8)\end{array}$

Using the least square solution to minimize the squared loss, Equation (8) can be written by

$\begin{array}{ll}{\displaystyle \underset{\text{p}}{min}}J(\text{p})={(\text{D}\text{p}-1_{N\times 1})}^T\text{H}(\text{D}\text{p}-1_{N\times 1})+\tau {\text{p}}^T\text{p},& (9)\end{array}$

where D = [l₁d(x₁)^T, …, l_Nd(x_N)^T]^T, the matrix H = diag(h₁, h₂, …, h_N), h_i = 1/|l_id(x_i)^Tp−1| for l_id(x_i)^Tp−1 < 0, and h_i = 0 otherwise. τ is the regularization parameter. Using the Ho–Kashyap iterative method (Leski, 2003), p can be computed by

$\begin{array}{ll}\text{p}={({\text{D}}^T\text{H}\text{D}+\tau \text{I})}^{-1}{\text{D}}^T\text{H}1,& (10)\end{array}$

where I is the identify matrix.

PCM Clustering

PCM clustering is a probability clustering based on FCM. Based on the framework of possibility theory, PCM not only takes into account the general criteria of clustering with the minimum distance within one class and the maximum distance between classes but also emphasizes the principle of the maximum membership value to avoid ordinary solution problems. The objective function of PCM is

$\begin{array}{l}{\displaystyle \underset{\text{U},\text{Y}}{min}}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{c=1}^C}{u}_{nc}^m{({\text{x}}_n-{\text{y}}_c)}^2+{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{c=1}^C}{\eta }_c{(1-u_{nc}^{})}^m,\\ s.t.u_{nc}^{}\in \left[0,1\right],\forall n,c& (11)\end{array}$

The closed solution of U and Y can be obtained by minimizing the objective function with respect to u_nc and y_c by.

$\begin{array}{llll}{\text{y}}_c& =& \frac{{\displaystyle \sum _{n=1}^N}{u}_{nc}^m{\text{x}}_n}{{\displaystyle \sum _{n=1}^N}{u}_{nc}^m}& (12)\end{array}$

$\begin{array}{llll}{u}_{nc}^{}& =& \frac{1}{1+{(\frac{{({\text{x}}_n-{\text{y}}_c)}^2}{{\eta }_c})}^{\frac{1}{m-1}}}& (13)\end{array}$

Possibilistic Clustering in Bayesian with Interclass Competitive Learning

Objective Function

A clustering method implements data partition with some certain degree of similarity. In the clustering process, the samples of one class will have a repulsive effect on the clustering center of other classes, especially in the overlapping regions of different classes of samples; the greater the overlap density, the greater the repulsive force. In these sample overlapping regions, clustering centers of different classes form the competitive learning relationship. On the one hand, the clustering centers are attracted by samples of this class; on the other hand, the clustering centers are excluded by different classes of samples and far away from the overlapping region. In this paper, this idea is embedded into PCM clustering. Based on the Bayesian framework, we propose the possibilistic clustering in Bayesian with interclass competitive learning.

Suppose a given binary classification dataset $\text{X}={\left\{{\text{x}}_n,l_n\right\}}_{n=1}^N$, in which ${\text{X}}_1={\left\{{\text{x}}_n,l_n\right\}}_{n=1}^{N_1}$ and ${\text{X}}_2={\left\{{\text{x}}_n,l_n\right\}}_{n=N_1+1}^N$ represent two class samples and l_n ∈ {+1, −1} is the class label of the nth sample. Let the cluster number of one class samples be C₁ and the cluster centers of the other class Z be priorly known $\text{Z}={\left[{\text{z}}_1\mathrm{\text{,}}{\text{z}}_2,\dots ,{\text{z}}_{{\text{c}}_2}\right]}^T$, where the cluster number is C₂. We suppose data X follows the normal distribution, and each sample x_i has an independent probability distribution. The maximum posterior estimation of data and parameters in X₁ is expressed by

$\begin{array}{l}p({\text{X}}_1,\text{U},\text{Y})=p({\text{X}}_1|\text{U},\text{Y})p(\text{U}|\text{Y})p(\text{Y})\\ \propto exp\left\{-\frac{1}{2}({\displaystyle \sum _{n=1}^{N_1}}{\displaystyle \sum _{c=1}^{C_1}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{y}}_c\Vert }^2+{\displaystyle \sum _{n=1}^{N_1}}{\displaystyle \sum _{c=C_1+1}^{C_1+C_2}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{z}}_c\Vert }^2)\right\}\times \\ \left[{\displaystyle \prod _{n=1}^{N_1}{\displaystyle \prod _{c=1}^{C_1+C_2}\text{exp}(-\frac{1}{2}{\eta }_c{(1-u_{nc})}^m)\times \text{exp}\left\{-\frac{1}{2}{\displaystyle \sum _{c=1}^{C_1}{\text{(}{y}_c-{\mu }_y)}^T{\displaystyle {\sum }_y^{-1}\text{(}{y}_c-{\mu }_y)}}\right\}}}\right],& (14)\end{array}$

where $\text{Y}={\left[{\text{y}}_1\mathrm{\text{,}}{\text{y}}_2,\dots ,{\text{y}}_{c_1}\right]}^T$ is the unknown cluster center matrix of one class sample. By taking the logarithm of Equation (14), the objective function of PCB-ICL method can be obtained as

$\begin{array}{l}J({\text{X}}_1,\text{U},\text{Y})={\displaystyle \sum _{n=1}^{N_1}}{\displaystyle \sum _{c=1}^{C_1}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{y}}_c\Vert }^2+{\displaystyle \sum _{n=1}^{N_1}}{\displaystyle \sum _{c=C_1+1}^{C_1+C_2}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{z}}_c\Vert }^2\\ +{\displaystyle \sum _{n=1}^{N_1}}{\displaystyle \sum _{c=1}^{C_1+C_2}}{\eta }_c{(1-u_{nc}^{})}^m\\ +{\displaystyle \sum _{c=1}^{C_1}{\text{(}{y}_c-{\mu }_y)}^T{\displaystyle \sum _y^{-1}\text{(}{y}_c-{\mu }_y)}}.& (15)\end{array}$

From Equations (14) and (15), we can see that (1) the PCB-ICL method shows the competition relationship between clustering centers of different classes. Different from the traditional PCM clustering method, PCB-ICL not only considers the label information of samples but also considers the competition relationship between clustering centers, as shown in the first two items. On the premise that the clustering centers of the other class are priorly known, the clustering centers of the current class will inevitably have a competition relationship with these known clustering centers in the overlapping region. (2) Due to simultaneously utilizing the global distribution structure and the discrimination information of the samples, the obtained antecedent part of fuzzy rules by PCB-ICL can realize the clarity of fuzzy space partition and enhance the interpretability of the fuzzy rules.

Parameter Learning

To obtain the optimal fuzzy partition matrix U, the PCB-ICL method uses the Metropolis–Hastings method (Chib and Greenberg, 1995; Elvira et al., 2017) to construct a Markov chain to make p(U|X₁, Y) stable. The conditional distribution p(U|X₁, Y) is proportional to the joint distribution p(X₁, U, Y) when the sample and clustering center are known and also is proportional to the conditional distribution p(U|X₁, Y). Therefore, we only need compute p(x_n, u_n|Y) of the sample x_n:

$\begin{array}{l}p({\text{x}}_n,{\text{u}}_n|\text{Y})=p({\text{x}}_n|{\text{u}}_n,\text{Y})p({\text{u}}_n|\text{Y})\\ \propto exp\left\{-\frac{1}{2}({\displaystyle \sum _{c=1}^{C_1}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{y}}_c\Vert }^2+{\displaystyle \sum _{c=C_1+1}^{C_1+C_2}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{z}}_c\Vert }^2)\right\}\\ \times {\displaystyle \prod _{c=1}^{C_1+C_2}}exp(-\frac{1}{2}{\eta }_c{(1-u_{nc}^{})}^m).& (16)\end{array}$

Thus, the process of the ith iteration of the Markov chain is

1) Generate a new state ${\text{u}}_n^{+}$ of u_n with a uniform distribution as

$\begin{array}{ll}{u}_n^{+}~\text{ Uniform}(0,1\text{),}\forall n& (17)\end{array}$

2) The newly generated membership ${\text{u}}_n^{+}$ is accepted by the probability a_u as

$\begin{array}{ll}{a}_u=\min \left\{1,\frac{p(x_{\text{n}},u_n^{+}|Y)}{p(x_{\text{n}},u_n|Y)}\right\}& (18)\end{array}$

Then accepting a_u as the current state with probability u_n,

$\begin{array}{ll}{\text{u}}_n^{}=\{\begin{array}{c}{\text{u}}_n^{+},\mu \le {\alpha }_{\text{u}}\\ {\text{u}}_n,\mu >{\alpha }_{\text{u}}\end{array}& (19)\end{array}$

where μ is a random number in [0, 1]. The distribution of the new state ${\text{u}}_n^{+}$ obtained by sampling is independent of the current sample, and the state ${\text{u}}_n^{+}/{\text{u}}_n^{}$ is independent, so a_u does not need Hasting correction.

3) Compare $p({\text{x}}_n\mathrm{\text{,}}{\text{u}}_n^{+}|{\text{Y}}_{}^{*}\mathrm{\text{)}}$ and $p({\text{x}}_n,{\text{u}}_n^{*}|{\text{Y}}_{}^{*})$, where Y^* and ${\text{u}}_n^{*}$ are the optimal values of Y and u_n. If, $p(x_n\mathrm{\text{,}}{u}_n^{+}\mathrm{\text{|}}{Y}^{*}\mathrm{\text{) >}}p(x_n,u_n^{*}\mathrm{\text{|}}{Y}^{*})$ ${\text{u}}_n^{+}$ is replaced by ${\text{u}}_n^{*}$.

When the matrix U is fixed, we use Metropolis–Hastings to sample the conditional distribution p(Y|X, U). In this case, p(Y|X, U) is proportional to the joint distribution p(X, U, Y). We estimate y_c by using the Gaussian distribution as

$\begin{array}{ll}{\text{y}}_c^{+}~{N}\left({\text{y}}_c,\frac{1}{\sigma }{{\displaystyle \sum }}_y\right)& (20)\end{array}$

where ${\text{y}}_c^{+}$ centers on the current value y_c. σ is a positive number and is used to control the compactness of cluster centers. In the experiment, we empirically set σ to 10.

For the newly generated ${\text{y}}_c^{+}$, it is independent of other clustering centers. Then the conditional distribution p(X, y_c|U) is represented by

$\begin{array}{l}p(\text{X},{\text{y}}_c|\text{U})=p(\text{X}|\text{U},{\text{y}}_c)p({\text{y}}_c)\\ \propto exp\left\{-\frac{1}{2}{\displaystyle \sum _{n=1}^{N_1}}{u}_{nc}^m{\Vert {\text{x}}_n-{\text{y}}_c\Vert }^2\right\}\\ \times \exp \left\{-\frac{1}{2}{\text{(}{y}_c-{\mu }_y)}^T{\displaystyle {\sum }_y^{-1}\text{(}{y}_c-{\mu }_y)}\right\}.& (21)\end{array}$

Similarly, the newly generated membership ${\text{y}}_c^{+}$ is accepted by the probability a_y as

$\begin{array}{ll}{a}_{\text{y}}=min\left\{1,\frac{p(\text{X},{\displaystyle {\text{y}}_c^{+}}|\text{U})}{p(\text{X},{\text{y}}_c|\text{U})}\right\}& (22)\end{array}$

Since the Gaussian distribution is symmetric, a_y does not need Hasting correction.

Finally, we compute p(X, U^*, Y^*) using Equation (15) and compare it with the current p(X, U, Y). If p(X, U, Y) > p(X, U^*, Y^*), the {U, Y} is replaced by {U^*, Y^*}.

Based on the above analysis, we give the procedure of the PCB-ICL method in Algorithm 1.

ALGORITHM 1

Algorithm 1. PCB-ICL method.

Noise-Insensitive TSK Fuzzy System via Interclass Competitive Learning

Antecedent Parameter Learning in PCB-ICL-TSK

In this section, we compute the antecedent parameters in PCB-ICL-TSK. The premise of PCB-ICL clustering in Algorithm 1 is that the clustering centers of other class are priorly known, which is obviously not feasible in practical application. To perform the fuzzy partition on the whole data set, we take the strategy of an alternating cycle to perform Algorithm 1 on different classes. In this case, the clustering results of one class influence the ones of the other class. Taking binary classification as an example, we perform Algorithm 1 on positive class X₁ and negative class X₂ alternately. The detailed fuzzy partition of the whole data is shown in Algorithm 2.

ALGORITHM 2

Algorithm 2. Fuzzy partition on the whole data.

The numbers of clustering in two classes are C₁ and C₂, and the cluster centers in two classes are Y₁ and Y₂, respectively. After applying Algorithm 2 on the whole data, the center matrix Y can be described by Y^* = [Y^(1)*; Y^(2)*].

Consequent Parameter Learning in PCB-ICL-TSK

In this section, we compute the noise-insensitive consequent parameters in PCB-ICL-TSK. As discussed before, using the obtained the antecedent parameters, the dataset $\text{X}={\left\{{\text{x}}_i,l_i\right\}}_{i=1}^N$ is represented as $S={\left\{(\tilde{\mu }({\text{x}}_i),l_i)\right\}}_{i=1}^N$, where $\tilde{\mu }({\text{x}}_i)={[{\tilde{\mu }}_1{({\text{x}}_i)}^T,{\tilde{\mu }}_2{({\text{x}}_i)}^T,\dots ,{\tilde{\mu }}_{(C_1+C_2)}{({\text{x}}_i)}^T]}^T$. Defining the vector $d({\text{x}}_i)={[{\tilde{\mu }}_1{({\text{x}}_i)}^T,{\tilde{\mu }}_2{({\text{x}}_i)}^T,\dots ,{\tilde{\mu }}_{(C_1+C_2)}{({\text{x}}_i)}^T,1]}^T$, the consequent vector ${\text{p}}^{*}={[p_0^1,p_0^2,...,p_0^{{}_{(C_1+C_2)}},w]}^T$ can be computed by

$\begin{array}{ll}f({\text{x}}_i)={({\text{p}}^{*})}^{T}d({\text{x}}_i)={{\text{p}}_0}^T\tilde{\mu }({\text{x}}_i)+w\{\begin{array}{c}\ge 0,{\text{x}}_i\in {\text{X}}_1\\ <0,{\text{x}}_i\in {\text{X}}_2\end{array}& (23)\end{array}$

where the vector ${\text{p}}_0={[p_0^1,p_0^2,...,p_0^{{}_{(C_1+C_2)}}]}^T$ and w is the decision threshold. If we multiply Equation (23) by the class label, Equation (23) is represented as l_i(p^*)^Td(x_i) ≥ 0 (i = 1, …, N). Then, the vector p^* can be computed by

$\begin{array}{ll}{l}_i{({\text{p}}^{*})}^{T}d({\text{x}}_i^{})\ge {\epsilon }_0& (24)\end{array}$

In particular, ε₀ = 1 leads to the classical SVM. For simplicity, we set ε₀ = 1, and Equation (24) can be written as l_i(p^*)^Td(x_i) ≥ 1. Thus, Equation (24) can be written as

$\begin{array}{ll}J(p^{*})={\displaystyle \sum _{i=1}^N(l_i}{(p^{*})}^{T}d(x_i)-1{)}^2& (25)\end{array}$

Denote the matrix D = [l₁d(x₁)^T, l₂d(x₂)^T, …, l_Nd(x_N)^T]^T and the error vector e = D^*p^* – 1. Equation (25) can be rewritten as

$\begin{array}{ll}{\displaystyle \underset{{\text{p}}^{*}}{min}}J({\text{p}}^{*})=\frac{1}{2}{(\text{D}{\text{p}}^{*}-1)}^T\text{H}(\text{D}{\text{p}}^{*}-1)& (26)\end{array}$

where the matrix H = (λ/N)diag(h₁, h₂, …, h_N), with h_i = 0 for error e_i ≥ 0 and 1 otherwise.

However, the misclassification error in Equation (24) is noise sensitive. To further improve the robustness of the TSK fuzzy system, we use the asymmetric expectile term, which is noise insensitive, especially to noise around the decision boundary. The weight h_i of the ith sample can be expressed by

$\begin{array}{ll}{h}_i=\{\begin{array}{c}q,e_i\ge 0\\ (1-q),e_i<0\end{array}& (27)\end{array}$

where h_i is the q (lower) expectile parameter. Obviously, when q = 0, the loss term obtained in Equation (27) is equal to the hinge loss, and when q = 0.5, the loss term is equal to the l₂ loss in Huang et al. (2014a,b).

At the same time, considering the regularization term, Equation (26) can be rewritten as

$\begin{array}{l}{\displaystyle \underset{{\text{p}}^{*}}{min}}J{({\text{p}}^{*})}^{(k)}=\frac{1}{2}{({\text{D}}^{*}{({\text{p}}^{*})}^{(k)}-1)}^T{\text{H}}^{(k)}({\text{D}}^{*}{({\text{p}}^{*})}^{(k)}-1)\\ +\frac{\tau }{2}{({{\text{p}}_0}^{(k)})}^T{{\text{p}}_0}^{(k)}& (28)\end{array}$

where τ is the regularization parameter. p^*(k), H^(k), and e^(k) are the kth iteration of p^*, H, and e, respectively.

The condition for optimality of Equation (28) in the kth iteration is obtained by setting dJ/dp^* = 0:

$\begin{array}{ll}{({\text{p}}^{*})}^{(k)}={({({\text{D}}^{*})}^T{\text{H}}^{(k)}{\text{D}}^{*}+\tau \tilde{\text{I}})}^{-1}{({\text{D}}^{*})}^T{\text{H}}^{(k)}1& (29)\end{array}$

where $\tilde{\text{I}}$ is the identity matrix with the last element on the main diagonal set to 0.

The consequent parameter learning in IB-TSK-FC on dataset X is shown in Algorithm 3.

ALGORITHM 3

Algorithm 3. Learning algorithm for consequent parameters.

Experiment

Experimental Settings

The real-world EEG signals have characters of high dimensionality and instability. Feature extraction is a necessary stage before classification for EEG signal recognition. In general, time domain and frequency domain feature extractions are two types of feature extraction methods (Wen and Zhang, 2017). In our experiments, we extract EEG features using kernel principal component analysis (KPCA) and short-time Fourier transform (STFT) (Blanco et al., 1997). The former is the time domain feature extraction, and the latter is the frequency domain feature extraction. In the experiment, we design eight classification tasks, namely, four binary classification and four three-class classification tasks, as shown in Table 2. We corrupt the original datasets with different amounts of random noises at 5, 10, and 15% noise levels.

TABLE 2

Table 2. EEG classification tasks in the experiment.

The experimental environment in this study is a computer with Intel Core i3-3317U 3.40-GHz CPU and 8-GB RAM. To validate the performance of MST-TSK, we compare three fuzzy systems (FS-FCSVM; et al., 2007, ε-margin-TSK-FS; Leski, 2005, and IB-TSK-FC; Gu et al., 2017b) and two robust classification methods (CS-SVM; Iranmehr et al., 2019 and FRSVM-ANCH; Gu et al., 2019). The Gaussian kernel is used for two SVM methods. The parameter settings for all methods are listed in Table 3. All parameters are obtained by a 5-fold cross-validation strategy.

TABLE 3

Table 3. Parameter settings for all methods in the experiment.

Classification Performance Comparison

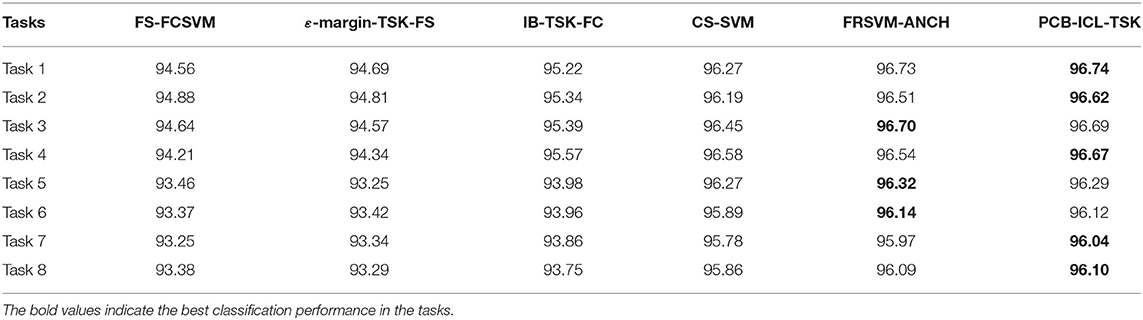
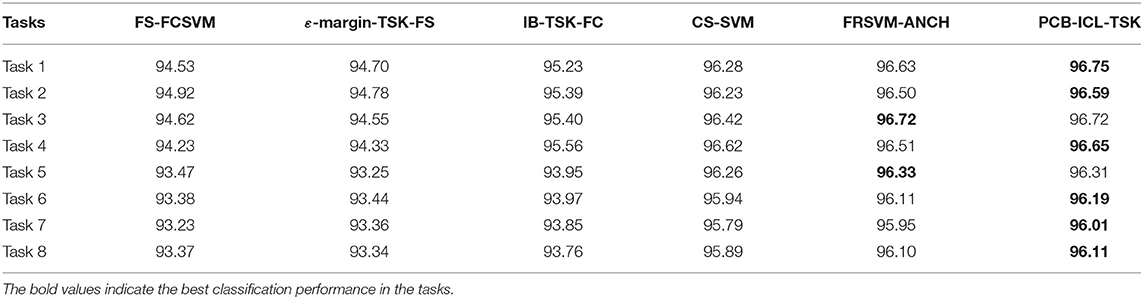
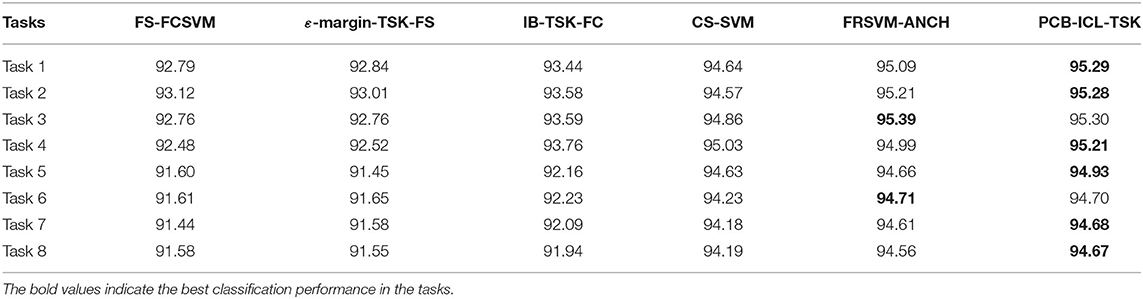
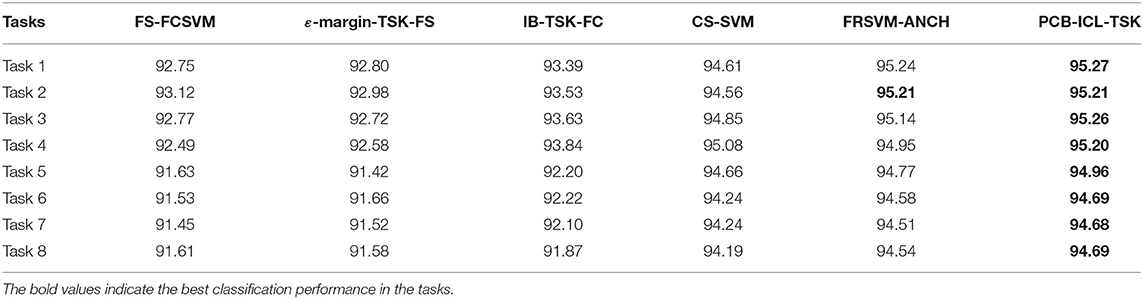
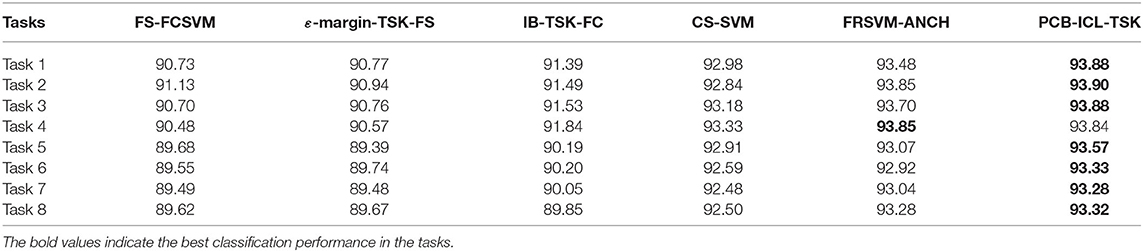
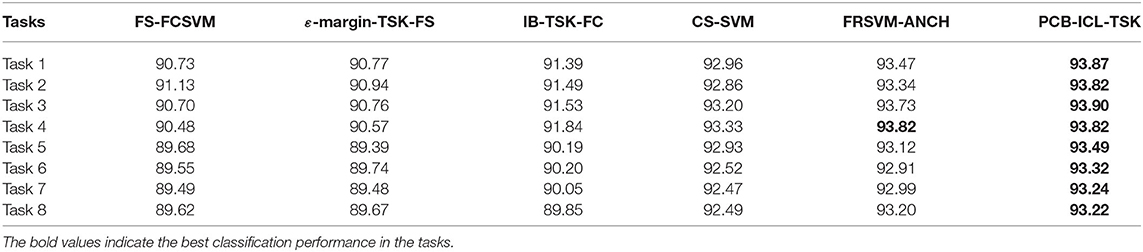
In this section, eight EEG classification tasks are used to verify the classification performance of PCB-ICL-TSK. Tables 4, 5 show the experimental results of six classification algorithms using STFT and KPCA feature extraction methods at the 5% noise level. Tables 6, 7 show the experimental results of six classification methods using STFT and KPCA feature extraction methods at the 10% noise level. Tables 8, 9 show the experimental results of six classification methods using STFT and KPCA feature extraction methods at the 15% noise level. From the experimental results, it can be seen that the noise data seriously affect the classification performance of the method. During the learning process, considering the noise of the data is helpful to promote the classification performance. Therefore, the performances of FS-FCSVM, ε-margin-TSK-FS, and IB-TSK-FC are poor. CS-SVM, FRSVM-ANCH, and PCB-ICL-TSK are not sensitive to noise, and they can achieve good classification results. In particular, PCB-ICL-TSK shows excellent classification performance in different levels of noise occasions, and it reflects strong robustness. Since PCB-ICL-TSK uses the PCB-ICL and Ho–Kashyap procedure with an asymmetric expectile term to compute antecedent and consequent parameters of fuzzy rules, it is noise insensitive. In addition, in the Bayesian framework, PCB-ICL obtains global optimal clustering results, and the strategy of competitive relationship of clustering centers can enhance the interpretability of the antecedents of fuzzy rules.

TABLE 4

Table 4. The classification accuracy for the 5% noise level using STFT features.

TABLE 5

Table 5. The classification accuracy for the 5% noise level using KPCA features.

TABLE 6

Table 6. The classification accuracy for the 10% noise level using STFT features.

TABLE 7

Table 7. The classification accuracy for the 10% noise level using KPCA features.

TABLE 8

Table 8. The classification accuracy for the 15% noise level using STFT features.

TABLE 9

Table 9. The classification accuracy for the 15% noise level using KPCA features.

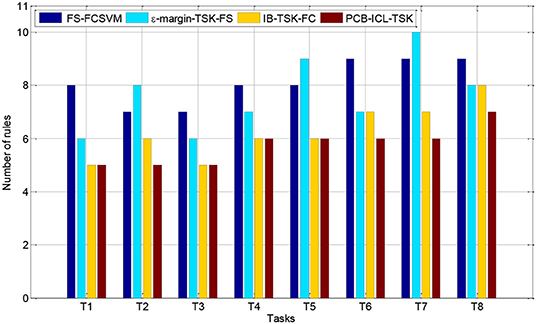
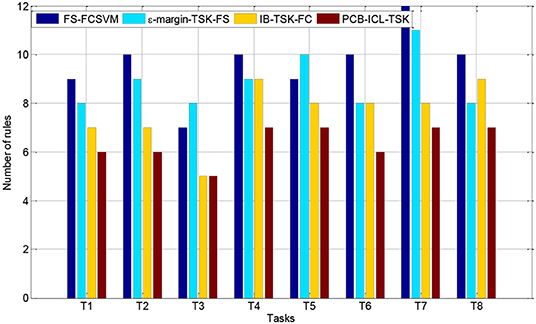
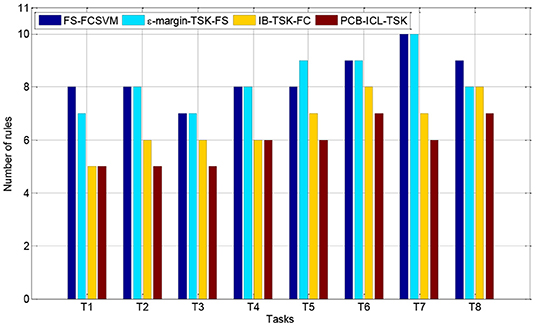
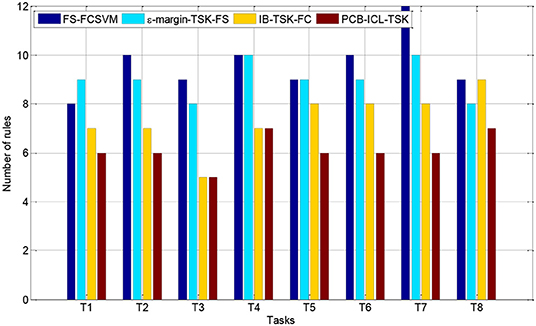
Interpretability Comparison

In this section, we compare the number of fuzzy rules of four fuzzy systems in Task 8. Figures 3, 4 show the number of fuzzy rules on the 5 and 15% noise levels for four fuzzy systems using KPCA features. Figures 5, 6 show the number of fuzzy rules on the 5 and 15% noise levels for four fuzzy systems using STFT features. From the results in Figures 3–6, compared with the three fuzzy systems, the number of fuzzy rules obtained by PCB-ICL-TSK is the least in all EEG classification tasks. It is known that for fuzzy systems, the interpretability of fuzzy rules is related to the number of fuzzy rules and the definition of fuzzy subsets. The fuzzy membership function obtained by PCB-ICL on Task 1 at the 5% noise level using KPCA features is shown in Figure 7. Because PCB-ICL clustering considers the influence of clustering centers of different classes in the process of clustering, that is, the competition relationship between different classes of clustering centers, PCB-ICL clustering can obtain clustering centers with a large interval, which guarantees the partition clarity of feature space and the classification accuracy of the obtained fuzzy system and the interpretation of rules.

FIGURE 3

Figure 3. The rules obtained by four fuzzy systems on the 5% noise level using KPCA features.

FIGURE 4

Figure 4. The rules obtained by four fuzzy systems on the 15% noise level using KPCA features.

FIGURE 5

Figure 5. The rules obtained by four fuzzy systems on the 5% noise level using STFT features.

FIGURE 6

Figure 6. The rules obtained by four fuzzy systems on the 15% noise level using STFT features.

FIGURE 7

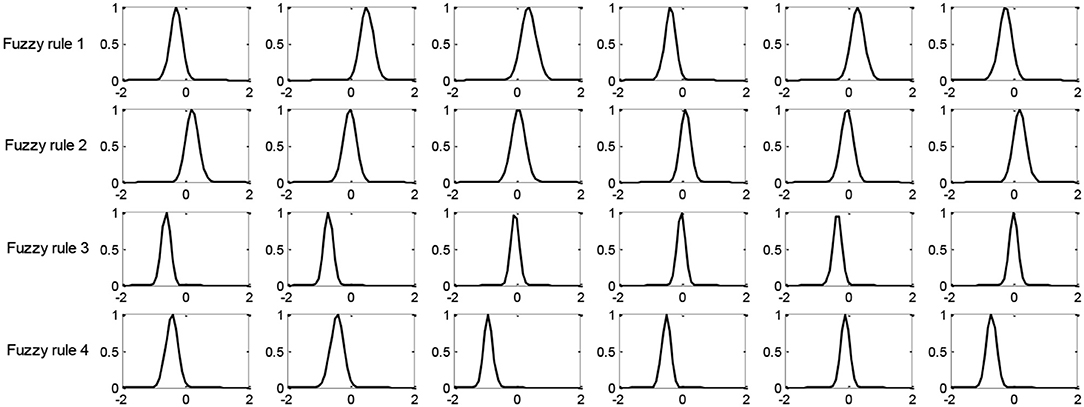
Figure 7. Fuzzy membership functions obtained by PCB-ICL on Task 1 with the 5% noise level using KPCA features.

Conclusion

The noise-insensitive PCB-ICL-TSK fuzzy system is proposed in this paper. In the learning of rule antecedent parameters, the proposed noise-insensitive PCB-ICL clustering based on the Bayesian probability model is used. PCB-ICL clustering considers the repulsion between different clustering centers, which can ensure the interpretability of the rule antecedent. PCB-ICL can learn the global optimal solution of clustering results by using the Markov model. PCB-ICL-TSK learns consequent parameters using the Ho–Kashyap procedure with an asymmetric expectile term. Thus, it not only has strong noise resistance but also has high classification performance. The experimental results of a real EEG dataset show that PCB-ICL-TSK has achieved satisfactory results in classification performance and high interpretability. Our future work is to further improve its practicability when the sample dimension is large.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: The dataset analyzed for this study can be found in the Department of Epileptology University of Bonn [http://epileptologie-bonn.de/cms/upload/workgroup/lehnertz/eegdata.html].

Author Contributions

TN and XG conceived and developed the theoretical framework of the manuscript. All authors carried out the experiment and data process and drafted the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 61806026 and by the Natural Science Foundation of Jiangsu Province under Grant BK20180956.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmadlou, M., and Adeli, H. (2011). Functional community analysis of brain: a new approach for EEG-based investigation of the brain pathology. Neuroimage 58, 401–408. doi: 10.1016/j.neuroimage.2011.04.070

PubMed Abstract | CrossRef Full Text | Google Scholar

Akhavan, A., and Moradi, M. H. (2018). Detection of concealed information using multichannel discriminative dictionary and spatial filter learning. IEEE Trans. Inform. Foren. Secur. 13, 2616–2627. doi: 10.1109/TIFS.2018.2825940

CrossRef Full Text | Google Scholar

Bezdek, J., Ehrlich, R., and Full, W. (1984). FCM: the fuzzy c-means clustering algorithm. Comp. Geosci. 10, 191–203. doi: 10.1016/0098-3004(84)90020-7

CrossRef Full Text | Google Scholar

Blanco, S., Kochen, S., Rosso, O. A., and Salgado, P. (1997). Applying time frequency analysis to seizure EEG activity. IEEE Eng. Med. Biol. Mag. 16, 64–71. doi: 10.1109/51.566156

PubMed Abstract | CrossRef Full Text | Google Scholar

Chib, S., and Greenberg, E. (1995). Understanding the metropolis-hastings algorithm. Am. Stat. 49, 327–335. doi: 10.1080/00031305.1995.10476177

CrossRef Full Text | Google Scholar

Cury, C., Maurel, P., Gribonval, R., and Barillot, C. (2019). A sparse EEG-informed fMRI model for hybrid EEG-fMRI neurofeedback prediction. Front. Neurosci. 13:1451. doi: 10.3389/fnins.2019.01451

PubMed Abstract | CrossRef Full Text | Google Scholar

Elvira, V., Míguez, J., and Djurić, P. M. (2017). Adapting the number of particles in sequential Monte Carlo methods through an online scheme for convergence assessment. IEEE Trans. Signal Process. 65, 1781–1794. doi: 10.1109/TSP.2016.2637324

CrossRef Full Text | Google Scholar

Glenn, T. C., Zare, A., and Gader, P. D. (2015). Bayesian fuzzy clustering. IEEE Trans. Fuzzy Syst. 23, 1545–1561. doi: 10.1109/TFUZZ.2014.2370676

CrossRef Full Text | Google Scholar

Gu, X., Chung, F., and Wang, S. (2017a). Bayesian Takagi-Sugeno-Kang fuzzy classifier. IEEE Trans. Fuzzy Syst. 25, 1655–1671. doi: 10.1109/TFUZZ.2016.2617377

CrossRef Full Text | Google Scholar

Gu, X., Chung, F. L., Ishibuchi, H., and Wang, S. (2017b). Imbalanced TSK fuzzy classifier by cross-class Bayesian fuzzy clustering and imbalance learning, IEEE Trans. Syst. Man Cybernet. Syst. 47, 2005–2020. doi: 10.1109/TSMC.2016.2598270

CrossRef Full Text | Google Scholar

Gu, X., Ni, T., and Fan, Y. (2019). A fast and robust support vector machine with anti-noise convex hull and its application in large-scale ncRNA data classification. IEEE Access. 7, 134730–134741. doi: 10.1109/ACCESS.2019.2941986

CrossRef Full Text | Google Scholar

Gu, X., and Wang, S. (2018). Bayesian Takagi-Sugeno-Kang Fuzzy model and its joint learning of structure identification and parameter estimation. IEEE Trans. Indust. Inform. 14, 5327–5337. doi: 10.1109/TII.2018.2813977

CrossRef Full Text | Google Scholar

Gummadavelli, A., Zaveri, H. P., Spencer, D. D., and Gerrard, J. L. (2018). Expanding brain-computer interfaces for controlling epilepsy networks: novel thalamic responsive neurostimulation in refractory epilepsy. Front. Neurosci. 12:474. doi: 10.3389/fnins.2018.00474

PubMed Abstract | CrossRef Full Text | Google Scholar

Hossain, M. S., Amin, S. U., Alsulaiman, M., and Muhammad, G. (2019). Applying deep learning for epilepsy seizure detection and brain mapping visualization, ACM Trans. Multimed. Comput. Commun. Appl. 15, 1–17. doi: 10.1145/3241056

CrossRef Full Text | Google Scholar

Huang, X. L., Shi, L., Pelckmansb, K., and Suykens, J. A. K. (2014a). Asymmetric ν-tube support vector regression. Comput. Stat. Data Anal. 77, 371–382. doi: 10.1016/j.csda.2014.03.016

CrossRef Full Text | Google Scholar

Huang, X. L., Shi, L., and Suykens, J. A. K. (2014b). Support vector machine classifier with pinball loss. IEEE Trans. Pattern Anal. Mach. Intell. 36, 984–997. doi: 10.1109/TPAMI.2013.178

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussein, R., Palangi, H., Ward, R. K., and Wang, Z. J. (2019). Optimized deep neural network architecture for robust detection of epileptic seizures using EEG signals. Clin. Neurophysiol. 130, 25–37. doi: 10.1016/j.clinph.2018.10.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Iranmehr, A., Shirazi, H. M., and Vasconcelos, N. (2019). Cost-sensitive support vector machines. Neurocomputing 343, 50–64. doi: 10.1016/j.neucom.2018.11.099

CrossRef Full Text | Google Scholar

Jiang, Y., Deng, Z., Chung, F., Wang, G., Qian, P., Choi, K. S., et al. (2017c). Recognition of epileptic EEG signals using a novel multiview TSK fuzzy system. IEEE Trans. Fuzzy Syst. 25, 3–20. doi: 10.1109/TFUZZ.2016.2637405

CrossRef Full Text | Google Scholar

Jiang, Y., Deng, Z., Chung, F., and Wang, S. (2015). Multi-task TSK fuzzy system modeling using inter-task correlation information. Inform. Sci. 298, 512–533. doi: 10.1016/j.ins.2014.12.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., Deng, Z., Chung, F., and Wang, S. (2017b). Realizing two-view TSK fuzzy classification system by using collaborative learning. IEEE Transac. Syst. Man Cybernet. Syst. 47, 145–160. doi: 10.1109/TSMC.2016.2577558

CrossRef Full Text | Google Scholar

Jiang, Y., Wu, D., Deng, Z., Qian, P., Wang, J., Wang, G., et al. (2017a). Seizure classification from EEG signals using transfer learning, semi-supervised learning and TSK fuzzy system. IEEE Trans. Neural Syst. Rehabil. Eng. 25, 2270–2284. doi: 10.1109/TNSRE.2017.2748388

PubMed Abstract | CrossRef Full Text | Google Scholar

Juang, C. F., Chiu, S. H., and Shiu, S. J. (2007). Fuzzy system learned through fuzzy clustering and support vector machine for human skin color segmentation. IEEE Trans. Syst. Man Cybernet. Part A Syst. Hum. 37, 1077–1087. doi: 10.1109/TSMCA.2007.904579

CrossRef Full Text | Google Scholar

Kabir, E., and Zhang, Y. (2016). Epileptic seizure detection from EEG signals using logistic model trees. Brain Inform. 3, 93–100. doi: 10.1007/s40708-015-0030-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnapuram, R., and Keller, J. M. (1993). A possibilistic approach to clustering. IEEE Trans. Fuzzy Syst. 1, 98–110. doi: 10.1109/91.227387

CrossRef Full Text | Google Scholar

Leski, J. M. (2003). Ho-Kashyap classifier with generalization control. Pattern Recogn. Lett. 24, 2281–2290. doi: 10.1016/S0167-8655(03)00054-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Leski, J. M. (2005). TSK-fuzzy modeling based on ε - insensitive learning. IEEE Trans. Fuzzy Syst. 13, 181–193. doi: 10.1109/TFUZZ.2004.840094

CrossRef Full Text | Google Scholar

Leski, J. M. (2015). Fuzzy (c+p)-means clustering and its application to a fuzzy rule-based classifier: towards good generalization and good interpretability. IEEE Trans. Fuzzy Syst. 23, 802–812. doi: 10.1109/TFUZZ.2014.2327995

CrossRef Full Text | Google Scholar

Li, X., Yang, H., Yan, J., Wang, X., Li, X., and Yuan, Y. (2019). Low-intensity pulsed ultrasound stimulation modulates the nonlinear dynamics of local field potentials in temporal lobe epilepsy. Front. Neurosci. 13:287. doi: 10.3389/fnins.2019.00287

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C. L., Xiao, B., Hsaio, W. H, and Tseng, V. S. (2019). Epileptic seizure prediction with multi-view convolutional neural networks. IEEE Access. 7, 170352–170361. doi: 10.1109/ACCESS.2019.2955285

CrossRef Full Text | Google Scholar

Martinez-Vargas, J. D., Strobbe, G., Vonck, K., Van Mierlo, P., and Castellanos-Dominguez, G. (2017). Improved localization of seizure onset zones using spatiotemporal constraints and time-varying source connectivity. Front. Neurosci. 11:156. doi: 10.3389/fnins.2017.00156

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, F., Li, Y., and Wu, W. (2017). RSTFC: a novel algorithm for spatio-temporal filtering and classification of single-trial EEG. IEEE Trans. Neural Netw. Learn. Syst. 26, 3070–3082. doi: 10.1109/TNNLS.2015.2402694

PubMed Abstract | CrossRef Full Text | Google Scholar

Razzak, I., Hameed, I. A., and Xu, G. D. (2019). Robust sparse representation and multiclass support matrix machines for the classification of motor imagery EEG signals. IEEE J. Transl. Eng. Health Med. 7, 2168–2372. doi: 10.1109/JTEHM.2019.2942017

PubMed Abstract | CrossRef Full Text | Google Scholar

Salgado, C. M., Viegas, J. L., Azevedo, C. S., Ferreira, M. C., Vieira, S. M., and Sousa, J. M. C. (2017). Takagi-Sugeno fuzzy modeling using mixed fuzzy clustering. IEEE Trans. Fuzzy Syst. 25, 1417–1429. doi: 10.1109/TFUZZ.2016.2639565

CrossRef Full Text | Google Scholar

Siuly, S., and Li, Y. (2015). Designing a robust feature extraction method based on optimum allocation and principal component analysis for epileptic EEG signal classification. Comput. Methods Prog. Biomed. 119, 29–42. doi: 10.1016/j.cmpb.2015.01.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Sreej, S. R., and Samanta, D. (2019). Classification of multiclass motor imagery EEG signal using sparsity approach. Neurocomputing 368, 133–145. doi: 10.1016/j.neucom.2019.08.037

CrossRef Full Text | Google Scholar

Takagi, T., and Sugeno, M. (1985). Fuzzy identification of systems and its application to modeling and control,. Trans. Syst. Man Cybernet. 15, 116–132. doi: 10.1109/TSMC.1985.6313399

CrossRef Full Text | Google Scholar

Truong, N. D., Nguyen, A., Kuhlmann, D. L., Bonyadi, M. R., Yang, J. W., Ippolito, S., et al. (2018). Integer convolutional neural network for seizure detection. IEEE J. Emerg. Select. Top. Circuits Syst. 8, 849–857. doi: 10.1109/JETCAS.2018.2842761

CrossRef Full Text | Google Scholar

Tzallas, A. T., Tsipouras, M. G., and Fotiadis, I. D. (2009). Epileptic seizure detection in EEGs using time-frequency analysis. IEEE Trans. Inform. Technol. Biomed. 13, 703–710. doi: 10.1109/TITB.2009.2017939

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, T., and Zhang, Z. (2017). Effective and extensible feature extraction method using genetic algorithm-based frequency-domain feature search for epileptic EEG multiclassification. Medicine 96:e6879. doi: 10.1097/MD.0000000000006879

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, K., Ni, T., Yin, H., and Chen, B. (2020). Cross-domain classification model with knowledge utilization maximization for recognition of epileptic EEG signals. IEEE/ACM Trans. Comput. Biol. Bioinformatics. doi: 10.1109/TCBB.2020.2973978. [Epub ahead of print].

PubMed Abstract | CrossRef Full Text | Google Scholar