- 1Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA, United States
- 2Department of Aeronautics and Astronautics, Stanford University, Stanford, CA, United States
The demand for advanced air mobility (AAM) operations is expected to be at a much larger scale than conventional aviation. Additionally, AAM flight operators are likely to compete in providing a range of on-demand services in congested airspaces, with varying operational costs. These characteristics motivate the need for the development of new traffic management algorithms for advanced air mobility. In this paper, we explore the use of traffic management protocols (“rules-of-the-road” for airspace access) to enable efficient and fair operations. First, we show that it is possible to avoid gridlock and improve efficiency by leveraging the concepts of cycle detection and backpressure. We then develop a cost-aware traffic management protocol based on the second-price auction. Using simulations of representative advanced air mobility scenarios, we demonstrate that our traffic management protocols can help balance efficiency and fairness, in both the operational and the economic contexts.
1 Introduction
As advanced air mobility (AAM) applications—including urban air mobility (UAM) and unmanned aircraft systems (UAS)—become more widespread, the skies will become more crowded. It is expected that the number of AAM operations will far exceed that of conventional aviation operations (Balakrishnan et al., 2018; Booz Allen, 2018; Crown Consulting, 2018). The predicted demand for AAM services has motivated large investments in drones and electric-powered Vertical Takeoff and Landing (eVTOL) aircraft (Drone Industry Insights, 2021; Karp, 2022). While the focus of research and development efforts have been on the vehicles themselves, there has been limited attention paid to the questions of how these large numbers of vehicles will operate collectively, and how the traffic will be managed. Although AAM aircraft will operate a diverse range of missions, we expect that the desired trajectories will strain limited airspace resources, leading to congestion. The consequence will be delays, namely, flights not being able to fly their desired routes at the desired times. Efficient traffic management should minimize such vehicle delays.
Conventional air traffic management (ATM) primarily involves actions taken by the air navigation service provider (ANSP) to mitigate congestion, namely, demand-capacity imbalances. However, operational concepts assume that ANSPs will not be responsible for providing traffic management services to AAM aircraft (Federal Aviation Administration, 2020; EUROCONTROL, 2022). Furthermore, in contrast to the centralized architecture of current ATM, traffic management services for AAM are expected to be provided by a federated network of service providers (Federal Aviation Administration, 2020). This shift in the service provider architecture necessitates the development of new decentralized approaches to traffic management.
Centralized optimization approaches to air traffic flow management assume that a central entity has complete knowledge of proposed flight trajectories in full. This assumption may not hold for AAM applications, where demand is expected to be more dynamic. While airline schedules are published months in advance and flight plans filed hours before scheduled departure, AAM demand may be known even to flight operators only minutes in advance. For applications like ridesharing or delivery services, the origins and destinations may also be dynamic in nature. AAM flight operators may hesitate to share trajectories in advance, as they may reveal information (e.g., areas of high demand for an air taxi company) that competitors can exploit. Even if willing to share it, AAM flight operators may not be able to reliably share trajectory information, since it can change as new customers materialize. Finally, mathematical formulations of centralized optimization approaches often scale poorly to large problem instances such as high-demand AAM scenarios (Bertsimas and Patterson, 1998).
While the above factors may suggest that the solution is to rely purely on tactical self-separation between aircraft for safety, such an approach can lead to a significant loss in efficiency, and even gridlock when traffic density is high. When aircraft perform tactical self-separation, further conflicts could arise. Therefore, we consider traffic management protocols that preserve operator privacy, while providing enough structure to mitigate efficiency loss. This approach is similar to how congestion is managed on road networks, where vehicles have freedom of route and destination, but must comply with general regulations (e.g., posted signs) and traffic lights.
In this work, we explore a decentralized congestion management protocol. In addition to being scalable, we design our protocols to preserve operator privacy by minimizing the amount of information shared. We propose a protocol with a prioritization scheme that tries to meet the following goals.
• Accommodate frequent re-planning: Many AAM applications are on-demand, so we want to allow for frequent re-planning of flight trajectories and destinations.
• Limited information-sharing: We want to preserve operator privacy and flexibility. Thus, we limit the amount of information shared, and the number of parties that information is shared with. Specifically, in each time step, operators only need to share their current sector position and the next sector that they want to proceed to in the next time step. In addition, operators do not need to broadcast their information to a central agent and only need to communicate with their current sector and desired next sector.
• Fairness and efficiency: We expect a large number of AAM operators competing to provide different types of services, so it is important that they are treated fairly. While there are many definitions for fairness, we use the standard deviation of delays as a metric of fairness in this paper.
• Cost-aware: Flights will likely have different delay costs which need to be accounted for while managing traffic. We do so by incorporating auctions as an optional prioritization mechanism. This allows operators to indicate or signal how much they value a flight, without revealing sensitive information like its payload, full trajectory, or destination.
In this paper, we build on our prior work on traffic management protocols and cost-aware prioritization schemes for AAM (Chin et al., 2021a; Qin and Balakrishnan, 2022). We design, analyze, and demonstrate through simulations, a congestion management protocol for AAM with the following characteristics.
1. Avoiding gridlock: We use the current sector position and desired next sector position of aircraft to create a directed graph. We identify “cycles” of aircraft, which are closed loops on the graph, and represent groups of aircraft where either all of them can proceed to their desired next sector, or none of them can. In Section 4.1, we show how to identify and prioritize cycles to avoid gridlock, even with limited information sharing.
2. Efficient sector deconfliction: When the number of incoming aircraft exceeds sector capacity, a sector needs to be “deconflicted”, where the sector decides which aircraft to prioritize and give permission to enter1. There may be multiple sectors that need to be deconflicted. Suboptimal ordering of sector deconfliction could result in conflicting control actions, making the order in which sectors are deconflicted important. In Section 4.2, we use a “backpressure” metric (which measures the length of the maximum incoming queue of aircraft) to decide the order in which sectors should be deconflicted. This allows the decentralized protocol to avoid assigning conflicting control actions.
3. Balancing efficiency, fairness, and operator privacy: We design a flexible protocol that can incorporate different prioritization schemes. We show that one of these prioritization schemes (backpressure) results in a minimum delay solution, for one time step. We also promote operator privacy by minimizing the amount of information sharing required.
4. Chained flight auctions: We propose a method for building flight bids and running an auction for conflicts across multiple intersections.
5. Cost-aware congestion management: We show how to account for variable operating costs, which allows us to achieve better economic efficiency.
The remainder of the paper is organized as follows. Section 2 describes the state-of-the-art and related works. Section 3 presents our problem setup and assumptions. Section 4 describes the proposed congestion management protocol. Section 5 discusses cost-neutral prioritization methods for our protocol, categorized into sector-based prioritization (Section 5.1) and aircraft-based prioritization (Section 5.2). Cost-aware prioritization methods are presented in Section 6. Section 7 presents the performance of our protocol and prioritization methods in a range of simulated AAM demand scenarios.
2 Related works
Most prior work on conventional air traffic management has focused on centralized approaches. Early work considered a single airport facing an arrival demand-capacity imbalance, and determined ground delays at the origin airport (Richetta and Odoni, 1993). The air traffic flow management problem (ATFMP), first formalized by Odoni, incorporated en route delays (i.e., considered reroutes due to reduced en route sector capacities (Bertsimas and Patterson, 1998). State-of-the-art distributed optimization approaches have been developed to solve large-scale instances of the ATFMP (Balakrishnan and Chandran, 2017). In addition to the above efforts that focused on efficiency, fairness has also been considered in the context of air traffic flows. In particular, researchers have considered the tradeooffs between efficiency and fairness, for different definitions of fairness (Bertsimas et al., 2012 and Bertsimas and Gupta, 2016). Prior work has extended these ideas to a centralized AAM setting, incorporating fairness and dynamic demands with re-planning (Chin et al., 2021b; 2022).
The proposed AAM architecture is a federated one, in which multiple service suppliers provide traffic management services through coordination (Kopardekar et al., 2016). Such coordination can be facilitated by a protocol for resource allocation. Congestion control protocols have been studied in several contexts, including communication networks (Low et al., 2002), surface transportation (Atta et al., 2018), and air traffic management (Khadilkar and Balakrishnan, 2014). Solution approaches proposed range from queue-length management protocols (Eryilmaz and Srikant, 2007) to dynamic traffic routing, demand management (Badrinath and Balakrishnan, 2022), backpressure algorithms (Gregoire et al., 2014; Sun and Yin, 2018), and optimal network flow management (Bertsimas and Patterson, 1998; Levin and Rey, 2017). Fair congestion control has been studied in the context of routing packets in communication networks (Lu et al., 1999). The simplifying assumptions typically made, such as infinite buffers at congested resources or high traffic volumes that can be approximated as fluid flows, are rarely satisfied in air traffic networks, be they conventional aviation or AAM. As a result, fairness in air traffic management has generally been evaluated either through first-come-first-served simulations (Evans et al., 2020) or in centralized settings with full information sharing (Bertsimas and Gupta, 2015; Chin et al., 2021b). By contrast, our congestion management protocol explicitly incorporates fairness preferences (Chin et al., 2021a). Other work has proposed protocols for air traffic management, including rules-of-the-road style protocols (Hwang et al., 2007), Markov decision process models (Ong and Kochenderfer, 2017), and speed control algorithms (Cruck and Lygeros, 2007). We incorporate fairness, reduced information sharing, and cost-aware prioritization schemes into this class of algorithms that have historically focused only on safety and efficiency.
Market-based approaches have been studied for strategic demand management and tactical deconfliction in the aviation context, including airport slot auctions (Ball et al., 2005), slot trading during Ground Delay Programs (Vossen and Ball, 2006), and mobility permits for airspace sector access (Corolli et al., 2014). More recently, there have proposals to consider auctions and other market-based mechanisms for AAM airspace use (Skorup, 2019; Seuken et al., 2021). While auctions have been a controversial topic in conventional aviation, especially in the United States (Grether et al., 1989), the proposed privatization of AAM service providers (Federal Aviation Administration, 2020) could make market-based mechanisms such as auctions feasible ways of allocating and pricing airspace resources. Auctions for congestion management have been studied primarily for road networks, including for congestion pricing in a downtown area (Teodorović et al., 2008) and for managing autonomous traffic in an intersection (Vasirani and Ossowski, 2012). The latter idea was extended to account for bids from chains of cars with a proportional payment mechanism, along with a “wallet” that controls how cars bid as they traverse their trajectory (Carlino et al., 2013).
3 Problem setup
We discretize space into a set of sectors
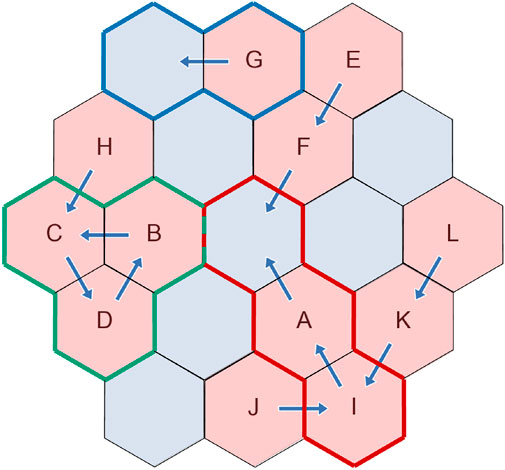
FIGURE 1. Grid setup for our protocol. Each red filled hexagon represents an occupied sector. The base of each arrow indicates the current sector occupied by an aircraft, while the head represents the desired next sector.
We make a few observations about this problem setup. First, if there is a sector into which only one aircraft wants to enter, then the optimal—and trivial—solution would be to set del(i, t) = 0 for that aircraft. Aircraft G and the blue bounded sectors in Figure 1 show an example of this. Second, in the scenario described by the green bounded sectors in Figure 1, we notice that aircraft C, B and D form a “cycle”. This means that either all of them are allowed to move, or none of them can. Furthermore, there is no feasible way in which any additional aircraft attempting to access the sectors occupied by the cycle (e.g., aircraft H) can be allowed to do so while the cycle exists, because of capacity constraints. Third, the red bounded sectors highlight a scenario in which there are multiple “connected” sectors where aircraft need to be deconflicted. A deconfliction decision at one of these sectors can have cascading effects on the decisions for the other sectors, so the order in which sectors are deconflicted is important.
3.1 Information-sharing constraints
In each time-step, each aircraft i occupies a sector x(i, t), which we call its current sector. Each aircraft i also has a desired next sector
Thus, we restrict our information sharing as follows. We require that each aircraft i conveys its intent to use sector
4 Protocol
Algorithm 1. Congestion-management protocol (x,
1:
2:
3:
4:
5:
6:
7:
8: B ←CalculateBackpressure
9: Sort
10: for
11:
12:
13: if
14: if
15:
16: else
17: while
18: p ← Prioritizeaircraft
19:
20:
21: end while
22: end if
23: end if
24:
25:
26: end for
27: return
We now present the framework for our congestion management protocol, which is run at every time-step. Figure 1 shows an example aircraft configuration for a time-step. Each arrow represents an aircraft: the tails represent their current sector x(i, t) and their heads represent their desired next sector
We divide our protocol into six steps, with references to the appropriate line numbers in Algorithm 1. Steps 1–3 are completed at the beginning of every time-step, and Steps 4–6 are performed for each sector with a conflict.
1. Initialization (Lines 1–3). We initialize two lists, a hold list
2. Identify and prioritize cycles (Lines 4–7). Cycles need to be identified and prioritized as soon as they appear. Until a cycle is cleared, it will block all sectors that it occupies. We identify aircraft in cycles
3. Compute sector prioritization (Lines 8–9). Now that the cycles for this time-step have been resolved, we need to decide the order in which to deconflict sectors. We calculate the backpressure at each sector and deconflict the sectors in decreasing order of backpressure. This ensures that the protocol never forces an aircraft to vacate a sector. We will formalize the notion of backpressure in Section 4.2, which provides a measure of the queue build-up incident on a sector.
4. Loop through sectors (Lines 10–12). Based on the sector order determined in step 3, we complete steps four to six for each sector. For the highest priority sector yet to be deconflicted, we split the aircraft that want to utilize this sector in the next time-step into two categories: undecided aircraft
5. Now, one of the two scenarios will occur:
a) Case of capacity exceeds demand (Lines 14–15). If the sector capacity is sufficiently high to allow all inbound traffic, then we add
b) Case of demand exceeds capacity (Lines 16–20). If there is insufficient capacity to allow all aircraft, then we use one of several prioritization schemes to choose which aircraft gets to proceed. These prioritization schemes can be sector-based or aircraft-based and are described in detail in Sections 5.1 and 5.2. Aircraft that are allowed to proceed are removed from
6. Delay all unassigned aircraft (Lines 24-25). If capacity is fully used and there are still aircraft in
4.1 Identifying cycles
After initialization, we identify and prioritize cycles first. The goal of this algorithm is for sectors to identify aircraft incoming into it that are in cycles under our limited information-sharing constraints. We use an adapted Rocha-Thatte cycle detection distributed algorithm (Rocha and Thatte, 2015). We have a finite directed graph
In each round, each sector s passes a message to its out-neighbors. That is, messages are passed along the edges E, between sectors. In the first round, this message contains the incoming aircraft into s,
Consider the example cycle of aircraft B, C, and D shown in Figure 2 (on the left, with sectors marked by dashed lines). Aircraft B in the red sector wants to proceed to the blue sector occupied by C. In the first round, the blue sector sends the identity (but not position) of B to the black sector (its in-neighbor) and receives the identity of Aircraft D from the red sector. In the next round, the blue sector sends a message of B, D to the black sector. Once the blue sector contains a message with aircraft B in it, it knows that B is part of a cycle and can prioritize it. Using Rocha-Thatte, sectors cannot extrapolate the precise location of aircraft in cycles longer than 3 aircraft.
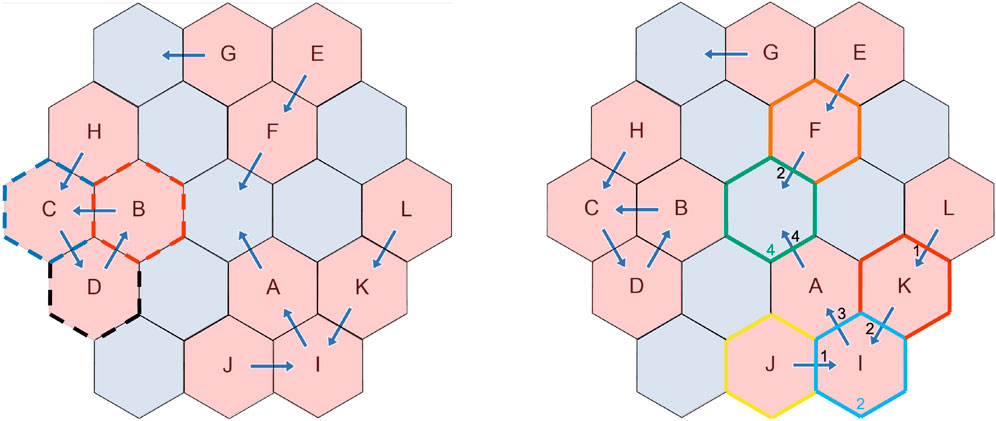
FIGURE 2. Examples of aircraft cycles referenced by Section 4.1 (left) and backpressure prioritization for conflict resolution referenced by Section 4.2 (right).
4.2 Calculating backpressure
After all cycles have been advanced, we use backpressure to determine the order in which to deconflict remaining sectors
We compute backpressure on all sectors not involved with a cycle, using a similar form of logic from Gregoire et al. (2014). The backpressure at each sector is equal to the maximum number of aircraft that could proceed if the sector allowed an aircraft to enter. To determine its backpressure, each sector needs to collect backpressure values from its in-neighbors. First, each sector s requests a backpressure value bq from all its in-neighbors
5 Prioritization schemes
When demand exceeds available capacity, the protocol decides which aircraft to allow to proceed using a prioritization scheme (Step 5b of the protocol). There are many potential prioritization schemes. We present several cost-agnostic prioritization schemes in this section; cost-aware prioritization schemes are shown in Section 6. We divide the cost-agnostic prioritization schemes into two categories: sector-based and aircraft-based. Sector-based prioritizations depend on the sectors that aircraft come from, whereas aircraft-based prioritizations depend on individual aircraft metrics. We could also consider operators that operate multiple aircraft. Operator-based prioritization schemes, which leverage operator-level metrics across multiple aircraft rather than individual aircraft metrics, are covered in Chin et al. (2021a).
5.1 Sector-based prioritizations
Random: With random prioritization, when there are aircraft coming from multiple sectors that want to access a sector, we choose the sector from which to accept an aircraft at random. We expect this prioritization method to perform poorly, but it serves as a useful baseline.
Round robin: With round-robin prioritization, we pre-define an adjacent sector priority order. For example, an interior sector has six adjacent sectors that we will label 1 through 6 starting from the top moving clockwise. A pre-defined priority order could be organized, where aircraft from a lower numbered sector get priority. If there is an aircraft coming from 1, it will be prioritized. But if there is no aircraft coming from 1, we prioritize the aircraft coming from 2 (if it exists), and so on. Once a sector has been prioritized, it moves to the back of the order. This mimics how stop-signs govern intersections on road traffic networks. The intent of round-robin prioritization is to treat adjacent sectors equally.
Backpressure: In Section 4.2, we showed how backpressure is calculated and used for determining the order in which sectors are deconflicted. We can also use backpressure as a prioritization mechanism. Specifically, a sector can prioritize aircraft coming from the adjacent sector with the highest backpressure. This allows the maximum possible number of aircraft to proceed. Note that it is possible for multiple adjacent sectors to have the same backpressure value. In that case, we break ties using round robin then randomly between the sectors that share the highest backpressure value. In Supplementary Appendix SA1, we prove that backpressure prioritization is optimal (i.e., results in minimal aircraft delay) in one time step, under unit sector capacity conditions.
5.2 Aircraft-based prioritizations
Accrued Delay: As aircraft travel toward their destination, they accrue delay over time. Accrued delay of a aircraft represents its cumulative delay up to a given time-step (Idris et al., 2019). Accrued delay prioritization orders aircraft based on their accrued delay, in descending order. The goal is to minimize additional delay for aircraft that have already been delayed.
Reversals: Each aircraft has a nominal schedule of when it will reach its destination and each en route sector. A reversal occurs when the relative scheduling order at a sector is not preserved (Bertsimas and Gupta, 2016). For example, if aircraft A was originally scheduled to arrive at a resource before aircraft B, but instead aircraft B arrives before A, we count this as one reversal for A (and zero for B, since it benefited). To determine whether a reversal occurred, aircraft need to communicate the original time that they intended to utilize a sector. Recall that we assume that aircraft are truthful, including when they report values, such as reversals, used for prioritization. Each aircraft keeps track of how many reversals it has experienced so far along its trajectory at previous sectors. We prioritize aircraft that have experienced more reversals.
6 Cost-aware prioritization schemes
In this section, we consider cost-aware prioritization schemes for aircraft. Aircraft have varying levels of need and urgency, and a corresponding cost of delays. These delay costs vary due to many different factors, such as environmental concerns, societal factors, operating costs, or others. For example, an aircraft carrying passengers may have a higher value of time than a single delivery drone, while a medical delivery could be more urgent than both. However, these factors cannot be expressed by agents using the previously-developed prioritization methods in Section 5.
To give agents more flexibility in expressing delay costs, we implement cost-aware prioritization methods. There are several properties we desire of the resulting methods.
1. Economic Efficiency: The sum of delay costs should be minimized and weighted throughput of aircraft should be maximized throughout the system.
2. Ex post rationality: Aircraft should rationally want to participate in the system, and the mechanism should never make an aircraft worse off (i.e., the operator should not pay more than their value of a timestep of delay).
3. Fairness: Costs of delay incurred should be evenly spread across aircraft in the system. In this section, we aim for the fair distribution of costs, instead of solely delay.
We use modified versions of the second price auction, which satisfies the first two properties (Shoham and Leyton-Brown, 2008) and gives a basis for exploring the third. The second price auction, also known as the Vickrey-Clarke-Groves mechanism, is a well-known result from game theory that distributes a good (in our case, an airspace sector) in the most efficient way. Second price mechanisms select the winner of the auction as the player with the highest bid, but the price paid by the winner is the second-highest bid. This ensures truthful reporting of player valuations in the bid and mechanism efficiency (the highest valuation actually wins), while also being budget-balanced.
To extend auctions to consider aircraft across multiple intersections, we also introduce the concept of proportional payment within the second price auction (Vasirani and Ossowski, 2012; Carlino et al., 2013). While previous work focused only on considering a single intersection, we combine the auction mechanism with backpressure to develop efficient prioritization methods that address flight delay costs for all aircraft in a subproblem.
6.1 Notation and setup
To incorporate cost-aware methods, we introduce some more notation to describe chains of aircraft and auction mechanisms.
In addition to each aircraft announcing a current sector x(i, t) and a desired next sector
We define a chain of m aircraft as a set L = {k1, k2, …, km}, kj ∈ V centered on the contested sector s, where
We define a valuation function
Each prioritization method will be treated as a mechanism with two parts: a choice mechanism χ(L): L → L that determines the chain of aircraft that will proceed, and a payment mechanism
For example, in Figure 3, there are 4 chains of different color: Lorange = {A}, Lpurple = {C, G}, Lbrown = {B, D}, and Lblue = {B, E, F}. The set L = {Lorange, Lpurple, Lbrown, Lblue} is the set of all chains; L/B would remove the aircraft B from both the brown and blue chains.
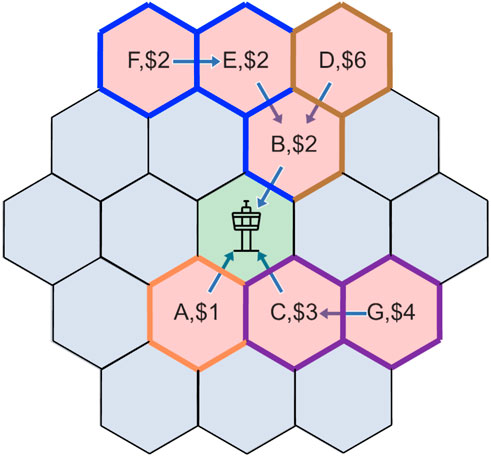
FIGURE 3. Example scenario for cost-aware prioritization. The central sector of conflict is the green sector, with the highest backpressure, contested by 3 aircraft (A–C) and 4 chains of aircraft (orange, purple, blue, and brown).
6.2 Second price
We first consider the simple case of the second-price mechanism that ignores backpressure, where we only consider the aircraft adjacent to the contested sector. We give χ and ρ truncated chains of length one. For contested sector s, let
The choice function selects the winning chain by examining the bids from the first aircraft in each chain (the aircraft adjacent to the contested sector) and choosing the highest bid as the winner. The payment function then selects the second highest price as the winner’s payment, while all other aircraft pay nothing (for losing aircraft k, the outcome from χ(X/k) and χ(X) is the same). This can also be seen as a method of prioritizing between chains of length 1, ignoring any backpressure or bids beyond the first aircraft. Note that the mechanism is considering X, instead of the set of chains L, similar to how round-robin or random prioritization methods might operate. Only one aircraft will advance when we run this mechanism, and later conflicts will be resolved by using the mechanism for lower backpressure sectors.
In Figure 4, the set of agents considered would be X = {A, B, C}. Aircraft C has the highest bid, so it advances. During the same time-step, aircraft G would advance as the protocol proceeded to deconflict lower backpressure sectors. Aircraft C pays the price of the second highest bid, which is $2 from aircraft B.
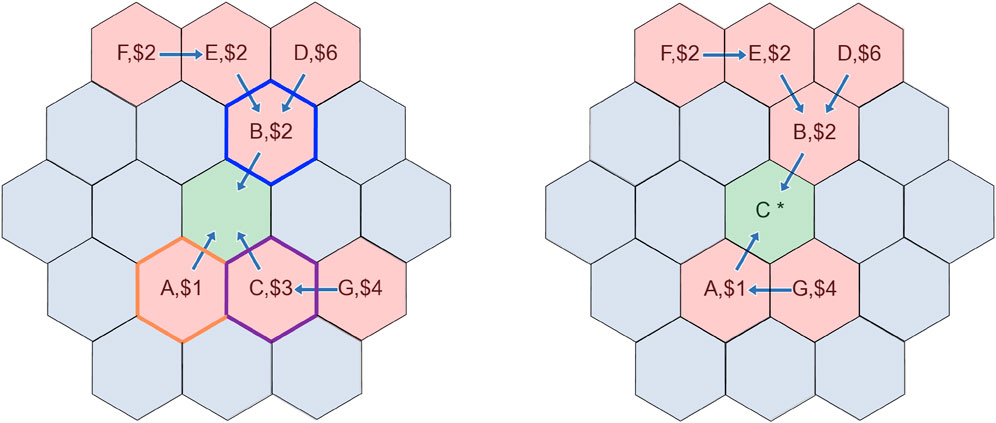
FIGURE 4. Before (left) and after (right) using the second price prioritization method, for the green sector marked. Aircraft C proceeds and has a payment of $2.
The above mechanism is straightforward, and maintains many of the positive traits of the VCG mechanism (including efficiency and truthfulness, among others). However, this ignores potentially serious delays incurred by aircraft not adjacent to the contested sector. In our previous example for instance, not selecting aircraft B also delays aircraft D, E, F, which together incur a very large delay cost. This motivates the following prioritization mechanism, which accounts for weighted backpressure and proportionally distributes costs along the winning chain.
6.3 Second backpressure
When we have multiple contests in a subproblem, the resolution of the highest backpressure sector has important implications for which subcontests must be resolved next. If we resolve sectors in a sequential manner, this could lead to inefficiencies as less efficient chains of aircraft are moved forward. For example, in Figure 4, if we resolve the central conflict at the green sector first, we may make a suboptimal decision, e.g., moving aircraft C when there are higher cost chains of aircraft. A more efficient mechanism would account for information from a broader set of aircraft to find the best solution for the entire subproblem.
In this section, we develop the second backpressure prioritization method, which accounts for the preferences of aircraft not immediately adjacent to the contested sector. We do this by adapting the backpressure prioritization method for agent bids—instead of the length of the chain, we consider the total sum of bids from aircraft along that chain. Second backpressure is one-step optimal with respect to agent bids (instead of to agents like in backpressure). To handle chains of aircraft together, we use proportional payment from Carlino et al. (2013). Proportional payment divides the cost charged to a group of agents proportionally to each agent based the fraction of their bid to the total bid of the group. For example, if an agent bid $3, and the total group bid was $8, then that agent would pay 3/8 of the cost to the group. This method allows chains to collectively bid together and then distribute the cost among its agents. We illustrate how subconflicts are also simultaneously resolved using the second backpressure method by creating distinct chains that may share aircraft.
We implement the mechanism as follows: for conflict s, let the list of chains originating at s be L = {L1, …, Lr}. Then:
There are three parts to this mechanism. First, our choice mechanism is χ(L), which selects the chain with the highest sum of bids (what we will call the chain bid). Next, the payment that the chain as a whole (ρi(L)) must make is the second highest chain bid. Finally, the payment is divided among aircraft in the winning chain using proportional payment (ρk(L), losing chains i have ρi(L) = 0). Proportional payment ensures that aircraft that bid more (and thus indicated greater need) are responsible for a greater share of the payment needed. In practice, the method does the following.
1. The central sector under conflict collects a list of all chains L and their bids
2. The central sector returns χ(L) and ρk(L), which is then disseminated back down the winning chain. In a real implementation, payments can be done through reporting to a centralized third-party handling payment transfers. We for now abstract away the information-sharing constraints.
3. Aircraft in the winning chain advance at the next time-step.
In Figure 5, we consider the sum of bids from the four chains in our example. The brown chain of {B, D} has the highest sum total bid of 8, with the second highest price of 7 coming from the purple chain. Thus, aircraft B pays a total of ρB = 7*2/8 = 7/4, and aircraft D pays ρD = 7*6/8 = 21/8.
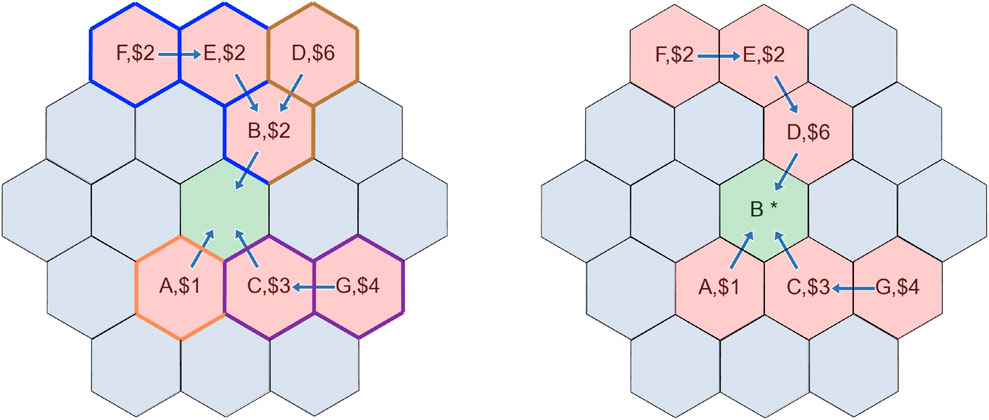
FIGURE 5. Before (left) and after (right) using the second backpressure prioritization method, for the green sector marked. We define 4 chains - orange, purple, brown and blue. The highest chain bid comes from brown, and aircraft B and D move forward with a payment of 7/4 and 21/8 respectively.
In Supplementary Appendix SA2, we show that second backpressure prioritization results in minimum weighted delay in one time step, under unit sector capacity conditions. The second backpressure method selects the most efficient chain of aircraft to proceed in a conflict, but it is not incentive compatible. Aircraft are able to achieve better outcomes for themselves by bidding untruthfully at values
7 Results
In this section, we demonstrate our protocol and prioritization methods on four simulated traffic scenarios. We compare the different prioritization methods shown in Sections 5, 6 on two main metrics: average delay μ (with the goal of minimizing delay) and standard deviation of delay σ across aircraft (with the goal of fairly distributing delay), in both unweighted forms
7.1 Scenarios
In each scenario, we utilize the hex grid setup shown in our examples. Each hex cell s in simulation consists of two sectors: a ground sector that aircraft depart from or land to and an airspace sector connected to all airspace sectors around it. We assume that there is one layer of airborne sectors (i.e., no vertical separation possibilities), but multiple layers could be explored in the future. We use a 7-radius (169 sector) hex grid for simulation. At time t, the protocol accepts requests bids from aircraft for sectors, then determines and gives approval to winners to enter their requested sector at time t + 1. Aircraft begin on the “ground”, and request access to the sector directly above their origin location. Once they receive approval, they move into the “air” and proceed to their destination sector. Aircraft “finish” their trajectory at the end of time-step tf, which is when they enter their destination sector (a ground sector). At tf + 1, the destination sector is available for other aircraft to use.
Trajectories are assumed to be the shortest path between origin and destination, determined by the hex cells intercepted by a straight line from the origin to destination sector. Each aircraft takes one time-step to traverse one sector. Aircraft are initialized with a random cost of travel p(x) between the integers [1, 10) in every scenario, used for cost-aware prioritization.
We demonstrate our protocol and simulation on 4 scenarios, with varying characteristics in the numbers of aircraft, the origin/destination locations, and the flight schedules.
1. Random: 124 aircraft travel across a radius 7 grid (169 cells). Origin and destination points are randomly and uniformly drawn across all hex cells in the grid, and departure times are uniformly drawn from between 0 and 50. This serves as a baseline example of the protocol and prioritization methods in action.
2. Bimodal: 126 aircraft travel across the same radius 7 grid. Origin and destination sectors are determined by assigning every sector a probability in [0, 1), with all probabilities summing to 1. Aircraft departure times were drawn between t = [0, 50], with
3. Crossing: The cross-flow scenario studies how the protocol and prioritization methods handle a heavy amount of traffic through central sectors. 3 “operators” each send aircraft from 4 origins along the top of the grid to 4 possible destinations on the opposite side. This creates a large amount of traffic in the central sectors, where many aircraft intersect. Departure times were generated using the above method from the bimodal scenario. 30, 40, and 30 aircraft were sent respectively from the top left, top, and top right sides towards the opposite sides of the grid.
4. Hub and Spoke: This scenario represents a package delivery system, where aircraft originate on the outskirts of the grid and move to destinations across the whole grid. Six “warehouses” on each corner of the grid send out 25 flights each. The start times are determined by a discrete Poisson process with μ = 2, and destinations are randomly and uniformly drawn from all hex cells in the grid.
The results are presented in Figure 6, averaged over 100 samples for each scenario. To measure efficiency and fairness for prioritization methods, we plot total delay (where less is more efficient) and standard deviation of delay across flights in that scenario (where less is more fair). These metrics can be measured in an unweighted form, where each aircraft is treated the same, or a weighted form, where the delay for each aircraft is normalized by the aircraft’s variable cost. We expect that cost-aware prioritization methods should perform less efficiently on unweighted metrics, and more efficiently for weighted metrics.
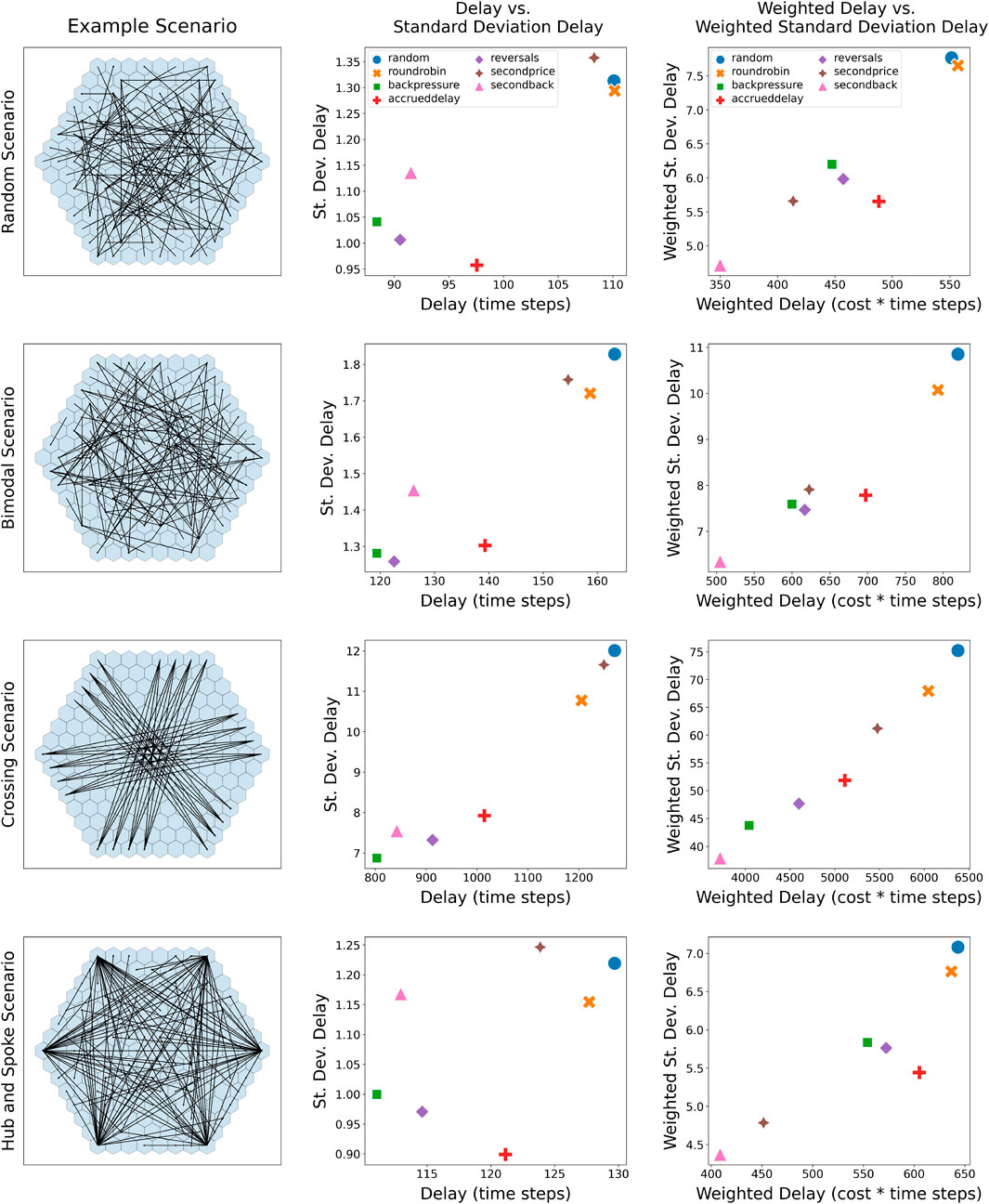
FIGURE 6. Simulation results of the protocol with all prioritization methods. Each scenario is in one row, with system metrics in columns 2 and 3.
7.2 Discussion
We first note that scenarios with more interactions between aircraft have higher delays and standard deviations of delay. This is most pronounced with the crossing scenario, which has the highest delays due to the congestion in the central hex grids. Among the cost-agnostic prioritization methods, random performs the worst, in terms of both delay and standard deviation. roundrobin performs slightly better than random in most cases. The three other cost-agnostic prioritization methods (Backpressure, accrueddelay, and reversals) have between 7% and 35% lower delay and 15%–37% lower standard deviation than these naive baselines. Backpressure consistently has the lowest delays, which makes sense given that it leads to minimal delay in one time-step. Backpressure also performs well in terms of standard deviation. Reversals and accrueddelay result in higher delay than backpressure, but sometimes have lower standard deviation (e.g., random and hub and spoke scenarios).
For the cost-aware prioritization methods, we can see that while secondback slightly underperforms backpressure in both raw delay and standard deviation of delay, it outperforms backpressure in both metrics after weighting by the variable cost of each aircraft. This makes sense because backpressure has been shown to be optimal in the unweighted case in Chin et al. (2021a), but its cost-agnostic approach leads it to suffer after weighting by variable costs. Secondprice is clustered with the other protocols methods as it ignores backpressure, but it outperforms the roundrobin and random protocols after weighting. This shows that adding second-price considerations to the prioritization protocol improves economic efficiency. Notably, secondback and secondprice compared to backpressure have high raw standard deviation of delay for the hub-and-spoke scenario (e.g., warehousing and delivery services), but much lower weighted standard deviation of delay.
Additional sensitivity analysis was done to study the sensitivity of our protocol and prioritization methods to different congestion levels, by varying the ratio of aircraft in a scenario to sectors. These results are presented in Supplementary Appendix SA3.
8 Conclusion
We have shown that a single time-step protocol for AAM congestion management can help preserve operator privacy and flexibility. To this end, we developed a congestion management protocol that avoids gridlock by identifying cycles, and deconflicting sectors in order of highest backpressure. The proposed protocol balances efficiency and fairness, and can accommodate different prioritization schemes. We explored cost-agnostic and cost-aware prioritization methods. We showed that backpressure and secondback prioritization are one time-step optimal in terms of delay and weighted delay, respectively. We also studied other prioritization schemes in simulation, and showed that our protocol balances efficiency and fairness, depending on the choice of prioritization scheme.
There are several interesting directions for further investigation. The protocol could be extended to accommodate sector capacities greater than one, and heterogeneous sector capacities could be explored. We are also interested in the interaction between optimization-based methods and our protocol, across different airspaces. Specifically, within certain regions of airspace (perhaps controlled by a single UAS service supplier), full information sharing may be possible, allowing for centralized optimization. However, protocols may be needed to coordinate hand-offs between these blocks of airspace controlled by different service suppliers. Our protocol focused on deconflicting one time-step at a time; it is worth considering extensions to handle multiple time-steps and partial trajectory information.
While the second-price auction is simple and powerful, alternative mechanisms can provide attractive properties such as truthfulness, or account for collusion (which can represent a scenario in which an operator has multiple flights). A concern with auctions and other monetary transactions is that they may impede airspace access to some users who cannot afford it. These concerns can be mitigated using mechanisms such as karma systems or mixed prioritization methods, and public policy solutions that ensure fair access to all.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. All authors contributed to the article and approved the submitted version.
Funding
The NASA University Leadership Initiative (grants 80NSSC21M0071 and 80NSSC20M0163) provided funds to assist the authors with their research, but this article solely reflects the opinions and conclusions of its authors and not any NASA entity. VQ was additionally supported in part by a Mathworks Fellowship.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpace.2023.1176969/full#supplementary-material
Footnotes
1In this paper, we use the term “deconfliction” to refer to such strategic deconfliction at the strategic level, rather than the tactical self-separation of vehicles.
References
Atta, A., Abbas, S., Khan, M. A., Ahmed, G., and Farooq, U. (2018). An adaptive approach: Smart traffic congestion control system. J. King Saud. University-Computer Inf. Sci. 32, 1012–1019. doi:10.1016/j.jksuci.2018.10.011
Badrinath, S., and Balakrishnan, H. (2022). Robust control of arrivals into a queuing network. IEEE Trans. Intell. Transp. Syst. 23, 4474–4489. doi:10.1109/TITS.2020.3045030
Balakrishnan, H., and Chandran, B. (2017). A distributed framework for traffic flow management in the presence of unmanned aircraft. ATM Seminar.
Balakrishnan, K., Polastre, J., Mooberry, J., Golding, R., and Sachs, P. (2018). Blueprint for the Sky: The roadmap for the safe integration of autonomous aircraft. Tech. rep. Airbus UTM.
Ball, M. O., Donohue, G. L., and Hoffman, K. (2005). “Auctions for the safe, efficient, and equitable allocation of airspace system resources,” in Combinatorial auctions. Editors P. Cramton, Y. Shoham, and R. Steinberg (The MIT Press), 507–538. doi:10.7551/mitpress/9780262033428.003.0021
Bertsimas, D., Farias, V. F., and Trichakis, N. (2012). On the efficiency-fairness trade-off. Manag. Sci. 58, 2234–2250. doi:10.1287/mnsc.1120.1549
Bertsimas, D., Farias, V. F., and Trichakis, N. (2011). The price of fairness. Oper. Res. 59, 17–31. doi:10.1287/opre.1100.0865
Bertsimas, D., and Gupta, S. (2015). Fairness and collaboration in network air traffic flow management: An optimization approach. Transp. Sci. 50, 57–76. doi:10.1287/trsc.2014.0567
Bertsimas, D., and Gupta, S. (2016). Fairness and collaboration in network air traffic flow management: An optimization approach. Transp. Sci. 50, 57–76. doi:10.1287/trsc.2014.0567
Bertsimas, D., and Patterson, S. S. (1998). The air traffic flow management problem with enroute capacities. Oper. Res. 46, 406–422. doi:10.1287/opre.46.3.406
Booz Allen, H. (2018). Urban air mobility (UAM) market survey. Tech. rep. NASA. Available at: Https://ntrs.nasa.gov/citations/20190001472.
Carlino, D., Boyles, S. D., and Stone, P. (2013). Auction-based autonomous intersection management. In 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013 IEEE), 529–534. doi:10.1109/ITSC.2013.6728285
Chin, C., Gopalakrishnan, K., Balakrishnan, H., Egorov, M., and Evans, A. (2022). Efficient and fair traffic flow management for on-demand air mobility. CEAS Aeronaut. J. 13, 359–369. doi:10.1007/s13272-021-00553-3
Chin, C., Gopalakrishnan, K., Balakrishnan, H., Egorov, M., and Evans, A. (2021a). “Protocol-based congestion management for advanced air mobility,” in Fourteenth USA/Europe Air Traffic Management Research and Development Seminar.
Chin, C., Gopalakrishnan, K., Egorov, M., Evans, A., and Balakrishnan, H. (2021b). Efficiency and fairness in unmanned air traffic flow management. IEEE Trans. Intell. Transp. Syst. 22, 5939–5951. doi:10.1109/TITS.2020.3048356
Corolli, L., Bolić, T., Castelli, L., and Rigonat, D. (2014). Tradable mobility permits for the strategic allocation of air traffic, 8.
Crown Consulting (2018). Urban air mobility (UAM) market survey. Tech. rep. NASA. Available at: Https://ntrs.nasa.gov/citations/20190002046.
Cruck, E., and Lygeros, J. (2007). “A mathematical framework for subliminal air traffic control,” in AIAA Guidance, Navigation and Control Conference and Exhibit, 6693.
Drone Industry Insights (2021). Drone Industry Insights. Available at: https://droneii.com/global-companies-invest-in-drones-despite-recession
Eryilmaz, A., and Srikant, R. (2007). Fair resource allocation in wireless networks using queue-length-based scheduling and congestion control. IEEE/ACM Trans. Netw. 15, 1333–1344. doi:10.1109/tnet.2007.897944
EUROCONTROL (2022). U-space ConOps (edition 3.10 U-space capabilities and services to enable Urban Air Mobility. Tech. rep. EUROCONTROL.
Evans, A. D., Egorov, M., and Munn, S. (2020). “Fairness in decentralized strategic deconfliction in UTM,” in AIAA Scitech 2020 Forum, 2203.
Federal Aviation Administration (2020). Urban air mobility (UAM) concept of operations version 1.0. Tech. rep. Washington, DC: Federal Aviation Administration.
Gregoire, J., Qian, X., Frazzoli, E., De La Fortelle, A., and Wongpiromsarn, T. (2014). Capacity-aware backpressure traffic signal control. IEEE Trans. Control Netw. Syst. 2, 164–173. doi:10.1109/tcns.2014.2378871
Grether, D. M., Isaac, R. M., and Plott, C. R. (1989). The allocation of scarce resources: experimental economics and the problem of allocating airport slots. Underground Classics in Economics (Westview Press).
Hwang, I., Kim, J., and Tomlin, C. (2007). Protocol-based conflict resolution for air traffic control. Air Traffic Control Q. 15, 1–34. doi:10.2514/atcq.15.1.1
Idris, H., Chin, C., and Evans, A. D. (2019). “Accrued delay application in trajectory-based operations,” in USA/Europe Air Traffic Management R&D Seminar.
Khadilkar, H., and Balakrishnan, H. (2014). Network congestion control of airport surface operations. J. Guid. Control, Dyn. 37, 933–940. doi:10.2514/1.57850
Kopardekar, P., Rios, J., Prevot, T., Johnson, M., Jung, J., and Robinson, J. E. (2016). “Unmanned aircraft system traffic management (utm) concept of operations,” in AIAA aviation forum.
Levin, M. W., and Rey, D. (2017). Conflict-point formulation of intersection control for autonomous vehicles. Transp. Res. Part C Emerg. Technol. 85, 528–547. doi:10.1016/j.trc.2017.09.025
Low, S. H., Paganini, F., and Doyle, J. C. (2002). Internet congestion control. IEEE control Syst. Mag. 22, 28–43.
Lu, S., Bharghavan, V., and Srikant, R. (1999). Fair scheduling in wireless packet networks. IEEE/ACM Trans. Netw. 7, 473–489. doi:10.1109/90.793003
Ong, H. Y., and Kochenderfer, M. J. (2017). Markov decision process-based distributed conflict resolution for drone air traffic management. J. Guid. Control, Dyn. 40, 69–80. doi:10.2514/1.G001822
Qin, V., and Balakrishnan, H. (2022). “Cost-aware congestion management protocols for advanced air mobility,” in 10th International Conference on Research in Air Transportation.
Richetta, O., and Odoni, A. R. (1993). Solving optimally the static ground-holding policy problem in air traffic control. Transp. Sci. 27, 228–238. doi:10.1287/trsc.27.3.228
Rocha, R. C., and Thatte, B. D. (2015). Distributed cycle detection in large-scale sparse graphs. doi:10.13140/RG.2.1.1233.8640
Seuken, S., Friedrich, P., and Dierks, L. (2021). “Market design for drone traffic management,” in Proceedings of the AAAI Conference on Artificial Intelligence. doi:10.1609/aaai.v36i11.21493
Shoham, Y., and Leyton-Brown, K. (2008). Multiagent systems: Algorithmic, game-theoretic, and logical foundations. Cambridge University Press.
Sun, X., and Yin, Y. (2018). A simulation study on max pressure control of signalized intersections. Transp. Res. Rec. 2672, 117–127. doi:10.1177/0361198118786840
Teodorović, D., Triantis, K., Edara, P., Zhao, Y., and Mladenović, S. (2008). Auction-based congestion pricing. Auction-based Congest. pricing 31, 399–416. doi:10.1080/03081060802335042
Vasirani, M., and Ossowski, S. (2012). A market-inspired approach for intersection management in urban road traffic networks. J. Artif. Intell. Res. 43, 621–659. doi:10.1613/jair.3560
Keywords: advanced air mobility, traffic management, congestion, efficiency, fairness, mechanism design
Citation: Chin C, Qin V, Gopalakrishnan K and Balakrishnan H (2023) Traffic management protocols for advanced air mobility. Front. Aerospace Engineering. 2:1176969. doi: 10.3389/fpace.2023.1176969
Received: 01 March 2023; Accepted: 27 April 2023;
Published: 17 May 2023.
Edited by:
Krishna Kalyanam, National Aeronautics and Space Administration, United StatesReviewed by:
Kaarthik Sundar, Los Alamos National Laboratory (DOE), United StatesPriyank Pradeep, Universities Space Research Association (USRA), United States
Jaewoo Jung, National Aeronautics and Space Administration, United States
Copyright © 2023 Chin, Qin, Gopalakrishnan and Balakrishnan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christopher Chin, Y2h5Y2hpbkBtaXQuZWR1; Victor Qin, dmljdG9ycWlAbWl0LmVkdQ==
†These authors have contributed equally to this work and share first authorship
 Christopher Chin
Christopher Chin Victor Qin
Victor Qin Karthik Gopalakrishnan2
Karthik Gopalakrishnan2 Hamsa Balakrishnan
Hamsa Balakrishnan
