Power Minimization Using Rate Splitting With Statistical CSI in Cloud-Radio Access Networks

Minimizing the power consumption in mobile communication networks while ensuring a minimum quality of service (QoS) for applications is essential in light of the unprecedented expected increase in the number of connected devices and the associated data traffic beyond the fifth generation of wireless networks (B5G). This paper considers a cloud-radio access network (C-RAN) model where a central processor (CP) is connected to the base stations (BSs) via limited capacity fronthaul links. In the context of our C-RAN setting, we consider the practical case where the CP has only statistical knowledge of channel state information (CSI). While conventional wireless systems adopt the treating interference as noise (TIN) strategy to deal with the interference in the network, this paper instead considers that the CP applies the rate splitting (RS) strategy by dividing each user’s message into two parts: a private part to be decoded by the intended user only and a common part to be decoded by a subset of users, for the sole reason of interference mitigation in the network. To best account for the channel estimation errors, this paper addresses the problem of transmit power minimization under minimum QoS constraints on the achievable ergodic rate per user, so as to determine the beamforming vectors of the private and common messages as well as the rate allocated to all the users. The considered problem is of stochastic, complex, and non-convex nature. This paper addresses the problem intricacies through an iterative approach that leverages both the sample average approximation (SAA) technique and the weighted minimum mean squared error (WMMSE) algorithm to obtain a stationary point of the optimization problem in the asymptotic regime. The numerical results demonstrate the gain achieved with the RS strategy as compared to TIN, especially under high QoS requirements.

1 Introduction

The sixth generation (6G) of mobile communication networks is expected to handle unprecedented amount of data traffic stemming from a wide spectrum of applications with the diverse nature of requirements (Saad et al., 2020). To date, traffic growth is driven by content-based applications such as Netflix and YouTube (Ericsson, 2019; Saad et al., 2020). However, with widespread deployment of Internet of things (IoT) systems that aim to connect an enormous number of people and devices, the focus of future 6G networks is limited not only to maximizing the achievable data rates of the users but also to efficiently using the available resources to satisfy the requirements of services requested from the network.

Hence, keeping the power consumption under manageable levels is essential for effective operation of 6G networks and also for reduction of CO2 emissions of information and communication technology (ICT) toward a green ICT industry. From the network architectural perspective, cloud-assisted radio access networks (C-RANs) enable dense networks and spatial reuse by taking advantage of cloud computing technologies to realize software-defined radio (SDR) concepts which can adapt the network resources to current traffic (Yang et al., 2019). Hence, the elasticity of provision of resources helps in optimizing the power consumption in the network while at the same time satisfying the requirements of users and their applications.

In C-RANs, the base stations (BSs) are connected to the central processor (CP) via limited capacity fronthaul links. Using advances of cloud computing technology, the CP centrally processes the user’s data and allows for efficient use of computing and radio resources. Through advanced multicell processing algorithms (Wubben et al., 2014), C-RAN helps in achieving a significant increase in spectral and energy efficiency of the wireless network. In particular, the CP jointly encodes the user’s data and shares the encoded data stream of each user with a subset of BSs. The CP then establishes cooperative transmission schemes among the BSs within each cluster by coordinating the beamforming design.

However, due to the limited fronthaul capacity, the cluster size of cooperating BSs for each data stream is limited. Hence, the interference cannot be removed using coordinated beamforming alone (Gesbert et al., 2010). In non-orthogonal multiple access–based wireless systems, the interference in the network becomes the main limiting factor for achieving a good performance, especially in dense networks (Gesbert et al., 2010).

Most works in the literature, which study multi-antenna systems in general (and C-RANs in particular), adopt treating interference as noise (TIN) as a transmission scheme. In TIN, the receiver ignores the interference resulting from communicating with other receivers and considers it as noise (Shi et al., 2015; Pan et al., 2017a) when decoding its own signals. However, future wireless networks are anticipated to be dense in order to address the challenges of emerging applications requiring massive connectivity under the IoT umbrella (Saad et al., 2020). In this context, it is essential to come up with a new multiple access scheme which accounts for the interference in the network. From the information theoretical perspective, TIN is in general not optimal and can lead to significant degradation of the performance in strong interference regimes (Etkin et al., 2008; Charafeddine et al., 2012). Alternatively, the rate splitting (RS) scheme which is first proposed in the late seventies by Carleial (1978) has been shown to achieve the best known performance in the information theoretical model of two-user interference channel (IC) (Te Han and Kobayashi, 1981; Etkin et al., 2008). Although the two-user IC is a simple model of non-orthogonal multiple access networks, the complete characterization of the capacity of the two-user IC is still an open problem in general.

To reach the full benefits of cooperative transmission strategies and the advanced multicell processing in C-RANs, the majority of works in the literature assume the availability of perfect channel state information at the transmitter (CSIT), an assumption which is rather optimistic and difficult to satisfy in practical systems. The CSI acquisition process in practice is subject to multiple sources of errors. For instance, in frequency-division duplex (FDD) systems, the imperfections in CSI can be due to limited resources in the feedback link (Love et al., 2008). Other sources of CSIT errors may be due to hardware imperfections (Maddah-Ali and Tse, 2010), outdated CSI (Zhang et al., 2009), or simply acquisition of partial CSI only which is reasonable specifically in dense networks to reduce the overhead (Shi et al., 2015; Razaviyayn et al., 2016). Inspired by the ability of the RS strategy to manage the interference in wireless networks, this paper employs a scalable and robust RS scheme in the C-RAN with limited fronthaul capacity links between the CP and the BSs. We study the problem of minimizing the weighted sum of power consumption subject to per-BS fronthaul constraints with minimum quality of service (QoS) guarantees for each user, under the assumption of CSIT imperfections. Next, we discuss the relevant works in the literature.

1.1 Related Work

Minimization of power consumption is an essential target for optimizing the performance of dense communication networks such as the C-RAN. For its importance, the problem of minimizing the network-wide power consumption while ensuring a QoS target for all users has been attracting the interest of research communication in the recent few years. Pan et al. (2017a) studied the problem of network power minimization in a green multiple-input multiple-output (MIMO) C-RAN system. A two-stage algorithm is proposed, where in stage I an admission control procedure is performed to guarantee the feasibility of stage II, which deals with joint precoding and BS selection to minimize the network power consumption. Pan et al. (2017b) studied the problem of joint precoding and user selection to minimize the total power consumption in dense C-RANs with incomplete CSI. Shi et al. (2014) studied the problem of coordinated sparse beamforming design minimizes the power consumption in C-RANs. Xia et al. (2018) investigated a mixed time-scale problem to minimize the network power consumption which includes the computation power at the CP and transmit power at the BSs. A joint transmit power and fronthaul transmission cost minimization problem in a downlink C-RAN with local caches was considered by Tao et al. (2016). Pan et al. (2019) also studied a C-RAN with imperfect CSIT. Pan et al. (2019) investigated a weighted sum-rate maximization problem in C-RANs with imperfect channel state information. They proposed a global optimization algorithm to find the global optimal solution of the problem. Furthermore, a polynomial complexity algorithm based on the WMMSE–rate relationship was proposed, which provides a suboptimal solution to the challenging non-convex problem at a lower computational cost. The numerical simulations show that the performance of the polynomial complexity algorithm is comparable to the performance of the exponential complexity global optimization algorithm.

All the works by Tao et al. (2016), Pan et al. (2017a), and Pan et al. (2017b) assume that the receivers apply the treating interference as noise (TIN) strategy. From an information theoretical perspective, TIN is in general a suboptimal strategy, especially in dense networks as C-RANs (Charafeddine et al., 2012; Gherekhloo et al., 2016). In the early 80s, Carleial (1978) and Te Han and Kobayashi (1981) showed that, for a basic interference channel (IC) which consists of two transmitters and two users, splitting the message of a user into a private part decoded solely by the intended receiver and a common part decoded by both receivers can significantly improve the achievable rates in such a network. The seminal work of Etkin et al. (2008) shows that such a rate splitting (RS) and common message decoding (CMD) strategy achieves to within one bit of the interference channel capacity. The work by Dahrouj and Yu (2011) conveys RS–CMD from the information theory territory and applies it to realistic scenarios. Dahrouj and Yu (2011) considered minimizing the transmit power in multicell networks subject to QoS requirements and adopted RS–CMD. Recently, RS is applied in different scenarios. In addition to TIN and RS, several works in the literature have studied the non-orthogonal multiple access (NOMA) scheme. Gu et al. (2018) investigated the outage probability from a stochastic geometry point of view in a downlink C-RAN assisted with NOMA. Gu et al. (2018) showed the efficiency of NOMA compared to state-of-the-art multiple access schemes in terms of spectral efficiency of the C-RAN and improved fairness among users. In Jaafar et al. (2020), several orthogonal and non-orthogonal multiple access schemes have been reviewed for an aerial network based on wireless communications of unmanned aerial vehicles (UAVs). Nevertheless, Mao et al. (2018) showed that RS generalizes classical linear precoding methods such as TIN and NOMA and can significantly improve the spectral efficiency in the downlink multiple-input single-output broadcast channel (MISO-BC). Recently, many works study the performance of RS techniques in the MISO-BC, and the benefits of such a multiple access scheme have been shown to significantly outperform the classical TIN transmission scheme (Clerckx et al., 2016; Dai et al., 2016; Joudeh and Clerckx, 2016b; Joudeh and Clerckx, 2017; Clerckx et al., 2019; Mao et al., 2019). Rate splitting multiple access (RSMA) in C-RANs has been explored by Yu et al. (2019) and Ahmad et al. (2020b), who considered the compression and data-sharing transmit strategies, respectively. Alameer Ahmad et al. (2019) and Ahmad et al. (2021) considered using RS–CMD in C-RANs to improve the spectral efficiency of the system and assumed perfect and statistical CSIT, respectively. Reifert et al. (2021) explored the problem of max–min fairness in a cache-assisted downlink C-RAN that applies the rate splitting multiple access scheme. In Reifert et al. (2021), we propose a polynomial time algorithm that is based on SAA and WMMSE–rate relationship to tackle the challenging non-convex optimization of the resource allocation problem. However, as opposed to the work by Reifert et al. (2021), the resource allocation problem is not guaranteed to be always feasible as the QoS user’s requirements could not be satisfied if, e.g., the channel state conditions are bad for some users. Hence, for instance, the clustering algorithm proposed by Reifert et al. (2021) does not apply to the problem formulated in this paper.

1.2 Contributions

This paper studies the problem of minimizing the network transmit power while satisfying ergodic QoS constraints. We consider a C-RAN assisted with RS techniques in which the CP only knows the distribution of the wireless channel. The RS design is linear with the number of users and only requires the knowledge of the users’ positions, which makes it scalable and robust against CSI imperfections.

The major contributions of this paper are as follows:

1) Novel problem formulation: We formulate a resource allocation problem in an RS-assisted C-RAN that tackles the ergodic nature of the QoS constraints. In contrast to the optimistic assumption of full CSIT, in this paper, we consider the practical setup in which the CP is assumed to have only access to the channel’s distribution, i.e., we consider the case of statistical CSIT. The resource allocation problem is then formulated so that the transmit power in C-RAN is minimized while the ergodic QoSs of all users are satisfied. The resulting problem is a mixed integer non-linear stochastic program (MINLSP) and known to be NP-hard. This paper proposes an optimization framework that first applies the sample average approximation (SAA) to the ergodic QoS expressions. After that, we propose a clustering approach to find a feasible solution to the discrete part of the problem. Finally, we adopt the weighted minimum mean squared error (WMMSE)–rate relationship to solve the resulting continuous non-convex problem using the alternating optimization approach.

2) Clustering: This work focuses on a C-RAN with the data-sharing strategy to describe the communication exchange between the CP and the set of BSs. Due to the limited capacity of the fronthaul links, each user can be served by a subset of BSs. We propose a clustering algorithm that takes the QoS requirements into account. As opposed to the clustering algorithm proposed by Ahmad et al. (2021), in this work, we formulate a general assignment problem to associate the users with the serving BSs.

3) Numerical simulations: We perform extensive numerical simulations to evaluate the performance of the proposed scheme against TIN in a practical C-RAN system. In particular, we show the gain of the proposed algorithm in different practical scenarios.

1.3 Notations

The notations used throughout this paper are as follows: (⋅)^T and (⋅)^H denote the transpose and Hermitian transpose operators, respectively, and 0_L denotes a column vector of length L with all elements equal to zero. We use lowercase letters to denote scalars and boldface lowercase letters to denote vectors. Let ${\mathbf{a}}_n\in {\mathbb{C}}^{L\times 1}\forall n\in \left\{1,\dots ,N\right\}$ denote a complex-valued vector of length N, then $\mathbf{a}\triangleq \text{vec}\left\{{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N\right\}$ is equivalent to the following operator: $\mathbf{a}\in {\mathbb{C}}^{NL\times 1}\triangleq {\left[{\mathbf{a}}_1^T,\dots ,{\mathbf{a}}_N^T\right]}^T$. Next, we give an overview of the organization of this paper.

1.4 Organization

The rest of this paper is organized as follows. Section 2 introduces the considered system model and the rate splitting scheme. Section 3 presents the signal model and the rate expressions, in the statistical CSI case, followed by formulation of the stochastic optimization problem. In Section 4, we discuss the optimization techniques to solve the problem where we discuss the SAA approach coupled with the WMMSE algorithm. Section 5 revisits the same problem under perfect CSIT. In Section 6, we present the simulation setup and the numerical results. At the end, this paper is summarized and concluded in Section 7.

2 System Model

The system model considered in this paper consists of the downlink rate splitting (RS)-enabled C-RAN with a set of multi-antenna BSs $\mathcal{N}=\left\{\mathrm{1,2},\dots ,N\right\}$, serving a set of single-antenna users $\mathcal{K}=\left\{\mathrm{1,2},\dots ,K\right\}$. Each BS $n\in \mathcal{N}$ is equipped with L ≥ 1 antennas and connected to a central processor (CP) at the cloud via a fronthaul link with limited capacity F_n, and an example of the system model is shown in Figure 1. The downlink communication can be explained as follows: The user k requires a message v_k, where the achievable data rate at user k is denoted R_k, which is a function of the channel state of user k, the rate splitting transmission schemes, the design of the cooperative transmission scheme, and the associated beamforming vector. In this work, we consider that each user needs to be served with a minimum data rate, denoted $r_k^{\text{Min}}$, which characterizes the quality of the service target of user k. The CP jointly processes the messages of all users, encodes them into streams s_k, $\forall k\in \mathcal{K}$, and forward the encoded streams with the BSs through the fronthaul links. The CP can share the encoded messages with the BSs if the sum-rate of users served by BS n does not exceed the fronthaul capacity limit F_n. In this scenario, the received signal model at user k is given by

$y_k={\mathbf{h}}_k^H\mathbf{x}+n_k,(1)$

where ${\mathbf{h}}_k\triangleq \text{vec}\left\{{\mathbf{h}}_{1,k},\dots ,{\mathbf{h}}_{N,k}\right\}\in {\mathbb{C}}^{NL\times 1}$ is the network-wide aggregate channel vector of user k to all BSs, $n_k\sim \mathcal{CN}\left(0,{\sigma }^2\right)$ is the additive white Gaussian noise (AWGN), and $\mathbf{x}\triangleq \text{vec}\left\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N\right\}\in {\mathbb{C}}^{NL\times 1}$ is the aggregate transmit signal from all BSs. Obviously, the transmit power from each BS must be finite. Therefore, the transmit signal x_n from BS n is subject to the following per-BS maximum transmit power constraint: $\mathbb{E}\left\{{\mathbf{x}}_n^H{\mathbf{x}}_n\right\}\le P_n^{\text{Max}}$. Next, we discuss the channel model adopted in this paper.

FIGURE 1

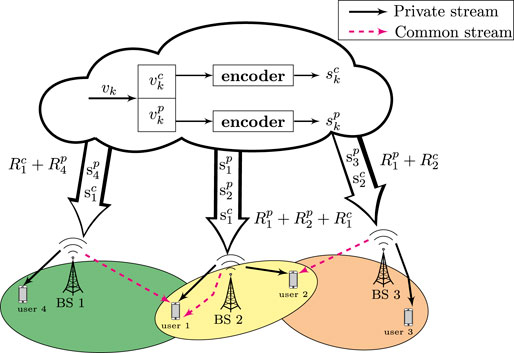
FIGURE 1. A C-RAN in the downlink with three BSs and four users. User 1 receives both its private and common messages from BS 2, while user 2 receives its private message from BS 2 and the common message from BS 3.

2.1 Stochastic CSI Model

We define the instantaneous channel state at time slot t as $\mathbf{h}(t)\triangleq \text{vec}\left\{{\mathbf{h}}_1(t),\dots ,{\mathbf{h}}_K(t)\right\}\in {\mathbb{C}}^{NLK\times 1}$. This paper considers a block-fading model in which the channel state h(t) remains constant over multiple time slots and may vary independently in a random fashion from one block to another according to some stochastic process. Specifically, in a block b with length t_b, the following relation in the block-fading model is satisfied:

$\mathbf{h}(t)=\mathbf{h}(b),\forall t\in \left\{(b-1)t_b+1,\dots ,b{t}_b\right\}.(2)$

We focus in this paper on optimizing the transmission strategy for a single transmission block. Hence, we drop next the dependency of the channel on the time variable and focus on the channel state in one block. We assume that the channel between BS n and user k follows the distribution ${\mathbf{h}}_{n,k}\sim \mathcal{CN}\left(0,{\mathbf{Q}}_{n,k}\right)$, where Q_n,k is a symmetric positive semi-definite matrix and depends mainly on the path loss between BS n and user k. To estimate the channel state within each transmission block at the CP, the receivers which are assumed to know the channel perfectly send a quantized feedback of their estimate to the CP. In this work, we distinguish between the following:

• Case 1: The CP estimates the channel state perfectly while the error due to quantized feedback is considered to be negligible, i.e., full CSIT case. In this case, the CP has knowledge of all elements in the vector h.

• Case 2: Obviously, a full CSIT case involves a large communication overhead between the users and the CP, which requires a huge amount of resources that may even be not affordable in dense networks. Alternatively, the CP can estimate the matrices $\left\{{\mathbf{Q}}_{n,k}|n\in \mathcal{N},k\in \mathcal{K}\right\}$, i.e., the CP has knowledge about channel distribution of all users. This case is referred to throughout this paper as statistical CSIT as the CP does not know the channel coefficients $\left\{{\mathbf{h}}_{n,k}|n\in \mathcal{N},k\in \mathcal{K}\right\}$ exactly, but their distribution is available to the CP. Note that the perfect estimate of the channel distribution can be easily done as it depends mainly on the user locations which can be accurately estimated using of-the-shelf global positioning system (GPS) devices (Cui et al., 2019).

In the next subsection, we describe the rate splitting (RS) procedure as performed at the CP for each requested message.

2.2 Rate Splitting in C-RAN With Data Sharing

As illustrated in Figure 1, the CP first creates two sub-messages out of v_k, the requested message by user k, namely, a private message denoted $v_k^p$ and a common message denoted $v_k^c$. Afterward, the CP encodes the private and common messages into $s_k^p$ and $s_k^c$, respectively. The coded messages $s_k^p$ and $s_k^c$ are assumed to be independent and identically distributed (i.i.d.) circularly symmetric complex Gaussian with zero mean and unit variance. The CP then shares the private stream $s_k^p$ with a cluster of BSs which exclusively sends the beamformed private stream to user k and the common stream $s_k^c$ with a cluster of BSs which exclusively sends the beamformed common stream to user k. We define the set of users which receive the private and common streams, respectively, from BS n as follows:

$\begin{array}{ll}\hfill {\mathcal{K}}_n^p& :=\left\{k\in \mathcal{K}|\mathbf{B}\mathbf{S}n\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}{s}_k^p\text{to\hspace{0.17em}user}k\right\},\hfill \end{array}(3)$

$\begin{array}{ll}\hfill {\mathcal{K}}_n^c& :=\left\{k\in \mathcal{K}|\mathbf{B}\mathbf{S}n\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}{s}_k^c\text{to\hspace{0.17em}user}k\right\}.\hfill \end{array}(4)$

Let the beamforming vector for transmitting the private message of user k from all BSs be ${\mathbf{w}}_k^p\in {\mathbb{C}}^{NL\times 1}\triangleq \text{vec}\left\{{\mathbf{w}}_{1,k}^p,{\mathbf{w}}_{2,k}^p,\dots ,{\mathbf{w}}_{N,k}^p\right\}$, then similarly we define the aggregate beamforming vector to transmit the common message of user k as follows: ${\mathbf{w}}_k^c\in {\mathbb{C}}^{NL\times 1}\triangleq \text{vec}\left\{{\mathbf{w}}_{1,k}^c,{\mathbf{w}}_{2,k}^c,\dots ,{\mathbf{w}}_{N,k}^c\right\}$, where ${\mathbf{w}}_{n,k}^p\in {\mathbb{C}}^{L\times 1}$ and ${\mathbf{w}}_{n,k}^c\in {\mathbb{C}}^{L\times 1}$ are the beamforming vectors to transmit the private and common streams, respectively, from BS n to user k. Since the capacity of the fronthaul link per BS is limited, the size of the BS’s cooperating cluster to serve the stream of each user cannot be very large, as each BS can only support a limited number of streams. Hence, if BS n does not participate in the cooperative transmission of the private or the common message to the k-th user, then ${\mathbf{w}}_{n,k}^p=0$ or ${\mathbf{w}}_{n,k}^c=0$ in the respective aggregate beamforming vectors. Thus, we can write the transmitted signal from the n-th BS as

${\mathbf{x}}_n=\sum _{k=1}^K\left({\mathbf{w}}_k^p{s}_k^p+{\mathbf{w}}_k^c{s}_k^c\right).(5)$

In the theoretical model two-user IC network, which is the simplest non-orthogonal multiple access model, each user needs to decode the common message of the other user. However, in a practical network as the RS-enabled C-RAN, we need to determine for each user the set of other users which decode its common message. To this end, let us denote the common message set of user k as ${\mathcal{M}}_k$ which is defined as

${\mathcal{M}}_k\triangleq \left\{j\in \mathcal{K}|\text{user}j\text{decodes}{s}_k^c\right\}.(6)$

In other words, the set ${\mathcal{M}}_k$ includes the indices of all users which decode the common message of user k. In a similar manner, we define the set of common messages decoded at user k as

${\mathrm{\Phi }}_k\triangleq \left\{j\in \mathcal{K}|k\in {\mathcal{M}}_j\right\}.(7)$

From Eqs 6, 7, we see that if the sets ${\left\{{\mathcal{M}}_k\right\}}_{k=1}^K$ are determined, then the sets ${\left\{{\mathrm{\Phi }}_k\right\}}_{k=1}^K$ are also determined, and vice versa. Next, we discuss the receiver model adopted in this paper.

2.3 Receiver Model

In this paper, we assume that each user employs a successive decoding order (SIC) strategy. Hence, the streams intended to be decoded at user k are decoded in a successive fashion according to some specific order. Figure 2 shows an example of the SIC receiver at user 1. Now, we can rewrite the received signal at user k as

$y_k=\underset{\text{Signals\hspace{0.17em}to\hspace{0.17em}be\hspace{0.17em}decoded}}{\underbrace{\left({\mathbf{h}}_k^H{\mathbf{w}}_k^p{s}_k^p+\sum _{j\in {\mathrm{\Phi }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_j^c{s}_j^c\right)}}+\underset{\text{Interference\hspace{0.17em}plus\hspace{0.17em}noise}}{\underbrace{\sum _{j\in \mathcal{K}\backslash \backslash k}{\mathbf{h}}_k^H{\mathbf{w}}_j^p{s}_j^p+\sum _{l\in {\mathrm{\Psi }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_l^c{s}_l^c+n_k.}}(8)$

FIGURE 2

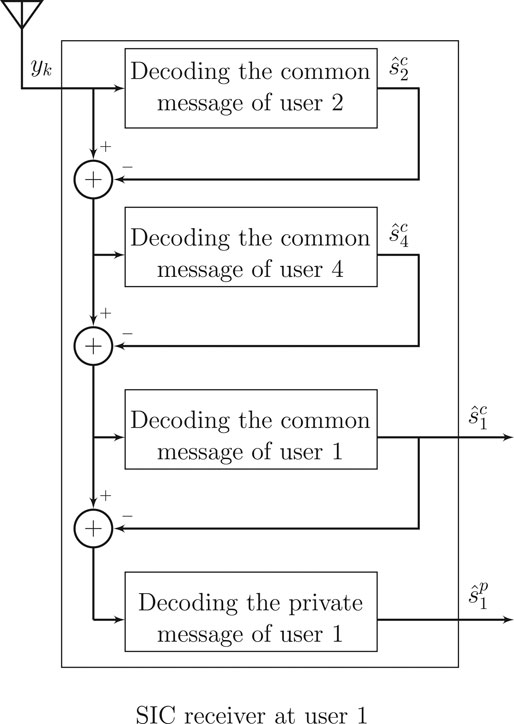
FIGURE 2. A block diagram for an SIC at user 1. In this example, the common messages decoded at user 1 are Φ₁ = {1, 2, 4}. The decoding order at user 1 is then given as π₁: Φ₁ → {3, 1, 2}.

Here, the set Ψ_k includes the indices of users whose common messages are not decoded at user k, i.e., ${\mathrm{\Psi }}_k=\{\mathcal{K}\backslash \backslash {\mathrm{\Phi }}_k\}$. Next, we discuss the expressions of instantaneous signal-to-interference-plus-noise ratio (SINR) and the achievable rates.

2.4 Instantaneous SINR and Achievable Rates

We assume that each user decodes its private stream at last, while the common messages are decoded according to specific order with the aim of maximizing the total achievable rate. The intuition behind this choice is that by decoding the common messages first, one would remove part of the interference from the received signal, thereby increasing the SINR when decoding the private stream, which leads to better achievable rates. The common messages of the users indexed by the set Φ_k are decoded according to the following order:

${\pi }_k(j):{\mathrm{\Phi }}_k\to \left\{\mathrm{1,2},\dots ,\left|{\mathrm{\Phi }}_k\right|\right\}.$

Here, the decoding order at user k, π_k(j), represents a bijective function of the set Φ_k with cardinality $\left|{\mathrm{\Phi }}_k\right|$, i.e., π_k(j) is the successive decoding step in which the message j ∈Φ_k is decoded at user k. In other words, π_k (j₁) > π_k (j₂) (where j₁ ≠ j₂) implies that the user k decodes the common message of user j₁ first and then the common message of user j₂. To this end, let ${\gamma }_k^p$ denote the SINR of user k when decoding its private message and ${\gamma }_{i,k}^c$ denote the SINR of user k when decoding the common message of user i, then we can write

$\begin{array}{ll}\hfill {\gamma }_k^p& =\frac{{\left|{\mathbf{h}}_k^H,{\mathbf{w}}_k^p\right|}^2}{\sum _{j\in \mathcal{K}\backslash \left\{k\right\}}^K{\left|{\mathbf{h}}_k^H,{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Psi }}_k}{\left|{\mathbf{h}}_k^H,{\mathbf{w}}_l^c\right|}^2+{\sigma }^2},\hfill \end{array}(9)$

$\begin{array}{ll}\hfill {\gamma }_{i,k}^c& =\frac{{\left|\right.\left|{\mathbf{h}}_k^H,{\mathbf{w}}_i^c\right|\left|\right.}^2}{{\sigma }^2+\sum _{j\in \mathcal{K}}{\left|{\mathbf{h}}_k^H,{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Psi }}_k}{\left|{\mathbf{h}}_k^H,{\mathbf{w}}_l^c\right|}^2+\sum _{\begin{array}{c}m\in {\mathrm{\Omega }}_{i,k}\end{array}}{\left|{\mathbf{h}}_k^H,{\mathbf{w}}_m^c\right|}^2}\cdot \hfill \end{array}(10)$

Here, ${\mathrm{\Omega }}_{i,k}\triangleq \left\{m\in {\mathrm{\Phi }}_k|{\pi }_k(m)>{\pi }_k(i)\right\}$. Based on the expressions in Eqs 9, 10, the instantaneous achievable rates for each user k satisfy the following expressions:

$\begin{array}{ll}\hfill {\gamma }_k^p\ge 2^{R_k^p/B}-1& \forall k\in \mathcal{K},\hfill \end{array}(11)$

$\begin{array}{ll}\hfill {\gamma }_{k,i}^c\ge 2^{R_k^c/B}-1& \forall i\in {\mathcal{M}}_k\text{and}\forall k\in \mathcal{K},\hfill \end{array}(12)$

where B is the transmit bandwidth, $R_k^p$ is the instantaneous achievable private rate, and $R_k^c$ is the instantaneous achievable common rate. Thus, the total achievable rate of user k is then defined as

$R_k=R_k^p+R_k^c.(13)$

From Eqs 9, 10, we note that the SINR expressions in an RS-enabled C-RAN depend not only on the beamforming vectors but also on the common message set choice and the decoding order for each user, i.e., ${\mathcal{M}}_k$ and π_k. Moreover, the expressions in Eqs 9–12 are deterministic only when the CP has full CSI. Hence, the instantaneous rates are achievable only in the full CSIT case. However, the uncertainty in the CSIT introduces some technical challenge for the transmitter design, and the instantaneous rate expressions are no longer valid. Next, we discuss the ergodic rate (ER) which is adopted in case of statistical CSIT.

2.5 Ergodic Rates

With perfect CSI at the CP, we can adapt the beamforming vectors and eventually the transmit rate to each channel state. Obviously, with full CSIT, we can achieve the best possible rate to send the streams to users. However, with statistical CSIT, the transmitter cannot adapt the beamforming vectors and the rate to each channel state as the latter is not known at the transmitter. In this case with the channel distribution knowledge at the CP, we instead consider sending the private and common streams of user k at the ergodic rates (ERs) (Goldsmith, 2005). The total ergodic rate of user k is defined as ${\mathbb{E}}_{\mathbf{h}}\left\{R_k^p+R_k^c\right\}\triangleq {\overline{R}}_k^p+{\overline{R}}_k^c$, where ${\overline{R}}_k^p$ is the ER to send the private stream and ${\overline{R}}_k^c$ is the ER to send the common stream of user k. The achievability relations of the ergodic private and common rates can be written as

$\begin{array}{ll}\hfill {\overline{R}}_k^p\le B{\mathbb{E}}_{\mathbf{h}}\left\{{\log }_2\left(1+{\gamma }_k^p\right)\right\}& \forall k\in \mathcal{K},\hfill \end{array}(14)$

$\begin{array}{ll}\hfill {\overline{R}}_k^c\le B{\mathbb{E}}_{\mathbf{h}}\left\{{\log }_2\left(1+{\gamma }_{k,i}^c\right)\right\}& \forall i\in {\mathcal{M}}_k\text{and}\forall k\in \mathcal{K}.\hfill \end{array}(15)$

Now, we are ready to discuss the problem we investigate in this paper.

3 Problem Formulation

We focus on the problem of joint optimization of coordinated beamforming vectors, clusters of BSs to serve private and common messages to all users, and the rate allocation per user such that the weighted transmit power consumption is minimized. We consider a data-sharing strategy between the CP and the BSs and apply rate splitting at the CP and BSs followed by a successive decoding strategy at the receivers. We assume all BSs operate in the active mode. Another option would be to consider minimizing the network power consumption by considering the set of active BSs as well as the power consumption due to computation operation which is necessary to perform the base band processing tasks, but this falls outside of the scope of the current paper and is left for our future investigation. We define the transmit power consumption as $P^{\text{Tr}}(\mathbf{w})\triangleq {\sum }_{k=1}^K{\alpha }_k({\sum }_{n=1}^N{‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2)$, where α_k is a coefficient which represents the weight associated with the transmit power assigned to user k. The weights α_k represent here the heterogeneity of the applications that request services from the cloud. For instance, an application which requires a service under the ultra-reliable low-latency communication (URLLC) category has higher priority than a service that requires some software update in an IoT category. Hence, the higher priority services should be associated with lower weights as compared with lower priority services. Next, we formulate the mathematical optimization problem describing the resource allocation to minimize the transmit power such that per-user QoS requirements are satisfied.

3.1 Optimization Problem

In the general setup where the CP only knows statistical CSI, the optimization is performed subject to per user-target ergodic rate constraints to account for the lack of full CSIT. The optimization problem considered in this paper can then be formulated in its general form as follows:

$\begin{array}{lll}({\mathrm{P}}_0):\underset{{\mathcal{V}}_0}{\text{minimize}}\hfill & \hfill & \sum _{k\in \mathcal{K}}{\alpha }_k\left({‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\hfill \end{array}(\mathrm{16a})$

$\begin{array}{ll}\text{subject\hspace{0.17em}to}\hfill & (9)\text{and}(10),\hfill \end{array}(\mathrm{16b})$

$\begin{array}{lll}\sum _{k\in {\mathcal{K}}_n^p}{\overline{R}}_k^p+\sum _{k\in {\mathcal{K}}_n^c}{\overline{R}}_k^c\le F_n\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{16c})$

$\begin{array}{lll}{\overline{R}}_k^p+{\overline{R}}_k^c\ge r_k^{\text{Min}}\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(\mathrm{16d})$

$\begin{array}{lll}{\overline{R}}_k^p\le {\mathbb{E}}_{\mathbf{h}}\left\{B{\log }_2(1+{\gamma }_k^p)\right\}\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(16e)$

$\begin{array}{lll}{\overline{R}}_k^c\le {\mathbb{E}}_{\mathbf{h}}\left\{B{\log }_2(1+{\gamma }_{k,i}^p)\right\}\hfill & \hfill & \forall i\in {\mathcal{M}}_k\text{and}\forall k\in \mathcal{K}.\hfill \end{array}(\mathrm{16f})$

Here, $r_k^{\text{Min}}$ is the minimum ergodic rate requested by user k, F_n is the fronthaul capacity of BS n, and ${\mathcal{V}}_0$ is the set of optimization variables given as

${\mathcal{V}}_0=:\left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,{\overline{R}}_k^p,{\overline{R}}_k^c,{\pi }_k,{\mathcal{M}}_k,{\mathcal{K}}_n^p,{\mathcal{K}}_n^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(17)$

The problem (P₀) is a mixed integer non-linear stochastic program (MINLSP) that is generally difficult to solve. The main difficulty stems from the combinatorial nature of the set of variables

$\left\{{\pi }_k,{\mathcal{M}}_k,{\mathcal{K}}_n^p,{\mathcal{K}}_n^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\},(18)$

besides that the constraints (Eq. 16b) are non-convex functions of the beamforming vectors and the constraints (Eqs 16e,f) are of stochastic nature, where the expected value has no closed-form expression. Thus, solving the problem (P₀) for global optimality is very challenging and may be computationally prohibitive even for small instances. In this paper, instead, we propose an optimization framework in which we first fix the set of common messages and the decoding order a priori. Furthermore, we use the sample average approximation (SAA) to deal with the stochastic constraints and WMMSE algorithm to resolve the joint optimization of beamforming vectors and rate allocation. Before presenting the optimization algorithm developed to solve the problem (P₀), we wish to note that, for the sake of numerical simplicity, the choice of the set of common messages adopted in this paper follows a distance-dependent heuristic. To this end, this paper next presents the approach this paper utilizes for determining the set of common messages, together with the decoding order. The next section, afterward, presents the optimization algorithm developed to solve the problem (P₀).

3.2 Common Message Set and Decoding Order

We suggest designing the common message set based on the network topology and avoiding the CSI to assure the robustness of the proposed RS scheme against channel imperfections. Hence, we propose a practical procedure that does not depend on the channel state’s knowledge and requires only the user’s geographical locations. The user’s positions can be easily obtained using global positioning system devices with little communication overhead. In particular, let $d_{k_1,k_2}$ denote the distance between users k₁ and k₂, then we define the common message set for user k as follows:

${\mathcal{M}}_k=\left\{j\in \mathcal{K}|d_{jk}\le \delta \right\},(19)$

where δ is a threshold in meters. Hence, in this procedure, the common message set of user k includes all users’ indices, which are located within a given distance of user k. While such a heuristic design of M_k has no optimality guarantees, the intuition behind such a simple design is that the user’s interference is at strongest when the users are spatially close to each other. Hence, decoding the common messages among such groups can significantly mitigate the interference and result in better achievable rates. Besides, the users in the proximity of the user k have potentially good channel quality to the serving cluster of BSs of the common stream of user k as they experience similar path-loss conditions. Hence, they achieve higher rates of the common stream of user k, as the common stream of user k is of multicast nature. Therefore, its achievable rate is determined by the weakest user. Next, we consider the design of the decoding order strategy at user k with statistical CSIT. We adopt the following rule: the SIC receiver at user k starts to decode the streams based on their proximity to user k. Hence, the common messages of users which are closer to user k are decoded before the common messages of users that are more distant from user k. Specifically, the common message of user i is decoded before the common message of user j if d_ik < d_jk. Again, this rule is heuristic; however, it is reasonable as by doing so, we make sure that the common rate of the users in the proximity of user k does not drop significantly, which potentially improves the total achievable rate and helps the users meeting their QoS requirements efficiently.

In what follows, we discuss another approach for determining the clustering variables, based on the general assignment formulation. Hence, we first determine the serving clusters so that the fronthaul constraint of each BS is satisfied. Afterward, we apply an optimization framework that merges the SAA approach with the WMMSE algorithm to find a KKT condition–satisfying solution of the resulting continuous stochastic optimization problem.

3.3 Clustering Variables and Assignment Problem

Let q_n,k be the channel quality between user k and BS n, measured as the inverse of path loss between them. We define the utility function of the assignment problem as

$U(n,k)=q_{n,k}.(20)$

The utility function in Eq. 20 measures the benefit of associating user k with BS n. The intuition behind this choice is that the utility function in Eq. 20 computes the benefit of associating user k with BS n based on the channel strength between them. Now, we can define the general assignment problem using Eq. 20 as follows:

$\begin{array}{lllll}\hfill & \underset{\mathbf{a}}{\text{maximize}}\hfill & \hfill & \sum _{(n,k)\in \mathcal{N}\times \mathcal{K}}{a}_{n,k}U(n,k)\hfill & \hfill \\ \hfill & \text{subject\hspace{0.17em}to}\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \sum _{k\in \mathcal{K}}{a}_{n,k}{r}_k^{\text{min}}\le F_n,\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{21a})$

$\begin{array}{lll}\sum _{n\in \mathcal{N}}{a}_{n,k}\le 1,\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(\mathrm{21b})$

$\begin{array}{l}{a}_{n,k}\in \left\{\mathrm{0,1}\right\}.\hfill \end{array}(\mathrm{21c})$

The optimization is carried over the binary association variables in set ${\mathcal{V}}_5$ which is defined as

$\mathbf{a}\triangleq \text{vec}\left\{a_{n,k}|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(22)$

Note that the constraint in Eq. 21a makes sure that the sum of the minimum rates required by users associated with BS n does not exceed its fronthaul capacity limit. Moreover, the constraint in Eq. 21b guarantees that each user is associated with at least one BS. The problem in Eqs 21a–c is an integer linear program that needs special solvers such as MOSEK and Gurobi. In this work, we use global optimization methods such as the branch and cut algorithm to find a solution to the problem in Eqs 21a–c. Note that the problem in Eqs 21a–c is an integer linear problem. Therefore, we can find its global optimal solution efficiently for the problem’s size considered in this paper. The binary variables in Eq. 22 associate users to BSs, which is equivalent to associating the private streams (e.g., in TIN) with the corresponding BSs. However, when using RS–CMD, both private and common streams need to be associated with the BSs. To accomplish this task, we propose the following procedure: First, for each common stream, we find a subset of BSs as a candidate serving cluster. Let ${\mathcal{D}}_k^c\triangleq {\mathcal{M}}_k$. Furthermore, let ${\mathcal{N}}_k^c$ denote the candidate cluster of BSs to serve common streams of user k. Since each common stream should be decoded by multiple users, each BS n in the candidate cluster ${\mathcal{N}}_k^c$ needs to have good channel quality to all users, which decode this particular stream. The quality of the channel is measured based on the large-scale fading coefficient. We propose a criterion based on the collective channel quality to all users decoding a specific stream. Let $q_{n,{\mathcal{D}}_k^c}$ denote the collective channel quality from BS n and to all the users decoding the common stream of user k, i.e., $s_k^c$. $q_{n,{\mathcal{D}}_k^c}$ is given as $q_{n,{\mathcal{D}}_k^c}=\frac{1}{|{\mathcal{D}}_k^c|}{\sum }_{j\in {\mathcal{D}}_k^c}{q}_{n,j}$. Here, q_n,j is the channel quality between user j and BS n and is inversely proportional to the path loss between them.

The candidate cluster of BSs serving the common messages of user k is then given as

${\mathcal{N}}_k^c=\left\{\{n_1,\dots ,n_{\mu }\}\subseteq \mathcal{N}|q_{n_1,{\mathcal{D}}_k^c}\ge \dots \ge q_{n_{\mu },{\mathcal{D}}_k^c}\right\},(23)$

where ${\mathcal{N}}_k^c$ is a set with cardinality μ. It contains the subset of BSs that have good channel quality to all users decoding the common message of user k.

After that, we use the solution of the assignment problem in Eqs 21a–c to specify the serving clusters for private streams. In particular, we choose the BS clusters for transmitting the private and common streams to the users as follows:

$\begin{array}{ll}\hfill {\mathcal{K}}_n^p& =\{k\in \mathcal{K}|a_{n,k}^p=1\},\hfill \end{array}(\mathrm{24a})$

$\begin{array}{ll}\hfill {\mathcal{K}}_n^c& =\{k\in \mathcal{K}|n\in {\mathcal{N}}_k^c\}.\hfill \end{array}(\mathrm{24b})$

We are now ready to discuss the algorithm to solve the problem P₂. Note that the choice of clusters in Eqs 24a,b preserves the feasibility of the assignment problem in Eqs 21a–c. Specifically, as a special case, we can set ${\mathcal{K}}_n^c=\{\varnothing \},\forall n\in \mathcal{N}$, i.e., we assign zero rates for the common streams. In this special case, both RS–CMD and TIN are equivalent. Any other option for the clusters serving the common messages allows RS–CMD to efficiently manage the interference, potentially resulting in a lower transmit power cost. Using the heuristic procedures in Eq. 19 to determine the common message sets and the problem in Eqs 21a–c together with Eqs 24a,b to determine the clustering variables, we get the following optimization problem formulation:

$\begin{array}{lllll}\hfill & ({\mathrm{P}}_2):\underset{{\mathcal{V}}_2}{\text{minimize}}\hfill & \hfill & \sum _{k\in \mathcal{K}}{\alpha }_k\left({‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\hfill & \hfill \\ \hfill & \text{subject\hspace{0.17em}to}\hfill & \hfill & (16f),(16e),(9),\text{and}(10),\hfill & \hfill \\ \hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^p}{\overline{R}}_k^p+\sum _{k\in {\mathcal{K}}_n^c}{\overline{R}}_k^c\le F_n,\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{25a})$

$\begin{array}{llllll}\hfill & \hfill & \hfill & {\overline{R}}_k^p+{\overline{R}}_k^c\ge r_k^{\text{min}},\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(\mathrm{25b})$

where the set of optimization variables is given by

${\mathcal{V}}_2\triangleq \left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,{\overline{R}}_k^p,{\overline{R}}_k^c|\forall i\in {\mathcal{M}}_k,\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(26)$

The next section discusses the optimization techniques to approach such a challenging stochastic and non-convex optimization problem.

4 Optimization Approach

4.1 WMMSE–Rate Relationships

We start this section by discussing the WMMSE–rate relationship, which turns out to be crucial in developing an efficient algorithm to solve the problem (P₂). To this end, each user estimates the intended transmit private and common streams using a linear receiver. Let ${\hat{s}}_k^p\triangleq u_k^p(y_k-{\sum }_{j\in {\mathrm{\Phi }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_j^c{s}_j^c)$ be the private stream estimate at user k after removing all the common messages, decoded at user k. Furthermore, let $u_{i,k}^c$ be the linear receiver used by user k to decode the common stream of user i, i.e., the estimated common stream of user i when decoded at user k is defined as ${ŝ}_{i,k}^c\triangleq u_{i,k}^c(y_k-\sum _{m\in {\mathrm{\Psi }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_m^c{s}_m^c)$.

To this end, let us define the mean squared error (MSE) when decoding the private stream at user k and the common stream of user i at user k as $e_k^p=\mathbb{E}\left\{|{ŝ}_k^p-s_k^p{|}^2\right\}$ and $e_{k,i}^c=\mathbb{E}\left\{|{ŝ}_{i,k}^c-s_k^c{|}^2\right\}$. Using Eq. 8, we can write the MSE’s expressions as follows:

$\begin{array}{ll}\hfill e_k^p& ={\left|u_k^p\right|}^2{T}_k^p-2\mathfrak{R}\left\{u_k^p{\mathbf{h}}_k^H{\mathbf{w}}_k^p\right\}+1,\hfill \end{array}(27)$

$\begin{array}{ll}\hfill e_{i,k}^c& ={\left|u_{i,k}^c\right|}^2{T}_{i,k}^c-2\mathfrak{R}\left\{u_{i,k}^c{\mathbf{h}}_k^H{\mathbf{w}}_i^c\right\}+1.\hfill \end{array}(28)$

Here, $T_k^p$ and $T_{i,k}^c$ are defined as

$\begin{array}{ll}\hfill T_k^p& ={\left|{\mathbf{h}}_k^H{\mathbf{w}}_k^p\right|}^2+\underset{I_k^p}{\underbrace{\sum _{j\in \mathcal{K}\backslash k}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Omega }}_k}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_l^c\right|}^2+{\sigma }^2}},\hfill \end{array}(29)$

$\begin{array}{ll}\hfill T_{i,k}^c& ={\left|{\mathbf{h}}_k^H{\mathbf{w}}_i^c\right|}^2+\underset{I_{i,k}^c}{\underbrace{\sum _{j\in \mathcal{K}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Omega }}_k}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_l^c\right|}^2+\sum _{m\in {\mathrm{\Psi }}_{i,k}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_m^c\right|}^2+{\sigma }^2}},\hfill \end{array}(30)$

where $I_k^p$ and $I_{i,k}^c$ are the interference plus noise at user k when decoding its private message and the common message of user i, respectively. By checking the first-order optimality of the expressions in Eqs 27, 28, we write

$\begin{array}{ll}\hfill \frac{\partial e_k^p}{\partial u_k^p}& =0\Rightarrow T_k^p{u}_{k,\text{mmse}}^p-{({\mathbf{w}}_k^p)}^H{\mathbf{h}}_k=0,\hfill \end{array}(31)$

$\begin{array}{ll}\hfill \frac{\partial e_{i,k}^c}{\partial u_{i,k}^c}& =0\Rightarrow T_{i,k}^c{u}_{i,k,\text{mmse}}^c-{({\mathbf{w}}_i^c)}^H{\mathbf{h}}_k=0.\hfill \end{array}(32)$

Thus, the optimal receiver coefficients that result in the minimum MSE, i.e., MMSE, are given as

$\begin{array}{ll}\hfill u_{k,\text{mmse}}^p& =\frac{{({\mathbf{w}}_k^p)}^H{\mathbf{h}}_k}{T_k^p},\hfill \end{array}(33)$

$\begin{array}{ll}\hfill u_{i,k,\text{mmse}}^c& =\frac{{({\mathbf{w}}_i^c)}^H{\mathbf{h}}_k}{T_{i,k}^c}\cdot \hfill \end{array}(34)$

By plugging the MMSE receiver’s expressions from Eqs 33, 34 in Eqs 27, 28, we get the expressions of the MMSE as

$\begin{array}{ll}\hfill e_{k,\text{mmse}}^p& =\frac{I_k^p}{T_k^p},\hfill \end{array}(35)$

$\begin{array}{ll}\hfill e_{i,k,\text{mmse}}^c& =\frac{I_{i,k}^c}{T_{i,k}^c}\cdot \hfill \end{array}(36)$

Before we proceed, we define the augmented MSEs when decoding the private stream of user k and the common stream of user k by user i as

${\zeta }_k^p\triangleq {\rho }_k^p{e}_k^p-{\log }_2({\rho }_k^p),{\zeta }_{k,i}^c\triangleq {\rho }_{k,i}^c{e}_{k,i}^c-{\log }_2({\rho }_{k,i}^c),(37)$

where ${\rho }_k^p$ and ${\rho }_{k,i}^c$ are some weighting coefficients.

An essential observation in this work is the following connection between the achievable ergodic rates and the WMMSE.

Proposition 1. The maximum achievable rate of user k when decoding its private stream and of user i when decoding the common stream of user k can be expressed as

$\begin{array}{ll}\hfill {\log }_2(1+{\gamma }_k^p)& =1+\underset{u_k^p,{\rho }_k^p}{\max }\left({\log }_2({\rho }_k^p)-{\rho }_k^p{e}_k^p\right)=1-{\zeta }_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p,\hfill \end{array}(38)$

$\begin{array}{ll}\hfill {\log }_2(1+{\gamma }_{k,i}^c)& =1+\underset{u_{k,i}^c,{\rho }_{k,i}^c}{\max }\left({\log }_2({\rho }_{k,i}^c)-{\rho }_{k,i}^c{e}_{k,i}^c+\right)=1-{\zeta }_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c,\hfill \end{array}(39)$

where ${\zeta }_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p$ and ${\zeta }_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c$ are the optimal augmented WMMSE expressions defined as

$\begin{array}{ll}\hfill {\zeta }_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p& \triangleq \underset{u_k^p,{\rho }_k^p}{\min }\left({\rho }_k^p{e}_k^p-{\log }_2({\rho }_k^p)\right),\hfill \end{array}(\mathrm{40a})$

$\begin{array}{ll}\hfill {\zeta }_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c& \triangleq \underset{u_{k,i}^c,{\rho }_{k,i}^c}{\min }\left({\rho }_{k,i}^c{e}_{k,i}^c-{\log }_2({\rho }_{k,i}^c)\right),\forall i\in {\mathcal{M}}_k.\hfill \end{array}(\mathrm{40b})$

Proof. To show the equivalence, let us look at the right-hand side of Eq. 38 which represents an unconstrained optimization problem. By checking the first-order optimality of this problem, through taking the partial derivative of the objective with respect to $u_k^p$ and setting the result to zero, we find out that the optimal receivers are in fact as given in Eq. 33, i.e., the MMSE receivers ${(u_k^p)}^{*}=u_{k,\text{mmse}}^p$. By taking the partial derivatives with respect to the weighting coefficient ${\rho }_k^p$ and setting the result to zero, we get the first-order optimal coefficients given as ${({\rho }_k^p)}^{*}=\frac{1}{e_{k,\text{mmse}}^p}$. By plugging the optimal values of $u_k^p$ and ${\rho }_k^p$ in Eq. 38 and using the value of $e_{k,\text{mmse}}^p$ as defined in Eq. 35, we get exactly the expression of the left-hand side of Eq. 38 which is the achievable rate of user k when decoding the private stream (assuming a normalized transmit bandwidth). By following the same proof steps, we show in a similar manner the equivalence in Eq. 39 which completes the proof.For the rest of this paper, we drop the word “augmented” and we use only “WMMSE” to refer to the quantities defined in Eqs 40a,b. Equations 38, 39 describe the instantaneous rate–WMMSE relationship. By taking the expectation over the channel variable of both sides, we get the following ergodic rate–ergodic WMMSE relationship:

$\begin{array}{ll}\hfill {\mathbb{E}}_{\mathbf{h}}\left\{{\log }_2(1+{\gamma }_k^p)\right\}& =1-{\mathbb{E}}_{\mathbf{h}}\{{\zeta }_{k,\text{mmse}}^p\},\hfill \end{array}(\mathrm{41a})$

$\begin{array}{ll}\hfill {\mathbb{E}}_{\mathbf{h}}\left\{{\log }_2(1+{\gamma }_{k,i}^c)\right\}& =1-{\mathbb{E}}_{\mathbf{h}}\{{\zeta }_{k,i,\text{mmse}}^c\}\forall i\in {\mathcal{M}}_k.\hfill \end{array}(\mathrm{41b})$

Here, ${\mathbb{E}}_{\mathbf{h}}\{{\log }_2(1+{\gamma }_k^p)\}$ and ${\min }_{i\in {\mathcal{M}}_k}{\mathbb{E}}_{\mathbf{h}}\{{\log }_2(1+{\gamma }_{k,i}^c)\}$ represent the maximum achievable private and common ergodic rates of user k. Moreover, ${\mathbb{E}}_{\mathbf{h}}\{{\zeta }_{k,\text{mmse}}^p\}$ and ${\max }_{i\in {\mathcal{M}}_k}{\mathbb{E}}_{\mathbf{h}}\{{\zeta }_{k,i,\text{mmse}}^c\}$ represent the minimum ergodic private and common WMMSEs of user k. Next, we discuss the sample average approximation approach to approximate the ergodic rate and ergodic WMMSE expressions.

4.2 SAA Method

The problem (P₂) is of stochastic nature, and the expected value in constraints in Eqs 16e,f is not in the closed form, which makes it very challenging. To overcome this obstacle, we assort to use the SAA (Shapiro et al., 2009) to approximate the ergodic rate and ergodic WMMSE expressions. To this end, we define an i.i.d. sample set of the wireless channel as follows:

${\mathcal{H}}^M=\{{\mathbf{h}}^m|1\le m\le M\},(42)$

where $M\in \mathbb{N}$ denotes the sample size and h^m is a realization of the aggregate channel state of all users given as ${\mathbf{h}}^m\in {\mathbb{C}}^{NKL\times 1}\triangleq \text{vec}\left\{{\mathbf{h}}_1^m,{\mathbf{h}}_2^m,\dots ,{\mathbf{h}}_K^m\right\}$.

The stochastic constraints can then be expressed as

$\begin{array}{ll}\hfill & {\overline{R}}_k^p-\frac{B}{M}\sum _{m=1}^M{\log }_2\left(1+{\gamma }_k^p(m)\right)\le 0\forall k\in \mathcal{K},\hfill \end{array}(43)$

$\begin{array}{ll}\hfill & {\overline{R}}_k^c-\frac{B}{M}\sum _{m=1}^M{\log }_2\left(1+{\gamma }_{k,i}^c(m)\right)\le 0\forall i\in {\mathcal{M}}_k,\forall k\in \mathcal{K}.\hfill \end{array}(44)$

Moreover, we define the SAA of the ergodic private and common WMMSEs in Eqs 41a,b as follows:

$\begin{array}{ll}\hfill & {\overline{\zeta }}_k^p(M)\triangleq \frac{1}{M}\sum _{m=1}^M{\zeta }_k^p(m),\hfill \end{array}(\mathrm{45a})$

$\begin{array}{ll}\hfill & {\overline{\zeta }}_{k,i}^c(M)\triangleq \frac{1}{M}\sum _{m=1}^M{\zeta }_{k,i}^c(m),\forall i\in {\mathcal{M}}_k.\hfill \end{array}(\mathrm{45b})$

Here, we made the dependency of the SINR expressions ${\gamma }_k^p(m),{\gamma }_{k,i}^c(m)$ in Eqs 43, 44, and the instantaneous private and common WMMSEs in Eqs 45a,b, respectively, on the channel realization h^m explicit. Note that, for simplicity of notations, we only keep the index of the channel realization in Eqs 43, 44, 45a,b. In particular, we have ${\zeta }_k^p(m)\triangleq {\zeta }_k^p({\mathbf{h}}^m,u_k^p(m),{\rho }_k^p(m))$ and ${\zeta }_{k,i}^c(m)\triangleq {\zeta }_{k,i}^c({\mathbf{h}}^m,u_{k,i}^c(m),{\rho }_{k,i}^c(m))$, where the receiver and MSE weights depend on the specific channel realization, i.e., $u_k^p(m)=u_k^p({\mathbf{h}}^m)$, $u_{k,i}^c(m)=u_{k,i}^c({\mathbf{h}}^m)$, ${\rho }_k^p(m)={\rho }_k^p({\mathbf{h}}^m)$, and ${\rho }_{k,i}^c(m)={\rho }_{k,i}^c({\mathbf{h}}^m)$. For each user k, let us define the following sample vectors: ${\mathbf{u}}_k^p\triangleq \text{vec}\{u_k^p(m)|1\le m\le M\}$ and ${\mathbf{u}}_{k,i}^c\triangleq \text{vec}\{u_{k,i}^c(m)|1\le m\le M\}$. Similarly, we define ${\mathit{\rho }}_k^p\triangleq \text{vec}\{{\rho }_k^p(m)|1\le m\le M\}$ and ${\mathit{\rho }}_{k,i}^c\triangleq \text{vec}\{{\rho }_{k,i}^c(m)|1\le m\le M\}$.

Let us introduce the SAA of the ergodic rate–ergodic WMMSE relationship as

$\begin{array}{ll}\hfill & \frac{1}{M}\sum _{m=1}^M{\log }_2\left(1+{\gamma }_k^p(m)\right)=1-{\overline{\zeta }}_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p(M),\hfill \end{array}(\mathrm{46a})$

$\begin{array}{ll}\hfill & \frac{1}{M}\sum _{m=1}^M{\log }_2\left(1+{\gamma }_{k,i}^c(m)\right)=1-{\overline{\zeta }}_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c(M)\forall i\in {\mathcal{M}}_k,\hfill \end{array}(\mathrm{46b})$

where ${\overline{\zeta }}_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p(M)$ and ${\overline{\zeta }}_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c(M)$ are the SAA of ergodic WMMSEs ${\mathbb{E}}_{\mathbf{h}}\{{\zeta }_{k,\text{mmse}}^p\}$ and ${\mathbb{E}}_{\mathbf{h}}\{{\zeta }_{k,i,\text{mmse}}^c\}$, using the channel sample ${\mathcal{H}}^M$, and are given as

$\begin{array}{ll}\hfill & {\overline{\zeta }}_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p(M)\triangleq \underset{{\mathbf{u}}_k^p,{\mathit{\rho }}_k^p}{\min }{\overline{\zeta }}_k^p(M),\hfill \end{array}(\mathrm{47a})$

$\begin{array}{ll}\hfill & {\overline{\zeta }}_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c(M)\triangleq \underset{{\mathbf{u}}_{k,i}^c,{\mathit{\rho }}_{k,i}^c}{\min }{\overline{\zeta }}_{k,i}^c(M)\forall i\in {\mathcal{M}}_k.\hfill \end{array}(\mathrm{47b})$

Here, the   min(⋅) operator is taken per channel realization.

Now, we can reformulate the stochastic problem (P₂) with the help of the rate–WMMSE relationship and the SAA approximation as follows:

$\begin{array}{llll}\hfill & ({\mathrm{P}}_3(M)):\underset{{\mathcal{V}}_3}{\text{minimize}}\hfill & \hfill & \sum _{k\in \mathcal{K}}{\alpha }_k\left({\left.‖{\mathbf{w}}_{n,k}^p\right|}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\hfill \end{array}(\mathrm{48a})$

$\begin{array}{llll}\hfill & \text{subject\hspace{0.17em}to}\hfill & \hfill & (47),(16c),(16d),\hfill \end{array}(\mathrm{48b})$

$\begin{array}{llllll}\hfill & \hfill & \hfill & {\overline{R}}_k^p-B(1-{\overline{\zeta }}_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p(M))\le 0\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(\mathrm{48c})$

$\begin{array}{llllll}\hfill & \hfill & \hfill & {\overline{R}}_k^c-B(1-{\overline{\zeta }}_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c(M))\le 0\hfill & \hfill & \forall i\in {\mathcal{M}}_k,\forall k\in \mathcal{K}.\hfill \end{array}(\mathrm{48d})$

Here, ${\mathcal{V}}_3$ is the set of optimization variables associated with the optimization problem (P₃(M)) defined as

${\mathcal{V}}_3=:\left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,{\overline{R}}_k^p,{\overline{R}}_k^c,{\mathbf{u}}_k^p,{\mathit{\rho }}_k^p,{\mathbf{u}}_k^c,{\mathit{\rho }}_k^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\},(49)$

where ${\mathbf{u}}_k^c\triangleq \text{vec}\{{\mathbf{u}}_{k,i}^c|\forall i\in {\mathcal{M}}_k\}$ and ${\rho }_k^c\triangleq \text{vec}\{{\rho }_{k,i}^c|\forall i\in {\mathcal{M}}_k\}$.

The problem (P₃(M)) is still non-convex and challenging to solve, and the optimization variable space is larger than that associated; however, it is more tractable than its stochastic counterpart (P₂). It is obvious that the optimization problem (P₃(M)) depends on the sample size M. As M grows large, the SAA becomes more accurate, at the cost of increasing the complexity of solving the problem (P₃(M)). Hence, in the asymptotic regime, when M → ∞, there is no loss in optimality of the stochastic problem (P₂) by solving the deterministic problem (P₃(M)), and this is captured in the following theorem.

Theorem 1. The set of global optimal solutions of the problem (P₃(M)) asymptotically converges to the set of optimal solutions of the problem (P₂) uniformly with probability one.

Proof. The proof is provided in the Appendix.Next, we discuss the iterative algorithm to provide a first-order optimal solution to the optimization problem (P₃(M)).

4.3 WMMSE-Based Algorithm

As discussed above, the optimization problem (P₃(M)) is non-convex, and it is difficult to solve for a global optimal. Hence, in this paper, we consider an iterative algorithm that converges in a finite number of iterations to a first-order optimal solution which satisfies Karush–Kuhn–Tucker (KKT) optimality conditions of the problem (P₃(M)). To this end, we first note that the feasible set of problem (P₃(M)) is non-convex due to constraints in Eqs 48c,d. Hence, the constraints in Eqs 48c,d are not jointly convex in the optimization variables. However, the SAA of the WMMSE expressions in Eqs 47a,b is convex in each set of variables independently. Based on this observation, the classical WMMSE algorithm uses the alternating optimization framework by optimizing over one set of variables and fixing all the rest. This process is repeated until convergence. However, in the problem (P₃(M)), we cannot apply the alternating optimization directly due to the constraint in Eq. 16c. The iterative algorithm starts by initializing the beamforming vectors to a feasible value. After that, we compute the optimal set of variables ${\mathbf{u}}_k^p,{\mathbf{u}}_k^c$ and ${\rho }_k^p,{\rho }_k^c$, separately. The advantage of the WMMSE algorithm is that this set of optimal variables can be found in the closed form as

$\begin{array}{ll}\hfill & u_k^p(m)=\frac{{({\mathbf{w}}_k^p)}^H{\mathbf{h}}_k^m}{T_k^p(m)},u_{k,i}^c(m)=\frac{{({\mathbf{w}}_k^c)}^H{\mathbf{h}}_i^m}{T_{k,i}^c(m)},\hfill \end{array}(50)$

$\begin{array}{ll}\hfill & {\rho }_k^p(m)=1/e_{k,\text{mmse}}^p(m),{\rho }_{k,i}^c(m)=1/e_{k,i,\text{mmse}}^c(m),\hfill \end{array}(51)$

where $e_{k,\text{mmse}}^p(m)$ and $e_{k,i,\text{mmse}}^c(m)$ are the optimal MMSEs as defined in Eqs 35, 36. The next step is to plug in the optimal values as defined in Eqs 50, 51 in the constraints in Eqs 48c,d by using the WMMSE expressions ${\zeta }_k^p$ and ${\zeta }_{k,i}^c$ as defined in Eq. 37. To express the approximate optimization problem in a compact manner, we define the following auxiliary variables:

$\begin{array}{ll}\hfill & {\overline{t}}_k^p=\frac{1}{M}\sum _{m=1}^M{\rho }_k^p(m){‖u_k^p(m)‖}_2^2,{\overline{t}}_{k,i}^c=\frac{1}{M}\sum _{m=1}^M{\rho }_{k,i}^c(m){‖u_{k,i}^c(m)‖}_2^2,\hfill \end{array}(52)$

$\begin{array}{ll}\hfill & {\overline{l}}_k^p=\frac{1}{M}\sum _{m=1}^M(1-{\rho }_k^p(m)+\log ({\rho }_k^p(m))),\hfill \end{array}(53)$

$\begin{array}{ll}\hfill & {\overline{l}}_{k,i}^c=\frac{1}{M}\sum _{m=1}^M(1-{\rho }_{k,i}^c(m)+\log ({\rho }_{k,i}^c(m))),\hfill \end{array}(54)$

$\begin{array}{ll}\hfill & {\overline{\mathbf{f}}}_k^p=\frac{1}{M}\sum _{m=1}^M{\rho }_k^p(m){\mathbf{h}}_k^m{(u_k^p(m))}^H,{\overline{\mathbf{f}}}_{k,i}^c=\frac{1}{M}\sum _{m=1}^M{\rho }_{k,i}^c(m){\mathbf{h}}_i^m{(u_{k,i}^c(m))}^H,\hfill \end{array}(55)$

$\begin{array}{ll}\hfill & {\overline{\mathbf{Y}}}_{k,k}^p=\frac{1}{M}\sum _{m=1}^M\left({\rho }_k^p(m){‖u_k^p(m)‖}_2^2{\mathbf{h}}_k^m{({\mathbf{h}}_k^m)}^H\right),\hfill \end{array}(56)$

$\begin{array}{ll}\hfill & {\overline{\mathbf{Y}}}_{k,i}^c=\frac{1}{M}\sum _{m=1}^M\left({\rho }_{k,i}^c(m){‖u_{k,i}^c(m)‖}_2^2{\mathbf{h}}_i^m{({\mathbf{h}}_i^m)}^H\right).\hfill \end{array}(57)$

By using Eqs 27, 28, 37, we define the approximate optimization problem as

$\begin{array}{llll}\hfill & ({\mathrm{P}}_4):\underset{{\mathcal{V}}_4}{\text{minimize}}\hfill & \hfill & \sum _{k\in \mathcal{K}}{\alpha }_k\left({‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\hfill \end{array}(\mathrm{58a})$

$\begin{array}{llll}\hfill & \text{subject\hspace{0.17em}to}\hfill & \hfill & (47),(16c),(76),\hfill \end{array}(\mathrm{58b})$

$\begin{array}{llll}\hfill & \hfill & \hfill & \sum _{j\in \mathcal{K}}{({\mathbf{w}}_j^p)}^H{\overline{\mathbf{Y}}}_{k,k}^p{\mathbf{w}}_j^p+\sum _{l\in {\mathrm{\Omega }}_k}{({\mathbf{w}}_l^c)}^H{\overline{\mathbf{Y}}}_{k,k}^p{\mathbf{w}}_l^c-2\mathfrak{R}\left\{{({\overline{\mathbf{f}}}_k^p)}^H{\mathbf{w}}_k^p\right\}+\hfill \\ \hfill & \hfill & \hfill & \frac{\log (2){\overline{R}}_k^p}{B}+{\sigma }^2{\overline{t}}_k^p-{\overline{l}}_k^p\le 0\forall k\in \mathcal{K},\hfill \end{array}(\mathrm{58c})$

$\begin{array}{llll}\hfill & \hfill & \hfill & \sum _{j\in \mathcal{K}}{({\mathbf{w}}_j^p)}^H{\overline{\mathbf{Y}}}_{k,i}^c{\mathbf{w}}_j^p+\sum _{l\in {\mathrm{\Omega }}_i}{({\mathbf{w}}_l^c)}^H{\overline{\mathbf{Y}}}_{k,i}^c{\mathbf{w}}_l^c+\sum _{m\in {\mathrm{\Psi }}_{k,i}}{({\mathbf{w}}_m^c)}^H{\overline{\mathbf{Y}}}_{k,i}^c{\mathbf{w}}_m^c\hfill \\ \hfill & \hfill & \hfill & +{({\mathbf{w}}_k^c)}^H{\overline{\mathbf{Y}}}_{k,i}^c{\mathbf{w}}_k^c-\hfill \\ \hfill & \hfill & \hfill & 2\mathfrak{R}\left\{{({\overline{\mathbf{f}}}_{k,i}^c)}^H{\mathbf{w}}_k^c\right\}+\frac{\log (2){\overline{R}}_k^c}{B}+{\sigma }^2{\overline{t}}_{k,i}^c-{\overline{l}}_{k,i}^c\le 0,\forall i\in {\mathcal{M}}_k,\forall k\in \mathcal{K},\hfill \end{array}(\mathrm{58d})$

where ${\mathcal{V}}_4$ is defined as

${\mathcal{V}}_4=:\left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,{\overline{R}}_k^p,{\overline{R}}_k^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(59)$

ALGORITHM 1

ALGORITHM 1. Joint rate allocation and beamforming for minimizing the sum-transmit power with stochastic QoS constraints.

The approximate optimization problem (P₄) is convex and can be solved efficiently, e.g., using an interior point method as implemented in commercial solvers (Grant and Boyd, 2014). After solving the optimization problem, we update the beamforming vectors. The detailed steps of the iterative algorithm are listed below.

Theorem 2. Let ${\left\{{\mathbf{q}}^u\right\}}_{u=1}^{\infty }\triangleq {\left\{{\mathbf{w}}^u,{\mathbf{u}}^u,{\mathbf{R}}^u,{\mathit{\rho }}^u\right\}}_{u=1}^{\infty }$ be the sequence generated by Algorithm 1, where u is the iteration number. The sequence ${\left\{{\mathbf{q}}^u\right\}}_{u=1}^{\infty }$ converges to a KKT solution of the problem P₃(M).

Proof. The details are given in Appendix B.

5 Special Case: Full CSIT

We start by discussing a special case in which the CP has full knowledge of CSI. In this scenario, the optimization is performed subject to per-BS maximum transmit power, fronthaul capacity, and user-target instantaneous rate constraints. The corresponding optimization problem can be expressed as

$\begin{array}{llll}\hfill ({\mathrm{P}}_6):& \underset{{\mathcal{V}}_6}{\text{minimize}}\hfill & \hfill & \sum _{k=1}^K{\alpha }_k\left(\sum _{n=1}^N\left({‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\right)\hfill \\ \hfill & \text{subject\hspace{0.17em}to}\hfill & \hfill & (9)\text{and}(10),\hfill \end{array}(\mathrm{60a})$

$\begin{array}{lllll}\hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^p}{\log }_2\left(1+{\gamma }_k^p\right)+\hfill & \hfill \\ \hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^c}\underset{i\in {\mathcal{M}}_k}{\min }\left\{{\log }_2\left(1+{\gamma }_{k,i}^c\right)\right\}\le F_n/B,\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{60b})$

$\begin{array}{lllll}\hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^p}{\log }_2\left(1+{\gamma }_k^p\right)+\hfill & \hfill \\ \hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^c}\underset{i\in {\mathcal{M}}_k}{\min }\left\{{\log }_2\left(1+{\gamma }_{k,i}^c\right)\right\}\ge r_k^{\text{min}},\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(\mathrm{60c})$

where ${\mathcal{V}}_6$ is the set of optimization variables associated with the problem P₆ and is given as

${\mathcal{V}}_6\triangleq \left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,R_k^p,R_k^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(61)$

The discrete variables ${\mathcal{K}}_n^p,{\mathcal{K}}_n^c$ are determined by solving the problem in Eqs 21a–and using Eqs 24a,b. In contrast to (P₀), the problem (P₆) is deterministic as the instantaneous rate expressions in Eqs 11, 12 are achievable, thanks to the full CSIT knowledge. Ahmad et al. (2020a) proposed an inner convex approximation (ICA)-based iterative algorithm to solve the class of optimization problems as the problem (P₆). However, in this paper, we assort to use the WMMSE-based iterative algorithm to solve both problems (P₆) and (P₀). In contrast to the ICA-based algorithm investigated by Ahmad et al. (2020a), our proposed WMMSE-based algorithm is scalable and its complexity is independent of the sample size M. Thus, the computational complexity is significantly reduced when using the WMMSE-based algorithm compared to the ICA-based algorithm.

To this end, we explain the WMMSE-based algorithm to solve the optimization problem (P₆) under the assumption of full CSIT knowledge. By using the instantaneous rate–WMMSE relationship, we reformulate the problem (P₆) as follows:

$\begin{array}{lllll}\hfill ({\mathrm{P}}_7):& \underset{{\mathcal{V}}_7}{\text{minimize}}\hfill & \hfill & \sum _{k=1}^K{\alpha }_k\left(\sum _{n=1}^N{‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\hfill & \hfill \\ \hfill & \text{subject\hspace{0.17em}to}\hfill & \hfill & (40),\hfill & \hfill \\ \hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^p}\left(1-{\zeta }_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p\right)+\hfill & \hfill \\ \hfill & \hfill & \hfill & \sum _{k\in {\mathcal{K}}_n^c}\underset{i\in {\mathcal{M}}_k}{\min }\left\{\left(1-{\zeta }_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c\right)\right\}\le F_{n/B},\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{62a})$

$\begin{array}{lllll}\hfill & \hfill & \hfill & \left(1-{\zeta }_{k,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^p\right)+\hfill & \hfill \\ \hfill & \hfill & \hfill & \underset{i\in {\mathcal{M}}_k}{\min }\left\{\left(1-{\zeta }_{k,i,\mathrm{m}\mathrm{m}\mathrm{s}\mathrm{e}}^c\right)\right\}\ge r_k^{\text{min}},\hfill & \hfill & \forall k\in \mathcal{K},\hfill \end{array}(\mathrm{62b})$

where ${\mathcal{V}}_7$ is the set of optimization variables associated with the problem (P₇) and is given as

${\mathcal{V}}_7\triangleq \left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,{\mathbf{u}}_k^p,{\mathit{\rho }}_k^p,{\mathbf{u}}_k^c,{\mathit{\rho }}_k^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(63)$

The problem (P₇) is still non-convex and challenging to solve as the expressions of the WMMSE in Eqs 40a,b are non-jointly convex in all the variables. Therefore, we propose to iteratively optimize over each independent set of variables for which the expressions become convex. To this end, by using the optimal values of the receiver and weighting coefficients, i.e., $\{{\mathbf{u}}_k^p,{\mathit{\rho }}_k^p,{\mathbf{u}}_k^c,{\mathit{\rho }}_k^c|\forall k\in \mathcal{K}\}$, and similar to the reformulation of the problem (P₄), we write

$\begin{array}{ll}\hfill ({\mathrm{P}}_8):& \underset{{\mathcal{V}}_8}{\text{minimize}}\sum _{k=1}^K{\alpha }_k\left(\sum _{n=1}^N{‖{\mathbf{w}}_{n,k}^p‖}_2^2+{‖{\mathbf{w}}_{n,k}^c‖}_2^2\right)\hfill \\ \hfill & \text{subject\hspace{0.17em}to}\hfill \\ \hfill & R_k^p+R_k^c\ge r_k^{\text{min}},\forall k\in \mathcal{K},\hfill \end{array}(\mathrm{64a})$

$\begin{array}{ll}\hfill & \sum _{k\in {\mathcal{K}}_n^p}{R}_k^p+\sum _{k\in {\mathcal{K}}_n^c}{R}_k^c\le F_n/B\forall n\in \mathcal{N},\hfill \end{array}(\mathrm{64b})$

$\begin{array}{ll}\hfill & \sum _{j\in \mathcal{K}}{({\mathbf{w}}_j^p)}^H{\mathbf{Y}}_{k,k}^p{\mathbf{w}}_j^p+\sum _{l\in {\mathrm{\Omega }}_k}{({\mathbf{w}}_l^c)}^H{\mathbf{Y}}_{k,k}^p{\mathbf{w}}_l^c-2\mathfrak{R}\left\{{({\mathbf{f}}_k^p)}^H{\mathbf{w}}_k^p\right\}\hfill \\ \hfill & +\frac{\log (2)R_k^p}{B}+{\sigma }^2{t}_k^p-l_k^p\le 0,\forall k\in \mathcal{K},\hfill \end{array}(\mathrm{64c})$

$\begin{array}{ll}\hfill & \sum _{j\in \mathcal{K}}{({\mathbf{w}}_j^p)}^H{\mathbf{Y}}_{k,i}^c{\mathbf{w}}_j^p+\sum _{l\in {\mathrm{\Omega }}_i}{({\mathbf{w}}_l^c)}^H{\mathbf{Y}}_{k,i}^c{\mathbf{w}}_l^c+\sum _{m\in {\mathrm{\Psi }}_{k,i}}{({\mathbf{w}}_m^c)}^H{\mathbf{Y}}_{k,i}^c{\mathbf{w}}_m^c\hfill \\ \hfill & +{({\mathbf{w}}_k^c)}^H{\mathbf{Y}}_{k,i}^c{\mathbf{w}}_k^c-2\mathfrak{R}\left\{{({\mathbf{f}}_{k,i}^c)}^H{\mathbf{w}}_k^c\right\}\hfill \\ \hfill & +\frac{\log (2)R_k^c}{B}+{\sigma }^2{t}_{k,i}^c-l_{k,i}^c\le 0,\forall i\in {\mathcal{M}}_k,\forall k\in \mathcal{K},\hfill \end{array}(\mathrm{64d})$

where

${\mathcal{V}}_8\triangleq \left\{{\mathbf{w}}_k^p,{\mathbf{w}}_k^c,R_k^p,R_k^c|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\right\}.(65)$

Here, the auxiliary variables $\left\{t_k^p,t_{k,i}^c,l_k^p,{\overline{l}}_{k,i}^c,{\mathbf{f}}_k^p,{\mathbf{f}}_{k,i}^c,{\mathbf{Y}}_{k,k}^p,{\mathbf{Y}}_{k,i}^c\right\}$ are the deterministic version of the sample average functions defined in Eqs 52–57, and they can be written as

$\begin{array}{llll}\hfill {\rho }_k^p& =1/e_{k,\text{mmse}}^p,\hfill & \hfill {\rho }_{k,i}^c& =1/e_{k,i,\text{mmse}}^c,\hfill \end{array}(66)$

$\begin{array}{llll}\hfill t_k^p& ={\rho }_k^p{‖u_k^p‖}_2^2,\hfill & \hfill t_{k,i}^c& ={\rho }_{k,i}^c{‖u_{k,i}^c‖}_2^2,\hfill \end{array}(67)$

$\begin{array}{llll}\hfill l_k^p& =(1-{\rho }_k^p+\log ({\rho }_k^p)),\hfill & \hfill l_{k,i}^c& =(1-{\rho }_{k,i}^c+\log ({\rho }_{k,i}^c)),\hfill \end{array}(68)$

$\begin{array}{llll}\hfill {\mathbf{f}}_k^p& ={\rho }_k^p{\mathbf{h}}_k{u}_k^p,\hfill & \hfill {\mathbf{f}}_{k,i}^c& ={\rho }_{k,i}^c{\mathbf{h}}_i{u}_{k,i}^c,\hfill \end{array}(69)$

$\begin{array}{llll}\hfill {\mathbf{Y}}_{k,k}^p& =\left({\rho }_k^p{‖u_k^p‖}_2^2{\mathbf{h}}_k{({\mathbf{h}}_k)}^H\right),\hfill & \hfill {\mathbf{Y}}_{k,i}^c& =\left({\rho }_{k,i}^c{‖u_{k,i}^c‖}_2^2{\mathbf{h}}_i{({\mathbf{h}}_i)}^H\right).\hfill \end{array}(70)$

The optimal receiver coefficients and the MMSE expressions are given by Eqs 50, 51. Note that the problem (P₈) is now convex. With the help of the general assignment problem in Eqs 21a–ca–cEqs 21a–c and Eqs 24a,b, we guarantee the fronthaul capacity constraints are respected. However, in contrast to the weighted sum-rate problem studied by Alameer Ahmad et al. (2019) and Ahmad et al. (2021), the feasibility of the problem (P₈) is not assured. If some users have poor channel quality, the network designer cannot make sure that all users can meet their requirements in Eq. 64a. The determination of the complete set of feasible values $r_k^{\text{min}}$ for a given CSI is, indeed, equivalent to the characterization of the capacity region for a multi-antenna interference channel, which remains an open problem in the communication theory area. Thus, solving the feasibility issue of problem (P₈) falls out of this paper’s scope. Instead, we focus on the feasible instances of the problem (P₈) in the analysis and numerical simulations. Now, we discuss the block coordinate descent algorithm to find a solution for the problem (P₇), whenever it is feasible. The idea is to iteratively solve the approximate problem (P₈) and enhance the approximation after each iteration. The detailed steps of such an approach, hereafter called Algorithm 2, are shown below.

ALGORITHM 2

ALGORITHM 2. Weighted sum-Power minimization subject to QoS constraints..

6 Numerical Simulations

This section illustrates the performance of the proposed algorithms in a realistic network setup. We first describe the adopted simulation parameters. Then, we present the numerical results in detail.

6.1 Simulation Parameters and Studied Schemes

The adopted channel model is standardized by the 3rd Generation Partnership Project (3GPP) (3GPP, 2015) and used in most of the works in the literature, e.g., Björnson and Jorswieck, 2013; Shi et al., 2014; Wei Yu and Yu, 2014:

${\mathbf{h}}_{n,k}=D_{n,k}{\mathbf{e}}_{n,k}.(71)$

Here, $D_{n,k}=10^{-\mathrm{P}\mathrm{L}(d_{n,k})/20}\sqrt{g_{n,k}{s}_{n,k}}$, where g_n,k is the shadowing coefficient, s_n,k is the antenna gain, and PL(d_n,k) is the path-loss coefficient defined as

$\mathrm{P}\mathrm{L}(d_{n,k})=128.1+37.6{\log }_{10}(d_{n,k}).(72)$

Here, d_n,k is the distance between BS n and user k in km. The coefficients ${\mathbf{e}}_{n,k}\in {\mathbb{C}}^{L\times 1}$ in Eq. 71 represent the small-fading component and are modeled as ${\mathbf{e}}_{n,k}\sim \mathcal{CN}({\mathbf{0}}_L,{\mathbf{I}}_L)$. In this work, we mean by a full CSIT scenario that the CP has full knowledge of the coefficients $\{{\mathbf{h}}_{n,k}|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\}$, i.e., both large-scale fading coefficients $\{D_{n,k}|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\}$ and small-scale fading coefficients $\{{\mathbf{e}}_{n,k}|\forall k\in \mathcal{K},\forall n\in \mathcal{N}\}$ are perfectly estimated at the CP. In the statistical CSIT, alternatively, we consider the CP can perfectly estimate the large fading coefficients D_n,k (Razaviyayn et al., 2013); however, the small-fading coefficients are unknown at the CP. Note that, in this scenario, the covariance matrix of the channel between user k and BS n is given by ${\mathbf{Q}}_{n,k}=D_{n,k}^2{\mathbf{I}}_L$. In the simulations, we use the proposed algorithms in full CSIT and in statistical CSIT scenarios, and we test dynamic and static clustering algorithms. The parameters for specifying the common message sets and the serving clusters are, respectively, given as δ = 150 m and μ = 5 unless we state otherwise. The noise spectral density is set to −120 dBm/Hz. The weights for the user’s rates are considered to be ${\alpha }_k=1\forall k\in \mathcal{K}$ unless otherwise mentioned. The transmit bandwidth is equal to 10 MHz. In the following simulations, we compare our proposed RS–CMD scheme with state-of-the-art multiple access schemes. Specifically, we consider the following schemes under the assumption of statistical knowledge of CSI at the CP:

1) TIN: The conventional TIN scheme.

2) RS-scheme 1: This benchmark is proposed by Joudeh and Clerckx (2016a). This scheme uses a broadcast transmit signal as a common message that must be decoded by all users in addition to the private messages that need to be decoded by intended users only.

3) NOMA: This scheme relies on superposition coding (SC) at the transmitter and successive interference cancellation at the receivers. In the simulations, we adopt the SC-SIC per group multi-antenna NOMA strategy, similar to the scheme adopted by Mao et al. (2018) for an MISO-BC.

6.2 Full CSIT

In this scenario, we consider the CP has perfect CSI. We perform a set of numerical simulations to evaluate the performance of the assignment algorithm that uses the solution of the optimization problem in Eqs 21a–c and Eqs 24a,b in addition to Algorithm 2. Both algorithms are used to solve the optimization problem (P₆) in the special case of full CSIT. Note that, in contrast to the optimization problem (P₂), the problem (P₆) is deterministic as the QoS constraints are given in terms of instantaneous rates. We compare our proposed RS–CMD transmission strategy to the conventional scheme TIN. The simulations are averaged over one hundred feasible network realizations. Note that the optimization problem (P₆) is not always feasible. The non-feasible problem instances are ignored. Nevertheless, the impact of both transmission schemes on the feasibility of the problem is analyzed.

6.2.1 Transmit Power as a Function of the Required Instantaneous QoS

In this simulation, we consider a C-RAN that consists of ten BSs, each equipped with two antennas and a fronthaul link with a capacity of 70 Mbps, serving a set of eight users. The required QoS per user is increased from 2 to 16 Mbps. Figure 3 shows the performance of RS–CMD and TIN transmission schemes in this setup. As expected, more transmit power is required in the C-RAN as the QoS demands become larger. However, the gain of RS–CMD considerably increases compared to that of TIN when the QoS values grow. Above a specific QoS value, both transmission schemes fail to find feasible solutions. Nevertheless, using RS–CMD, the C-RAN can accommodate higher QoS demands.

FIGURE 3

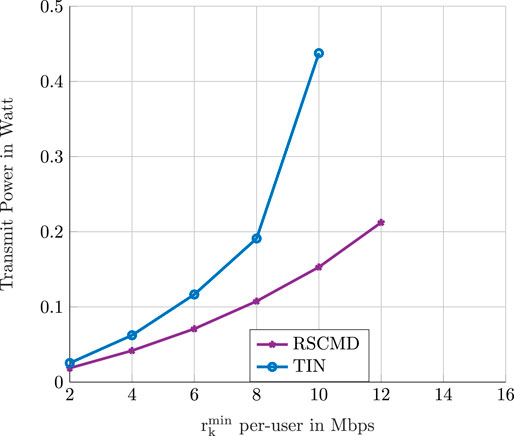
FIGURE 3. The optimal value of the optimization problem (P₆) as a function of the deterministic required QoS per user.

Next, we explore the impact of the user’s number on the performance.

6.3 Transmit Power as a Function of the User’s Number

In this simulation, we generate a C-RAN of five BSs, each equipped with two antennas and a fronthaul link with a capacity of 100 Mbps. We increase the number of users from two to ten and investigate two scenarios. The first one considers a minimum rate of ${\text{r}}_{\text{k}}^{\text{min}}=6$ Mbps per user, and in the second one, each user requests a minimum rate of ${\text{r}}_{\text{k}}^{\text{min}}=8$ Mbps. As shown in Figure 4, the results coincide with our expectation; when increasing the QoS demands, both transmission schemes require more transmit power to satisfy the user requirements. The gain of RS–CMD becomes significant as the number of users and their demands increase, which shed light on the importance of the RS–CMD transmission scheme enabling future communication networks satisfying the demands of a large number of users. In the following section, we discuss the statistical CSIT case and investigate the role of RS–CMD in such a network setup.

FIGURE 4

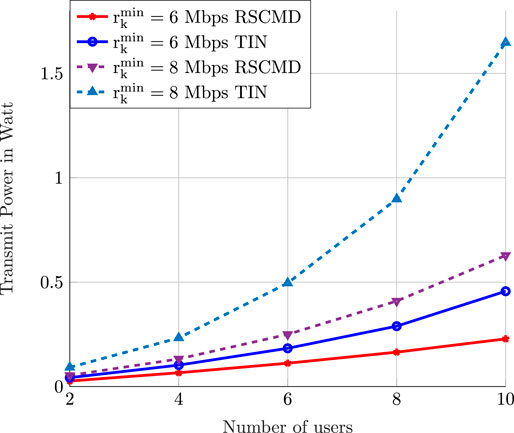
FIGURE 4. The optimal value of the optimization problem (P₆) with deterministic QoS constraints as a function of the number of users.

6.4 Statistical CSIT

This scenario considers that the CP only acquires the channel distribution and not the full CSI. Numerical simulations are performed to analyze the performance of RS–CMD and TIN transmission schemes. We deploy the optimization algorithm (Algorithm 1). The simulations are averaged over one hundred feasible network realizations. For each network realization, the CP uses the statistical CSI knowledge for generating a Monte Carlo sample to perform the SAA. The sample consists of M = 1000 independent and identically distributed (i.i.d.) channel realizations.

6.4.1 Impact of Sample Size on the Accuracy of SAA

The accuracy of SAA that approximates the ergodic rate (or equivalently the MMSE expressions) depends on the sample size M. We know from Theorem 1 that the SAA converges almost surely to the ergodic rate expressions.

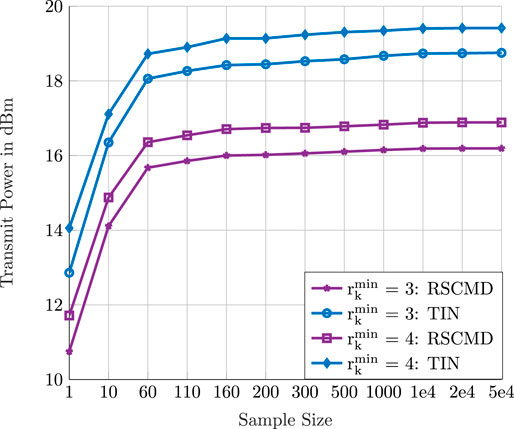
As aforementioned, in the numerical examples, we choose the sample size to be M = 1000, representing a reasonable value that balances the complexity versus accuracy. To justify this choice, we investigate the impact of the sample size on the convergence of the SAA. We generate a C-RAN that consists of eight BSs, each equipped with two antennas, serving six users. We consider two scenarios; in the first one, each user requests a minimum ergodic rate of 3 Mbps. In the second scenario, each user requests a minimum ergodic rate of 4 Mbps. Thus, we solve the optimization problem (P₂), using different sample sizes, as shown in Figure 5. Each point on Figure 5 is averaged over one hundred feasible network realizations. We note that our proposed RS–CMD scheme significantly outperforms the conventional TIN in both scenarios. Interestingly, the SAA converges from sample size M = 500 onward. Thus, the changes after M = 500 are minimal and can be ignored. That is, the sample size choice of M = 1000 is reasonable and can accurately approximate the ergodic rate expressions using the SAA. We emphasize here that the main advantage of the rate–WMMSE optimization approach adopted in this paper is that the complexity of solving the problem (P₂) becomes independent of the sample size.

FIGURE 5

FIGURE 5. The optimal value of the optimization problem P₂ as a function of the sample size.

Next, we investigate the impact of the number of users on the achievable network transmit power and the feasibility of the optimization problem (P₂).

6.5 Impact of the Number of Users on the Transmit Power

In this simulation, we study the performance of RS–CMD and TIN transmission schemes as the number of users increases from two to ten. We consider a C-RAN of fifteen BSs, each with two antennas and a fronthaul link with a capacity of 40 Mbps. The minimum ergodic rate requested by each user is considered to be 5 Mbps.

As shown in Figure 6, the RS–CMD strategy outperforms the conventional TIN and achieves less sum-transmit power. The gain of RS–CMD increases as the number of users increases. That is, when the number of users becomes larger, the interference level increases. Interestingly, the feasibility of the problem is considerably improved. Specifically, under the same physical conditions, RS–CMD can accommodate up to nine users, while the conventional TIN stops at five users. As shown in Figure 6, under the same sum-power, we can serve up to seven users using RS–CMD, while we can serve five users using TIN. Note that, for each point, the number of feasible realizations drops below 50% of the studied network realizations. That is, we consider the transmission strategy is not able to accommodate the corresponding number of users. The feasibility percentage of each studied scenario for both transmission schemes is depicted in Table 1.

FIGURE 6

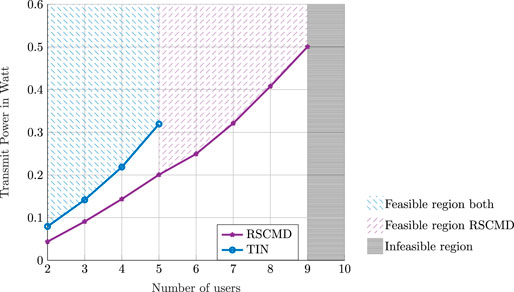
FIGURE 6. The optimal value of the optimization problem (P₂) as a function of the number of users. We compare the performance of TIN and RS–CMD transmission strategies.

TABLE 1

TABLE 1. Percentage of feasible instances of the optimization problem (P₂) when deploying TIN and RS–CMD transmission strategies.

The feasibility percentage is measured by simulating two hundred network realizations. The result in Table 1 is very interesting. It says by using the RS–CMD transmission strategy, we can significantly extend the feasible region without using additional complicated measures, e.g., admission control. In the next generation of wireless communication networks, using RS–CMD may, therefore, be indispensable to fulfill the heterogeneous QoS of many applications. Next, we discuss the impact of the requested QoS on the performance of both considered transmission schemes.

6.6 Impact of the Stochastic QoS on the Transmit Power

In this simulation, we generate a C-RAN of five users and ten BSs each with two antennas and a fronthaul capacity of 40 Mbps. We increase the minimum ergodic rate requested by each user from 1 Mbps to 8 Mbps. The performances of RS–CMD and TIN transmission schemes are compared. As a benchmark, we also consider the case when the CP has full CSIT knowledge. As shown in Figure 7, when the CP has perfect CSIT, the C-RAN requires less transmit power to satisfy the user’s requirements. Moreover, with RS–CMD, the C-RAN can achieve lower sum-transmit power compared to the case when TIN is employed. This result can also be interpreted as follows: With the same sum-transmit power, by adopting the RS–CMD transmit strategy, the C-RAN can accommodate users with higher QoS requirements compared to that when adopting TIN.

FIGURE 7

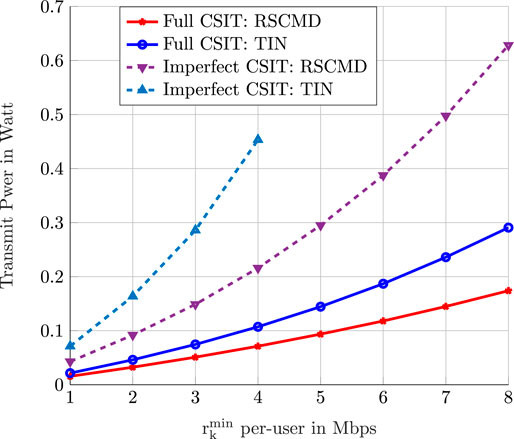
FIGURE 7. The optimal value of the optimization problem (P₂) as a function of the minimum ergodic rate requested by users. We compare the performance of TIN and RS–CMD transmission strategies. Each BS has two antennas.

To shed light on the effect of increasing the number of transmit antennas on the performance, we simulate the same C-RAN, but we increase the number of antennas per BS to four antennas. The result of simulating this network is depicted in Figure 8. The performance of all studied schemes improves as the number of antennas becomes larger. However, the performance gap between TIN and RS–CMD shrinks, compared to the previous scenario. Thus, with a higher number of antennas, the C-RAN can efficiently mitigate the interference. Moreover, the optimization problem’s feasibility improves, especially for the transmission scheme TIN. To investigate the feasibility of both studied schemes, we illustrate the percentage of feasible instances of the optimization problem (P₂) when using TIN and RS–CMD for both scenarios, that is, when the number of antennas per BS is equal to two and four, in Tables 2, 3, respectively. The transmission scheme RS–CMD significantly extends the feasibility region of the optimization problem, especially when the user’s demands increase, and the optimization problem becomes more challenging. Specifically, when the minimum QoS ergodic rate requested by each user is equal to 6 Mbps, the percentage of feasible instances using RS–CMD is equal to 94.4%. This percentage drops down to 8.4% when using TIN in the case, where each BS is equipped with two antennas. When we double the number of antennas per BS, the percentage of feasible instances increases to 97.2% when using RS–CMD and reaches up to 12.4% using TIN for the same value of the requested QoS per user. Thus, the benefits of employing RS–CMD are not limited to increasing the network throughout as we saw in our previous works or minimizing the network transmit power as illustrated in this section. However, RS–CMD can also help extending the feasibility region and therefore enabling the C-RAN to accommodate a higher number of users and greater demands, without extra psychical resources.

FIGURE 8

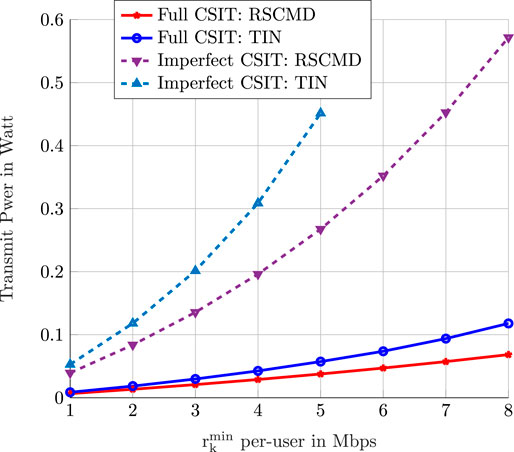
FIGURE 8. The optimal value of the optimization problem (P₂) as a function of the minimum ergodic rate requested by users. We compare the performance of TIN and RS–CMD transmission strategies. Each BS has four antennas.

TABLE 2

TABLE 2. Percentage of feasible instances of the optimization problem (P₂) when deploying TIN and RS–CMD transmission strategies. Each BS is equipped with two antennas.

TABLE 3

TABLE 3. Percentage of feasible instances of the optimization problem (P₂) when deploying TIN and RS–CMD transmission strategies. Each BS is equipped with four antennas.

6.7 Comparison With Other Benchmark Schemes

In this simulation, we compare the performance of our proposed RS–CMD scheme with different multiple access schemes. In particular, we consider the performance of NOMA as described by Mao et al. (2018) and of the RS scheme as proposed by Joudeh and Clerckx (2016a) in addition to the conventional TIN as benchmarks. We consider a C-RAN that consists of five BSs and the fronthaul capacity link of 80 Mbps per BS. Figure 9 illustrates the performance of all studied schemes. Figure 9 shows that the RS-based multiple access schemes achieve the best performance. Moreover, NOMA also outperforms TIN, especially as the number of users increases the gain of the RS-based scheme, and NOMA becomes more pronounced. This result coincides with the findings by Mao et al. (2018) as it is shown that RS-based schemes generalize and outperform both TIN and NOMA in the MISO-BC. Interestingly, the feasibility of the problem significantly improves as the fronthaul capacity per BS increases.

FIGURE 9

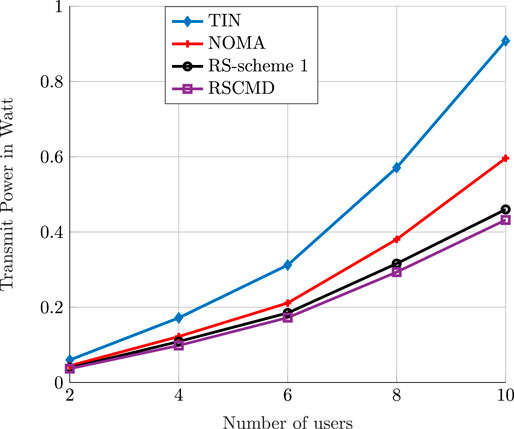
FIGURE 9. The optimal value of the optimization problem (P₂) as a function of the number of users. We compare the performance of TIN, NOMA, RS-scheme 1, and RS–CMD transmission strategies.

Figure 10 shows the performance as a function of the QoS requirements per user with the number of users set to 8. Figure 10 also shows the superiority of the RS-based transmission scheme. Again, our proposed RS–CMD scheme achieves the best performance among all studied multiple access schemes. The gain increases as the problem becomes more challenging by increasing the required QoS per user.

FIGURE 10

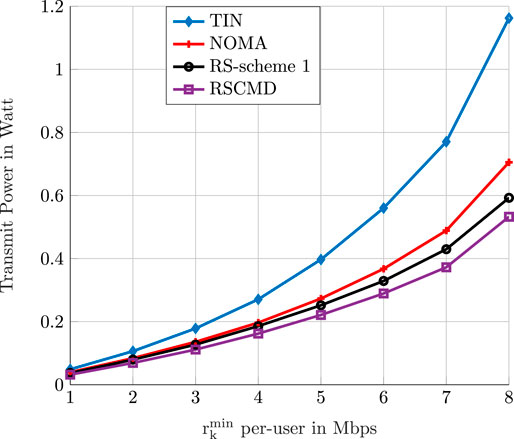
FIGURE 10. The optimal value of the optimization problem (P₂) as a function of the minimum ergodic rate requested by users. We compare the performance of TIN, NOMA, RS-scheme 1, and RS–CMD transmission strategies. Each BS has two antennas.

7 Conclusion

This paper demonstrates the benefits of using RS–CMD in the C-RAN. In particular, it sheds light on the significant gain in minimizing the transmit power costs in the network while ensuring the minimum QoS for the users. We consider two scenarios: the full CSIT in which the QoS constraints are expressed in terms of the minimum instantaneous rate required by each user and the statistical CSIT where the CP has only the channel’s distribution information. In this case, QoS constraints are stochastic and expressed in terms of the minimum ergodic rate required by each user. In the full CSIT scenario, we formulate first an assignment problem that exploits the full CSIT to associate the BSs with users. Afterward, we use the WMMSE algorithm to solve the resulting non-convex optimization problem. The statistical CSIT is more challenging as the QoS constraints are stochastic and non-convex. In this case, we first use the assignment problem to associate the BSs with users by exploiting the statistical information of the CSI. The resulting non-convex stochastic problem is tackled by leveraging both SAA and WMMSE algorithms. The proposed RS–CMD significantly outperforms the conventional TIN in reducing the network transmit power subject to QoS constraints. Furthermore, the benefit of using QoS is particularly high in terms of maximizing the feasible set of admitted users as compared to the classical TIN approach.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AA made substantial contributions to the conception or design of the work and the acquisition, analysis, or interpretation of data in this work. HD and AS revised the article critically for important intellectual content. AC, AS, TA-N, JS, and M-SA provided approval for publication of the content.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Robert-Jeron Reifert for helping out with preparing the figures in this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frcmn.2021.716618/full#supplementary-material

References

3GPP (2015). “Evolved Universal Terrestrial Radio Access (E-UTRA); Further Advancements for E-UTRA Physical Layer Aspects,” 3rd Generation Partnership Project (3GPP), Technical Specification (TS) 36.814 version 9.

Google Scholar

Ahmad, A. A., Dahrouj, H., Chaaban, A., Sezgin, A., Al-Naffouri, T. Y., and Alouini, M.-S. (2020). “Power Minimization via Rate Splitting in Downlink Cloud-Radio Access Networks,” in 2020 IEEE International Conference on Communications Workshops, Dublin, Ireland. ICC Workshops, 1–6. doi:10.1109/iccworkshops49005.2020.9145363

CrossRef Full Text | Google Scholar

Ahmad, A. A., Mao, Y., Sezgin, A., and Clerckx, B. (2020). “Rate Splitting Multiple Access in C-RAN,” in 2020 IEEE 31st Annual International Symposium on Personal Indoor Mobile Radio Commun., London, United Kingdom, 1–6.

CrossRef Full Text | Google Scholar

Ahmad, A. A., Mao, Y., Sezgin, A., and Clerckx, B. (2021). Rate Splitting Multiple Access in C-RAN: A Scalable and Robust Design. IEEE Trans. Commun. doi:10.1109/tcomm.2021.3085343

CrossRef Full Text | Google Scholar

Alameer Ahmad, A., Dahrouj, H., Chaaban, A., Sezgin, A., and Alouini, M. (2019). Interference Mitigation via Rate-Splitting and Common Message Decoding in Cloud Radio Access Networks. IEEE Access. 7, 80 350–80365. doi:10.1109/access.2019.2921626

CrossRef Full Text | Google Scholar

Björnson, E., and Jorswieck, E. (2013). Optimal Resource Allocation in Coordinated Multi-Cell Systems. Found. Trends Commun. Inf. Theory 9 (2-3), 113–381. doi:10.1561/0100000069

CrossRef Full Text | Google Scholar

Carleial, A. (1978). Interference Channels. IEEE Trans. Inform. Theor. 24 (1), 60–70. doi:10.1109/tit.1978.1055812

CrossRef Full Text | Google Scholar

Charafeddine, M. A., Sezgin, A., Han, Z., and Paulraj, A. (2012). Achievable and Crystallized Rate Regions of the Interference Channel with Interference as Noise. IEEE Trans. Wireless Commun. 11 (3), 1100–1111. doi:10.1109/twc.2012.010312.110497

CrossRef Full Text | Google Scholar

Clerckx, B., Joudeh, H., Hao, C., Dai, M., and Rassouli, B. (2016). Rate Splitting for MIMO Wireless Networks: a Promising PHY-Layer Strategy for LTE Evolution. IEEE Commun. Mag. 54 (5), 98–105. doi:10.1109/mcom.2016.7470942

CrossRef Full Text | Google Scholar

Clerckx, B., Mao, Y., Schober, R., and Poor, H. V. (2020). Rate-Splitting Unifying SDMA, OMA, NOMA, and Multicasting in MISO Broadcast Channel: A Simple Two-User Rate Analysis. IEEE Wireless Commun. Lett. 9 (3), 349–353. doi:10.1109/LWC.2019.2954518

CrossRef Full Text | Google Scholar

Cui, W., Shen, K., and Yu, W. (2019). Spatial Deep Learning for Wireless Scheduling. IEEE J. Select. Areas Commun. 37 (6), 1248–1261. doi:10.1109/jsac.2019.2904352

CrossRef Full Text | Google Scholar

Dahrouj, H., and Yu, W. (2011). Multicell Interference Mitigation with Joint Beamforming and Common Message Decoding. IEEE Trans. Commun. 59 (8), 2264–2273. doi:10.1109/tcomm.2011.060911.100554

CrossRef Full Text | Google Scholar

Dai, M., Clerckx, B., Gesbert, D., and Caire, G. (2016). A Rate Splitting Strategy for Massive MIMO with Imperfect CSIT. IEEE Trans. Wireless Commun. 15 (7), 4611–4624. doi:10.1109/twc.2016.2543212

CrossRef Full Text | Google Scholar

Ericsson (2019). Ericsson Mobility Report November 2019. Tech. Rep. MSU-CSE-06-2. Available: https://www.ericsson.com/en/mobility-report/reports/november-2019.

Google Scholar

Etkin, R. H., Tse, D. N. C., and Wang, H. (2008). Gaussian Interference Channel Capacity to within One Bit. IEEE Trans. Inform. Theor. 54 (12), 5534–5562. doi:10.1109/tit.2008.2006447

CrossRef Full Text | Google Scholar

Gesbert, D., Hanly, S., Huang, H., Shamai Shitz, S., Simeone, O., and Yu, W. (2010). Multi-cell Mimo Cooperative Networks: A New Look at Interference. IEEE J. Select. Areas Commun. 28 (9), 1380–1408. doi:10.1109/jsac.2010.101202

CrossRef Full Text | Google Scholar

Gherekhloo, S., Chaaban, A., Di, C., and Sezgin, A. (2016). (Sub-)Optimality of Treating Interference as Noise in the Cellular Uplink with Weak Interference. IEEE Trans. Inform. Theor. 62 (1), 322–356. doi:10.1109/tit.2015.2499189

CrossRef Full Text | Google Scholar

Goldsmith, A. (2005). Capacity of Wireless Channels. CA, United States: Stanford University, 99–125. doi:10.1017/cbo9780511841224.005

CrossRef Full Text

Grant, M., and Boyd, S. (2014). Data From: Matlab Software for Disciplined Convex Programming. version 2.1. http://cvxr.com/cvx.

Google Scholar

Gu, X., Ji, X., Ding, Z., Wu, W., and Peng, M. (2018). Outage Probability Analysis of Non-orthogonal Multiple Access in Cloud Radio Access Networks. IEEE Commun. Lett. 22 (1), 149–152. doi:10.1109/lcomm.2017.2761828

CrossRef Full Text | Google Scholar

Jaafar, W., Naser, S., Muhaidat, S., Sofotasios, P. C., and Yanikomeroglu, H. (2020). Multiple Access in Aerial Networks: From Orthogonal and Non-orthogonal to Rate-Splitting. IEEE Open J. Veh. Technol. 1, 372–392. doi:10.1109/ojvt.2020.3032844

CrossRef Full Text | Google Scholar

Joudeh, H., and Clerckx, B. (2017). Rate-Splitting for Max-Min Fair Multigroup Multicast Beamforming in Overloaded Systems. IEEE Trans. Wireless Commun. 16 (11), 7276–7289. doi:10.1109/twc.2017.2744629

CrossRef Full Text | Google Scholar

Joudeh, H., and Clerckx, B. (2016a). Robust Transmission in Downlink Multiuser MISO Systems: A Rate-Splitting Approach. IEEE Trans. Signal. Process. 64 (23), 6227–6242. doi:10.1109/tsp.2016.2591501

CrossRef Full Text | Google Scholar

Joudeh, H., and Clerckx, B. (2016b). Sum-Rate Maximization for Linearly Precoded Downlink Multiuser MISO Systems with Partial CSIT: A Rate-Splitting Approach. IEEE Trans. Commun. 64 (11), 4847–4861. doi:10.1109/tcomm.2016.2603991

CrossRef Full Text | Google Scholar

Love, D., Heath, R., N. Lau, V., Gesbert, D., Rao, B., and Andrews, M. (2008). An Overview of Limited Feedback in Wireless Communication Systems. IEEE J. Select. Areas Commun. 26 (8), 1341–1365. doi:10.1109/jsac.2008.081002

CrossRef Full Text | Google Scholar

Maddah-Ali, M. A., and Tse, D. (2010). “Completely Stale Transmitter Channel State Information Is Still Very Useful,” in 2010 48th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, United States. (Allerton), 1188–1195. doi:10.1109/allerton.2010.5707049

CrossRef Full Text | Google Scholar

Mao, Y., and Clerckx, B. (2020). Beyond Dirty Paper Coding for Multi-Antenna Broadcast Channel with Partial CSIT: A Rate-Splitting Approach. IEEE Trans. Commun. 68 (11), 6775–6791. doi:10.1109/tcomm.2020.3014153

CrossRef Full Text | Google Scholar

Mao, Y., Clerckx, B., and Li, V. O. K. (2018). Rate-Splitting for Downlink Multi-User Multi-Antenna Systems: Bridging NOMA and Conventional Linear Precoding. EURASIP J. Wireless Commun. Netw.

Google Scholar

Mao, Y., Clerckx, B., and Li, V. O. K. (2019). Rate-Splitting for Multi-Antenna Non-orthogonal Unicast and Multicast Transmission: Spectral and Energy Efficiency Analysis. IEEE Trans. Commun. 67 (12), 8754–8770. doi:10.1109/tcomm.2019.2943168

CrossRef Full Text | Google Scholar

Pan, C., Ren, H., Elkashlan, M., Nallanathan, A., and Hanzo, L. (2019). Weighted Sum-Rate Maximization for the Ultra-dense User-Centric TDD C-RAN Downlink Relying on Imperfect CSI. IEEE Trans. Wireless Commun. 18 (2), 1182–1198. doi:10.1109/twc.2018.2890474

CrossRef Full Text | Google Scholar

Pan, C., Zhu, H., Gomes, N. J., and Wang, J. (2017). Joint Precoding and RRH Selection for User-Centric Green MIMO C-RAN. IEEE Trans. Wireless Commun. 16 (5), 2891–2906. doi:10.1109/twc.2017.2671358

CrossRef Full Text | Google Scholar

Pan, C., Zhu, H., Gomes, N. J., and Wang, J. (2017). Joint User Selection and Energy Minimization for Ultra-dense Multi-Channel C-RAN with Incomplete CSI. IEEE J. Select. Areas Commun. 35 (8), 1809–1824. doi:10.1109/jsac.2017.2710858

CrossRef Full Text | Google Scholar

Reifert, R.-J., Ahmad, A. A., Mao, Y., Sezgin, A., and Clerckx, B. (2021). “Rate-Splitting Multiple Access in Cache-Aided Cloud-Radio Access Networks.” arXiv [Epub ahead of print].

Google Scholar

Razaviyayn, M., Hong, M., and Luo, Z.-Q. (2013). Linear Transceiver Design for a Mimo Interfering Broadcast Channel Achieving max-min Fairness. Signal. Process. 93, 3327–3340. Elsevier. doi:10.1016/j.sigpro.2013.02.017

CrossRef Full Text | Google Scholar

Razaviyayn, M., Sanjabi, M., and Luo, Z.-Q. (2016). A Stochastic Successive Minimization Method for Nonsmooth Nonconvex Optimization with Applications to Transceiver Design in Wireless Communication Networks. Math. Program. 157 (2), 515–545. doi:10.1007/s10107-016-1021-7

CrossRef Full Text | Google Scholar

Saad, W., Bennis, M., and Chen, M. (2020). A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 34, 134–142. doi:10.1109/mnet.001.1900287

CrossRef Full Text | Google Scholar

Shapiro, A., Dentcheva, D., and Ruszczyński, A. P. (2009). Lectures on Stochastic Programming: Modeling and Theory. Philadelphia, PA, USA: SIAM.

Shi, Y., Zhang, J., and Letaief, K. B. (2014). Group Sparse Beamforming for Green Cloud-RAN. IEEE Trans. Wireless Commun. 13 (5), 2809–2823. doi:10.1109/twc.2014.040214.131770

CrossRef Full Text | Google Scholar

Shi, Y., Zhang, J., and Letaief, K. B. (2015). Optimal Stochastic Coordinated Beamforming for Wireless Cooperative Networks with CSI Uncertainty. IEEE Trans. Signal. Process. 63 (4), 960–973. doi:10.1109/tsp.2014.2385669

CrossRef Full Text | Google Scholar

Tao, M., Chen, E., Zhou, H., and Yu, W. (2016). Content-Centric Sparse Multicast Beamforming for Cache-Enabled Cloud RAN. IEEE Trans. Wireless Commun. 15 (9), 6118–6131. doi:10.1109/twc.2016.2578922

CrossRef Full Text | Google Scholar

Te Han, T., and Kobayashi, K. (1981). A New Achievable Rate Region for the Interference Channel. IEEE Trans. Inform. Theor. 27 (1), 49–60. doi:10.1109/tit.1981.1056307

CrossRef Full Text | Google Scholar

Wei Yu, B., and Yu, W. (2014). Sparse Beamforming and User-Centric Clustering for Downlink Cloud Radio Access Network. IEEE Access. 2, 1326–1339. doi:10.1109/access.2014.2362860

CrossRef Full Text | Google Scholar

Wubben, D., Rost, P., Bartelt, J. S., Lalam, M., Savin, V., Gorgoglione, M., et al. (2014). Benefits and Impact of Cloud Computing on 5G Signal Processing: Flexible Centralization through Cloud-RAN. IEEE Signal. Process. Mag. 31, 35–44. doi:10.1109/msp.2014.2334952

CrossRef Full Text | Google Scholar

Xia, W., Zhang, J., Quek, T. Q. S., Jin, S., and Zhu, H. (2018). Power Minimization-Based Joint Task Scheduling and Resource Allocation in Downlink C-RAN. IEEE Trans. Wireless Commun. 17 (11), 7268–7280. doi:10.1109/twc.2018.2865955

CrossRef Full Text | Google Scholar

Yang, P., Xiao, Y., Xiao, M., and Li, S. (2019). 6G Wireless Communications: Vision and Potential Techniques. IEEE Netw. 33, 70–75. doi:10.1109/mnet.2019.1800418

CrossRef Full Text | Google Scholar

Yu, D., Kim, J., and Park, S.-H. (2019). An Efficient Rate-Splitting Multiple Access Scheme for the Downlink of C-RAN Systems. IEEE Wireless Commun. Lett. 8 (6), 1555–1558. doi:10.1109/lwc.2019.2927206

CrossRef Full Text | Google Scholar

Zhang, J., Heath, R. W., Kountouris, M., and Andrews, J. G. (2009). Mode Switching for the Multi-Antenna Broadcast Channel Based on Delay and Channel Quantization. EURASIP J. Adv. Signal Process. 2009. doi:10.1155/2009/802548

CrossRef Full Text | Google Scholar