- Department of Mathematical and Computing Science, Tokyo Institute of Technology, Tokyo, Japan
Theory of point processes, in particular Palm calculus within the stationary framework, plays a fundamental role in the analysis of spatial stochastic models of wireless communication networks. Neveu’s exchange formula, which connects the respective Palm distributions for two jointly stationary point processes, is known as one of the most important results in the Palm calculus. However, its use in the analysis of wireless networks seems to be limited so far and one reason for this may be that the formula in a well-known form is based upon the Voronoi tessellation. In this paper, we present an alternative form of Neveu’s exchange formula, which does not rely on the Voronoi tessellation but includes the one as a special case. We then demonstrate that our new form of the exchange formula is useful for the analysis of wireless networks with hotspot clusters modeled using cluster point processes.
1 Introduction
Spatial stochastic models have been widely accepted in the literature as mathematical models for the analysis of wireless communication networks, where irregular locations of wireless nodes, such as base stations (BSs) and user devices, are modeled using spatial point processes on the Euclidean plane (see, e.g., (Baccelli and Błaszczyszyn, 2009a; Baccelli and Błaszczyszyn, 2009b; Haenggi and Ganti, 2009; Haenggi, 2013; Mukherjee, 2014; Błaszczyszyn et al., 2018) for monographs and (Andrews et al., 2016; ElSawy et al., 2017; Hmamouche et al., 2021; Lu et al., 2021) for recent survey and tutorial articles). In such analysis of wireless networks, the theory of point processes, in particular Palm calculus within the stationary framework, plays a fundamental role. Neveu’s exchange formula, which connects the respective Palm distributions for two jointly stationary point processes, is known as one of the most important results in the Palm calculus. However, its use in the analysis of wireless networks seems to be limited so far and one reason for this may be that the formula in a well-known form is based upon the Voronoi tessellation [see, e.g., (Baccelli et al., 2020, Section 6.3)]. In this paper, we present an alternative form of Neveu’s exchange formula, which does not rely on the Voronoi tessellation but includes the one as a special case, and then demonstrate that it is useful for the analysis of spatial stochastic models based on cluster point processes.
A cluster point process represents a state such that there exist a large number of clusters consisting of multiple points and is used to model the locations of wireless nodes in an (urban) area with a number of hotspots. Indeed, many researchers have adopted the cluster point processes in their models of various wireless networks such as ad hoc networks (Ganti and Haenggi, 2009), heterogeneous networks (Chun et al., 2015; Suryaprakash et al., 2015; Saha et al., 2017, 2018; Afshang and Dhillon, 2018; Saha et al., 2019; Yang et al., 2021), device-to-device (D2D) networks (Afshang et al., 2016), wireless powered networks (Chen et al., 2017), unmanned aerial vehicle assisted networks (Turgut and Gursoy, 2018), and so on. In this paper, we focus on so-called stationary Poisson-Poisson cluster processes (PPCPs) [see, e.g., (Błaszczyszyn and Yogeshwaran, 2009; Miyoshi, 2019)] and apply the new form of the exchange formula to the analysis of stochastic models based on them.
We first use the exchange formula for the Palm characterization, where we derive the intensity measure, the generating functional and the nearest-neighbor distance distribution for a stationary PPCP under its Palm distribution. Although these results are known in the literature [see, e.g., (Baudin, 1981; Ganti and Haenggi, 2009)], we here give them simple and unified proofs using the new form of the exchange formula. We next consider some applications to wireless networks modeled using stationary PPCPs, where we examine the problems of coverage and device discovery in a D2D network. The coverage analysis of a D2D network model based on a cluster point process was considered in (Afshang et al., 2016), where a device communicates with another device in the same cluster. In contrast to this, we assume here that a device receives messages from the nearest transmitting device, which is possibly in a different cluster because clusters may overlap in space. For this model, we derive the coverage probability using the exchange formula. On the other hand, in the problem of device discovery, transmitting devices transmit broadcast messages and a receiving device can detect the transmitters if it can successfully decode the broadcast messages. Such a problem was studied in (Hamida et al., 2008; Baccelli et al., 2012; Kwon and Choi, 2014) when the devices are located according to a homogeneous Poisson point process (PPP) and in (Kwon et al., 2020) when the devices are located according to a Ginibre point process [see, e.g., (Miyoshi and Shirai, 2014, 2016), for the Ginibre point process and its applications to wireless networks]. We consider the case where the devices are located according to a stationary PPCP and derive the expected number of transmitting devices discovered by a receiving device. We should note that Neveu’s exchange formula is also introduced in a more general form in (Last and Thorisson, 2009; Last, 2010; Gentner and Last, 2011), so that the form presented in the paper may be within its scope. Nevertheless, we see in the rest of the paper that our new form would be valuable and could spread the application fields of the exchange formula.
The rest of the paper is organized as follows. The new form of Neveu’s exchange formula is derived in the next section, where the relations with the existing forms are also discussed. In Section 3, the exchange formula is applied to the Palm characterization of a stationary PPCP, where alternative proofs of the intensity measure, the generating functional and the nearest-neighbor distance distribution under the Palm distribution are given. In Section 4, some applications to wireless network models are examined, where for a D2D network model based on a stationary PPCP, the coverage probability and the expected number of discovered devices are derived using the exchange formula. The results of numerical experiments are also presented there. Concluding remarks are provided in Section 5.
2 Neveu’s Exchange Formula
In this section, we discuss point processes on the d-dimensional Euclidean space
Let
Theorem 1. For the two jointly stationary point processes
1)
2)
where
Proof. As with the proof of the exchange formula in (Baccelli et al., 2020, Theorem 6.3.7), we start our proof with the mass transport formula [see, e.g., (Baccelli et al., 2020, Theorem 6.1.34)]; that is, for any measurable function ξ:
Let ξ(y) = W◦θy Ψ0({y}) on {Φ({0}) = 1}. Then, the left-hand side of Eq. 2 becomes
On the other hand, the right-hand side of Eq. 2 is reduced to
where the first equality follows from
Remark 1: Let W ≡ 1 in (Eq. 1). Then, we have
3 Applications to Cluster Point Processes
In this section, we demonstrate that Neveu’s exchange formula (Eq. 1) in Theorem 1 is useful to characterize the Palm distribution of stationary cluster point processes. A cluster point process is, roughly speaking, constructed by placing point processes (usually with finite points), called offspring processes, around respective points of another point process, called a parent process, and is used to represent a state such that there exist a large number of clusters consisting of multiple points (see Figure 1). In particular, we focus here on a stationary PPCP described next.

FIGURE 1. A sample of a 2-dimensional cluster point process (


3.1 Poisson-Poisson Cluster Processes
Let
The PPCP Ψ constructed as above is stationary since the parent process Φ is stationary and the offspring processes Ψn,
3.2 Characterization of Palm Distribution
For a stationary point process Ψ, let Ψ!≔Ψ − δ0 on the event {Ψ({0}) = 1}, which is referred to as the reduced Palm version of Ψ.
Lemma 1. For the stationary PPCP Ψ described in Section 3.1, the intensity measure of the reduced Palm version Ψ! (with respect to the Palm distribution) is given by
where |⋅| denotes the Lebesgue measure on
Proof. Since the offspring processes Ψn,
Taking the expectation with respect to
where λΨ = λΦμ is used in the second equality, the third equality follows because, for any
which completes the proof.
Remark 2. The second term on the right-hand side of (Eq. 4) is of course equal to μ∫Q(B + y) Q(dy). We adopt the form in Lemma 1 due to its interpretability. Since Q is the distribution for the position of an offspring point viewed from its parent, Q− represents the distribution for the location of the parent of the offspring point at the origin on the event {Ψ({0}) = 1}. On the other hand, μ Q(B − y) gives the expected number of offspring points falling in
Proposition 1. For the stationary PPCP
for any measurable function h:
and
Note that in Proposition 1 above,
Proof. As stated in the proof of Lemma 1, once the parent process
where the generating functional of a PPP is applied in the second equality. Taking the expectation with respect to
where Campbell’s formula for Ψ0 is applied in the last equality. By Slivnyak’s theorem and the stationarity for Φ, we have
Remark 3. The right-hand side of (Eq. 5) is given as the generating functional
3.3 Nearest-Neighbor Distance Distributions
For a stationary point process Ψ on
Proposition 2. For the stationary PPCP Ψ described in Section 3.1, the complementary nearest-neighbor distance distribution is given by
where
Proof. As with the proof of Proposition 1, we consider the conditional probability given the parent process
where the second equality follows from Slivnyak’s theorem and the third does because Ψ! is conditionally an inhomogeneous PPP with the intensity measure
Remark 4. In (Eq. 8), the term
4 Applications to Wireless Networks With Hotspot Clusters
In this section, we apply Theorem 1 to the analysis of a D2D network with hotspot clusters modeled using a stationary PPCP. We here suppose d = 2, but unless otherwise specified, the discussion holds for d ≥ 2 theoretically.
4.1 Model of a Device-To-Device Network
Wireless devices are distributed on
where N denotes a constant representing noise at the origin. We suppose that the typical device can successfully decode a message from the device at
4.2 Coverage Analysis
We here suppose that a device in the receiving mode communicates with the nearest device in transmission mode. The probability that the typical device can successfully decode a message from its partner is called the coverage probability and is given by
where 1 − p on the right-hand side indicates that the typical device must be in the receiving mode and the sum over
Theorem 2. For the model of a D2D network described in Section 4.1 with the devices deployed according to a stationary PPCP in Section 3.1, the coverage probability is given by
where Q− is given in Lemma 1 and
Before proceeding on the proof of Theorem 2, we give an intuitive interpretation to the result of it. First, as stated in the preceding section, Q− denotes the distribution for the location of the parent point of the typical device at the origin. Thus, pμI1,θ(t) and pμI2,θ(t) in (Eq. 12) represent the cases where the typical device, whose parent is located at
Proof. Similar to the proof of Proposition 1, once the parent process
where 1A denotes the indicator function for set A and we use
Furthermore, the generating functional of a PPP applying to the above expectation yields
Plugging this into (Eq. 14), taking the expectation with respect to
where we note the existence of X0 = 0 on {Φ({0}) = 1} in the second equality and apply Campbell’s formula in the third equality. Noting that X0 = 0 on {Φ({0}) = 1}, we separate the expectation in (Eq. 15) into
and consider the two terms on the right-hand side of (Eq. 16) one by one. For the first term, the generating functional of a PPP yields (1st term of (Eq. 16))
On the other hand, applying Campbell’s formula and the generating functional for Φ to the second term on the right-hand side of (Eq. 16), we have (2nd term of (Eq. 16))
Finally, plugging (Eqs 17, 18) into (Eq. 16), and then into (Eq. 15), we have (Eq. 12) and the proof is completed.When d = 2 and the distribution Q for the locations of offspring points depends only on the distance; that is, Q(dy) = fo(‖y‖) dy for
Corollary 1. When d = 2 and Q(dy) = fo(‖y‖) dy,
where
Proof. Since the distribution Q depends only on the distance, it holds that Q−(dt) = Q(dt) = fo(‖t‖) dt,
where the polar coordinate conversion is applied in the second equality and
Therefore, we have
Plugging this into (Eq. 21), we have (Eq. 19) and the proof is completed.
4.3 Device Discovery
We next consider the problem of device discovery. Devices in the transmission mode transmit broadcast messages, whereas a device in the receiving mode can discover the transmitters if it can successfully decode the broadcast messages. When a device in the receiving mode receives the signal from one transmitting device, the signals from all other transmitting devices work as interference. Then, the expected number of transmitting devices discovered by the typical device is represented by
Proposition 3. Consider the D2D network model described in Section 4.1 with the devices deployed according to a stationary PPCP given in Section 3.1. Then, the expected number
Proof. Since
4.4 Numerical Experiments
We present the results of numerical experiments for the analytical results obtained in Sections 4.2, 4.3. We set d = 2 and the distribution Q for the location of the offspring points as Q(dy) = fo(‖y‖) dy and
The numerical results for the coverage probability are given in Figure 2, where the values of
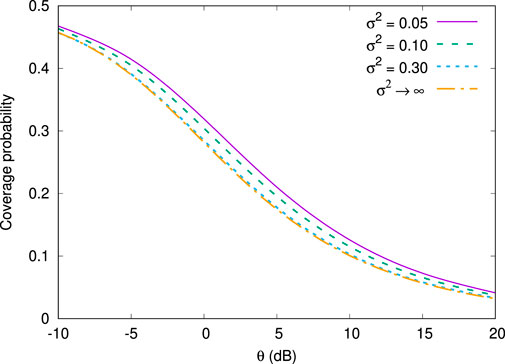
FIGURE 2. Coverage probability as a function of SINR threshold (λΦ = π−1, μ = 10, p = 0.5, β = 4 and N = 0).
The results of the device discovery is given in Figure 3, where we know that the closed form expression of the expected number of discovered devices is obtained as
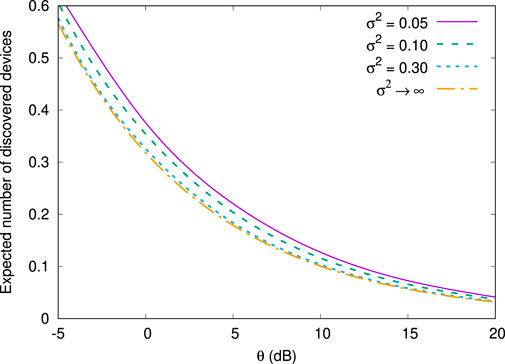
FIGURE 3. Expected number of discovered devices as a function of SINR threshold (λΦ = π−1, μ = 10, p = 0.5, β = 4 and N = 0).
5 Conclusion
In this paper, we have presented an alternative form of Neveu’s exchange formula for jointly stationary point processes on
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was supported by the Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for Scientific Research (C) 19K11838.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Afshang, M., Dhillon, H. S., and Chong, P. H. J. (2016). Modeling and Performance Analysis of Clustered Device-To-Device Networks. IEEE Trans. Wirel. Commun. 15, 4957–4972. doi:10.1109/twc.2016.2550024
Afshang, M., and Dhillon, H. S. (2018). Poisson Cluster Process Based Analysis of HetNets with Correlated User and Base Station Locations. IEEE Trans. Wirel. Commun. 17, 2417–2431. doi:10.1109/twc.2018.2794983
Afshang, M., Saha, C., and Dhillon, H. S. (2017a). Nearest-Neighbor and Contact Distance Distributions for Matérn Cluster Process. IEEE Commun. Lett. 21, 2686–2689. doi:10.1109/lcomm.2017.2747510
Afshang, M., Saha, C., and Dhillon, H. S. (2017b). Nearest-neighbor and Contact Distance Distributions for Thomas Cluster Process. IEEE Wirel. Commun. Lett. 6, 130–133.
Andrews, J. G., Gupta, A. K., and Dhillon, H. S. (2016). A Primer on Cellular Network Analysis Using Stochastic Geometry. ArXiv:1604.03183 [cs.IT]. doi:10.48550/arXiv.1604.03183
Andrews, J. G., Baccelli, F., and Ganti, R. K. (2011). A Tractable Approach to Coverage and Rate in Cellular Networks. IEEE Trans. Commun. 59, 3122–3134. doi:10.1109/tcomm.2011.100411.100541
Baccelli, F., Błaszczyszyn, B., and Karray, M. (2020). Random Measures, Point Processes, and Stochastic Geometry. Available at: https://hal.inria.fr/hal-02460214.
Baccelli, F., and Błaszczyszyn, B. (2009a). Stochastic Geometry and Wireless Networks: Volume I Theory. FNT Netw. 3, 249–449. doi:10.1561/1300000006
Baccelli, F., and Błaszczyszyn, B. (2009b). Stochastic Geometry and Wireless Networks: Volume II Applications. FNT Netw. 4, 1–312. doi:10.1561/1300000026
Baccelli, F., Khud, N., Laroia, R., Li, J., Richardson, T., Shakkottai, S., et al. (2012). “On the Design of Device-To-Device Autonomous Discovery,” in 2012 Fourth International Conference on Communication Systems and Networks (Bangalore, India: COMSNETS), 1–9. doi:10.1109/comsnets.2012.6151335
Baudin, M. (1981). Likelihood and Nearest-Neighbor Distance Properties of Multidimensional Poisson Cluster Processes. J. Appl. Probab. 18, 879–888. doi:10.2307/3213062
Błaszczyszyn, B., Haenggi, M., Keeler, P., and Mukherjee, S. (2018). Stochastic Geometry Analysis of Cellular Networks. Cambridge: Cambridge University Press.
Błaszczyszyn, B., and Yogeshwaran, D. (2009). Directionally Convex Ordering of Random Measures, Shot Noise Fields, and Some Applications to Wireless Communications. Adv. Appl. Probab. 41, 623–646.
Chen, L., Wang, W., and Zhang, C. (2017). Stochastic Wireless Powered Communication Networks with Truncated Cluster Point Process. IEEE Trans. Veh. Technol. 66, 11286–11294. doi:10.1109/tvt.2017.2726003
Chiu, S. N., Stoyan, D., Kendall, W. S., and Mecke, J. (2013). Stochastic Geometry and its Applications. 3rd edn. Wiley.
Chun, Y. J., Hasna, M. O., and Ghrayeb, A. (2015). Modeling Heterogeneous Cellular Networks Interference Using Poisson Cluster Processes. IEEE J. Sel. Areas Commun. 33, 2182–2195. doi:10.1109/jsac.2015.2435271
Daley, D. J., and Vere-Jones, D. (2003). An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods. 2nd edn. Switzerland: Springer.
Daley, D. J., and Vere-Jones, D. (2008). An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. 2nd edn. Switzerland: Springer.
Dhillon, H. S., Ganti, R. K., Baccelli, F., and Andrews, J. G. (2012). Modeling and Analysis of K-Tier Downlink Heterogeneous Cellular Networks. IEEE J. Sel. Areas Commun. 30, 550–560. doi:10.1109/jsac.2012.120405
ElSawy, H., Sultan-Salem, A., Alouini, M.-S., and Win, M. Z. (2017). Modeling and Analysis of Cellular Networks Using Stochastic Geometry: A Tutorial. IEEE Commun. Surv. Tutorials 19, 167–203. doi:10.1109/comst.2016.2624939
Ganti, R. K., and Haenggi, M. (2009). Interference and Outage in Clustered Wireless Ad Hoc Networks. IEEE Trans. Inf. Theory 55, 4067–4086. doi:10.1109/tit.2009.2025543
Gentner, D., and Last, G. (2011). Palm Pairs and the General Mass-Transport Principle. Math. Z. 267, 695–716. doi:10.1007/s00209-009-0642-4
Haenggi, M., and Ganti, R. K. (2009). Interference in Large Wireless Networks. Found. Trends Netw. 3, 127–248.
Haenggi, M. (2013). Stochastic Geometry for Wireless Networks. Cambridge: Cambridge University Press.
Hamida, E. B., Chelius, G., Busson, A., and Fleury, E. (2008). Neighbor Discovery in Multi-Hop Wireless Networks: Evaluation and Dimensioning with Interference Considerations. Discrete Math. Theor. Comput. Sci. 10, 87–114.
Hmamouche, Y., Benjillali, M., Saoudi, S., Yanikomeroglu, H., and Renzo, M. D. (2021). New Trends in Stochastic Geometry for Wireless Networks: A Tutorial and Survey. Proc. IEEE 109, 1200–1252. doi:10.1109/jproc.2021.3061778
Kwon, T., and Choi, J.-W. (2014). Spatial Performance Analysis and Design Principles for Wireless Peer Discovery. IEEE Trans. Wirel. Commun. 13, 4507–4519. doi:10.1109/twc.2014.2321142
Kwon, T., Ju, H., and Lee, H. (2020). Performance Study for Random Access-Based Wireless Mutual Broadcast Networks with Ginibre Point Processes. IEEE Commun. Lett. 24, 1581–1585. doi:10.1109/lcomm.2020.2987913
Last, G. (2010). “Modern Random Measures: Palm Theory and Related Models,” in New Perspectives in Stochastic Geometry. Editors W. S. Kendall, and I. Molchanov (United Kingdom: Oxford University Press), 77–110.
Last, G., and Penrose, M. (2017). Lectures on the Poisson Process. Cambridge: Cambridge University Press.
Last, G., and Thorisson, H. (2009). Invariant Transports of Stationary Random Measures and Mass-Stationarity. Ann. Probab. 37, 790–813. doi:10.1214/08-aop420
Lu, X., Salehi, M., Haenggi, M., Hossain, E., and Jiang, H. (2021). Stochastic Geometry Analysis of Spatial-Temporal Performance in Wireless Networks: A Tutorial. IEEE Commun. Surv. Tutorials 23, 2753–2801. doi:10.1109/comst.2021.3104581
Miyoshi, N. (2019). Downlink Coverage Probability in Cellular Networks with Poisson-Poisson Cluster Deployed Base Stations. IEEE Wirel. Commun. Lett. 8, 5–8. doi:10.1109/lwc.2018.2845377
Miyoshi, N., and Shirai, T. (2014). A Cellular Network Model with Ginibre Configured Base Stations. Adv. Appl. Probab. 46, 832–845. doi:10.1239/aap/1409319562
Miyoshi, N., and Shirai, T. (2016). Spatial Modeling and Analysis of Cellular Networks Using the Ginibre Point Process: A Tutorial. IEICE Trans. Commun. E99-B, 2247–2255. doi:10.1587/transcom.2016nei0001
Mukherjee, S. (2014). Analytical Modeling of Heterogeneous Cellular Networks: Geometry, Coverage, and Capacity. Cambridge: Cambridge University Press.
Pandey, K., Dhillon, H. S., and Gupta, A. K. (2020). On the Contact and Nearest-Neighbor Distance Distributions for the ${n}$ -Dimensional Matérn Cluster Process. IEEE Wirel. Commun. Lett. 9, 394–397. doi:10.1109/lwc.2019.2957221
Saha, C., Afshang, M., and Dhillon, H. S. (2018). 3GPP-inspired HetNet Model Using Poisson Cluster Process: Sum-Product Functionals and Downlink Coverage. IEEE Trans. Commun. 66, 2219–2234. doi:10.1109/tcomm.2017.2782741
Saha, C., Afshang, M., and Dhillon, H. S. (2017). Enriched $K$ -Tier HetNet Model to Enable the Analysis of User-Centric Small Cell Deployments. IEEE Trans. Wirel. Commun. 16, 1593–1608. doi:10.1109/twc.2017.2649495
Saha, C., Dhillon, H. S., Miyoshi, N., and Andrews, J. G. (2019). Unified Analysis of HetNets Using Poisson Cluster Processes under Max-Power Association. IEEE Trans. Wirel. Commun. 18, 3797–3812. doi:10.1109/twc.2019.2917904
Suryaprakash, V., Moller, J., and Fettweis, G. (2015). On the Modeling and Analysis of Heterogeneous Radio Access Networks Using a Poisson Cluster Process. IEEE Trans. Wirel. Commun. 14, 1035–1047. doi:10.1109/twc.2014.2363454
Tanaka, U., Ogata, Y., and Stoyan, D. (2008). Parameter Estimation and Model Selection for Neyman-Scott Point Processes. Biom. J. 50, 43–57. doi:10.1002/bimj.200610339
Turgut, E., and Gursoy, M. C. (2018). Downlink Analysis in Unmanned Aerial Vehicle (UAV) Assisted Cellular Networks with Clustered Users. IEEE Access 6, 36313–36324. doi:10.1109/access.2018.2841655
Keywords: stationary point processes, Palm calculus, Neveu’s exchange formula, cluster point processes, device-to-device networks, hotspot clusters, coverage probability, device discovery
Citation: Miyoshi N (2022) Neveu’s Exchange Formula for Analysis of Wireless Networks With Hotspot Clusters. Front. Comms. Net 3:885749. doi: 10.3389/frcmn.2022.885749
Received: 28 February 2022; Accepted: 17 May 2022;
Published: 28 June 2022.
Edited by:
Harpreet S. Dhillon, Virginia Tech, United StatesReviewed by:
Mehrnaz Afshang, Other, United StatesPraful Mankar, International Institute of Information Technology, India
Copyright © 2022 Miyoshi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Naoto Miyoshi , bWl5b3NoaUBpcy50aXRlY2guYWMuanA=
 Naoto Miyoshi
Naoto Miyoshi