Cell signaling error control for reliable molecular communications

1 Introduction

The communication paradigm for micro- and nanoscale implantable devices in biological tissues, termed molecular communication (MC), is a promising bio-inspired method that uses molecules as information carriers instead of traditional electromagnetic waves (Honary and Wysocki, 2021). This promising communication technology provides potential nanomedicine and health-sensing applications, contributing to coordinated tasks in vivo, such as smart drug delivery and their more accurate release in the body (Kumari et al., 2023). Due to the advantages of biological MC systems, such as increased biocompatibility and energy efficiency, researchers have investigated a range of biologically inspired methods and abstracted them into models for assembling and characterizing systems for encoding in-body data communication (Akyildiz et al., 2019). There are two main classes of information coding schemes for MC. One depends on the type of particle used (e.g., DNA molecules, neurotransmitters, or messengers inside cells) and the other relies on how the particles are propagated (e.g., free diffusion and cell–cell signaling) (Farsad et al., 2016).

Designing a reliable MC is challenging. Each communication has specific propagation characteristics and noises that cause errors. For instance, the free-diffusion and cell–cell signaling channels have communication errors generated by noises such as symbol distortion (i.e., bit-0 is incorrectly identified as bit-1 and vice versa) and symbol transposition (i.e., bits exchange their positions) (Jamali et al., 2019; Wei et al., 2020). Nevertheless, the factors that create these errors differ in each channel (Borges et al., 2021b). Thus, each channel characteristic is crucial for the performance of implantable device communication, where novel mechanisms for dealing with noise due to cellular signaling dynamics (e.g., the cell-signaling process involving chemical reactions that occur stochastically) must emerge. Besides this, the intra-body network development must consider that medical applications will operate under different conditions. This includes healthy cells and cells affected by pathologies that can increase molecular noise, such as Alzheimer’s disease, which disrupts the cells’ molecular equilibrium (Toivari et al., 2011). Therefore, controlling errors in these networks requires characterizing the dynamics of the cellular environment, such as factors that increase noise.

The literature on cell-signaling MC networks follows a unidirectional communication with a single information carrier approach, generally based on calcium molecules (Nakano et al., 2005; Barros, 2017; He et al., 2018), which brings advances in the research field but still requires advances in performance and error control. Furthermore, the characterization of communication noise produced by signaling cells affected by pathologies remains an open issue. Some studies point to interesting and tractable error control solutions in free diffusion channels (Felicetti et al., 2017; Marcone et al., 2018; Rouzegar and Spagnolini, 2019; Wei et al., 2020; Byun, 2023). However, these works focus on a different type of channel (free diffusion) that is not in the scope of this work, in which the molecules are suspended in a fluid and move randomly in the absence of chemical reactions (Kuran et al., 2020). Also, the studies assume a two-way communication for the error control proposal. This is not applicable to synthetic networks based on cell signaling channels. The communication between a transmitter and receiver in these networks is assumed to be unidirectional (Nakano and Liu, 2010; Heren et al., 2013; Barros et al., 2015; He et al., 2018), as detailed in Section 3.1.

This work proposes an adaptive error control for cell signaling-based MC (i.e., that which encodes information based on the concentration of molecules) governed by reaction–diffusion processes mediated by gap junctions. Cell-signaling MC is found in cells such as astrocytes, epithelial cells, and smooth muscle cells (present in the heart, brain, kidneys, muscles, among others) (Barros et al., 2015). Networks based on cell signaling perform tasks directly in the tissue. Bio-devices coupled to natural tissues can monitor pathologies associated with failures in cellular communication that affect the performance of natural cellular processes (Blackiston et al., 2021). An example is of approaches that use molecular communications to detect tumors (Bong and Monteith, 2018). Implantable devices with synthetic molecular receptors (i.e., developed through synthetic biology) have improved cancer detection efficiency and accuracy by identifying tumor-associated molecules in biological communication (Stephenson-Brown et al., 2015). Among the pathologies that occur in signaling cells that these synthetic networks could address is breast cancer caused by damage to epithelial cell genes (Wang et al., 2012), Alzheimer’s disease associated with molecular disorders in astrocytes, and vascular diseases in smooth muscle cells that can present intrinsic defects due to monogenic diseases (Shi et al., 2020).

Since the technique relies on the signaling of cells to achieve the error control goals, it is termed CELLEC (cell signaling error control for reliable MC). CELLEC comprises an adaptive retransmission scheme and an error control coding technique. The coding aims to reduce symbol distortion to get a near–error-free transmission (i.e., compared to the single-carrier approach followed in the literature). The self-adaptive retransmission intends to obtain code word reliability. Natural cells exhibit a variety of molecules with corresponding signaling pathways, which can be harnessed in synthetic MC to create a redundancy of information carriers (i.e., considering the principles of the multi-carrier system) (Borges et al., 2020). Thus, the proposed error control capitalizes on this bio-inspired diversity and molecules’ non-linear relationships to control error with a multi-molecule encoding mechanism. The retransmission scheme uses the average noise measured in the environment (source) and its relation to the bit error probability to define the retransmission strategy.

This work followed the development of a theoretical approach in line with existing models of cell-signaling MC (Barros et al., 2018; He et al., 2018). Advances in this research domain occur mainly through simulations that are used to identify and evaluate new communication solutions. This study focuses on the error control proposal for cell signaling–based MC channels. Thus, this work uses astrocytes and inositol triphosphate (IP₃) and calcium (Ca²⁺) molecules as reference models. Astrocytes are fundamental cells in the brain that control synaptic functions and present a high degree of molecular diversity (Khakh et al., 2015). The astrocytes’ most important information molecules are the IP₃ and Ca²⁺, which are also important for other signaling cell types in the body (epithelial and smooth muscle cells, among others) (Decrock et al., 2013; Barros, 2017). Studies have demonstrated that astrocytes support molecular intercellular propagation of up to 100 μm while propagating in a regenerative fashion (Kuga et al., 2011) and reach 450 μm² when the calcium signaling is mechanically induced (Peters et al., 2005). The cellular signaling processes of astrocytes are similar to those found in other cells, such as epithelial and smooth muscle cells (i.e., governed by reaction–diffusion processes mediated by gap junctions). Astrocytes and these molecules have already been studied to develop artificial communication systems at the nanoscale (Heren et al., 2013; Barros, 2017; Barros et al., 2018). The evaluation scenarios have considered a mathematical model of the 3D cellular environment composed of connected astrocytes (i.e., syncytium) in which the synthetic MC system is incorporated. The analyses consider that the environment surrounding the transmitter and receiver devices comprises biological cells that exchange molecules as their regulatory process.

This study looks into the noises (spatial noise) that come from/to the communication system in healthy cells and cells affected by one pathology. Thus, the communication model assumes an additive white Gaussian tissue noise (AWGTN) generated by intercellular propagation in healthy tissues due to their intrinsic relationship with internal cellular properties, such as their molecular diffusion mechanisms in the cellular communication system (He et al., 2018). Astrocytes are known to become reactive in Alzheimer’s disease, and their molecular equilibrium can be disturbed by the interaction of released and accumulated transmitters (e.g., peptides, serotonin) (Toivari et al., 2011; Price et al., 2021). Thus, the model also takes into account the noise produced by reactive cells. The simulation results indicate that communication channels are more affected in reactive cells. For instance, the path loss in reactive cells is 18.78% higher for the calcium and 33.05% higher for the IP₃. Besides that, the reactive tissues present a higher amplitude of signal-to-noise ratio (21.4%). The results show that CELLEC (the hybrid mechanism that comprises an error control coding technique and an adaptive retransmission scheme) improves communication channel performance by reducing the error probability.

This article proceeds as follows: Section 2 overviews the related works. Section 3 details the signaling-based MC model, the noise model of healthy cells, and the noise model for reactive cells. Section 4 describes the error control technique for tackling the noise. Section 5 describes the evaluation method and discusses the results. Finally, Section 6 concludes the article.

2 Related works

Due to the noisy characteristics of MC channel models, error control schemes are primordial to provide reliable communication. Therefore, channel coding techniques are commonly employed to tackle the intersymbol interference (ISI) effects with low complexity. In the MC literature, some solutions propose modulation schemes based on particle release. The reduction of transposition error information results from three main approaches: i) counting the number of released particles or alternating two different particles in two subsequent time slots; ii) sending the information in two types of molecules: one for symbol-1 and another for symbol-0; and iii) sending two different molecules at the same time, subtracting their concentration and identifying the equalized signal.

Kuran et al. (2011) proposed a modulation scheme called molecular shift keying (MoSK), in which information is encoded in the molecule type. For the transmission of one symbol, the scheme employs two different molecules, each representing a combination of the two different n-bit sequences. In the 2-bit constellation of the MoSK modulation called quadruple MoSK (QMoSK), four types of molecules modulate two information symbols. Noises generating ISI are molecules from other sources and residue molecules from the previous symbol (additive Gaussian white noise). Results show that BMoSK and QMoSK implementations exhibit more robustness against noise than the concentration shift keying (CSK) modulation, which uses only one molecule concentration to encode the information.

Chen et al. (2020) proposed a generalized version of MoSK modulation called generalized MoSK (GMoSK) that simultaneously activates several types of molecules to increase data rate and mitigate ISI. The free-diffusion channel model assumes a counting noise generated by the type of molecules that is not due to the transmitter but due to other similar transmission or chemical reactions in the environment. Despite results showing higher data rates at higher transmission powers, GMoSK requires a higher receptor complexity than MoSK does. However, for the two presented modulation techniques, the receiver must have multiple receptors on its surface and the transmitter must synthesize different types of molecules (Kuran et al., 2020).

In the proposed MCSK scheme by Arjmandi et al. (2013), two different types of molecules in two subsequent time slots are used in a 1D diffusion channel. The transmitter uses one molecule type in odd time slots and another type in even time slots. Only one type of molecule is used in all time slots. In a similar work, Keshavarz-Haddad et al. (2019) proposed the crossover resistant coding with time gap (CRCTG) for a one-dimensional noiseless channel. The modulation uses one molecule to transmit the code words in odd intervals and another molecule to transmit the code words in even intervals. The key idea is to deploy a time gap between consecutive code words to reduce the ISI.

In addition to mitigating intersymbol interference (ISI), error correction codes aim to reduce the bit error rate. There are two different error control techniques: forward error correction (FEC) and backward error correction (BEC). In the FEC technique, the sender encodes the message in a redundant way to improve the quality of the channel. For example, some redundant symbols assist in detecting and correcting errors in the receiver (i.e., error correction information is transmitted along with the message, similar to the Hamming codes). In the BEC technique, the receiver detects an error and requests the transmitter to retransmit the message (i.e., a block of data that was not correctly received). BEC techniques were proposed for MC. Some proposals apply the stop-and-wait automatic repeat request (SW-ARQ) method in free-diffusion (Wang et al., 2014; 2013; 2014; Furuhashi et al., 2018; Singh et al., 2023).

Variations of this technique send duplicated messages and acknowledgment (ACK) to improve reliability. According to the method, the ACK control message performs multiple tasks, such as triggering the next information in the transmitter, stopping and releasing information molecules, and changing the type of molecule (Felicetti et al., 2017; Ningthoujam et al., 2020). The Reed–Solomon code is one of the few FEC that can detect and correct various random symbol errors by adding verification symbols to data, but they require high energy consumption. This algorithm was used as an error recovery tool to enhance reliability in a multi-user diffusion-based MC system. The process involved increases the minimum distance of the code word and the number of molecules emitted per bit (Dissanayake et al., 2017).

Regarding free–diffusion–based MC, there are several ISI-resistant coding schemes based on the number of received molecules and error control techniques (Akhkandi et al., 2016). The MC literature has shown that modulation techniques that apply distinct molecules to encode information have better performance in dealing with channel noise (Kuran et al., 2011; Akhkandi et al., 2016; Chen et al., 2020; Kuran et al., 2020). However, these works focus on a different type of MC that is not in the scope of this work. Even though they consider intersymbol interference (ISI), the source of the ISI is different in signaling channels.

The literature on cell signaling–based MC networks focuses mainly on channel modeling and modulation schemes required to establish a communication link among bio-devices. Cell signaling has been studied since the initial proposal of the MC paradigm for nanonetworks (Nakano et al., 2005). Nakano et al. (2007) have suggested using the signaling processes of cells to engineer biological communication to allow nanomachines (small-scale biological devices artificially engineered from biological materials that perform sensing, processing, and actuation) to communicate through chemical signals. They proposed using calcium ions to encode information due to their abundance in the human body and their use in natural communication between cells (cell signaling). In this way, researchers have focused on studying how to use calcium to implement molecular communications in intra-body networks.

In Nakano and Liu (2010), the authors applied an information theory approach to propose a channel capacity model for a one-dimensional calcium signaling system. The capacity analysis presented values lower than 0.3 bits, even for short transmission ranges. Heren et al. (2013) extended the model to include the intercellular dynamics of IP₃. The researchers explored the channel capacity of astrocytes, highlighting the need for further studies on concentration frequency variation and noise model development in molecular communication. Barros et al. (2016) modeled the channel diversity for MC considering three distinct signaling cells: astrocytes, epithelial cells, and muscle cells. They demonstrated that electronically designed nanomachines (e.g., chips inside a cell) or synthetically engineered ones can be embedded into cellular tissues and communicate using calcium signaling.

Barros et al. (2015) studied the capacity, delay, and intracellular communication behavior considering a 3D tissue. They considered the simulation of the gap junctions (i.e., channels that physically connect adjacent cells to exchange molecules) of astrocytes, epithelial cells, and muscle cells. They investigated how the behavior of gap junctions between cells impacted the capacity of the communication channel within the tissue. In this type of MC, each signaling cell connects to several other cells through these gates (gap junctions), and as they have a stochastic behavior, diffusion turns to cells that are not the destination cells, generating noises and losses. The study found that biological systems are affected by molecular noise caused by their inherent stochastic properties. Intercellular calcium (Ca²⁺) signaling is a complex and chaotic process where random signaling constantly occurs in the channel as a part of the cells’ self-regulation processes. In their study, Barros et al. (2016) have highlighted the importance of developing techniques to reduce noise and adaptive methods to address the diverse characteristics of cellular tissue.

Similarly, Bicen et al. (2016) explored biological reactions for communication engineering in body area networks. They presented a channel model for both intracellular and intercellular Ca²⁺ signaling via the gap junction in astrocytes. They investigated the error probability for binary transmission, gain, and delay of Ca²⁺ waves traveling through a 1D array of cells. In their model, Ca²⁺ signals of astrocytes function as the communication relay. These studies follow a single-carrier approach based only on Ca²⁺ molecules with an on–off keying (OOK) modulation, which transmits molecules in bit-1 periods and does not transmit molecules in bit-0 periods. However, OOK modulation has demonstrated low performance (Barros et al., 2014).

Borges et al. (2020) proposed to use the diversity of molecules and their relationships to improve performance and reliability in MC. They used Ca²⁺ and IP₃ channels, following the principles of multi-carrier systems. The analyses considered two different scenarios: i) independence between IP₃ and Ca²⁺ channels and ii) dependence between these two channels. The capacity and channel gain results were compared with the single-carrier approach based on calcium. The results indicate that the cooperation between these two channels, i.e., IP₃ and Ca²⁺, improves data encoding and transmission compared to the single carrier. Borges et al. (2021a) validated molecular shift keying (MSK) modulation to reduce bit errors. The channel noise makes it difficult to correctly identify the symbol zero (bit-0) in OOK modulation. MSK avoids this error by using two types of molecules (IP₃ and Ca²⁺) to differentiate the symbols (bit-0 and bit-1).

Despite advances in research, there is still a need for error control techniques for systems based on cell signaling that take into account the specific characteristics of the channel (e.g., types of noise, reactions, communication, gap junctions, and molecules already present in the environment) and their applications (e.g., synthetic cell networks coupled to natural tissues for the identification and treatment of cellular tissue pathology). The intra-body MC applications, such as health monitoring, will operate on healthy tissues and tissues with pathologies that affect communication and increase environmental noise. However, the literature has not yet studied how this tissue characteristic impacts MC systems; consequently, there are no adaptive solutions for error control.

3 System model

This section describes cell signaling-based molecular communication and network entities. Subsequently, it details the molecular channel with IP₃ and Ca²⁺ cellular signaling. It also explores biological channel characteristics, such as the gap junction model that influences intercellular diffusion and the 3D model of the cellular tissue, and details the models of cell signaling noise. The development follows a theoretical approach (i.e., a mathematical model) in line with existing models to simulate the behavior of molecular communication based on cell signaling.

3.1 Molecular communication system

This work considers a synthetic molecular communication system between bio-devices incorporated into a biological cellular environment. The error control design assumes a unidirectional single-hop MC system composed of a hybrid transmitter, receiver bio-devices (i.e., biological devices based on cells with electronic parts), and a channel (biological cells that are between transmitter and receiver bio-devices). The cell signaling cannot withstand bidirectional communication for a few reasons, such as i) the fact that transceivers have not yet been demonstrated for calcium–cell signaling–based communication (i.e., the transmitter always remains a transmitter and does not have a receiver mode and vice versa for the receivers) (Nakano et al., 2012; Bi et al., 2021); ii) calcium flows unidirectionally depending on the source of the calcium signal; and iii) a bidirectional communication has not yet been demonstrated for cell signaling–based channels (Nakano and Liu, 2010; Heren et al., 2013; Barros, 2017; He et al., 2018).

The transmitter (Tx) is a bio-device capable of storing or producing molecules to encode information and has additional resources, such as i) microfluidic channels with dynamics purely driven by diffusion reactions that control the release of molecules by concentration and type. These channels can be implemented using microfiltration techniques (Zeman and Zydney, 2017; Akdeniz and Egan, 2021) and ii) a sensor capable of measuring the concentration of molecules and translating the biochemical information into an electrical equivalent format of the binary data (i.e., bit-0 or bit-1). One potential solution is to utilize new micro-/nanosensors that are capable of detecting chemical and biological signals (Bicen et al., 2016) [e.g., based on light emission and confocal microscopy (Russell, 2011)]. When specific molecules release energy from chemical bonds, they can emit visible light through bioluminescence. This process can be utilized to transduce biochemical signals into bits (Fouad et al., 2020).

The transmitter can encode data by concentrations of two types of information molecules. It follows MSK modulation to transmit M1 molecules (Ca²⁺) in symbol-1 periods (bit-1), whereas it transmits M2 molecules (IP₃) in symbol-0 periods (bit-0) (Borges et al., 2021a). The Tx node executes the retransmission procedures based on the adaptive error control proposal described in Section 4. Exploiting synthetic biology techniques has value in the designing of signal processing circuits, as was suggested by Akyildiz et al. (2015). Artificial manipulation has enabled cells to produce engineered molecules, serving several approaches, such as developing synthetic cell signaling. Genetic circuit engineering in biological cells also paves the way toward realizing programmable synthetic bio-devices (Bi and Deng, 2021). The statistical processing and information exchange between engineered cells (i.e., based on molecules and biochemical reactions) has been studied for noise measurement in error control techniques (Bi and Deng, 2021).

The receiver Bionano device (Rx) has additional resources to measure the molecules’ concentration per type and conduct statistical processing. Rx receives the molecules and decodes the data transported by them. Rx measures the concentration of molecules upon contact. There is a set of IP₃ and calcium receptors within the cell responsible for the distributed adhesion of molecules and quantifying the concentration of received molecules. In the receiver, the symbol interference occurs when the transmitted signal is overlaid in the initially allocated range by noisy molecules (i.e., due to the constant fluctuations in molecular concentrations), causing a symbol distortion (i.e., bit-0 incorrectly is identified as bit-1 and vice versa).

The channel comprises the propagation of IP₃ and Ca²⁺. It includes the intracellular and intercellular signaling stages. Within the cell (intracellular), several chemical reactions regulate the molecules’ concentration. Cell-to-cell communication (intercellular) occurs when gap junctions in the cells open. Then, molecules propagate through cytosol (i.e., the liquid that fills the cell cytoplasm) between a pair of neighboring cells. To get near–error-free transmission, we propose using the binary erasure channel concept. As in the binary channel, Tx sends a bit with just one of two symbols (i.e., bit-0 or bit-1). The Rx receives the symbol (i.e., bit-0 or bit-1) or the erasure symbol (i.e., no estimate for the transmitted symbol is obtained). Thus, if the Rx receives a symbol, it assumes that this was, in fact, the send symbol. If the receiver cannot identify the symbol due to noises, it discards it and awaits retransmission. The transmitter automatically initiates the retransmission based on the noise measure in the source and its relation to the bit error probability, as detailed in Section 4.

We consider that only the transmitting and receiving nodes are bio-devices with additional resources to encode/decode information based on the concentration of molecules. These bio-devices use the body’s own cells to transmit information (i.e., biological cells already present in the environment that are not genetically manipulated and do not have additional resources). The use of molecules naturally present in the body as information carriers and the use of the biological environment as a channel is the essence of MC proposals for intra-body networks between implanted bio-devices (Nakano et al., 2005; 2007; Heren et al., 2013; Barros, 2017), standing out for considering biocompatibility issues.

3.2 Molecular channel and 3D tissue model

This work considers the cellular environment with an area composed of i × j × k astrocytes (c) following a three-dimensional grid organization where c_i,j,k (i = 1, …, I; j = 1, …, J; and k = 1, …, K) indicates the position of an arbitrary cell that contains both intracellular and intercellular reactions and N distinguishable types of molecules {M₁, …, M_N}. The cells are connected with a maximum of six neighboring cells through gap junctions. The model for connections between cells follows the study of topologies found in astrocytes (Lallouette et al., 2014). The network uses Ca²⁺ and IP₃ signaling in astrocytes, once these cells support the molecular propagation for long distances (Khakh et al., 2015). The mesoscopic-type of diffusion of Ca²⁺ and IP₃ molecules is mediated by gap junctions that connect the cytosol of two cells (Figure 1). The communication model applies the Exact Stochastic Chemical Reaction–Diffusion ordinary differential equation (ODE) solution from the Gillespie algorithm. The ODE-based simulations produce accurate variability of the chemical reactions and serve to study noise effects caused by inherent stochastic behavior (Nakano and Liu, 2010).

Figure 1

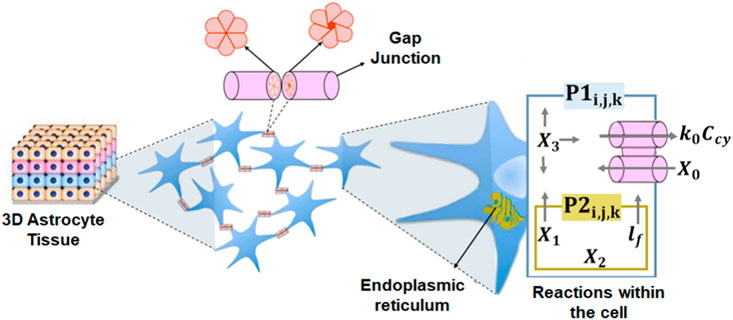
Figure 1. Three-dimensional tissue with the intracellular and intercellular processes. P1 is the flow of IP₃ or Ca²⁺ from the cytosol into the extracellular space and P2 is the diffusion of Ca²⁺ from the ER to the cell cytosol.

Since the neighboring cells of the communication system (between Tx and Rx) are part of the natural environment, they can receive and transmit molecules (i.e., as part of their regulatory process), which can cause interference in synthetic communication. To simulate the behavior of the natural MC environment, this work follows a baseline model for calcium signaling based on the well-accepted ODEs of Lavrentovich and Hemkin (2008) that describe the molecules’ oscillations in astrocytes. This algorithm was previously used by Borges et al. (2020) to simulate cellular MC channels to validate the use of Ca²⁺ and IP₃ molecules for multi-carrier molecular communication. The use of these molecules to differentiate the symbols (i.e., Ca²⁺ for bit-1 and IP₃ for bit-0) was also validated in Borges et al. (2021a). The study found that the signal-to-noise ratio showed a low overlap between the concentrations of molecules, which reduces the risk of interference between symbols. The model considers the molecules’ storage areas (pools) for the variation of Ca²⁺ concentration in the cytosol (C_cy) Eq. (1); the variation of Ca²⁺ concentration in the endoplasmic reticulum (C_er) Eq. (2); and the variation of IP₃ concentration $(I{P}_{3cy})$ in the cytosol Eq. (3).

$\frac{C_{cy}}{dt}=\chi -{\kappa }_{0_{\beta }}+4M_1\left(\frac{k_A^n{b}^n}{\left(C_{cy}^n+k_A^n\right)\left(C_{cy}^n+k_I^n\right)}\right).\left(\frac{I{P}_3^m}{k_{I{P}_3}^m+I{P}_3^m}\right).f-M_2\frac{C_{er}^2}{k_2^2+C_{er}^2}+f,(1)$

$\begin{array}{c}\frac{C_{er}}{dt}=M_2\frac{C_{er}^2}{k_2^2+C_{er}^2}-4M_1\left(\frac{k_A^n{C}_{cy}^n}{\left(C_{cy}^n+k_A^n\right)\left(C_{cy}^n+k_I^n\right)}\right).\left(\frac{I{P}_3^m}{k_{I{P}_3}^m+I{P}_3^m}\right)f-f,\hfill \end{array}(2)$

$\begin{array}{c}\frac{{IP}_{3cy}}{dt}=\left(M_p\frac{C_{er}^2}{C_{er}^2+k_p^2}\right)-{IP}_{3_{{\kappa }_{\mathit{deg}}}},\hfill \end{array}(3)$

where χ is the flow concentration of Ca²⁺ from the extracellular space to the cytosol; ${\kappa }_{0_{\beta }}$ is the efflux rate of Ca²⁺ from the cytosol to the extracellular space; M₁ is the maximum flux of Ca²⁺ into the cytosol; k_A and k_I relate, respectively, to the activation and inhibition factors for IP₃; k₂ and $k_{{IP}_3}$ are threshold constants; and m and n are regular Hill coefficients (i.e., used to describe the level of cooperation between two biological processes). The term M₂ is the maximum Ca²⁺ flux in this process; k is the saturation constant for the cytosolic Ca²⁺ concentration; and f (i.e., C_cy − C_er) is the leak flow rate from the endoplasmic reticulum (ER) to the cytosol. Ca_er describes IP₃ generation by the phosphoinositide phospholipase C (PLC) protein, where M_p is the maximum Ca²⁺ flux in this process; K is the saturation constant for the cytosolic Ca²⁺ concentration; and p is the Hill coefficient; $I{P}_{3_{{\kappa }_{\mathit{deg}}}}$ is the rate of IP₃ degeneration per second; and C_er represents the Ca²⁺ flow rate from the ER to the cytosol (Figure 1).

Equation (4) describes the fraction of active IP₃ receptors on the endoplasmic reticulum membrane (IP₃R).

$I{P}_{3}R=\left(V_{{IP}_3}R\left(Rec\right)-V_{{IP}_3}\left(Inac\right)R\right)+\sqrt{\frac{1}{Na{V}_{\mathit{cyt}}}}\left(\sqrt{V_{{IP}_{3}R\left(Rec\right)}}-\sqrt{V_{{IP}_{3}R\left(Inac\right)}}\right),(4)$

where

$V_{I{P}_3}R\left(Rec\right)=\frac{K_{\mathit{rci}}{k}_1^2}{k_i+C_{cy}^2},(5)$

$V_{I{P}_3}R\left(Inac\right)=K_{\mathit{rci}}I{P}_{3}R.(6)$

The term K_rci is the rate constant of IP₃ receptor inactivation; k₁ is the half-saturation constant for Ca²⁺ inhibition of the IP₃ receptor; V_cyt is the volume of the cytosol; and N_A represents the Avogadro’s number (i.e., the number of atoms per mole of a given particle such as molecules). According to the findings of Goldbeter et al. (1990), calcium molecular concentration can exhibit oscillatory behavior either by spontaneous initiation (without dependence on the IP₃ stimulations) or through an external stimulus. The oscillations are characterized by regular spikes in concentration occurring at varying intervals. However, the oscillation frequency is not a consistent process for astrocytes displaying spontaneous activity.

The gap junctions are composed of two connexons, one in each connecting cell, which are formed by six proteins (connexins). The gap junction model followed in this work (Baigent et al., 1997) considers the connexin Cx43 found in astrocytes. Connexin 43 (Cx43) forms gap junctions that mediate the direct intercellular diffusion of ions and small molecules between adjacent cells such as calcium and IP₃ (Niessen et al., 2000; Kang et al., 2014). The model introduced by Baigent et al. (1997) represents the intercellular channels’ stochastic opening/closing behavior. The model represents voltage-sensitive gap junctions (i.e., gates formed by two cylindrical particles called connexons, one in each connecting cell, which is formed by six proteins called connexins) with two conductance states for each gate: open, meaning high conductance, and closed, meaning low conductance. Thus, three possible combinations for all states of each connexin of the connexon exist: i) state g_hl—the first gate is in a high conductance state and the second is in low conductance; ii) state g_hc—both gates in the communicating cells are in high conductance; and iii) state g_lh—first gate is in a low conductance state and the second is in high conductance.

$\frac{g_{hl}}{dt}={\beta }_1\left(\vartheta j\right)\times g_{hc}-{\xi }_1\left(\vartheta j\right)\times g_{lh},(7)$

$\frac{d{g}_{lh}}{dt}={\beta }_2\left(\vartheta j\right)\times g_{hc}-{\xi }_2\left(\vartheta j\right)\times g_{hl}.(8)$

The control of the gap junction permeability is mediated by the voltage difference (ϑ_j) between two adjacent cell membranes. ξ is the gate opening rate and β is the gate closing rate. The terms are defined as ${\xi }_1({\vartheta }_j)=\lambda e^{-A\xi ({\vartheta }_j-{\vartheta }_0)}$; ${\xi }_2({\vartheta }_j)=\lambda e^{A\xi ({\vartheta }_j-{\vartheta }_0)}$; ${\beta }_1({\vartheta }_j)=\lambda e^{A_{\beta }({\vartheta }_j-{\vartheta }_0)}$; ${\beta }_2({\vartheta }_j)=\lambda e^{-A_{\beta }({\vartheta }_j-{\vartheta }_0)}$, where ϑ₀ is the voltage of the gap junction at which ξ = β. λ, Aξ, and Aβ are constants indicating the responsiveness of a gap to its voltage. The permeability values considered are based on experimental data (Baigent et al., 1997; Valiunas et al., 2000; Bukauskas et al., 2001). The model for connections between cells follows the study of the topologies found in astrocytes (Lallouette et al., 2014). Thus, each cell connects to other cells (up to six adjacent cells) through a gap junction, and as they have a stochastic behavior, diffusion can turn to cells that are not the destination cells. The model presented in Baigent et al. (1997) does not include a mechanism to control the behavior of gap junctions.

The molecular diffusion follows a model that captures the spatiotemporal dynamics of intercellular signaling based on mesoscopic diffusion principles (Nakano and Liu, 2010).

$Z\mathrm{\Delta }\left(i,j,k,n,m,l\right)=\frac{D_m}{v_{\mathit{cell}}}\left(\mid Z_{n,m,l}-Z_{i,j,k}|\right)\times p\left(.\right),(9)$

where ZΔ(i, j, k, n, m, l) is the molecular concentration difference between neighboring cells. i, j, k is the position of the transmitter cell and n, m, l is the position of the receiver cell, where m is the molecule type. This value follows $\frac{D_m}{v}(\mid Z_{n,m,l}-Z_{i,j,k}|)$, where D defines the molecular diffusion coefficient for Ca²⁺ or IP₃; v is the cell volume; and (|Z_n,m,l − Z_i,j,k|) is the variation in the concentration of molecules between transmitter and receiver cells. The probabilities p(.) assume the open and close rates for each gate, selected by the stochastic model and based on the states g_hl, g_hc, and g_lh [Eqs (7) and (8)].

3.3 Additive white Gaussian tissue noise

Molecular signaling can result in excessive noise due to variations in the concentrations of molecules during intracellular and intercellular signaling. Internal noise (intracellular) occurs due to the constant fluctuations in the concentrations of molecules within cells due to the stochastic events of chemical reactions. External noise occurs due to the stochastic behavior of the intercellular channels, and it is generated due to fluctuations in the concentration of the molecules coming from neighboring cells (Figure 2). To represent this behavior, there are the internal noises for IP₃ and Ca²⁺ molecules based on the formulation of Yu et al. (2009). It is commonly accepted that the internal noise intensity is proportional to the square root of the concentration of the molecule and inversely proportional to the cell volume (He et al., 2018). The noise is modeled by the terms W₁, W₂, and W₃ [Eqs (10)–(12)] and refers to chemical reactions [Eqs (1)–(3)] that occur in astrocytes.

$W_1=\frac{1}{\sqrt{v}}\left(w{0}_{i,j,k}\sqrt{{\chi }_0}-w{1}_{i,j,k}\sqrt{{\kappa }_{0_{\beta }}}+w{2}_{i,j,k}\sqrt{{\chi }_1}-w{3}_{i,j,k}\sqrt{{\chi }_2}+w{4}_{i,j,k}\sqrt{f}\right),(10)$

$W_2=\frac{1}{\sqrt{v}}=\left(w{3}_{i,j,k}\sqrt{{\chi }_2}-w{2}_{i,j,k}\sqrt{{\chi }_1}-w{4}_{i,j,k}\sqrt{f}\right),(11)$

$W_3=\frac{1}{\sqrt{v}}\left(w_{6,i,j,k}\sqrt{{\chi }_3}-w_{7,i,j,k}\sqrt{I{P}_{3_{K_{\mathit{deg}}}}}\right),(12)$

where

${\chi }_1=4M_1\left(\frac{k_A^n{C}_{cy}^n}{\left(C_{cy}^n+k_A^n\right)\left(C_{cy}^n+k_I^n\right)}\right).\left(\frac{I{P}_3^m}{k_{I{P}_3}^m+I{P}_3^m}\right).f,(13)$

${\chi }_2=M_2\frac{C_{er}^2}{k_2^2+C_{er}^2},(14)$

${\chi }_3=M_p\frac{C{a}_{er}^2}{C{a}_{er}^2+k_p^2}.(15)$

W₁ and W₂ represent the internal calcium noise in the cytoplasm and the ER, respectively. W₃ is the IP₃ noise that includes the degradation of IP₃, according to Eq. (3). The Gaussian variables w0_i,j,k … w7_i,j,k are independent with null means (zero) and unit variance; v is the cell volume. The term X₁ models the Ca²⁺ flow rate from the ER to the cytosol under IP₃ stimulus. χ₀ is the flow concentration of Ca²⁺ from the extracellular space to the cytosol, f is the leak flow rate from the ER to the cytosol, and κ₀β efflux rate of Ca²⁺ from the cytosol to the extracellular space.

Figure 2

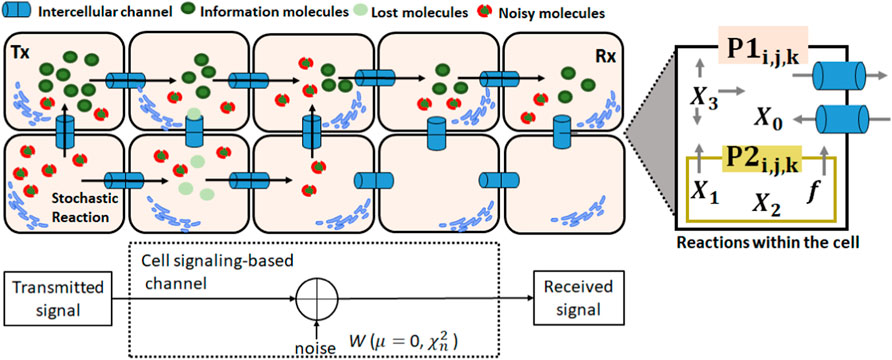
Figure 2. Cellular signaling with the intracellular/intercellular processes and noise (AWGTN). P1 is the flow of IP₃ or Ca²⁺ from the cytosol into the extracellular space and P2 is the diffusion of Ca²⁺ from the ER to the cell cytosol.

This mechanism directly affects the cytosolic concentration of Ca²⁺. M₁ is the maximum flux of Ca²⁺ into the cytosol; k₂ and $k_{I{P}_3}$ are threshold constants; and m and n are regular Hill coefficients (i.e., used to describe the level of cooperation between two biological processes). k_A and k_I relate, respectively, to the activation and inhibition factors for IP₃. χ₂ [Eq. (14)] models the efflux of Ca²⁺ from the sarco(endo)plasmic reticulum to the endoplasmic reticulum. Finally, χ₃ [Eq. (15)] describes IP₃ generation by the PLC protein, where M_p is the maximum Ca²⁺ flux in this process, k is the saturation constant for the cytosolic Ca²⁺ concentration, and p is the Hill coefficient. The presented formulation leads to Gaussian distributed noise that is intrinsic to the channel and has a uniform power spectrum density, as shown in He et al. (2018). Therefore, this article theorizes that the presented noise is an additive white Gaussian tissue noise (AWGTN) of healthy tissues.

3.4 Reactive tissue noise

In addition to ATP receptors, astrocytes also have receptors for other neurotransmitters in their plasma membranes, such as serotonin (5-hydroxytryptamine, 5-HT) and glutamate. Studies of brain activity with electrophysiological and ion calcium images have shown that the concentration of 5-HT causes the release of molecules from intracellular deposits and their intercellular propagation. Thus, disturbance in astrocyte signaling is prone to cause alterations in brain activity patterns, which are related to various neurological disorders (Seifert et al., 2006). The accumulation of amyloid-beta (Aβ)–containing neuritic plaques and neurofibrillary tangles are considered hallmarks of Alzheimer’s disease since they contribute to the altered cellular signaling in the brain (Mattson, 2004). For example, the Aβ25–35 has been shown to induce transient changes in intracellular calcium ions concentration in astrocytes (Abramov et al., 2004).

Experimental results point out that the transient component in cytosolic calcium concentration was induced by the activation of the metabotropic receptor (mR) due to Ca²⁺ stimuli/release from the internal stores. By contrast, the activation of the ionotropic receptor (iR) mediates the supported component (Di Garbo et al., 2007). Similarly, results of the experiments performed by Toivari et al. (2011) indicate that 5-HT affects Ca²⁺ of the cytosol. In a solution with normal external calcium, the 5-HT induced a transient peak together with a more sustained increase in the cytosol. When the 5-HT (1 mM) was added for 20 s in Ca²⁺-free medium, a single peak occurred, indicating Ca²⁺ release from intracellular stores. Based on the reference model proposed by Toivari et al. (2011), the noise of reactive cells assumed in this work is created by 5-HT, which affects cytosolic calcium through ionotropic and metabotropic receptors.

$W_{4_{\left({\chi }_{1_{iR}}\right)}}=M_{1_{\left(iR\right)}}\frac{{\left[input\right]}^{1.4}}{{\kappa }_{0_{\beta }}+{\left[input\right]}^{1.4}},(16)$

where ${\text{W}}_{4_{({\chi }_{1_{iR}})}}$ models the noise generated by Ca²⁺ flux from the endoplasmic reticulum to the cytosol induced by the activation of the metabotropic receptor (mR) due to stimuli-/input-evoked Ca²⁺, whereas the activation of the ionotropic receptor $M_{1_{(iR)}}$ represents the maximal rate of stimuli-evoked ionotropic Ca²⁺ flux and ${\kappa }_{0_{\beta }}$ is the half-saturation constant for stimuli-evoked Ca²⁺.

The activation of G protein and PLCβ pathways, induced by metabotropic receptors, to promote IP₃ production follows the equation:

$W_5\left({\nu }_{\mathit{PLC\beta }}\right)=kmR\frac{\left[input\right]}{Kd+\left[input\right]}.(17)$

The term k_mR represents the maximal rate of IP₃ production mediated by the metabotropic receptor and k_d is the dissociation constant for the binding of the ligand and metabotropic receptor. Equation (18) describes the time-series behavior of cytosolic IP₃ in reactive cells with ionic disturbance.

$W_6\left(I{P}_3\right)=\left(V_{\mathit{PLC\beta }}+V_{\mathit{PLC\delta }}-V_{I{P}_{3\left(Kdeg\right)}}\right)+\frac{1}{\sqrt{Na{V}_{\mathit{cyt}}}}\left(\sqrt{V_{\mathit{PLC\beta }}}+\sqrt{V_{\mathit{PLC\delta }}}-\sqrt{V_{I{P}_{3_{\left(kdeg\right)}}}}\right).(18)$

The term V_PLCβ models the IP₃ production induced by metabotropic receptors, V_PLCδ is the astrocytic IP₃ increase via PLC protein, ${\text{V}}_{I{P}_{3_{(Kdeg)}}}$ is the rate constant of IP₃ degradation, and NaV_cyt is the volume for the cytosol.

4 Cell signaling error control for reliable MC

The cellular environment contains variable conditions that produce different sources and noise patterns. Noise from dynamic tissue signaling leads to low data rates and high latency due to the absence of error control, which is critical for reliable communication. Hence, this article proposes an adaptive error control for cell signaling–based molecular communications. The components of the hybrid mechanism comprise a retransmission scheme and an error control coding technique. Coding aims to mitigate inter-symbol interference (i.e., caused by the noisy concentration of molecules interfering with symbols’ correct identification) to get near–error-free transmission (i.e., compared to the literature, a single-carrier approach for cell signaling–based nanonetworks) and the self-adaptive retransmission intends to obtain code word or event-level reliability. Using an efficient combination of these techniques is expected to achieve reliable communication. This section details the components of the proposed error control technique, considering the restrictions imposed by the molecular environment and bio-devices’ computational limitations.

4.1 Adaptive symbol retransmission and error control coding

The error control proposal assumes an asynchronous single-hop MC system composed of a hybrid transmitter, receiver bio-devices, and channel. The synthetic communication (i.e., coding based on concentration and type of molecules released at the transmitter in a controlled manner) is propagated cell to cell (i.e., molecules pass for each biological cell until they arrive at the receiver) by a diffusion process. The biological cells follow the MC model presented in Section 3.2 and the two conditions for astrocytes: healthy (Section 3.3) and reactive (Section 3.4). This work assumes a unidirectional communication (i.e., the direction of encoded data flow only occurs from transmitter to receiver bio-device). Unidirectionality restricts error correction techniques based on two-way messages (e.g., exchanging bidirectional messages between nodes when an error occurs and the receiver sending a symbol retransmission request). Therefore, the proposed error control evaluates the need for retransmission according to the algorithm that calculates the bit error probability based on channel noise. This process comprises two phases: i) molecular noise inference and ii) retransmission adaptation, consisting of five steps, as is depicted in Figure 3.

Figure 3

Figure 3. Adaptive retransmission overview.

In Phase 1, the transmitter node listens to its adjacent cells, i.e., up to six cells connected directly to the transmitter by gap junctions following the 3D tissue model for connection between astrocytes based on the study of Lallouette et al. (2014). This phase involves collecting data from the communication behavior in the source to perform the inference process. This process is essential because channel cells and cells neighboring to the transmitter are part of the natural environment; they can receive and transmit molecules, causing interference (the Gillespie algorithm simulates the stochastic communication in adjacent cells, as described in Section 5). Since each cell connects to several other cells through gap junctions with an opening/closing stochastic behavior (following the gap junction model presented in Section 3.2), diffusion can turn to cells that are not the destination cells (generating noises). Thus, the noisy molecules propagated by the cells connected to the transmitter can reach the receiver, as shown in the example in Figure 2.

The transmitter bio-device must receive molecules from neighboring cells to conduct the inference process. Intercellular diffusion only occurs when both connections are open simultaneously; thus, the stochastic nature of intercellular channels can cause the gap junction connected to the transmitter to close, disrupting the molecules’ diffusion process. In astrocytes, the gap junctions are often opened, allowing more free diffusion (i.e., compared to other cells such as epithelial and smooth muscle cells) (Barros et al., 2015). This characteristic, combined with the natural mechanism of the cells’ functions that quickly expel molecules through intercellular channels, benefits the inference process. The collected data (i.e., molecule concentration received from adjacent cells) is analyzed using statistical processing to measure noise (i.e., the average molecular spatiotemporal concentration peak). Then, information theory metrics such as the signal-to-noise ratio (i.e., SNR = 20log₁₀(P/W_j), where W_j is the power of noise determined by the average peak of molecular concentration and P is the power of the signal that is the predefined concentration per molecule type send in a bit), and error probability [Eq. (19)] are employed to estimate the retransmission necessity based on a decision rule explained below.

In Phase 2, the source adapts to the requirement to retransmit a symbol according to Eq. (19), which indicates to the error probability of the channel that is based on the measured noise. Retransmission is a common technique to achieve reliable communication. It allows a receiver to recover from a lost symbol. As previously explained, the destination node does not send an acknowledgment message (a vital mechanism to manage retransmissions) to the source due to unidirectional communication. Thus, the symbol retransmission starts after the expected lifetime of a molecular symbol in the environment that respects a time interval (t_r) defined according to the time required for synthesizing molecules at the receiver plus the estimated time for possible noise generated by the system fading away. A time slot (t_b) controls the transmitter release of each symbol (i.e., symbol time interval). The code word C is a binary code that encodes information into a string of length l symbols (s₁, s₂ … ,s_n). For example, a block code of length l with M words consists of a collection of M integers, where all integers from 1 to M occur as messages with equal probability 1/M. At each time interval, a symbol (i.e., bit-0 or bit-1) is selected at the transmitter and sent to the receiver. However, this transmission is subject to interference (e.g., noises), which result in the received value s_i of the i-th bit being equal to si + xi, where xi denotes an independent Gaussian random variable with variance N. As a result, the probability of error in transmitting a message can be calculated as

$P_e=\frac{1}{M}{\displaystyle \sum _{i=s_i}^M}{C}_{e_i}.(19)$

${\text{C}}_{e_i}$ denotes the probability (under the Gaussian distribution) of a code word w_i being decoded as an integer other than i. To estimate the probability of error for the code of length l containing M words, each of power P, and noise disturbance of variance W, the following noises are considered: noises in healthy cells [W₁: Eq. (10), W₂: Eq. (11), and W₃: Eq. (12)] and in reactive cells [W₄: Eq. (16), W₅: Eq. (17), and W₆: Eq. (18)]. Thus, the symbol error probability (P_e) concerning the molecular signal-to-noise ratio (i.e., SNR = 20log₁₀(P/W_j) follows P_e [M, l, 20log₁₀(P/W_j)], where W_j is the power of noise and j denotes the specific noise type, that is, j = 1, 2, 3 for noises in healthy cells (W₁, W₂, W₃) and j = 4, 5, 6 for noises in reactive cells (W₄, W₅, W₆), and P is the power of the signal that is the predefined concentration per molecule type sent in a bit. The probability of a bit being transmitted correctly (P_t) is complementary to the error probability (P_e). If the probability of successful transmission is high, the probability of error will be low and vice versa. Thus, Eqs (20), (21) are used as a benchmark to determine when retransmission is necessary (i.e., adaptation step).

$P_t=1-P_e(20)$

$\text{Retransmission}=\left\{\begin{array}{cc}1,\hfill & \text{if\hspace{0.17em}}{P}_t<T\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.(21)$

If the probability of a bit being transmitted correctly (P_t) is inferior to the threshold (T), then the retransmission value is set to 1, indicating that retransmission should be conducted. Otherwise, if the error probability is less than or equal to the threshold, the retransmission value is set to 0, indicating that retransmission is not required.

Given the computing limitations of bio-devices, very simple coding schemes must be considered for MC. The literature on cell signaling–based networks has followed a single-carrier approach based only on Ca²⁺ molecule (Nakano et al., 2005; Barros et al., 2015; He et al., 2018). Thus, the studies follow the OOK modulation that transmits molecules in bit-1 periods (with a certain concentration) and does not transmit molecules in bit-0 periods (concentration is zero). However, channel noise makes it difficult to identify the symbol zero correctly. For instance, the receiver may receive a calcium concentration during the transmission of bit-0 (channel silence period), causing symbol interference (i.e., similarly to a symbol distortion of conventional communications). As a result, the receiver interprets a bit that was meant to be 0 as 1. In order to reduce the symbol distortion mentioned above, this work proposes using a binary modulation technique with a binary erasure channel.

Therefore, this work considers a multi-carrier molecular communication model where each type of molecule performs the role of a channel (i.e., two channels following the IP₃/Ca²⁺ information carrier pathway). The information is encoded using the MSK modulation technique with distinct molecules to discretize the symbols (i.e., calcium for bit-1 and IP₃ for bit-0). We assume the independence between IP₃ and Ca²⁺ channels (i.e., each molecule transmission does not depend on each other). However, it is important to emphasize that encoded information (molecules) is propagated in the biological environment (cell-to-cell molecular diffusion through gap junctions) under natural cell-signaling conditions that involve a range of chemical reactions and processes (Section 3.2). The use of these molecules to differentiate the symbols was validated in Borges et al. (2021a). The signal-to-noise ratio results (considering an end-to-end communication with a distance of eight cells between the transmitter and receiver) showed that the overlap between the concentrations of molecules is low, which reduces the risk of symbol interference (symbol distortion) compared to the OOK single-carrier approach followed in the cell signaling–based literature.

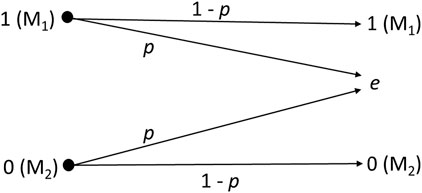
Unlike conventional communications employing the binary erasure channel, cell signaling does not occur as a complete transaction between symbols 1 and 0. Thus, the receiver estimates the symbol based on a predefined concentration range for molecules M₁ and M₂. Then, the receiver employs this estimate to make a decision. Figure 4 describes the binary erasure channel model, where 1-p is the channel capacity (1 bit per transmission), with erasure probability p, and e is the erasure symbol (i.e., no estimate for the transmitted symbol is obtained). The network operates with positive concentration values for each molecule based on a predefined range, and any value belonging to the range means being symbol-1 (Ca²⁺) or symbol-0 (IP₃), according to the molecule whose concentration was measured [Eq. (22)]. Thus, different molecules represent each symbol to reduce the probability of symbol interference due to the noisy molecules coming from neighboring cells (i.e., generated by the stochastic behavior of the chemical reactions or those that get in the cell due to the stochastic behavior of the gap junction).

$Mol\left(s\right)=\left\{\begin{array}{cc}\hfill M_1\hfill & \hfill \text{if\hspace{0.17em}}bit\left(s\right)=1\hfill \\ \hfill M_2\hfill & \hfill \text{if\hspace{0.17em}}bit\left(s\right)=0\hfill \end{array}\right.,(22)$

where Mol(s) indicates the molecules that are released by the transmitter node in a s-th symbol, M₁ is the concentration of Ca²⁺ molecules that are emitted if the bit is 1, and M₂ is the concentration of IP₃ molecules if the bit is 0. The transmitter node decides which molecule to send, relying on the data message. A time slot is reserved for the release of each symbol (i.e., a bit time interval) based on the propagation time plus the time required for synthesizing molecules (i.e., considering the estimated time for possible noise generated by the system fades away) to avoid errors. The decoding process is based on the molecular concentration value with a predefined threshold detector and occurs at the receiver side [Eq. (23)]. If molecules M1 and M2 exceed or fall below the threshold, the erasure symbol is output from the molecule detector in the receiver.

$RXdecode\left(s\right)=\left\{\begin{array}{cc}\text{bit}-1\hfill & \hfill \text{if\hspace{0.17em}}{M}_1\left(s\right)XϵR/\left\{r_{m1}\le x\le r_{m1}\right\}\hfill \\ \text{bit}-\text{0}\hfill & \hfill \text{if\hspace{0.17em}}{M}_2\left(s\right)XϵR/\left\{r_{m2}\le x\le r_{m2}\right\}\hfill \\ \hfill \text{erasure\hspace{0.17em}symbol}\hfill & \hfill \text{if\hspace{0.17em}}\left(M_1\left(s\right)XϵR/\left\{r_{m1}\le x\le r_{m1}\right\}\right)\text{\hspace{0.17em}and\hspace{0.17em}}\hfill \\ \hfill \hfill & \hfill \left(M_2\left(s\right)XϵR/\left\{r_{m2}\le x\le r_{m2}\right\}\right)\hfill \end{array}\right.(23)$

Figure 4

Figure 4. Binary erasure channel.

The receiver identifies whether the concentration has reached the predefined concentration range per type of molecule (i.e., r_m1 for Ca²⁺ and r_m2 for IP₃) in each symbol duration to determine the sent symbol. If both M1 and M2 concentrations exceed their respective thresholds, the receiver will discard the message and wait for symbol retransmission.

5 Performance evaluation

This section describes the performance evaluation of the proposed error control technique. The evaluation focuses on end-to-end channel path loss, the end-to-end spatiotemporal concentration of IP₃ and Ca²⁺ molecules, and how intracellular and spatial noises affect signal propagation inside astrocytes. The evaluation scenario follows the model presented in Section 3. The calcium signaling–based molecular communication simulator (CalComSim) (Barros et al., 2015) was extended to allow proposal evaluation considering the different noise sources. CalComSim is a simulator implemented in Python for molecular communication systems utilizing calcium signaling. It can simulate synthetic and natural cell communications in various human tissues. The simulator models different cell types, such as epithelial cells, smooth muscle cells, and astrocytes, incorporating biological models based on real experimental data.

Simulations follow parameter values based on experimental results from the literature (Goldbeter et al., 1990; Baigent et al., 1997; Baigent et al., 1997; Venance et al., 1997; Valiunas et al., 2000; Bukauskas et al., 2001; Höfer et al., 2002; Di Garbo et al., 2007; Lavrentovich and Hemkin, 2008; Di Garbo, 2009; Toivari et al., 2011), such as Ca_cy = 0.1 (μM), Ca_er = 1.5 (μM), IP₃ = 1.44 (μM), χ₀ = 0.05 (μM), κ_o = 0.5 (s⁻¹), f = 0.5 (s⁻¹), κ_deg = 0.08 (s⁻¹), M₂ = 15 (μM/s), M_p = 0.05 (μM/s), k_p = 0.3 (μM), n = 2.02, k_A = 0.15 (μM), k_I = 0.15 (μM), k₂ = 0.1 (μM), M₃ = 40.0 (s⁻¹), m = 2.2, $D_{C{a}^{2+}}$ = 350 (μm²/s), D_IP3 = 280 (μm²/s), l = 15 (μM), = 141.13 (μm³), λ = 0.37, ϑ_j mV = 90, ϑ₀ mV = 60, Aξ(mV)⁻¹ = 0.008, Aβ(mV)⁻1 = 0.67. M1_iR = 0.08 (μm²/s), k_mR = 0.5 (μM), κ_0β = 0.5 (μm²/s), K_D = 10 (μM), β = 35, and V_cyt = 0.4 X v_cell.

Simulations based on the Gillespie algorithm are effective for studying the effects of noise due to the inherent stochastic behavior. They produce precise variability of chemical reactions, as stated in the study by Nakano and Liu (2010). Thus, in a previous work (Borges et al., 2020), the Exact Stochastic Chemical Reaction–Diffusion ordinary differential equation (ODE) from the Gillespie algorithm (Gillespie, 1977) used for calcium signaling in the mathematical framework CalComSim (Barros et al., 2015) was advanced to create a multi-carrier communication model. This advancement allowed the analysis of molecular path loss and capacity using two molecules (IP₃ and Ca²⁺) to encode information.

The ODE solution from the Gillespie algorithm leads to the dynamic intracellular/intercellular concentration (Gillespie, 1992). The stochastic mathematical framework (CalComSim adapted for multi-carrier MC) executes the Gillespie algorithm at each time step to select a random cell and determine the dynamic intracellular/intercellular concentration of molecules in each pool over time. It chooses a random internal reaction for the cell and schedules a time step (t) to that reaction. The execution of each reaction (R) follows a two-phase scheduling process: i) selecting a reaction and ii) selecting a time step. Each reaction is allocated to a reaction constant (a_r). Considering that τ₀ is the sum of all a_r of R, the following reaction is chosen (r_u) and given by Eq. (24).

$\begin{array}{c}{r}_u=MAX\left\{\frac{a_{rj}}{{\tau }_0}=\frac{a_{rj}}{{\sum }_{j=1}^{\mid R\mid }{a}_{rj}}\right\}.\hfill \end{array}(24)$

The reaction selection is based on the roulette wheel function, which is biased on the reactions’ probability values. However, a roulette wheel selection (u) must satisfy the condition [Eq. (25)]:

${\displaystyle \sum _{j=1}^{u-1}}\frac{{\tau }_{rj}}{{\tau }_0}<{\rho }_1\le {\displaystyle \sum _{j=1}^u}\frac{{\tau }_{rj}}{{\tau }_0},(25)$

where ρ₁ is a binary uniform random variable. It computes a time-lapse (δ_t) at each time step (t) based on the initial τ₀ as ${\tau }_0.{\delta }_t=1n\frac{1}{{\rho }_2}$, where ρ₂ is another binary uniform random variable. The end condition is ${\sum }_{t=0}^{\mid T\mid }{\delta }_i<t_0$, where T is the t set and t₀ is the predefined simulation time. Reactions are then time-varying variables based on the changes in pool values (i.e., according to the differential equations). A predefined reaction-changing constant influences the set of values based on the positive or negative result of the reaction. With regard to intercellular reactions, a_r is replaced by ZΔ, as observed in Eq. (9).

5.1 End-to-end path loss

Path loss is the reduction in energy density (attenuation) of a carrier wave propagating through space. This metric includes channel gain values and can be adapted to fit other aspects that affect communications for analysis, such as interference and multipath fading. In MC, molecules may not arrive at the receiver due to their diffusion direction probability in gap junction channels [Eq. (9)]. Thus, the path loss [Eq. (26)] is applied to assist in analyzing this behavior considering the system noise (i.e., the noise produced by molecules emitted from each cell as part of its regulation process). Equation (26) is a derivative of the formula proposed in Barros et al. (2015) to estimate the molecular communication end-to-end channel gain.

$\mathrm{\Gamma }{\left(f\right)}^M=20{\log }_{10}\left(\frac{{\mathrm{\Gamma }}_T\left(f\right)}{{\mathrm{\Gamma }}_{T_0}\left(f\right)}\right).(26)$

Here, Γ_T(f) and ${\mathrm{\Gamma }}_{T_0}(f)$ are the molecular concentration average peak in the destination (i.e., the amplitude of the received signal) and the initial peak of molecules in the source, respectively. (f) represents the frequency of spontaneous oscillation of Ca²⁺ and IP₃ in hertz (Hz). Equation (27) calculates the path loss for Ca²⁺ and Eq. (28) for IP₃ molecules.

$\mathrm{\Gamma }{\left(f\right)}^{M_1}=20{\log }_{10}\left(\frac{{\mathrm{\Gamma }}_T^{C{a}^{2+}}\left(f\right)}{{\mathrm{\Gamma }}_{T_0}^{C{a}^{2+}}\left(f\right)}\right)+SysN\left(W_i\right),(27)$

$\mathrm{\Gamma }{\left(f\right)}^{M_2}=20{\log }_{10}\left(\frac{{\mathrm{\Gamma }}_T^{I{P}_3}\left(f\right)}{{\mathrm{\Gamma }}_{T_0}^{I{P}_3}\left(f\right)}\right)+SysN\left(W_i\right).(28)$

The terms ${\mathrm{\Gamma }}_T^{C{a}^{2+}}(f)$ and ${\mathrm{\Gamma }}_T^{I{P}_3}(f)$ are the average peak concentration of Ca²⁺ and IP₃, respectively; ${\mathrm{\Gamma }}_{T_0}^{C{a}^{2+}}(f)$ and ${\mathrm{\Gamma }}_{T_0}^{I{P}_3}(f)$ are the initial peak of molecules for Ca²⁺ and IP₃. SysN(W_i) is the internal system noise factor for each tissue condition and molecule type, satisfying Eqs (10)–(12).

5.2 Results

The spatiotemporal molecular concentration for each molecule determines the concentration threshold values for the encoding mechanism. This article also explores how noises in healthy and reactive cellular tissue that are generated inside the cell and propagated through the gap junctions affect communication. Due to the characteristics of cell signaling channels, the noise can occur in different forms. The source noise arises from molecules of the cells surrounding the transmitter after initial stimulation. The destination noise is due to recurrent ion signals from the cells surrounding the receiver after a cell gets stimulated by molecules.

Figures 3, 4 show results for Ca²⁺ and IP₃ molecule concentrations at the transmitter (Tx) and receiver (Rx), and the source and destination noise generated by cells surrounding the Tx and Rx after initial stimulation, considering healthy and reactive cells. The oscillation frequency of the concentration levels in astrocytes is 0.1 Hz, and the distance is eight cells in 3 × (3 × l) × (20 × l) (μm) cellular tissue. The amplitude of oscillations is 2.5 μm for IP₃ and 0.6 μm for Ca²⁺ measured by the maximum level of molecules.

The spatial–temporal concentration analysis considers, for both molecules, that the initial concentration at the Rx is 500 nM and the Tx initial concentration is 2 × 10³ nM (Figures 5, 6). The analysis shows that the concentration levels alone yield different behaviors and varying concentration rates for each molecule. Thus, the defined concentration thresholds for the decoding process in the Rx nodes are as follows: for Ca²⁺, bit-1 if M₁ × ϵ R/{0.15 nM–0.25 nM} and for IP₃, bit 0 if M₂ ×ϵ R/{0.18 nM–1 nM} based on the spatiotemporal concentration results. These thresholds were validated in a previous study (Borges et al., 2020). Figures 5A, 6A results indicate that at least 30 s are required to transmit each symbol (symbol duration). The spatiotemporal concentration of the Ca²⁺ and IP₃ intercellular noise presented in Borges et al. (2020) showed that the noise propagation time is very close to the time required to transmit a symbol (a few seconds less). Based on these results, we arbitrarily chose to use 60 s for the time interval for data transmission t_r (indicating how long the transmitter must wait before starting the symbol transmission/retransmission).

Figure 5

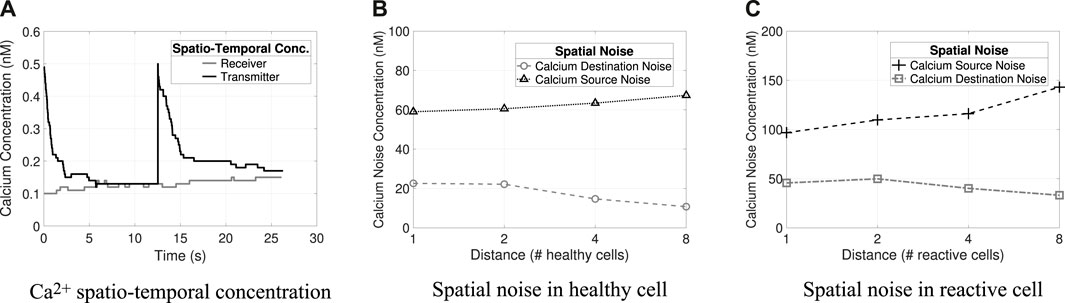
Figure 5. Calcium spatio-temporal concentrations and noises (i.e., source and destination). (A) Spatio-temporal concentration of Ca²⁺ in transmitter and receiver. (B) Spatial noise of Ca²⁺ at varying distances in healthy cells. (C) Spatial noise of Ca²⁺ at varying distances in reactive cells.

Figure 6

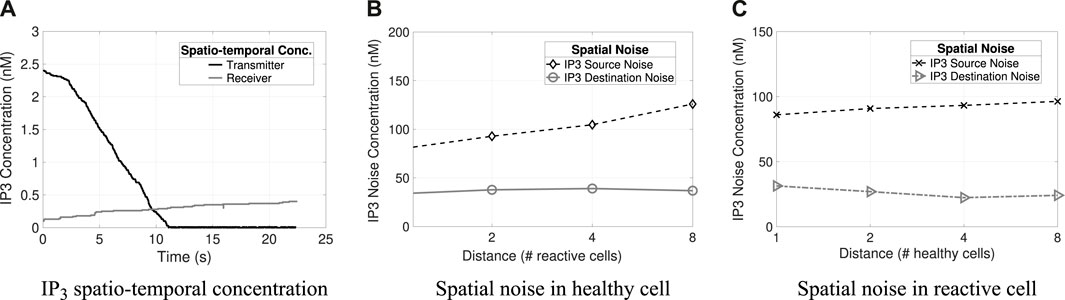
Figure 6. Spatio-temporal concentrations and noises (i.e., source and destination) of IP₃. (A) Transmitter and receiver IP₃ spatio-temporal concentration. (B) IP₃ spatial noise concerning varying distances for healthy cells. (C) Spatial noise of IP₃ at varying distances in reactive cells.

Figures 5B, 6C and Figures 4B, C illustrate the different types of noises produced by Ca²⁺ and IP₃ molecules, respectively, and their differences concerning varying distances in healthy and reactive cells. Tx concentration is 50 nM and Rx concentration is 500 nM (the results refer to the average value considering 32 repetitions). The highest quantity of noise in the system is the source noise. At the same time, the lowest amount is contributed from the cells surrounding the receiver (i.e., destination noise: Dest) for all combinations analyzed (i.e., molecule types and cell conditions). Besides that, the reactive cells have higher ionic disturbance concentrations for both molecules. However, noise is more expressive in calcium channels (i.e., the amplitude of 143 nM), explained by Ca²⁺ regeneration in the astrocyte that produces and releases new molecules.

Figure 7 presents the cumulative distribution function (CDF) of the signal-to-noise ratio (SNR) for healthy and reactive astrocytes. This analysis considers the IP₃ and Ca²⁺ accumulative source and destination noises. The cellular environment surrounding the network (i.e., a pair of nodes connected by intercellular channels at a distance of eight cells that play the role of a channel) causes fluctuations in the molecular concentration of both cells (healthy and reactive). The results refer to the average value considering 32 rounds. The source presents similar behavior patterns in both cells. However, the signal-to-noise ratio of the calcium molecule shows a higher amplitude in the reactive cells (21.4%). The signal-to-noise ratio is more critical in the reactive tissue, which presents overlaps in the concentrations of molecules, than in the healthy tissue with only one intercalation. The destination interference in the SNR results supports the need for an adaptive technique to deal with tissue variable conditions that make the decoding process prone to errors introduced by the channel properties, in which noises are inevitable.

Figure 7

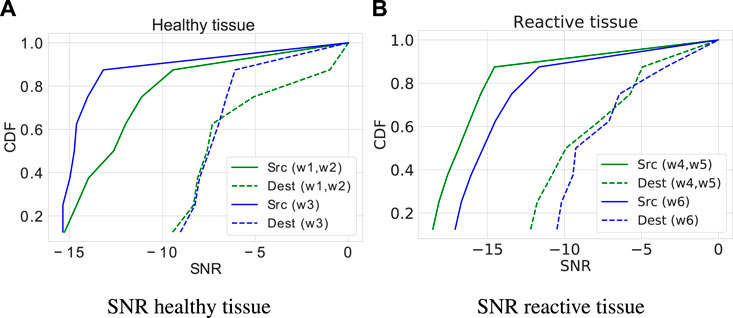
Figure 7. Cumulative Distribution Function (CDF) of the Signal-to-Noise Ratio (SNR). (A) SNR in healthy cells. (B) SNR in reactive cells.

Figure 8A shows the path loss that results in using Ca²⁺ and IP₃ in healthy and reactive tissue, concerning varying distances of one to eight cells. The results represent the average value obtained from 32 repetitions, considering each distance. The Tx concentration is 50 nM and the Rx concentration is 500 nM. The distance is eight cells. Compared to the performance of pure Ca²⁺ molecules or pure IP₃, the results show that Ca²⁺ performs better in path loss. However, it is just considering the stochastic behavior of gap junctions that causes the loss of information molecules (Figure 2). In healthy cells, the spatial system noise considers the interference represented by the terms W₁, W₂, and W₃ [Eqs (9)–(12) and (26)] and in reactive tissues by W₄, W₅, and W₆ [Eqs (9), (16)–(18)]. The effects of noise include communication degradation and changes in patterns of information carriers’ propagation behavior. However, communication channels are more affected as cellular tissue undergoes disease. For example, considering the transmitter–receiver distance of eight cells, the end-to-end path loss is 18.78% higher in reactive tissues for the calcium molecule and 33.05% higher for IP₃.

Figure 8

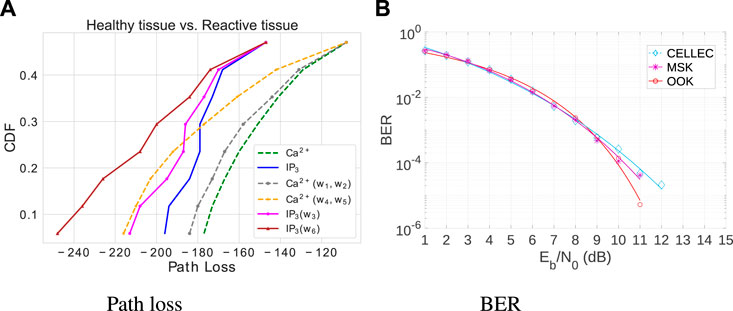
Figure 8. Cumulative Distribution Function (CDF) of Path Loss in healthy and reactive cells, along with a comparative analysis of Bit Error Rate (BER) in reactive cells. (A) Path loss over a distance of eight cells. (B) BER versus Molecular Signal-to-Noise Ratio.

Figure 8B presents the bit error rate (BER) results versus the molecular signal-to-noise ratio in astrocytes. This figure compares the result of the following modulations in reactive cells since it has the worst noise conditions: i) MSK modulation technique with distinct molecules to discretize the symbols, i.e., calcium for bit-1 and IP₃ for bit-0 and ii) the proposed MSK modulation combined with error control CELLEC (a cell signaling adaptive error control technique for reliable MC). This study arbitrarily established a threshold of 0.3, indicating that the transmitter should conduct the retransmission if the error probability surpasses 30%. CELLEC performs better as the E_b/N₀ increases over the channel. CELLEC also benefits the communication system by decreasing the bit error probability (18%).

6 Conclusion

Short-range molecular communication (MC) based on cellular signaling is a promising approach for in vivo communication. However, the signaling behavior affects the communication channel’s reliability because of different noise sources. This article shows how error conditions, such as signal fading, spatial noise, and tissue conditions, impact molecular communication and presents a novel error control technique. The analysis revealed that identical cell types exhibited varying noise patterns, highlighting the necessity for an adaptive approach to address tissue-specific conditions that led to communication errors. Results indicate that combining the encoded information with two information carriers (i.e., IP₃ and Ca²⁺ molecules) with the proposed adaptive error control technique improves molecular communication and reduces the bit error rate.

Data availability statement

Publicly available data sets were analyzed in this study. These data can be found at: https://github.com/michaelbarros/astrocytes_population_sim, https://github.com/ccscresearch/nanonetwork.

Author contributions

LB: Conceptualization, investigation, methodology, software, validation, and manuscript writing–original draft. MB: Conceptualization, formal analysis, methodology, project administration, software, and manuscript writing–review and editing. MN: Project administration, supervision, and manuscript writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Coordination for the Improvement of Higher Education Personnel (CAPES), grant #88882.382196/2019-01 and National Council for Scientific and Technological Development (CNPq), grants #313844/2020-8 and #426701/2018-6.

Acknowledgments

The authors thank CAPES (grant #88882.382196/2019-01) and CNPq (grants #313844/2020-8 and #426701/2018-6) for their support to this research. The content of this article has been presented in part at the IEEE International Conference on Communications—ICC (Borges et al., 2020) and IEEE Global Communications Conference—GLOBECOM (Borges et al., 2021a).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abramov, A. Y., Canevari, L., and Duchen, M. R. (2004). Calcium signals induced by amyloid β peptide and their consequences in neurons and astrocytes in culture. Biochimica Biophysica Acta (BBA)-Molecular Cell Res. 1742, 81–87. doi:10.1016/j.bbamcr.2004.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Akdeniz, B. C., and Egan, M. (2021). Molecular communication for equilibrium state estimation in biochemical processes on a lab-on-a-chip. IEEE Trans. NanoBioscience 20, 193–201. doi:10.1109/tnb.2021.3062473

PubMed Abstract | CrossRef Full Text | Google Scholar

Akhkandi, P., Keshavarz-Haddad, A., and Jamshidi, A. (2016). “A new channel code for decreasing inter-symbol-interference in diffusion based molecular communications,” in 8th International Symposium on Telecommunications (IST) (IEEE), Tehran, Iran, 27-28 September 2016, 277–281. doi:10.1109/istel.2016.7881825

CrossRef Full Text | Google Scholar

Akyildiz, I. F., Pierobon, M., and Balasubramaniam, S. (2019). Moving forward with molecular communication: from theory to human health applications [point of view]. Proc. IEEE 107, 858–865. doi:10.1109/jproc.2019.2913890

CrossRef Full Text | Google Scholar

Akyildiz, I. F., Pierobon, M., Balasubramaniam, S., and Koucheryavy, Y. (2015). The internet of bio-nano things. IEEE Commun. Mag. 53, 32–40. doi:10.1109/mcom.2015.7060516

CrossRef Full Text | Google Scholar

Arjmandi, H., Gohari, A., Kenari, M. N., and Bateni, F. (2013). Diffusion-based nanonetworking: a new modulation technique and performance analysis. IEEE Commun. Lett. 17, 645–648. doi:10.1109/lcomm.2013.021913.122402

CrossRef Full Text | Google Scholar

Baigent, S., Stark, J., and Warner, A. (1997). Modelling the effect of gap junction nonlinearities in systems of coupled cells. J. Theor. Biol. 186, 223–239. doi:10.1006/jtbi.1996.0351

CrossRef Full Text | Google Scholar

Barros, M., Balasubramaniam, S., and Jennings, B. (2016). Ca2+-signalling-based molecular communication systems towards nanomedicine development. Waterford Institute of Technology. Ph.D. thesis.

Google Scholar

Barros, M. T. (2017). Ca2+-signaling-based molecular communication systems: design and future research directions. Nano Commun. Netw. 11, 103–113. doi:10.1016/j.nancom.2017.02.001

CrossRef Full Text | Google Scholar

Barros, M. T., Balasubramaniam, S., and Jennings, B. (2015). Comparative end-to-end analysis of ca²⁺-signaling-based molecular communication in biological tissues. IEEE Trans. Commun. 63, 5128–5142. doi:10.1109/tcomm.2015.2487349

CrossRef Full Text | Google Scholar

Barros, M. T., Balasubramaniam, S., Jennings, B., and Koucheryavy, Y. (2014). Transmission protocols for calcium-signaling-based molecular communications in deformable cellular tissue. IEEE Trans. Nanotechnol. 13, 779–788. doi:10.1109/tnano.2014.2321492

CrossRef Full Text | Google Scholar

Barros, M. T., Silva, W., and Regis, C. D. M. (2018). The multi-scale impact of the alzheimer’s disease on the Topology diversity of astrocytes molecular communications nanonetworks. IEEE Access 6, 78904–78917. doi:10.1109/access.2018.2885518

CrossRef Full Text | Google Scholar

Bi, D., Almpanis, A., Noel, A., Deng, Y., and Schober, R. (2021). A survey of molecular communication in cell biology: Establishing a new hierarchy for interdisciplinary applications. IEEE Commun. Surv. Tutorials 23, 1494–1545. doi:10.1109/comst.2021.3066117

CrossRef Full Text | Google Scholar

Bi, D., and Deng, Y. (2021). “Spatiotemporal control of genetic circuit with pulse generation for molecular communication,” in 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 07-11 December 2021 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Bicen, A. O., Akyildiz, I. F., Balasubramaniam, S., and Koucheryavy, Y. (2016). Linear channel modeling and error analysis for intra/inter-cellular ca 2+ molecular communication. IEEE Trans. Nanobioscience 15, 488–498. doi:10.1109/tnb.2016.2574639

PubMed Abstract | CrossRef Full Text | Google Scholar

Blackiston, D., Lederer, E., Kriegman, S., Garnier, S., Bongard, J., and Levin, M. (2021). A cellular platform for the development of synthetic living machines. Sci. Robotics 6, eabf1571. doi:10.1126/scirobotics.abf1571

PubMed Abstract | CrossRef Full Text | Google Scholar

Bong, A. H., and Monteith, G. R. (2018). Calcium signaling and the therapeutic targeting of cancer cells. Biochimica Biophysica Acta (BBA)-Molecular Cell Res. 1865, 1786–1794. doi:10.1016/j.bbamcr.2018.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Borges, L. F., Barros, M. T., and Nogueira, M. (2020). “A multi-carrier molecular communication model for astrocyte tissues,” in IEEE International Conference on Communications (ICC), Dublin, Ireland, 07-11 June 2020 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Borges, L. F., Barros, M. T., and Nogueira, M. (2021a). “A synchronization protocol for multi-user cell signaling-based molecular communication,” in IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 07-11 December 2021 (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Borges, L. F., Barros, M. T., and Nogueira, M. (2021b). Toward reliable intra-body molecular communication: an error control perspective. IEEE Commun. Mag. 59, 114–120. doi:10.1109/mcom.001.2000487

CrossRef Full Text | Google Scholar

Bukauskas, F. F., Bukauskiene, A., Bennett, M. V., and Verselis, V. K. (2001). Gating properties of gap junction channels assembled from connexin43 and connexin43 fused with green fluorescent protein. Biophysical J. 81, 137–152. doi:10.1016/s0006-3495(01)75687-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Byun, H. (2023). Feedback-controlled adaptive signal detection scheme for diffusion-based molecular communication systems. Appl. Sci. 13, 2171. doi:10.3390/app13042171

CrossRef Full Text | Google Scholar

Chen, X., Huang, Y., Yang, L.-L., and Wen, M. (2020). Generalized molecular-shift keying (gmosk): principles and performance analysis. IEEE Trans. Mol. Biol. Multi-Scale Commun. 6, 168–183. doi:10.1109/tmbmc.2020.3021281

CrossRef Full Text | Google Scholar

Decrock, E., De Bock, M., Wang, N., Gadicherla, A. K., Bol, M., Delvaeye, T., et al. (2013). Ip3, a small molecule with a powerful message. Biochimica Biophysica Acta (BBA)-Molecular Cell Res. 1833, 1772–1786. doi:10.1016/j.bbamcr.2012.12.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Garbo, A. (2009). Dynamics of a minimal neural model consisting of an astrocyte, a neuron, and an interneuron. J. Biol. Phys. 35, 361–382. doi:10.1007/s10867-009-9143-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Garbo, A., Barbi, M., Chillemi, S., Alloisio, S., and Nobile, M. (2007). Calcium signalling in astrocytes and modulation of neural activity. Biosystems 89, 74–83. doi:10.1016/j.biosystems.2006.05.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Dissanayake, M. B., Deng, Y., Nallanathan, A., Ekanayake, E., and Elkashlan, M. (2017). Reed solomon codes for molecular communication with a full absorption receiver. IEEE Commun. Lett. 21, 1245–1248. doi:10.1109/lcomm.2017.2671858

CrossRef Full Text | Google Scholar

Farsad, N., Yilmaz, H. B., Eckford, A., Chae, C.-B., and Guo, W. (2016). A comprehensive survey of recent advancements in molecular communication. IEEE Commun. Surv. Tutorials 18, 1887–1919. doi:10.1109/comst.2016.2527741

CrossRef Full Text | Google Scholar

Felicetti, L., Femminella, M., and Reali, G. (2017). Congestion control in molecular cyber-physical systems. IEEE Access 5, 10000–10011. doi:10.1109/access.2017.2707597

CrossRef Full Text | Google Scholar

Fouad, H., Hashem, M., and Youssef, A. E. (2020). A nano-biosensors model with optimized bio-cyber communication system based on internet of bio-nano things for thrombosis prediction. J. Nanoparticle Res. 22, 1–17. doi:10.1007/s11051-020-04905-8

CrossRef Full Text | Google Scholar

Furuhashi, K., Suzuki, J., Mitzman, J. S., Nakano, T., Okaie, Y., and Fukuda, H. (2018). “Impacts of sw-arq on the latency and reliability of diffusive, in-sequence molecular communication,” in IEEE International Conference on Sensing, Communication and Networking (IEEE), Hong Kong, China, 11-11 June 2018, 1–4. doi:10.1109/seconw.2018.8396350

CrossRef Full Text | Google Scholar

Gillespie, D. T. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361. doi:10.1021/j100540a008

CrossRef Full Text | Google Scholar

Gillespie, D. T. (1992). A rigorous derivation of the chemical master equation. Phys. A Stat. Mech. its Appl. 188, 404–425. doi:10.1016/0378-4371(92)90283-v

CrossRef Full Text | Google Scholar

Goldbeter, A., Dupont, G., and Berridge, M. J. (1990). Minimal model for signal-induced ca2+ oscillations and for their frequency encoding through protein phosphorylation. Proc. Natl. Acad. Sci. 87, 1461–1465. doi:10.1073/pnas.87.4.1461

PubMed Abstract | CrossRef Full Text | Google Scholar

He, P., Nakano, T., Mao, Y., Lio, P., Liu, Q., and Yang, K. (2018). Stochastic channel switching of frequency-encoded signals in molecular communication networks. IEEE Commun. Lett. 22, 332–335. doi:10.1109/lcomm.2017.2768537

CrossRef Full Text | Google Scholar

Heren, A. C., Kuran, M. S., Yilmaz, H. B., and Tugcu, T. (2013). “Channel capacity of calcium signalling based on inter-cellular calcium waves in astrocytes,” in The 3rd IEEE International Workshop on Molecular and Nano Scale Communication, Budapest, Hungary, 09-13 June 2013. doi:10.1109/iccw.2013.6649341

CrossRef Full Text | Google Scholar

Höfer, T., Venance, L., and Giaume, C. (2002). Control and plasticity of intercellular calcium waves in astrocytes: a modeling approach. J. Neurosci. 22, 4850–4859. doi:10.1523/jneurosci.22-12-04850.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Honary, V., and Wysocki, T. A. (2021). Molecular communication system with non-absorbing receiver. Nano Commun. Netw. 28, 100335–100342. doi:10.1016/j.nancom.2020.100335

CrossRef Full Text | Google Scholar

Jamali, V., Ahmadzadeh, A., Wicke, W., Noel, A., and Schober, R. (2019). Channel modeling for diffusive molecular communication—a tutorial review. Proc. IEEE 107, 1256–1301. doi:10.1109/jproc.2019.2919455

CrossRef Full Text | Google Scholar

Kang, M., Lin, N., Li, C., Meng, Q., Zheng, Y., Yan, X., et al. (2014). Cx43 phosphorylation on s279/282 and intercellular communication are regulated by ip3/ip3 receptor signaling. Cell Commun. Signal. 12, 58–12. doi:10.1186/s12964-014-0058-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Keshavarz-Haddad, A., Jamshidi, A., and Akhkandi, P. (2019). Inter-symbol interference reduction channel codes based on time gap in diffusion-based molecular communications. Nano Commun. Netw. 19, 148–156. doi:10.1016/j.nancom.2019.01.001

CrossRef Full Text | Google Scholar

Khakh, M. V., Baljit, S., and Sofroniew, Y. (2015). Diversity of astrocyte functions and phenotypes in neural circuits. Nat. Neurosci. 18, 942–952. doi:10.1038/nn.4043

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuga, N., Sasaki, T., Takahara, Y., Matsuki, N., and Ikegaya, Y. (2011). Large-scale calcium waves traveling through astrocytic networks in vivo. J. Neurosci. 31, 2607–2614. doi:10.1523/jneurosci.5319-10.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumari, S., Singh, S., Singh, R. K., Pandey, V., Singh, D. K., Singh, S. P., et al. (2023). Performance investigation of molecular nano communication over channels under dynamic scenarios. Wirel. Personal. Commun. 131, 471–488. doi:10.1007/s11277-023-10440-1

CrossRef Full Text | Google Scholar

Kuran, M. Ş., Yilmaz, H. B., Demirkol, I., Farsad, N., and Goldsmith, A. (2020). A survey on modulation techniques in molecular communication via diffusion. IEEE Commun. Surv. Tutorials 23, 7–28. doi:10.1109/comst.2020.3048099

CrossRef Full Text | Google Scholar

Kuran, M. S., Yilmaz, H. B., Tugcu, T., and Akyildiz, I. F. (2011). “Modulation techniques for communication via diffusion in nanonetworks,” in IEEE international conference on communications (ICC), Kyoto, Japan, 05-09 June 2011 (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Lallouette, J., De Pittà, M., Ben-Jacob, E., and Berry, H. (2014). Sparse short-distance connections enhance calcium wave propagation in a 3d model of astrocyte networks. Front. Comput. Neurosci. 8, 45–18. doi:10.3389/fncom.2014.00045

PubMed Abstract | CrossRef Full Text | Google Scholar

Lavrentovich, M., and Hemkin, S. (2008). A mathematical model of spontaneous calcium (ii) oscillations in astrocytes. J. Theor. Biol. 251, 553–560. doi:10.1016/j.jtbi.2007.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcone, A., Pierobon, M., and Magarini, M. (2018). Parity-check coding based on genetic circuits for engineered molecular communication between biological cells. IEEE Trans. Commun. 66, 6221–6236. doi:10.1109/tcomm.2018.2859308

CrossRef Full Text | Google Scholar

Mattson, M. P. (2004). Pathways towards and away from alzheimer’s disease. Nature 430, 631–639. doi:10.1038/nature02621

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakano, T., and Liu, J.-Q. (2010). Design and analysis of molecular relay channels: an information theoretic approach. IEEE Trans. NanoBioscience 9, 213–221. doi:10.1109/tnb.2010.2050070

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakano, T., Moore, M. J., Wei, F., Vasilakos, A. V., and Shuai, J. (2012). Molecular communication and networking: Opportunities and challenges. IEEE Trans. nanobioscience 11, 135–148. doi:10.1109/tnb.2012.2191570

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakano, T., Suda, T., Koujin, T., Haraguchi, T., and Hiraoka, Y. (2007). “Molecular communication through gap junction channels:system design, experiments and modeling,” in IEEE Bionetics, Nagoya, Japan, 15-15 July 2005 (IEEE), 139–146.

CrossRef Full Text | Google Scholar

Nakano, T., Suda, T., Moore, M., Egashira, R., Enomoto, A., and Arima, K. (2005). “Molecular communication for nanomachines using intercellular calcium signaling,” in IEEE NANO, Nagoya, Japan, 15-15 July 2005 (IEEE), 478–481.

Google Scholar

Niessen, H., Harz, H., Bedner, P., Krämer, K., and Willecke, K. (2000). Selective permeability of different connexin channels to the second messenger inositol 1, 4, 5-trisphosphate. J. cell Sci. 113, 1365–1372. doi:10.1242/jcs.113.8.1365

PubMed Abstract | CrossRef Full Text | Google Scholar

Ningthoujam, S., Chingkheinganba, T., and Chakraborty, S. K. (2020). Finding an effective distance between t-cell and b-cell using s/w arq in an immune system communication. China Commun. 17, 174–185. doi:10.23919/jcc.2020.01.014

CrossRef Full Text | Google Scholar

Peters, J. L., Earnest, B. J., Tjalkens, R. B., Cassone, V. M., and Zoran, M. J. (2005). Modulation of intercellular calcium signaling by melatonin in avian and mammalian astrocytes is brain region-specific. J. Comp. Neurology 493, 370–380. doi:10.1002/cne.20779

PubMed Abstract | CrossRef Full Text | Google Scholar

Price, B. R., Johnson, L. A., and Norris, C. M. (2021). Reactive astrocytes: the nexus of pathological and clinical hallmarks of alzheimer’s disease. Ageing Res. Rev. 68, 101335. doi:10.1016/j.arr.2021.101335

PubMed Abstract | CrossRef Full Text | Google Scholar

Rouzegar, S. R., and Spagnolini, U. (2019). Diffusive mimo molecular communications: channel estimation, equalization, and detection. IEEE Trans. Commun. 67, 4872–4884. doi:10.1109/tcomm.2019.2910252

CrossRef Full Text | Google Scholar

Russell, J. T. (2011). Imaging calcium signals in vivo: a powerful tool in physiology and pharmacology. Br. J. Pharmacol. 163, 1605–1625. doi:10.1111/j.1476-5381.2010.00988.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Seifert, G., Schilling, K., and Steinhäuser, C. (2006). Astrocyte dysfunction in neurological disorders: a molecular perspective. Nat. Rev. Neurosci. 7, 194–206. doi:10.1038/nrn1870

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, J., Yang, Y., Cheng, A., Xu, G., and He, F. (2020). Metabolism of vascular smooth muscle cells in vascular diseases. Am. J. Physiology-Heart Circulatory Physiology 319, H613–H631. doi:10.1152/ajpheart.00220.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, S. P., Rai, R., Awasthi, S., Singh, D. K., and Lakshmanan, M. (2023). Vlsi implementation of error correction codes for molecular communication. Wirel. Personal. Commun. 130, 2697–2713. doi:10.1007/s11277-023-10399-z

CrossRef Full Text | Google Scholar

Stephenson-Brown, A., Acton, A. L., Preece, J. A., Fossey, J. S., and Mendes, P. M. (2015). Selective glycoprotein detection through covalent templating and allosteric click-imprinting. Chem. Sci. 6, 5114–5119. doi:10.1039/c5sc02031j

PubMed Abstract | CrossRef Full Text | Google Scholar

Toivari, E., Manninen, T., Nahata, A. K., Jalonen, T. O., and Linne, M.-L. (2011). Effects of transmitters and amyloid-beta peptide on calcium signals in rat cortical astrocytes: Fura-2am measurements and stochastic model simulations. PloS One 6, 17914–17923. doi:10.1371/journal.pone.0017914

PubMed Abstract | CrossRef Full Text | Google Scholar

Valiunas, V., Weingart, R., and Brink, P. R. (2000). Formation of heterotypic gap junction channels by connexins 40 and 43. Circulation Res. 86, e42–e49. doi:10.1161/01.res.86.2.e42

PubMed Abstract | CrossRef Full Text | Google Scholar

Venance, L., Stella, N., Glowinski, J., and Giaume, C. (1997). Mechanism involved in initiation and propagation of receptor-induced intercellular calcium signaling in cultured rat astrocytes. J. Neurosci. 17, 1981–1992. doi:10.1523/jneurosci.17-06-01981.1997

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Higgins, M. D., and Leeson, M. S. (2013). “Stop-and-wait automatic repeat request schemes for molecular communications,” in First International Black Sea Conference on Communications and Networking (BlackSeaCom), Batumi, Georgia, 03-05 July 2013 (IEEE), 84–88.

CrossRef Full Text | Google Scholar

Wang, X., Higgins, M. D., and Leeson, M. S. (2014). Simulating the performance of sw-arq schemes within molecular communications. Simul. Model. Pract. Theory 42, 178–188. doi:10.1016/j.simpat.2013.12.006

CrossRef Full Text | Google Scholar

Wang, Y.-Y., Lehuédé, C., Laurent, V., Dirat, B., Dauvillier, S., Bochet, L., et al. (2012). Adipose tissue and breast epithelial cells: a dangerous dynamic duo in breast cancer. Cancer Lett. 324, 142–151. doi:10.1016/j.canlet.2012.05.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., Li, B., Hu, W., Guo, W., and Zhao, C. (2020). Hamming–luby rateless codes for molecular erasure channels. Nano Commun. Netw. 23, 100280. doi:10.1016/j.nancom.2019.100280

CrossRef Full Text | Google Scholar

Yu, G., Yi, M., Jia, Y., and Tang, J. (2009). A constructive role of internal noise on coherence resonance induced by external noise in a calcium oscillation system. Chaos, Solit. Fractals 41, 273–283. doi:10.1016/j.chaos.2007.12.001

CrossRef Full Text | Google Scholar

Zeman, L. J., and Zydney, A. L. (2017). Microfiltration and ultrafiltration: principles and applications.

Google Scholar