- Department of Electrical and Computer Engineering, University of Victoria, Victoria, BC, Canada
Multiple-input multiple-output (MIMO) technology is employed to improve the reliability and capacity of wireless communication systems. However, the wireless communication environment creates vulnerabilities to spoofing attacks. Furthermore, the authentication challenges posed by the heterogeneous characteristics of wireless applications increase as diverse technologies facilitate the growing number of Internet of Things (IoT) devices. To address these challenges, adaptive physical-layer authentication (PLA) leveraging the inherent antenna diversity in MIMO systems is examined, and an information-theoretic perspective on PLA in MIMO systems is given. The real and imaginary components of the received reference signals are used as attributes with a single-class classification support vector machine (SCC-SVM). It is shown that the authentication performance improves with the number of antennas, and the proposed scheme provides robust authentication.
1 Introduction
The number of wireless devices has increased significantly as a result of Internet of Things (IoT) development. However, the limited bandwidth for applications and limited device capabilities make it challenging to deliver reliable services in wireless networks. Multiple-input multiple-output (MIMO) technology can improve the effectiveness and capacity of wireless communication networks without increasing bandwidth resources (Zhang et al., 2020).
Information-theoretic security metrics for secrecy, privacy, authentication, stealth, and covertness have been developed and fundamental limits derived (Liang et al., 2008; Bloch et al., 2021). Shannon (1949) presented the first information-theoretic study of a cryptography model. Cryptography is the science of securing communications. It involves the transformation of plaintext into ciphertext, which can be intercepted by an attacker. A key K is a secret parameter used in conjunction with an algorithm to encrypt or decrypt data. The message M represents the data that need to be protected. For encryption, K is used to transform M into a ciphertext E. The goal is to maximize the secret information rate between legitimate users. Wyner (1975) presented information-theoretic security limits for a discrete memoryless wiretap channel. It was shown that security is possible if the capacity Cm between legitimate users is higher than the wiretap channel capacity Cw between the transmitter and attacker. Abdi et al. (2001) extended the model proposed by Wyner (1975) to a Gaussian wiretap channel. It was shown that secure communication can be achieved if Cs = Cm − Cw > 0. However, Cs is degraded by wireless channels due to factors such as fading (Zou et al., 2016).
The model proposed by Wyner (1975) was extended to MIMO systems (Khisti and Wornell, 2010a), and this was improved by Khisti and Wornell (2010b). It was shown that increasing the number of antennas can improve Cs. Bloch et al. (2008) considered quasi-static fading. The outage probability Pout was shown to depend on the user location and path loss, where Pout = P(Cs < Rs) and Rs is the secrecy rate. Information-theoretic security for MIMO systems was considered by Oggier and Hassibi (2011), but the channel state information (CSI) was assumed to be known. Security without knowledge about the attacker CSI was considered by He et al. (2011).
A MIMO scheme for practical physical-layer security was presented by Ishikawa et al. (2021). It employs chaos-based unitary matrices to eliminate the need for channel estimation. Unlike conventional approaches, an imperfect key agreement in high-mobility scenarios was considered, and an algorithm for reconciling chaotic sequences between legitimate parties was given. Simulation results were presented which show that the performance is superior to that with conventional chaos-based MIMO schemes assuming perfect CSI.
Downlink security in cell-free massive MIMO systems with imperfect channel estimation was investigated by Tubail et al. (2023). Two power allocation algorithms using artificial noise were introduced to combat passive eavesdropping. Imperfect channel estimation was considered as it leads to artificial noise leakage which impacts performance. The results show that the proposed algorithm improves the security through robust authentication.
In this paper, physical-layer authentication (PLA) for MIMO systems is examined from an information-theoretic perspective. The authentication boundary is determined using machine learning (ML). For training, a single-class classification support vector machine (SCC-SVM) is used with only legitimate user data. The real and imaginary components of the received reference signals are employed as attributes. These attributes vary slowly over time as a result of factors such as mobility (Hou et al., 2014; Ferrante et al., 2015; Wang et al., 2015; Wang et al., 2016; Fang et al., 2020). As a result, the SCC-SVM authentication boundary is updated to ensure reliable authentication. The authentication rate (AR) is shown to improve with antenna diversity. The contributions of this paper are as follows.
• PLA for MIMO systems is examined from an information-theoretic perspective.
• The real and imaginary components of the received signals are used as attributes to improve PLA performance.
• A practical approach is presented to extract attributes from cellular network reference signals.
• The effectiveness of the proposed PLA scheme is evaluated and validated in urban environments.
The remainder of this paper is organized as follows: the system model is presented in Section 2; Section 3 introduces SCC-SVM and the proposed PLA scheme; the performance evaluation metrics are given in Section 4; Section 5 provides the simulation results; and Section 6 provides some concluding remarks.
2 System model
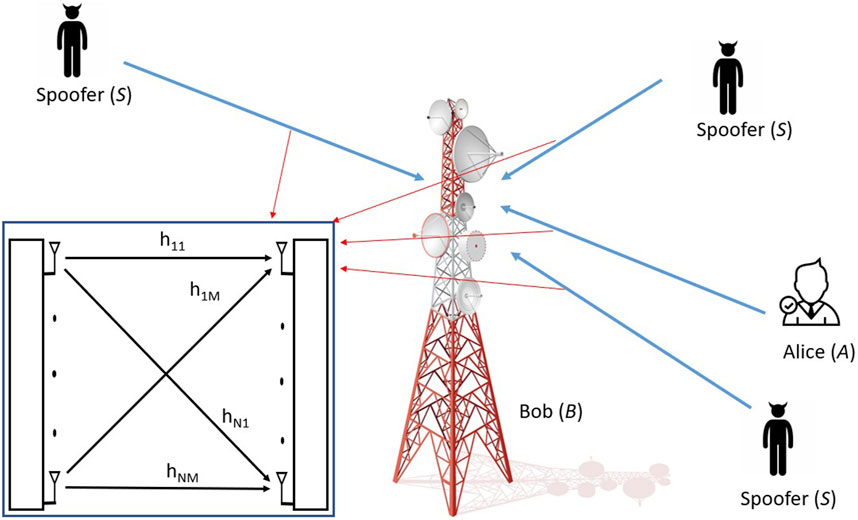
The system model for the proposed authentication scheme is shown in Figure 1. In this scheme, Alice (A) represents a user requiring authentication from Bob (B), while the spoofer (S) is an attacker attempting to impersonate A. B must ascertain the legitimacy of A and also reject S. Consequently, B must decide between the two hypotheses
Thus,
Reference signals are transmitted in cellular networks to facilitate CSI estimation. In particular, sounding reference signals are repeated every 28 symbols or 56 symbols (GPP, version 15.2.0, 2018). The received signal at B can be expressed as
where x is the transmitted reference signals, H is the channel matrix, and W is independent additive white Gaussian noise (AWGN). The channel matrix for the M × N MIMO system can be partitioned according to the transmit and receive antennas as follows:
where hnm represents the channel from the mth transmit antenna to the nth receive antenna. H can be estimated from Y corresponding to the known reference signals (Schindler and Mellein, 2011; Germain et al., 2020). Y is used to obtain the data for SCC-SVM training and testing.
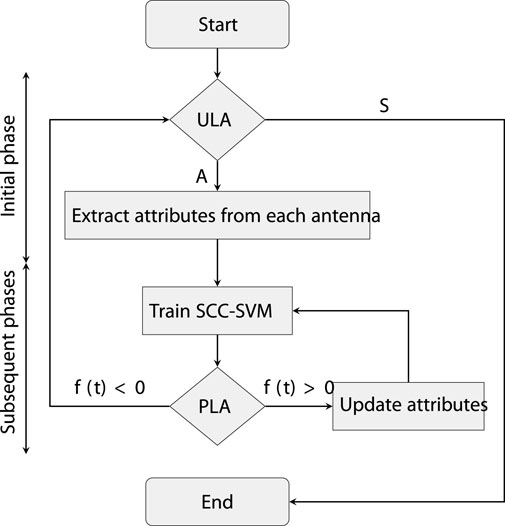
The proposed scheme is implemented in the uplink and has an initial phase (T1), followed by subsequent phases (T2, T3, … , Tn). During the initial phase, upper-layer authentication (ULA) is conducted, and SCC-SVM training is performed at B using the received reference signals from A. The real and imaginary components of these signals for each transmit–receive antenna pair are obtained to provide 2 × M attributes per antenna for a total of 2 × M × N attributes. In subsequent phases, SCC-SVM testing is conducted at B to validate the legitimacy of the received signals, which may originate from either A or a spoofer S. Hence, the received signals during these phases are treated as being from an unknown user U. If successful, the attributes are updated, and SCC-SVM training is repeated. Conversely, if testing fails, the connection is terminated.
SCC-SVM training is used in the initial phase to establish an authentication boundary. In subsequent phases, SCC-SVM testing is used to determine whether the received signal attributes fall within this boundary. In this case, the test is successful, and authentication continues. The received signal is rejected if the attributes fall outside the boundary. The proposed scheme leverages the spatial independence of A and S as the physical-layer attributes for authentication are independent. Furthermore, transmit and receive antenna diversity is exploited to generate a large number of attributes. These attributes vary slowly over time due to factors such as mobility (Hou et al., 2014; Ferrante et al., 2015; Wang et al., 2015; Wang et al., 2016; Fang et al., 2020). Consequently, the SCC-SVM authentication boundary is dynamically updated in each subsequent phase to ensure reliable authentication.
3 The proposed scheme
3.1 Single-class classification support vector machine
SCC is a machine learning technique that can be employed to distinguish between A and S using training data from A. The goal is to find the optimal authentication boundary that surrounds most of the training data from A (Tax and Duin, 2004). In this paper, the SCC-SVM algorithm proposed by Schölkopf et al. (2001) is employed. SCC-SVM computes a decision function f which encompasses the majority of the training data [Senigagliesi et al. (2020); Abdrabou and Gulliver (2022c); Abdrabou and Gulliver, 2022a; Abdrabou and Gulliver, 2023]. First, the following optimization problem is solved (Hoang et al., 2021); (Schölkopf et al., 2001):
where w is the weight vector, ρ is the distance from the origin to the boundary, Φ is a feature mapping determined based on the kernel employed, gi is the ith feature vector used for SCC-SVM training, si is the corresponding slack variable, ℓ is the number of training samples, and η is the percentage of data considered as outliers (Senigagliesi et al., 2020). SCC-SVM maps data to a feature space using kernels and then separates the features using a boundary. The optimization problem in Eq. 1 provides w and ρ which determine the boundary used in the decision function Eq. 3. Using Lagrange multipliers pi, qi ≥ 0 yields (Schölkopf et al., 2001)
Setting the derivatives with respect to w, s, and ρ as zero yields (Schölkopf et al. 2001)
The decision function used to test a new sample t is expressed as follows (Senigagliesi et al. 2020); (Hoang et al. 2021):
and substituting w from Eq. 2 yields
The kernel expansion is defined as (Schölkopf et al. 2001)
so the decision function is
A test sample t is accepted if f(t) > 0, which indicates that it is within the authentication boundary (Senigagliesi et al., 2020).
3.2 Proposed scheme
The proposed scheme employs SCC-SVM with antenna diversity. The received signal at the nth receive antenna from the mth transmit antenna is
where xm is the transmitted reference symbol and hnm and nnm are the corresponding channel coefficients and AWGN, respectively. The WINNER II channel model for non-line-of-sight (NLOS) urban environments (Kyösti et al., 2007) is considered here. The received MIMO signals can be expressed as
This matrix is employed to obtain features for SCC-SVM training and testing. Binary phase-shift keying (BPSK) modulation is assumed, so the transmitted signal is (Chatzidiamantis et al., 2011)
where g(t) is the pulse shaping function, 0 ≤ t ≤ Ts, Ts is the symbol time, fs is the carrier frequency, and φk ∈ [0, π] is the phase of the kth symbol. The real (R) and imaginary (I) components are used as attributes so that
Figure 2 illustrates the proposed scheme. In the initial phase T1 following ULA authentication, data are obtained from the legitimate user (A) for SCC-SVM training. In subsequent phases, reference signal data from U are utilized by B for testing and training. If testing is successful in a given phase, the corresponding data are employed to update the attributes for training. A sliding window is used so the oldest data are discarded. Conversely, if testing fails, the connection is terminated.
The initial authentication is performed in phase T1 with A through ULA. Then, the reference signal data from A are used to construct the training sample vector di. The ith data sample is then
SCC-SVM training is performed using the vectors di, where i = 1, 2, … , ℓ, to obtain the authentication boundary. In subsequent phases, SCC-SVM is utilized to test new samples t, as shown in Eq. 4, originating from U, where U could be A or S. If testing is successful, U is accepted and the attributes are updated, followed by SCC-SVM training. Otherwise, the connection is terminated.
The ℓ training samples from A in the initial phase are
and the testing sample from U is
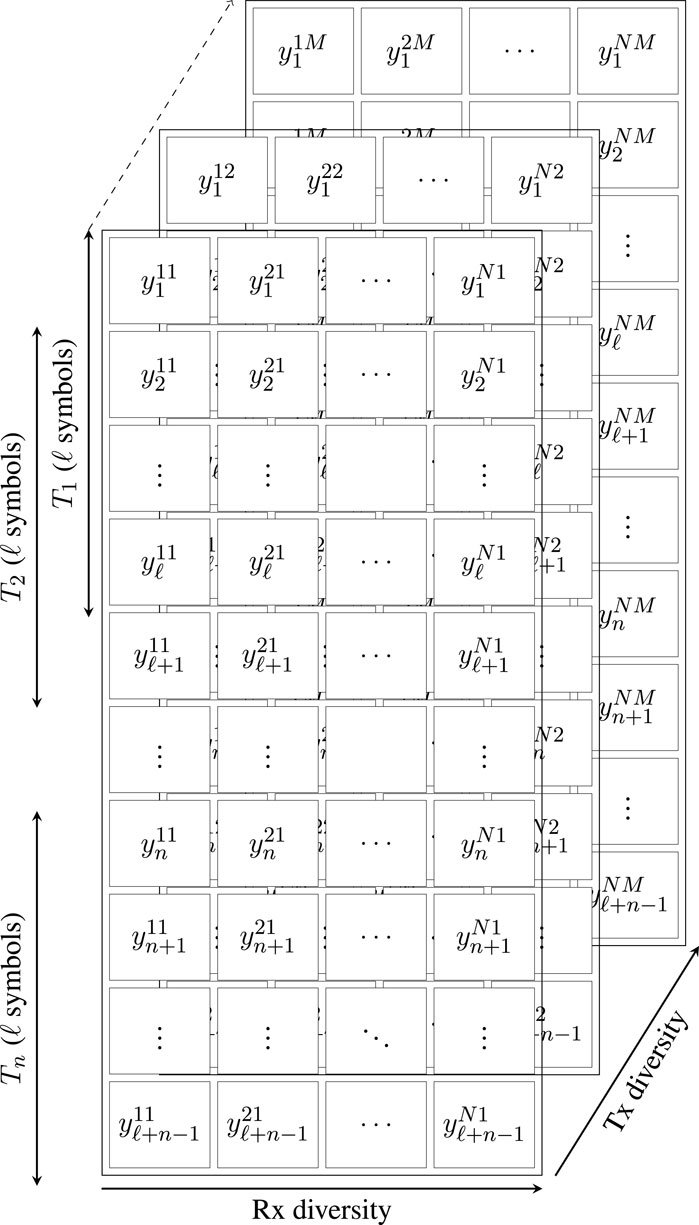
Figure 3 illustrates the sliding window update process for the attributes. In phase T1, the training data from A consist of ℓ matrices Y, where each matrix is represented by a vector as shown in Eq. 5. Subsequently, in phase T2 a new data vector t is tested (following scaling), and if accepted, the data matrix is updated by discarding the first row d1 and adding the new data vector as row ℓ + 1. Consequently, if the first e new data vectors are accepted, the training data matrix is
so ℓ vectors are used for training.
Each attribute undergoes separate minimum–maximum scaling
to obtain
where
and mmin,r is the minimum value in mr and mmax,r is the maximum value in mr. The feature matrix for training is then
and the elements of t are scaled using mmin,r and mmax,r from the training data as follows:
to form the test vector t. The proposed scheme is summarized in Algorithm 1.
Algorithm 1.Proposed scheme.
ULA for A.
Obtain the received reference signals from each antenna.
Extract the real (R) and imaginary (I) components from the received reference signals.
Construct the training samples di using Eq. 5.
Train SCC-SVM to establish the authentication boundary.
Test SCC-SVM with the sample t as in Eq. 6.
if (f(t) > 0) then
Accept the user.
Update the attributes.
Retrain SCC-SVM.
else if (f(t) ≤ 0) then
Terminate the connection.
end if
3.3 Information-theoretic PLA
The authentication performance can be improved with antenna diversity (Abdrabou and Gulliver, 2022b; 2024). This is indicated by the mutual information between the training and testing attributes from A I(TrA; TeA), which is greater than the mutual information between the training attributes from A and testing attributes from S I(TrA; TeS). The mutual information authentication rate IAR can be defined as
First, a single-input multiple-output system (SIMO) and independent channels based on user location and mobility are considered. The mutual information that characterizes the legitimacy of A at the receiver is a function of the wireless link at two consecutive time instances (training and testing). The mutual information between the transmit antenna and receive antennas is
Each element of this matrix characterizes the received reference signal at times t − 1 (training) and t (testing), so it can be reformulated as
where yi (t − 1) is the training data from A and yi(t) is the testing data from U, so then,
Now, a MIMO system is considered. The mutual information between the transmit antennas and receive antennas can be expressed as
Each element of this matrix characterizes the received reference signal at times t − 1 and t, so
where y*(t − 1) is the training data from A and y*(t) is the testing data from U, and therefore,
Since mutual information is greater than or equal to zero [Cover and Thomas, 2006, (2.90)],
The joint mutual information for independent channels in a SIMO system can be formulated as
so
For a MIMO system, this is
so
These results show that the authentication performance improves with the number of receive and transmit antennas so that
where u and p are the number of receive antennas and v and q are the number of transmit antennas.
3.4 Channel capacity for PLA
The channel capacity C is defined as the maximum mutual information (Cover and Thomas, 2006),
The capacity of a MIMO system depends on several factors such as the signal-to-noise ratio (SNR). It can be obtained using singular value decomposition (SVD) to decompose the channel matrix H and obtain the singular values and unitary matrices for the transmitter and receiver as (Golub and Van Loan, 2013)
where U is the unitary matrix corresponding to the transmitter, Σ is a diagonal matrix containing the singular values, and VH is the conjugate transpose of the unitary matrix corresponding to the receiver. The singular values are
and the corresponding channel capacity is (Tse and Viswanath, 2005)
where n is the number of singular values and λi is the ith singular value of the channel matrix.
4 Performance evaluation
The performance is evaluated using the confusion matrix which includes true positive (TP), the acceptance of A, true negative (TN), the rejection of S, false negative (FN), the erroneous rejection of A, and false positive (FP), the erroneous acceptance of S. The evaluation metrics are the missed detection rate (MDR), false alarm rate (FAR), precision or positive predictive value (PPV), false discovery rate (FDR), and authentication rate (AR) (Senigagliesi et al., 2020; Abdrabou and Gulliver, 2022b):
where γ is used to balance between A and S and is given by
The AR improves with the number of antenna (Abdrabou and Gulliver, 2022b), and the corresponding PPV increases, so
and the FDR decreases, so
and therefore,
5 Simulation results
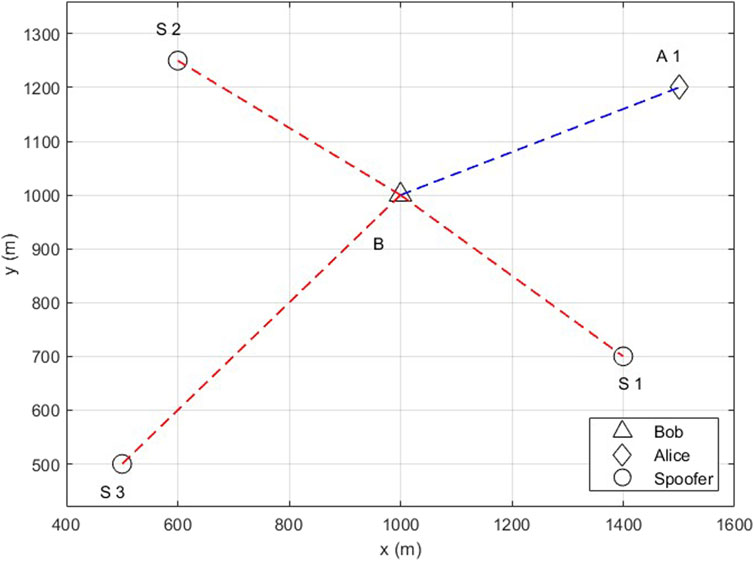
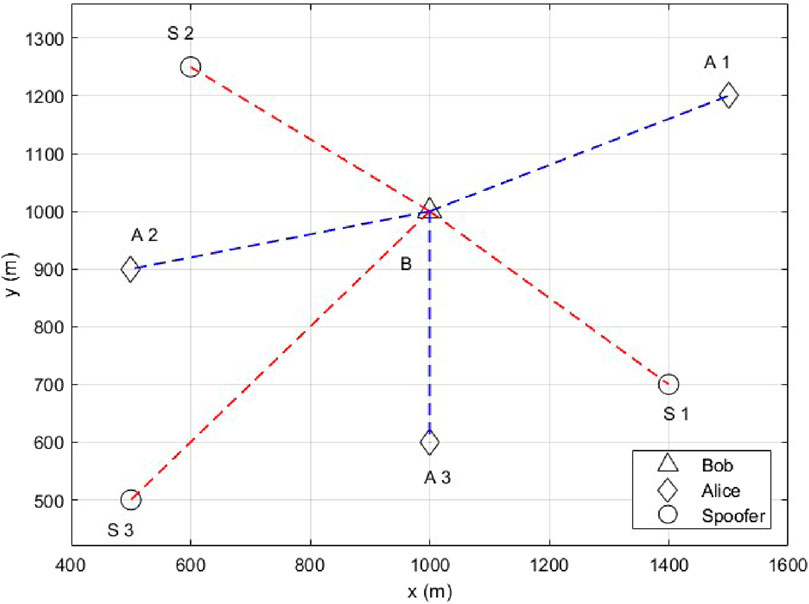
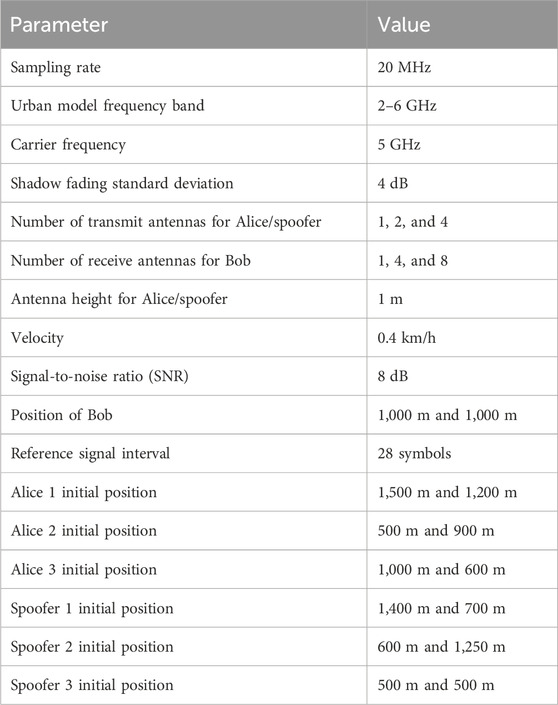
In this section, the performance of the proposed scheme is evaluated in multipath fading channels via Monte Carlo simulation. BPSK modulation is employed with the WINNER II channel model for NLOS urban environments (Kyösti et al., 2007). The single-user scenario has one Alice and three spoofers, while the multiple-user scenario has three Alice and three spoofers, as shown in Figures 4, 5, respectively. In these scenarios, Bob is stationary, while Alice and spoofers move arbitrarily and independently. SCC-SVM is implemented using the scikit-learn library in Python. For the single-user scenario,
Figure 6 presents the MDR, FAR, and AR for the single-user scenario with an SNR of 8 dB, velocity of 0.4 km/h, and 1, 4, and 8 receive antennas. This shows that MDR, FAR, and AR improve with an increase in the number of antennas. For instance, with a single transmit antenna, the MDR decreases from 26.0% with 1 receive antenna to 17.8% with four receive antennas and 2.9% with eight receive antennas. Similarly, with four receive antennas, the MDR decreases from 17.8% with one transmit antenna to 4.0% with two transmit antennas and 1.7% with four transmit antennas. The FAR with a single transmit antenna decreases from 11.9% with one receive antenna to 1.9% with four receive antennas and 0.3% with eight receive antennas. In the case of four receive antennas, the FAR decreases from 1.9% with one transmit antenna to 0.2% with two transmit antennas and only 0.1% with four transmit antennas. The AR increases with an increase in the number of antennas. For example, with four receive antennas, the AR increases from 90.2% with one transmit antenna to 97.9% with two transmit antennas and 99.1% with four transmit antennas. These results illustrate the impact of antenna diversity on performance.
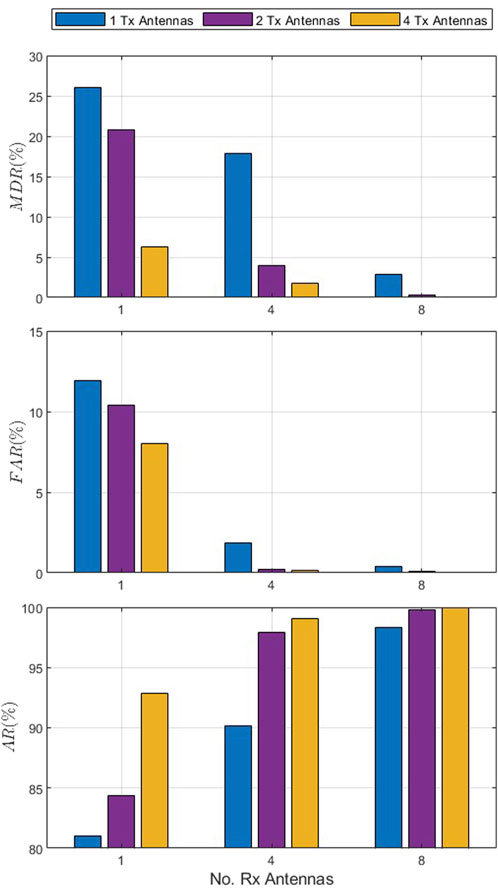
Figure 6. MDR, FAR, and AR versus the number of receive antennas for the single-user scenario with a signal-to-noise ratio (SNR) of 8 dB, velocity of 0.4 km/h, and 1, 4, and 8 receive antennas.
Figure 7 presents C, PPV, FDR, and PPV − FDR versus the number of receive antennas in the single-user scenario with an SNR of 8 dB, velocity of 0.4 km/h, and 1, 4, and 8 receive antennas. This shows that increasing the number of antennas improves C and thus, the information authentication rate IAR. With a single transmit antenna, C increases from 1.15 bps with one receive antenna to 4.75 bps with four receive antennas and 5.95 bps with eight receive antennas. Furthermore, the PPV increases, FDR decreases, and PPV − FDR increases with an increase in the number of antennas. For instance, with one transmit antenna, the PPV increases from 77.2% with one receive antenna to 84.6% with four receive antennas and 97.2% with eight receive antennas, while with four receive antennas, the PPV increases from 84.6% with one transmit antenna to 96.2% with two transmit antennas and 98.3% with four transmit antennas. In addition, with four receive antennas, the FDR decreases from 15.4% with one transmit antenna to 3.8% with two transmit antennas and 1.7% with four transmit antennas. The PPV − FDR also improves with an increase in the number of antennas as with four receive antennas, it increases from 69.2% with one transmit antenna to 92.3% with two transmit antennas and 96.6% with four transmit antennas. These results further illustrate the impact of antenna diversity on performance.
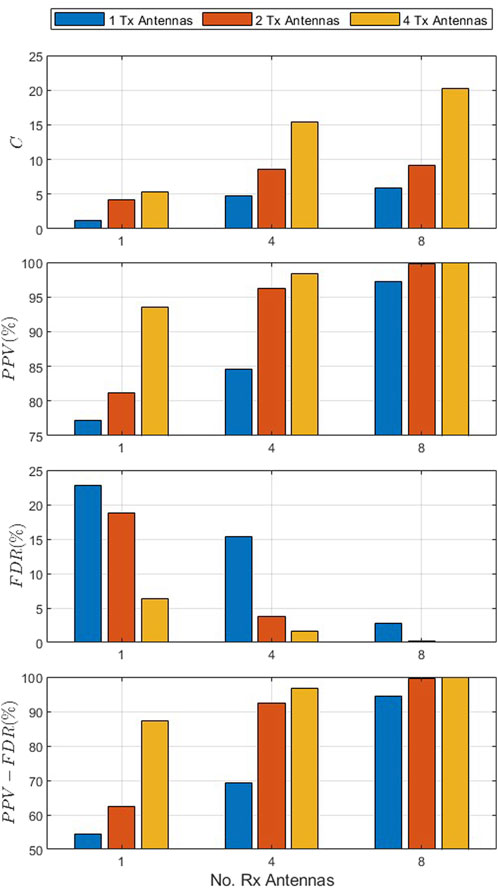
Figure 7. C, PPV, FDR, and PPV − FDR versus the number of receive antennas for the single-user scenario with an SNR of 8 dB, velocity of 0.4 km/h, and 1, 4, and 8 receive antennas.
Figure 8 presents the MDR, FAR, and AR versus the number of receive antennas with an SNR of 8 dB, velocity of 0.4 km/h, and one transmit antenna for the single- and multiple-user scenarios. This shows that the MDR, FAR, and AR increase with the number of receive antennas in both scenarios. For instance, in the multiple-user scenario, the MDR decreases from 44.9% with one receive antenna to 40.1% with four receive antennas and 31.9% with eight receive antennas. The corresponding FAR decreases from 17.7% with 1 receive antenna to 3.7% with four receive antennas and 2.0% with eight receive antennas, while the AR increases from 68.7% with one receive antenna to 78.1% with four receive antennas and 83.1% with eight receive antennas. These results also indicate that the MDR, FAR, and AR are better in the single-user scenario than in the multiple-user scenario. For instance, with four receive antennas, the MDR for the single- and multiple-user scenarios is 17.8% and 40.1%, respectively, while the corresponding FAR and AR are 1.9% and 3.7%, and 90.2% and 78.1%, respectively.
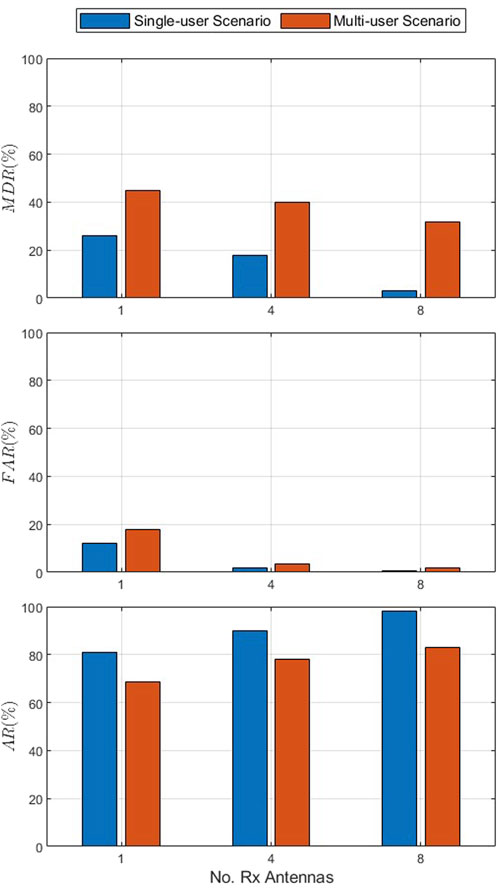
Figure 8. MDR, FAR, and AR versus the number of receive antennas with an SNR of 8 dB, velocity of 0.4 km/h, and 1 transmit antenna for the single- and multiple-user scenarios.
Figure 9 presents the MDR, FAR, and AR versus the number of receive antennas with an SNR of 8 dB, velocity of 0.4 km/h, and one transmit antenna for the single-user scenario, and η = 0.2 and 0.8. An increase in η means that a higher percentage of the data is treated as outliers, which decreases the MDR, so the probability of accepting spoofers is reduced. For example, with two receive antennas, the MDR is 26.6% for η = 0.2 and decreases to 10.9% for η = 0.8. However, an increase in η also results in a higher FAR, which increases the likelihood of rejecting Alice. For instance, with one receive antenna, the FAR is 8.7% for η = 0.2 and increases to 22.5% for η = 0.8. These results indicate that an increase in η will increase the AR. For example, with four receive antennas, the AR is 87.3% for η = 0.2 and increases to 92.0% for η = 0.8. Thus, η has a significant impact on the authentication performance and, therefore, should be chosen appropriately.
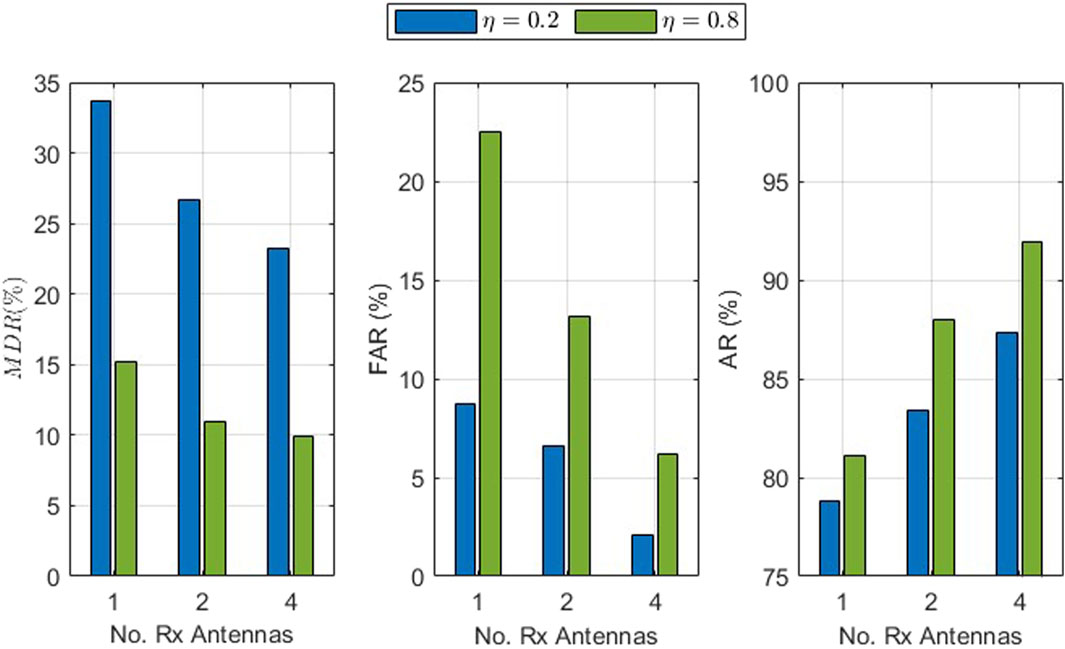
Figure 9. MDR, FAR, and AR versus the number of receive antenna with an SNR of 8 dB, velocity of 0.4 km/h, and 1 transmit antenna for the single-user scenario and η = 0.2 and 0.8.
Figure 10 presents the AR versus the velocity with an SNR of 8 dB, 1 transmit antenna, and 4 receive antennas using the real and imaginary components of the received signals as features (proposed scheme) and using only the magnitude, as in Pei et al. (2014). This shows that the AR with the proposed scheme is higher for all velocities. For example, the AR at a velocity of 0.4 km/h using the real and imaginary components of the signals as features is 89.2%, but it is only 56.7% using only the magnitude.
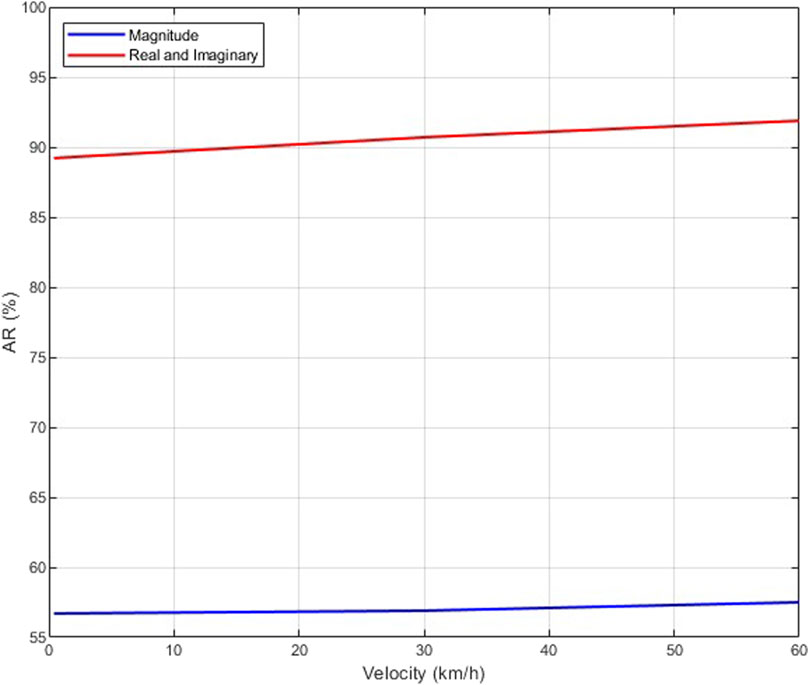
Figure 10. AR versus velocity with an SNR of 8 dB, 1 transmit antenna, and 4 receive antennas using the real and imaginary components of the received signals as features (proposed scheme) and using only the magnitude, as in Pei et al. (2014).
6 Conclusion
An adaptive PLA scheme was proposed that leverages ML and the antenna diversity in MIMO communication systems. Authentication robustness is achieved via a sliding window to continually update the attributes. Furthermore, an information-theoretic perspective was given for PLA in MIMO systems. The results presented illustrate the relationship between authentication performance and the number of antennas; in particular, the mutual information authentication rate IAR improves with the number of antennas.
Data availability statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Author contributions
MA: writing–original draft and writing–review and editing. TAG: writing–original draft and writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdi, A., Tepedelenlioglu, C., Kaveh, M., and Giannakis, G. (2001). On the estimation of the K parameter for the Rice fading distribution. IEEE Commun. Lett. 5, 92–94. doi:10.1109/4234.913150
Abdrabou, M., and Gulliver, A. (2022a). Authentication for satellite communication systems using physical characteristics. IEEE Open J. Veh. Technol. 4, 48–60. doi:10.1109/ojvt.2022.3218609
Abdrabou, M., and Gulliver, T. A. (2022b). Adaptive physical layer authentication using machine learning with antenna diversity. IEEE Trans. Commun. 70, 6604–6614. doi:10.1109/tcomm.2022.3196648
Abdrabou, M., and Gulliver, T. A. (2022c). Physical layer authentication for satellite communication systems using machine learning. IEEE Open J. Commun. Soc. 3, 2380–2389. doi:10.1109/ojcoms.2022.3225846
Abdrabou, M., and Gulliver, T. A. (2023). Adaptive physical layer authentication for IoT in MIMO communication systems using support vector machine. IEEE Internet Things J. 10, 19861–19873. doi:10.1109/jiot.2023.3282214
Abdrabou, M., and Gulliver, T. A. (2024). Game theoretic spoofing detection for space information networks using physical attributes. IEEE Trans. Commun., 1. doi:10.1109/tcomm.2024.3370433
Bloch, M., Barros, J., Rodrigues, M. R., and McLaughlin, S. W. (2008). Wireless information-theoretic security. IEEE Trans. Inf. Theory 54, 2515–2534. doi:10.1109/tit.2008.921908
Bloch, M., Günlü, O., Yener, A., Oggier, F., Poor, H. V., Sankar, L., et al. (2021). An overview of information-theoretic security and privacy: metrics, limits and applications. IEEE J. Sel. Areas Inf. Theory 2, 5–22. doi:10.1109/jsait.2021.3062755
Chatzidiamantis, N. D., Karagiannidis, G. K., Kriezis, E. E., and Matthaiou, M. (2011). “Diversity combining in hybrid RF/FSO systems with PSK modulation,” in IEEE international conference on communications (Japan: Kyoto).
Cover, T. M., and Thomas, J. A. (2006). Elements of information theory. 2nd Ed. USA: John Wiley & Sons.
Fang, H., Wang, X., and Xu, L. (2020). Fuzzy learning for multi-dimensional adaptive physical layer authentication: a compact and robust approach. IEEE Trans. Wirel. Commun. 19, 5420–5432. doi:10.1109/twc.2020.2993175
Ferrante, A., Laurenti, N., Masiero, C., Pavon, M., and Tomasin, S. (2015). On the error region for channel estimation-based physical layer authentication over Rayleigh fading. IEEE Trans. Inf. Forensics Secur. 10, 941–952. doi:10.1109/tifs.2015.2392565
Germain, K. S., and Kragh, F. (2020). “Physical-layer authentication using channel state information and machine learning,” in International Conference on Signal Processing and Communication Systems, Australia, 6 - 8 September 2023 (IEEE).
Golub, G. H., and Van Loan, C. F. (2013). Matrix computations. China: The John Hopkins University Press.
GPP version 15.2.0 (2018). NR; Physical channels and modulation. 3rd Gener. Partnersh. Proj. Tech. Specif. 38, 211.
He, X., Khisti, A., and Yener, A. (2011). “MIMO broadcast channel with arbitrarily varying eavesdropper channel: secrecy degrees of freedom,” in IEEE Global Telecommunications Conference, Houston, TX, USA, 29 November 2004 (IEEE).
Hoang, T. M., Duong, T. Q., Tuan, H. D., Lambotharan, S., and Hanzo, L. (2021). Physical layer security: detection of active eavesdropping attacks by support vector machines. IEEE Access 9, 31595–31607. doi:10.1109/access.2021.3059648
Hou, W., Wang, X., Chouinard, J.-Y., and Refaey, A. (2014). Physical layer authentication for mobile systems with time-varying carrier frequency offsets. IEEE Trans. Commun. 62, 1658–1667. doi:10.1109/tcomm.2014.032914.120921
Ishikawa, N., Hamamreh, J. M., Okamoto, E., Xu, C., and Xiao, L. (2021). Artificially time-varying differential MIMO for achieving practical physical layer security. IEEE Open J. Commun. Soc. 2, 2180–2194. doi:10.1109/ojcoms.2021.3112486
Khisti, A., and Wornell, G. W. (2010a). Secure transmission with multiple antennas I: the MISOME wiretap channel. IEEE Trans. Inf. Theory 56, 3088–3104. doi:10.1109/tit.2010.2048445
Khisti, A., and Wornell, G. W. (2010b). Secure transmission with multiple antennas—part II: the MIMOME wiretap channel. IEEE Trans. Inf. Theory 56, 5515–5532. doi:10.1109/tit.2010.2068852
Kyösti, P., Meinilä, J., Jämsä, T., et al. (2007). WINNER II channel models. China: Information Society Technologies. Technical Report IST-4-027756 WINNER II D1.1.2 V1.2.
Liang, Y., Poor, H. V., and Shamai (Shitz), S. (2008). Information theoretic security. Found. Trends® Commun. Inf. Theory 5, 355–580. doi:10.1561/0100000036
Oggier, F., and Hassibi, B. (2011). The secrecy capacity of the MIMO wiretap channel. IEEE Trans. Inf. Theory 57, 4961–4972. doi:10.1109/tit.2011.2158487
Pei, C., Zhang, N., Shen, X. S., and Mark, J. W. (2014). “Channel-based physical layer authentication,” in IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2024 (IEEE), 4114–4119.
Schölkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J., and Williamson, R. C. (2001). Estimating the support of a high-dimensional distribution. Neural Comput. 13, 1443–1471. doi:10.1162/089976601750264965
Senigagliesi, L., Baldi, M., and Gambi, E. (2020). Comparison of statistical and machine learning techniques for physical layer authentication. IEEE Trans. Inf. Forensics Secur. 16, 1506–1521. doi:10.1109/tifs.2020.3033454
Shannon, C. E. (1949). Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715. doi:10.1002/j.1538-7305.1949.tb00928.x
Tax, D. M., and Duin, R. P. (2004). Support vector data description. Mach. Learn. 54, 45–66. doi:10.1023/b:mach.0000008084.60811.49
Tse, D., and Viswanath, P. (2005). Fundamentals of wireless communication. Cambridge: Cambridge University Press.
Tubail, D. A., Alsmadi, M., and Ikki, S. (2023). Physical layer security in downlink of cell-free massive MIMO with imperfect CSI. IEEE Trans. Inf. Forensics Secur. 18, 2945–2960. doi:10.1109/tifs.2023.3272769
Wang, W., Chen, Y., and Zhang, Q. (2015). Privacy-preserving location authentication in Wi-Fi networks using fine-grained physical layer signatures. IEEE Trans. Wirel. Commun. 15, 1218–1225. doi:10.1109/twc.2015.2487453
Wang, W., Sun, Z., Piao, S., Zhu, B., and Ren, K. (2016). Wireless physical-layer identification: modeling and validation. IEEE Trans. Inf. Forensics Secur. 11, 2091–2106. doi:10.1109/tifs.2016.2552146
Wyner, A. D. (1975). The wire-tap channel. Bell Syst. Tech. J. 54, 1355–1387. doi:10.1002/j.1538-7305.1975.tb02040.x
Zhang, P., Shen, Y., Jiang, X., and Wu, B. (2020). Physical layer authentication jointly utilizing channel and phase noise in MIMO systems. IEEE Trans. Commun. 68, 2446–2458. doi:10.1109/tcomm.2020.2967393
Keywords: physical-layer authentication, single-class classification, information theory, machine learning, MIMO systems
Citation: Abdrabou M and Gulliver TA (2024) Secure authentication in MIMO systems: exploring physical limits. Front. Comms. Net 5:1370496. doi: 10.3389/frcmn.2024.1370496
Received: 14 January 2024; Accepted: 05 March 2024;
Published: 03 May 2024.
Edited by:
Pantea Nadimi Goki, Sant’Anna School of Advanced Studies, ItalyReviewed by:
Lei Guan, Xidian University, ChinaChanapha Bast, Udon Thani Rajabhat University, Thailand
Copyright © 2024 Abdrabou and Gulliver. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammed Abdrabou, YWJkcmFib3VAb3V0bG9vay5jb20=
 Mohammed Abdrabou
Mohammed Abdrabou T. Aaron Gulliver
T. Aaron Gulliver