- 1Department of Statistical Data Science, Institute of Statistical Mathematics, Tachikawa, Japan
- 2Department of Civil Engineering, Kobe University, Kobe, Japan
Transportation networks have a hierarchical structure, and the spatial scale of their impact on urban growth differs depending on the hierarchy. However, in empirical analyses of the impacts that transportation has on land use and prices, such hierarchy is often examined using dummy variables, and the network dependence and heterogeneity of impacts are often ignored. Thus, this study develops a spatial regression method that considers not only spatial dependence, but also network dependence within a hierarchical transportation network. This method was developed by extending the random effects eigenvector spatial filtering approach. Subsequently, it was applied to a pre-existing analysis that focused on the impacts that high-speed rail (HSR) had on residential land prices in Japan over the last 30 years. The results of the analysis suggested that HSR lines had hierarchical effects on residential land prices. The results also provide interesting insight into the ongoing problem of Japanese urban hierarchy; that is, the excessive concentration of population and industry in the Tokyo metropolitan area.
Introduction
Transportation networks are hierarchical. For example, a road network consists of expressways, national roads, prefectural roads, municipal roads, and others. The commuter rail network has major stations where rapid transit services are available and other stations where it is not. Such hierarchical transportation networks have heterogeneous impacts on urban structures, which is evidenced in the vast amounts of existing research regarding the interactions between land use and transportation (e.g., Newman and Kenworthy, 1996; Stanley, 2014).
High-speed rail (HSR) is one of the most influential transportation systems within urban structures in Japan (Takami and Hatoyama, 2008), China (Chen and Hall, 2011), and Europe (e.g., Garmendia et al., 2012). The presence of HSR causes a concentration of economic activities around stations and creates hierarchies within the urban network (Jiao et al., 2017). For example, Albalate and Bel (2012) suggested that Japanese HSR encouraged rapid growth in major cities, such as in Tokyo and Osaka, leading to a concentrated urban hierarchy. Similar results were obtained in Spain (Garmendia et al., 2012) and China (Jiao et al., 2017). Contrastingly, the HSR in France was found to encourage rapid growth in minor cities and create a dispersed hierarchy in the city network (Cervero and Bernick, 1996).
Moreover, HSR typically has rapid trains that only stop at major stations, and local trains that stop at every station. Such a hierarchy within the HSR network may create an urban hierarchy. However, in empirical analyses, such a hierarchy in transportation networks is often solely considered through the use of dummy variables that indicate differences in services, whilst ignoring network dependence.
To quantify the hierarchical impacts of HSR on urban growth, this study develops a spatial regression method that considers (i) network dependence, (ii) city-wise heterogeneity in each hierarchy, and (iii) spatial dependence (decaying with respect to Euclidean distance) by extending the random effects eigenvector spatial filtering (RE-ESF) approach (Griffith, 2003; Murakami and Griffith, 2015). Although it is typical to use spatial econometric models to consider spatial dependences (Anselin and Griffith, 1988; LeSage and Pace, 2009; Yamagata and Seya, 2019), the RE-ESF framework is flexible and can easily be applied to models for transportation research, as Yu et al. (2020) showed and as we will show later.
The number of studies considering network dependence is relatively limited. Cressie et al. (2006) and Garreta et al. (2010) considered network dependence on river networks, and Lu et al. (2017) and Ver Hoef (2018) considered dependence through road networks. Yet, these studies utilize either network dependence alone or compared Euclidean and network distances, then merely choosing the model with better accuracy. In the case of land prices, however, while there is spatial dependence, they may also be affected by network dependence and station-wise heterogeneity. Moreover, these variables can affect multiple hierarchies in the city network, as explained above. Based on our literature review, no regression studies simultaneously consider variables (i)–(iii).
This study analyzes the impact that HSR development has on land prices in Japan. Since 1964 when Japan's first HSR, the Shinkansen, first opened, major cities have been connected by the HSR network and urbanization has accelerated along rail lines. As discussed by Seya and Timmermans (2018), a properly executed transportation project may improve the land accessibility. An improvement in accessibility may be reflected in both the price of land and the concentration of development. Typically, the effect of transport on land use and development can take a relatively long time to observe, whereas the effect of transport on property values can occur sooner (Stokenberga, 2014). Existing studies have attempted to examine both the former and the latter. The results of the analysis, as explained below, indicate that both spatial dependence and HSR network dependence influence residential land prices. This suggests the importance of considering network dependence when analyzing interactions between land use and transport. We also observed a hierarchical pattern in which both major and minor cities were affected by network dependence. However, the former was further affected by another global network dependence.
The subsequent sections are organized as follows: Section methodology explains the method employed, section empirical analysis applies this method to an analysis that evaluates the influence that HSR has on urbanization in Japan, and section concluding remarks states the conclusions from this study.
Methodology
Data Model
This study assumes the following model for the land price yi at the i-th location:
where xi, k denotes the k-th explanatory variable, βk is the regression coefficient, si denotes (iii) spatially dependent process, and zi, m denotes influence from the m-th HSR network characterized by (i) and (ii). εi represents data noise with variance σ2. Following land price modeling studies (e.g., Tsutsumi and Seya, 2009; Kunimi and Seya, 2021), land price has been log-transformed.
This study considers M transportation networks, each of which has the same network structure but different set of stations/nodes; the m-th network has the stations/nodes that the m-th class train stops1. Later, we analyze the impact of the rapid and local HSR networks on urban hierarchy, assuming M = 2. The influence from the m-th network zi, m is modeled as follows:
The nearest station from the i-th location in the m-th network is indexed by I(m). nI(m) models (i) the dependence through the m-th network, and models (ii) the station-wise heterogeneity. While nI(m) and are stochastic processes defined by the network, they are assumed to influence the land price nearby the I(m)-th station (i.e., spill-over from the station). While the expectations of these processes are assumed to be zero, the bm parameter estimates the mean increase of the logged land price at each station owing the m-th transport network. wi, I determines the strength of the influence that the i-th location receives from the nearest station I(m). It is specified as follows:
where di, I(m) is the Euclidian distance between the i-th location and the I(m)-th station. RI(m) represents the distance that the spatial spillover extends from the I(m)-th station. This study parameterizes it as RI(m) = RmAI(m) where Rm is a range parameter and AI(m) is a multiplier adjusting the range according to the scale of the I(m)-th station. Later, it is given by the square root of the number of passengers at the station.
In short, Equation (1) models logged land price using explanatory variables {xi, 1, …, xi, K}, (iii) spatial dependent effects si, (i) dependent and (ii) heterogenous effects induced by the M transportation networks , and noise εi. Since si, nI(m), and can be collinear each other, these effects must be identified and analyzed carefully.
Process Model
Spatially Dependent Process si
Moran coefficient (MC; Griffith, 2000) is a diagnostic statistic of spatial dependence. The MC value for a vector y is defined as follows:
where C is a symmetric spatial proximity matrix with zero diagonals. M = I−11′/N is a centering matrix where I is an identity matrix 1 is a vector of ones. In the absence of spatial dependence in y, the expectation of MC[y] equals . If N is sufficiently large, MC[y] > 0 if y is positively dependent while MC[y] < 0 if it is negatively dependent.
It is known that the MC of the p-th eigenvector ep of the MCM matrix yields (Griffith, 2003).
Equation (5) suggests that ep has a positively dependent map pattern if λp > 0 while the opposite is true if λp < 0. In other words, the P eigenvectors e1, …, eP corresponding positive eigenvalues {λ1, …, λP} explains positive spatial dependence. Thus, the P eigenvectors are sufficient for modeling positively dependent spatial processes, which is predominant in most real-world cases.
Using the P eigenvectors, RE-ESF models positively dependent spatial process as follows:
where ei, p is the i-th element of ep and τ2 denotes the variance of the process (e.g., τ2 = 0 means no spatially dependent variation). The α parameter determines the scale or the MC value of the process. Specifically, the expectation of I[s] where approaches the theoretical maxima, which implies the largest-scale map pattern, as α → ∞, while the expectation approaches zero, which implies the smallest-scale map pattern, as α → −∞. Thus, Equation (6) attempts to estimate the structure of the underlying process through the τ2 and α parameters (see Murakami and Griffith, 2021).
Network Dependent Process nI(m)
Equation (6) is readily extended to model dependence among stations through the m-th network as follows:
where and λqm are the qm-th eigen-pair corresponding positive eigenvalue extracted from a doubly centered proximity matrix MmCmMm on the m-th network. The (I(m), J(m))-th element of the Cm matrix may be defined by a function decaying with respect to the shortest-path distance, travel time, or other distances between the stations I(m) and J(m). The parameters and αm estimate the variance and scale of the dependent process upon the network. While Equation (7) models a dependence on the m-th network, it influences on the land prices nearby the I(m)-th station though a spillover, that decays with respect to wi, I(m), as previously explained.
Station-Wise Heterogenous Process
The following station-wise random intercept is assumed for :
where is a variance parameter. The random intercepts take uniformly zero values when , while the intercepts have large variation across stations when is large. In general, consideration of such a group effect is crucial to avoid estimation bias attributed to the heterogeneity by groups (ecological fallacy; see Piantadosi et al., 1988).
Summary
By substituting the process models (6–8) into Equation (1), our model is written as follows:
Equation (9) is a mixed effects model with random coefficients regularized by the variance parameters . While the model estimation can be slow for large samples because of the need to optimize the 2 + 3M variance parameters, Murakami and Griffith (2019) developed a fast restricted maximum likelihood (REML) method to estimate a spatial mixed effects model (see Murakami et al., 2020) including Equation (9). The model is estimated using the REML. Since the original fast REML does not assume the Rm parameter in wi, I(m), it is optimized though a grid search (grid size: 1 km) in the subsequent empirical part. Therefore, the fast REML is iterated while varying the r value, and the value maximizing the restricted likelihood is adopted.
Empirical Analysis
Outline
This section applies the developed model to the HSR to examine the HSR's effects on urbanization between 1984 and 2014 through land price analysis. The study area included the main island of Japan (Honshu) and the Kyushu region where the HSR runs. The explained variable is the logged officially assessed residential land price per area [JPY/m2] (source: National Land Numerical Information download service (NLNI); https://nlftp.mlit.go.jp/ksj/). The yearly sample size ranged between 26,264 (1984) and 45,008 (1998). In this study, the static model is estimated on an annual basis (i.e., for each cross-section).
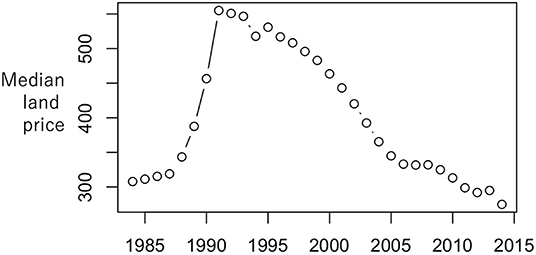
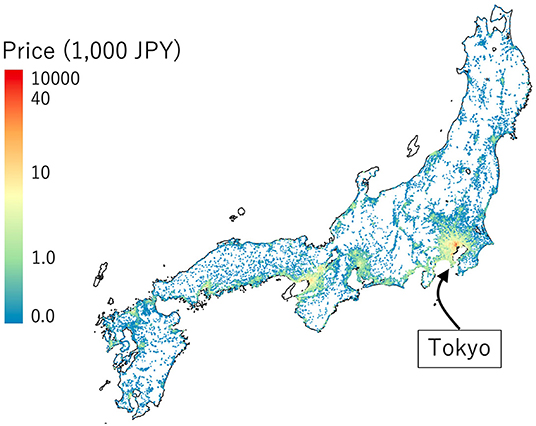
Figures 1, 2 display the temporal and spatial distributions of the land prices. As shown in Figure 1, the median land price peaked in 1991 when Japan was in a bubble economy, which lasted from 1986 until 1991. After that, the economy stagnated and land price began a gradual decline. This was especially true around major urban areas, including the Tokyo metropolitan area (see Figure 2).
As shown in Figure 3, the HSR stretches outwards from Tokyo in every direction. Among the HSR lines summarized in Table 1, the Tokaido-Sanyo Shiknansen, which connects Tokyo and Hakata through Nagoya, Kyoto, and Osaka with the maximum speed of 275–300 km/h, is the busiest line. This line is thought to have had a huge impact on urban growth. The other lines which connect Tokyo to other major cities have maximum speeds between 240 and 320 km/h.2
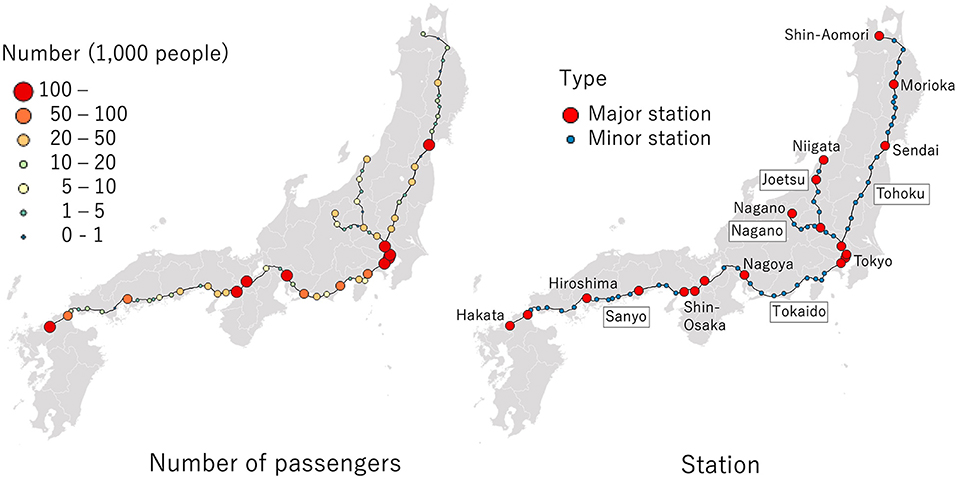
Figure 3. Study area and the high-speed rail network. The major stations and other stations are shown in the right panel while the number of passengers is shown in the left. In the right panel, route names are surrounded by black border while station names are not. The major stations are considered as the nodes of the global network while all the stations are considered as the nodes of the local network.
Each of these lines have rapid trains that only stop at major stations. This is indicated by red circles in Figure 3 (left). However, local trains stop at every station. In other words, Japanese HSR has a global-level HSR network, whose proximity matrix C1 is defined by the distance among the major stations that the rapid trains stop, and a local-level network with proximity matrix C2 being defined by the network distance among all the HSR stations. The (I(m), J(m))-th element of the Cm matrix is given by where the distance dI(m), J(m) between stations is given using the shortest travel time, which is defined as (network distance) × (the maximum speed). The rm value is given by the longest distance between two adjacent stations/nodes in the M-th network3. The rm value acts as a prior for the scale of the network dependence, and the scale is adjusted to fit the data by estimating the αm parameter as explained in section summary.
Regarding AI(m), to determine the range of the spillover from the I(m)-th station (see Equation 3), the square-root of the average number of daily passengers in 2013 (source: NLNI) is used4. The resulting range is RI(m) = RmAI(m), wherein the spillover becomes larger for stations with more passengers. The Rm parameter is estimated by maximizing the restricted likelihood.
The explanatory variables considered as are follows: Euclidean distance to the nearest railway station among stations including those for non-high-speed rail lines (Sta_dist [km]), bus stop (Bus_dist [km]), airport (Air_dist [km]), and prefectural government official (Gov_dist [km]); and dummy variables for residential land (Res), commercial land (Com), and industrial land (Ind). All these variables were acquired from NLNI.
The objective of this empirical analysis is to examine if the HSR network has hierarchical effects influencing the major cities though the global-level network and the major and local cities through the local-level network. Section accuracy comparison result verifies the existence of global and local effects through accuracy comparison. Section estimation results visualized the estimated effects.
Accuracy Comparison Result
The accuracy of the models summarized in Table 2 were compared using Bayesian Information Criterion (BIC). The BIC values of all the spatial models are considerably smaller, and therefore better, than LM, suggesting the presence of the conventional spatial dependence (si). Figure 4 plots the differences in the BIC values between SM and {SM_G, SM_L, SM_GL}. Based on this figure, consideration of both the global and local networks can improve the BIC. In particular, throughout the target period, the best accuracy was achieved by SM_L and SM_GL which consider the local-level effects. The local network dependence appears more influential on land price than the global network dependence is. Based on that result, land prices near minor stations may be strongly influenced by network dependence from Tokyo, for example. From 1984 to 1988, SM_L achieved the best, or smallest, BIC values in 4 or 5 years. After 1989, SM_GL achieved the best BIC values out of all of the years that were analyzed. Both the HSR's global and local networks may affect land prices. Based on this result, we report an estimated result of SM_GL in the subsequent sections.
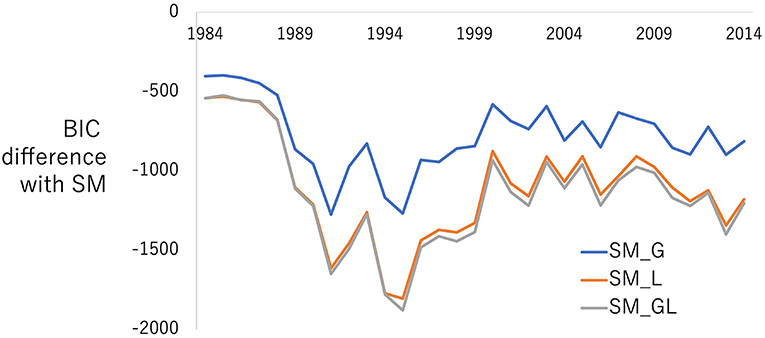
Figure 4. BIC differences between SM and {SM_G, SM_L, SM_GL}. A larger negative value means better model accuracy relative to SM.
Estimation Results
Figure 5 plots the estimated range rI(m) of the spillover effects from the Tokyo station. The range, which ~20 km in the 80s and gradually increased during 90s, became ~40 km in 2000. The HSR may have encouraged urban development and, therefore, urban sprawl (Bagan and Yamagata, 2012) in this period. Contrastingly, the range gradually declined after 2000. Note that this pattern is similar to the net population inflow to the Tokyo metropolitan area (Ministry of Land Infrastructure Transport and Tourism (MLIT), 2014, p. 3), which increased from just after the end of the bubble in 1991 until the 2008 financial crisis, although it peaked a slightly earlier. As the optimized range values are a bit noisy as shown in the gray line in Figure 5, we smoothed the value as shown in the black line and used in the subsequent SM_GL model estimation.
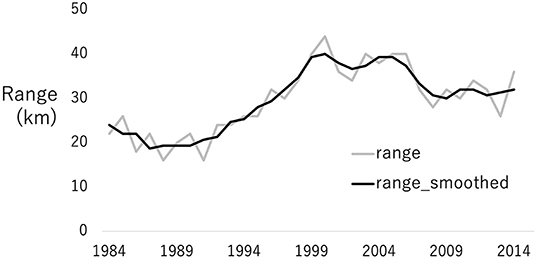
Figure 5. Estimated range of the spatial spill-over from the Tokyo station. The gray line represents the raw estimates, and the black line represents the smoothed estimates, which are used in the subsequent analysis.
Figure 6 plots the regression coefficients estimated in each year. Sta_dist, Bus_dist, Gov_dist, which are accessibility measures, are negatively significant within certain periods. The coefficients on Sta_dist is smaller than Bus_dist, meaning that railway station has a long-range effect whereas the bus stop has a short-range effect. The result is reasonable given that buses are typically responsible for local transportation. The coefficients for Gov_dist are smaller than those for Sta_dist and Bus_dist, indicating longer-range effects. Again, this is reasonable given that only 41 prefectural offices cover the entire study area. The coefficients on Air_dist had values near zero and tended to be statistically insignificant.
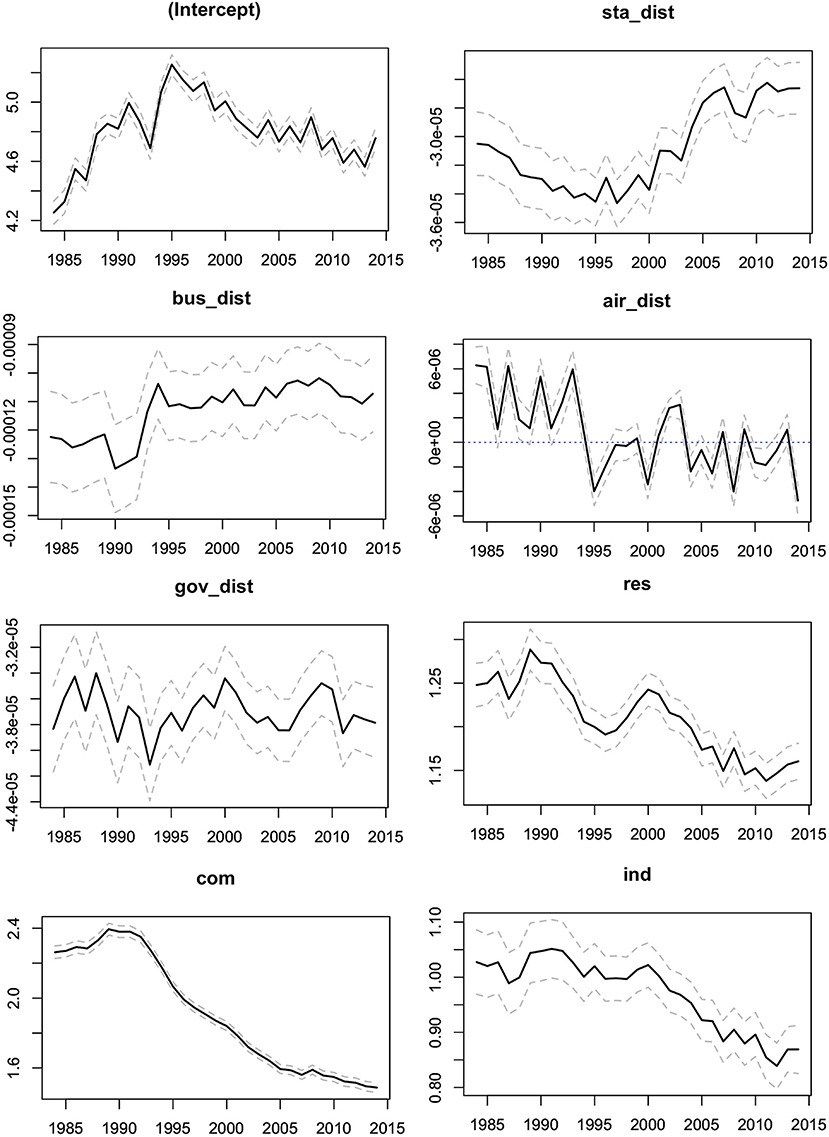
Figure 6. Coefficients estimated from SM_GL. Solid line represents the coefficient estimates and dashed lines represent the upper and lower limits of the 95 percent confidence intervals.
Res, Com, and Ind were all positively significant. Among the three, Com was the largest and Ind was the smallest coefficient. Commercial land, which has many urban facilities, was found to be the most popular area. Meanwhile, industrial land, which may suffer from air pollution and noise, was the cheapest area of the three land types.
Based on the fact that the coefficients for Sta_dist, Res, Com, and Ind all declined over the study period, a decline in land prices during a stagnate economy appeared to be especially severe in urban areas, specifically those that were near railway stations.
The left panel in Figure 7 plots the estimated spatially dependent process (si). The process identified two hotspots around Tokyo and Osaka, which are two major urban areas. However, Osaka's hotspot gradually diminished, whereas Tokyo is still the dominant hotspot as of 2014. This result suggests that there has been a popular residential area concentrated around Tokyo for years.
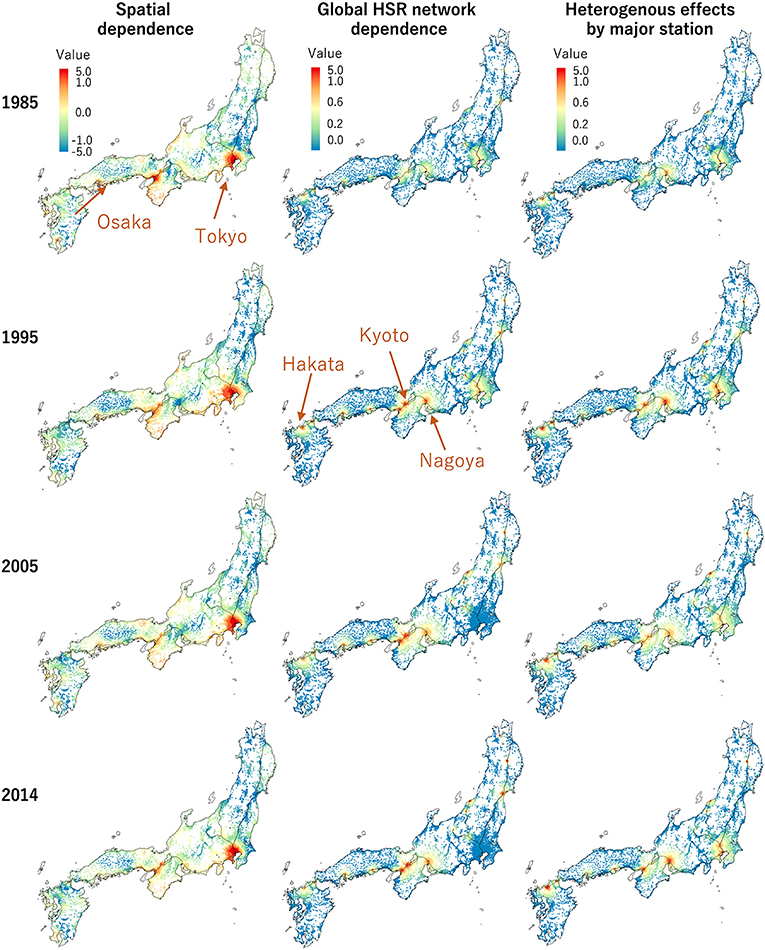
Figure 7. Estimated spatial dependent effects and spill-over effects from the global network dependence through the HSR (1985, 1995, 2005, 2014). For comparison, the same color scale is assumed for all the panels in this figure and Figure 8 except for the left four panels in this figure.
The middle panel of Figure 7 maps the effects of the global-level network dependence (wi, I(1)(b1 + nI(1))). The dependence was estimated to increase the land price around the major stations, including the Nagoya and Hakata stations in Tokaido-Sanyo Shinkansen. The increase was substantial in Osaka and Kyoto. Because these cities dramatically improved their accessibility to Tokyo through the HSR, the increase in land price was reasonable. Similar increases in land price were also found around major stations outside Tokyo, likely due to the accessibility to Tokyo and other major cities caused by the HSR. Contrastingly, the global-level network dependence did not increase land prices in Tokyo after 2005. In short, the global-level network dependence is especially beneficial for major cities outside Tokyo.
Based on the right panels in Figure 7 showing the global-level station-wise effects (), land price along Tokaido-Sanyo Shinkansen increased not only dependently through the network but also heterogeneously/independently within each major city. Given that Tokaido-Sanyo Shinkansen runs along Taiheiyo Belt, which covers a concentration of various industries, this heterogeneity is attributable to differences in industrial structure in each major city. Unlike the global-level network dependence (middle column of Figure 7), the station-wise effect increases land prices in the Tokyo metropolitan area. The land price patterns in Tokyo are estimated to be highly heterogeneous, relative to other major cities.
Figure 8 plots the estimated local-level effects. The local-level network dependence strongly increases land prices between Tokyo and Sendai, along the Tohoku Shinkansen. The increase in land price is substantial in the city of Utsunomiya, which has a minor station. This result is intuitively consistent given that the HSR allowed Utsunomiya to become a commuter town for Tokyo. It follows that the section of the Tohoku Shinkansen near Tokyo benefitted strongly from aspects of the local-level HSR network.
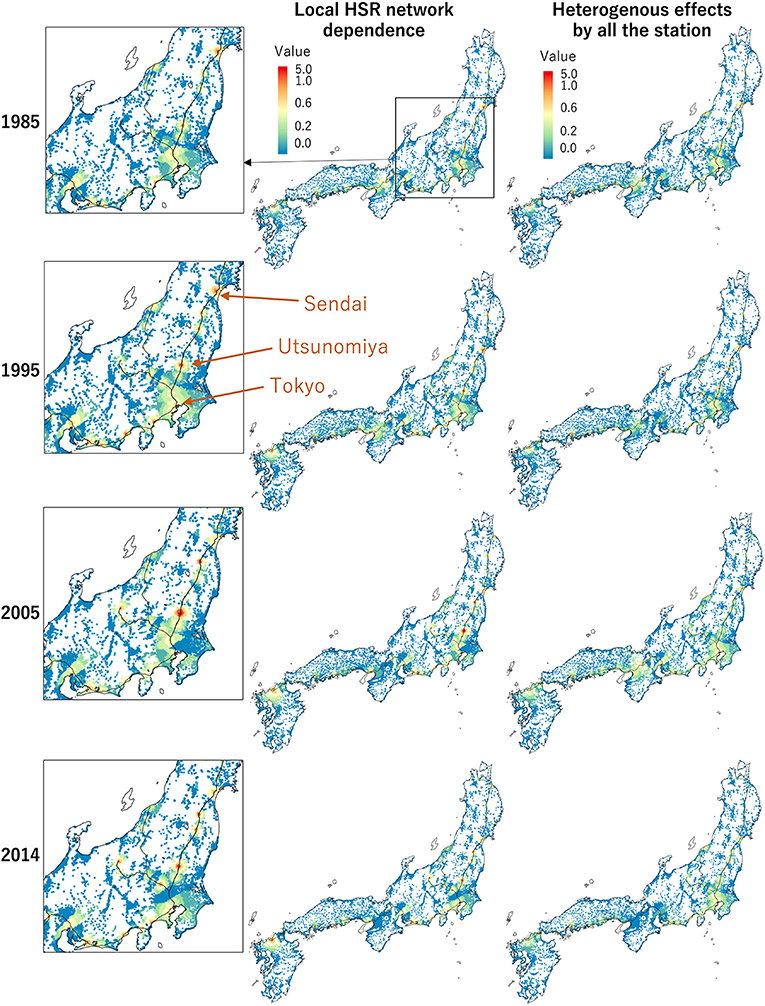
Figure 8. Estimated spatial dependent effects and spill-over effects from the local network dependence through the HSR (1985, 1995, 2005, 2014). The former around Tokyo is zoomed. See Figure 7 for the color scale.
This study verified the existence of hierarchical effects that influence major cities along the HSR lines due to the global-level network, and minor cities due to the local-level network. Further, the effects of HSR are heterogenous in different spaces. Regarding trends over time, the Tokyo metropolitan area's role as the largest metropolitan area in Japan has not changed during the studied period. However, its contents have changed. When compared to the 1980s, the influence that spatial dependence had has gradually strengthened and that of HSR networks has weakened since the 2000s. That is, the spillover effect that the Tokyo metropolitan area experiences from other metropolitan areas is weakening. This is a phenomenon that can only be understood when both spatial and network dependences are considered.
Concluding Remarks
Transportation networks encourage a hierarchy within urban growth. However, in extant literature, these hierarchies are usually examined by simply using dummy variables, and the network dependence within the impacts is often ignored. Using the example of HSR in Japan, this study proposed a regression method for the simultaneous estimation of spatial dependence, network dependence among stations, and station-specific heterogeneity. The empirical results verified that there are hierarchical effects along HSR lines. The findings provide an interesting insight into an ongoing problem within the Japanese urban hierarchy; that is, the fact that the spillover effect that the Tokyo metropolitan area experiences from other metropolitan areas is weakening.
The proposed method allows for modeling dependencies on multiple networks simultaneously and can achieve efficient computation through an extension of the RE-ESF approach. However, several issues remain to be examined in future studies. For example, although this study focused on railway networks, the proposed modeling method can be applied to other transportation networks, including airports and ports. Additionally, this model can be expanded into a spatiotemporal model that allows for the consideration of dynamic processes that underly urbanization. Therefore, it may also be pivotal to consider a network's direction (e.g., Tokyo strongly influences Osaka, but the opposite might be less remarkable). Similarly, although this study considered only two levels with HSR lines, there are more levels to be examined in future research.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
DM developed the model and applied the model to land price analysis. HS created the land price dataset and provided ideas for model development. DM and HS contributed in writing the manuscript. Both authors contributed to the article and approved the submitted version.
Funding
This work was supported by JSPS KAKENHI, Grant Numbers 20K13261, 21H01447, and 18H03628. Part of this research was conducted under the project, Research on the evaluation of spatial economic impacts of building bus termini (Principal Investigator: Prof. Yuki Takayama, Kanazawa University), supported by the Committee on Advanced Road Technology, the MLIT, Japan.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor DG declared a past co-authorship with the DM.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^The M networks can also be defined by different transportation networks (e.g., bus and railway networks).
2. ^Mini-Shinkansen that goes through conventional railway is not considered in this study because their maximum speed is 130 km/h, which is considerably slower than our targets and impacts may be different.
3. ^It is an analog of relevant studies (e.g., Murakami and Griffith, 2015) that gave the same range parameter by the longest distance between two adjacent nodes in a network connecting all sample sites for modeling spatial dependence.
4. ^Area in the Rm distance radius equals . Therefore, it is reasonable assume that population in the radius is proportion to . In other words, , or equivalently, . Given that, we assume the square-root of the number of passengers as the adjustment factor AI(m) for the distance range parameter Rm.
References
Albalate, D., and Bel, G. (2012). High-speed rail: lessons for policy makers from experiences abroad. Public Adm. Rev. 72, 336–349. doi: 10.1111/j.1540-6210.2011.02492.x
Anselin, L., and Griffith, D. A. (1988). Do spatial effects really matter in regression analysis? Papers Reg. Sci. 65, 11–34. doi: 10.1111/j.1435-5597.1988.tb01155.x
Bagan, H., and Yamagata, Y. (2012). Landsat analysis of urban growth: how Tokyo became the world's largest megacity during the last 40 years. Remote Sens. Environ. 127, 210–222. doi: 10.1016/j.rse.2012.09.011
Cervero, R., and Bernick, M. (1996). High-Speed Rail and Development of California's Central Valley: Comparative Lessons and Public Policy Considerations. IURD Working Paper, p. 675.
Chen, C. L., and Hall, P. (2011). The impacts of high-speed trains on British economic geography: a study of the UK's InterCity 125/225 and its effects. J. Transp. Geogr. 19, 689–704. doi: 10.1016/j.jtrangeo.2010.08.010
Cressie, N., Frey, J., Harch, B., and Smith, M. (2006). Spatial prediction on a river network. J. Agric. Biol. Environ. Stat. 11, 127–150. doi: 10.1198/108571106X110649
Garmendia, M., Romero, V., Ureña, J., Md. Coronado, J. M., and Vickerman, R. (2012). High-speed rail opportunities around metropolitan regions: Madrid and London. J. Infrastructure Syst. 18, 305–313. doi: 10.1061/(ASCE)IS.1943-555X.0000104
Garreta, V., Monestiez, P., and Ver Hoef, J. M. (2010). Spatial modelling and prediction on river networks: up model, down model or hybrid? Environmetrics 21, 439–456. doi: 10.1002/env.995
Griffith, D. A.. (2000). A linear regression solution to the spatial autocorrelation problem. J. Geogr. Syst. 2, 141–156. doi: 10.1007/PL00011451
Griffith, D. A.. (2003). Spatial Autocorrelation and Spatial Filtering Gaining Understanding Through Theory and Scientific Visualization. Berlin: Springer. doi: 10.1007/978-3-540-24806-4_4
Jiao, J., Wang, J., and Jin, F. (2017). Impacts of high-speed rail lines on the city network in China. J. Trans. Geogr. 60, 257–266. doi: 10.1016/j.jtrangeo.2017.03.010
Kunimi, T., and Seya, H. (2021). Identification of the geographical extent of an area benefiting from a transportation project: a generalized synthetic control. J. Trans. Land Use 14, 25–45. doi: 10.5198/jtlu.2021.1784
LeSage, J. P., and Pace, R. K. (2009). Introduction to Spatial Econometrics. Chapman and Hall/CRC. doi: 10.1201/9781420064254
Lu, B., Brunsdon, C., Charlton, M., and Harris, P. (2017). Geographically weighted regression with parameter-specific distance metrics. Int. J. Geogr. Inf. Sci. 31, 982–998. doi: 10.1080/13658816.2016.1263731
Ministry of Land Infrastructure Transport Tourism (MLIT) (2014). On the Situation of Excess Concentration in the Tokyo Metropolitan Area (in Japanese). Available online at: https://www.mlit.go.jp/common/001042017.pdf
Murakami, D., and Griffith, D. A. (2015). Random effects specifications in eigenvector spatial filtering: a simulation study. J. Geogr. Syst. 17, 311–331. doi: 10.1007/s10109-015-0213-7
Murakami, D., and Griffith, D. A. (2019). Spatially varying coefficient modeling for large datasets: eliminating N from spatial regressions. Spat. Stat. 30, 39–64. doi: 10.1016/j.spasta.2019.02.003
Murakami, D., and Griffith, D. A. (2021). Balancing spatial and non-spatial variation in varying coefficient modeling: a remedy for spurious correlation. Geogr. Anal. doi: 10.1111/gean.12310. [Epub ahead of print].
Murakami, D., Kajita, M., and Kajita, S. (2020). Scalable model selection for spatial additive mixed modeling: application to crime analysis. ISPRS Int. J. Geo-Information 9:577. doi: 10.3390/ijgi9100577
Newman, P. W., and Kenworthy, J. R. (1996). The land use-transport connection: an overview. Land Use Policy 13, 1–22. doi: 10.1016/0264-8377(95)00027-5
Piantadosi, S., Byar, D. P., and Green, S. B. (1988). The ecological fallacy. Am. J. Epidemiol. 127, 893–904. doi: 10.1093/oxfordjournals.aje.a114892
Seya, H., and Timmermans, H. (2018). “An overview of Asian studies on transport and land use,” in Routledge Handbook of Transport, eds A. J. Zhang and F. Cheng-Min (London: Routledge), 314–336. doi: 10.4324/9781315739618-14
Stanley, J. K.. (2014). Land use/transport integration: Starting at the right place. Res. Trans. Econ. 48, 381–388. doi: 10.1016/j.retrec.2014.09.067
Stokenberga, A.. (2014). Does Bus rapid transit influence urban land development and property values: a review of the literature. Trans. Rev. 34, 276–296. doi: 10.1080/01441647.2014.902404
Takami, K., and Hatoyama, K. (2008). “Sustainable regeneration of a car-dependent city: the case of Toyama toward a compact city,” in cSUR-UT Series: Library for Sustainable Urban Regeneration (Tokyo: Springer), 183–200. doi: 10.1007/978-4-431-78147-9_10
Tsutsumi, M., and Seya, H. (2009). Hedonic approaches based on spatial econometrics and spatial statistics: application to evaluation of project benefits. J. Geogr. Syst. 11, 357–380. doi: 10.1007/s10109-009-0099-3
Ver Hoef, J. M.. (2018). Kriging models for linear networks and non-euclidean distances: cautions and solutions. Methods Ecol. Evol. 9, 1600–1613. doi: 10.1111/2041-210X.12979
Yamagata, Y., and Seya, H., (eds.) (2019). Spatial Analysis Using Big Data: Methods and Urban Applications. Cambridge: Academic Press.
Yu, D., Murakami, D., Zhang, Y., Wu, X., Li, D., Wang, X., et al. (2020). Investigating high-speed rail construction's support to county level regional development in China: an eigenvector based spatial filtering panel data analysis. Trans. Res. Part B Methodol. 133, 21–37. doi: 10.1016/j.trb.2019.12.006
Keywords: high-speed rail, network dependence, spatial regression, Moran eigenvectors, land prices, urban form
Citation: Murakami D and Seya H (2022) Spatial Regression in the Presence of a Hierarchical Transportation Network: Application to Land Price Analysis. Front. Sustain. Cities 4:905967. doi: 10.3389/frsc.2022.905967
Received: 28 March 2022; Accepted: 02 May 2022;
Published: 23 May 2022.
Edited by:
Daniel A. Griffith, The University of Texas at Dallas, United StatesReviewed by:
Jan Hauke, Adam Mickiewicz University, PolandPeter Rogerson, University at Buffalo, United States
Copyright © 2022 Murakami and Seya. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daisuke Murakami, ZG11cmFrYUBpc20uYWMuanA=
 Daisuke Murakami
Daisuke Murakami Hajime Seya2
Hajime Seya2