1
ISI Foundation, Torino, Italy
2
Laboratoire de Neurophysique et Physiologie, Université Paris Descartes, Paris, France
3
UMR 8119, CNRS, Paris, France
Persistent activity observed in neurophysiological experiments in monkeys is thought to be the neuronal correlate of working memory. Over the last decade, network modellers have strived to reproduce the main features of these experiments. In particular, attractor network models have been proposed in which there is a coexistence between a non-selective attractor state with low background activity with selective attractor states in which sub-groups of neurons fire at rates which are higher (but not much higher) than background rates. A recent detailed statistical analysis of the data seems however to challenge such attractor models: the data indicates that firing during persistent activity is highly irregular (with an average CV larger than 1), while models predict a more regular firing process (CV smaller than 1). We discuss here recent proposals that allow to reproduce this feature of the experiments.
Since the beginning of the seventies, experiments on awake monkeys performing memory tasks have provided a wealth of information about the neural basis of working memory (Funahashi et al., 1989
; Fuster and Alexander, 1971
; Fuster and Jervey, 1981
; Goldman-Rakic, 1995
; Miyashita, 1988
). During these experiments, the animals are trained to perform a task in which they have to remember for short times the identity or the location of a visual stimulus. These tasks share in common a ‘delay period’ during which the monkey has to maintain in ‘working’ memory information needed to solve the task after the end of the delay period. One of the major findings of these experiments is that neurons in several areas of the association cortex (e.g. prefrontal cortex, posterior parietal cortex and inferotemporal cortex) exhibit selective ‘persistent activity’ during delay period – they increase their firing rates compared to the baseline period, selectively for one or several cues whose identity is needed for the monkey to perform the task correctly after the end of the delay period.
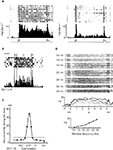
Three examples of such experiments are shown in Figure 1
. The first example (Figure 1
A) shows an example of an ‘object’ working memory task (memory of the identity of a stimulus). This type of short-term memory has been investigated by the delay-match-to-sample (DMS) experiment (Fuster and Jervey, 1981
; Miyashita, 1988
) in which the animal is required to retain the identity of a sample stimulus (an image shown on a computer screen) during the delay interval, and respond differently if the following test stimulus was identical or different from the sample stimulus. Figure 1
A shows rasters and trial-averaged firing rates of a cell recorded in IT cortex, both in the case in which the presented stimulus was familiar (left panel), and in the case in which the stimulus was unfamiliar (right panel) (Miyashita, 1988
). For stimuli that are familiar, the elevated rate distribution during the delay period is stimulus specific, i.e. each visual stimulus evokes a characteristic pattern of delay activity. When unfamiliar stimuli are presented, the recorded neurons may have elevated selective rates during stimulation, but no delay activity after the stimulus is removed.
Figure 1. Experimental evidence of persistent activity. (A) Persistent activity of a cell in IT cortex of a monkey performing a DMS task. Raster and trial-averaged firing rate of in trials during which the picture that elicits the highest delay activity is shown as a sample (left) and trials when an unfamiliar picture is shown (right). From Miyashita (1988)
, reprinted by permission from Nature, © 1988 Macmillan Publishers Ltd. (B) Persistent activity of a cell in PFC of a monkey performing an ODR task. Raster and trial-averaged firing rate of a neuron when a cue is presented at 270 (top panel), the preferred cue location for that neuron (C: cue period; D: delay period; R: response period). From Funahashi et al. (1989)
, used with permission. (C) average firing rate during the delay period vs. cue location, for the neuron shown in (B). From Funahashi et al. (1989)
, used with permission. (D) Persistent activity of a cell in PFC of a monkey performing a delayed somatosensory discrimination task. Top panel: Rastergrams of a PFC cell arranged according to frequency of the base stimulus (indicated on the left). Middle panel: Trial averaged firing rate for several stimulus frequencies showing the monotonic response as a function of stimulus frequency. Bottom panel: Tuning curve of the cell in the delay period. From Romo et al. (1999)
, reprinted by permission from Nature, © 1989 Macmillan Publishers Ltd.
The second example, shown in Figure 1
B, presents a ‘spatial’ working memory task, the oculomotor-delayed-response (ODR) task (Funahashi et al., 1989, 1990, 1991) in which the animal is required to remember the location of a light spot on a screen during the delay interval, and respond at the end of the delay interval, making a saccade towards this location. Figure 1
B shows rasters and trial averaged firing rate of a cell recorded in the PF cortex during the four phases of the task: in the first phase the monkey fixates a central spot on a screen; in the second phase a light spot at one of eight possible angles is presented (in this period the monkey continues to fixate the central spot); the third phase is the ‘delay period’ which starts with the removal of the stimulus and lasts for some seconds; finally, when the central spot disappears the monkey has to respond by making a saccade towards the location of the presented stimulus. Figure 1
C shows the activity of the recorded cell during the delay period: this activity is maximal at a particular cue location (270°) and decreases away from that preferred location. This stimulus-selective, spatially tuned delay activity is observed for many of the recorded cells in PFC.
Our last example is shown in Figure 1
D. It represents a ‘parametric’ working memory task (Romo et al., 1999
). In this task a monkey was trained to compare and discriminate the frequencies of two vibrotactile stimuli separated by a delay period. Figure 1
D shows a cell in the inferior convexity that has persistent activity that varies monotonically with the cue frequency (indicated on the left and by the different curves).
These experimental findings have been interpreted as manifestations of attractor dynamics in local cortical modules (see e.g. Amit, 1995
; Brunel, 2004
; Wang, 2001
). The basic idea is that the selective delay activity is not a single neuron property. Rather, after the removal of a familiar stimulus, cells with enhanced activity are participating in the collective dynamics of a subpopulation of neurons. These neurons excite each other in such a way that the enhanced activity is self-sustained throughout the delay period, even in the absence of the sensory event that triggered this process. The dynamics of the network, and in particular the feedback mechanism, is governed by the synaptic connectivity matrix.
The attractor network picture clearly separates two forms of memory: a short-term component, maintained by the persistent activation of an ensemble of neurons; and a long-term memory component, maintained by persistent changes in synaptic efficacies which governs the dynamics of the network. These ideas, that can be traced back to Hebb (1949) and have been implemented in many simplified network models since (Amari, 1972
; Amit, 1995
; Amit and Brunel, 1997
; Hopfield, 1982
; Tsodyks and Feigel’man, 1989
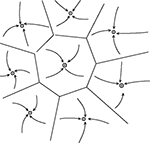
), imply that the information about the identity of the stimuli is stored through synaptic plasticity mechanisms that form or modifies the synaptic connections during learning. The set of synaptic connections then determines the dynamics of the network and in particular its stable states (attractors). Each attractor can be thought of as an internal representation of a stimulus. When a visual stimulus is presented, it selects one of these internal representations by determining the initial state activation of the network. Following the removal of the stimulus, the network dynamics is attracted towards one of the stable patterns of activity, which represents the response of the network. Figure 2
gives a visual representation of an attractor landscape: the white stable state represents the activity in absence of any stimulus (background activity), while the many black states represents the ‘memory’ states in which different fractions of neurons fire at higher rates (persistent activity). In the case of the DMS task, each attractor is associated with the memory of one of the familiar stimuli; while in the case of the ODR task (or the vibrotactile discrimination task), there is a continuum of attractors associated with all possible orientations along a circle (or all possible stimulation frequencies).
Figure 2. Schematic depiction of the space of states of an attractor network. Stable states are shown as filled circles. The represented network has one background state (shown schematically as a grey circle in the center) and several memory states (black circles). Arrows represents the dynamics of the network towards an attractor, following presentation of a stimulus. Lines represents the limits of the basin of attraction of each attractor. From Brunel (2004)
.
Consistent with the collective origin of the delay activity, degraded versions of familiar stimuli, evoke different visual responses during the stimulation, but the same mean activity during the delay interval (Amit et al., 1997
). This means that all stimuli leading to the same pattern of delay activity (i.e. the same basin of attraction which is marked by the lines in Figure 2
) share the same internal representation during the delay period. This fact is important because in presence of large basin of attraction the network can perform as an ‘associative memory’, i.e. it can retrieve the stored information from a partial cue (Amit et al., 1997
).
The behaviour of attractor networks is in qualitative agreement with enhanced persistent activity observed in subsets of neurons in the relevant areas of associative cortex. But can this agreement be made quantitative? In particular, can network models based on the Hebbian scenario reproduce the statistics of firing of recorded neurons in the areas where persistent activity is observed?
Firing Rates
The first question is whether models can reproduce the firing rates of neurons in IT or PFC. One of the prominent features of the experiments reported in Figure 1
, as well as other experiments in awake behaving animals, is that all recorded cells exhibit a pronounced background (or baseline, or spontaneous) activity, typically of a few Hertz. The question of how a network with heavy recurrent connectivity can sustain activity at low rates was addressed by several groups in the nineties (Amit and Brunel, 1997
; Tsodyks and Sejnowski, 1995
; van Vreeswijk, 1996
; van Vreeswijk and Sompolinsky, 1998
). These studies showed that networks with strong recurrent connectivity can indeed give rise to low irregular activity, provided recurrent inhibition is strong enough to control the mean firing rate of the network.
The next observation that had to be accounted for is that neurons with persistent selective activity have rates which are not much higher than background rates – typical values are in the 10–30 Hz range, and these rates tend to be about three times the background rates (Nakamura and Kubota, 1995
), while even smaller ratios have been reported (Miller, et al., 1996
). These values are much lower than saturation rates of pyramidal cells, that should in principle be able to fire at much higher rates (McCormick et al., 1985
). This is a problem with naive ‘firing rate’ models with sigmoidal transfer functions (or f-I curve) describing how rate depends on input current, which typically give persistent activity close to saturation levels. This issue was addressed by Daniel Amit and his collaborators in the nineties, using networks composed of leaky integrate-and-fire (LIF) neurons, one of the simplest spiking neuron models. These studies showed that this model has a f-I curve that has a crucial difference from the sigmoidal form typically assumed by earlier models: the inflexion point of such a curve typically occurs at a rate which is much lower than the saturation rate (the precise value depends on the value of the noise), while sigmoidal f-I curves have inflexion points which are exactly at half the saturation rates (Amit and Tsodyks, 1991a,
b
). Importantly, this inflexion point determines to a large extent the range of values of persistent activity (Brunel, 2000
). In fact, by studying the bifurcation diagrams showing how firing rates in background and persistent activity states change as a function of the synaptic strength connecting neurons with similar selectivity properties, models with various levels of realism (Amit and Brunel, 1997
; Brunel, 2000
; Brunel and Wang, 2001
) showed that networks of LIF neurons can exhibit both background and memory states in rough quantitative agreement with experimental values. However, in all these models, the strength of the selective excitatory connectivity has to be tuned rather precisely to obtain low persistent activity, in order to be close to the bifurcation at which the persistent state appears.
CVS
After the issue of firing rates has been settled, the next question is whether these models can reproduce higher-order statistics of inter-spike intervals (ISI). In particular, one popular measure of the variability of ISIs is the CV, which is equal to the standard deviation of ISIs, divided by the mean. A CV equal to 0 signals a periodically firing neuron, while a CV of order one indicates strong irregularity, similar to a Poisson process. A neuron firing as a Poisson process has exponentially distributed ISIs and consequently a CV equal to 1. Several studies have shown consistently that in cortex the CV of pyramidal cells is typically of order 1, consistent with neurons firing approximately as Poisson processes (Shadlen and Newsome, 1994
; Softky and Koch, 1993
). This high variability is consistent with neurons operating in a ‘sub-threshold’ mode, with fluctuating inputs that drive the neuron to fire due to fluctuations around a mean input which is below threshold.
Several recent studies have analysed the variability of firing of prefrontal cortex neurons during delayed response tasks (Compte et al., 2003
; Shinomoto et al., 1999
). In particular, a recent study (Compte et al., 2003
) found that neurons fire in a highly irregular fashion in all periods of an ODR task (see Figure 3
). They found that the average coefficient of variation is close to 1 in the baseline period (spontaneous activity state) as in the case of a Poisson process, and is higher than 1 in the delay period, both for preferred and non-preferred stimuli. This is shown in Figure 3
A in which the distribution of the CVs of the recorded cells is displayed, both before the cue presentation (fixation epoch) and during the delay period, for preferred and non-preferred stimuli. Figure 3
B shows that the average CV during the delay period is higher than during fixation and higher than 1 for all the three classes of neurons.
Figure 3. Variability of spiking activity of prefrontal neurons of monkeys performing an ODR task. Measures of ISI variability are high in all epochs of the task. From Compte et al. (2003)
, used with permission. (A) Distribution of CVs over recorded cells for each task condition (FIXATION, F): before stimulus presentation; PREFERRED (PR): delay period following the preferred stimulus; NONPREFERRED (NP): delay period following the non-preferred stimulus). (B) Mean and SD of the CV in each task condition. The right panel shows mean and SD of the CV for three classes of neurons (‘Poisson’, ‘Refractory’, and ‘Bursty’) defined according to features of their power spectrum. See Compte et al. (2003)
for more details.
Are these experimental results consistent with standard attractor network models reviewed above? It turns out that the answer is no. The major problem encountered with these models is that, while high irregularity can be obtained robustly in the baseline period, provided inhibition is sufficiently strong, because neurons receive synaptic inputs that are sub-threshold in average and firing is due to temporal fluctuations in these inputs (Amit and Brunel, 1997
; van Vreeswijk and Sompolinsky, 1996, 1998
), persistent activity states typically involve neurons which receive suprathreshold inputs (Brunel, 2000
; Renart et al., 2007
) and therefore exhibit much more regular firing.
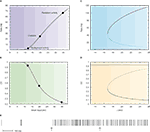
This is shown in Figure 4
A in which the intersections between the response function of the neuron and the straight line are the solutions of the mean field equation that give the states of the network for a particular value of the synaptic efficacy (Barbieri and Brunel, 2007
; Brunel, 2000
). While the solution at low rates (spontaneous activity) is in the sub-threshold region of the response function in which the firing is due to fluctuations that bring the neuron to threshold, the solution at high rates (persistent activity) is always found above the inflexion point of the response function (supra-threshold region) in which the firing is governed by the mean synaptic input and hence is close to being periodic. This is reflected by the behaviour of the CV as a function of the mean synaptic input (Figure 4
B) in which the spontaneous activity has a CV close to 1, while the CV of the persistent activity is close to zero. This is true for any value of the synaptic efficacy as showed by the bifurcation diagrams displayed in Figure 4
D.
Figure 4. Standard attractor network models produce highly regular persistent activity. Mean firing rate and CV of a population of excitatory leaky integrate-and-fire neurons with low reset (10 mV below threshold) connected by linear excitatory synapses (see Barbieri and Brunel, 2007
for more details). (A) f-I curve (firing rate of a single LIF neuron as a function of mean input). The intersections between the f-I curve (thick line) of the LIF neuron and the straight line (thin line) correspond to solutions of the mean-field equation, shown by diamonds, for a particular value of the synaptic efficacy. The three solutions correspond to the background activity state (stable), the limit of the basin of attraction (unstable) and the persistent activity state (stable). (B) CV-I curve (CV of a single LIF neuron as a function of mean input). Diamonds: Values of the CV for the three states shown in (A). (C) Bifurcation diagram showing firing rate of the excitatory network as a function of synaptic strength J. The background activity corresponds to the horizontal curve (lowest branch), the dotted curve (intermediate branch) is the boundary of the basin of attraction and the black curve (highest branch) represents the evolution of the persistent activity. (D) Bifurcation diagram showing how the CV depends on J: the persistent activity (black curve, lowest branch) has a CV which is well below the CV of the background activity (highest branch, red curve) for all values of J. (E) Spike train of one of the cells of the network (simulation of a network of 1000 neurons). Arrows indicate beginning and end of presentation of the stimulus, so the second arrow indicates the beginning of the delay period. Note the high regularity of the spike train in the delay period.
The experimental observations on the irregularity of firing during the delay period have triggered a burst of studies that propose mechanisms for generating irregularity during persistent activity. Interestingly, all these studies propose models which build on standard attractor networks, but with modifications leading to high irregularity, rather than proposing a radically new scenario. For instance, to our knowledge, no model in which persistence is induced by single neuron dynamics is able to reproduce bistability between two highly irregular states – in fact, models relying on single cell dynamics typically produce extremely regular spike trains (see e.g. Fransén et al., 2006
).
Balancing Excitation and Inhibition in Both Background and Persistent States
A possible solution was proposed recently by Renart et al. (2007)
. The idea is to have both inhibitory and excitatory neurons involved in the sub-population which is activated by any given external stimulus. In this way, both excitatory and inhibitory increase their rates in the persistent states; if both are balanced, the mean inputs to both populations does not increase in a pronounced fashion, but the variance does increase significantly compared to the background state. Since CV increases with variance when the mean is constant, this model explains the high CV in the persistent state observed experimentally. However, a limitation of this model is that the bistability range is small in this scenario, and that it in fact vanishes in the limit of large number of connections per neuron.
Another scenario involves a Hopfield-type memory structure on top of unstructured random excitatory connections (Roudi and Latham, 2007
), together with inhibitory neurons maintaining a balance with excitation in both background and persistent states, due to the increase of inhibition triggered by the increase of the firing rate of activated excitatory neurons. These authors showed that this mechanism does produce CVs which are comparable in background and persistent states, however at a quantitative level the values of the CVs seem significantly below 1 – on the order of 0.8.
High Reset Potential and Short-Term Depression
We have reconsidered recently a simple recurrent network in which multistability is induced by recurrent excitation (Barbieri and Brunel, 2007
), and found that this type of network can lead to persistent activity that is more irregular than background activity, provided two conditions are fulfilled: (1) post-spike reset is close to threshold (i.e. neurons do not have a pronounced hyperpolarization following a spike, see also Troyer and Miller, 1997
) and (2) post-synaptic currents saturate at high pre-synaptic firing rates, due to short-term depression (STD) (Tsodyks and Markram, 1997
).
The model we used is a fully connected network of LIF neurons which receive a Gaussian and δ-correlated external input. This network can be thought as a sub-population of cells selective to a particular stimulus, which are embedded in a larger network which represents a cortical column.
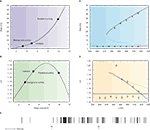
The first condition is important because the behaviour of the CV as function of the mean synaptic input changes drastically as a function of the reset potential Vr: when Vr is large enough, the CV I curve becomes non-monotonic – as shown in Figure 5
B, it first increases when the mean input increases, reaches a maximum at a value which is smaller than Vr, and then decreases monotonically as the mean inputs go towards the suprathreshold range. Hence, there is a large region of mean inputs for which the CV is larger than one, contrary to the low reset case illustrated in Figure 4
. The reason for a maximum in CV for mean inputs smaller than the reset is that in these conditions, the instantaneous firing probability is higher just after firing that it is afterwards – hence, there is a higher probability of short ISIs, compared to a Poisson process with the same rate. However, this fact alone is not sufficient to account for irregularity, because a neuron in the persistent activity state receives suprathreshold inputs, that lead to CV out of the region of the peak. While increasing Vr does increase the CV of both background and persistent activity states, the large gap between the CV in the background state and the one in the persistent state persists (see Barbieri and Brunel, 2007
for more details).
Figure 5. An excitatory network with high reset potentials of individual neurons and short-term depression of excitatory synapses produce highly irregular persistent activity. Mean firing rate and CV of a population of excitatory leaky integrate-and-fire neurons with high reset (5 mV below threshold) connected by excitatory synapses with short-term depression (see Barbieri and Brunel, 2007
for more details). (A) f-I curve (solid line) plotted together with the current-rate relationship for synapses with short-term depression (dotted curve). Intersections between these two curves (diamonds) yield the solutions of the mean-field equation. They correspond to background, unstable and persistent fixed points, respectively. (B) CV-I curve. Diamonds: Values of the CV for the three intersection points shown in (A). (C) Bifurcation diagram showing firing rate vs. J. The black curve correspond to the persistent state (stable), the dotted one to the boundary of the basin of attraction (unstable) and the horizontal one to the background state (stable). (mean-field: lines; simulations: symbols). (D) CV vs. J bifurcation diagram. There exists a finite range of values of the synaptic efficacy for which the CV in the persistent state is larger than in the background one (370 mV < J < 420 mV in the figure). Mean-field: lines; simulations: symbols. (E) Spike train of one cell in a simulated network of 1000 neurons; arrows indicate beginning and end of the stimulus presentation. Note the high irregularity of this spike train during the delay period, contrary to the one shown in Figure 4
.
The problem can be solved using a mechanism that limit the magnitude of the input afferent to a neuron. Such a mechanism is, in our model, synaptic STD between pyramidal neurons. We used the phenomenological model proposed by Tsodyks and Markram (1997)
, that models depression due to vesicle depletion and recovery after an action potential.
The introduction of STD leads to a frequency-dependent synaptic efficacy (Romani et al., 2006
; Tsodyks and Markram, 1997
): the mean synaptic input saturates as a function of the mean firing rate. This saturation brings the persistent state solution in the sub-threshold region of the response function. This is shown in Figure 5
A that display the solutions of the mean field equations: these are the intersections between the response function and a non-linear curve which saturates at a particular frequency. The upper intersection between the two curves, which represents the persistent state solution, is shifted towards the sub-threshold region of the f I curve, thanks to the saturation effect mentioned above. Figure 5
B shows where the values of the CV of the three solutions are located on the CV-I curve. The persistent state solution is now in the range in which the CV displays a peak. In fact, the CV of the persistent state is greater than the CV of the spontaneous state. This property holds in a fairly large range of synaptic efficacies, as shown by Figures 5
C,D, which display the bifurcation diagrams for rates and CV, respectively. The large gap in the CV between background state and persistent state that was found for linear synapses is now reduced to a few percent, since both solutions are now located in the sub-threshold region dominated by fluctuations around the mean input. The mean-field results are in good agreement with numerical simulations of networks of 1000 neurons (symbols in Figures 5
C,D). Qualitatively similar results hold in networks with a ring architecture that allows to reproduce the tuning curves of neurons in the delay period (see Barbieri and Brunel, 2007
for more details).
We have discussed here network models that address the issue of irregularity in persistent activity. These models rely either on balancing excitation and inhibition (Renart et al., 2007
; Roudi and Latham, 2007
) or on a combination of high reset and STD of excitatory synapses (Barbieri and Brunel, 2007
). In all these studies, persistent rates are significantly larger than background rates, unless synaptic weights are extremely finely tuned. Though some experiments find persistent rates that are significantly larger than background rates (Funahashi et al., 1989
; Miyashita, 1988
; Nakamura and Kubota, 1995
), others find much smaller differences between both (see e.g. Shafi et al., 2007
). A recent experiment by Rainer and Miller (2002)
even finds that persistent activity vanishes during part of the delay period. This would be incompatible with the standard models discussed above, unless a mechanism of short-term facilitation is introduced (Mongillo et al., 2008
). In the Mongillo et al. (2008)
model, an item is maintained in working memory by short-term synaptic facilitation mediated by increased calcium levels at the pre-synaptic terminals of the neurons that code for this item. The process of removal of the residual calcium is a relatively slow process that can last about 1 s (Wang et al., 2006
). This allows memory maintenance with rates that are very close to background rates, thereby reducing the metabolic cost of maintenance. Though Mongillo et al. (2008)
do not discuss the issue of irregularity in their model, one can speculate that in the regime in which background and persistent rates are very close, spike trains are likely to be strongly irregular in both cases. In that regime memory has to be refreshed by non-selective external inputs to persist longer than the facilitation time constants. In an other regime, memory can be maintained through repetitive population spikes due to the interplay between depression and facilitation. In this regime, one would rather predict that irregularity is much smaller in the background state, because of the highly periodic nature of population spikes. The model has a third regime which is essentially similar to previous attractor network models, and therefore the irregularity in this regime should be controlled by the same parameters that were discussed above.
Most models so far have considered persistent activity to be a stationary process. This is again consistent with part of the published data, but electrophysiological recordings often find that many cells exhibit significant non-stationarity in the delay period (see e.g. Brody et al., 2003
). To our knowledge, these non-stationarities have not yet found a satisfactory theoretical explanation, and are likely to be the focus of future theoretical research.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.