- 1 Department of Physiology, Northwestern University, Chicago, IL, USA
- 2 Department of Biomedical Engineering, Northwestern University, Evanston, IL, USA
- 3 Rehabilitation Institute of Chicago, Chicago, IL, USA
- 4 Department of Biological Sciences, University of Illinois at Chicago, Chicago, IL, USA
- 5 Department of Neuroscience and Brain Technologies, Italian Institute of Technology, Genova, Italy
- 6 Department of Robotics, Brain and Cognitive Sciences, Italian Institute of Technology, Genova, Italy
- 7 Department of Human Physiology, University of Ferrara, Ferrara, Italy
- 8 Department of Biomedical Engineering, Ben Gurion University, Beer Sheva, Israel
- 9 Department of Informatics, Systems and Telematics, University of Genova, Genova, Italy
Brain-machine interfaces (BMIs) are mostly investigated as a means to provide paralyzed people with new communication channels with the external world. However, the communication between brain and artificial devices also offers a unique opportunity to study the dynamical properties of neural systems. This review focuses on bidirectional interfaces, which operate in two ways by translating neural signals into input commands for the device and the output of the device into neural stimuli. We discuss how bidirectional BMIs help investigating neural information processing and how neural dynamics may participate in the control of external devices. In this respect, a bidirectional BMI can be regarded as a fancy combination of neural recording and stimulation apparatus, connected via an artificial body. The artificial body can be designed in virtually infinite ways in order to observe different aspects of neural dynamics and to approximate desired control policies.
Introduction
The possibility of controlling the motion of a robotic arm “by mere thought,” as suggested by popular media since the advent of brain-machine interfaces (BMIs), has captured the imagination of fiction writers and science journalists. The image of a magician displacing objects by mental powers can be entertaining. But is mind control a reasonable or even a desirable practical goal for the future of neuroprosthetics? If the ultimate clinical objective is to endow amputees and paralyzed people with the ability to act naturally through the interaction of their brain with an artificial limb, then “controlling by thought” is not quite an appropriate objective. The fact is that, as we carry out the simplest actions, such as operating the handle of a door, we do not occupy our minds with what we are doing. We do not think about opening up the grasp, closing it on the handle, twisting the wrist and so on. This is because motor acts are stored in the brain in hierarchically organized goal-directed actions. The addressing of a given action representation is the only thing the brain must do in order to cause the cascade of events leading to execution. In other words, our nervous systems do all that is needed without loading our thought processes, apart from the explicit activation of a very general action procedure. It is only in the early stages of learning that one must be aware of the details of one’s detailed movements. Once a skill is practiced it becomes automatic and requires minimal thinking. The goal of this review is to provide a perspective that emerged from work by our group and others on how BMIs, based on the bidirectional flow of information between a neural population and a controlled device, may lead to the creation of automatic behavior. But there is more. These interactions are also a fundamental tool for investigating how information is processed by the brain.
In the early 90s, Sharp, Abbott and Marder, introduced a new method to bridge the gap between experimental and computational analysis of neural behavior (Sharp et al., 1992 , 1993 ). They established a direct dialogue between a computer simulation and a group of neurons in a dish. The technique is called “dynamic clamp” and is based on an exquisitely simple idea: to simulate on a computer the input/output properties of a membrane conductance by obtaining the input membrane potential from an actual neuron and injecting the output – a current – into another neuron. To derive the current from the potential, one must integrate a system of ordinary differential equations; a task that can be done in real-time if the size of the system is within the available computational power. The difference between this and a more standard computer simulation is that the variables in question are exchanged between simulation and real neurons. The dynamic clamp establishes a symbiosis between the artificial computation and the biological element, or, to quote Sharp and colleagues (Sharp et al., 1993 ): “the dynamic clamp behaves as if the channels described by the programmed equations were located at the tip of the microelectrode.”
The concepts that led to the dynamic clamp can be extended from the cellular to the system’s level of analysis. A number of recent studies provided a similar closed-loop feedback to neural systems involved in motor task learning. In this focused review, we discuss how the physical connection between biological neural systems and artificial computational processes established by BMIs may lead to new paths for understanding neural information processing and be harnessed to benefit people suffering from paralysis. We begin by describing a simple neuro-robotic system, in which a small mobile robot provides an artificial body to a brain preparation maintained in a Ringer’s solution. We discuss how the analysis of the coupled behavior may provide insight on the connectivity of the neural system that transforms input stimuli into output control signals. Then, we review more recent work aimed at characterizing the dynamical behavior of a neural system engaged in a two-way interaction with an external device. This knowledge is likely to be critical, also for pursuing the goal of “programming” the operation of BMIs by gaining control on the plastic properties of neurons. We conclude with a new perspective on tuning the maps implemented by bidirectional interfaces so as to approximate the desired behavior of a control system expressed as a force field.
A Neurally Controlled Vehicle
Almost three decades ago, Valentino Braitenberg wrote a small manifesto in semi-fictional form (Braitenberg, 1984 ). He considered a family of hypothetical vehicles, endowed with various sensors and motor-driven wheels, in the form of mobile robots. The book narrates in entertaining but also thoughtful terms, how the electrical connections between sensors and wheels determine a repertoire of different responses to the stimuli in the environment. It presents two distinct viewpoints: one is the viewpoint of an electrical engineer who puts together the wiring scheme starting from a desired behavior of the vehicle; the other is the analytical viewpoint of a scientist who observes the behavior and attempts to find out how it derives from some possible “neural wiring”. The insight that we obtained from Braitenberg’s vehicles is that neural structures and properties can be established by artificially constraining the relation between neural system and behavior. This guided our group to develop an experimental approach, in which the behavior of a simple artificial device is generated by an isolated neural preparation (Reger et al., 2000 ; Karniel et al., 2005 ).
Figure 1 presents the scheme of our initial setup. The brains of sea lamprey larvae were extracted and placed in a recording chamber where they were maintained at constant physiologically relevant temperature in a Ringer’s solution. We placed two stimulation microelectrodes, one on the right and one on the left side of the midline, among the axons of the rhombencephalic vestibular pathways. We also placed two recording glass-electrodes, one on each side of the brainstem’s midline, among visually identified reticulospinal neurons of the reticular formation, which represent the final command neurons to activate and maintain locomotion in vertebrates (Grillner et al., 2008 ). A simple interface decoder converted the spiking activities detected by the recording electrodes into driving signals for the corresponding wheels of a small robot (a Khepera, by K-Team). A set of optical sensors on the robot measured the light coming from the right and left side, implementing two very rudimentary “electronic eyes”. The light intensities were then mapped by the interface encoder into the frequencies of two impulse generators connected to the two stimulating electrodes. This was effectively the first implementation of a bidirectional interface, which closed the loop from recorded neural activities to electrical stimulation via a robotic device. It was quite impressive to see the small robot responding to a shining light by movements that were most often directed toward it. This response is called “positive phototaxis” and reflects the predominance of excitatory pathways crossing the brainstem’s midline (Figure 2 ). This was indeed one of the first models discussed in Braitenberg’s book: if the right sensor is connected to the left wheel and vice-versa, then a light shining on one side will cause the wheel on the opposite side to spin faster. As a result, the vehicle will tend to orient itself toward the light and to proceed in the forward direction. However, positive phototaxis was not the only observed behavior of the neuro-robotic system exposed to a light source. Negative phototaxis – a tendency to move away from the light source- was observed as well (Karniel et al., 2005 ) and reflected the action of ipsilateral connections between vestibular and reticular neurons.
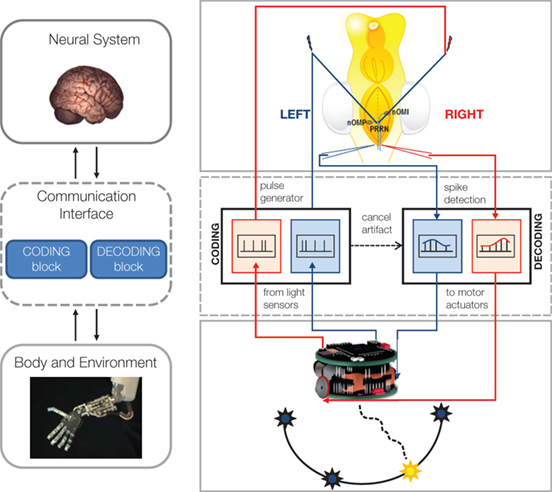
Figure 1. Bi-directional BMIs. Left. The general scheme includes a brain model, a communication interface characterized by one coding and one decoding block, and a robotic body. Right. Implementation of the first BMI realized at Northwestern University: a hybrid neuro-robotic system connecting a lamprey’s brainstem to a small mobile robot. Signals from the optical sensors of the robot (bottom) are encoded by the communication interface into electrical stimuli, whose frequency depends linearly upon the light intensity. Stimuli are delivered by tungsten microelectrodes to the right and left vestibular pathways (top. nOMI and nOMP: intermediate and posterior octavomotor nuclei). The whole brain is immersed in artificial cerebro-spinal fluid within a recording chamber. Glass microelectrodes record extracellular responses to the stimuli from the posterior rhombencephalic reticular nuclei (PRRN). Recorded signals from right and left PRRNs are decoded by the interface, which generates the commands to the robot’s wheels. These commands are set to be proportional to the estimated average firing rate on the corresponding side of the lamprey’s brainstem. The robot is placed in a circular arena with light sources on the periphery. The neural system between stimulation and recording electrodes determines the motions in response to each light source (modified from Mussa-Ivaldi and Miller, 2003 ).
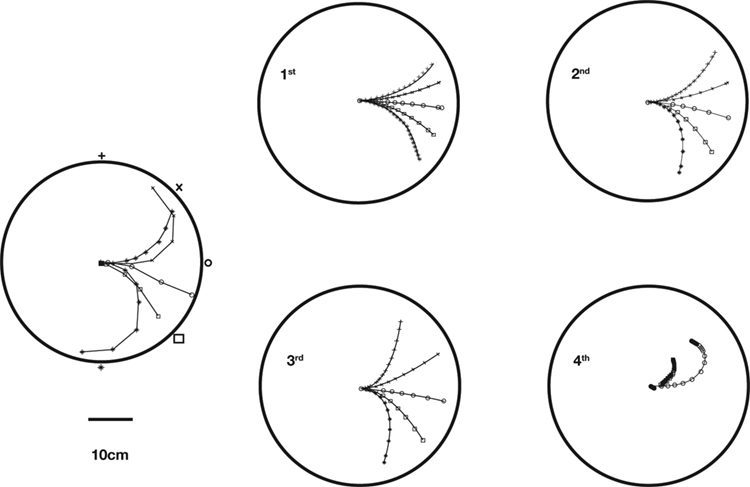
Figure 2. Actual and simulated robot trajectories. Leftmost panel: Trajectories generated by the neuro-robotic system. The five light bulbs placed on the circular boundary of the workspace were turned on in sequence. Movements toward the lateral lights were curved, with an initial part in the forward direction, followed by a turn toward the light. The four panels on the right show the simulation results obtained after fitting the neural responses of the neural preparation with polynomial surfaces of various degrees, from linear to 4th degree. The data for the fit were generated in a separate session, in which stimulation patterns with different frequencies were applied to the two electrodes placed among vestibular axons. The responses were collected from the two recording electrodes in the posterior rhombencephalic reticular nuclei (PRRN) on the right and left side of the midline. Thus, the data were a collection of points 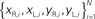 (x: stimulus, y: response) from the right and left side. These were used to derive, by least squares, the parameters W in Eq. 3.
(x: stimulus, y: response) from the right and left side. These were used to derive, by least squares, the parameters W in Eq. 3.
As the robot was exposed to a single source of light, it moved along rather complex and curvilinear pathways. It was immediately evident that the neural circuitry responsible for the observed movements had properties that go beyond the structure of a simple linear feedforward network. A notable feature of this neuro-robotic interaction is that it allowed us to make a direct comparison between behaviors generated by the neural preparation and behaviors generated by a computational model. This was possible (a) because the robotic system was a simple artificial body whose dynamics were simpler and much better known than those of any biological body, and (b) because the interactions between the robot and the neural preparation were confined to a set of well defined signals. The dynamics of the robot were captured by two first-order ordinary differential equations that yield the translational and rotational velocities as functions of the orientation and of the spinning rates of the two wheels. The sensor response to a source of light depended upon the orientation of the robot with respect to the source and was inversely proportional to the square of the distance between the source and the sensor. These are simple relations that allowed us to predict (a) the motion of the robot, given the recorded output activity, and (b) the neural stimulus as a function of the motion of the robot. The remaining, very important, part is the neural tissue between stimulation and recording electrodes. A simple model of the transformation performed by the tissue is a static algebraic non-linear mapping, i.e.

where x = (xL, xR) is a vector of input stimuli on the left and right electrodes, y = (yL, yR)is a vector of recorded responses from the two sides and W is a matrix of “weights”, parametrizing the outputs as functions of the inputs. In a simpler form, this can be a static linear mapping, as in

More complex, yet particular, non-linear relations can also be considered. For example polynomials of higher degree, as
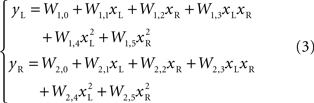
By analyzing the responses of the neural preparation to stimuli of different frequencies applied to both stimulation electrodes, it was possible to estimate the W parameters in polynomial models (Karniel et al., 2005 ). Then, the models were used to predict the motor behavior of the robot in the presence of a fixed light stimulus. Figure 2 shows a comparison between actual trajectories, and trajectories simulated using models from linear to 4th degree. As the polynomial degree increases from linear to cubic, there is a visible increase of the model’s ability to reproduce the data. However, with the 4th degree polynomial there is a clear collapse in performance. This kind of failure was due to over-fitting the measured data; however, more importantly as described below, the performance of these kinds of models is limited since the actual neural system is dynamic rather than static.
Karniel et al. (2005) modified the linear model (2) by adding a simple first-order dynamic component. The dynamic component was expressed as a linear dependence of the neural output at an instant of time upon the neural output at a previous instant
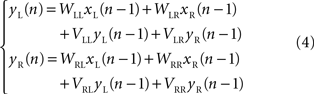
They found that, with this correction the performance of the model was much better than higher order polynomial models, despite a reduced number in free approximation parameters.
The Dimension of Closed-Loop Dynamics
The interaction between a neural system and an external device provides a framework for further investigating the dynamical properties of a neural system (Kositsky et al., 2003 , 2009 ). The diagram of Figure 3 describes this framework schematically. The interaction between device and neural tissue is entirely self-contained. To simplify our discussion, we assume that the nervous system and the artificial device are governed by some deterministic dynamics. Of course, while the dynamics of the external device are generally well known, the neural dynamics are unknown and are the object of study. The external device does not need to be a physical one. It can be a computer simulation, for example, of a spring-mass system. The use of simulated devices is particularly useful for investigating specific properties of the neural system. Moving along the diagram of Figure 3 in a clockwise direction, the device sends an output vector variable to the input interface, which encodes this variable into a stimulus pattern, e.g., a frequency of a pulse train. The neural preparation receives the stimulus and responds to it with a pattern of activities. These are recorded either extracellularly or intracellularly with one or more electrodes, depending on the experimental setup. Here, again, we need to make the critical assumption that the recorded activities depend in a deterministic way upon the stimulus. Of course, such assumption is likely to be violated in reality – and in various ways. In fact, an important but difficult task facing the experimenter is to ensure that the preparation is isolated as much as possible from external influences, which tend to create time-dependent fluctuations in the observed neural activity. And, of course, such fluctuations need to be analyzed as a form of “experimental noise”. Finally, the loop is closed by an output interface, which converts the recorded activity into an input vector to the external device.
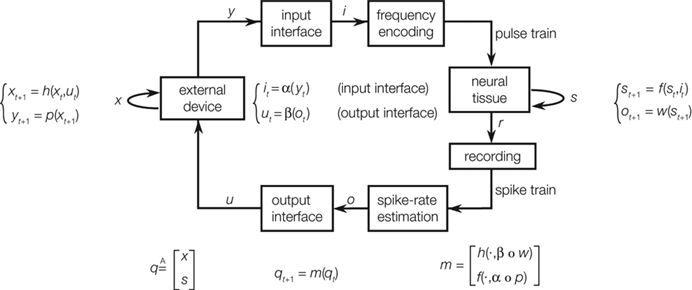
Figure 3. Computational maps associated with an ideal closed-loop interaction between a device and a neural preparation. The external device and the neural tissue dynamics are described by a state equation, yielding the next state as a function of the current state and the input. The output of the device is mapped into a stimulation pattern by the input interface. The recorded neural activities are mapped into a control signal for the external device. By combining these dynamical equations, one obtains an autonomous system [qt+1 = m(qt)] whose behavior is entirely determined by its initial conditions (from Kositsky et al., 2009 ).
A fundamental parameter of any dynamical system is the minimum number of independent state variables that are needed to predict the response to an external input. More concisely, this is the dimension of the state space, also known as dynamical dimension. A point mass in free space has dimension 6, as its state is determined by 3 position and 3 velocity coordinates. A spring-mass system constrained to move along a line has dimension 2. The dynamical dimension of neural systems is unknown. However, the closed-loop system described in Figure 3 can be used to estimate it by exploiting the simple fact that the dimension of the neural (s) and artificial (x) component combine by addition to yield the dimension of the closed-loop hybrid system (q)
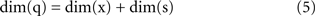
The unknown dimension of the neural system – dim(s) – is derived by subtracting the known dimension of the external device from the measured dimension of the combined system. Therefore, the problem is reduced to measuring the dimension of the combined system. Fortunately, this can be done with rather standard techniques – see (Abarbanel, 1996 ) for a review. The combined system is autonomous by construction, as it does not receive any external input and we make the assumption that its parameters are time-independent (at least within sufficiently long time intervals.) A well known theorem (Arnold, 1973 ) establishes that, under broad conditions of smoothness, the solutions of an ordinary differential equation are unique. This implies that the state-space trajectories of an autonomous system , corresponding to different initial conditions, do not overlap. This fact is exploited by a technique (Kaplan and Glass, 1992 ; Kaplan, 1994 ) which seeks to find the dimension of a dynamical system by embedding observed trajectories into candidate state-spaces of increasing dimension, until all intersections are removed (Figure 4 , bottom left panel). Applying this technique, Kositsky et al. (2009 ) were able to estimate the dynamical dimension of several preparations from the lamprey’s brainstem. Importantly, as t is shown in Figure 4 , the estimated dimension of the neural tissue remained unchanged as the dimension of the simulated external system varied from two to four.
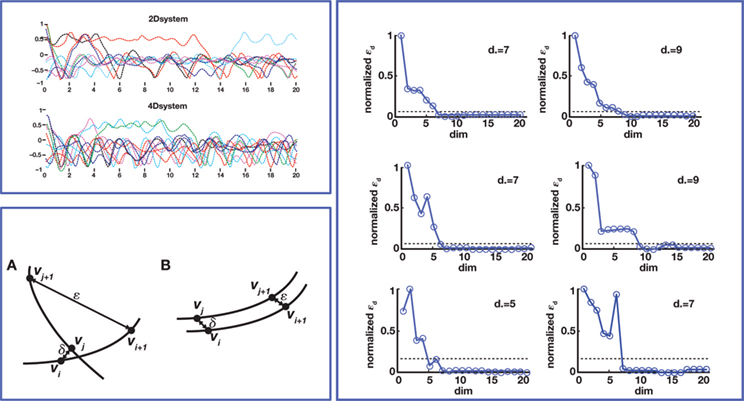
Figure 4. Dynamical dimension analysis. Top left: device trajectories. Two simulated devices were connected to a neural preparation – the lamprey’s brainstem with a stimulation electrode in the vestibulo-reticular pathway and a recording electrode in the PRRN. One of the devices was governed by a 2nd order differential equation, the other by a 4th order equation. The trajectories obtained by setting a variety of initial conditions are plotted in different colors, over a time span of 20 s. Bottom left: Kaplan’s δ–ε analysis (Kaplan 1994
). It considers pairs of points (vi, vj), and their successors along corresponding trajectories (vi + 1, vj + 1). Let δ = |vi−vj|, ε = |vi + 1−vj + 1|. When small δ bear large ε, it is interpreted as intersecting trajectories. If the trajectories do not intersect, small δ always bear small ε. Surrogate state vectors are constructed from a one-dimensional output signal by combining values of the signal at different delays. So, an n-dimensional state vector s(t) is obtained from the output signal y(t) as 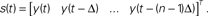 The method consists in building surrogate state vectors of increasing dimension until one can assess that the trajectories do not have self-intersections, using the Kaplan’s method. Right: Results of the δ–ε analysis for three preparations. The dynamical dimension of the combined system is assessed as the dimension that makes ε vanish when δ approaches zero. This was empirically assessed by setting a small threshold for epsilon. The plots on the left are with the 2D external system, those on the right are with the 4D system. This is consistently reflected by the difference in the corresponding estimated dimensions (from Karniel et al., 2005
; Kositsky et al., 2009
).
The method consists in building surrogate state vectors of increasing dimension until one can assess that the trajectories do not have self-intersections, using the Kaplan’s method. Right: Results of the δ–ε analysis for three preparations. The dynamical dimension of the combined system is assessed as the dimension that makes ε vanish when δ approaches zero. This was empirically assessed by setting a small threshold for epsilon. The plots on the left are with the 2D external system, those on the right are with the 4D system. This is consistently reflected by the difference in the corresponding estimated dimensions (from Karniel et al., 2005
; Kositsky et al., 2009
).
Bi-Directional Interfaces for Understanding and Controlling Neural Plasticity
Bidirectional BMIs may lead to a new level of understanding of neural plasticity and its role in shaping new behaviors. While different forms of neural plasticity, such as long term potentiation (LTP) (Bliss and Lomo, 1973 ) and long-term depression (Ito, 1989 ), are currently seen as important components of the neurobiological basis for learning and memory, the connection between changes in neural excitability, observable at the cellular level, and purposeful modifications of behavior remains largely unexplored. This is because the macroscopic scale of behavior is often orders of magnitude larger than the cellular scale. Bidirectional BMIs open new pathways of investigation because they connect observable behaviors with the activities that are recorded from a population of neurons and convey feedback from behavior directly to another population in the proximity of the stimulation electrodes. This provides a new tool for manipulating the mechanisms of Hebbian plasticity (Hebb, 1949 ; Abbott and Nelson, 2000 ) by controlling the relation between presynaptic signals associated with the stimulation and the postsynaptic activities that generate the behavior.
Karniel et al. (2005) tested the possibility of inducing plastic changes in the Lamprey’s vestibulo-reticular pathways by performing an “artificial lesion” in the robotic system of Figure 1 . This is another peculiar opportunity offered by such hybrid systems: they allow us to produce reversible changes in the communications between external device and neural preparation. Then, to assess the occurrence of a plastic change in the neural preparation, one can observe the difference between the behavior that takes place after the lesion is reversed and the behavior before the lesion was applied. The investigators performed this experiment by temporarily “blinding” the left electronic eye of the mobile robot. For this, it was sufficient to reduce the gain of the left optical sensor by a factor of 0.1. Then, they exposed the system to random light stimulation for about 20 min. At the end of this period, they restored the initial optical gain and tested the system on a set of standard light sources. Exposure to the unilateral reduction of the optical gain was sufficient to induce a sustained tendency of the robot to veer toward the right after the balance between the sensors was reestablished. This effect could be explained in two ways: either by a reduction of the spinning rate in the right wheel or by an acceleration of the left wheel (or both). The comparison of this behavioral observation with the prediction of a simple computational model driven by the recorded stimulus/activity patterns revealed that the main change was likely caused by a reduction of the recurrent dynamical gain which relates the activity of the right population of reticular neurons to their own state of firing (the term VRR in eq. 4). This indicates a general reduction of excitability in the output population contralateral to the lesion and can be attributed to the fact that this population received a reduced input from the lesioned site for an extended period of time.
Is it possible to modify the connectivity in a biological neural network to achieve a desired behavior? The theory of artificial neural networks (Bishop, 1996 ) has grown and advanced precisely on this premise. But can we exploit the actual mechanisms of neural plasticity to create a desired behavior of the external device? This question has not yet been answered; however, there are signs of progress. Different groups around the world (DeMarse et al., 2001 ; Martinoia et al., 2004 ; Bakkum et al., 2008 ; Marom et al., 2009 ) are working on systems conceptually similar to that described in Figure 3 , but using a different biological model. The neural preparation in these studies is a culture of dissociated neurons from rat cortices grown onto micro-electrode arrays (MEAs). Each electrode of the MEA is able to both record and stimulate the extracellular activity of the cultured network. The external device is a simulated or a real vehicle that navigates over an arena. Even with different methods and approaches, these groups succeeded to “program” the unstructured neuron culture in order to make the vehicle able to solve specific behavioral tasks, such as obstacle avoidance. In one example, the network was programmed by the delivery of tetanic stimulation (Chiappalone et al., 2008 ) to “punish” the wrong behavior of the robot in case of a collision with an obstacle. After repeated stimulation, an improvement in the robot’s performances (i.e., a lower number of collisions) was observed (Novellino et al., 2007 ). While this is still a very preliminary result, it demonstrates that – at least in principle – it may be possible to reach the goal of programming the behavior of a bidirectional BMI by inducing controlled changes in neural excitability. A critical milestone, still unreached, is the controlled induction of plastic changes in both directions (potentiation and depression) with brief exposure to targeted conditioning signals.
Future Directions
Most work on BMIs, so far, has developed decoding paradigms to translate the neural activities captured by surface electrodes or by MEAs into commands for an external device. This requires the users to keep a constant focus of attention on the execution of detailed motor commands. In these setups, feedback is limited to vision, which involves long delays and requires gaze to be constantly on the moving device. Furthermore, non-kinematic information, such as the weight, rigidity and temperature of a manipulated object, are not directly sensed. These limits have propelled investigations toward the development of goal-decoding interfaces (Musallam et al., 2004 ) and of bidirectional BMI’s (Mussa-Ivaldi and Miller, 2003 ; Fagg et al., 2007 ). Bidirectional BMI’s are devices that can not only decode neural activity but also encode external information in the form of brain stimuli. If successful, BMI prosthetic control systems are to be developed which will surely require the use of a trainable bidirectional interface.
A bidirectional interface can, in principle, be programmed to implement a pattern of neural stimuli and responses capable of approximating a desired behavior of the controlled system (Chao et al., 2008 ). Mathematically, this process corresponds to translating the behavior of the neural system into a control policy that maps the current observed state of the controlled system into a corresponding action. This concept is closely related to earlier evidence that spinal interneurons organize muscles into synergy groups whose mechanical outputs are force fields acting upon the limbs (Bizzi et al., 1991 ; Giszter et al., 1993 ; Tresch and Bizzi, 1999 ). These studies demonstrated a simple mechanism of vector summation capable of generating a rep ertoire of control policies out of a small set of non-linear force fields (Mussa-Ivaldi et al., 1994 ; Mussa-Ivaldi and Bizzi, 2000 ). As a future direction, we propose to program bidirectional BMIs for generating control policies in the form of force fields acting on the controlled external devices. We call “dynamic shaping” the interface algorithm that implements this neuro-mechanical translation (Figure 5 ). Dynamic shaping has two components: (1) a decoder that maps the recorded output activity into a force vector, and (2) an encoder that maps the state of the device into a pattern of stimuli. If the dimension of the vector field is smaller than the number of recorded units, the transformation from recorded activities to force vector involves a dimensionality reduction (e.g., by principal component analysis.) In a dynamically shaped interface, the external neural input sets an initial condition and the dynamic field – in the absence of other influences– determines the ensuing trajectory. This approach would free the user from the need to guide the connected device instant by instant. At the same time, however, the user would be able to perform a continuous control, thus guiding the device through arbitrary paths. So far, we have implemented and tested dynamic shaping with a simulated neural system, a simple feedforward neural network model of the biological component (Figure 5 ).
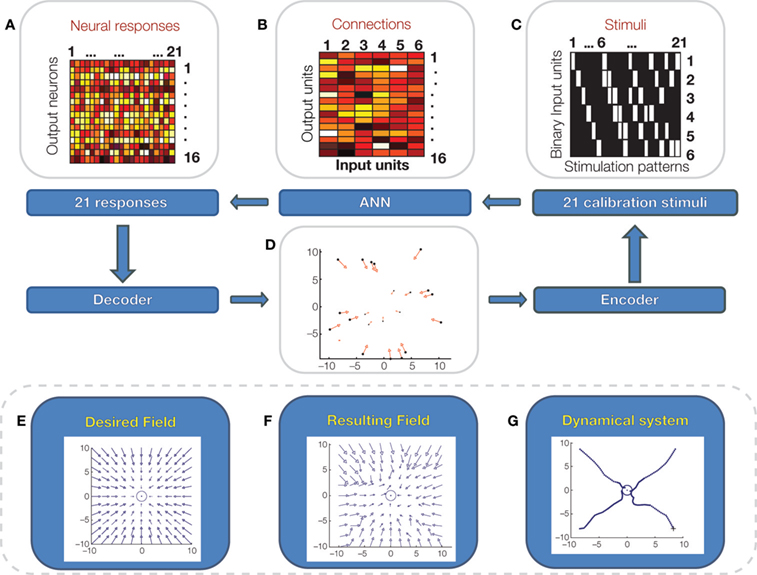
Figure 5. Dynamic shaping simulation. A simple artificial feedforward neural network is connected to a pattern of stimuli, delivered to 6 binary input units (C; white: on, black off) and generates responses over a set of 16 output neurons. In this model, there are no hidden units between input and output units but there is a set of four hidden “noise” units that generate random inputs to the output units. Input and output units are connected by a “synaptic matrix” (B) with positive and negative weights. The output units respond to the weighted sum of their input via a sigmoid transfer function. A set of 21 calibration stimuli (C) are presented in sequence to the input units and 21 responses (A) are recorded from the output units. The calibration stimuli and responses are used to approximate a desired force field (E), acting on a mass-damping system. To perform the calibration, the two top principal components of the 21 neural responses are mapped over the ranges of the force vector components in the desired field. This mapping is performed by the linear decoder. Then, for each force vector, the corresponding point of application is determined and is associated to the stimulus pattern that generated the force vector (D). A simple form of the stimulus encoder maps the current location of the mass-damping system into the nearest point determined in the calibration. The resulting field generated by the encoder/decoder system (F) is a fragmented approximation of the desired field. (G): Simulated trajectories of the spring-damper system under the field generated by the interface.
As dynamic clamps provide us with the means for isolating particular elements of cellular physiology, such as individual channels, the bidirectional interactions between brain and machines – either physical or simulated – provide the nervous system with artificial bodies that are endowed with well known properties and that communicate through well defined channels. This marriage of the nervous system with artificial devices offers an unparalleled opportunity to acquire knowledge about neural computation and plasticity while opening a path for restoring functions lost to accident or disease.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by ONR grant N000149910881, NINDS grants NS048845 and 1R21HD053608 to FAM-I and EU grants Neurobotics, RobotCub and Poeticon to Luciano Fadiga. We are grateful to Dr. Citlali Lopez-Ortiz for comments on the manuscript.
Key Concepts
Brain-machine interface: Hardware and software systems that enable the communication between the brain and an external device. BMI research received a strong boost from advances in micro-electrode technologies and in the decoding of neural signals. A bidirectional BMI involves translating neural signals into commands to the external device and translating signals from the device into neural stimulation.
Dynamical system: A system that evolves in time under the influence of its environment. The state of a dynamical system is any minimal set of variables that is sufficient to determine the future evolution of the system under the action of a known external input. The state equation is an ordinary differential equation that relates the rate of change of the state to the state and to the external input.
Autonomous system: A system governed by a differential equation that contains no explicit dependence upon time. This corresponds to the system being isolated from external influences. Determinism implies that the state trajectories of an autonomous system do not intersect each other, each trajectory being completely determined by the initial state.
References
Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183.
Bakkum, D. J., Chao, Z. C., and Potter, S. M. (2008). Spatio-temporal electrical stimuli shape behavior of an embodied cortical network in a goal-directed learning task. J. Neural Eng. 5, 310.
Bizzi, E., Mussa-Ivaldi, F., and Giszter, S. (1991). Computations underlying the execution of movement: a biological perspective. Science 253, 287–291.
Bliss, T. V. P., and Lomo, T. (1973). Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. J. Physiol. (Lond.) 232, 331–356.
Chao, Z. C., Bakkum, D. J., and Potter, S. M. (2008). Shaping embodied neural networks for adaptive goal-directed behavior. PLoS Comput. Biol. 4. doi: 10.1371/journal.pcbi.1000042.
Chiappalone, M., Massobrio, P., and Martinoia, S. (2008). Network plasticity in cortical assemblies. Eur. J. Neurosci. 28, 221.
DeMarse, T. B., Wagenaar, D. A., Blau, A. W., and Potter, S. M. (2001). The neurally controlled animat: biological brains acting with simulated bodies. Auton. Robots 11, 305–310.
Fagg, A. H., Hatsopoulos, N. G., de Lafuente, V., Moxon, K. A., Nemati, S., Rebesco, J. M., Romo, R., Solla, S. A., Reimer, J., Tkach, D., Phlmeyer, E. A., and Miller, L. E. (2007). Biomimetic brain machine interfaces for the control of movement. J. Neurosci. 27, 11842.
Giszter, S. F., Mussa-Ivaldi, F. A., and Bizzi, E. (1993). Convergent force fields organized in the frog’s spinal cord. J. Neurosci. 13, 467–491.
Grillner, S., Wallén, P., Saitoh, K., Kozlov, A., and Robertson, B. (2008). Neural bases of goal-directed locomotion in vertebrates—an overview. Brain Res. Rev. 57, 2–12.
Kaplan, D. T., and Glass, L. (1992). Direct test for determinism in a time series. Phys. Rev. Lett. 68, 427–430.
Karniel, A., Kositsky, M., Fleming, K. M., Chiappalone, M., Sanguineti, V., Alford, S. T., and Mussa-Ivaldi, F. A. (2005). Computational analysis in vitro: dynamics and plasticity of a neuro-robotic system. J. Neural Eng. 2, S250–S265.
Kositsky, M., Chiappalone, M., Alford, S. T., and Mussa-Ivaldi, F. A. (2009). Brain-machine interactions for assessing the dynamics of neural systems. Front. Neurorobotics 3, 1–12. doi: 10.3389/neuro.12.001.2009.
Kositsky, M., Karniel, A., Alford, S., Fleming, K. M., and Mussa-Ivaldi, F. A. (2003). Dynamical dimension of a hybrid neuro-robotic system. IEEE Trans. Neural. Syst. Rehabil. Eng. 11, 155–159.
Marom, S., Meir, R., Braun, E., Gal, A., Kermany, E., and Eytan, D. (2009). On the precarious path of reverse neuro-engineering. Front. Comput. Neurosci. 3. doi:10.3389/neuro.10.005.2009.
Martinoia, S., Sanguineti, V., Cozzi, L., Berdondini, L., Van Pelt, J., Tomas, J., Le Masson, G., and Davide, F. (2004). Towards an embodied in vitro electrophysiology: the NeuroBIT project. Neurocomputing 58, 1065–1072.
Musallam, S., Corneil, B. D., Greger, B., Scherberger, H., and Andersen, R. A. (2004). Cognitive control signals for neural prosthetics. Science 305, 258–262.
Mussa-Ivaldi, F. A., and Bizzi, E. (2000). Motor learning through the combination of primitives. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 355, 1755–1769.
Mussa-Ivaldi, F. A., Giszter, S. F., and Bizzi, E. (1994). Linear combinations of primitives in vertebrate motor control. Proc. Natl. Acad. Sci. U.S.A. 91, 7534–7538.
Mussa-Ivaldi, F. A., and Miller, L. E. (2003). Brain-machine interfaces: computational demands and clinical needs meet basic neuroscience. Trends Neurosci. 26, 329–334.
Novellino, A., D’Angelo, P., Cozzi, L., Chiappalone, M., Sanguineti, V., and Martinoia, S. (2007). Connecting neurons to a mobile robot: an in vitro bidirectional neural interface. Comput. Intell Neurosci. 2007, 12725.
Reger, B. D., Fleming, K. M., Sanguineti, V., Alford, S., and Mussa-Ivaldi, F. A. (2000). Connecting brains to robots: an artificial body for studying the computational properties of neural tissue. Artif. Life 6, 307–324.
Sharp, A. A., Abbott, L. F., and Marder, E. (1992). Artificial electrical synapses in oscillatory networks. J. Neurophysiol. 1691–1694.
Sharp, A. A., O’Neil, M. B., Abbott, L. F., and Marder, E. (1993). The dynamic clamp: artificial conductances in biological neurons. Trends Neurosci. 16, 389.
Keywords: brain-machine interface, dynamical system, dynamical dimension, neural plasticity, lamprey
Citation: Mussa-Ivaldi S, Alford ST, Chiappalone M, Fadiga L, Karniel A, Kositsky M, Maggiolini E, Panzeri S, Sanguineti V, Semprini M and Vato A (2010) New perspectives on the dialogue between brains and machines. Front. Neurosci. 4,1: 44Â52. doi:10.3389/neuro.01.008.2010
Received: 30 September 2009;
Paper pending published: 14 October 2009;
Accepted: 24 November 2009;
Published online: 15 May 2010
Edited by:
Steve M. Potter, Georgia Institute of Technology, USAReviewed by:
Antonio Novellino, Institute for Health and Consumer Protection – Joint Research Centre, ItalyThomas DeMarse, University of Florida, USA
Copyright: © 2010 Mussa-Ivaldi, Alford, Chiappalone, Fadiga, Karniel, Kositsky, Maggiolini, Panzeri, Sanguineti, Semprini and Vato. This is an open-access publication subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Ferdinando (Sandro) Mussa-Ivaldi, has a degree (Laurea) in Physics and a Ph.D. in Biomedical Engineering. He is Professor at Northwestern University, and a Senior Research Scientist at the Rehabilitation Institute of Chicago, where he founded the Robotics Laboratory. His main research contributions are in motor system and computational neuroscience. His team created the first hybrid system, in which neural tissue from the Lamprey’s brain stem was bi-directionally interfaced with a mobile robot. Mussa-Ivaldi is also studying the mechanisms of motor remapping in a clinical context.c2FuZHJvQG5vcnRod2VzdGVybi5lZHU=










