1
Network Dynamics Group, Max Planck Institute for Dynamics and Self-Organization, Göttingen, Germany
2
Bernstein Center for Computational Neuroscience, Göttingen, Germany
A commentary on
On dynamics of integrate-and-fire neural networks with conductance based synapses
by Bruno Cessac and Thierry Viéville
Distributed spiking activity underlies the dynamics and function of neuronal circuits and thus their computational capabilities. Beyond a simple rate, often the timing of spikes also essentially contributes to information processing in these systems (Hahnloser et al., 2002
; Riehle et al., 1996
; Rieke et al., 1996
; Rokem et al., 2006
). A thorough understanding and analysis of the very notion of spike timing is therefore pivotal for understanding brain function.
For instance, it is widely accepted that abstract discrete time models of interacting neurons, with spike times fixed to a temporal grid, may well describe the spike rates of neurons, e.g., for balanced cortical activity (van Vreeswijk and Sompolinsky, 1996
), but the timing of spikes is not modeled exactly. In this respect, even simple integrate-and-fire type models are more accurate because they describe neural dynamics in continuous time and thus may exhibit spikes at any chosen time (Brette et al., 2007
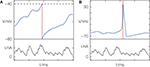
). One may argue that the manually implemented reset in integrate-and-fire models, leading to exact spike times, merely serves as a low-level compromise between detailed biological modeling and mathematical tractability. Generating an action potential takes a time of the order of 1 ms, but one may easily introduce a defined time of a spike by interpreting it, e.g., as the time of peak voltage during a biophysical action potential (cf. Figure 1
).
Figure 1. Definition of spike timing (A) in models with threshold and reset and (B) in models with active spike generation. (A) Membrane potential V of a leaky integrate-and-fire model receiving excitatory input current I; when V crosses the threshold (dashed line) from below, a spike is generated and the membrane potential is reset. (B) Hodgkin–Huxley models with active spike generation. In (A) the spike time (red) has infinite precision due to the artificial reset; in (B) the spike has some temporal extent but a spike time can equally be exactly identified (e.g., by the peak potential).
Nevertheless, continuous time models, in general, face the conceptual problem that information contained in the timing of only a single spike is infinite. In contrast, discrete time models exhibit bounds on the information carried by a spike but it may seem questionable how real biological systems would conform to time discretization.
Moreover, in raster plots displaying experimentally recorded spike trains of neurons there is actually a raster, a non-zero time resolution discretizing time into small but positive intervals. However, the current high temporal resolution, often 10 kHz or more, may make us forget such discretization issues.
In their recent contribution to Frontiers in Neuroscience, Cessac and Viéville (2008)
emphasize that the main issue is not about how fine the resolution actually is, in models or data, but whether or not there is a discretization at all. So not even the most subtle description, neither experimentally nor in modeling, can characterize the timing of spikes with arbitrarily high precision. The authors now show an alternative way of modeling spiking neural circuits by lifting a recent mathematical work (Cessac, 2008
) to the level of networks with conductance-based synapses and by pointing out (and explicitly highlighting for their system) a number of prerequisites needed to fully grasp what neural network modeling is all about – how to define “spikes” and what is their “timing”, how could we come by conceptual problems of discrete resolution and how well do (arbitrarily detailed) mathematical models characterize an actual neural systems’ dynamics. They combine continuous time evolution with a discretization of spike times and identify situations where minute disturbances in spike times may crucially change the circuit dynamics. That work certainly does not provide the final word on the subject, but highlights one key problem: it is not fully self-evident a priori how precise the timing of action potentials really is and what we actually mean by “timing”, neither in experimental data nor in idealized mathematical models.
Cessac and Viéville (2008)
argue that the very notion of spike timing is not well understood in itself and thus can lead to conceptual difficulties. For instance, in integrate-and-fire type models the reset implies that the neuron’s membrane potential after reset is completely independent of its value before reset. A very recent work (Kirst et al., 2009
) on a state- and input-dependent reset partially resolves this issue. One might expect that the problem of spike timing is overcome completely when considering biophysically more detailed models, such as Hodgkin–Huxley or compartment models; but even for arbitrarily refined, high-dimensional differential equation models, any reasonable time scale described must be much larger than intrinsic time scales characterizing, e.g., individual ion channels, because otherwise the very description by differential equations looses its meaning.
The study of Cessac and Viéville (2008)
, pushing further an alternative discrete-time view onto the world of biological neural network modeling, naturally raises more questions than it answers: in their model, discrete spike times themselves are defined arbitrarily precise (namely on the lattice) such that it remains debatable in how far the above precision problem is actually solved. More generally, how does noise affect the spike timing in networks and what is the impact of the dynamics of action potential initiation (cf. Naundorf et al., 2006
)? We also need to reconsider related questions about creating (or removing) additional spikes by small perturbations and about the reliability of spikes (Jahnke et al., 2008
; Teramae and Fukai, 2008
). For computations in neural systems it finally seems most relevant how precisely spike times can actually be detected by neurons and read out for further processing (Tiesinga et al., 2008
). We definitely need to take some time to precisely think about timing before recording, simulating or analyzing the timing of action potentials in neural circuits.
This work was supported by the Federal Ministry of Education and Research (BMBF) Germany by grant number 01GQ0430 to the Bernstein Center for Computational Neuroscience (BCCN) Göttingen and by a grant of the Max Planck Society to MT. We thank L. J. Deutsch for help with manuscript preparation.
Brette, R., Rudolph, M., Carnevale, T., Hines, M., Beeman, D., Bower, J. M., Diesmann, M., Morrison, A., Goodman, P. H., Harris, F. C. Jr., Zirpe, M., Natschläger, T., Pecevski, D., Ermentrout, B., Djurfeldt, M., Lansner, A., Rochel, O., Vieville, T., Muller, E., Davison, A. P., El Boustani, S., and Destexhe, A. (2007). Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci. 23, 349–398.