1
Program in Applied and Computational Mathematics, Center for the Study of Brain, Mind and Behavior, Princeton University, Princeton, NJ, USA
2
Section of Neurobiology, Center for Perceptual Systems, Department of Psychology, The University of Texas at Austin, TX, USA
Recent neurophysiological studies in awake, behaving primates have revealed that neurons in certain brain areas appear to integrate sensory evidence over time during the performance of perceptual decision-making tasks. Neurons in the lateral intraparietal area (LIP) of rhesus monkeys exhibit such decision-related signals while the animals view and judge the direction of a visual motion display. Further investigation of this temporal integration process using brief perturbations of the sensory evidence has suggested that LIP neurons do not integrate evidence in a perfect, linear manner. We describe how a biophysically-plausible attractor network model can account for many aspects of the temporal dynamics of neural activity during these perceptual decisions. We also review a larger set of models and explain how the dynamics during and after temporal integration can help to distinguish the underlying neural mechanisms. Finally, we propose some crucial theoretically-motivated experiments that are needed to test among models.
Perceptual decision-making provides systems neuroscientists a tractable arena for the physiological and computational analysis of higher cognitive function. Building on the large bodies of systems neuroscience work investigating the circuits and signals involved in sensory and motor functions, this subfield of cognitive neuroscience has targeted the sensorimotor brain structures that link sensation and action. Here, we describe a set of intertwined experimental and theoretical work within one particular model system of interest – primate’s perceptual decisions about the direction of visual motion (Shadlen and Newsome, 1996
). In particular, we focus on how recent emphases on the temporal dynamics of visual motion decisions yield insights into how the brain accumulates evidence. We note that this is a narrow but deeply-developed vein within a larger set of neurophysiological work on perceptual decision-making and oculomotor choice behavior (Glimcher, 2003
; Gold and Shadlen, 2007
; Schall, 2001
, 2003
; Sugrue et al., 2005
).
The motion-perception direction-discrimination framework grew out of basic visual neurophysiological studies of the middle temporal visual area, commonly referred to as MT (or V5). Early studies of the basic physiological properties demonstrated that the vast majority of cells in this area were selective to the direction of visual motion but were notably insensitive to many other visual features. Further inquiry by Newsome, Movshon, Britten, Salzman, Shadlen and colleagues followed, with a series of lesion, microstimulation, and computational modeling studies assessing the relation between direction-selective MT signals and monkeys’ judgements of the direction of motion (Newsome et al., 1989
; Salzman et al., 1990
; Shadlen et al., 1996
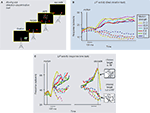
). These studies employed a now-standard task in which monkeys viewed a dynamic random dot display, decided the direction of motion in a two-alternative forced-choice paradigm (e.g., either left or right), and communicated their decision by moving their eyes to a corresponding choice target on the screen (Figure 1
A). Difficulty was controlled (and manipulated across trials) by varying the proportion of dots moving coherently in one direction; the rest were replotted randomly like analog television “snow”. This integrated series of studies demonstrated that MT signals play a causal role in direction perception, and that the statistical properties of these signals are sufficient to explain several aspects of these perceptual judgments (Newsome, 1997
; Parker and Newsome, 1998
).
Figure 1. Visual motion direction discrimination task. (A) Task protocol: (i) monkey fixates a central fixation point; (ii) choice targets are presented, one in the response field (RF) of the LIP neuron under study, and the other well outside it; (iii) monkey views random dot motion, decides which direction was presented, and communicates its choice by making an eye movement to the corresponding choice target. (B) Fixed duration version of the direction discrimination task (Shadlen and Newsome, 2001
): The moving dots are presented for a short, experimenter-controlled duration. The monkey watches the entire moving dot presentation and is them allowed to make its eye movement response (saccade) after a “go” signal (removal of fixation point). Bold (dashed) traces: LIP activities with saccades into (away from) neuron’s RF; different colors indicate different motion strengths (see legend). (C) LIP activity during a response-time version of the direction discrimination task (Huk and Shadlen, 2005
; Roitman and Shadlen, 2002
). Monkey views dots until they have made their decision, at which point they can interrupt dot viewing by making a saccadic eye movement. This provides a measure of the decisions accuracy (correct or incorrect) as well as the time it took. Left panel, LIP response as a function of time relative to the onset of the moving dot display. Right panel, same LIP responses aligned to the time of the saccadic response. Otherwise same format as panel (B). Adapted from Mazurek et al. (2003)
, with permission; original data from Shadlen and Newsome (2001)
(B), and Roitman and Shadlen (2002)
(C).
Although these studies elegantly supported a relation between neural signals and perception, they did not directly address how those sensory signals were “read out” by later brain areas that transformed them into decisions and corresponding actions. The direct attack began when Shadlen and Newsome (2001)
lowered their electrodes into a particularly promising part of the primate posterior parietal lobe, the lateral intraparietal area (LIP). Basic properties of LIP suggested it would be a good place to investigate the neural transformations linking sensory inputs and motor outputs. Even in simple tasks, LIP neurons appear to carry signals involved in sensorimotor integration (Gnadt and Andersen, 1988
). For example, each LIP neuron responds when a spot of light is placed in a particular location in the visual field, termed the neuron’s “response field”. In addition to this visual response, these cells will maintain a steady rate of action potential discharge until the monkey is allowed to make a saccadic eye-movement to the location of the target. Such persistent activity is even observed when the target is merely flashed briefly, and the monkey must remember the location of the target until executing the eye-movement (Churchland et al., 2008
; Kiani et al., 2008
; Roitman and Shadlen, 2002
; Shadlen and Newsome, 2001
). This “memory activity” is conventionally considered to be a hallmark of higher cognitive function (Fuster, 1988
).
Consistent with this conjecture, single neurons in LIP exhibited decision-related activity while the monkeys performed the direction-discrimination task. Again, monkeys viewed a moving dot stimulus of variable direction and motion strength for a fixed amount of time, decided their direction, and then waited until a “go” signal to make their eye movement response. The time course of LIP responses suggested these neurons were involved in the accumulation of directional “evidence” over time, perhaps going as the time-integral of the instantaneous estimate of motion coming from MT. This interpretation came from the fact that (trial-averaged) spike rates in individual LIP neurons rose (or fell) while the monkey viewed the dots and decided their direction; responses rose on trials in which the monkey’s ultimate decision involved an eye movement response to a target inside the neuron’s response field, and fell when the monkey chose the target outside the neuron’s response field (Figure 1
B). More compellingly, responses rose or fell monotonically, and the rate of these ramping responses was dependent on difficulty. When more dots moved coherently in one direction, responses rose or fell more steeply. Analysis of error trials also demonstrated that these ramps were better correlated with the monkey’s choice than with the veridical sensory stimulus, bolstering the interpretation that these signals were decision-related. Similar signals have been observed or inferred in other oculomotor planning areas as well (e.g., Glimcher and Sparks, 1992
; Hanes et al., 1995
).
The ramping nature of these LIP decision signals was further clarified by Roitman and Shadlen (2002)
, who modified the direction-discrimination task to allow the monkeys to communicate their decision as soon as they had made up their mind (instead of waiting for an experimenter-controlled “go” signal). This response-time protocol provided further insight into the temporal dynamics of decision formation. Each trial thus ended, not after a fixed amount of time, but when the monkey had accumulated sufficient evidence to commit to a choice. This provides richer behavioral data for models to consider (e.g., the time it takes to make each decision, in addition to its accuracy), and also removes the ambiguity of whether later parts of fixed-duration trials were used by the monkey, or were ignored after a decision had already been made. Consistent with this latter improvement, this response time protocol revealed more linear ramping in LIP (Figure 1
C). The time courses of these ramps have been shown to be consistent with the observed speed and accuracy of the monkeys’ decisions (Mazurek et al., 2003
).
In summary, the evolution of the direction-discrimination protocol has provided an arena for the neuroscientific study of simple perceptual decision making. In particular, the ramping responses in LIP suggest that the temporal dynamics of decision formation are empirically accessible. Because higher cognition involves the dissociation of sensory inputs from subsequent outward actions, temporal aspects of information processing during decision making may be particularly informative. Probing these temporal dynamics further has recently proven to be a fruitful endeavor, as described below.
Early models of perceptual decision making come from cognitive psychological research, borrowing ideas from signal detection theory, wave difference theory and diffusion models (Busemeyer and Townsend, 1993
; Gold and Shadlen, 2001
; Laming, 1968
; Link, 1992
; Link and Heath, 1975
; Mazurek et al., 2003
; Palmer et al., 2005
; Ratcliff, 1978
; Ratcliff and McKoon, 2008
; Stone, 1960
). These sequential sampling models are based on the competing temporal accumulation of sensory information among alternative choices (Ratcliff and Smith, 2004
; Smith and Ratcliff, 2004
). In particular, one-dimensional diffusion models posit a drift (accumulation) rate which is proportional to the relative difference between opposing sensory signals, representing the accumulation of sensory evidence toward one of two decision thresholds (Figure 2
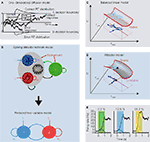
A). By definition, there is no leak in the integration, so these models assume perfect, linear integration of sensory information over time.
Figure 2. The diffusion and the attractor models in two-choice tasks. (A) Basic features of a one-dimensional drift-diffusion model of Ratcliff (1978)
for two-choice reaction time tasks. (B) Network architecture of Wang (2002)
(top), and its reduced “mean-field” version (Wong and Wang, 2006
) (bottom). (C,D) “Potential landscapes” of models in decision firing rate space and its 2-dimensional projection during sensory integration. U: “potential” of the system. rLeft and rRight: neural activity of populations selective to leftward and rightward motion, respectively. Sensory stimulus is unbiased for clearer illustration. (C) Linear neural network model with large and balanced decay and inhibition can exhibit approximately one-dimensional diffusion-like processes. (D) Attractor model which has an unstable saddle-like steady-state (black filled circle) that is associated with a stable and unstable “manifold” that direct the network dynamics in two dimensions. (E) Persistent neural activity of the model in Wong and Wang (2006)
showing the formation of the decision (0–1 s) and sustaining the categorical memory of decision made during the delay period (1–2 s), in a task similar to Shadlen and Newsome (2001)
. Left-right: motion coherences of 3.2%, 6.4% and 12.8%. (A) adapted from Ratcliff and McKoon (2008)
, with permission; (B,E) from Wong and Wang (2006)
, with permission. See text for details.
Diffusion models yield analytical solutions for reaction time (RT) and accuracy, typically fit human psychophysical data well, and also optimize reward rate (Bogacz, 2007
; Bogacz et al., 2006
; Palmer et al., 2005
; Ratcliff and McKoon, 2008
; Ratcliff et al., 1999
). Many of these models were developed before neuronal recordings of behaving animals became commonplace, but their basic feature of accumulation toward some decision threshold turns out to be surprisingly similar to that found in recent electrophysiological studies (Gold and Shadlen, 2007
).
A Neurally- and Biophysically-Plausible Attractor Network Model
Wang (2002)
proposed a biophysically-plausible network model that was more directly inspired by the decision-making neurophysiology. The network architecture was borrowed from a cortical microcircuit model originally used for modeling primate working memory (Brunel and Wang, 2001
) (Figure 2
B, top). The model consisted of a network of four populations: two populations of excitatory pyramidal cells selective to the presented stimulus (blue for choice left or 1 and red for choice right or 2), one excitatory population (black, NS) not selective to the stimulus, and one population of inhibitory interneurons (green, I). These leaky integrate-and-fire spiking neurons were connected by synapses with realistic dynamics. Glutamatergic excitatory synapses (pointed arrows) were mediated by AMPA and NMDA, while inhibitory synapses (circular arrows) were mediated by GABAA. Probabilistic choice behaviors were mainly provided by background noise outside this local microcircuit, filtered by AMPA receptors.
This model reproduced the psychophysical and neuronal data of Shadlen and Newsome (2001) and Roitman and Shadlen (2002)
. Importantly, the model could both integrate sensory information during decision formation, and also self-sustain this categorical decision during a blank period after the offset of the visual stimulus (Figure 2
E). This working memory capacity is achieved by endowing the network model with relatively stronger recurrent excitatory synapses from Hebbian learning (denoted by w+ in Figure 2
B) within the population of cells selective to the presented stimulus. However, in many strongly recurrent attractor network
models, the behavior is dominated by their steady states; the network is either not sensitive to (weak) inputs, or rapidly switches between steady states by (strong) inputs. In contrast, the kind of attractor network proposed by Wang (2002)
has the ability to exhibit prolonged responses to transient inputs, with a characteristic time constant of up to a second, that can subserve integration computations in decision processes. The co-existence of a strong recurrent network (needed for working memory) and the long integration time (needed for reliable processing of sensory information) can be robustly achieved by incorporating slow NMDA-mediated synapses in its recurrent connections. An extended version of the Wang (2002)
model was implemented by Lo and Wang (2006)
, accounting for a more biologically plausible decision threshold mechanism.
Temporal Dynamics of the Attractor Model
Wong and Wang (2006)
performed a systematic parameter reduction to gain additional insights into the behavior of the Wang (2002)
model. A mean-field approach reduced the four populations of spiking neurons into four neural units, each representative of their population-averaged activity. The network dynamics were assumed to be dominated by their slowest dynamics, that of the average NMDA-mediated receptors of the two competing pyramidal cell populations, thus reducing the Wang (2002)
network to only two dynamical variables (Figure 2
B, bottom). The neural population dynamics, and the AMPA and GABAA synaptic dynamics, were therefore assumed to be relatively fast in approaching their stationary states. This reduced the original network to its simplest form and was more conducive for theoretical analysis (e.g. using dynamical systems theory
). For example, the reduced model showed that slow integration could be enhanced not only by NMDA-mediated synapses but also by having the network to integrate near a transition point of network stability – a bifurcation
.
Other theoretical work has shown that linear neural networks coupled with leakage and mutual inhibition can also exhibit decision-making dynamics (e.g., Bogacz et al., 2006
; Brown and Holmes, 2001
; Brown et al., 2005
; Usher and McClelland, 2001
). Inhibition allows inputs early in the trial to be predominant, whereas leakage favors signals at later times in the trial (Usher and McClelland, 2001
). In particular, Bogacz et al. (2006)
(see also Brown and Holmes, 2001
; Brown et al., 2005
), has shown that these linear networks can exhibit dynamics that approximate a one-dimensional linear diffusion-like process. Doing so requires leakage to balance inhibition, and for both leakage and inhibition to be large. However, Wong and Wang (2006)
found that the decision network has difficulty reducing its dynamics to a one-dimensional diffusion-like integration process, when the recurrent synapses is dominated by the slow dynamics of NMDA receptors.
Figures 2
C,D illustrate this in a decision firing-rate space. Assuming a “potential” can be defined, Bogacz et al. (2006)
show that the state of a balanced linear network (shown by the noisy blue trajectory) can traverse quickly and be confined in a one-dimensional linear decision space (Figure 2
C). With an unbiased or weak stimulus (illustrated here), noise will dominate the trajectory in this one-dimensional space, ultimately making a close to random choice. This should be compared to more general unbalanced linear networks (with inhibition larger than their decay) (Bogacz et al., 2006
; Brown and Holmes, 2001
; Brown et al., 2005
; Usher and McClelland, 2001
), or to nonlinear attractor network endowed with slow excitatory recurrent synaptic dynamics and fast feedback inhibition (Wang, 2002
; Wong and Wang, 2006).
These attractor networks will have an unstable saddle-like steady state
(black filled dot, Figure 2
D) that forces the network to move to either of the two choices, even when the stimulus is unbiased. Note the saddle point in Figure 2
D is associated with a stable (brown) attracting and an unstable (magenta) repelling “manifold”, but there is no such saddle point in balanced linear network models (Figure 2
C). Moreover, nonlinear attractor network models with strong recurrent excitation as in Wang (2002), Wong and Wang (2006), and Roxin and Ledberg (2008)
would result in stronger repelling dynamics (larger curvature along the unstable “manifold”).
This analysis suggests that models can be distinguished according to the structure of their stable or unstable steady states during transient dynamics. We further explore how the classes of network circuits can be distinguished using time-varying task protocols below.
Electrophysiological recordings from LIP, as well as theoretical analyses of an attractor model, both point to temporal dynamics as a key element for understanding the computations underlying perceptual decisions. This motivates more direct theoretical and experimental manipulations of the temporal properties of the stimulus and task. Wang (2002)
proposed a time-varying stimulus protocol in which mid-trial changes of motion strength and direction could reverse decisions. Simulations showed that for a weak motion direction change, there was a maximum time onset when decisions could be reversed, attributable to the existence of a categorical choice attractor. This theoretical work motivated a similar time-varying protocol in an experimental study that employed motion pulses to more directly characterize the mechanisms of neural time-integration during decision making.
A Direct Experimental Test of Temporal Integration with Motion Pulses
Although prior experimental work provided both qualitative and quantitative evidence that the ramping activity in LIP neurons reflected the temporal accumulation of evidence over time (e.g., Figure 1
), all of these inferences were derived from experiments in which the visual motion display was of constant strength and direction over time. In order to more compellingly test the case for temporal integration and to more precisely quantify its form, it was necessary to characterize the relation between visual motion inputs and LIP spiking outputs using time-varying stimuli.
Huk and Shadlen (2005)
experimentally characterized the temporal integration mechanisms in LIP neurons by employing a time-varying version of the direction-discrimination task. Monkeys were trained to discriminate the direction of a moving dot display in a response time paradigm, just as in prior experiments. However, in these new experiments, there was also a dim, dynamic texture drawn behind the standard moving dots. On some trials, this background texture was simply dynamic pixel noise, and hence added no systematic motion signal. But on one-third of trials, this background texture briefly shifted in the same direction as the moving dots, and on another third of trials, the background briefly shifted in the opposite direction of the dots. These 100 ms-long motion pulses served as a brief perturbation of the time course of visual motion that could be inserted and manipulated independently of the standard moving dot display.
These subtle motion pulses were used to assay the temporal integration properties in LIP. If one conceives of the motion pulses as an impulse input, the output of a perfect time-integrator would of course be a “step” response that persists infinitely in time. Deviations from this relation would reflect deviations from perfect integration, and the specific form of these deviations might reveal the particular neural mechanisms for approximating time integration.
In this motion-pulse version of the moving dot direction discrimination, the monkey subjects were still rewarded for choosing the correct direction of the dots, and hence were motivated to ignore the subtle, added background motion pulses (if they noticed them at all). However, the motion pulses proved impossible for the monkeys to completely ignore: The subtle pulses exerted systematic effects on both the accuracy and speed of the choices, consistent with the addition (or subtraction) of a small amount of additional motion evidence in favor of one direction (or the other).
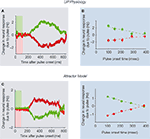
The firing rates of LIP neurons were also perturbed by the pulses in a similarly direction-selective manner. As LIP responses ramped up or down due to the dot motion, the background pulses bumped the response rate up or down in a direction-selective manner. Figure 3
A shows the relative change in LIP spike rate due to a pulse; the ramping responses have been subtracted off to isolate the pulse effects. Critically, this deviation in spike rate persisted for several hundreds of msec after the offset of the motion pulse, and thus approximated the “step” response of an integrator. The temporal persistence of these pulse effects revealed that LIP spike rates are a function of the entire time course of the motion evidence, and do not just reflect the instantaneous sensory input. These persistent neural signals may reflect the psychological process of accumulating evidence over time.
Figure 3. Brief motion pulses exert persistent effects on neural activity. (A) A brief 100 ms
motion pulse during motion discrimination of random dot stimulus exerts a long-lasting change
in LIP neuronal firing rates. Green (red) trace: positive (negative) pulse in the same (opposite)
direction as the random dot motion coherence. Data grouped over all pulse onset times
and motion coherences. (B) Violation of time-shift invariance (TSI): instantaneous change in LIP
activity due to pulse is not a constant, but decreases with later motion pulse onset time relative
to the random dot motion stimulus onset. Green and red: same as (A). (C) Attractor model
reproduces experimental data (A,B). (A,B) adapted from Huk and Shadlen (2005)
, with permission;
(C) from Wong et al. (2007)
.
Although the pulse-probe perturbation paradigm portrayed powerful perseverance, potential problems persisted. In particular, the effects of the pulses gradually decayed over time (a seeming deviation from perfect integration), and pulses presented earlier during motion viewing exerted larger effects than later pulses (a violation of time-shift invariance; Figure 3
B). Further computational analyses, described in the next section, explain why some but not all of these phenomena were consistent with perfect integration. In contrast, an attractor model might be able to explain these temporal dynamics.
Modeling Studies of the Motion Pulse Experiment
It may initially be tempting to interpret the gradual fall-off of pulse effects over time (Figure 3
A) as indicating “leakiness” of the integration process (an apparent deviation from the perfect integration assumed in classical diffusion models described above). However, further consideration reveals that when a perfect integrator’s activity terminates at a bound (i.e., when it reaches the decision threshold), the observed time course of the average pulse effect will decline over time as the bound is approached. This is simply a result of conditionalization when averaging multiple trials that terminate at different times. Each trial ends when the integrator’s activity level reaches a decision bound: as time goes on, the only surviving traces are from trials in which the decision process had not yet hit the decision bound. Thus, the average response eventually asymptotes at the decision bound, but this does not directly indicate integrator leak. This is equivalent to a saturation or ceiling effect, but it occurs at the level of data analysis, and should not be interpreted as reflecting neural saturation or leakiness per se.
To further explore these dynamics, Huk and Shadlen (2005)
used a simple neural model that incorporated realistic MT responses to motion, but which simply asserted (i.e., without a neurophysiological implementation) that LIP reflected the perfect time integral of the MT signals. This “neural-diffusion” model confirmed that the time course of pulse effects observed in LIP neurons was similar to that expected by nearly perfect integration up to a decision bound. Bounded temporal integration could not, however, explain the failure of time-shift invariance observed in the LIP pulse effects. This departure suggested that the accumulation of evidence depends on time-varying neural dynamics that are experimentally distinguishable from the perfect, linear, time-invariant integration posited by early mathematical models and originally used to describe LIP firing rates.
In contrast, the attractor model inherently contains the sort of time-varying dynamics needed to explain failures of time-shift invariance, due to its unique unstable dynamics (Figure 2
D). Wong et al. (2007)
showed that the attractor model could account for a wider range of the experimental data of Huk and Shadlen (2005)
than the perfect integrator model. The attractor model reproduced the basic pulse effects on the monkey’s decisions, and also matched the temporal persistence of pulse effects on LIP spike rates (Figure 3
C), confirming that it could approximate temporal integration. It was, however, also able to reproduce the violation of time-shift invariance in the original data (Figure 3
C, right), which the perfect integrator model was not able to do. Taken together, these modeling analyses demonstrate that a neural implementation of the diffusion model based on perfect, linear integration is able to account for many – but not all – of the effects of time-varying inputs. In contrast, the attractor model accounts for the basic effects as well as the distinctive deviation from time-shift invariance.
Model Challenges Based on Other Temporal Dynamics in the Data
Much emphasis has been placed on the temporal dynamics of LIP activity during the dot viewing period, such as the coherence-dependent ramping responses and the persistent effects of brief motion pulses. However, LIP neurons display other temporal dynamics during trials in the direction discrimination task, and it is interesting to consider whether the attractor model can also account for these elements. Indeed, several seemingly peripheral aspects of LIP responses turn out to place important constraints on the computational mechanisms.
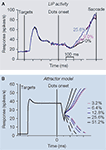
First, LIP neurons exhibit strong responses at the very beginning of each trial, when the response targets are illuminated before the onset of the dots (Figure 4
A). Second, LIP neurons exhibit a dip-and-rise immediately after the onset of dots, which is independent of the dot motion direction or strength (see Huk and Shadlen, 2005
; Roitman and Shadlen, 2002
, and Figures 1
C and 4
A). These dynamics challenge attractor models, which must remain capable of performing integration when starting from a high response level (the target-onset response) and be robust to stereotyped perturbations (the dip-and-rise).
Figure 4. Other temporal dynamics observed
in the direction-discrimination protocol.
(A) Dynamics of population-averaged LIP firing rate
throughout a trial in a 4-choice reaction time task
(Churchland et al., 2008
), similar to Roitman and Shadlen
(2002)
. Note the high firing rate right after choice
targets onset and the signature dip-and-rise before
ramping of activity after motion onset. Only saccades
into the response field of LIP neurons are shown.
(B) Attractor network model of Wong et al. (2007)
that reproduces similar features as in the monkey
experiments. Trial-averaged neural responses. (A)
adapted from Churchland et al. (2008)
, with permission;
(B) from Wong et al. (2007)
.
To take the high baseline firing rate into account, the attractor model can be amended to incorporate symmetrical target inputs to the two competing neural populations, thus matching the high initial firing rates observed in LIP after the onset of the choice targets (Figure 4
B). These symmetrical target inputs create a high stable steady-state to match the observed neural responses, but it does so without allowing competition between the populations to set in. This steady-state has to be less than ∼100 Hz, as observed in experiments, which is automatically accounted for in the model with its nonlinear saturation of NMDA at the recurrent synapses (Wang, 1999, 2002
; Wong and Wang, 2006
). The model can also be modified to follow the dip-and-rise observed in real LIP neurons, by virtue of adding a time-varying input associated with the onset of the trial. Even under these conditions, the attractor model remains capable of performing temporal integration (Figure 4
B) when the moving dot stimulus appears.
These are important extensions because they show that a model with nonlinear attractor dynamics can not only approximate temporal integration, but can do so when starting at a relatively high (but non-competitive) activity level. In general, attractor models appear to be more stable and robust in the face of high activity levels than general intuition may have suggested. Moreover, adding symmetrical pre-stimulus target inputs into the model brings the system closer to the saddle-like unstable steady-state, moving it toward more one-dimensional (although still nonlinear) dynamics along the unstable manifold (compare Wong et al., 2007
with Wong and Wang, 2006
, and Figure 2
D).
Experimental Challenges Based on Insights from Models
Wong et al. (2007)
explored a multiple-pulse protocol to further elucidate the neural computation of temporal integration by assessing how multiple sequential pulses interact over time. These pulses would have the same amplitude but their directions would be the same or opposite to each other (Figure 5
A). A perfect integrator (like the diffusion model) predicts that the individual pulses would cancel each other exactly. In contrast, a leaky integrator would depend more on the second pulse, and a network with strong recurrent excitation would depend more on the first pulse (Figure 5
B). These multiple-pulse protocols can be translated into new experimental work and promise to further expose nonlinearities in LIP (A. Huk, unpublished observations).
Figure 5. Multiple pulse protocol and predictions
of the attractor model. (A) One out of four possible
combinations of the double-pulse experimental protocol
proposed in Wong et al. (2007)
. (B) Model predictions
for double-pulse effects on monkeyâÂÂs choices. Second
pulse has a weaker effect than the first, resulting
in differential effects between the paired-pulse from
the linear sum of the individual pulses. (A,B) adapted
from Wong et al. (2007)
.
The attractor model also makes strong predictions for the relations between memory activity and temporal integration within individual LIP neurons. LIP cells are typically selected based upon the persistence of firing rates during the delay period. It is not clear whether LIP neurons with little or no such persistent activity can still integrate sensory information. Such simple experiments are currently in progress, and will be important for constraining the class of possible models, especially knowing that memory and rate of integration are fundamentally linked in the attractor model discussed in this paper (Wong and Wang, 2006
). Likewise, further tests of whether accumulation and memory are based on a common mechanism can be assessed by using tasks that that involve multiple periods of stimulus viewing bridged by blank memory periods, similar to that of Romo et al. (1999)
. Simultaneous recording from multiple single-units over different brain areas may also help to elucidate whether LIP neural networks can locally sustain memory or require interaction from other brain areas.
The attractor model’s implementation of the choice target inputs can be tested by introducing additional targets, because it predicts that the response to any target is normalized by the overall response to all targets. Consistent with this proposition, Churchland et al. (2008) and Basso and Wurtz (1997)
have shown that increasing the number of choice targets lowers the level of neuronal activity before the onset of the stimulus to be discriminated. It would also be interesting to investigate the effects of asymmetrically biasing the salience of choice targets.
Although these initial interactions between experiments and models have begun to clarify the possible neural computations that underlie decision making, these early experimental and theoretical considerations of time-varying dynamics are just early steps in understanding how the brain integrates sensory evidence in more complex, realistic instances. Mastering this model system will hopefully pave the way for studying more complex decision processes that involve reward, learning, “top-down” cognitive controls, and other factors known to play a role in real behavior. The successes to date bolster the notion that theory and experiments can be fruitfully intertwined, even when studying higher brain function.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors would like to thank Miriam Meister (Huk Lab), Michael Shadlen and Xiao-Jing Wang for helpful comments on an earlier version of the manuscript. The authors especially thank Xiao-Jing Wang for sharing and discussing ideas reviewed in this paper. KFW is supported by PHS grants MH 58480 and 62196. ACH is supported by NIH REI R01-EY017366.
Unstable saddle-like steady state: Also called a saddle fixed (equilibrium) point in dynamical systems theory, this meta-stable fixed point locally has one or more dimensions associated with an unstable, repelling dynamics (along an unstable “manifold”). See Figure 2
D for illustration.