Diffusion State Transitions in Single-Particle Trajectories of MET Receptor Tyrosine Kinase Measured in Live Cells

Single-particle tracking enables the analysis of the dynamics of biomolecules in living cells with nanometer spatial and millisecond temporal resolution. This technique reports on the mobility of membrane proteins and is sensitive to the molecular state of a biomolecule and to interactions with other biomolecules. Trajectories describe the mobility of single particles over time and provide information such as the diffusion coefficient and diffusion state. Changes in particle dynamics within single trajectories lead to segmentation, which allows to extract information on transitions of functional states of a biomolecule. Here, mean-squared displacement analysis is developed to classify trajectory segments into immobile, confined diffusing, and freely diffusing states, and to extract the occurrence of transitions between these modes. We applied this analysis to single-particle tracking data of the membrane receptor MET in live cells and analyzed state transitions in single trajectories of the un-activated receptor and the receptor bound to the ligand internalin B. We found that internalin B-bound MET shows an enhancement of transitions from freely and confined diffusing states into the immobile state as compared to un-activated MET. Confined diffusion acts as an intermediate state between immobile and free, as this state is most likely to change the diffusion state in the following segment. This analysis can be readily applied to single-particle tracking data of other membrane receptors and intracellular proteins under various conditions and contribute to the understanding of molecular states and signaling pathways.

Introduction

Cells sense their environment through membrane proteins, and extracellular stimuli are translated into intracellular signaling cascades and a cellular response. This process often begins with ligands that bind to membrane receptors, induce receptor oligomerization, and recruit other proteins such as co-receptors. The formation of receptor oligomers and signaling platforms reduce the receptor mobility and change its diffusion behavior (Stone et al., 2017; Dietz and Heilemann, 2019). Single-particle tracking (SPT) is a method to measure and to reveal subtle changes in the diffusion of membrane receptors in cells and at the molecular level (Manzo and Garcia-Parajo, 2015; Shen et al., 2017). SPT requires low molecular densities, in order to allow single-molecule detection and assignment of these into single-protein trajectories. Such low molecular densities can be achieved by substoichiometric labeling, by the introduction of a photoactivatable fluorophore, or by using transiently binding labels that specifically target the membrane protein (Manley et al., 2008; Giannone et al., 2010). SPT provides information on diffusion coefficients and on the type of motion, i.e. free diffusion, spatially confined movement, and immobile particles (Michalet, 2010). It may also occur that a molecule switches between different diffusion states within a single trajectory; such transitions can be analyzed by comparing the experimental dataset to Monte Carlo simulations (Wieser et al., 2008), using hidden Markov models (Persson et al., 2013; Sungkaworn et al., 2017; Liu et al., 2019), analytic diffusion distribution analysis (Vink et al., 2020), local MSD exponent values (Hubicka and Janczura, 2020), and unsupervised Gibbs sampling (Karslake et al., 2021).

Receptor tyrosine kinases (RTKs) constitute a family of membrane receptors comprising 58 different proteins (Lemmon and Schlessinger, 2010). One subfamily is the MET receptor family containing the hepatocyte growth factor receptor, also known as MET. MET was first discovered as an oncogene in 1984 (Cooper et al., 1984). The role of MET together with its physiological ligand hepatocyte growth factor/scatter factor (HGF/SF) is manifold: It is essential in embryogenesis, is involved in growth, and regulates cell migration (Bladt et al., 1995; Schmidt et al., 1995; Uehara et al., 1995). MET overexpression was found to be of relevance in several cancers and is targeted in cancer therapy (Ichimura et al., 1996; Goyal et al., 2013; Mo and Liu, 2017). Next to its canonical ligand HGF, MET is targeted by the surface protein internalin B (InlB) secreted by the pathogenic bacterium Listeria monocytogenes that causes human listeriosis (Braun et al., 1998). InlB triggers similar cellular responses as HGF/SF and induces bacterial invasion into hepatocytes (Dramsi et al., 1995; Shen et al., 2000; Niemann et al., 2007).

Here, we apply a segmentation analysis to single-molecule trajectories of un-activated and InlB-bound MET and extract the diffusion states and transitions between these diffusion states. To follow activated MET, we used the N-terminal internalin domain of InlB (InlB₃₂₁) that binds to the extracellular domain of MET and induces MET phosphorylation (Banerjee et al., 2004; Niemann et al., 2007; Ferraris et al., 2010; Dietz et al., 2013), and that we used in previous work to measure the diffusion of MET in living HeLa cells with single-particle tracking (Harwardt et al., 2017). We found that MET bound to InlB diffuses slower than resting receptors and that the immobile population increases. This immobilization was assigned to interactions with the actin cytoskeleton as well as to recruitment of MET to endocytosis sites. Using a segmentation approach, we now present an extended analysis of these data by taking into account that single receptors may switch between different diffusive states within single trajectories. For this analysis, single trajectories were divided into segments showing uniform movement. These segments were analyzed separately with regard to their diffusion mode (free, confined, immobile) (Rossier et al., 2012; Harwardt et al., 2017; Orré et al., 2021). In addition, we extracted the transitions between different segments within single trajectories, which report on functional transitions of the MET receptor signaling complex. For MET, we found that upon InlB activation the immobile state becomes more stable and transitions into immobile states occur more often. The confined diffusion state acts as an intermediate state between immobile and free, as this state is most likely to change the diffusion state in the following segment. This straight-forward analysis routine can be transferred to SPT data of other biological targets.

Methods

Data Acquisition

The SPT data used within this study, together with experimental details on data acquisition and sample preparation, were previously published (Harwardt et al., 2017). In brief, the universal point accumulation for imaging in nanoscale topography (uPAINT) method (Giannone et al., 2010) was applied to measure the dynamics of the MET receptor in living HeLa cells. For the resting receptor, an ATTO 647N-labeled, non-activating Fab antibody fragment was used. The ligand-bound state was probed using the InlB₃₂₁ ligand site-specifically labeled with ATTO 647N which was fully functional (Dietz et al., 2013; Dietz et al., 2019). Imaging was performed in total internal reflection fluorescence (TIRF) mode using an N-STORM microscope (Nikon, Japan). For both un-activated MET and InlB-bound MET, 60 cells were analyzed.

Single-Molecule Localization

The MET receptor was targeted with fluorescent labels and its position in a cell membrane determined by analyzing image stacks with the ThunderSTORM plugin (version dev-2016-09-10-b1) (Ovesný et al., 2014) implemented in the image processing program Fiji (Schindelin et al., 2015). Camera settings were adjusted according to the manufacturer’s manual and the base level was estimated by averaging the pixel intensity with the shutter closed. Deviations from ThunderSTORM default settings are the chosen fitting method “maximum likelihood”, activated “multi-emitter fitting analysis” with a “maximum numbers of molecules per fitting region” of 3 and a “limit intensity range” spanning the 2-sigma interval of the photon distribution in log-space, extracted from detected emitters with “multi-emitter fitting analysis” disabled. The localizations were filtered by applying “remove duplicates”.

Single-Particle Tracking

Trajectories of MET receptors were obtained by loading single-molecule localization data provided by ThunderSTORM into the swift tracking software (version 0.4.2) (Endesfelder et al., manuscript in prep). Parameters for swift analysis were determined using the SPTAnalyser software. A detailed description is added to the manual at https://github.com/JohannaRahm/SPTAnalyser. The parameters “diffraction_limit” = 14 nm, “exp_displacement” = 85 nm (Fab)/75 nm (InlB), “p_bleach” = 0.010 (Fab)/0.014 (InlB), and “p_switch” = 0.01 were set globally for all cells. The parameters “exp_noise_rate” and “precision” were calculated individually per cell. swift divides trajectories into segments if the diffusion behavior of the particle changes.

Diffusion State Analysis

The diffusion state analysis was performed with SPTAnalyser. Diffusion coefficients of individual segments were calculated by optimizing the parameters of a linear diffusion model on the basis of the first four time steps of the mean squared displacement using the method of least squares (Eq. 1). Segments with a diffusion coefficient below 0 were discarded.

$MSD\left(\Delta t\right)=4D\Delta t(1)$

Segments with a minimum length of 20 frames (400 ms) were classified into diffusion states as previously reported (Rossier et al., 2012; Harwardt et al., 2017; Orré et al., 2021). First, the segments were separated into immobile and mobile diffusion applying a diffusion coefficient threshold D_min. The threshold is derived from the dynamic localization error (Eq. 2) which was calculated for each cell, with average values of MSD(0) and diffusion coefficient D (Savin and Doyle, 2005; Michalet, 2010). The third quartile was used to determine D_min (Eq. 3), where n is the number of time steps used in the linear model to extract the diffusion coefficient. All segments with a diffusion coefficient below D_min = 0.0028 μm²/s were classified as immobile.

${\sigma }_{dyn}=\sqrt{\frac{\langle MSD\left(0\right)\rangle +\frac{4}{3}\langle D\rangle \cdot dt}{4}}(2)$

$D_{\mathit{min}}=\frac{{\sigma }_{dyn}^2}{4\cdot n\cdot dt}(3)$

Mobile segments were separated by fitting 60% of the MSD plot with Eq. 4, where r_c is the confined diffusion radius and τ is a time constant. Segments with τ smaller than half the time interval used to compute the MSD (120 ms) are classified as confined diffusion, and values higher than that as free diffusion.

$MSD\left(\Delta t\right)=\frac{4}{3}{r}_c^2·\left(1-e^{-\Delta t/\tau }\right)(4)$

Transition Counting

For each single trajectory in which at least two segments were identified, the transition of the diffusion state between the segments was determined. For the three diffusion states of immobile (i), confined (c), and freely diffusing (f) particles, nine different transitions are distinguished: i-i, i-c, i-f, c-i, c-c, c-f, f-i, f-c, f-f. Segments with a length of less than 20 frames, or with a negative diffusion coefficient, were not classified. Transitions between a classified and an unclassified segment were neglected. Unclassified segments that occurred between two classified segments, and that had a length of up to 19 frames, were masked, and the transition between the segment before and after the unclassified segment was considered in the analysis. This means that all segments that were shorter or equal than the mask length of 19 frames were removed from the trajectories, and that transitions between the preceding and the succeeding segment were counted. The mask value was synchronized to the minimum length a segment must exceed to be classified into a diffusion state. Transition counts were normalized per cell and summed to one to compare the occurrences of transition types. Transition counts were normalized per diffusion state so that the counts of transition types proceeding from the same diffusion state summed up to one to compare the occurrences of diffusion states in adjacent segments.

Statistical Analysis

Mean values are listed with respective standard errors of the mean (SEM). Mean values and SEMs were determined for each cell and globally averaged. Nonparametric tests were chosen as populations partly rejected the hypothesis of being normally distributed (tested with the Shapiro-Wilk test for normality, significance level = 0.05). Wilcoxon signed rank tests were used to validate the comparison of distributions within a treatment group (Supplementary Tables S2, S5). Mann-Whitney U tests were used to validate the comparison of distributions from two treatment groups (Supplementary Tables S1, S3, S4, S6). Levels of significance were classified as follows: p > 0.05 no significant difference (n.s.), p < 0.05 significant difference (*), p < 0.01 very significant difference (**), p < 0.001 highly significant difference (***). All tests were performed with SciPy (version 1.6.2) (Virtanen et al., 2020).

Simulations

To evaluate the error rate of the diffusion state classification, simulations of single-particle trajectories were performed. For this purpose, the software ermine (Estimate Reaction-rates by Markov-based Investigation of Nanoscopy Experiments) was used to create simulations of trajectories of freely diffusing particles. The probability distribution was defined by the expectation value of the mean squared displacement $r²$ within a timestep t (Eq. 5). The apparent mean squared displacement $r²$ was calculated based on the apparent diffusion coefficient $D$ and the static error $\epsilon$ (Savin and Doyle, 2005) (Eq. 6). In order to match the simulation close to the experimental data, the following parameters were chosen: for $D$, the average diffusion coefficient of 0.12 ${\text{μm}}^2/\text{s}$ of the mobile population (confined and free) was used, $t$ corresponds to the camera integration time of 0.02 s, $\tau$ to the time lag between two consecutive frames of 0.02 s, and $\epsilon$ to the average localization error of 29 nm.

$p\left(r|\langle r^2\rangle \right)=\frac{2r}{\langle r^2²\rangle }·e^{-\left(\frac{r^2²}{\langle r^2²\rangle }\right)}(5)$

$\langle r^2²\rangle =4D\left(t-\frac{\tau }{3}\right)+4{\mathrm{\epsilon }}^2(6)$

The error rate of the diffusion state classification model was estimated by classifying the simulated trajectories of freely diffusing particles into confined or free by fitting their MSD values with Eq. 4 (see Diffusion State Analysis Section). The false negative rate was calculated as the number of confined classified trajectories divided by the sum of confined and free classified trajectories.

Availability

The analysis procedure introduced in this work can be straight-forward applied to other single-particle tracking data. Localizations can be detected with rapidSTORM (Wolter et al., 2012) or ThunderSTORM (Ovesný et al., 2014) and connected to trajectories with swift. Swift version 0.4.2, used in this manuscript, and all subsequent versions of the swift software, as well as documentation and test data sets, can be obtained on the swift beta-testing repository (http://bit.ly/swifttracking). The home-written software SPTAnalyser in Python (3.7.6) estimates parameters for tracking with swift and executes diffusion state analysis and transition counting. SPTAnalyser has a graphical user interface with adaptable analysis parameters and assists in processing large amounts of data by creating macros for ThunderSTORM and batch files for swift. SPTAnalyser is compatible with PALMTracer (Bordeaux Imaging Center), which is a software for localization and tracking available as a plugin for MetaMorph (Molecular Devices, Sunnyvale, CA, USA). The source code of SPTAnalyser, together with a detailed manual, is available from https://github.com/JohannaRahm/SPTAnalyser. Simulations of trajectories of freely diffusing particles were conducted with ermine version 0.1 (https://github.com/SMLMS/ermine-tutorial).

Results

Extraction of Different Diffusion States Within Single-Molecule Trajectories

We developed a data analysis workflow that extracts transitions between diffusion states from single-particle trajectories (Figure 1A, Supplementary Figure S1). We applied this analysis to single-particle tracking data of MET receptors in live HeLa cells recorded using the uPAINT principle (Giannone et al., 2010). For that purpose, MET receptors were either labeled with a monoclonal Fab fragment, which binds to but does not activate the receptor, or with the bacterial ligand InlB, which binds and activates the receptor (Figure 1B). Both ligands were conjugated to the fluorophore ATTO 647N. The positions of the fluorophore labels were measured in live cells using TIRF microscopy and subsequently linked to trajectories (Figure 1A). Individual trajectories were divided into segments that exhibited uniform motion. Segments were classified as immobile (i), confined (c), and freely diffusing (f) states and transitions between diffusion states within single trajectories were analyzed.

FIGURE 1

FIGURE 1. Analysis pipeline of single-particle tracking data of the MET membrane receptor. (A) Diffraction limited signal of membrane-bound fluorescently labeled receptors is localized with subpixel accuracy (scale bar 1 μm) (left). Localizations are connected over time to trajectories and changes in diffusion behavior within a trajectory give separated segments (schematic scale bar 100 nm) (middle). Segments are classified into the diffusion states immobile (blue), confined (green), and free (orange) (right). Gray segments are below the necessary length to be classified and have no diffusion state label. Transitions between diffusion states are counted. (B) Membrane bound MET receptors are labeled extracellularly with a monoclonal Fab fragment that binds but does not activate and with InlB that binds and activates the receptor. Both ligands carry ATTO 647N as a fluorescent label. The movement of bound labels is detected and analyzed. The segment properties (C) diffusion coefficient, (D) population of diffusion states, (E) segment length, and (F) confinement radius are displayed as violin plots; dashed lines mark the quartiles. For each condition, Fab (blue) and InlB (gray), the average segment values of 60 cells are displayed.

Segments of single trajectories of Fab- and InlB-bound receptors exhibit different properties in terms of their mobility, population of diffusion states, lengths, and confinement radii (Figures 1C–F). Diffusion states (free, confined, immobile) were determined by analyzing the MSD plots of the segments (for details see Methods). The diffusion coefficients of the InlB/MET complexes are significantly smaller compared to Fab/MET for the confined (D_InlB = 0.051 ± 0.003 μm²/s vs D_Fab = 0.094 ± 0.007 μm²/s) and free (D_InlB = 0.084 ± 0.003 μm²/s vs D_Fab = 0.134 ± 0.004 μm²/s) population (Figure 1C). The diffusion coefficients for the immobile populations are smaller than the precision of the method and result from segments below the detection limit of mobility (see Methods). Upon activation with InlB, the population of the freely diffusing particles is reduced and driven towards the immobile state (Figure 1D). Segment lengths are drastically shorter for confined segments compared to the other two diffusion states (Figure 1E). For example, in InlB-treated cells, a segment classified as confined diffusion lasts an average of 0.64 ± 0.02 s compared to 1.19 ± 0.03 s for immobile and 1.00 ± 0.04 s for a free diffusion. InlB-bound receptors generally move in a more confined manner, as confinement radii calculated for the confined and free populations are smaller compared to un-activated MET (Figure 1F). Interestingly, the confinement radii of the free diffusion state are in the order of magnitude of the cell sizes.

To evaluate the accuracy of the classification model, simulated trajectories of freely diffusing particles were classified. An error rate was calculated from freely diffusing particles particles that were classified as confined diffusion (Supplementary Figure S2). This error rate decreased with increasing trajectory length. In addition, trajectories of freely diffusing particles were simulated with number and trajectory length corresponding to the distribution of trajectories in the Fab experiments, resulting in an error rate of 15%. This suggests the possibility that trajectories of freely diffusing particles contribute to the confined population and reduce the average trajectory length, as a misclassification is more likely with shorter trajectories.

The number of transition events observed for all trajectories of a cell is 184 ± 11 within a measurement period of 20 s. Compared to the average number of 1440 ± 90 trajectories per cell, this number appears relatively small, which is because such events rarely occur within the observed time window of a trajectory (1.36 ± 0.06 s). More transition events occur in longer trajectories (Supplementary Figure S1A). However, 70% of the trajectories do not change their diffusion mode and consist of only one segment (Supplementary Figure S1B). The number of transition counts increases by up to 30% by masking unclassified segments, i.e. segments with a length below the threshold of 20 frames. For this, the transitions of adjacent segments with a defined diffusion state around the masked segment are counted. Without masking, the average is 22.2 ± 0.6% of transitions between segments with a defined diffusion state. With masking, this value is increased to 71.6 ± 0.7% (Supplementary Figure S1C). Mostly no significant changes are observed between the relative frequencies of transitions when masking or without masking (Supplementary Figures S1D,E). Only transitions between immobile and free diffusion benefited slightly less from masking than those of the other transition types.

MET Receptor Activation With InlB Changes Diffusion State Transitions Between Segments

Segments of single-molecule trajectories of Fab-bound as well as InlB-bound MET receptors were classified into freely diffusing, confined moving, and immobile particles as described above. Exemplary cells with color-coded segments are shown in Figures 2A,B for resting and activated MET, respectively. In the zoom-ins only trajectories with at least one transition are displayed. In InlB-treated cells, the number of confined and especially immobile segments increases in comparison to Fab-treated cells, while at the same time the occurrence of freely diffusing particles is significantly lower. In addition, an increased confinement of InlB-bound receptors is visible. These observations are in accordance with the increased fractions of immobile and confined receptors (Figure 1D) and the decreased confinement radius of InlB-bound MET trajectories.

FIGURE 2

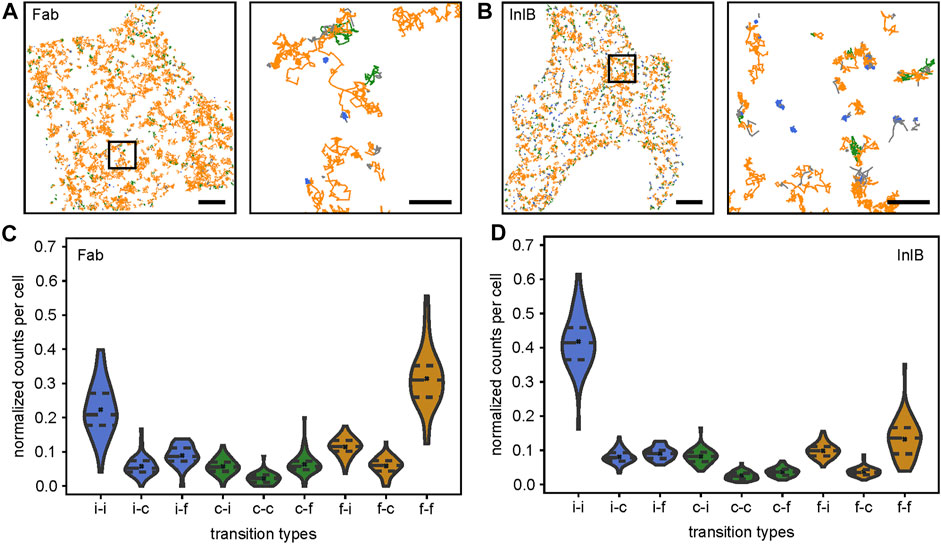
FIGURE 2. Single-molecule trajectories and quantification of transitions within trajectories. Single-molecule trajectories of (A) Fab-bound and (B) InlB-bound MET receptors within exemplary cells. Diffusion states of segments are highlighted in colors (free: orange, confined: green, immobile: blue). Highlighted regions in the overview images are shown as zoom-ins (right). In the zoom-ins only trajectories showing at least one transition are displayed. Scale bars 5 μm, zoom-ins 1 μm. Violin plots of the nine different diffusion state transitions between segments within trajectories in (C) Fab-bound and (D) InlB-bound cells (i = immobile, c = confined, f = free). Counts are normalized to one per cell. For each condition 60 cells were analyzed. Dashed lines mark the quartiles, crosses correspond to the means.

In the next step, we quantified the probability of specific transitions between segments in individual trajectories (Figures 2C,D). From this analysis, we found a probability of 22 ± 1% for Fab-bound receptors and 42 ± 2% for InlB-bound receptors that an immobile particle stays immobile. A similar observation is made for freely diffusing receptors, which mainly stay in this diffusion state (Fab: 31 ± 2%, InlB: 13.2 ± 0.8%). Homogeneous transitions of the confined diffusion state are less probable (Fab: 2.2 ± 0.3%, InlB: 2.6 ± 0.2%). This is interesting, as the confined and immobile states for Fab-bound receptors (immobile: 15.6 ± 0.5%, confined: 17.4 ± 0.4%) are nearly equally populated (Figure 1D), but significantly less homogeneous transitions occur in the confined population. Regarding heterogeneous transitions, transitions from free to immobile (Fab: 11.4 ± 0.4%, InlB: 9.8 ± 0.3%), immobile to free (Fab: 8.9 ± 0.4%, InlB: 9.1 ± 0.3%), and confined to free for Fab-bound MET (6.3 ± 0.4%) and confined to immobile for InlB-bound MET (8.2 ± 0.3%) are most frequent.

Interestingly, when comparing the frequencies of transitions between resting and InlB-bound MET receptors they mostly differ highly significantly (Supplementary Figure S2). Only the transitions from immobile to free and from confined to confined do not change significantly. The transition from immobile to immobile segments, from immobile to confined segments, as well as from confined to immobile segments increases for the activated cells. At the same time, transitions to the freely diffusing state occur less probable out of the InlB-activated state.

To visualize the differences between the different diffusion states, we normalized the transitions with regard to the respective diffusion state (Supplementary Figure S3). For both, Fab-bound and InlB-bound MET receptor trajectories, it clearly shows that the immobile and the free state are relatively stable diffusion states, which we infer from the high probability that an immobile particle stays immobile in the next segment and a freely diffusing molecule remains freely diffusing (Supplementary Figures S3 A,B). The confined state appears to be a more intermediate state: a confined diffusing receptor very likely changes its diffusion state in the next segment, either getting immobilized or switching to free diffusion. When comparing resting and InlB-activated MET mobility most transitions significantly change (Supplementary Figure 3C). Transitions towards the immobile state become more likely and to the freely diffusing state less probable in activated cells. The transitions involving the confined diffusing state change less significantly.

Discussion

We report an analysis method for single-particle tracking data that resolves segments of different diffusional states within single trajectories. The method is sensitive to report segments of free, confined, and immobile states within single trajectories, and transitions between these diffusion states. This allowed us to relate dynamic information on protein mobility to functional states of a protein in a membrane, e.g. the immobilization upon binding of a ligand to a receptor. This additional information from single-particle tracking data complements the available portfolio on analyzing mobility data of single proteins (Rossier et al., 2012; Calebiro et al., 2013; Ibach et al., 2015; Sungkaworn et al., 2017).

As a showcase example, we investigated the diffusion of the MET receptor in living HeLa cells by analyzing available single-particle tracking data of resting and InlB-activated MET (Harwardt et al., 2017). Our analysis reports similar diffusion coefficients for resting and InlB-bound MET. In addition, we were able to segment trajectories and to reveal transitions between diffusion states within single trajectories; this information was so far averaged out by a global MSD analysis of single-particle trajectories. The analysis of segments in single MET receptor trajectories revealed that upon activation, MET transits from a free diffusion state to confined and immobile states and the immobile state becomes more stable, which is in line with the canonical model of receptor tyrosine kinase activation and internalization (Li et al., 2005; Chung et al., 2010). Interestingly, we found that the confined state has a short lifetime which is reflected in the segment lengths as well as the transition probabilities. This diffusion state can be seen as an intermediate state of MET. Upon entry into this state, it is probable that the receptor is soon either immobilized, e.g. prior to endocytosis, or returns to a highly mobile state, e.g. searching for interaction partners.

Our analysis procedure can be applied to single-particle tracking data of other molecules and provides straight-forward access to transitions in the mobility of proteins that can be related to functional states. Future developments may focus on extending the trajectory length and extracting the kinetics of transitions within single trajectories. This could be achieved by either using more stable fluorescent probes such as quantum dots (Hagen et al., 2009; Li et al., 2012; Cognet et al., 2014), or by recording single-molecule data with very low illumination intensity and in combination with image analysis-assisted localization through e.g. denoising algorithms (Kefer et al., 2021). Another exciting extension is dual-color SPT (Wilmes et al., 2015, 2020), which in combination with segmentation analysis may relate changes in diffusion states to molecular interactions such as the formation of transient complexes between two receptors.

Data Availability Statement

The dataset analyzed in this study can be found at the EMBL/EBI BioStudies server; https://www.ebi.ac.uk/biostudies/studies/S-BSST712.

Author Contributions

MH conceptualized the study. JR, MD, and MH conceived the experiments. UE provided software, and JR, UE, and SM developed data analysis protocols. JR performed data analysis. All authors discussed the results, contributed to manuscript revision, read, and approved the final submitted version.

Funding

MH and JR acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - Project number 414985841, GRK 2566.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Marie-Lena Harwardt for providing the single-particle tracking data for the analysis and discussing their analysis, Claudia Catapano for testing the SPTAnalyser software and valuable input, as well as Marc Endesfelder and Bartosz Turkowyd for helpful discussions on the tracking analysis.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2021.757653/full#supplementary-material

References

Banerjee, M., Copp, J., Vuga, D., Marino, M., Chapman, T., van der Geer, P., et al. (2004). GW Domains of the Listeria Monocytogenes Invasion Protein InlB Are Required for Potentiation of Met Activation. Mol. Microbiol. 52, 257–271. doi:10.1111/j.1365-2958.2003.03968.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bladt, F., Riethmacher, D., Isenmann, S., Aguzzi, A., and Birchmeier, C. (1995). Essential Role for the C-Met Receptor in the Migration of Myogenic Precursor Cells into the Limb Bud. Nature 376, 768–771. doi:10.1038/376768a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Braun, L., Ohayon, H., and Cossart, P. (1998). The InlB Protein ofListeria Monocytogenesis Sufficient to Promote Entry into Mammalian Cells. Mol. Microbiol. 27, 1077–1087. doi:10.1046/j.1365-2958.1998.00750.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Calebiro, D., Rieken, F., Wagner, J., Sungkaworn, T., Zabel, U., Borzi, A., et al. (2013). Single-molecule Analysis of Fluorescently Labeled G-Protein-Coupled Receptors Reveals Complexes with Distinct Dynamics and Organization. Proc. Natl. Acad. Sci. 110, 743–748. doi:10.1073/pnas.1205798110

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, I., Akita, R., Vandlen, R., Toomre, D., Schlessinger, J., and Mellman, I. (2010). Spatial Control of EGF Receptor Activation by Reversible Dimerization on Living Cells. Nature 464, 783–787. doi:10.1038/nature08827

PubMed Abstract | CrossRef Full Text | Google Scholar

Cognet, L., Leduc, C., and Lounis, B. (2014). Advances in Live-Cell Single-Particle Tracking and Dynamic Super-resolution Imaging. Curr. Opin. Chem. Biol. 20, 78–85. doi:10.1016/j.cbpa.2014.04.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooper, C. S., Park, M., Blair, D. G., Tainsky, M. A., Huebner, K., Croce, C. M., et al. (1984). Molecular Cloning of a New Transforming Gene from a Chemically Transformed Human Cell Line. Nature 311, 29–33. doi:10.1038/311029a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietz, M. S., Haße, D., Ferraris, D. M., Göhler, A., Niemann, H. H., and Heilemann, M. (2013). Single-molecule Photobleaching Reveals Increased MET Receptor Dimerization upon Ligand Binding in Intact Cells. BMC Biophys. 6, 6. doi:10.1186/2046-1682-6-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietz, M. S., and Heilemann, M. (2019). Optical Super-resolution Microscopy Unravels the Molecular Composition of Functional Protein Complexes. Nanoscale 11, 17981–17991. doi:10.1039/c9nr06364a

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietz, M. S., Wehrheim, S. S., Harwardt, M.-L. I. E., Niemann, H. H., and Heilemann, M. (2019). Competitive Binding Study Revealing the Influence of Fluorophore Labels on Biomolecular Interactions. Nano Lett. 19, 8245–8249. doi:10.1021/acs.nanolett.9b03736

PubMed Abstract | CrossRef Full Text | Google Scholar

Dramsi, S., Biswas, I., Maguin, E., Braun, L., Mastroeni, P., and Cossart, P. (1995). Entry of Listeria Monocytogenes into Hepatocytes Requires Expression of InIB, a Surface Protein of the Internalin Multigene Family. Mol. Microbiol. 16, 251–261. doi:10.1111/j.1365-2958.1995.tb02297.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferraris, D. M., Gherardi, E., Di, Y., Heinz, D. W., and Niemann, H. H. (2010). Ligand-mediated Dimerization of the Met Receptor Tyrosine Kinase by the Bacterial Invasion Protein InlB. J. Mol. Biol. 395, 522–532. doi:10.1016/j.jmb.2009.10.074

PubMed Abstract | CrossRef Full Text | Google Scholar

Giannone, G., Hosy, E., Levet, F., Constals, A., Schulze, K., Sobolevsky, A. I., et al. (2010). Dynamic Superresolution Imaging of Endogenous Proteins on Living Cells at Ultra-high Density. Biophysical J. 99, 1303–1310. doi:10.1016/j.bpj.2010.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Goyal, L., Muzumdar, M. D., and Zhu, A. X. (2013). Targeting the HGF/c-MET Pathway in Hepatocellular Carcinoma. Clin. Cancer Res. 19, 2310–2318. doi:10.1158/1078-0432.ccr-12-2791

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagen, G. M., Lidke, K. A., Rieger, B., Lidke, D. S., Caarls, W., Arndt-Jovin, D. J., et al. (2009). Dynamics of Membrane Receptors: Single-Molecule Tracking of Quantum Dot Liganded Epidermal Growth Factor. Single Molecule Dyn. Life Sci. 117, 117–130. doi:10.1002/9783527626137.ch6

CrossRef Full Text | Google Scholar

Harwardt, M.-L. I. E., Young, P., Bleymüller, W. M., Meyer, T., Karathanasis, C., Niemann, H. H., et al. (2017). Membrane Dynamics of Resting and Internalin B-Bound MET Receptor Tyrosine Kinase Studied by Single-Molecule Tracking. FEBS Open Bio 7, 1422–1440. doi:10.1002/2211-5463.12285

PubMed Abstract | CrossRef Full Text | Google Scholar

Hubicka, K., and Janczura, J. (2020). Time-dependent Classification of Protein Diffusion Types: A Statistical Detection of Mean-Squared-Displacement Exponent Transitions. Phys. Rev. E 101, 022107. doi:10.1103/physreve.101.022107

PubMed Abstract | CrossRef Full Text | Google Scholar

Ibach, J., Radon, Y., Gelléri, M., Sonntag, M. H., Brunsveld, L., Bastiaens, P. I. H., et al. (2015). Single Particle Tracking Reveals that EGFR Signaling Activity Is Amplified in Clathrin-Coated Pits. PLoS One 10, e0143162. doi:10.1371/journal.pone.0143162

PubMed Abstract | CrossRef Full Text | Google Scholar

Ichimura, E., Maeshima, A., Nakajima, T., and Nakamura, T. (1996). Expression Ofc-Met/HGF Receptor in Human Non-small Cell Lung Carcinomasin Vitroandin Vivoand its Prognostic Significance. Jpn. J. Cancer Res. 87, 1063–1069. doi:10.1111/j.1349-7006.1996.tb03111.x

CrossRef Full Text | Google Scholar

Karslake, J. D., Donarski, E. D., Shelby, S. A., Demey, L. M., DiRita, V. J., Veatch, S. L., et al. (2021). SMAUG: Analyzing Single-Molecule Tracks with Nonparametric Bayesian Statistics. Methods 193, 16–26. doi:10.1016/j.ymeth.2020.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Kefer, P., Iqbal, F., Locatelli, M., Lawrimore, J., Zhang, M., Bloom, K., et al. (2021). Performance of Deep Learning Restoration Methods for the Extraction of Particle Dynamics in Noisy Microscopy Image Sequences. Mol. Biol. Cel 32, 903–914. doi:10.1091/mbc.e20-11-0689

CrossRef Full Text | Google Scholar

Lemmon, M. A., and Schlessinger, J. (2010). Cell Signaling by Receptor Tyrosine Kinases. Cell 141, 1117–1134. doi:10.1016/j.cell.2010.06.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Duan, Z.-W., Xie, P., Liu, Y.-R., Wang, W.-C., Dou, S.-X., et al. (2012). Effects of Paclitaxel on EGFR Endocytic Trafficking Revealed Using Quantum Dot Tracking in Single Cells. PLoS One 7, e45465. doi:10.1371/journal.pone.0045465

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, N., Xiang, G.-S., Dokainish, H., Ireton, K., and Elferink, L. A. (2005). The Listeria Protein Internalin B Mimics Hepatocyte Growth Factor-Induced Receptor Trafficking. Traffic 6, 459–473. doi:10.1111/j.1600-0854.2005.00290.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y.-L., Chou, C.-K., Kim, M., Vasisht, R., Kuo, Y.-A., Ang, P., et al. (2019). Assessing Metastatic Potential of Breast Cancer Cells Based on EGFR Dynamics. Sci. Rep. 9, 3395. doi:10.1038/s41598-018-37625-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Manley, S., Gillette, J. M., Patterson, G. H., Shroff, H., Hess, H. F., Betzig, E., et al. (2008). High-density Mapping of Single-Molecule Trajectories with Photoactivated Localization Microscopy. Nat. Methods 5, 155–157. doi:10.1038/nmeth.1176

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzo, C., and Garcia-Parajo, M. F. (2015). A Review of Progress in Single Particle Tracking: from Methods to Biophysical Insights. Rep. Prog. Phys. 78, 124601. doi:10.1088/0034-4885/78/12/124601

PubMed Abstract | CrossRef Full Text | Google Scholar

Michalet, X. (2010). Mean Square Displacement Analysis of Single-Particle Trajectories with Localization Error: Brownian Motion in an Isotropic Medium. Phys. Rev. E 82, 041914. doi:10.1103/physreve.82.041914

PubMed Abstract | CrossRef Full Text | Google Scholar

Mo, H.-N., and Liu, P. (2017). Targeting MET in Cancer Therapy. Chronic Dis. Translational Med. 3, 148–153. doi:10.1016/j.cdtm.2017.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemann, H. H., Jäger, V., Butler, P. J. G., van den Heuvel, J., Schmidt, S., Ferraris, D., et al. (2007). Structure of the Human Receptor Tyrosine Kinase Met in Complex with the Listeria Invasion Protein InlB. Cell 130, 235–246. doi:10.1016/j.cell.2007.05.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Orré, T., Joly, A., Karatas, Z., Kastberger, B., Cabriel, C., Böttcher, R. T., et al. (2021). Molecular Motion and Tridimensional Nanoscale Localization of Kindlin Control Integrin Activation in Focal Adhesions. Nat. Commun. 12, 3104. doi:10.1038/s41467-021-23372-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Ovesný, M., Křížek, P., Borkovec, J., Švindrych, Z., and Hagen, G. M. (2014). ThunderSTORM: a Comprehensive ImageJ Plug-In for PALM and STORM Data Analysis and Super-resolution Imaging. Bioinformatics 30, 2389–2390. doi:10.1093/bioinformatics/btu202

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, F., Lindén, M., Unoson, C., and Elf, J. (2013). Extracting Intracellular Diffusive States and Transition Rates from Single-Molecule Tracking Data. Nat. Methods 10, 265–269. doi:10.1038/nmeth.2367

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossier, O., Octeau, V., Sibarita, J.-B., Leduc, C., Tessier, B., Nair, D., et al. (2012). Integrins β1 and β3 Exhibit Distinct Dynamic Nanoscale Organizations inside Focal Adhesions. Nat. Cel Biol. 14, 1057–1067. doi:10.1038/ncb2588

CrossRef Full Text | Google Scholar

Savin, T., and Doyle, P. S. (2005). Static and Dynamic Errors in Particle Tracking Microrheology. Biophysical J. 88, 623–638. doi:10.1529/biophysj.104.042457

PubMed Abstract | CrossRef Full Text | Google Scholar

Schindelin, J., Rueden, C. T., Hiner, M. C., and Eliceiri, K. W. (2015). The ImageJ Ecosystem: An Open Platform for Biomedical Image Analysis. Mol. Reprod. Dev. 82, 518–529. doi:10.1002/mrd.22489

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, C., Bladt, F., Goedecke, S., Brinkmann, V., Zschiesche, W., Sharpe, M., et al. (1995). Scatter Factor/hepatocyte Growth Factor Is Essential for Liver Development. Nature 373, 699–702. doi:10.1038/373699a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, H., Tauzin, L. J., Baiyasi, R., Wang, W., Moringo, N., Shuang, B., et al. (2017). Single Particle Tracking: From Theory to Biophysical Applications. Chem. Rev. 117, 7331–7376. doi:10.1021/acs.chemrev.6b00815

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Y., Naujokas, M., Park, M., and Ireton, K. (2000). InlB-Dependent Internalization of Listeria Is Mediated by the Met Receptor Tyrosine Kinase. Cell 103, 501–510. doi:10.1016/s0092-8674(00)00141-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Stone, M. B., Shelby, S. A., and Veatch, S. L. (2017). Super-Resolution Microscopy: Shedding Light on the Cellular Plasma Membrane. Chem. Rev. 117, 7457–7477. doi:10.1021/acs.chemrev.6b00716

PubMed Abstract | CrossRef Full Text | Google Scholar

Sungkaworn, T., Jobin, M.-L., Burnecki, K., Weron, A., Lohse, M. J., and Calebiro, D. (2017). Single-molecule Imaging Reveals Receptor-G Protein Interactions at Cell Surface Hot Spots. Nature 550, 543–547. doi:10.1038/nature24264

PubMed Abstract | CrossRef Full Text | Google Scholar

Uehara, Y., Minowa, O., Mori, C., Shiota, K., Kuno, J., Noda, T., et al. (1995). Placental Defect and Embryonic Lethality in Mice Lacking Hepatocyte Growth Factor/scatter Factor. Nature 373, 702–705. doi:10.1038/373702a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Vink, J. N. A., Brouns, S. J. J., and Hohlbein, J. (2020). Extracting Transition Rates in Particle Tracking Using Analytical Diffusion Distribution Analysis. Biophysical J. 119, 1970–1983. doi:10.1016/j.bpj.2020.09.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., et al. (2020). SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 17, 261–272. doi:10.1038/s41592-019-0686-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wieser, S., Axmann, M., and Schütz, G. J. (2008). Versatile Analysis of Single-Molecule Tracking Data by Comprehensive Testing against Monte Carlo Simulations. Biophysical J. 95, 5988–6001. doi:10.1529/biophysj.108.141655

CrossRef Full Text | Google Scholar

Wilmes, S., Beutel, O., Li, Z., Francois-Newton, V., Richter, C. P., Janning, D., et al. (2015). Receptor Dimerization Dynamics as a Regulatory Valve for Plasticity of Type I Interferon Signaling. J. Cel Biol. 209, 579–593. doi:10.1083/jcb.201412049

CrossRef Full Text | Google Scholar

Wilmes, S., Hafer, M., Vuorio, J., Tucker, J. A., Winkelmann, H., Löchte, S., et al. (2020). Mechanism of Homodimeric Cytokine Receptor Activation and Dysregulation by Oncogenic Mutations. Science 367, 643–652. doi:10.1126/science.aaw3242

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolter, S., Löschberger, A., Holm, T., Aufmkolk, S., Dabauvalle, M.-C., van de Linde, S., et al. (2012). rapidSTORM: Accurate, Fast Open-Source Software for Localization Microscopy. Nat. Methods 9, 1040–1041. doi:10.1038/nmeth.2224

PubMed Abstract | CrossRef Full Text | Google Scholar