RWAFormer: a lightweight road LiDAR point cloud segmentation network based on transformer

Point cloud semantic segmentation technology for road scenes plays an important role in the field of autonomous driving. However, accurate semantic segmentation of large-scale and non-uniformly dense LiDAR road point clouds still faces severe challenges. To this end, this paper proposes a road point cloud semantic segmentation algorithm called RWAFormer. First, a sparse tensor feature encoding module (STFE) is introduced to enhance the network’s ability to extract local features of point clouds. Secondly, a radial window attention module (RWA) is designed to dynamically select the neighborhood window size according to the distance of the point cloud data from the center point, effectively aggregating the information of long-distance sparse point clouds to the adjacent dense areas, significantly improving the segmentation effect of long-distance point clouds. Experimental results show that our method achieves an average intersection over union (mIoU) of 75.3 and 82.0% on the Semantickitti and Nuscenes datasets, and an accuracy (Acc) of 94.5 and 97.4%. These results validate the effectiveness and superiority of RWAFormer in road point cloud semantic segmentation.

1 Introduction

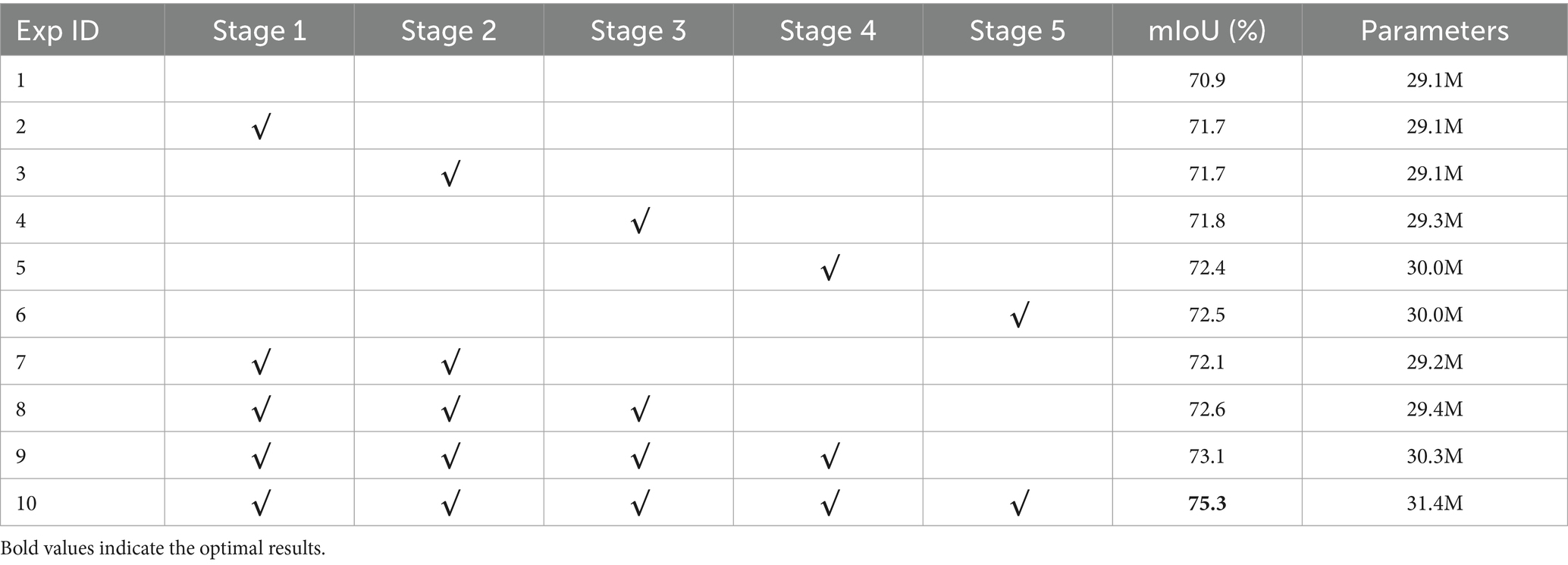
In recent years, the rapid advancement of 3D sensing technology (Song, 2014) has significantly improved the quality of 3D point cloud data. Point cloud data, with its ability to preserve rich spatial information, has led to notable achievements in 3D computer vision tasks, further driving its application in various 3D scenarios, large-scale road point clouds are increasingly utilized in fields such as autonomous driving, intelligent transportation systems, and urban planning. Studies Poulose et al. (2022) demonstrate that 3D LiDAR point cloud maps enable centimeter-accurate vehicle positioning via NDT matching, though this requires precise semantic scene understanding. In road scenes, road point cloud semantic segmentation (Zhang et al., 2020) serves as a foundational task for perceiving and understanding the environment, aiming to assign a specific semantic label to each point in the cloud. For example, in autonomous driving, objects such as pedestrians, vehicles, and traffic lights must be accurately identified and understood to guide subsequent decision-making processes. However, LiDAR-based road point clouds are characterized by their large scale and uneven density, as illustrated in Figure 1, posing significant challenges to achieving both accurate and efficient semantic segmentation.

Figure 1

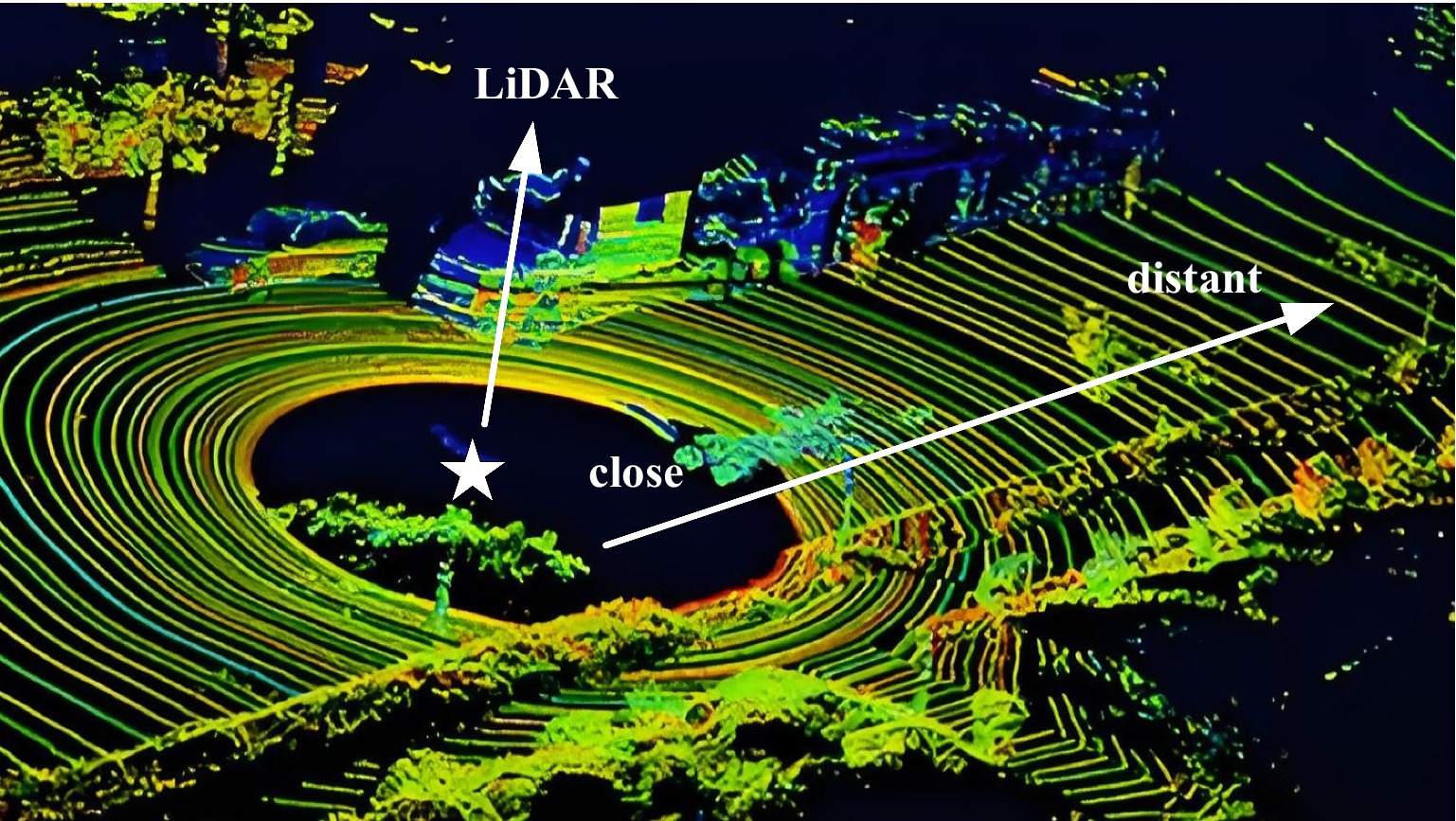
Figure 1. Large-scale and uneven density characteristics of LiDAR-based road point clouds. Image reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0.

In recent years, deep learning techniques have been widely applied to road point cloud segmentation in traffic scenarios. PointNet, proposed by Qi et al. (2017), utilizes a single-branch architecture that deepens the network and generates a score for each point by combining global and local features. This method’s capability to directly process unordered point clouds lays the groundwork for subsequent research. However, its deficiency in lacking local feature interactions leads to limited representation ability of sparse points at long distances. Recent studies (Liu et al., 2019) have shown that PointNet’s global max-pooling operation discards fine-grained spatial relationships, making it unsuitable for complex road scenes where small objects (e.g., traffic signs) require precise localization. Since the introduction of PointNet++ (Qi et al., 2017) and D-PointNet++ (Xu et al., 2024), which employ farthest point sampling (FPS) to aggregate local features in point clouds, incorporating local feature aggregation modules has become a dominant trend for hierarchically extracting local features. FPS ensures a uniform distribution of points by sampling, facilitating the aggregation of local features. However, the computational complexity introduced by the hierarchical structure limits its application in large-scale scenarios. Empirical evidence (Hu et al., 2020) suggests that FPS-based methods suffer from up to 30% performance degradation on distant objects (>50 m) due to excessive point sparsity. DGCNN (Wang et al., 2019) leverages k-nearest neighbors (k-NN) to construct a local neighborhood graph and dynamically updates the graph to expand the receptive field as much as possible, approaching the diameter of the point cloud. In LiDAR road scenes, dynamic changes in traffic elements (such as moving vehicles) lead to frequent changes in the neighborhood graph structure, causing a decrease in the computational efficiency of DGCNN in real-time segmentation tasks. A recent benchmark (Tang et al., 2020) reported that DGCNN’s graph update module consumes over 40% of inference time on nuScenes dataset, highlighting its inefficiency for dynamic environments. PointMLP (Choy et al., 2019) introduces a geometric affine module that enables local point features to be effectively extracted both before and after the aggregation process. However, the inherent uneven density characteristic of road point clouds (such as dense near points and sparse distant points) diminishes the feature representation capability of the geometric affine module, particularly resulting in poor performance in the segmentation of distant small targets (like traffic signs). Comparative experiments (Zhang et al., 2021) reveal that PointMLP’s accuracy drops by 22.5% on SemanticKITTI’s “traffic-sign” class compared to close-range objects, underscoring its density sensitivity.

Beyond these methods, voxel-based approaches like VoxelNet (Zhou and Tuzel, 2018) partition point clouds into 3D grids to enable efficient convolution operations. While they achieve real-time processing, their fixed grid resolution causes quantization errors that misclassify thin structures (e.g., poles). On SemanticKITTI, voxelization artifacts reduce pole segmentation accuracy by 15% (Thomas et al., 2019).

In addition, Transformer-based architectures (Liu et al., 2021) have achieved notable success in visual tasks, the core advantage lies in establishing long-range dependencies through the dot-product self-attention mechanism (Touvron et al., 2021), which enables the dynamic modeling of spatial correlations between any two points in the point cloud. To further capture spatial characteristics in higher-order feature interactions, HorNet introduces a recursive structure called gnConv (Rao et al., 2022). While the networks proposed in the aforementioned research have demonstrated strong performance in point cloud semantic segmentation, they have yet to fully address the inherent challenges of road point cloud data, such as its natural disorder, large volume, and irregular scene distribution.

In the field of point cloud semantic segmentation, early works focused on improving segmentation accuracy and efficiency through innovative network architectures and attention mechanisms. As early as 2020, Varney et al. (2020) constructed the large-scale aerial LiDAR dataset DALES, which laid an important data foundation for subsequent research in this field, though it did not involve specific network architecture innovations. In 2022, Zhao et al. (2022) proposed SVASeg, which captures contextual information through hash table lookup of non-empty neighboring voxels, local region multi-head attention, and sparse voxel-based multi-head attention (SMHA), but it neglects the modeling of fine-grained spatial relationships among local points. Later that year, Cen et al. (2022) put forward the REAL framework to address open-world segmentation, handling unknown categories and incremental learning through redundancy classifiers, while its focus lies in category recognition rather than spatial feature extraction.

In 2023, Wang et al. (2023) designed 3D-ARSS to optimize real-time segmentation on edge devices via spatial and channel attention modules, with sparse tensor implementation for efficient computation, yet it does not involve high-dimensional spatial encoding of each point. Meanwhile, Jhaldiyal and Chaudhary (2023) reviewed projection-based methods, emphasizing their advantages in reducing computational overhead, though such methods generally suffer from the loss of 3D topological information during projection. In 2024, Feng et al. (2024) proposed LSK3DNet, optimizing 3D perception through dynamic sparse kernels and channel selection, but it relies on convolutional operations and does not explicitly model spatial relationships of local points. Around the same time, Wu et al. (2024) presented Point Transformer V3, achieving efficient attention mechanisms via point cloud serialization, yet its serialization strategy may lose local geometric correlations.

In contrast, our method effectively fills the gaps in existing research through a sparse tensor feature extraction module to preserve spatial position information of points, a radial window attention module to explicitly model spatial relationships of local points, and a skip self-attention mechanism to enhance computational efficiency.

This article investigates the LiDAR road point cloud dataset in traffic scenarios and introduces a novel U-Net-based (Ronneberger et al., 2015) architecture to address the semantic segmentation of large-scale LiDAR road point clouds by leveraging the unique characteristics of this data. The main contributions of this work are as follows:

(1) We design a lightweight semantic segmentation algorithm for road point clouds, called RWAFormer, based on Transformer architecture.

(2) We propose a sparse tensor feature extraction module that encodes each point into a high-dimensional vector through sparse tensor encoding while preserving its spatial position. The encoded point cloud is then processed through multiple continuous convolutional layers. Additionally, a radial window attention module is introduced to incorporate spatial perception into the multi-head attention mechanism by modeling the spatial relationships of local neighborhood points. A skip self-attention mechanism is used to reduce Transformer computations and improve the efficiency of the attention mechanism, enabling faster road point cloud segmentation.

(3) We demonstrate the effectiveness of the proposed RWAFormer on the SemanticKITTI and nuScenes datasets, outperforming several state-of-the-art point cloud semantic segmentation methods.

The subsequent sections of this paper are organized as follows: In Chapter 2, we elaborate on the proposed sparse tensor extraction module and the radial window attention module; Chapter 3 verifies the effectiveness of the proposed method through extensive experiments; finally, Chapter 4 summarizes the full text and discusses potential future research directions.

2 Our method

The network is implemented in three stages: (1) The sparse tensor feature extraction module captures key geometric and spatial features from the input point cloud data. (2) The radial window attention module aggregates local features and global contextual information across different levels. (3) We design a codec with a structure similar to U-Net, incorporating skip connections between different levels to facilitate feature fusion.

2.1 Overall network architecture

Road point cloud data contains rich semantic information, represented by numerous three-dimensional coordinate points that detail the road and its surrounding environment. Each data point typically includes multiple dimensions of information, such as point coordinates (x, y, z), normal vectors, and colors. The Transformer network utilizes the self-attention mechanism to achieve global perception, effectively capturing the global relationships between points in the point cloud and enhancing the understanding of the structure and semantic information of the entire point cloud. Additionally, the Transformer network employs positional encoding to process the positional information of points, helping the network better grasp the relative positional relationships of points in space. This positional information aids the Transformer in classifying data points more accurately. Hence, we selected the Transformer network structure for this task.

The overall network architecture of the model is shown in Figure 2. We integrate the vector attention mechanism with the U-Net encoder-decoder framework, which comprises 5 encoders and 5 decoders. The encoder includes a downsampling module, a sparse tensor feature extraction module (STFE), and the radial window attention module (RWA) proposed in this paper to capture features. The decoder includes an upsampling module, STFE, and RWA to map features. The RWA, based on radial window self-attention, effectively extracts feature information from distant points in dense point areas, addresses the issue of sparse distant point disconnection, and expands the effective receptive field.

Figure 2

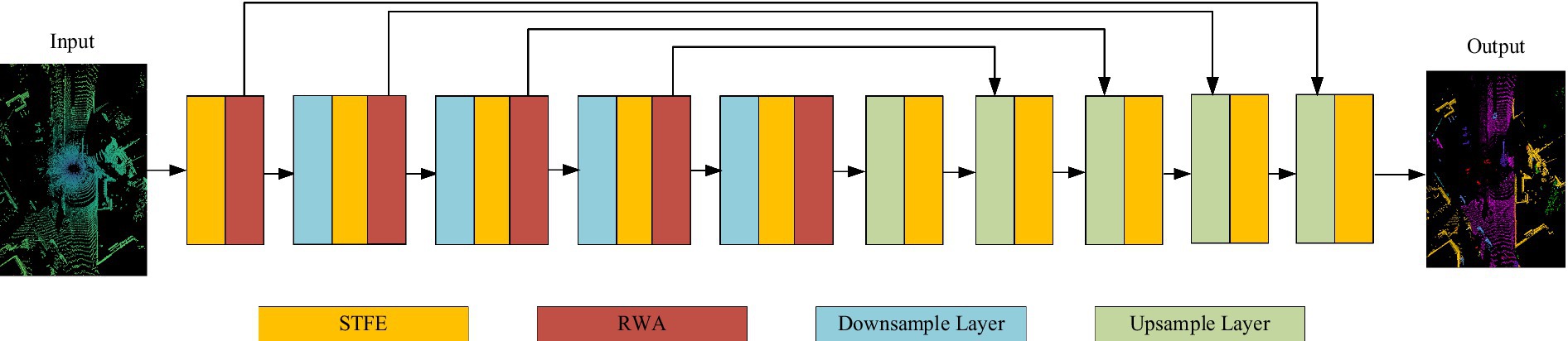
Figure 2. RAWFormer network architecture. Images reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0.

RWAFormer adopts an encoder-decoder structure, connecting fine-grained features from the encoder to the decoder through skip connections. This design allows the network to effectively integrate features at various levels and achieve precise segmentation at the pixel level. The RWA module is stacked at the end of each encoding stage.

2.2 Sparse tensor feature extraction module

Road scenes often contain a large number of scattered points, necessitating efficient processing for road point cloud segmentation to meet practical application requirements. The sparse tensor feature extraction module processes the original point cloud directly through continuous convolution operations, avoiding conversion to a dense voxel grid. This approach preserves the sparsity of the point cloud and reduces computational resource consumption. As illustrated in Figure 3, its network architecture design is shown.

Figure 3

Figure 3. Sparse tensor feature extraction module. The yellow blocks represent Minkowski convolutional layers. NNS, nearest neighbor search; BN, batch normalization; ReLU, activation function. Image reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0

The input point cloud data undergoes sparse tensor encoding, converting each point into a high-dimensional vector while preserving its spatial position information. These encoded point clouds are then processed through 8 consecutive Minkowski convolutional layers, effectively extracting both local and global features while maintaining data sparsity. Activation functions and regularization layers are interspersed between these convolutional layers to enhance the network’s ability to fit nonlinearities and prevent overfitting.

Sparse tensor encoding is the first and central step in the sparse tensor feature extraction module for processing point cloud data. It represents each point as a high-dimensional vector while recording its spatial position information. This encoding method not only preserves the geometric characteristics of point clouds but also provides an appropriate input format for subsequent continuous convolution operations. The specific encoding method is as follows:

The module employs sparse tensors to represent point cloud data, dividing it into two components: the coordinate matrix C and the feature matrix F, as defined in Equation 1.

$C=\left[\begin{array}{cccc}{x}_1& y_1& z_1& b_1\\ ⋮& ⋮\\ x_N& y_N& z_N& b_N\end{array}\right],F=\left[\begin{array}{c}{f}_1^T\\ ⋮\\ f_N^T\end{array}\right]\text{ (1)}$

In this representation, (x_i, y_i, z_i) contains the coordinates of the point cloud, $b_i$ indicates which point cloud belongs to the batch, N represents the total number of points in a batch, and $f_i^T$ represents the feature of the i-th point. This method effectively saves space and boosts computational efficiency.

In the LiDAR point cloud data of this paper, the feature $f_{\mathrm{i}}^T$ represents intensity information, which is used to describe the strength of the LiDAR return signal. Intensity information can reflect the surface properties of the objects corresponding to the point cloud; for example, objects with higher reflectivity (such as metals) usually have higher intensity values, while those with lower reflectivity (like vegetation) typically have lower intensity values. By incorporating intensity information into the feature matrix F, the network can better capture the semantic information of the point cloud, thereby improving segmentation accuracy.

The coordinate matrix C has a shape of N × 4, storing the spatial location (x, y, z) and batch index b of each point; the feature matrix F has a shape of N × 1, storing only the intensity information of each point. This representation method avoids information loss and computational redundancy inherent in traditional voxelization methods.

Another core component of the sparse tensor feature extraction module is the continuous convolutional layer. Unlike traditional convolution, it operates directly on the original point cloud data without relying on any grid structure. The continuous convolutional layers use a differentiable nearest neighbor search algorithm (NNS) to locate points within the local neighborhood of each point, after which the Minkowski convolution operations are applied within these local neighborhoods to generate local feature maps. Minkowski convolution preserves the inherent sparsity of the point cloud data while efficiently capturing local features.

The Sparse Tensor Feature Extraction (STFE) module establishes a feature extraction mechanism that adapts to the unordered and sparse nature of point clouds. This module achieves multi-level feature learning based on stacked Minkowski sparse convolutions, specifically divided into three stages: Shallow Feature Extraction (Layers 1–3) employs asymmetric convolution kernels (3 × 3 × 1), densely sampling neighborhood points in the horizontal direction (x-y plane) to capture local geometric structures such as road surfaces, vehicles, and pedestrians. Meanwhile, it compresses the convolution range in the vertical direction (z-axis) to suppress sparse noise interference; Mid-Level Feature Extraction (Layers 4–6) further extracts global semantic information from the point cloud. By using strided convolutions (stride = 2), it gradually expands the receptive field to capture large-scale objects in road scenes (such as buildings and vegetation) and their spatial distribution; Deep Feature Extraction (Layers 7–8) optimizes feature representation capabilities. Through deep convolution modeling of long-range dependencies, it enhances adaptability to complex scenes (like intersections and dense traffic flows).

This hierarchical feature extraction mechanism effectively retains the local geometric details and global semantic information of point clouds. Additionally, by leveraging the sparse computation characteristics of Minkowski convolutions, it significantly improves computational efficiency and ensures the network’s robustness to the unordered nature of point clouds.

As a result, the STFE module better maintains the spatial structure of point cloud data, which is essential for accurately identifying and segmenting objects with non-uniform distributions, such as roads and vehicles.

2.3 Radial window attention module

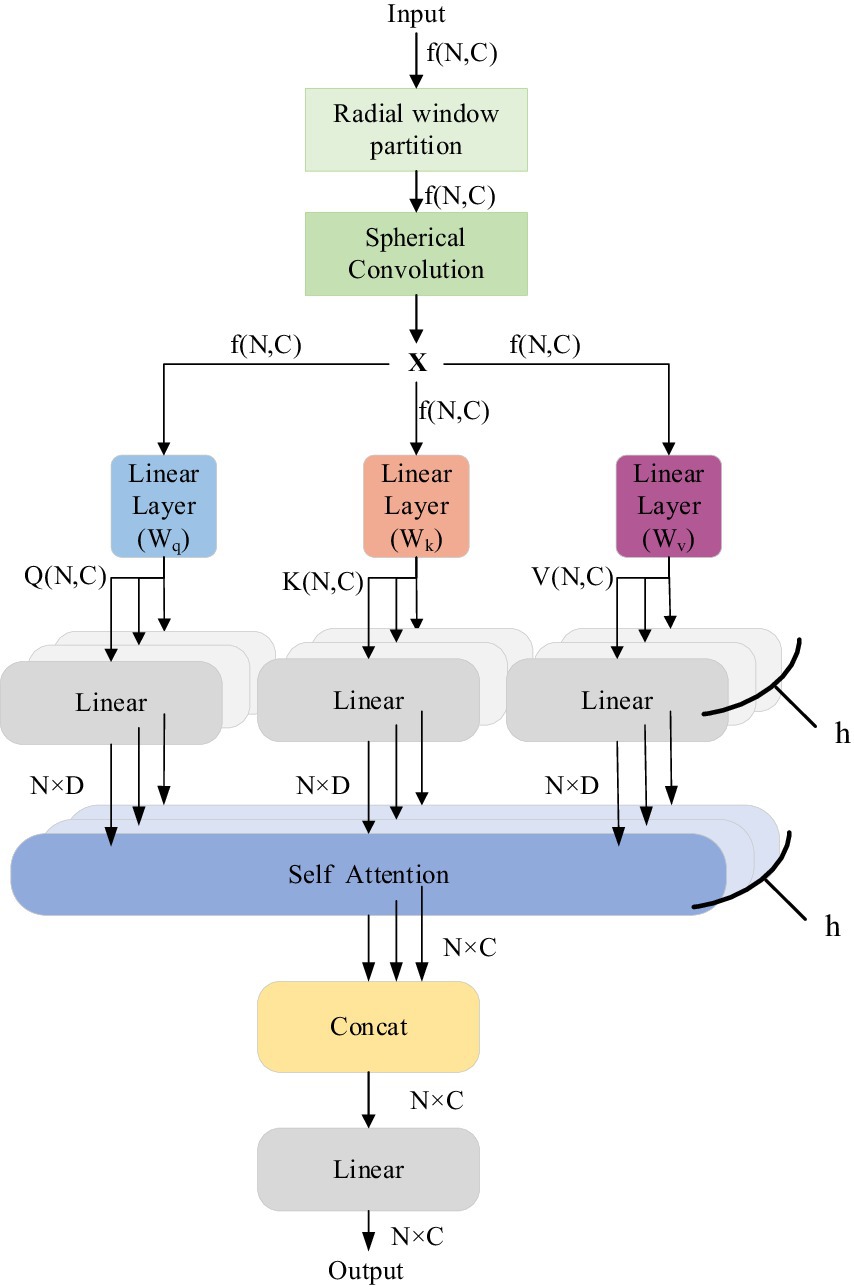
Due to the sparsity of LiDAR point cloud distribution, the lack of neighboring points near sparse distant points causes a disconnection in feature information, which hinders the expansion of the receptive field and results in poor segmentation performance for distant points. The RWA module proposed in this article effectively captures both global and local information in point clouds, aggregating long-distance feature information into a single operator to adapt to the sparse distribution of point clouds. The overall network structure is highly modular, as shown in Figure 4, allowing for flexible integration into existing point cloud processing networks.

Figure 4

Figure 4. Radial window attention module.

The input is an N × C local feature matrix extracted by the sparse tensor feature extraction module. We first dynamically select the local features of the input based on the radius of the center point using a radial window mechanism to determine the size of the local neighborhood. Next, we apply spherical convolution to the input features. By designing a convolution kernel that adapts to the spherical surface, spherical convolution can more accurately extract the local geometric features of the point cloud while preserving the spatial information. This method is particularly suited for processing point cloud data with irregular distribution characteristics. After spherical convolution, RWA employs a multi-head attention mechanism, allowing the model to learn information from multiple different feature subspaces simultaneously, which helps capture complex dependencies between various features. Following a series of spherical convolutions and multi-head attention processing, RWA integrates the extracted features.

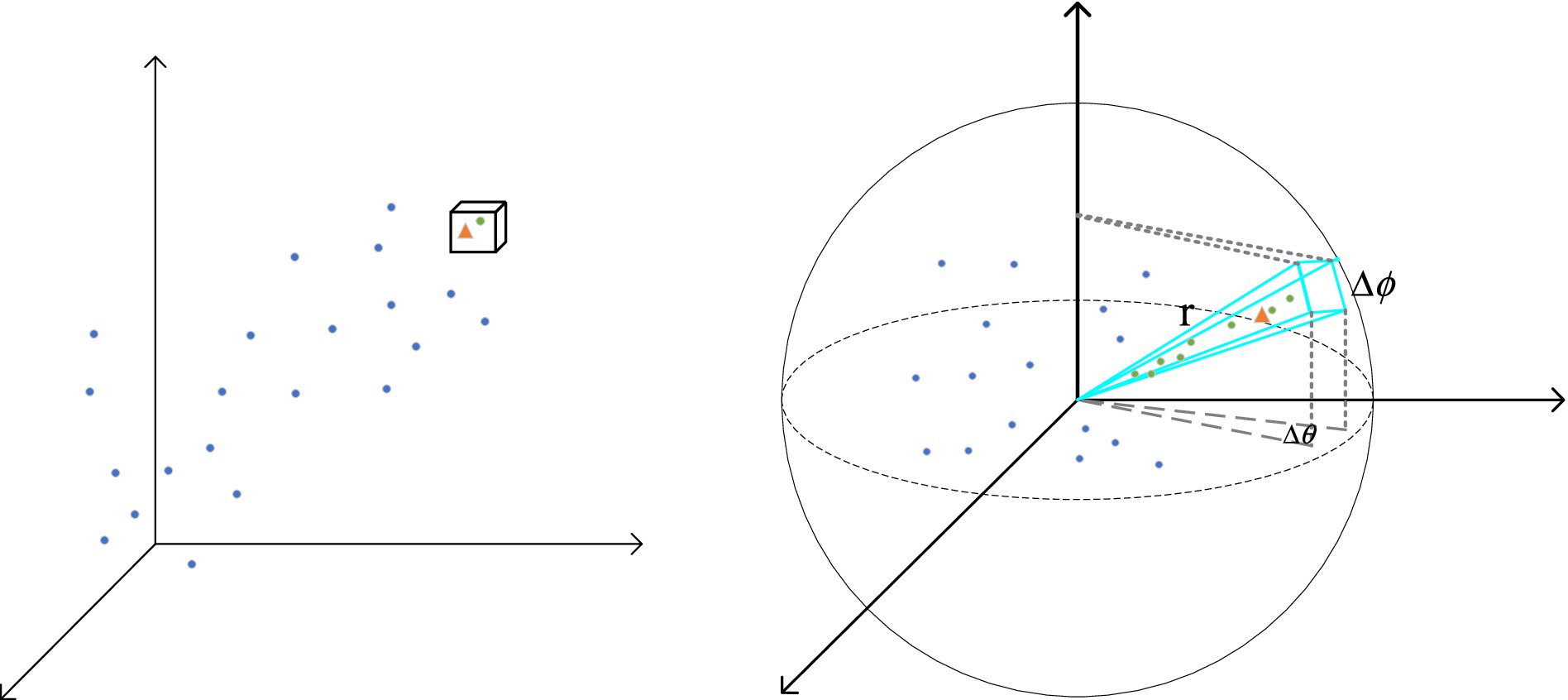
The radial window partitioning mechanism enhances the efficiency and accuracy of feature extraction by dynamically adjusting the neighborhood range to adapt to the sparse distribution characteristics of point clouds. The core idea of this mechanism is to dynamically adjust the neighborhood range based on the radius distance between points and a center point. For each center point p_i, its neighborhood range Neighborhood (p_i) is determined by the radius r_i. This relationship is formulated in Equation 2:

$\begin{array}{ll}\text{Neighborhood}\left(p_i\right)=\{p_j\mid \parallel p_j-p_i\parallel \le r_i\}& (2)\end{array}$

Here, $p_i$ represents the center point, $p_j$ represents a neighboring point, $p_j-p_i$ denotes the Euclidean distance between point $p_j$ and the center point $p_i$ , and $r_i$ is the radius dynamically adjusted based on the sparsity of the point cloud.

To dynamically adjust the radius $r_i$ , this paper proposes calculating it based on the local density characteristics of the point cloud. The local density ${\rho }_i$ around a center point $p_i$ represents the number of points within a unit volume surrounding. The radius $r_i$ is dynamically adjusted using the following Equation 3:

$\begin{array}{ll}{r}_i=r_{\text{base}}\cdot \frac{{\rho }_{\mathrm{ref}}}{{\rho }_i}& (3)\end{array}$

Where $r_{\text{base}}$ is the base radius, used to control the minimum value of the neighborhood range; ${\rho }_{\mathrm{ref}}$ is the reference density, used to normalize the impact of local density; and ${\rho }_i$ is the local density around the center point $p_i$ . The local density ${\rho }_i$ is calculated using Equation 4:

$\begin{array}{ll}{\rho }_i=\frac{\mid \{p_j\mid \parallel p_j-p_i\parallel \le r_{\text{init}}\}\mid }{\frac{4}{3}\pi r_{\text{init}}^3}& (4)\end{array}$

Here, $r_{\text{init}}$ is the initial radius used for calculating the local density; $\mid \{p_j\mid \parallel p_j-p_i\parallel \le r_{\text{init}}\}\mid$ represents the number of points within the initial radius $r_{\text{init}}$ ; and $\frac{4}{3}\pi r_{\text{init}}^3$ is the volume of the sphere corresponding to the initial radius $r_{\text{init}}$ . Based on the aforementioned formula, the neighborhood range $\text{Neighborhood}\left(p_i\right)$ is dynamically adjusted according to the changes in the local density ${\rho }_i$ .

Unlike the cubic window partition mechanism, a radial window mechanism determines the size of the local neighborhood based on the radius from the center point. Figure 5 compares the cube window mechanism with the radial window mechanism. The cube window is shown in (Figure 5a), while the radial window is presented in (Figure 5b). This radial window partitioning mechanism forms the core of RWA. By utilizing this approach, RWA effectively handles point cloud data with uneven density, enhancing both the adaptability and robustness of feature extraction.

Figure 5

Figure 5. Comparison between cube window and radial window.

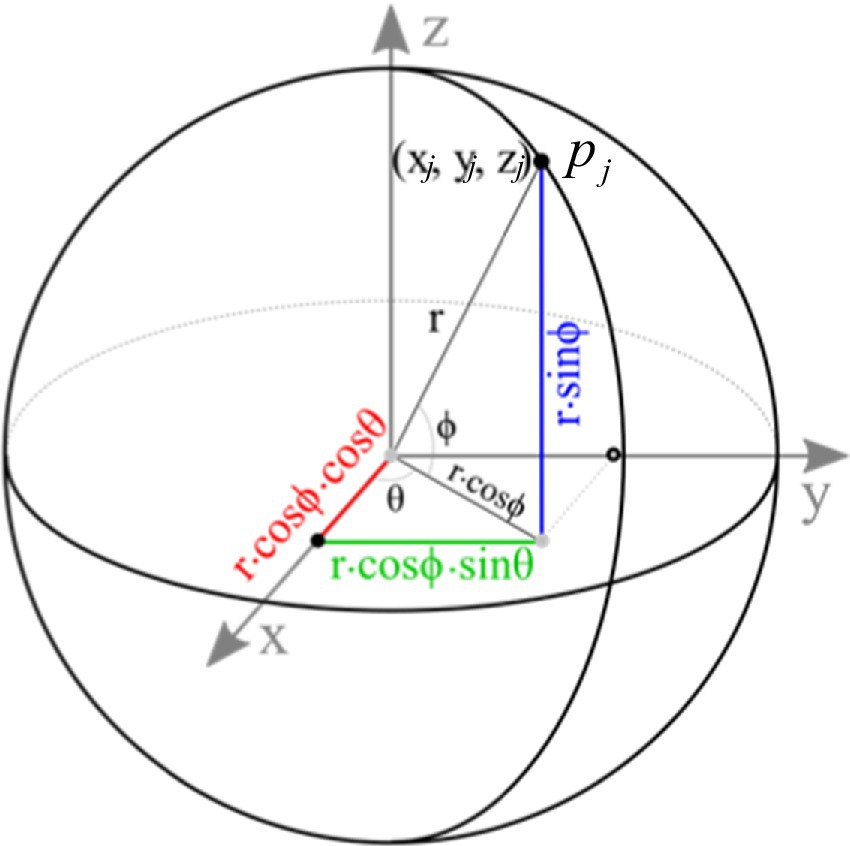
The core idea of spherical convolution is to map the local neighborhood of point clouds to a spherical coordinate system and design convolution kernels in this coordinate system to extract geometric features. For each central point $p_i$ , its neighboring points $p_j$ are mapped to the spherical coordinate system. Figure 6 illustrates the construction process of the spherical coordinate system, where the central point $p_i$ serves as the origin O $(x,y,z)$ . The spherical coordinates are represented by radius $r$ , polar angle $\theta$ , and azimuthal angle $\varphi$ , with the formulas given by Equations 5–7:

$\begin{array}{ll}r=\parallel p_j-p_i\parallel & (5)\end{array}$

$\begin{array}{ll}\theta =arccos\left(\frac{z_j-z_i}{r}\right)& (6)\end{array}$

$\begin{array}{ll}\varphi =arctan\left(\frac{y_j-y_i}{x_j-x_i}\right)& (7)\end{array}$

where $(x_i,y_i,z_i)$ and $(x_j,y_j,z_j)$ are the Cartesian coordinates of the central point $p_i$ and neighboring point $p_j$ respectively.

Figure 6

Figure 6. The construction process of the spherical coordinate system.

In the spherical coordinate system, the convolution kernel $K(r,\theta ,\varphi )$ is designed as a function adapted to the spherical geometric structure. The kernel weights $W(r,\theta ,\varphi )$ are generated by a neural network, which takes the spherical coordinates $(r,\theta ,\varphi )$ as input and outputs the kernel weights $W(r,\theta ,\varphi )$ . The weights for the convolution kernel are generated by a multilayer perceptron (MLP), as described by Equation 8:

$\begin{array}{ll}W(r,\theta ,\varphi )=\mathit{MLP}(r,\theta ,\varphi )& (8)\end{array}$

In the spherical coordinate system, the convolution operation is performed to extract local geometric features from the point cloud. The specific convolution operation is formulated in Equation 9:

$\begin{array}{ll}{F}_{\text{out}}\left(p_i\right)=\sum _{p_j\in \text{Neighborhood}\left(p_i\right)}W(r,\theta ,\varphi )\cdot F_{\text{in}}\left(p_j\right)& (9)\end{array}$

RWA also incorporates the multi-head attention mechanism, a core component of the Transformer model, to capture both global and local features. The multi-head attention mechanism efficiently processes sequential data and captures long-range dependencies by splitting the input sequence into multiple “heads.” Each head learns different representations of the input, and these representations are merged to capture diverse aspects of the data. In complex road point cloud segmentation scenarios, this mechanism significantly enhances model performance by extracting multi-scale features and improving the ability to detect features of various scales and positions.

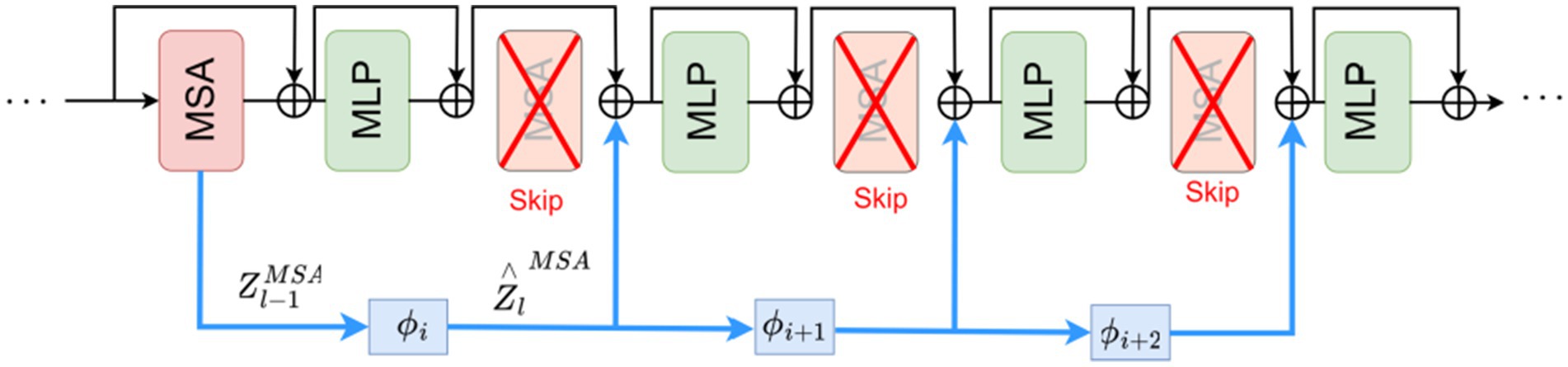
Each layer of the Transformer consists of a Multi-head Self-Attention (MSA) module and a Multi-Layer Perceptron (MLP) module. The conventional MSA module in Transformers suffers from high computational complexity, making it difficult to adapt to large-scale point cloud data. Research findings reveal high correlations between the output representations Z^MSA across different layers. Building upon this discovery, we propose an approach that reuses Z^MSA from previous layers as input to a SKIPAT parametric function, skips the MSA operations in one or more subsequent Transformer layers, and then feeds the features output by the SKIPAT parametric function into the MLP module, as illustrated in Figure 7.

Figure 7

Figure 7. Transformer network framework with SKIPAT.

The output feature representation at layer $l$ can be computed as Equation 10:

$\begin{array}{l}{Z}_l\leftarrow \Phi \left(Z_{l-1}^{\mathrm{MSA}}\right)+Z_{l-1}\\ Z_l\leftarrow \mathrm{MLP}\left(Z_l\right)+Z_l\end{array}\text{ (10)}$

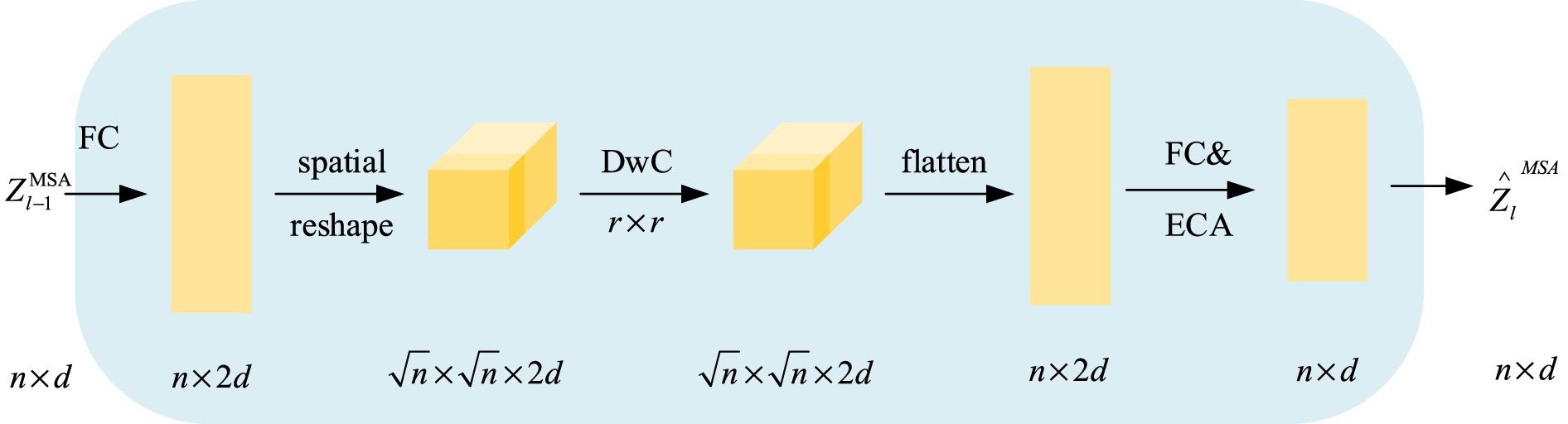
To ensure that cross-layer reuse of self-attention blocks maintains performance, we introduce a simple parameter function, SKIPAT, which not only accelerates the process but also enhances performance. Figure 8 shows the specific implementation of the SKIPAT parameter function. SKIPAT consists of two linear layers (Fully Connected, FC) and a Depthwise Convolution (DwC) (Chollet, 2017). We first feed the point cloud block embedding vectors into the initial linear layer, FC, to expand the channel dimension: $R^{n\times d}\to R^{n\times 2d}$ . Then, DwC extracts relational features between point cloud elements using a $\gamma \times \gamma$ convolution kernel: $R^{\sqrt{n}\times \sqrt{n}\times 2d}\to R^{\sqrt{n}\times \sqrt{n}\times 2d}$ . Before applying the depthwise convolution, we reshape the matrix into a feature tensor. Afterward, we reshape the output of DwC back into a matrix and pass it through the final fully connected layer, FC: $R^{n\times 2d}\to R^{n\times d}$ , reducing the channel dimension back to the initial dimension $d$ . Finally,we apply an Efficient Channel Attention (ECA) module after FC to strengthen cross-channel dependencies, producing the output ${\widehat{Z}}_l^{\mathrm{MSA}}$ . The corresponding computation is expressed in Equation 11:

$\begin{array}{ll}{\widehat{Z}}_l^{\mathrm{MSA}}:\mathrm{ECA}\left({\mathrm{FC}}_2\right(\mathrm{DwC}\left({\mathrm{FC}}_1\right(Z_{l-1}^{\mathrm{MSA}}\left)\right)\left)\right)& (11)\end{array}$

Figure 8

Figure 8. SKIPAT parameter function computation flow.

Therefore, to reduce the computational burden on the Transformer’s core computational component within the RWA module, we propose utilizing a skip self-attention mechanism. This mechanism improves the Transformer’s computational efficiency by reducing redundant operations in attention calculation. Specifically, it enables the model to “jump” between layers, allowing lower layers to directly interact with higher layers without passing information through each intermediate layer.

The radial window attention module designed in this study opens new possibilities for point cloud processing. By enhancing processing efficiency and strengthening the model’s ability to analyze and interpret complex point cloud data through precise feature extraction and dependency capture, RWA has the potential for broad application across fields such as autonomous driving, robotic perception, and virtual reality.

3 Experimental results and analysis

3.1 Dataset description

To evaluate the effectiveness of the proposed RWAFormer method, we conducted experiments using two publicly available large-scale LiDAR point cloud datasets: SemanticKITTI (Behley et al., 2019) and NuScenes (Caesar et al., 2020) both datasets were collected in real road environments, providing highly realistic and authentic point cloud data. These characteristics make them ideal for research in fields like autonomous driving and robotics.

3.1.1 SemanticKITTI

This dataset extends the KITTI Vision Benchmark Suite (Geiger et al., 2012) by providing semantic annotations that assign a category label to each point, such as buildings, vehicles, and pedestrians. These labels offer rich semantic information, making the dataset ideal for tasks like semantic segmentation and object detection. Figure 9 illustrates the SemanticKITTI dataset, showing how point cloud distribution becomes sparser as the distance from the LiDAR sensor increases, with points further away appearing more dispersed than those closer to the sensor.

Figure 9

Figure 9. Visualization example of the SemanticKITTI dataset. Images reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0.

Semantickitti contains a large amount of point cloud sequence data, the total includes point cloud sequences 00-21, each sequence corresponds to a scene or a section of the road video recordings, a total of more than 45,000 point cloud frames, a total of 22 categories, of which there are 19 categories that can be frequently seen in the driving scene, this study for the semantic segmentation of these 19 categories, and the sequence 08 as an independent test set.

3.1.2 NuScenes

The NuScenes dataset consists of 1,000 driving scenes from Boston and Singapore, where each LiDAR point in the keyframes is annotated with one of 32 semantic labels. For the LiDAR point cloud semantic segmentation tasks, it focuses on 16 primary semantic classes. This dataset contains 1.4 billion annotated points, covering 40,000 point clouds across 1,000 scenes, with 850 scenes designated for training and validation, and 150 for testing. The scenes are scanned by a 32-line LiDAR, resulting in a sparser point cloud compared to the Semantichitti dataset. Figure 10 highlights this, where densely-packed nearby cars are encircled in green, while sparsely-distributed distant bicycles are marked in red.

Figure 10

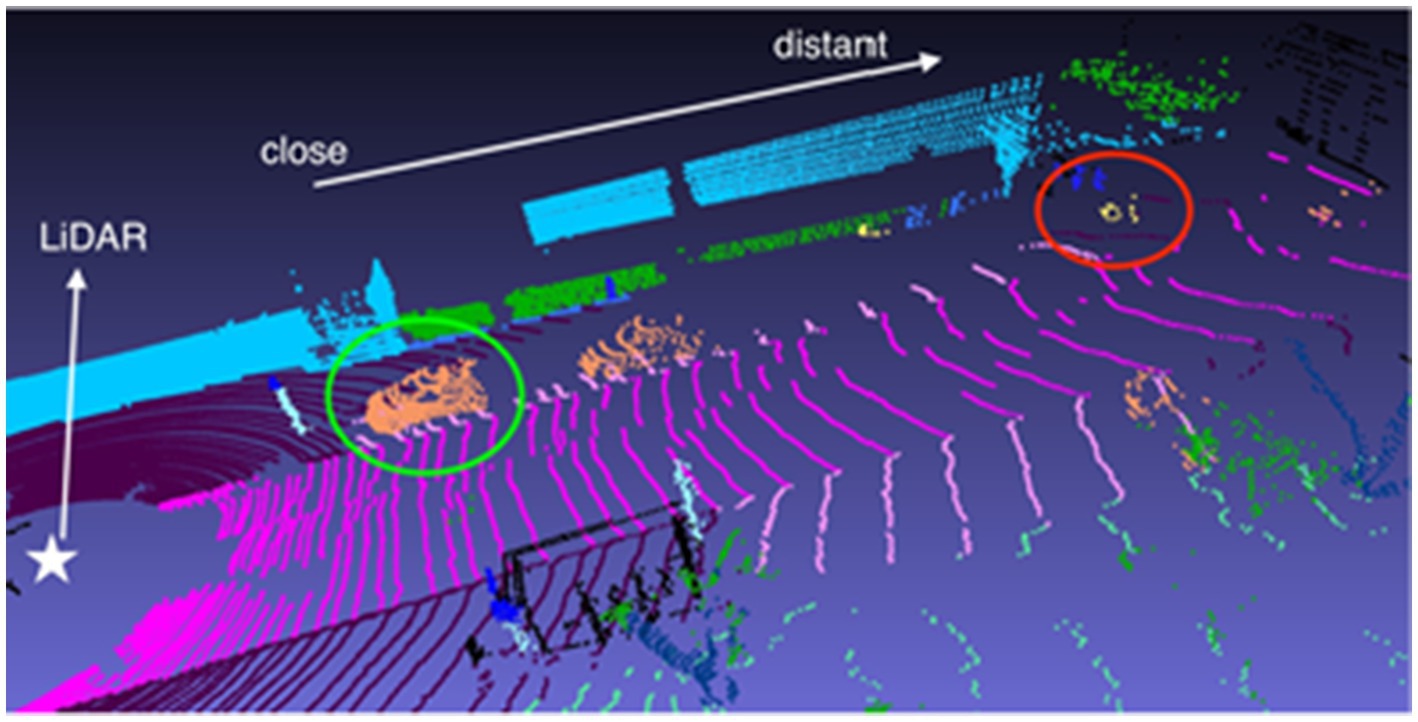
Figure 10. Visualization of the NuScenes dataset. Image reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0.

3.2 Evaluation metrics

In the experiment, we selected Acc and mIoU as evaluation metrics to assess the model’s performance. Acc measures the proportion of correctly segmented points in the point cloud relative to all points, while IoU represents the intersection-over-union ratio between the true labels and predicted labels of points in a specific category. mIoU calculates the average IoU across all categories in multi-class scenarios. These metrics are crucial for evaluating the accuracy of 3D point cloud segmentation. The formulas for overall accuracy (Acc) and mean Intersection over Union (mIoU) are given by Equations 12, 13 respectively:

$\begin{array}{ll}\mathrm{Acc}=\frac{T}{N}& (12)\end{array}$

$\begin{array}{ll}\text{mIoU}=\frac{1}{c}\sum _{i=0}^c\frac{C_{\mathit{ii}}}{\sum _{j=0}^c{C}_{\mathit{ji}}+\sum _{j=0}^c{C}_{\mathit{ij}}-C_{\mathit{ii}}}& (13)\end{array}$

In practical applications of road point cloud segmentation, besides accurately identifying pedestrians, vehicles, and traffic lights, the network must also operate efficiently within hardware constraints. The number of parameters and floating point operations (FLOPs) are core metrics for evaluating the computational complexity of a model. FLOPs represent the total number of floating-point operations required for a single forward pass, which in point cloud networks primarily includes convolution/attention operations for feature extraction, neighborhood search, and coordinate transformation. The number of parameters refers to the total count of learnable weights and biases in a deep learning model. It directly impacts the model’s storage size and initialization time. Generally, models with more parameters have greater capacity, but they also demand higher computational and storage resources. This metric reflects the model’s complexity, computational cost, and potential generalization capability.

3.3 Experimental setting

This article validates the effectiveness of RWAFormer through semantic segmentation results of 3D road scene point clouds on the Semantichitti and Nuscenes datasets. We built the entire code project using PyTorch and conducted training and testing on an RTX 3090 graphics card. We trained the model for 50 epochs using the AdamW optimizer (Loshchilov and Hutter, 2017) and the “poly” scheduler. We set the learning rate to 0.006 and the weight decay to 0.01, with a batch size of 2. All algorithms used consistent patch sizes for the same tasks. To better extract semantic information from road point clouds, we set the patch sizes for Semantichitti tasks to [0.05, 0.05, 0.05], and for Nuscenes tasks to [0.1, 0.1, 0.1]. For the proposed RWAFormer method, we set the window size to [120 m, 2°, 2°] (r, θ, ϕ), while for other comparative experiments, the window size was set to 50 m (cube edge length). During data preprocessing, we limited the input scenario of Semantichitti to [−51.2 m, −51.2 m, −4 m] to [51.2 m, 51.2 m, 2.4 m]. The voxel size for Semantichitti tasks was set to 0.1 m, and for Nuscenes tasks, it was set to 0.05 m.

3.4 Experimental results

3.4.1 Experiments on the SemanticKITTI task

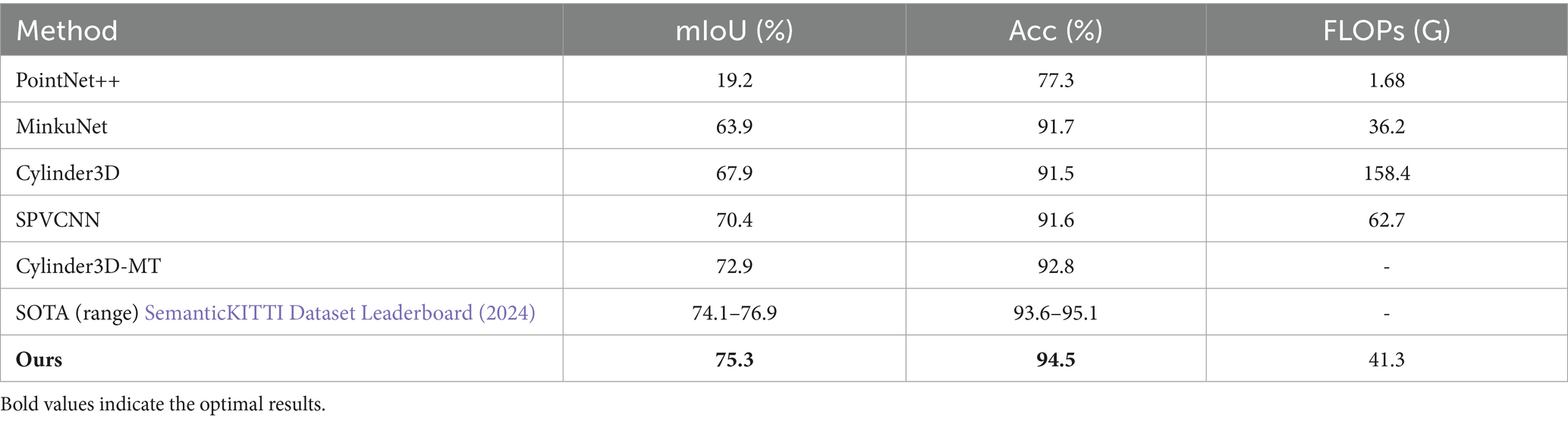
To evaluate the segmentation performance of RWAFormer on the Semantichitti dataset, we present the overall experimental results and IoU results for each category compared with different algorithms in Tables 1, 2. Table 1 shows that using point cloud data directly as input and performing layer-by-layer sampling and grouping operations, as in the PointNet++ method, results in an mIoU of only 19.2%. The MinkowskiNet (Jia and Leibe, 2021) method, which applies dynamic graph convolution to process point cloud data with multi-scale convolution operations, increases the mIoU to 63.9%. The Cylinder3D (Zhu et al., 2021) method, which maps point cloud data into cylindrical space and processes it using 3D convolutional neural networks (CNNs), further improves mIoU to 67.9%, demonstrating good robustness for large-scale scenes. SPVCNN (Tang et al., 2020), which employs spherical pyramid pooling to aggregate local features and combines multi-level convolution operations for global feature extraction, achieves an mIoU of 70.4% and effectively handles complex point cloud shapes.

Table 1

Table 1. Experimental results on the SemanticKITTI task.

Table 2

Table 2. IoU (%) results for each category on the Semantickitti dataset.

To ensure our comparison encompasses the most recent advancements, we benchmark our results against the official SemanticKITTI leaderboard (access date: May 2024). The top-performing published method on the leaderboard is Cylinder3D-MT (Zhu et al., 2021), which achieves 72.9% mIoU. Furthermore, the leading methods (including unpublished entries) have pushed the performance boundary to between 74.1 and 76.9% mIoU, primarily through model ensembles and extensive test-time augmentations.

In this competitive context, the RWAFormer method proposed in this article achieves a notably high mIoU of 75.3%. It is important to emphasize that while the top leaderboard entries (76.9% mIoU) employ computationally expensive strategies unsuitable for real-time applications, our method establishes this competitive result as a single model without any ensemble or complex test-time tricks. Compared to the strongest published single-model method (Cylinder3D-MT, 72.9%), RWAFormer improves the overall mIoU by 2.4% and accuracy (Acc) by 1.7%, demonstrating the effectiveness of our architectural innovation.

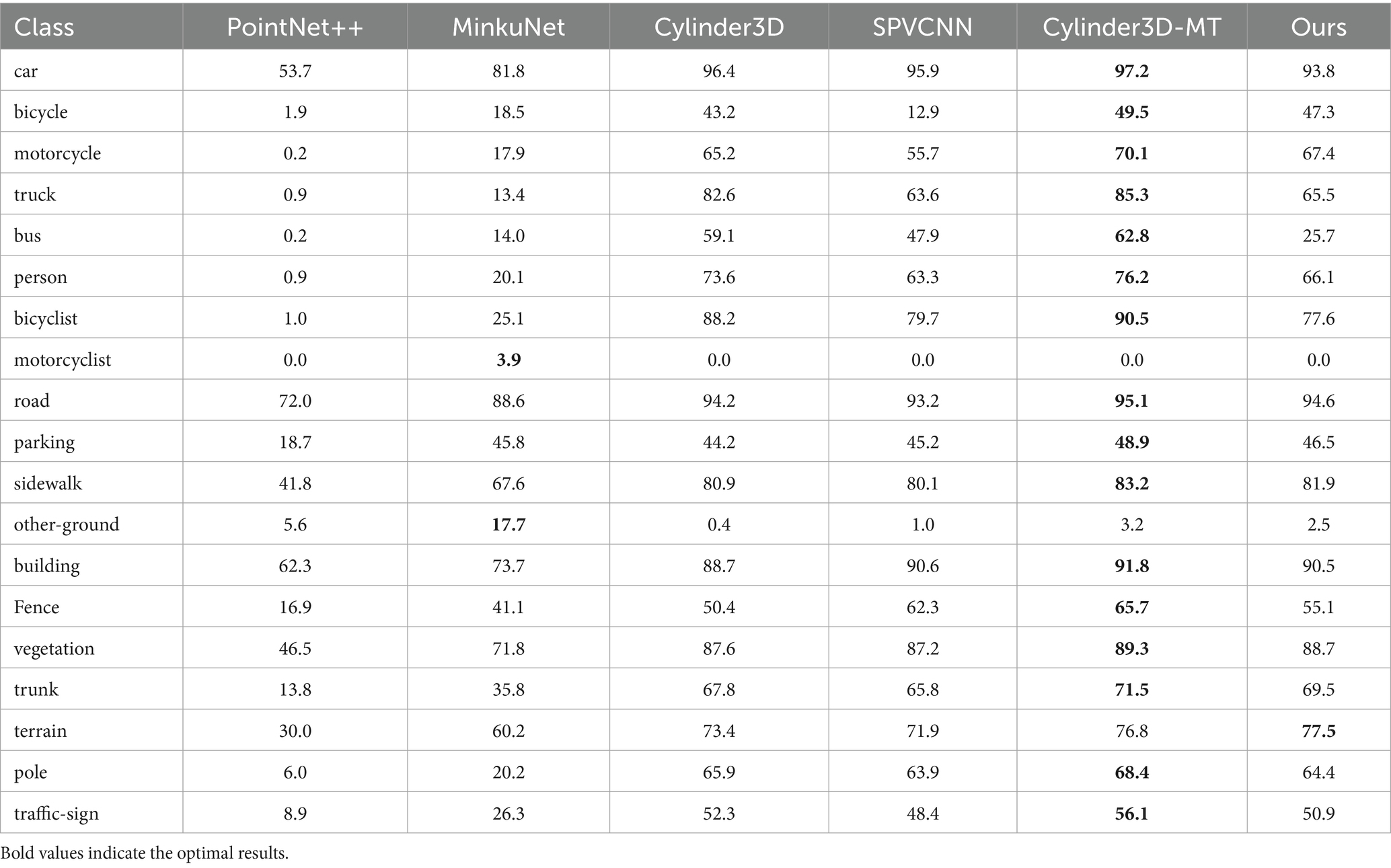
It also achieves competitive results in specific categories such as roads (94.6%), vehicles (93.8%), and buildings (90.5%), as shown in Table 2.

Our method achieves a mIoU of 75.3% (representing a 4.9–56.1% relative improvement) while operating at 2.6–3.8 × lower FLOPs than state-of-the-art (SOTA) approaches. This “optimal performance with moderate computation” characteristic makes it particularly suitable for resource-constrained autonomous driving scenarios.

As shown in Table 2, the detailed per-category IoU results provide further insights into the strengths of our approach. When compared with the current best published method Cylinder3D-MT, our RWAFormer demonstrates competitive or superior performance on multiple categories, particularly in recognizing thin structures (e.g., bicycle, motorcycle) and ground elements (e.g., road, parking, sidewalk, terrain). This can be attributed to our radial window attention mechanism, which better captures long-range dependencies and fine-grained features critical for these challenging categories. The performance comparison confirms that our method achieves a more balanced performance profile across categories with a simpler and more efficient architecture.

As shown in Figure 11, different colors represent different segmentation labels, and distant objects with sparse point cloud distribution are highlighted with blue boxes. The brown box is a zoomed-in display of the blue box, and the last two columns are a plot of the difference from the true value, with incorrectly segmented points labelled in red and correct ones in black. We visually compare the optimal model (i.e., SPVCNN) with the RWAFormer model proposed in this paper. It is clear from the figure that there are fewer incorrectly segmented points than SPVCNN using our proposed RWAFormer model, which has a higher accuracy for sparse long-range object recognition.

Figure 11

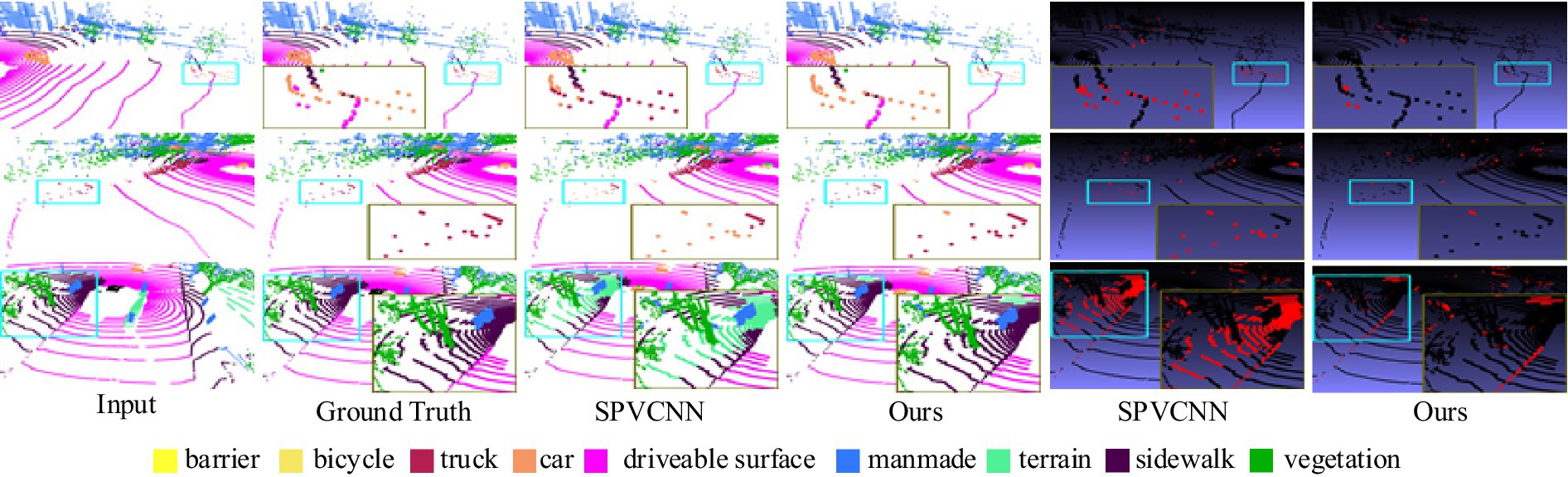
Figure 11. Comparison of semantic segmentation results between SPVCNN and the proposed model on the SemanticKITTI task. Image reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0.

3.4.2 Experiments on the Nuscenes task

To verify the generalization ability of RWAFormer, we conducted further experiments using the Nuscenes LiDAR road point cloud dataset. Table 3 compares the semantic segmentation results of several classic point cloud semantic segmentation networks with those of the RWAFormer model proposed in this paper.

Table 3

Table 3. Experimental results on the NuScenes task.

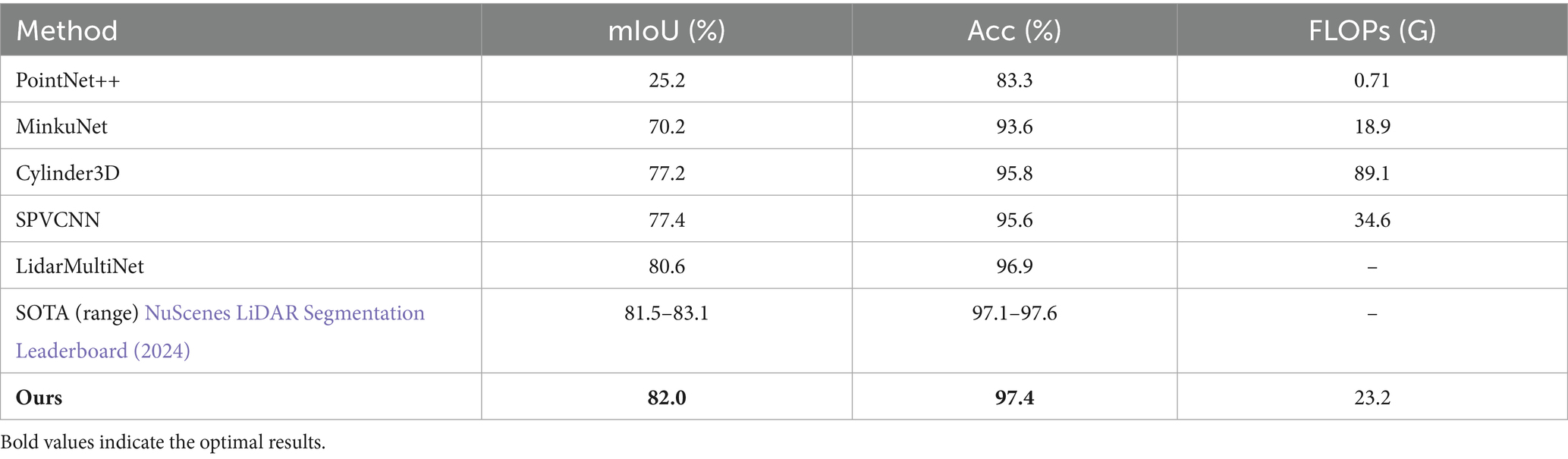
To firmly establish the competitive standing of our work, we reference the official NuScenes LiDAR segmentation leaderboard (2024). The leading published method on this benchmark, LidarMultiNet (Li et al., 2022), reports a score of 80.6% mIoU. The current state-of-the-art, including unpublished entries that utilize ensembles, achieves between 81.5 and 83.1% mIoU.

Our RWAFormer model achieves 82.0% mIoU on this dataset. This result clearly outperforms the best previously published result (LidarMultiNet, 80.6% mIoU) by 1.4%. More importantly, our method achieves this as a single-model solution, while the top leaderboard entries rely on computationally prohibitive ensemble strategies. This consistent high performance across two distinct large-scale datasets underscores the robustness and effectiveness of our proposed architecture.

Experimental results show our approach attains 82.0% mIoU with merely 23.2G FLOPs on nuScenes 1.5–3.8 times more efficient than SOTA solutions, coupled with 4.6–56.8% relative accuracy gains, establishing substantial improvements over existing best methods.

The consistent superiority of RWAFormer across both SemanticKITTI and nuScenes datasets demonstrates its robust generalization capability. The performance gain is particularly significant when compared to the best published methods on both benchmarks. Our radial window attention mechanism provides a more unified and efficient solution, enabling effective feature learning across diverse sensor configurations and urban environments. This demonstrates that our architectural innovation offers a superior balance between performance and practicality compared to existing approaches.

In addition, Figure 12 gives a comparison graph of the visual segmentation effect of the SPVCNN model, which has the best segmentation effect so far, with our proposed RWAFormer method, where different colors represent different segmentation labels, and the last two columns are the difference graphs from the real values, with the points that are incorrectly segmented marked in red and the correct ones marked in black. From the figure, we can see that our model segments more points correctly than SPVCNN, which can identify the category of the object more accurately and segment it completely, and the red box highlights the places where the segmentation effect contrasts significantly.

Figure 12

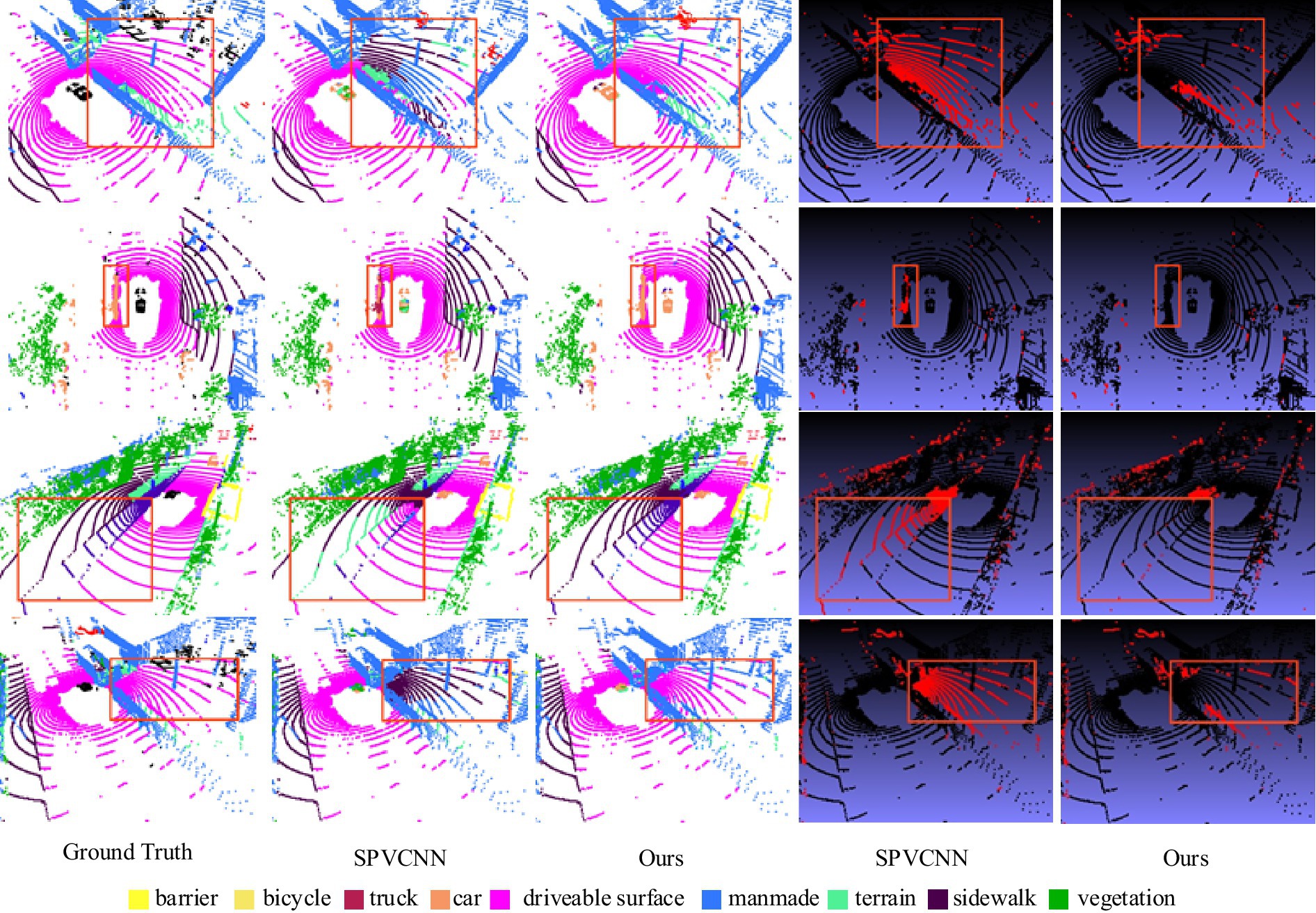
Figure 12. Comparison of visual segmentation results between SPVCNN and our proposed method on the NuScenes task. Image reproduced with permission from Behley et al. (2019): https://arxiv.org/abs/1904.01416 under CC BY-NC-SA 4.0.

3.5 Ablation study

To verify the effectiveness of each module in the proposed RWAFormer method, we conducted ablation experiments on the Semantichitti dataset. The experimental results are presented in Table 4.

Table 4

Table 4. Ablation experiment results.

Experiment 1 used the U-Net point cloud processing network architecture without incorporating the STFE and RWA modules. The road point cloud segmentation accuracy was the lowest at this stage, with an mIoU of 66.2% and an accuracy of 82.3%. This outcome indicates that U-Net may suffer from information loss when processing large 3D scenes due to excessive downsampling and pooling.

Experiment 2 introduced the STFE module, which improved mIoU and accuracy by 2.7 and 5.3%, respectively, with only a minor increase in parameters. This result demonstrates that the STFE module effectively handles sparse and spatially irregular point cloud data, efficiently extracting both local and global features relevant to road scenes. This capability enhances performance in road point cloud segmentation tasks, providing significant support for applications such as autonomous driving.

Experiment 3 added the RWA module, which captures global and local information in point cloud data through spherical convolution operations. It uses a skip attention mechanism to calculate self-attention, leveraging outputs from the MSA blocks of each layer to represent high correlations between ZMSAs and skipping MSA operations in subsequent Transformer layers. The parameter count decreased by 5.1 M to 29.1 M, while mIoU and accuracy improved by 4.7 and 9.4%, respectively. This demonstrates that RWA can effectively mitigate the adverse effects of the near-dense and far-sparse characteristics of road point cloud data on segmentation performance, reduce Transformer computations, and enhance segmentation efficiency.

Experiment 4 included both the RWA and STFE modules. Although the number of parameters was slightly higher than in Experiment 3, both mIoU and accuracy significantly improved. This indicates that combining RWA and STFE can enhance road point cloud segmentation accuracy with a relatively small increase in parameters.

To assess the effect of inserting the RWA module at different stages, we compared Experiment 1 and Experiment 3, confirming that introducing the RWA module was effective, with a 4.7% mIoU performance gain. This result highlights the benefits of aggregating length information using the radial window shape.

Additionally, we examined the effect of RWA insertion positions, as shown in Table 5. From Experiment 2 to Experiment 6, applying RWA to a single stage from Stage 1 to Stage 5 resulted in gradual performance improvements. In Experiment 6, inserting RWA in Stage 5 yielded a 2% mIoU performance gain, with negligible impact on inference time and model parameter count. Adding RWA to additional stages (Experiments 7 to 10) resulted in continuous performance enhancement.

Table 5

Table 5. Ablation experiments when inserting RWA modules into different stages.

This ablation study indicates that we can balance performance and efficiency by choosing the stage for insertion. For efficiency, adding RWA to the latter stages may be preferred, while for higher performance, incorporating it into more stages provides greater gains. In our experiments, we inserted RWA at the end of each encoding stage to achieve optimal performance.

4 Conclusion

This article thoroughly examines the distribution characteristics of LiDAR road point cloud data and introduces a road point cloud segmentation method named RWAFormer. This method features the STFE (Sparse Tensor Feature Extraction) module, which processes raw point clouds directly through continuous convolution operations, avoiding the need to convert data into dense voxel representations. This approach preserves the point cloud’s sparsity and efficiently handles sparse data. To enhance the model’s ability to capture features across various scales and positions and improve performance in road point cloud segmentation, this paper proposes a radial window attention strategy and develops the RWA (Radial Window Attention) module. This module allows sparse radar points that are far from the sensor to effectively aggregate crucial information from nearby dense points, compensating for information loss due to distance.

Despite the significant achievements of the RWAFormer proposed in this paper on LiDAR road point cloud segmentation tasks, there remain several issues that warrant further investigation and improvement. Future research directions could be explored from the following aspects:

1) While LiDAR point cloud data can provide rich three-dimensional geometric information, its performance may be limited under certain conditions (such as adverse weather or low-light conditions). Future research could investigate the fusion of LiDAR point cloud data with multi-modal data such as camera images and radar data to enhance the model’s robustness and segmentation accuracy in complex environments.

2) Current point cloud segmentation methods primarily rely on large amounts of annotated data for training, while the cost of annotating point cloud data is relatively high. Future exploration into self-supervised learning or weakly supervised learning methods could utilize unannotated or partially annotated data for model training, thereby reducing reliance on annotated data.

In conclusion, LiDAR road point cloud segmentation is a field with significant research value and application prospects. The study in this paper provides an efficient and accurate solution for this field but leaves many questions that deserve further exploration. In the future, with the continuous development of deep learning technology and sensor technology, point cloud segmentation algorithms will play an even more crucial role in areas such as autonomous driving and intelligent transportation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZL: Writing – original draft, Writing – review & editing. LC: Writing – original draft, Writing – review & editing. YL: Writing – review & editing. SZ: Writing – review & editing. QG: Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The financial support for this paper was provided by the following project: Science and Technology Department of Jilin Province, Project Number 20230203028SF.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Behley, J., Garbade, M., Milioto, A., Quenzel, J., Behnke, S., Stachniss, C., et al. SemanticKITTI: a dataset for semantic scene understanding of LiDAR sequences. In ICCV (2019)

Google Scholar

Caesar, H., Bankiti, V., Lang, A. H., Vora, S., Liong, V. E., Xu, Q., et al. nuscenes: a multimodal dataset for autonomous driving. In CVPR, (2020).

Google Scholar

Cen, J., Yun, P., Zhang, S., Cai, J., Luan, D., Wang, M. Y., et al. (2022). Open-world semantic segmentation for LIDAR point clouds. arXiv [Preprint]. arXiv:2207.01452v1.

Google Scholar

Chollet, F. Xception: deep learning with depthwise separable convolutions. In CVPR, (2017). 4, 8.

Google Scholar

Choy, C., Gwak, J. Y., and Savarese, S. 4D spatio-temporal convnets: Minkowski convolutional neural networks. In CVPR, (2019).

Google Scholar

Feng, T., Wang, W., Ma, F., and Yang, Y. (2024). LSK3DNet: towards effective and efficient 3D perception with large sparse kernels. arXiv [Preprint]. arXiv:2403.15173v1.

Google Scholar

Geiger, A., Lenz, P., and Urtasun, R. Are we ready for autonomous driving? The Kitti vision benchmark suite. 2012 IEEE conference on computer vision and pattern recognition. IEEE, (2012):3354–3361.

Google Scholar

Hu, Q., Yang, B., Xie, L., Rosa, S., Guo, Y., Wang, Z., et al. Randla-net: efficient semantic segmentation of large-scale point clouds. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. (2020): 11108–11117.

Google Scholar

Jhaldiyal, A., and Chaudhary, N. (2023). Semantic segmentation of 3D LiDAR data using deep learning: a review of projection-based methods. Appl. Intell. 53, 6844–6855.

Google Scholar

Jia, D., and Leibe, B. (2021). Person-MinkUNet: 3D person detection with LiDAR point cloud. arXiv [Preprint]. arXiv:2107.06780.

Google Scholar

Li, Z., Wang, W., Li, H., Xie, E., Lin, C., and Liu, Q. (2022). Lidarmultinet: towards a unified multi-task network for lidar perception. IEEE Robot. Autom. Lett. 7, 11096–11103.

Google Scholar

Liu, Y., Fan, B., Xiang, S., and Pan, C. Relation-shape convolutional neural network for point cloud analysis. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. (2019): 8895–8904.

Google Scholar

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., et al. Swin transformer: hierarchical vision transformer using shifted windows. In Proceedings of the 2021 IEEE/CVF international conference on computer vision (ICCV), Montreal, QC, Canada, (2021); pp. 10012–10022.

Google Scholar

Loshchilov, I., and Hutter, F. (2017). Decoupled weight decay regularization. arXiv [Preprint]. arXiv:1711.05101.

Google Scholar

NuScenes LiDAR Segmentation Leaderboard. (2024). Available online at: http://www.semantic-kitti.org/ (Accessed August 15, 2024).

Google Scholar

Poulose, A., Baek, M., and Han, D. S. Point cloud map generation and localization for autonomous vehicles using 3D LiDAR scans. 2022 27th Asia Pacific conference on communications (APCC). IEEE, (2022): 336–341.

Google Scholar

Qi, C. R., Su, H., Mo, K., and Guibas, L. J., Pointnet: deep learning on point sets for 3D classification and segmentation. Proceedings of the IEEE conference on computer vision and pattern recognition. (2017): 652–660.

Google Scholar

Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017). Pointnet++: deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 30, 5105–5114.

Google Scholar

Rao, Y., Zhao, W., Tang, Y., Zhou, J., Lim, S. N., and Lu, J. (2022). Hornet: efficient high-order spatial interactions with recursive gated convolutions. arXiv [Preprint]. arXiv:2207.14284.

Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. U-net: convolutional networks for biomedical image segmentation. In MICCAI, (2015)

Google Scholar

SemanticKITTI Dataset Leaderboard. (2024). Available online at: http://www.semantic-kitti.org/ (Accessed August 16, 2024).

Google Scholar

Song, J. (2014). Research on registration methods for 3D point cloud data. Harbin, China: Harbin Engineering University.

Google Scholar

Tang, H., Liu, Z., Zhao, S., Lin, Y., Lin, J., Wang, H., et al. Searching efficient 3D architectures with sparse point-voxel convolution. European conference on computer vision. Cham: Springer International Publishing, (2020): 685–702.

Google Scholar

Thomas, H., Qi, C. R., Deschaud, J. E., Marcotegui, B., Goulette, F., and Guibas, L. J. Kpconv: flexible and deformable convolution for point clouds. Proceedings of the IEEE/CVF international conference on computer vision. (2019): 6411–6420.

Google Scholar

Touvron, H., Cord, M., Douze, M., Massa, F., Sablayrolles, A., and Jégou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the 38th international conference on machine learning, virtual, (2021); pp. 10347–10357. Available online at: http://proceedings.mlr.press/v139/touvron21a/touvron21a.pdf (Accessed March 29, 2024)

Google Scholar

Varney, N., Asari, V. K., and Graehling, Q. (2020). DALES: a large-scale aerial LiDAR data set for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (1–10).

Google Scholar

Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M., and Solomon, J. M. (2019). Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. 38, 1–12. doi: 10.1145/3326362

Crossref Full Text | Google Scholar

Wang, F., Wu, Z., Yang, Y., Li, W., Liu, Y., and Zhuang, Y. (2023). Real-time semantic segmentation of LiDAR point clouds on edge devices for unmanned systems. IEEE Trans. Instrum. Meas. 72, 1–11. doi: 10.1109/TIM.2023.3292948

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, X., Jiang, L., Wang, P. -S., Liu, Z., Liu, X., Qiao, Y., et al. (2024). Point transformer V3: simpler, faster, stronger. arXiv [Preprint]. arXiv:2312.10035v2.

Google Scholar

Xu, J., Liu, H., Shen, Y., Zeng, X., and Zheng, X. (2024). Individual nursery trees classification and segmentation using a point cloud-based neural network with dense connection pattern. Sci. Hortic. 328:112945. doi: 10.1016/j.scienta.2024.112945

Crossref Full Text | Google Scholar

Zhang, Z., Hua, B.-S., Rosen, D. W., and Yeung, S. -K. (2021). Rotation invariant point cloud classification: where local geometry meets global topology. Pattern Recogn. 109:107567.

Google Scholar

Zhang, J., Zhao, X., and Chen, Z. (2020). A review of deep learning-based point cloud semantic segmentation. Prog. Laser Optoelectron. 57, 28–46.

Google Scholar

Zhao, L., Xu, S., Liu, L., Ming, D., and Tao, W. (2022). SVASeg: sparse voxel-based attention for 3D LiDAR point cloud semantic segmentation. Remote Sens 14:4471. doi: 10.3390/rs14184471

Crossref Full Text | Google Scholar

Zhou, Y., and Tuzel, O. Voxelnet: end-to-end learning for point cloud based 3d object detection. Proceedings of the IEEE conference on computer vision and pattern recognition. (2018): 4490–4499.

Google Scholar

Zhu, X., Zhou, H., Wang, T., Hong, F., Li, W., Ma, Y., et al. (2021). Cylindrical and asymmetrical 3D convolution networks for LiDAR-based perception. IEEE Trans. Pattern Anal. Mach. Intell. 44, 9527–9540.

Google Scholar

Zhu, X., Zhou, H., Wang, T., Hong, F., Ma, Y., Li, W., et al. Cylindrical and asymmetrical 3D convolution networks for LiDAR segmentation. In CVPR, (2021)

Google Scholar