Multimedia privacy protection: an N-round cascaded cryptosystem based on merged multi-chaotic maps under various image attacks

Due to the widespread use and variety of wireless networks and their applications in open environments, security techniques need to be more robust, reliable, and flexible, incorporating multi-stage and interfered secret key (S_key) capabilities. This research article presents an efficient cryptographic approach through the construction of a cascaded series of processes. It proposes a multi-number of encrypting processes (N-round chaos-based) cryptosystem containing N secret keys based on data classification and the environment. The article also outlines the simple criteria for determining the number of rounds (N-round). Several chaos-based encryption techniques have been utilized to construct the proposed algorithm, and various scenarios of the N-round mechanism over different classified images have been presented. In the majority of relevant published studies, two critical issues have been overlooked: the selection criteria for required and suitable security levels and the rules and conditions for robust security keys. These essential issues have been discussed in this research article. Various grayscale images are used in the computer simulation experiments conducted to demonstrate the robustness, reliability, and applicability of the proposed cryptographic algorithm. The experiments consider the presence of various attacks, such as speckle, salt-and-pepper, and Gaussian noise. Based on the results from the standard database (Hlevkin, USA CANVAS), the proposed algorithm is robust and suitable for applications in noise/attack environments. As clarified by the results, the similarity of extracted images is 100% to the original plaintext in the absence of attacks, while in the presence of noise and attacks, the similarity remains above 99%. The quality of the decrypted images is superior to that of the majority of existing cryptosystems.

1 Introduction

In recent years, the world has made significant advancements in mobile wireless communication networks and security tools to meet requirements and combat various attacks (Al-Eryani and Hossain, 2019). We are experiencing a continuous evolution through generations of mobile wireless communication, starting from 1G, progressing through 2G, 3G, and 4G, to the emergence of 5G networks. The 5G networks offer numerous benefits, including higher transmission rates with lower latency, better system performance and reliability, smaller device sizes, and more energy-efficient designs for devices and networks (Liu et al., 2020). 5G networks aim to facilitate a wider range of applications, such as real-time closed-loop robotic control, large-scale Internet of Things (IoT), autonomous vehicles, and augmented and virtual reality (AR/VR). The fifth-generation (5G) system includes three distinct technical features: ultra-reliable low-latency communications (uRLLC), massive machine-type communications (mMTC), and enhanced mobile broadband (eMBB) (Tomkos et al., 2020; Chowdhury et al., 2020).

Despite the advantages provided by the fifth generation, it faces many challenges that affect its performance in various applications. A fully automated, intelligent network that offers everything as a service and a fully immersive experience is not something that 5G networks will be able to provide. In 10 years, 5G communication networks will not be able to meet the demands of emerging intelligent and automated systems despite their enormous advances over current systems. On the other hand, due to the significant advancements of different wireless networks and various application fields of these networks, trusted and robust security techniques must be developed continuously to meet the security requirements of these critical applications. Therefore, many researchers are interested in proposing suggestions for enhancing the security algorithms of mobile wireless communications. High-level security must be provided for the transferred data, given the expected immense amount of devices and data on the network, according to the vision of the advanced wireless/mobile network (Alraih et al., 2022; Shen et al., 2021).

With the variations of wireless networks and their applications covering military, civil, and medical fields, new threats will emerge and be invented. To counter these new threats, highly efficient security techniques must be utilized to guarantee the reliability and integrity of the data transferring over the open environment applications of these mobile/wireless networks (Penttinen, 2021; Uusitalo et al., 2021). Artificial Intelligence (AI)-based security using machine learning (ML) and deep learning (DL) techniques has been proposed in several research studies (Quy et al., 2023; Hong et al., 2022; Alsabah et al., 2021) as strong security solutions. AI-based techniques are essential to address emerging threats related to artificial intelligence attacks, such as backdoor embedding and the poisoning of training data in federated learning. Additionally, the 5G network lacks a global standard to enhance security strategies in various scenarios to meet diverse security requirements while reducing overall costs (Letaief et al., 2022). For example, when the remaining battery power of the device decreases, the complexity of the security systems used must be adjusted to provide longer device operation time. With the increasing heterogeneity, dynamics, and complexity in advanced wireless/mobile networks, security must be adaptively customizable for different services, power conditions, and other variable characteristics over time (Bhat and Alqahtani, 2021). These issues are considered in our presented research article through a proposed security state diagram that controls different security levels based on the available power, data classification, and the surrounding environment of communication (Viswanathan and Mogensen, 2020).

In this study, high levels of privacy and reliability have been considered through a proposed cascaded N-Round crypto algorithm based on chaotic encryption techniques. The proposed approach consists of integrating encryption-chaotic-based techniques and secret key (S_key) management. The proposed algorithm has been constructed by combining various security layers to achieve a high level of privacy and confidentiality on the network. Additionally, the transition between these layers of security can be controlled by previous roles or automatically based on a simple AI model. The proposed security approach considers the essential factors in wireless network applications, which are consumed power and node lifetime, through the concept of an energy-saving security algorithm (ESSA) on the network, as described in the following sections.

1.1 The main contributions

In this research article, a developed interactive and expandable crypto algorithm is proposed based on cryptographic techniques integrated within a multi-round secret key using an efficient chaos-based system. Chaotic-based encryption is one of the most widely used types of image encryption, built by employing one or more chaotic maps, such as the Baker, logistic, cat, Henon maps, and others, for encrypting the plaintext.

- The various chaos maps have been used in the proposed crypto algorithm. The chaos-based Baker Map (BM) is chosen for its resistance to various types of noise and attacks, making it suitable for executing additional rounds and merging S_key or overlapping them. The Logistic Chaos Map (LM), the second chaos tool, is used to encrypt the classified data. Due to its high sensitivity to noise and tampering, it is used to ensure the detection of any modifications or attacks. In the proposed crypto algorithm, it is utilized only in the final round.

- The standard and un-standards images such as Hlevkin datasets and open sources are utilized in the evaluation of the proposed crypto algorithm.

- The presented robust crypto approach is an advanced and reliable variant of existing approaches and the recently published related works. It can be considered an enhancement of classic security techniques due to the following reasons:

- Interactivity: Users can modify interactive security levels by choosing the number of rounds and types of cryptographic tools based on four key factors. These factors include available resources (AR), which cover Available Power (AP) or ‘battery level’ and Available Memory size (AM), open/closed environments (O/CE), device/node types (homogeneous/Heterogeneous) (DTHH), and the secret classification level (SCL) of the data being transferred.

- Better/robust security: Due to the multi-overlapping crypto process, the presented approach is robust against various attacks. The cascaded security processes are not reversible because of the sensitivity of LCM in the case of any tiny tampering in the cipher.

- AI-based management capabilities: Given the variety of security layers and the flexible number of rounds, hash conditions, and environmental variations, AI can be employed to manage appropriate security levels and rounds based on real-time conditions.

- Flexibility: The presented algorithm is flexible in choosing the N-round in the chaos BM stage. The levels and layers of the proposed crypto-security algorithm can be managed and selected to decrease the computational overhead due to the N-round.

The evaluation of the proposed cryptosystem is performed based on computerized simulation experiments utilizing two scenarios: free noise and attacks/noising and the presence of various attacks such as Gaussian noise, salt-and-pepper, and speckle attacks. The computer-based simulation experiments have been utilized as a tool to evaluate and test the performance, applicability, and practicability of the proposed encryption algorithms. The results of this evaluation method are not enough; they present a true indication of the expected performance of the hardware implementation. The real implementation and hardware design of the proposed cryptosystem will be considered in future research studies utilizing FBGA and employing recent logic-style approaches such as full swing-gate diffusion input (FS-GDI). Furthermore, the computational complexity of the proposed cryptosystem has been included in the objective evaluation metrics. The proposed cryptosystem is an N-round cascaded algorithm designed to provide multilayered security based on accepted complexity. In fact, the multi-round encryption increases the complexity, resulting in computational overhead. This drawback has been addressed by binding the number of rounds to the degree of classification of the transferred message, the nature of the transmission circumstances, the available resources of the networks, and the nodes of the application. Hence, the overhead computation due to the number of rounds is optional; it can be controlled by determining the degree of security needs in relation to the available resources.

The rest of this article is organized as follows: Section 2 presents the related work and literature review. Section 3 describes the proposed anti-forgery algorithm. Section 4 presents the objective metrics utilized for the proposed techniques. Section 5 discusses the results of the computer simulation experiments. Section 6 presents conclusions.

2 Literature review

The recent related research studies have been discussed in this section. It presents the recently published studies that propose various image security approaches. The majority of the proposed security approaches are based on the combination of different techniques. The literature review is presented as follows.

Sabry et al. (2023) demonstrates a high degree of security for image plaintext. The authors presented an algorithm that enhances the Rossler system. The research provides high encryption strength for images, which blends DNA technology with Baker map techniques. This method works with 16×16 images. To create a highly secure encrypted image, the CBC mode is used for encryption, followed by the application of DNA technology and the Baker map approach. This study presents a technique for simultaneously encrypting several images. This technique uses a hyper-chaotic system to combine a collection of images into a single image. The Baker map technique is used to encode the image. A zigzag method is used to process the encoded image, raising the security level. As a result, this study not only encodes several images simultaneously but also provides a high level of security (Liu, 2024). The combining-based algorithm has been proposed in Zhou et al. (2024). It utilizes image encoding and data-hiding watermarking, using DCT and DWT with Baker Map techniques. This approach relies on integrating the watermark of the original image to transform it into a watermark image. The watermark image is encrypted using the encryption techniques employed in this approach.

In Abodawood et al. (2024), the authors presented an approach to improve image encryption based on chaotic maps. They used eight chaotic maps for image encryption performance. The approach employed to enhance image encryption relies on two different processes during encryption: confusion and diffusion. One of these processes alters the position of the data, while the other changes the value of the data, leading to robust image encryption. In Nasr et al. (2024), the authors proposed an approach that relies on both hiding and encryption. This research utilized the chaotic map to encrypt images and hide them within an audio file. It also employed data transformation to convert between the spatial domain and the frequency domain. The approach depends on transforming the audio using the DWT to hide the image after it has been encrypted with one of the chaotic maps, such as the Baker map. After that, the audio is returned to the spatial domain using the IDWT. The audio file is then sent over the communication channel. This method demonstrated high efficiency in securing images by relying on both hiding and encryption techniques. The multilayer algorithm for encrypting audio files was presented in Abdallah and Meshoul (2023). This algorithm relies on merging the audio file with a speech file after transforming it into the frequency domain using DWT. Then, the merged file is recovered to the spatial domain, followed by applying DCT to the file. After that, the file is encrypted using a Baker map to produce an encrypted audio file in the frequency domain. This multilayer algorithm and the transformations between the frequency domain and the spatial domain provide a higher level of encryption for audio files.

The authors in Fetteha et al. (2023) presented an algorithm for image encryption based on chaotic systems and DNA. The algorithm relies on changing the pixel values of images for a high-security rate. It encrypts images at two levels. At the first level, images are encrypted using a chaotic map. Then, the images pass to the second level to enhance encryption using DNA. The resulting image is multi-level encrypted, making it difficult to hack. This algorithm provides a high level of security for images through multi-level encryption.

In Sabir and Guleria (2023), the authors presented an approach to encrypting a set of images using multiple levels of encryption. This approach relies on three levels of encryption using AHC, RP2DFrHT, and 2D AM. The method combines several images into one and passes through different levels of encryption to obtain an encrypted image. These different levels of encryption provide a high level of security for the original image, making it difficult to access.

The encrypting algorithm for medical images based on the chaotic map has been presented in Toledo et al. (2023). The algorithm encrypts health images using logistic colors. The encrypted image is sent over the network using IoT, offering a high level of security for patient data and preventing unauthorized access.

Authors in Fotsing et al. (2023) discussed an approach to encrypting medical images on 5G networks. This approach relies on 2D logistic encryption with the SHA-256 protocol. In this approach, the SHA protocol is responsible for generating encryption keys. The 2D logistic encryption method encodes images based on permutation and diffusion logistics using the encryption keys generated from the SHA-256 protocol. An algorithm for securing colored images on 5G networks using a colored watermark is proposed in Su et al. (2024). The proposed algorithm relies on dividing both the colored images and the colored watermark into three parts: R, G, and B. The parts of the image are segmented into a set of blocks, while the parts of the watermark are converted into digital information. The watermark is integrated into its digital form within the image parts. The image is then reconstructed to form a colored image with the watermark.

Security enhancements in 5G networks have been considered in Shi et al. (2023); Zhang et al. (2023); Alrikabi et al. (2024). In Shi et al. (2023), the study presents an approach for encrypting and hiding data on 5G networks. This approach relies on RDHEI, ASS, and ABPP for encrypting and hiding data. The cover image is encrypted using this approach and then divided into several parts. Each part of the encrypted image participates in hiding the secret data. The parts of the image are then combined again to produce the encrypted cover image, which contains the hidden secret data. In Zhang et al. (2023), the authors present an algorithm for a strong watermark to secure images on 5G networks. The proposed algorithm relies on DTT and DC. In this algorithm, the color image is divided into the R, G, and B channels, while the watermark is transformed into a consecutive series of binary numbers. The algorithm combines parts of the image with the binary numbers representing the watermark. The image parts are then gathered again to produce the color image embedded with the watermark. In Alrikabi et al. (2024), the research article presents a system for data encryption on 5G networks. The proposed system relies on a chaotic map for data encryption. In this system, data are encrypted through pseudo-random numbers. The proposed system is characterized by its ability to encrypt different types of data. The system is used to encrypt images, audio, and waves.

The watermarking technique has been considered for securing images on 5G networks in Mehraj et al. (2023). This approach relies on encrypting the watermark using chaotic and DNA techniques. In this method, colored images are divided into two channels, with each channel transformed into the frequency domain using DCT. The encrypted watermark is embedded in each channel, which is then converted back to the spatial domain using IDCT. The two channels are merged again to produce the colored image embedded with the watermark. Embedding the watermark in the frequency domain provides a high level of security for this approach. A unique strategy for protecting medical data in 5G communications networks is presented in Murmu et al. (2024) for wireless edge computing, aiming to create collaborative deep learning (DL) models using dependable federated learning (FL)-based CusIAFL with the Flower framework. Additionally, a new GAN-based Pix2Pix model is employed to categorize tumors into multiple classes and to identify and generate realistic image features. Moreover, private key generation procedures are conducted using the Flower framework with a GAN-based architecture to ensure strong security against attackers. To guarantee consistency in time series data, the model utilizes a hybrid technique. In addition, image-to-image (I-to-I) translation for synthesizing color images is performed using the Pix2Pix method. The Flower framework is also employed as a global paradigm to enhance performance. The confidentiality of multimedia transmission is considered in Sabry and Mohsen (2022), where the authors propose efficient security tools for securing the transfer of multimedia signals based on a chaos-error control scheme merging.

As clarified in the previous discussion of related research studies, the majority of these studies considered the concepts of merging and combining. The data-hiding techniques and encryption tools merge to achieve robust security algorithms. Conversely, our proposed crypto algorithm has lower computation compared to the combining and merging-based security algorithms (Su et al., 2024; Shi et al., 2023; Zhang et al., 2023; Alrikabi et al., 2024; Mehraj et al., 2023). The chaos-based crypto algorithm, featuring optional N-round encryption, ensures lightweight complexity. The computational overhead is determined by the number of rounds (N) and variations in the secret keys for each round, as clarified in the simulation experiments section.

Due to the widespread use of wireless networks and their applications, security techniques should be more robust, reliable, and flexible to manage various levels of merging or combining secret keys. Additionally, the rates of multimedia forgery and cyber-attacks grow hand in hand with multimedia applications. Several authors have proposed a chaos encryption approach based on utilizing multiple chaos maps (Sabry et al., 2021; Osama et al., 2024; Hayam et al., 2022).

3 The methodology of the proposed cryptosystem

Based on the previous section, the recent and existing cryptographic algorithms are primarily constructed by merging data hiding, chaotic maps, and data transformation techniques. Therefore, the proposed N-round cryptosystem aims to harness the advantages of chaos-based cryptography and data transformation methods while modeling multiple security levels in a simple, robust, and efficient algorithm. This section discusses the contents, construction, and mechanism of the proposed N-round cryptosystem, emphasizing its robustness alongside low complexity (Mohsen and Abou El-Azm, 2019).

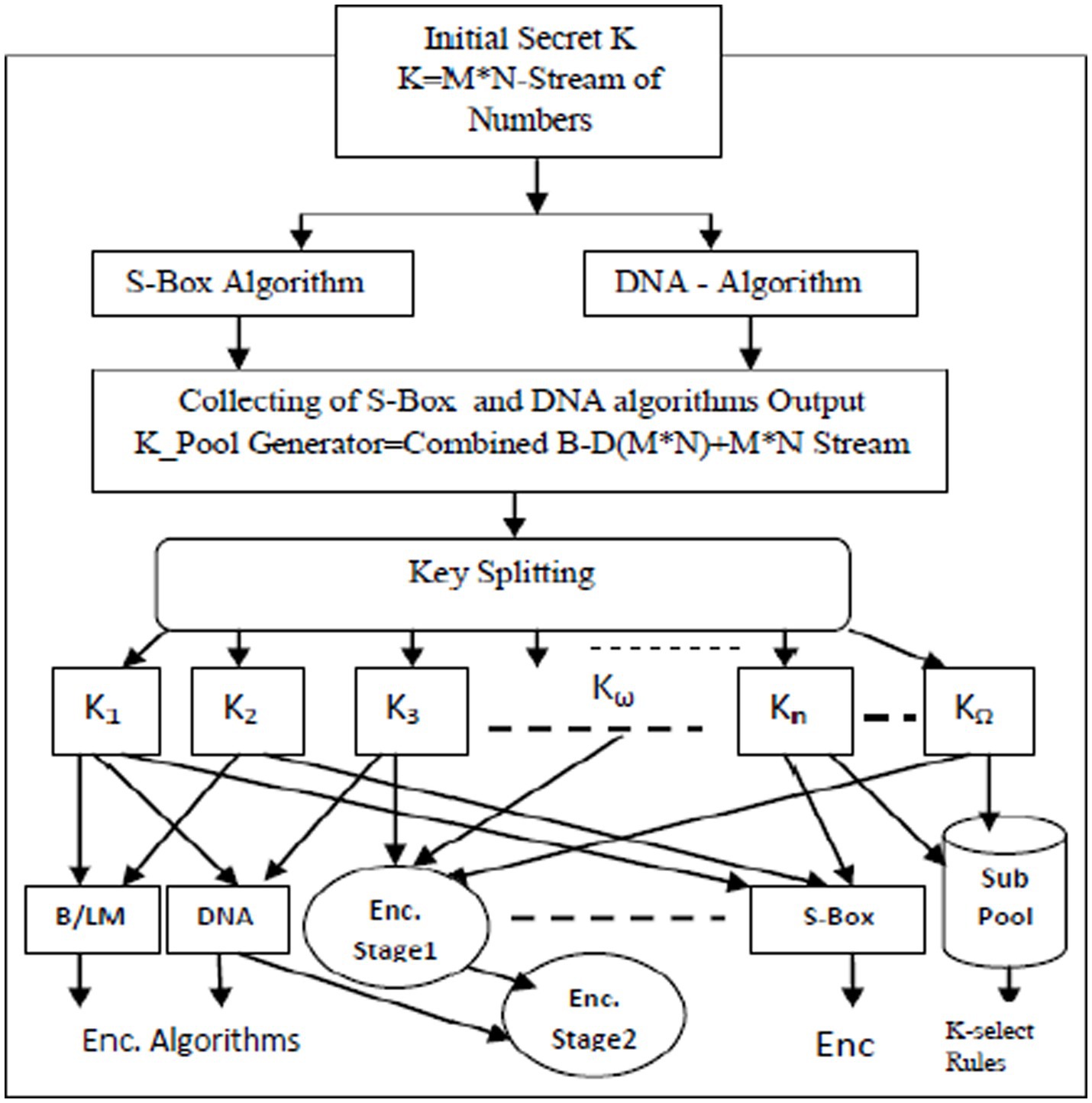
The proposed cryptographic algorithm is built on generating multi-secret keys from the original plaintext message. Figure 1 presents multiple scenarios for applying the proposed algorithm. The chaos-based encryption approach is flexible enough to achieve the highest degree of security while considering the power efficiency and the targets of the proposed crypto algorithm, as mentioned before (Murugan and Karthigai Kumar, 2018).

Figure 1

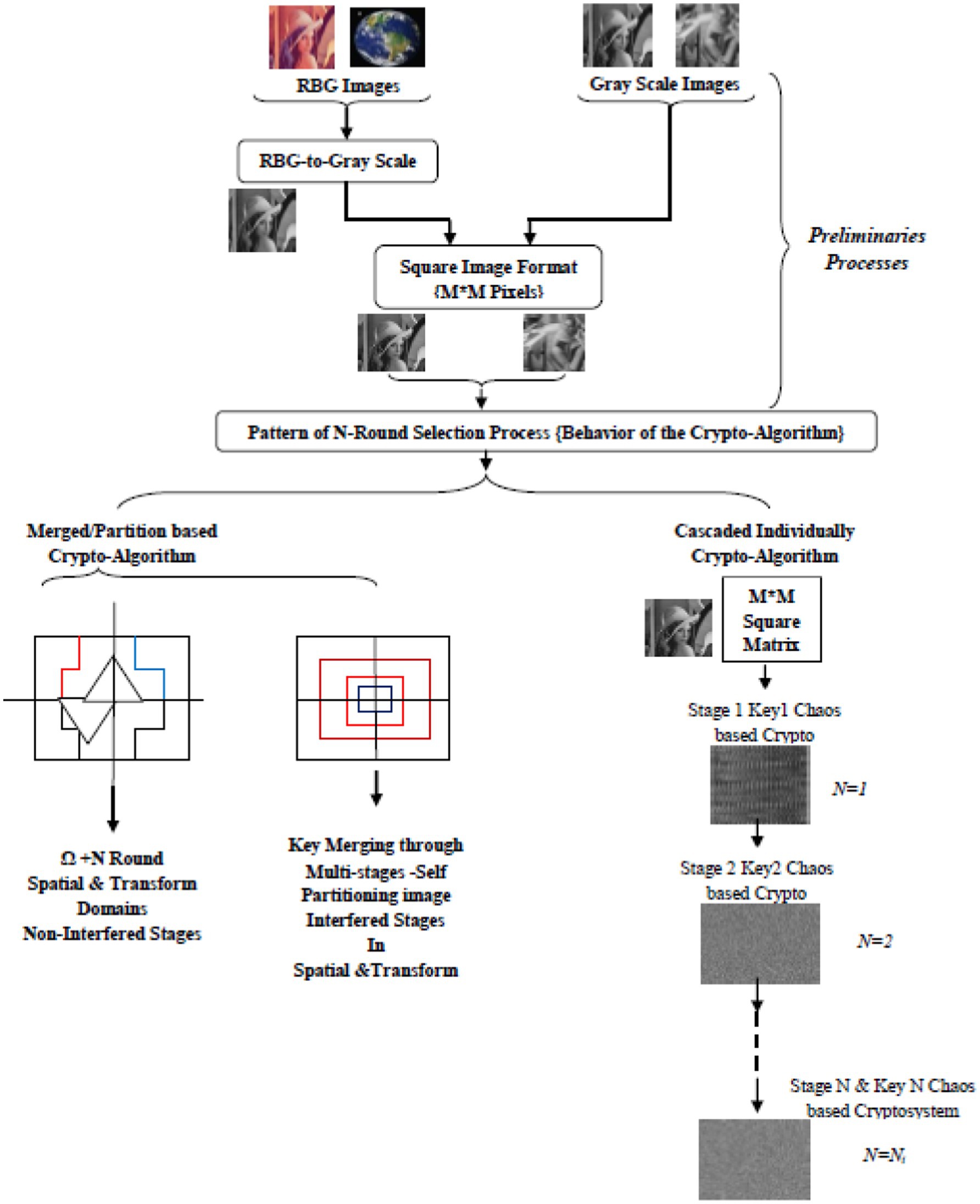
Figure 1. The first stages of the proposed N-round chaos/transform crypto-system (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, “Earth”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/planets/Earth.bmp and “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm, licensed under CC BY 4.0).

3.1 The construction of the proposed crypto algorithm

The construction of the proposed N-round cascaded crypto algorithm is described in this section. The proposed crypto algorithm is based on various scenarios, including the splitting of classified images and encrypting each section with a different secret key, as well as processing the entire set of classified images with different secret keys in each round based on their degree of classification in a series process. The chaos-based encryption utilizing different chaotic maps is the core of the proposed crypto algorithm. The various techniques are presented in the following section.

3.1.1 Cryptography techniques

Cryptography keeps data stored on the network from unauthorized access. It is extremely important to securely transmit data. Cryptography is an efficient technique utilized to store and send data in a secure format, allowing only the intended user to access and process the data (Osama et al., 2024). In cryptography, encryption is defined as the process of converting valuable data into an unrecognizable form to protect it from unauthorized access (Hayam et al., 2022). Data encryption techniques are commonly utilized by all cryptographic techniques to send data on an insecure network (Mohsen and Abou El-Azm, 2019). Data encryption techniques are divided into two main types: symmetric encryption and asymmetric encryption (Murugan and Karthigai Kumar, 2018).

Systematic encryption is a data encryption method that encrypts data at the sender using an encryption key. At the receiver, data are decrypted with the same encryption key used by the sender, meaning that encryption and decryption use the same key. Systematic encryption involves encrypting data at the sender with a key called the public key. Data are then decrypted at the receiver using another encryption key called the private key. Therefore, encryption and decryption are performed using different encryption keys (Zia et al., 2022; Ghosha et al., 2021; Sajitha Rekh, 2022).

Based on the widely used chaos maps, specifically the Baker Map (BM) and the Logistic Map (LM), the proposed N-Round cryptographic system is proposed. The execution of the algorithm, as clarified in Figure 2, allows the round to be performed on the same chaos map to exhibit the cascaded algorithm behavior or to merge various chaos maps to demonstrate self/partitioning behavior (Hamouda, 2020; Singh and Singh, 2022; Priyanka Singh, 2022; Muthu and Murali, 2021; Zhang and Liu, 2023; Zolfaghari and Koshiba, 2022; Wu and Wang, 2022; Jiang and Liu, 2023).

Figure 2

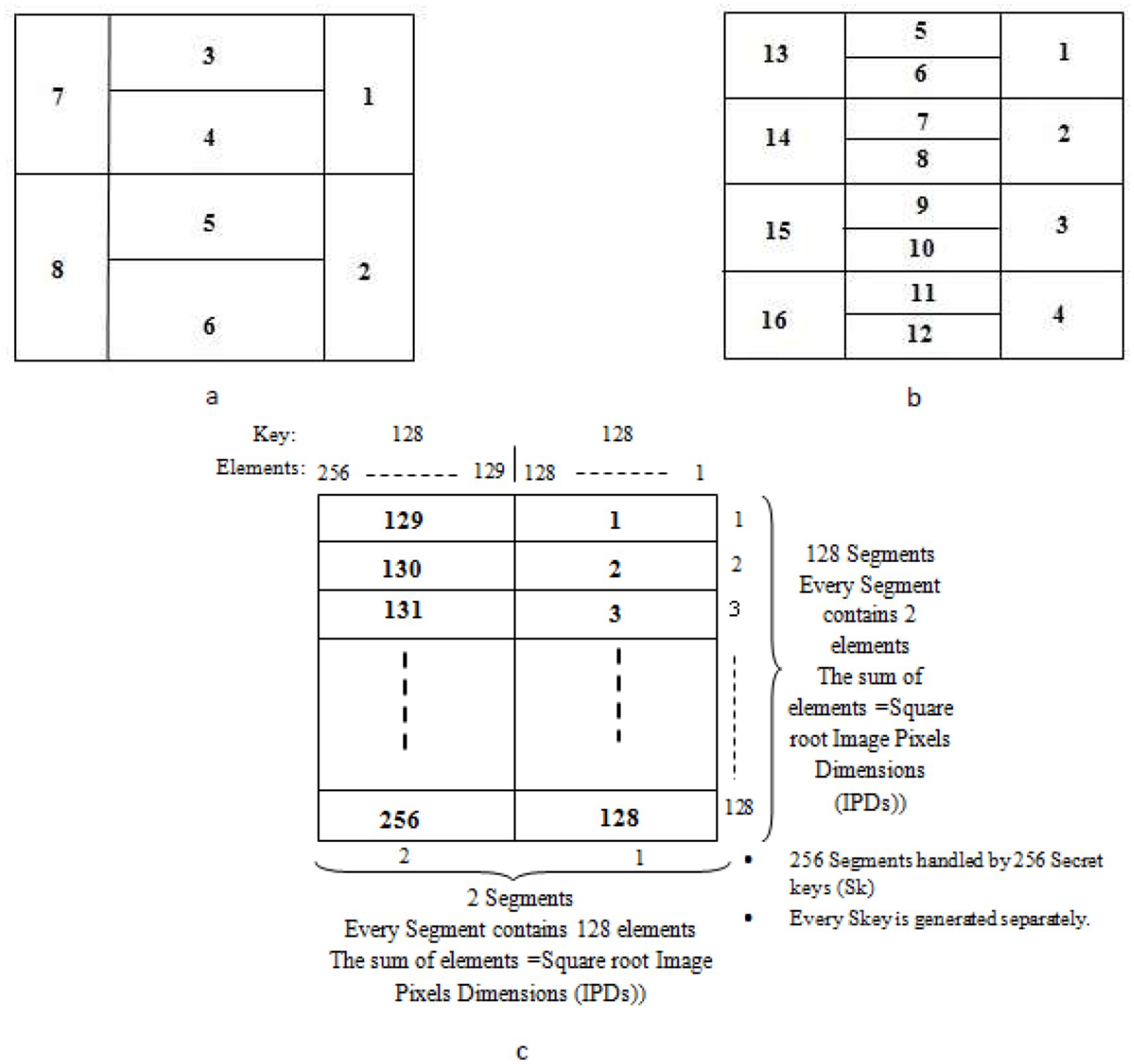
Figure 2. Examples of square image segmentation based on Baker Map (BM) chaos cryptography and image size: (a) S_key = {2, 4, 2}; (b) S_key = {4, 8, 4}; (c) S_key = {128, 128}.

3.1.2 2-D Chaos Baker map (BM) based (multi-round)

The Baker map is defined as a two-dimensional chaotic map that transforms a square matrix into itself after operations similar to randomization. The Baker map can be considered an efficient tool to randomize a square matrix of data (Sabry and Mohsen, 2022). The Baker map is described mathematically, as shown in Equation 1 (Muthu and Murali, 2021; Zhang and Liu, 2023).

$\begin{array}{c}\hfill B\left(x,y\right)=\left(2x,y/2\right),0\le x<1/2\hfill \\ \hfill B\left(x,y\right)=\left(2x-1,y∕2+1∕2\right),1∕2\le x<1\hfill \end{array}\text{ (1)}$

The discredited map can be represented for an M * M matrix, as shown in Figure 3, which represents a 2D chaotic encryption of an 8 * 8 matrix. Figure 3 shows the mechanism of the 2D chaotic BM operation, as mentioned in Figure 2. There is a dependency on the Baker map encryption for the stretch-and-fold concept. This means that the plain image is randomly distributed in the encrypted image (Zolfaghari and Koshiba, 2022).

Figure 3

Figure 3. S_keys management and relations for the proposed N-round cryptosystem.

3.1.3 2-D Chaos logistic map (LM)

The 2-D logistic map is a discrete dynamic system in which the evolution of orbits and attractors demonstrates chaotic behavior. The behavior of 2-D logistics is more complex than that of 1-D logistic behavior (Wu and Wang, 2022). Several cryptographic features, such as the wider range of parameters for chaotic behaviors and the fewer periodic windows in bifurcation diagrams, are present in 2D logistic maps. Due to its great sensitivity to initial parameters, uncomplicated expression, fast computation, and strong chaotic properties, 2D logistics has many applications (Jiang and Liu, 2023). Given the two-dimensional nature of image data, secure image encryption requires an efficient chaos-generating technique. The implementation of a two-dimensional logistic map satisfies these criteria. With its basin and attractor characteristics, a 2-D logistic map produces chaotic behavior and generates more complicated random number patterns (Faragallah et al., 2021). The mathematical representation of the 2-D logistic map as shown in Equation 2:

$\mathit{xi}+1=r\left(3yi+1\right)\mathit{xi}\left(1-\mathit{xi}\right)$

$\begin{array}{ll}yi+1=r\left(3\mathit{xi}+1+1\right)yi\left(1-yi\right)& (2)\end{array}$

(xi and yi) is the point at the ith iteration. Further, (xi and yi) and r denote the initial values and system parameters of this map. The previously defined equation for the 2-D logistic map describes a complex dynamical system (Hamza et al., 2017; Liu et al., 2019).

Due to the flexible key management of BM, the N-round is performed in the algorithm by BM, while the last round is executed by LM. The LM-based chaotic encryption technique is highly sensitive to noise and attacks; any tampering in the ciphertext makes it suitable for the last round.

3.2 Description of the proposed N-round chaos/transform-based algorithm

The following processes and multimedia handling stages are listed to clarify the smoothing and robustness of the proposed crypto algorithm.

- In the case of the RGB image (I), the first step is to convert it to a grayscale image.

- Generating Square image I=I (M*M).

- Pattern/behavior selection of the cryptosystem algorithm.

- The separated/cascaded chaos/transform N-rounds of encryption.

- OR self/partitioning images {merged N-round encryption processes}.

- Secret keys (S_keys) generation: All predetermined S_keys can be generated once for all subsequent rounds or one-by-one for each round.

- Real-time S_keys generation or retrieval from the pre-establishing S_keys pool.

The first stage of the proposed crypto algorithm is depicted in Figure 1, which illustrates the details of multimedia signal handling within the algorithm. The last round generates Ni-round encrypted images utilizing sufficient secret keys as recommended based on the previously mentioned conditions.

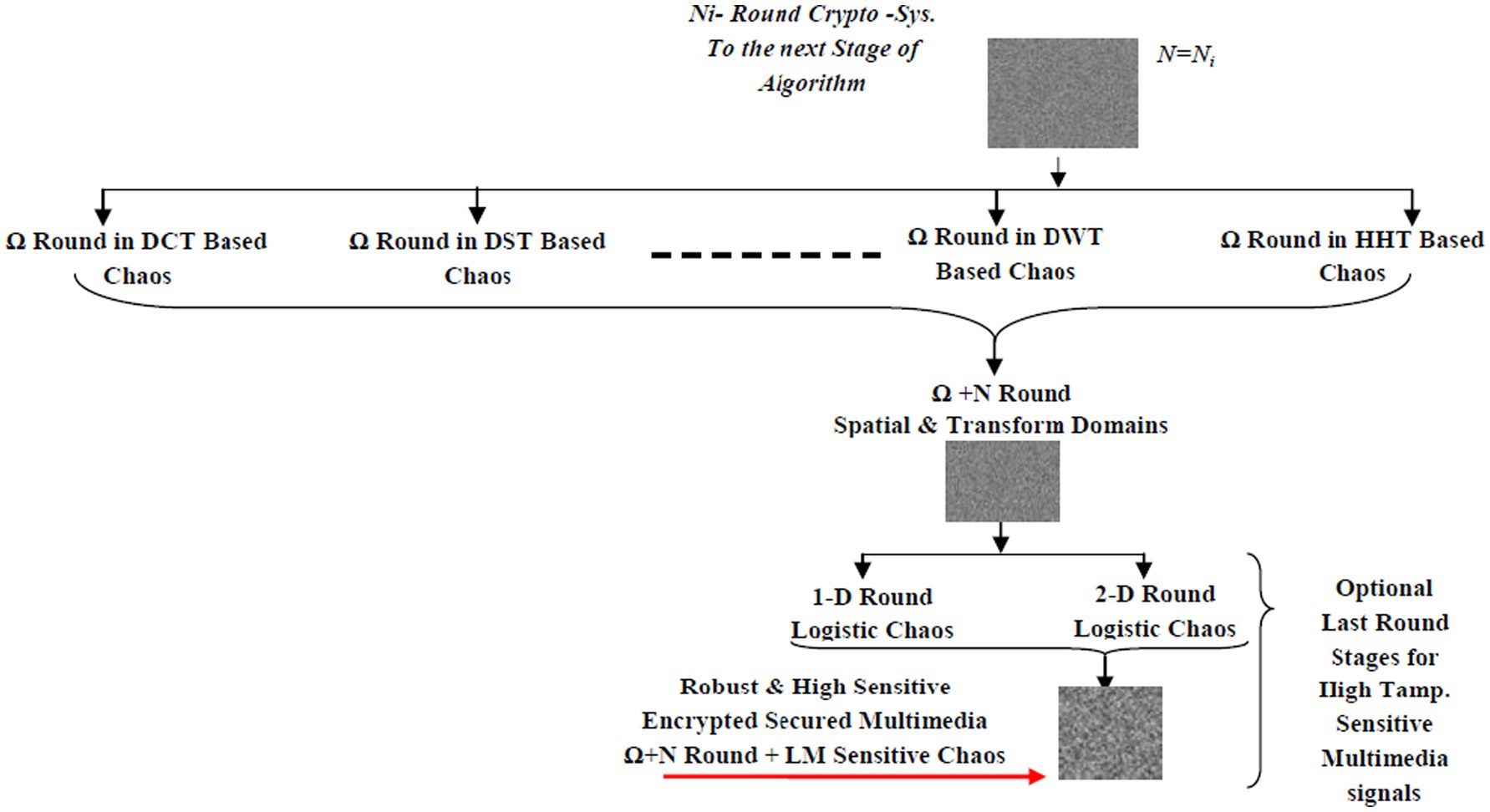
The product of stage 1 in the proposed algorithm will be the input data for the optional next stage, as illustrated in Figure 4. In this additional stage, there are two key aspects: first, employing a number of rounds after transforming the pre-encrypted data; second, the chaotic cryptosystem round contains one or more rounds using the highly sensitive Logistic Map (LM)-based cryptography in the form of one-dimensional (1-D) LM and two-dimensional (2-D) processing, to detect and capture any minute tampering.

Figure 4

Figure 4. Next stages of the operational mechanism of the proposed N-round crypto algorithm.

The last contribution in this article is clarified in Figure 3; this contribution establishes the basis for a robust and complex algorithm for building a large secret key database (S_keys pool). The proposed S_key generation algorithm is based on three processes: splitting, randomizing, and classic tool merging. S_key generation is discussed in a straightforward manner; however, this generation process is not reliable for highly classified plaintext. Therefore, the Hybrid Algorithm is designed to be the engine of S_key generation, combating various attacks such as brute force attacks (Murugan and Karthigai Kumar, 2018).

The secret key is controlled and determined based on the size of the managed plaintext. The degree of confusion effectiveness can be controlled by the contents and elements of the secret key. As shown in Figures 2a–c, the degree of BM chaos-based cryptographic robustness depends on the format of S_keys and the size of the plaintext. The examples presented in Figures 2a,b represent the semi-similar key generation rules. Each segment has been manipulated separately by unique S_keys. The third shape in Figure 2c gives an example of a fully similar S_key; additionally, each segment is encrypted with a unique and separate S_key.

The complexity is considered in Murugan and Karthigai Kumar (2018); the chaos-based interleaver is presented to enhance the forward error correction (FEC) schemes. The operational mechanism of this scheme is presented in Murugan and Karthigai Kumar (2018) with S_key = (2, 4, 2). The secret key is controlled and determined based on the size of the managed plaintext. The degree of confusion effectiveness can be influenced by the contents and elements of the secret key.

The simple equations have been presented to manage the automatic generation of the keys as follows.

The steps for generating secret keys to construct the key pool can be expressed as follows.

Let the image pixel dimensions be (m, n, and x) for RGB images. The image must first be converted to a two-dimensional grayscale image of size (M × M).

$\mathrm{I}\left[\mathrm{M},\mathrm{N}\right]=\mathrm{imresize}\left(\mathrm{I}\left(\mathrm{m},\mathrm{n},\mathrm{and}\mathrm{x}\right)\right)\text{.}$

Reshaping to a square matrix.

$\mathrm{I}\left(\mathrm{Square}\right)=\mathrm{reshape}\left(\mathrm{I}\left[\mathrm{M},\mathrm{N}\right],\mathrm{Sqrt}\left({\mathrm{M}}^{\ast }\mathrm{N}\right)\mathrm{Sqrt}\left({\mathrm{M}}^{\ast }\mathrm{N}\right)\right]\text{.}$

The key elements must be equal to the Sqrt (M*N):

${\mathrm{S}}_{\mathrm{key}}=\left(\mathrm{e}1,\mathrm{e}2,\mathrm{e}3,\mathrm{e}4,----------\mathrm{e}\mathrm{n}\right).=\mathrm{Squar}:\mathrm{root}\left({\mathrm{M}}^{\ast }\mathrm{N}\right)\text{.}$

To automatically generate the key, two approaches are used: systematic auto-key generation, as shown in Equation 3, and semi-systematic auto-key generation, as shown in Equation 6. Simple examples for systematic key generation are provided in Equations 4, 5.

Systematic auto-key generation:

$\mathrm{TheAuto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}=\left[\begin{array}{l}\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\dots \dots \\ \dots \dots \dots \dots \dots \dots \dots \dots \dots .,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}}\end{array}\right]\text{ (3)}$

$\mathrm{The}\mathrm{Auto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}.\mathrm{Example}\mathrm{Let}\mathrm{I}\left(256\ast 256\right)$

$\mathrm{if}\mathrm{z}=2,\mathrm{then}\mathrm{Key}=\left[\begin{array}{c}\hfill \frac{\mathrm{sr}\left(256\ast 256\right)}{2},\frac{\mathrm{sr}\left(256\ast 256\right)}{2}\hfill \\ \hfill \left(128,128\right)\hfill \end{array}\right]\text{ (4)}$

$\mathrm{if}\mathrm{z}=4,\mathrm{then}\mathrm{Key}=\left[\begin{array}{c}\hfill \begin{array}{l}\frac{\mathrm{sr}\left(256\ast 256\right)}{4},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\\ \frac{\mathrm{sr}\left(256\ast 256\right)}{4},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\end{array}\hfill \\ \hfill \left(64,64,64,64\right)\hfill \end{array}\right]\text{ (5)}$

The semi-systematic auto-gen example is (2, 4, 2) for image (8*8) pixels or (4, 8, 4) for image (16 * 16) pixels. As shown in Equation 4, there are two variables that control the elements of secret keys z and y. As shown in example (2, 4, 2), the z = 4 and y = 2 are the same for the stream of (4, 8, 4).

The Semi-Systematic auto-key Gen=

$\mathrm{The}\mathrm{Auto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}=\left[\begin{array}{l}\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{y}},\\ \frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\dots \dots \dots \dots \\ \dots ,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{y}},\dots \dots .,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}}\end{array}\right]\text{ (6)}$

$\mathrm{The}\mathrm{Auto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}.\mathrm{Example}\mathrm{Let}\mathrm{I}\left(256\ast 256\right)$

$\mathrm{if}\mathrm{z}=2,\mathrm{y}=4\mathrm{then}\mathrm{the}\mathrm{key}=\left[\begin{array}{c}\hfill \begin{array}{l}\frac{\mathrm{sr}\left(256\ast 256\right)}{4},\\ \frac{\mathrm{sr}\left(256\ast 256\right)}{2}\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\end{array}\hfill \\ \hfill \left(64,128,64\right)\hfill \end{array}\right]\text{ (7)}$

The second behavior of two variables for semi-systematic auto-generating of the key elements is given in Equations 7–9:

$\mathrm{if}\mathrm{z}=8,\mathrm{y}=4\mathrm{then}\mathrm{the}\mathrm{key}=\left[\begin{array}{c}\hfill \begin{array}{l}\frac{\mathrm{sr}\left(256\ast 256\right)}{8},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\\ \frac{\mathrm{sr}\left(256\ast 256\right)}{8},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\end{array}\hfill \\ \hfill \left(32,64,32,64\right)\hfill \end{array}\right]\text{ (8)}$

$\mathrm{if}\mathrm{z}=8,\mathrm{y}=4\mathrm{then}\mathrm{the}\mathrm{key}=\left[\begin{array}{c}\hfill \begin{array}{l}\frac{\mathrm{sr}\left(256\ast 256\right)}{8},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\\ \frac{\mathrm{sr}\left(256\ast 256\right)}{4},\frac{\mathrm{sr}\left(256\ast 256\right)}{8}\end{array}\hfill \\ \hfill \left(32,64,64,32\right)\hfill \end{array}\right]\text{ (9)}$

Moreover, the semi-systematic key auto-generation can be controlled by three variables: x, z, and y, as shown in Equations 10, 11. Simple examples of the three variables are shown in Equations 12, 13, the third x variable is denied.

The semi-systematic auto-key generation:

$\mathrm{TheAuto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{Semi}-\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}=\left[\begin{array}{l}\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{y}},\\ \frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\dots \dots ,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{x}}\\ \dots \dots ,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{y}},\dots ,\dots .,\\ \frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{x}},\dots ,\dots .,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}}\end{array}\right]\text{ (10)}$

$\mathrm{TheAuto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{Semi}-\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}=\left[\begin{array}{l}\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}},\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{y}},\\ \frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{x}},\dots \dots ,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}}\\ \dots \dots ,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{y}},\dots ,\dots .,\\ \frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{x}},\dots ,\dots .,\frac{\mathrm{sr}\left(\mathrm{m}\ast \mathrm{n}\right)}{\mathrm{z}}\end{array}\right]\text{ (11)}$

$\mathrm{TheAuto}.\mathrm{G}\mathrm{e}\mathrm{n}.\mathrm{S}\mathrm{y}\mathrm{s}.\mathrm{Keys}.\mathrm{Example}\mathrm{Let}\mathrm{I}\left(256\ast 256\right)$

$\begin{array}{l}\mathrm{if}\mathrm{z}=16,\mathrm{y}=8,\\ \mathrm{x}=\mathrm{deny},\mathrm{then}\mathrm{the}\mathrm{key}=\left[\begin{array}{c}\hfill \begin{array}{l}\frac{\mathrm{sr}\left(256\ast 256\right)}{4},\frac{\mathrm{sr}\left(256\ast 256\right)}{2}\\ \frac{\mathrm{sr}\left(256\ast 256\right)}{4}\end{array}\hfill \\ \hfill \left(64,128,64\right)\hfill \end{array}\right]\end{array}\text{ (12)}$

$\begin{array}{l}\mathrm{if}\mathrm{z}=8,\mathrm{y}=4,\mathrm{z}=2,\\ \mathrm{x}=\mathrm{deny},\mathrm{then}\mathrm{the}\mathrm{key}=\left[\begin{array}{c}\hfill \begin{array}{l}\frac{\mathrm{sr}\left(256\ast 256\right)}{8},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\\ \frac{\mathrm{sr}\left(256\ast 256\right)}{8},\frac{\mathrm{sr}\left(256\ast 256\right)}{4}\end{array}\hfill \\ \hfill \left(32,64,32,64\right)\hfill \end{array}\right]\end{array}\text{ (13)}$

As shown in the previous examples of auto-secret key generation for the systematic and semi-systematic keys, this process can be controlled by one, two, or more variables. For simplicity, the keys with one and two variables are considered in the simulation experiments.

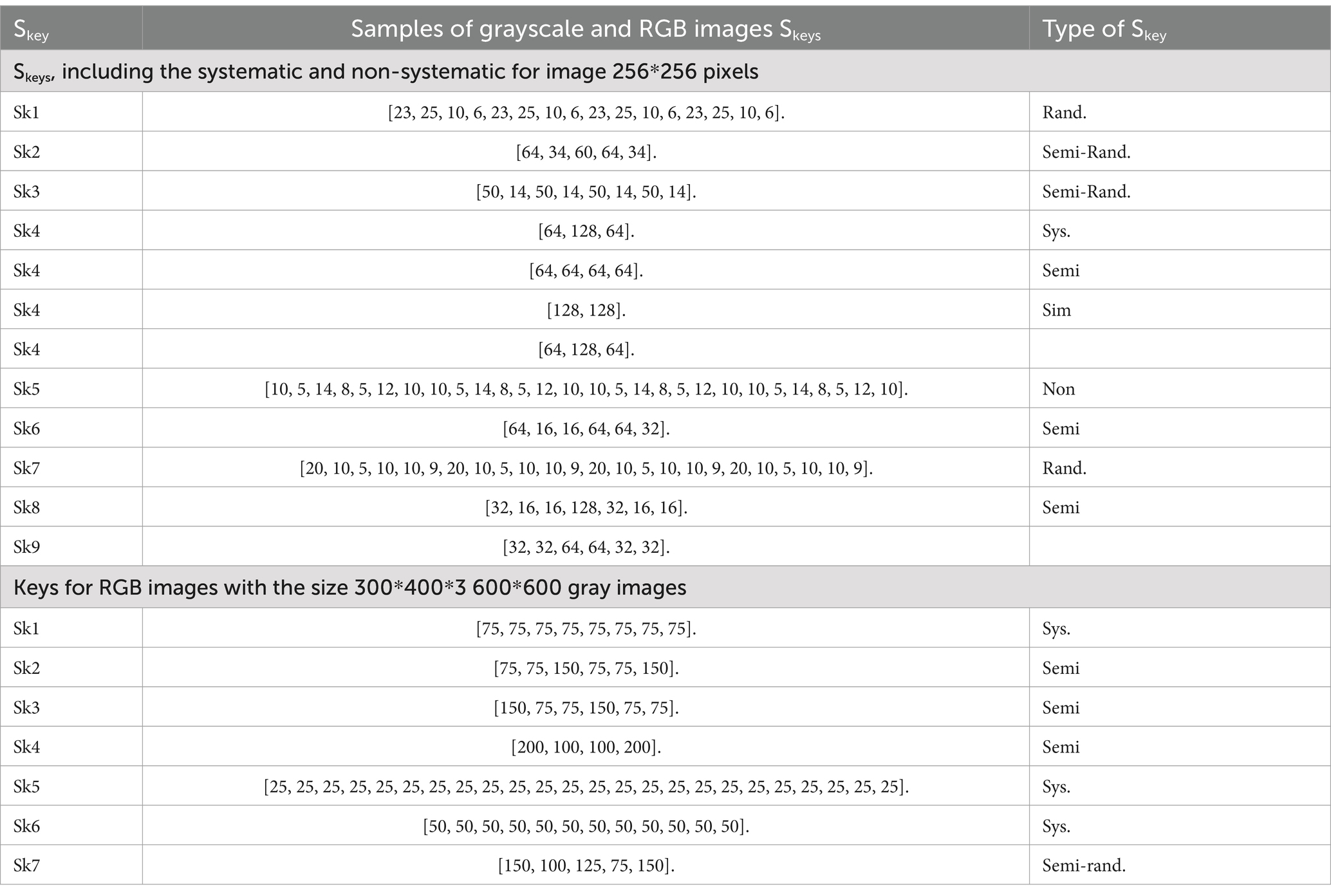
The proposed pool formatting, as shown in Table 1, contains the systematic, semi-systematic, and random secret keys utilized in the proposed N-Round Cryptography algorithm. This cryptographic algorithm is designed with the highest level of security, incorporating a variety of rounds according to multiple predetermined conditions. The evaluation process of the algorithm is conducted using two methods: the systematic behavior, which examines the correlation between the plaintext message and the cipher, expects a lower Cr to yield a stronger secret key for a robust cipher. The second scenario involves the random selection of keys for each round. The number of rounds is flexible, with no limit imposed based on the required level of security, AR, overhead computation, power, environment, and so on.

Table 1

Table 1. Samples of S_keys pool contents based on the generating method.

4 The objective metrics: performance evaluations

The efficiency, reliability, applicability, and complexity of the proposed cascaded cryptosystem are measured by evaluating the processing time, the quality of the extracted/decrypted images, and the number of rounds (Latha Prasath, 2020).

This section defines the different performance metrics. Many metric tools are employed to measure the similarities between the plaintext and the decrypted version. Additionally, the algorithm’s efficiency is evaluated based on the quality of the deciphered text. The metrics used are described as follows:

• Correlation coefficient (Cr):

It is one of the common metrics for measuring the degree of closeness between two functions. This metric can be used to determine the extent to which two images are close to each other, as given in Equation 14.

$\begin{array}{ll}Cr=\mathit{Corr}(F\left(x,y\right),f\left(X,Y\right)& (14)\end{array}$

Thus, it provides a direct measure of the proposed algorithm’s efficiency. The most efficient algorithms produce images with correlation ratios closer to unity (Alrubaie et al., 2023).

• Mean square error (MSE):

MSE is one of the most important image quality evaluation metrics, and it can be defined as the average of the squares of the differences between the intensities of two examined images. It can be mathematically represented as in Equation 15,

$\begin{array}{ll}MSE=\frac{1}{MN}{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^N}{\left(f\left(i,j\right)-f^{\prime }\left(i,j\right)\right)}^2\text{,}& (15)\end{array}$

where f (i, j) is the original image, and f′(i, j) is the marked image. Higher values of MSE mean that the image is of poor quality (Iqbal et al., 2023).

• Peak Signal-to-Noise Ratio (PSNR):

The PSNR can be formulated mathematically as Equation 16:

$\begin{array}{ll}\mathit{PSNR}\left(\mathit{dB}\right)=10log\left(\raisebox{1ex}{${255}^2$}\!\left/ \!\raisebox{-1ex}{$MSE$}\right.\right)& (16)\end{array}$

A higher value of PSNR is better (Roselinkiruba, 2023).

• Structural Similarity (SSIM):

The SSIM is a recently proposed image fidelity measure that has proven highly effective in assessing the fidelity of signals. The human visual system is particularly sensitive to structural distortions and can easily compensate for non-structural ones. The primary purpose of the SSIM is to simulate this functionality; it is calculated as follows (Megías et al., 2021):

Let x = {xi|i = 1, 2, …, N} and y = {yi|i = 1, 2, …, N} be the original and the test image signals, respectively. Then, the SSIM can be expressed as Equation 17:

$\begin{array}{c}\hfill \mathit{SSIM}=\frac{4{\sigma }_{xy}{x}^{\prime }{y}^{\prime }}{\left({\sigma }_x^2+{\sigma }_y^2\right)\left[{\left(x^{\prime }\right)}^2+{\left(y^{\prime }\right)}^2\right]}\hfill \\ \hfill \mathrm{It}\mathrm{can}\mathrm{also}\mathrm{be}\mathrm{expressed}\mathrm{b}\mathrm{y}\mathrm{the}\mathrm{following}\mathrm{formula}:\hfill \\ \hfill \mathit{SSIM}=\frac{{\sigma }_{xy}}{{\sigma }_x{\sigma }_y}.\frac{2x^{\prime }{y}^{\prime }}{{\left(x^{\prime }\right)}^2+{\left(y^{\prime }\right)}^2}.\frac{2{\sigma }_x{\sigma }_y}{{\sigma }_x^2+{\sigma }_y^2}\hfill \end{array}\text{ (17)}$

The results of the executed experiments indicate that the SSIM is more accurate than the correlation coefficient metric. The SSIM metric captures more details in similarity than the Cr (Dala and Juneja, 2021).

• Computational and Time Complexity (CC&TE):

The fifth metric tool is the complexity of the proposed cryptosystem compared to existing security techniques. The term ‘complexity’ refers to three related concepts: computational complexity, which involves the number of operations needed to execute the cryptosystem for encrypting and decrypting plaintext; time complexity (TE), which concerns the execution time of the cryptosystem algorithms; and power complexity, which pertains to the amount of power required to perform the algorithms of the cryptosystem. These three terms are interconnected. In this study, the time complexity is measured to evaluate the processing time of the encryption algorithms within the proposed N-round cryptosystem (Nezami et al., 2022; Kumar and Jung, 2019; Bhavani et al., 2021; Singh et al., 2018).

• Presence attacks:

The robustness and reliability of the proposed N-round cryptosystem have been evaluated to measure its resistance to attacks and noise. The quality of the extracted classified images has been assessed while considering the presence of various types of image attacks, including Gaussian noise, salt-and-pepper noise, and speckle attacks (Rasmia et al., 2019; Nashat and Mamdouh, 2019; Abdel-Wahab et al., 2021; Alshoura et al., 2021; Abushhiwa and Abdussalam, 2024).

5 Computer simulation result discussion

Various computerized simulation experiments have been conducted to demonstrate the effectiveness of an N-round chaos-based cascaded cryptographic approach. Simulation tests were run using Windows 10 and MATLAB version 2017.

The simulation experiments were conducted on a variety of images that differed in size and grayscale (black and white), as shown in Figure 5, to assess the applicability of the proposed crypto algorithm.

Figure 5

Figure 5. The utilized image in the computer simulation experiments including the gray scale and RGB images (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

5.1 Result of 2-D BM-based chaos N-round crypto algorithm on gray images

In this section, we present the results of the simulation experiments for the idea of Chaos-based BM Round. The simulation experiments were conducted on several different grayscale images of size 256×256. Various encryption keys were applied in accordance with the idea of a Chaos-based BM Round. This idea aims to encrypt the image using multiple encryption keys to create a significant distance between the original and the encrypted images. The large distance between the images adds a high level of encryption strength, making it difficult to access the original image easily. This is shown in the results presented later. The results are divided into four parts: 1-Round, 2-Round, 3-Round, and 4-Round.

5.1.1 Chaos N-round crypto algorithm: one S_key (N = 1)

Figure 6 illustrates the encryption and decryption of the image using the Chaos-based BM Round technique. The image was encrypted using one encryption key: S_key1 = [23, 25, 10, 6, 23, 25, 10, 6, 23, 25, 10, 6, 23, 25, 10, 6] − {Semi-random key}.

Figure 6

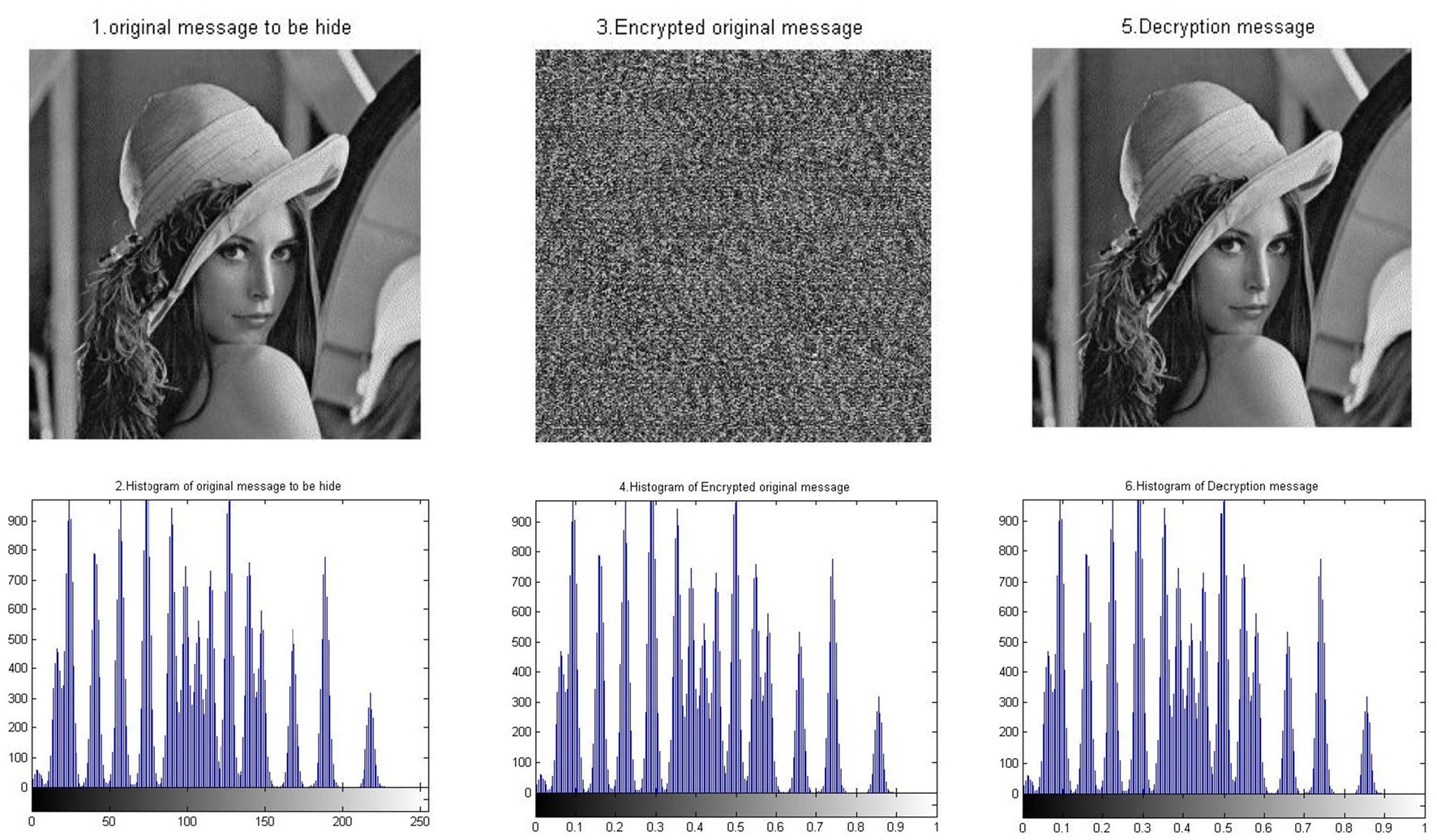
Figure 6. Sample results of the chaos N-round crypto algorithm: one S_key (N = 1) (reproduced “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, licensed under CC BY 4.0).

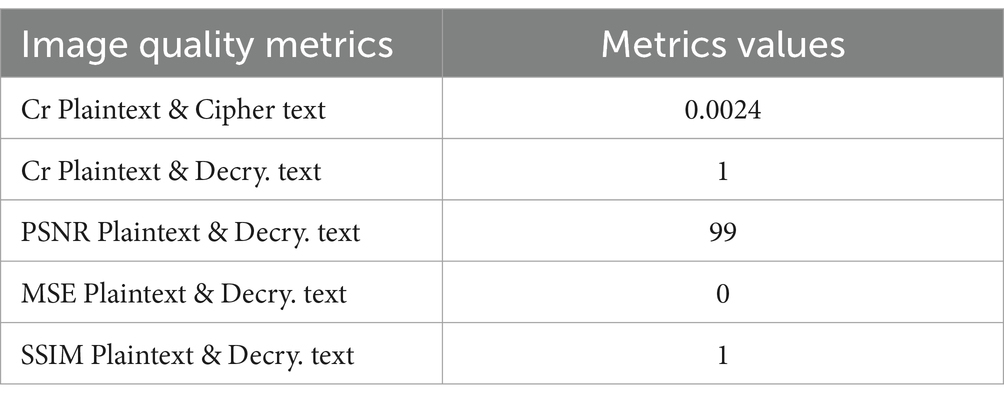
The figure shows a significant difference between the original image and the encrypted image. This difference indicates the strength of the encryption technique used. It also shows a match between the original image and the decrypted image, which indicates the high quality of the BM in recovering the original image without any loss. This means that the BM is a lossless data technique. Table 2 presents the results of the experiments and confirms what is shown in Figure 6.

Table 2

Table 2. Chaos N-round crypto algorithm: one S_key (N = 1 round).

Table 2 illustrates the encryption strength of the chaos-based BM in data encryption. This is shown in the correlation value between the original image and the encrypted image, which is 0.0024, a value less than 1. This indicates the degree of separation between the two images. Additionally, the table shows the high quality of the BM in recovering the original data without loss. This is reflected in the degree of similarity between the original image and the decrypted image, where the correlation coefficient between them equals 1. This correlation is also shown in the PSNR and MSE values. This indicates the efficiency of the BM in encryption and decryption, confirming that the BM is a lossless data technique.

5.1.1.1 The applicability measurement of the one-round cryptosystem

In this section, the experiments demonstrate the applicability of the one-round cryptographic algorithm within the one S_key. Various standard and non-standard images are utilized in these experiments, where different metrics are used to evaluate the quality of the extracted plaintext after the one-round process.

Table 3 shows the results of simulation experiments using a single encryption key for various 256×256 images.

Table 3

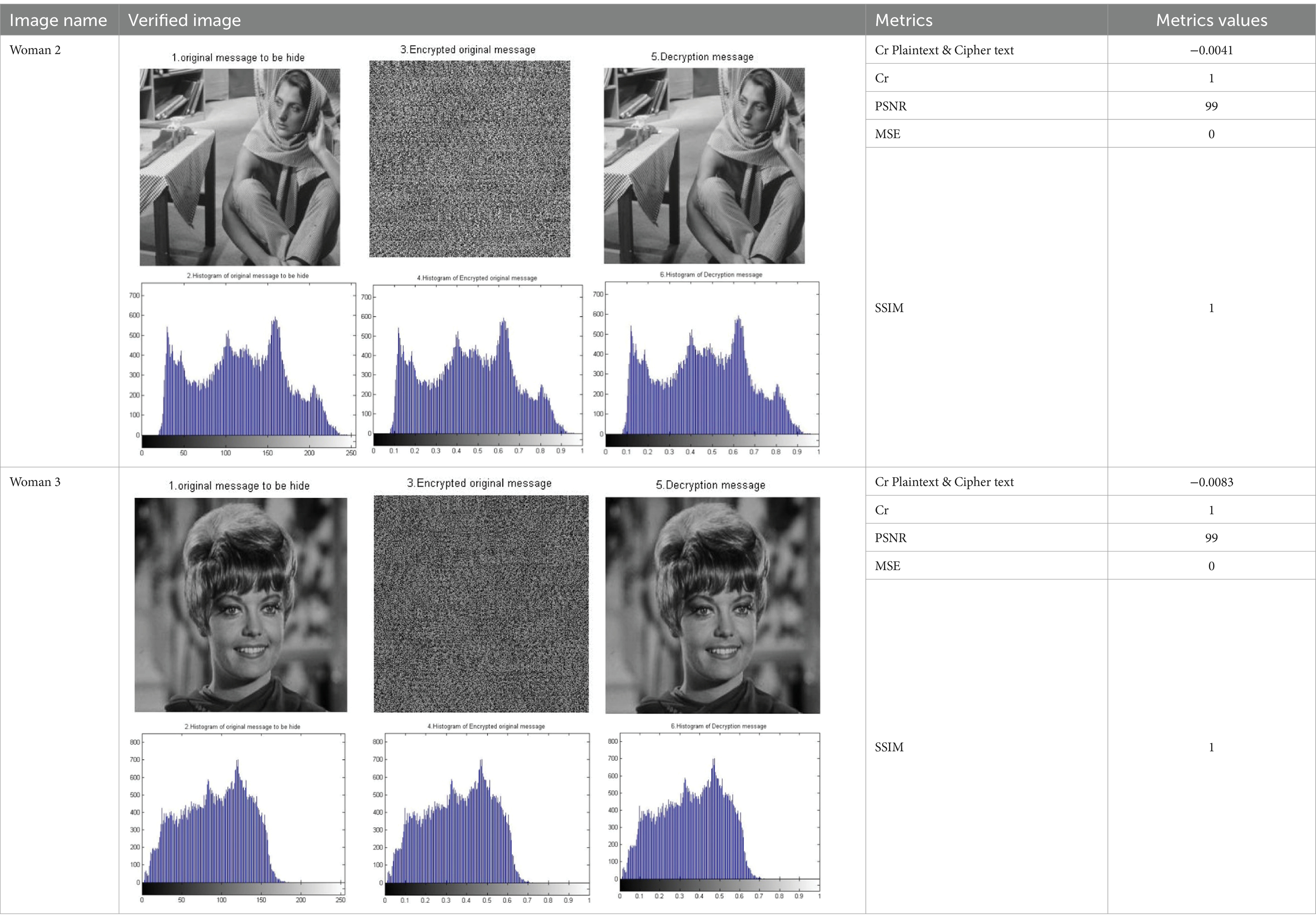
Table 3. Chaos N-round crypto algorithm: one S_key (N = 1) (reproduced from “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

The encryption key used is S_key1 = [23,25,10,6,23,25,10,6,23,25,10,6,23,25,10,6] − {Semi-random key}.

The results presented in the table illustrate the strength of the Baker map in data encryption. We observe a significant difference between the original image and the encrypted image in the first and second images of the woman. In the first image, the correlation coefficient between the original image and the encrypted image is −0.0041, while in the second image, it is −0.0083. These values are less than 1, indicating the strength of the encryption. The results also demonstrate the effectiveness of the Baker map in recovering data without loss. In both images, the correlation coefficient between the original image and the decrypted image is 1, indicating the efficiency of the Baker map in data recovery without any loss.

Two standard images are used to evaluate the algorithm’s applicability and to observe the effect of S_key on the encrypted images. As shown in the results, the Cr between the plaintext and the encrypted version varies based on the plaintext structure. The algorithm with the N-round on-S_key produces high-quality extracted images.

5.1.2 Chaos N-round crypto algorithm: two cascaded S_keys (N = 2)

As shown in Figures 1, 4, which present the construction and processing details of the proposed cryptosystem algorithm, two different secret keys are used to encrypt the plaintext in two separate cascaded processes. The utilized keys are merely examples, while the proposed cryptosystem algorithm manages a vast number of secret keys with flexible generating rules to construct a pool of secret keys.

Figure 7 illustrates the encryption and decryption of the image using the Chaos-based BM 2-round technique. The image was encrypted with two encryption keys:

S_key1 = [23,25,10,6,23,25,10,6,23,25,10,6,23,25,10,6] − {Semi-random key}.

S_key2 = [64, 34, 60, 64, 34] − {Semi-random key}.

Figure 7

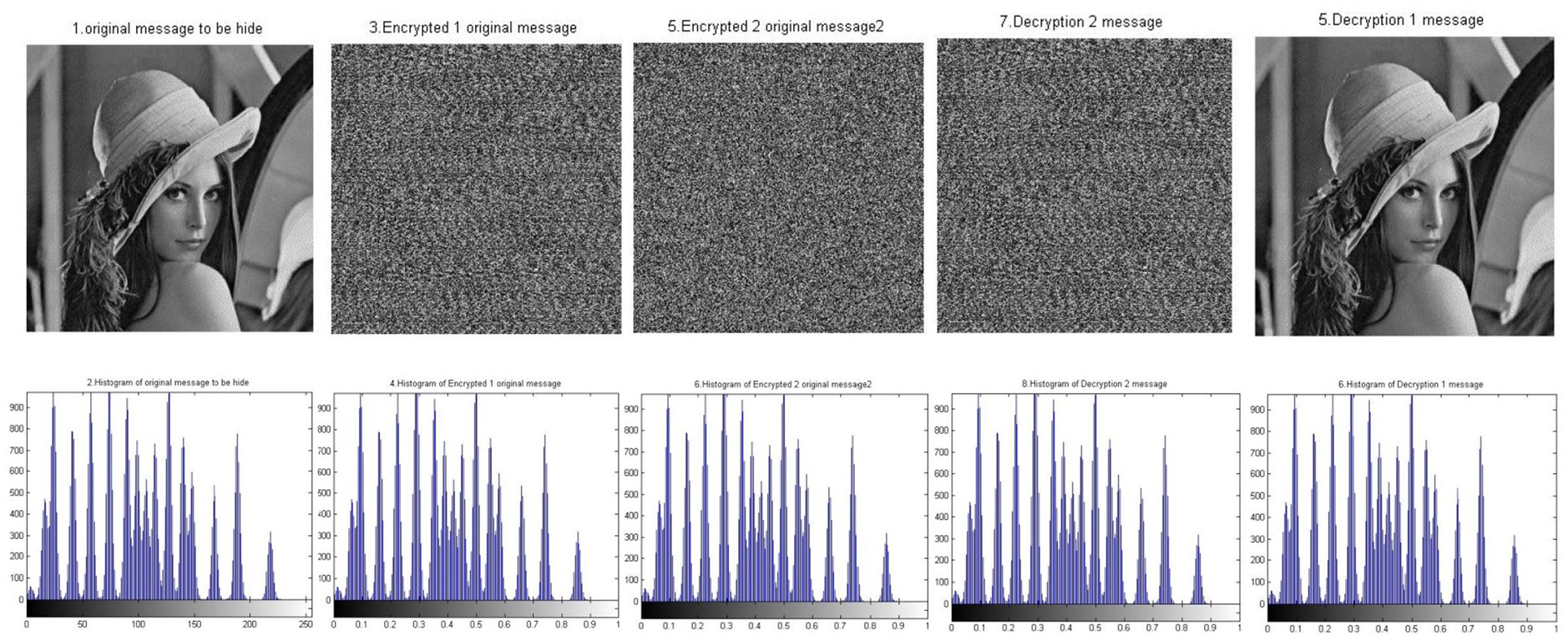
Figure 7. Sample results of the chaos N-round crypto algorithm: two cascaded S_keys (N = 2) (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, licensed under CC BY 4.0).

Figure 7 shows a significant difference between the original image and the encrypted images. This difference reflects the strength of encryption using the BM Round technique. It also reveals a match between the original image and the decrypted image. This match demonstrates the high quality of the BM Round in recovering the original image without any loss. Thus, the BM Round is a lossless data technique. Table 4 presents the experiment results and reinforces the findings shown in Figure 7.

Table 4

Table 4. Tabulated results of chaos N-round crypto algorithm: two cascaded S_keys (N = 2).

Table 4 illustrates the encryption strength of the BM Round in data encryption. This is shown in the correlation value between the original image and encrypted image 1, which equals 0.0024. Moreover, the correlation coefficient between the original image and encrypted image 2 is 0.0021. These values, being less than 1, indicate the degrees of separation between the original image and the encrypted images. Additionally, the table demonstrates the high quality of the BM in recovering the original data without loss. This is reflected in the degree of similarity between the original image and the decrypted image, where the correlation coefficient equals 1. This correlation is also shown in the PSNR and MSE values. This indicates the efficiency of the chaos BM N-(2) round in encryption and decryption, indicating that the proposed crypto algorithm is a lossless data technique.

5.1.2.1 The applicability measuring of the two-cascaded N-2 round cryptosystem

In this section, the experiments demonstrate the applicability of the 2-cascaded cryptographic algorithm within two different S_keys. Various standard and Nan images are utilized in these experiments, where different metrics are used to evaluate the quality of the extracted plaintext after the two cascaded processes.

The results of these experiments are shown in Table 5, which presents the outcomes of simulation experiments using two encryption keys for various images sized 256×256. The encryption keys used are as follows:

S_key1 = [23,25,10,6,23,25,10,6,23,25,10,6,23,25,10,6].

S_key2 = [64, 34, 60, 64, 34].

Table 5

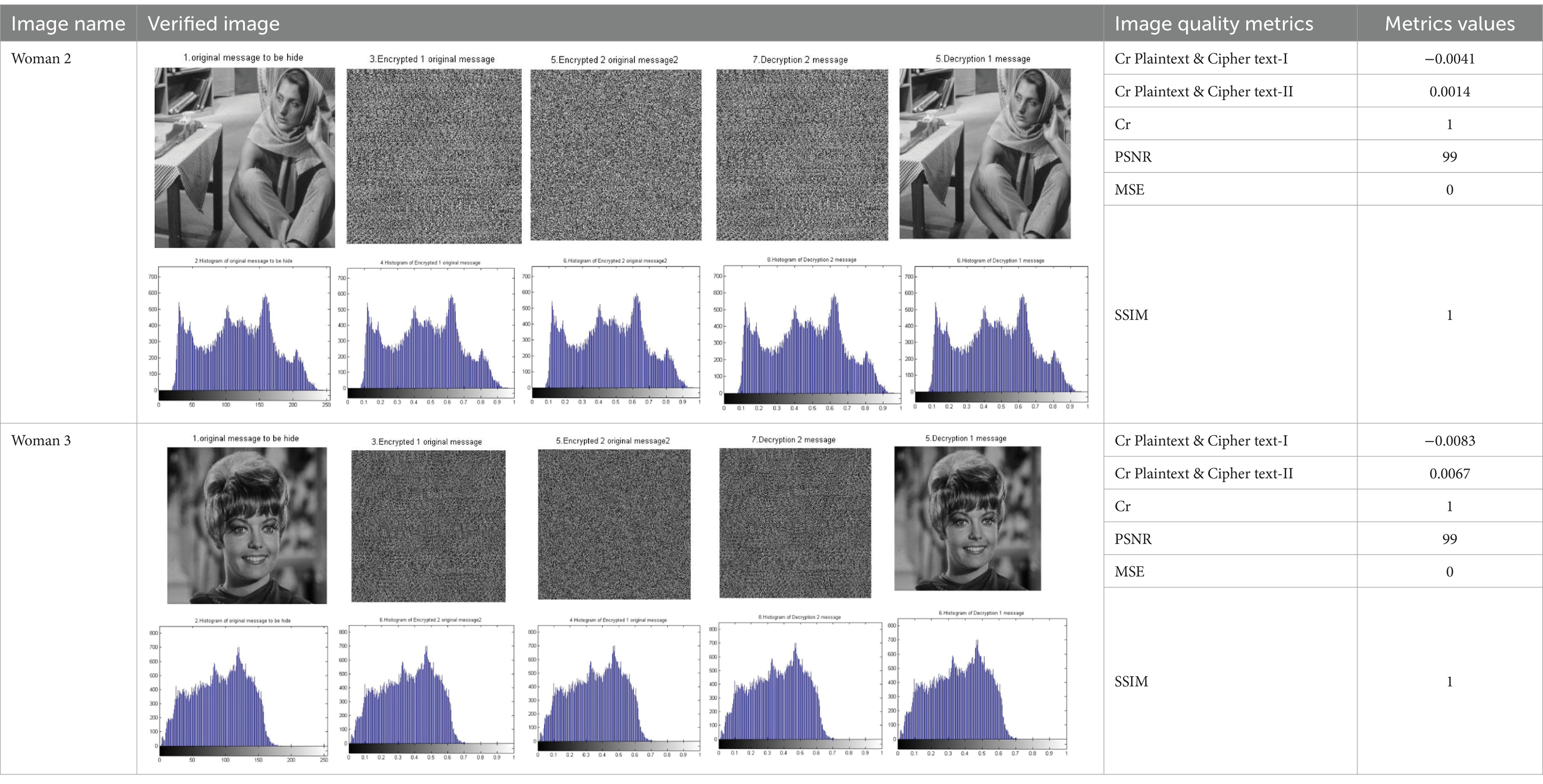
Table 5. Tabulated results of applicability measurement for the chaos N-round crypto algorithm: two cascaded S_keys (N = 2) (reproduced from “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

The results presented in the table illustrate the strength of the Baker map round in data encryption. We observe a significant difference between the original image and the encrypted images in the first and second images of the woman.

• In the first image, the correlation coefficient between the original image and the encrypted image 1 is −0.0041.

• The second stage in the two cascaded cryptosystems, the original image and the encrypted image 2 is 0.0014.

• In the second image, the correlation coefficient between the original image and the encrypted image 1 is −0.0083.

• The Cr value between the original image and the encrypted image 2 is 0.0067.

• These values are close to zero and, in some experiments, are less than zero, indicating a “Negative Correlation.

5.1.3 Chaos N-round crypto algorithm: three cascaded S_keys (N = 3)

As shown in Figures 1, 4, which present the construction and processing details of the proposed cryptosystem algorithm, three different secret keys are used to encrypt the plaintext within three separate cascaded processes. The keys used are only examples, while the proposed cryptosystem algorithm manages numerous S_keys with flexible generating rules to construct the pool of secret keys.

Figure 8 illustrates the encryption and decryption of the image using the Chaos-based BM 3-Round technique. The image was encrypted using three encryption keys:

S_key1 = [23,25,10,6,23,25,10,6,23,25,10,6,23,25,10,6].

S_key2 = [64, 34, 60, 64, 34].

S_key3 = [50, 14, 50, 14, 50, 14, 50, 14].

Figure 8

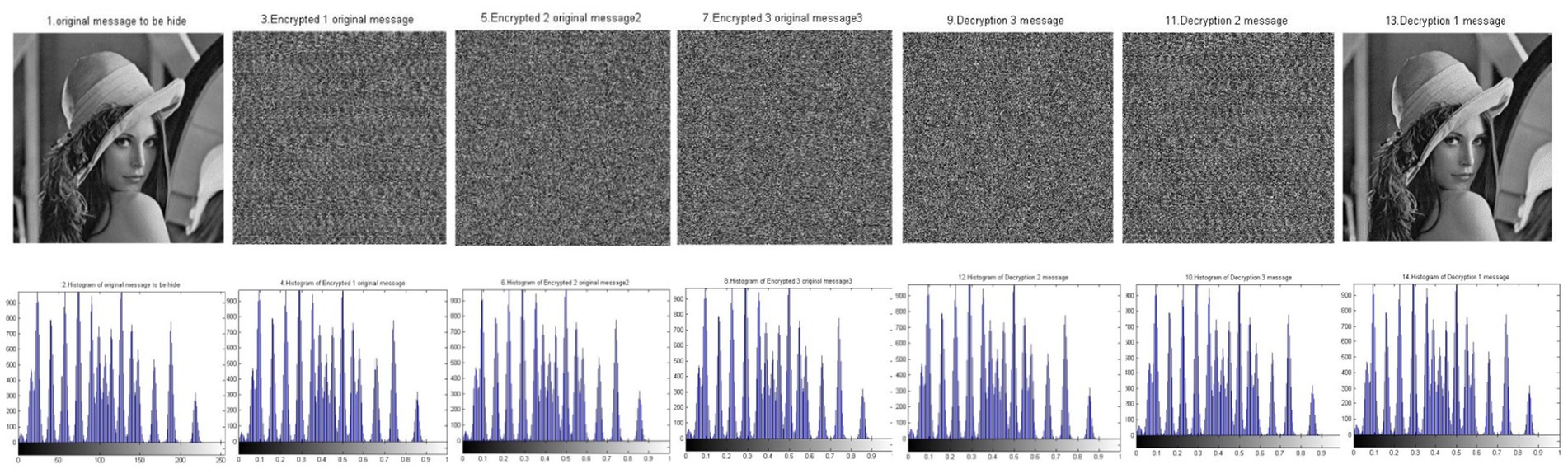
Figure 8. Sample results of the chaos N-round crypto algorithm: three cascaded S_keys (N = 3) (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, licensed under CC BY 4.0).

Figure 8 shows a significant difference between the original image and the encrypted images. This difference indicates the strength of encryption using the BM Round technique. Table 6 presents the results of the experiments and confirms what is shown in Figure 8.

Table 6

Table 6. Tabulated results of the chaos N-round crypto algorithm: three cascaded S_keys (N = 3).

Table 6 illustrates the encryption strength of the BM Round in data encryption. This is shown by the correlation value between the original image and encrypted image 1, which equals 0.0024. Additionally, the correlation coefficient between the original image and encrypted image 2 is 0.0021, while the correlation coefficient between the original image and encrypted image 3 is −0.0007. These values are all less than 1, indicating the degree of separation between the original image and the encrypted images. The table also shows the high quality of the BM in recovering the original data without loss. This is reflected in the degree of similarity between the original image and the decrypted image, where the correlation coefficient between them equals 1. This correlation is also evident in the PSNR and MSE values, indicating the efficiency of the chaos BM N-(3) Round in encryption and decryption. It also means that the BM Round is a lossless data technique.

5.1.3.1 The applicability measurement of the three-cascaded N-3 round cryptosystem

In this section, we demonstrate the experiments designed to measure the applicability of the 3-cascaded cryptographic algorithm across three different S_keys. Standard images and NaN are used in these experiments, employing various metrics to evaluate the quality of the extracted plaintext after the three-cascaded process.

The results of these experimental groups have been tabulated in Table 7; it shows the results of simulation experiments on two encryption keys for different images of size 256 × 256. The encryption keys used are as follows:

S_key1 = [23, 25, 10, 6, 23, 25, 10, 6, 23, 25, 10, 6, 23, 25, 10, 6].

S_key2 = [64, 34, 60, 64, 34].

S_key3 = [50, 14, 50, 14, 50, 14, 50, 14].

Table 7

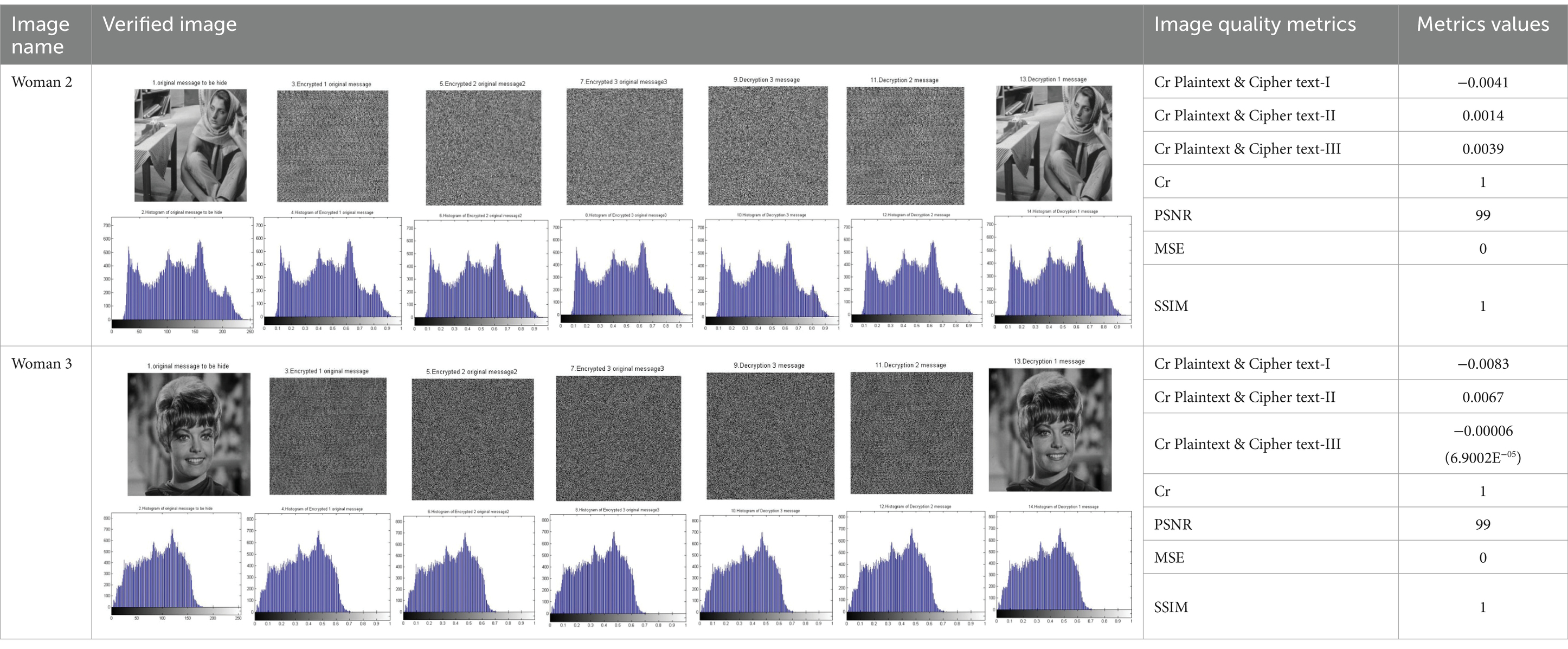
Table 7. Tabulated results of the applicability measurement of the chaos N-round crypto algorithm: three cascaded keys (N = 3) (reproduced from “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

The results presented in the table illustrate the strength of the Baker map round in data encryption. We observe a significant difference between the original image and the encrypted images in the first and second images of the woman.

• In the first image, the correlation coefficient between the original image and the encrypted image 1 is −0.0041.

• The second stage in the two cascaded cryptosystems, the original image and encrypted image 2, is 0.0014.

• The third stage in the two cascaded cryptosystems, the original image and encrypted image 3, is 0.0039.

• In the second image, the correlation coefficient between the original image and encrypted image 1 is −0.0083.

• The Cr value between the original image and the encrypted image 2 is 0.0067.

• The Cr value between the original image and the encrypted image 3 is −0.00006.

• These values are close to zero, and in some experiments, they are less than zero, indicating a “Negative Correlation.”

5.1.4 Chaos N-round crypto algorithm: four cascaded S_keys (N = 4)

Figure 9 illustrates the encryption and decryption of the image using the BM round technique. The image was encrypted using four encryption keys:

S_key1 = [23,25,10,6,23,25,10,6,23,25,10,6,23,25,10,6].

S_key2 = [64, 34, 60, 64, 34].

S_key3 = [50, 14, 50, 14, 50, 14, 50, 14].

S_key4 = [64, 128, 64].

Figure 9

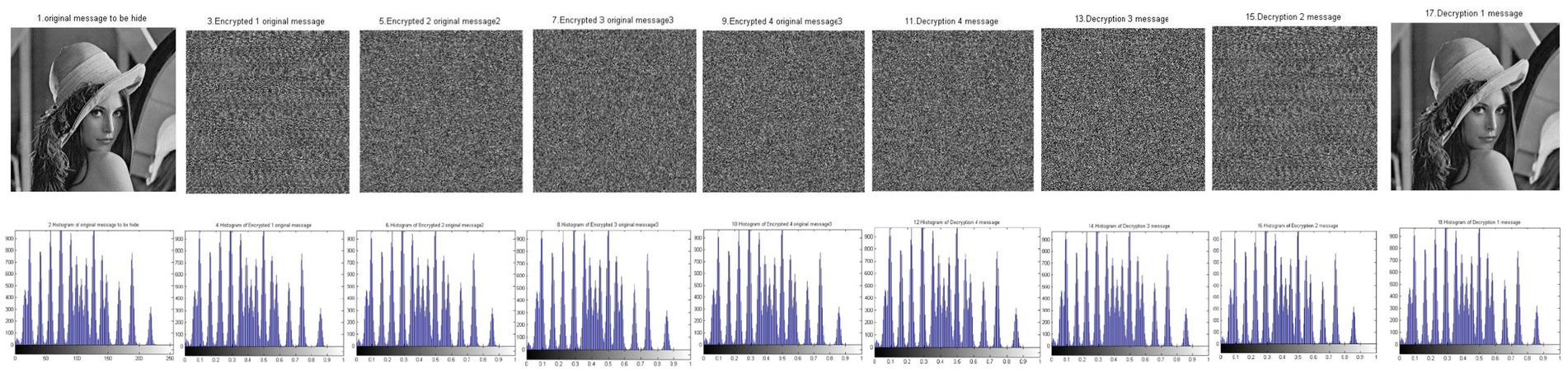
Figure 9. Sample results of the chaos N-round crypto algorithm: four cascaded S_keys (N = 4) (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, licensed under CC BY 4.0).

Figure 9 shows a significant difference between the original image and the encrypted images. This difference highlights the robustness and reliability of encryption using the BM Round technique. Table 8 presents the results of the experiments and confirms the findings shown in Figure 9.

Table 8

Table 8. Chaos N-Round Crypto-Algorithm: Four S_key (N = 4).

Table 8 illustrates the encryption strength of the BM Round in data encryption. This is indicated by the correlation value between the original image and encrypted image 1, which equals 0.0024. Moreover, the correlation value between the original image and encrypted image 2 is −0.0084. Additionally, the correlation value between the original image and encrypted image 3 is −0.0028.

C_r between the original image and encrypted image 4 is −0.0005.

As clarified in these results, the cascaded encryption processing and the generation of the cipher from the cipher have minimal effects on the decrypted image. Each stage in the algorithm is considered an enhancement of the cipher, as shown in Tables 5, 7. The Cr of the plaintext and cipher can be adversely affected during the multi-round process.

5.1.4.1 The applicability measuring of the four-cascaded N-4 round cryptosystem

In this section, the experiments demonstrate the applicability of the four-cascaded cryptographic algorithm across the four different S_keys. Various image standards and Nan are utilized in these experiments, where different metrics are used to evaluate the quality of the extracted plaintext after the four cascaded processes.

Table 9 shows the results of simulation experiments using four encryption keys on various images sized 256×256. The encryption keys used are as follows:

S_key1 = [23,25,10,6,23,25,10,6,23,25,10,6,23,25,10,6].

S_key2 = [64, 34, 60, 64, 34].

S_key3 = [50, 14, 50, 14, 50, 14, 50, 14].

S_key4 = [64, 128, 64].

Table 9

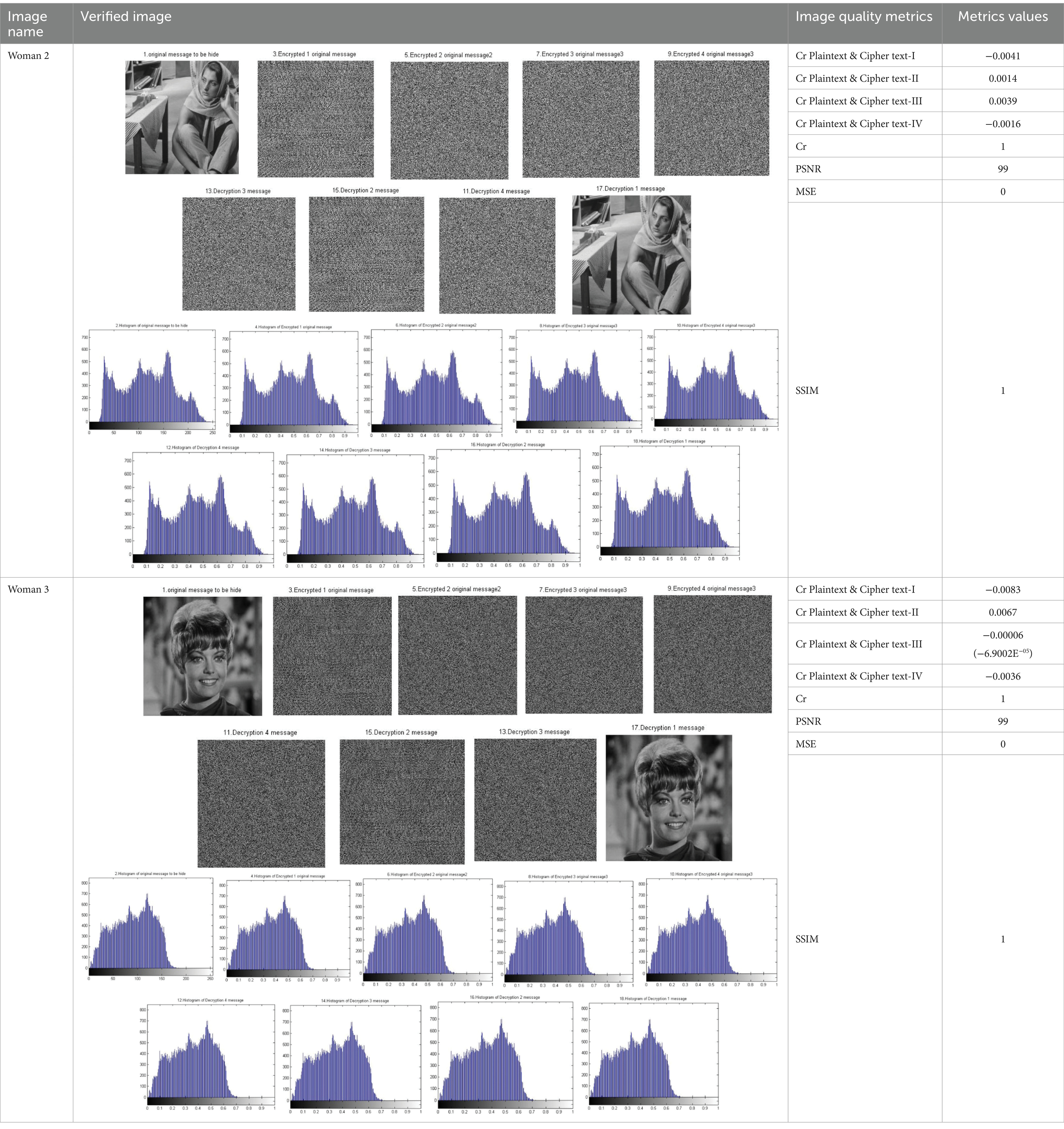
Table 9. Tabulated results of the applicability measurement of the chaos N-round crypto algorithm: four cascaded S_keys (N = 4) (reproduced from “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

The results presented in the table illustrate the strength of the BM Round in data encryption. We observe a significant difference between the original image and the encrypted images in the first and second images of the woman.

In the first image, the C_r value between the original and encrypted image 1 is −0.0041. In the second stage, C_r = 0.0014, while Cr = 0.0039 in the third stage. In the fourth stage, Cr ₌ −0.0016, as shown in Table 9. In a second experiment with a different image, the C_r values are −0.0083, 0.0067, −0.00006, and 0.0036 for stages 1, 2, 3, and 4, respectively. These results are also presented in Table 9.

As shown in the previous results of the experiments, the proposed algorithm provides high flexibility in the number of rounds while ensuring high quality in the extracted classified images. The similarity between the plaintext and the deciphered image across different rounds is 100% because the values of the metrics C_r and SSIM are equal to 1.

Moreover, as clarified by the experiments on the algorithm’s applicability, it is reliable and effective because it performs better with a variety of images selected from widely used image databases {Hlevkin, USA CANVAS}. The S_keys used in the previous experiments across different rounds are very flexible and can be changed, as shown in Table 1.

5.1.5 Strategy of S_key for the Chaos N-round crypto algorithm

This section examines the performance of the 4-round chaos cryptosystem by varying the strategy for selecting the secret key to achieve a highly robust encrypted plaintext. The C_r of the cipher image is measured in each round. In the four cascaded crypto algorithms, four secret keys are selected to ensure a significant difference between the ciphertext and the original plaintext similarity. Figure 10 illustrates the steps of the proposed algorithm with N-Round (four). The selection of S_keys is based on the C_r between the plaintext and ciphertext for each round individually. As shown in the results, the distinction between the plaintext and ciphertext has increased in each round due to the S_key.

Figure 10

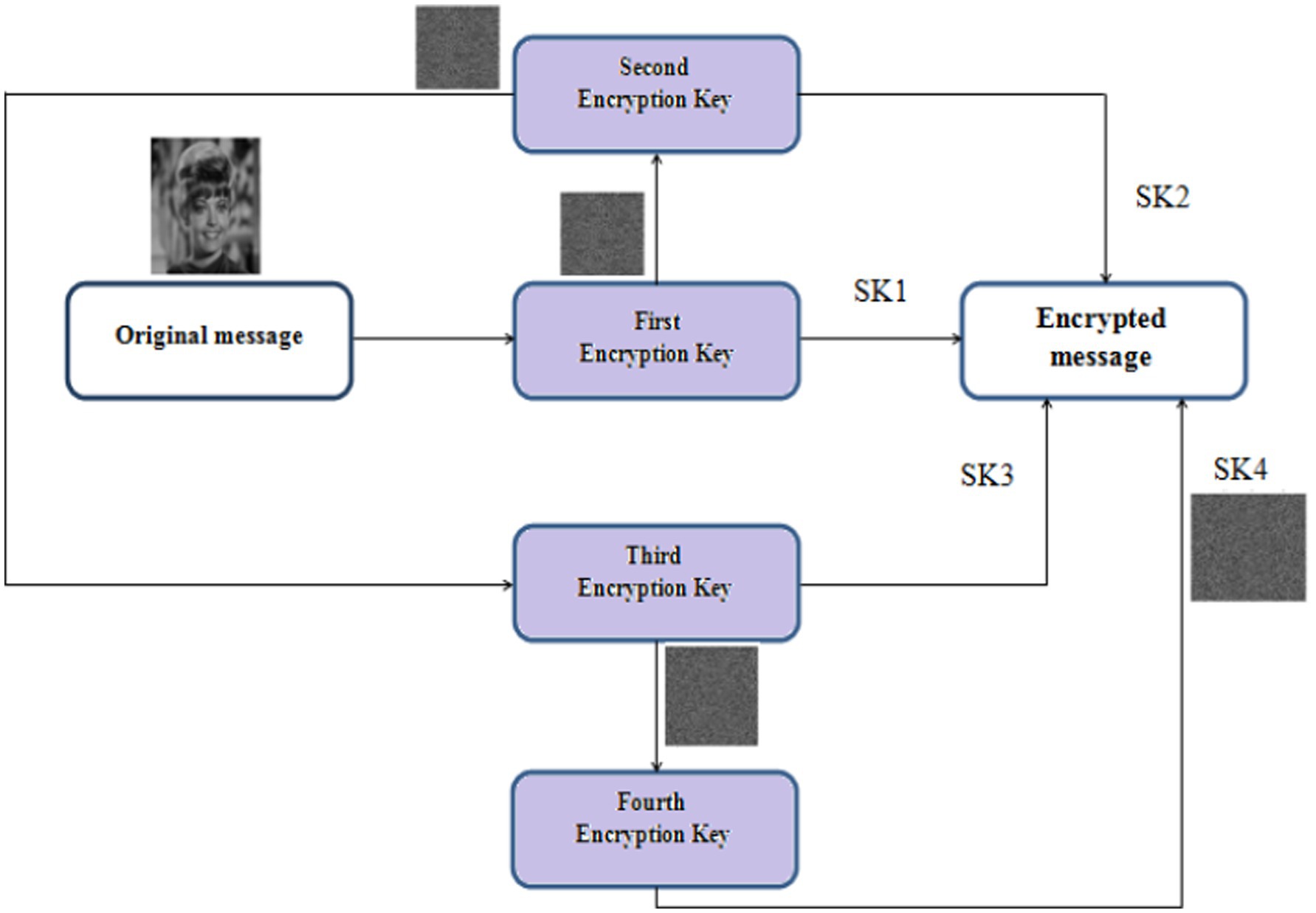
Figure 10. Mechanism of chaos N-round crypto algorithm: four cascaded S_keys (N = 4) with different domains consideration (reproduced from “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

Table 10 shows the results of simulation experiments on four additional encryption keys for various images of size 256 × 256. The encryption key for Woman 1 is as follows:

Table 10

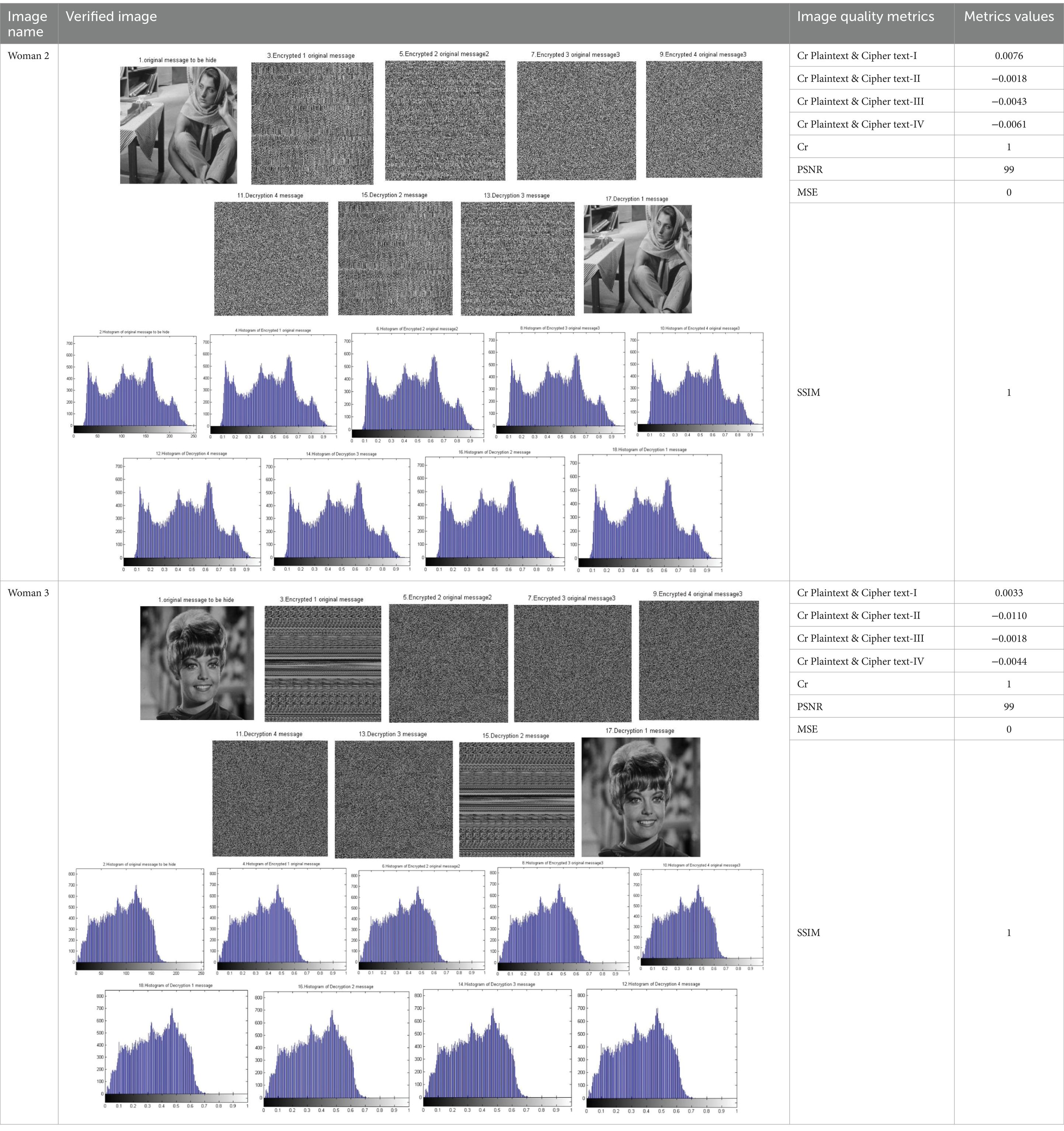
Table 10. Tabulated results of the chosen strategy for Cr S_keys and the applicability measurement of the chaos N-round crypto algorithm: four cascaded S_keys (N = 4) (reproduced from “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

Case I:

S_key1 = [10,5,14,8,5,12,10,10,5,14,8,5,12,10,10,5,14,8,5,12,10,10,5,14,8,5,12,10].

S_key2 = [64, 16, 16, 64, 64, 32].

S_key3 = [50, 14, 50, 14, 50, 14, 50, 14].

S_key4 = [20,10,5,10,10,9,20,10,5,10,10,9,20,10,5,10,10,9,20,10,5,10,10,9].

The encryption key for the woman 2 image is as follows:

Case II:

S_key1 = [32, 16, 16, 128, 32, 16, 16].

S_key2 = [50, 14, 50, 14, 50, 14, 50, 14].

S_key3 = [32, 32, 64, 64, 32, 32].

S_key4 = [23, 25, 10, 6, 23, 25, 10, 6, 23, 25, 10, 6, 23, 25, 10, 6].

To follow the differentiation of plaintext and cipher per stage/S_key, the results are tabulated in Table 10. The Cr values for Woman1’s image are 0.0076, −0.0018, −0.0043, and −0.0061 for stages 1, 2, 3, and 4, respectively. Meanwhile, the Cr for Woman2’s image ranges from 0.0033 to −0.0044, as shown in Table 10.

The results of the Chaos N-round indicate the strength of data encryption and the efficiency of data retrieval without loss. However, we observe that with different images, the results varied between the original image and the encrypted image. Additionally, using different encryption keys on the same images led to variations in the encryption results between the original and the encrypted images. Some results demonstrated a significant difference between the original and encrypted images when applying an encryption key. In contrast, applying another encryption key resulted in the original image being very close to the encrypted image, while yet another encryption key caused a substantial difference again. Therefore, encryption keys must be chosen very carefully to maintain a significant difference between the plaintext and the cipher, ensuring high encryption strength that is difficult to break easily.

5.2 Attacks presence consideration {gray scale images}

In this section, the performance of the proposed crypto algorithm is evaluated by considering the presence of various attacks. The simulation experiments were conducted using numerous different grayscale images. Image attacks are divided into several types, including noise, filtering, geometric, image enhancement, compression, and image temporal attacks.

The executed simulation experiments in this section have considered three different types of image attacks: Gaussian, salt and pepper, speckle, random, and Poisson noise (Singh et al., 2022; Naffouti et al., 2022). Three images are used to test the robustness of the algorithm and its resistance to noise and attacks. The noises are applied with various values, as shown in the results. Three different image attacks—Gaussian noise, salt and pepper, and speckle attacks—are applied with different values of α (0.1, 0.01, and 0.001). The results of the three deciphered images are tabulated in Tables 11–13 for α = 0.1, α = 0.01, and α = 0.001, respectively.

Table 11

Table 11. Deciphered image samples of the N-round chaos cryptosystem with respect to the various image attacks: {four cascaded S_key (N = 4) and (α = 0.1)} (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and "Zelda", Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

Table 12

Table 12. Deciphered image samples of N-round crypto-chaos algorithm with respect to the presence of various attacks: {four cascaded S_keys (N = 4) and (α = 0.01)} (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

Table 13

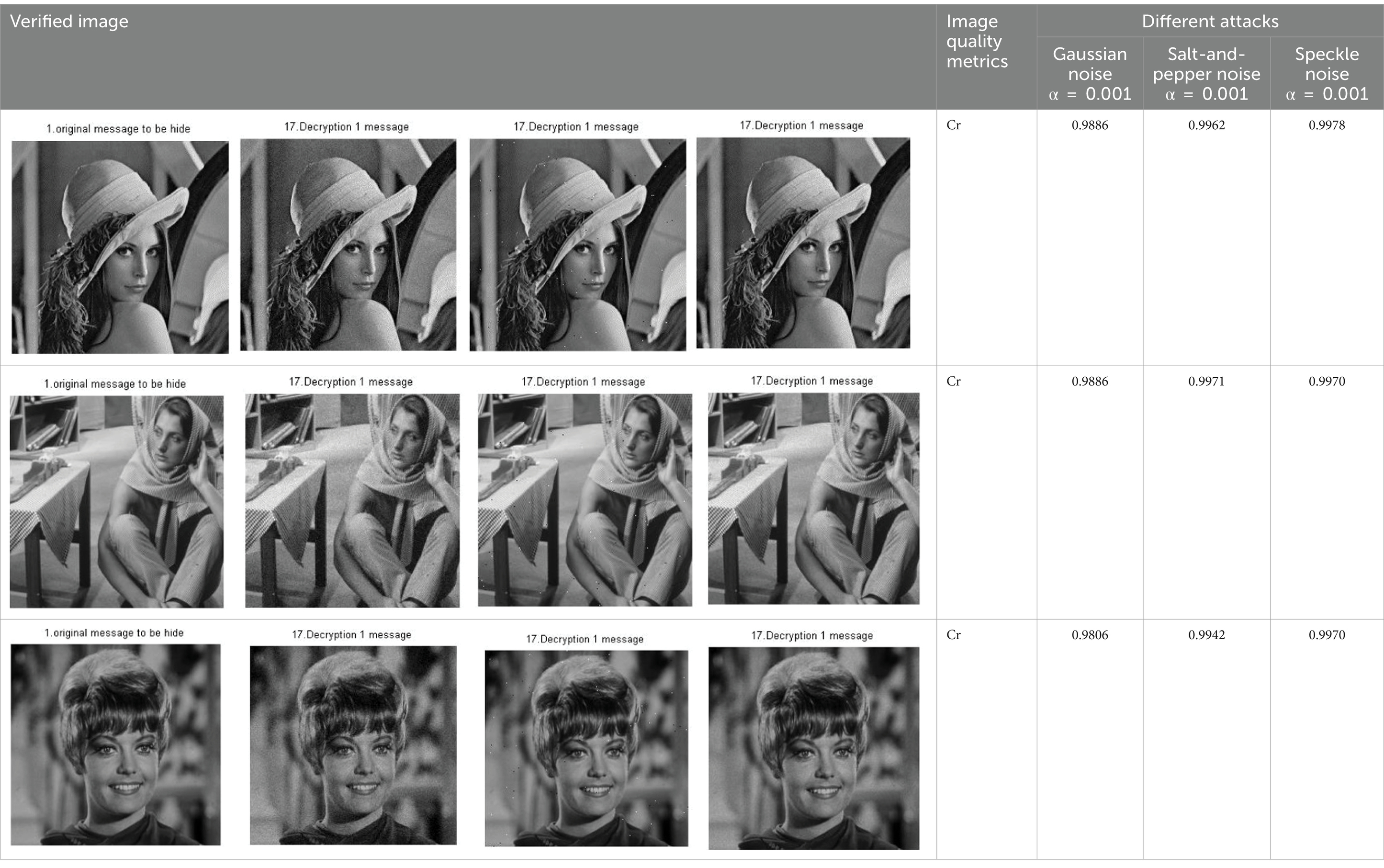
Table 13. Deciphered image samples of the crypto algorithm on grayscale images with different attacks: {four cascaded S_keys (N = 4) and (α = 0.001)} (reproduced from “Lenna”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/lenna.bmp, “barbara”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/barbara.pgm and “Zelda”, Mathship/Hlevkin database, https://www.hlevkin.com/hlevkin/TestImages/zelda.bmp, licensed under CC BY 4.0).

As shown in Table 11, these results represent the worst-case scenario, with {α = 0.1}. The ordinary quality metrics mentioned in Section 4 are utilized to evaluate the deciphered images. Gaussian noise adversely affects the images compared to salt and speckle noise. Sometimes, the effects of this noise vary from one image to another due to pixel values, as illustrated by the differences between Image 1 (Cr = 0.543) and Image 3 (Cr = 0.4372) for Gaussian noise. In contrast, the metric values for speckle noise are very similar, as shown in the tabulated results in Table 11. Therefore, based on these results, it is clear that the proposed algorithm is more resilient to salt-and-pepper and speckle noise than to Gaussian noise.

As shown in Tables 12, 13, the extracted images have been improved, as clarified by the metric values. From the tabulated results in Table 12, the deciphered image in the presence of Gaussian noise is affected more, with C_r = 0.9038, compared to C_r = 0.9637 for salt-and-pepper noise and Cr = 0.9782 for speckle noise in the same scenario. In the case of speckle noise, the metric values are very close, as shown in the tabulated results in Table 13. Therefore, it is clear that the proposed N-round chaos-crypto algorithm performs better in the presence of moderate noise; the quality of the extracted deciphered classified image is good. With a lower noise level, the proposed security algorithm succeeds in extracting the image with very high quality, as verified by the tabulated results in Table 13. Consequently, the results of the previous experiments demonstrate the robustness, applicability, and reliability of the proposed crypto algorithm in the presence of various attacks and noise.

The degree of robustness of the encryption process of the crypto algorithm, compared to recent related research studies, is considered in Table 14. This simple comparison takes into account the Cr of plaintext, cipher similarity, and the techniques/methodology utilized in different research works. As clarified in the tabulated results in Table 14, the proposed crypto algorithm based on the cascaded N-round chaos maps performs better than existing algorithms. On the other hand, the methodology and techniques utilized confirm the superiority of our algorithm due to lower overhead computation and the optional number of cascaded rounds in the algorithm.

Table 14

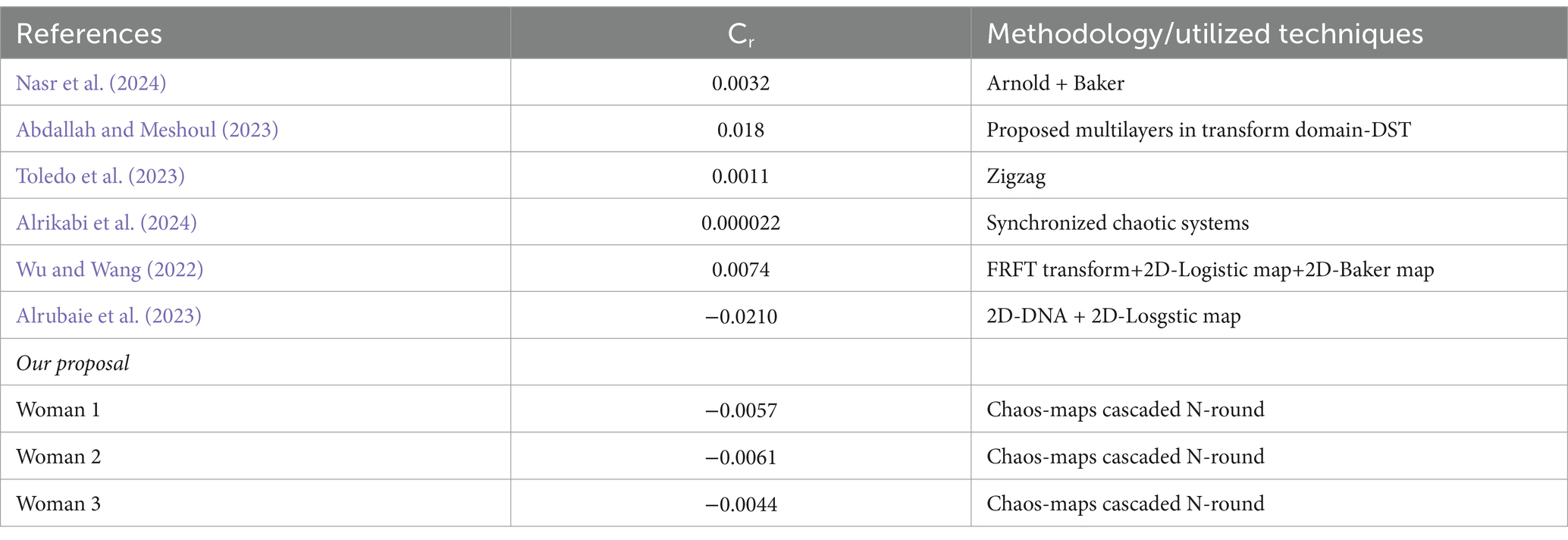
Table 14. Comparison of the proposed cryptographic algorithm and related studies with respect to C_r and the methodology/techniques utilized.

6 Conclusion

Due to the widespread use of multimedia applications and the variety of cyber-attacks, this study presents an efficient cryptographic algorithm to support multimedia privacy and combat various image cyber-attacks. The N-round chaos-based crypto algorithm has been proposed to provide a robust and reliable multimedia/image security approach with high flexibility in controlling the number of rounds. The construction of the security algorithm is based on merging various chaos maps in the spatial and frequency domains to enhance the security capabilities of the algorithm. Additionally, the study presents multiple strategies for applying the N-round concepts: cascaded, self-partitioning, and hybrid behavior. Several experiments have been conducted to evaluate the performance of the proposed N-Round crypto algorithm, both with and without the presence of noise and attacks. Both standard and non-standard grayscale images have been utilized in the dedicated experiments to measure the applicability and reliability of the proposed algorithm. The results of the experiments reveal that the proposed crypto algorithm is suitable and applicable for colored images in the presence of various attacks. Based on the results of the cascaded multi-round crypto algorithm, it is robust, reliable, and applicable for grayscale images. Furthermore, it features an interactive multi-round crypto approach. In future work, various behaviors of the N-round crypto algorithm will be explored, utilizing the auto-generation of the S_key algorithm.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

TS: Writing – original draft, Writing – review & editing. AE-R: Writing – original draft, Writing – review & editing. ME-B: Writing – original draft, Writing – review & editing. ME: Writing – original draft, Writing – review & editing. AA: Writing – original draft, Writing – review & editing. BN: Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdallah, H., and Meshoul, S. (2023). A multilayered audio signal encryption approach for secure voice communication. Electronics. 12, 1–15. doi: 10.3390/electronics12010002

Crossref Full Text | Google Scholar

Abdel-Wahab, O., Khalaf, A., Hussein, A., and Hamed, H. (2021). Hiding data using efficient combination of RSA cryptography, and compression steganography techniques. IEEE Access. 9, 31805–31815. doi: 10.1109/ACCESS.2021.3060317

Crossref Full Text | Google Scholar

Abodawood, M., Khalil, A., Amer, H., and Ata, M. (2024). Enhancing image encryption using chaotic maps: a multi-map approach for robust security and performance optimization. Clust. Comput. 27, 14611–14635. doi: 10.1007/s10586-024-04672-4

Crossref Full Text | Google Scholar

Abushhiwa, H., and Abdussalam, M. (2024). Network attacks and network security threats and preventions. Int. J. Adv. Eng. Manage. 6, 276–283. doi: 10.35629/5252-0602276283

Crossref Full Text | Google Scholar

Al-Eryani, Y., and Hossain, E. (2019). The D-OMA method for massive multiple access in 6G: performance, security, and challenges. IEEE Veh. Technol. Mag. 14, 92–99. doi: 10.1109/MVT.2019.2919279

Crossref Full Text | Google Scholar

Alraih, S., Shayea, I., Behjati, M., Nordin, R., Abdullah, N. F., Abu-Samah, A., et al. (2022). Revolution or evolution? Technical requirements and considerations towards 6G mobile communications. Sensor 22, 1–29. doi: 10.3390/s22030762

PubMed Abstract | Crossref Full Text | Google Scholar

Alrikabi, H., Aljazaery, I., and Alaidi, A. (2024). Using a chaotic digital system to generate random numbers for secure communication on 5G networks. Eng. Technol. Appl. Sci. Res. 14, 13598–13603. doi: 10.48084/etasr.6938

Crossref Full Text | Google Scholar

Alrubaie, A., Abid, M., and Talib, A. (2023). Image encryption based on 2DNA encoding and chaotic 2D logistic map. J. Eng. Appl. Sci. 1–21. doi: 10.1186/s44147-023-00228-2

Crossref Full Text | Google Scholar

Alsabah, M., Naser, M., Mahmmod, B., Abdulhussain, S., Eissa, M., Al-Baidhani, A., et al. (2021). 6G wireless communications networks: A comprehensive survey. IEEE Access 9, 148191–148243. doi: 10.1109/ACCESS.2021.3124812

Crossref Full Text | Google Scholar

Alshoura, W., Zainol, Z., Teh, J., Alawida, M., and Alabdulatif, A. (2021). Hybrid SVD based image watermarking schemes: A review. IEEE Access 9, 32931–32968. doi: 10.1109/ACCESS.2021.3060861

Crossref Full Text | Google Scholar

Bhat, J., and Alqahtani, A. (2021). 6G ecosystem: Current status and future perspective. IEEE Access 9, 43134–43167. doi: 10.1109/ACCESS.2021.3054833

Crossref Full Text | Google Scholar

Bhavani, Y., Kamakshi, P., Sri, E., and Sai, Y. (2021). A survey on image steganography techniques using least significant bit. Intelligent Data Communication Technologies and Internet of Things.

Google Scholar

Chowdhury, M., Shahjalal, M., Ahmed, S., and Jang, M. (2020). 6G wireless communication systems: applications, requirements, technologies, challenges, and research directions. IEEE Open J. Commun. Soc. 1, 957–975. doi: 10.1109/OJCOMS.2020.3010270

PubMed Abstract | Crossref Full Text | Google Scholar

Dala, M., and Juneja, M. (2021). A survey on information hiding using video steganography. Artif. Intell. Rev. 54, 5831–5895. doi: 10.1007/s10462-021-09968-0

Crossref Full Text | Google Scholar

Faragallah, O., Naeem, E., El-Shafai, W., Ramadan, N., Ahmed, H., Abd Elnaby, M., et al. (2021). Efficient chaotic-baker-map-based cancelable face recognition. J. Ambient. Intell. Humaniz. Comput. 14, 1837–1875. doi: 10.1007/s12652-021-03398-0

Crossref Full Text | Google Scholar

Fetteha, M., Sayed, W., and Said, L. (2023). A lightweight image encryption scheme using DNA coding and chaos. Electronics 12, 1–15. doi: 10.3390/electronics12244895

Crossref Full Text | Google Scholar

Fotsing, J., Kakmeni, J., Tiedeu, A., and Fotsin, H. (2023). Image encryption algorithm based on 2D logistic map system in IoHT using 5G network. Multimed. Tools Appl. 83, 30819–30845. doi: 10.1007/s11042-023-16730-x

Crossref Full Text | Google Scholar

Ghosha, G., Kavitab, D., Vermab, S., Talibc, N., and Hussain, M. (2021). A systematic review on image encryption techniques. Turk. J. Comput. Math. Educ. 12, 3055–3059.

Google Scholar

Hamouda, B. (2020). Comparative study of different cryptographic algorithms. J. Inf. Secur. 11, 138–148. doi: 10.4236/jis.2020.113009

Crossref Full Text | Google Scholar

Hamza, R., Muhammad, K., Arunkumar, N., and Ramí Rez-Gonzá Lez, G. (2017). Hash based encryption for Keyframes of diagnostic hysteroscopy. IEEE Access.

Google Scholar

Hayam, A., Noha, R., Walid, E., Ashraf, A., Hossam Eldin, H., Said, E., et al. (2022). Cancelable biometric security system based on advanced chaotic maps. Vis. Comput.

Google Scholar

Hong, E. K., Lee, I., Shim, B., Ko, Y. C., Kim, S., Pack, S., et al. (2022). 6G R &D vision: requirements and candidate technologies. J. Commun. Networks 24, 232–245. doi: 10.23919/JCN.2022.000015

Crossref Full Text | Google Scholar

Iqbal, N., Hussain, I., Adnan, M., Abbas, S., and Yousaf, S. (2023). An efficient image cipher based on the 1D scrambled image and 2D logistic chaotic map. Multimed. Tools Appl. 82, 40345–40373. doi: 10.1007/s11042-023-15037-1

Crossref Full Text | Google Scholar

Jiang, Z., and Liu, X. (2023). Image encryption algorithm based on discrete quantum baker map and chen hyperchaotic system. Int. J. Theor. Phys. 62, 1–28. doi: 10.1007/s10773-023-05277-0

PubMed Abstract | Crossref Full Text | Google Scholar

Kumar, R., and Jung, K. (2019). A systematic survey on block truncation coding based data hiding techniques. Multimed. Tools Appl.

Google Scholar

Latha Prasath, A. (2020). Chaos based 2 dimensional logistic map for image security. J. Crit. Rev.

Google Scholar

Letaief, K., Shi, Y., Lu, J., and Lu, J. (2022). Edge artificial intelligence for 6G: vision, enabling technologies, and applications. IEEE J. Sel. Areas Commun. 40, 5–36. doi: 10.1109/JSAC.2021.3126076

Crossref Full Text | Google Scholar

Liu, K. (2024). Integrate encryption of multiple images based on a new hyperchaotic system and baker map. Multimedia Syst.

Google Scholar

Liu, Y., Yuan, X., Xiong, Z., Kang, J., Wang, X., and Niyato, D. (2020). Federated learning for 6G communications: challenges, methods, and future directions. China Commun.

Google Scholar

Liu, H., Zhao, B., and Huang, L. (2019). A remote-sensing image encryption scheme using DNA bases probability and two-dimensional logistic map. IEEE Access 7, 65450–65459. doi: 10.1109/ACCESS.2019.2917498

Crossref Full Text | Google Scholar

Megías, D., Mazurczyk, W., and Kuribayashi, M. (2021). Data hiding and its applications: digital watermarking and steganography. Appl. Sci.

Google Scholar

Mehraj, S., Mushtaq, S., Parah, A., Giri, K., Sheikh, J., Gandomi, A., et al. (2023). RBWCI: Robust and blind watermarking framework for cultural images. IEEE Trans. Consum. Electron. 69, 128–139. doi: 10.1109/TCE.2022.3217974

Crossref Full Text | Google Scholar

Mohsen, A., and Abou El-Azm, A. (2019). Complexity considerations: efficient image transmission over mobile communications channels. Multimed. Tools Appl. 78, 16633–16664. doi: 10.1007/s11042-018-6843-2

Crossref Full Text | Google Scholar

Murmu, A., Kumar, P., Moparthi, N., Namasudra, S., and Lorenz, P. (2024). Reliable federated learning with GAN model for robust and resilient future healthcare system. IEEE Trans. Netw. Services Manag.

Google Scholar

Murugan, C., and Karthigai Kumar, P. (2018). Survey on image encryption schemes, bio cryptography and efficient encryption algorithms. Mob. Netw. Appl.

Google Scholar

Muthu, J., and Murali, P. (2021). Review of chaos detection techniques performed on chaotic maps and systems in image encryption. SN Computer Science 2, 1–24. doi: 10.1007/s42979-021-00778-3

Crossref Full Text | Google Scholar

Naffouti, S., Kricha, A., and Sakly, A. (2022). A sophisticated and provably gray scale image watermarking system using DWT-SVD domain. Vis. Comput.

Google Scholar

Nashat, D., and Mamdouh, L. (2019). An efficient Steganographic technique for hiding data. J. Egypt. Math. Soc.

Google Scholar

Nasr, M., El-Shafai, W., El-Rabaie, E., El-Fishawy, A., El-Hoseny, H., Abd El-Samie, F., et al. (2024). A robust audio steganography technique based on image encryption using different chaotic maps. Sci. Rep. 14:22054. doi: 10.1038/s41598-024-70940-3

PubMed Abstract | Crossref Full Text | Google Scholar

Nezami, Z., Ali, H., Asif, M., Aljuaid, H., Hamid, I., and Ali, Z. (2022). An efficient and secure technique for image steganography using a hash function. Peer J. Comput. Sci. 8:e1157. doi: 10.7717/peerj-cs.1157

PubMed Abstract | Crossref Full Text | Google Scholar

Osama, S., Farouk, M., Hala, S., and Mohsen, A. M. (2024). Speech cryptography algorithms: utilizing frequency and time domain techniques merging. J. Ambient. Intell. Humaniz. Comput. 15, 3617–3649. doi: 10.1007/s12652-024-04838-3

Crossref Full Text | Google Scholar

Penttinen, J. (2021). On 6G Visions and Requirements. J. ICT Standard.

Google Scholar

Priyanka Singh, A. (2022). A survey of image encryption for healthcare applications. Evol. Intel.

Google Scholar

Quy, K. V., Chehri, A., Quy, M. N., Han, D. N., and Ban, T. N. (2023). Innovative trends in the 6G era: A comprehensive survey of architecture, applications, technologies, and challenges. IEEE Access 11, 39824–39844. doi: 10.1109/ACCESS.2023.3269297

Crossref Full Text | Google Scholar

Rasmia, A., Arunkumar, B., and Anees, V. (2019). A comprehensive review of digital data hiding techniques. Pattern Recogn. Image Analy. 29, 639–646. doi: 10.1134/S105466181904014X

PubMed Abstract | Crossref Full Text | Google Scholar

Roselinkiruba, R. (2023). Reversible data hiding using optimization, interpolation and binary image encryption techniques. Multimed. Tools Appl.

Google Scholar

Sabir, S., and Guleria, V. (2023). Multi-layer security based multiple image encryption technique. Comput. Electr. Eng. 106:108609. doi: 10.1016/j.compeleceng.2023.108609

PubMed Abstract | Crossref Full Text | Google Scholar

Sabry, M., EL Akkad, M., Merras, M., Satori, K., EL-shafai, W., ALtameem, T., et al. (2023). Securing images using high dimensional chaotic maps and DNA encoding techniques. IEEE Access. 11, 100856–100878. doi: 10.1109/ACCESS.2023.3315658

Crossref Full Text | Google Scholar

Sabry, S., and Mohsen, A. M. (2022). Confidentiality considerations: multimedia signals transmission over different wireless channels utilized efficient secured model. Multimed. Tools Appl. 81, 25707–25744. doi: 10.1007/s11042-022-12297-1

Crossref Full Text | Google Scholar

Sabry, S., Osama, S., and Mohsen, A. M. (2021). Reliable mark-embedded algorithm for verifying archived/encrypted image contents in presence different attacks with FEC utilizing consideration. Wirel. Pers. Commun. 119, 37–61.

Google Scholar

Sajitha Rekh, A. (2022). Review on various image encryption schemes. Materials Today Proc.

Google Scholar

Shen, S., Yu, C., Zhang, K., Ni, J., and Ci, S. (2021). Adaptive and dynamic security in AI-empowered 6G: from an energy efficiency perspective. IEEE Commun. Stand. Mag.

Google Scholar

Shi, H., Zhou, Z., Qin, J., Geng, J., and Li, M. (2023). A reversible data hiding in encrypted image based on additive secret sharing with adaptive bit-plane prediction. Multimed. Tools Appl.

Google Scholar

Singh, R., Saraswat, M., Ashok, A., Mittal, H., Tripathi, A., Pandey, A., et al. (2022). From classical to soft computing based watermarking techniques: a comprehensive review. Futur. Gener. Comput. Syst.

Google Scholar

Singh, M., and Singh, A. (2022). A comprehensive survey on encryption techniques. Multimed. Tools Appl.

Google Scholar

Singh, L., Singh, A., and Singh, P. (2018). Secure data hiding techniques: A survey. Multimed. Tools Appl.

Google Scholar

Su, Q., Chen, S., Wang, H., Cao, H., and Hu, F. (2024). An efficient watermarking scheme for dual color image with high security in 5G environment. Expert Syst. Appl.

Google Scholar

Toledo, D., Bonilla, O., Guerrero, E., Elizondo, J., Valdez, J., Perez, U., et al. (2023). Real-time medical image encryption for H-IoT applications using improved sequences from chaotic maps. Integration.

Google Scholar

Tomkos, I., Klonidis, D., Pikasis, E., and Theodoridis, S. (2020). Toward the 6G network era: Opportunities and challenges. IT Prof.

Google Scholar

Uusitalo, A., Rugeland, P., Boldi, R. M., Strinati, C. E., Demestichas, P., Ericson, M., et al. (2021). 6G vision, value, use cases and technologies from European 6G flagship project Hexa-X. IEEE Access.

Google Scholar

Viswanathan, H., and Mogensen, E. (2020). Communications in the 6G era. IEEE Access 8, 57063–57074. doi: 10.1109/ACCESS.2020.2981745

Crossref Full Text | Google Scholar

Wu, W., and Wang, Q. (2022). Block image encryption based on chaotic map and fractional Fourier transformation. Multimed. Tools Appl. 82, 10367–10395. doi: 10.1007/s11042-022-13675-5

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, B., and Liu, L. (2023). Chaos-based image encryption: review, application, and challenges. Mathematics.

Google Scholar

Zhang, X., Su, Q., Sun, Y., and Chen, S. (2023). A robust and high-efficiency blind watermarking method for color images in the spatial domain. Multimed. Tools Appl. 82, 27217–27243. doi: 10.1007/s11042-023-14479-x

PubMed Abstract | Crossref Full Text | Google Scholar

Zhou, N., Wu, J., Chen, M., and Wang, M. (2024). A quantum image encryption and watermarking algorithm based on QDCT and baker map. Int. J. Theor. Phys. 63, 1–24. doi: 10.1007/s10773-024-05630-x

Crossref Full Text | Google Scholar

Zia, U., McCartney, M., Scotney, B., Martinez, J., Abu Tair, M., Memon, J., et al. (2022). Survey on image encryption techniques using chaotic maps in spatial, transform and spatiotemporal domains. Int. J. Inf. Secur. 21, 917–935. doi: 10.1007/s10207-022-00588-5

Crossref Full Text | Google Scholar

Zolfaghari, B., and Koshiba, T. (2022). Chaotic image encryption: state-of-the-art, ecosystem, and future roadmap. Appl. Syst. Innov.

Google Scholar