Brownian motion models: cryptographic applications, capabilities, and limitations

Brownian motion (BM) is a stochastic model that has been extensively studied in physics, finance, and engineering. However, its potential use in cryptographic applications remains underexplored. This paper presents a comprehensive review of the capabilities, limitations, and cryptographic properties of various BM models, including the Wiener process, geometric BM, fractional BM, Ornstein–Uhlenbeck process, multidimensional BM, and reflected BM. We reviewed the mathematics of these models, simulate their random evolutions, and compare their cryptanalytic properties. A comparison of these sources highlights unique characteristics that can provide cryptographic resilience, including long-range dependence, multidimensional modeling of noise, and constraints on randomness. We also describe the main limitations and potential weaknesses of each model. This paper addresses gaps in the application of stochastic process to cryptographic design and provides a foundational guideline for the continued development of secure systems based on Brownian dynamics.

1 Introduction

Brownian motion (BM) is the random movement of particles suspended in a fluid, first reported by Brown in 1827 (Chen et al., 2023). It has been widely used to model stochastic processes in physics (Tawade et al., 2022), finance (Thapa et al., 2022), biology, and engineering. The Wiener process, geometric Brownian motion (GBM), and advanced generalizations such as fractional Brownian motion (fBM) (Wang et al., 2022) and the Ornstein–Uhlenbeck (OU) process are commonly employed to characterize randomness, diffusion, and mean-reverting processes within complex systems (Ibrahim et al., 2021; Urumov et al., 2024).

The mathematical application of BM to real-world problems has been extensively studied but, to the best of our knowledge, the cryptographic aspect of this model has remained largely unexplored. Given the growing importance of high-entropy randomness, secure communication, and adaptive encryption protocols in contemporary cryptographic underpinnings, BM-like models show promise (Kumar et al., 2022; Santra et al., 2021). Their stochasticity, long-range dependence, and self-similarity may serve as sources of entropy or as frameworks for designing robust, noise-resistant security protocols.

This paper aims to bridge the gap between stochastic process modeling and cryptography. We provide a rigorous review and simulation-based comparison of six BM models, assessing their capabilities and limitations in the context of cryptographic requirements. Our contributions are as follows:

• Analyze and simulate key BM variants (Wiener, GBM, fBM, OU, multidimensional, and reflected BM) to demonstrate their structural differences and stochastic behaviors.

• Explore their cryptographic applicability for pseudo-random number generation.

• Present a comparative evaluation highlighting security benefits, implementation complexity, and limitations for each model.

• Identify challenges in real-world adoption and propose future directions for integrating BM models into cryptographic system design.

Recent advances in BM models have significantly deepened our understanding of randomness, diffusion, and long-range dependence in complex systems. In this work, we review and simulate the six key variants of Brownian motion models to assess their structural distinctions and stochastic behaviors within a cryptographic context. By aligning the historical evolution and advanced modeling techniques of BM with critical cryptographic challenges such as pseudo-random number generation, this paper defines the scope and aims of our project. Our comparative evaluation not only details the operational benefits and complexities of each model but also utilizes the potential for BM-based approaches to contribute to the development of more secure, and adaptive encryption mechanisms.

Despite the mathematical maturity of Brownian models, their integration into practical cryptographic primitives remains underexplored. Most existing work either applies BM in unrelated domains or theorizes its potential without experimental grounding. This paper addresses this gap by classifying major BM models for cryptographic relevance and evaluating their implementation feasibility.

2 Brownian motion models

2.1 Wiener process

The Wiener process, also known as standard BM, is the fundamental continuous-time stochastic process used in probability theory. It serves as the building block for many stochastic models, including those applied in financial modeling, physics, and control theory (Durrett, 2019). A Wiener process $W\left(t\right)$ is a stochastic process that satisfies the following conditions (Kleinert, 2009):

Initial condition: $W\left(0\right)=0$ .

The increments $W\left(t\right)$ − $W\left(s\right)$ for s < t are independent of past values.

For s < t, the increment $W\left(t\right)$ − $W\left(s\right)$ follows the normal distribution $W\left(t\right)$ − $W\left(s\right)$ ∼ $N$ (0, t − s).

The function $W\left(t\right)$ is continuous in t with probability 1.

The expected value of the process given past values is equal to the current value: E[ $W\left(t\right)$ ∣ $W\left(s\right)$ ] = $W\left(s\right)$ for s < t.

The function $W\left(t\right)$ has continuous sample paths with probability 1, in the topological sense, not to the likelihood of the process taking a particular value or direction. The key statistical property is that the increments $W\left(t\right)-W\left(s\right)$ (for s < t) are normally distributed with mean zero and variance t−s, and these increments are independent of the past values of the process. This ensures that while the motion is continuous in time, its direction and magnitude remain entirely random.

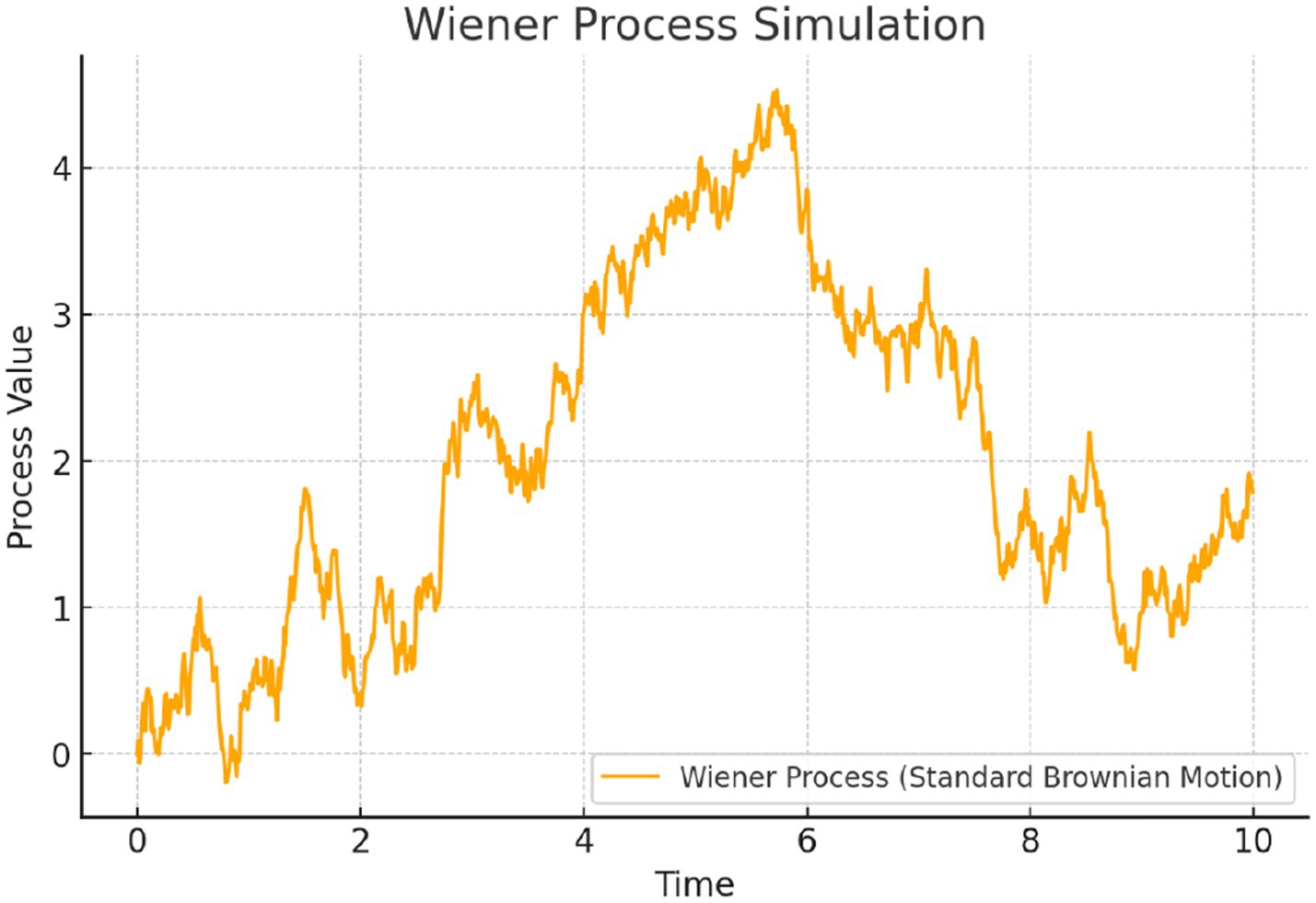
These properties define standard BM, which has applications in physics, finance, and mathematics. The differential form of the Wiener process is given by d $W\left(t\right)$ ∼ N(0, dt), where d $W\left(t\right)$ represents an infinitesimal change in the Wiener process, and dt is an infinitesimal time increment. Since d $W\left(t\right)$ is Gaussain increment with mean zero and variance dt, it serves as the driving force for many stochastic differential equations. Figure 1 presents a sample plot of the Wiener process simulation.

Figure 1

Figure 1. Sample plot of Wiener process.

2.2 Geometric Brownian motion

Geometric BM is used to model processes where the logarithm of the variable follows BM with drift. It is commonly applied in financial mathematics to model stock prices (Hull, 2017). The stochastic differential equation (SDE) for GBM is:

$\begin{array}{ll}\mathrm{d}S\left(t\right)=\mathit{\mu S}\left(t\right)\mathrm{d}t+\mathit{\sigma S}\left(t\right)\mathrm{d}S\left(t\right),& (1)\end{array}$

where $S\left(t\right)$ is the value of the process at time t, μ is the drift coefficient, σ is the volatility coefficient, d $W\left(t\right)$ is the increment of the standard Wiener process $W\left(t\right)$ , and dt represents an infinitesimal time increment.

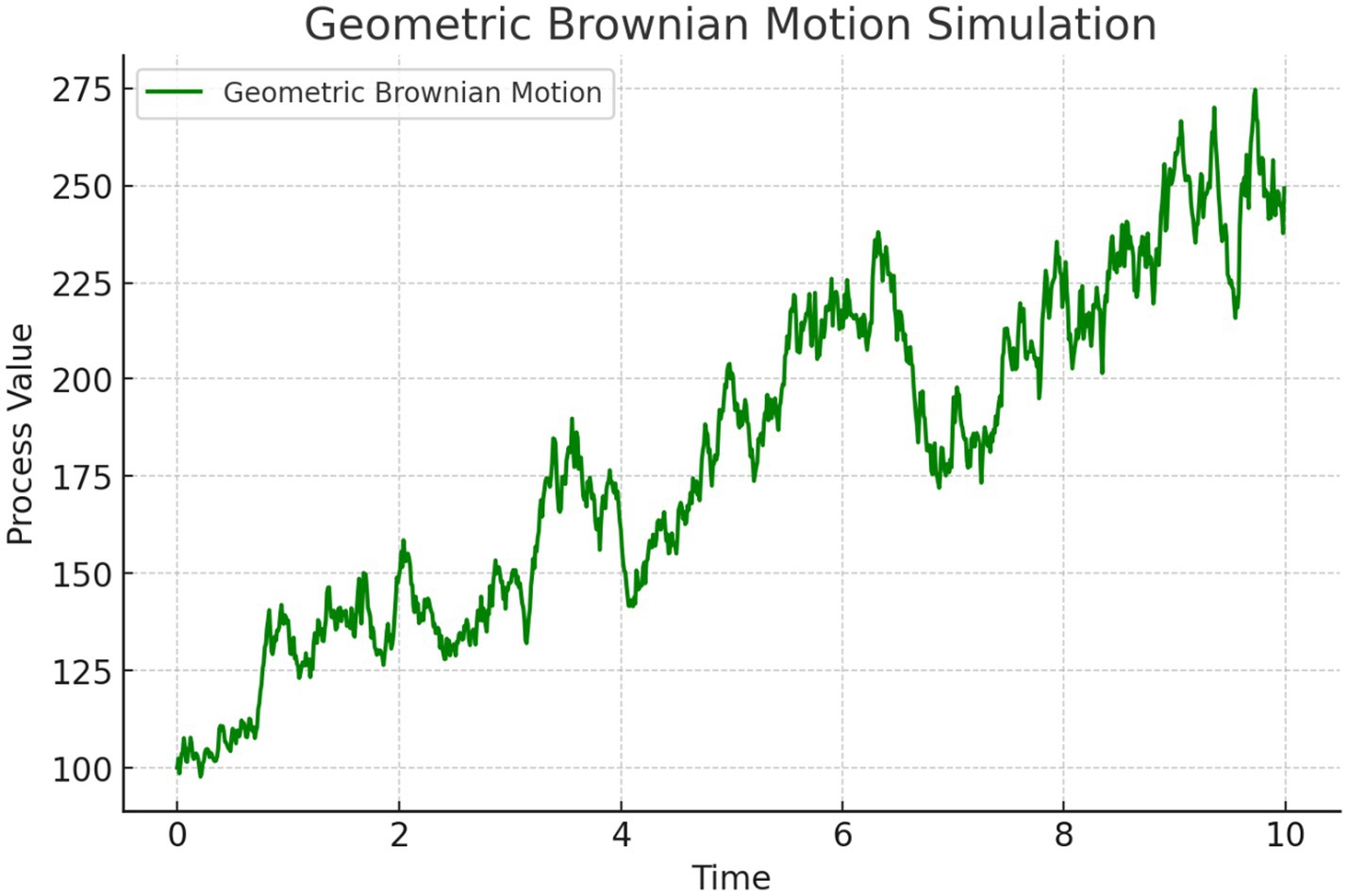
In cryptography, GBM can model the evolution of certain security parameters over time, aiding in the assessment of long-term security. It is utilized in option pricing and modeling stock prices. The GBM model assumes that asset prices follow exponential BM, ensuring that prices remain positive. Applying Itô’s lemma to solve the SDE yields the explicit solution.

$\begin{array}{ll}S\left(t\right)=S\left(0\right)\cdot exp\left[\right(\mu -{\sigma }^2/2)\cdot t+\sigma \cdot W(t\left)\right],& (2)\end{array}$

where S(0) is the initial price at time t = 0, and the term $(\mu -\frac{{\sigma }^2}{2})$accounts for drift correction due to the variance of the stochastic term. Figure 2 presents a plot of a GBM simulation. The process models the evolution of a stock price over time, incorporating both drift (μ = 0.1) and volatility (σ = 0.2). The exponential growth pattern is evident, along with random fluctuations introduced by the BM component.

Figure 2

Figure 2. Sample plot of GBM.

2.3 Fractional Brownian motion

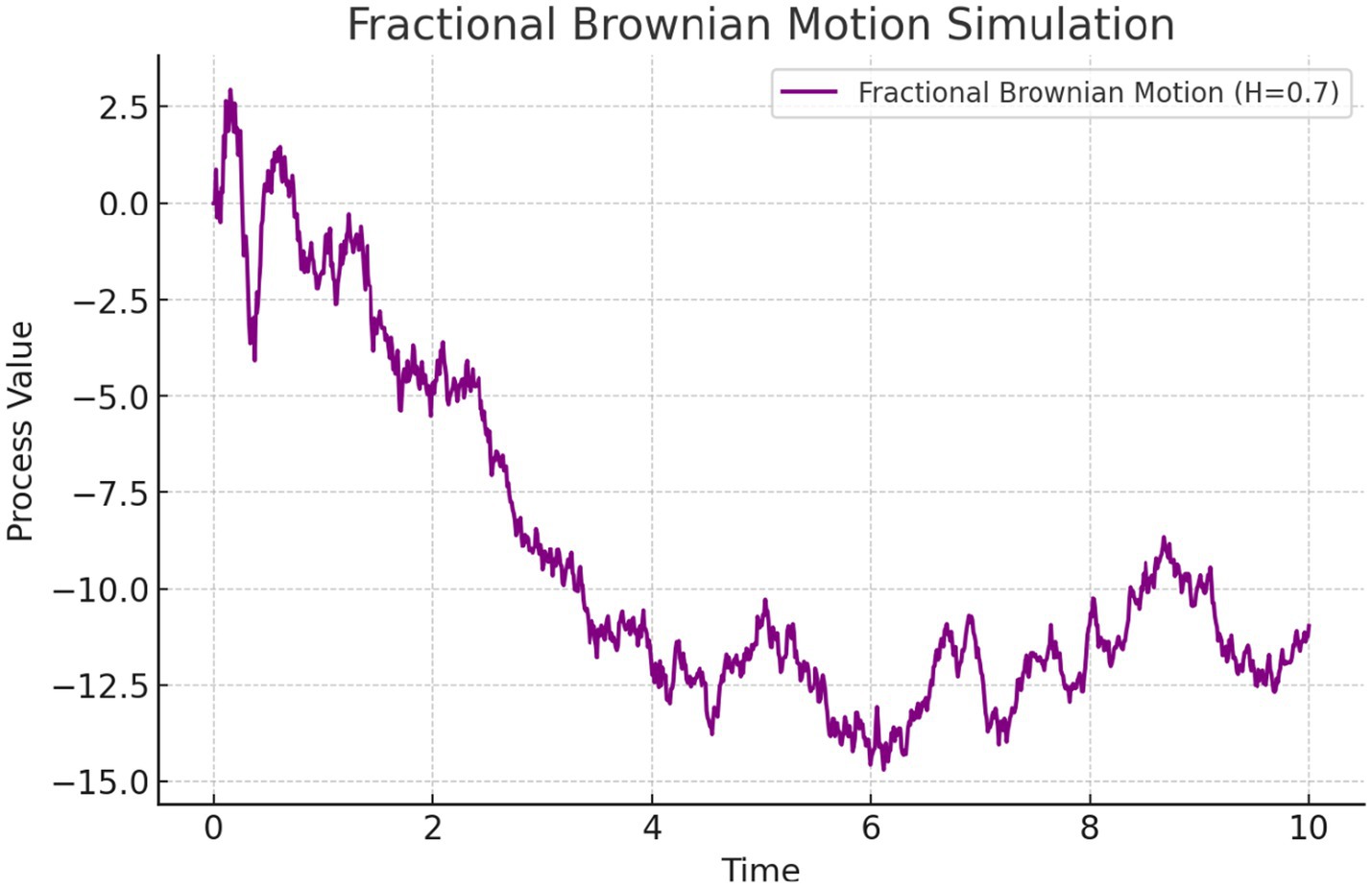
fBM is a generalization of standard BM that incorporates long-range dependence and self-similarity (Biagini et al., 2008). It is widely used in fields such as finance, network traffic modeling, and image processing, where memory effects play a crucial role. Fractional BM, B_H(t), is a Gaussian process with mean zero and covariance function.

$\begin{array}{ll}E\left[B_H\right(t\left)B_H\right(s\left)\right]=\frac{1}{2}(t^{2H}+s^{2H}-\mid t-s\mid 2H),& (3)\end{array}$

where H is the Hurst exponent, which controls the correlation structure (if H = 0.5, fBM reduces to standard BM; if H > 0.5, the process exhibits positive correlation; and if H < 0.5, the process exhibits negative correlation), and s and t are two time points. Note that s and t denote two distinct instants in time at which the process is observed, with s < t in the standard formulation. They are used to evaluate the covariance structure of the fractional BM. The distinction is that s represents the earlier time point and t the later time point, so that the difference t-s determines the time lag over which statistical dependence is measured.

Unlike standard BM, fBM is not a Markov process and does not have independent increments. A common way to define fBM is via the Mandelbrot–van Ness representation, given as:

$B_H\left(t\right)=\frac{1}{\Gamma (H+\frac{1}{2})}\left(\begin{array}{l}{\int }_{-\infty }^0[{(t-s)}^{H-\frac{1}{2}}-{(-s)}^{H-\frac{1}{2}}]\\ \mathrm{d}W\left(s\right)+{\int }_0^t{(t-s)}^{H-\frac{1}{2}}\mathrm{d}W\left(s\right)\end{array}\right),\text{ (4)}$

where $W\left(s\right)$ is a standard Wiener process and Γ(·) is the gamma function. This integral representation ensures that B_H(t) satisfies the required covariance structure. Figure 3 presents a sample plot of an fBM simulation with Hurst parameter H = 0.7. The process exhibits long-range dependence and self-similarity, characteristic of fBM.

Figure 3

Figure 3. Sample plot of fBM.

2.4 Ornstein–Uhlenbeck process

The Ornstein–Uhlenbeck (OU) process describes the velocity of a particle undergoing BM with friction. It is defined by the SDE.

$\begin{array}{ll}\mathrm{d}X\left(t\right)=\theta (\mu -X(t\left)\right)\mathrm{d}t+\sigma \mathrm{d}W\left(t\right),& (5)\end{array}$

where $X\left(t\right)$ is the value of the process at time t, θ is the rate of reversion to the mean, μ is the long-term mean, σ is the volatility coefficient, and d $W\left(t\right)$ is the increment of a Wiener process (Vasicek, 1977).

In cryptography, the OU process can model the fluctuation of certain security metrics around a desired level, facilitating the design of adaptive security systems. It is a mean-reverting stochastic process that describes how a system tends to drift toward a long-term mean over time. It is widely deployed in financial modeling, physics, and biology. It is commonly used in finance to model interest rates and mean reversion. Applying Itô’s lemma and solving the SDE yields the explicit solution for $X\left(t\right)$ :

$\begin{array}{ll}X\left(t\right)=X_0{e}^{-\mathit{\theta t}}+\mu (1-e^{-\mathit{\theta t}})+\sigma {\int }_0^t{e}^{-\theta (t-s)}\mathrm{d}W\left(s\right)& (6)\end{array}$

This equation shows that $X\left(t\right)$ exponentially tends to μ with rate θ, and the stochastic integral refers to the random part around this mean. The key property of the model is mean reversion: if $X\left(t\right)$  > μ, the drift term θ(μ −  $X\left(t\right)$ ) brings it down toward μ, and if $X\left(t\right)$  < μ, the drift term pulls it upward toward μ.

The second property is the stationary distribution: as t → ∞, the random variable $X\left(t\right)$ becomes normally distributed:

$\begin{array}{ll}X\left(t\right)~\mathcal{N}(\mu ,\frac{{\sigma }^2}{2\theta }),& (7)\end{array}$

where the variance $\frac{{\sigma }^2}{2\theta }$ decreases as θ increases. Thus, faster mean reversion leads to lower fluctuations.

The third property is the autocorrelation function: $X\left(t\right)$ can be expressed as

$\begin{array}{ll}cov\left(X\right(s),X(t\left)\right)=\frac{{\sigma }^2}{2\theta }{e}^{-\theta \mid t-s\mid }& (8)\end{array}$

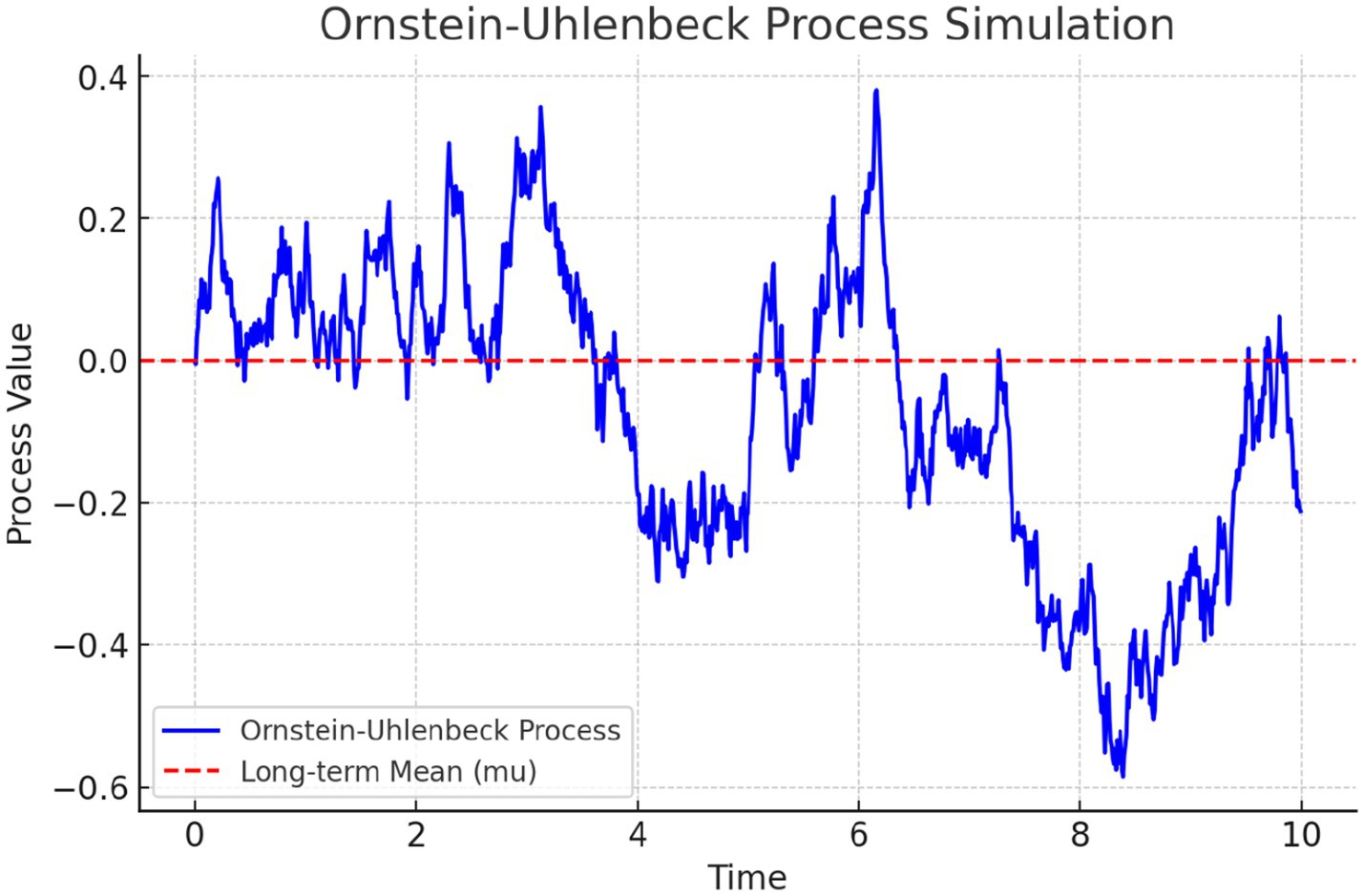
This shows that correlations decay exponentially over time. Finally, the OU process has the Markov property: the future behavior of $X\left(t\right)$ depends only on its present value, not past values. Figure 4 illustrates a sample plot of an OU process simulation. The blue line represents the simulated process over time, and the red dashed line indicates the long-term mean μ = 0. This process illustrates the tendency of mean reversion over time.

Figure 4

Figure 4. Sample plot of OU process.

2.5 Multidimensional Brownian motion

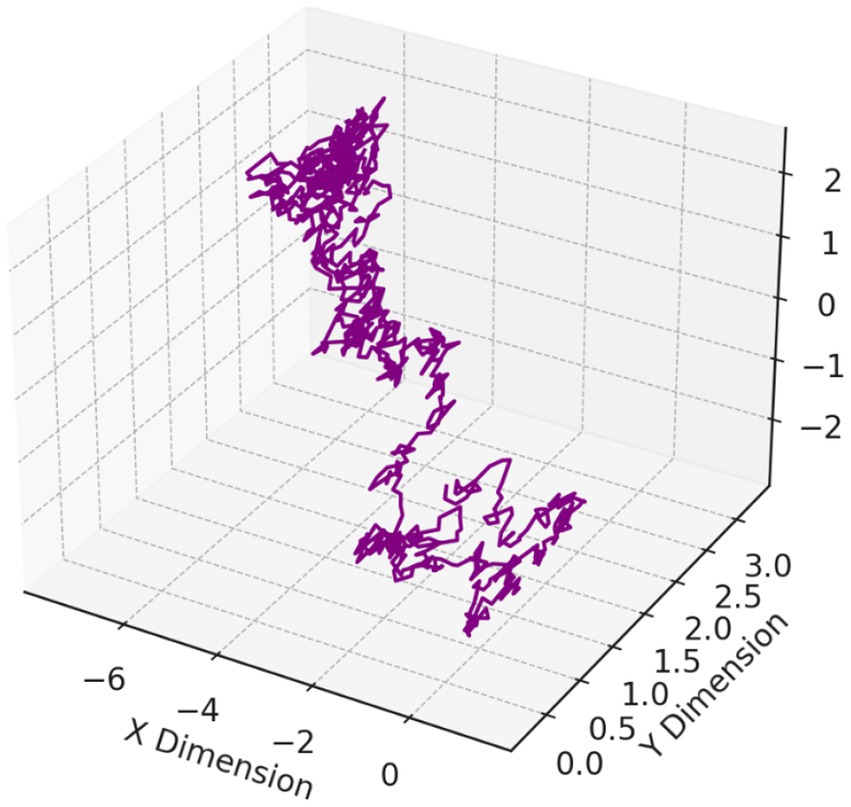
Multidimensional BM (also called vector-valued BM) is a generalization of one-dimensional BM, with the process defined in a multidimensional space. It models random motion in higher dimensions and is widely deployed in financial models, diffusion processes, and statistical physics. In this case, the process is represented as a vector of BMs, where each component represents BM in one dimension (Vasicek, 1977).

Let $W\left(t\right)$ = ( $W_1\left(t\right),W_2\left(t\right),\dots ,W_d\left(t\right)){}^{\mathrm{T}}$ represent multidimensional BM in ℝ ^d , where each component $W_i\left(t\right)$ is a standard Wiener process (one-dimensional BM). The components are mutually independent for different i, with each following the distribution

$\begin{array}{ll}\mathrm{d}{W}_i\left(t\right)~\mathcal{N}(0,\mathrm{d}t)& (9)\end{array}$

The covariance structure of multidimensional BM is given by $cov\left(W_i\right(t),W_j(s\left)\right)=min(s,t){\delta }_{\mathit{ij}}$ , where ${\delta }_{\mathit{ij}}$ is the Kronecker delta (i.e., components are independent if $i\ne j$ ). More generally, a multidimensional BM can be defined with covariance matrix $\Sigma$ , so that $cov\left(W\right(t\left)\right)=\mathit{t\Sigma }$ . In this paper, we consider the standard case where the components are independent, corresponding to $\Sigma =I_d.$

The multidimensional BM $W\left(t\right)$ is a vector-valued process and can be written as

$\begin{array}{ll}\mathbf{d}{W}_t={\left(\mathrm{d}{W}_1\right(t),\mathrm{d}{W}_2(t),\dots ,\mathrm{d}{W}_d(t\left)\right)}^{\mathrm{T}},& (10)\end{array}$

where $W_t={\left(W_1\right(t),W_2(t),\dots ,W_d(t\left)\right)}^{\mathrm{T}}$ is the multidimensional BM vector at time t, each $W_i\left(t\right)$ is one-dimensional BM, and the components $W_i\left(t\right)$ are mutually independent. Figure 5 presents a 3D plot of multidimensional BM. The random path illustrates the stochastic behavior of BM extended to a multidimensional space.

Figure 5

Figure 5. Sample plot of multidimensional BM (3D).

2.6 Reflected Brownian motion

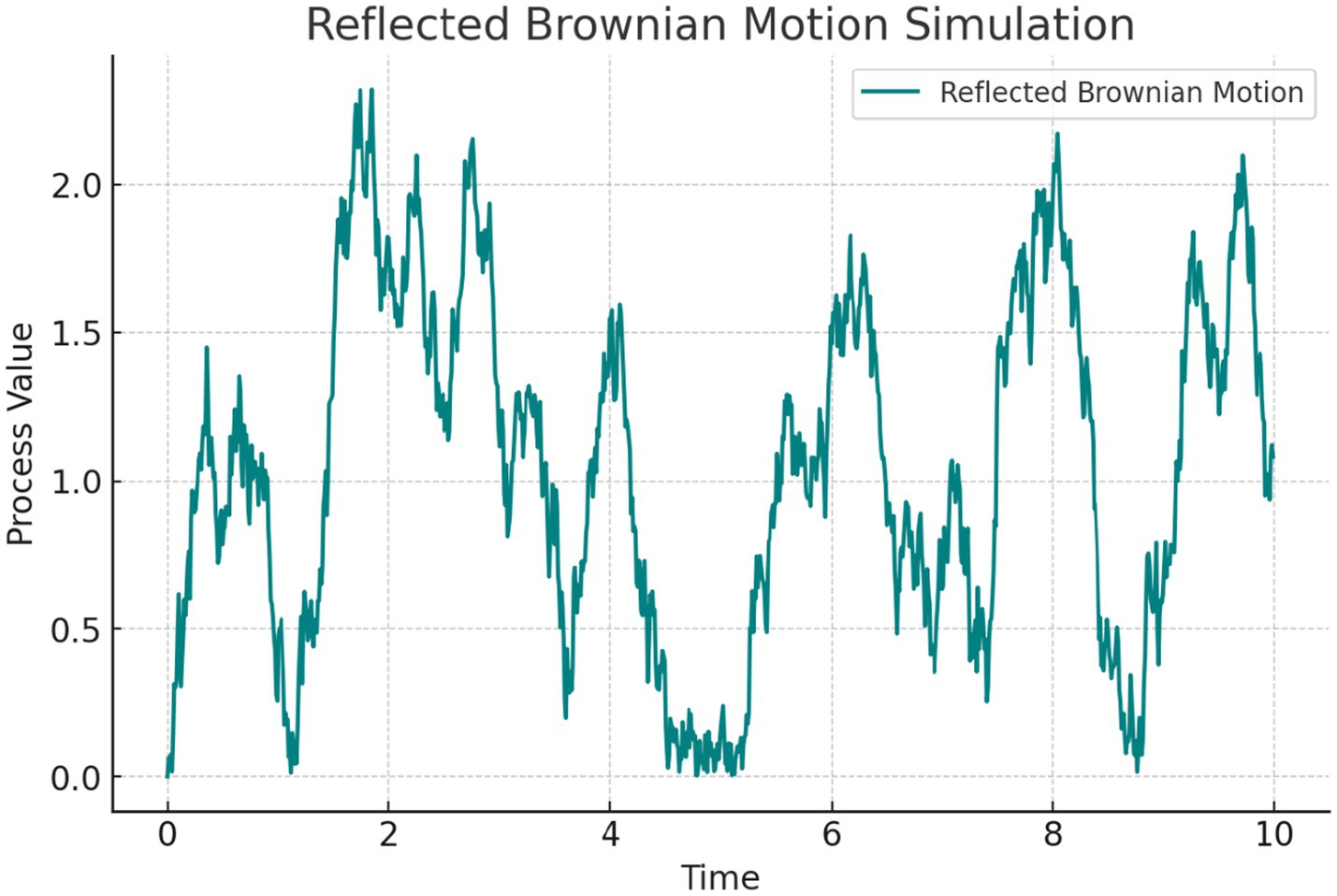
Reflected Brownian motion (RBM) is a constrained form of BM that cannot cross a specified boundary (Øksendal, 2003). It is often used to model queueing systems, diffusion processes in confined spaces, and other constrained stochastic processes. In one dimension, a standard reflected BM Z(t) with a lower reflecting barrier at 0 is defined as:

$\begin{array}{ll}Z\left(t\right)=\mid B\left(t\right)\mid ,& (11)\end{array}$

where B(t) is standard BM. This definition ensures that Z(t) never takes negative values by “reflecting” any negative excursions back into the positive domain. For a general reflected BM in a domain D with reflection at the boundary, the process satisfies:

$\begin{array}{ll}\mathrm{d}{X}_t=\mu \mathrm{d}t+\sigma \mathrm{d}W\left(t\right)+\mathrm{d}R\left(t\right),& (12)\end{array}$

where $X\left(t\right)$ is the reflected BM, μ is the drift coefficient, σ is the volatility, $W\left(t\right)$ denotes standard Wiener process, and $R\left(t\right)$ is non-decreasing and increases only when $X\left(t\right)$ is on the boundary. This process enforces the constraint $X\left(t\right)$ ∈ D and increases only when $X\left(t\right)$ is on the boundary, where D is the domain constraining the reflected BM. This model has several properties; for example, it ensures that the process never falls below the defined boundary. RBM is often formulated as a Skorokhod problem, where a correction term is introduced to keep the process within the allowed domain. Figure 6 presents a sample plot of a reflected BM simulation. The process behaves similarly to standard BM but reflects at zero, ensuring that the process value remains non-negative. The process is constrained such that it cannot take negative values, and whenever it reaches zero, it is reflected back into the positive domain. This reflection mechanism creates a lower bound but does not impose any positive limit or asymptotic upper bound. The fluctuations above zero remain stochastic and unbounded over time, determined by the volatility parameter σ and the drift μ of the underlying Wiener process.

Figure 6

Figure 6. Sample plot of reflected BM.

3 Applications of Brownian motion

3.1 Applications of Wiener process

The Wiener process is a fundamental concept in stochastic processes, with applications in finance, physics, biology, mathematics, and engineering. In finance, it is used to model stock prices and option pricing. Its increments are independent and normally distributed, making it a key component of models such as the Black–Scholes model, which is central to option pricing and risk control (Bian, 2024). It also supports the prediction of stock price movements, capturing the volatility and uncertainties present in financial markets. This process is invaluable for traders and financial analysts, who rely on such probabilistic models to predict prices.

In physics, the Wiener process appears in many fields, including statistical mechanics and thermodynamics. It is used to model the BM of a particle suspended in a fluid, providing insights into the effects of thermal fluctuations. Moreover, it is applied to noise modeling of electronic devices, where the Gaussian Wiener process helps analyze and cancel noise in systems such as high-electron-mobility transistors (Mohammadzade et al., 2021).

In biology, the Wiener process is employed to describe nerve firing rates and growth and development processes. It captures the chance variations in population size, which are important in the study of interactions between species and ecosystem dynamics. The continuous nature of the Wiener process enables the simulation of stochastic fluctuations in biological systems, making it an important resource in evolutionary biology and ecology (Bevia et al., 2021).

Mathematically, the Wiener process plays a key role in stochastic calculus and is used as a building block to construct more sophisticated mathematical objects. It is a natural setting for studying systems perturbed by randomness (Li and Qian, 2020). The process has also been applied to advanced mathematical theories—for example, cubature on Wiener space, which develops approximations for expectations of functionals of diffusion processes, and is important in mathematical finance (Hayakawa and Tanaka, 2021).

In engineering, the Wiener process is commonly adopted in reliability engineering and deterioration modeling. It is employed to estimate the remaining useful life of systems and components, and its random character is valuable for interpreting and estimating degradation patterns (Li et al., 2020; Shangguan, 2023). For example, it has been applied in the reliability evaluation of hard disk drives and lithium-ion batteries (Muhammad et al., 2022; Zhu et al., 2022). The Wiener process is also important in the maintenance of engineering systems, helping to optimize inspection and preventive replacement policies (Gao et al., 2023).

3.2 Applications of geometric Brownian motion

GBM is important in various disciplines. Its features, particularly price log-normality and the capacity to model continuous paths with drift and volatility, support the analysis and forecasting of dynamic systems.

In the financial sector, GBM is commonly used for stock and option pricing. The Black–Scholes model of investment, which has had a profound effect on financial markets, is based on the assumption that the prices of financial assets follow a GBM process. This allows the development of closed-form solutions for option prices, enabling traders and analysts to compute the fair value of options using the volatility and expected returns of the underlying asset (Brătian et al., 2021; Lv and Wang, 2020). GBM is also used to forecast the price of commodities, such as crude oil; it contributes to the interpretation of price fluctuations and supports investment decision-making (Pangestika, 2023; Moroz and Yalymova, 2021).

In economics, GBM has been used to represent various economic phenomena and indicators, such as inflation rates and market behaviors (Sun et al., 2022). For example, GBM has been applied to analyze stock market index dynamics and to understand market efficiency and the behavior of asset prices in different economic scenarios (Brătian et al., 2021). In addition, the GBM model has been adopted in supply chain financing, where it can assist decision-making by representing the uncertainty of financial flows (Zhao et al., 2020).

GBM is applied to reliability analysis and risk estimation in engineering systems. It can model the deterioration of parts, allowing engineers to estimate failure rates and plan maintenance schedules. It is also implemented in telecommunications to model signal distortion and noise in communication systems (Sun et al., 2022).

In biology, GBM is used as a basis for modeling population dynamics and disease spread. Epidemiologists have used it to study the spread of pandemics, such as COVID-19, and predict future outbreaks from past data. GBM’s ability to capture noise inherent in biological systems is becoming invaluable to ecologists examining population growth and disease spread (Fabiano and Radenović, 2021).

GBM can be utilized in stochastic calculus and is a fundamental part of many mathematical fields, such as SDEs. It also serves as a tool for studying noise-induced phenomena in systems described by deterministic mathematical models. GBM’s characteristics can be used to investigate complex mathematical issues, such as relationships among averages used in finance (Kipp and Koziol, 2020). It also has potential applications in time series analysis for modeling auto-correlated processes and improving forecasting accuracy.

3.3 Applications of fractional Brownian motion

fBM is a generalization of BM with long-range dependence and self-similarity, and it is applied in multiple disciplines. The properties of this model enable it to portray more complex systems than a simple model. The complexity of fractional BM comes from the Hurst exponent, which determines whether the process shows long-range dependence (H > 0.5) or anti-persistence (H < 0.5). This makes fBM capable of capturing correlations across multiple time scales, giving it memory, fractal geometry, and self-similarity that standard BM lacks.

In finance, fBM is more suitable for fitting asset prices and financial derivatives than classical models. It accounts for the long-memory behavior of financial time series required to understand market dynamics and volatility clustering (Sun et al., 2022). fBM has been utilized in option pricing with fractional stochastic volatility models for the realistic pricing of derivatives in markets with long-memory volatility.

In physics, fBM describes several special cases with fractal properties and long-range correlations. For example, it has been used to model turbulent flows (Gao and Sun, 2021) and diffusion processes, as its self-similar nature is consistent with the complex dynamics of such systems. Its application to SDEs allows for the modeling of systems with memory effects and the universal properties of a wide range of physical processes. Furthermore, fBM has been used to describe the dynamics of noise-driven systems to investigate heat transfer and light propagation (Suryawan, 2020).

fBM can also be used to extend the representation of long-range dependence in biological phenomena. It has been found particularly useful for modeling the ontogenetic allometries of populations, where its long-memory feature is required to model the erratic fluctuations found in field population data (Li and Qian, 2020; Sun et al., 2022). Moreover, fBM has been used to model the spread of infectious diseases, yielding valuable insights into outbreak dynamics and the efficacy of control measures (Gao and Sun, 2021).

fBM is also used to model traffic patterns in networks exhibiting self-similarity and long-range dependence. Classical models often fail to capture such characteristics, making fBM a more appropriate choice (Li and Qian, 2020; Suryawan, 2020). A better understanding of such patterns is essential for network design, resource management, and improving the quality of service (Zhao et al., 2020).

In image processing, fBM is used for texture analysis and image synthesis. Its recursive properties make it useful for modeling natural textures, which are typically fractal in nature. For example, fBM is applied to synthesize texture patterns that match the statistical characteristics of natural images, supporting the generation of realistic computer graphics (Bou et al., 2021). It is also deployed in image de-noising and enhancement, especially when noise with memory can be modeled as such—that is, when the quality of an image indicates the presence of noise of the same type (Suryawan, 2020).

3.4 Applications of Ornstein–Uhlenbeck process

The OU process is a stochastic process utilized in many fields and domains. Its properties, including mean reversion and normally distributed increments, make it suitable for modeling processes that tend to return to a mean level.

In finance, the OU process is used to describe interest rates and asset prices. It forms the basis of the Vasicek interest rate model, which captures how interest rates change over time (Wu et al., 2021). It is also applied to model the volatility of financial assets, helping explain return dynamics and the effect of shocks on prices.

In physics, it models the movement of particles in viscous fluids, acting as a prototype for the velocity of particles subject to random forces and friction. It is also useful for understanding system dynamics in thermal equilibrium (Mariani et al., 2023). The process is studied in the context of stochastic resonance, providing insights into how noise can enhance the detection of weak signals in physical systems (Mariani et al., 2023). It is also applied in optical tweezers, where the motion of trapped particles is simulated to study their behavior under different conditions.

In biology, the OU process is used in evolutionary dynamics and population genetics. It models the adaptive evolution of traits in populations (for example, how traits increase with skill level), where mean reversion reflects the tendency of traits to stabilize around an optimal value (Giorno and Nobile, 2022). The OU process is also applied in neuroscience to simulate neuronal activity and analyze the time-dependent fluctuations in firing rates. This contributes to understanding neural coding and information processing in the brain.

In economics, the OU process is used to simulate indicators such as inflation rates and GDP growth. Its mean-reverting nature makes it suitable for modeling the cyclical characteristics of economic variables, helping economists examine the stability and oscillation of economic systems. It is also implemented in econometrics to model time series data and study relationships among several economic variables over time (Wu et al., 2021).

3.5 Applications of multidimensional Brownian motion

MBM is a stochastic process that generalizes BM to multiple dimensions. It has many useful applications, as it allows for the modeling of nonlinear systems composed of many parts.

In finance, MBM is important for capturing the dynamics of several correlated assets. It is used to price multi-asset options, where asset dependencies and covariances must be considered. For example, it is applied to portfolio optimization and is useful in analyzing the risk and return properties of portfolios containing multiple assets (Guillaume, 2024).

In physics, MBM models the motion of systems of particles in multiple dimensions, particularly when the particles interact. It is also used to study diffusion in complex media where particles move under multiple forces acting in different directions (Zhou, 2024). MBM is useful in statistical mechanics, as it simplifies the study of systems with many degrees of freedom.

In engineering, MBM is utilized in control and signal processing. It provides a framework for multidimensional noise modeling in communication systems. For example, it is useful for constructing optimal control policies for randomly perturbed systems (Bouaicha et al., 2022). MBM is also applied to simulate multidimensional diffusion, which is important in predicting the behavior of complicated engineering structures under uncertainty.

In machine learning, MBM is used for anomaly detection and pattern discovery in high-dimensional data. It has recently been shown that features extracted using MBM can be effectively used in learning methods. MBM can also help identify patterns, as well as rare or abnormal events, in complex data sets (Muñoz-Gil et al., 2021). It is adopted in stochastic models that incorporate prediction uncertainty, thereby increasing the robustness of machine learning algorithms (Abdar et al., 2021; Kirichenko, 2023).

3.6 Applications of reflected Brownian motion

RBM is a stochastic process suitable for describing systems with constraints. It is applied across a range of disciplines, such as queueing theory, finance, biology, and engineering, because it captures the dynamics of systems undergoing reflection at transitions.

In queueing theory, RBM is used for systems whose queue length cannot become negative, reflecting a common physical characteristic of service systems. Ascione et al. (2022) proposed delayed RBM in association with fractional queues, suggesting its usefulness for heavy traffic approximations in performance analysis under limiting conditions. Similarly, Dai et al. (2022) applied RBM to queues in series, verifying its potential for representing network traffic as it approaches Gaussian processes.

In finance, asset prices and risk management strategies can be modeled by RBM. The concept of reflection applies to situations where asset prices are bounded below. Banerjee et al. (2022) discussed the use of RBM in financial contexts, particularly in analyzing heavy traffic approximations in queueing systems within financial models. Additionally, RBM is relevant in optimal stopping and singular control problems, where the reflection at a boundary represents a critical decision threshold (Ata, 2024).

In biology, RBM models population dynamics and ecological systems where populations cannot fall below a certain level. Here, the reflection property represents a minimum viable population size, below which the population cannot decline. This is essential for understanding species survival and ecosystem dynamics under various environmental pressures. Although direct references to RBM are less common in biological studies, the principles of reflected processes can be adapted to systems with such constraints.

In engineering, RBM is applied in areas such as control systems and reliability analysis. For example, it can model the dynamics of systems whose output must remain non-negative despite random disturbances. Menshikov discussed RBM behavior in generalized parabolic domains, which are relevant to engineering applications involving diffusion and boundary conditions (Menshikov, 2023). RBM is also used to analyze stochastic networks, helping to assess the performance and reliability of systems subject to random inputs and constraints.

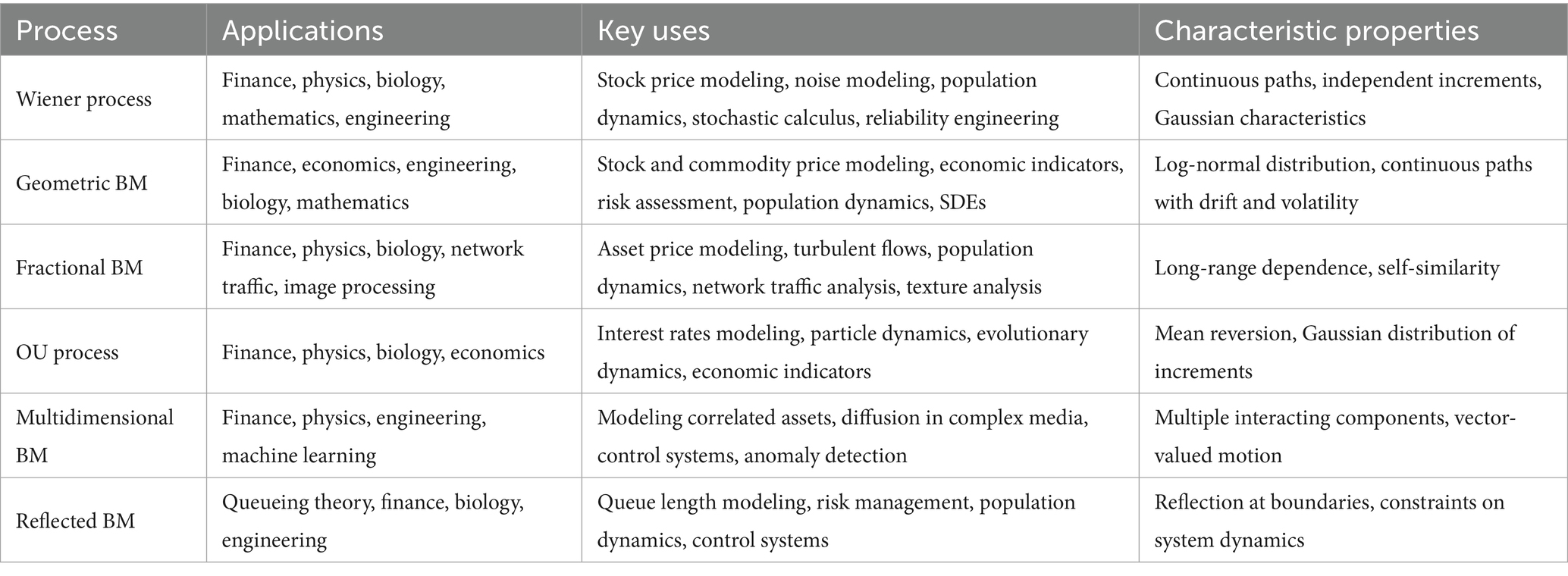
Table 1 summarizes the applications and characteristic properties of each process discussed in this chapter.

4 Applications of Brownian motion in cryptography

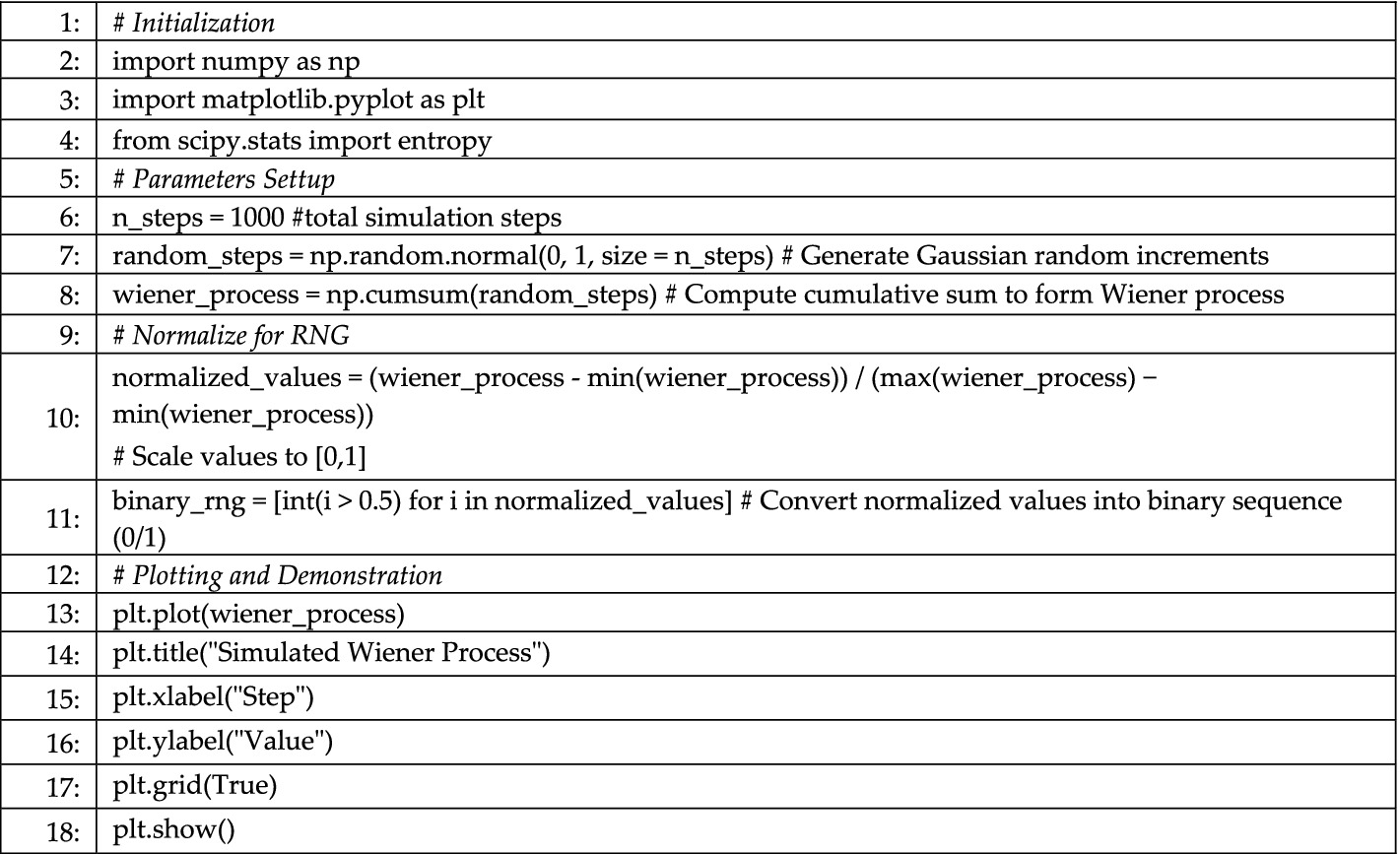
One important application of the Wiener process in cryptography is the generation of true random numbers. To demonstrate its cryptographic potential, we used a simulated Wiener process to generate random numbers, as shown in Algorithm 1. These numbers were evaluated for randomness and entropy characteristics. We implemented a simple Python-based simulation using NumPy, modeling the Wiener process by adding a random Gaussian value at each time step to simulate Brownian increments. The normalized values were binarized using a 0.5 threshold to yield a random bitstream. This bitstream was then evaluated for Shannon entropy using Method 1. The output entropy of the 1,000-bit stream was approximately 0.998, indicating a high level of randomness (ideal = 1.0). These results suggest that even basic BM models can serve as effective sources of entropy. With further refinement, such systems could support cryptographically secure random number generation.

ALGORITHM 1

ALGORITHM 1. BM-based random number generator.

METHOD 1

METHOD 1. Compute entropy.

Table 1

Table 1. Summary of BM models.

Table 2

Table 2. Limitations of BM models.

In Dey et al. (2021), Suwais (2023), Suwais and Almanasra (2023), Suwais (2022), Gilardi-Velázquez et al. (2023), and de la Fraga and Ovilla-Martínez (2024), the researchers highlighted that true random number generators, which are crucial for secure cryptographic algorithms, can be derived from the stochastic dynamics of particles undergoing BM. The randomness inherent in the collisions between particles and ambient molecules results in nondeterministic outputs, making BM suitable for cryptographic applications where unpredictability is paramount (Bian, 2024). This capability is essential to ensure that the keys generated in encryption algorithms are not only random but also secure against prediction.

In the context of public key cryptography, the Wiener process has been shown to enhance the security of existing algorithms. For example, Ranasinghe discussed how the Rivest–Shamir–Adleman algorithm can be improved by utilizing properties of the Wiener process to defend against specific attacks, such as Wiener’s attack (Mohammadzade et al., 2021). By incorporating stochastic elements derived from the Wiener process, the robustness of cryptographic systems can be significantly increased.

One important aspect of GBM is its ability to model asset prices that incorporate randomness and volatility, such as financial derivatives. The randomness in GBM can be employed to design secure cryptographic keys and protocols. For example, it can generate uncertain keys, which are indispensable in secure communications and data encryption (Bevia et al., 2021). Prices modeled by GBM follow a log-normal distribution, enabling the generation of random and unpredictable keys that are resistant to attack. Furthermore, different types of financial instruments can be valued using GBM. This ability to simulate asset prices allows GBM to be used to devise efficient pricing strategies. For example, the valuation of Asian options based on the average price of an asset over a specified time interval is described by GBM (Li and Qian, 2020). This feature can be extended to cryptographic protocols involving option-pricing systems for secure transactions.

A key feature of fBM is its ability to generate true random numbers with cryptographically-valid entropies. The high degree of randomness produced by fBM is important for cryptographic applications, including secure key generation systems that generate unpredictable and attack-resistant random keys (Hayakawa and Tanaka, 2021). This is particularly relevant in applications requiring high-quality randomness, such as secure communications and data encryption. Another application of fBM is in the construction of secure communication protocols, as its properties make it suitable for describing noise in communication channels, which could be a key factor for designing secure cryptosystems. By implementing fBM in cryptographic schemes, the security of data communication over potentially insecure networks can be improved (Li et al., 2020).

A possible application of the OU process is the creation of pseudorandom numbers. The OU model can generate sequences of numbers that satisfy the properties of randomness, while its mean-reverting property ensures that these numbers do not drift too far from a central value. This is important in cryptographic applications where controlled randomness is desired (Shangguan, 2023). Its ability to incorporate noise processes and communication channel dependencies also makes it useful for modeling noise and developing robust security strategies (Muhammad et al., 2022).

Random number generation is one of the key cryptographic applications of MBM. Its stochastic nature makes it suitable for generating random sequences required in cryptography. These sequences can be designed or accessed by protocol designers and relevant parties during the generation of secure keys that are rare yet unpredictable, and thus resistant to cryptographic attack (Zhu et al., 2022). Secure communication protocols can be enhanced with MBM, whose properties allow for effective modeling of noise and channel fluctuations. MBM can also be used in cryptographic algorithms to increase the security of data transfer over insecure networks (Gao et al., 2023).

Finally, RBM can be used to model noise and fluctuations in communication channels, supporting secure communication over data transmission channels. When combined with a cryptologic algorithm, RBM has the potential to support cryptographic techniques that are resistant to many forms of attack (Lv and Wang, 2020). In finance, RBM is often used to model the evolution of asset prices that are nonlinear to barriers. This application could be repeated in cryptography, particularly in the pricing of financial derivatives such as options (Pangestika, 2023).

5 Limitations of Brownian motion in cryptography

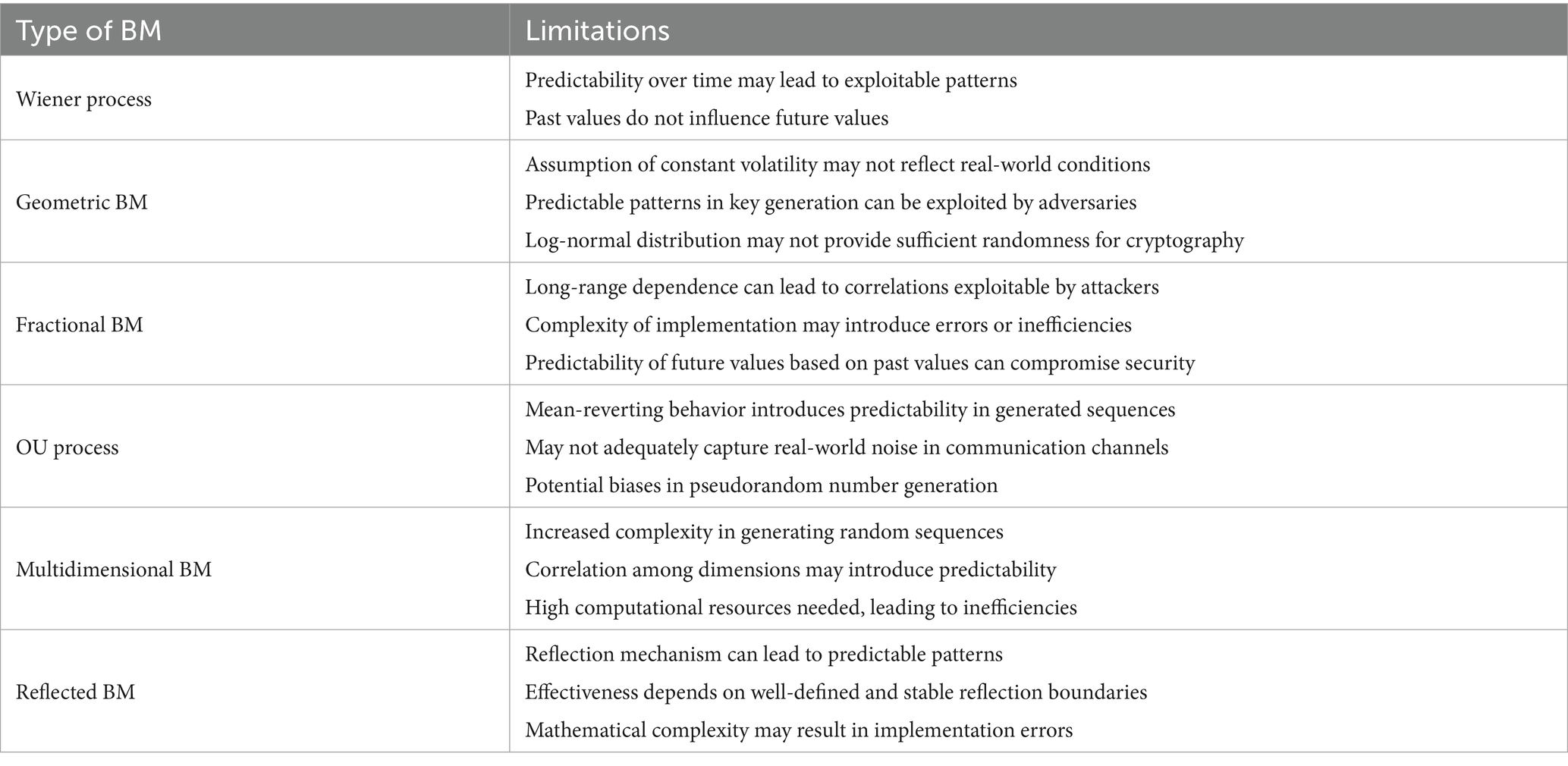
Although the Wiener process has proven useful for cryptographic applications, its inherent limitations may restrict its broader applicability. One key limitation is that it can be predicted at given moments. Although its outputs are random, the mathematical structure of the Wiener process can produce patterns that can be exploited by attackers. For example, if an attacker can predict some of the process’s outputs, this will weaken the security of generated cryptographic keys (Gharari et al., 2024; Hematpour et al., 2024; Alia and Suwais, 2020).

Although GBM is widely used in financial models, it has some drawbacks in encryption scenarios. A major limitation of this model is the assumption of constant volatility, which is unrealistic in markets. In encryption key creation, such constant volatility may result in patterns with attackable sequences (Bevia et al., 2021). Furthermore, although GBM can produce random numbers, and the log-normal distribution of prices might be sufficiently random for certain applications, it may not be random enough for cryptographic applications. The predictability in the prices of underlying assets, as modeled by GBM, can yield a wider range of vulnerabilities in cryptosystems that use such values for key generation and secure communication (Li and Qian, 2020).

fBM incorporates the concept of long-range dependence, which can be both advantageous and disadvantageous in cryptography. Since fBM produces true random number sequences with self-similarity, its long memory might result in correlations that an adversary can exploit. In cryptographic applications, this may lead to a different class of vulnerability when the predictability of future outputs depends on past outputs (Hayakawa and Tanaka, 2021). Moreover, realizing fBM in practical cryptographic protocols could be difficult, which may compromise the security of cryptographic protocols based on this model (Li et al., 2020).

The OU process is mean-reverting, which can be disadvantageous in cryptography. Mean reversion results in some predictability in the generated sequences, which makes it possible for attackers to predict future values given observed values. This regularity can be exploited to attack the OU process, raising questions about the security of keys generated by the process (Shangguan, 2023; Muhammad et al., 2022). Moreover, its use to obtain pseudorandom numbers may introduce biases that can be exploited to break cryptographic systems (Zhu et al., 2022).

A related model is the multiple beta model, which can represent complex systems with many correlated dimensions. However, it has some limitations for cryptographic use, such as a more complicated process for generating random sequences. The inherently multivariate character of this model can make it difficult to ensure the independence of generated values (Gao et al., 2023). Moreover, correlations between dimensions may introduce predictability into the output sequences. This creates the potential for adversaries to exploit such correlations and make inferences about the rules or keys, or the data being protected (Brătian et al., 2021). Finally, the computational cost of simulating MBM can be high, reducing its suitability for cipher systems with real-time key generation (Lv and Wang, 2020).

RBM is a useful model for constrained stochastic processes; however, it may have drawbacks in cryptographic settings. One such limitation is the potential for its reflection property to be exploited to predict patterns, particularly if an adversary can assume or determine the reflection boundaries. This can reduce the unpredictability of RBM-generated random numbers (Pangestika, 2023). Although RBM can model noise in communication channels, any improvement to security resulting from dithering may be limited by the nature of the reflection boundaries. If these boundaries are not well-defined or change dynamically, the robustness of some cryptographic protocols based on RBM may be compromised (Moroz and Yalymova, 2021). Furthermore, the computational overhead of RBM may introduce vulnerabilities to basic forms of cryptanalysis (Sun et al., 2022).

Table 2 summarizes the limitations of the different BM models.

6 Conclusion

This paper has provided a systematic review of the cryptographic potential of BM and its key variants, including the Wiener process, GBM, fBM, the OU process, multidimensional BM, and reflected BM. By examining their mathematical foundations and simulating their stochastic behaviors, we have shown how features such as long-range dependence, mean reversion, multidimensional noise, and reflection constraints highlights the strengths and the weaknesses of these models when considered for cryptographic use.

Our exploratory simulations, such as the Wiener-based bitstream and entropy evaluation, are viewed as illustrative demonstrations of entropy potential rather than as a concrete cryptographic implementations. These experiments confirm that BM models are rich in stochastic structure and can provide high levels of randomness. The comparative analysis across the six models highlights that while BM offers valuable building blocks for entropy generation and noise modeling, further refinement is required before these processes can serve as practical cryptographic primitives.

Our findings suggest two clear paths for future research. First, more extensive benchmarking is needed to transform BM-based entropy sources into robust pseudorandom number generators. Second, hybrid designs that integrate BM dynamics with established cryptographic protocols—potentially in post-quantum settings or adaptive systems that respond to real-time noise—may deliver resilient architectures.

Author contributions

AZ: Methodology, Data curation, Investigation, Formal analysis, Visualization, Resources, Writing – original draft. KS: Conceptualization, Validation, Supervision, Project administration, Methodology, Writing – review & editing. HE-B: Supervision, Investigation, Writing – review & editing. IA: Investigation, Supervision, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors would like to thank Arab Open University in the Kingdom of Saudi Arabia for supporting this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., et al. (2021). A review of uncertainty quantification in deep learning: techniques, applications and challenges. Inf. Fusion 76, 243–297. doi: 10.1016/j.inffus.2021.05.008

Crossref Full Text | Google Scholar

Alia, M., and Suwais, K. (2020). Improved steganography scheme based on fractal set. Int. Arab J. Inf. Technol. 17, 128–136. doi: 10.34028/iajit/17/1/15

Crossref Full Text | Google Scholar

Ascione, G., Leonenko, N., and Pirozzi, E. (2022). Skorokhod reflection problem for delayed Brownian motion with applications to fractional queues. Symmetry 14:615. doi: 10.3390/sym14030615

Crossref Full Text | Google Scholar

Ata, B. (2024). Singular control of (reflected) Brownian motion: a computational method suitable for queueing applications. Queueing Syst. 108, 215–251. doi: 10.1007/s11134-024-09910-5

Crossref Full Text | Google Scholar

Banerjee, S., Budhiraja, A., and Estevez, B. (2022). The inert drift atlas model. Commun. Math. Phys. 399, 2083–2147. doi: 10.1007/s00220-022-04589-2

Crossref Full Text | Google Scholar

Bevia, V., Burgos, C., López, J., and Micó, R. (2021). Uncertainty quantification of random microbial growth in a competitive environment via probability density functions. Fractal Fract. 5:26. doi: 10.3390/fractalfract5020026

Crossref Full Text | Google Scholar

Biagini, F., Hu, Y., Øksendal, B., and Zhang, T. (2008). Stochastic calculus for fractional Brownian motion and applications. London: Springer.

Google Scholar

Bian, S. (2024). The Brownian motion, wiener process, and pu migration as examples of random walk. Theor. Nat. Sci. 38, 229–234. doi: 10.54254/2753-8818/38/20240556

Crossref Full Text | Google Scholar

Bou, D., Bocar, B., and Moussa, T. (2021). Method of construction of the stochastic integral with respect to fractional Brownian motion. Am. J. Appl. Math. 9:156. doi: 10.11648/j.ajam.20210905.11

Crossref Full Text | Google Scholar

Bouaicha, N., Chighoub, F., Alia, I., and Sohail, A. (2022). Conditional LQ time-inconsistent Markov-switching stochastic optimal control problem for diffusion with jumps. Mod. Stoch.: Theory Appl. 9, 157–205. doi: 10.15559/22-vmsta199

Crossref Full Text | Google Scholar

Brătian, V., Acu, A., Oprean-Stan, C., Dinga, E., and Ionescu, G. (2021). Efficient or fractal market hypothesis? A stock indexes modelling using geometric Brownian motion and geometric fractional Brownian motion. Mathematics 9:2983. doi: 10.3390/math9222983

Crossref Full Text | Google Scholar

Chen, Y., Chen, W., Xiang, X., Deng, L., Qian, J., Cui, W., et al. (2023). Pollen-inspired shell–core aerosol particles capable of Brownian motion for pulmonary vascularization. Adv. Mater. 35:e2207744. doi: 10.1002/adma.202207744

PubMed Abstract | Crossref Full Text | Google Scholar

Dai, H., Dawson, D. A., and Zhao, Y. Q. (2022). Exact tail asymptotics for a three-dimensional Brownian-driven tandem queue with intermediate inputs. ESAIM Probab. Stat. 26, 26–68. doi: 10.1051/ps/2021018

Crossref Full Text | Google Scholar

de la Fraga, L. G., and Ovilla-Martínez, B. (2024). Generating pseudo-random numbers with a Brownian system. Integration 96:102135. doi: 10.1016/j.vlsi.2023.102135

PubMed Abstract | Crossref Full Text | Google Scholar

Dey, R., Ghosh, S., Kundu, A., and Banerjee, A. (2021). Simultaneous random number generation and optical tweezers calibration employing a learning algorithm based on the Brownian dynamics of a trapped colloidal particle. Front. Phys. 8:576948. doi: 10.3389/fphy.2020.576948

Crossref Full Text | Google Scholar

Durrett, R. (2019). Probability: theory and examples. Cambridge: Cambridge University Press.

Google Scholar

Fabiano, N., and Radenović, S. (2021). Geometric Brownian motion and a new approach to the spread of COVID-19 in Italy. Gulf J. Math. 10, 25–30. doi: 10.56947/gjom.v10i2.516

Crossref Full Text | Google Scholar

Gao, L., and Sun, X. (2021). Almost periodic solutions to impulsive stochastic delay differential equations driven by fractional Brownian motion with 12 < H < 1. Front. Phys. 9:783125. doi: 10.3389/fphy.2021.783125

Crossref Full Text | Google Scholar

Gao, W., Wang, Y., Zhang, X., and Wang, Z. (2023). Quasi-periodic inspection and preventive maintenance policy optimisation for a system with wiener process degradation. Eksploat. Niezawodn. Maint. Reliab. 25:162433. doi: 10.17531/ein/162433

Crossref Full Text | Google Scholar

Gharari, F., Hematpour, N., Bakouch, H. S., and Popović, P. M. (2024). Fractional duals of the Poisson process on time scales with applications in cryptography. Bull. Malays. Math. Sci. Soc. 47:145. doi: 10.1007/s40840-02401737-w

Crossref Full Text | Google Scholar

Gilardi-Velázquez, H. E., Echenausia-Monroy, J. L., Escalante-González, R. J., and Campos, E. (2023). Codification of images based on deterministic Brownian motion. Chaotic Modeling and Simulation International Conference. 143–156. Cham: Springer.

Google Scholar

Giorno, V., and Nobile, A. (2022). On the absorbing problems for wiener, Ornstein–Uhlenbeck, and feller diffusion processes: similarities and differences. Fractal Fract. 7:11. doi: 10.3390/fractalfract7010011

Crossref Full Text | Google Scholar

Guillaume, T. (2024). Rainbow step barrier options. J. Risk Financ. Manag. 17:356. doi: 10.3390/jrfm17080356

Crossref Full Text | Google Scholar

Hayakawa, S., and Tanaka, K. (2021). Monte Carlo construction of cubature on wiener space. Jpn. J. Ind. Appl. Math. 39, 543–571. doi: 10.1007/s13160-021-00496-6

Crossref Full Text | Google Scholar

Hematpour, N., Gharari, F., Ors, B., and Yalcin, M. E. (2024). A novel S-box design based on quantum tent maps and fractional stochastic models with an application in image encryption. Soft. Comput. 28, 6235–6268. doi: 10.1007/s00500-023-09478-x

Crossref Full Text | Google Scholar

Hull, J. C. (2017). Options, futures, and other derivatives. 10th Edn. London: Pearson.

Google Scholar

Ibrahim, S. N. I., Misiran, M., and Laham, M. F. (2021). Geometric fractional Brownian motion model for commodity market simulation. Alex. Eng. J. 60, 955–962. doi: 10.1016/j.aej.2020.10.023

Crossref Full Text | Google Scholar

Kipp, M., and Koziol, C. (2020). Which is the correct discount rate? Arithmetic versus geometric mean. Credit Capital Markets 53, 355–381. doi: 10.3790/ccm.53.3.355

Crossref Full Text | Google Scholar

Kirichenko, L. (2023). Probabilistic machine learning methods for fractional Brownian motion time series forecasting. Fractal Fract. 7:517. doi: 10.3390/fractalfract7070517

Crossref Full Text | Google Scholar

Kleinert, H. (2009). Path integrals in quantum mechanics, statistics, polymer physics, and financial markets. Singapore: World Scientific.

Google Scholar

Kumar, M., Kumar, S., Budhiraja, R., Das, M., and Singh, S. (2022). Cryptanalysis and improvement of novel image encryption technique using hybrid method of discrete dynamical chaotic maps and Brownian motion. Multimed. Tools Appl. 81, 6571–6584. doi: 10.1007/s11042-021-11810-2

Crossref Full Text | Google Scholar

Li, T., Pei, H., Pang, Z., Si, X., and Zheng, J. (2020). A sequential Bayesian updated wiener process model for remaining useful life prediction. IEEE Access 8, 5471–5480. doi: 10.1109/access.2019.2962502

Crossref Full Text | Google Scholar

Li, J., and Qian, Z. (2020). Large deviation principle for fractional Brownian motion with respect to capacity. Potential Anal. 54, 655–685. doi: 10.1007/s11118-020-09844-6

Crossref Full Text | Google Scholar

Lv, L., and Wang, L. (2020). Option pricing based on modified advection-dispersion equation: stochastic representation and applications. Discret. Dyn. Nat. Soc. 2020, 1–8. doi: 10.1155/2020/7168571

PubMed Abstract | Crossref Full Text | Google Scholar

Mariani, M., Asante, P., Kubin, W., Tweneboah, O., and Beccar-Varela, M. (2023). Determining the background driving process of the Ornstein–Uhlenbeck model. Electron. J. Differ. Equations, 193–207. doi: 10.58997/ejde.sp.02.m1

Crossref Full Text | Google Scholar

Menshikov, M. (2023). Reflecting Brownian motion in generalized parabolic domains: explosion and superdiffusivity. Ann. Inst. Henri Poincaré Probab. Stat. 59, 1813–1843. doi: 10.1214/22-aihp1309

Crossref Full Text | Google Scholar

Mohammadzade, A., Abdipour, A., and Askarpour, A. (2021). Time-domain signal and noise modelling and analysis of millimetre-wave and THz high electron mobility transistors. IET Microwaves Antennas Propag. 15, 1636–1648. doi: 10.1049/mia2.12173

Crossref Full Text | Google Scholar

Moroz, V., and Yalymova, I. (2021). Modeling the volatity of cryptocurrency markets. Bull. Natl. Tech. Univ. KHPI 1, 59–68. doi: 10.20998/2411-0558.2021.02.08

Crossref Full Text | Google Scholar

Muhammad, I., Wang, X., Li, C., Yan, M., Mukhtar, M., and Muhammad, M. (2022). Reliability analysis with wiener-transmuted truncated normal degradation model for linear and non-negative degradation data. Symmetry 14:353. doi: 10.3390/sym14020353

Crossref Full Text | Google Scholar

Muñoz-Gil, G., Corominas, G., and Lewenstein, M. (2021). Unsupervised learning of anomalous diffusion data: an anomaly detection approach. J. Phys. A: Math. Theor. 54:504001. doi: 10.1088/1751-8121/ac3786

Crossref Full Text | Google Scholar

Øksendal, B. (2003). Stochastic differential equations: an introduction with applications. Berlin: Springer.

Google Scholar

Pangestika, V. (2023). Application of the geometric Brownian motion model in West Texas intermediate crude oil price prediction. Gema Wiralodra 14, 1061–1068. doi: 10.31943/gw.v14i3.546

Crossref Full Text | Google Scholar

Santra, I., Basu, U., and Sabhapandit, S. (2021). Active Brownian motion with directional reversals. Phys. Rev. E 104:L012601. doi: 10.1103/physreve.104.l012601

PubMed Abstract | Crossref Full Text | Google Scholar

Shangguan, A. (2023). Reliability modeling based on multiple wiener degradation-shock competing failure process and dynamic failure threshold. Eksploat. Niezawodn. Maint. Reliab. 25:174248. doi: 10.17531/ein/174248

Crossref Full Text | Google Scholar

Sun, L., Chen, J., and Lu, X. (2022). Parameter estimation for discretized geometric fractional Brownian motions with applications in Chinese financial markets. Adv. Contin. Discret. Models 2022:69. doi: 10.1186/s13662-022-03743-3

Crossref Full Text | Google Scholar

Suryawan, H. (2020). Weighted local times of a sub-fractional Brownian motion as Hida distributions. J. Mat. Integr. 15:81. doi: 10.24198/jmi.v15.n2.23350.81

Crossref Full Text | Google Scholar

Suwais, K. (2022). Stream cipher based on game theory and DNA coding. Intell. Autom. Soft Comput. 33, 1815–1834. doi: 10.32604/iasc.2022.025076

Crossref Full Text | Google Scholar

Suwais, K. (2023). Enhanced parallelized DNA-coded stream cipher based on multiplayer prisoners’ dilemma. Comput. Mater. Contin. 75, 2685–2704. doi: 10.32604/cmc.2023.036161

Crossref Full Text | Google Scholar

Suwais, K., and Almanasra, S. (2023). Strike: stream cipher based on stochastic lightning strike behaviour. Appl. Sci. 13:4669. doi: 10.3390/app13084669

Crossref Full Text | Google Scholar

Tawade, J. V., Guled, C. N., Noeiaghdam, S., Fernandez-Gamiz, U., Govindan, V., and Balamuralitharan, S. (2022). Effects of thermophoresis and Brownian motion for thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet. Results Eng. 15:100448. doi: 10.1016/j.rineng.2022.100448

Crossref Full Text | Google Scholar

Thapa, S., Park, S., Kim, Y., Jeon, J.-H., Metzler, R., and Lomholt, M. A. (2022). Bayesian inference of scaled vs fractional Brownian motion. J. Phys. A: Math. Theor. 55:194003. doi: 10.1088/1751-8121/ac60e7

Crossref Full Text | Google Scholar

Urumov, G., Chountas, P., and Chaussalet, T. (2024). Fuzzy fractional Brownian motion: review and extension. Algorithms 17:289. doi: 10.3390/a17070289

Crossref Full Text | Google Scholar

Vasicek, O. (1977). An equilibrium characterization of the term structure. J. Financ. Econ. 5, 177–188. doi: 10.1016/0304-405X(77)90016-2

Crossref Full Text | Google Scholar

Wang, W., Metzler, R., and Cherstvy, A. (2022). Anomalous diffusion and nonergodicity of scaled Brownian motion. Phys. Chem. Chem. Phys. 24, 18482–18504. doi: 10.1039/d2cp01741e

Crossref Full Text | Google Scholar

Wu, Y., Hu, J., and Yang, X. (2021). Moment estimators for parameters of Lévy-driven Ornstein–Uhlenbeck processes. J. Time Ser. Anal. 43, 610–639. doi: 10.1111/jtsa.12630

Crossref Full Text | Google Scholar

Zhao, W., Mao, Z., and Tao, X. (2020). Application of fractal dimension of fractional Brownian motion to supply chain financing and operational comprehensive decision-making. Fractals 28:2040019. doi: 10.1142/s0218348x20400198

Crossref Full Text | Google Scholar

Zhou, T. (2024). Feynman–Kac equation for Brownian non-Gaussian polymer diffusion. J. Phys. A: Math. Theor. 57:285001. doi: 10.1088/1751-8121/ad57b4

Crossref Full Text | Google Scholar

Zhu, Y., Liu, S., Wei, K., Zuo, H., Du, R., and Shu, X. (2022). A novel based-performance degradation wiener process model for real-time reliability evaluation of lithium-ion battery. J Energy Storage 50:104313. doi: 10.1016/j.est.2022.104313

Crossref Full Text | Google Scholar