Adaptive graph-theoretic localization of radiation sources via real-time density-aware clustering for IoT

The increasing complexity of Internet of Things and modern battlefield electromagnetic environments poses significant challenges to radiation source localization, especially under electronic countermeasures, cross-density distributions, and iterative data updates. Existing methods based on fixed-parameter clustering or single geometric discrimination often fail to handle localization divergence caused by dynamic density variations. To overcome this limitation, this paper proposes an adaptive graph-theoretic localization method via real-time density-aware clustering, integrating dynamic density clustering, probabilistic model verification, and graph clique analysis. This approach enables real-time discrimination of potential noise during data density fluctuations and reconstructs trusted subsets for radiation source localization. During the dynamic clustering stage, an adaptive Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm is employed to rapidly separate preliminary the potential noise from target clusters. Subsequently, Gaussian Mixture Model (GMM) is utilized for the secondary partitioning of ambiguous clusters, enhancing the accuracy of target identification. In the clique analysis phase, a probabilistic adjacency matrix is constructed based on the outputs of GMM. Through the application of maximum clique algorithms, consistent targets are effectively extracted from the adjacency matrix, enabling precise localization. Experimental results show that the proposed method improves localization accuracy by at least 70% in dynamic updating scenarios compared to conventional techniques, demonstrating strong practical applicability and scalability for real-world deployments.

1 Introduction

With the rapid advancement of information technology, radiation source localization has emerged as a key technology in modern communication, navigation, and public safety systems. Its applications span across military electronic warfare and diverse civilian sectors (Feng et al., 2024; Sun et al., 2023). In civilian contexts, stringent requirements are imposed on radiation source localization for efficient radio spectrum resource management, collaborative positioning of Unmanned Aerial Vehicle (UAV) swarms, and emergency signal tracking in urban environments (Chen et al., 2025b; Feng et al., 2024). For instance, in smart cities, the proliferation of densely deployed Internet of Things (IoT) devices demands precise spectrum monitoring to minimize signal interference; emergency rescue operations rely on the swift localization of distress signals from casualties; and the burgeoning low-altitude economy necessitates real-time perception and analysis of surrounding radio frequency signals for UAV path planning and obstacle avoidance. However, in complex electromagnetic environments, the lack of prior information fundamentally hinders the deterministic discrimination between correct and incorrect measurements. This limitation also precludes the accurate quantification of radiation source cardinality and spatial coordinates. In addition, the inclusion of incorrect measurements in localization algorithms exacerbates spatiotemporal overlapping interference among target signals. Under these operational constraints, instead of attempting an explicit binary classification of the measurement validity, a more resilient approach is to select trusted subsets from raw measurements based on statistical regularity and internal consistency for subsequent processing. As such, the development of reliable measurement subset selection mechanisms under zero/weak prior knowledge conditions has become a critical technological bottleneck (Wang et al., 2024; Chen et al., 2025a; Lu et al., 2022).

In order to address the issue of corrupted radiation source localization estimates, it is essential to distinguish between correct and incorrect measurements arising from density variations. Upon achieving such a differentiation, invalid measurements can be excluded from the updating process, thereby enabling the recovery of accurate localization estimates. These existing methods primarily employ geometric triangulation techniques or fixed-parameter clustering algorithms, such as K-means and Density-Based Spatial Clustering of Applications with Noise (DBSCAN). Although these methods demonstrate satisfactory performance in scenarios with predefined target numbers or low-noise environments, their effectiveness is significantly compromised when applied to dynamic open environments characterized by operational complexity (Tin et al., 2024; Zhou et al., 2022a). Firstly, fixed-parameter clustering algorithms encounter fundamental challenges in adapting to spatiotemporal variations in radiation source density. For instance, significant disparities in signal distribution between urban cores and suburban areas are frequently observed, where preset neighborhood radii are found to induce missed detections in sparse regions and false clustering in dense zones. Secondly, conventional methods exhibit inherent limitations in separating overlapping targets effectively. When multiple radiation sources (e.g., RF signals from adjacent base stations or densely deployed sensor nodes) are spatially proximate, they are prone to being erroneously aggregated into singular clusters by the algorithm, inducing significant deviations of localization results from ground truth values increasingly. Lastly, in complex scenarios with dynamically updating data, certain measurements identified as potential noise at time t-1 may become valid positioning data at time t as measurements accumulate. This necessitates algorithmic capabilities for real-time reconstruction of trusted data and potential noise. However, existing methods exhibit significant limitations in handling such dynamic data density variations (Zhou et al., 2022b; Liu et al., 2025; Zhang et al., 2023).

To address the aforementioned challenges, this paper proposes an adaptive graph-theoretic localization method for radiation sources via real-time density-aware clustering, integrating dynamic density clustering, probabilistic model verification, and maximum clique algorithms. The proposed method enables an instantaneous response to measurement data variations during density fluctuations, simultaneously reconstructing real-time potential noise and identifying trusted data subsets. This capability effectively mitigates overlapping interference in dense multi-target scenarios, thereby achieving high-precision, real-time localization of radiation sources. In the dynamic clustering layer, an adaptive Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm is implemented, which incorporates k-Nearest-Neighbor (k-NN) statistics and quantile-based adjustment mechanisms. This design dynamically optimizes the neighborhood radius and minimum sample size according to local signal density distributions, thereby achieving efficient preliminary segregation of noise from target clusters with high computational efficiency. At the probabilistic verification layer, Gaussian Mixture Model (GMM) are employed for secondary partitioning of initial clustering results. A dual-validation mechanism, which integrates the Bayesian Information Criterion (BIC) for model selection and silhouette coefficients for cluster compactness evaluation, is introduced to precisely distinguish overlapping signal sources and select trustworthy measurement subsets. To rigorously analyze intra-cluster measurement consistency under conditions of absent prior information, a GMM-driven probabilistic framework is developed to construct dynamic adjacency matrices. This formulation transforms the problem of identifying reliable measurements into a maximum clique problem, where high-dimensional adjacency matrices are decomposed into optimized submatrix blocks via spectral graph partitioning to facilitate trusted subset selection. Experimental results demonstrate that the proposed algorithm exhibits significant advantages over conventional methods in noise suppression, overlapping target separation, and real-time processing capabilities. This breakthrough establishes a robust framework for fast radiation source localization in complex electromagnetic environments. The main contributions of our work can be summarized as follows:

• This paper proposes a novel methodology capable of real-time adaptation to measurement data density fluctuations, thereby reconstructing the potential noise components and trusted subsets to provide accurate input for reliable radiation source localization without a priori information.

• The paper proposes an adaptive clustering method that integrates k-nearest neighbor statistics and adaptive quantile thresholding. This enables online parameter adaptation through localized density characterization, effectively addressing the limitations of conventional methods in handling complex environments.

• By transforming pairwise consistency maximization into maximum clique problems, the paper enhances the radiation source localization accuracy. This approach leverages graph theory to improve the reliability and scalability of radiation source localization systems.

The remaining of the paper is organized as follows. Section 2 gives a review of the existing literature. Section 3 presents the mathematical formulation of the problem. Section 4 presents a complete overview of the method. The experimental results are shown in Section 5. Lastly, Section 6 concludes this paper.

2 Related work

In the field of radiation source localization, numerous studies have focused primarily on enhancing conventional algorithms such as Angle of Arrival (AOA), Direction of Arrival (DOA), and Time Difference of Arrival (TDOA) to improve localization accuracy. However, due to noise interference and environmental distortions, raw measurements inevitably contain noise or “outliers” (Pang et al., 2025; Feng et al., 2025; Zhou et al., 2018). However, existing methods lack robust mechanisms for selecting trusted subsets from raw datasets under conditions where prior information is absent.

Recent advancements in radiation source localization have addressed challenges posed by complex electromagnetic environments, non-Gaussian noise, and GPS-denied scenarios. Traditional methods, such as Time Difference of Arrival (TDOA) and Received Signal Strength (RSS), have been enhanced to improve robustness. A Gaussian Mixture Model (GMM)-based RSS localization algorithm was designed using semidefinite relaxation (GMM-SDP) to handle non-Gaussian noise, achieving superior performance in wireless sensor networks (Wang et al., 2018). Yuan proposed K-means clustering with grid density peak clustering (DPC) for initial localization of nearby targets, effectively mitigating angular estimation errors caused by sensor inaccuracies (Yuan et al., 2025). Passive bistatic radar (PBR) systems have also gained traction, as demonstrated in (Ummenhofer et al. 2019), who utilized direction-of-arrival (DOA) estimation and single-frequency network (SFN) configurations to achieve 3D target localization in air traffic control scenarios.

The integration of machine learning and multi-agent systems has further propelled the field. (Chen et al. 2025b) developed a distributed deep reinforcement learning framework (MURPPO) for multi-UAV collaborative localization, which improved convergence speed and accuracy by 38.5% compared to traditional methods. In GPS-denied environments, (Mascarich et al. 2018) combined visual-inertial odometry with radiation sensors on aerial robots, enabling autonomous source localization and mapping under limited dwell time constraints. For urban environments, the PYRL method was proposed in (Feng et al. 2024), which converts electromagnetic field strength data into grayscale maps and employs YOLO networks for real-time localization, achieving an average error of 4.8 meters. Multi-station fusion techniques (He et al., 2025; Zhang et al., 2017), such as He et al. (2025) spectrum energy-based approach, reduced localization errors by 25% through normalized power calculations and propagation attenuation modeling. (Zhou and Abawajy 2025) and (Zhou et al. 2021) combined an improved clustering algorithm with reinforcement learning to achieve dynamic adaptive optimization of parameters, providing an important reference for the method of real-time adjustment of clustering parameters in scenarios lacking prior information. These innovations highlight a shift toward hybrid methodologies that combine physical propagation models with data-driven algorithms to address multipath effects and non-line-of-sight challenges.

Clustering techniques have evolved significantly, driven by demands for efficiency and adaptability in high-dimensional and noisy datasets. (Cai 2016) addressed the maximum weight clique problem (MWCP) in massive graphs by interleaving clique construction and graph reduction, achieving optimal solutions in sub-second timescales. CLIPPER+ was introduced in (Fathian and Summers 2024), which reformulated maximum clique estimation via semidefinite relaxation and graph pruning, enabling outlier-robust point cloud alignment with over 99% outlier rejection. Density-based methods, the FDP-DBSCAN method (Wang et al., 2018) automated cluster center selection by iteratively applying density peak clustering and DBSCAN, resolving initialization dependencies inherent in traditional K-means.

Comparative studies have underscored the strengths of specific clustering paradigms. (Omari et al. 2025) evaluated nine algorithms for image compression, identifying K-means, divisive clustering, and CLIQUE as optimal for balancing compression ratios and structural similarity. In customer segmentation, (Ling and Weiling 2025) demonstrated K-means++'s superiority over Gaussian mixture models (GMM) and DBSCAN, achieving higher silhouette scores (0.62) in RFM-based e-marketing analytics. Meanwhile, the graph-theoretic formulation was used to transform pairwise consistency maximization into maximum clique problems to improve multi-robot SLAM accuracy (Cai, 2016; Mangelson et al., 2018). These advancements emphasize the importance of algorithm hybridization—e.g., combining density peaks with spectral clustering or integrating geometric constraints with deep learning (Kassir et al., 2024) to handle heterogeneous data structures and improve scalability.

The reviewed studies illustrate a symbiotic relationship between radiation source localization and clustering algorithms. Although current research efforts have been predominantly focused on front-end radiation source measurement techniques, critical back-end data processing modules have been systematically overlooked. They do not focus on internal set consistency as we do. This work proposes a novel approach that constructs dynamic adjacency matrices and a multi-criteria optimization framework to differentiate potential noise from raw measurement datasets in real-time while selecting trusted subsets. This offers a paradigm-shift solution for reliable radiation source localization in electromagnetically complex environments.

3 Problem formulation

This paper aims to select the optimal localization subsets given all the available information provided by different platforms, either incrementally or in batch. We assume that $D_t=\left\{x_1,x_2,\dots ,x_n\right\},(x_i\in {ℝ}^d)$ denotes number of the raw measurements is n at time t. The dataset D_t can be decomposed into the union of multiple clusters, formally, there exist N disjoint clusters C₁, C₂, …, C_N, such that: $D_t={\bigcup }_{i=1}^N{C}_i$, where C_i denote the cluster of measurement points associated with the i−th radiation source. Each radiation source corresponds to a distinct cluster C_i exhibiting high intra-cluster similarity, while maintaining inter-cluster statistical independence. This characteristic aligns with the empirical observation that distinct radiation sources follow heterogeneous spatial-temporal distributions. In more complex scenarios characterized by a non-stationary number of radiation sources, spatially overlapping clusters C_i∩C_j≠∅, C_N(∃i≠j), and dynamic changes in data density, the selection of a reliable trusted subset $D_t^{*}$ from the raw measurements D_t becomes imperative. The trusted subset $D_t^{*}$ can be formulated as

$\begin{array}{ll}{D}_t^{*}=\left\{{\displaystyle \bigcup _{i=1}}{S}_i^{*}\right\}& (1)\end{array}$

$\begin{array}{l}{S}_i^{*}=arg{\displaystyle \underset{C_i\subseteq D}{max}}({\text{λ}}_1·Consistency(C_i)\oplus {\text{λ}}_2·Noise(C_i))\end{array}$

where λ₁ and λ₂ denotes the weighting coefficient, Noise(C_i) represents outliers within the i−th cluster, and Consistency(C_i) corresponds to the internal consistency function of cluster i, the operator ⊕ indicates that, under the current state, each initial cluster consists of a consistent subset and potential noise. It should be noted that the term “potential noise” herein refers to certain measurement information that is temporarily regarded as noise at the current moment during the dynamic update process, but may be re-identified as new radiation sources in subsequent data updates due to data accumulation, as shown in Figure 1.

Figure 1

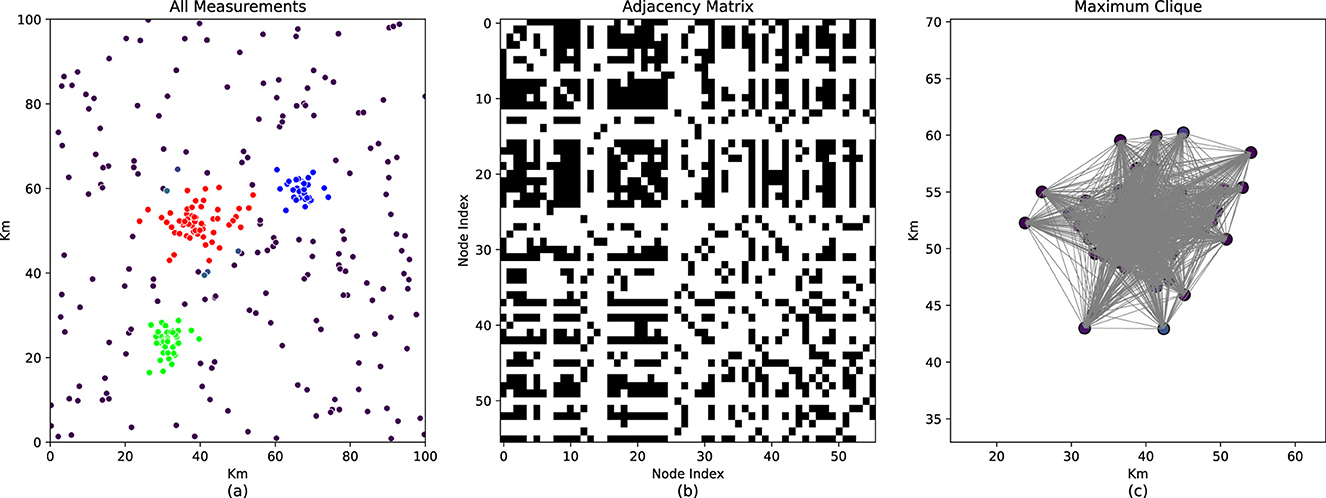
Figure 1. An illustration of the largest consistent subset maximization method for fast radiation sources localization. (a) These are a large amount of radiation source position information detected without prior information, which are then subjected to initial clustering. The gray points denote potential noise at the current moment, implying that they might be identified as new radiation sources in the subsequent dynamic update process. (b) For each initial cluster, an internal adjacency matrix is constructed, whose advantage lies in converting a huge high dimension into multiple matrix blocks. (c) The optimization problem is transformed into a maximum clique problem to obtain a trustworthy internally consistent subset, thereby enabling the rejection of erroneous measurements.

Existing methods do a good job of handling outlier measurements in the constant radiation source localization, but not in the Consistency(C_i) since no prior estimate of initial situation information in general. This paper aims to select corresponding trustworthy measurement subsets for each radiation source from the raw dataset containing potential noise. The next section describes our method for doing so.

4 Methodology

This section first establishes an adaptive clustering framework, and subsequently formulates the selection of radiation source measurement data as a combinatorial optimization problem, whose objective is to identify maximal consistent subsets in the current stage. The proposed method adopts a three-stage architecture, namely “adaptive clustering, probabilistic verification, and graph-theoretic optimization,” integrating the following key technical components.

4.1 Dynamic parameter-adaptive DBSCAN algorithm

In the absence of prior information, direct discrimination between inliers and outliers within measurement data is inherently intractable. Therefore, instead of performing explicit inlier-outlier classification, this study first partitions the measurement dataset into multiple subsets with intrinsic intra-cluster consistency using the proposed DBSCAN algorithm. The method adopts a self-adaptive parameter strategy that integrates k-nearest-neighbor statistics and adaptive quantile thresholding, allowing online parameter adaptation through localized density characterization. This approach effectively addresses the limitation of traditional approaches in adapting to instantaneous data density variations in complex environments, which leads to the absence of prior information.

For each data point in the measurement set D, we compute the Euclidean distance (eps, minPts) to its k−th nearest neighbor (k − NN), iteratively constructing the k distance sequence D_k = {d_{k, 1}, d_{k, 2}, …, d_{k, n}∣d_{k, i} = ||x_k−x_i||₂}, where k is adaptively determined based on the dataset cardinality to ensure coverage of local density characteristics. Then, we apply the Interquartile Range (IQR) method to eliminate outliers in D_k, defining the valid range χ = [Q₁−γ·IQR, Q₃+γ·IQR], where Q₁ and Q₃ represent the first and third quartiles of D_k and γ denotes the outlier detection coefficient. This process yields the filtered valid distance sequence $D_k^{\prime }=\left\{d_{k,i}\in D_k\mid d\in \chi \right\}$. Now, the key parameter neighborhood radius eps of the DBSCAN algorithm is adaptively determined in real-time by selecting the α−th quantile of the dataset $D_k^{\prime }$, $eps=Percentile(D_k^{\prime },\alpha )$, where α is dynamically adjusted according to the local density distribution. This strategy enables dynamic adaptation to local density characteristics, thereby circumventing misclassification artifacts induced by fixed parameterization in both sparse and dense regions. The DBSCAN algorithm's other critical parameter, the minimum neighborhood size minPts, is configured as a scaling function $minPts=\gamma ·{log}_{10}(\left|D_k^{\prime }\right|)$, where γ is a density-aware coefficient derived from the dataset cardinality $\left|D_k^{\prime }\right|$. The parameter minPts meets concurrent suppression of small-scale noise and adaptive accommodation of density variations across heterogeneous data scales through its cardinality- sensitive formulation.

Building upon this framework, we achieve preliminary dataset classification through adaptive tuning of DBSCAN's critical parameters (eps, minPts). From the measurement data containing potential noise at the current time, we obtain initial clusters represented by three colors (red, green, and blue), as shown in Figure 1a. This generates high-fidelity initial clusters, which are critical for subsequent GMM validation and maximal clique analysis, serving as the core foundation for the system to achieve high-precision localization.

4.2 Misclustering problem

Following the previous section, we obtain an initial candidate cluster set C = {C₁, C₂, …, C_m}. Then the system conducts subsequent analysis on clustering errors characterized by excessive inter-cluster proximity or abnormal intra-cluster variance, thereby addressing the misclustering issues induced by dense target overlap and noise corruption. A probabilistic segmentation framework integrating GMM with the Bayesian Information Criterion (BIC) is developed to refine the partitioning of anomalous clusters through model-order optimization. The misclustering identification criteria are mainly based on inter-cluster distance and intra-cluster variance. A cluster is flagged for segmentation if the minimum centroid distance to neighboring clusters falls below an adaptive threshold d_min, or if its covariance matrix trace exceeds the variance threshold σ_max, triggering GMM-based probabilistic decomposition. Based on the two aforementioned criteria, we iteratively traverse all clusters to select those satisfying threshold d_min or σ_max, obtaining cluster set C′.

Then, we construct GMM to probabilistically partition each selected cluster. To prevent overfitting and underfitting, the number of mixture components K is dynamically configured as $K=min(K_{max},max(2,\lfloor \frac{N_{\text{cluster}}}{\delta }\rfloor ))$ during each algorithmic invocation, where N_cluster denotes the intra-cluster point cardinality, K_max specifies the maximum allowable component count, and δ represents the size-adaptive scaling factor, thereby achieving self-adaptive parameter optimization. We further calculate the BIC values before and after segmentation. The mathematical formulation is formulated as

$\begin{array}{ll}BIC=-2lnL+klnN& (2)\end{array}$

where L denotes the model likelihood, k represents the number of model parameters, and N is the sample size. Only segmentation results with statistically significant BIC reduction are retained, specifically executing the partition when the post-segmentation BIC value decreases beyond the proportional threshold β, formally expressed as BIC_post < BIC_pre(1 − β), where β = 0.15 denotes the empirically optimized significance level.

The BIC constrains model complexity to prevent overfitting induced by excessive component counts. The component count K is dynamically adjusted in real-time based on cluster scale, ensuring statistical validity of partitioned sub-clusters while accommodating varying density distributions. The current computed candidate cluster set $C^{\prime }=\left\{C_1^{\prime },C_2^{\prime },\dots ,C_n^{\prime }\right\}$ has considerably mitigated the impact of noisy measurements on localization. However, the consistency of measurements within individual clusters remains undetermined, indicating that erroneous measurements may still persist within clusters. Now, we attempt to extract the highconfidence target core regions, also called trusted subset $S_i^{*}$, from each candidate cluster $C_i^{\prime }$ to calculate the radiation source positions, where the measurements exhibit high consistency across both spatial and temporal dimensions. However, it should be noted that computing intracluster measurement consistency may require evaluating all possible combinations of measurements, which has been proven to exhibit exponential computational complexity. By formulating the problem as the maximum clique problem in graph theory, we can effectively leverage existing theoretical frameworks to achieve efficient solutions or approximate estimations. In practical applications, it has been observed that pairwise consistency checks demonstrate sufficient constraint strength to effectively filter out inconsistent measurements in datasets with full-degree-of-freedom observations.

4.3 Selecting trust subsets via maximum clique

The maximum clique problem seeks to identify the largest fully-connected subgraph where all nodes are pairwise adjacent, which essentially aims to find the largest subset in a dataset satisfying strict consistency constraints. In radiation source localization scenarios, we model measurement data within candidate cluster C′ as a graph structure where nodes represent measurement points and edges denote spatial consistency relationships between point pairs. By constructing a probabilistic adjacency matrix and solving the maximum clique, this approach effectively identifies the target's core distribution regions while eliminating peripheral noise points and low-confidence measurements.

In graph theory, a clique is defined as a subset of vertices in an undirected graph where every pair of distinct vertices is connected by an edge. A graph may contain multiple cliques, with a maximal clique being one that cannot be extended by incorporating additional adjacent vertices—that is, no superset of vertices in the graph forms a larger clique. The foundational consideration in clique analysis lies in the rigorous definition of pairwise adjacency relationships between vertices. This paper employs GMM probabilistic framework to adaptively assess pairwise spatial consistency between measurement points.

For the measurement data in each candidate cluster $C_k^{\prime }$, it is assumed that their error distributions follow a multimodal Gaussian mixture model. For cluster $C_k^{\prime }=\left\{x_1^k,x_2^k,\dots ,x_n^k\mid x_i^k\in {ℝ}^2\right\}$, we assume that it follows a mixture distribution composed of K Gaussian components, and the model is then trained to capture the mixture characteristics of the noise and target distributions.

$\begin{array}{ll}p(x\mid C_j)={\displaystyle \sum _{k=1}^K}{\pi }_{jk}N\left(x\mid {\mu }_{jk},{\sigma }_{jk}^2\right)& (3)\end{array}$

Where K denotes the number of Gaussian components, π_jk represents the mixture weights, μ_jk and ${\sigma }_{jk}^2$ correspond to the mean and variance of the component, respectively.

Based on the GMM posterior probability $p(x\in C_k^{\prime })$, we compute the consistency weight associated with their pairwise distance, for any two points $x_i^k$ and $x_j^k$ within cluster $C_k^{\prime }$, the adjacency condition is formally defined as H(i, j),:

$\begin{array}{ll}H(i,j)=\{\begin{array}{l}1,p\left(d_{ij}\right)>\tau (\rho )\hfill \\ 0,\text{\hspace{1em} otherwise }\hfill \end{array}& (4)\end{array}$

where τ(ρ) denotes the dynamic threshold function and ρ represents the local density. The elements of the adjacency matrix H are binary-valued, where an entry of 1 denotes the existence of an edge between the corresponding vertices, and 0 indicates the absence of a connecting edge.

The threshold adaptively increases with higher densities to mitigate over-connection, while relaxing constraints under sparser densities to prevent missed detection. In this paper, the dynamic threshold function is formulated as

$\begin{array}{ll}\tau (\rho )={\tau }_0(1+log(1+\rho ))& (5)\end{array}$

where τ₀ serves as the fundamental threshold parameter. When the number of adjacency edges falls below a predefined lower bound, a Euclidean distance-based fallback mechanism is activated to enforce edge creation, thereby guaranteeing graph connectivity. By iteratively processing all measurement data within the cluster $C_k^{\prime }$ through the described operations, we obtain an adjacency matrix H of dimension n × n, where n represents the cardinality of measurement points in the cluster. Inherent to the undirected graph representation, the adjacency matrix H constitutes a symmetric matrix with zero-valued main diagonal entries, satisfying the fundamental properties H(i, j) = H(j, i), ∀i≠j, and H(i, i) = 0 by definition, as shown in Figure 1b.

The adjacency matrix and the undirected graph representations are mutually convertible, where a zero-valued element in the matrix indicates the absence of the corresponding edge in the graph. As a preliminary step, we introduce fundamental graph-theoretic concepts: an undirected graph G is formally defined as G = {V, E}, where V denotes the vertex set and E⊆{{i, j}∣i, j∈V, i≠j} represents the edge set. For each candidate cluster $C_k^{\prime }$, we construct its corresponding undirected graph G_k = {V_k, E_k} and extract the maximum clique S

$\begin{array}{ll}S=arg{\displaystyle \underset{S\subseteq D}{max}}{\displaystyle \sum _{x_i,x_j\in S}}{\text{H}}_{ij},\text{s.t.}\left|S\right|\ge m_{min}& (6)\end{array}$

where m_min denotes the threshold of the minimum clique cardinality.

Now, the meanings of the nodes and edges in the undirected graph G_k have changed. The measurement data within a cluster become the nodes of the undirected graph, and whether an edge exists between two measurement nodes depends on whether the corresponding element in the adjacency matrix H is greater than the threshold. Considering the fully connected property of the clique model, the nodes in a clique represent that all measurements satisfy pairwise internal consistency. Since the proposed algorithm has achieved a relatively high accuracy in clustering radiation sources, our objective is to find the corresponding maximum clique $S_k^{*}$ in each undirected graph.

$\begin{array}{ll}{S}^{*}=arg{\displaystyle \underset{S\subseteq D}{max}}({\text{λ}}_1·Consistency(S)\oplus {\text{λ}}_2·Noise(S))& (7)\end{array}$

where the maximum clique $S_k^{*}$ represents the trusted subset with the largest cardinality in the graph. As shown in Figure 1c, the purple points represent the trust subset selected by the proposed algorithm at the current moment, which comply with the full connectivity of the clique. The existence of edges between nodes indicates that consistency is satisfied between them. Now, we have extracted a trust subset $D^{*}=\left\{{\bigcup }_{i=1}{S}_i^{*}\right\}$ with high internal consistency from the raw data containing potential noise, thus improving the accuracy of localization in the absence of prior information.

Note that for dynamically updated radiation source localization, the trustworthy subsets selected by the proposed algorithm cannot guarantee the identification of all correct measurements. This is because, due to the lack of prior information in the measurement data, the measurement points regarded as potential noise at the current moment may be incorporated into the clique in the next moment as a result of supplementary new measurement data. However, it can be confirmed that the trust subsets selected by the proposed algorithm at the current moment have effectively excluded potential noise, enabling the fast localization of radiation sources under the condition of zero/weak prior information.

5 Experiment evaluation

This section aims to evaluate the accuracy of the proposed algorithm through simulation analyzes. The proposed method is implemented in python language. We collected real radiation source localization datasets and conducted comparative performance assessments against K-means clustering, DBSCAN, and GMM methods (Tin et al., 2024). During experimental validation, we observed that the number of radiation source significantly influences measurement precision. Specifically, higher amounts of radiation sources may introduce additional outlier measurements, thereby substantially degrading the localization accuracy. Consequently, our data preprocessing workflow incorporates comparative analysis across varying target source populations to quantify these effects. The experiments are mainly designed from three scenarios: high-noise scenarios, densely overlapping scenarios, and Cross-Density Scenarios scenarios. It should be noted that the algorithm proposed in this paper aims to solve the problem that density changes during the dynamic incremental update of measurement data lead to the failure of traditional algorithms, rather than merely clustering static data. It places more emphasis on the robustness of the algorithm to density and noise.

5.1 Boundary noise robustness assessment

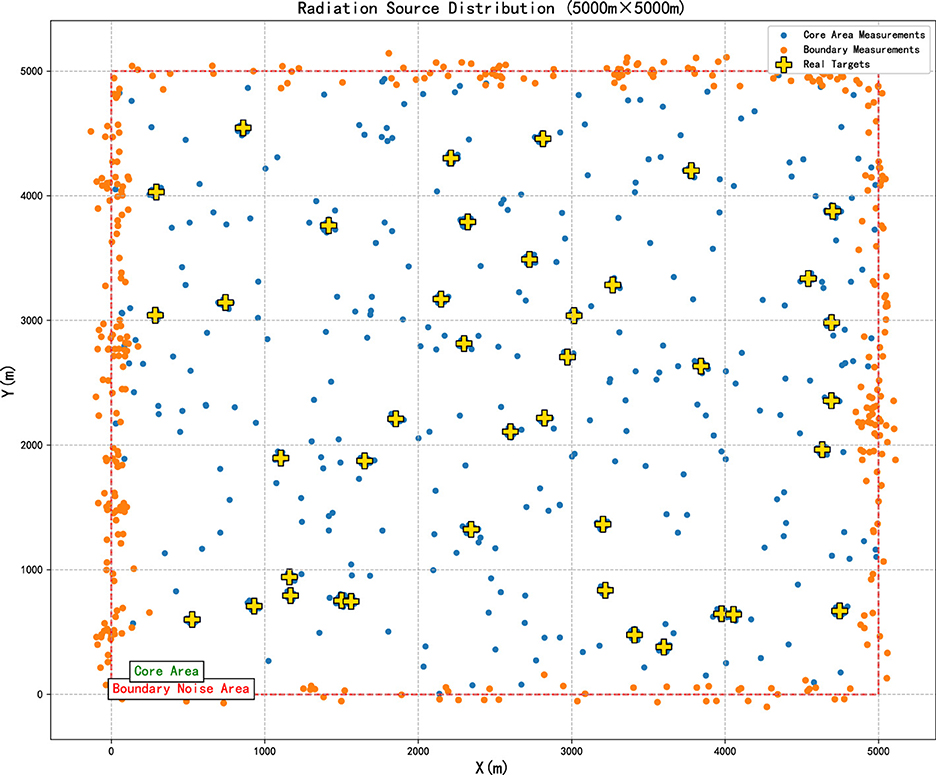
In complex electromagnetic environments, radiation source distributions often exhibit significant spatial heterogeneity. The real targets typically reside in core regions with measurement data conforming to Gaussian distributions, while global background noise (conventional noise points) follows a uniform distribution. However, boundary interference zones contain high-intensity aggregated noise formed by boundary noise points and interference clusters. These adverse factors cause substantial performance degradation in boundary regions for conventional methods. Thus, we first evaluate the proposed algorithm's robustness against boundary noise.

The simulation scenario includes an area of [0, 5, 000]m × [0, 5, 000]m, where the width of the boundary noise band is 100 m. Forty real targets are uniformly distributed in the core area of [200, 4,800] m × [200, 4, 800]m. Conventional noise (Gaussian noise with σ = 20) accounts for 15% of the total number of points and is uniformly distributed throughout the area. Boundary noise (Gaussian noise with σ = 60) accounts for 10% of the total number of points and is intensively distributed in the boundary noise area. Ten interference clusters are distributed in the boundary noise area to simulate false targets, as shown in Figure 2.

Figure 2

Figure 2. Simulation results of radiation source distribution.

The proposed algorithm, K-means clustering, DBSCAN, and GMM methods are run for distribution to extract cluster sets, and the False Positive Count (FPC) of the quantization algorithm mistakenly judging boundary noise as real targets is quantified.

$\begin{array}{ll}FPC={\displaystyle \sum _{n=1}}I(C_k\text{is false target})& (8)\end{array}$

where C_k is the target cluster output by the algorithm, and I denotes the indicator function.Then, each cluster is sequentially traversed to check whether it simultaneously satisfies the following two criteria, and if both are satisfied, it is counted into the FPC. Criteria 1: The centroid of the cluster is located in the boundary noise area; Criteria 2: The proportion of boundary noise within the cluster is greater than 70%,

$\begin{array}{ll}\frac{\left|\left\{x_i\in C_k^{\prime }\mid x_i\in \partial \text{Ω}\right\}\right|}{\left|C_k^{\prime }\right|}\ge 0.7& (9)\end{array}$

Where ∂Ω is the boundary noise region. During the experimental analysis, we comprehensively analyze the performance of different algorithms using the Monte Carlo idea, repeating the experiments 20 times with different random seeds.

Figures 3a, b show the trend of variation and the average results of the FPC, respectively. The reason for the poor result of the DBSCAN method lies in the excessive clustering of fixed parameters in the dense boundary area. The experimental results demonstrate that the proposed algorithm exhibits higher robustness to boundary noise compared with other methods. This is because the adaptive DBSCAN method proposed in this paper automatically increases eps in the sparse boundary region to prevent small noise from forming clusters. Meanwhile, the clique model eliminates low-confidence clusters and only retains highly consistent clusters. The experimental result of FPC < 1 indicates that the proposed algorithm achieves a “FPC approaching zero” in the strong interference boundary region, which can meet complex scenarios.

Figure 3

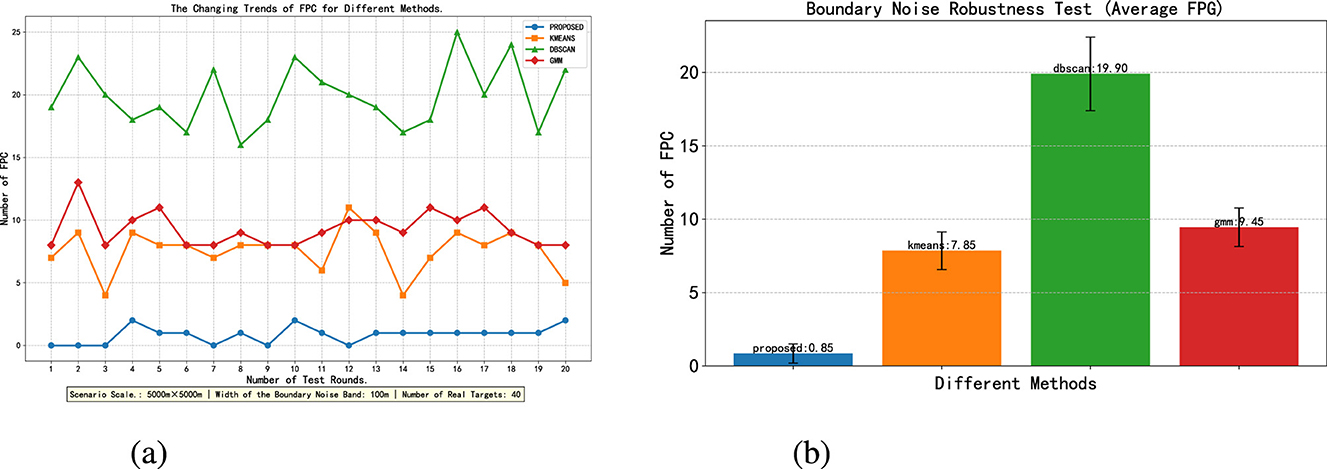
Figure 3. The simulation results of Scenario 1. (a) Simulation results of the FPC trend. (b) Schematic diagram of FPC error bars.

5.2 Dense overlapping scenarios assessment

In the previous section, we validated the robustness of the proposed method against boundary noise. In this section, we verify its effectiveness in overlapping scenarios. In dense overlapping scenes, the spatial positions of multiple radiation sources may exhibit high proximity (partial or complete overlap), compounded by adverse factors such as high noise, dynamic data distributions, and heterogeneous interference. These conditions cause traditional methods to be prone to misclustering, target adhesion, and noise misclassification in such scenarios. Therefore, in this section, we establish simulation scenarios to simulate extreme environments where multiple radiation source positions exhibit high proximity and signals mutually interfere, to systematically test the proposed method's robustness, accuracy, and adaptability under complex electromagnetic conditions. The average positioning error (Euclidean distance) is mainly used to verify the accuracy of the proposed algorithm. The mathematical expression of the average localization error is

$\begin{array}{ll}{E}_{\text{avg}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\displaystyle \underset{j}{min}}||x_i-t_j||& (10)\end{array}$

where x_i denotes the measurement data derived from the algorithm, t_j represents the location of the true radiation source, and N is the detection count.

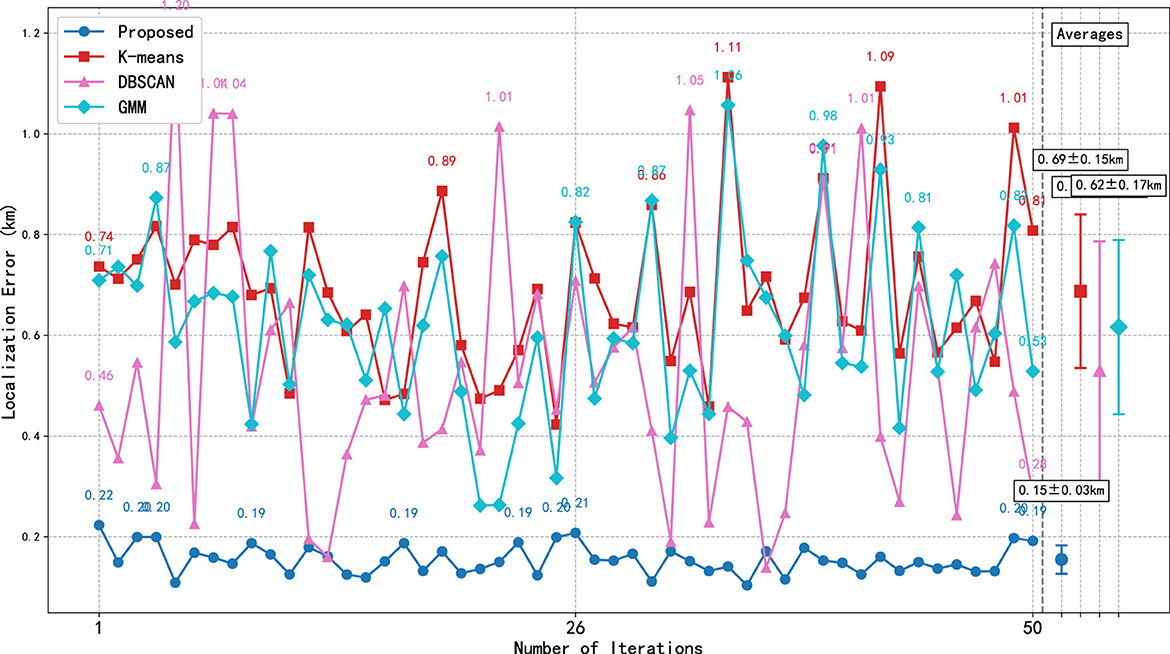
The experimental scenario includes five groups of radiation sources, where the number of radiation sources in each group can be dynamically adjusted for experimental analysis. Figure 4 shows the Monte Carlo experiment with 50 simulations per run. The dashed line represents the average error of the method in one Monte Carlo experiment, and the length of the vertical error bar indicates the standard deviation of the localization error of each method in each run. The maximum spacing constraint within a group is < 2.0 km, and the offset range of radiation sources within a group is [–1.0, 1.0] km. To ensure the universality of the data, each radiation source generates 40 Gaussian points distributed with rotational perturbation, and 20% uniformly distributed random noise points are added. As mentioned above, the increase in the number of radiation sources in dense scenarios deteriorates the positioning error of the algorithm. In the experiment, the number of radiation sources in each group gradually increased from 3 to 10, which means that the total number of measurements in the measurement area increased from 600 to 2,000.

Figure 4

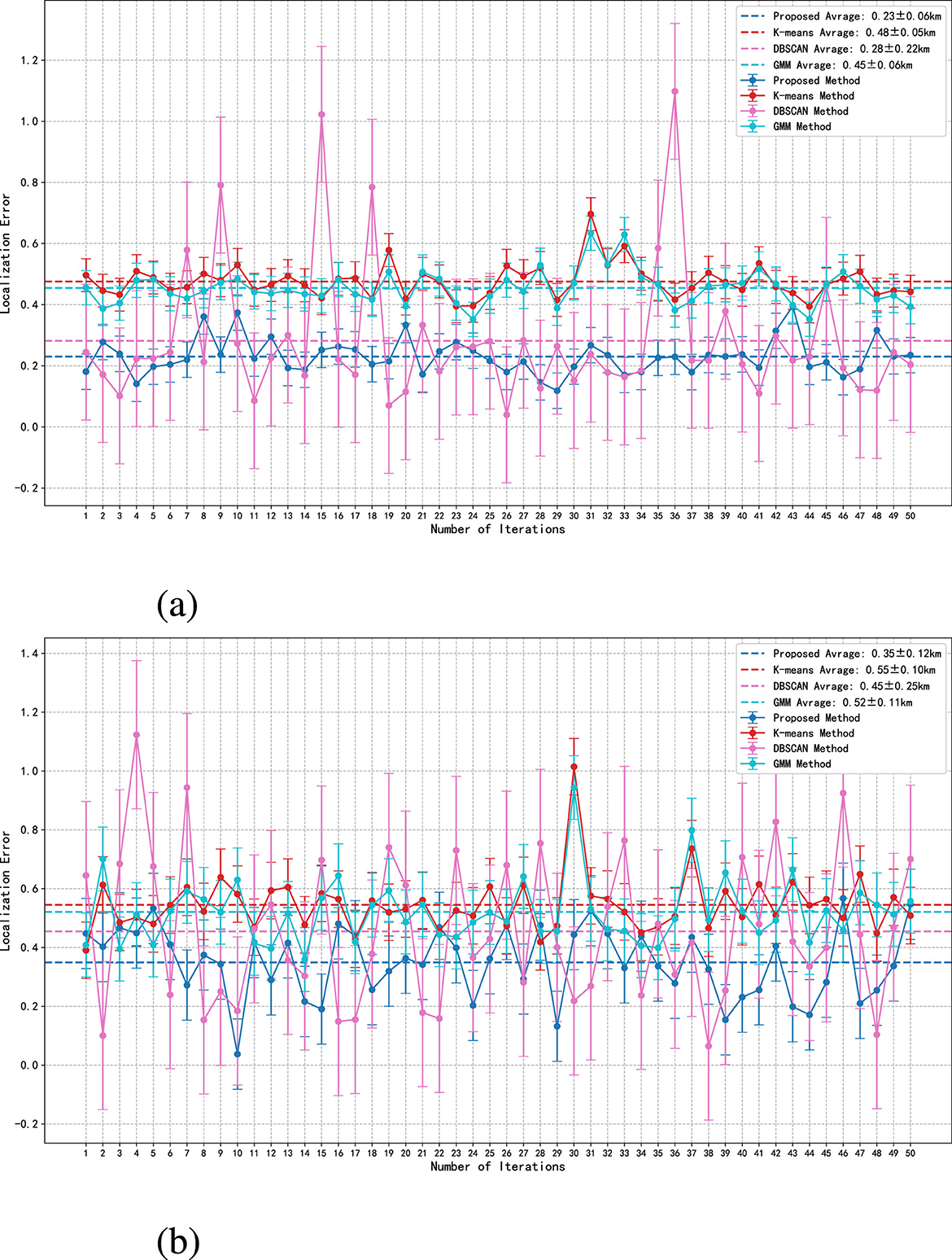
Figure 4. Experiment on localization error in dense scenarios. (a) Number of radiation sources per group is 3. (b) Number of radiation sources per group is 10.

In dense scenarios, the proposed algorithm simultaneously considers geometric distances and radiation source attribution relationships, significantly improving the accuracy of point-to-point associations. This ensures that each real radiation source retains only one high-quality cluster, avoiding repeated detections. In Figure 4, the error curve of the proposed method is consistently at the bottom, while the error fluctuation ranges of other algorithms are significantly larger. During simulation, traditional methods exhibit error spikes (misidentification in dense regions). And as the number of radiation sources per group increases, the localization error of the method gradually increases, yet the proposed method always maintains a significant advantage. The traditional DBSCAN method uses a fixed parameter eps, making it impossible to adapt to regions with different densities. As a result, a large number of boundary points in dense scenarios are misclassified as noise, leading to the worst localization performance.

5.3 Cross-density scenarios assessment

Sections 5.1 and 5.2 analyze the anti-noise capacity of the method under low-density conditions and the localization accuracy in high-density environments. In this section, we further analyze the consistency of the proposed algorithm in cross-density scenarios, that is, evaluate the effectiveness of the algorithm when the data volume dynamically changes by simulating different conditions of data distribution (sparse-transition-dense). Figure 5 shows the localization results of different algorithms in the sparse, transition, and dense regions, respectively, for an arbitrary single trial. In the simulation experiments in this section, we extend the experimental scenario to [0, 10] km. The generation of measurement data includes three phases. Phase 1 is referred to as the sparse region, where the density of measurement data is assumed to be 5 /km². Phase 2 is the transition region, with a data density of 20 /km² and 30 /km². Finally, Phase 3 is assumed to be the dense region, where the density of measurement data is 50 /km². The procedure begins with initial sparse-phase measurement data and gradually increases the number of measurement points to elevate the density. This thus verifies that the proposed method can dynamically handle potential noise at different moments, ensuring the consistency of the trust subset. Based on the Monte Carlo method, multiple simulation analyzes were conducted.

Figure 5

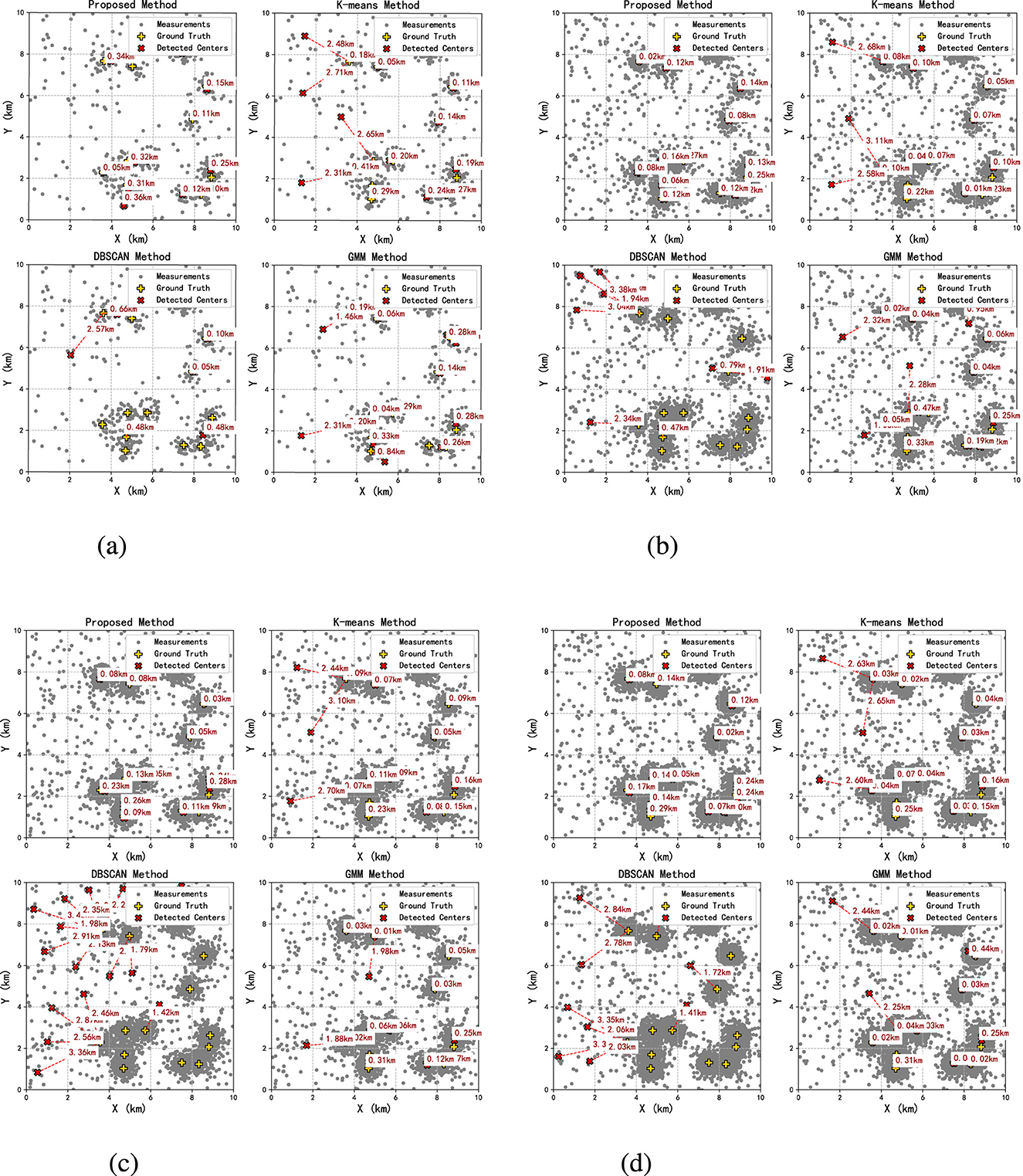
Figure 5. Experiment on localization error in cross-density scenarios. The gray points may be initially regarded as noise, and as the measurement information gradually increases, they are detected as new radiation sources. (a) Simulation results of the spare region. (b) Simulation results of the transition region 1. (c) Simulation results of the transition region 2. (d) Simulation results of the dense region.

As shown in Figure 5a, the measurement data of radiation sources are approximately 600 in the initial stage, which are relatively sparse, and the proportion of noise points is high (30%). Traditional methods are disturbed by noise, leading to large deviations in the positioning results. It should be noted that the measurement data are relatively sparse under the current state, with some correct measurement data being temporarily classified as potential noise. To allow the simulation to gradually enter Stage 2 (transition region), we adopt an incremental update approach to increase the density of measurement data, as shown in Figures 5b, c. In this phase, the measurement count exceeds 2,000, yet the data distribution exhibits non-uniformity with mixed-density regions in the scenario. Traditional K-means/GMM methods fail to accommodate both density variations and inhomogeneity, thereby amplifying localization deviations. It can be observed that with the dynamic update of measurement data, the measurement points previously regarded as potential noise are re-selected into the trust subset at the current moment, which verifies the adaptability of the proposed algorithm to dynamic scenarios. In the dense region of Stage 3, the number of measurement points exceeded 5,000, as shown in Figure 5d. The accumulation of a large volume of measurement data reduces inter-cluster distances, which may readily lead to incorrect associations between distinct clusters—despite the fact that they do not actually belong to the same cluster. The proposed method leverages the dynamic threshold of the GMM adjacency matrix to effectively mitigate the issue of erroneous association between adjacent clusters in cross-density scenarios. It prevents the incorrect merging of different clusters while improving localization accuracy.

Figure 5 visually illustrates the variation of localization accuracy among different algorithms during the iterative update process of the measurement data. A quantitative analysis of this phenomenon is now presented. Figure 6 displays the polylines of localization error and the average errors of different algorithms statistically obtained from 50 Monte Carlo experiments. The simulation results indicate that the localization error of the proposed algorithm is 0.2, and its localization accuracy is improved by approximately 70% compared to the other three methods. As is clearly observed in the figure, the error curve of the proposed algorithm appears smoother, which confirms its superior robustness against noise and density variations.

Figure 6

Figure 6. Simulation results of radiation source localization errors.

6 Conclusions

For the challenges of high noise, target overlap, and dynamic density variations present in radiation source measurement data within complex environments, this paper proposes a novel radiation source localization framework that integrates adaptive clustering, probabilistic validation, and graph-theoretic optimization. This paper establishes a framework incorporating adaptive clustering, probabilistic validation, and graph-based optimization to address the challenges associated with processing incrementally updated datasets. The proposed approach resolves the limitations of conventional methods in adapting to instantaneous density variations by dynamically partitioning the data into intrinsically consistent subsets. Furthermore, it employs a graph-based formulation, translating the maximization of pairwise consistency into a maximum clique problem, thereby enhancing localization accuracy. Experimental results demonstrate that the proposed framework significantly improves localization performance in complex scenarios. Specifically, it achieves an average positioning error of 0.15 km in cross-density scenarios, significantly outperforming traditional algorithms. This research provides a engineering feasible solution for radiation source localization in complex environments, and its modular architecture lays the groundwork for future multisource fusion applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

WC: Writing – original draft. ZQ: Writing – review & editing. LJ: Writing – review & editing. QM: Writing – review & editing. HX: Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, S. (2016). “Fast solving maximum weight clique problem in massive graphs,” in International Joint Conference on Artificial Intelligence.

Google Scholar

Chen, J., Chen, A., Wang, J., and Liu, Y. (2025a). Research on a radioactive source localization algorithm based on UAV aerial survey data. Radiat. Meas. 184, 107437. doi: 10.1016/j.radmeas.2025.107437

Crossref Full Text | Google Scholar

Chen, J., Zhang, Z., Fan, D., Hou, C., Zhang, Y., Hou, T., et al. (2025b). Distributed decision making for electromagnetic radiation source localization using multi-agent deep reinforcement learning. Drones 9, 216. doi: 10.3390/drones9030216

Crossref Full Text | Google Scholar

Fathian, K., and Summers, T. (2024). Clipper+: a fast maximal clique algorithm for robust global registration. IEEE Robot. Autom. Lett. 9, 3562–3569. doi: 10.1109/LRA.2024.3368233

Crossref Full Text | Google Scholar

Feng, M., Luo, Y., Shao, W., Jin, J., Liu, Y., Lu, H., et al. (2024). “Pyrl: a radiation source localization method in urban environments,” in 2024 14th International Symposium on Antennas, Propagation and EM Theory (ISAPE), 1–4. doi: 10.1109/ISAPE62431.2024.10841005

Crossref Full Text | Google Scholar

Feng, R., Wu, W., Qian, L., Chang, Y., Yousaf, M. Z., Khan, B., et al. (2025). A hybrid tdoa and aoa visible light indoor localization method using irs. Electronics 14:2158. doi: 10.3390/electronics14112158

Crossref Full Text | Google Scholar

He, G., Hao, Y., and Xie, Y. (2025). The multi-station fusion-based radiation source localization method based on spectrum energy. Sensors 25:1339. doi: 10.3390/s25051339

Crossref Full Text | Google Scholar

Kassir, H. A., Kantartzis, N. V., Lazaridis, P. I., Sarigiannidis, P., Goudos, S. K., Christodoulou, C. G., et al. (2024). Improving doa estimation via an optimal deep residual neural network classifier on uniform linear arrays. IEEE Open J. Antennas Propag. 5, 460–473. doi: 10.1109/OJAP.2024.3362061

Crossref Full Text | Google Scholar

Ling, L. S., and Weiling, C. T. (2025). Enhancing segmentation: a comparative study of clustering methods. IEEE Access 13, 47418–47439. doi: 10.1109/ACCESS.2025.3550339

Crossref Full Text | Google Scholar

Liu, X., Wu, W., and Xie, M. (2025). Adaptive weighted noise constraint-based low-rank representation learning for robust multi-view subspace clustering. Appl. Intell. 55:816. doi: 10.1007/s10489-025-06502-5

Crossref Full Text | Google Scholar

Lu, J., Wu, Q., and Wu, C. (2022). “A new density clustering method based on dynamic local density,” in 2022 IEEE International Conference on Networking, Sensing and Control (ICNSC), 1–6. doi: 10.1109/ICNSC55942.2022.10004074

Crossref Full Text | Google Scholar

Mangelson, J. G., Dominic, D., Eustice, R. M., and Vasudevan, R. (2018). “Pairwise consistent measurement set maximization for robust multi-robot map merging,” in 2018 IEEE International Conference on Robotics and Automation (ICRA), 2916–2923. doi: 10.1109/ICRA.2018.8460217

Crossref Full Text | Google Scholar

Mascarich, F., Wilson, T., Papachristos, C., and Alexis, K. (2018). “Radiation source localization in gps-denied environments using aerial robots,” in 2018 IEEE International Conference on Robotics and Automation (ICRA). doi: 10.1109/ICRA.2018.8460760

Crossref Full Text | Google Scholar

Omari, M., Kaddi, M., Salameh, K., and Alnoman, A. (2025). Advancing image compression through clustering techniques: a comprehensive analysis. Technologies 13:123. doi: 10.3390/technologies13030123

Crossref Full Text | Google Scholar

Pang, D., Wang, G., and Ho, K. C. (2025). Hybrid aoa-tdoa localization of a moving source by single receiver. IEEE Trans. Commun. 73, 4088–4104. doi: 10.1109/TCOMM.2024.3511932

Crossref Full Text | Google Scholar

Sun, C., Zhou, J., Jang, K.-S., and Kim, Y. (2023). Intelligent mesh cluster algorithm for device-free localization in wireless sensor networks. Electronics 12:3426. doi: 10.3390/electronics12163426

Crossref Full Text | Google Scholar

Tin, T. T., Hao, Y. J., Yeou, Y. C., Mooi, L. S., Yew, G. T., Olugbade, T. O., et al. (2024). Natural disaster clustering using k-means, dbscan, som, gmm, and mean shift: an analysis of fema disaster statistics. Int. J. Adv. Comput. Sci. Applic. 15, 667–681. doi: 10.14569/IJACSA.2024.0150968

Crossref Full Text | Google Scholar

Ummenhofer, M., Kohler, M., Schell, J., and Ohagan, D. W. (2019). “Direction of arrival estimation techniques for passive radar based 3D target localization,” in 2019 IEEE Radar Conference (RadarConf19). doi: 10.1109/RADAR.2019.8835841

Crossref Full Text | Google Scholar

Wang, Y., Han, L., Zhang, X., Sun, G.-C., Zhang, Z., Xing, M., et al. (2024). A passive signal focusing algorithm based on synthetic aperture technique for multiple radiation source localization. IEEE Trans. Geosci. Rem. Sens. 62, 1–16. doi: 10.1109/TGRS.2024.3370390

Crossref Full Text | Google Scholar

Wang, Z., Huang, M., Du, H., and Qin, H. (2018). “A clustering algorithm based on fdp and dbscan,” in 2018 14th International Conference on Computational Intelligence and Security, 8563058. doi: 10.1109/CIS2018.2018.00039

Crossref Full Text | Google Scholar

Yuan, Z., Wang, X., Chen, F., and Ma, X. (2025). Improved k-means algorithm for nearby target localization. IEEE Access 13, 14872–14880. doi: 10.1109/ACCESS.2024.3479091

Crossref Full Text | Google Scholar

Zhang, L., Zhang, M., Xu, J., and Xu, Y. (2023). Cluster-based jrpca algorithm for wi-fi fingerprint localization. Electronics 12:153. doi: 10.3390/electronics12010153

Crossref Full Text | Google Scholar

Zhang, Y., Xing, S., Zhu, Y., Yan, F., and Shen, L. (2017). Rss-based localization in wsns using gaussian mixture model via semidefinite relaxation. IEEE Commun. Lett. 21, 1329–1332. doi: 10.1109/LCOMM.2017.2666157

Crossref Full Text | Google Scholar

Zhou, Z., and Abawajy, J. (2025). Reinforcement learning-based edge server placement in the intelligent internet of vehicles environment. IEEE Trans. Intell. Transport. Syst. 2025, 1–11. doi: 10.1109/TITS.2025.3557259

Crossref Full Text | Google Scholar

Zhou, Z., Abawajy, J., Chowdhury, M., Hu, Z., Li, K., Cheng, H., et al. (2018). Minimizing sla violation and power consumption in cloud data centers using adaptive energy-aware algorithms. Future Gener. Comput. Syst. 86, 836–850. doi: 10.1016/j.future.2017.07.048

Crossref Full Text | Google Scholar

Zhou, Z., Shojafar, M., Abawajy, J., Yin, H., and Lu, H. (2022a). ECMS: an edge intelligent energy efficient model in mobile edge computing. IEEE Trans. Green Commun. Netw. 6, 238–247. doi: 10.1109/TGCN.2021.3121961

Crossref Full Text | Google Scholar

Zhou, Z., Shojafar, M., Alazab, M., Abawajy, J., and Li, F. (2021). AFED-EF: an energy-efficient VM allocation algorithm for IoT applications in a cloud data center. IEEE Trans. Green Commun. Netw. 5, 658–669. doi: 10.1109/TGCN.2021.3067309

Crossref Full Text | Google Scholar

Zhou, Z., Shojafar, M., Alazab, M., and Li, F. (2022b). IECL: an intelligent energy consumption model for cloud manufacturing. IEEE Trans. Ind. Inform. 18, 8967–8976. doi: 10.1109/TII.2022.3165085

Crossref Full Text | Google Scholar