- 1Department of Neurosurgery, the Affliliated Hospital, Southwest Medical University, Luzhou, Sichuan, China
- 2Department of Geriatric Medicine, The Affliliated Hospital, Southwest Medical University, Luzhou, Sichuan, China
- 3Department of Urology or Nursing, Sichuan Provincial People's Hospital East Sichuan Hospital & Dazhou First People’s Hospital, Dazhou, Sichuan, China
A Commentary on
Molecular and immunological features of TREM1 and its emergence as a prognostic indicator in glioma
by Lin Zhang, Xun Qu, Yangyang Xu (2024). Front. Immunol. 15: 1324010. doi: 10.3389/fimmu.2024.1324010
We read with great interest the recently reported study published in Front. Immunol. by Zhang et al. (1). The researchers employed both univariate and multivariate Cox regression analysis to validate TREM1 as an independent prognostic biomarker for gliomas. Following this, they developed a nomogram utilizing the TREM1 expression level, WHO grade, gender, age, radiotherapy, chemotherapy, and IDH status, sourced from the TCGA cohort, to forecast the 1-year, 3-year, and 5-year survival probabilities of glioma patients. This study demonstrated that the nomogram possessed satisfactory predictive capability. Acknowledging the significant contributions of this study, we have identified certain deviations in the authors’ application of the Cox proportional hazards (CoxPH) model that are still unstated and unresolved.
Mixed censoring results (i.e., interval-censoring and right-censoring occurrences) could arise from the established criteria (2). Interval censoring may occur if the end event of glioma identified by medical records takes place in between follow-ups. Right censoring may occur if the diagnosis is made between the conclusion of the follow-up and the data analysis period. Dealing with right-censoring data is the main emphasis of the CoxPH model. The accelerated failure time (AFT) model, on the other hand, is usually chosen for situations that involve an extensive variety of censored data types (3). By adequately modifying the likelihood function, the AFT model may effectively handle data that has been left, right, or interval censored (4). The R packages (‘icenReg’ and ‘survival’) are useful for fitting and analyzing mixed censored data as well as estimating event timings (5).
Furthermore, from the standpoint of modeling strategy, the CoxPH model assumes that the hazard ratio is constant over the course of the follow-up period, meaning that the influence of covariates does not change over time (6). Inaccurate prediction findings and skewed statistical conclusions drawn from the model may result from breaking the proportional hazards (PH) assumption (7, 8). However, a number of factors may contribute to the frequent emergence of nonproportionality of hazards in practice (9). Schoenfeld residuals or other alternative methods should be used by the investigators to evaluate the PH assumption of the association between covariates and outcomes (10). If there is a consistent pattern of change over time in the residuals, it suggests that the covariate’s effect may fluctuate over time. Instead of using the conventional Cox proportional hazards model, writers should use the Cox model including time-varying effects, the stratified Cox model, or the AFT model when the proportional hazards assumption fails to be met (11–13).
Similarly, we performed the univariate and multivariate Cox regression analysis (Figure 1A) of relevant clinical parameters as conducted by Zhang et al. (1) on glioma patients from the TCGA cohort, and verified the PH assumption for the multivariate Cox regression model (Table 1). Afterwards, we built a nomogram (Figure 1B) utilizing multivariate Cox regression results and plotted calibration curves (Figure 1C) to demonstrate the predictive value of the nomogram in prognosis. The findings indicated that the global test failed to meet the PH assumption, potentially undermining the statistical credibility and precision of the predictive model introduced by Zhang et al. (1) (Table 1).
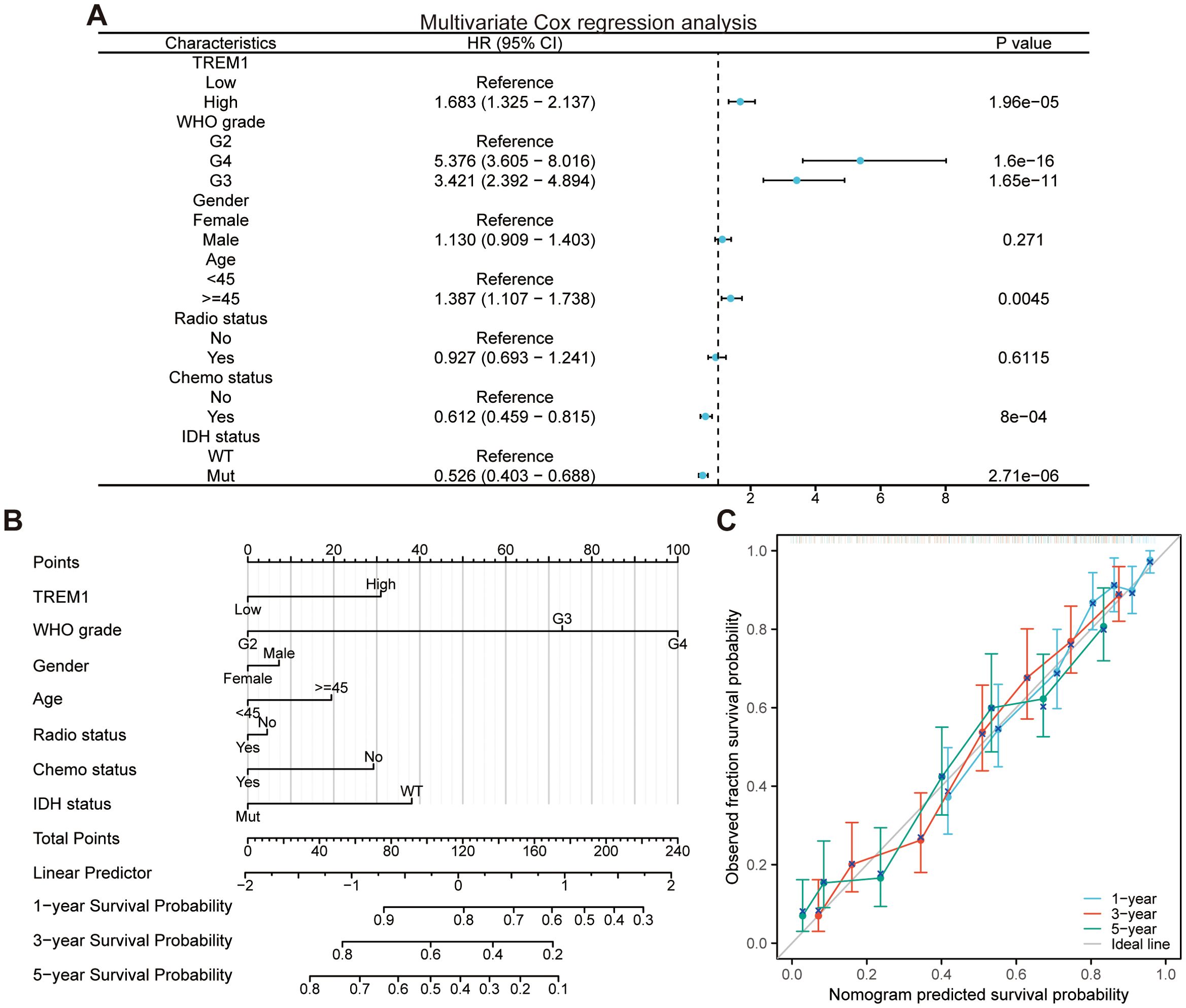
Figure 1. Development and evaluation of the nomogram. (A) Multivariate Cox regression analysis in the TCGA cohort. (B) Nomogram for predicting the survival probability of glioma patients. (C) Calibration curves for predicting the 1-year, 3-year, and 5-year survival probability of glioma patients.
As a predictive model based on statistical principles, the accuracy of nomograms largely depends on the richness and diversity of the training data. Nonetheless, the sample size incorporated in the development of the nomograms within this research is comparatively modest, thereby fundamentally limiting the predictive precision and the capacity for generalization of the models in question. Furthermore, they did not utilize an external validation dataset to evaluate the predictive performance of the nomogram model subsequent to its development, thereby failing to demonstrate the applicability of the model across different patient populations. To address these challenges, future studies should strive to collect more extensive and representative multicenter datasets for the development of nomogram models. Concurrently, after the construction of the model, a rigorous validation using independent external cohorts should be carried out to comprehensively assess the predictive performance of the model.
In conclusion, taking into account the proportionate hazards assumption and the possible ramifications of censoring events, we conclude that a reevaluation is necessary. Despite our concerted efforts to underscore the prerequisites for utilizing multivariate Cox regression model and developing nomogram, numerous publications continue to overlook the PH assumption in their investigations. This underscores the fact that the meticulous validation of models remains an overlooked yet indispensable component within the realm of scientific inquiry. Therefore, we strongly recommend that the scientific community adopts strict and standardized methods when constructing predictive models, and ensures compliance with the prerequisites for the appropriate use of these models.
Author contributions
JX: Writing – original draft, Writing – review & editing. ZL: Writing – original draft, Writing – review & editing. TW: Writing – original draft, Writing – review & editing. QY: Writing – review & editing. LC: Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Natural Science Foundation of Southwest Medical University, Grant (No. 2023QN008 and 2023QN103). This work was further supported by the National Natural Science Foundation project (No. 82372825).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Zhang L, Qu X, and Xu Y. Molecular and immunological features of trem1 and its emergence as a prognostic indicator in glioma. Front Immunol. (2024) 15:1324010. doi: 10.3389/fimmu.2024.1324010
2. Thomas LE, Turakhia MP, and Pencina MJ. Competing risks, treatment switching, and informative censoring. JAMA Cardiol. (2021) 6:871–3. doi: 10.1001/jamacardio.2021.1239
3. Lee KH, Rondeau V, and Haneuse S. Accelerated failure time models for semi-competing risks data in the presence of complex censoring. Biometrics. (2017) 73:1401–12. doi: 10.1111/biom.12696
4. Ning J, Qin J, and Shen Y. Score estimating equations from embedded likelihood functions under accelerated failure time model. J Am Stat Assoc. (2014) 109:1625–35. doi: 10.1080/01621459.2014.946034
5. Crowther MJ, Royston P, and Clements M. A flexible parametric accelerated failure time model and the extension to time-dependent acceleration factors. Biostatistics. (2023) 24:811–31. doi: 10.1093/biostatistics/kxac009
6. Stensrud MJ, Aalen JM, Aalen OO, and Valberg M. Limitations of hazard ratios in clinical trials. Eur Heart J. (2018) 40:1378–83. doi: 10.1093/eurheartj/ehy770
7. Bardo M, Huber C, Benda N, Brugger J, Fellinger T, Galaune V, et al. Methods for non-proportional hazards in clinical trials: A systematic review. Stat Methods Med Res. (2024) 33:1069–92. doi: 10.1177/09622802241242325
8. Stensrud MJ and Hernán MA. Why test for proportional hazards? Jama. (2020) 323:1401–2. doi: 10.1001/jama.2020.1267
9. Jiang N, Wu Y, and Li C. Limitations of using cox proportional hazards model in cardiovascular research. Cardiovasc Diabetol. (2024) 23:219. doi: 10.1186/s12933-024-02302-2
10. Xue X, Xie X, Gunter M, Rohan TE, Wassertheil-Smoller S, Ho GYF, et al. Testing the proportional hazards assumption in case-cohort analysis. BMC Med Res Method. (2013) 13:88. doi: 10.1186/1471-2288-13-88
11. Gregson J, Sharples L, Stone GW, Burman CF, Öhrn F, and Pocock S. Nonproportional hazards for time-to-event outcomes in clinical trials: jacc review topic of the week. J Am Coll Cardiol. (2019) 74:2102–12. doi: 10.1016/j.jacc.2019.08.1034
12. Xu L and Xu Y. Misuse of the cox proportional hazards model and alternative approaches in kidney outcome research. Kidney Int. (2024) 106:1186. doi: 10.1016/j.kint.2024.08.026
Keywords: proportional hazards (PH) assumption, glioma, Cox regression, nomogram, prediction
Citation: Xue J, Luo Z, Wang T, Yin Q and Chen L (2025) Commentary: Molecular and immunological features of TREM1 and its emergence as a prognostic indicator in glioma. Front. Immunol. 16:1577773. doi: 10.3389/fimmu.2025.1577773
Received: 16 February 2025; Accepted: 28 May 2025;
Published: 17 June 2025.
Edited by:
Dermot Kelleher, University of British Columbia, CanadaReviewed by:
Zhenyu Gong, Technical University of Munich, GermanyCopyright © 2025 Xue, Luo, Wang, Yin and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qijia Yin, cWlqaWF5aW4wODEwQDE2My5jb20=; Ligang Chen, Y2hlbmdsaWdhbmcuY29vbEAxNjMuY29t
†These authors have contributed equally to this work and share first authorship
 Jihao Xue
Jihao Xue Zhilin Luo2†
Zhilin Luo2† Ligang Chen
Ligang Chen