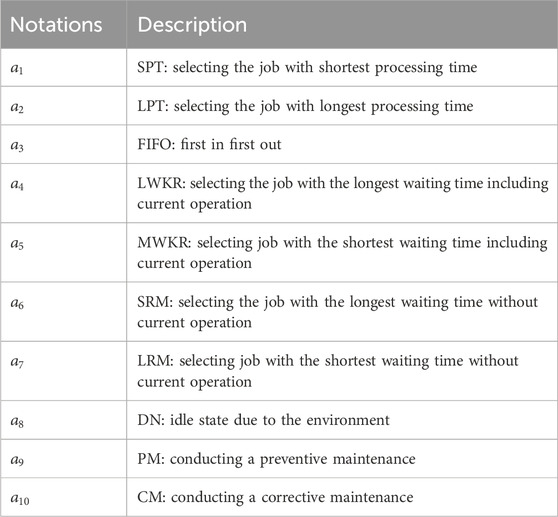
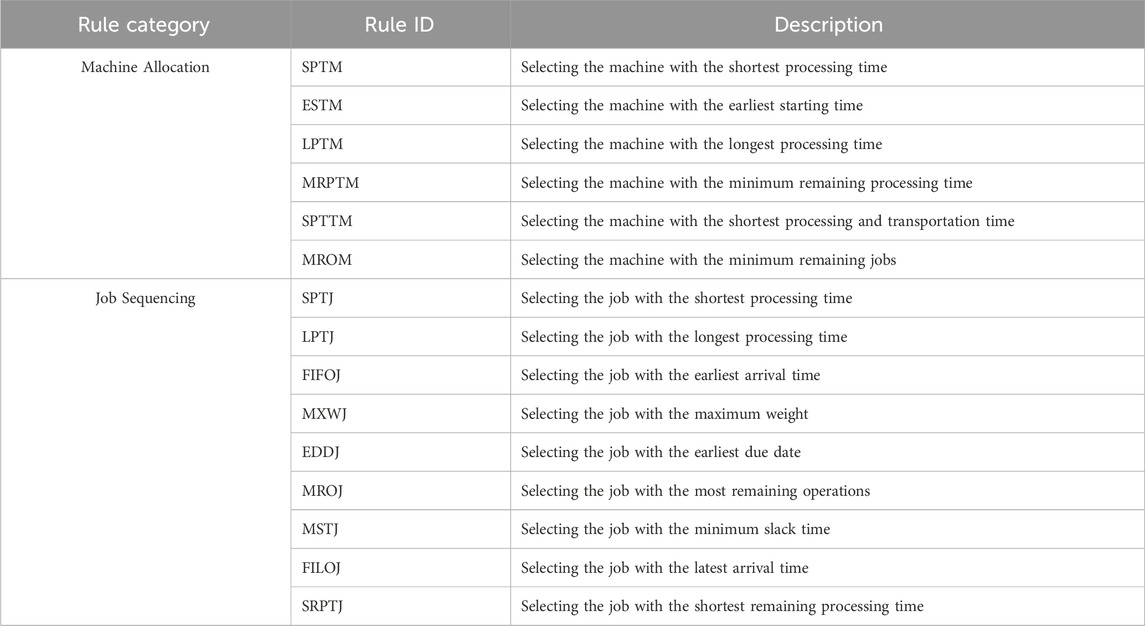
- 1College of Information Science and Engineering, Henan University of Technology, Zhengzhou, China
- 2School of Artificial Intelligence and Big Data, Henan University of Technology, Zhengzhou, China
- 3Research Institute for Science & Technology, Tokyo University of Science, Tokyo, Japan
- 4Faculty of Science & Techology, Tokyo University of Science, Tokyo, Japan
This paper presents a systematic and comprehensive review of multi-agent reinforcement learning (MARL) methodologies and their applications in addressing the flexible shop scheduling problem (FSSP), a fundamental yet challenging optimization paradigm in contemporary manufacturing systems. While conventional optimization approaches exhibit limitations in handling the inherent multi-resource constraints, dynamics and stochastic characteristics of real-world FSSP scenarios, MARL has emerged as a promising alternative framework, particularly due to its capability to effectively manage complex, decentralized decision-making processes in dynamic environments. Through a rigorous analytical framework, this study synthesizes and evaluates the current state-of-the-art MARL implementations in FSSP contexts, encompassing critical aspects such as problem formulation paradigms, agent architectural designs, learning algorithm frameworks, and inter-agent coordination mechanisms. We conduct an in-depth examination of the fundamental challenges inherent in MARL applications to FSSP, including the optimization of state-action space representations, the design of effective reward mechanisms, and the resolution of scalability constraints. Furthermore, this review provides a comparative analysis of diverse MARL paradigms, including centralized training with decentralized execution, fully decentralized approaches, and hierarchical methodologies, critically evaluating their respective advantages and limitations within the FSSP domain. The study culminates in the identification of significant research gaps and promising future research directions, with particular emphasis on theoretical foundations and practical implementations. This comprehensive review serves as an authoritative reference for researchers and practitioners in the field, providing a robust theoretical foundation and practical insights for advancing the application of MARL in flexible shop scheduling and related manufacturing optimization domains. The findings presented herein contribute to the broader understanding of intelligent manufacturing systems and computational optimization in Industry 4.0 contexts.
1 Introduction
With the development of intelligent and digital technologies, the production technology and capabilities of the manufacturing industry have seen rapid improvements. However, manufacturing enterprises face significant competitive pressures in the market. When production capabilities and scales are comparable, formulating scientific and rational production plans and resource scheduling schemes has become a critical approach and key technology for enterprises to gain a competitive advantage. Shop scheduling involves not only the upper level production planning, but also the operation management within the shop floor. How to reasonably allocate and efficiently coordinate production equipment and resources, while integrating various production objectives and fully considering various production resource constraints and processing technology constraints, has become a major challenge in enhancing the efficiency of manufacturing.
The flexible shop scheduling problem (FSSP) is a combination of several classic shop scheduling problems, such as flow-shop scheduling problem (FSP) and job-shop scheduling problem (JSP). Hence, FSSP can be divided into two major types: flexible job-shop scheduling problem (FJSP) and flexible flow shop scheduling problem, which is commonly known as hybrid flow-shop scheduling problem (HFSP) (Fan K. et al., 2018). FSSP is a class of combinatorial optimization problems with NP-hard characteristics, which has a wide range of applications in the fields of chemical engineering, machinery, textile, metallurgy, pharmaceuticals, logistics, etc., (Ruiz and Vázquez-Rodríguez, 2010). Therefore, the study of FSSP has important theoretical significance and practical application value, especially in the context of intelligent manufacturing, solving FSSP problems can help enterprises achieve more efficient production management and resource allocation.
With the continuous deepening of research, the simple FSSP can no longer meet the requirements of modern production. FSSP is an extremely complex problem in the manufacturing industry, involving the arrangement of operations in multiple stages, and each stage may include parallel machines. With the development of Industry 4.0 and intelligent manufacturing, the traditional FSSP model is no longer sufficient to cope with the increasing production demands and technological progress. The complexity of actual production processes and processing environments requires scheduling algorithms to not only handle static, idealized scenarios but also adapt to dynamically changing, uncertain environments. Therefore, researchers have begun to focus on extended FSSP problems, such as batch FSSP considering job constraints, distributed FSSP considering factory constraints, and dynamic FSSP considering production environment constraints. With the increasing complexity of production processes and processing environments, FSSP has expanded from simple models to more complex forms to meet the needs of actual production. The specific extended problems of FSSP will be introduced in the second section of this paper. These extended forms not only increase the complexity of the problem but also increase the requirements for scheduling algorithms.
In recent years, reinforcement learning (RL) has made remarkable progress in solving various sequential decision-making problems in machine learning due to its strong adaptability, flexibility, and generalization ability, and has become the main research method in the field of multi-agent systems (MAS). RL is widely used in fields such as robot control (Schwab et al., 2018), autonomous driving (Natan and Miura, 2022), and traffic signal control (Kodama et al., 2022). The combination of RL and evolutionary algorithms applied to FSSP has been studied in detail (Drugan, 2019). Cao et al. (2024) conducted various numerical experiments. Compared with several classical heuristics, the results show that the proposed method is superior to other similar methods in finding high-quality solutions in a reasonable time. With the advancement of deep learning technology and computing power, multi-agent reinforcement learning (MARL) has emerged. MARL has better performance in dealing with high-dimensional state-action spaces and nonlinear decision-making problems in complex environments than traditional RL, overcoming some inherent drawbacks of traditional RL algorithms, and endowing MAS with stronger collaboration and adaptability, providing a powerful tool and method for solving complex decision-making problems in practical applications.
Although MARL has made significant progress in theory, framework, and application, there is still a certain distance from the large-scale application of higher intelligence in life and production. At present, the field is still in the early stage of research and still faces a series of challenges such as scalability (Kim and Sung, 2023; Yang et al., 2022), sparse rewards (Fu et al., 2022), partial observability (Xu et al., 2020; Ortiz et al., 2020), and credit allocation (Seo et al., 2019).
In this survey, a comprehensive review and analysis was conducted on the relevant papers that applied MARL to FSSP. Primarily, Scopus and Web of Science (WOS) databases were searched using the following keywords in the whole articles:
(“multi-agent reinforcement learning” OR “multi agent” OR “distributed reinforcement learning” OR “multiagent reinforcement learning” OR “cooperative reinforcement learning”)
AND
(“hybrid flow shop” OR “flexible job shop” OR “flexible flow shop” OR “flexible scheduling” OR “flexible process” OR “manufacturing scheduling” OR “production scheduling” OR “scheduling”)
The initial research involved a comprehensive literature search to ensure that no papers in this field were overlooked. By scanning all the search results by reading the abstracts of the papers, this was achieved as the result of the comprehensive search. Firstly, these papers were examined from the perspective of problem types, and those involving network scheduling, routing scheduling, computing resource scheduling, etc. were eliminated. Then, the solution methods in the remaining papers were analyzed, and those papers that only involved multi-agent systems but did not include reinforcement learning methods were eliminated. After these exclusions, 41 papers were found within the scope of this study.
Currently, experts and scholars have published review papers in the field of MARL, but their perspectives differ from that of this paper. For instance, Bahrpeyma and Reichelt (2022) have reviewed the application of MARL in smart factories, providing a comprehensive overview and future research directions for five smart factory issues. Oroojlooy and Hajinezhad (2023) reviewed cooperative MARL problems, introducing five common cooperative reinforcement learning methods, discussing in detail their principles, challenges, and countermeasures, and looking forward to emerging research areas and potential future research directions. However, no scholars have directly reviewed the application of MARL in FSSP. From the above discussion, it is evident that as research deepens, the complexity of HFSP continues to increase, and MARL, with its unique advantages, has become an effective tool for handling such complex scheduling problems. Therefore, the motivation for this paper stems from the need to summarize and analyze existing research. Future research should further explore how to better utilize MARL to solve extended problems in HFSP and successfully apply it to actual production environments. This paper provides a comprehensive and up-to-date review of MARL for FSSP. In terms of methodology, we have conducted a more thorough study from the perspectives of multi-agent training paradigms and multi-agent collaboration methods. From the perspective of problem research, we analyze the scalability issues of FSSP and future research trends, and propose research recommendations. Thus, this paper can assist managers and practitioners in making practical and targeted decisions. Compared to previous work, we have made the following contributions:
(1) This paper analyzes recently published literature on MARL for shop scheduling problems; We have conducted a dedicated analysis of MARL for solving FSSP and summarized the key challenges of existing FSSP solution methods;
(2) This paper has reviewed the current state of MARL methods in handling FSSP from aspects such as multi-agent training paradigms, multi-agent collaboration methods, problem complexity, and optimization objectives;
(3) This paper has discussed the key challenges of MARL in terms of dimensional issues in large-scale scenarios and Scenario scalability;
(4) By analyzing the limitations and challenges of MARL, we propose future research directions.
The organization of this paper is as follows: Section 1 introduces the method of this study. Section 2 introduces the flexible shop scheduling, including its classification, extended types, and optimization objectives, and also introduces the reinforcement learning method, as well as the MARL method. Section 3 introduces the application of MARL in the shop scheduling field, especially focusing on FSSP. Section 4 elaborates on a specific application case of MARL in the FSSP. The two cases help to gain a deeper understanding of the core roles and advantages of MARL in solving the FSSP. Section 5 identifies the key challenges of MARL in the application of FSSP and analyzes the number of publications from multiple perspectives to derive future research directions. Section 6 summarizes this paper.
2 Fundamentals and concepts
2.1 Flexible shop scheduling problem
According to the constraints of the scheduling problem, FSSP can be divided into HFSP, FJSP and flexible open-shop scheduling problem (FOSP) (Fan K. et al., 2018). Both HFSP and FJSP are complex production scheduling problems, but they have significant differences in machine configuration, process paths, and scheduling complexity. HFSP focuses more on assigning operations to multiple parallel machines within each stage, while FJSP needs to determine the specific machine selection for each process, and the path is more flexible. Nevertheless, both have a lot in common in terms of optimization objectives, dynamics, and uncertainty, all aiming to improve production efficiency and resource utilization. FOSP is also theoretically a subset of FSSP. However, due to its inherent openness and complexity, characterized by unstructured job processing routes and minimal constraints, FOSP has received significantly less attention in existing research (Fan K. et al., 2018). Notably, FJSP and HFSP are currently the most studied and representative branches of FSSP within the MARL domain. In contrast, FOSP and other shop types entail greater complexity, including unstructured routing and expanded state-action spaces. This introduces distinct challenges, leaving their exploration within MARL research in a relatively nascent stage. Therefore, this paper mainly focuses on the related content of HFSP and FJSP.
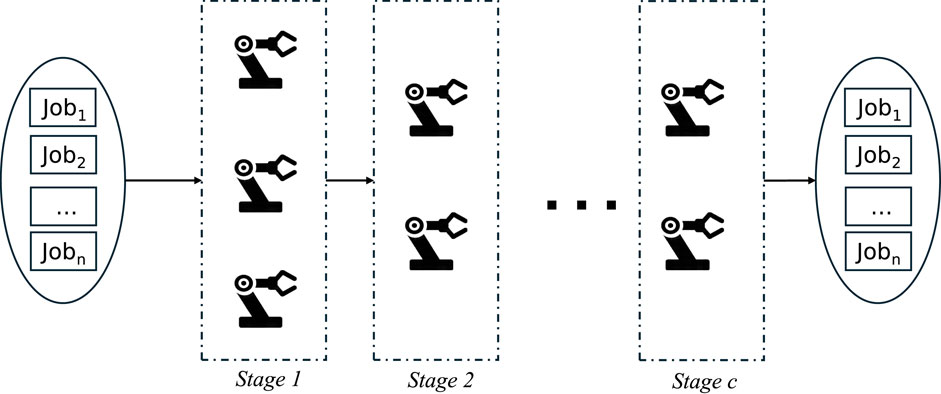
2.1.1 Hybrid flow-shop scheduling problem
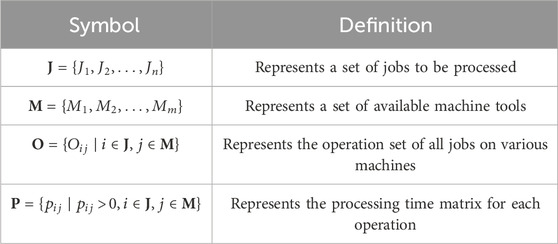
The hybrid flow-shop scheduling problem is a complex production scheduling problem that involves multiple stages of processing. Each job must go through a series of processing steps in a specific order. The basic components of HFSP include jobs, machines, stages, and operations. Formally, HFSP can be defined as a quadruple
As shown in Figure 1, the HFSP problem includes a set of
The main objective of this problem, based on the processing times of all jobs provided, is to determine the sequence of
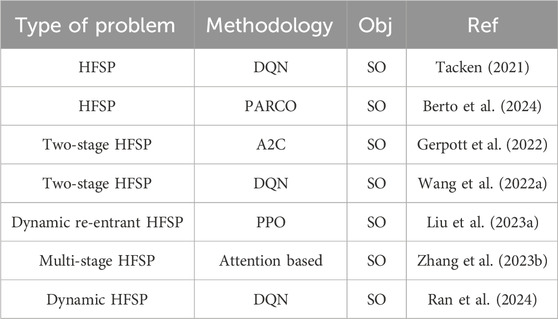
With the increasing complexity of the production environment and demands, HFSP has also expanded into more problems to adapt to different actual situations, and the summarized results are shown in Table 2.
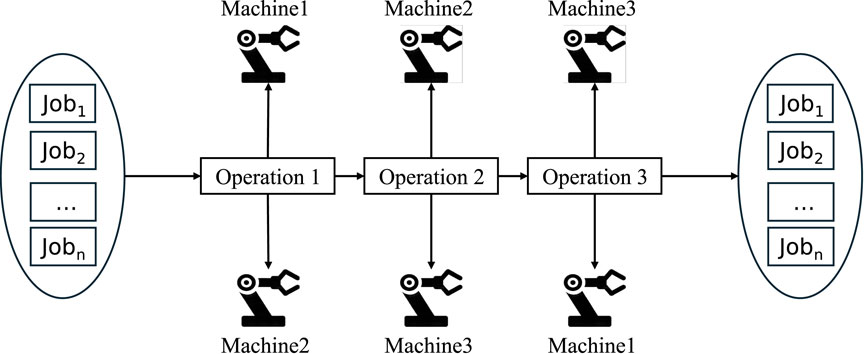
2.1.2 Flexible job-shop scheduling problem
The flexible job-shop scheduling problem is an important and complex problem in the field of shop scheduling. Different from HFSP, each job in FJSP can have multiple process paths, and each path corresponds to a different sequence of machines, which provides greater flexibility for scheduling. The goal of FJSP is to find the best job scheduling plan under a series of constraints to optimize production efficiency and resource utilization. The basic components of FJSP include: jobs, machines, operations, and process routes. Formally, FJSP can be defined as a quintuple
The FJSP problem can be stated as follows: In a job shop,
These operations follow specific sequence constraints, i.e., the second operation cannot start until the first operation is completed. At the same time, each operation corresponds to a set of machines with processing capabilities. These machines have the characteristics of non-preemptive and non-interruptive, i.e., once a machine starts processing a job, it cannot be preempted by other jobs, and the processing cannot be interrupted until the current job is processed. The basic assumptions of FJSP usually include:
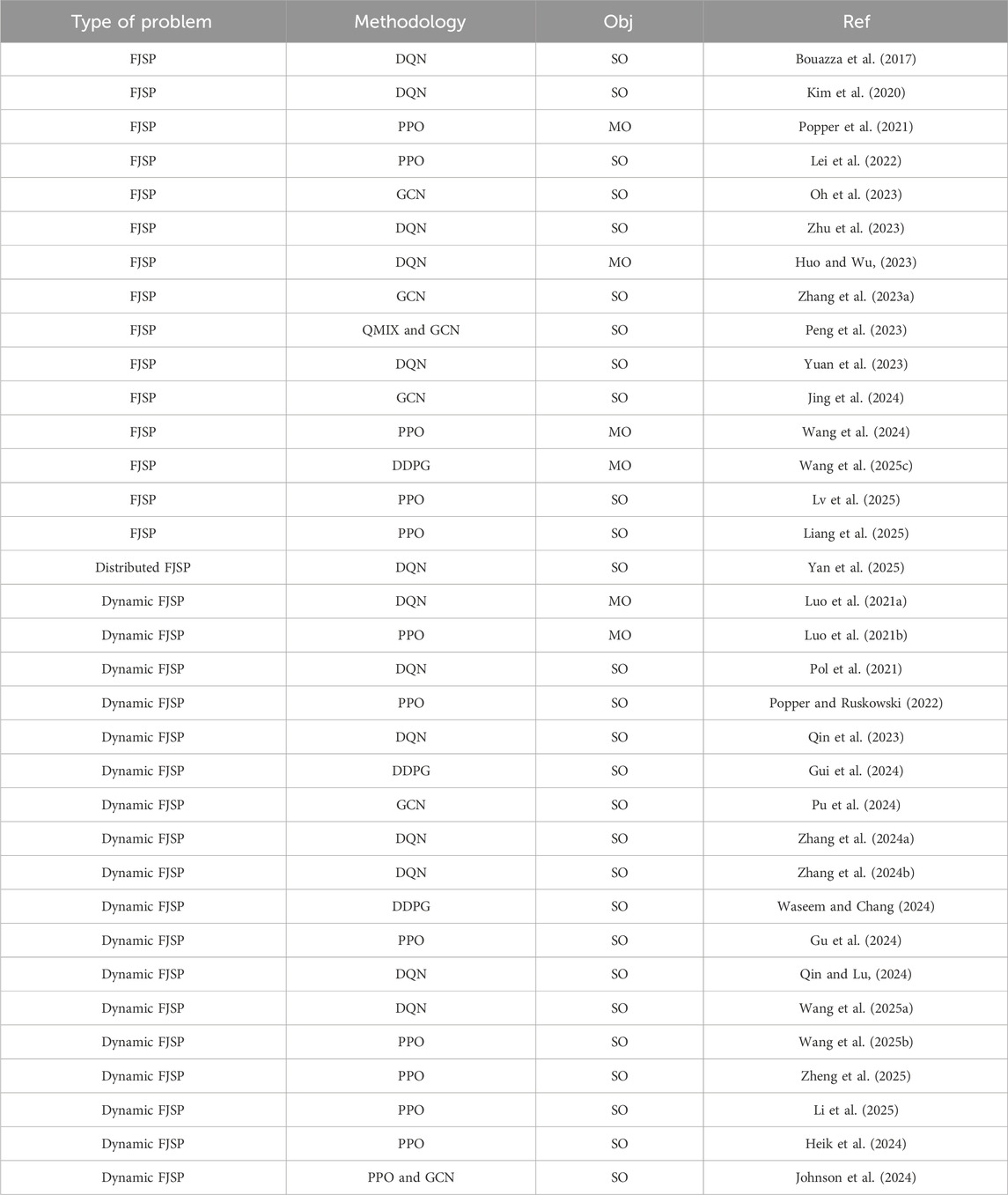
With the increasing complexity of the production environment and demands, FJSP has also expanded into more variants to adapt to different actual situations. The following are some common extended problems of FJSP as shown in Table 4.
2.2 Single-agent RL
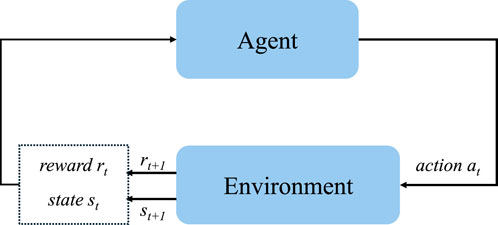
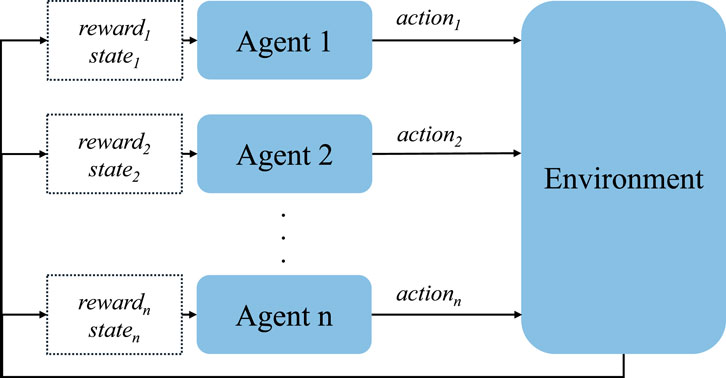
RL is a subfield of machine learning (ML). The main purpose of reinforcement learning is to maximize the rewards obtained by an agent in actions about environmental states. Unlike other machine learning algorithms, it does not directly tell the agent which action to choose, but allows the agent to learn which action has the greatest reward through trial and error (Liu and Wang, 2009). In the standard RL model, an agent is a decision-making unit that observes the environment and takes actions. Each action will produce a result, and according to the state of the environment, this result can be a reward or a punishment. The rewards or punishments obtained from the environment are used to evaluate the behavior. The agent decides which actions it will take, considering which action will produce the greatest reward. The result of taking actions is evaluated by a reward function about the current state and the current action. The algorithm retains the value of actions and the current state of the environment at each decision step and uses this information to evaluate the next time step (Kaelbling et al., 1996). The framework of reinforcement learning is shown in Figure 3.
At each decision step
2.2.1 Markov decision process
RL mainly solves a Markov decision process (MDP) consisting of a quintuple
In an environment where the agent has full observability of the state and the environment is stationary, meaning that the transition probability function and rewards remain constant over time, this setting is referred to as a MDP with fully observable states. The case where the agent does not have a fully observable state is called partially observable Markov decision process (POMDP). A policy
The discount factor
When dealing with MDP, reinforcement learning methods can be divided into two major categories based on whether the interactive environment is known: model based and model free. Model based methods are mainly dynamic programming (DP), while model free methods are mainly represented by monte carlo (MC), temporal difference (TD) and policy gradient (PG) methods. These four categories form the core of reinforcement learning and are the foundation for the subsequent development of deep reinforcement learning (DRL) and MARL algorithms. Mainstream reinforcement learning algorithms include Q-learning (QL) algorithm, state-action-reward-state-action (SARSA) algorithm, actor–critic (A2C) algorithm, and proximal policy optimization (PPO) algorithm.
Most MDP solving methods can be divided into three categories: value function based, policy based and model based methods. Two model free methods are introduced in the following section.
2.2.2 Value function based methods
Value function based methods learn the value function and derive the optimal policy from the optimal value function. There are two kinds of value functions, the state-value function and the action-value function. With the optimal state-value function and the optimal action-value function, we can obtain the optimal policy
The state-value function and the action-value function are given in Equations 2, 3.
The QL algorithm maps from states to the probabilities of each possible action in the Q-table, aiming to maximize future rewards. It is worth noting that it does not require prior knowledge of the environment’s dynamics. QL is a non-policy learning algorithm that allows learning from experience, even if the current policy is suboptimal (Mnih et al., 2015). Its goal is to iteratively improve the Q-values that change over time through experience and learning from the consequences of different actions in different states. This process helps the agent learn a strategy that maximizes the cumulative reward over time.
In QL, the Q-function yields the discounted cumulative reward with the discount factor
The optimal action-value is obtained according to the action-value function as shown in Equation 5.
The Q-value is updated each time an action is taken. Equation 6 proposed by Tacken (2021) essentially updates the Q-value of the current state-action pair based on immediate rewards and estimated future cumulative rewards.
Other reinforcement learning algorithms can refer to the literature review by Kayhan and Yildiz (2023), and due to limited space, they will not be detailed here.
The emergence of deep neural networks (DNN) has greatly expanded the application range of RL. Compared with traditional table based RL methods, DNN can handle more complex tasks because they can generalize past experiences rather than just relying on stored values. This generalization ability allows DNN to handle problems with such large state spaces that they cannot be represented in tabular form. In RL, DNN can store and approximate value functions that predict the expected rewards for taking specific actions in given states. This approach is particularly suitable for “unseen” situations, i.e., new states that have not been encountered during training. Deep Q-network (DQN) is a typical example that uses DNN to approximate the Q-function, enabling effective decision-making in complex tasks.
2.2.3 Policy based methods
Policy based methods in RL directly search for the optimal policy by optimizing the parameters of a policy function that outputs the probability distribution over actions. The optimal policy is typically obtained through gradient ascent on the expected return with respect to the policy parameters. Specifically, the policy network’s weights are iteratively updated to favor state-action pairs that yield higher rewards.
The update rule for the policy parameters is shown in Equation 7.
Policy based methods are particularly effective in continuous and stochastic environments where they can learn specific probabilities for each action and appropriate levels of exploration. However, these methods often suffer from low sample efficiency because new gradient estimates are independent of past estimates, leading to high variance in the gradient estimates due to sparse rewards and limited state-action space exploration.
In summary, policy based methods directly optimize the policy parameters to maximize the expected return, making them suitable for complex environments but challenging in terms of sample efficiency and variance control.
2.3 Multi-agent RL
2.3.1 Multi-agent RL problem representation
MARL is a technology where multiple agents interact and learn optimal strategies in a shared environment. In MARL, the actions of each agent not only affect themselves but also indirectly affect the states and rewards of other agents, leading to the non-stationarity of the environment. Non-stationarity means that the environment is dynamically changing for each agent because the actions of other agents change the state of the environment, making previous experiences and strategies invalid. Interactions between agents can be cooperative, competitive, or mixed. The framework of reinforcement learning is shown in Figure 4.
In the context of MAS, particularly in centralized training and decentralized execution (CTDE), decentralized partially observable Markov decision process (Dec-POMDP) offer a robust modeling framework (Zhang et al., 2021). Widely employed in MARL, Dec-POMDPs are formally defined by the tuple
At each time step, each agent
where
Dec-POMDP provide a formal framework for modeling MAS characterized by limited and local observations. In such settings, agents must operate independently based on their partial information while coordinating their actions to achieve a shared goal and maximize collective rewards. This framework is particularly valuable in applications requiring high levels of cooperation and coordination among multiple autonomous entities, such as robotics, network management, and resource allocation. By addressing the challenges posed by partial observability and decentralized decision-making, Dec-POMDP offer effective solutions for complex multi-agent environments, ensuring that agents can efficiently achieve their objectives despite the inherent limitations of their observations and the need for decentralized operation.
Thus, Dec-POMDPs not only facilitate the design of sophisticated MAS but also enhance our ability to manage and optimize these systems in real-world applications where centralized control is impractical or impossible.
2.3.2 Multi-agent RL methods
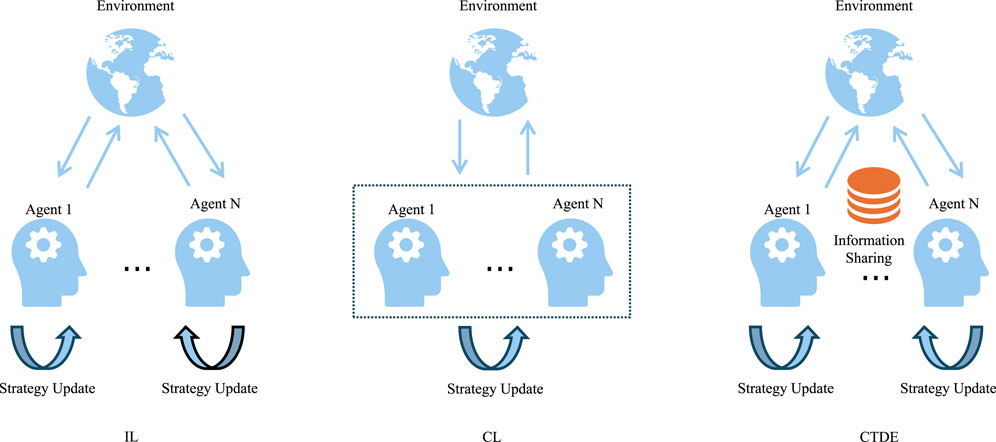
There are three main learning paradigms in MARL shown in Figure 5:
Independent learning (IL) paradigm, where each agent independently optimizes its behavior strategy, treating other agents as part of the environment. Independent learning allows agents to learn without collaboration or information sharing, suitable for discrete state-action spaces and small-scale multi-agent tasks, with good scalability. However, due to the independence of each agent, this approach is prone to environmental non-stationarity issues, such as independent Q-learning (IQL).
Centralized learning (CL) paradigm involves centralizing the decision-making process of all agents into a single learning algorithm. In this mode, a central controller or algorithm has access to information from all agents, including the state, actions, and rewards of each agent, as well as the global state of the entire environment. Centralized learning is particularly suitable for tasks that require precise coordination and cooperation, but due to the exponential growth of the state space with the increase in the number of agents, this method may encounter dimensional disaster, making it difficult for the algorithm to converge to the optimal strategy, and poor scalability (Nowé et al., 2012).
CTDE combines the advantages of independent learning and centralized learning. During the training phase, all agents share information and guide the learning process of the agents through centralized training to maximize global performance; during the execution phase, agents make decisions independently based on their own perceptions and historical experiences. This approach overcomes the convergence and cooperation issues of centralized learning while retaining the flexibility and efficiency of distributed decision-making, making it an important direction for MARL research and practice in recent years.
According to the different ways of handling value functions, the CTDE paradigm can be divided into two major categories: value function decomposition methods and centralized value function methods. The former decomposes the global value function into local value functions for each agent, meaning that each agent only needs to focus on its own local value function without needing to know all the information about other agents, thereby simplifying the learning process. This approach not only alleviates the environmental non-stationarity issues faced by independent learning algorithms but also solves the contribution allocation problem in the CTDE paradigm.
Value decomposition network (VDN) (Sunehag et al., 2017) is a cooperative multi-agent learning method based on team rewards, which decomposes the global value to each agent and calculates the contribution of each agent to the team’s total reward through gradient backpropagation. VDN well solves the credit allocation problem, but due to its linear decomposition characteristics, the scope of application is limited. Similar to this, QMIX algorithm (Chen, 2021) combines the local value functions of each agent in a nonlinear manner through a mixing network and maintains the monotonicity constraint between the global value function and the local value functions, enhancing the algorithm’s approximation ability for different decomposition tasks. However, the “monotonicity” constraint still limits the decomposition form and performs poorly in handling non-monotonic tasks.
QTRAN algorithm overcomes the monotonicity constraints of QMIX and VDN, allowing more flexible value function decomposition, making it suitable for a wider range of cooperative multi-agent tasks, especially those involving non-monotonicity complex tasks (Son et al., 2019). However, the QTRAN algorithm has high computational complexity and is often accompanied by large computational overhead and slow convergence speed. WQMIX algorithm points out the shortcomings in the design of QMIX, introduces a weighted mixing network, allowing the algorithm to dynamically adjust the weights of local value functions according to different states, enhancing the adaptability to complex tasks (Rashid et al., 2020). However, the design of WQMIX is relatively complex, and additional hyperparameters need to be adjusted during the training process, increasing the difficulty of model optimization.
To solve the limitations of QMIX in handling non-monotonic tasks, QPLEX algorithm (Wang et al., 2020) designed a dual-track adversarial structure value function decomposition method, making the algorithm more effective in dealing with non-monotonic tasks. Qatten algorithm (Yang et al., 2020) used a multi-head attention mechanism to approximate and decompose the joint Q-function, providing a solid theoretical basis for value decomposition methods through detailed theoretical derivation.
MARL algorithms based on value function decomposition have the advantages of independent learning, distributed computing, and local information. Due to the characteristics of value function decomposition and locality, these algorithms are more scalable and manageable when dealing with complex multi-agent environments, but there are still limitations when dealing with distributed control problems in continuous action spaces.
In contrast, centralized value function methods use global information to train the value network and guide each agent’s policy network to learn independently through the value network. Most of these methods use the actor-critic architecture, separating policy learning and value learning, thus showing obvious advantages in flexibility and stability.
3 MARL for FSSP
This section provides a review of common scheduling problems according to the types of MARL methods, the complexity of research issues, and the number of optimization objectives, with a particular focus on FSSP.
Before surveying the applications of MARL in FSSP, it is essential to revisit the fundamental backgrounds of single-agent and MAS (Busoniu et al., 2008). In the context of single-agent RL, the environment is modeled as a MDP. Within this framework, the agent’s objective is to select a sequence of actions that maximizes cumulative rewards over time. To achieve this goal, the single-agent must learn a value function that guides its decision-making process toward optimal outcomes.
The environment becomes more complex in MAS, where multiple agents share the same environment and their behaviors influence each other. Each agent has its own set of states, actions, and potentially its own value function. Multi-agent tasks can be categorized based on the nature of interactions between agents into fully cooperative, fully competitive, or mixed-type tasks. Furthermore, static tasks versus dynamic tasks pose different requirements for defining MAS. In static tasks, agents’ strategies can converge to a fixed point, whereas in dynamic environments, agents must continuously adapt to changes in other agents’ behaviors.
MARL aims to address the complexities introduced by MAS, enabling agents to discover solutions dynamically rather than relying on pre-programmed behaviors (Baer et al., 2019). MARL algorithms typically focus on two key objectives: ensuring stability during the learning process and adapting to changes in other agents’ behaviors. MARL offers a novel and effective approach to solving FSSP by leveraging the collaborative characteristics among agents, overcoming challenges posed by high complexity and dynamic changes that traditional methods struggle with.
As research deepens and technology advances, MARL is expected to play an increasingly important role in future intelligent manufacturing systems. Through systematic analysis of relevant literature, we have found that MARL has significant advantages in solving FSSP, especially in dealing with dynamic and uncertain environments. Existing studies have shown that MARL can find better scheduling solutions through the collaboration of multiple agents and has demonstrated good performance in a variety of application scenarios. However, there are also some challenges, such as high training complexity and coordination difficulties. In addition, the literature has proposed various improvement methods, such as VDN, QMIX, IQL, and CTDE, which play an important role in enhancing the performance and scalability of MARL algorithms.
3.1 MARL for HFSP
MARL has shown significant potential in addressing scheduling issues in HFSP. Gerpott et al. (2022) proposed a distributed advantage A2C method for production scheduling in a two-stage HFSP manufacturing system, aiming to minimize total tardiness and maximum completion time. This work uses identical scheduling agents that explore different parts of the problem space and share their gradients with the critic. The study utilizes a global parameter shared by several agents exploring the environment simultaneously. As a synchronous and deterministic method, A2C waits for each agent to complete the corresponding part of the experiment before executing a global update by taking the average of all gradients received from the participants. A coordinator manages the collection of local gradients and passes them to the global network.
Zhang N. et al. (2023) proposed a counterfactual attention-based multi-agent reinforcement learning (CAMARL) framework to address the joint condition-based maintenance and production scheduling problems in multi-stage hybrid flow-shops. The study models production scheduling and equipment maintenance as interacting activities and establishes a model through a Dec-POMDP considering the machine wear process. The framework consists of three main modules: an attention mechanism module, an action abstraction representation module, and a coordination control unit, aiming to reduce the dimensionality of the state space, handle high-dimensional action spaces, and accelerate the search for optimal production strategies. To validate the effectiveness of the proposed CAMARL method in a two-level HFSP with five independent machines, numerical experiments were conducted. By comparing with seven benchmark methods under different production scenarios, the effectiveness of the CAMARL method was demonstrated. This study not only promotes the application of MARL in complex manufacturing systems theoretically but also shows its effectiveness and superiority under various manufacturing environment conditions experimentally. In Section 4.1, a detailed introduction to this case is provided.
Berto et al. (2024) proposed a new method called parallel auto regressive combinatorial optimization (PARCO), which addresses multi-agent combinatorial optimization problems such as path planning and scheduling through parallel autoregressive decoding. The core of PARCO lies in its innovative model architecture, which includes multiple pointer mechanisms and priority based conflict handling schemes, as well as communication layers specifically designed to facilitate effective collaboration between agents. These designs enable PARCO to construct solutions among different agents simultaneously and efficiently, significantly improving the construction efficiency and quality of solutions. Through extensive experiments on representative multi-agent combinatorial problems in routing and scheduling domains, PARCO demonstrated its competitive performance in solution quality and computational efficiency compared to classic heuristic methods and neural baseline methods. Especially in the flexible flow-shop problem, PARCO not only improved solution quality but also significantly accelerated decoding speed and reduced the number of required decoding steps. In addition, PARCO showed good generalization ability when dealing with unseen scales and numbers of agents, indicating its potential and flexibility in practical applications.
Tacken (2021) discussed a MARL method for solving HFSP in hospitals. The core of the study is to construct an MARL framework, and the case study demonstrates the effectiveness of the framework in solving general HFSP problems. The framework not only achieves solutions comparable to benchmark solutions but also can generate reasonable solutions in real-time for new, unseen problem instances during training. This feature is very promising when quick scheduling solutions for new scenarios are needed. The thesis first reviews hospital scheduling problems and the application of reinforcement learning methods in solving scheduling problems. The authors point out that there is a lack of literature on applying MARL to HFSP, especially in the context of hospital scheduling. Wang M. et al. (2022) proposed an independent double deep Q-network multi-agent reinforcement learning method (MA-IDDQN) for solving online two-stage hybrid flow-shop scheduling problems, especially in batch machine environments. This problem is complex and challenging because it needs to consider job arriving over time. The researchers transformed the online scheduling problem into a cooperative MDP and constructed the model by defining the state space, action space, and reward function for different agents. They designed two agents, which are trained through double DQN to handle batch formation tasks and scheduling tasks, and achieved multi-agent cooperation through inter-agent behavioral analysis mechanisms. In addition, they designed an
Liu et al. (2023a) proposed a novel solution for the dynamic re-entrant hybrid flow-shop scheduling problem (DRHFSP) by integrating DRL and MAS. This study takes into account two key factors: worker fatigue and skill levels. By constructing a self-organizing MAS and developing two DRL models, the study effectively addresses the sub-decision problems of job sequence, machine selection, and worker assignment. In particular, their proposed reward shaping techniques and attention-based network models not only improve decision-making efficiency but also demonstrate excellent performance in dynamic environments. Ran et al. (2024) presented a dynamic hybrid flow shop scheduling strategy for multi-agent manufacturing systems, integrating DRL and federated transfer learning to address privacy concerns and enhance scheduling efficiency in Industry 4.0 discrete manufacturing. The study formulated the problem as a MDP, modeling each machine as an independent agent that interacts with the environment to maximize long-term rewards. The state space included static features and dynamic features, while the action space comprised job processing requests and method selections. The reward function combined job timeliness, processing efficiency, and machine utilization. A federated knowledge transfer module was introduced to adaptively aggregate model parameters, enabling knowledge sharing among agents while preserving data privacy. Experimental validation using classic MK benchmark examples showed that the proposed strategy outperformed GA, hybrid intelligent algorithms HIA, and single-agent DRL, with up to 8.3% lower objective values and 21% reduced computation time in complex scenarios. The approach demonstrated enhanced adaptability to dynamic job arrivals and equipment changes, highlighting its potential for real-world multi-agent manufacturing systems.
A summary of the application of MARL in HFSP is provided in Table 5.
3.2 MARL for FJSP
In recent years, MARL technology has been widely applied to solve FJSP. DQN, a value iteration based reinforcement learning method, guides action decisions by learning the value of state-action pairs and is used to optimize task scheduling strategies in FJSP. Bouazza et al. (2017) proposed a distributed QL method for production scheduling, treating products as intelligent agents, aiming to emphasize the significant contribution of considering adjustment time in decision-making to overall performance. Intelligent product agents can decompose decision-making into the selection of machine selection rules and scheduling rules. However, although agents have individual impacts on the environment, this work does not show the common impact of the decisions made by the agents on the environment and each other. Kim et al. (2020) proposed a multi-Agent DQN based method that can learn from dynamic environments and make better decisions in job assignment and task prioritization for mass customization. Different manufacturing component-based DQN agents evaluate job priorities and negotiate scheduling while continuously learning to improve their decision-making performance. Huo and Wu (2023) proposed a solution for the multi-objective FJSP based on MARL algorithm. The researchers transformed the objective of shortening the maximum completion time and reducing machine load into a problem that can be solved through reinforcement learning. By establishing state, action, and reward functions and introducing QL, the researchers proposed a MARL optimization algorithm. The algorithm was applied to the Brandimarte benchmark example for simulation verification, and compared with other intelligent algorithms, the algorithm showed faster convergence speed and higher utilization rate of processing machines. Using this algorithm in the MK01 example, the minimum maximum completion time was 40, validating the feasibility, accuracy, and efficiency of the proposed intelligent optimization algorithm. Zhu et al. (2023) conceptualized a multi-task multi-agent reinforcement learning framework designed for real-time scheduling in a dual-resource flexible job shop environment, enhancing decision-making processes in complex manufacturing systems. The framework utilizes a mixture-of-experts model with double DQN for process planning, job sequencing, and machine selection, demonstrating effective scheduling solutions under various constraints. Yuan et al. (2023) proposed a multi-agent double DQN framework for the FJSP, transforming it into a multi-stage sequence decision problem via an event-driven workshop environment model based on state machine and event stream mechanisms. The model decouples the workshop environment from the decision analysis model, using job and machine agents to make decisions based on global and local state features, with Boltzmann exploitation to maximize cumulative rewards and avoid local optima. Numerical experiments show that multi-agent double DQN outperforms traditional methods like genetic algorithms in large-scale instances, achieving better makespan results and real-time scheduling capabilities, with an average performance improvement of 3.01% over single optimal policies and faster response speeds. Yan et al. (2025) proposed a multi-agent deep reinforcement learning approach to address the distributed FJSP with random job arrivals, modeling it as a MDP and designing a distribute agent (DA) and a sequence agent (SA). The DA is configured with 12 state features, 5 candidate actions, and a reward based on production tardiness, while the SA has 7 state features, 6 candidate actions, and rewards reflecting delay conditions, both utilizing a DQN framework with a linearly decreasing threshold probability for exploration-exploitation balance. Comparative experiments on randomly generated instances demonstrate the effectiveness of the DA alone and in conjunction with the SA, showcasing the approach’s superiority in minimizing tardiness compared to composite dispatching rules and other optimization algorithms.
To address dynamic problems, numerous experts and scholars have conducted further research. Pol et al. (2021) proposed the challenge of achieving cooperation among multiple agents in MARL to achieve scheduling purposes in manufacturing systems, such as minimizing the maximum completion time. The authors developed a experience logic that can quickly estimate an effective reference completion time based on the total sum of operation times for each job. They proposed a dense local reward and sparse global reward augmented by a global reward factor to achieve cooperation among agents. Their work is based on DQN, simply including information from other agents in each agent’s state space, enabling smarter decision-making in dynamic multi-agent environments. Due to the fixed topology structure of the manufacturing system, communication is implicitly implemented, with agents sharing DQN to simplify the training process. To address the credit assignment problem, training is divided into two stages, first using local rewards, and then retaining local rewards enhanced by the global reward factor. In addition, they proposed using sparse rewards given to each agent at the end of an episode to replace global rewards, simplifying the process of learning to cooperate. Luo et al. (2021a) proposed a two-layer hierarchical reinforcement learing (HRL) production scheduling method. The paper uses a high-level DDQN agent to determine global optimization objectives, and a low-level DDQN is responsible for selecting appropriate scheduling rules. However, using a high-level controller agent in the HRL method increases the depth of the RL problem, thus reducing the chances of the learning process converging. Qin et al. (2023) proposed an innovative multi-agent dueling deep reinforcement learning method to address dynamic FJSP. The method learns scheduling strategies in a static training phase and directly applies these strategies to real-time scheduling that includes random processing times and unexpected machine failures. Through extensive simulation experiments under different production environment conditions, the study proves the effectiveness of the proposed method in optimizing production scheduling, especially in handling dynamic changes in mass personalized production. This achievement provides new solutions for dynamic scheduling problems in intelligent manufacturing systems and demonstrates the potential of deep reinforcement learning in improving the flexibility and adaptability of production scheduling. Zhang et al. (2024a) proposed a multi-agent reinforcement learning framework to address dynamic FJSP with transportation constraints, enabling collaboration between machine and job agents. The study formulates the problem as a POMDP and designs a reward-sharing mechanism to tackle delayed rewards and facilitate policy learning. An improved multi-agent dueling double deep Q network algorithm is developed, demonstrating superior performance in shortening weighted flow time compared to state-of-the-art methods across trained and unseen scenarios. Meanwhile, Zhang et al. (2024b) proposed a dynamic FJSP strategy based on heterogeneous MARL. The strategy achieves centralized optimization and decentralized decision-making through the collaboration between job agents and machine agents, with the heterogeneous multi-agent scheduling framework. The researchers first modeled the dynamic FJSP problem as a heterogeneous multi-agent POMDP and introduced a reward shaping mechanism to organize work and machine agents to minimize the weighted tardiness of dynamic jobs. The method demonstrated significant adaptability when encountering new scenarios, highlighting the advantages of using a scheduling method based on heterogeneous MARL in addressing dynamic and flexible challenges. The detailed introduction about this case will be provided in Section 4.2. Wang H. et al. (2025) considered uncertain processing and transportation times in dynamic FJSP, constructed a MAS based on this problem model, and proposed a method based on multi-agent deep reinforcement learning. The study aims to optimize the makespan, which is the maximum completion time of all orders. Experimental results show that it has better convergence and generalization ability in large-scale task processing. Qin and Lu (2024) presented a knowledge graph-enhanced MARL approach for adaptive scheduling in smart manufacturing, aiming to address the challenges of mass personalization by integrating interoperable communication via Knowledge Graphs with adaptive manufacturing control through Reinforcement Learning. The study formulated the dynamic FJSP, considering manufacturing requirements and dynamic events such as stochastic processing times and unplanned machine breakdowns. A machine graph was constructed to represent machine capability, availability, and preference information, enabling semantic communication among manufacturing entities. The framework redesigned agent observation, action, reward, and cooperation mechanisms to incorporate machine preferences, using a density-based clustering algorithm to extract preference information from historical data. The model was trained using a Dueling DQN approach, with the Machine Graph guiding agents to narrow down search spaces and accelerate learning. Experimental results on 12 testing instances showed that the approach outperformed individual Reinforcement Learning and heuristic rules in both training efficiency and makespan optimization, particularly under dynamic events. The approach demonstrated improved convergence speed and robustness, highlighting the effectiveness of integrating domain knowledge via Knowledge Graphs to enhance scheduling adaptability in dynamic manufacturing environments.
PPO, an improved policy gradient method, enhances training stability by limiting the magnitude of policy updates, helping to find better solutions in FSSP. Lei et al. (2022) proposed a multi-agent framework based on deep reinforcement learning for solving FJSP. The researchers designed an end-to-end deep reinforcement learning framework that uses graph neural networks to automatically learn strategies for solving FJSP. In the FJSP environment, reinforcement agents need to schedule an operation of a job to a suitable machine from a set of compatible machines at each time step. This requires the agent to control multiple actions simultaneously, thus such multi-action problems are formulated as a multi MDP. To solve MDP, the researchers proposed a multi-pointer graph network architecture and designed a training algorithm called multi-PPO to learn two sub-policies: job operation action policy and machine action policy, thereby allocating job operations to machines. The MPGN architecture consists of two encoder-decoder components, defining the job operation action policy and machine action policy, to predict probability distributions on different operations and machines. The researchers introduced a discontinuous graph representation for FJSP and used graph neural network embeddings for local states encountered during scheduling. Computational experimental results show that the agent can learn high-quality scheduling strategies that perform better than hand-crafted heuristic scheduling rules and metaheuristic algorithms in terms of solution quality and running time. In addition, the researchers tested the generalization performance of the learned strategies on random and benchmark instances, showing that the strategy has good generalization performance on real-world instances and larger-scale instances. Popper et al. (2021) studied FJSP and proposed an innovative MARL. This method not only considers production efficiency but also integrates sustainable objective variables, such as energy consumption and machine usage efficiency. Through experimental validation, this method has shown excellent performance in multi-objective optimization, especially in dealing with dynamic changes and uncertainties in the production process. This study provides a new perspective for scheduling problems in intelligent manufacturing systems, emphasizing the importance of considering sustainability in production planning, and demonstrates the potential of MAS in achieving this goal. Lv et al. (2025) proposed a type-aware MARL strategy to address real-time schedule repair for FJSP under machine breakdowns, modeling the problem as a multi-agent MDP. The approach uses a heterogeneous graph to represent relationships between machine agents and operations, extracting machine node embeddings via a meta-path type-aware recurrent neural network and operation embeddings through a heterogeneous graph attention network, with a hypernetwork enabling parameter adaptation for node types, edge types, and locations. Experimental results show that the proposed MARL outperforms heuristic rules and other MARL algorithms, achieving the minimum stability objective while reducing makespan, demonstrating its effectiveness in handling machine breakdowns and maintaining production stability. Li et al. (2025) proposed a real-time scheduling method for the dynamic FJSP with AGVs using MARL, aiming to minimize total tardiness cost in the face of machine flexibility, limited logistics equipment, and frequent dynamic events. The study designed a real-time scheduling framework with a multiagent architecture comprising a task selection agent, machine selection agent, and AGV selection agent. It introduced an action space and efficient action decoding algorithm based on priority dispatching rule weighting and adjustment, enabling agents to explore high-quality solution spaces. The state space was generalized to include job, machine, and AGV attributes, while the reward function considered machine idle time and handled four disturbance events to enhance robustness. The model was trained using MAPPO. Experimental results showed that the proposed method outperformed priority dispatching rules, genetic programming, and four popular RL based methods, with performance improvements often exceeding 10%. It demonstrated strong robustness in handling various disturbance events, providing appropriate scheduling schemes for uncertain manufacturing systems. Liang et al. (2025) proposed a MARL with structural information optimization framework (MARLSIO) for large-scale FJSP, decomposing the problem into operation selection and machine allocation sub-tasks and training job agents using the multi agent PPO algorithm. The framework introdsuced a structural information-based state and action abstraction to capture complex machine-operation relationships, using structural entropy to optimize hierarchical state and action representations, which enhanced agents’ learning efficiency and policy quality. Experimental results showed that MARLSIO outperformed traditional methods in both synthetic and public benchmark instances, demonstrating better computational efficiency and generalization ability, especially in large-scale FJSP scenarios with varying sizes and characteristics. Wang et al. (2024) proposed an end-to-end multiagent proximal policy optimization (E2E-MAPPO) approach for the multitarget FJSP, integrating makespan, processing energy consumption, standby energy consumption, and transportation energy consumption as optimization targets. The approach modeled FJSP as a disjunctive graph, using graph isomorphism network and graph attention network to encode subtask and machine node features, and designed job and machine agents to make decisions based on vectorized value functions and local critic networks. Experimental results showed that E2E-MAPPO outperformed traditional priority dispatching rules and state-of-the-art deep reinforcement learning methods in terms of solution quality, online computation time, stability, and generalization, especially in large-scale and unseen testing instances.
Popper and Ruskowski (2022) proposed an innovative MARL method for solving dynamic FJSP. By constructing a MAS that includes machine agents and factory agents, this method achieves dynamic scheduling of production tasks. The factory agent is responsible for coordinating machine agents and tracking the status of order processing, while the machine agent decides whether to accept new production tasks based on the task weight values generated by its neural network. This MARL based method can not only handle variable-sized orders but also achieve online scheduling and can easily integrate more production participants. In addition, by optimizing the production factory globally, it avoids the local minimum problems that may occur in sequential planning. Preliminary experimental results show that the system can match the planning quality of common heuristic algorithms, and even perform better in some aspects, providing a new solution for flexible job-shop scheduling problems. Luo et al. (2021b) developed a hierarchical multi-agent proximal policy optimization (HMAPPO) method as a means to address dynamic multi-objective flexible job-shop scheduling problems, where some operations are subject to no-wait constraints. The method includes three types of agents, including objective agents, job agents, and machine agents. Object agents periodically specify temporary optimization objectives, job agents select job selection rules, and machine agents choose machine allocation rules for the corresponding temporary objectives. Through HRL, the method learns at different levels of abstraction, where the high-level controller learns strategies at a high level. This means that some jobs need to be processed continuously without interruption. However, the architecture in HRL is not fully decentralized, as there should be a high-level controller at the top layer. It should also be noted that the HRL method does not guarantee the optimality of the overall multi-agent strategy. Gu et al. (2024) proposed a dynamic scheduling mechanism for intelligent workshops based on a MAS architecture and a deep reinforcement learning method. The researchers designed an IoT-based multi-agent manufacturing system and established a mathematical model for FJSP. To construct agents in the intelligent workshop, the article proposed a data-based combination of virtual and physical agents (DB-VPA), which includes the information layer, software layer, and physical layer. Wang W. et al. (2025) proposed a hierarchical MARL framework to address the dynamic FJSP with transportation, decomposing the decision space into high-level job prioritization, mid-level machine assignment, and low-level transbot allocation. The framework integrates an imitation learning strategy to leverage heuristic methods, using a variable state space representation and scaled dense rewards to enhance adaptability and convergence speed. Experimental results on generated instances and benchmark datasets demonstrate that multi agent PPO outperforms traditional heuristic and single-agent DRL methods in makespan, robustness, and computational efficiency, showcasing its scalability for complex manufacturing scenarios. Zheng et al. (2025) proposed a MARL approach based on cross-attention networks for the dynamic FJSP, aiming to address the complexity and uncertainty of actual production processes. The study formulated the dynamic FJSP as an MDP, designing a job selection agent and a machine allocation agent. It innovatively represented job processing data and production Gantt charts as state matrices, and employed a multi-head cross-attention network to extract state features, enabling the model to capture complex relationships between jobs and machines. The model was trained using an IPPO algorithm, allowing agents to learn efficient scheduling strategies. Experimental results on numerous static and dynamic scheduling instances demonstrated that the algorithm outperformed traditional heuristic rules and other advanced algorithms, such as maskable PPO and multi agent PPO, with strong learning efficiency and generalization capability. The algorithm showed superior performance in minimizing makespan and handling dynamic job arrivals, highlighting the effectiveness of cross-attention networks and multi-agent frameworks in solving complex scheduling problems. Heik et al. (2024) explored the application of single-agent and multi-agent RL to dynamic scheduling in the growing complexity of manufacturing environments, using the Industrial IoT test bed as a case study. The research aimed to enhance manufacturing system efficiency by optimizing resource consumption and minimizing makespan. The study formulated the dynamic FJSP as an RL problem, evaluating heuristic, meta-heuristic, and RL methods. It designed a state space representation capturing operational details and used PPO for training. The MARL architecture, with individual agents for each manufacturing operation, demonstrated superior performance in managing resources and improving system efficiency. The reward function was carefully designed to balance makespan minimization and machine utilization, and the study investigated the impact of different state representations and reward parameters on model performance. Experimental results showed that the multi-agent PPO approach outperformed heuristic methods, with significant improvements in makespan and robustness against disturbances. The study highlighted the potential of MARL in handling complex manufacturing dynamics and provided insights into designing effective RL policies for real-world industrial systems.
Graph convolutional networks (GCN) excels in handling graph-structured data, capturing task dependencies and resource allocation information in FJSP. Oh et al. (2023) explored FJSP, a complex scheduling problem involving the modeling of production systems. Traditionally, mathematical optimization and metaheuristic methods have been widely used to solve FJSP. With the advancement of DRL, particularly the combination of MARL and GNN, new approaches have emerged for FJSP. In previous studies, work and machines were defined as agents, but due to the dynamic nature of the number of work agents, there were scalability issues when the number of work agents increased. To overcome this limitation, this study modeled FJSP as a graph structure of machine pairs and applied GNN to reflect the cooperation between agents. Through experiments, the researchers demonstrated that the proposed method outperformed existing heuristic rules and metaheuristic algorithms in reducing the weighted delay of dynamic jobs. These results indicate that the combination of MARL and GNN has potential in solving FJSP and can achieve efficient scheduling through learned strategies in real-time scheduling environments. Zhang J.-D. et al. (2023) proposed an innovative model DeepMAG, which combines DRL and MARL to address this issue. By constructing multi-agent graphs, DeepMAG can simulate the operational relationships between machines and jobs, enabling agents to work together to find the best scheduling strategy. The experimental results of the study show that DeepMAG can significantly improve scheduling efficiency and effectiveness compared to traditional methods when dealing with complex scheduling problems with a large number of machines and jobs. This achievement provides a new solution for scheduling problems in intelligent manufacturing systems and demonstrates the potential of deep learning and MAS in solving practical industrial problems. Jing et al. (2024) proposed a CTDE framework based on GCN to address the challenges of high flexibility, agility, and robustness in FJSP. The study transformed the FJSP into a topological graph structure prediction problem by constructing a directed acyclic graph (DAG) probability model of the product processing network and the job shop environment, and used GCN to extract interaction information between job agents, achieving efficient scheduling in complex and dynamic environments. This method not only improves machine utilization but also enhances adaptability to personalized production, providing a new perspective for the application of FJSP in intelligent manufacturing.
Peng et al. (2023) proposed a double Q-value mixing (DQMIX) algorithm specifically for extended flexible job-shop scheduling problems (FJSP-DT) with dual flexibility and variable transportation times. By modeling FJSP-DT as Dec-POMDP and combining GCN to handle high-dimensional state and observation spaces, the DQMIX algorithm effectively addresses the curse of dimensionality and enhances the adaptability and real-time performance of scheduling. The algorithm introduces a dual-critic network structure to enhance the exploration and exploitation capabilities of the algorithm, while integrating mechanical constraints into the learning process to further improve performance. Experimental results demonstrate the significant advantages of the DQMIX algorithm in solving FJSP-DT problems in terms of solution accuracy, stability, and generalization, especially in handling large-scale scheduling problems, where the DQMIX algorithm shows exceptional performance. Pu et al. (2024) proposed an innovative MARL method for solving dynamic FJSP, which is of great significance in intelligent manufacturing. By constructing a distributed multi-agent scheduling architecture, each job is regarded as an agent, and reinforcement learning algorithms are used to achieve collaboration among agents to optimize production scheduling. Through graph neural networks and heterogeneous GNN encoding of state nodes, the researchers can effectively calculate scheduling strategies including machine matching and process selection. Furthermore, through the multi-agent proximal policy optimization algorithm, the method excels in minimizing energy consumption and improving resource efficiency, surpassing existing scheduling rules and RL-based methods in terms of solution accuracy and stability. Experimental results validate the effectiveness and generalization capability of the method in handling large-scale problems, providing new solutions for real-time dynamic scheduling in intelligent manufacturing. Johnson et al. (2024) introduced the continuous dynamic FJSP to address the challenges of mass personalization in smart manufacturing, where job orders arrived continuously, products were diverse, and urgent orders disrupted traditional scheduling. They proposed MAC-Sched, a graph based MARL model, to tackle this problem. MAC-Sched represented the manufacturing environment as a heterogeneous graph, with nodes for operations and machines and edges for processing capabilities and sequences. Each machine acted as an agent, using a heterogeneous GNN to extract state embeddings, and a shared actor-critic policy was trained via PPO. Conflicts between agents selecting the same job order were resolved through a bidding mechanism prioritizing machines with fewer options and shorter processing times. The reward function was based on minimizing estimated mean tardiness. Experiments on the Brandimarte Dataset showed that MAC-Sched outperformed 18 combinations of heuristic rules, particularly at high machine utilization rates. It demonstrated strong generalization to factories with varying numbers of machines, product diversity, and utilization levels, highlighting its reliability in dynamic, continuous manufacturing environments.
Gui et al. (2024) proposed a new dynamic scheduling method by constructing the manufacturing system as a self-organizing MAS and using MARL. The method transforms the complex scheduling problem into a collaborative decision-making task between agents through a partially observable Markov game (POMG) based on the contract net protocol. Through training with the MADDPG algorithm, agents can learn to choose the best scheduling rule weights at each decision point, thus optimizing the collaborative scheduling decision-making between heterogeneous manufacturing equipment. The research not only advances the application of MARL in complex manufacturing systems theoretically but also demonstrates its effectiveness and superiority in the dynamic FJSP scenario through experiments, providing new solutions for dynamic scheduling in intelligent manufacturing systems. Waseem and Chang (2024) proposed a method that combines Nash games with MADDPG algorithms, called Nash-MADDPG. This method developed a multi-agent control scheme for allocating mobile robots to load/unload different product types on different machines by observing the system’s permanent production loss (PPL) and market demand for each product type. First, the authors developed a Nash game among mobile robots and defined a cooperative cost to improve cooperation, which was then used in the reward function of the MADDPG algorithm. Secondly, the actions were defined based on the action values from the MADDPG and the strategies of the mobile robots in the Nash game, thereby updating the environment to a new state. Wang X. et al. (2025) proposed a MADRL system with game theory to address the FJSP, aiming to minimize Makespan, total energy consumption, and human factor’s comfort. The study formulates the FJSP as a MDP, using a deep convolutional neural network to extract state features from processing time, task assignment, and adjacency matrices, and employs simple constructive heuristics as candidate actions for scheduling decisions. A game model combining Nash equilibrium and Pareto optimality is established to unify multi-objective optimization into a reward strategy, and a MADDPG framework is designed to train the model, demonstrating superior performance in solving real-world production scheduling problems compared to traditional algorithms. A summary of the application of MARL in FJSP is provided in Table 6.
4 Case study of FSSP by MARL
To facilitate a clearer understanding of the role of MARL in the FSSP, this section will present two concrete case studies. These case studies focus on the HFSP and FJSP, respectively, and cover discussions on the MDP formulations, MARL algorithms, and numerical experiments. The choice of these two cases was based on several key criteria: problem complexity, real-world relevance, current research trends, and their potential for further development within the context of MARL.
4.1 Case study of HFSP by MARL
Zhang N. et al. (2023) proposed a CAMARL approach to solve the joint optimization problem of maintenance and production scheduling in manufacturing systems. Its main advantage is the ability to handle large-scale, dynamic environments and boost performance through counterfactual attention and collaboration mechanisms. This problem considers a setting where each stage comprises multiple parallel machines, and jobs sequentially pass through all stages, with each stage selecting one machine for processing. While frequent maintenance can reduce failure rates, it inevitably leads to downtime, impacting production efficiency. Conversely, neglecting maintenance increases the risk of machine failures, necessitating corrective maintenance (CM), which escalates costs and downtime. Machine degradation is influenced by various factors, including workload and environmental conditions. The objective is to optimize production scheduling and maintenance strategies, balancing production efficiency and maintenance costs to minimize total costs.
4.1.1 Decentralized partially observable Markov decision process
This section models the HFSP as a Dec-POMDP and defines the key components of MARL: state, action, and reward. The observation result at the decision moment serves as input for the agent to guide its action selection.
The state is divided into three categories of information: job information, machine information, and system-level information. Job information includes actual processing time, the quantity of jobs in the waiting queue, and the index of available jobs. This information reflects the current demands and task status of production scheduling. Machine information is represented as a tuple
At the decision moment
A real-time reward settlement mechanism is designed. Once the action
For production-related actions, the reward is proportional to the difference between the completion time
4.1.2 Algorithm description
This section provides a detailed introduction to the framework and implementation steps of the CAMARL algorithm, including action abstraction, coordination control, attention mechanisms, counterfactual reasoning, and the training process. The goal of the algorithm is to optimize the problem through multi-agent collaboration, minimizing the total cost. The framework of the CAMARL algorithm is shown in Figure 6.
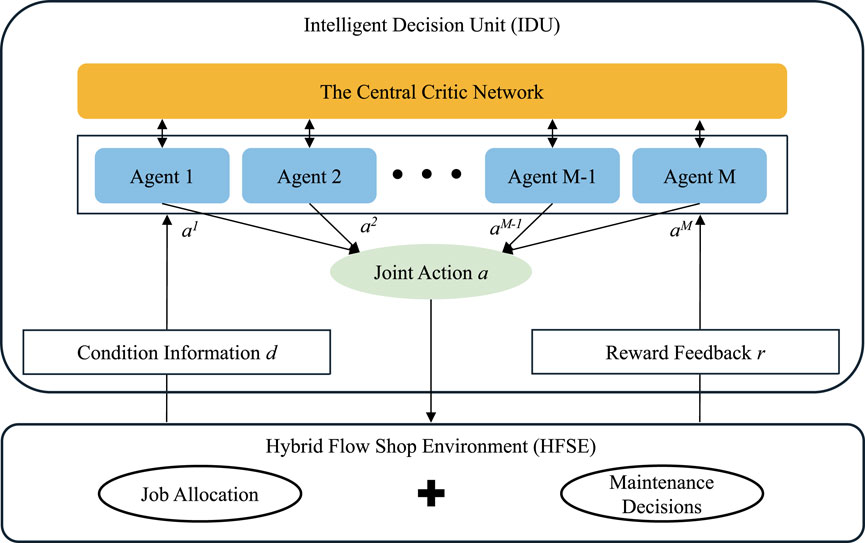
Figure 6. The heterogeneous multi-agent based scheduling framework in Zhang N. et al. (2023).
The problem involves a large-scale action space, and directly handling it can lead to the curse of dimensionality. Action abstraction reduces the action space by clustering similar actions.
In the multi-agent system, the agents’ action selections may conflict with one another. The coordination control module avoids invalid actions and accelerates exploration by generating a legal action space. Each agent has limited local observations and struggles to directly obtain global information. The attention mechanism integrates local observations to generate global information by quantifying the importance of agents.
Traditional attention mechanisms can lead to unstable training, especially when the number of agents dynamically changes. Counterfactual attention reduces training variance and improves adaptability by comparing an agent’s actual contribution with a baseline. CAMARL adopts a CTDE framework, and the specific algorithm flow is shown in Algorithm 1.

Algorithm 1. Training Algorithm of CAMARL in Zhang et al. (2023b).
4.1.3 Experimental results and analysis
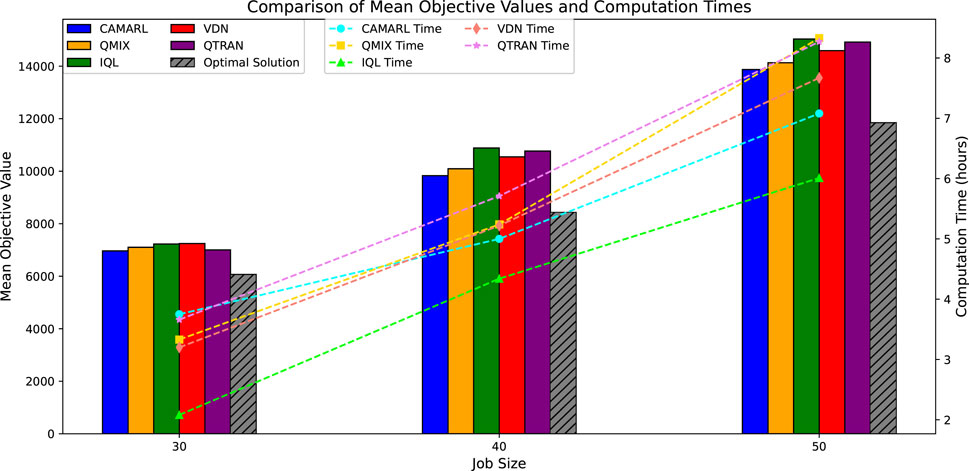
The experiment was conducted in a two-stage HFSP consisting of five independent machines. Three different types of jobs were considered, with varying initial processing times on different machines. This case focuses on the comparison between CAMARL and other reinforcement learning methods, primarily analyzing the objective values and computational time.
To evaluate the performance of CAMARL, the authors compared it with four reinforcement learning methods: QMIX, IQL, VDN, and QTRAN. Table 8 lists the mean objective values of the five MARL algorithms compared to the optimal solution and the computation times (in hours) for all algorithms. The data visualization analysis of the comparison of the average target value and the computation time is shown in Figure 7.
In contrast, QMIX, IQL, VDN, and QTRAN showed larger gaps, indicating that CAMARL is closer to the optimal solution. Numerical studies demonstrate that CAMARL performs exceptionally well in joint maintenance and production scheduling problems.
4.2 Case study of FJSP by MARL
Zhang et al. (2024b) first modeled the dynamic FJSP problem as a heterogeneous multi-agent POMDP and introduced a reward shaping mechanism to organize work and machine agents to minimize the weighted tardiness of dynamic jobs. The researchers proposed an extension of the dynamic FJSP that incorporates transportation times. In this extended formulation, jobs are allowed to arrive dynamically within the system, and each job can be processed by a set of available machines, with each machine having different processing times for the operations. Under these conditions, information about the jobs is not visible until they arrive, and the transportation time between machines is also non-negligible. This paper aims to minimize the average weighted tardiness of dynamic jobs as outlined.
4.2.1 Multi-agent partially observable MDP
Each job’s state is precisely described by a set of feature parameters, specifically including: the current job ID, arrival time, earliest possible start time, remaining number of jobs, average remaining processing time, list of available machines for processing, job weight, and due date. These features collectively provide a comprehensive description of job requirements and priorities.
For machine states, the representation focuses on several key indicators: residual processing time for the current task, total residual processing time, and the number of jobs in the buffer zone. This information aids agents in evaluating the machine’s workload and potential task scheduling over the coming period.
The observation space of an agent encompasses detailed information about all pending jobs in its queue, such as the aforementioned job state attributes. Utilizing a POMDP framework, agents make decisions based on limited yet critical information. This setup not only enhances system adaptability and robustness but also promotes collaboration among different agents, thereby improving the overall performance of the dynamic FJSP. This method ensures that each agent can operate efficiently within a broader, more adaptive system environment, thereby enhancing the performance outcomes of the entire manufacturing system.
For job agents, the action space is discrete and specified across six dimensions, as shown in Table 9.
This table lists a series of heuristic rules guiding the allocation of machines to specific operations. Once a rule is selected, subsequent machine selection is determined based on priority values calculated according to the chosen rule. This means that, depending on the attribute values under the selected rule, the agent evaluates the suitability of each candidate machine and ultimately decides which machine is most appropriate for the current task. After selecting a machine, considering transportation time, the relevant job is placed in the machine’s buffer zone awaiting further processing.
For machine agents, their action space is also discrete but extends to nine dimensions, as detailed in Table 9.
This table lists various heuristic rules applied to job sequencing within the buffer zone. When a rule is adopted, the machine agent assesses all candidate jobs based on this rule and assigns them corresponding priority values. The job with the highest priority is then selected for processing. This design enables machines to respond quickly to dynamic changes while ensuring high-quality scheduling decisions.
In dynamic FJSP, job tardiness cannot be realized until the last operation of each job is completed, leading to sparse rewards during the learning process for both job and machine agents. To address this issue, the authors propose a reward shaping mechanism where the completion reward of a job is shared between the job and the machine agents involved in its processing. Specifically, when a job is completed, weighted tardiness serves as the shared reward for all agents involved in the completion process. Thus, job agents receive rewards directly aligned with optimization goals, and these rewards are distributed among machine agents corresponding to the set of machines completing the job operations.
The introduction of this reward shaping mechanism ensures that each decision experience provides feedback directly related to the optimization objective. This approach effectively mitigates the problem of sparse rewards and establishes a collaborative environment among heterogeneous agents with different decision points, aiming to achieve common optimization goals. Consequently, agents can learn faster and improve strategies, significantly enhancing the overall system performance.
4.2.2 Algorithm description
Zhang et al. (2024b) proposed a dynamic FJSP strategy based on heterogeneous MARL. The strategy achieves centralized optimization and decentralized decision-making through the collaboration between job agents and machine agents, with the heterogeneous multi-agent scheduling framework. The scheduling framework based on heterogeneous multi-agent is shown in Figure 8.
Figure 8. The heterogeneous multi-agent based scheduling framework in Zhang et al. (2024b).
To solve this problem, the researchers developed an adversarial double deep Q-network algorithm combined with the reward shaping mechanism to determine the optimal strategy for machine assignment and job sequencing. This approach not only solves the problem of sparse rewards but also accelerates the learning process. Numerical experiments validated the effectiveness of the proposed method, showing its superiority over existing state-of-the-art baselines in reducing the weighted tardiness of dynamic jobs.
The simplified algorithm flow is shown in Algorithm 2.
4.2.3 Experimental results and analysis
This study performs a comparative analysis of the proposed method against four benchmark approaches for solving the dynamic FJSP across various scenarios. Initially, it evaluates the performance of different combinations of machine allocation and job sequencing rules within the action space, which includes 54 composite heuristic rules. Following this evaluation, the best composite heuristic rule (BCHR) for each instance is selected as one of the baseline methods. Additionally, two advanced methodologies are included in the comparison: a novel cooperative coevolution genetic programming (CCGP) approach, as described by Zhang et al. (2020), and a multi-agent double deep Q-network (MADDQN) method, as detailed in Liu et al. (2022). Furthermore, an heterogeneous multi-agent dueling double deep Q-network (HMAD3QN) approach is incorporated to evaluate the improvements brought about by the reward-shaping mechanism. The study deliberately excludes meta-heuristic-based approaches from the comparison. The rationale is that comparing rescheduling and real-time scheduling methods, which require time-consuming iterations during dynamic events, would introduce bias and inequity in the evaluation framework.
Weighted tardiness is an important evaluation criterion, and its calculation is shown in Equation 10.
Wherein,
The article evaluates weighted tardiness in different scenarios, and the experimental results obtained are shown in Table 10.
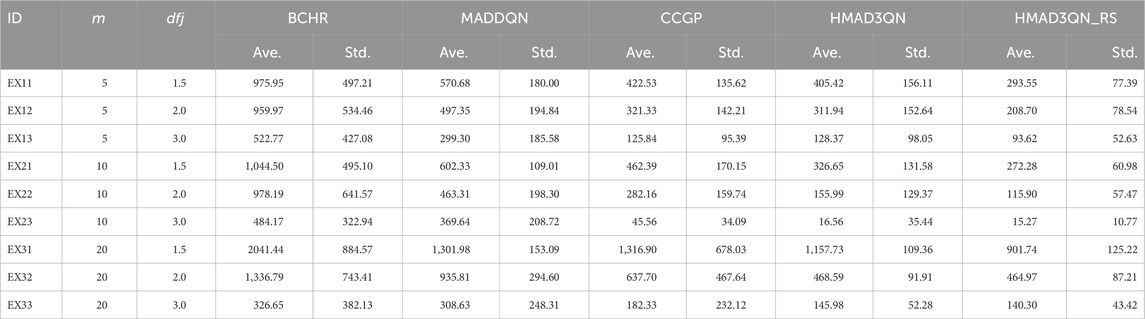
Table 10. Average and standard deviation of weighted tardiness for different scenarios in Zhang et al. (2024b).
The empirical results demonstrate that HMAD3QN-RS consistently achieves the lowest average weighted tardiness across all evaluated scenarios. This finding underscores the significant improvement in scheduling performance attributable to the incorporation of reward shaping mechanisms. This finding underscores the significant improvement in scheduling performance attributable to the incorporation of reward shaping mechanisms. Additionally, HMAD3QN-RS not only outperforms other methods in terms of mean performance but also exhibits lower standard deviations in most cases, indicating both its efficiency and consistency.
To clearly dissect the outcomes, we assign rank values to the algorithms by sorting them in descending order based on their ave values. Figure 9 illustrates the ranking results. It is evident that HMAD3QN-RS attains the best “Ave.” values across all instances in terms of mean performance, indicating its superior effectiveness. Notably, HMAD3QN, which can be regarded as a variant of HMAD3QN-RS without the specific optimization strategy RS, consistently ranks second or third. This observation underscores the competitive advantage of incorporating the RS optimization strategy into the HMAD3QN algorithm, significantly enhancing its convergence performance.
These graphical representations provide deeper insights into the comparative performance metrics across various scenarios, thereby supporting the authors’ assertions with clear and accessible evidence. Notably, the proposed method demonstrates remarkable adaptability. Even when applied to a new environment featuring 20 machines, a scenario not encountered during training, the learned Q-functions remain highly efficient. This underscores the robustness and generalizability of the proposed approach.
5 Challenges and future directions
In this study, a comprehensive review of the application of MARL to shop scheduling, especially flexible shop scheduling, was conducted from a technical and analytical perspective. Specifically, the application of MARL in FSSP was studied, with a particular emphasis on HFSP and FJSP. A comparative analysis was provided for different shop scheduling problems and MARL methods, representing how to select different MARL characteristics to implement corresponding MARL solutions. The research presented in this paper indicates that MARL has become one of the excellent methods for solving flexible shop scheduling problems due to its ability to handle uncertainties in a self-organized manner within multi-agent and decentralized systems.
5.1 Analysis and findings
This study comprehensively collected 78 relevant data and conducted a detailed classification of these data. After screening, a total of 39 research papers were finally identified. These papers cover different research questions and methods, providing a solid foundation for follow-up research.
5.1.1 Problem distribution analysis
From the perspective of problem analysis: Currently, there are relatively few studies on HFSP (only 7 papers), while there are more studies on FJSP (34 papers). Future research should pay more attention to HFSP, especially in the application of MARL methods. By filling this research gap, the development of MARL in a wider range of industrial application scenarios can be promoted. As depicted in the outer section of Figure 10, which utilizes a donut chart representation.
In FSSP research, optimization objectives vary, including minimizing makespan, reducing machine load, improving resource utilization, reducing energy consumption, shortening average waiting time, and balancing workload. Different studies may focus on single or multi-objective optimization depending on the needs of the application scenario. As shown in the middle section of Figure 10 which displays the visual analysis of the number of optimization objectives. These analyses help us understand the distribution and focus of current research, providing guidance for future research directions.
5.1.2 Methodology analysis
From the perspective of method analysis: Currently, there are relatively few studies on centralized methods (only 3 papers), while there are more studies on CTDE methods (38 papers). Future research can focus more on the application of centralized methods in scheduling problems, exploring their strengths and limitations in different scenarios. As shown in the inner section of Figure 10.
Through collaboration among agents, MARL achieves more efficient resource allocation and task scheduling in the FSSP, thereby enhancing production efficiency and reducing costs. In Section 3 of this paper, we reviewed the base MARL methods applied to FSSP, including DQN, A2C, PPO, GCN, DDPG, QMIX, Attention-based mechanisms, and Parallel decoding techniques. DQN, a value iteration-based reinforcement learning method, guides action decisions by learning the value of state-action pairs and is used to optimize task scheduling strategies in FSSP. A2C combines the advantages of policy gradient and value function methods, accelerating the learning process by training multiple agents in parallel to quickly find approximate optimal scheduling strategies. PPO, an improved policy gradient method, enhances training stability by limiting the magnitude of policy updates, helping to find better solutions in FSSP. GCN excels in handling graph-structured data, capturing task dependencies and resource allocation information in FSSP, and strengthens the MARL algorithm’s understanding and prediction of complex scheduling problems. DDPG is suitable for problems with continuous action spaces, improving learning effects through deterministic policies, and dealing with dynamic machine load adjustments in FSSP. QMIX, a value decomposition-based learning method, promotes cooperation in multi-agent environments by decomposing global value into individual value contributions, coordinating agent behaviors to achieve common optimization goals. Attention-based methods highlight key information in the input, effectively handling long sequence dependencies in FSSP, and improving scheduling quality. Parallel decoding technology speeds up learning by distributing computational tasks among multiple agents, increasing the efficiency of exploring the solution space in FSSP. As shown in Figure 11, we conducted statistical and visual analysis of the number of literature used.
5.2 Key challenges
Addressing the dimensional disaster in large-scale scenarios and scalability issues can be achieved through independent learning, task decomposition, simplifying network structures, transfer learning, and knowledge reuse. Each method has its advantages and limitations, and the most suitable technology needs to be selected according to the specific scenario in practical applications. Through these methods, the performance and scalability of MAS can be effectively improved.
5.2.1 Dimensional issues in large-scale scenarios
For the dimensional disaster that occurs in large-scale clusters with unknown or continuous state-action spaces, leading to slow convergence or even failure of the algorithm, there are two main existing solutions: First, independent learning is used to deal with large-scale cluster problems to avoid the complexity brought by centralized learning; second, for algorithms with centralized learning architecture, optimization algorithms and network itself are optimized, that is, task decomposition, simplifying network structures, and information compression to alleviate dimensional disasters.
5.2.1.1 Independent learning
Independent learning inherently does not have scalability issues and does not need to consider the state-action of other agents in the cluster, making independent decisions, thus not affected by system scale. Fan T. et al. (2018) and Long et al. (2018) proposed independent QL based multi-robot collision avoidance algorithms. Each robot uses radar to perceive the surrounding environment as input variables of the network. Embedding independent QL algorithms in the multi-agent platform effectively solves the action decision problem for a large number of agents. DIAL (Foerster et al., 2016) and CommNet (Sukhbaatar et al., 2016) algorithms introduced communication mechanisms between agents to learn communication protocols through feedback mechanisms, making independent learning methods effectively solve the dimensional disaster problem. Zhang et al. (Zhang et al., 2019) proposed a QCOMBO algorithm for optimizing the global traffic state of large-scale road networks. By combining the advantages of independent and centralized learning and selecting actions from separate optimized utility functions, scalability is ensured. This utility function is maximized through a new consistency regularization loss between separate utilities and global action-value functions. Wang et al. (Wang W. et al., 2022) used the independent learning paradigm to extend single-agent reinforcement learning algorithms to multi-agent scenarios, solving the scalability problem of UAV swarms. Although the above methods can effectively avoid dimensional disasters and improve the convergence speed of the algorithm, this approach has no communication with the outside world, leading to environmental non-stationarity and partial observability issues (Nguyen et al., 2020), which limits the application of such algorithms.
5.2.1.2 Task decomposition and simplifying network structures
The CTDE paradigm can effectively avoid the partial observability and non-stationarity issues of independent learning and is currently the most widely used learning architecture. For this type of learning method, the convergence of the algorithm and the learning of the strategy are easily affected by the scale of the cluster. To address the scalability issues of CTDE-type algorithms, the mainstream ideas mainly include two aspects: First, using the idea of hierarchical reinforcement learning, complex tasks are decomposed into multiple levels, each level handles smaller sub-tasks, simplifying the decision-making process and reducing the dimension of the joint decision space (Yin et al., 2020). Second, on the network structure level, the model architecture is lightened by pruning and quantization to improve computational efficiency and performance. Hierarchical reinforcement learning aims to accelerate learning and improve performance by organizing complex tasks into different levels. In hierarchical reinforcement learning, the actions and decisions of agents are organized into a multi-level structure, with each level responsible for different decision-making issues. This method can greatly reduce the complexity of the action space and provide more effective learning and generalization capabilities. Xu et al. (2023) proposed a hierarchical reinforcement learning framework to improve the scalability of multi-domain elastic optical networks. The framework consists of a high-level DRL module and multiple low-level DRL modules that collaborate with each other. The proposed HRL framework retains the autonomy of each domain while providing efficient network performance through the cooperation of high-level and low-level DRL modules. Li (2022) proposed a hierarchical architecture learning paradigm that combines multi-agent algorithms and single-agent algorithms. By learning hierarchical strategies and the independence of each level in the model, macro operations are introduced to reduce the original action space, cleverly alleviating the scalability issue. Kim and Sung (2023) addressed the issue that using the same shared parameters among multiple agents limits the representative capacity of the joint policy, leading to a decline in collaborative performance. The study applied structured pruning to deep neural networks, increasing the representative capacity of the joint policy without introducing additional parameters, and auxiliary parameter sharing improved the model’s scalability.
5.2.2 Scenario scalability
MARL has demonstrated tremendous potential in a variety of application scenarios, but it also faces the issue of scalability. Scalability is a significant challenge in the field of MARL, especially when it comes to dealing with a large number of agents and complex environments. Here are some key points regarding scalability issues in MARL application scenarios:
The scalability of MARL in scenarios mainly refers to the ability of the algorithm to effectively transfer the optimal policy from the source task to a similar but not identical target task, thereby accelerating the learning process of the target task, reducing resource consumption in the target task, and improving the collaboration efficiency and effectiveness among multi-agents. Research on the scalability of MARL across scenarios mainly involves three key issues: First, the transfer between different task domains, where the state and action spaces of the source and target domains differ, and the mapping relationship between the two needs to be considered. Second, when there are multiple available source strategies, how to choose the source strategy that best fits the target domain to achieve better transfer and avoid negative transfer. Finally, how to choose the appropriate transfer learning solution based on the characteristics of the source domain-target domain task is related to the final effect of cross-scenario scalability.
Knowledge reuse usually refers to the transfer of learned models, parameters, rules, or experience to new problems or domains to improve learning efficiency, accelerate model training, or improve system performance. Knowledge reuse can be achieved through various technologies and methods, such as transfer learning, model fine-tuning, and shared model parameters. Through knowledge reuse, similar knowledge does not need to be learned repeatedly, saving training time and resources, and improving system performance and scalability. In recent years, many scholars have been committed to using the idea of parameter sharing to address the scalability issues of MARL. In terms of algorithm innovation, as early as 2017, Peng et al. (2017) proposed the BiCNet algorithm to solve the scalability issue in large-scale environments by introducing a parameter sharing mechanism, allowing agents to share model parameters, and showed significant effects in the game of StarCraft. In the same year, Gupta et al. (2017) applied DDPG, TRPO, DQN algorithms, and RNN in multi-agent environments, improving the scalability of the algorithm by introducing parameter sharing and curriculum learning mechanisms. Chu and Ye (2017) studied the scalability issue of MADDPG under local observation conditions and proposed a parameter-sharing deterministic policy gradient method based on neural networks, including three variants: Actor-Critic sharing, Actor sharing, and full Actor sharing. However, simply using the original parameter sharing often leads to a high degree of homogeneity in agents. This lack of learning adjustment for task or individual specificity often suppresses the diversity between individuals, leading to uneven model performance and even poor performance on some specific tasks. Parameter sharing, as an effective means to address the scalability issues of MARL, has shown its significant advantages in many studies. However, simple parameter sharing often leads to a lack of diversity in agents and insufficient policy diversity. Therefore, optimizing the sharing mechanism, such as introducing clustering grouping, network structured pruning, or identity mapping, etc., has effectively improved the training efficiency and convergence of the model, enhanced the policy diversity and collaboration ability between agents, but further improvements are needed in terms of dynamic adaptability, scalability in complex environments, balance between individuality and collaboration, and the ability to cope with non-stationarity issues.
5.3 Future research directions
5.3.1 Literature quantity comparison analysis
A statistical comparison of the literature quantity in the Scetion 3 of this paper was conducted, comparing the research quantities of HFSP, FJSP, and other scheduling problems. Through comparative analysis, it can be found that the research on HFSP and FJSP is relatively scarce. This finding provides an important reference direction for future research.
5.3.2 Optimizing the coordination and cooperation between agents
Due to the increasing complexity of the problem, MARL needs to further optimize the coordination and cooperation mechanisms between agents. Specifically, this can be achieved by introducing more efficient communication mechanisms, designing reasonable reward and punishment mechanisms, and developing new algorithms to enhance the collaborative ability of agents.
5.3.3 Reducing training duration and improve convergence speed
In response to the issues of long training duration and difficulty in convergence in MARL, future research can start from the following aspects:
5.3.4 Problem modeling enhancement
Modeling complex scheduling problems is an important direction for future research. More refined and accurate mathematical models need to be developed to describe scheduling problems so that they can be better applied to MARL methods. At the same time, it is also necessary to consider how to effectively integrate the constraints of actual production into the model.
6 Conclusion
The FSSP is one of the core issues in the field of production scheduling. Effectively solving manufacturing scheduling problems is an extremely challenging task. In recent years, despite significant progress made through RL methods, traditional single-agent RL approaches still have limitations when facing large-scale problems. Therefore, MARL has emerged as an innovative technology and is gradually becoming an important means to solve FSSP. The recognition of MARL’s potential in solving FSSP is continuously increasing, leading to sustained attention from both academia and industry. Over the past 5 years, the number of research papers in this field has been growing, proving that MARL for handling FSSP will become a hot research topic.
This study begins with a brief description of FSSP and explores the current state of research on its extended problems, while also summarizing the progress in MARL research, laying the foundation for subsequent MARL solutions to FSSP. Then, we proceed from the application of MARL in other shop scheduling problems to the study of FSSP. We organize cutting-edge research from multiple perspectives, including research questions, methods, and optimization objectives, and demonstrate its practical effects and theoretical innovation. Finally, we conclude with a visual analysis of the paper data and draw the following conclusions.
(1) The lower volume of published studies on HFSP and FJSP, as compared to other scheduling domains, indicates a relative lack of exploration in relation to MARL solution approaches. This finding provides an important reference direction for future research. Given the limited research on MARL in HFSP, future studies should focus on these two areas. By filling this research gap, we can promote the development of MARL in a broader range of industrial application scenarios.
(2) In the field of MARL, researchers prefer to apply DQN methods. Due to the relative simplicity and high efficiency of QL methods, they have been widely recognized and adopted in both practical applications and theoretical research.
(3) Current research on FSSP mainly focuses on single-objective optimization problems. However, through literature analysis, it has been observed that scholars have already achieved promising results by using MARL to solve FSSP. Therefore, the future trend could expand into multi-objective optimization research to better meet the diverse needs of actual industrial environments.
(4) When dealing with large-scale problems, MARL should adopt methods of problem decomposition to simplify problems and network structures, and design effective multi-agent collaboration mechanisms to achieve efficient cooperation among agents. This approach can enhance the scalability and practicality of the algorithms.
Through the aforementioned research results, we have identified new scenarios to focus on in FSSP and proposed an approach to decompose more complex problems into multiple sub-problems for resolution. At the level of MARL methods, we need to consider how to design agents and how to structure MDP, while ensuring efficient collaboration among the agents. With the continuous improvement of MARL methods, MARL is expected to solve more complex FSSP such as FOSP. These research directions will not only help advance MARL technology but also provide new perspectives and solutions for tackling complex scheduling problems in the industrial sector.
Author contributions
WX: Conceptualization, Formal Analysis, Methodology, Supervision, Writing – review and editing. JG: Conceptualization, Data curation, Investigation, Methodology, Writing – original draft, Writing – review and editing. WZ: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing – review and editing. MG: Conceptualization, Data curation, Formal Analysis, Supervision, Validation, Writing – review and editing. HO: Conceptualization, Formal Analysis, Validation, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. Science & Technology Research Project of Henan Province (232102211049), Open Fund of Key Laboratory of Grain Information Processing and Control, Ministry of Education (KFJJ2023005), Zhengzhou Science and Technology Collaborative Innovation Project (21ZZXTCX19), Open Fund of Institute for Complexity Science, Henan University of Technology (CSKFJJ-2024-29), and Scientific Research (C) of Japan Society of Promotion of Science (JSPS) (19K12148).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Andrew, A. M., and Barto, A. G. (1999). Reinforcement learning: an introduction by Richard S. Sutton and Andrew G. Barto, Adaptive computation and machine learning series, MIT Press (bradford book), Cambridge, Mass., 1998, xviii + 322 pp, ISBN 0-262-19398-1, (hardback, £31.95). Robotica 17, 229–235. doi:10.1017/s0263574799211174
Baer, S., Bakakeu, J., Meyes, R., and Meisen, T. (2019). “Multi-agent reinforcement learning for job shop scheduling in flexible manufacturing systems,” in 2019 Second International Conference on Artificial Intelligence for Industries (AI4I), Laguna Hills, CA, USA, 25-27 September 2019 (IEEE), 22–25.
Bahrpeyma, F., and Reichelt, D. (2022). A review of the applications of multi-agent reinforcement learning in smart factories. Front. Robotics AI 9, 1027340. doi:10.3389/frobt.2022.1027340
Berto, F., Hua, C., Luttmann, L., Son, J., Park, J., Ahn, K., et al. (2024). PARCO: learning parallel autoregressive policies for efficient multi-agent combinatorial optimization. arXiv preprint arXiv:2409.03811.
Bouazza, W., Sallez, Y., and Beldjilali, B. (2017). A distributed approach solving partially flexible job-shop scheduling problem with a q-learning effect. IFAC-PapersOnLine 50, 15890–15895. doi:10.1016/j.ifacol.2017.08.2354
Busoniu, L., Babuska, R., and De Schutter, B. (2008). A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man, Cybern. Part C Appl. Rev. 38, 156–172. doi:10.1109/tsmcc.2007.913919
Cao, Z., Lin, C., Zhou, M., and Wen, X. (2024). Learning-based genetic algorithm to schedule an extended flexible job shop. IEEE Trans. Cybern. 54, 6909–6920. doi:10.1109/tcyb.2024.3413054
Chen, Q. (2021). NQMIX: non-Monotonic value function factorization for deep multi-agent reinforcement learning. arXiv preprint arXiv:2104.01939.
Chu, X., and Ye, H. (2017). Parameter sharing deep deterministic policy gradient for cooperative multi-agent reinforcement learning. arXiv preprint arXiv:1710.00336.
Deng, L., Di, Y., and Wang, L. (2024). A reinforcement-learning-based 3-d estimation of distribution algorithm for fuzzy distributed hybrid flow-shop scheduling considering on-time-delivery. IEEE Trans. Cybern. 54, 1024–1036. doi:10.1109/tcyb.2023.3336656
Drugan, M. M. (2019). Reinforcement learning versus evolutionary computation: a survey on hybrid algorithms. Swarm Evol. Comput. 44, 228–246. doi:10.1016/j.swevo.2018.03.011
Du, Y., Li, J., Li, C., and Duan, P. (2024). A reinforcement learning approach for flexible job shop scheduling problem with crane transportation and setup times. IEEE Trans. Neural Netw. Learn. Syst. 35, 5695–5709. doi:10.1109/tnnls.2022.3208942
Fan, K., Zhai, Y., Li, X., and Wang, M. (2018a). Review and classification of hybrid shop scheduling. Prod. Eng. 12, 597–609. doi:10.1007/s11740-018-0832-1
Fan, T., Long, P., Liu, W., and Pan, J. (2018b). Fully distributed multi-robot collision avoidance via deep reinforcement learning for safe and efficient navigation in complex scenarios. arXiv preprint arXiv:1808.03841.
Foerster, J., Assael, I. A., De Freitas, N., and Whiteson, S. (2016). Learning to communicate with deep multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 29. doi:10.48550/arXiv.1605.06676
Fu, Q., Qiu, T., Pu, Z., Yi, J., and Yuan, W. (2022). “A cooperation graph approach for multiagent sparse reward reinforcement learning,” in 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18-23 July 2022 (IEEE), 1–8.
Gao, J., Sun, L., and Gen, M. (2008). A hybrid genetic and variable neighborhood descent algorithm for flexible job shop scheduling problems. Comput. and Operations Res. 35, 2892–2907. doi:10.1016/j.cor.2007.01.001
Gerpott, F. T., Lang, S., Reggelin, T., Zadek, H., Chaopaisarn, P., and Ramingwong, S. (2022). Integration of the a2c algorithm for production scheduling in a two-stage hybrid flow shop environment. Procedia Comput. Sci. 200, 585–594. doi:10.1016/j.procs.2022.01.256
Gholami, H., and Sun, H. (2023). Toward automated algorithm configuration for distributed hybrid flow shop scheduling with multiprocessor tasks. Knowledge-Based Syst. 264, 110309. doi:10.1016/j.knosys.2023.110309
Gu, W., Liu, S., Guo, Z., Yuan, M., and Pei, F. (2024). Dynamic scheduling mechanism for intelligent workshop with deep reinforcement learning method based on multi-agent system architecture. Comput. and Industrial Eng. 191, 110155. doi:10.1016/j.cie.2024.110155
Gui, Y., Zhang, Z., Tang, D., Zhu, H., and Zhang, Y. (2024). Collaborative dynamic scheduling in a self-organizing manufacturing system using multi-agent reinforcement learning. Adv. Eng. Inf. 62, 102646. doi:10.1016/j.aei.2024.102646
Guirchoun, S., Martineau, P., and Billaut, J.-C. (2005). Total completion time minimization in a computer system with a server and two parallel processors. Comput. and Operations Res. 32, 599–611. doi:10.1016/j.cor.2003.08.007
Gupta, J. K., Egorov, M., and Kochenderfer, M. (2017). “Cooperative multi-agent control using deep reinforcement learning,” in Autonomous Agents and Multiagent Systems: AAMAS 2017 Workshops, Best Papers, São Paulo, Brazil, May 8-12, 2017 (Springer), 66–83.
Heik, D., Bahrpeyma, F., and Reichelt, D. (2024). Study on the application of single-agent and multi-agent reinforcement learning to dynamic scheduling in manufacturing environments with growing complexity: case study on the synthesis of an industrial iot test bed. J. Manuf. Syst. 77, 525–557. doi:10.1016/j.jmsy.2024.09.019
Huo, S., and Wu, W. (2023). “Multi-objective FJSP based on multi-agent reinforcement learning algorithm,” in 2023 6th International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 22-24 September 2023 (IEEE), 341–343.
Jing, X., Yao, X., Liu, M., and Zhou, J. (2024). Multi-agent reinforcement learning based on graph convolutional network for flexible job shop scheduling. J. Intelligent Manuf. 35, 75–93. doi:10.1007/s10845-022-02037-5
Johnson, D., Chen, G., and Lu, Y. (2024). “Multi-agent scheduler for the continuous dynamic flexible job shop scheduling problem,” in 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Bari, Italy, 28 August 2024–01 September 2024 (IEEE), 2924–2930.
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996). Reinforcement learning: a survey. J. Artif. Intell. Res. 4, 237–285. doi:10.1613/jair.301
Kayhan, B. M., and Yildiz, G. (2023). Reinforcement learning applications to machine scheduling problems: a comprehensive literature review. J. Intelligent Manuf. 34, 905–929. doi:10.1007/s10845-021-01847-3
Kim, W., and Sung, Y. (2023). Parameter sharing with network pruning for scalable multi-agent deep reinforcement learning. arXiv preprint arXiv:2303.00912.
Kim, Y. G., Lee, S., Son, J., Bae, H., and Chung, B. D. (2020). Multi-agent system and reinforcement learning approach for distributed intelligence in a flexible smart manufacturing system. J. Manuf. Syst. 57, 440–450. doi:10.1016/j.jmsy.2020.11.004
Kodama, N., Harada, T., and Miyazaki, K. (2022). Traffic signal control system using deep reinforcement learning with emphasis on reinforcing successful experiences. IEEE Access 10, 128943–128950. doi:10.1109/access.2022.3225431
Lei, K., Guo, P., Zhao, W., Wang, Y., Qian, L., Meng, X., et al. (2022). A multi-action deep reinforcement learning framework for flexible job-shop scheduling problem. Expert Syst. Appl. 205, 117796. doi:10.1016/j.eswa.2022.117796
Li, B. (2022). “Hierarchical architecture for multi-agent reinforcement learning in intelligent game,” in 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18-23 July 2022 (IEEE), 1–8.
Li, Y., Wang, Q., Li, X., Gao, L., Fu, L., Yu, Y., et al. (2025). Real-time scheduling for flexible job shop with agvs using multiagent reinforcement learning and efficient action decoding. IEEE Trans. Syst. Man, Cybern. Syst. 55, 2120–2132. doi:10.1109/tsmc.2024.3520381
Liang, L., Sun, S., Hao, Z., and Yang, Y. (2025). Structural entropy-based scheduler for job planning problems using multi-agent reinforcement learning. Int. J. Mach. Learn. Cybern., 1–18. doi:10.1007/s13042-024-02504-w
Lin, C.-C., Peng, Y.-C., Chang, Y.-S., and Chang, C.-H. (2024). Reentrant hybrid flow shop scheduling with stockers in automated material handling systems using deep reinforcement learning. Comput. and Industrial Eng. 189, 109995. doi:10.1016/j.cie.2024.109995
Liu, R., Piplani, R., and Toro, C. (2022). Deep reinforcement learning for dynamic scheduling of a flexible job shop. Int. J. Prod. Res. 60, 4049–4069. doi:10.1080/00207543.2022.2058432
Liu, W.-B., and Wang, X.-J. (2009). Dynamic decision model in evolutionary games based on reinforcement learning. Syst. Engineering-Theory and Pract. 29, 28–33. doi:10.1016/s1874-8651(10)60008-7
Liu, Y., Fan, J., Zhao, L., Shen, W., and Zhang, C. (2023a). Integration of deep reinforcement learning and multi-agent system for dynamic scheduling of re-entrant hybrid flow shop considering worker fatigue and skill levels. Robotics Computer-Integrated Manuf. 84, 102605. doi:10.1016/j.rcim.2023.102605
Liu, Y., Shen, W., Zhang, C., and Sun, X. (2023b). Agent-based simulation and optimization of hybrid flow shop considering multi-skilled workers and fatigue factors. Robotics Computer-Integrated Manuf. 80, 102478. doi:10.1016/j.rcim.2022.102478
Long, P., Fan, T., Liao, X., Liu, W., Zhang, H., and Pan, J. (2018). “Towards optimally decentralized multi-robot collision avoidance via deep reinforcement learning,” in 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21-25 May 2018 (IEEE), 6252–6259.
Luo, S. (2020). Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning. Appl. Soft Comput. 91, 106208. doi:10.1016/j.asoc.2020.106208
Luo, S., Zhang, L., and Fan, Y. (2021a). Dynamic multi-objective scheduling for flexible job shop by deep reinforcement learning. Comput. and Industrial Eng. 159, 107489. doi:10.1016/j.cie.2021.107489
Luo, S., Zhang, L., and Fan, Y. (2022). Real-time scheduling for dynamic partial-no-wait multiobjective flexible job shop by deep reinforcement learning. IEEE Trans. Automation Sci. Eng. 19, 3020–3038. doi:10.1109/tase.2021.3104716
Lv, L., Fan, J., Zhang, C., and Shen, W. (2025). A multi-agent reinforcement learning based scheduling strategy for flexible job shops under machine breakdowns. Robotics Computer-Integrated Manuf. 93, 102923. doi:10.1016/j.rcim.2024.102923
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236
Natan, O., and Miura, J. (2023). End-to-end autonomous driving with semantic depth cloud mapping and multi-agent. IEEE Trans. Intelligent Veh. 8, 557–571. doi:10.1109/tiv.2022.3185303
Nguyen, T. T., Nguyen, N. D., and Nahavandi, S. (2020). Deep reinforcement learning for multiagent systems: a review of challenges, solutions, and applications. IEEE Trans. Cybern. 50, 3826–3839. doi:10.1109/tcyb.2020.2977374
Nowé, A., Vrancx, P., and De Hauwere, Y.-M. (2012). “Game theory and multi-agent reinforcement learning,” in Reinforcement learning: state-of-the-art (Springer), 441–470.
Oh, S. H., Cho, Y. I., and Woo, J. H. (2023). “Applying multi-agent reinforcement learning and graph neural networks to flexible job shop scheduling problem,” in IFIP International Conference on Advances in Production Management Systems (Springer), 506–519.
Oroojlooy, A., and Hajinezhad, D. (2023). A review of cooperative multi-agent deep reinforcement learning. Appl. Intell. 53, 13677–13722. doi:10.1007/s10489-022-04105-y
Ortiz, A., Weber, T., and Klein, A. (2021). Multi-agent reinforcement learning for energy harvesting two-hop communications with a partially observable system state. IEEE Trans. Green Commun. Netw. 5, 442–456. doi:10.1109/tgcn.2020.3026453
Peng, P., Wen, Y., Yang, Y., Yuan, Q., Tang, Z., Long, H., et al. (2017). Multiagent bidirectionally-coordinated nets: emergence of human-level coordination in learning to play starcraft combat games. arXiv preprint arXiv:1703.10069.
Peng, S., Xiong, G., Yang, J., Shen, Z., Tamir, T. S., Tao, Z., et al. (2023). Multi-agent reinforcement learning for extended flexible job shop scheduling. Machines 12 (8), 8. doi:10.3390/machines12010008
Pol, S., Baer, S., Turner, D., Samsonov, V., and Meisen, T. (2021). Global reward design for cooperative agents to achieve flexible production control under real-time constraints. Proc. 23rd Int. Conf. Enterp. Inf. Syst. 1, 515–526. doi:10.5220/0010455805150526
Popper, J., Motsch, W., David, A., Petzsche, T., and Ruskowski, M. (2021). “Utilizing multi-agent deep reinforcement learning for flexible job shop scheduling under sustainable viewpoints,” in 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, Mauritius, 07-08 October 2021 (IEEE), 1–6.
Popper, J., and Ruskowski, M. (2022). Using multi-agent deep reinforcement learning for flexible job shop scheduling problems. Procedia CIRP 112, 63–67. doi:10.1016/j.procir.2022.09.039
Pu, Y., Li, F., and Rahimifard, S. (2024). Multi-agent reinforcement learning for job shop scheduling in dynamic environments. Sustainability 16, 3234. doi:10.3390/su16083234
Qin, Z., Johnson, D., and Lu, Y. (2023). Dynamic production scheduling towards self-organizing mass personalization: a multi-agent dueling deep reinforcement learning approach. J. Manuf. Syst. 68, 242–257. doi:10.1016/j.jmsy.2023.03.003
Qin, Z., and Lu, Y. (2024). Knowledge graph-enhanced multi-agent reinforcement learning for adaptive scheduling in smart manufacturing. J. Intelligent Manuf., 1–24. doi:10.1007/s10845-024-02494-0
Ran, P., Jiang, B., Wang, S., Li, X., and Qin, L. (2024). “Dynamic hybrid flow shop scheduling in multi-agent manufacturing systems via federated transfer learning,” in 2024 43rd Chinese Control Conference (CCC) (IEEE), 6893–6898.
Rashid, T., Farquhar, G., Peng, B., and Whiteson, S. (2020). Weighted qmix: expanding monotonic value function factorisation for deep multi-agent reinforcement learning. Adv. neural Inf. Process. Syst. 33, 10199–10210. Available online at: https://proceedings.neurips.cc/paper_files/paper/2020/hash/73a427badebe0e32caa2e1fc7530b7f3-Abstract.html.
Rossi, A., and Dini, G. (2007). Flexible job-shop scheduling with routing flexibility and separable setup times using ant colony optimisation method. Robotics Computer-Integrated Manuf. 23, 503–516. doi:10.1016/j.rcim.2006.06.004
Ruiz, R., and Vázquez-Rodríguez, J. A. (2010). The hybrid flow shop scheduling problem. Eur. J. Operational Res. 205, 1–18. doi:10.1016/j.ejor.2009.09.024
Schwab, D., Zhu, Y., and Veloso, M. (2018). “Zero shot transfer learning for robot soccer,” in Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, 2070–2072.
Seo, M., Vecchietti, L. F., Lee, S., and Har, D. (2019). Rewards prediction-based credit assignment for reinforcement learning with sparse binary rewards. IEEE Access 7, 118776–118791. doi:10.1109/access.2019.2936863
Shen, L., Dauzère-Pérès, S., and Neufeld, J. S. (2018). Solving the flexible job shop scheduling problem with sequence-dependent setup times. Eur. J. Operational Res. 265, 503–516. doi:10.1016/j.ejor.2017.08.021
Son, K., Kim, D., Kang, W. J., Hostallero, D. E., and Yi, Y. (2019). “Qtran: learning to factorize with transformation for cooperative multi-agent reinforcement learning,” in International conference on machine learning (PMLR), Cambridge, MA, 5887–5896. Available online at: https://proceedings.mlr.press/v97/son19a.html.
Sukhbaatar, S., Szlam, A., and Fergus, R. (2016). Learning multiagent communication with backpropagation. Adv. Neural Inf. Process. Syst. 29. doi:10.48550/arXiv.1605.07736
Sunehag, P., Lever, G., Gruslys, A., Czarnecki, W. M., Zambaldi, V., Jaderberg, M., et al. (2017). Value-decomposition networks for cooperative multi-agent learning. arXiv preprint arXiv:1706.05296.
Tacken, A. M. L. (2021). “Msc thesis A multi-agent reinforcement learning approach for the hybrid flow shop problem,”. Ph.D. thesis (Tilburg University). Available online at: https://arno.uvt.nl/show.cgi?fid=157805.
Wang, H., Lin, W., Peng, T., Xiao, Q., and Tang, R. (2025a). Multi-agent deep reinforcement learning-based approach for dynamic flexible assembly job shop scheduling with uncertain processing and transport times. Expert Syst. Appl. 270, 126441. doi:10.1016/j.eswa.2025.126441
Wang, J., Ren, Z., Liu, T., Yu, Y., and Zhang, C. (2020). Qplex: Duplex dueling multi-agent q-learning. arXiv preprint arXiv:2008.01062.
Wang, M., Zhang, J., Zhang, P., Cui, L., and Zhang, G. (2022a). Independent double DQN-based multi-agent reinforcement learning approach for online two-stage hybrid flow shop scheduling with batch machines. J. Manuf. Syst. 65, 694–708. doi:10.1016/j.jmsy.2022.11.001
Wang, R., Jing, Y., Gu, C., He, S., and Chen, J. (2025). End-to-end multi-target flexible job shop scheduling with deep reinforcement learning. IEEE Internet Things J. 12, 4420–4434. doi:10.1109/jiot.2024.3485748
Wang, W., Wang, L., Wu, J., Tao, X., and Wu, H. (2022b). Oracle-guided deep reinforcement learning for large-scale multi-uavs flocking and navigation. IEEE Trans. Veh. Technol. 71, 10280–10292. doi:10.1109/tvt.2022.3184043
Wang, W., Zhang, Y., Wang, Y., Pan, G., and Feng, Y. (2025b). Hierarchical multi-agent deep reinforcement learning for dynamic flexible job-shop scheduling with transportation. Int. J. Prod. Res., 1–28. doi:10.1080/00207543.2025.2511239
Wang, X., Liang, Z., Zhong, P., Li, D., Li, H., and Liu, M. (2025c). Multi-objective scheduling for green flexible assembly job-shop system via multi-agent deep reinforcement learning with game theory. IEEE Access 13, 103417–103438. doi:10.1109/access.2025.3577044
Waseem, M., and Chang, Q. (2024). From nash q-learning to nash-MADDPG: advancements in multiagent control for multiproduct flexible manufacturing systems. J. Manuf. Syst. 74, 129–140. doi:10.1016/j.jmsy.2024.03.004
Xu, L., Huang, Y.-C., Xue, Y., and Hu, X. (2023). Hierarchical reinforcement learning in multi-domain elastic optical networks to realize joint RMSA. J. Light. Technol. 41, 2276–2288. doi:10.1109/jlt.2023.3235039
Xu, Y., Yu, J., and Buehrer, R. M. (2020). The application of deep reinforcement learning to distributed spectrum access in dynamic heterogeneous environments with partial observations. IEEE Trans. Wirel. Commun. 19, 4494–4506. doi:10.1109/twc.2020.2984227
Yan, Y., Yi, W., Pei, Z., and Chen, Y. (2025). Multi-agent reinforcement learning for distributed flexible job shop scheduling with random job arrival. IEEE Access 13, 80941–80957. doi:10.1109/access.2025.3564433
Yang, N., Ding, B., Shi, P., and Feng, D. (2022). “Improving scalability of multi-agent reinforcement learning with parameters sharing,” in 2022 IEEE International Conference on Joint Cloud Computing (JCC), Fremont, CA, USA, 15-18 August 2022 (IEEE), 37–42.
Yang, Y., Hao, J., Liao, B., Shao, K., Chen, G., Liu, W., et al. (2020). Qatten: a general framework for cooperative multiagent reinforcement learning. arXiv preprint arXiv:2002.03939.
Yin, C., Yang, R., Zhu, W., Qiu, X., and Li, F. (2020). A survey on multi-agent hierarchical reinforcement learning. CAAI Trans. Intell. Syst. 15, 646–655. Available online at: https://tis.hrbeu.edu.cn/EN/oa/darticle.aspx?type=viewi&id=201909027.
Yuan, M., Huang, H., Li, Z., Zhang, C., Pei, F., and Gu, W. (2023). A multi-agent double deep-q-network based on state machine and event stream for flexible job shop scheduling problem. Adv. Eng. Inf. 58, 102230. doi:10.1016/j.aei.2023.102230
Zhang, F., Mei, Y., Nguyen, S., and Zhang, M. (2021). Evolving scheduling heuristics via genetic programming with feature selection in dynamic flexible job-shop scheduling. IEEE Trans. Cybern. 51, 1797–1811. doi:10.1109/tcyb.2020.3024849
Zhang, J.-D., He, Z., Chan, W.-H., and Chow, C.-Y. (2023a). DeepMAG: deep reinforcement learning with multi-agent graphs for flexible job shop scheduling. Knowledge-Based Syst. 259, 110083. doi:10.1016/j.knosys.2022.110083
Zhang, K., Yang, Z., and Başar, T. (2021). “Multi-agent reinforcement learning: a selective overview of theories and algorithms,” in Handbook of reinforcement learning and control, 321–384.
Zhang, L., Yan, Y., and Hu, Y. (2024a). Dynamic flexible scheduling with transportation constraints by multi-agent reinforcement learning. Eng. Appl. Artif. Intell. 134, 108699. doi:10.1016/j.engappai.2024.108699
Zhang, L., Yan, Y., Yang, C., and Hu, Y. (2024b). Dynamic flexible job-shop scheduling by multi-agent reinforcement learning with reward-shaping. Adv. Eng. Inf. 62, 102872. doi:10.1016/j.aei.2024.102872
Zhang, N., Shen, Y., Du, Y., Chen, L., and Zhang, X. (2023b). Counterfactual-attention multi-agent reinforcement learning for joint condition-based maintenance and production scheduling. J. Manuf. Syst. 71, 70–81. doi:10.1016/j.jmsy.2023.08.011
Zhang, Z., Yang, J., and Zha, H. (2019). Integrating independent and centralized multi-agent reinforcement learning for traffic signal network optimization. arXiv preprint arXiv:1909.10651.
Zheng, J., Zhao, Y., Li, Y., Li, J., Wang, L., and Yuan, D. (2025). Dynamic flexible flow shop scheduling via cross-attention networks and multi-agent reinforcement learning. J. Manuf. Syst. 80, 395–411. doi:10.1016/j.jmsy.2025.03.005
Keywords: flexible shop scheduling problem, flexible job-shop scheduling problem, hybrid flow-shop scheduling problem, multi-agent reinforcement learning, reinforcement learning
Citation: Xu W, Gu J, Zhang W, Gen M and Ohwada H (2025) Multi-agent reinforcement learning for flexible shop scheduling problem: a survey. Front. Ind. Eng. 3:1611512. doi: 10.3389/fieng.2025.1611512
Received: 14 April 2025; Accepted: 14 July 2025;
Published: 31 July 2025.
Edited by:
Dimitrios Bechtsis, International Hellenic University, GreeceReviewed by:
Juan Carlos Seck Tuoh Mora, Autonomous University of the State of Hidalgo, MexicoLixiang Zhang, Beijing Institute of Technology, China
Copyright © 2025 Xu, Gu, Zhang, Gen and Ohwada. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenqiang Zhang, emhhbmd3cUBoYXV0LmVkdS5jbg==
 Weitao Xu1
Weitao Xu1 Jinghan Gu
Jinghan Gu Wenqiang Zhang
Wenqiang Zhang Mitsuo Gen
Mitsuo Gen