- 1Faculty of Science, Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, Netherlands
- 2Bacterial Cell Biology, Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, Netherlands
According to the recently-revived adder model for cell size control, newborn cells of Escherichia coli will grow and divide after having added a constant size or length, ΔL, irrespective of their size at birth. Assuming exponential elongation, this implies that large newborns will divide earlier than small ones. The molecular basis for the constant size increment is still unknown. As DNA replication and cell growth are coordinated, the constant ΔL could be based on duplication of an equal amount of DNA, ΔG, present in newborn cells. To test this idea, we measured amounts of DNA and lengths of nucleoids in DAPI-stained cells growing in batch culture at slow and fast rates. Deeply-constricted cells were divided in two subpopulations of longer and shorter lengths than average; these were considered to represent large and small prospective daughter cells, respectively. While at slow growth, large and small prospective daughter cells contained similar amounts of DNA, fast growing cells with multiforked replicating chromosomes, showed a significantly higher amount of DNA (20%) in the larger cells. This observation precludes the hypothesis that ΔL is based on the synthesis of a constant ΔG. Growth curves were constructed for siblings generated by asymmetric division and growing according to the adder model. Under the assumption that all cells at the same growth rate exhibit the same time between initiation of DNA replication and cell division (i.e., constant C+D-period), the constructions predict that initiation occurs at different sizes (Li) and that, at fast growth, large newborn cells transiently contain more DNA than small newborns, in accordance with the observations. Because the state of segregation, measured as the distance between separated nucleoids, was found to be more advanced in larger deeply-constricted cells, we propose that in larger newborns nucleoid separation occurs faster and at a shorter length, allowing them to divide earlier. We propose a composite model in which both differential initiation and segregation leads to an adder-like behavior of large and small newborn cells.
Introduction
The early ideas of Koppes et al. (1978a,b) and Voorn et al. (1993) that Escherichia coli cells grow by adding a constant length between divisions, were based on measurements of cell lengths and the rate of DNA replication in pulse-labeled cells grown in batch culture and prepared for electron microscopic autoradiography. This view has recently been revived in several studies (Amir, 2014; Campos et al., 2014; Jun and Taheri-Araghi, 2014); in the new experiments on cell size homeostasis (Campos et al., 2014; Taheri-Araghi et al., 2015; Wallden et al., 2016), the bacteria are grown in microfluidic chambers and observed by fluorescence light microscopy.
Whereas Koppes et al. (1978a,b) were able to measure only the length increment between initiation of DNA replication and the start of cell constriction, the extensive measurements of Jun and co-workers on large numbers of individual E. coli cells growing in a microfluidic “mother machine” (Wang et al., 2010) under a wide range of growth conditions covered the entire cell cycle (Taheri-Araghi et al., 2015). They confirm that at the population level, average cell size depends on growth rate exponentially (Schaechter et al., 1958); more importantly, they also show at the single cell level, that all cells in a particular growth medium grow in size at the same exponential rate and increase in size by the same amount (ΔL) between birth and division irrespective of their newborn size. Consequently, a large newborn cell will synthesize ΔL faster and will divide at a slightly earlier age than a small newborn cell, thus contributing to homeostasis (Figure 3 in Taheri-Araghi et al., 2015).
In several recent studies it has been discussed that the chromosome could play a role in establishing the constant size increment inherent to the adder model (Campos et al., 2014; Robert, 2015). Such constancy could be based on the chromosome serving as a “measuring stick” if newborn cells contain the same amount of DNA independent of their size at birth. For signaling cell division after duplicating this amount of DNA, a tight relation would have to exist between nucleoid replication/segregation and the peptidoglycan synthesizing machinery for cell division (Woldringh et al., 1991; Typas et al., 2012). This could be established via the so-called transertion process that involves transcription–translation and translocation of membrane proteins (Norris, 1995; Woldringh, 2002; Rabinovitch et al., 2003) and has been proposed to interfere with the assembly of the FtsZ-ring through nucleoid occlusion (Woldringh et al., 1991; Wu and Errington, 2012).
To detect whether newborn cells indeed contain equal amounts of DNA irrespective of their birth size, we have measured the DNA in nucleoids of large and small prospective daughter cells that can be assumed to give rise to large and small newborn cells. Cells were obtained from populations grown in batch cultures under steady state conditions at two different growth rates. As to be expected, only a small difference in DNA content (6%) was observed in newborn cells at slow growth. However, at fast growth and in the presence of multifork replication, large and small prospective daughter cells contained significantly different amounts of DNA (20%). This observation makes it unlikely that newborn cells base their constant length increment, ΔL, on the synthesis of equal amounts of DNA.
Graphical constructions of the adder cell cycle were made under the assumption that large and small newborn cells, generated by asymmetric division, have the same C+D-period. The constructions of length growth and genome content of single cells show that at fast growth large newborn cells exhibit a transient increase in the amount of DNA compared to small newborns, in agreement with the measurements. This lends support to the assumption that all individual newborns in a population have the same C+D-period and that large and small newborn cells initiate DNA replication at different sizes. Moreover, the advanced state of segregation, measured as the distance between separated nucleoids, found in the larger deeply-constricted cells, allows for differential segregation and earlier division in the larger cells, as required by the adder model and for obtaining homeostasis.
Materials and Methods
Cells and Growth Medium
Escherichia coli strain PJ4271 (strain MC1000 transformed with pBR322) was grown at 37°C in MOPS-buffered minimal medium (Neidhardt et al., 1974) with 100 mg/ml ampicillin according to Jensen et al. (1999), except that NaCl was added (about 27 ml of 2 M NaCl to 500 ml of MOPS-medium) to increase the osmolality to 300 mOsm. For slow growth the medium was supplemented with succinate (4 g per l), giving a doubling time Td of 122 min. For rapid growth glucose (5 g per l) and 20 amino acids (at millimolar concentrations according to Neidhardt et al., 1974) were added, giving a Td of 29 min. Exponentially growing cultures with constant OD450/cell (determined with a Coulter counter) were grown to OD450 of 0.1 to 0.2 and processed for microscopy (cf. Stuger et al., 2002).
Fluorescence Microscopy and Image Analysis
DNA was labeled by addition of DAPI (4′,6-diamino-2-phenylindole dihydrochloride, Molecular Probes) at a final concentration of 0.05 mg/ml to cells fixed with OsO4 (0.1% w/v). After at least 15 min the cells were concentrated by centrifugation (1 min at 13000 rpm) and attached to microscopy slides coated with a thin layer of 1% agarose in culture medium. Pictures were taken with an Olympus BX60 fluorescence microscope equipped with a 100W mercury lamp and a Princeton RTE 1317-k-1 cooled CCD-camera. To limit photobleaching and DNA damage by ultraviolet light we focused the cells in phase contrast mode before photography. In this way all cells were exposed to the same (limited) amount of UV light.
DNA content per cell (expressed in chromosome equivalents) was measured after mixing the fixed E. coli PJ4271 cells with fixed E. coli pbpA(Ts) cells that contain one, or two fully replicated chromosomes when grown into stationary phase at the permissive temperature (30°C) for at least 48 h (Vischer et al., 1999) and after staining the mixture with DAPI. The pbpA mutant cells used for calibration could be distinguished from the PJ4271 cells because of their larger diameter and spherical shape. Cells were measured using the program “Coli-Inspector”1. This is a specialized software package developed for the analysis of shape and fluorescence related properties of bacterial cells. The program runs in combination with ImageJ with plug-in ObjectJ (see Figure 1 in Vischer et al., 2015). Amounts of DNA were calculated by assuming that the value of integrated fluorescence per cell of the left peak of the DNA distribution of pbpA cells equals 1 chromosome equivalent (Supplementary Figures S1A,B; cf. Huls et al., 1999).
To calculate integrated fluorescence (see Vischer et al., 1999), the modal value of the entire image was considered as background and was subtracted before subsequent image analysis.
Determination of C and C+D-Periods
For the construction of the cell cycles at the two growth rates (succinate with Td = 122 min and glucose plus amino acids with Td = 29 min), the C- and D-periods have to be known. These were determined by image-cytometric measurement of the amount of DNA per cell during run-off DNA synthesis after inhibiting initiations with 300 μg/ml rifampicin, as previously described (see Figure 3 in Huls et al., 1999). In similar experiments the accumulation of DNA per cell (and per nucleoid) reached a plateau value after about 70 or 53 min in succinate or glucose plus amino acids medium, respectively. With these population values of the C-periods, the D-periods were subsequently calculated from the values of average chromosome equivalents per cell Gc, using the expression Gc = {Td/C.ln2}{2(C+D)/Td-2D/Td} (Cooper and Helmstetter, 1968; Bremer and Churchward, 1977). It should be emphasized that this formula is only applicable to cell populations in steady-state growth. In our experiments this was verified by a constancy of average cell mass (OD450/cell counts) during the 5 h preceding cell sampling.
From the experimental values for Gc of 1.5 and 3.7 chromosome equivalents per cell in the slowly (Td = 122 min) and rapidly (Td = 29 min) growing populations, the D-periods were calculated to be 40 and 25 min (cf. Figures 2B,D below). The values are comparable with those reported by Huls et al. (1999); note that the growth temperature in those experiments was 28°C, whereas it is 37°C in the present study. Variations in the values for C- and D-periods have also been reported for E. coli K-12 strains grown at 30°C (Michelsen et al., 2003).
Results
Measurement of DAPI-Stained Nucleoids in Prospective Daughter Cells
To determine the amount of DNA in large and small prospective daughter cells, we stained fixed cells with DAPI and measured the fluorescence of the nucleoids and the size of the cells in fast- and slow-growing populations. From the subpopulations of constricting cells we sampled the deeply-constricted cells, defined as those having a diameter at the constriction site that is smaller than the mean constriction diameter (Table 1, column 9). These deeply-constricted cells that were just about to divide, were assumed to represent prospective newborn cells (see Grover and Woldringh, 2001, for a similar analysis). Although the average length of the deeply-constricted cells with respect to all constricting cells had slightly increased (by 1–4%; see Table 1, compare columns 7 and 10), they largely covered the range of all constricting cells (Supplementary Figure S2), indicating a limited elongation during the constriction process.
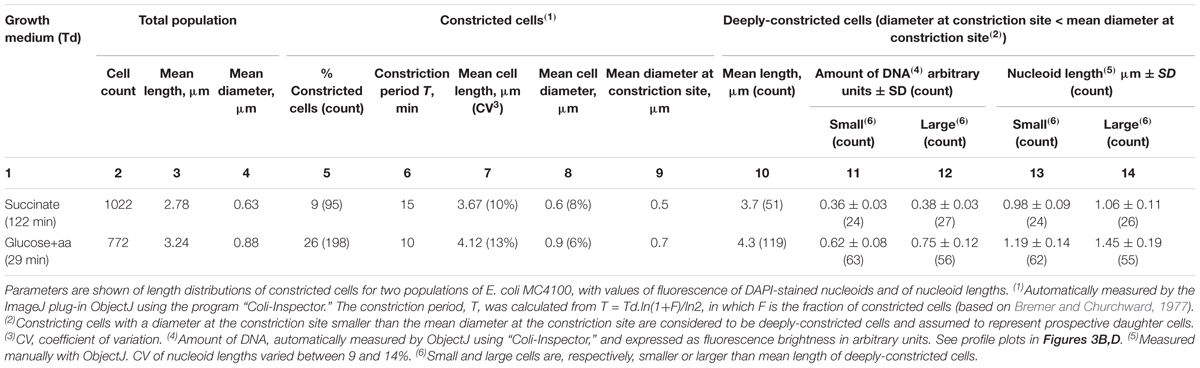
TABLE 1. Properties of small and large newborn cells as estimated from deeply-constricted cells assumed to represent prospective daughter cells.
Figures 1A,B show examples of deeply-constricted cells with their nucleoids from slow (Td = 122 min) and fast (Td = 29 min) growing cultures. The separated nucleoids can be seen to have a more extended shape in the longer constricted cells (right panels). As will be discussed below the distances between the segregated daughter nucleoids are larger in these cells.
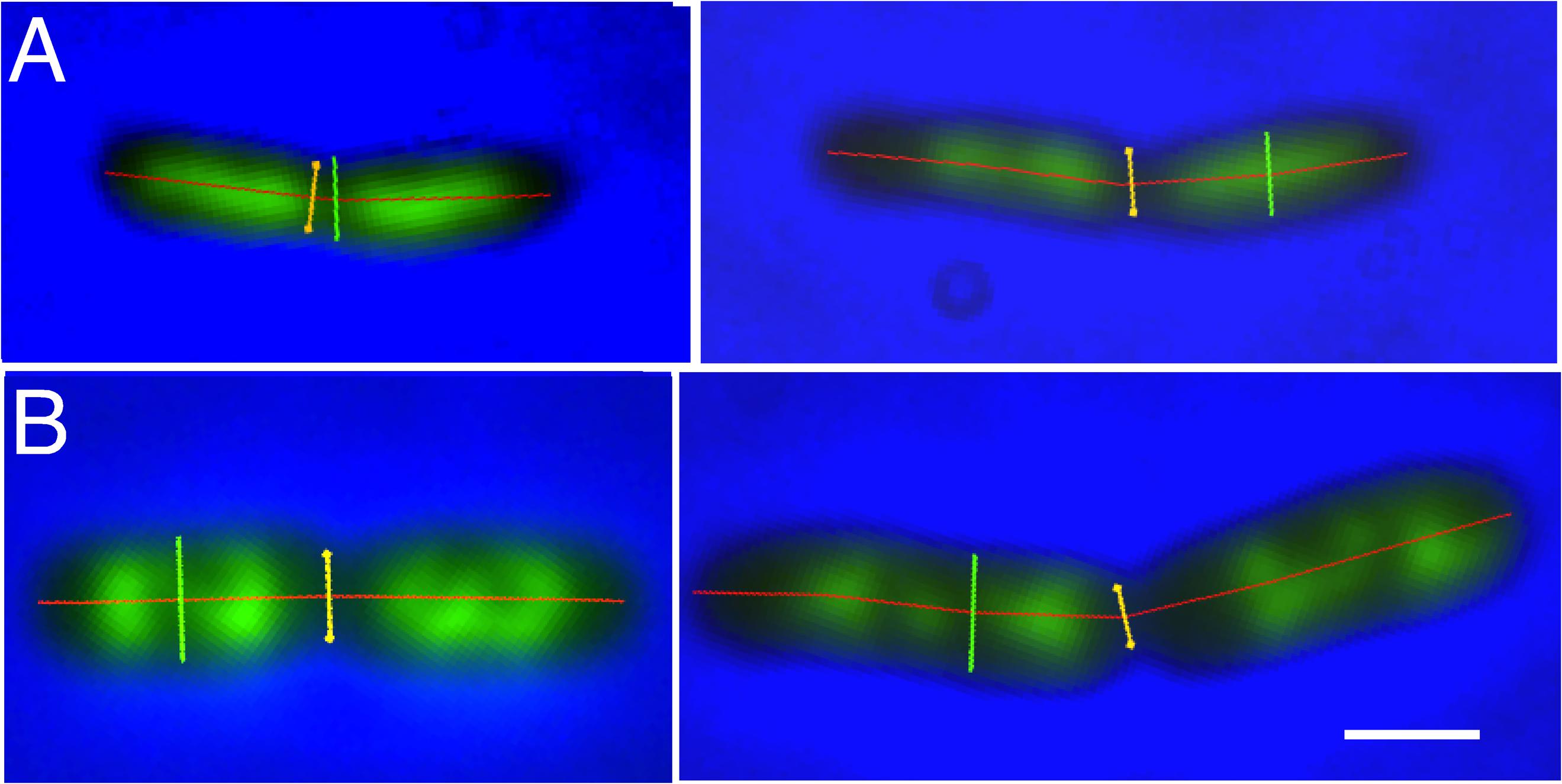
FIGURE 1. Examples of deeply-constricted Escherichia coli MC1000 cells, fixed with osmium tetroxide and stained with DAPI. Fluorescence images are overlaid with phase-contrast images and with markers, transiently displayed upon the images, for cell length (red), cell diameter (green) and the diameter at the constriction site (yellow), as measured by “Coli-Inspector” with ImageJ plugin ObjectJ. (A) Slow growing cells in succinate medium (Td = 122 min). Left and right panel, cell shorter and longer than 3.7 μm, respectively. (B) Fast growing cells in glucose plus amino acids medium (Td = 29 min). Left and right panel, cell shorter and longer than 4.3 μm, respectively. See mean lengths in Table 1, column 10. DAPI fluorescence is seen in green. Scale bar equals 1 μm.
In Figures 2A,C, the cell boundaries (magenta) and DNA fluorescence (green) of all individual cells in the two populations are arranged in so-called maps of cell profiles according to length, using the ImageJ plugin ObjectJ with software “Coli-Inspector” (see section “Materials and Methods”). In Figures 2B,D, histograms of all cells and of constricting cells (gray and red distributions, respectively) are shown together with a plot of the amount of DNA per cell (in chromosome equivalents) as a function of cell length. The plots indicate that in slow-growing cells (Figure 2B), DNA synthesis starts after a short B-period and slows down at the end, indicative of termination and a D-period. Because of overlapping DNA replication cycles (multifork replication) in the fast growing cells, such decreases in the rate of DNA synthesis are absent in Figure 2D.
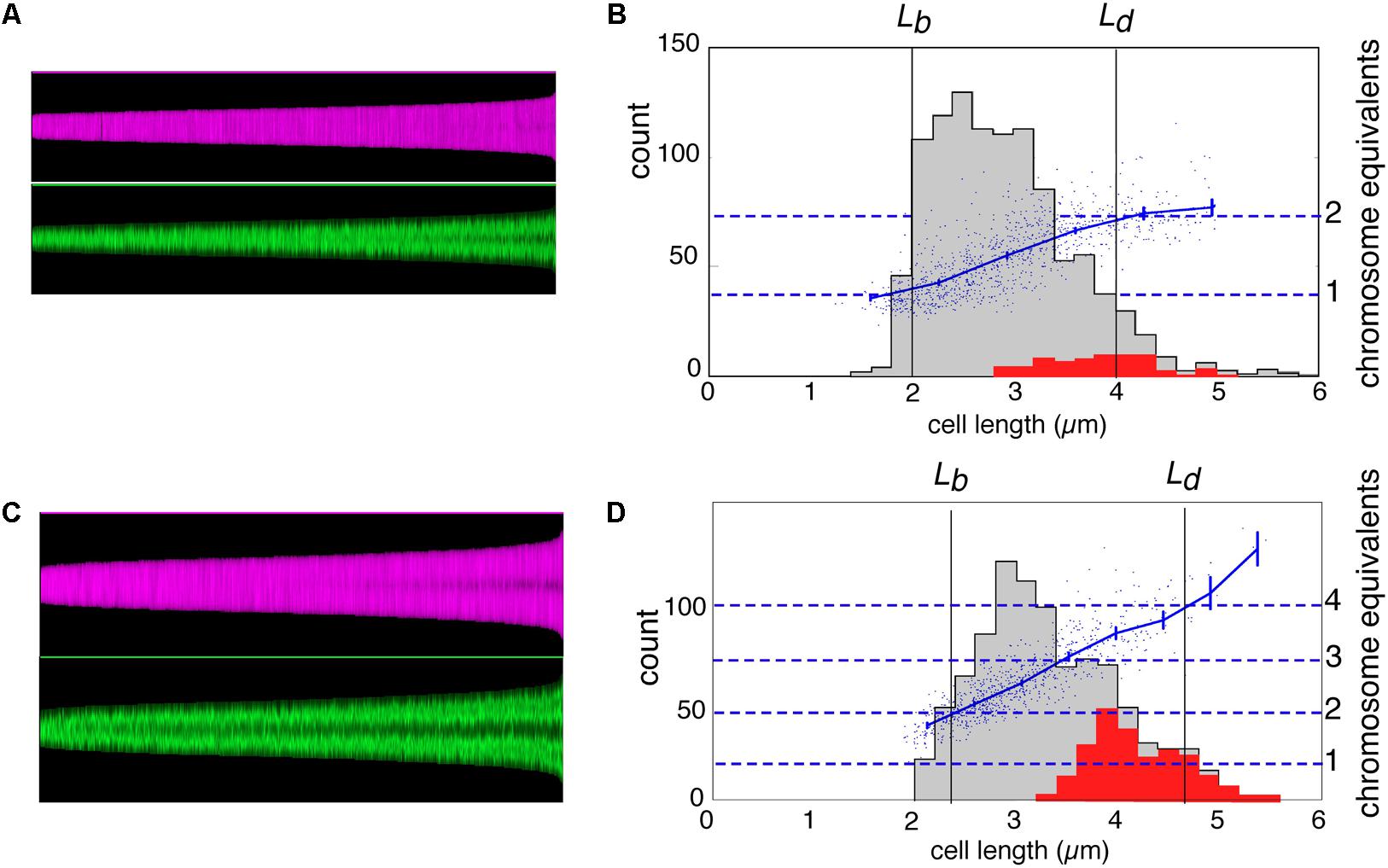
FIGURE 2. Maps of cell profiles and distributions of cell lengths. (A,C) Map of cell profiles, sorted according to ascending cell length. Each cell is visualized as a 1-pixel-wide column with a height corresponding to the cell length (in pixels) and showing local diameter (magenta) or the local fluorescence (green). The profile map visualizes the development of the constriction before cell division (magenta band becomes darker in the center due to the smaller diameter at the constriction site) and the change in fluorescence distribution of the (segregating) nucleoids along the cell length (green) (see Vischer et al., 2015). (B,D) Distribution of cell length of the total population (gray) and of constricting cells (red) with the lengths of newborn (Lb) and dividing cells (Ld) indicated. Lb was calculated from Lb = < L > /2ln2, in which < L > is the mean length of all cells, under the assumption of exponential elongation. In addition, the total DAPI-fluorescence per cell is shown by a scatter plot, with a line through the averages of binned data with vertical 95% confidence error bars in blue (in chromosome equivalents, right-hand ordinate). (A,B) Slow growing cells in succinate medium (Td = 122 min). (C,D) Fast growing cells in glucose plus amino acids medium (Td = 29 min).
The maps of DNA profiles in Figures 2A,C illustrate the gradual elongation of both cells (magenta) and nucleoids (green). At fast growth a second segregation event can be seen to occur in the largest deeply-constricted cells (Figures 3C,D, right panels), indicative of re-initiation of DNA replication (see below).
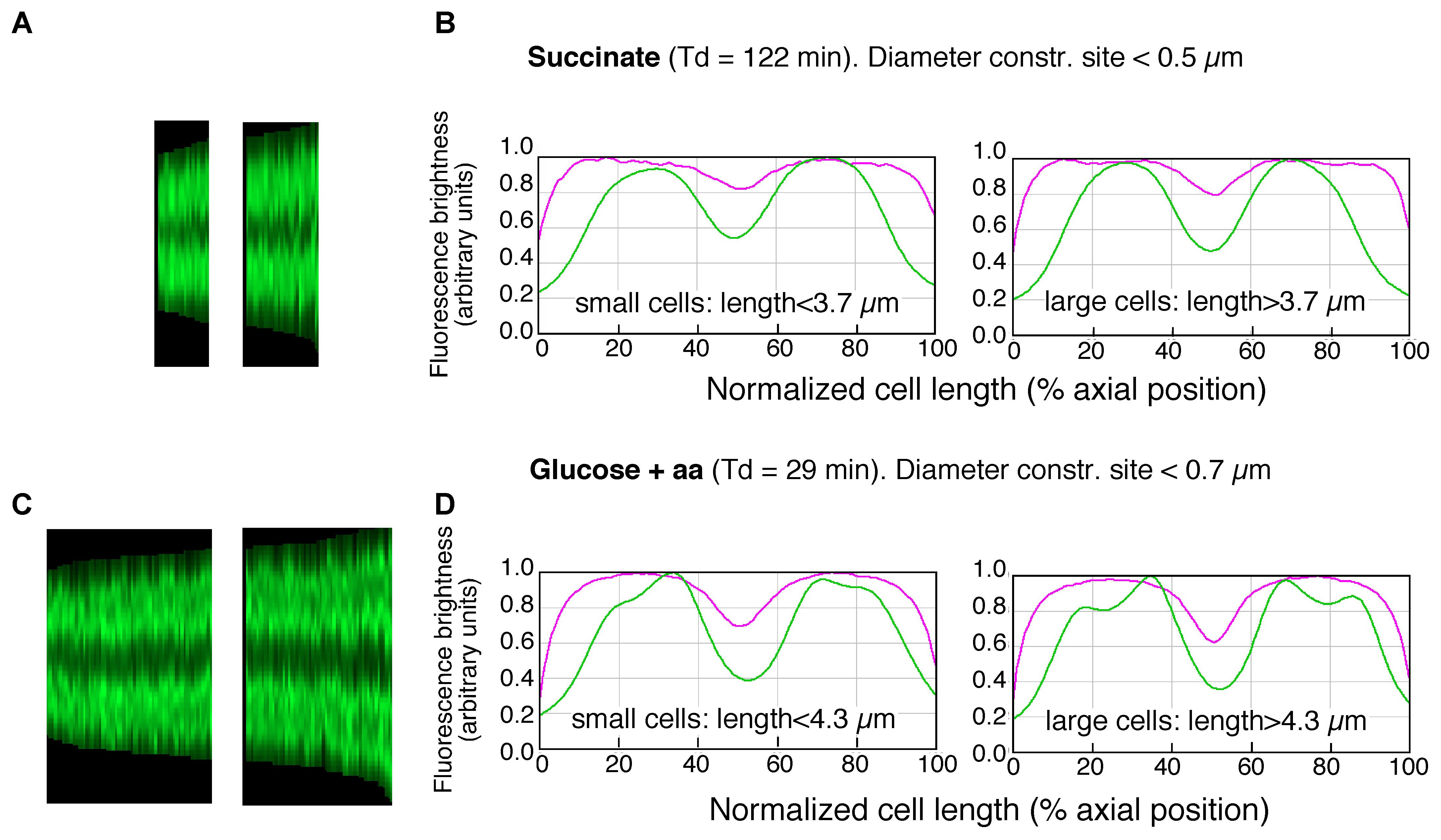
FIGURE 3. Maps of profiles and collective plots. (A,C) Maps of profiles of DAPI-fluorescence (cf. lower panels in Figures 2A,C) of deeply-constricted cells in slow (A) and fast (C) growing populations; subpopulations of small and large deeply-constricted cells are shown in left and right panels, respectively. (B,D) Collective profiles created from all cell profiles in the maps (A,C) by resampling to a normalized cell length of 100 data points and averaging to a single plot. Mean diameter- (magenta) and DAPI-fluorescence (green) are plotted in arbitrary units of brightness as a function of normalized cell length for slow (B) and fast (D) growing cells; subpopulations of small and large deeply-constricted cells are shown in left and right panels, respectively.
To determine the amount of DNA in large and small newborn cells, we measured the integrated fluorescence per nucleoid and the cellular positions and lengths of the nucleoids for cells smaller and larger than the mean length of deeply-constricted cells, all of which contained two separated daughter nucleoids. The results are presented in Figure 3 and Table 1. Because the nucleoids in the fast growing cells show rather irregular, lobular shapes characteristic of multifork replication (cf. Figure 1B), we also measured from the same cell populations nucleoid lengths manually (Table 1, columns 13 and 14).
Both the integrated fluorescence intensities, which represent the amount of DNA per nucleoid (Figures 3B,D and Table 1, columns 11 and 12), and the measurements of nucleoid lengths (Table 1, columns 13 and 14) indicate that the difference in DNA between small and large deeply-constricted cells at the fast growth rate is highly significant (p < 10-8, as determined by a two-tail t-test); at the slow growth rate, the difference remains significant, but just barely (p = 0.035). These differences are difficult to reconcile with a fixed amount of DNA (ΔG) serving as a constant in both large and small newborn cells, on which the constant length increment (ΔL) of the adder model could be based.
The State of Nucleoid Segregation
The measurements of the amount of DNA in small and large constricting cells also give information on the state of segregation in deeply constricted cells, defined as the distance between their segregated nucleoids. The distances between nucleoids in deeply-constricted cells have been measured manually (Table 2, columns 4 and 5). Nucleoid separation was evaluated by eye for each individual cell. If some DAPI fluorescence could still be seen between nucleoids (usually after contrast enhancement) they were considered not to have segregated. In addition, distances between the centers of mass of segregated nucleoids have been calculated from the DNA profile plots as shown in Figures 3B,D (Table 2, columns 6 and 7).

TABLE 2. Distances between segregated nucleoids in deeply-constricted cells from slow and fast growing populations of E. coli MC1000.
The results in Table 2 (columns 4 and 5) indicate that the difference between the distances measured manually in the large and those in the small deeply-constricted cells at the fast growth rate, is very highly significant (p < 10-8). At the slow growth rate, the difference is still statistically significant but much less so (p = 0.0006). The same holds for the differences between the centers of mass (Table 2, columns 6 and 7) calculated from the profile plots for slow (p < 10-6) and fast growth (p < 10-20).
The present experimental set-up cannot provide information about the segregation-period of individual cells, S (the time during which two separated nucleoids exist or, in other words, the time between visible separation of daughter nucleoids and cell division). We can, however, determine the average S-period, on a population level, from the percentage of cells containing two nucleoids (Table 2, column 2, just as the duration of constriction, T, was calculated from the percentage of constricting cells (Table 1, column 6). Whether large and small newborn cells exhibit the same S- and T-periods can only be estimated from time-lapse studies (e.g., Wallden et al., 2016). In the Discussion we will argue that the more advanced state of segregation at the end of the cell cycle of large, deeply-constricted cells could result from the larger space available to the nucleoids when being pushed apart in the long cell axis by the invaginating envelope during the constriction process (Supplementary Figure S3).
Generation of Large and Small Newborn Cells
Different newborn cell sizes can be assumed to originate either from stochastically postponed or premature symmetric divisions, or from asymmetric cell divisions. We do not know what their relative contributions are to the length distributions in the present populations. However, the coefficients of variation of the so-called K(L) distributions (length of prospective daughter cell/length constricting cell; Trueba, 1982), indicative of the degree of asymmetry, were found to be 9.5 and 4.9% for the succinate and glucose+amino acids populations, respectively. This suggests that asymmetric divisions do contribute to the subpopulations of large and small prospective daughter cells that we consider here.
Siblings generated by asymmetric division will have the same DNA content (G) present in a larger or smaller cell volume (see shaded insert in Figures 4A,B). To understand their behavior in subsequent cell cycles, we constructed for slow and fast growing cells their growth curves assuming exponential elongation. Consequently, after adding a constant length (gray upward arrows, ΔL, in Figure 4), the large newborns divide at a younger age than the small newborns, thus decreasing the difference in the size at division and leading to homeostasis (Taheri-Araghi et al., 2015). In the graphs of the cell cycles of single slow and fast growing newborn cells, we also depict the time of initiation of DNA replication by subtracting the C+D-period from the time of division under the assumption that all newborn cells have the same C+D-period. The graphs show that the size differences at birth induced by the asymmetric division, become less at division, reaching steady state after about four cycles (Figure 4B), as predicted by the adder model (cf. Figure 3 in Taheri-Araghi et al., 2015). The adder principle and the constant C+D-period cause initiations to occur at different lengths (Li, open red circles in Figure 4). These differences also return to the steady state of initiation length Li after about four cycles.
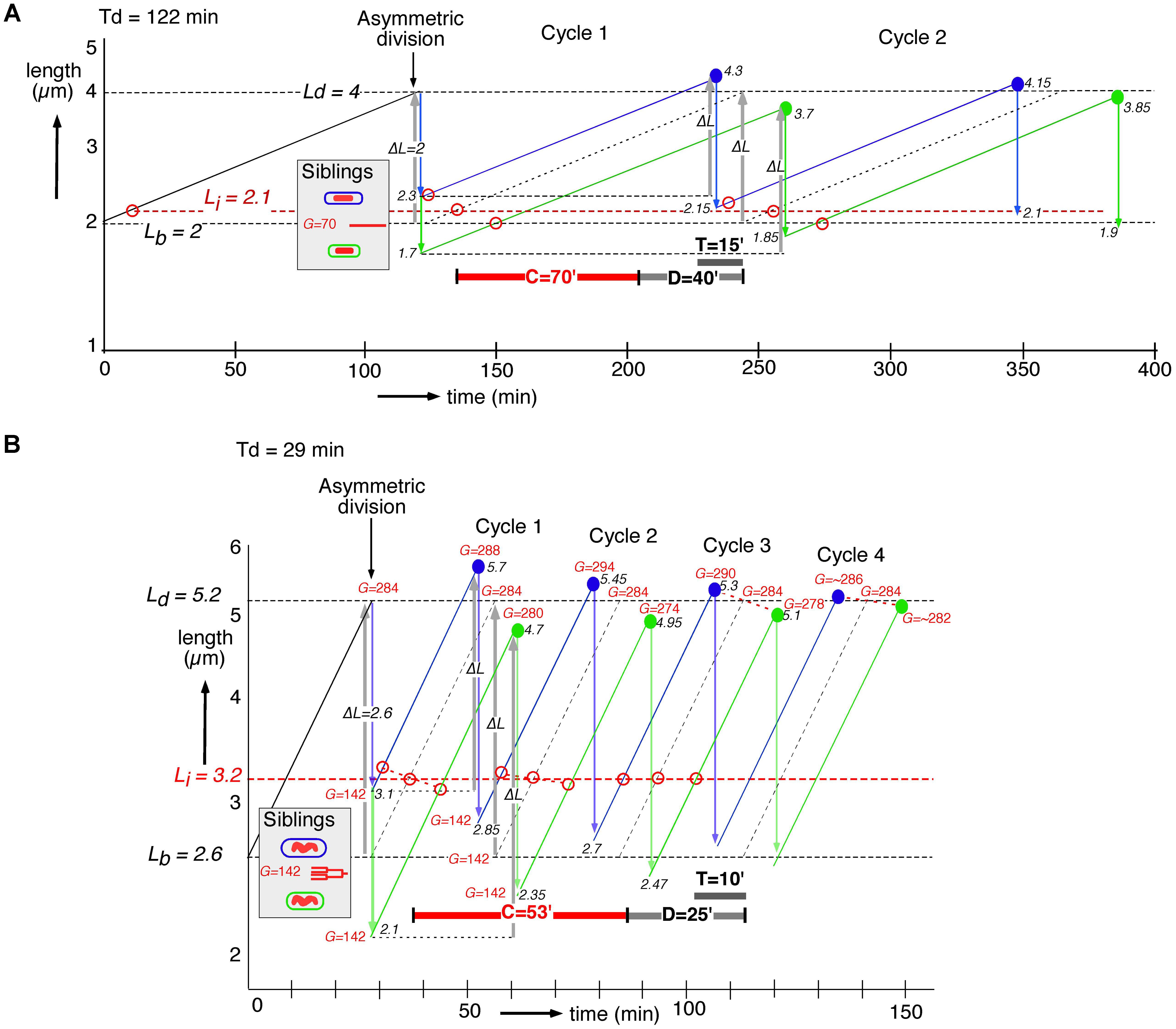
FIGURE 4. Construction of length growth curves of large (blue lines) and small (green lines) siblings, generated by asymmetric division. Cells elongate exponentially (elongation rate proportional to length); note log scale of the ordinate. Cell lengths can be considered to represent cell volumes if cell diameter is assumed to remain constant during the cell cycle. The graphs are inspired by, but different from Figure 6 in Koppes et al. (1978b), where the constant length increment was assumed to occur between initiation of DNA replication and initiation of constriction. Average lengths at birth (Lb) and division (Ld) are indicated by dashed horizontal black lines. The first division of an average cell is assumed to occur asymmetrically producing a large (Lb + 1 SD) and a small (Lb – 1 SD) newborn cell. Each newborn cell is constrained to add a fixed length, ΔL (gray upward arrows) before division. Lengths at division for large and small newborn cells are indicated by solid blue and green circles, respectively; their subsequent symmetrical divisions are indicated by blue and green downward arrows. Black numbers refer to cell lengths L (μm) at division or birth. The time of initiation of DNA replication (open red circles) is determined by subtracting the C+D-period from the time of division dictated by the adder model. The original length at initiation (Li) is indicated by a dashed horizontal red line. Red numbers refer to genome content, G, expressed in minutes; division by C = 70 or 53 min gives G in genome equivalents. (A) An individual cell from a slow growing succinate population (Td = 122 min) with a length at birth of Lb = 2 μm, equal to the average length of newborn cells (CV = 15%), dividing after a size increment of ΔL = 2 μm. (B) Similar construction of an individual cell growing in glucose plus amino acids medium (Td = 29 min) with a length at birth Lb = 2.6 (CV = 15%) and a size increment of ΔL = 2.6 μm.
In the slow growing population with C+D = 110 min (Figure 4A), both large and small newborn cells can be seen to exhibit a short B-period and a relatively long D-period (cf. Figure 2B). In the fast growing population with C+D = 78 min (Figure 4B), large newborn cells will initiate very early in their cycle. This means that some newborn cells could have already initiated prior to their birth (i.e., in the previous generation), in accordance with the observation of a second segregation event in Figures 3C,D (right panels) and with the theoretical predictions of Taheri-Araghi (2015).
The average values of C and D measured for the two populations (see section “Materials and Methods”) were used to calculate the genome contents (G) of the dividing cells indicated in Figure 4B. It can be seen that after asymmetric division siblings with identical chromosomes and the same multifork chromosome structure, acquire different genome contents at their subsequent divisions (during about three cycles). It follows that the adder model together with the assumed constant C+D-period predict a transient increase of the amount of DNA in the progeny of large newborn cells (see red G-numbers in Figure 4), in qualitative agreement with the present observations (Table 1). The same behavior is obtained when constructing the cycles of large and small newborn cells after stochastically premature or postponed divisions, for instance, due to variations in the C+D-period.
Discussion
According to the adder model (Amir, 2014; Campos et al., 2014; Osella et al., 2014; Taheri-Araghi et al., 2015), individual cells sense neither time nor absolute size but “measure” a fixed increase in length between divisions. The differences in size at division predicted by the three models, sizer, timer, and adder are rather small (Figure 5 in Zaritsky and Woldringh, 2015), but the observed positive correlation between sizes at division and at birth falsifies the sizer model, while the timer model is falsified by the negative correlation between generation time and size at birth (Figure 1D in Taheri-Araghi et al., 2015).
The adder mechanism requires that an individual cell monitor a property that is equal in all newborn cells. A constant total number of proteins per cell in different newborns and growth conditions were proposed to trigger cell division after reaching a threshold in each generation (Taheri-Araghi et al., 2015; Sauls et al., 2016). Alternatively, the absolute constant amount of DNA per nucleoid could serve as the signal. If equal in all newborn cells, the duplicating nucleoid could function as a “molecular ruler” to monitor a constant size increment (Campos et al., 2014; Zaritsky, 2015; Zaritsky and Woldringh, 2015). The present results, however, have shown that large newborn cells in a fast growing population, contain significantly more DNA (20%; Table 1) than small newborns, precluding the possibility that the adder model is based on duplication of a fixed amount of DNA in all newborn cells.
We based our observations of the amount of DNA in prospective daughters on the evaluation of the degree of constriction in fixed cells visualized by phase contrast microscopy using the software package of ObjectJ (see section “Materials and Methods”; for an elaborate analysis of constricting E. coli cells see Reshes et al., 2008). Classification of the degree of constriction has been performed previously on E. coli cells prepared by agar filtration and visualized by electron microscopy (Koppes and Nanninga, 1980; Grover et al., 1987; Vardi and Grover, 1993; Grover and Woldringh, 2001). However, subtle shape changes like the degree of constriction and the variation in cell width during cell elongation (Trueba and Woldringh, 1980) can also be observed using light microscopy of living or fixed (Supplementary Figure S5) cells. Such studies could prove very informative with large populations growing in a microfluidics device (Taheri-Araghi et al., 2015; Wallden et al., 2016).
To understand better how differences in the amount of DNA in large and small newborn cells could arise, we constructed length growth curves according to the adder model and calculated the genome contents (G) of large and small siblings that initiate DNA replication C+D min before division (Figure 4). Large newborn cells initiate earlier and at a larger length (Li) than small newborns (red open circles), and at fast growth they also develop transiently a higher genome content during the first three cycles (G and red numbers in Figure 4B). This qualitative agreement with the measurements of DNA contents (Table 1) supports the assumption of an equal C+D-period in all individual cells, consistent with the observations of Wallden et al. (2016). A mathematical framework for these graphical constructions has been presented before (Amir, 2014; Ho and Amir, 2015; Taheri-Araghi, 2015; Taheri-Araghi et al., 2015). The implied differential initiation could be explained by assuming that the differently-sized siblings, although born with identical chromosomes, have a different balance between the amount of their DNA and cytoplasmic initiators such as DnaA or other regulators (Hansen et al., 1991; Katayama et al., 2010; Skarstad and Katayama, 2013). The chromosome in the sibling with a larger volume could consequently initiate earlier than that in the smaller sibling if the cell contained more initiators. The open circles at Cycle 1 in Figure 4 indicate that large and small siblings initiate at different lengths, deviating from the average length for initiation as indicated by Li (dashed horizontal red line in Figure 4). Here, cell length represents cell volume if diameter remains constant during the cell cycle. It should be noted that to our knowledge the earlier division in the larger sibling has not directly been observed in, for instance, time-lapse studies with cells growing in microfluidic channels (Taheri-Araghi et al., 2015; Wallden et al., 2016).
The question remains as to what the dominant mechanism is behind the adder phenomenon of cell growth. Do large and small newborn cells monitor their size (ΔL) from birth on, dividing after a fixed size increment that is based on some constant property other than the amount of DNA (cf. “birth-centric” view; Amir, 2016)? Or do different newborns initiate DNA replication at different sizes and divide after a constant C+D-period, causing large newborns to have shorter and small newborns longer generation times as though growing according to the adder principle? This “initiation-centric” or “adder-per-origin” model has been described by Ho and Amir (2015) and Zheng et al. (2016). The model is based on sensing the activity of initiation proteins (cf. Hansen et al., 1991) rather than on the need for cells to “measure” a size increment that depends on the synthesis of many macromolecules. However, the model still requires an additional timing mechanism for triggering cell division at the end of the C+D-period. As previously suggested (Campos et al., 2014; Zaritsky and Woldringh, 2015), this could be established by the sequence of events occurring in elongating cells starting with replication and the concomitant segregation of chromosome arms (Wiggins et al., 2010; Youngren et al., 2014; Woldringh et al., 2015; Männik et al., 2016) during the C-period. After termination and relief of nucleoid occlusion (Woldringh et al., 1991; Wu and Errington, 2012; Cambridge et al., 2014), the D-period starts by assembling the FtsZ-ring (den Blaauwen et al., 1999; Aarsman et al., 2005), followed by divisome maturation (van der Ploeg et al., 2013; Vischer et al., 2015) and visible cell constriction (T-period; Reshes et al., 2008; Tsukanov et al., 2011).
These latter processes, occurring during the D-period, can all be expected to proceed in a growth-rate dependent way. But because at higher growth rate cell width will increase, the duration of the joint processes of FtsZ-ring assembly, divisome maturation and polar-cap peptidoglycan synthesis, may remain the same. The effect of a higher growth rate is thus compensated by the increased surface of the polar cap to be synthesized, causing a constant D-period. Such phenomenon is supported by the observation that the T-period is more or less constant for doubling times shorter than 60 min (Woldringh et al., 1977; Zaritsky et al., 2006). Under conditions of thymine limitation, when cell width increases without a compensating change in growth rate (Zaritsky and Pritchard, 1973), the D-period has been found to increase (Zaritsky et al., 1999).
At slow growth (Figure 4A), the earlier initiation in the larger sibling and the constant C+D-period enable it to divide earlier in the first cycle than the average newborn cell. At fast growth (Figure 4B), the earlier initiation in the larger sibling will trigger a division event also after C+D min, but occurring in the third cycle. How then can the large sibling already divide earlier than the average newborn cell in the first cycle, as dictated by the adder model and how does chromosome segregation accord with this adder principle? The unexpected observation of an increased distance (∼20%) between segregated nucleoids in large, deeply-constricted cells (Table 2) could explain the necessary acceleration of the cell cycle in large siblings. We envisage that a faster segregation of the nucleoid in the larger sibling could transiently occur because of the larger space along the length axis, accelerating the onset of constriction and division already in the first cycle. That the constriction process itself can enhance nucleoid separation has been demonstrated previously (Huls et al., 1999; Aarsman et al., 2005). It is also suggested here by the gradual increase in the distance between nucleoids during advancing constriction in both slow and fast growing cells (Supplementary Figure S3) and by the increased distance between separated nucleoids in constricting cells as a function of their length (Supplementary Figure S4). Whether the separation of daughter nucleoids also occurs faster in large elongating cells before the onset of constriction can only be ascertained by direct observation of live cells growing in microfluidics channels.
That cell volume regulates initiation of DNA replication seems well-established (Si et al., 2016; Zheng et al., 2016). That cell length regulates initiation of constriction has been proposed previously (Grover and Woldringh, 2001). This length model predicts the decrease observed in cell diameter during elongation (Trueba and Woldringh, 1980), and the correlations between cell dimensions and the coefficients of variation of cell length and volume at specific events like the onset of constriction. The proposal here thus comes down to a composite model in which both cell volume (for initiation of DNA replication) and cell length (for initiation of Z-ring assembly) play roles in determining cell division. Just as in the case of the larger sibling where the greater volume enables the chromosome to initiate earlier than average, its longer length enables faster segregation and earlier division, as dictated by the adder principle. Visualizing and measuring nucleoids at the single-cell level in vivo would establish whether or not differently-sized siblings indeed initiate DNA replication at different cell volumes and segregate nucleoids and initiate cell constrictions at different cell lengths. Such information could well be obtained using quantitative time-lapse imaging of mutants with enhanced asymmetric division (Männik et al., 2017).
Author Contributions
PH performed the research and reviewed the manuscript. NV analyzed the data and reviewed the manuscript. CW wrote the paper.
Funding
This work was inspired by the observations of L. J. H. Koppes, who developed the constant length increment model long before the others. However, he lacked the opportunity to continue his experimental work. His theoretical work was greatly supported by N. B. Grover, resulting in a paper the abstract of which reads: “Two statistical hypotheses for the occurrence of cell division were tested by observed distributions of cell size during steady-state growth. The 30 year old so-called sloppy-size model could be rejected, whereas the newly-developed incremental-size model was accepted (by lack of alternatives)” (see Voorn et al., 1993). Revival of the incremental model occurred in 2014 in Boston (see Amir, 2014) and San Diego (see Jun and Taheri-Araghi, 2014).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Arieh Zaritsky for his continuous support and stimulation and N. B. Grover for the critical remarks that greatly improved the manuscript and for the statistical tests. Nanne Nanninga, Charles Helmstetter, Suckjoon Jun, Jim Walker, Ariel Amir, Frank Trueba, and Vic Norris are thanked for the stimulating discussions and suggestions. We are indebted to Rogier Stuger for the E. coli strain and to Tanneke den Blaauwen for the comments and laboratory facilities.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2018.00664/full#supplementary-material
Footnotes
- ^ https://sils.fnwi.uva.nl/bcb/objectj/examples/Coli-Inspector/Coli-Inspector-MD/coli-inspector.html
References
Aarsman, M. E. G., Piette, A., Fraipont, C., Vinkenvleugel, T. M. F., Nguyen-Disteche, M., and den Blaauwen, T. (2005). Maturation of Escherichia coli divisome occurs in two steps. Mol. Microbiol. 55, 1631–1645. doi: 10.1111/j.1365-2958.2005.04502.x
Amir, A. (2014). Cell size regulation in bacteria. Phys. Rev. Lett. 112:208102. doi: 10.1103/PhysRevLett.112.208102
Bremer, H., and Churchward, G. (1977). An examination of the Cooper-Helmstetter theory of DNA replication in bacteria and its underlying assumptions. J. Bacteriol. 69, 645–654. doi: 10.1016/0022-5193(77)90373-3
Cambridge, J., Blinkova, A., Magnan, D., Bates, D., and Walker, J. R. (2014). A replication-inhibited unsegregated nucleoid at mid-cell blocks Z-ring formation and cell division independently of SOS and the SlmA nucleoid occlusion protein in Escherichia coli. J. Bacteriol. 196, 36–49. doi: 10.1128/JB.01230-12
Campos, M., Surovtsev, I. V., Kato, S., Paintdakhi, A., Beltran, B., Ebmeier, S. E., et al. (2014). A constant size extension drives bacterial cell size homeostasis. Cell 159, 1433–1446. doi: 10.1016/j.cell.2014.11.022
Cooper, S., and Helmstetter, C. E. (1968). Chromosome replication and the division cycle of Escherichia coli B/r. J. Mol. Biol. 31, 519–540. doi: 10.1016/0022-2836(68)90425-7
den Blaauwen, T., Buddelmeijer, N., Aarsman, M. E. G., Hameete, C. M., and Nanninga, N. (1999). Timing of FtsZ assembly in Escherichia coli. J. Bacteriol. 181, 5167–5175.
Grover, N. B., and Woldringh, C. L. (2001). Dimensional regulation of cell-cycle events in Escherichia coli during steady-state growth. Microbiology 147, 171–181. doi: 10.1099/00221287-147-1-171
Grover, N. B., Woldringh, C. L., and Koppes, L. J. (1987). Elongation and surface extension of individual cells of Escherichia coli B/r: comparison of theoretical and experimental size distributions. J. Theor. Biol. 129, 337–348. doi: 10.1016/S0022-5193(87)80006-1
Hansen, F. G., Christensen, B. B., and Atlung, T. (1991). The initiator titration model: computer simulation of chromosome and minichromosome control. Res. Microbiol. 142, 161–167. doi: 10.1016/0923-2508(91)90025-6
Ho, P. Y., and Amir, A. (2015). Simultaneous regulation of cell size and chromosome replication in bacteria. Front. Microbiol. 6:662. doi: 10.3389/fmicb.2015.00662
Huls, P. G., Vischer, N. O. E., and Woldringh, C. L. (1999). Delayed nucleoid segregation in Escherichia coli. Mol. Microbiol. 33, 959–970. doi: 10.1046/j.1365-2958.1999.01535.x
Jensen, P. R., Van Der Weijden, C. C., Jensen, L. B., Westerhoff, H. V., and Snoep, J. L. (1999). Extensive regulation compromises the extent to which DNA gyrase controls DNA supercoiling and growth rate of Escherichia coli. Eur. J. Biochem. 266, 865–877. doi: 10.1046/j.1432-1327.1999.00921.x
Jun, S., and Taheri-Araghi, S. (2014). Cell-size maintenance: universal strategy revealed. Trends Microbiol. 23, 4–6. doi: 10.1016/j.tim.2014.12.001
Katayama, T., Ozaki, S., Keyamura, K., and Fujimitsu, K. (2010). Regulation of the replication cycle: conserved and diverse regulatory systems for DnaA and oriC. Nat. Rev. Microbiol. 60, 351–375. doi: 10.1038/nrmicro2314
Koppes, L. J. H., and Nanninga, N. (1980). Positive correlation between size at initiation of chromosome replication in Escherichia coli and size at initiation of cell constriction. J. Bacteriol. 143, 89–99.
Koppes, L. J. H., Overbeeke, N., and Nanninga, N. (1978a). DNA replication patterns and cell wall growth in Escherichia coli PAT84. J. Bacteriol. 133, 1053–1061.
Koppes, L. J. H., Woldringh, C. L., and Nanninga, N. (1978b). Size variations and correlation of different cell cycle events in slow-growing Escherichia coli. J. Bacteriol. 134, 423–433.
Männik, J., Bailey, M. W., O’Neill, J. C., and Männik, J. (2017). Kinetics of large-scale chromosomal movement during asymmetric division in Escherichia coli. PLoS Genet. 13:e1006638. doi: 10.1371/journal.pgen.1006638
Männik, J., Castillo, D. E., Yang, D., Siopsis, G., and Männik, J. (2016). The role of MatP, ZapA and ZapB in chromosomal organization and dynamics in Escherichia coli. Nucleic Acids Res. 44, 2016–2026. doi: 10.1093/nar/gkv1484
Michelsen, O., Teixeira de Mattos, M. J., Jensen, P. R., and Hansen, F. G. (2003). Precise determinations of C and D periods by flow cytometry in Escherichia coli K-12 and B/r. Microbiology 149, 1001–1010. doi: 10.1099/mic.0.26058-0
Neidhardt, F. C., Bloch, P. L., and Smith, D. F. (1974). Culture medium for enterobacteria. J. Bacteriol. 119, 736–747.
Norris, V. (1995). Hypothesis: chromosome separation in Escherichia coli involves autocatalytic gene expression, translation and membrane-domain formation. Mol. Microbiol. 16, 1051–1057. doi: 10.1111/j.1365-2958.1995.tb02330.x
Osella, M., Nugent, E., and Cosentino Lagomarsino, M. (2014). Concerted control of Escherichia coli cell division. Proc. Natl. Acad. Sci. U.S.A. 111, 3431–3435. doi: 10.1073/pnas.1313715111
Rabinovitch, A., Zaritsky, A., and Feingold, M. (2003). DNA-membrane interactions can localize bacterial cell center. J. Theor. Biol. 225, 393–396. doi: 10.1016/S0022-5193(03)00292-3
Reshes, G., Vanounou, S., Fishov, I., and Feingold, M. (2008). Timing the start of division in E. coli: a single-cell study. Phys. Biol. 5:046001. doi: 10.1088/1478-3975/5/5/4/046001
Robert, L. (2015). Size sensors in bacteria, cell cycle control, and size control. Front. Microbiol. 6:515. doi: 10.3389/fmicb.2015.00515
Sauls, J., Li, D., and Jun, S. (2016). Adder and a coarse-grained approach to cell size homeostasis in bacteria. Curr. Opin. Cell Biol. 38, 38–44. doi: 10.1016/j.ceb.2016.02.004
Schaechter, M., Maaløe, O., and Kjeldgaard, N. O. (1958). Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. J. Gen. Microbiol. 19, 592–606. doi: 10.1099/00221287-19-3-592
Si, F., Li, D., Cox, S. E., Sauls, J. T., Azizi, O., Sou, C., et al. (2016). Invariance of initiation mass and predictability of cell size in Escherichia coli. Curr. Biol. 27, 1278–1287. doi: 10.1016/j.cub.2017.03.022
Skarstad, K., and Katayama, T. (2013). Regulating DNA replication in bacteria. Cold Spring Harb. Perspect. Biol. 5:a012922. doi: 10.1101/cshperspect.a012922
Stuger, R., Woldringh, C. L., van der Weijden, C. C., Vischer, N. O. E., Bakker, B. M., van Spanning, R. J. M., et al. (2002). DNA supercoiling by gyrase is linked to nucleoid compaction. Mol. Biol. Rep. 29, 79–82. doi: 10.1023/A:1020318705894
Taheri-Araghi, S. (2015). Self-consistent examination of Donachie’s constant initiation size at the single-cell level. Front. Microbiol. 6:1349. doi: 10.3389/fmicb.2015.01349
Taheri-Araghi, S., Bradda, S., Sauls, J. T., Hill, N. S., Levin, P. A., Paulsson, J., et al. (2015). Cell-size control and homeostasis. Curr. Biol. 25, 1–7. doi: 10.1016/j.cub.2014.12.009
Trueba, F. J. (1982). On the precision and accuracy achieved by Escherichia coli cells at fission about their middle. Arch. Microbiol. 131, 55–59. doi: 10.1007/BF00451499
Trueba, F. J., and Woldringh, C. L. (1980). Changes in cell diameter during the division cycle of Escherichia coli. J. Bacteriol. 142, 869–878.
Tsukanov, R., Reshes, G., Carmon, G., Fischer-Friedrich, E., Gov, N. S., Fishov, I., et al. (2011). Timing of Z-ring localization in Escherichia coli. Phys. Biol. 8:066003. doi: 10.1088/1478-3975/8/6/066003
Typas, A., Banzhaf, M., Gross, C. A., and Vollmer, W. (2012). From the regulation of peptidoglycan synthesis to bacterial growth and morphology. Nat. Rev. Microbiol. 10, 123–135. doi: 10.1038/nrmicro2677
van der Ploeg, R., Verheul, J., Vischer, N. O. E., Alexeeva, S., Hoogendoorn, E., Postma, M., et al. (2013). Colocalization and interaction between elongasome and divisome during a preparative cell division phase in Escherichia coli. Mol. Microbiol. 87, 1074–1087. doi: 10.1111/mmi.12150
Vardi, E., and Grover, N. B. (1993). Shape changes in Escherichia coli B/rA during agar filtration. Cytometry 14, 173–178. doi: 10.1002/cyto.990140209
Vischer, N. O. E., Huls, P. G., Ghauharali, R. I., Brakenhoff, G. J., Nanninga, N., and Woldringh, C. L. (1999). Image cytometric method for quantifying the relative amount of DNA in bacterial nucleoids using Escherichia coli. J. Microsc. 196, 61–68. doi: 10.1046/j.1365-2818.1999.00597.x
Vischer, N. O. E., Verheul, J., Postma, M., van den Berg van Saparoea, B., Galli, E., Natale, P., et al. (2015). Cell age dependent concentration of Escherichia coli divisome proteins analyzed with ImageJ and ObjectJ. Front. Microbiol. 6:586. doi: 10.3389/fmicb.2015.00586
Voorn, W. J., Koppes, L. J. H., and Grover, N. B. (1993). Mathematics of cell division in Escherichia coli: comparison between sloppy-size and incremental-size kinetics. Curr. Top. Mol. Gen. 1, 187–194.
Wallden, M., Fange, D., Lundius, E. G., Baltekin, O., and Elf, J. (2016). The synchronization of replication and division cycles in individual E. coli cells. Cell 166, 729–739. doi: 10.1016/j.cell.2016.06.052
Wang, P., Robert, L., Pelletier, J., Dang, W. L., Taddei, F., Wright, A., et al. (2010). Robust growth of Escherichia coli. Curr. Biol. 20, 1099–1103. doi: 10.1016/j.cub.2010.04.045
Wiggins, P. A., Cheveralls, K. C., Martin, J. S., Lintner, R., and Kondev, J. (2010). Strong intranucleoid interactions organize the Escherichia coli chromosome into a nucleoid filament. Proc. Natl. Acad. Sci. U.S.A. 107, 4991–4995. doi: 10.1073/pnas.0912062107
Woldringh, C. L. (2002). The role of co-transcriptional translation and protein translocation (transertion) in bacterial chromosome segregation. Mol. Microbiol. 45, 17–29. doi: 10.1046/j.1365-2958.2002.02993.x
Woldringh, C. L., de Jong, M. A., van den Berg, W., and Koppes, L. (1977). Morphological analysis of the division cycle of two Escherichia coli substrains during slow growth. J. Bacteriol. 131, 270–279.
Woldringh, C. L., Hansen, F. G., Vischer, N. O. E., and Atlung, T. (2015). Segregation of chromosome arms in growing and non-growing Escherichia coli cells. Front. Microbiol. 6:448. doi: 10.3389/fmicb.2015.00448
Woldringh, C. L., Mulder, E., Huls, P. G., and Vischer, N. (1991). Toporegulation of bacterial division according to the nucleoid occlusion model. Res. Microbiol. 142, 309–320. doi: 10.1016/0923-2508(91)90046-D
Wu, L. J., and Errington, J. (2012). Nucleoid occlusion and bacterial cell division. Nat. Rev. Microbiol. 10, 8–12. doi: 10.1038/nrmicro2671
Youngren, B., Nielsen, H. J., Jun, S., and Austin, S. (2014). The multifork Escherichia coli chromosome is a self-duplicating and self-segregating thermodynamic ring polymer. Genes Dev. 28, 71–84. doi: 10.1101/gad.231050.113
Zaritsky, A. (2015). Cell-shape homeostasis in Escherichia coli is driven by growth, division, and nucleoid complexity. Biophys. J. 109, 178–181. doi: 10.1016/j.bpj.2015.06.026
Zaritsky, A., and Pritchard, R. H. (1973). Changes in cell size and shape associated with changes in the replication time of the chromosome of Escherichia coli. J. Bacteriol. 114, 824–837.
Zaritsky, A., van Geel, A., Fishov, I., Pas, E., Einav, M., and Woldringh, C. L. (1999). Visualizing multiple constrictions in spheroidal Escherichia coli cells. Biochimie 81, 897–900. doi: 10.1016/S0300-9084(99)00206-0
Zaritsky, A., and Woldringh, C. L. (2015). Chromosome replication, cell growth, division and shape: a personal perspective. Front. Microbiol. 6:756. doi: 10.3389/fmicb.2015.00756
Zaritsky, A., Woldringh, C. L., Einav, M., and Alexeeva, S. (2006). Use of thymine limitation and thymine starvation to study bacterial physiology and cytology. J. Bacteriol. 188, 1667–1679. doi: 10.1128/JB.188.5.1667-1679.2006
Keywords: Escherichia coli, deeply-constricted cells, newborn cells, DAPI-stained nucleoid, DNA segregation, adder growth model, ObjectJ
Citation: Huls PG, Vischer NOE and Woldringh CL (2018) Different Amounts of DNA in Newborn Cells of Escherichia coli Preclude a Role for the Chromosome in Size Control According to the “Adder” Model. Front. Microbiol. 9:664. doi: 10.3389/fmicb.2018.00664
Received: 04 December 2017; Accepted: 21 March 2018;
Published: 05 April 2018.
Edited by:
Marc Bramkamp, Ludwig-Maximilians-Universität München, GermanyReviewed by:
Johannes Geiselmann, Université Grenoble Alpes, FranceDennis Claessen, Leiden University, Netherlands
Copyright © 2018 Huls, Vischer and Woldringh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Conrad L. Woldringh, Yy53b2xkcmluZ2hAZ21haWwuY29t
 Peter G. Huls1
Peter G. Huls1 Norbert O. E. Vischer
Norbert O. E. Vischer Conrad L. Woldringh
Conrad L. Woldringh