- 1Division of Biomedical Statistics and Informatics, Center for Individualized Medicine, Mayo Clinic, Rochester, MN, United States
- 2School of Statistics and Mathematics, Zhongnan University of Economics and Law, Wuhan, China
- 3Department of Health Outcomes Research and Policy, Harrison School of Pharmacy, Auburn University, Auburn, AL, United States
- 4Department of Statistics, Texas A&M University, College Station, TX, United States
Fueled by technological advancement, there has been a surge of human microbiome studies surveying the microbial communities associated with the human body and their links with health and disease. As a complement to the human genome, the human microbiome holds great potential for precision medicine. Efficient predictive models based on microbiome data could be potentially used in various clinical applications such as disease diagnosis, patient stratification and drug response prediction. One important characteristic of the microbial community data is the phylogenetic tree that relates all the microbial taxa based on their evolutionary history. The phylogenetic tree is an informative prior for more efficient prediction since the microbial community changes are usually not randomly distributed on the tree but tend to occur in clades at varying phylogenetic depths (clustered signal). Although community-wide changes are possible for some conditions, it is also likely that the community changes are only associated with a small subset of “marker” taxa (sparse signal). Unfortunately, predictive models of microbial community data taking into account both the sparsity and the tree structure remain under-developed. In this paper, we propose a predictive framework to exploit sparse and clustered microbiome signals using a phylogeny-regularized sparse regression model. Our approach is motivated by evolutionary theory, where a natural correlation structure among microbial taxa exists according to the phylogenetic relationship. A novel phylogeny-based smoothness penalty is proposed to smooth the coefficients of the microbial taxa with respect to the phylogenetic tree. Using simulated and real datasets, we show that our method achieves better prediction performance than competing sparse regression methods for sparse and clustered microbiome signals.
1. Introduction
The human microbial community (a.k.a., microbiota) is the collection of microorganisms associated with the human body. These microorganisms, their genomes, and the environment they reside in are collectively known as the human “microbiome.” The human microbiome plays a critical role in health and disease (Cho and Blaser, 2012). For instance, the human gut microbiome aids the digestive system with inaccessible nutrients, synthesizes beneficial nutrients and protects us against pathogens. An abnormal microbiome has been implicated in many human diseases including various cancer types (Ahn et al., 2013; Bultman, 2014; Walther-Antonio et al., 2016; Peters et al., 2017). Dysbiosis of the microbiome has been observed in obesity, type II diabetes, rheumatoid arthritis and multiple sclerosis (Turnbaugh et al., 2009; Kinross et al., 2011; Honda and Littman, 2012; Pflughoeft and Versalovic, 2012; Qin et al., 2012; Chen et al., 2016; Jangi et al., 2016). Therefore, the human microbiome holds great potential for various clinical applications such as disease diagnosis, patient stratification and drug response prediction. Building up an efficient microbiome-based predictor could thus empower microbiome-based precision medicine (Kashyap et al., 2017).
Advances in low-cost, high-throughput DNA sequencing technologies such as Illumina Solexa sequencing has enabled researchers to study the microbiome composition by directly sequencing the microbial DNA. Two main approaches have been employed to sequence the microbiome: gene-targeted sequencing and shotgun metagenomic sequencing (Kuczynski et al., 2011). Compared to the shotgun metagenomic sequencing, where all microbial DNA is sequenced, the gene-targeted approach only sequences a “fingerprint” region of a “molecular clock” gene such as the 16S rRNA gene in the bacteria. Although the shotgun metagenomic sequencing provides more biological information, the targeted approach is still the dominant approach for large-scale microbiome studies due to its lower cost and high scalability (McDonald et al., 2018). In the targeted sequencing, standard practices involve clustering the sequencing reads into operational taxonomic units (OTUs) or amplicon sequence variants (ASVs) based on their sequence similarities (Schloss et al., 2009; Caporaso et al., 2010, 2012; Chen et al., 2013b, 2017; Edgar, 2013; Rideout et al., 2014; Callahan et al., 2016; Amir et al., 2017). A taxonomic lineage is further assigned to each OTU/ASV by comparing their sequence to existing 16S rRNA gene databases. Finally, a phylogenetic tree, which characterizes the evolutionary relationships among OTUs/ASVs, is constructed based on their sequence divergences (Price et al., 2010). For shotgun metagenomic sequencing, a phylogenetic tree can also be constructed based on the reference genomes of the detected species (Kembel et al., 2011). As a result, a typical microbiome sequencing study is usually summarized as a table of the read counts of the detected OTUs/ASVs/Species, together with a phylogenetic tree, reflecting the community structure and composition of the studied microbiome. For simplicity, hereafter, we use the term “OTU” to stand for the basic taxonomic units (e.g., OTU, ASV, species, taxa) from any sequencing experiment/bioinformatics pipeline. Compared to other types of omics sequencing data, one important characteristic of microbiome sequencing data (microbial community data) is the phylogenetic tree that relates all the OTUs. The phylogenetic tree provides prior knowledge about how the OTUs are evolutionarily related. Related OTUs, which usually share similar biological functions, are more likely to be simultaneously associated with the outcome, forming “clustered signals” at varying phylogenetic depths (Garcia et al., 2014; Martiny et al., 2015). Therefore, the phylogeny creates linkages among OTUs and induces a grouping structure, allowing more efficient linkage between the OTUs and the phenotype. As the microbial community data moves into even higher resolutions such as strain-level resolution (Mallick et al., 2017; Edgar, 2018), the phylogenetic relationship becomes even more important for OTU data analysis. Clearly, it is not sensible to treat OTUs with only 1% sequence divergence in the same way as the OTUs with more than 10% sequence divergence. Indeed, incorporating the tree structure has proven to make the analyses more efficient and robust for various statistical tasks ranging from ordination to microbiome-wide multiple testing (Purdom, 2011; Chen et al., 2012, 2013a; Evans and Matsen, 2012; Wang and Zhao, 2017; Xiao et al., 2017).
One important task for microbiome analysis is to predict the phenotype/outcome (either quantitative or qualitative) based on the features of the underlying microbial community (relative abundances of the OTUs and their phylogeny). This process is also known as predictive modeling or supervised learning in machine learning literature, where we try to derive some function from the training data that can be used to predict the outcome of future data, and to learn which features (i.e., OTUs) are predictive of the outcome. For clinical applications, the outcome includes disease state, treatment response, and drug toxicity. To enable prediction based on microbial community data, general-purpose predictive methods have been applied (Knights et al., 2011; Statnikov et al., 2013; Pasolli et al., 2016). These methods include classical machine learning methods (e.g., Random Forest and Support Vector Machine) and modern regression methods for high-dimensional data [e.g., Lasso (Tibshirani, 1996), MCP (Zhang, 2010), and Elastic Net (Zou and Hastie, 2005)], focusing on modeling the nonlinear relationship between the outcome and the microbiome as well as selecting the most predictive OTUs for better interpretation. However, these methods do not fully exploit the information in the microbiome data, particularly the phylogenetic relationship among OTUs. The phylogenetic tree is an informative prior since the microbial community changes are usually not randomly distributed but tend to occur in clades at varying phylogenetic depths (clustered signal). In other words, the phylogenetic structure offers a biologically motivated grouping structure, through which we can aggregate sparse OTU data to enrich signals and achieve better predictive performance. The objective of the proposed study is thus to provide a data-adaptive approach to use the tree structure when constructing the predictive model, i.e., let the data determine how much phylogenetic information and what level of phylogenetic depth we should use to achieve optimal performance. The inputs of our method are the OTU count table, the phylogenetic tree of the OTUs and the outcome measurements, and the outputs are the selected OTUs and the predictive function based on their abundances.
Many previous attempts have been made to incorporate the tree information into prediction, particularly in the regression framework (Tanaseichuk et al., 2014; Chen et al., 2015; Ning and Beiko, 2015; Wang and Zhao, 2017; Randolph et al., 2018; Xiao et al., 2018). These methods are advantageous over previous methods by taking into account the tree. However, they still have many limitations. For example, some methods do not perform variable selection in model building (Wang and Zhao, 2017; Randolph et al., 2018; Xiao et al., 2018), and hence their prediction performance is subpar for sparse-signal scenarios (i.e., only a subset of OTUs are associated with outcome). For methods that perform variable weighting or selection (Tanaseichuk et al., 2014; Ning and Beiko, 2015), they usually rely solely on the tree topology. The branch lengths, which provide more detailed evolutionary history, are usually ignored. Therefore, there is still a need to develop prediction methods for sparse clustered signals while exploiting the full information of the phylogenetic tree, which consists of both the tree topology and branch lengths.
Previously, we developed glmgraph (Chen et al., 2015), a graph-regularized sparse regression model for structured genomic data. In the glmgraph framework, besides a sparsity penalty, a graph Laplacian-based structure penalty (Laplacian penalty) was imposed to smooth the coefficients with respect to the graph structure. It also encourages structurally related predictors to be selected simultaneously (Huang et al., 2011). In principle, a graph Laplacian can be constructed based on the pair-wise distances between OTUs with respect to the phylogenetic tree. However, the Laplacian penalty has two major drawbacks for microbiome applications. First, the Laplacian-induced smoothing/grouping effects are susceptible to the interference by a large number of distantly related OTUs since the graph is fully connected. It is well- known that distantly related OTUs have very different biological characteristics, and thus their contribution to the smoothing should be minimized. Second, the smoothing effects induced by the Laplacian penalty is completely driven by the external graph structure. This is in stark contrast to the l2 penalty-induced smoothing effects (Zou and Hastie, 2005; Huang et al., 2016), which are mainly driven by the internal correlation structure in the data. In case of a misspecified tree, the Laplacian penalty cannot reduce to the l2 penalty. Therefore, it does not possess the data-driven smoothing property, which has been shown to be important to improve prediction performance under certain scenarios (Waldron et al., 2011).
In this work, in parallel to our previous prediction method for “dense and clustered” microbiome signals (Xiao et al., 2018), we develop a phylogeny-regularized sparse regression model for “sparse and clustered” microbiome signals. The proposed method uses a novel phylogeny-based smoothness penalty, which is defined based on the inverse of the phylogeny-induced correlation matrix. The new penalty addresses the two major drawbacks of the Laplacian penalty: it encourages local smoothing, i.e., smoothing effects from more immediate neighbors, as well as enjoys the data-driven smoothing property if the tree is misspecified. In summary, the sparse nature of the distribution of OTUs in complex microbiome data can be better captured by our model because it provides a data-adaptive way to group the OTUs according to their phylogeny as well as to select the most predictive OTUs, which leads to improved prediction and interpretation.
2. Methods
2.1. A Phylogeny-Induced Correlation Structure Among OTUs
We first introduce a phylogeny-induced correlation structure, on which our phylogeny-based smoothness penalty will be defined. Suppose we have p OTUs on a phylogenetic tree, following the evolutionary model proposed in Martins and Hansen (1997), the correlation of the traits between OTU i and j can be modeled as
where dij is the patristic distance between OTU i and j (i.e., the length of the shortest path linking the two OTUs on the tree) and the parameter α∈(0, ∞) characterizes the evolutionary rate. When α = 0, cij = 1 ∀i, j, indicating all the traits are the same and there is no evolution. When α → ∞, cij = 0 ∀i≠j, indicating that the traits evolve independently. The parameter α is also related to the phylogenetic depth of trait conservation (Martiny et al., 2015), with a smaller α value indicating a greater phylogenetic depth at which the trait is conserved (i.e., a large clade of OTUs share the trait). In other words, the parameter α has a (soft) grouping effect and groups the OTUs at various phylogenetic depths. Compared to the taxonomic grouping, where the OTUs are grouped at a specific taxonomic level, such phylogeny-based grouping not only achieves more resolutions, but also circumvents the difficulty of the uncertainty in taxonomy assignments. Therefore, in the context of predictive modeling, the parameter α can be treated as a tuning parameter, which allows us to explore different phylogenetic depths to optimize prediction. Also to be noted, the pairwise distance dij can be simply the genetic distance based on pairwise comparison of the DNA sequences without the need for explicit tree construction.
2.2. Phylogeny-Regularized Sparse Generalized Linear Model
To account for the high dimensionality and the phylogenetic tree structure in microbiome-based prediction, we introduce a phylogeny-regularized sparse generalized linear model. We assume that there are n samples with the abundances of p OTUs being profiled. For the ith sample, let yi denote the outcome variable, which can be binary or continuous, and xi = (xi1, xi2, … , xip)T denote the normalized and properly transformed abundance vector of the p OTUs. We further assume the data have been standardized (). The goal is to predict yi based on xi. We will use a generalized linear model
where β0 is the intercept, β = (β1, β2, …, βp) and g(.) is a link function (identity and logit link for continuous and binary outcome, respectively). Since p > n, we need to make some sparsity assumption in order for the model to be estimable. Additional assumption will be imposed on the structural relationship among the model parameters to make the estimation more efficient. To this end, we propose the following penalized log-likelihood to estimate the regression coefficients:
where
The penalized likelihood estimate can be obtained by solving the optimization problem
The two penalty terms in Equation (2) play distinct roles. is the sparsity penalty, which induces a sparse solution and has been demonstrated to improve both the prediction performance and model interpretability (Tibshirani, 1996) in the high-dimensional setting. is the smoothness penalty, which encourages smoothness of the estimated coefficients with respect to the phylogenetic tree (i.e., encourage similar coefficients for clustered OTUs at a certain phylogenetic depth).
For the sparsity penalty , we choose to use MCP (Minimax Concave Penalty) (Zhang, 2010):
where λ1 ≥ 0 is the tuning parameter, (.)+ indicates the nonnegative part and the parameter γ (1 ≤ γ ≤ +∞) controls the degree of concavity. Larger values of γ make ρ less concave. By varying the value of γ from 1 to +∞, the MCP provides a continuum of penalties with the hard-threshold penalty as γ → 1 and the convex l1 penalty at γ = +∞. In practice, γ is usually fixed to a reasonable value without the need for further tuning. An important advantage of the MCP over the l1 penalty is that it leads to a nearly unbiased estimator and achieves selection consistency under weaker conditions. More detailed discussions of MCP could be found in Zhang (2010).
Our major contribution is the design of a novel structure-based smoothness penalty to achieve efficient phylogeny-based smoothing. One common approach to accommodate structure/graph information in sparse regression model is through the use of a graph Laplacian penalty , where the Laplacian matrix L is defined based on the connectivity, or adjacency among predictors. The penalized likelihood estimator resulted from the combination of the MCP and Laplacian penalty, termed as Sparse Laplacian Shrinkage (SLS) estimator, has been shown to have nice properties such as selection consistency and generalized grouping (Huang et al., 2011). For microbiome applications, a graph Laplacian for microbiome data can be defined using the phylogeny-induced correlation (Equation 1) as the adjacency measure. However, we found that this approach did not always achieve better prediction performance than the procedure without the Laplacian penalty. The subpar performance is partly due to the interference by a large number of distantly related OTUs since the phylogeny-induced graph is fully connected. To achieve better prediction performance, it is important to reduce the contribution of smoothing effects from the large number of distantly related OTUs. Although this can be achieved by sparsifying L, in practice, the degree of sparsity to achieve optimal prediction depends on the data and it is difficult to set a universal degree of sparsity for all applications. To overcome the limitation of the graph Laplacian approach, we propose to use an alternative smoothness penalty
where C(α) = (cij(α))p × p is the phylogeny-induced correlation structure defined in the previous section. The inverse correlation matrix Ω≜C−1 also implies a graph structure among predictors but encourages more local smoothing, that is, the coefficient smoothing is mainly contributed by its immediate neighbors. To demonstrate a stronger local smoothing effect by Ω than L, we plot Ωij, Lij, the elements of the Ω and L, against the pairwise patristic distances between OTUs (Figure 1). As the pairwise distance increases, Ωij approaches zero quickly while Lij does not decrease as fast. Since |Ωij|, |Lij| determine the contribution of the smoothing effect of OTU i to OTU j, a faster rate to zero suggests a stronger local smoothing effect.
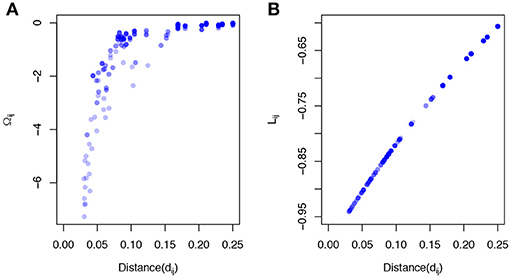
Figure 1. Local smoothing effects of the proposed smoothness penalty. The data was generated based on a simulated phylogenetic tree (p = 200,“rcoal” from R “ape” package). The correlation C(α) was calculated based on the pairwise patristic distances with α = 2. (A) The elements of inverse correlation matrix (Ωij) are plotted against pairwise patristic distances (dij). (B) The elements of Laplacian matrix (Lij) are plotted against pairwise patristic distances (dij).
In the phylogeny-regularized sparse generalized linear model, we have three parameters λ1, λ2 and α, which need to be tuned in the training step for optimal prediction performance. These three parameters, respectively control the model sparsity (i.e., how many OTUs are predictive of the outcome), the phylogeny-based smoothing effects (i.e., how much smoothing effects should be induced by the tree), and the phylogenetic depth of the signal (i.e., what level of clustering is needed to achieve better prediction). With the inverse correlation matrix-based smoothness penalty, we call the resulting penalized likelihood estimator Sparse Inverse Correlation Shrinkage (SICS) estimator. The proposed approach also has a Bayesian interpretation: it assumes that the coefficient β has a prior multivariate normal component with the covariance matrix τC and the penalized likelihood estimate can be viewed as the MAP (maximum a posteriori) estimate from a Bayesian perspective.
2.3. Connection With Existing Methods
The proposed smoothness penalty βTΩβ, the graph Laplacian penalty βTLβ and the l2 penalty βT β are all special cases of a general class of quadratic penalties βTΣβ, where Σ is a positive semi-definite matrix. When α → ∞, the proposed penalty becomes l2 penalty and the SICS estimator is reduced to the Mnet estimator (Huang et al., 2016). It is well-known that l2 penalty induces a grouping effect based on the correlation structure in the data (data-driven smoothing). As α decreases, the phylogeny-driven smoothing will take control (prior-driven smoothing). Thus, α also provides some tradeoff between data-driven and prior-driven smoothing (Theorem 1). To better understand the behavior of the proposed smoothness penalty, we rewrite it as
where sjk = sgn(−Ωjk) is the sign of −Ωjk. Note that the second part has the same form as the Laplacian penalty (Huang et al., 2011). Thus, the proposed smoothness penalty is a combination of a weighted l2 penalty (first part) and a Laplacian penalty (second part) with the adjacency coefficients −Ωij. For the phylogeny-induced correlation structure, all the off-diagonal elements Ωij are negative and the magnitude controls the prior-driven smoothing effect. The weighted l2 penalty, on the other hand, offers the data-driven smoothing effect. In contrast, the Laplacian penalty cannot reduce to the l2 penalty and does not have the data-driven smoothing effect.
Since the proposed smoothness penalty has a weighted l2 component, some degree of shrinkage in the coefficient estimate is expected (Zou and Hastie, 2005). For orthogonal designs, rescaling could remove the bias due to l2 shrinkage without significantly increasing the variance. However, we find that, for more general designs, rescaling could instead increase the variance of the SICS estimator and decrease the prediction performance. Therefore, we will not rescale the coefficients in the implementation.
2.4. Some Theoretical Properties
We further investigate the smoothing effect and grouping property of the proposed SICS estimator. Previously, Li and Li (2008) derived the smoothing effect and grouping property for the penalty combining l1 and Laplacian penalty, and Huang et al. (2016) demonstrated a similar property for the Mnet estimator. Here, we demonstrate such property for our SICS estimator under a linear regression model and a simple graph design. The proof of the theorem can be found in the Supplementary File.
Without loss of generality, we assume that the whole graph (as characterized by Ω) corresponding to the index set {1, …, p} is divided into disjoint cliques V1, …, VJ. We further assume that the patristic distances between OTUs are the same in each clique so that the phylogeny-induced correlation coefficient cij are the same. Thus, Ω has a special block-diagonal structure: Ω = diag(Ω1, …, ΩJ) with Ωg = (Ωg, lm)vg × vg, where vg = |Vg| for g = 1, …, J, for Ωg, κg > 0, l = 1, …, vg and for 1 ≤ l, m ≤ vj, l≠m. Also, denote (data-induced correlation between OTU i and OTU j). For the SICS estimator based on this inverse correlation matrix Ω, we have the following smoothing and grouping property:
Theorem 1. Denote and
Then for j, k ∈ Vg and g ∈ {1, …, J}, we have
Especially, if ρjk = 0, we have
Based on Theorem 1, both the prior-induced correlation cjk (which in turn determines and ξ) and the data-induced correlation ρjk contribute to the smoothing effect. With the tuning parameter α, cjk can vary from 0 to 1 (equivalently, varies from 0 to ∞). We can thus increase and decrease the prior-driven smoothing by varying α. The optimal level of prior-driven smoothing effect can be tuned based on the data.
2.5. Model Estimation and Computational Complexity
Since the proposed penalty is convex with respect to β, coordinate descent algorithm, which is developed for sparse regression model with convex and non-convex sparsity penalties (Friedman et al., 2010; Breheny and Huang, 2011) can be readily extended to our case. For the linear regression model, we have a closed-form solution for each coordinate update. For the logistic regression model, we solve a series of structure-regularized sparse linear regression model at each iteratively reweighed least squares step. Coordinate descent continues until a certain convergence criterion is reached. More details could be found in Chen et al. (2015). We implemented the method in the R package SICS (https://github.com/lichen-lab/SICS), which depends on our previously developed glmgraph R package (Chen et al., 2015).
The computation complexity of the proposed method consists of two parts: coordinate descent and matrix inversion. For each coordinate descent loop, it requires O(n+p) arithmetic operations, and a full cycle through the p OTUs requires O(np+p2) operations. Assume the number of iterations to reach convergence is c1 and the number of tuning parameter combinations is c2. The overall complexity for the coordinate descent algorithm is thus . In addition, taking inverse of the correlation matrix typically has a computational complexity of O(p3) (some algorithm may reduce it, but could not bring down to O(p2)). A total of is required to perform matrix inversion, where c3 is the number of grid points for the tuning parameter α. Therefore, the total computational complexity for SICS is . Usually, c1, c2, c3 are treated as fixed, so the computational complexity for SICS is O(np+p3). Thus it is highly scalable with the sample size but not with the number of OTUs. Since we usually perform OTU filtering before running the algorithm, it is computationally efficient for typical microbiome datasets with p < 1000.
3. Simulation studies
3.1. Simulation Strategy
We performed extensive simulations to evaluate the prediction performance of SICS for both continuous and binary outcome. For the continuous outcome, we simulated 100 samples in the training set and 200 samples in the testing set. For the binary outcome, we simulated an equal number of 50 samples for both case and control groups in the training set, and an equal number of 100 samples in case and control groups in the testing set. We used a Dirichlet-multinomial distribution with parameters estimated from a real microbiome data to simulate OTU counts and generated the outcome based on the abundances of the outcome-associated OTUs. We investigated the effect of the informativeness of the phylogenetic tree and the level of signal strength on the prediction performance. The simulation studies were aimed to reveal the scenarios in which our model performed favorably and also to test whether our model was robust when the phylogenetic tree was not informative or misspecified.
3.1.1. Simulating OTU Abundance Data
We included 200 OTUs in the simulation. The OTU counts were generated using a Dirichlet-multinomial distribution with the parameter values (dispersion, mean proportions) estimated based on a real dataset from the human upper respiratory tract microbiome (Charlson et al., 2010). Only the count data from the 200 most abundant OTUs were used in the parameter estimation. Accordingly, the phylogenetic tree was trimmed to contain the 200 OTUs. For each sample, the total read count was sampled from a negative binomial distribution with mean 5,000 and dispersion 25, reflecting a typical sequencing depth for a targeted sequencing experiment. The OTU counts were normalized into OTU proportions by dividing the total read counts.
3.1.2. Selecting Outcome-Associated OTUs
We simulated both phylogeny-informative and non-informative scenarios to study the performance of the proposed method with respect to the informativeness of the phylogenetic tree. In the phylogeny-informative scenarios, we selected outcome-associated OTUs (“aOTUs”) from an OTU cluster and let their effects in the same direction. In the phylogeny-non-informative scenarios, we either randomly selected OTUs or let the effects of the aOTUs in a cluster have opposite effects, which violates the assumption that closely related aOTUs should have similar effects. To construct OTU clusters, we partitioned the 200 OTUs into 20 clusters using the partitioning-around-medoids (PAM) algorithm based on their patristic distances. The simulation strategy was illustrated in Figure 2 and the detailed settings for four scenarios were presented below,
• S1: The phylogenetic tree was informative. One cluster with 12 aOTUs formed an outcome-associated cluster (“aCluster”). In the aCluster, the aOTUs had the same effect size and the effect direction was also the same.
• S2: The phylogenetic tree was informative. On top of S1, we varied the effect size of each aOTU but the effect direction was still the same.
• S3: The phylogenetic tree was non-informative. We randomly selected 12 OTUs to be aOTUs. We restricted one cluster to have only one aOTU.
• S4: The phylogenetic tree was non-informative. On top of S1, we reversed the effect direction for half of the aOTUs.
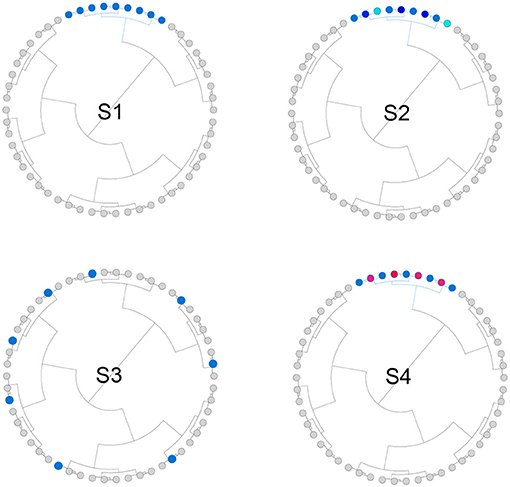
Figure 2. Illustration for the simulation strategy. We simulated both phylogeny-informative scenarios (S1 and S2) and phylogeny-non-informative scenarios (S3 and S4). Blue and red color indicate the direction of the effect while the darkness of the color indicates the magnitude of the effect.
3.1.3. Generating the Outcome Based on the Outcome-Associated OTUs
Denote as the set containing the indices of aOTUs, and let xij be the proportion of OTU j in sample i. We first generated ηi based on the following linear relationship
For a continuous outcome,
For a binary outcome,
We simulated different levels of signal strength (effect size). The signal strength was defined as for the continuous outcome and (xj denotes the abundance for the jth OTU) for the binary outcome. In the simulation, we investigated a signal strength at 1.0, 1.5, and 2.0 for continuous outcome and 5.0, 10.0, and 20.0 for binary outcome to represent low, medium and high signal strength. The detailed parameter settings for the four scenarios were included in the Supplementary File.
3.2. Competing Methods, Model Selection and Evaluation
3.2.1. Competing Methods
We compared the proposed method (SICS) to Lasso, MCP and Elastic Net (Enet), the three sparse regression models without considering the phylogenetic tree. We also compared SICS to a Laplacian-regularized sparse regression model as implemented in glmgraph (SLS) (Chen et al., 2015). The Laplacian matrix L was constructed using the same phylogeny-induced correlation matrix C as the adjacency matrix. L was further sparsified to 90% sparsity level to reduce the adverse effects of distantly related OTUs on the outcome prediction. Besides those sparse regression models, we also compared SICS to a representative machine learning method, Random Forest (RF), which has been demonstrated good prediction performance on microbiome data (Pasolli et al., 2016). The parameter settings for the competing methods were shown in Box 1.
Box 1. Parameter settings for competing methods
• Lasso: glmnet R package, all parameters were set as the default.
• Elastic Net (Enet): glmnet R package. Tuning parameter for l2 penalty was searched on the grid .
• MCP: ncvreg R package, all parameters were set as the default.
• SLS: glmgraph R package, the search grid for λ2 and α were set the same as SICS.
• Random Forest (RF): randomForest R package, parameters were set as default.
3.2.2. Model Selection and Evaluation
For SICS, the parameters (λ1, λ2, α) were tuned to achieve optimal model sparsity and phylogenetic depth. Specifically, we searched their best combination over a three-dimensional grids. λ2 was searched on the grid , and α on the grid , while λ1 was selected from a finer grid on a log scale from the most sparse to a very dense model as implemented in glmgraph and glmnet.
The best tuning parameter values were selected based on 5-fold cross-validation (CV), where the training samples were randomly divided into 5-folds with 4-folds for model fitting and the remaining fold for testing . We used PMSE (Predicted Mean Square Error) as the CV criterion for a continuous outcome and AUC (Area Under the Curve) for a binary outcome as in Xiao et al. (2018). Once the optimal tuning parameters were selected, we fit the final model using all the training samples and evaluated the prediction on independent testing samples.
To evaluate the prediction performance, we used PMSE (“Brier score” for a binary outcome), which quantifies the discrepancy between the predicted and observed values. In addition, we also investigated the R2, which quantifies the (squared) correlation between the predicted and observed values and ranges from 0 (no correlation) to 1 (perfect correlation). Detailed definition of R2 could be found in Xiao et al. (2018).
Although we focused our evaluation on outcome prediction, variable selection and parameter estimation performance were also investigated to gain more insights about the improved prediction performance of SICS. Variable selection was assessed by sensitivity and specificity, where sensitivity is the true positive rate, i.e., the proportion of aOTUs that are selected, and specificity is true negative rate, i.e., the proportion of irrelevant OTUs that are not selected. The parameter estimation performance was evaluated using MSE (Estimation Mean-Squared Error). Each simulation setting was repeated 50 times and the averages and standard errors of the performance measures were reported.
3.3. Simulation Results
3.3.1. Results for Continuous-Outcome Data
We evaluated the prediction performance in terms of both R2 and PMSE across different scenarios and signal strengths (Figure 3). We observed a general increase in performance for all methods when the signal strength increased. When the phylogenetic tree was informative (Scenario S1 and S2), SICS outperformed other methods substantially with a much larger R2 and lower PMSE across all levels of signal strength. The improvement of SICS over other methods was more evident when the signal strength decreased, indicating the importance of using the tree prior to pool signals when the signal was weak. Under the weak signal, SICS had a clear advantage over SLS, which uses the Laplacian penalty to smooth the coefficients, demonstrating the benefit of using the proposed smoothness penalty that encourages more local smoothing. SICS and SLS were both significantly better than other sparse regression methods and RF across different levels of signal strength. The lower performance of these sparse regression methods was due to their inability to exploit the phylogenetic structure. The improved prediction performance of SICS could be explained by more accurate parameter estimation evidenced by a lower MSE (Figure S1) and an increased sensitivity to retain the aOTUs (Figure S2). Although the increased sensitivity was at the cost of a slightly lower specificity (Figure S3), inclusion of aOTUs was more important than exclusion of non-aOTUs to improve prediction. We also observed that SICS performed similarly in Scenario S1, S2, indicating the robustness of SICS to the variation of the effect size of individual aOTUs as long as the effects are in the same direction.
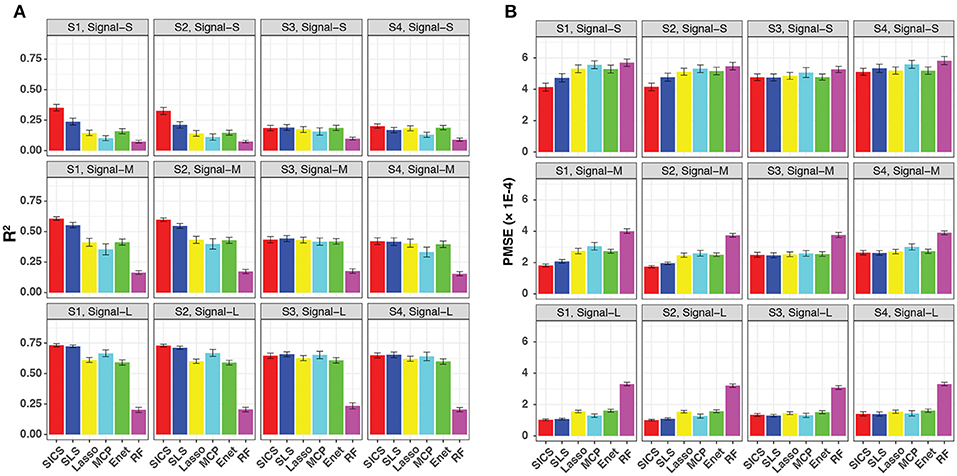
Figure 3. Prediction performance for continuous-outcome simulations across different signal levels and scenarios. Both R2 (A) and PMSE (B) were used for evaluation. S1, S2: phylogeny-informative scenarios, and S3, S4: phylogeny-non-informative scenarios; Signal-S, -M, and -L represent weak, medium and strong signals, respectively.
It should be noted that SICS achieved similar performance as other sparse regression methods in its unfavorable scenarios, when the phylogenetic tree was not informative (Scenarios S3 and S4), demonstrating the robustness of SICS. The comparable performance could be explained by that the additional parameters λ2, α, which makes MCP and Enet as special cases of SICS.
3.3.2. Results for Binary-Outcome Data
We repeated the same simulations for binary-outcome data and presented the results in Figure 4. Compared to the continuous outcome-based simulations, the prediction improvement of SICS was even more striking when the phylogenetic tree was informative (Scenarios S1 and S2). SICS achieved a significantly larger R2 and smaller Brier Score than other methods across different levels of signal strength. The advantage was even evident when the signal was strong, which was not observed for continuous-outcome data. Overall, a similar trend was observed: SICS had the best performance, followed by SLS under an informative phylogeny; SICS was comparable to other methods for a non-informative phylogeny. The advantage of SICS could be explained by a higher sensitivity of selecting aOTUs (Figure S4) at some cost of specificity (Figure S5).
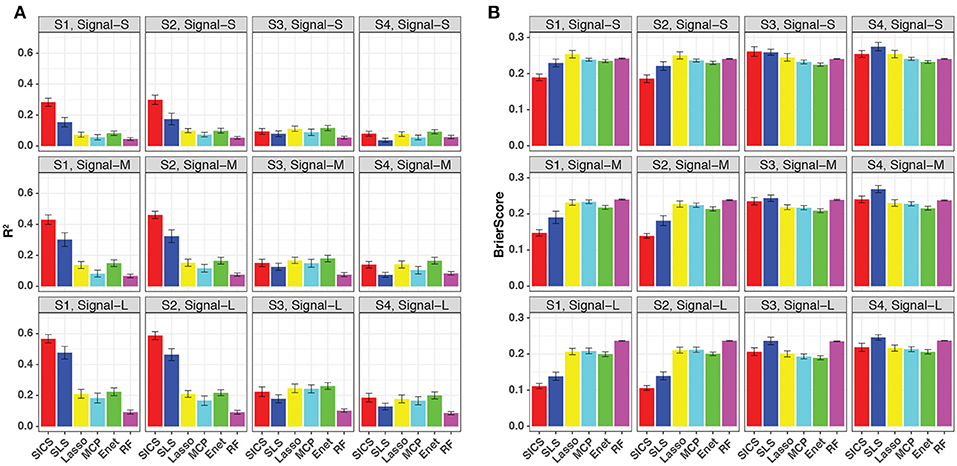
Figure 4. Prediction performance for binary-outcome simulations across different signal levels and scenarios. Both R2 (A) and Brier score (B) were used for evaluation. S1, S2: phylogeny-informative scenarios, and S3, S4: phylogeny-non-informative scenarios; Signal-S, -M, and -L represent weak, medium and strong signals, respectively.
3.3.3. Comparison to SLS With Different Sparsity Levels in the Laplacian Matrix
In the above simulation, we adopted a sparsity level of 90% in the Laplacian matrix L for SLS, which generally resulted a satisfactory prediction performance. To further investigate the impact of sparsity level on the prediction performance of SLS, we compared SICS to SLS with different levels of sparsity in L. We tested sparsity levels at 0, 10, 30, 50, 70, and 90% and 0% sparsity indicates no sparsification.
For the continuous-outcome data, SICS consistently outperformed SLS in Scenario S1 & S2 when the signal was weak or medium, and was on par with SLS when the signal was strong (Figures S6, S7). When the tree was not informative (Scenarios S3, S4), SLS was not sensitive to the sparsity level as expected and the performance was similar to SICS. For binary-outcome data, the performance difference between SICS and SLS was even more striking and SICS performed much better across levels of signal strength when the phylogeny was informative (Figures S8, S9). We also found that the performance of SLS varied for different levels of sparsity, and SLS generally achieved the best prediction at a sparsity level of 90%. In contrast, SICS did not need to select the optimal sparsity level and had an overall better performance than SLS, regardless of the sparsity level used.
4. Real Data Applications
We applied SCIS to two real microbiome datasets and compared it to the competing methods evaluated in the simulations. We compared to two versions of SLS: SLS without sparsifying L matrix (SLS(0)) and SLS with 90% sparsity level (SLS(0.9)). In addition, we compared to glmmTree, a phylogeny-regularized linear model for dense and clustered microbiome signals (Xiao et al., 2018). The first dataset came from a study of the impact of the long-term dietary pattern on the gut microbiome. We used the caffein intake as the continuous outcome (Wu et al., 2011). The second dataset came from a study of the smoking effect on the human upper respiratory tract microbiome (Charlson et al., 2010). We used the microbiome data from the left side of the throat and treated the smoking status as the binary outcome.
4.1. Caffeine Intake Data
The caffeine intake data was taken from a cross-sectional study of long-term dietary effects on the human gut microbiome in a general population (Wu et al., 2011). The dataset was downloaded from Qiita (https://qiita.ucsd.edu/) with study ID 1011, which consists of 98 samples and 6674 OTUs. We selected the caffeine intake as the outcome of interest since caffeine intake was found to have a significant impact on the gut microbiota (Jaquet et al., 2009). We aimed to predict the caffeine intake based on the OTU abundances. Before applying the prediction methods, we implemented a series of preprocessing steps designed in Xiao et al. (2018) to make the microbiome data more amenable to predictive modeling. First, we removed outlier samples based on an outlier index defined on Bray-Curtis distance and removed rare OTUs with prevalence < 10% to reduce the dimensionality of OTUs, leaving 98 samples and 499 OTUs. Second, we normalized OTU raw read counts using GMPR (Chen et al., 2018) followed by a replacement of outlier counts using winsorization at 97% quantile. Third, we transformed the normalized OTU abundance data using square-root transformation to reduce the influence of highly abundant observation. Finally, we applied quantile transformation to the caffeine intake to make it approximately normally distributed.
To have an objective evaluation of the prediction performance, the dataset was randomly divided 50 times into 5 folds each time, among which 4 folds were used for training and the remaining one for testing. In the training set, tuning parameter selection was based on CV as in the simulation. R2 and PMSE were used as metrics for prediction performance based on the testing set. The results were presented in Figures 5A,B. SICS achieved the best performance for caffeine intake prediction as indicated by the highest R2 and lowest PMSE, followed by Elastic Net, SLS and Random Forest. On the other hand, Elastic Net and SLS, which had data-driven smoothing and prior-driven smoothing, respectively, did improve over Lasso and MCP, which only exploited the model sparsity. To verify whether the improvement of prediction was statistically significant, we performed paired Wilcoxon signed-rank test between SICS and any other methods based on R2, PMSE values obtained from the fifty random divisions. SICS achieved significantly higher R2, and significantly lower PMSE than any other method (P < 0.05).
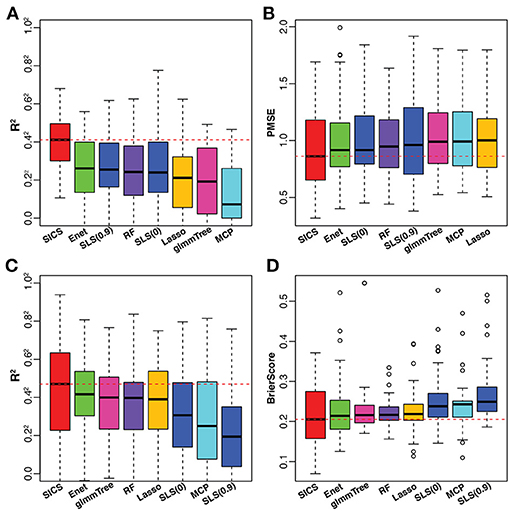
Figure 5. Performance comparison on the caffeine intake data (A,B) and smoking data (C,D). The red dashed line indicates the median value of various performance measures for SICS. SLS(0): SLS without sparsification; SLS(0.9): SLS with 90% sparsity level in the Laplacian matrix.
4.2. Smoking Data
The smoking data was from a study of the smoking effect on the human upper respiratory tract microbiome (Charlson et al., 2010). We aimed to predict the smoking status based on the microbiome profile. All the data processing steps were carried out as described in the previous example. After preprocessing, the final dataset consisted of 32 non-smokers and 28 smokers with 174 OTUs. For smoking vs. non-smoking prediction, SICS still achieved the highest R2 and lowest Brier Score, followed by Elastic Net, glmmTree and Random Forest (Figures 5C,D). However, SLS did not improve the prediction performance compared to Lasso and MCP. We also noticed that SLS(0) and SLS(0.9) performed differently (R2 P = 0.01; Brier Score P = 0.12). Overall, SICS achieved the best prediction performance for both continuous caffeine intake and dichotomous smoking status.
5. Discussion
The power of a predictive model depends on its capability to exploit the full information in the data, which usually requires domain knowledge. For microbiome data, one unique characteristic is the phylogenetic relationship relating all OTUs, which is important prior information that could be utilized to improve prediction performance. In this paper, we proposed a phylogeny-regularized sparse regression model for capturing sparse and clustered microbiome signals. In the model, a novel phylogeny-based smoothness penalty was designed based on the inverse of phylogeny-induced correlation matrix. We show that such inverse correlation-based smoothness penalty improved over the traditional Laplacian-based smoothness penalty for microbiome applications, due to its local smoothing property as well as the dual smoothing effects (i.e., data-driven and prior-driven smoothing). Moreover, an additional tuning parameter in the smoothness penalty allows our model to capture signals at various phylogenetic depths, further improving its prediction power. We demonstrated the robustness of the proposed method when the tree was not informative or misspecified. A noisy or misspecified tree could be resulted from applying an inappropriate tree construction method or be due to the fact that DNA sequence similarity does not necessarily reflect biological similarity. Interestingly, the proposed method could reduce to Mnet (Huang et al., 2016), which possesses the data-driven smoothing effect.
Similar to other sparse regression models, the proposed method builds on the assumption that the model is sparse: only a few OTUs are associated with the outcome. It is thus expected to be a powerful predictive tool when the signal is sparse. Many diseases have been shown to be associated with a small number of “marker” taxa. For example, in the case of colorectal cancer or arthritis (Scher et al., 2013; Zeller et al., 2014), individual marker taxa were found to be associated to the disease state, whereas effects on the overall composition were very mild. In contrast, other disease states were associated with marked shifts in the overall composition as in the case of obesity and inflammatory bowel disease (Manichanh et al., 2012; Le Chatelier et al., 2013). In such “dense-signal” scenario, sparse regression models including the proposed approach may not work well. Instead, a prediction model based on the global community similarity, such as our recently proposed glmmTree (Xiao et al., 2018), is expected to be more powerful. Exploratory analysis of the microbiome data should be performed before selecting a suitable model.
In the model, we assume a linear relationship between the OTU abundance and the outcome. Although the assumption is usually reasonable after the abundance data is properly normalized and transformed, it may fail to capture complex nonlinear relationship for some applications. Our model can be extended to capture more complex nonlinear effects. The simplest strategy is to apply various transformations, e.g., Box-cox transformation (Sakia, 1992), to the OTU abundance data and selects the best transformation function based on cross-validation. In the case of Box-cox transformation, the power parameter can be treated as another tuning parameter (Xiao and Chen, 2017; Xiao et al., 2018). Alternatively, one could apply an additive model, which is more flexible and allows OTU-specific nonlinear effects (Wood, 2006). However, a larger sample size may be needed to achieve good performance.
Finally, the distribution of OTU abundances is very skewed, and a large number of OTUs are rare and of low-abundance. For these rare OTUs, their sampling variability is very large. Accommodating the sampling error in the predictive model could potentially improve the prediction performance. Jointly modeling the microbiome and the outcome data is thus a promising direction. We leave these extensions as our future work.
Author Contributions
JX analyzed the data, wrote the paper, prepared figures and tables, reviewed drafts of the paper. LC analyzed the data, wrote the paper, prepared figures and tables, wrote the software, reviewed drafts of the paper. YY prepared figures and tables, reviewed drafts of the paper. XZ contributed substantial expertise to improve the paper and revised the paper. JC conceived and designed the experiments, analyzed the data, wrote the paper, wrote the software, prepared figures and tables.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by Mayo Clinic Gerstner Family Career Development Awards, Mayo Clinic Center for Individualized Medicine, U01 FD005875, Food and Drug Administration and the National Natural Science Foundation of China (no.61773401 and no.11801571).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2018.03112/full#supplementary-material
References
Ahn, J., Sinha, R., Pei, Z., Dominianni, C., Wu, J., Shi, J., et al. (2013). Human gut microbiome and risk for colorectal cancer. J. Natl. Cancer Inst. 105, 1907–1911. doi: 10.1093/jnci/djt300
Amir, A., McDonald, D., Navas-Molina, J. A., Kopylova, E., Morton, J. T., Xu, Z. Z., et al. (2017). Deblur rapidly resolves single-nucleotide community sequence patterns. MSystems 2, e00191–16. doi: 10.1128/mSystems.00191-16
Breheny, P., and Huang, J. (2011). Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Ann. Appl. Stat. 5, 232–253. doi: 10.1214/10-AOAS388
Bultman, S. J. (2014). Emerging roles of the microbiome in cancer. Carcinogenesis 35, 249–255. doi: 10.1093/carcin/bgt392
Callahan, B. J., McMurdie, P. J., Rosen, M. J., Han, A. W., Johnson, A. J., and Holmes, S. P. (2016). Dada2: high-resolution sample inference from illumina amplicon data. Nat. Methods 13, 581–583. doi: 10.1038/nmeth.3869
Caporaso, J. G., Kuczynski, J., Stombaugh, J., Bittinger, K., Bushman, F. D., Costello, E. K., et al. (2010). Qiime allows analysis of high-throughput community sequencing data. Nat. Methods 7:335. doi: 10.1038/nmeth.f.303
Caporaso, J. G., Lauber, C. L., Walters, W. A., Berg-Lyons, D., Huntley, J., Fierer, N., et al. (2012). Ultra-high-throughput microbial community analysis on the illumina hiseq and miseq platforms. ISME J. 6:1621. doi: 10.1038/ismej.2012.8
Charlson, E. S., Chen, J., Custers-Allen, R., Bittinger, K., Li, H., Sinha, R., et al. (2010). Disordered microbial communities in the upper respiratory tract of cigarette smokers. PLoS ONE 5:e15216. doi: 10.1371/journal.pone.0015216
Chen, J., Bittinger, K., Charlson, E. S., Hoffmann, C., Lewis, J., Wu, G. D., et al. (2012). Associating microbiome composition with environmental covariates using generalized unifrac distances. Bioinformatics 28, 2106–2113. doi: 10.1093/bioinformatics/bts342
Chen, J., Bushman, F. D., Lewis, J. D., Wu, G. D., and Li, H. (2013a). Structure-constrained sparse canonical correlation analysis with an application to microbiome data analysis. Biostatistics 14, 244–258. doi: 10.1093/biostatistics/kxs038
Chen, J., Wright, K., Davis, J. M., Jeraldo, P., Marietta, E. V., Murray, J., et al. (2016). An expansion of rare lineage intestinal microbes characterizes rheumatoid arthritis. Genome Med. 8:43. doi: 10.1186/s13073-016-0299-7
Chen, L., Liu, H., Kocher, J. P., Li, H., and Chen, J. (2015). glmgraph: an r package for variable selection and predictive modeling of structured genomic data. Bioinformatics 31, 3991–3993. doi: 10.1093/bioinformatics/btv497
Chen, L., Reeve, J., Zhang, L., Huang, S., Wang, X., and Chen, J. (2018). Gmpr: A robust normalization method for zero-inflated count data with application to microbiome sequencing data. PeerJ 6:e4600. doi: 10.7717/peerj.4600
Chen, W., Zhang, C. K., Cheng, Y., Zhang, S., and Zhao, H. (2013b). A comparison of methods for clustering 16s rrna sequences into otus. PLoS ONE 8:e70837. doi: 10.1371/journal.pone.0070837
Chen, X., Johnson, S., Jeraldo, P., Wang, J., Chia, N., Kocher, J. A., et al. (2017). Hybrid-denovo: a de novo otu-picking pipeline integrating single-end and paired-end 16s sequence tags. Gigascience 7, 1–7. doi: 10.1093/gigascience/gix129
Cho, I., and Blaser, M. J. (2012). The human microbiome: at the interface of health and disease. Nat. Rev. Genet 13, 260–270. doi: 10.1038/nrg3182
Edgar, R. C. (2013). Uparse: highly accurate otu sequences from microbial amplicon reads. Nat. Methods 10, 996–998. doi: 10.1038/nmeth.2604
Edgar, R. C. (2018). Updating the 97% identity threshold for 16s ribosomal rna otus. Bioinformatics 1:5. doi: 10.1093/bioinformatics/bty113
Evans, S. N., and Matsen, F. A. (2012). The phylogenetic kantorovich-rubinstein metric for environmental sequence samples. J. R. Stat. Soc. B 74, 569–592. doi: 10.1111/j.1467-9868.2011.01018.x
Friedman, J., Hastie, T., and Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. J. Stat. Sofw. 33, 1–22. doi: 10.18637/jss.v033.i01
Garcia, T. P., Muller, S., Carroll, R. J., and Walzem, R. L. (2014). Identification of important regressor groups, subgroups and individuals via regularization methods: application to gut microbiome data. Bioinformatics 30, 831–837. doi: 10.1093/bioinformatics/btt608
Honda, K., and Littman, D. R. (2012). The microbiome in infectious disease and inflammation. Annu. Rev. Immunol. 30, 759–795. doi: 10.1146/annurev-immunol-020711-074937
Huang, J., Breheny, P., Lee, S., Ma, S., and Zhang, C. (2016). The mnet method for variable selection. Stat. Sin. 26, 903–923. doi: 10.5705/ss.202014.0011
Huang, J., Ma, S., Li, H., and Zhang, C. H. (2011). The sparse laplacian shrinkage estimator for high-dimensional regression. Ann. Stat. 39, 2021–2046. doi: 10.1214/11-AOS897
Jangi, S., Gandhi, R., Cox, L. M., Li, N., von Glehn, F., Yan, R., et al. (2016). Alterations of the human gut microbiome in multiple sclerosis. Nat. Commun. 7:12015. doi: 10.1038/ncomms12015
Jaquet, M., Rochat, I., Moulin, J., Cavin, C., and Bibiloni, R. (2009). Impact of coffee consumption on the gut microbiota: a human volunteer study. Int. J. Food Microbiol. 130, 117–121. doi: 10.1016/j.ijfoodmicro.2009.01.011
Kashyap, P. C., Chia, N., Nelson, H., Segal, E., and Elinav, E. (2017). Microbiome at the frontier of personalized medicine. Mayo Clin. Proc. 92, 1855–1864. doi: 10.1016/j.mayocp.2017.10.004
Kembel, S. W., Eisen, J. A., Pollard, K. S., and Green, J. L. (2011). The phylogenetic diversity of metagenomes. PLoS ONE 6:e23214. doi: 10.1371/journal.pone.0023214
Kinross, J. M., Darzi, A. W., and Nicholson, J. K. (2011). Gut microbiome-host interactions in health and disease. Genome Med. 3:14. doi: 10.1186/gm228
Knights, D., Costello, E. K., and Knight, R. (2011). Supervised classification of human microbiota. FEMS Microbiol. Rev. 35, 343–359. doi: 10.1111/j.1574-6976.2010.00251.x
Kuczynski, J., Lauber, C. L., Walters, W. A., Parfrey, L. W., Clemente, J. C., Gevers, D., et al. (2011). Experimental and analytical tools for studying the human microbiome. Nat. Rev. Genet 13, 47–58. doi: 10.1038/nrg3129
Le Chatelier, E., Nielsen, T., Qin, J., Prifti, E., Hildebrand, F., Falony, G., et al. (2013). Richness of human gut microbiome correlates with metabolic markers. Nature 500:541. doi: 10.1038/nature12506
Li, C., and Li, H. (2008). Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics 24, 1175–1182. doi: 10.1093/bioinformatics/btn081
Mallick, H., Ma, S., Franzosa, E. A., Vatanen, T., Morgan, X. C., and Huttenhower, C. (2017). Experimental design and quantitative analysis of microbial community multiomics. Genome Biol. 18:228. doi: 10.1186/s13059-017-1359-z
Manichanh, C., Borruel, N., Casellas, F., and Guarner, F. (2012). The gut microbiota in ibd. Nat. Rev. Gastroenterol. Hepatol. 9:599. doi: 10.1038/nrgastro.2012.152
Martins, E. P., and Hansen, T. F. (1997). Phylogenies and the comparative method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. Amer. Nat. 149, 646–667. doi: 10.1086/286013
Martiny, J. B., Jones, S. E., Lennon, J. T., and Martiny, A. C. (2015). Microbiomes in light of traits: a phylogenetic perspective. Science 350:aac9323. doi: 10.1126/science.aac9323
McDonald, D., Hyde, E., Debelius, J. W., Morton, J. T., Gonzalez, A., Ackermann, G., et al. (2018). American gut: an open platform for citizen science microbiome research. mSystems 3, e00031–18. doi: 10.1128/mSystems.00031-18
Ning, J., and Beiko, R. G. (2015). Phylogenetic approaches to microbial community classification. Microbiome 3:47. doi: 10.1186/s40168-015-0114-5
Pasolli, E., Truong, D. T., Malik, F., Waldron, L., and Segata, N. (2016). Machine learning meta-analysis of large metagenomic datasets: tools and biological insights. PLoS Comput. Biol. 12:e1004977. doi: 10.1371/journal.pcbi.1004977
Peters, B. A., Wu, J., Pei, Z., Yang, L., Purdue, M. P., Freedman, N. D., et al. (2017). Oral microbiome composition reflects prospective risk for esophageal cancers. Cancer Res. 77, 6777–6787. doi: 10.1158/0008-5472.CAN-17-1296
Pflughoeft, K. J., and Versalovic, J. (2012). Human microbiome in health and disease. Annu. Rev. Pathol. 7, 99–122. doi: 10.1146/annurev-pathol-011811-132421
Price, M. N., Dehal, P. S., and Arkin, A. P. (2010). Fasttree 2-approximately maximum-likelihood trees for large alignments. PLoS ONE 5:e9490. doi: 10.1371/journal.pone.0009490
Purdom, E. (2011). Analysis of a data matrix and a graph: metagenomic data and the phylogenetic tree. Ann. Appl. Stat. 5, 2326–2358. doi: 10.1214/10-AOAS402
Qin, J., Li, Y., Cai, Z., Li, S., Zhu, J., Zhang, F., et al. (2012). A metagenome-wide association study of gut microbiota in type 2 diabetes. Nature 490, 55–60. doi: 10.1038/nature11450
Randolph, T. W., Zhao, S., Copeland, W., Hullar, M., and Shojaie, A. (2018). Kernel-penalized regression for analysis of microbiome data. Ann. Appl. Stat. 12, 540–566. doi: 10.1214/17-AOAS1102
Rideout, J. R., He, Y., Navas-Molina, J. A., Walters, W. A., Ursell, L. K., Gibbons, S. M., et al. (2014). Subsampled open-reference clustering creates consistent, comprehensive otu definitions and scales to billions of sequences. PeerJ 2:e545. doi: 10.7717/peerj.545
Sakia, R. (1992). The box-cox transformation technique: a review. Statistician 63, 169–178. doi: 10.2307/2348250
Scher, J. U., Sczesnak, A., Longman, R. S., Segata, N., Ubeda, C., Bielski, C., et al. (2013). Expansion of intestinal prevotella copri correlates with enhanced susceptibility to arthritis. elife 2:e01202. doi: 10.7554/eLife.01202
Schloss, P. D., Westcott, S. L., Ryabin, T., Hall, J. R., Hartmann, M., Hollister, E. B., et al. (2009). Introducing mothur: open-source, platform-independent, community-supported software for describing and comparing microbial communities. Appl. Environ. Microbiol. 75, 7537–7541. doi: 10.1128/AEM.01541-09
Statnikov, A., Henaff, M., Narendra, V., Konganti, K., Li, Z., Yang, L., et al. (2013). A comprehensive evaluation of multicategory classification methods for microbiomic data. Microbiome 1:11. doi: 10.1186/2049-2618-1-11
Tanaseichuk, O., Borneman, J., and Jiang, T. (2014). Phylogeny-based classification of microbial communities. Bioinformatics 30, 449–56. doi: 10.1093/bioinformatics/btt700
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58, 267–288.
Turnbaugh, P. J., Hamady, M., Yatsunenko, T., Cantarel, B. L., Duncan, A., Ley, R. E., et al. (2009). A core gut microbiome in obese and lean twins. Nature 457, 480–484. doi: 10.1038/nature07540
Waldron, L., Pintilie, M., Tsao, M.-S., Shepherd, F. A., Huttenhower, C., and Jurisica, I. (2011). Optimized application of penalized regression methods to diverse genomic data. Bioinformatics 27, 3399–3406. doi: 10.1093/bioinformatics/btr591
Walther-Antonio, M. R., Chen, J., Multinu, F., Hokenstad, A., Distad, T. J., Cheek, E. H., et al. (2016). Potential contribution of the uterine microbiome in the development of endometrial cancer. Genome Med. 8:122. doi: 10.1186/s13073-016-0368-y
Wang, T., and Zhao, H. (2017). Constructing predictive microbial signatures at multiple taxonomic levels. J. Am. Stat. Assoc. 112, 1022–1031. doi: 10.1080/01621459.2016.1270213
Wood, S. N. (2006). Generalized Additive Models: An Introduction With R. London: Chapman and Hall/CRC.
Wu, G. D., Chen, J., Hoffmann, C., Bittinger, K., Chen, Y.-Y., Keilbaugh, S. A., et al. (2011). Linking long-term dietary patterns with gut microbial enterotypes. Science 334, 105–108. doi: 10.1126/science.1208344
Xiao, J., Cao, H., and Chen, J. (2017). False discovery rate control incorporating phylogenetic tree increases detection power in microbiome-wide multiple testing. Bioinformatics 33, 2873–2881. doi: 10.1093/bioinformatics/btx311
Xiao, J., and Chen, J. (2017). “Phylogeny-based kernels with application to microbiome association studies,” in New Advances in Statistics and Data Science, eds D. G. Chen, Z. Jin, G. Li, Y. Li, A. Liu, and Y. Zhao (Cham: Springer), 217–237.
Xiao, J., Chen, L., Johnson, S., Yu, Y., Zhang, X., and Chen, J. C. (2018). Predictive modeling of microbiome data using a phylogeny-regularized generalized linear mixed model. Front. microbiol. 9:1391. doi: 10.3389/fmicb.2018.01391
Zeller, G., Tap, J., Voigt, A. Y., Sunagawa, S., Kultima, J. R., Costea, P. I., et al. (2014). Potential of fecal microbiota for early-stage detection of colorectal cancer. Mol. Syst. Biol. 10:766. doi: 10.15252/msb.20145645
Zhang, C. H. (2010). Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 58, 267–288. doi: 10.1214/09-AOS729
Keywords: microbiome, phylogenetic tree, sparse generalized linear model, predictive model, statistical modeling, high-dimenisonal statistics
Citation: Xiao J, Chen L, Yu Y, Zhang X and Chen J (2018) A Phylogeny-Regularized Sparse Regression Model for Predictive Modeling of Microbial Community Data. Front. Microbiol. 9:3112. doi: 10.3389/fmicb.2018.03112
Received: 31 August 2018; Accepted: 03 December 2018;
Published: 19 December 2018.
Edited by:
Qi Zhao, Liaoning University, ChinaReviewed by:
Jonathan Badger, National Cancer Institute (NCI), United StatesAdina Howe, Iowa State University, United States
Copyright © 2018 Xiao, Chen, Yu, Zhang and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Li Chen, bGkuY2hlbkBhdWJ1cm4uZWR1
Jun Chen, Y2hlbi5qdW4yQG1heW8uZWR1
 Jian Xiao1,2
Jian Xiao1,2 Li Chen
Li Chen Xianyang Zhang
Xianyang Zhang Jun Chen
Jun Chen