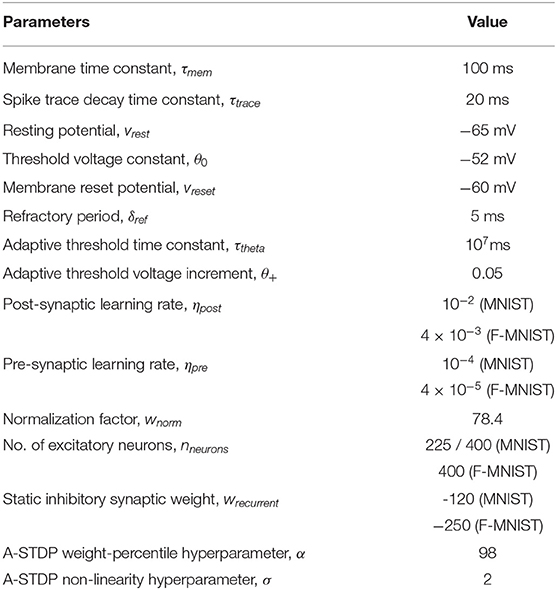
- 1School of Electrical Engineering and Computer Science, Pennsylvania State University (PSU), University Park, PA, United States
- 2Department of Computer Science and Information Systems, Birla Institute of Technology and Science Pilani, Goa Campus, India
Neuromorphic computing is emerging to be a disruptive computational paradigm that attempts to emulate various facets of the underlying structure and functionalities of the brain in the algorithm and hardware design of next-generation machine learning platforms. This work goes beyond the focus of current neuromorphic computing architectures on computational models for neuron and synapse to examine other computational units of the biological brain that might contribute to cognition and especially self-repair. We draw inspiration and insights from computational neuroscience regarding functionalities of glial cells and explore their role in the fault-tolerant capacity of Spiking Neural Networks (SNNs) trained in an unsupervised fashion using Spike-Timing Dependent Plasticity (STDP). We characterize the degree of self-repair that can be enabled in such networks with varying degree of faults ranging from 50 to 90% and evaluate our proposal on the MNIST and Fashion-MNIST datasets.
1. Introduction
Neuromorphic computing has made significant strides over the past few years—both from hardware (Merolla et al., 2014; Sengupta and Roy, 2017; Davies et al., 2018; Singh et al., 2020) and algorithmic perspective (Diehl and Cook, 2015; Neftci et al., 2019; Sengupta et al., 2019; Lu and Sengupta, 2020). However, the quest to decode the operation of the brain have mainly focused on spike based information processing in the neurons and plasticity in the synapses. Over the past few years, there has been increasing evidence that glial cells, and in particular astrocytes, play a crucial role in a multitude of brain functions (Allam et al., 2012). As a matter of fact, astrocytes represent a large proportion of the cell population in the human brain (Allam et al., 2012). There have been also suggestions that complexity of astrocyte functionality can significantly contribute to the computational power of the human brain. Astrocytes are strategically positioned to ensheath tens of thousands of synapses, axons and dendrites among others, thereby having the capability to serve as a communication channel between multiple components and behave as a sensing medium for ongoing brain activity (Chung et al., 2015). This has led neuroscientists to conclude that astrocytes play a major role in higher order brain functions like learning and memory, in addition to neurons and synapses. Over the past few years, there have been multiple studies to revise the neuron-circuit model for describing higher order brain functions to incorporate astrocytes as part of the neuron-glia network model (Allam et al., 2012; Min et al., 2012). These investigations clearly indicate and quantify that incorporating astrocyte functionality in network models influence neuron excitability, synaptic strengthening and, in turn, plasticity mechanisms like Short-Term Plasticity and Long-Term Potentiation, which are important learning tools used by neuromorphic engineers.
The key distinguishing factors of our work against prior efforts can be summarized as follows:
(i) While recent literature reports astrocyte computational models and their impact on fault-tolerance and synaptic learning (Allam et al., 2012; De Pittà et al., 2012; Gordleeva et al., 2012; Min et al., 2012; Wade et al., 2012), the studies have been mostly confined to small scale networks. This work is a first attempt to explore the self-repair role of astrocytes at scale in unsupervised SNNs in standard visual recognition tasks.
(ii) In parallel, there is a long history of implementing astrocyte functionality in analog and digital CMOS implementations (Irizarry et al., 2013; Nazari et al., 2015; Ranjbar and Amiri, 2015; Lee and Parker, 2016; Liu et al., 2017; Amiri et al., 2018; Karimi et al., 2018). More recently, emerging physics in post-CMOS technologies like spintronics are also being leveraged to mimic glia functionalities at a one-to-one level (Garg et al., 2020). However, the primary focus has been on a brain-emulation perspective, i.e., implementing astrocyte computational models with high degree of detail in the underlying hardware. We explore the aspects of astrocyte functionality that would be relevant to self-repair in the context of SNN based machine learning platforms and evaluate the degree of bio-fidelity required.
(iii) While Refs. (Hazan et al., 2019; Saunders et al., 2019b) discusses impact of faults in unsupervised STDP enabled SNNs, self-repair functionality in such networks have not been studied previously.
While neuromorphic hardware based on emerging post-CMOS technologies (Jo et al., 2010; Kuzum et al., 2011; Ramakrishnan et al., 2011; Jackson et al., 2013; Sengupta and Roy, 2017) have made significant advancements to reduce the area and power efficiency gap of Artificial Intelligence (AI) systems, such emerging hardware are characterized by a host of non-idealities which has greatly limited its scalability. Our work provides motivation toward autonomous self-repair of such faulty neuromorphic hardware platforms. The efficacy of our proposed astrocyte enabled self-repair process is measured by the following steps: (i) Training SNNs using unsupervised STDP learning rules in networks equipped with lateral inhibition and homeostasis, (ii) Introducing “faults”1 in the trained weight maps by setting a randomly chosen subset of the weights to zero and (iii) Implementing self-repair by re-training the faulty network with astrocyte functionality augmented STDP learning rules. We also compare our proposal with sole STDP based re-training strategy and substantiate our results on the MNIST and F-MNIST datasets.
2. Materials and Methods
2.1. Astrocyte Preliminaries
In addition to astrocyte mediated meta-plasticity for learning and memory (Nadkarni and Jung, 2004, 2007; Volman et al., 2007; Wade et al., 2012), there has been indication that retrograde signaling via astrocytes probably underlie self-repair in the brain. Computational models demonstrate that when faults occur in synapses corresponding to a particular neuron, indirect feedback signal (mediated through retrograde signaling by the astrocyte via endocannabinoids, a type of retrograde messenger) from other neurons in the network implements repair functionality by increasing the transmission probability across all healthy synapses for the affected neuron, thereby restoring the original operation (Wade et al., 2012). Astrocytes modulate this synaptic transmission probability (PR) through two feedback signaling pathways: direct and indirect, responsible for synaptic depression (DSE) and potentiation (e-SP), respectively. Multiple astrocyte computational models (Nadkarni and Jung, 2004, 2007; Volman et al., 2007; Wade et al., 2012) describe the interaction of astrocytes and neurons via the tripartite synapse where the astrocyte's sensitivity to 2-arachidonyl glycerol (2-AG), a type of endocannabinoid, is considered. Each time a post synaptic neuron fires, 2-AG is released from the post synaptic dendrite and can be described as:
where, AG is the quantity of 2-AG, τAG is the decay rate of 2-AG, rAG is the 2-AG production rate and tsp is the time of the post-synaptic spike.
The 2-AG binds to receptors (CB1Rs) on the astrocyte process and instigates the generation of IP3, which subsequently binds to IP3 receptors on the Endoplasmic Reticulum (ER) to open channels that allow the release of Ca2+. It is this increase in cystolic Ca2+ that causes the release of gliotransmitters into the synaptic cleft that is ultimately responsible for the indirect signaling. The Li-Rinzel model (Li and Rinzel, 1994) uses three channels to describe the Ca2+ dynamics within the astrocyte: Jpump models how Ca2+ is pumped into the ER from the cytoplasm via the Sarco-Endoplasmic-Reticulum Ca2+-ATPase (SERCA) pumps, Jleak describes Ca2+ leakage into the cytoplasm and Jchan models the opening of Ca2+ channels by the mutual gating of Ca2+ and IP3 concentrations. The Ca2+ dynamics is thus given by:
The details of the equations and their derivations can be obtained from Wade et al. (2012) and De Pittà et al. (2009).
The intracellular astrocytic calcium dynamics control the glutamate release from the astrocyte which drives e-SP. This release can be modeled by:
where, Glu is the quantity of glutamate, τGlu is the glutamate decay rate, rGlu is the glutamate production rate and tCa is the time of the Ca2+ threshold crossing. To model e-SP:
where, τeSP is the decay rate of e-SP and meSP is a scaling factor. Equation (4) substantiates that the level of e-SP is dependent on the quantity of glutamate released by the astrocyte.
The released 2-AG also binds directly to pre-synpatic CB1Rs (direct signaling). A linear relationship is assumed between DSE and the level of 2-AG released by the post-synaptic neuron as:
where, AG is the amount of 2-AG released by the post-synaptic neuron and is found from Equation (1) and KAG is a scaling factor. The PR associated with each synapse is given by the following equation:
where, PR(t0) is the initial PR of the synapses, e-SP and DSE are given by Equations (4) and (5), respectively. In the computational models, the effect of DSE is local to the synapses connected to a particular neuron whereas all the tripartite synapses connected to the same astrocyte receive the same e-SP. Under no-fault condition, the DSE and e-SP reach a dynamic equilibrium where the PR is unchanged over time, resulting in a fixed firing rate for the neurons. When a fault occurs, this balance subsides and the PR changes according to Equation (6) to restore the firing rate to its previous value. To showcase this effect consider for instance, Figure 1 where a simple SNN with two post-synaptic neurons is depicted. Let us assume that each post-neuron receives input spikes from 10 pre-neurons. The initial PR of the synapses were set to 0.5. Figure 1A is the case with no faults, while in Figure 1B, faults have occurred after some time in 70% of the synapses associated with post-neuron N2 (Figure 2). Note, here “faults” imply that the synapses do not take part in transmission of the input spikes i.e., have a PR of 0. This results in a drop of the firing frequency associated with N2 while operation of N1 is not impacted. Thus, the amount of 2-AG released by N2 decreases, which increases DSE and in turn increases the PR of the associated synapses of N2 where no faults have occurred. Hence, we observe in Figure 2D that the increased PR recovers the firing rate and approaches the ideal firing frequency. Note that the degree of self-recovery, i.e., the difference between the recovered and ideal frequency is a function of the fault probability. The simulation conditions and parameters for the modeling are based on Wade et al. (2012). Interested readers are directed to Wade et al. (2012) for an extensive discussion on the astrocyte computational model and the underlying processes governing the retrograde signaling.
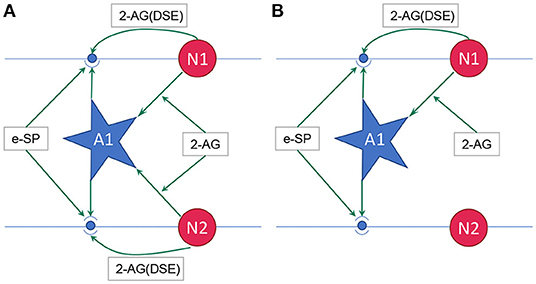
Figure 1. (A) Network with no faults, (B) Network with fault occurring in synapse associated with neuron N2 (Wade et al., 2012). 2-AG is local signal associated with each synapse while e-SP is a global signal. A1 is the astrocyte.
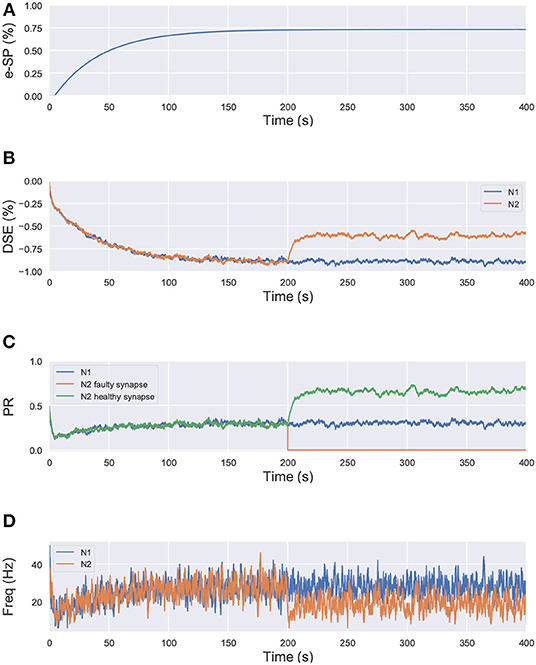
Figure 2. Simulation results of the network in Figure 1 using the computational model of astrocyte mediated self-repair from Wade et al. (2012). Total simulation time is 400 s. At 200 s, faults are introduced in 70% of the synapses connected to N2. All the synapses have PR(t0)=0.5. (A) e-SP of N1 and N2. It is the same for both N1 and N2 since e-SP is a global function, (B) DSE of N1 and N2. It is different for each neuron as it is dependent upon the neuron output. At 200 s, after the introduction of the faults in N2, only DSE of N2 changes, (C) PR of different types of synapses connected to N1 and N2, and (D) Firing rate of neurons N1 and N2.
A key question that we have attempted to address in this work is the computational complexity at which we require to model the feedback mechanism to implement autonomous repair in such self-learning networks. Simplifying the feedback modeling would enable us to implement such functionalities by efficient hardware primitives. For instance, the core functionality of astrocyte self-repair occurs in conjunction with STDP based learning in synapses. Figure 3 shows a typical STDP learning rule where the change in synaptic weight varies exponentially with the spike time difference between the pre- and post-neuron (Liu et al., 2018), according to measurements performed in rat glutamatergic synapses (Bi and Poo, 2001). Typically, the height of the STDP weight update for potentiation/depression is constant (A+/A−). However, astrocyte mediated self-repair suggests that the weight update should be a function of the firing rate of the post-neuron (Liu et al., 2018). Assuming the fault-less expected firing rate of the post-neuron to be fideal and the non-ideal firing rate to be f, the synaptic weight update window height should be a function of Δf = fideal − f. The concept has been explained further in Figure 3 and is also in accordance with Figure 2 where the PR increase after fault introduction varies in a non-linear fashion over time and eventually stabilizes once the self-repaired firing frequency approaches the ideal value. The functional dependence is assumed to be that of a sigmoid function—indicating that as the magnitude of the fault, i.e., deviation in the ideal firing frequency of the neuron increases, the height of the learning window increases in proportion to compensate for the fault (Liu et al., 2018). Note that the term “fault” for the machine learning workloads, described herein, refers to synaptic weights (symbolizing PR) stuck at zero. Therefore, with increasing amount of synaptic faults, f << fideal, thereby increasing the STDP learning window height significantly. During the self-healing process, the frequency deviation gradually reduces and thereby the re-learning rate also becomes less pronounced and finally saturates once the ideal frequency is reached. While our proposal is based on Liu et al. (2018), prior work has been explored in the context of a prototype artificial neural network with only 4 input neurons and 4 output neurons. Extending the framework to an unsupervised SNN based machine learning framework therefore requires significant explorations, highlighted next.
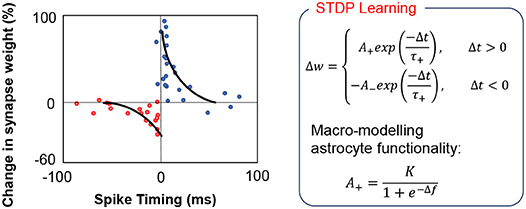
Figure 3. In the above equations, the STDP learning window height is a non-linear increasing function of the deviation Δf from the ideal firing frequency of the post-neuron.
2.2. Neuron Model and Synaptic Plasticity
We utilized the Leaky Integrate and Fire (LIF) spiking neuron model in our work. The temporal LIF neuron dynamics are described as,
where, v(t) is the membrane potential, τmem is the membrane time constant, vrest is the resting potential and I(t) denotes the total input to the neuron at time t. The weighted summation of synaptic inputs is represented by I(t). When the neuron's membrane potential crosses a threshold value, vth(t), it fires an output spike and the membrane potential is reset to vreset. The neuron's membrane voltage is fixed at the reset potential for a refractory period, δref, after it spikes during which it does not receive any inputs.
In order to ensure that single neurons do not dominate the firing pattern, homeostasis (Diehl and Cook, 2015) is also implemented through an adaptive thresholding scheme. The membrane threshold of each neuron is given by the following temporal dynamics,
where, θ0 > vrest, vreset and is a constant. τtheta is the adaptive threshold time constant. The adaptive threshold, θ(t) is increased by a constant quantity θ+, each time the neuron fires, and decays exponentially according to the dynamics in Equation 8.
A trace (Morrison et al., 2008) based synaptic weight update rule was used for the online learning process (Diehl and Cook, 2015; Saunders et al., 2019b). The pre and post-synaptic traces are given by xpre and xpost, respectively. Whenever the pre (post) - synaptic neuron fires, the variable xpre (xpost) is set to 1, otherwise it decays exponentially to 0 with spike trace decay time constant, τtrace. The STDP weight update rule is characterized by the following dynamics,
where, ηpre/ηpost denote the learning rates for pre-synaptic/post-synaptic updates, respectively. The weights of the neurons are bounded in the range of [0, wmax]. It is worth mentioning here that the sum of the weights associated with all post-synaptic neurons is normalized to a constant factor, wnorm (Saunders et al., 2019a).
2.3. Network Architecture
Our SNN based unsupervised machine learning framework is based on single layer architectures inspired from cortical microcircuits (Diehl and Cook, 2015). Figure 4 shows the network connectivity of spiking neurons utilized for pattern-recognition problems. Such a network topology has been shown to be efficient in several problems, such as digit recognition (Diehl and Cook, 2015) and sparse encoding (Knag et al., 2015). The SNN, under consideration, has an Input Layer with the number of neurons equivalent to the dimensionality of the input data. Input neurons generate spikes by converting each pixel in the input image to a Poisson spike train whose average firing frequency is proportional to the pixel intensity. This layer connects in an all-to-all fashion to the Output Layer through excitatory synapses. The Output layer has nneurons LIF neurons characterized by homeostasis functionality. It also has static (constant weights) recurrent inhibitory synapses with weight values, wrecurrent, for lateral inhibition to achieve soft Winner-Take-All (WTA) condition. Each neuron in the Output Layer has an inhibitory connection to all the neurons in that layer except itself. Trace-based STDP mechanism is used to learn the weights of all synapses between the Input and Output Layers. The neurons in the Output Layer are assigned classes based on their highest response (spike frequency) to input training patterns (Diehl and Cook, 2015).
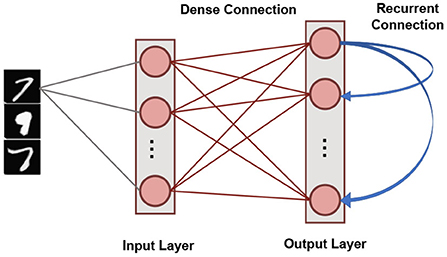
Figure 4. The single layer SNN architecture with lateral inhibition and homeostasis used for unsupervised learning.
2.4. Challenges and Astrocyte Augmented STDP (A-STDP) Learning Rule Formulation
One of the major challenges in extending the astrocyte based macro-modeling in such self-learning networks lies in the fact that the ideal neuron firing frequency is a function of the specific input class the neuron responds to. This is substantiated by Figure 5 which depicts the histogram distribution of the ideal firing rate of the wining neuron in the fault-less network. Further, due to sparse neural firing, the total number of output spikes of the winning neurons over the inference window is also small, thereby limiting the amount of information (number of discrete levels) that can be encoded in the frequency deviation, Δf. This leads to the question: Can we utilize another surrogate signal that gives us information about the degree of self-repair occurring in the network over time while being independent of the class of the input data?
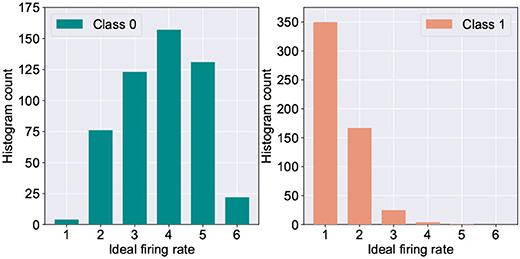
Figure 5. Histogram count of the ideal firing rate of neurons responding to digit “0” vs. digit “1” (measured from 5,000 test examples of the MNIST dataset).
While the above challenge is related to the process of reducing the STDP learning window over time, we observed that using sole STDP learning or with a constant enhanced learning rate consistently reduced the network accuracy over time (Figure 6). Figure 7 also depicts that normal STDP retraining with faulty synapses slowly loses their learnt representations over time. Re-learning all the healthy synaptic weights uniformly using STDP with an enhanced learning rate should at least result in some accuracy improvement for the initial epochs of re-training, even if the modulation of learning window height over time is not incorporated in the self-repair framework. The degradation of network accuracy starting from the commencement of the retraining process signified that some additional factors may have been absent in the astrocyte functionality macro-modeling process, which is independent from the above challenge of modulating the temporal behavior of the STDP learning window.
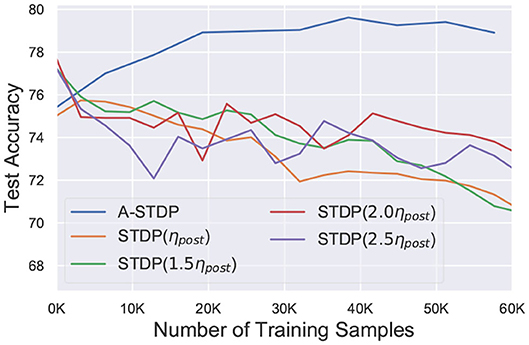
Figure 6. Test accuracy of a 225 neuron network on the MNIST dataset with 70% faulty connections with normal and enhanced learning rates during STDP re-training process. Re-training with A-STDP rule is also depicted.
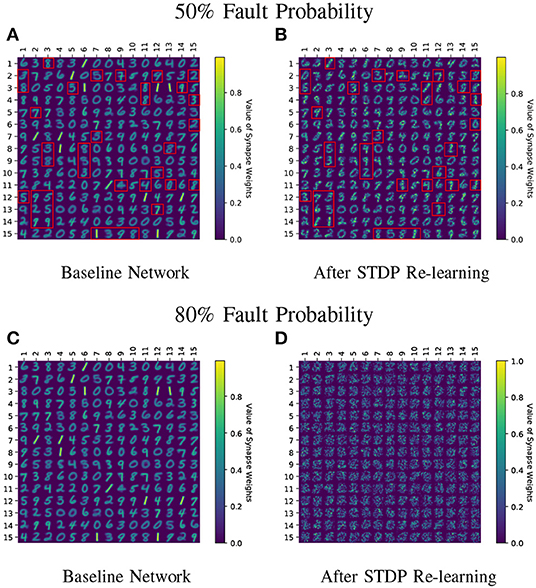
Figure 7. (A–D) Learnt weight patterns for 225 neuron network on the MNIST dataset are shown. Re-training the network with sole STDP learning causes distortion of the weight maps (50 and 80% fault cases are plotted). The red boxes in (A,B) highlight how the neurons can change association toward a particular class during re-learning thereby forgetting their original learnt representations. Receptive fields of all neurons undergo distortion for the 80% fault case.
In that regard, we draw inspiration from Equation (6), where we observe that the initial fault-free value of the PR acts as a scaling factor for the self-repair feedback terms DSE and e-SP. We perform a similar simulation for the network shown in Figure 1, with each neuron receiving input from 10 synapses. However in this case, we set the initial PR of all of the synapses to 0.5, except one connected to N2; for which the initial PR was set to 0.1. In other words, 9 of the synapses connected to N2 have a PR(t0)=0.5, while for one PR(t0)=0.1. The lower initial PR value symbolizes a weaker connection. The network is simulated for 400 s and at 200 s, the associated PR of 8 of the synapses with higher initial PR are reduced to 0 to signify faulty condition (Figure 8). We observe that after the introduction of the faults, the PR of the synapses with the higher initial PR value is enhanced greatly compared to the one with the lower initial PR. This leads us to the conclusion that synapses that play a greater role in postsynaptic firing also play a greater role in the self-repair process compared to other synapses.
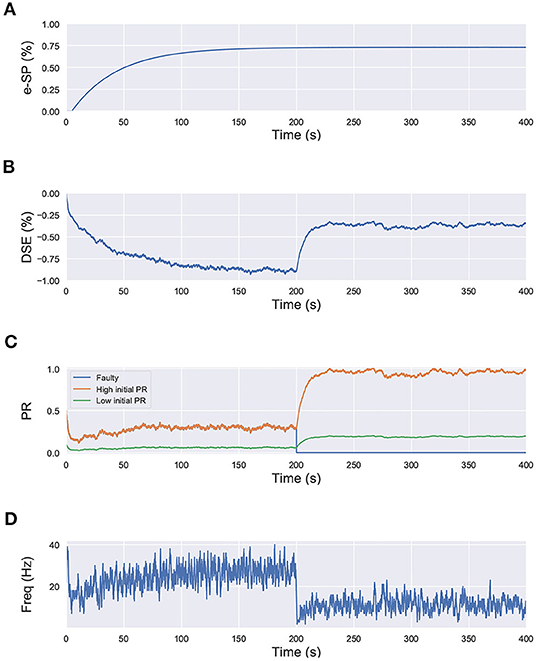
Figure 8. Simulation results of the network in Figure 1 using the computational model of Wade et al. (2012) with synapses having different initial PR values. Total simulation time is 400 s. At 200 s, faults are introduced in 8 synapses with high initial PR connected to N2. (A) e-SP of N1 and N2, (B) DSE of N2, (C) PR of the 3 types of synapses connected to N2 (orange: healthy synapse with PR(t0)=0.5, green: healthy synapse with PR(t0)=0.1 and blue: faulty synapse with PR(t0)=0.5 till 200 s and PR(t0)=0 afterwards) and (D) Firing rate of neuron N2.
Since our unsupervised SNN is characterized by analog synaptic weights in the range of [0, wmax], we hypothesized that this characteristic might underlie the reason for the accuracy degradation and designed a preferential self-repair learning rule for healthier synapses. This was found to result in significant accuracy improvement during the retraining process (discussed in next section). Our formulated A-STDP learning rule formulation is therefore also guided by the following question: Can we aggressively increase the healthy synaptic weights during the initial learning epochs which preserves the original representations learnt by the network?
Driven by the above observations, we formulated our Astrocyte Augmented STDP (A-STDP) learning rule during the self-repair process as,
where, wα represents the weight value at the α-th percentile of the network and serves as the surrogate signal to guide the retraining process. Figure 9 depicts the temporal behavior of wα for the 98-th percentile of the weight distribution. After faults are introduced, wα is significantly reduced and slowly increases over time during the re-learning process. It finally saturates off at the bounded value wmax. The term w/wα ensures that the effective learning rate for healthier synapses (w > wα) is much higher than the learning rate for weaker connections (w < wα) while σ dictates the degree of non-linearity. Since wα increases over time, the enhanced learning process also reduces and finally stops once wα saturates. It is worth mentioning here that wα, σ and wmax are hyperparameters for the A-STDP learning rule. All hyperparameter settings and simulation details are presented in the next section.
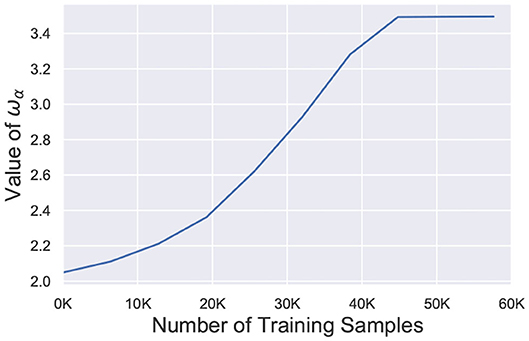
Figure 9. Value of wα (98-th percentile from weight distribution of the entire network) during the self-repair process using A-STDP learning rule for a 225 neuron network on the MNIST Dataset with 80% faulty connections.
3. Results
We evaluated our proposal in the context of unsupervised SNN training on standard image recognition benchmarks under two settings: scaling in network size and scaling in network complexity. We used MNIST (LeCun and Cortes, 2010) and Fashion-MNIST (Xiao et al., 2017) datasets for our analysis. Both datasets contain 28 × 28 grayscale images of handwritten digits / fashion products (belonging to one of 10 categories) with 60,000 training examples and 10,000 testing examples. All experiments are run in PyTorch framework using a single GPU with a batchsize of 16 images. In addition to standard input pre-processing for generating the Poisson spike train, the images in F-MNIST dataset also undergo Sobel filtering for edge detection before being converted to spike trains. The SNN implementation is done using a modified version of the mini-batch processing enabled SNN simulation framework (Saunders et al., 2019b) in BindsNET (Hazan et al., 2018), a PyTorch based package (Link). In addition to dataset complexity scaling, we also evaluated two networks with increasing size (225 and 400 neurons) on the MNIST dataset. For the MNIST dataset, the baseline test accuracy of the ideal network was 89.53 and 92.02%, respectively. A 400-neuron network was used for the F-MNIST dataset with 77.35% accuracy. The baseline test accuracies are superior/comparable to prior reported accuracies for unsupervised learning on both datasets. For instance, Diehl and Cook (2015) reports 87% accuracy for an STDP trained network with 400 neurons while Zhu and Wang (2020) reports the best accuracy of 73.1% for state-of-the-art clustering methods on the F-MNIST dataset. Table 1 lists the network simulation parameters used in this work. It is worth mentioning here that all hyperparameters were kept unchanged (from their initial values during training) in the self-repair process. We also kept the hyperparameters, wα and σ for the A-STDP rule unchanged for all fault simulations. Figure 10 shows a typical ablation study of the hyperparameters α and σ. For this study, we trained a 225-neuron network with 90% faults. We divided the training set into training and validation subsets in the ratio of 5:1, respectively, through random sampling. The two accuracy plots shown in Figure 10 are models retrained on the training subset and then evaluated on the new validation set. Further hyperparameter optimizations for different fault conditions can potentially improve the accuracy improvement even further.
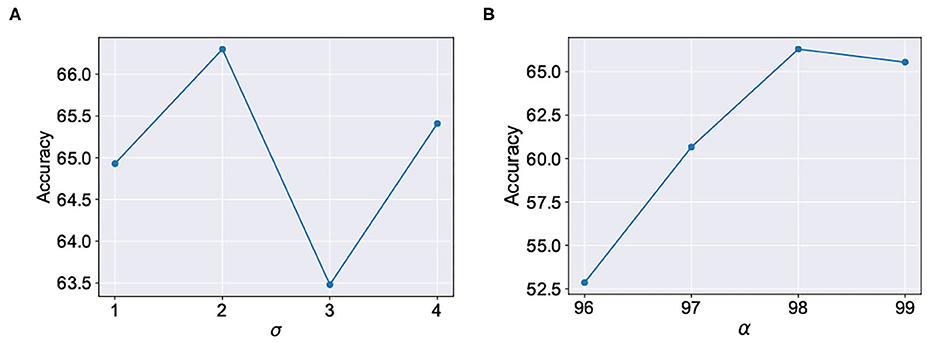
Figure 10. Ablation studies for the hyperparameters (A) σ (with fixed α = 98) and (B) α (with fixed σ = 2) in A-STDP learning rule.
The network is first trained with sole STDP learning rule for 2 epochs and the maximum test accuracy network is chosen as the baseline model. Subsequently, faults are introduced by randomly deleting synapses (from the Input to the Output Layer) post-training. Each synaptic connection was assigned a deletion probability, pdel, to decide whether the connection would be retained in the faulty network. For this work, pdel was varied between 0.5 and 0.9 to analyze the network and re-train after introducing faults. Note that A-STDP learning rule is only used during this self-repair phase. It is worth mentioning here, that weight normalization by factor wnorm (mentioned in section 2.2) is used before starting the re-training process. This helps to adjust the magnitude of firing threshold relative to the weights of the neurons (since the resultant magnitude diminishes due to fault injection).
Figure 11 shows the test classification accuracy as a function of re-learning epochs for a 225/400 neuron network with 80% probability for faulty synapses. After the faults are introduced, the network accuracy improves over time during the self-repair process. The mean and standard deviation of test accuracy from 5 independent runs are plotted in Figure 11. Figure 12 depicts the initial and self-repaired weight maps of the 225 (MNIST) and 400 (F-MNIST) neuron networks, substantiating that original learnt representations are preserved during the re-learning process. Table 2 summarizes our results for all networks with varying degrees of faults. The numbers in parentheses denote the standard deviation in accuracy from the 5 independent runs. Since sole STDP learning resulted in accuracy degradation for most of the runs, the accuracy is reported after 1 re-learning epoch. For some cases, some accuracy improvement through normal STDP was also observed. The maximum accuracy is reported for the A-STDP re-training process. After repair through A-STDP, the network is able to achieve accuracy improvement across all level of faults, ranging from 50 to 90%. Interestingly, A-STDP is able to repair faults even in a 90% faulty network and improve the testing accuracy by almost 9% (5%) for the MNIST (F-MNIST) dataset. Further, the accuracy improvement due to A-STDP scales up with increasing degree of faults. Note that the standard deviation of the final accuracy over 5 independent runs is much smaller for A-STDP than normal STDP re-training, signifying that the astrocyte enabled self-repair is consistently stable, irrespective of the initial fault locations.
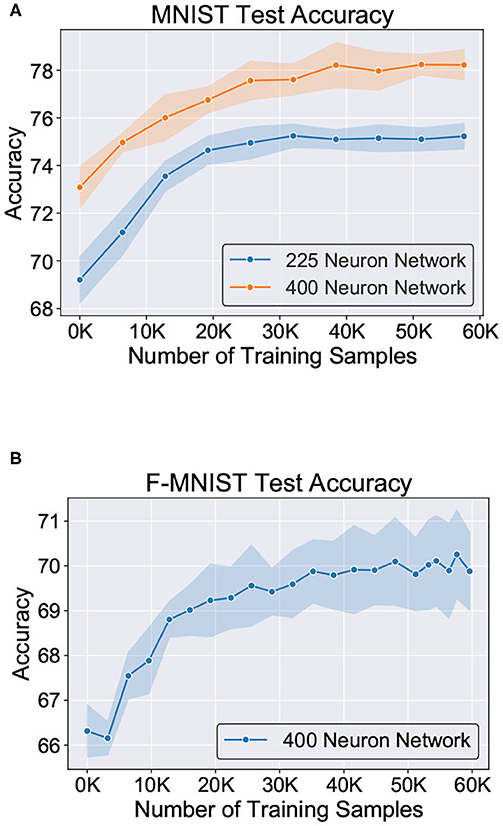
Figure 11. Improvement of test accuracy during re-learning is depicted as a function of the training samples using A-STDP learning rule on the (A) MNIST (225 and 400 neuron networks) and (B) F-MNIST datasets (400 neuron network). Mean and standard deviation of the accuracy is plotted for 80% fault simulation in the networks.
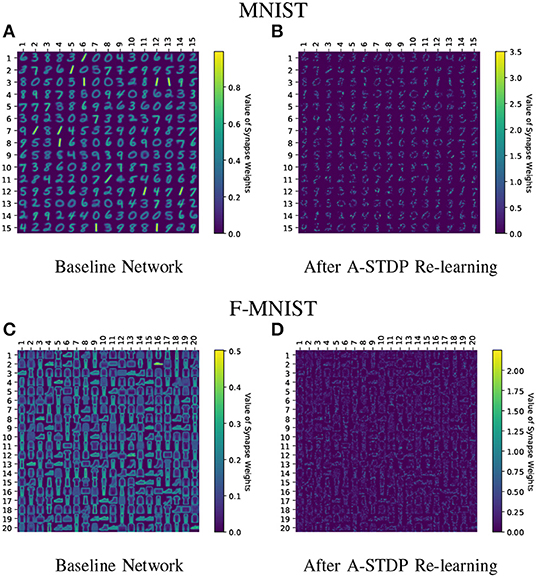
Figure 12. (A–D) Initial and self-repaired weight maps of the 225 (400) neuron network trained on MNIST (F-MNIST) dataset corresponding to 80% fault simulations.
4. Discussion
The work provides proof-of-concept results toward the development of a new generation of neuromorphic computing platforms that are able to autonomously self-repair faulty non-ideal hardware operation. Extending beyond just unsupervised STDP learning, augmenting astrocyte feedback in supervised gradient descent based training of SNNs needs to be explored along with their implementation on neuromorphic datasets (Orchard et al., 2015). In this work, we also focused on aspects of astrocyte operation that would be relevant from a macro-modeling perspective for self-repair. Further investigations on understanding the role of neuroglia in neuromorphic computing can potentially forge new directions related to synaptic learning, temporal binding, among others.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author Contributions
AS developed the main concepts. MR, SL, and NI performed all the simulations. All authors assisted in the writing of the paper and developing the concepts.
Funding
The work was supported in part by the National Science Foundation grants BCS #2031632, ECCS #2028213, and CCF #1955815.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^Note that “faults” are disjoint from the concept of “dropout” (Srivastava et al., 2014) used in neural network training. In dropout, neurons are randomly deleted (along with their connections) only during training to avoid overfitting. In contrast, faults in our work refer to static non-ideal stuck at zero synaptic connections present during both the re-training and inference stages.
References
Allam, S. L., Ghaderi, V. S., Bouteiller, J.-M. C., Legendre, A., Nicolas, A., Greget, R., et al. (2012). A computational model to investigate astrocytic glutamate uptake influence on synaptic transmission and neuronal spiking. Front. Comput. Neurosci. 6:70. doi: 10.3389/fncom.2012.00070
Amiri, M., Nazari, S., and Janahmadi, M. (2018). Digital configuration of astrocyte stimulation as a new technique to strengthen the impaired astrocytes in the tripartite synapse network. J. Comput. Electron. 17, 1382–1398. doi: 10.1007/s10825-018-1207-8
Bi, G.-Q., and Poo, M.-M. (2001). Synaptic modification by correlated activity: Hebb's postulate revisited. Annu. Rev. Neurosci. 24, 139–166. doi: 10.1146/annurev.neuro.24.1.139
Chung, W.-S., Allen, N. J., and Eroglu, C. (2015). Astrocytes control synapse formation, function, and elimination. Cold Spring Harbor Perspect. Biol. 7:a020370. doi: 10.1101/cshperspect.a020370
Davies, M., Srinivasa, N., Lin, T., Chinya, G., Cao, Y., Choday, S. H., et al. (2018). Loihi: a neuromorphic manycore processor with on-chip learning. IEEE Micro 38, 82–99. doi: 10.1109/MM.2018.112130359
De Pittà, M., Goldberg, M., Volman, V., Berry, H., and Ben-Jacob, E. (2009). Glutamate regulation of calcium and ip 3 oscillating and pulsating dynamics in astrocytes. J. Biol. Phys. 35, 383–411. doi: 10.1007/s10867-009-9155-y
De Pittà, M., Volman, V., Berry, H., Parpura, V., Volterra, A., and Ben-Jacob, E. (2012). Computational quest for understanding the role of astrocyte signaling in synaptic transmission and plasticity. Front. Comput. Neurosci. 6:98. doi: 10.3389/fncom.2012.00098
Diehl, P. U., and Cook, M. (2015). Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 9:99. doi: 10.3389/fncom.2015.00099
Garg, U., Yang, K., and Sengupta, A. (2020). Emulation of astrocyte induced neural phase synchrony in spin-orbit torque oscillator neurons. arXiv preprint arXiv:2007.00776. Available online at: https://arxiv.org/abs/2007.00776
Gordleeva, S. Y., Stasenko, S. V., Semyanov, A. V., Dityatev, A. E., and Kazantsev, V. B. (2012). Bi-directional astrocytic regulation of neuronal activity within a network. Front. Comput. Neurosci. 6:92. doi: 10.3389/fncom.2012.00092
Hazan, H., Saunders, D., Sanghavi, D., Siegelmann, H., and Kozma, R. (2019). Lattice map spiking neural networks (LM-SNNs) for clustering and classifying image data. Ann. Math. Artif. Intell. 88, 1237–1260. doi: 10.1007/s10472-019-09665-3
Hazan, H., Saunders, D. J., Khan, H., Patel, D., Sanghavi, D. T., Siegelmann, H. T., and Kozma, R. (2018). Bindsnet: a machine learning-oriented spiking neural networks library in Python. Front. Neuroinform. 12:89. doi: 10.3389/fninf.2018.00089
Irizarry-Valle, Y., Parker, A. C., and Joshi, J. (2013). “A cmos neuromorphic approach to emulate neuro-astrocyte interactions,” in The 2013 International Joint Conference on Neural Networks (IJCNN) (Dallas, TX), 1–7.
Jackson, B. L., Rajendran, B., Corrado, G. S., Breitwisch, M., Burr, G. W., Cheek, R., et al. (2013). Nanoscale electronic synapses using phase change devices. ACM J. Emerg. Technol. Comput. Syst. 9:12. doi: 10.1145/2463585.2463588
Jo, S. H., Chang, T., Ebong, I., Bhadviya, B. B., Mazumder, P., and Lu, W. (2010). Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 10, 1297–1301. doi: 10.1021/nl904092h
Karimi, G., Ranjbar, M., Amirian, M., and Shahim-Aeen, A. (2018). A neuromorphic real-time VLSI design of Ca2+ dynamic in an astrocyte. Neurocomputing 272, 197–203. doi: 10.1016/j.neucom.2017.06.071
Knag, P., Kim, J. K., Chen, T., and Zhang, Z. (2015). A sparse coding neural network ASIC with on-chip learning for feature extraction and encoding. IEEE J. Solid State Circ. 50, 1070–1079. doi: 10.1109/JSSC.2014.2386892
Kuzum, D., Jeyasingh, R. G., Lee, B., and Wong, H.-S. P. (2011). Nanoelectronic programmable synapses based on phase change materials for brain-inspired computing. Nano Lett. 12, 2179–2186. doi: 10.1021/nl201040y
LeCun, Y., and Cortes, C. (2010). MNIST Handwritten Digit Database 2010. Available online at: http://yann.lecun.com/exdb/mnist/
Lee, R. K., and Parker, A. C. (2016). “A CMOS circuit implementation of retrograde signaling in astrocyte-neuron networks,” in 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS) (Shanghai), 588–591.
Li, Y.-X., and Rinzel, J. (1994). Equations for InsP3 receptor-mediated Ca2+ i oscillations derived from a detailed kinetic model: a Hodgkin-Huxley like formalism. J. Theor. Biol. 166, 461–473. doi: 10.1006/jtbi.1994.1041
Liu, J., Harkin, J., Maguire, L. P., McDaid, L. J., and Wade, J. J. (2017). SPANNER: a self-repairing spiking neural network hardware architecture. IEEE Trans. Neural Netw. Learn. Syst. 29, 1287–1300. doi: 10.1109/TNNLS.2017.2673021
Liu, J., McDaid, L. J., Harkin, J., Karim, S., Johnson, A. P., Millard, A. G., et al. (2018). Exploring self-repair in a coupled spiking astrocyte neural network,” IEEE Trans. Neural Netw. Learn. Syst. 30, 865–875. doi: 10.1109/TNNLS.2018.2854291
Lu, S., and Sengupta, A. (2020). Exploring the connection between binary and spiking neural networks. arXiv preprint arXiv:2002.10064. doi: 10.3389/fnins.2020.00535
Merolla, P. A., Arthur, J. V., Alvarez-Icaza, R., Cassidy, A. S., Sawada, J., Akopyan, F., et al. (2014). A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 345, 668–673. doi: 10.1126/science.1254642
Min, R., Santello, M., and Nevian, T. (2012). The computational power of astrocyte mediated synaptic plasticity. Front. Comput. Neurosci. 6:93. doi: 10.3389/fncom.2012.00093
Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybernet. 98, 459–478. doi: 10.1007/s00422-008-0233-1
Nadkarni, S., and Jung, P. (2004). Dressed neurons: modeling neural–glial interactions. Phys. Biol. 1:35. doi: 10.1088/1478-3967/1/1/004
Nadkarni, S., and Jung, P. (2007). Modeling synaptic transmission of the tripartite synapse. Phys. Biol. 4:1. doi: 10.1088/1478-3975/4/1/001
Nazari, S., Faez, K., Amiri, M., and Karami, E. (2015). A digital implementation of neuron–astrocyte interaction for neuromorphic applications. Neural Netw. 66, 79–90. doi: 10.1016/j.neunet.2015.01.005
Neftci, E. O., Mostafa, H., and Zenke, F. (2019). Surrogate gradient learning in spiking neural networks. IEEE Signal Process. Mag. 36, 61–63. doi: 10.1109/MSP.2019.2931595
Orchard, G., Jayawant, A., Cohen, G. K., and Thakor, N. (2015). Converting static image datasets to spiking neuromorphic datasets using saccades. Front. Neurosci. 9:437. doi: 10.3389/fnins.2015.00437
Ramakrishnan, S., Hasler, P. E., and Gordon, C. (2011). Floating gate synapses with spike-time-dependent plasticity. IEEE Trans. Biomed. Circ. Syst. 5, 244–252. doi: 10.1109/TBCAS.2011.2109000
Ranjbar, M., and Amiri, M. (2015). An analog astrocyte–neuron interaction circuit for neuromorphic applications. J. Comput. Electron. 14, 694–706. doi: 10.1007/s10825-015-0703-3
Saunders, D. J., Patel, D., Hazan, H., Siegelmann, H. T., and Kozma, R. (2019a). Locally connected spiking neural networks for unsupervised feature learning. Neural Netw. 119, 332–340. doi: 10.1016/j.neunet.2019.08.016
Saunders, D. J., Sigrist, C., Chaney, K., Kozma, R., and Siegelmann, H. T. (2019b). Minibatch processing in spiking neural networks. arXiv preprint arXiv:1909.02549.
Sengupta, A., and Roy, K. (2017). Encoding neural and synaptic functionalities in electron spin: a pathway to efficient neuromorphic computing. Appl. Phys. Rev. 4:041105. doi: 10.1063/1.5012763
Sengupta, A., Ye, Y., Wang, R., Liu, C., and Roy, K. (2019). Going deeper in spiking neural networks: VGG and residual architectures. Front. Neurosci. 13:95. doi: 10.3389/fnins.2019.00095
Singh, S., Sarma, A., Jao, N., Pattnaik, A., Lu, S., Yang, K., et al. (2020). “Nebula: a neuromorphic spin-based ultra-low power architecture for SNNs and ANNs,” in 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA) (Valencia), 363–376.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958. doi: 10.5555/2627435.2670313
Volman, V., Ben-Jacob, E., and Levine, H. (2007). The astrocyte as a gatekeeper of synaptic information transfer. Neural Comput. 19, 303–326. doi: 10.1162/neco.2007.19.2.303
Wade, J., McDaid, L. J., Harkin, J., Crunelli, V., and Kelso, S. (2012). Self-repair in a bidirectionally coupled astrocyte-neuron (AN) system based on retrograde signaling. Front. Comput. Neurosci. 6:76. doi: 10.3389/fncom.2012.00076
Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv arXiv:1708.07747.
Keywords: astrocytes, unsupervised learning, spiking neural networks, spike-timing dependent plasticity, self-repair
Citation: Rastogi M, Lu S, Islam N and Sengupta A (2021) On the Self-Repair Role of Astrocytes in STDP Enabled Unsupervised SNNs. Front. Neurosci. 14:603796. doi: 10.3389/fnins.2020.603796
Received: 07 September 2020; Accepted: 27 November 2020;
Published: 14 January 2021.
Edited by:
Mostafa Rahimi Azghadi, James Cook University, AustraliaReviewed by:
Bharath Ramesh, National University of Singapore, SingaporeJason Kamran Jr. Eshraghian, University of Michigan, United States
Copyright © 2021 Rastogi, Lu, Islam and Sengupta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abhronil Sengupta, c2VuZ3VwdGFAcHN1LmVkdQ==
 Mehul Rastogi1,2
Mehul Rastogi1,2 Sen Lu
Sen Lu Nafiul Islam
Nafiul Islam Abhronil Sengupta
Abhronil Sengupta