Hamza Hasnaoui1,2
Mirko Lobino- 1INFN TIFPA, Trento Institute for Fundamental Physics and Applications, Trento, Italy
- 2Department of Industrial Engineering, University of Trento, Trento, Italy
- 3Dipartimento di Fisica, Università di Trento, Trento, Italy
- 4INFN, Sezione di Padova, Padova, Italy
- 5Università di Padova, Dipartimento di Fisica e Astronomia, Padova, Italy
Integrated optics is one of the most promising platforms for quantum technologies. Integrated nonlinear waveguides have been used for the generation of quantum states of light for several applications. Here we discuss a project for the generation of squeezed vacuum in periodically poled waveguides made on a lithium niobate substrate. This non-classical optical state has been used for enhancing high precision measurements in gravitational wave detectors. However, in this application bulk sources of squeezed vacuum states have been employed. Integrated optics can provide a more robust and reliable way for the generation of these states which have great potential not only for interferometric GW detectors, but also for other high-precision optical measurements as well as for quantum computing purposes.
1 Introduction
High-precision laser-based measurements, such as gravitational wave interferometry (The LIGO Scientific Collaboration, 2015), precision metrology (Giovannetti et al., 2004), and quantum information (Wang et al., 2020), rely heavily on the quantum properties of light. These measurements, while crucial for scientific advancements, are often limited by quantum noise, specifically shot noise and radiation pressure noise. The challenge lies in finding ways to improve the sensitivity of these measurements beyond the standard noise limits imposed by quantum mechanics with systems that are robust and high performing. To address this, researchers have turned to quantum engineering, particularly the use of squeezed vacuum states (Takeno et al., 2007), which offers a promising route to overcoming these limitations. At present the highest level of squeezing has been generated from a bulk optics apparatus (Vahlbruch et al., 2016) that used a semi-monolithic cavity configuration. The development and application of an integrated squeezed vacuum source (Kashiwazaki et al., 2023) have great potential for many fields including gravitational wave detection, quantum sensing (Casacio et al., 2021), and quantum computing (Eli Bourassa et al., 2021; Larsen et al., 2025) since it can greatly simplify the experimental set-ups currently built with hundreds of bulk optics components (Takeno et al., 2007).
Here we will focus on the potential of the use of lithium niobate periodically poled waveguides (Lenzini et al., 2018) and their suitability for the generation of highly squeezed states that can be used for GW detection when the squeezing is measured in the acoustic band between 10 Hz and 10 kHz, which is the most sensitive frequency region of the interferometric GW detectors, and quantum computation for the high frequency region. This material is characterized by large second order nonlinearity and the compatibility with several fabrication techniques for making optical waveguides. Proton exchanged (Lenzini et al., 2018) and titanium in-diffused (Stefszky et al., 2017) waveguides have been used in the past for the generation of squeezed vacuum, but more recently other approaches based on thin film lithium niobate (Zhu et al., 2021) (TFLN) geometries have been used. These devices include ridge TFLN waveguide (Nehra et al., 2022), strip-loaded waveguide (Peace et al., 2022), and bonding-dicing waveguides (Kashiwazaki et al., 2023).
2 Quantum noise in interferometric gravitational wave detectors
In interferometric measurements, quantum noise manifests in two primary forms: shot noise and radiation pressure noise. Shot noise arises from the statistical fluctuation in the number of photons detected, which results in a variation of the photocurrent, while radiation pressure noise is due to the fluctuation of the momentum transferred between photons and mechanical objects. In most cases, shot noise dominates; however, radiation pressure noise becomes significant when very light mechanical objects or very high laser powers are involved, such as in interferometric GW detectors.
A common approach to mitigate shot noise is by increasing the laser power. Since shot noise scales with the square root of the circulating power while the signal scales linearly, increasing the power improves the signal-to-noise ratio (SNR). However, this strategy is not without its challenges. The power required to achieve the desired SNR might exceed the capabilities of the laser systems available, or the optical components might not be able to handle the increased power without introducing additional noise. Furthermore, increasing power beyond a certain threshold can also introduce additional radiation pressure noise, which may negate the benefits of reducing shot noise. In these situations, quantum engineering offers a viable alternative.
The fundamental limit to reducing both shot noise and radiation pressure noise simultaneously arises from the Heisenberg uncertainty principle, which dictates that the amplitude and phase fluctuations of the coherent vacuum state cannot be minimized at the same time. However, it is possible to engineer specific quantum states of light, such as squeezed states, in which one type of noise is reduced at the expense of increasing the other. Squeezing a quantum state involves reducing the uncertainty in one quadrature (such as amplitude) while increasing the uncertainty in the conjugate quadrature (such as phase).
By applying squeezed vacuum states, the sensitivity of high-precision instruments can be enhanced. For instance, in gravitational wave detectors like Advanced LIGO and Advanced Virgo during the observational run O3, squeezed light has been used to reduce shot noise (Virgo Collaboration Aga et al., 2019; Tse et al., 2019), resulting in an increase of the Universe explorable volume by approximately 50%. This improvement is particularly crucial: to achieve the same sensitivity by merely increasing the laser power in the interferometer, it will require almost doubling the amount currently present in the interferometric GW detector, something that is technically challenging with current technology. In a more recent observational run (O4) the observable universe has been further increased up to 65% using well engineered squeezed vacuum states (Ganapathy et al., 2023) (see Figure 1). These are generated by exploiting the dispersion in reflection of a detuned optical cavity to which a frequency-independent squeezing field is injected. This technology is the baseline design of all current and future detectors such as the Einstein Telescope (Einstein Telescope, 2020) and Cosmic Explorer (Cosmic Explorer, 2019), providing them with the sensitivity to detect signals that are nowadays impossible to measure.
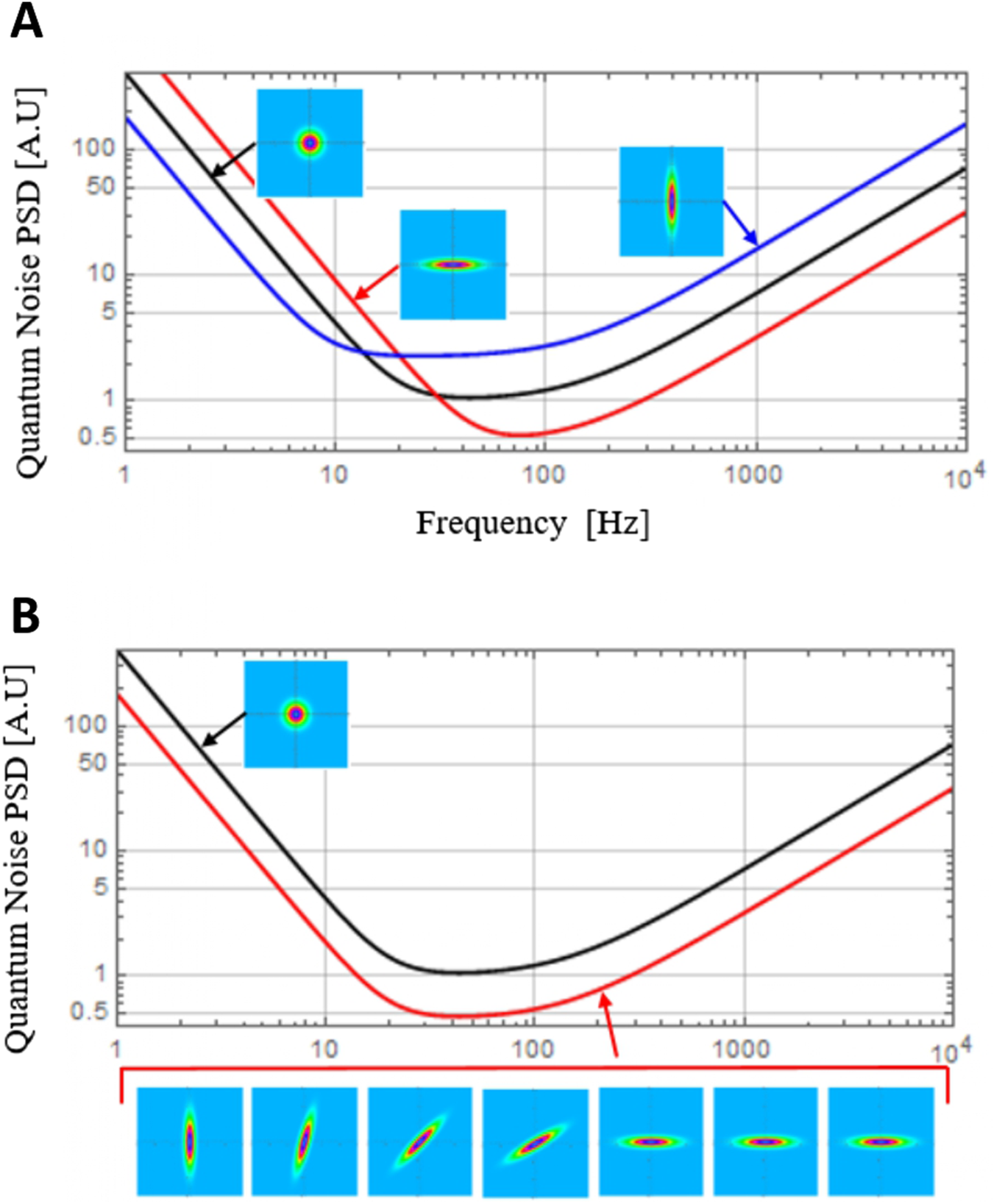
Figure 1. Frequency dependent squeezing for GW detectors. (A) Power Spectral Density (PSD) of the standard quantum noise (black line) and for the case where the coherent vacuum field is replaced with a phase (red line) or amplitude (blu line) squeezed vacuum state. Injecting frequency-independent squeezed light, quantum noise can be lowered in a portion of the spectrum while it is increased in the other. (B) PSD of the noise with the injection of squeezed light with an optimized frequency-dependent squeezing angle (red).
While squeezed vacuum sources have demonstrated their potential in improving the sensitivity of gravitational wave detectors, their implementation remains complex. These systems often require extensive infrastructure, expert knowledge, and dedicated space, which make them difficult to integrate into existing experimental setups. Additionally, traditional squeezed vacuum sources are typically bulky and require delicate alignment and tuning.
To overcome these challenges, researchers have focused on the development of integrated squeezed vacuum sources that are compact, stable, and easily adaptable to existing experimental frameworks. One promising approach is the use of integrated optical devices, such as lithium niobate (LiNbO3) waveguides, which offer a range of advantages over bulk optical sources. These integrated devices can provide the necessary nonlinear response to generate squeezed states through processes like parametric down-conversion, with the added benefits of stability and scalability.
3 Development of integrated optical squeezed vacuum sources
Lithium niobate has become a leading material for integrated quantum technologies due to its excellent nonlinear optical properties, low propagation loss, and electro-optical reconfigurability. Moreover, the creation of periodically-poled nonlinear waveguides and its transparency window that goes from UV to mid infrared allows the generation of squeezed light over a broad spectral range. Among the different fabrication techniques mentioned in the introduction, devices based on thin film lithium niobate (TFLN) (Saravi et al., 2021) offer greater nonlinear conversion efficiency because of the strongest confinement when compared to proton exchanged or titanium in-diffused waveguides which are generally long several centimeters. The bonding-dicing (Kashiwazaki et al., 2023) approach has shown great potential for the generation of highly squeezed states. These devices are fabricated by bonding a TFLN layer over a carrier substrate and then carving ridges a few microns wide, depending on the working wavelength, with a high precision, self-polishing dicing saw (Berry et al., 2019) (see Figure 2C). This saw leaves the sidewall of the device extremely smooth achieving propagation losses as low as 0.1 dB/cm (Kashiwazaki et al., 2021) compared to the 0.3 dB/cm of etched ridge waveguides (Luke et al., 2020). This type of waveguide has demonstrated the generation of more than 8 dB squeezing (Kashiwazaki et al., 2023), resulting in the highest value reported from an integrated device. They also have a lower numerical aperture which makes the collection of the generated squeezed light easier than from ridge waveguides. Figures 2A,B shows some results of parametric gain and squeezing measured at 1,550 nm in our laboratory via homodyne detection at the 8 MHz sideband. While the set-up still requires optimization in terms of losses of the optical components to improve the level of squeezing, it is quite simple to build and operate compared to bulk optical systems. Furthermore, to measure squeezing in the frequency region of interest for GW detection (from 10 Hz to 10 kHz), schemes for the reduction of low frequency noise are required such as the coherent control described in the next section, and low noise electronics for the circuitry of the homodyne detector.
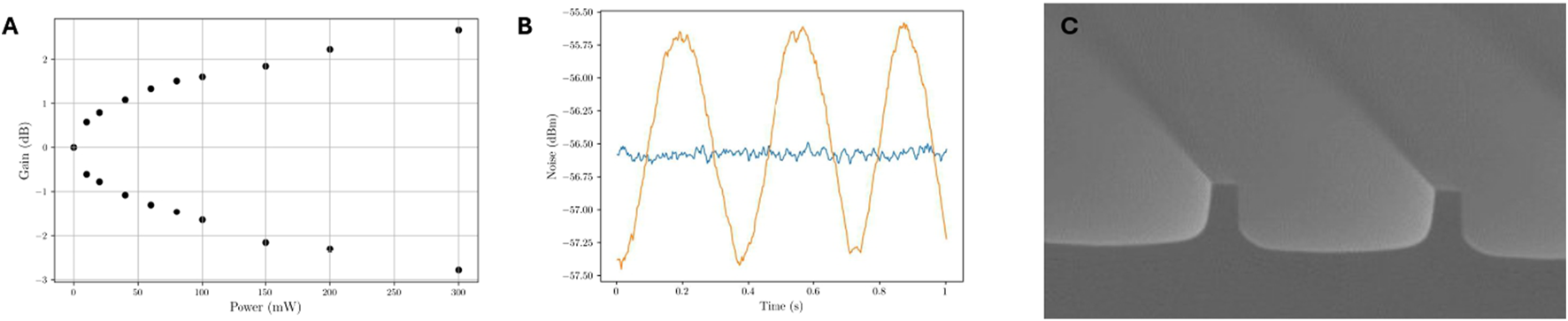
Figure 2. (A) Parametric gain measured at 1,550 nm from a MgO:PPLN waveguide as a function of the pump power at 775 nm. (B) Squeezing measured from a spectrum analyzer at 8 MHz in zero span mode. The blue line represents the shot noise level. (C) Scanning electron microscope image of diced ridge waveguides in MgO:PPLN from Berry et al. (2019).
The main limitation of this type of waveguides is that because of the dicing step, only straight waveguides can be fabricated, while the other techniques can integrate on a single chip optical circuits with multiple functionalities such as nonlinear waveguides, directional couplers, modulators, MMIs and more.
3.1 Coherent control of squeezed states
The detection of highly squeezed states also poses challenges. In particular, the phase of the local oscillator used for homodyne measurements needs to be stabilized with respect to potential phase drifts of the generated squeezed state, otherwise the noise reduction is reduced because of mixing between the squeezed and anti-squeezed quadratures. For this reason, active control techniques are required.
To improve the performance of the squeezed vacuum source, it is necessary to implement a technique known as coherent control (CC) (Vahlbruch et al., 2007). This technique stabilizes the phase of the squeezed light to ensure that it remains aligned with one of the detector’s reference beams, so that the measurement is always performed on the quadrature with reduced quantum noise. The CC protocol involves injecting a sideband offset by a few MHz from the carrier frequency of the squeezed light into the nonlinear waveguide and subsequent optical path, where it generates another sideband through difference-frequency generation with the pump used for spontaneous down conversion. The beat between the two sidebands encodes the information of the pump phase and is used as an error signal to stabilize it. Since the CC sidebands co-propagate with the squeezed light, their beat notes with the local oscillator (LO), measured by the homodyne detector, can be used to extract information on the relative phase between the squeezed field and the LO, providing an error signal to stabilize the phase of the squeezed state. The two error signals ensure a complete stabilization of the phase and orientation of a squeezed state of light. This approach requires a sophisticated setup, including custom optics and electronics, to integrate the CC technique with standard squeezed vacuum systems. The aim is to achieve phase stabilization of the squeezed light with high precision, ensuring that the generated squeezed states maintain their purity and effectiveness in suppressing quantum noise. This aspect becomes essential to exploit all the noise reduction of highly squeezed states for either sensing of computation.
3.2 Applications for gravitational wave detection and quantum technologies
The development of an integrated squeezed vacuum source has far-reaching implications for both gravitational wave detection and quantum technologies. In the context of interferometric GW detectors, the ability to implement a compact squeezed light source directly into the experimental setup will significantly improve the sensitivity of future detectors and extend the time available for observation runs. The next-generation of gravitational wave observatories, such as the Einstein Telescope (Einstein Telescope, 2020), will rely on such technologies to detect faint signals from distant cosmic events, but for achieving the required sensitivity goals, around 10 dB of squeezing delivered to the interferometer are needed. Whether waveguide sources can achieve this level of performance is an open question, but recent results are promising (Nehra et al., 2022). The mode matching and coupling of the squeezed light from the waveguide into the mode of the GW interferometer is also a challenging task. However, mode mismatching sensing techniques have been proposed and experimentally demonstrated (Magaña-Sandoval et al., 2019) and adaptive mode matching techniques are currently in place in gravitational wave detectors (Srivastava et al., 2022). These techniques are directly applicable to the mode of ridge waveguide for GW interferometers.
Beyond gravitational wave detection, squeezed light sources have applications in quantum metrology, quantum sensing, and quantum computing. In particular, they are a key resource for continuous variable quantum computing (Luke et al., 2020) and for quantum computational advantage, demonstrated via Gaussian Boson sampling (Zhong et al., 2020). In this context the level of squeezing is closely related to the fidelity of the quantum gate used to perform computation which makes the generation of highly squeezed states essential.
4 Conclusion
The development of integrated quantum sources for squeezed vacuum has the potential to revolutionize high-precision measurements in interferometric GW detectors, quantum metrology, and quantum technologies. By addressing the limitations imposed by quantum noise, such as shot noise and radiation pressure noise, these devices enable measurements beyond the standard quantum limit, enhancing the sensitivity and performance of scientific instruments. The integration of squeezed light sources into experimental setups will significantly reduce costs, improve ease of implementation, and open the door to new discoveries in the field of gravitational wave detection and quantum technologies.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
HH: Investigation, Formal analysis, Writing – review and editing. MaL: Writing – original draft, Writing – review and editing. J-PZ: Writing – original draft, Writing – review and editing. MB: Writing – original draft, Writing – review and editing. MiL: Writing – original draft, Writing – review and editing.
Funding
The authors declare that financial support was received for the research and/or publication of this article. This work was supported by the experiment Squeeze from INFN-CSN5.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Berry, S. A., Carpenter, L. G., Gray, A. C., Smith, P. G. R., and Gawith, C. B. E. (2019). Zn-indiffused diced ridge waveguides in MgO:PPLN generating 1 watt 780 nm SHG at 70% efficiency. OSA Contin. 2, 3456–3464. doi:10.1364/OSAC.2.003456
Casacio, C. A., Madsen, L. S., Terrasson, A., Waleed, M., Barnscheidt, K., Hage, B., et al. (2021). Quantum-enhanced nonlinear microscopy. Nat. Photonics 594, 201–206. doi:10.1038/s41586-021-03528-w
Cosmic Explorer (2019). Cosmic explorer. Available online at: https://cosmicexplorer.org/.
Einstein Telescope (2020). Einstein telescope. Available online at: https://www.et-gw.eu/index.php.
Eli Bourassa, J., Alexander, R. N., Vasmer, M., Patil, A., Tzitrin, I., Matsuura, T., et al. (2021). Blueprint for a scalable photonic fault-tolerant quantum computer. Quantum 5, 392. doi:10.22331/q-2021-02-04-392
Ganapathy, D., Jia, W., Nakano, M., Xu, V., Aritomi, N., Cullen, T., et al. (2023). Broadband quantum enhancement of the LIGO detectors with frequency-dependent squeezing. Phys. Rev. X 13, 041021. doi:10.1103/PhysRevX.13.041021
Giovannetti, V., Lloyd, S., and Maccone, L. (2004). Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336. doi:10.1126/science.1104149
Kashiwazaki, T., Yamashima, T., Takanashi, N., Umeki, T., and Furusawa, A. (2021). Fabrication of low-loss quasi-single-mode PPLN waveguide and its application to a modularized broadband high-level squeezer. Appl. Phys. Lett. 119, 251104. doi:10.1063/5.0063118
Kashiwazaki, T., Yamashima, T., Enbutsu, K., Kazama, T., Inoue, A., Fukui, K., et al. (2023). Over-8-dB squeezed light generation by a broadband waveguide optical parametric amplifier toward fault-tolerant ultra-fast quantum computers. Appl. Phys. Lett. 122, 234003. doi:10.1063/5.0144385
Larsen, M. V., Bourassa, J. E., Kocsis, S., Tasker, J. F., Chadwick, R. S., González-Arciniegas, C., et al. (2025). Integrated photonic source of gottesman–kitaev–preskill qubits. Nature 642, 587–591. doi:10.1038/s41586-025-09044-5
Lenzini, F., Janousek, J., Thearle, O., Villa, M., Haylock, B., Kasture, S., et al. (2018). Integrated photonic platform for quantum information with continuous variables. Sci. Adv. 4, eaat9331. doi:10.1126/sciadv.aat9331
Luke, K., Kharel, P., Reimer, C., He, L., Loncar, M., and Zhang, M. (2020). Wafer-scale low-loss lithium niobate photonic integrated circuits. Opt. Express 28, 24452. doi:10.1364/OE.401959
Magaña-Sandoval, F., Vo, T., Vander-Hyde, D., Sanders, J. R., and Ballmer, S. W. (2019). Sensing optical cavity mismatch with a mode-converter and quadrant photodiode. Phys. Rev. D. 100, 102001. doi:10.1103/PhysRevD.100.102001
Nehra, R., Sekine, R., Ledezma, L., Guo, Q., Gray, R. M., Roy, A., et al. (2022). Few-cycle vacuum squeezing in nanophotonics. Science 377, 1333–1337. doi:10.1126/science.abo6213
Peace, D., Zappacosta, A., Cernansky, R., Haylock, B., Boes, A., Mitchell, A., et al. (2022). Picosecond pulsed squeezing in thin-film lithium niobate strip-loaded waveguides at telecommunication wavelengths. J. Phys. Photonics 4, 035002. doi:10.1088/2515-7647/ac80e2
Saravi, S., Pertsch, T., and Setzpfandt, F. (2021). Lithium niobate on insulator: an emerging platform for integrated quantum photonics. Adv. Opt. Mater. 9, 2100789. doi:10.1002/adom.202100789
Srivastava, V., Mansell, G., Makarem, C., Noh, M., Abbott, R., Ballmer, S., et al. (2022). Piezo-deformable mirrors for active mode matching in advanced LIGO. Opt. Express 30, 10491–10501. doi:10.1364/OE.445088
Stefszky, M., Ricken, R., Eigner, C., Quiring, V., Herrmann, H., and Silberhorn, C. (2017). Waveguide cavity resonator as a source of optical squeezing. Phys. Rev. Appl. 7, 044026. doi:10.1103/PhysRevApplied.7.044026
Takeno, Y., Yukawa, M., Yonezawa, H., and Furusawa, A. (2007). Observation of -9 dB quadrature squeezing with improvement of phase stability in homodyne measurement. Opt. Express 15, 4321–4327. doi:10.1364/OE.15.004321
The LIGO Scientific Collaboration (2015). Advanced LIGO. Class. Quantum Grav. 32, 074001. doi:10.1088/0264-9381/32/7/074001
Tse, M., Yu, H., Kijbunchoo, N., Fernandez-Galiana, A., Dupej, P., Barsotti, L., et al. (2019). Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy. Phys. Rev. Lett. 123, 231107. doi:10.1103/PhysRevLett.123.231107
Vahlbruch, H., Chelkowski, S., Hage, B., Franzen, A., Danzmann, K., and Schnabel, R. (2007). Coherent control of vacuum squeezing in the gravitational-wave detection band. Phys. Rev. Lett. 97, 011101. doi:10.1103/PhysRevLett.97.011101
Vahlbruch, H., Mehmet, M., Danzmann, K., and Schnabel, R. (2016). Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency. Phys. Rev. Lett. 117, 110801. doi:10.1103/PhysRevLett.117.110801
Virgo Collaboration Agathos, M., Aiello, L., Allocca, A., Amato, A., Ansoldi, S., et al. (2019). Increasing the astrophysical reach of the advanced Virgo detector via the application of squeezed vacuum states of light. Phys. Rev. Lett. 123, 231108. doi:10.1103/PhysRevLett.123.231108
Wang, J., Sciarrino, F., Laing, A., and Thompson, M. G. (2020). Integrated photonic quantum technologies. Nat. Photonics 14, 273–284. doi:10.1038/s41566-019-0532-1
Zhong, H.-S., Wang, H., Deng, Y.-H., Chen, M.-C., Peng, L.-C., Luo, Y.-H., et al. (2020). Quantum computational advantage using photons. Science 370, 1460–1463. doi:10.1126/science.abe8770
Keywords: integrated optics, squeezed light, quantum sensing, lithium niobate, quantum photonics
Citation: Hasnaoui H, Leonardi M, Zendri J-P, Bazzan M and Lobino M (2025) Integrated waveguide sources of squeezed vacuum for gravitational wave detection and quantum metrology. Front. Sens. 6:1603365. doi: 10.3389/fsens.2025.1603365
Received: 31 March 2025; Accepted: 06 November 2025;
Published: 01 December 2025.
Edited by:
Vincenzo Guidi, University of Ferrara, ItalyReviewed by:
Massimo Minuti, Universities and Research, ItalyRay-Kuang Lee, National Tsing Hua University, Taiwan
Guido Zavattini, University of Ferrara, Italy
Copyright © 2025 Hasnaoui, Leonardi, Zendri, Bazzan and Lobino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mirko Lobino, bWlya28ubG9iaW5vQHVuaXRuLml0