- 1Department of Applied Mathematics and Statistics, Stony Brook University, Stony Brook, NY, USA
- 2De Vinci Finance Lab, École Supérieure d'Ingénieurs Léonard de Vinci, Paris, France
Today's mainstream economics, embodied in Dynamic Stochastic General Equilibrium (DSGE) models, cannot be considered an empirical science in the modern sense of the term: it is not based on empirical data, is not descriptive of the real-world economy, and has little forecasting power. In this paper, I begin with a review of the weaknesses of neoclassical economic theory and argue for a truly scientific theory based on data, the sine qua non of bringing economics into the realm of an empirical science. But I suggest that, before embarking on this endeavor, we first need to analyze the epistemological problems of economics to understand what research questions we can reasonably ask our theory to address. I then discuss new approaches which hold the promise of bringing economics closer to being an empirical science. Among the approaches discussed are the study of economies as complex systems, econometrics and econophysics, artificial economics made up of multiple interacting agents as well as attempts being made inside present main stream theory to more closely align the theory with the real world.
Introduction
In this paper we analyze the status of economics as a science: Can neoclassical economics be considered an empirical science, eventually only in the making? Are there other approaches that might better bring economics into the realm of empirical science, with the objective of allowing us to forecast (at least probabilistically) economic and market phenomena?
While our discussion is centered on economic theory, our considerations can be extended to finance. Indeed, mainstream finance theory shares the basic framework of mainstream economic theory, which was developed in the 1960s, 1970s in what is called the “rational expectations revolution.” The starting point was the so-called Lucas critique. University of Chicago professor Robert Lucas observed that changes in government policy are made ineffective by the fact that economic agents anticipate these changes and modify their behavior. He therefore advocated giving a micro foundation to macroeconomics—that is, explaining macroeconomics in function of the behavior of individual agents. Lucas was awarded the 1995 Nobel Prize in Economics for his work.
The result of the Lucas critique was a tendency, among those working within the framework of mainstream economic theory, to develop macroeconomic models based on a multitude of agents characterized by rational expectations, optimization and equilibrium1. Following common practice we will refer to this economic theory as neoclassical economics or mainstream economics. Mainstream finance theory adopted the same basic principles as general equilibrium economics.
Since the 2007–2009 financial crisis and the ensuing economic downturn—neither foreseen (not even probabilistically) by neoclassical economic theory—the theory has come under increasing criticism. Many observe that mainstream economics provides little knowledge from which we can make reliable forecasts—the objective of science in the modern sense of the term (for more on this, see Fabozzi et al. [1]).
Before discussing these questions, it is useful to identify the appropriate epistemological framework(s) for economic theory. That is, we need to understand what questions we can ask our theory to address and what types of answers we might expect. If economics is to become an empirical science, we cannot accept terms such as volatility, inflation, growth, recession, consumer confidence, and so on without carefully defining them: the epistemology of economics has to be clarified.
We will subsequently discuss why we argue that neoclassical economic and finance theory is not an empirical science as presently formulated—nor can it become one. We will then discuss new ideas that offer the possibility of bringing economic and finance theory closer to being empirical sciences,—in particular, economics (and finance) based on the analysis of financial time series (e.g., econometrics) and on the theory of complexity. These new ideas might be referred to collectively as “scientific economics.”
We suggest that the epistemological framework of economics is not that of physics but that of complex systems. After all, economies are hierarchical complex systems made up of human agents—complex systems in themselves—and aggregations of human agents. We will argue that giving a micro foundation to macroeconomics is a project with intrinsic limitations, typical of complex systems. These limitations constrain the types of questions we can ask. Note that the notion of economies as complex systems is not really new. Adam Smith's notion of the “invisible hand” is an emerging property of complex markets. Even mainstream economics represents economic systems as complex systems made up of a large number of agents—but it makes unreasonable simplifying assumptions.
For this and other reasons, economics is a science very different from the science of physics. It might be that a true understanding of economics will require a new synthesis of the physical and social sciences given that economies are complex systems made up of human individuals and must therefore take into account human values, a feature that does not appear in other complex systems. This possibility will be explored in the fourth part of our discussion, but let's first start with a review of the epistemological foundations of modern sciences and how our economic theory eventually fits in.
The Epistemological Foundations of Economics
The hallmark of modern science is its empirical character: modern science is based on theories that model or explain empirical observations. No a priori factual knowledge is assumed; a priori knowledge is confined to logic and mathematics and, perhaps, some very general principles related to the meaning of scientific laws and terms and how they are linked to observations. There are philosophical and scientific issues associated with this principle. For example, in his Two Dogmas of Empiricism, van Orman Quine [2] challenged the separation between logical analytic truth and factual truth. We will herein limit our discussion to the key issues with the bearing on economics. They are:
a. What is the nature of observations?
b. How can empirical theories be validated or refuted?
c. What is the nature of our knowledge of complex systems?
d. What scientific knowledge can we have of mental processes and of systems that depend on human mental processes?
Let's now discuss each of these issues.
What is the Nature of Observations?
The physical sciences have adopted the principles of operationalism as put forward by Bridgman [3], recipient of 1946 Nobel Prize in Physics, in his book The Logic of Modern Physics. Operationalism holds that the meaning of scientific concepts is rooted in the operations needed to measure physical quantities2. Operationalism rejects the idea that there are quantities defined a priori that we can measure with different (eventually approximate) methods. It argues that the meaning of a scientific concept is in how we observe (or measure) it.
Operationalism has been criticized on the basis that science, in particular physics, uses abstract terms such as “mass” or “force,” that are not directly linked to a measurement process. See, for example, Hempel [4]. This criticism does not invalidate operationalism but requires that operationalism as an epistemological principle be interpreted globally. The meaning of a physical concept is not given by a single measurement process but by the entire theory and by the set of all observations. This point of view has been argued by many philosophers and scientists, including Feyerabend [5], Kuhn [6], and van Orman Quine [2].
But how do we define “observations”? In physics, where theories have been validated to a high degree of precision, we accept as observations quantities obtained through complex, theory-dependent measurement processes. For example, we observe temperature through the elongation of a column of mercury because the relationship between the length of the column of mercury and temperature is well-established and coherent with other observations such as the change of electrical resistance of a conductor. Temperature is an abstract term that enters in many indirect observations, all coherent.
Contrast the above to economic and finance theory where there is a classical distinction between observables and hidden variables. The price of a stock is an observable while the market state of low or high volatility is a hidden variable. There are a plethora of methods to measure volatility, including: the ARCH/GARCH family of models, stochastic volatility, and implied volatility. All these methods are conceptually different and yield different measurements. Volatility would be a well-defined concept if it were a theoretical term that is part of a global theory of economics or finance. But in economics and finance, the different models to measure volatility use different concepts of volatility.
There is no global theory that effectively links all true observations to all hidden variables. Instead, we have many individual empirical statements with only local links through specific models. This is a significant difference with respect to physical theories; it weakens the empirical content of economic and finance theory.
Note that the epistemology of economics is not (presently) based on a unified theory with abstract terms and observations. It is, as mentioned, based on many individual facts. Critics remark that mainstream economics is a deductive theory, not based on facts. This is true, but what would be required is a deductive theory based on facts. Collections of individual facts, for example financial time series, have, as mentioned, weak empirical content.
How Can Empirical Theories Be Validated or Refuted?
Another fundamental issue goes back to the eighteenth century, when the philosopher-economist David Hume outlined the philosophical principles of Empiricism. Here is the issue: No finite series of observations can justify the statement of a general law valid in all places and at all times, that is, scientific laws cannot be validated in any conclusive way. The problem of the validation of empirical laws has been widely debated; the prevailing view today is that scientific laws must be considered hypotheses validated by past data but susceptible of being invalidated by new observations. That is, scientific laws are hypotheses that explain (or model) known data and observations but there is no guarantee that new observations will not refute these laws. The attention has therefore shifted from the problem of validation to the problem of rejection.
That scientific theories cannot be validated but only refuted is the key argument in Carl Popper's influential Conjectures and Refutations: The Growth of Scientific Knowledge. Popper [7] argued that scientific laws are conjectures that cannot be validated but can be refuted. Refutations, however, are not a straightforward matter: Confronted with new empirical data, theories can, to some extent, be stretched and modified to accommodate the new data.
The issue of validation and refutation is particularly critical in economics given the paucity of data. Financial models are validated with a low level of precision in comparison to physical laws. Consider, for example, the distribution of returns. It is known that returns at time horizons from minutes to weeks are not normally distributed but have tails fatter than those of a normal distribution. However, the exact form of returns distributions is not known. Current models propose a range from inverse power laws with a variety of exponents to stretched exponentials, but there is no consensus.
Economic and financial models—all probabilistic models—are validated or refuted with standard statistical procedures. This leaves much uncertainty given that the choice among the models and the parameterization of different models are subject to uncertainty. And in most cases there is no global theory.
Economic and financial models do not have descriptive power. This point was made by Friedman [8], University of Chicago economist and recipient of the 1976 Nobel Prize in Economics. Friedman argued that economic models are like those in physics, that is to say, mathematical tools to connect observations. There is no intrinsic rationality in economic models. We must resist the temptation to think that there are a priori truths in economic reasoning.
In summary, economic theories are models that link observations without any pretense of being descriptive. Their validation and eventual rejection are performed with standard statistical methods. But the level of uncertainty is great. As famously observed by Black [9] in his article “Noise,” “Noise makes it very difficult to test either practical or academic theories about the way that financial or economic markets work. We are forced to act largely in the dark.” That is to say, there is little evidence that allows us to choose between different economic and financial models.
What is the Nature of Our Knowledge of Complex Systems?
The theory of complex systems has as its objective to explain the behavior of systems made up of many interacting parts. In our Introduction, we suggested that the theory of complexity might be relevant to the analysis of economies and financial time series. The key theoretical questions are:
 Can the behavior of complex systems be explained in terms of basic laws?
Can the behavior of complex systems be explained in terms of basic laws?
 Can complex systems be spontaneously created in non-complex media? Can they continue to evolve and transform themselves? If so, how?
Can complex systems be spontaneously created in non-complex media? Can they continue to evolve and transform themselves? If so, how?
 Can complex systems be described and, if so, how?
Can complex systems be described and, if so, how?
The first question is essentially the following: Can we give a micro foundation to economics? The second question asks: How do economies develop, grow, and transform themselves? The last question is: Using the theory of complex systems, what type of economic theory we can hope to develop?
The principle of scientific reductionism holds that the behavior of any physical system can be reduced to basic physical laws. In other words, reductionism states that we can logically describe the behavior of any physical system in terms of its basic physical laws. For example, the interaction of complex molecules (such as molecules of drugs and target molecules with which they are supposed to interact) can in principle be described by quantum mechanical theories. The actual computation might be impossibly long in practice but, in theory, the computation should be possible.
Does reductionism hold for very complex physical systems? Can any property of a complex system be mathematically described in terms of basic physical laws? Philip Warren Anderson, co-recipient of the 1977 Nobel Prize in Physics, conjectured in his article “More is different” [10] that complex systems might exhibit properties that cannot be explained in terms of microscopic laws. This does not mean that physical laws are violated in complex systems; rather it means that in complex systems there are aggregate properties that cannot be deduced with a finite chain of logical deductions from basic laws. This impossibility is one of the many results on the limits of computability and the limits of logical deductions that were discovered after the celebrated theorem of Goedel on the incompleteness of formal logical systems.
Some rigorous results can be obtained for simple systems. For example, Gu et al. [11] demonstrated that an infinite Ising lattice exhibits properties that cannot be computed in any finite time from the basic laws governing the behavior of the lattice. This result is obtained from well-known results of the theory of computability. In simple terms, even if basic physical laws are valid for any component of a complex system, in some cases the chains of deduction for modeling the behavior of aggregate quantities become infinite. Therefore, no finite computation can be performed.
Reductionism in economic theory is the belief that we can give a micro foundation to macroeconomics, that is, that we can explain aggregate economic behavior in terms of the behavior of single agents. As mentioned, this was the project of economic theory following the Lucas critique. As we will see in Section What Is the Cognitive Value of Neoclassical Economics, Neoclassical Finance? this project produced an idealized concept of economies, far from reality.
We do not know how economic agents behave, nor do we know if and how their behavior can be aggregated to result in macroeconomic behavior. It might well be that the behavior of each agent cannot be computed and that the behavior of the aggregates cannot be computed in terms of individuals. While the behavior of agents has been analyzed in some experimental setting, we are far from having arrived at a true understanding of agent behavior.
This is why a careful analysis of the epistemology of economics is called for. If our objective is to arrive at a science of economics, we should ask only those questions that we can reasonably answer, and refrain from asking questions and formulating theories for which there is no possible empirical evidence or theoretical explanation.
In other words, unless we make unrealistic simplifications, giving a micro foundation to macroeconomics might prove to be an impossible task. Neoclassical economics makes such unrealistic simplifications. A better approximation to a realistic description of economics might be provided by agent-based systems, which we will discuss later. But agent-based systems are themselves complex systems: they do not describe mathematically, rather they simulate economic reality. A truly scientific view of economics should not be dogmatic, nor should it assume that we can write an aggregate model based on micro-behavior.
Given that it might not be possible to describe the behavior of complex systems in terms of the laws of their components, the next relevant question is: So how can we describe complex systems? Do complex systems obey deterministic laws dependent on the individual structure of each system, which might be discovered independently from basic laws (be they deterministic or probabilistic)? Or do complex systems obey statistical laws? Or is the behavior of complex systems simply unpredictable?
It is likely that there is no general answer to these questions. A truly complex system admits many different possible descriptions in function of the aggregate variables under consideration. It is likely that some aggregate properties can be subject to study while others are impossible to describe. In addition, the types of description might vary greatly. Consider the emission of human verbal signals (i.e., speech). Speech might indeed have near deterministic properties in terms of the formation rules, grammar, and syntax. If we move to the semantic level, speech has different laws in function of cultures and domains of interest which we might partially describe. But modeling the daily verbal emissions of an individual likely remains beyond any mathematical and computational capability. Only broad statistics can be computed.
If we turn to economics, when we aggregate output in terms of prices, we see that the growth of the aggregate output is subject to constraints, such as the availability of money, that make the quantitative growth of economies at least partially forecastable. Once more, it is important to understand for what questions we might reasonably obtain an answer.
There are additional fundamental questions regarding complex systems. For example, as mentioned above: Can global properties spontaneously emerge in non-complex systems and if so, how? There are well-known examples of simple self-organizing systems such as unsupervised neural networks. But how can we explain the self-organizing properties of systems such as economic systems or financial markets? Can it be explained in terms of fundamental laws plus some added noise? While simple self-organizing behavior has been found in simulated systems, explaining the emergence and successive evolution of very complex systems remains unresolved.
Self-organization is subject to the same considerations made above regarding the description of complex systems. It is well possible that the self-organization of highly complex systems cannot be described in terms of the basic laws or rules of behavior of the various components. In some systems, there might be no finite chain of logical deductions able to explain self-organization. This is a mathematical problem, unrelated to the failure or insufficiency of basic laws. Explaining self-organization becomes another scientific problem.
Self-organization is a key concept in economics. Economies and markets are self-organizing systems whose complexity has increased over thousands of years. Can we explain this process of self-organization? Can we capture the process that makes economies and markets change their own structure, adopt new models of interaction?
No clear answer is yet available. Chaitin [12] introduced the notion of metabiology and has suggested that it is possible to provide a mathematical justification for Darwinian evolution. Arguably one might be able to develop a “metaeconomics” and provide some clue as to how economies or markets develop3.
Clearly there are numerous epistemological questions related to the self-organization of complex systems. Presently these questions remain unanswered at the level of scientific laws. Historians, philosophers, and social scientists have proposed many explanations of the development of human societies. Perhaps the most influential has been Hegel's Dialectic, which is the conceptual foundation of Marxism. But these explanations are not scientific in the modern sense of the term.
It is not obvious that complex systems can be handled with quantitative laws. Laws, if they exist, might be of a more general logical nature (e.g., logical laws). Consider the rules of language—a genuine characteristic of the complex system that is the human being: there is nothing intrinsically quantitative. Nor are DNA structures intrinsically quantitative. So with economic and market organization: they are not intrinsically quantitative.
What Scientific Knowledge Can We Have of Our Mental Processes and of Systems That Depend on Them?
We have now come to the last question of importance to our discussion of the epistemological foundations of modern science: What is the place of mental experience in modern science? Can we model the process through which humans make decisions? Or is human behavior essentially unpredictable? The above might seem arcane philosophical or scientific speculation, unrelated to economics or finance. Perhaps, Except that whether or not economics or finance can be studied as a science depends, at least to some extent, on if and how human behavior can be studied as a science.
Human decision-making shapes the course of economies and financial markets: economics and finance can become a science if human behavior can be scientifically studied, at least at some level of aggregation or observability. Most scientific efforts on human behavior have been devoted to the study of neurodynamics and neurophysiology. We have acquired a substantial body of knowledge on how mental tasks are distributed to different regions of the brain. We also have increased our knowledge of the physiology of nervous tissues, of the chemical and electrical exchanges between nervous cells. This is, of course, valuable knowledge from both the practical and the theoretical points of view.
However, we are still far from having acquired any real understanding of mental processes. Even psychology, which essentially categorizes mental events as if they were physical objects, has not arrived at an understanding of mental events. Surely we now know a lot on how different chemicals might affect mental behavior, but we still have no understanding of the mental processes themselves. For example, a beam of light hits a human eye and the conscious experience of a color is produced. How does this happen? Is it the particular structure of molecules in nerve cells that enables vision? Can we really maintain that structure “generates” consciousness? Might consciousness be generated through complex structures, for example with computers? While it is hard to believe that structure in itself creates consciousness, consciousness seems to appear only in association with very complex structures of nerve cells.
John von Neumann [13] was the first to argue that brains, and more in general any information processing structure, can be represented as computers. This has been hotly debated by scientists and philosophers and has captured popular imagination. In simple terms, the question is: Can computers think? In many discussions, there is a more or less explicit confusion between thinking as the ability to perform tasks and thinking as having an experience.
It was Alan Turing who introduced a famous test to determine if a machine is intelligent. Turing [14] argued that if a machine can respond to questions as a human would do, then the machine has to be considered intelligent. But Turing's criterion says nothing as regards the feelings and emotions of the machine.
In principle we should be able to study human behavior just as we study the behavior of a computer as both brain and computer are made of earthly materials. But given the complexity of the brain, it cannot be assumed that we can describe the behavior of functions that depend on the brain, such as economic or financial decision-making, with a mathematical or computational model.
A key question in studying behavior is whether we have to include mental phenomena in our theories. The answer is not simple. It is common daily experience that we make decisions based on emotions. In finance, irrational behavior is a well-known phenomenon (see Shiller [15]). Emotions, such as greed or fear, drive individuals to “herd” in and out of investments collectively, thereby causing the inflation/deflation of asset prices.
Given that we do not know how to represent and model the behavior of complex systems such as the brain, we cannot exclude that mental phenomena are needed to explain behavior. For example, a trader sees the price of a stock decline rapidly and decides to sell. It is possible that we will not be able to explain mathematically this behavior in terms of physics alone and have to take into account “things” such as fear. But for the moment, our scientific theories cannot include mental events.
Let's now summarize our discussion on the study of economies or markets as complex systems. We suggested that the epistemological problems of the study of economies and markets are those of complex systems. Reductionism does not always work in complex systems as the chains of logical deductions needed to compute the behavior of aggregates might become infinite. Generally speaking, the dynamics of complex systems needs to be studied in itself, independent of the dynamics of the components. There is no unique way to describe complex systems: a multitude of descriptions corresponding to different types of aggregation are possible. Then there are different ways of looking at complex systems, from different levels of aggregation and from different conceptual viewpoints. Generally speaking, truly complex systems cannot be described with a single set of laws. The fact that economies and markets are made up of human individuals might require the consideration of mental events and values. If, as we suggest, the correct paradigm for understanding economies and finance is that of complex systems, not that of physics, the question of how to do so is an important one. We will discuss this in Section Econophysics and Econometrics.
Table 1 summarizes our discussion of the epistemology of economics.
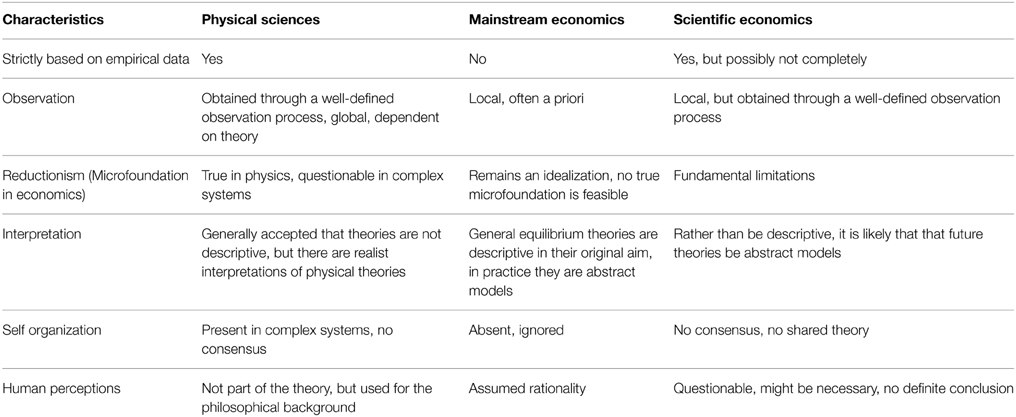
Table 1. Similarities and differences between the physical sciences, mainstream economics, and hypothetical future scientific economics.
What Is the Cognitive Value of Neoclassical Economics, Neoclassical Finance?
As discussed above, there are difficult epistemological questions related to the study of economics and finance, questions that cannot be answered in a naïve way, questions such as “What do we want to know?”, “What can we know?”, or questions that cannot be answered at all or that need to be reformulated. Physics went through a major conceptual crisis when it had to accept that physical laws are probabilistic and do not describe reality but are subject to the superposition of events. In economics and finance, we have to think hard to (re)define our questions—they might not be as obvious we think: economies and markets are complex systems; the problems must be carefully conceptualized. We will now analyze the epistemological problems of neoclassical economics and, by extension, of neoclassical finance.
First, what is the cognitive value of neoclassical economics? As observed above, neoclassical economics is not an empirical science in the modern sense of the term; rather neoclassical economics is a mathematical model of an idealized object that is far from reality. We might say that the neoclassical economics has opened the way to the study of economics as a complex system made of agents which are intelligent processors of information, capable of making decisions on the basis of their forecasts. However, its spirit is very different from that of complex systems theory.
Neoclassical economics is essentially embodied in Dynamic Stochastic General Equilibrium (DSGE) models, the first of which was developed by Fynn Kidland and Edward Prescott, co-recipients of the 2004 Nobel Prize in Economics. DSGEs were created to give a micro foundation to macroeconomics following the Lucas critique discussed above. In itself sensible, anchoring macro behavior to micro-behavior, that is, explaining macroeconomics in terms of the behavior of individuals (or agents), is a challenging scientific endeavor. Sensible because effectively the evolution of economic quantities depends ultimately on the decisions made by individuals using their knowledge but also subject to emotions. Challenging, however, because (1) rationalizing the behavior of individuals is difficult, perhaps impossible and (2) as discussed above, it might not be possible to represent mathematically (and eventually to compute) the aggregate behavior of a complex system in terms of the behavior of its components.
These considerations were ignored in the subsequent development of economic and finance theory. Instead of looking with scientific humility to the complexity of the problem, an alternative idealized model was created. Instead of developing as a science, mainstream economics developed as highly sophisticated mathematical models of an idealized economy. DSGEs are based on three key assumptions:
 Rational expectations
Rational expectations
 Equilibrium
Equilibrium
 Optimization
Optimization
From a scientific point of view, the idealizations of neoclassical economics are unrealistic. No real agent can be considered a rational-expectations agent: real agents do not have perfect knowledge of future expectations. The idea of rational expectations was put forward by Muth [16] who argued that, on average, economic agents make correct forecasts for the future—clearly a non-verifiable statement: we do not know the forecasts made by individual agents and therefore cannot verify if their mean is correct. There is little conceptual basis in arguing that, on average, people make the right forecasts of variables subject to complex behavior. It is obvious that, individually, we are uncertain about the future; we do not even know what choices we will have to make in the future.
There is one instance where average expectations and reality might converge, at least temporarily. This occurs when expectations change the facts themselves, as happens with investment decision-making where opinions lead to decisions that confirm the opinions themselves. This is referred to as “self-reflectivity.” For example, if on average investors believe that the price of a given stock will go up, they will invest in that stock and its price will indeed go up, thereby confirming the average forecast. Investment opinions become self-fulfilling prophecies. However, while investment opinions can change the price of a stock, they cannot change the fundamentals related to that stock. If investment opinions were wrong because based on a wrong evaluation of fundamentals, at a certain point opinions, and subsequently the price, will change.
Forecasts are not the only problem with DSGEs. Not only do we not know individual forecasts, we do not know how agents make decisions. The theoretical understanding of the decision-making process is part of the global problem of representing and predicting behavior. As observed above, individual behavior is the behavior of a complex system (in this case, the human being) and might not be predictable, not even theoretically. Let's refine this conclusion: We might find that, at some level of aggregation, human behavior is indeed predictable—at least probabilistically.
One area of behavior that has been mathematically modeled is the process of rational decision-making. Rational decision-making is a process of making coherent decisions. Decisions are coherent if they satisfy a number of theoretical axioms such as if choice A is preferred to choice B and choice B is preferred to choice C, then choice A must be preferred to choice A. Coherent decisions can be mathematically modeled by a utility function, that is a function defined on every choice such that choice A is preferred to choice B if the utility of A is higher than the utility of B. Utility is purely formal. It is not unique: there are infinite utility functions that correspond to the same ordering of decisions.
The idea underlying the theory of decisions and utility functions is that the complexity of human behavior, the eventual free will that might characterize the decision-making process, disappears when we consider simple business decisions such as investment and consumption. That is, humans might be very complex systems but when it comes to questions such as investments, they all behave in the same formal way, i.e., they all maximize the utility function.
There are several difficulties with representing agent decision-making as utility maximization. First, real agents are subjects to many influences, mutual interactions and other influences that distort their decisions. Numerous studies of empirical finance have shown that people do not behave according to the precepts of rational decision making. Although DSGEs can be considered a major step forward in economics, the models are, in fact, mere intellectual constructions of idealized economies. Even assuming that utility maximization does apply, there is no way to estimate the utility function(s) of each agent. DSGEs do not describe real agents nor do they describe how expectations are formed. Real agents might indeed make decisions based on past data from which they might make forecasts; they do not make decisions based on true future expectations. Ultimately, a DSGE model in its original form cannot be considered scientific.
Because creating models with a “realistic” number of agents (whatever that number might be) would be practically impossible, agents are generally collapsed into a single representative agent by aggregating utility functions. However, as shown by Sonnensheim-Mantel-Debreu [17], collapsing agents into a single representative agent does not preserve the conditions that lead to equilibrium. Despite this well-known theoretical result, models used by central banks and other organizations represent economic agents with a single aggregate utility functional.
Note that the representative agent is already a major departure from the original objective of Lucas, Kidland, and Prescott to give a micro foundation to macroeconomics. The aggregate utility functional is obviously not observable. It is generally assumed that the utility functional has a convenient mathematical formulation. See for example, Smets and Wouters [18] for a description of one such model.
There is nothing related to the true microstructure of the market in assuming a global simple utility function for an entire economy. In addition, in practice DSGE models assume simple processes, such as AutoRegressive processes, to make forecasts of quantities, as, for example, in Smets and Wouters [18] cited above.
What remains of the original formulation of the DSGE is the use of Euler equations and equilibrium conditions. But this is only a mathematical formalism to forecast future quantities. Ultimately, in practice, DSGE models are models where a simple utility functional is maximized under equilibrium conditions, using additional ad hoc equations to represent, for example, production.
Clearly, in this formulation DSGEs are abstract models of an economy without any descriptive power. Real agents do not appear. Even the forward-looking character of rational expectations is lost because these models obviously use only past data which are fed to algorithms that include terms such as utility functions that are assumed, not observed.
How useful are these models? Empirical validation is limited. Being equilibrium models, DSGEs cannot predict phenomena such as boom-bust business cycles. The most cogent illustration has been their inability to predict recent stock market crashes and the ensuing economic downturns.
Econophysics and Econometrics
In Section The Epistemological Foundations of Economics, we discussed the epistemological issues associated with economics; in Section What Is the Cognitive Value of Neoclassical Economics, Neoclassical Finance? We critiqued mainstream economics, concluding that it is not an empirical scientific theory. In this and the following section we discuss new methods, ideas, and results that are intended to give economics a scientific foundation as an empirical science. We will begin with a discussion of econophysics and econometrics.
The term Econophysics was coined in 1995 by the physicist Eugene Stanley. Econophysics is an interdisciplinary research effort that combines methods from physics and economics. In particular, it applies techniques from statistical physics and non-linear dynamics to the study of economic data and it does so without the pretense of any a priori knowledge of economic phenomena.
Econophysics obviously overlaps the more traditional discipline of econometrics. Indeed, it is difficult to separate the two in any meaningful way. Econophysics also overlaps economics based on artificial markets formed by many interacting agents. Perhaps a distinguishing feature of econophysics is its interdisciplinarity, though one can reasonably argue that any quantitative modeling of financial or economic phenomena shares techniques with other disciplines. Another distinguishing feature is its search for universal laws; econometrics is more opportunistic. However, these distinctions are objectively weak. Universality in economics is questionable and econometrics uses methods developed in pure mathematics.
To date, econophysics has focused on analyzing financial markets. The reason is obvious: financial markets generate huge quantities of data. The availability of high-frequency data and ultra-high-frequency data (i.e., tick-by-tick data) has facilitated the use of the methods of physics. For a survey of Econophysics, see in particular Lux [19] and Chakraborti et al. [20]; see Gallegati et al. [21] for a critique of econophysics from inside.
The main result obtained to date by econophysics is the analysis and explanation of inverse power law distributions empirically found in many economic and financial phenomena. Power laws have been known and used for more than a century, starting with the celebrated Pareto law of income distribution. Power law distributions were proposed in finance in the 1950s, for example by Mandelbrot [22]. More recently, econophysics has performed a systematic scientific study of power laws and their possible explanations.
Time series or cross sectional data characterized by inverse power law distributions have special characteristics that are important for economic theory as well as for practical applications such as investment management. Inverse power laws characterize phenomena such that very large events are not negligibly rare. The effect is that individual events, or individual agents, become very important.
Diversification, which is a pillar of classical finance and investment management, becomes difficult or nearly impossible if distributions follow power laws. Averages lose importance as the dynamics of phenomena is dominated by tail events. Given their importance in explaining economic and financial phenomena, we will next briefly discuss power laws.
Power Laws
Let's now look at the mathematical formulation of distributions characterized by power laws and consider some examples of how they have improved our understanding of economic and financial phenomena.
The tails of the distribution of a random variable r follow an inverse power law if the probability of the tail region decays hyperbolically:
The properties of the distribution critically depend on the magnitude of the exponent α. Values α < 2 characterize Levy distributions with infinite variance and infinite mean if α < 1; values α > 2 characterize distributions with finite mean and variance.
Consider financial returns. Most studies place the value of α for financial returns at around 3 [19]. This finding is important because values α < 2 would imply invariance of the distribution, and therefore of the exponent, with respect to summation of variables. That is, the sum of returns would have the same exponent of the summands. This fact would rule out the possibility of any diversification and would imply that returns at any time horizon have the same distribution. Instead, values of α at around 3 imply that variables become normal after temporal aggregation on sufficiently long time horizons. This is indeed what has been empirically found: returns become normal over periods of 1 month or more.
Power laws have also been found in the autocorrelation of volatility. In general the autocorrelation of returns is close to zero. However, the autocorrelation of volatility, (measured by the autocorrelation of the absolute value of returns, or the square of returns), decays as an inverse power law:
The typical exponent found empirically is 0.3. Such a small exponent implies a long-term dependence of volatility.
Power laws have been found in other phenomena. Trading volume decays as a power law; power laws have also been found in the volume and number of trades per time unit in high-frequency data; other empirical regularities have been observed, especially for high-frequency data.
As for economic phenomena more in general, power laws have been observed in the distribution of loans, the market capitalization of firms, and income distribution - the original Pareto law. Power laws have also been observed in non-financial phenomena such as the distribution of the size of cities4.
Power law distributions of returns and of volatility appear to be a universal feature in all liquid markets. But Gallegati et al. [21] suggest that the supposed universality of these empirical findings (which do not depend on theory) is subject to much uncertainty. In addition, there is no theoretical reason to justify the universality of these laws. It must be said that the level of validation of each finding is not extraordinarily high. For example, distributions other than power laws have been proposed, including stretched exponentials and tempered distributions. There is no consensus on any of these findings. As observed in Section The Epistemological Foundations of Economics, the empirical content of individual findings is low; it is difficult to choose between the competing explanations.
Attempts have been made to offer theoretical explanations for the findings of power laws. Econophysicists have tried to capture the essential mechanisms that generate power laws. For example, it has been suggested that power laws in one variable naturally lead to power laws in other variables. In particular, power law distributions of the size of market capitalization or similar measures of the weight of investors explain most other financial power laws [23]. The question is: How were the original power laws generated?
Two explanations have been proposed. The first is based on non-linear dynamic models. Many, perhaps most, non-linear models create unconditional power law distributions. For example, the ARCH/GARCH models create unconditional power laws of the distribution of returns though the exponents do not fit empirical data. The Lux-Marchesi dynamic model of trading [24] was the first model able to explain power laws of both returns and autocorrelation time. Many other dynamic models have since been proposed.
A competing explanation is based on the properties of percolation structures and random graph theory, as originally proposed by Cont and Bouchaud [25]. When the probability of interaction between adjacent nodes approaches a critical value that depends on the topology of the percolation structure or the random graph, the distribution of connected components follows a power law. Assuming financial agents can be represented by the nodes of a random graph, demand created by aggregation produces a fat-tailed distribution of returns.
Random Matrices
Econophysics has also obtained important results is in the analysis of large covariance and correlation matrices, separating noise from information. For example, financial time series of returns are weakly autocorrelated but strongly correlated. Correlation matrices play a fundamental role in portfolio management and many other financial applications.
However, estimating correlation and covariance matrices for large markets is problematic due to the fact that the number of parameters to estimate (i.e., the entries of the covariance matrix) grows with the square of the number of time series, while the number of available data is only proportional to the number of time series. In practice, the empirical estimator of a large covariance matrix is very noisy and cannot be used. Borrowing from physics, econophysicists suggest a solution based on the theory of random matrices which has been applied to solve problems in quantum physics.
The basic idea of random matrices is the following. Consider a sample of N time series of length T. Suppose the series are formed by independent and identically distributed zero mean normal variables. In the limit of N and T going to infinity with a constant ratio Q = T/N, the distribution of the eigenvalues of these series was determined by Marchenko Pastur [26]. Though the law itself is a simple algebraic function, the demonstration is complicated. The remarkable finding is that there is a universal theoretical distribution of eigenvalues in an interval that depends only on Q.
This fact suggested a method for identifying the number of meaningful eigenvalues of a large covariance matrix: Only those eigenvalues that are outside the interval of the Marcenko-Pastur law are significant (see Plerou et al. [27]). A covariance matrix can therefore be made robust computing the Principal Components Analysis (PCA) and using only those principal components corresponding to meaningful eigenvalues. Random matrix theory has been generalized to include correlated and autocorrelated time series and non-normal distributions (see Burda et al. [28]).
Econometrics and VAR Models
As mentioned above, the literature on econophysics overlaps with the econometric literature. Econometricians have developed methods to capture properties of time series and model their evolution. Stationarity, integration and cointegration, and the shifting of regimes are properties and models that come from the science of econometrics.
The study of time series has opened a new direction in the study of economics with the use of Vector Auto Regressive (VAR) models. VAR models were proposed by Christopher Sims in the 1980s (for his work, Sims shared the 2011 Nobel Prize in Economics with Thomas Sargent). Given a vector of variables, a VAR model represents the dynamic of the variables as the regression of each variable over lagged values of all variables:
The use of VAR models in economics is typically associated with dimensionality reduction techniques. As currently tens or even hundreds of economic time series are available, PCA or similar techniques are used to reduce the number of variables so that the VAR parameters can be estimated.
What are the similarities and differences between econometrics and econophysics? Both disciplines try to find mathematical models of economic and/or financial variables. One difference between the two disciplines is perhaps the fact that econophysics attempts to find universal phenomena shared by every market. Econometricians, on the other hand, develop models that can be applied to individual time series without considering their universality. Hence econometricians focus on methods of statistical testing because the applicability of models has to be tested in each case. This distinction might prove to be unimportant as there is no guarantee that we can find universal laws. Thus far, no model has been able to capture all the features of financial time series: Because each model requires an independent statistical validation, the empirical content is weak.
New Directions in Economics
We will now explore some new directions in economic theory. Let's start by noting that we do not have a reasonably well-developed, empirically validated theory of economics. Perhaps the most developed field is the analysis of instabilities as well as economic simulation. The main lines of research, however, are clear and represent a departure from the neoclassical theory. They can be summarized thus:
1. Social values and objectives must be separated from economic theory, that is, we have to separate political economics from pure economic theory. Economies are systems in continuous evolution. This fact is not appreciated in neoclassical economics which considers only aggregated quantities.
2. The output of economies is primarily the creation of order and complexity, both at the level of products and social structures. Again, this fact is ignored by neoclassical economics, which takes a purely quantitative approach without considering changes in the quality of the output or the power structure of economies.
3. Economies are never in a state of equilibrium, but are subject to intrinsic instabilities.
4. Economic theory needs to consider economies as physical systems in a physical environment; it therefore needs to take into consideration environmental constraints.
Let's now discuss how new directions in economic theory are addressing the above.
Economics and Political Economics
As mentioned above, economic theory should be clearly separated from political economics. Economies are human artifacts engineered to serve a number of purposes. Most economic principles are not laws of nature but reflect social organization. As in any engineering enterprise, the engineering objectives should be kept separate from the engineering itself and the underlying engineering principles and laws. Determining the objectives is the realm of political economics; engineering the objectives is the realm of economic theory.
One might object that there is a contradiction between the notion of economies as engineered artifacts and the notion of economies as evolving systems subject to evolutionary rules. This contradiction is akin to the contradiction between studying human behavior as a mechanistic process and simultaneously studying how to improve ourselves.
We will not try to solve this contradiction at a fundamental level. Economies are systems whose evolution is subject to uncertainty. Of course the decisions we make about engineering our economies are part of the evolutionary process. Pragmatically, if not philosophically, it makes sense to render our objectives explicit.
For example, Acemoglu, Robinson, and Verdier wrote an entry in the VOX CEPR's Policy Portal (http://www.voxeu.org/article/cuddly-or-cut-throat-capitalism-choosing-models-globalised-world) noting that we have the option to choose between different forms of capitalism (see, for example, in Hall and Soskice [29]), in particular, between what they call “cuddly capitalism” or “cut-throat capitalism.” It makes sense, pragmatically, to debate what type of system, in this case of capitalism, we want. An evolutionary approach, on the other hand, would study what decisions were/will be made.
The separation between objectives and theory is not always made clear, especially in light of political considerations. Actually, there should be multiple economic theories corresponding to different models of economic organization. Currently, however, the mainstream model of free markets is the dominant model; any other model is considered either an imperfection of the free-market competitive model or a failure, for example Soviet socialism. This is neither a good scientific attitude nor a good engineering approach. The design objectives of our economies should come first, then theory should provide the tools to implement the objectives.
New economic thinking is partially addressing this need. In the aftermath of the 2007–2009 financial crisis and the subsequent questioning of mainstream economics, some economists are tackling socially-oriented issues, in particular, the role and functioning of the banking system, the effect of the so-called austerity measures, and the social and economic implications of income and wealth inequality.
There is a strain of economic literature, albeit small, known as meta-economics, that is formally concerned with the separation of the objectives and the theory in economics. The term metaeconomics was first proposed by Karl Menger, an Austrian mathematician and member of the Vienna Circle5. Influenced by David Hilbert's program to give a rigorous foundation to mathematics, Menger proposed metaeconomics as a theory of the logical structure of economics.
The term metaeconomics was later used by Schumacher [30] to give a social and ethical foundation to economics, and is now used in this sense by behavioral economists. Metaeconomics, of course, runs contrary to mainstream economics which adheres to the dogma of optimality and excludes any higher-level discussion of objectives.
Economies as Complex Evolving Systems
What are the characteristics of evolutionary complex systems such as our modern economies? An introduction can be found in Beinhocker [31]. Associated with the Institute for New Economic Thinking (INET)6, Beinhocker attributes to Nicholas Georgescu-Roegen many of the new ideas in economics that are now receiving greater attention.
Georgescu-Roegen [32] distinguishes two types of evolution, slow biological evolution and the fast cultural evolution typical of modern economies. Thus, the term bioeconomics. The entropy accounting of the second law of thermodynamics implies that any local increase of order is not without a cost: it requires energy and, in the case of the modern economies, produces waste and pollution. Georgescu-Roegen argued that because classical economics does not take into account the basic laws of entropy, it is fundamentally flawed.
When Georgescu-Roegen first argued his thesis back in the 1930s, economists did not bother to respond. Pollution and depletion of natural resources were not on any academic agenda. But if economics is to become a scientific endeavor, it must consider the entropy accounting of production. While now much discussed, themes such as energy sources, sustainability, and pollution are still absent from the considerations of mainstream economics.
It should be clear that these issues cannot be solved with a mathematical algorithm. As a society, we are far from being able, or willing, to make a reasonable assessment of the entropy balance of our activities, economic and other. But a science of economics should at least be able to estimate (perhaps urgently) the time scales of these processes.
Economic growth and wealth creation are therefore based on creating order and complexity. Understanding growth, and eventually business cycles and instabilities, calls for an understanding of how complexity evolves—a more difficult task than understanding the numerical growth of output.
Older growth theories were based on simple production functions and population growth. Assuming that an economy produces a kind of composite good, with appropriate production functions, one can demonstrate that, setting aside capital, at any time step the economy increases its production capabilities and exhibits exponential growth. But this is a naïve view of the economy. An increase of complexity is the key ingredient of economic growth.
The study of economic complexity is not new. At the beginning of the twentieth century, the Austrian School of Economics introduced the idea, typical of complex systems, that order in market systems is a spontaneous, emerging property. As mentioned above, this idea was already present in Adam Smith's invisible hand that coordinates markets. The philosopher-economist Friedrick Hayek devoted much theoretical thinking to complexity and its role in economics.
More recently, research on economies as complex systems started in the 1980s at The Santa Fe Institute (Santa Fe, New Mexico). There, under the direction of the economist Bryan Arthur, researchers developed one of the first artificial economies. Some of the research done at the Santa Fe Institute is presented in three books titled The Economy as an Evolving Complex System, published by The Santa Fe Institute.
At the Massachusetts Institute of Technology (MIT), the Observatory on Economic Complexity gathers and publishes data on international trade and computes various measures of economic complexity, including the Economic Complexity Index (ECI) developed by Cesar Hidalgo and Ricardo Hausmann. Complexity economics is now a subject of research at many universities and economic research centers.
How can systems increase their complexity spontaneously, thereby evolving? Lessons from biology might help. Chaitin [12] proposed a mathematical theory based on the theory of algorithmic complexity that he developed to explain Darwinian evolution. Chaitin's work created a whole new field of study—metabiology—though his results are not universally accepted as proof that Darwinian evolution works in creating complexity.
While no consensus exists, and no existing theory is applicable to economics, it is nevertheless necessary to understand how complexity is created if we want to understand how economies grow or eventually fail to grow.
Assuming the role of complexity in creating economic growth and wealth, how do we compare the complexity of objects as different as pasta, washing machines and computers? And how do we measure complexity? While complexity can be measured by a number of mathematical measures, such as those of the algorithmic theory of complexity, there is no meaningful way to aggregate these measures to produce a measure of the aggregate output.
Mainstream economics uses price—the market value of output—to measure the aggregate output. But there is a traditional debate on value, centered on the question of whether price is a measure of value. A Marxist economist would argue that value is the amount of labor necessary to produce that output. We will stay within market economies and use price to measure aggregate output. The next section discusses the issues surrounding aggregation by price.
The Myth of Real Output
Aggregating so many (eventually rapidly changing) products7 quantitatively by physical standards is an impossible task. We can categorize products and services, such as cars, computers, and medical services but what quantities do we associate to them?
Economics has a conceptually simple answer: products are aggregated in terms of price, the market price in free-market economies as mentioned above, or centrally planned prices in planned economies. The total value of goods produced in a year is called the nominal Gross National Product (GNP). But there are two major problems with this.
First, in practice, aggregation is unreliable: Not all products and services are priced; many products and services are simply exchanged or self-produced; black and illegal economies do exist and are not negligible; data collection can be faulty. Therefore, any number which represents the aggregate price of goods exchanged has to be considered uncertain and subject to error.
Second, prices are subject to change. If we compare prices over long periods of time, changes in prices can be macroscopic. For example, the price of an average car in the USA increased by an order of magnitude from a few thousand dollars in the 1950s to a tens of thousands of dollars in the 2010s. Certainly cars have changed over the years, adding features such as air conditioning, but the amount of money in circulation has also changed.
The important question to address is whether physical growth corresponds to the growth of nominal GNP. The classical answer is no, as the level of prices changes. But there is a contradiction here: to measure the eventual increase in the price level we should be able to measure the physical growth and compare it with the growth of nominal GNP. But there is no way to measure realistically physical growth; any parameter is arbitrary.
The usual solution to this problem is to consider the price change (increase or decrease) of a panel of goods considered to be representative of the economy. The nominal GNP is divided by the price index to produce what is called real GNP. This process has two important limitations. First, the panel of representative goods does not represent a constant fraction of the total economy nor does it represent whole sectors, such as luxury products or military expenditures. Second, the panel of representative goods is not constant as products change, sometimes in very significant ways.
Adopting an operational point of view, the meaning of the real GNP is defined by how it is constructed: it is the nominal GNP weighted with the price of some average panel of goods. Many similar constructions would be possible in function of different choices of the panel of representative goods. There is therefore a fundamental arbitrariness in how real GNP is measured. The growth of the real GNP represents only one of many different possible concepts of growth. Growth does exist in some intuitive sense, but quantifying it in some precise way is largely arbitrary. Here we are back to the fundamental issue that economies are complex systems.
Describing mathematically the evolution of the complexity of an economy is a difficult, perhaps impossible, task. When we aggregate by price, the problem becomes more tractable because there are constraints to financial transactions essentially due to the amount of money in circulation and rules related to the distribution of money to different agents.
But it does not make sense to aggregate by price the output of an entire country. We suggest that it is necessary to model different sectors and understand the flows of money. Some sectors might extend over national boundaries. Capital markets, for example, are truly international (we do not model them as purely national); the activity of transnational corporations can span a multitude of countries. What is required is an understanding of what happens under different rules.
Here we come upon what is probably the fundamental problem of economics: the power structure. Who has the power to make decisions? Studying human structures is not like studying the behavior of a ferromagnet. Decisions and knowledge are intertwined in what the investor George Soros has called the reflexivity of economies.
Finance, the Banking System, and Financial Crises
In neoclassical economics, finance is transparent; in real-world economies, it is far from being the case. Real economies produce complexity and evolve in ways that are difficult to understand. Generally speaking, the financial and banking systems allow a smooth evolution of the economic system, providing the money necessary to sustain transactions, thereby enabling the sale and purchase of goods and services. While theoretically providing the money needed to sustain growth, the financial and banking systems might either provide too little money and thereby constrain the economy, or provide too much money and thereby produce inflation, especially asset inflation.
Asset inflation is typically followed by asset deflation as described by Minsky [33] in his financial instability hypothesis. Minsky argued that capitalist economies exhibit asset inflations due to the creation of excess money, followed by debt deflations that, because of the fragile financial systems, can end in financial and economic crises. Since Minsky first formulated his financial instability hypothesis, many changes and additional analysis have occurred.
First, it has become clear that the process of money creation is endogenous, either by the central banks or commercial banks. What has become apparent, especially since the 2007–2009 financial crisis, is that central banks can create money greatly in excess of economic growth and that this money might not flow uniformly throughout the economy but follow special, segregated paths (or flows), eventually remaining in the financial system, thereby producing asset inflation but little to no inflation in the real economy.
Another important change has been globalization, with the free flow of goods and capital in and out of countries, in function of where it earns the highest returns or results in the lowest tax bill. As local economies lost importance, countries have been scrambling to transform themselves to compete with low-cost/low-tax countries. Some Western economies have been successful in specializing in added-value sectors such as financial services. These countries have experienced huge inflows of capital from all over the world, creating an additional push toward asset inflation. In recent years, indexes such as the S&P500 have grown at multiples of the nominal growth of their reference economies.
But within a few decades of the beginning of globalization, some of those economies that produced low-cost manufactured goods have captured the entire production cycle from design, engineering, manufacturing, and servicing. Unable to compete, Western economies started an unprecedented process of printing money on a large scale with, as a result, the recurrence of financial crashes followed by periods of unsustainable financial growth.
Studying such crises is a major objective of economics. ETH-Zurich's Didier Sornette, who started his career as a physicist specialized in forecasting rare phenomena such as earthquakes, made a mathematical analysis of financial crises using non-linear dynamics and following Minsky's financial instability hypothesis. Together with his colleague Peter Cauwels, Sornette and Cauwels [34] hypothesize that financial crises are critical points in a process of superexponential growth of the economy.
Artificial Economies
As discussed above, the mathematical analysis of complex system is difficult and might indeed be an impossible task. To overcome this problem, an alternative route is the development of agent-based artificial economies. Artificial economies are computer programs that simulate economies. Agent-based artificial economies simulate real economies creating sets of artificial agents whose behavior resembles the behavior of real agents.
The advantage of artificial economies is that they can be studied almost empirically without the need to perform mathematical analysis, which can be extremely difficult or impossible. The disadvantage is that they are engineered systems whose behavior depends on the engineering parameters. The risk is that one finds exactly what one wants to find. The development of artificial markets with zero-intelligence agents was intended to overcome this problem, studying those market properties that depend only on the trading mechanism and not on agent characteristics.
There is by now a considerable literature on the development of artificial economies and the design of agents. See Chakraborti et al. [20] for a recent review. Leigh Tesfatsion at Iowa State University keeps a site which provides a wealth of information on agent-based systems: http://www2.econ.iastate.edu/tesfatsi/ace.htm.
Evolution of Neoclassical Economics
Among classical economists, efforts are underway to bring the discipline closer to an empirical science. Among the “new” classical economists is David Colander, who has argued that the term “mainstream” economics does not reflect current reality because of the many ramifications of mainstream theories.
Some of the adjustments underway are new versions of DSGE theories which now include a banking system and deviations from perfect rationality as well as the question of liquidity. As observed above, DSGE models are a sort of complex system made up of many intelligent agents. It is therefore possible, in principle, to view complex systems as an evolution of DSGEs. However, most basic concepts of DSGEs, and in particular equilibrium, rational expectations, and the lack of interaction between agents, have to be deeply modified. Should DSGEs evolve as modern complex systems, the new generations of models will be very different from the current generation of DSGEs.
Conclusions
In this paper we have explored the status of economics as an empirical science. We first analyzed the epistemology of economics, remarking on the necessity to carefully analyze what we consider observations (e.g., volatility, inflation) and to pose questions that can be reasonably answered based on observations.
In physics, observables are processes obtained through the theory itself, using complex instruments. Physical theory responds to empirical tests in toto; individual statements have little empirical content. In economics, given the lack of a comprehensive theory, observations are elementary observations, such as prices, and theoretical terms are related to observables in a direct way, without cross validation. This weakens the empirical content of today's prevailing economic theory.
We next critiqued neoclassical economics, concluding that it is not an empirical science but rather the study of an artificial idealized construction with little connection to real-world economies. This conclusion is based on the fact that neoclassical economics is embodied in DSGE models which are only weakly related to empirical reality.
We successively explored new ideas that hold the promise of developing economics more along the lines of an empirical science. Econophysics, an interdisciplinary effort to place economics on a sure scientific grounding, has produced a number of results related to the analysis of financial time series, in particular the study of inverse power laws. But while econophysics has produced a number of models, it has yet to propose a new global economic theory.
Other research efforts are centered on looking at economies as complex evolutionary systems that produce order and increasing complexity. Environmental constraints due to the accounting of energy and entropy are beginning to gain attention in some circles. As with econophysics, the study of the economy as a complex system has yet produced no comprehensive theory.
The most developed area of new research efforts is the analysis of instabilities, building on Hyman Minsky's financial instability hypothesis. Instabilities are due to interactions between a real productive economy subject to physical constraints, and a financial system whose growth has no physical constraints.
Lastly, efforts are also being made among classical economists to bring their discipline increasingly into the realm of an empirical science, adding for example the banking system and boundedly rational behavior to the DSGE.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^By “neoclassical economics,” we refer to an economic theory based on the notions of optimization, the efficient market hypothesis, and rational expectations. Among the major proponents of neoclassical economic thinking are Robert Lucas and Eugene Fama, both from the University of Chicago and both recipients of the Nobel Prize in Economics. Because neoclassical economic (and finance) theory is presently the dominating theory, it is also often referred to as “mainstream” theory or “the prevailing” theory. Attempts are being made to address some of the shortfalls of neoclassical economics, such as the consideration of the banking system, money creation and liquidity.
2. ^For example, in the Special Relativity Theory, the concept of simultaneity of distant events is not an a priori concept but depends on how we observe simultaneity through signals that travel at a finite speed. To determine simultaneity, we perform operations based on sending and receiving signals that travel at finite speed. Given the invariance of the speed of light, these operations make simultaneity dependent on the frame of reference.
3. ^The term “metaeconomics” is currently used in a different sense. See Section Econophysics and Econometrics below. Here we use metaeconomics in analogy with Chaitin's metabiology.
4. ^Power laws are ubiquitous in physics where many phenomena, such as the size of ferromagnetic domains, are characterized by power laws.
5. ^Karl Menger was the son of the economist Carl Menger, the founder of the Austrian School of Economics.
6. ^The Institute for New Economic Thinking (INET) is a not-for profit think tank whose purpose is to support academic research and teaching in economics “outside the dominant paradigms of efficient markets and rational expectations.” Founded in 2009 with the financial support of George Soros, INET is a response to the global financial crisis that started in 2007.
7. ^Beinhocker [31] estimates that, in the economy of a city like New York, the number of Stock Keeping Units or SKUs, with each SKU corresponding to a different product, to be in the order of tens of billions.
References
1. Fabozzi FJ, Focardi SM, Jonas C. Investment Management: A Science to Teach or an Art to Learn? Charlottesville: CFA Institute Research Foundation (2014).
2. van Orman Quine W. Two Dogmas of Empiricism (1951). Available online at: http://www.ditext.com/quine/quine.html)
3. Bridgman WP. The Logic of Modern Physics (1927). Available online at: https://archive.org/details/logicofmodernphy00brid
4. Hempel CG. Aspects of Scientific Explanation and Other Essays in the Philosophy of Science. New York: Free Press (1970).
6. Kuhn TS. The Structure of Scientific Revolutions. 3rd ed. Chicago: University of Chicago Press (1962).
7. Popper C. Conjectures and Refutations: The Growth of Scientific Knowledge. London: Routledge Classics (1963).
11. Gu M, Weedbrook C, Perales A, Nielsen MA. More really is different. Phys D (2009) 238:835–9. doi: 10.1016/j.physd.2008.12.016
14. Turing A. Computing machinery and intelligence. Mind (1950) 49:433–60. doi: 10.1093/mind/LIX.236.433
16. Muth JF. Rational expectations and the theory of price movements. Econometrica (1961) 29:315–35. doi: 10.2307/1909635
17. Mantel R. On the characterization of aggregate excess demand. J Econ Theory (1974) 7:348–53. doi: 10.1016/0022-0531(74)90100-8
18. Smets F, Wouters R. An estimated stochastic dynamic general equilibrium model of the euro area. In: Working Paper No. 171, European Central Bank Working Paper Series. Frankfurt (2002). doi: 10.2139/ssrn.1691984
19. Lux T. Applications of statistical physics in finance and economics. In: Kiel Working Papers 1425. Kiel: Kiel Institute for the World Economy (2008).
20. Chakraborti A, Muni-Toke I, Patriarca M, Abergel F. Econophysics review: I. empirical facts. Quant Finance (2011) 11:991–1012. doi: 10.1080/14697688.2010.539248
21. Gallegati M, Keen S, Lux T, Ormerod P. Worrying trends in econophysics. Phys A (2006) 370:1–6 doi: 10.1016/j.physa.2006.04.029
22. Mandelbrot B. Stable Paretian random functions and the multiplicative variation of income. Econometrica (1961) 29:517–43. doi: 10.2307/1911802
23. Gabaix X, Gopikrishnan P, Plerou V, Stanley HE. A theory of power-law distributions in financial market fluctuations. Nature (2003) 423:267–70. doi: 10.1038/nature01624
24. Lux T, Marchesi M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature (1999) 397:498–500.
25. Cont R, Bouchaud J-P. Herd behavior and aggregate fluctuations in financial markets. Macroecon Dyn. (2000) 4:170–96. doi: 10.1017/s1365100500015029
26. Marchenko VA, Pastur LA. Distribution of eigenvalues for some sets of random matrices. Mathematics (1967) 72:507–536.
27. Plerou V, Gopikrishnan P, Rosenow B, Amaral LAN, Guhr T, Stanley HE. Random matrix approach to cross correlations in financial data. Phys Rev E (2002) 65:066126-1—18. doi: 10.1103/physreve.65.066126
28. Burda Z, Jurkiewicz J, Nowak MA, Papp G, Zahed I. Levy matrices and financial covariances (2001). arXiv:cond-mat/0103108
29. Hall P, Soskice D. Varieties of Capitalism: The Institutional Foundations of Comparative Advantage. Oxford: Oxford University Press (2001). doi: 10.1093/0199247757.001.0001
30. Schumacher F. Small is Beautiful: A Study of Economics as Though People Mattered. London: Blond & Briggs Ltd. (1973). 352 p.
31. Beinhocker ED. The Origin of Wealth: The Radical Remaking of Economics and What It Means for Business and Society. Boston: Harvard Business Review Press (2007).
32. Georgescu-Roegen N. The Entropy Law and the Economic P5rocess. Cambridge: MA University Press (1971). doi: 10.4159/harvard.9780674281653
34. Cauwels P, Sornette D. The Illusion of the Perpetual Money Machine, Paper No. 12-40. Geneva: Swiss Finance Institute Research (2012). Available online at: http://ssrn.com/abstract=2191509 (Accessed October 27, 2012).
Keywords: economics, empirical science, epistemology of economics, econophysics, complex systems, financial crises
Citation: Focardi SM (2015) Is economics an empirical science? If not, can it become one? Front. Appl. Math. Stat. 1:7. doi: 10.3389/fams.2015.00007
Received: 07 April 2015; Accepted: 29 June 2015;
Published: 21 July 2015.
Edited by:
Sergio Ortobelli Lozza, University of Bergamo, ItalyReviewed by:
Byung Hwa Lim, The University of Suwon, South KoreaNaoshi Tsuchida, Bank of Japan, Japan
Copyright © 2015 Focardi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sergio M. Focardi, Department of Applied Mathematics and Statistics, Stony Brook University, Stony Brook, NY 11794, USA,c2VyZ2lvLmZvY2FyZGlAc3Rvbnlicm9vay5lZHU=
 Sergio M. Focardi
Sergio M. Focardi