General equilibrium pricing with information asymmetry

1. Introduction

General equilibrium theory deals with an economy consisting of multiple agents in a market endowed with initial resources and willing to exchange commodities with others. It considers the behavior of the economy as a closed and inter-related system. In a general equilibrium perspective, each agent in the market optimizes his/her behavior to achieve maximum consumption utility. Agents' optimal behavior represents the behavior of the economy. Equilibrium prices are determined endogenously. The existence of such an equilibrium is based on the assumption of perfect competition among agents. In other words, the model assumes all individuals are price-takers, i.e., that they have zero price impact. This type of model is often called Walrasian equilibrium, from the Walras [1] theory of markets. The modern version of general equilibrium theory was formalized by Arrow and Debreu [2], Debreu [3] and McKenzie [4]. In the Arrow-Debreu model, the market is static and deterministic. Radner [5–7] and Jordan and Radner [8] explore the competitive equilibrium in the case of uncertainty. In a Radner-type economy, different market agents are allowed to have different information. Agents in such an economy maximize their expected utility with respect to the their own information. The work opens the possibility of applying general equilibrium to financial markets to explain the prices of financial assets. Breeden [9] develops the Consumption-Based Capital Asset Pricing Model (CCAPM) that connects continuous-time general equilibrium to characteristics of returns on securities. Cox et al. [10] also examine the price behavior in a general equilibrium. Duffie and Zame [11] further study and extend the approach.

Demarzo and Skiadas [12] further investigate asset pricing in economies with asymmetric information, although not in a dynamic setting. The concept of quasi-completeness is introduced to describe the feasibility of consumption conditioned on the agents individual information. Also, in Yannelis [13] and Glycopantis and Yannelis [14], the core of an economy and its related concepts are introduced and discussed to study information asymmetry. In Lengwiler [15], Heer and Maussner [16], Black and Glaser [17], Starr [18], and Ludvigson [19], the modern general equilibrium pricing theory are elaborated and reviewed. Recently, Biais et al. [20, 21] develop a two-date equilibrium with differential information and demonstrates that information is partially revealed by the price. Fama and French [22] investigate the effects of disagreement and preference differences on asset prices in a CAPM setting. Ostrovsky [23] uses an extended sequential auction model based on market scoring rules to study information aggregation with partially informed trades. Iyer et al. [24] develop a market with heterogeneous traders and a market maker to give a condition for information aggregation. Equilibrium under information asymmetry has also been studied in many other papers, including Bernardo and Judd [25], Breon-Drish [26], Cao and Ou-yang [27], Gao et al. [28], Banerjee and Green [29], among others. Meanwhile there also exist many literatures investigating in the extensions of CAPM theory, including Campbell and Cochrane [30], Dionne [31], Breeden and Litzenberger [32], Barberis and Greenwood [33], among others.

Our work is in line with the formalization of the Consumption-based Capital Pricing Models in Duffie [34] and Demarzo and Skiadas [12] model with differential information among agents. We model asset price formation in a multi-period general equilibrium framework. The concept of equivalent martingale measure under quasi-completeness as in Demarzo and Skiadas [12] and related concepts will be rephrased in a CCAPM context. In our framework, the state-price can be extended to a broader sense, so that it stays universal while difference agent views it asymmetrically. It provides a convenient tool for asset valuation. Also, the similar result that agents will come to asymmetric betas in their beta form asset pricing, as the CAPM in Demarzo and Skiadas [12]. The difference is that our beta is based on consumption, thus not requiring the strict mean-variance utility.

In Section 2, we describe the setup of our model. In Section 3, we re-introduce the concepts of arbitrage, state price and martingale measure in the context of asymmetric information. In Section 4, we define the equilibrium and discuss the characteristics of the equilibrium price. Section 5 provides several examples to illustrate the differences in equilibrium prices between the case with information asymmetry and the one without. Mispricing as a consequence of asymmetric information is also discussed.

2. The Setup

In this section, We formulate a general equilibrium model with information asymmetry in discrete time. In our setting, there are finite number of agents in economy. As in other general equilibrium models, the agents are assumed to be price takers. Agents make their consumption plans based on not only their own private information but also the information generated by the price process. An agent prices a consumption process by her own pricing function, which is obtained from maximizing her utility. That means, for some consumption process, the prices as seen by different agents are allowed to be different. However, since agents are price takers and the market must clear, it is shown that there exists a so-called quasi pricing kernel such that the pricing function of each agent is the optimal projection of the quasi pricing kernel onto her own information filtration. Equivalently, there exists a probability measure, a so-called quasi equivalent martingale measure, under which a security price is viewed as a martingale for each agent (i.e., conditioned on individual information filtration).

2.1. Uncertainty

There are T + 1 dates: 0, 1, …, T. Denote by ${T}$ = {0, 1, …, T} the time horizon. Then uncertainty is modeled by the probability space (Ω, ${F}$, P) equipped with filtration 𝔽 = {${F}$₀, ${F}$₁, …, ${F}$_T}. ${F}$_t denotes the information up to time t and ${F}$_T =${F}$. Ω denotes the state space. P is the physical probability measure. Let L be the space of all 𝔽-adapted processes.

2.2. Economy

In our economy, there are n agents. Denote by I = {1, …, n} the set of agents. Each agent i ∈ I is characterized by individual belief (represented by probability measure P⁽ⁱ⁾), utility function U⁽ⁱ⁾, endowment e⁽ⁱ⁾, and information flow, represented by the filtration ${\text{𝔽}}^{(i)}={\left\{{{F}}_t^{(i)}\right\}}_{t\in {T}}$.

Each individual filtration satisfies ${{F}}_t^{(i)}\subseteq {{F}}_t$. It means each agent can access some subset of the total information, which allows that information available to agents is not symmetric. Denote the common information by ${\underset{\_}{{F}}}_t={\bigcap }_{i\in I}{{F}}_t^{(i)}$, and the largest information that can be accessed by all agents as whole by ${\overline{{F}}}_t={\vee }_{i\in I}{{F}}_t^{(i)}$ which is the smallest σ-algebra contains all ${{F}}_t^{(i)}$. Each agent knows her endowment process very well. In another word, e⁽ⁱ⁾ is 𝔽⁽ⁱ⁾-adapted for each i ∈ I. Denote the aggregated endowment by $e(t)=\sum _{i\in I}{e}^{(i)}(t)$.

There exist m assets; denote by J = {1, …, m} the set of assets. Each asset j ∈ J is associated with its dividend process δ_j = (δ_j(t)). δ = (δ₁(t), δ₂(t), …, δ_m(t)) denotes dividend process, which is adapted to 𝔽. Assume that all agents can observe dividends, i.e., σ(δ_u: u ≤ t) ⊆ $\underset{\_}{{F}}$_t for all t ∈ ${T}$.

Definition 1 (Economy). The economy is defined as a collection

$ℰ=\{(\Omega ,{F},\text{\hspace{0.17em}𝔽},P),{(P^{(i)},U^{(i)},{\text{𝔽}}^{(i)},e^{(i)})}_{i\in I},\delta \}.$

For simplicity, we also assume all agents share the same (physical) probability measure, i.e., P⁽ⁱ⁾ = P for all i ∈ I.

2.3. Security Prices

The security price at time t is denoted by S(t) = (S₁(t), …, S_m(t)). (S(t)) is adapted to 𝔽. Security price is public information, thus given price process S, each agent i observes the information generated by S as well as private information ${F}$⁽ⁱ⁾. Denote by ${G}$_t = σ(S_u:u ≤ t) for t ∈ ${T}$ the filtration generated by prices. Assume that all agents are price-takers, thus the securities' prices S is the exact price at which agents trade.

2.4. Trading Strategies and Consumption

Agents in the economy will choose their trading strategies to optimize their satisfaction (which will be represented by utility later). However, the trading strategies each agent can access are restricted by the information she can access. More information will give more choice of trading strategies. This means that an agent's trading strategies are adapted to the information available to her.

Definition 2 (Feasible trading strategies). A trading strategy ${\theta }^{(i)}={({\theta }^{(i)}(t))}_{t\in {T}}$ is feasible for agent i given price S if θ⁽ⁱ⁾(t) is ${{G}}_t\vee {{F}}_t^{(i)}$-measurable, and the consumption process c(t; θ, S) ∈ ℝ₊₊ which is given by the budget constraint:

$\begin{array}{l}{\theta }^{(i)}(t)·S(t)={\displaystyle \sum _{\tau =0}^{t-1}{\theta }^{(i)}}(\tau )·(S(\tau +1)-S(\tau )+\delta (\tau +1))\\ +{\displaystyle \sum _{\tau =0}^t{e}^{(i)}}(t)-{\displaystyle \sum _{\tau =0}^{t}c}(t;\theta ,S)a.s.\end{array}$

or equivalently,

$\begin{array}{l}c(t;\theta ,S)=e(t)+\theta (t-1)·(S(t)+\delta (t))-\theta (t)·S(t),\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} for }t=1,\mathrm{\dots },T,\text{and}\\ c(0;\theta ,S)=e(0)-\theta (0)·S(0).\end{array}$

The budget constraint makes sure that the consumption cannot exceed the sum of endowment, dividends and trading profit. Additionally, for convenience, we can define a strategy-generated dividend process as follows.

Definition 3. Let θ(−1) = 0, then define the dividend process generated by trading strategy θ as

${\delta }^{\theta }(t)=\theta (t-1)·(S(t)+\delta (t))-\theta (t)·S(t).t\in {T}$

The dividend generated by trading strategy θ can be interpreted as the trading profit generated from price changes and dividends. Then the feasible consumption set for agent i and a given price process S can be written as

$X^{(i),S}=\left\{e^{(i)}+{\delta }^{\theta }\in L_{+}:\theta \in L^{(i),S}\right\}.$

3. Arbitrage, State Price Deflator, Martingale

Definition 4 (Arbitrage). We call a trading strategy an arbitrage for given (δ, S) if δ^θ > 0.

Recall L denotes the space of all 𝔽-adapted processes and similarly denote by L^{(i), S} the space of process adapted to the filtration generated by ${\left\{{{F}}_t^{(i)}\vee {{G}}_t\right\}}_{t\in {T}}$. Then M^{(i), S} = {δ^θ:θ ∈ L^{(i), S}} and M = {δ^θ:θ ∈ L} are linear subspaces of the space of L.

Proposition 1. There is no arbitrage strategy in L′ if and only if there is a strictly increasing linear function F:L → ℝ such that F(δ^θ) = 0 for any θ ∈ L′. Here L′ can be L or L^{(i), S} for some i ∈ I.

Corollary 1. If there is no arbitrage in $\overline{L}$ the space of all processes adapted to the filtration generated by ${\left\{{\overline{{F}}}_t\vee {{G}}_t\right\}}_{t\in {T}}$ for a given S, then there is no arbitrage in L^{(i), S} for all i ∈ I.

Remark. When (δ, S) admits arbitrage in the trading strategy space L, it is not necessary that there exists an arbitrage in a smaller space L′ ⊂ L. That means an agent could not be able to find arbitrage due to the lack of information. See the following example.

Example 1 (Arbitrage in case of information asymmetry). Let time ${T}$ = 0, 1, 2, 3, and let there be one risky asset which pays dividend δ(t), t = 0, 1, 2, where δ(t) satisfies

$\delta (t)=f(t)+{ϵ}_D(t),$

where f(t) is the fundamental value satisfying

$f(t)=f(t-1)+{ϵ}_f(t),t=1,2,3\text{ and\hspace{0.17em}}f(0)=1,$

and ϵ_D(t) is pure noise with ϵ_D(0) = 0, and ϵ_D(t), t = 1, 2, 3 are i.i.d Bernoulli distributed

${ϵ}_D(t)=\{\begin{array}{l}0,\text{ with probability }p\hfill \\ 1,\text{ with probability }q\hfill \end{array}$

and ϵ_f(t) is the pure noise with ϵ_f(0) = 0 and ϵ_f(t), t = 1, 2, 3 are i.i.d Bernoulli distributed

${ϵ}_f(t)=\{\begin{array}{l}0,\text{ with probability }\mu \hfill \\ 1,\text{ with probability }\nu \hfill \end{array}$

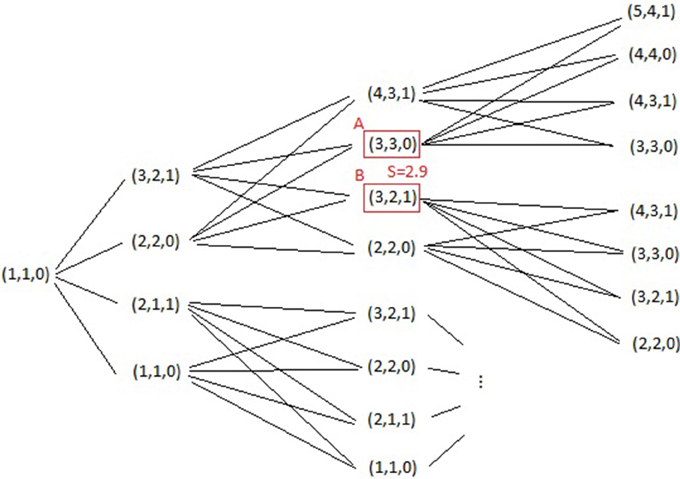
Then this example can be illustrated by the tree with (δ(t), f(t), ϵ_D(t)) as nodes, as shown in Figure 1.

FIGURE 1

Figure 1. Example: Arbitrage opportunity in case of information asymmetry.

Now suppose there two agents. One is uninformed and can only observe dividends, and the other is an insider who knows the true fundamental. Thus, the uninformed agent cannot distinguish the two nodes A,B as shown in the red boxes, and the insider can distinguish between the two nodes. Let price given by probability measure p = 0.2, q = 0.8, μ = 0.5, ν = 0.5, then the prices for the non-informed agent for state A and B are the same, S = 2.9. However, the insider can easily obtain an arbitrage opportunity by making a strategy as (i) Buy if state A happens, (ii) Sell if state B happens, (iii) No trade if none of them happens.

3.1. Classic Case

Lemma 1. For each linear function F:L → ℝ, there exists a unique π in L such that for any x ∈ L

$F(x)={\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^T\pi }(t)x(t)\right].$

π is called the Riesz representation of F. If F is strictly increasing, then π is strictly positive.

Proof. Apply Riesz representation theorem to the Hilbert space L, where inner product is defined as $\langle x,y\rangle ={\text{𝔼}}^{\mathbb{P}}\left[\sum _{t=0}^{T}x(t)y(t)\right],x,y\in L$.          □

We call a strictly positive process π, which is adapted to 𝔽, a state-price deflator if, for all t ∈ ${T}$,

$S(t)=\frac{1}{\pi (t)}{\text{𝔼}}^P\left[{\displaystyle \sum _{j=t+1}^T\pi }(j)\delta (j)|{{F}}_t\right].$

Proposition 2. A strict positive process π ∈ L is a state-price deflator if and only if, for any trading strategy θ ∈ L,

$\theta (t)·S(t)=\frac{1}{\pi (t)}{\text{𝔼}}^P\left[{\displaystyle \sum _{j=t+1}^T\pi }(j){\delta }^{\theta }(j)|{{F}}_t\right],t<T.$

Suppose there exists a risk-free short-rate process $r^f={(r^f(t))}_{t\in {T}}$, define the discount factor

$R(s,t)={\displaystyle \prod _{j=s}^{t-1}(1+r^f(}j)).$

Definition 5 (Equivalent Martingale Measure). We call a probability measure Q an equivalent martingale measure (EMM) if, Q is equivalent to P and

$S(t)={\text{𝔼}}^Q\left[{\displaystyle \sum _{j=t+1}^T\frac{1}{R(t,j)}}\delta (j)|{{F}}_t\right],t<T.$

Theorem 1. π is a state-price deflator if and only if there exists an equivalent martingale measure Q with the density process ξ such that

$\xi (t)=\frac{R(0,t)\pi (t)}{\pi (0)},$

where the density process ξ is defined by

$\xi (t)={\text{𝔼}}^P\left[\frac{dQ}{dP}|{{F}}_t\right].$

Proof. See Duffie [35] p. 30.          □

3.2. Case of Asymmetric Information

In the classic case of symmetric information, a security's price equals the expectation of aggregated future discounted dividend flow under the equivalent martingale measure, and also equals the expectation of aggregated discounted future dividend flows under the physical probability measure. To extend the analysis to asymmetric information, we allow each agent to have her ownstate-price deflator, which is the optimal projection of the universal state-price deflator to her own information.

Let us first investigate some process X ∈ L for a smaller filtration ℍ = {${H}$_t}_{t ∈ ${T}$}, where ${H}$_t ⊆ ${F}$_t for all t. Denote by X^ℍ the optimal projection of X onto ℍ, i.e.,

$X^{\text{ℍ}}(t)={\text{𝔼}}^P\left[X(t)|{{H}}_t\right].$

Some simple facts:

Fact 1. X^ℍ = X ⇔ X is adapted to ℍ.

Fact 2. X^ℍ is ℍ-martingale if X is 𝔽-martingale under same probability measure.

Fact 3. If X is a 𝔽-martingale, and adapted to ℍ, then X is a ℍ-martingale.

For an equivalent probability measure Q, we define its density process ξ^ℍ on some smaller filtration ℍ as the optimal projection of ξ onto ℍ, i.e.,

${\xi }^{\text{ℍ}}(t)={\text{𝔼}}^P\left[\frac{dQ}{dP}|{{H}}_t\right]={\text{𝔼}}^P\left[\xi (t)|{{H}}_t\right].$

Claim. If Q is an equivalent martingale measure, and π is the corresponding state-price deflator as in Theorem 1, and R(s, t) is ${H}$_t-measurable for all 0 ≤ s < t ≤ T, then

${\xi }^{\text{ℍ}}(t)=\frac{R(0,t){\pi }^{\text{ℍ}}(t)}{{\pi }^{\text{ℍ}}(0)}.$

If there exists no arbitrage in L, and let π be the state-price deflator, then the price viewed by the partially informed agent at time t can be represented by

$S(t)=\text{𝔼}[S(t)|{{H}}_t]={\text{𝔼}}^P\left[\frac{1}{\pi (t)}{\displaystyle \sum _{j=t+1}^T\pi }(j)\delta (j)|{{H}}_t\right],$

where ${H}$_t is the information set can be accessed at time t, and S(t) is ${H}$_t-measurable, which means security prices are public information. Moreover, for any strategy in L^ℍ, the space of ℍ-adapted processes,

$\theta (t)·S(t)={\text{𝔼}}^P\left[\frac{1}{\pi (t)}{\displaystyle \sum _{j=t+1}^T\pi }(j){\delta }^{\theta }(j)|{{H}}_t\right].$

Now, bearing in mind that all agents are price takers, we can start to construct the martingale measure and state-price deflator for asymmetric information. Assume that the risk-free rate is known to all agents.

3.2.1. Assumption

R(s, t), s ≤ t ≤ T, is ${{F}}_t^{(i)}$-measurable for all i ∈ I.

Definition 6 (Quasi Equivalent Martingale Measure). We call an equivalent probability measure Q a quasi equivalent martingale measure (Quasi-EMM) if, for all i ∈ I,

$S(t)={\text{𝔼}}^Q\left[{\displaystyle \sum _{j=t+1}^T\frac{1}{R(t,,j)}}\delta (j)|{{F}}_t^{(i)}\vee {{G}}_t\right],t<T.$

Denote the density processes of Q respect to P for the filtrations ${{F}}^{(i)}\vee {{G}}_t,i\in I$ by

${\xi }^{(i)}(t)={\text{𝔼}}^P\left[\frac{dQ}{dP}|{{F}}_t^{(i)}\vee {{G}}_t\right].$

Under a Quasi-EMM, a security's price equals the expectation of discounted future dividends conditioned on individual information for every agent. All agents in our economy agree on the same (fair) prices of securities, which are exactly consistent with the assumption that all agents are price takers. Correspondingly, we can define a quasi state-price deflator as follows.

Definition 7 (Quasi State-price Deflator). A strictly positive process π is called a quasi state-price deflator if, for all i ∈ I,

$S(t)=\frac{1}{{\pi }^{(i)}(t)}{\text{𝔼}}^P\left[{\displaystyle \sum _{j=t+1}^T{\pi }^{(i)}}(j)\delta (j)|{{F}}_t^{(i)}\vee {{G}}_t\right],$

where π⁽ⁱ⁾ is the optimal projection of π onto ${\left\{{{F}}_t^{(i)}\vee {{G}}_t\right\}}_{t\in {T}}$.

Proposition 3. If π is a quasi state-price deflator, then for any trading strategy θ⁽ⁱ⁾ ∈ L^{(i), S}, i ∈ I,

${\theta }^{(i)}(t)·S(t)=\frac{1}{{\pi }^{(i)}(t)}{\text{𝔼}}^P\left[{\displaystyle \sum _{j=t+1}^T{\pi }^{(i)}}(j){\delta }^{{\theta }^{(i)}}(j)|{{F}}_t^{(i)}\vee {{G}}_t\right],t<T.$

The following theorem shows the relationship between a quasi-EMM and a quasi state-price deflator, which is similar to the classic case of symmetric information.

Theorem 2. π is a quasi state-price deflator if and only if there exists an quasi equivalent martingale measure Q with the density process ξ such that

${\xi }^{(i)}(t)=\frac{R(0,t){\pi }^{(i)}(t)}{{\pi }^{(i)}(0)},foralli\in I,$

where the density process ξ is defined by

${\xi }^{(i)}(t)={\text{𝔼}}^P\left[\frac{dQ}{dP}|{{F}}_t^{(i)}\vee {{G}}_t\right],i\in I.$

The following proposition gives a strong condition for the existence of a quasi state-price deflator, which is actually for the case of symmetric information.

Proposition 4. If there exists a quasi state-price deflator, then there is no arbitrage in L^{(i), S} for all i ∈ I. If there is no arbitrage in $\overline{L}$, then there exists a quasi state-price deflator.

3.2.2. Pricing Consumption Process

The use of quasi state-price deflator π is to price any consumption process, that is, the price of a consumption process c in L₊ is given by ${\text{𝔼}}^{\mathbf{\text{P}}}\left[\sum _{t=0}^{T}c(t)\pi (t)\right]$. Thus, π will be also called a pricing kernel.

If c ∈ X^{(i), S} for some i, then the price for this particular agent i is given by

${\text{𝔼}}^{\text{P}}\left[{\displaystyle \sum _{t=0}^{T}c}(t)\pi (t)\right]={𝔼}^{\text{P}}\left[{\displaystyle \sum _{t=0}^{T}c}(t){\pi }^{(i)}(t)\right].$

But for some other agent j in whose information c is not accessible, then the price will be

${\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^{T}c}(t){\pi }^{(j)}(t)\right],$

which does not necessarily coincide with Π(c). The difference between them comes from asymmetry of information, thus for agent j to access this consumption c, she will have to pay a fee to obtain more information. This, fee, which we call an information fee η, should be

$\eta ={\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^{T}c}(t)\pi (t)\right]-{\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^{T}c}(t){\pi }^{(i)}(t)\right]>0.$

This argument can be extended to any consumption c ∈ L₊. The price of any consumption c ∈ L₊ for an agent i is

${\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^{T}c}(t){\pi }^{(i)}(t)\right].$

And the information fee η is

$\eta ={\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^{T}c}(t)\pi (t)\right]-{\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^{T}c}(t){\pi }^{(i)}(t)\right]\ge 0.$

Thus, η = 0 when c ∈ X^{(i), S}.

4. Equilibrium

4.1. Individual Agent Optimality

The objective of each agent is to maximize her individual utility by choosing the optimal feasible trading strategy. Then the optimization problem for agent i can be written as

$\begin{array}{rc}\underset{{}_{c\in X^{(i),S}}}{\text{max}}{U}^{(i)}(c).& \left(1\right)\end{array}$

The following claims show the relation between arbitrage and individual optimization problem.

Proposition 5. The optimization problem (1) for agent i and given S has a solution ⇒ there exists no arbitrage in L^{(i), S}.

Corollary 2. There exists no arbitrage in L^{(i), S} and U⁽ⁱ⁾ is continuous ⇒ Optimization problem for agent i given S has a solution.

4.1.1. First-order Condition

If the individual optimization (1) has a strictly positive solution c*, and U⁽ⁱ⁾ is continuously differentiable at c*, then

$\nabla U^{(i)}(c^{\ast };{\delta }^{\theta })=0,\forall \theta \in L^{(i),S},$

where ∇U(x; y) denotes the ∇U(x) at y, i.e.,

$\nabla U(x;y)\equiv \underset{\alpha \to 0}{\lim }\frac{U^{(i)}(x+\alpha y)-U^{(i)}(x)}{\alpha }.$

Note that ∇U⁽ⁱ⁾(c*; ·): L → ℝ is a linear function. The following proposition shows that this linear function gives the pricing kernel for the individual agent.

Proposition 6. Suppose the individual optimization problem (1) has a strict positive solution c* and U has a strictly positive continuous derivatives at c*. Then the Riesz representation π of ∇U⁽ⁱ⁾(c*; ·) satisfies that

$S(t)=\frac{1}{{\pi }^{(i)}(t)}{\text{𝔼}}^P\left[{\displaystyle \sum _{j=t+1}^T{\pi }^{(i)}}(j)\delta (j)|{{F}}_t^{(i)}\vee {{G}}_t\right].$

If we restrict utility satisfying additive form, then we can have the following. Suppose U⁽ⁱ⁾, for each i ∈ I, has the additive form:

$U^{(i)}(c)={\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^T{u}_t^{(i)}}(c(t))\right].$

Then for any t ≤ τ,

$\begin{array}{l}S(t)=\frac{1}{u_t^{\prime }(c^{\ast }(t))}{\text{𝔼}}^P[S(\tau )u_{\tau }^{\prime }(c^{\ast }(\tau ))\\ +{\displaystyle \sum _{j=t+1}^{\tau }\delta }(j)u_j^{\prime }(c^{\ast }(j))|{{F}}^{(i)}\vee {{G}}_t].\end{array}$

4.2. Equilibrium Asset Pricing

Definition 8. A security-spot market equilibrium (SSE) is a collection $\left\{{({\theta }^{(i)})}_{i\in I},S\right\}$, such that, for each i, θ⁽ⁱ⁾ solves individual optimization

$\begin{array}{rc}\underset{{}_{c\in X^{(i),S}}}{\text{max}}{U}^{(i)}(c),& \left(2\right)\end{array}$

under market clearing condition

$\begin{array}{rc}{\displaystyle \sum _{i\in I}{\theta }^{(i)}}=0.& \left(3\right)\end{array}$

If a SSE equilibrium exists, that means the equilibrium consumption

$c^{\ast }=(c^{{(1)}^{\ast }},c^{{(2)}^{\ast }},\mathrm{\dots },c^{{(n)}^{\ast }})$

solves all individual optimization problems. From last section, we have the result that there is no arbitrage opportunity for each individual agent. Also, each ∇U⁽ⁱ⁾(c⁽ⁱ⁾*; ·) gives this agent i a pricing kernel π⁽ⁱ⁾, which is adapted to individual information filtration, up to a positive multiplier. In order to construct a universal pricing kernel π, such that π⁽ⁱ⁾ equals to the optimal project of π on individual information. If this universal pricing kernel π exists, then π is a quasi state-price deflator, and Π(c) ≤ Π(e) implies Π⁽ⁱ⁾(c) ≤ Π⁽ⁱ⁾(e⁽ⁱ⁾) for all $c\in L_{+}^{(i),S}$, where Π(·) = 〈π, ·〉, Π⁽ⁱ⁾(·) = 〈π⁽ⁱ⁾, ·〉.

Proposition 7. Suppose that there exist an equilibrium satisfying (2)(3), then (π⁽¹⁾, …, π⁽ⁿ⁾) obtained from Proposition 6 admits a quasi state-price deflator.

Definition 9. We say the market is quasi-complete if for each i ∈ I,

$L^{(i),S}=\left\{(\theta (t)·\delta (t)):\theta \in L^{(i),S}\right\}.$

When the market is quasi-complete, the existence of the universal π will reduce the individual optimization to the following form:

$\begin{array}{rc}\underset{c\in L_{+}^{(i),S}}{\text{max}}{U}^{(i)}(c)\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}subject to }\Pi (c)\le \Pi (e^{(i)}).& \left(4\right)\end{array}$

Since U⁽ⁱ⁾ is strictly increasing, there is a Lagrange multiplier λ⁽ⁱ⁾ such that the optimization above is equivalent to

$\underset{{}_{c\in L_{+}^{(i),S}}}{\max }{\lambda }^{(i)}{U}^{(i)}(c)-\left(\Pi (c)-\Pi (e^{(i)})\right).$

Define the utility function U_λ: L₊ → ℝ by

$U_{\lambda }(x)=\underset{{}_{c^{(i)}\in L_{+}^{(i),S},i\in I}}{\max }{\displaystyle \sum _{i\in I}{\lambda }^{(i)}}{U}^{(i)}(c^{(i)})\text{subject to }{\displaystyle \sum _{i\in I}{c}^{(i)}}\le x.$

Proposition 8. Suppose that there exists an equilibrium satisfying (2)(3) for a quasi-complete market, then the equilibrium consumption solves

$\underset{{}_{c^{(i)}\in L_{+}^{(i),S},i\in I}}{\max }{\displaystyle \sum _{i\in I}{\lambda }^{(i)}}{U}^{(i)}(c^{(i)})subjectto{\displaystyle \sum _{i\in I}{c}^{(i)}}\le {\displaystyle \sum _{i\in I}{e}^{(i)}}.$

Corollary 3. Moreover, if for each i that U⁽ⁱ⁾ is of additive form

$U^{(i)}(c)={\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^T{u}_t^{(i)}}(c(t))\right],$

then U_λ is also of additive form

$U_{\lambda }(c)={\text{𝔼}}^P\left[{\displaystyle \sum _{t=0}^T{u}_{\lambda t}}(c(t))\right].$

where

$u_{\lambda t}(x)=\underset{{}_{c^{(i)}\in L_{+}^{(i),S},i\in I}}{\max }{\displaystyle \sum _{i\in I}{\lambda }^{(i)}}{u}^{(i)}(c^{(i)})subjectto{\displaystyle \sum _{i\in I}{c}^{(i)}}\le x.$

for any t ≤ τ,

$\begin{array}{l}S(t)=\frac{1}{u_t^{\prime }(c^{\ast }(t))}{\text{𝔼}}^P[S(\tau )u_{\tau }^{\prime }(c^{\ast }(\tau ))\\ +{\displaystyle \sum _{j=t+1}^{\tau }\delta }(j)u_j^{\prime }(c^{\ast }(j))|{{F}}^{(i)}\vee {{G}}_t].\end{array}$

4.3. State-price Beta Model

Denote by 𝔼_{i, t} the expectation conditioned on ${{F}}_t^{(i)}\vee {{G}}_t$, by Var_{i, t} the variance conditioned on ${{F}}_t^{(i)}\vee {{G}}_t$, and by Cov_{i, t} the covariance conditioned on ${{F}}_t^{(i)}\vee {{G}}_t$.

Now, let us define the capital returns generated by a trading strategy θ by

$r^{\theta }(t)=\frac{\theta (t-1)·(S(t)+\delta (t))}{\theta (t-1)·S(t-1)}$

Denote by r^{(i), 0}(t) the risk-free return for agent i. Thus, r^{(i), 0} is the return of a strategy θ₀, such that,

${\theta }_0\in L^{(i),S},{\text{ and corr}}_{i,t-1}^P(r^{(i),0},\pi (t))=0,$

where corr_{i, t} is the correlation conditioned on ${{F}}_t^{(i)}\vee {{G}}_t$.

Each agent also believes in her own market portfolio. That is, for each agent i, she constructs the optimal market portfolio from L^{(i), S} by maximizing the the correlation with π conditioned on their own information. That is, at time t, the market portfolio is given by

$\underset{\theta \in L^{(i),S}}{\max }{\text{ corr}}_{i,t-1}^P\left(r^{\theta }(t),\pi (t)\right).$

Let r^{(i), M}(t) denote the market return. Then the maximization implies

$\pi (t)=r^{(i),M}(t)+ϵ(t),$

where ${Cov}_{i,t-1}^{\mathbf{\text{P}}}\left(ϵ(t),r^{\theta }(t)\right)=0$ for all θ ∈ L^{(i), S}. Note that

${\text{Cov}}_{i,t-1}^P\left(r^{\theta }(t),\pi (t)\right)={\pi }^{(i)}(t-1)\left(1-\frac{{\text{𝔼}}_{i,t-1}^P\left[r^{\theta }(t)\right]}{{\text{𝔼}}_{i,t-1}^P\left[r^{(i),0}(t)\right]}\right).$

Then we can obtain the beta form of the CAPM:

${\text{𝔼}}_{i,t-1}^P\left[r^{\theta }(t)-r^{(i),0}(t)\right]={\beta }_{i,t-1}^{\theta }{\text{𝔼}}_{i,t-1}^P\left[r^{(i),M}(t)-r^{(i),0}(t)\right]$

where

${\beta }_{i,t-1}^{\theta }=\frac{{\text{Cov}}_{i,t-1}^P\left(r^{\theta }(t),r^{(i),M}(t)\right)}{{\text{Var}}_{i,t-1}^P\left(r^{(i),M}(t)\right)}.$

5. Examples and Discussion

5.1. Equilibrium Price

Example 2 (Quasi-EMM and Price in Case of No Private Information) Let time ${T}$ = 0, 1, 2, and there is one risky asset which pays dividend δ(t) satisfying

$\delta (t)=f(t)+{ϵ}_D(t),t=0,1,2,$

where f(t) is the fundamental value satisfying

$f(t)=f(t-1)+{ϵ}_f(t),t=1,2,\text{ and }f(0)=1,$

and ϵ_D(t) is noise with ϵ_D(0) = 0, and ϵ_f(t) is noise with ϵ(0) = 0. Assume that ϵ_D(1), ϵ_D(2), ϵ_f(1), ϵ_f(2) are jointly normally distributed.

Now suppose no agents has private information, i.e., the only information agents can access are generated by dividend and price.

Let (Quasi-)EMM be the probability measure under which ϵ_D(1), ϵ_D(2), ϵ_f(1), ϵ_f(2) are independent standard normally distributed N(0, 1). Then the price given by the following is valid,

$S(1)={\text{𝔼}}^Q\left[{\delta }_2|\delta (1),S(1)\right]=\frac{1}{3}\delta (1)+\frac{2}{3}$

$S(0)={\text{𝔼}}^Q[\delta (1)+\delta (2)]=2$

In this case, price reveals no additional information beyond dividends.

Example 3 (Quasi-EMM and Price in Case of Symmetric Private Information). Within the framework as in Example 2, we additionally introduce one signal process y(t) satisfying

$y(t)=f(t)+{ϵ}_y(t),t=1,2,\text{ and }y(0)=1,$

where ϵ_y(t) is noise. All agents can access signal y as their private information.

Case 1. Let Quasi-EMM be the probability measure under which ϵ_D(1), ϵ_D(2), ϵ_f(1), ϵ_f(2), ϵ_y(1) are independent standard normally distributed N(0, 1). Then the price given by the following is valid,

$S(1)={\text{𝔼}}^Q\left[{\delta }_2|\delta (1),S(1),y(1)\right]=\frac{1}{3}\delta (1)+\frac{1}{3}y(1)+\frac{1}{3}$

$S(0)={\text{𝔼}}^Q[\delta (1)+\delta (2)]=2$

Case 2. Let Quasi-EMM be the probability measure under which ϵ_f(1), ϵ_D(1), ϵ_y(1), ϵ_f(2), ϵ_D(2) are jointly normally distributed with mean 0 and covariance matrix

$\left[\begin{array}{ccccc}1& \frac{3}{4}& \frac{1}{2}& 0& 0\\ \frac{3}{4}& 1& \frac{1}{4}& 0& 0\\ \frac{1}{2}& \frac{1}{4}& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right].$

Then the price given by the following is valid,

$S(1)={\text{𝔼}}^Q\left[{\delta }_2|\delta (1),S(1),y(1)\right]=\frac{1}{2}\delta (1)+\frac{1}{2}$

$S(0)={\text{𝔼}}^Q[\delta (1)+\delta (2)]=2$

In this example, we can see when there exists private information, either case can happen: (i) the signal is incorporated into price as factor, and (ii) price is very inefficient and reveals no private information.

Example 4 (Quasi-EMM and Price in Case of Asymmetric Private Information). As in Example 3, we introduce not one but two signal processes y₁(t) and y₂(t) satisfying

$y_1(t)=f(t)+{ϵ}_1(t),t=1,2,\text{ and }{y}_1(0)=1,$

$y_2(t)=f(t)+{ϵ}_2(t),t=1,2,\text{ and }{y}_2(0)=1,$

where ϵ_y(t) is noise. There are two agents in economy, agent 1 can access signal y₁, and agent 2 can access signal y₂.

Let Quasi-EMM be the probability measure under which ϵ_D(1), ϵ_D(2), ϵ_f(1), ϵ_f(2), ϵ₁(1), ϵ₂(1) are independent standard normally distributed N(0, 1). Then the price given by the following is valid,

$\begin{array}{l}S(1)={\text{𝔼}}^Q\left[{\delta }_2|\delta (1),S(1),y_1(1)\right]\\ ={\text{𝔼}}^Q\left[{\delta }_2|\delta (1),S(1),y_2(1)\right]\\ =\frac{1}{4}\delta (1)+\frac{1}{4}{y}_1(1)+\frac{1}{4}{y}_2(1)+\frac{1}{4}\end{array}$

$S(0)={\text{𝔼}}^Q[\delta (1)+\delta (2)]=2$

In this example, price reflects aggregated private information.

5.2. Mispricing

Suppose we have a pricing kernel π and that its optimal projections on individual information filtration are π⁽ⁱ⁾'s. Consider a derivative written by agent w and it is traded at time 0. This derivative pays dividend δ^θ, where θ is a trading strategy in L^{(w), S}. That means the writer, agent w, can replicate this derivative and that the value of this derivative is 0. Agent w want to sell this derivative to other agents. The question is what would be the fair price of this derivative for some agent i.

If θ ∈ L^{(i), S}, agent i can replicate this derivative easily, and also the consumption process c = e⁽ⁱ⁾ + δ^θ cannot increase the utility of this agent i. Thus, agent i will not pay any positive price for this derivative.

If θ ∉ L^{(i), S}, agent i cannot reach this dividend with a trading strategy based on her own information. Thus, agent i will buy this derivative if the consumption process c = e⁽ⁱ⁾ + δ^θ can increase her maximum utility, i.e., U⁽ⁱ⁾(c) > U⁽ⁱ⁾(c⁽ⁱ⁾*). The maximum price at which agent i will to pay will be Π⁽ⁱ⁾(c)−Π⁽ⁱ⁾(c⁽ⁱ⁾*). In this case, agent w is just taking advantage of better information than agent i. The true value of this derivative is in fact 0, since some agent can get this dividend without any cost. This mis-pricing can be regarded as a bubble, since agents still want to buy this derivative even though they know the price of this derivative is higher than its true value.

6. Conclusion

In this paper, we formulate a general equilibrium asset pricing model in discrete time. It is shown that with the existence of differential information, agents can still achieve agreement on a universal trading price. This equilibrium price reflects the private information through the individual choice of consumption. As an inter-related system, the equilibrium price is also viewed as a public information resource by each agent. The information asymmetry also influences individuals portfolio choices and the consumption beta. This is rooted in the fact that agents price the same consumption choices differently. Mispricing is also discussed as a consequence of these facts.

Author Contributions

Both authors contributed significantly to all aspects of this work.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Many thanks to Professor Svetlozar Rachev, Professor Noah Smith, Professor Haipeng Xing, and Professor Aaron Kim for stimulating discussions. Without their help, this paper could not be finished.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/article/10.3389/fams.2015.00008

References

1. Walras L. Études D' économie Politique Appliquée : (Théorie de la Production de la Richesse Sociale). Lausanne: F. Rouge (1989).

2. Arrow KJ, Debreu G. Existence of an equilibrium for a competitive economy. Econometrica (1954) 22:265–90. doi: 10.2307/1907353

CrossRef Full Text | Google Scholar

3. Debreu G. Market equilibrium. Proc Natl Acad Sci USA. (1956) 42:876–8. doi: 10.1073/pnas.42.11.876

PubMed Abstract | CrossRef Full Text | Google Scholar

4. McKenzie L. On equilibrium in graham's model of world trade and other competitive systems. Econometrica (1954) 22:147–61. doi: 10.2307/1907539

CrossRef Full Text | Google Scholar

5. Radner R. Competitive equilibrium under uncertainty. Econometrica (1968) 36:31–58. doi: 10.2307/1909602

CrossRef Full Text | Google Scholar

6. Radner R. Existence of equilibrium of plans, prices, and price expectations in a sequence of markets. Econometrica (1972) 40:289–303. doi: 10.2307/1909407

CrossRef Full Text | Google Scholar

7. Radner R. Rational expectations equilibrium: generic Existence and the information revealed by prices. Econometrica (1979) 47:655–78. doi: 10.2307/1910413

CrossRef Full Text | Google Scholar

8. Jordan JS, Radner R. Rational expectations in microeconomic models: an overview. J Econ Theory (1982) 26:201–23. doi: 10.1016/0022-0531(82)90001-1

CrossRef Full Text | Google Scholar

9. Breeden DT. An intertemporal asset pricing model with stochastic consumption and investment opportunities. J Financ Econ. (1979) 7:265–96. doi: 10.1016/0304-405X(79)90016-3

CrossRef Full Text | Google Scholar

10. Cox JC, Ingersoll JE, Ross SA. An intertemporal general equilibrium model of asset prices. Econometrica (1985) 53:363–84. doi: 10.2307/1911241

CrossRef Full Text | Google Scholar

11. Duffie D, Zame W. The consumption-based capital asset pricing model. Econometrica (1989) 57:1279–97. doi: 10.2307/1913708

CrossRef Full Text | Google Scholar

12. DeMarzo P, Skiadas C. Aggregation, determinacy, and informational efficiency for a class of economies with asymmetric information. J Econ Theory (1998) 80:123–52. doi: 10.1006/jeth.1998.2398

CrossRef Full Text | Google Scholar

13. Yannelis NC. The core of an economy with differential information. Econ Theory (1991) 1:183–97.

Google Scholar

14. Glycopantis D, Yannelis N. Differential Information Economies. Princeton, NJ: Springer Science & Business Media (2006).

Google Scholar

15. Lengwiler Y. Microfoundations of Financial Economics: An Introduction to General Equilibrium Asset Pricing. Princeton, NJ: Princeton University Press (2009).

Google Scholar

16. Heer B, Maussner A. Dynamic General Equilibrium Modeling: Computational Methods and Applications. Dordrecht; New York, NY: Springer Science & Business Media (2009).

Google Scholar

17. Black FS, Glaeser EL. Exploring General Equilibrium. Cambridge, MA: The MITPress (2010).

Google Scholar

18. Starr RM. General Equilibrium Theory: An Introduction. New York, NY: Cambridge University Press (2011).

Google Scholar

19. Ludvigson SC. Advances in consumption-based asset pricing: empirical tests. In: Working Paper 16810, National Bureau of Economic Research (2011). Available online at: http://www.nber.org/papers/w16810

20. Biais B, Bossaerts P, Spatt CS. Equilibrium Asset Pricing Under Heterogeneous Information. Rochester, NY: Social Science Research Network (2004).

Google Scholar

21. Biais B, Bossaerts P, Spatt C. Equilibrium asset pricing and portfolio choice under asymmetric information. Rev Financ Stud. (2010) 23:1503–43. doi: 10.1093/rfs/hhp113

CrossRef Full Text | Google Scholar

22. Fama EF, French KR. Disagreement, tastes, and asset prices. J Financ Econ. (2007) 83:667–89.

Google Scholar

23. Ostrovsky M. Information aggregation in dynamic markets with strategic traders. Econometrica (2012) 80:2595–647. doi: 10.3982/ECTA8479

CrossRef Full Text | Google Scholar

24. Iyer K, Johari R, Moallemi CC. Information aggregation and allocative efficiency in smooth markets. Manag Sci. (2014) 60:2509–24. doi: 10.1287/mnsc.2014.1929

CrossRef Full Text | Google Scholar

25. Bernardo AE, Judd KL. Asset market equilibrium with general tastes, returns, and informational asymmetries. J Financ Mark. (2000) 3:17–43. doi: 10.1016/S1386-4181(99)00011-7

CrossRef Full Text | Google Scholar

26. Breon-Drish B. Asymmetric Information in Financial Markets: Anything Goes. (2010). Working Paper, Stanford University.

27. Cao HH, Ou-Yang H. Differences of opinion of public information and speculative trading in stocks and options. Rev Financ Stud. (2009) 22:299–335. doi: 10.1093/rfs/hhn020

CrossRef Full Text | Google Scholar

28. Gao F, Song F, Wang J. Rational expectations equilibrium with uncertain proportion of informed traders. J Financ Mark. (2013) 16:387–413. doi: 10.1016/j.finmar.2012.04.001

CrossRef Full Text | Google Scholar

29. Banerjee S, Green BS. Signal or noise? Uncertainty and learning about whether other traders are informed. J Financ Econ. (2014) 117:398–423. doi: 10.2139/ssrn.2139771

CrossRef Full Text | Google Scholar

30. Campbell JY, Cochrane JH. By force of habit: a consumption-based explanation of aggregate stock market behavior. In: Working Paper 4995, National Bureau of Economic Research. (1995).

Google Scholar

31. Dionne G, Li J. A Theoretical Extension of the Consumption-Based CAPM Model. Rochester, NY: Social Science Research Network (2011).

Google Scholar

32. Breeden DT, Litzenberger RH, Jia T. Consumption-based asset pricing: research and applications. Annu Rev Financ Econ. (2015) 7.

Google Scholar

33. Barberis N, Greenwood R, Jin L, Shleifer A. X-CAPM: an extrapolative capital asset pricing model. J Financ Econ. (2015) 115:1–24. doi: 10.1016/j.jfineco.2014.08.007

CrossRef Full Text | Google Scholar

34. Duffie D. Dynamic Asset Pricing Theory. Princeton, NJ: Princeton University Press (2010).

Google Scholar

35. Duffie D. Dynamic Asset Pricing Theory, 3rd Edn. Princeton, NJ: Princeton University Press (2001).