Detecting Violations of Unidimensionality by Order-Restricted Inference Methods

Introduction

Assessing the data-model fit forms the most essential part of psychometric modeling before any theoretical or practical conclusions can be derived from a model under consideration. The most crucial feature of many psychometric models is the assumption of undimensionality. That is, that a single latent trait accounts for the statistical dependence among the items of a psychological test in the entire population; and that the items are statistically independent in each subpopulation of examinees that are homogenous with respect to the latent trait (local independence). An assessment aimed at identifying and measuring inter-individual differences on some attribute necessarily requires unidimensionality. Consequently, unidimensionality must hold before either a total score is calculated under true score theory, or person parameters are estimated using item response theory (IRT) and Rasch [1] models. Violation of unidimensionality may bias item and person estimates [2–4] and will result in wrong conclusions about the nature of latent traits. Applying reliable methods to assess unidimensionality is therefore of critical importance before any theoretical and/or practical conclusions can be drawn from psychometric test data.

Because measurements can only be made of continuous quantities [5, 6], the claim of unidimensionality is essentially equivalent to the hypothesis that individual differences in test performance are caused by the behavior of a single, relevant and quantitative psychological attribute. It is frequently stated that “Unidimensionality refers to the existence of a single trait or construct underlying a set of measures” ([7], p. 186) or, likewise, “A unidimensional test may be defined simply as a test in which all items are measuring the same thing” ([8], p. 268). We do not regard these merely conceptual definitions as sufficiently unambiguous because they reach too far into a premature causal interpretation of unidimensionality leaving too many questions open what is meant, for example, by an “underlying” trait or the “same thing” (see also [9]). Therefore, in order to avoid conceptual confusions which might arise from those definitions, we think it is important to stress the point that unidimensionality does not necessarily imply that a single psychological or physiological attribute or process determines the responses on a set of items. Even a large number of attributes/processes can affect item responses and unidimensionality will hold (see [10, 11] for a classical illustration and explanation). As long as the different attributes/processes determining those responses affect the item responses in the same manner, that is, are held constant among the items, unidimensionality will hold. So, in order to avoid any conceptual ambiguities related to the psychological interpretation of unidimensionality, our definition of unidimensionality will therefore strictly refer to the statistical definition of local independence of a set of random observed variables conditional on a hypothetical variable, that is, the person parameter from the parameter space of a psychometric model. That is, let Y₁, Y₂,…,Y_K be random observed variables and θ be a single hypothetical variable, then P[Y₁, Y₂,…,Y_K] constitutes the joint probability of the observed variables and P[Y₁| θ]P[Y₂| θ]…P[Y_K| θ] denotes the conditional probabilities. If the hypothetical variable θ alone accounts for the dependencies among the observed variables, then the joint probability equals the product of the conditional probabilities:

$\begin{array}{ll}P\left[Y_1,Y_2,\dots ,Y_K|\theta \right]=P\left[Y_1|\theta \right]·P\left[Y_2|\theta \right]{·}_{\dots }·P\left[Y_K|\theta \right].& (1)\end{array}$

This definition relies on strict tests of unidimensionality which are in fact difficult to achieve in practice. Consequently, weaker definitions of unidimensionality exist, such as Stout's [12] definition of essential unidimensionality which states that on average, the conditional covariances over all item pairs must be small in magnitude and is thus based on assessing only the dominant dimensions. At first sight it seems therefore to be questionable why strict unidimensionality, as proposed in this paper, should be of any practical value. While it is presumably true that strict unidimensionality rarely holds in psychology it is important to note that the main aim of this paper is not to contribute once more to the debate of how multidimensional a test can be without disturbing conclusions about the dominant latent trait assessed by a test. More importantly, the main aim of this paper is to investigate the more fundamental assumption of quantitative measurement within psychological testing which presupposes the requirement of unidimensionality. Thus, unidimensionality is a necessary but not sufficient condition for quantitative measurement to hold. Note that the fit of a certain item response model does not necessarily imply that the psychological attribute is quantitative and can therefore not serve as a test of quantitative measurement. As Suppes and Zanotti [13] have shown, there always (i.e., for every joint distribution) exists a scalar-valued latent trait variable such that conditional independence holds. This implies that any IRT model with a continuous latent trait is equivalent to a model with a discrete latent trait. Since psychologists conceptualize many latent variables as continuous, testing this assumption within a framework of strict unidimensionality is required.

Consequently, and as noted above, the problem of unidimensionality is twofold; and it is therefore essential not only to test local independence but also the (usually implicitly assumed) hypothesis that the attribute under consideration is quantitative. By quantitative, it is meant that the relations amongst the degrees (levels) of the attribute are consistent with the ordinal, additive and continuity conditions proven by Hölder [14] as being necessary for quantity (c.f., [15] for an English translation). The base quantities of physics, notably mass, length and time, are unidimensional quantities. Derived quantities, notably three dimensional space, consist of these base unidimensional quantities (c.f., [16]).

Within psychometrics, it has been argued that the Rasch model [1] is a probabilistic form of conjoint measurement [17] and so hence constitutes a means of “fundamental measurement” for the behavioral sciences [18]. This is because arrays of Rasch model probabilities exhibit ordinal relations consistent with the cancelation axioms of conjoint measurement [19]. Given the Rasch model is also considered a strict test of the assumption of unidimensionality (e.g., [20]), application of the model is considered a stringent test of the hypothesis of the existence of a single, quantitative and unidimensional psychological variable.

Application of the Rasch model, however, is unlikely to lead to the quantification of human cognitive abilities. Firstly, there is no logical substantive, theoretical or scientific reason that the empirical sample estimates of Rasch model probabilities, the item response proportions, must also exhibit ordinal relations consist with the cancelation axioms of conjoint measurement. Studies testing the conjoint measurement cancelation axioms directly via order constrained probabilistic frameworks (e.g., [21–23]) have found that such proportions violate these axioms, even though the Rasch model may fit the data.

Secondly, a rather more severe conceptual problem is the “Rasch Paradox” identified by Michell [24]. Suppose X is a set of items ostensibly designed to assess a particular intellectual ability and A is a set of persons. Guttman's [25] model is such that:

$\begin{array}{ll}\left(a,x\right)\in B\iff f\left(a\right)>g\left(x\right)& (2)\end{array}$

where 〈ℜ, >〉 are the real numbers and f: A ↦ ℜ and g: X ↦ ℜ; and B is a biorder.

The uniqueness of Equation (2) is such that for (f, g) and (f′, g′) there exists a monotonically increasing function K such that:

$\begin{array}{ll}f\prime =K\circ f\text{ and }g\prime =K\circ g& (3)\end{array}$

where “∘” designates function composition [26]. Therefore, ability estimates in Guttman's model are unique up to monotonic transformations only [27]. Hence Guttman's model is ordinal and not quantitative.

Michell ([24], p. 122) argued the Rasch model is a “woolly” version of Guttman's theory because it posits that:

$\begin{array}{ll}Pr \left(a,x\right)\iff f\left(a\right)\ge g\left(x\right)+\epsilon =\Omega \left({\theta }_a-b_x\right)& (4)\end{array}$

where ε is an error term, Ω is the logistic cumulative distribution function, θ_a is the ability of a and b_x is the difficulty of x.

Because Guttman's model is ordinal (Equation 2), Rasch's quantitative and the only difference between them being error, it follows that the Rasch model's status as a quantitative theory is derived exclusively through the theoretical error term of Equation (4). This creates a paradoxical situation, because in physics and metrology, error is a measurement confound. Physicists and metrologists work to create observational methodologies that reduce measurement error precisely because such methods lead to better measurement [28]. However, removal of the error term from Equation (4) results in Equation (1) and the result is an ordinal, not quantitative, scale. Hence the elimination of error from the model renders measurement impossible. But in science, eliminating would lead to perfect scientific measurement, not the impossibility of measurement; and so hence a paradox is obtained.

Sijtsma [29] disputed the Rasch Paradox, claiming it did not exist. However, he mistook the arguments of Michell [24] as pertaining to the presence or absence of error in test data, rather than the Paradox residing at the theoretical level of the model itself [30].

The Rasch Paradox implies that it may never be possible for the Rasch or other IRT model to scientifically quantify human cognitive abilities. Hence perhaps the most rigorous way to quantify human abilities (and also assess unidimensionality) is to directly test the cancelation axioms of conjoint measurement upon test data.

The Theory of Conjoint Measurement

Let A = {a, b, c,…} and X = {x, y, z,…} be non-empty (and possibly infinite) sets of magnitudes of the same quantity. Let $\underset{˜}{\succ }$ be a simple order (i.e., one that is transitive, antisymmetric and strongly connected) holding upon the set A × X = {(a, x), (b, x),…, (c, z)}, which is the set of all ordered pairs of the elements of A and X. The relation $\underset{˜}{\succ }$ upon A × X satisfies single cancelation if and only if (cf. [31]):

• For all a, b in A and x in X, (a, x) $\underset{˜}{\succ }$ (b, x) implies for every w in X that (a, w) $\underset{˜}{\succ }$ (b, w);

• For all x, y in X and a in A, (a, x) $\underset{˜}{\succ }$ (a, y) implies for every d in A that (d, x) $\underset{˜}{\succ }$ (d, y).

Satisfaction of the single cancelation axiom means that the ordinal and equivalence relations holding upon the levels of A are independent of the levels of X and vice versa.

The relation $\underset{˜}{\succ }$ upon A×X satisfies double cancelation if and only if for every a, b, c in A and x, y, z in X, (a, y) $\underset{˜}{\succ }$ (b, x) and (b, z) $\underset{˜}{\succ }$ (c, y) therefore (a, z) $\underset{˜}{\succ }$ (c, x). Satisfaction of double cancelation means that A and X are additive and are therefore quantitative (c.f., [32]). Double cancelation can be difficult to empirically test as some instances of it are redundant (i.e., they trivially hold if single cancelation is true; [33]). A weaker form of double cancelation, in which the relation $\underset{˜}{\succ }$ is replaced by the equivalence relation ~, is known as the Thomsen condition [32]. Luce and Steingrimsson [34] argued that conjoint commutativity and the Thomsen condition are preferable to double cancelation as this redundancy is avoided, although it is worth mentioning that in decision-making contexts, double cancelation is often easier to test and it can be evaluated via preferences, as opposed to indifferences (see [35, 36]).

The cancelation axioms place rather stringent ordinal restrictions upon a dataset, which if satisfied, can produce compelling evidence of unidimensionality. This has been found in applications of conjoint measurement in the assessment of attitudes (e.g., [37–39]), where the dominant path condition of Coombs' [40] theory of unidimensional unfolding has satisfied single and double cancelation. However, dominant paths supporting single cancelation yet rejecting double cancelation were discovered by Kyngdon and Richards [41]. They also found that Andrich's [42] unidimensional IRT unfolding model fitted this data well. Yet application of conjoint measurement in psychometrics has been limited [43, 44]. Its most effective formal use thus far has been in the study of decision making under conditions of risk and uncertainty (c.f., [45]). Most prominently, conjoint measurement served as the formal proof to Kahneman and Tversky's [46] prospect theory, for which Kahneman received the 2002 Nobel Economics Memorial Prize [47].

As conjoint measurement is non-stochastic, attempts at applying it to invariably noisy psychometric test data are problematic [48, 49]. Moreover, the ordinal constraints posed by the cancelation axioms render the application of common statistical procedures invalid [50]. Scheiblechner [51] proposed a class of order-restricted non-parametric probabilistic IRT models. Karabatsos [21] extended this approach by integrating the theory of conjoint measurement [17] with order-restricted inference and Markov Chain Monte Carlo methods (MCMC). The integration of these concepts into a MCMC framework enables one to test the order-restricted approach statistically, that is, to assess the degree of stochastic approximation to the conjoint measurement axioms. The present study is aimed to show that this approach can be used to assess data-model fit in regard to the common problem of violations of unidimensionality in psychological test data.

Using Order-Restricted Response Models to Detect Violations of Unidimensionality

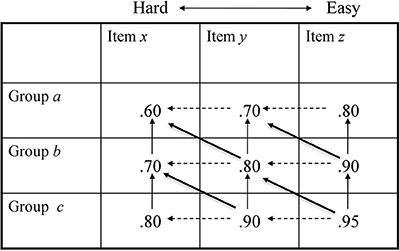
At first glance, it seems odd to use order-restricted response models to detect violations of unidimensionality. However, as previous studies have shown, unmodeled multidimensionality can heterogeneously affect item slope parameters, resulting in crossing Item Response Functions (IRFs; [52–54]). Consequently, for the case of the Rasch model, Glas and Verhelst [20] have shown that the likelihood ratio test by Andersen [55], originally aimed to detect violations of non-intersecting IRFs, has also reasonable power against violations of unidimensionality. However, a major drawback of tests of parametric item response models exists because they rest on the assumption that the estimated model parameters are true population parameters, hence unspoiled by random or systematic measurement error. As Karabatsos [21] has shown if data contain such noise, the estimated IRFs contain noise and model violations are—to an unknown extend—absorbed. The approach suggested by Karabatsos, on the other hand, is not based on estimated parameters but on the degree to which the observed data matrix conforms to the restrictions imposed by an order-restricted non-parametric probabilistic IRT model. That is, item and person response functions of the observed data are constrained by non-numerical order restrictions of the conjoint measurement cancelation axioms. However, the number of tests of the double cancelation axiom in m × n conjoint matrices per dataset equals $\left(\begin{array}{l}m\hfill \\ 3\hfill \end{array}\right)\left(\begin{array}{l}m\hfill \\ 3\hfill \end{array}\right)$ [56]. In the present study (and explained below), we constructed 3 × 30 conjoint data matrices from replicated data sets. This poses a major computational problem because, even with a single conjoint matrix of order 3 × 30, there are 4060 tests of the double cancelation axiom. However, with multidimensional data and as described above, we expected a violation already of the single cancelation axiom, that is, violations of the requirement that the IRFs for any particular response category are non-decreasing and non-intersecting. Thus, if single cancelation is violated, there is no logical point in testing double cancelation. At this point it is essential to recognize that the isotonic ordinal probabilistic model (ISOP; [51]) imposes order relations implying single cancelation. In general, the ISOP model defines non-intersecting and non-decreasing non-parametric IRFs, therefore implying double monotonicity, that is, the probability of a positive response increases monotonically with the person parameter and the probability of a positive response is also monotonically decreasing with the item difficulty parameter, where the order of the item difficulty is invariant over the response categories. It is important to note that the ISOP model differs from the Rasch model (which was used to simulate the data sets in this study) because the IRFs can take any positive monotonic functions, unlike the Rasch model, assuming the logistic function. Hence, the ISOP model also covers non-parametric models with non-intersecting IRFs such as the Mokken [57] and the Guttman model [58]. Note that since the IRFs of the ISOP model need not to be parallel (as in the case of parametric functions) but only positively monotonic and non-intersecting, the joint scale of item and person parameters is on an ordinal metric. The general structure of the order restrictions characterizing the ISOP model resulting from the restriction on the row- (respondents) and column-wise (items) ordered data matrix are illustrated by in Figure 1.

FIGURE 1

Figure 1. Graphical representation of the single cancelation axiom (row and column independence).

The ISOP model, within the context of Karabatsos' [21] framework, can be formally expressed as follows. The matrix of observed proportions of correct item responses corresponding to Figure 1 can be defined as:

$\begin{array}{rc}\text{p}=\left(p_{ax}|a=1,\dots ,3;x=1,\dots ,3\right)\in {\left[0,1\right]}^9.& (2)\end{array}$

The matrix of expected proportions of correct responses is defined as:

$\begin{array}{rc}\Theta =\left({\theta }_{ax}|a=1,\dots ,3;x=1,\dots ,3\right)\in {\left[0,1\right]}^9.& (3)\end{array}$

The posterior distribution for Θ, conditional upon the data (p), is given by Bayes' Theorem:

$\begin{array}{ll}p\left(\Theta |\text{p}\right)=\frac{L\left(\text{p}|\Theta \right)\pi \left(\Theta \right)}{{\int }_{\Omega }L\left(\text{p}|\Theta \right)\pi \left(\Theta \right)d\Theta },& (4)\end{array}$

where π(Θ) is the order constraining prior distribution of the parameters in Θ. This distribution restricts Θ to lie within the proper subset Ω of [0,1]⁹. Karabatsos and Sheu [22] state that the prior distribution has the form:

$\pi \left(\Theta \right)=\{\begin{array}{ll}\hfill & >0\iff \Theta \in \Omega \hfill \\ \hfill & 0\iff \Theta \notin \Omega .\hfill \end{array}$

The likelihood, L(p|Θ), is assumed to be a product of independent binomial distributions such that:

$\begin{array}{ll}L\left(\text{p}|\Theta \right)={\prod }_{a=1}^3{\prod }_{x=1}^3\left(\begin{array}{c}{N}_{ax}\\ n_{ax}\\ \end{array}\right){\theta }_{ax}^{n_{ax}}{\left(1-{\theta }_{ax}\right)}^{N_{ax}-n_{ax}}.& (5)\end{array}$

Equation (5) assumes independence of the data conditional on the parameters in Θ, with the product operation directly corresponding to the local independence condition stated in Equation (1) [22]. The denominator of the posterior distribution, the marginal density, is not of closed form and therefore numerical methods must be used to obtain a solution. To this end, Karabatsos [21] proposed an MCMC algorithm, a hybrid Metropolis Hastings–Gibbs sampler. The prior distribution, π(Θ), constrains the order upon the elements of Θ to accord with the cancelation axioms of conjoint measurement. Two different order constraining prior distributions are proposed for π(Θ). For the ISOP model, the prior π(θ_I) subjects each parameter θ_ax to the constraint:

$\begin{array}{ll}0\le max\left\{{\theta }_{\left(a-1\right)x},{\theta }_{a\left(x-1\right)}\right\}\le {\theta }_{ax}\le min\left\{{\theta }_{\left(a+1\right)x},{\theta }_{a\left(x+1\right)}\right\}\le 1& (6)\end{array}$

for all a, x. Additionally, θ_0x ≡ θ_a0 ≡ 0 and θ_(A+1)x ≡ θ_a(X+1) ≡ 1.

The monotone homogeneity (MH) model is a weaker form of the ISOP model in that IRFs are monotonically increasing but intersect. For the MH model, the prior π(Θ_MH) subjects each parameter θ_ax to the constraint:

$\begin{array}{ll}0\le {\theta }_{\left(a-1\right)x}\le {\theta }_{ax}\le {\theta }_{\left(a+1\right)x}\le 1& (7)\end{array}$

for all a, x. Additionally, θ_0x ≡ 0 and θ_(A+1)x ≡ 1.

To initiate the algorithm, a set of starting values ${\Theta }^{\left(0\right)}=\left({\theta }_{ax}^{\left(0\right)}|a=1,\dots ,3;x=1,\dots ,3\right)\in {\left[0,1\right]}^9$ is randomly drawn from a uniform distribution under constraint that the elements follow the ordinal restrictions imposed by the prior. For any element of Θ at iteration t, two steps determine ${\theta }_{ax}^{\left(t\right)}$ :

Step 1. A random number r_ax~Unif[0, 1] is drawn and a candidate ${\theta }_{ax}^{\left(*\right)}$ is sampled from the order restrictions defined by the prior uniform distribution on [min(θ_ax), max(θ_ax)].

Step 2. Decide:

$\begin{array}{ll}{\theta }_{ax}^{\left(t\right)}=\{\begin{array}{l}{\theta }_{ax}^{\ast }\text{\hspace{0.17em}iff\hspace{0.17em}}{r}_{ax}\le \frac{L\left(p|{\theta }_{ax}^{\ast },{\theta }_{<a\left(1\le x\le X\right)}^{\left(t\right)},{\theta }_{a\left(<x\right)}^{\left(t\right)},{\theta }_{a\left(>x\right)}^{\left(t-1\right)},{\theta }_{>a\left(1\le x\le X\right)}^{\left(t-1\right)}\right)}{L\left(p|{\theta }_{ax}^{\left(t-1\right)},{\theta }_{<a\left(1\le x\le X\right)}^{\left(t\right)},{\theta }_{a\left(<x\right)}^{\left(t\right)},{\theta }_{a\left(>x\right)}^{\left(t-1\right)},{\theta }_{>a\left(1\le x\le X\right)}^{\left(t-1\right)}\right)}\hfill \\ {\theta }_{ax}^{\left(t-1\right)}\text{\hspace{0.17em}otherwise}.\hfill \end{array}\hfill & (8)\end{array}$

In Step 1, $min\left({\theta }_{ax}\right)=max\left\{{\theta }_{\left(a-1\right)x}^t,{\theta }_{a\left(x-1\right)}^t\right\}$ and $max\left({\theta }_{ax}\right)=min\left\{{\theta }_{\left(a+1\right)x}^{t-1},{\theta }_{a\left(x+1\right)}^{t-1}\right\}$ when the ISOP model is tested. For the MH model, $min\left({\theta }_{ax}\right)={\theta }_{\left(a-1\right)x}^t$ and $max\left({\theta }_{ax}\right)={\theta }_{\left(a+1\right)x}^{\left(t-1\right)}$. Support of the ISOP model (Figure 1) logically implies that Item z > Item y > Item x, where > is the relation of “is easier than”; and that Group c > Group b > Group a, where > is the relation of “has more ability than.” As “item easiness” is simply the amount of ability needed to correctly respond to an item, both A and X are instances of the same attribute (viz., a cognitive ability of some kind). From the ISOP model, it can only be concluded that A and X are ordinal attributes. Via the binary relation of transitivity (i.e., if a > b and b > c, then a > c), single cancelation determines only half the number of the relations between the diagonally adjacent cells of a conjoint matrix. Michell [6] calls such relations left leaning diagonals. Figure 1 shows that because single cancelation has determined that (b, y) ≥ (b, x) and (b, x) ≥ (a, x), via transitivity it follows that (b, y) ≥ (a, x). But the relation between (a, y) and (b, x) remains logically undetermined. These particular relations, the right leaning diagonals, are determined by double cancelation.

The ISOP model and double cancelation constitutes what Scheiblechner [51] calls a complete additive conjoint ISOP model or CADISOP model. In this model, the prior π(Θ_D), for each 3 × 3 submatrix, constrains the elements of Θ such that:

$\begin{array}{r}0\le max\left\{{\theta }_{\left(a-1\right)x},{\theta }_{a\left(x-1\right)},{\theta }_{\left(a+1\right)\left(x-1\right)}\right\}\le {\theta }_{ax}\\ \le min\left\{{\theta }_{\left(a+1\right)x},{\theta }_{a\left(x+1\right)},{\theta }_{\left(a-1\right)(x+1)}\right\}\le 1\hfill & (9)\end{array}$

for all a, x. Additionally, θ_0x ≡ θ_a0 ≡ θ_(A+1)x ≡ θ_a(X+1) ≡ 0 and θ_0x ≡ θ_a0 ≡ θ_(A+1)x ≡ θ_a(X+1) ≡ 1. In Step 1 of Karabatsos' [21] algorithm, $min\left({\theta }_{ax}\right)=max\left\{{\theta }_{\left(a-1\right)x}^t,{\theta }_{a\left(x-1\right)}^t,{\theta }_{\left(a+1\right)\left(x-1\right)}^{t-1}\right\}$ and $max\left({\theta }_{ax}\right)=min\left\{{\theta }_{\left(a+1\right)x}^{t-1},{\theta }_{a\left(x+1\right)}^{t-1},{\theta }_{\left(a-1\right)\left(x+1\right)}^t\right\}$.

In the weaker MH model, single cancelation holds only upon the rows of Figure 1 and so hence it can only be concluded that Group c > Group b > Group a.

Methods

Data Simulations

ConQuest [59] was used to simulate 900 data matrices according to a fully-crossed 2 × 3 × 3 design. In order to investigate the power of the ISOP approach to detect violations of unidimensionality, that is, to calculate Type II error rates, two-dimensional data according to a between-item multidimensionality Rasch model [60] were simulated. A total of 30 items were chosen to represent an “average” length. Person and item parameters for each dimension were both drawn from a standard normal distribution. The design included two levels of sample sizes (250 and 500) and three degrees of correlations between both dimensions (r₁₂ = 0.30, 0.50, and 0.80). Finally, the proportion of items reflecting each dimension was varied across three different ratios (25:5, 20:10, and 15:15). For each of the resulting 18 conditions, 100 data replications were generated. This simulation design was chosen in order to reflect a representative range of possible violations of unidimensionality a test constructor can encounter in practical test construction. Most psychological scales are constructed to measure a single variable but are in fact composed of item subsets measuring different aspects of the variable. Note that the size of these subsets and the correlation between both dimensions being meausured by those subsets can vary from test to test and both factors should therefore be varied in a simulation study. Thus, the condition with an item ratio of 25:5 and a low correlation between both dimensions of 0.30 stands for the situation that the data matrix is formed from a major dimension of interest but that there is also a minor dimension that accounts for some of the shared covariance between variables. The opposite case, that is, an equal number of items in each subset with a high correlation between both dimensions was defined by the condition of an equal item ratio of 15:15 on both dimensions with a correlation of 0.80. (See, for example, [61, 62], for practical examples of typical violations of unidimensionality in psychology).

Besides investigating the power of the ISOP approach with respect to violations of unidimensionality, the often implicitly made assumption of quantitative measurement also needs to be tested. As already noted above, it has been argued that fit of the Rasch model [1] is not only a stringent test of the hypothesis of unidimensionality but is also tantamount for the existence of a quantitative variable [19]. This assertion can be directly tested by analyzing Rasch-fitting data should under the ISOP model. We therefore analyzed simulated unidimensional and Rasch-fitting data under the ISPO model. To do so, we also generated Rasch-fitting data of 30 dichotomous items with sample sizes N = 250 and N = 500 with person and item parameters being drawn from a standard normal distribution and 100 replicated data sets under each sample size condition.

The order constrained Bayesian MCMC inference approach was conducted by using a modified version of the original S-Plus program by Karabatsos [21], adapted by the second author for R [63] and can be obtained from the first author. This R program differed from the original version with respect to the calculation of the posterior distribution quantiles needed for the MCMC approach, by using the method recommended by Hyndman and Fan [64] which gives median-unbiased estimates of the quantiles independent of the distribution. The MCMC approach assesses the degree of stochastic approximation to the measurement axioms of a model under consideration and offers three methods focusing on different aspects to evaluate model fit.

Firstly, the MCMC algorithm generates samples from p(θ^(I) | p^(I)), p(θ^(MH) | p^(MH)) and p(θ^(D) | p^(D)). It is therefore possible to It is therefore possible to conduct the following three tests of fit – p = p^(I), p^(MH) and p = p^(D)— by comparing p to the posterior-predictive distribution [22]. To estimate the posterior-predictive distribution from a given data matrix, the Gibbs sampling algorithm needs to be repeated for a sufficiently large number of T times [65] to find a good starting point for the MCMC algorithm. Usually (cf., 63), iterations at the beginning of an MCMC run (“burn-in” samples) should be discarded because they are affected by the arbitrary starting values required to initiate the Gibbs algorithm. Note that in the present study, we used 500 “burn-in” samples {t = 1,…,500} and 5000 MCMC iterations {t = 501,…,5000} for sufficient precision in the posterior estimates. As Geyer [66] has demonstrated, using at least 1% of T usually results in sufficient precision. For a future value p*, this posterior-predictive distribution is:

$\begin{array}{ll}p\left({\text{p}}^{*}|\text{p}\right)=\int p\left({\text{p}}^{*}|\Theta \right)p\left(\Theta |\text{p}\right)d\Theta & (10)\end{array}$

which can be estimated as a simple byproduct of the MCMC algorithm used to calculate p(θ | p). A posterior-predictive or “Bayesian” p-value [67] of the Pearson χ² discrepancy statistic can therefore be obtained such that:

$\begin{array}{ll}{\chi }^2\left(\text{p}|\Theta \right)={\displaystyle \sum _{a=0}^A}{\displaystyle \sum _{x=1}^X}\left[\left(N_{ax}{p}_{ax}-N_{ax}{\theta }_{ax}\right)∕N_{ax}{\theta }_{ax}\right]& (11)\end{array}$

and

$\begin{array}{ll}p\mathrm{\text{ value}}\left(\text{p}|\Theta \right)=Pr\left[{\chi }^2\left({\text{p}}^{*}|\Theta \right)\ge {\chi }^2\left(\text{p}|\Theta \right)|\text{p}\right].& (12)\end{array}$

Given the set of MCMC samples (Θ^(t) | t = 1, …, T), whereby T should be reasonable large (i.e., T = 5000 as in the present study) the above equation is estimated by:

$\begin{array}{ll}\frac{1}{T}{\displaystyle \sum _{t=1}^T}I\left({\chi }^2\left({\text{p}{}^{*}}^{\left(t\right)}|{\Theta }^{\left(t\right)}\right)\ge {\chi }^2\left(\text{p}|{\Theta }^{\left(t\right)}\right)\right)& (13)\end{array}$

where I(·) is the indicator function [22]. This Bayesian p-value is therefore the probability that the χ²-value of “future” data is greater or equal to the χ²-value of the observed data [67]. Hence it indicates if the data can be described by the model, assuming the model is correct. Large values are indicative of global model fit whereas low values (such as the conventional p < 0.05) suggest poor fit.

Secondly, since the Bayesian p-value does not provide information whether a certain model is correct but rather that it is one of possibly many fitting models [68], the Deviance Information Criterion (DIC; [69]) serves as a decision criterion to select a model with the highest generalizability over future observations of the same conditions which generated the actual data set. Thus, the DIC serves as a criterion for Bayesian model selection and model comparison and is thus a measure of relative model fit. For the matrix of observed proportions of correct item responses corresponding to Figure 1, the deviance function obtained from the MCMC algorithm is as follows:

$\begin{array}{ll}D\left(\Theta \right)=2{\displaystyle \sum _{j=1}^9}\left[\left(n_j\right)ln\left(\frac{n_j}{N_j{\theta }_j}\right)+\left(N_j-n_j\right)ln\left(\frac{N_j-n_j}{N_j-N_j{\theta }_j}\right)\right]& (14)\end{array}$

where n_j is the number of correct responses and N_j is the total number of responses corresponding to the j-th cell of the conjoint array. The DIC is given by:

$\begin{array}{ll}\mathrm{\text{DIC}}=D\left(\overline{\Theta }\right)+2\left(\overline{D\left(\Theta \right)}-D\left(\overline{\Theta }\right)\right)& (15)\end{array}$

where $D\left(\overline{\Theta }\right)$ is the deviance evaluated at the posterior mean, $\left(\overline{D\left(\Theta \right)}-D\left(\overline{\Theta }\right)\right)$ penalizes the complexity of an axiom and $\overline{D\left(\Theta \right)}$ is the posterior mean of the deviance [70].

In our study, the DIC was used in order to compare the fit of the ISOP model compared to the monotone homogeneity model (MH; [22]), differing from the ISOP model with respect to conjoint matrices in which the single cancelation axiom holds upon only the rows of the matrix, that is, allowing for intersecting item response functions. According to Spiegelhalter et al. [71], a difference of less than five in the DIC measures between models does not provide sufficient evidence favoring one model over another. Thirdly, local model fit, that is, the fit of any cell of proportions of correct responses in the observed data matrix, can be judged by constructing a Bayesian 95% confidence interval around the observed proportions. Based on that, one can construct an unstandardized effect size measure of approximate model fit as the number of proportions within their 95% corresponding confidence interval.

It is important to note that with 30 items and sample sizes of 250 and 500, as in our study, the dimensionality of the row- (respondents) and column-wise (items) ordered data matrix of observed proportions becomes huge, increasing computational time of the MCMC method drastically. Therefore, the conjoint matrices were constructed by defining only three score groups based on the quantiles q_33% and q_66%, resulting in 3 × 30 conjoint matrices of the replicated data sets, simulated as described above. Furthermore, extreme scores (i.e., persons with scores of either 0 or 30) were automatically deleted before each analysis of the replicated data sets.

Results

Two-Dimensional Data

The observed statistical power (i.e., rate of correct rejections) of the ISOP χ²-model test to detect violations of unidimensionality was 100% under all simulation conditions. Furthermore, the relative frequencies of proportions within their 95% confidence interval as an unstandardized effect size measure of model violations indicated clear deviations from the requirements of the ISOP model under all conditions as shown in Figures 2, 3.

FIGURE 2

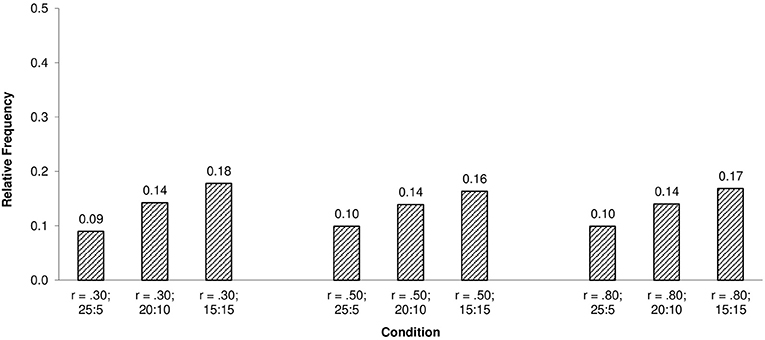
Figure 2. Relative frequencies of proportions correct within their 95% confidence interval for the ISOP model and N = 250.

FIGURE 3

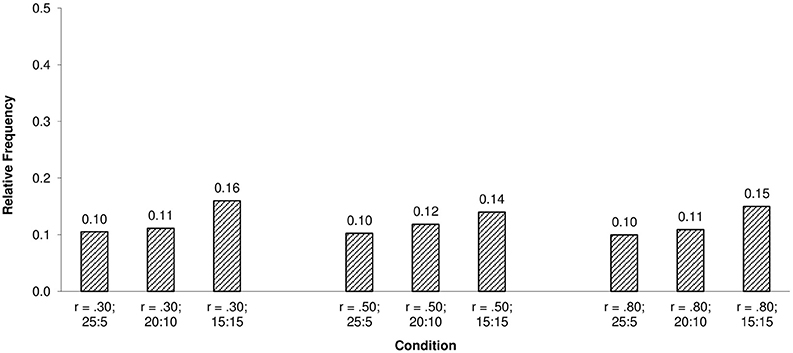
Figure 3. Relative frequencies of proportions correct within their 95% confidence interval for the ISOP model and N = 500.

As the results show, relative frequencies of the proportions within their confidence intervals were low under all simulation conditions, indicating gross violations of the order restrictions imposed by the ISOP model. The slight positive relationship between the relative frequencies of proportions within their 95% confidence interval and the item ratio may seem surprising at the first glance but can be explained by a compensation effect of the positively correlated dimensions.

To begin with, recall that the ISOP model requires non-decreasing and non-intersecting IRFs and that the estimated proportions of correct responses within their 95% confidence interval are indicating whether the IRFs are monotonically increasing and non-intersecting. Now, note that the ability of each person i within each quantile score group is determined by their parameter values θ_ij and θ_ik on the two dimensions j and k. As long as both dimensions are not perfectly positively correlated, each quantile score group consists of subgroups characterized by different ability configurations (θ_ij, θ_ik). Clearly, three types of parameter configurations within each quantile score group can be distinguished: θ_ij = θ_ik, θ_ij > θ_ik and θ_ij < θ_ik. For persons with θ_ij > θ_ik items of the first dimension are easier, whereby for θ_ij < θ_ik items of the second dimension are easier and for persons with θ_ij = θ_ik items are equally difficult. Because both types of parameter configurations θ_ij > θ_ik and θ_ij < θ_ik are part of each score group, effects of item heterogeneity, are—to a certain extend—compensated. Furthermore, because item homogeneity holds for persons in subgroups characterized by the parameter configuration θ_ij = θ_ij which are also included in each subgroup, effects of multidimensionality/item heterogeneity are even more reduced. In general, this effect is of course more pronounced if the ratio of items belonging to each dimension approaches one as the results show. Nevertheless, the very low relative frequencies of proportions within their 95% confidence interval leave no doubt about the strong violations of the single cancelation axiom and the sensitivity of the presented approach to detect violations of unidimensionality, regardless of the described slight compensation effect.

The violation of the single cancelation axiom is also demonstrated in Table 1 showing the means and standard deviations of the DIC from the replicated data sets per simulation condition.

TABLE 1

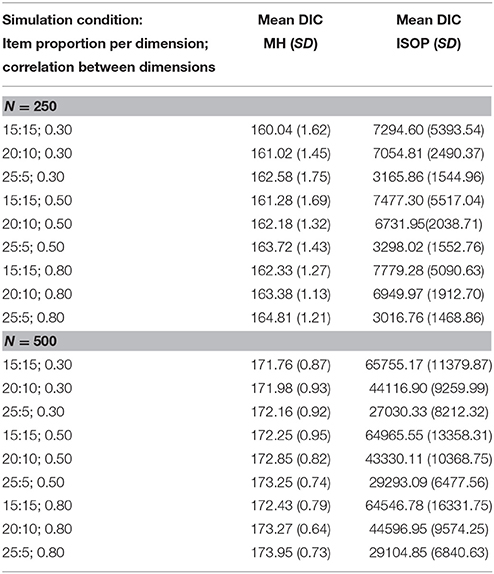
Table 1. Mean and (Standard Deviations) of the DIC statistic under different conditions of multidimensionality for the MH and ISOP model.

Under both sample size conditions the mean DIC statistic clearly indicate a better relative model fit of the MH model than the ISOP model [71], suggesting violation of the single cancelation axiom on both rows and columns of the conjoint matrices due to violations of unidimensionality. Furthermore, under the condition with N = 500 of the ISOP model, there is a clear positive relationship between mean DIC-values and the number of items assigned to each of the two dimensions as well as higher mean DIC-values can be observed when both dimensions are less correlated. With N = 250 and in contrast to the positive relationship between the number of items per dimension and mean DIC-values under the condition with N = 500, higher mean DIC-values are obtained when both dimensions are more strongly correlated. Presently we can only speculate on this effect. Because sample size bias has also been observed with the special cases of the DIC, Akaike's Information Criterion and Bayesian information criterion (cf. [72]), it is likely that sample sizes within each of the three quantile score groups with approximately 83 simulated persons per score group are too small to obtain unbiased estimates of the DIC statistic.

Rasch-Fitting Data

The analysis of the unidimensional Rasch-fitting data with the ISOP χ²-model test resulted in a 100% rejection rate under both sample size conditions, implying clear violations of the of single cancelation axiom. This was also supported by the mean DIC statistic indicating a better relative fit of the MH model under both sample size conditions as shown in Table 2.

TABLE 2

Table 2. Mean and (Standard Deviations) of the DIC statistic for the MH and ISOP model under different sample size conditions with Rasch-fitting data.

Furthermore, relative frequencies of the proportions within their 95% confidence intervals were low under both sample size conditions with 17 (N = 250) and 7% (N = 500), showing clear violations of the order restrictions imposed by the ISOP model implying quantitative measurement.

For the sake of completeness, we furthermore applied the generalization of Karabatsos' [21] algorithm recently developed by [23]. Domingue developed an improved version of the “jumping”/proposal function (cf., [73], p. 295f.) used in the Metropolis-Hastings algorithm to check both single and double cancelation. To keep the presented results of this study comprehensive, we decided to apply this approach to selected yet meaningful conditions only. We therefore chose the conditions of Rasch-fitting data with N = 500 and two-dimensional data with r₁₂ = 0.30, N = 500, and an item proportion per dimension of 15:15. Domingue's approach uses mean percentages of checks that detected violations from adjacent 3 × 3 matrices from a conjoint matrix, weighted by the number of individuals at each sum score level to reduce the impact of possible volatility at extreme abilities. Interestingly, we found practically no difference between the weighted means of these conditions with which were 0.27 and 0.28, respectively. We can only speculate on the reasons for the finding that Karabatsos' approach seems to be highly sensitive to departures from unidimensionality but Domingue's is not, for the experimental conditions realized in this study. In future studies, it might be worth checking randomly formed 3 × 3 because those turned to be more sensitive as first findings indicate (Domingue, personal communication, June, 2014).

Discussion

Before the study results are interpreted, it should be noted that the presented study was carried out under specific conditions of the distribution of the person and item parameters, test length, sample size and degrees of model violation. Under these restrictions, the results of this simulation study clearly demonstrated the power of the order-restricted inference approach to detect violations of unidimensionality by imposing the restrictions of the single cancelation axiom of conjoint measurement, using the ISOP model and integrated within a MCMC framework. Under each condition of different degrees of violations of unidimensionality the χ²-model test of the discrepancy statistics between the observed and expected data always rejected the hypothesis of the data-model fit under the assumption of unidimensionality. Furthermore, relative frequencies of proportions of correct responses within their 95% confidence interval as unstandardized effect size measures demonstrated gross violations of the unidimensionality assumption. These results were supported by comparing a nonparametric item response model assuming monotone homogeneity with the ISOP model, assuming double monotonicity or single cancelation, respectively. By applying the DIC statistic the results always showed a superior data-model fit of the monotone homogeneity model when compared to the ISOP model. Furthermore, for N = 500 higher mean DIC statistics (i.e., less fitting models) were observed when dimensions were less correlated. However, the somewhat biased results observed under the smaller sample size condition (N = 250), where higher mean DIC-values are obtained when both dimensions were more strongly correlated, possibly indicate that the suggested approach should only be used with big sample sizes (N ≥ 500).

In general, this study demonstrates that stochastic tests of the conjoint measurement cancelation axioms are highly sensitive with regard to different degrees of violations of the unidimensionality assumption. Because these axioms imply certain order relations upon the cells of a conjoint matrix, being violated in case of multidimensional data, they can also be employed in the context of applied psychometrics without relying on assumptions of most parametric tests of unidimensionality. Even more important, as a direct result of testing these cancelation axioms, the presented approach enables one to test the only implicitly assumed hypothesis of most psychometrical models that the attribute under consideration is a continuous quantity. Given that “…psychologists are quite cavalier in their use of the loaded term ‘measure”’ [74] because they have not yet attempted an explicit unit of measurement [75, 76], testing the assumption of continuous quantity is of critical importance for the advancement of a science.

It has nevertheless been argued that the measurement axioms used in this study are too restrictive for psychological data because factors extraneous to the attribute (measurement errors) affect test performances and that item response models, accounting for measurement error by assuming monotonically increasing IRFs (cf. [77]), should be preferred. Even more importantly, and as already alluded in the introduction of this article, it is argued that the Rasch model in particular produces quantitative measurements [19, 78]. If this assertion is true, how come was violation of single cancelation observed in data which fitted the unidimensional Rasch model?

A possible explanation for this was advanced by Michell [24]. The Rasch model is considered a stochastic version of an older IRT model proposed by Guttman [58], in that test score data which fit the Rasch model are stochastic realizations of Guttman item response patterns. But this leads to a contradiction which Michell [24] called the Rasch Paradox.

Let Guttman's model be formally defined as follows. Suppose X is a set of items ostensibly designed to assess a particular intellectual ability and A is a set of persons. Let aRx be the relation “Person a responds to item x correctly.” Ducamp and Falmagne ([26], Theorem 3) found that for x, y ∈ X and a, b ∈ A;

$\begin{array}{ll}\mathrm{\text{If }}aRx,\text{ not }aRy, \text{and }bRy \text{then }bRx& (16)\end{array}$

This then has the representation:

$\begin{array}{ll}\left(a,x\right)\in B\iff f(a)>g(x)& (17)\end{array}$

where 〈ℜ, >〉 are the real numbers and f:A ↦ ℜ and g:X ↦ ℜ; and B is a biorder. In psychometrics, a Guttman scale is inferred when the Boolean tableau of “1”s and “0's of persons” responses corresponding to Equation (16) are separated by a staircase type function [79] such that a Guttman scalogram results:

$\begin{array}{ll}\left(\begin{array}{ccc} & x& y\\ a& 1& 0\\ b& 1& 1\\ \end{array}\right)& (18)\end{array}$

Thus, a biorder is the empirical relational structure underlying Guttman scalograms. However, there is a problem with Equation (17) in that Equation (18) does not always empirically hold [26]. Suppose that:

$\begin{array}{ll}\left(\begin{array}{ccc} & x& y\\ a& 1& 0\\ b& 0& 1\\ \end{array}\right)& (19)\end{array}$

which indicates that person b did not get item x correct. Thus, Equation (17) with Equation (18) implies a contradiction, in that g(y) ≥ f(a) > g(x) and g(x) ≥ f(b) > g(y) [26]. Hence the uniqueness of the representation in Equation (17) depends upon the support of Equation (18) and so hence the negation of Equation (19). Therefore, the uniqueness of Equation (17) is such that for (f, g) and (f′, g′) then there exists a monotonically increasing function K such that:

$\begin{array}{ll}f\prime =K\circ f\text{ and }g\prime =K\circ g& (20)\end{array}$

where “ ∘ ” designates function composition [26]. Therefore, measurements in Guttman's model are unique up to monotonic transformations only [27]. Hence Guttman's model is merely ordinal, not quantitative.

Michell ([24], p. 122) argued the Rasch model is a “woolly” version of Guttman's theory because it posits that:

$\begin{array}{ll}\left(a,x\right)\iff f\left(a\right)\ge g\left(x\right)+\epsilon & (21)\end{array}$

where error is assumed to form a logistic distribution. Michell [24] contended that because Guttman's model is ordinal, Rasch's quantitative and the only difference between them being error, it follows that the Rasch model's status as a quantitative theory is derived exclusively through the error term of Equation (21). This creates a paradoxical situation, because in physics and metrology, error is perceived as a measurement confound. Metrologists work to create observational methodologies that reduce measurement error precisely because such methods lead to better measurement (c.f., [16]). If error were completely eliminated, physical measurement would be perfect. But with the Rasch model, if the error was eliminated, then the “measurements” of the Rasch model reduce only to mere order (i.e., the Guttman model is obtained). Measurement would therefore be impossible. But eliminating error must by definition lead to better measurement, not the impossibility of measurement, and so hence the paradox.

In the present study, the ISOP model stochastically tested the single cancelation condition. It therefore tested only for order. Given a Rasch model simulation yields stochastic Guttman response patterns (i.e., Guttman response patterns contaminated by error), and if the Rasch Paradox is true, then it can reasonably be expected that Rasch model simulations lead to violations of single cancelation. Such violation was indeed observed in the present study.

What the ISOP analyses of the present study perhaps reveal is the effect of adding error to ordinal data. That psychometric test score data are fundamentally ordinal is by no means contentious. As directly observed and absent descriptive theories of the item response process, test score response patterns form partial orders [5, 80, 81]. Partial orders are not measureable, yet they have been mistakenly argued to provide a foundation for the measurement of cognitive abilities (e.g., [81, 82]). Partial orders also violate the cancelation axioms as the latter propose that simple orders must hold upon persons and items, whilst the former implies that simple orders are not possible.

Three different conclusions may be drawn from the present study. Firstly, it is possible that human cognitive abilities, or at least those aspects of cognition which cause individual differences in psychometric test performance, simply are not quantitative. Application of all psychometric models to test score data that assume continuous and quantitative latent traits is therefore misguided and other non-quantitative theories should be explored. To a large extent this has already occurred with non-parametric IRT models such as the Mokken model [57], which assume that abilities can only be ordered. Non parametric IRT has received serious attention in theoretical psychometrics, with Applied Psychological Measurement (2001, 25(3)) devoting a special issue to the topic. The Mokken [57] model has been successfully applied in quality of life research (e.g., [83, 84]) and in tests of inductive reasoning [85]. Moreover, in an investigation of 36 person fit statistics, including both parametric and non-parametric indices, Karabatsos [86] found that the Mokken H^T statistic outperformed all others in detecting aberrant response behavior such as guessing and cheating. The idea of non-quantitative measures may not to every taste because it undermines psychology's self-conception as a quantitative science with a strong resemblance to the natural sciences. As Schönemann ([87], p. 151) put it: “…it also requires a willingness to accept empirical results which conflict with traditional beliefs.” We doubt that psychologists are willing to pay the price of falsification of theories being based on the claim of quantitative measures (cf., [88, 89]). Yet “solving” the problem by ignoring the possible non-quantitative properties of psychological phenomena is a pleasant self-delusion at the expense of falsifiability, resting on the dubious implicit assumption that knowledge is the “…result of ‘processing’ rather than discovery” ([90], p. 259).

Secondly, it could be that the traditional psychometric test, as an observational methodology, is simply far too crude to enable the application of the theory of conjoint measurement to human cognitive abilities. Our current theoretical understanding of what it means for an attribute to be quantitative and measureable may simply exceed our capacity to observe cognitive abilities. Cliff ([43], p. 189) already pointed to this problem by observing: “The levels of variables are never infinitely fine, as is often required in the proofs” (see [87], p. 153 for an illustration). Effort may therefore be needed in developing better observational methodologies, perhaps using information technology. Whether the development of better observational methodologies would reveal a quantitative structure of at least some psychological phenomena is, admittedly, speculative. One could, on the other hand, argue that this could shift the current focus from processing to discovery mentioned above. To us, the current and problematic state of affair in this respect is provided by Schönemann ([91], p. 200): “Numerous ‘general scientific methods’ came and went, ranging from multidimensional scaling (…) to latent trait theory, IRT, linear structural models (…), and meta-analysis and log-linear models. None of them (…) helped answer any of the basic theoretical questions (…).”

Thirdly, it could be the case that cognitive abilities are quantitative, but that psychometricians have mostly failed to develop and test behavioral theories of individual differences in ability test performance [92]. Without explicit behavioral theory, it is difficult to tell whether or not the zero in the test score response pattern (1, 1, 0, 1), for example, is truly an item response error or something that genuinely reflects the behavior of the relevant cognitive ability. In this respect, Kyngdon [92] applied the theory of conjoint measurement to data from the Lexile Framework for Reading [93], which argues that individual differences in performance upon reading tests are caused by differences in readers' verbal working memory capacities and vocabularies. He found the cancelation axioms were supported only when the columns of the relevant conjoint array were permuted. This suggested that reading ability was quantitative but that the Lexile Framework is not a complete behavioral account of individual differences in reading test performance. Such findings might make things worse in the short term because it would just be easier to show how poorly the theoretical claims are connected to the data. However, such disapointing surprises might pay off scientifically in the long run.

It is likely that psychometricians would not welcome the conclusions of this article and judge them as too severe for practical testing purposes. However, it is they who continue to argue that cognitive abilities are quantitative and measureable “latent traits” (e.g., [94]). If this argument is correct, then once item response error is controlled for using an order restricted inference framework, test score response data should be consistent with the cancelation axioms of conjoint measurement; and the stringent unidimensionality that they entail. If test data does not, then testing need not be dispensed with. Most practical applications of testing only require that persons be ordered with respect their cognitive abilities (cf., [95]) and something like Stout's [12] notion of essential unidimensionality may be useful in practical testing contexts. In any case, the stochastic ISOP model, integrated in an MCMC framework that implies the cancelation axioms of the theory of conjoint measurement, is perhaps the most stringent test of the unidimensionality hypothesis currently available.

Author Contributions

All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The Handling Editor declared a shared affiliation, though no other collaboration, with one of the authors AK and states that the process nevertheless met the standards of a fair and objective review.

The other authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Danish Institute for Educational Research (1960).

Google Scholar

2. Drasgow F. Study of the measurement bias of two standardized psychological tests. J Appl Psychol. (1987) 72:19–29. doi: 10.1037/0021-9010.72.1.19

CrossRef Full Text | Google Scholar

3. Harrison DA. Robustness of IRT parameter estimation to violations of the unidimensionality assumption. J Educ Stat. (1986) 11:91–115. doi: 10.2307/1164972

CrossRef Full Text | Google Scholar

4. Reckase MD. Unifactor latent trait models applied to multifactor tests: results and implications. J Educ Stat. (1979) 4:207–30. doi: 10.2307/1164671

CrossRef Full Text | Google Scholar

5. Michell J. An Introduction to the Logic of Psychological Measurement. Hillsdale, NJ: Erlbaum (1990).

Google Scholar

6. Michell J. The psychometricians' fallacy: too clever by half? Br J Math Stat Psychol. (2009) 62:41–55. doi: 10.1348/000711007X243582

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gerbing DW, Anderson JC. An updated paradigm for scale development incorporating unidimensionality and its assessment. J Market. Res. (1988) 25:186–92. doi: 10.2307/3172650

CrossRef Full Text | Google Scholar

8. Lumsden J. The construction of unidimensional tests. Psychol Bull. (1961) 58:122. doi: 10.1037/h0048679

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Maraun M. Myths and Confusions: Psychometrics and the Latent Variable Model. Unpublished manuscript, Department of Psychology, Simon Fraser University (2006). Retrieved from: http://www.sfu.ca/~maraun/myths-and-confusions.html

10. Thomson GH. A hierarchy without a general factor. Br J Psychol. (1916) 8:271–81. doi: 10.1111/j.2044-8295.1916.tb00133.x

CrossRef Full Text | Google Scholar

11. Thomson GH. On the cause of hierarchical order among the correlation coefficients of a number of variates taken in pairs. Proc R Soc Lond A (1919) 95:400–8. doi: 10.1098/rspa.1919.0018

CrossRef Full Text | Google Scholar

12. Stout W. A nonparametric approach for assessing latent trait unidimensionality. Psychometrika (1987) 52:589–617. doi: 10.1007/BF02294821

CrossRef Full Text | Google Scholar

13. Suppes P, Zanotti M. When are probabilistic explanations possible? Synthese (1981) 48:191–99. doi: 10.1007/BF01063886

CrossRef Full Text | Google Scholar

14. Hölder O. Die Axiome Der Quantität und die Lehre vom Maß. Berichte über die Verhandlungen der königlich sächsischen, Gesellschaft der Wissenschaften zu Leipzig (1901).

15. Michell J, Ernst C. The axioms of quantity and the theory of measurement. J Math Psychol. (1997) 41:345–56. doi: 10.1006/jmps.1997.1178

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bureau International des Poids et Mesures (BIPM) (2006). The International System of Units (SI), 8th Edn. Retrieved from: http://www.bipm.org/en/si/sibrochure/

17. Luce RD, Tukey JW. Additive conjoint measurement: a new type of fundamental measurement. J Math Psychol. (1964b) 1:1–27. doi: 10.1016/0022-2496(64)90015-X

CrossRef Full Text | Google Scholar

18. Bond TG, Fox CM. Fundamental Measurement in the Human Sciences. Chicago, IL: Institute for Objective Measurement (2007).

Google Scholar

19. Perline R, Wright BD, Wainer H. The Rasch model as additive conjoint measurement. Appl Psychol Meas. (1979) 3:237–255. doi: 10.1177/014662167900300213

CrossRef Full Text | Google Scholar

20. Glas CAW, Verhelst ND. Testing the Rasch model. In: Fischer G, Molenaar IW, editors, Rasch Models - Foundations, Recent Developments, and Applications. New York, NY: Springer. pp. 69–95.

21. Karabatsos G. The Rasch model, additive conjoint measurement, and new models of probabilistic measurement theory. J Appl Meas. (2001) 2:389–423.

PubMed Abstract | Google Scholar

22. Karabatsos G, Sheu C. Order-constrained Bayes inference for dichotomous models of unidimensional nonparametric IRT. Appl Psychol Meas. (2004) 28:110–25. doi: 10.1177/0146621603260678

CrossRef Full Text | Google Scholar

23. Domingue B. Evaluating the equal-interval hypothesis with test score scales. Psychometrika (2014) 79:1–19. doi: 10.1007/s11336-013-9342-4

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Michell J. Conjoint measurement and the Rasch paradox: a response to Kyngdon. Theory Psychol. (2008) 18:119–24. doi: 10.1177/0959354307086926

CrossRef Full Text | Google Scholar

25. Guttman L. A basis for scaling qualitative data. Am Sociol Rev. (1944) 91:139–50. doi: 10.2307/2086306

CrossRef Full Text

26. Ducamp A, Falmagne J-C. Composite measurement. J Math Psychol. (1969) 6:359–90. doi: 10.1016/0022-2496(69)90012-1

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Narens L. On the scales of measurement. J Math Psychol. (1981) 24:249–75. doi: 10.1016/0022-2496(81)90045-6

PubMed Abstract | CrossRef Full Text | Google Scholar

28. de Boer J. On the history of quantity calculus and the international system. Metrologia (1994/1995) 31: 405–29. doi: 10.1088/0026-1394/31/6/001

CrossRef Full Text | Google Scholar

29. Sijtsma K. Psychological measurement between physics and statistics. Theory Psychol. (2012) 22:786–809. doi: 10.1177/0959354312454353

CrossRef Full Text | Google Scholar

30. Michell J. Constructs, inferences, and mental measurement. New Ideas Psychol. (2013) 31:13–21. doi: 10.1016/j.newideapsych.2011.02.004

CrossRef Full Text | Google Scholar

31. Michell J. Some problems in testing the double cancellation condition in conjoint measurement. J Math Psychol. (1988) 32:466–73. doi: 10.1016/0022-2496(88)90024-7

CrossRef Full Text | Google Scholar

32. Krantz DH, Luce RD, Suppes P, Tversky A. Foundations of Measurement, Vol. I: Additive and Polynomial Representations. New York, NY: Academic Press (1971).

Google Scholar

33. Gigerenzer G, Strube G. Are there limits to binaural additivity of loudness? J Exp Psychol Hum Percept Perform. (1983) 9:126–36. doi: 10.1037/0096-1523.9.1.126

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Luce RD, Steingrimsson R. Theory and tests of the conjoint commutativity axiom for additive conjoint measurement. J Math Psychol. (2011) 55:379–85. doi: 10.1016/j.jmp.2011.05.004

CrossRef Full Text | Google Scholar

35. Luce RD. Behavioral assumptions for a class of utility theories: a program of experiments. J Risk Uncertain. (2010a) 41:19–37. doi: 10.1007/s11166-010-9098-5

CrossRef Full Text | Google Scholar

36. Luce RD. Interpersonal comparisons of utility for 2 of 3 types of people. Theory Decis. (2010b) 68:5–24. doi: 10.1007/s11238-009-9138-2

CrossRef Full Text | Google Scholar

37. Johnson T. Controlling the effect of stimulus context change on attitude statements using Michell's binary tree procedure. Aust J Psychol. (2001) 53:23–8. doi: 10.1080/00049530108255118

CrossRef Full Text | Google Scholar

38. Michell J. Measuring dimensions of belief by unidimensional unfolding. J Math Psychol. (1994) 38:224–73. doi: 10.1006/jmps.1994.1016

CrossRef Full Text | Google Scholar

39. Kyngdon A. An empirical study into the theory of unidimensional unfolding. J Appl Meas. (2006) 7:369–93.

PubMed Abstract | Google Scholar

40. Coombs CH. A Theory of Data. New York, NY: Wiley (1964).

Google Scholar

41. Kyngdon A, Richards B. Attitudes, order and quantity: deterministic and direct probabilistic tests of unidimensional unfolding. J Appl Meas. (2007) 8:1–34.

PubMed Abstract | Google Scholar

42. Andrich D. Hyperbolic cosine latent trait models for unfolding direct responses and pairwise preferences. Appl Psychol Meas. (1995) 19:269–90. doi: 10.1177/014662169501900306

CrossRef Full Text | Google Scholar

43. Cliff N. Abstract measurement theory and the revolution that never happened. Psychol Sci. (1992) 3:186–90. doi: 10.1111/j.1467-9280.1992.tb00024.x

CrossRef Full Text | Google Scholar

44. Narens L, Luce RD. Further comments on the “non revolution” arising from axiomatic measurement theory. Psychol Sci. (1993) 4:127–30. doi: 10.1111/j.1467-9280.1993.tb00475.x

CrossRef Full Text | Google Scholar

45. Luce RD. Utility of Gains and Losses: Measurement-Theoretic and Experimental Approaches. Mahwah, NJ: Erlbaum (2000).

46. Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk. Econometrica (1979) 47:263–91. doi: 10.2307/1914185

CrossRef Full Text | Google Scholar

47. Birnbaum MH. New paradoxes of risky decision making. Psychol Rev. (2008) 115:463–501. doi: 10.1037/0033-295X.115.2.463

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Luce RD, Narens L. Fifteen problems concerning the representational theory of measurement. In: Suppes P editor. Philosophy of Physics, Theory Structure, Measurement Theory, Philosophy of Language, and Logic. Vol. 2. Dordrecht: Kluwer Academic Publishers (1994). pp. 219–49.

49. Ramsay JO, Bloxom B, Cramer, EM. Reviews. Psychometrika (1975) 40:257–66.

PubMed Abstract | Google Scholar

50. Iverson G, Falmagne JC. Statistical issues in measurement. Math Soc Sci. (1985) 10:131–53. doi: 10.1016/0165-4896(85)90031-9

CrossRef Full Text | Google Scholar

51. Scheiblechner H. Isotonic ordinal probabilistic models (ISOP). Psychometrika (1995) 60:281–304. doi: 10.1007/BF02301417

CrossRef Full Text | Google Scholar

52. Masters GN. Item discrimination: when more is worse. J Educ Meas. (1988) 25:15–29. doi: 10.1111/j.1745-3984.1988.tb00288.x

CrossRef Full Text | Google Scholar

53. Tuerlinckx F, De Boeck P. Non-modeled item interactions lead to distorted discrimination parameters: a case study. Methods Psychol Res Online (2001) 6:159–74. Retrieved from: https://ppw.kuleuven.be/okp/_pdf/Tuerlinckx2001NMII.pdf

Google Scholar

54. Tuerlinckx F, De Boeck P. Two interpretations of the discrimination parameter. Psychometrika (2005) 70:629–50. doi: 10.1007/s11336-000-0810-3

CrossRef Full Text | Google Scholar

55. Andersen EB. A goodness of fit test for the Rasch model. Psychometrika (1973) 38:123–40. doi: 10.1007/BF02291180

CrossRef Full Text | Google Scholar

56. McClelland G. A note on Arbuckle and Larimer, “The number of two-way tables satisfying certain additivity axioms.” J Math Psychol. (1977) 15:292–5. doi: 10.1016/0022-2496(77)90035-9

CrossRef Full Text | Google Scholar

57. Mokken RJ. A Theory and Procedure of Scale Analysis. The Hague: Mouton (1971).

Google Scholar

58. Guttman L. The basis for scalogram analysis. In: Stouffer SA, Guttman L, Suchman EA, Lazarsfeld PF, Star SA, Clausen JA. Measurement and Prediction, The American Soldier. New York, NY: Wiley (1950).

PubMed Abstract

59. Wu M, Adams RJ, Wilson M. ACER ConQuest: Generalized Item Response Modeling Software [Computer Software and Manual]. Australian Council for Educational Research (2002). Camberwell.

60. Adams RJ, Wilson M, Wang W. The multidimensional random coefficients multinomial logit model. Appl Psychol Meas. (1997) 21:1–23. doi: 10.1177/0146621697211001

CrossRef Full Text | Google Scholar

61. DeYoung CG, Quilty LC, Peterson JB. Between facets and domains: 10 aspects of the Big Five. J Pers SocPsychol. (2007) 93:880. doi: 10.1037/0022-3514.93.5.880

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Andrich D. On the Fractal Dimension of a Social Measurement: I. Unpublished paper, Social Measurement Laboratory, Murdoch University, Perth, Australia (2006). Retrieved from: http://scseec.edu.au/site/DefaultSite/filesystem/documents/Reports/ArchivePublications/Miscellaneous/ARC documents/ARC-Report03_FractalDimension_II.pdf

Google Scholar

63. Core Development Team (2015). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Retrieved from: http://www.R-project.org

64. Hyndman RJ, Fan Y. Sample quantiles in statistical packages. Am Stat. (1996) 50:361.

Google Scholar

65. Tierney L. Markov chains for exploring posterior distributions. Ann Stat. (1994) 22:1701–28. doi: 10.1214/aos/1176325750

CrossRef Full Text | Google Scholar

66. Geyer CJ. Practical Markov chain Monte Carlo. Stat Sci. (1992) 7:473–511. doi: 10.1214/ss/1177011137

CrossRef Full Text | Google Scholar

67. Myung JI, Karabatsos G, Iverson GJ. A Bayesian approach to testing decision making axioms. J Math Psychol. (2005) 49:205–25. doi: 10.1016/j.jmp.2005.02.004

CrossRef Full Text | Google Scholar

68. Carlin BP, Louis TA. Bayes and empirical Bayes methods for data analysis. Stat Comput. (1997) 7:153–4. doi: 10.1023/A:1018577817064

CrossRef Full Text | Google Scholar

69. Spiegelhalter DJ, Best NG, Carlin BP, van der Linde, A. Bayesian measures of model complexity and fit. J R Stat Soc B (2002) 64:583–639. doi: 10.1111/1467-9868.00353

CrossRef Full Text | Google Scholar

70. Karabatsos G, and Ullrich JR. Enumerating and testing conjoint measurement models. Math Soc Sci. (2002) 43:485–504.

Google Scholar

71. Spiegelhalter DJ, Thomas A, Best NG, Lunn D. WinBUGS Users Manual. MRC Biostatistics Unit, Cambridge (2004). Retrieved from: http://www.mrc-bsu.cam.ac.uk/bugs/

72. Burnham KP, Anderson DR. Multimodel inference. Sociol Methods Res. (2004) 33:261. doi: 10.1177/0049124104268644

CrossRef Full Text | Google Scholar

73. Gelman A, Carlin JB, Stern HS, and Rubin DB. Bayesian data Analysis (Vol. 2). Boca Raton, FL: Chapman and Hall/CRC (2014).

Google Scholar

74. Schönemann PH, Thompson WW. Hit-rate bias in mental testing. Curr Psychol Cogn. (1996) 15:3–28.

Google Scholar

75. Heene M. An old problem with a new solution, raising classical questions: a commentary on humphry. Measurement (2011) 9:51–4. doi: 10.1080/15366367.2011.558790

CrossRef Full Text | Google Scholar

76. Kyngdon A. Psychological measurement needs units, ratios and real quantities – a commentary on Humphry. Measurement (2011c) 9:55–8. doi: 10.1080/15366367.2011.558791

CrossRef Full Text | Google Scholar

77. Borsboom D, Mellenbergh GJ. Why psychometrics is not pathological. Theory Psychol. (2004) 14:105–20. doi: 10.1177/0959354304040200

CrossRef Full Text

78. Wright BD, Linacre JM. Observations are always ordinal; measurements, however, must be interval. Arch Phys Med Rehabil. (1989) 70:857.

PubMed Abstract | Google Scholar

79. Christophe J, Doignon JP, Fiorini, S. Counting biorders. J Integer Seq. (2003) 6:1–10.

PubMed Abstract | Google Scholar

80. Kane M. The benefits and limitations of formality. Measurement (2008) 6:101–8. doi: 10.1080/15366360802035562

CrossRef Full Text | Google Scholar

81. Kyngdon A. Partial orders cannot be measured. Measurement (2011b) 9:159–162. doi: 10.1080/15366367.2011.603618

CrossRef Full Text | Google Scholar

82. Black P, Wilson M, Yao SY. Roadmaps for learning: a guide to the navigation of learning progressions. Measurement (2011) 9:71–123. doi: 10.1080/15366367.2011.591654

CrossRef Full Text | Google Scholar

83. van der Heiden PGM, van Buuren S, Fekkes M, Radder J, Verrips E. Unidimensionality and reliability under Mokken scaling of the Dutch language version of the SF-36. Qual Life Res. (2003) 12:189–98. doi: 10.1023/A:1022269315437

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Ringdal K, Ringdal GI, Kaasa S, Bjordal K, Wisløff F, Sundstrøm S, et al. Assessing the consistency of psychometric properties of the HRQoL scales within the EORTC QLQ-C30 across populations by means of the Mokken scaling model. Qual Life Res. (1999) 8:25–43. doi: 10.1023/A:1026419414249

PubMed Abstract | CrossRef Full Text | Google Scholar

85. de Koning E, Sijstma K, Hamers JHM. Comparison of four IRT models when analyzing two tests for inductive reasoning. Appl Psychol Meas. (2002) 26:302–20. doi: 10.1177/0146621602026003005

CrossRef Full Text | Google Scholar

86. Karabatsos G. Comparing the aberrant response detection performance of thirty-six person-fit statistics. Appl Meas Educ. (2003) 16:277–98. doi: 10.1207/S15324818AME1604_2

CrossRef Full Text | Google Scholar

87. Schönemann, P. H. (1994). Measurement: the reasonable ineffectiveness of mathematics in the social sciences. In: Borg I, Mohler P, editors. Trends and Perspectives in Empirical Social Research, Berlin; New York, NY: Walter de Gruyter, pp. 149–160.

88. Ferguson CJ, Heene M. A vast graveyard of undead theories publication bias and psychological science's aversion to the null. Perspect Psychol Sci. (2012) 7:555–61. doi: 10.1177/1745691612459059

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Heene M. Additive conjoint measurement and the resistance toward falsifiability in psychology. Front Quant Psychol Meas. (2013) 4:246. doi: 10.3389/fpsyg.2013.00246

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Koch S. The nature and limits of psychological knowledge: Lessons of a century qua “science.” Am Psychol. (1981) 36:257. doi: 10.1037/0003-066X.36.3.257

CrossRef Full Text | Google Scholar

91. Schönemann PH. Psychometrics of intelligence. In: Kemp-Leonard K, editors. Encyclopedia of Social Measurement. Vol. 3 (2005). Oxford, UK: Elsevier. pp. 193–201.

PubMed Abstract

92. Kyngdon A. Plausible measurement analogies to some psychometric models of test performance. Br J Math Stat Psychol. (2011a) 64:478–97. doi: 10.1348/2044-8317.002004

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Stenner AJ, Burdick H, Sanford EE, Burdick DS. How accurate are Lexile text measures? J Appl Meas. (2006) 7:307–22.

PubMed Abstract | Google Scholar

94. Markus KA, Borsboom D. The cat came back: evaluating arguments against psychological measurement. Theory Psychol. (2011). 22:452–66. doi: 10.1177/0959354310381155

CrossRef Full Text | Google Scholar

95. Cliff N, Keats JA. Ordinal Measurement in the Behavioral Sciences. Mahwah, NJ: Erlbaum (2003).

Google Scholar