- Graduate School of Natural Sciences, International Christian University, Tokyo, Japan
In this paper, we present the self-similar symmetry (SSS) model that describes the hierarchical structure of the universe. The model is based on the concept of self-similarity, which explains the symmetry of the cosmic microwave background (CMB). The approximate length and time scales of the six hierarchies of the universe—grand unification, electroweak unification, the atom, the pulsar, the solar system, and the galactic system—are derived from the SSS model. In addition, the model implies that the electron mass and gravitational constant could vary with the CMB radiation temperature.
1. Introduction
What determines the values of the physical constants and whether they will remain constant over time are fundamental questions in physics. A long-standing conundrum associated with the physical constants is that large dimensionless numbers that are seemingly unrelated can be linked by a scale factor of 1039 [1–5]. The Dirac large numbers hypothesis (LNH) tackles this problem. It claims that the gravitational constant G is inversely proportional to the age of the universe. The LNH is based on the coincidences between three very large dimensionless numbers . N1, the ratio of the radius of the observable universe to the radius of the electron, is approximately 1039; N2, the ratio of the electromagnetic and gravitational forces between a proton and an electron, is also approximately 1039; and N, the number of protons in the observable universe, is approximately 1078. The Dirac LNH argues that “any two of the very large dimensionless numbers occurring in Nature are connected by a simple mathematical relation, in which the coefficients are of the order of unity”[1].
In this paper, we present the self-similar symmetry (SSS) model in which the relationships among these seemingly unrelated physical quantities are represented using a simple geometric sequence for which the first term and the geometric ratio are given by dimensionless ratios of masses. Based on the LNH, the first term of the geometric sequence corresponds to the cosmic microwave background (CMB) radiation temperature, which points to the possibility that the values of the physical constants are determined by the CMB radiation temperature.
2. The Self-Similar Symmetry Model
In the SSS model, the CMB has a symmetrical self-similar structure and the physical constants are dimensionless, otherwise they would not have universality. Therefore, the fundamental dimensionless mass ratios are defined as follows:
where mpr is the proton mass, me is the electron mass, and mpl is the Planck mass, and the fundamental dimensionless time and length ratios are defined as
where t and l are the time and length scales of the hierarchies and tpl and lpl are the Planck time and Planck length, respectively. The similarity dimension D is defined using these dimensionless parameters:
We then assume that hierarchical structures are constructed according to the following sequences:
where n and m are natural numbers that represent the hierarchical level. In addition, the time scales of each hierarchy are calculated using Equation (3).
3. Verification of the SSS Model
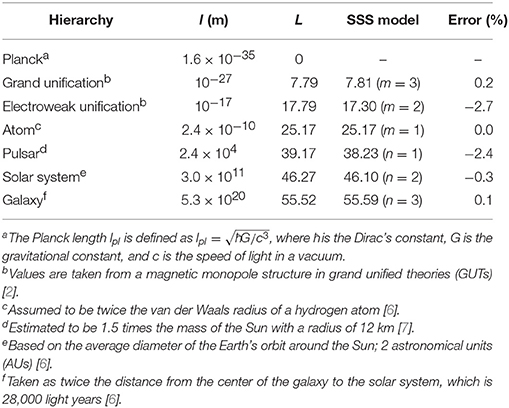
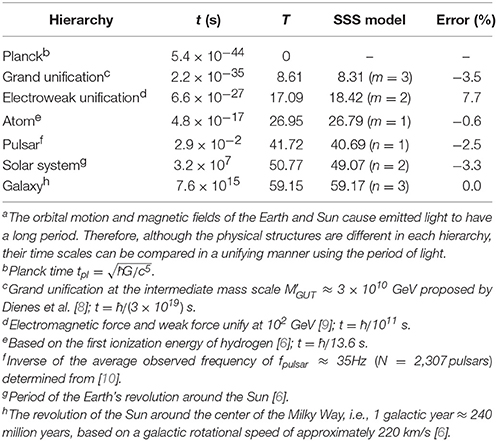
To verify the SSS model, we compared values obtained with it against reference values. Tables 1, 2 summarize the length and time scales, respectively, of the grand unification, electroweak unification, atom, pulsar, solar system, and galactic system hierarchies of the universe. The SSS model values agree well with the reference values. Figure 1 shows the hierarchy time scale as a function of the length scale. The coincidences in the figure confirm the validity of the SSS model.
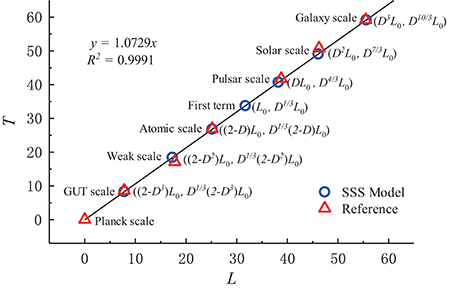
Figure 1. Time scale as a function of the length scale for the SSS model and reference values. The gradient of the fit of the SSS model values to the reference values is 1.0729(R2 = 0.9991). Note the symmetry about the first term L0, which corresponds to the CMB radiation temperature. This symmetry leads to speculation about the approximate length and time scale of the universe, which are 4.1 × 1028 m and 5.2 × 1016 years, respectively.
4. Discussion
From Equation (1), 2A = −logαG, where is the gravitational coupling constant, the following coincidences occurs:
Equation (7) shows that αG plays an important role in forming the hierarchical structure of the universe. In addition,
Thus, if Lu is the length of the universe, the following hierarchy holds:
Therefore, the ratios of the coincidences between the length scales of the hierarchies are
from which we get
From Equation (12), we see that ra ≠ rb ≠ 1.
With respect to the first term of the geometric sequence, L0, we find that
where Tpl is the Planck temperature. The value in Equation (13) is consistent with the CMB radiation temperature TCMB[11]. Assuming the right-hand side of Equation (13) represents the TCMB, if LNH is applied to Equation (13) and we define the dimensionless temperature ratio τCMB = TCMB/Tpl, we get
Similarly,
Thus, both αG and β are power functions of TCMB.
Substituting TCMB = Tpl, an initial condition of the universe, into Equations (14) and (15) yields α = β = 1, which means that the entire hierarchy was contained in a single point and that the electron, proton, and Planck masses were equivalent. These masses have varied since that initial single point such that me ≪ mpr ≪ mpl, in response to the changing TCMB, where TCMB ≪ Tpl. Assuming that TCMB → 0 is the ultimate fate of the universe, then α → ∞, β → 0, and L0 → ∞, indicating that me → 0 and G → 0 as the universe expands to infinity.
5. Conclusions
Our SSS model describes the large-scale structure of the universe and shows that the six hierarchies of the universe are self-similar to the CMB, indicating that the CMB is key to unifying quantum theory with general relativity. In addition, the SSS model leads to the conclusion that me and G vary with TCMB. Any errors arising from the SSS model are problems to be tackled in the future.
Author Contributions
TS conceived the study and prepared the manuscript.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author thanks M. B. Greenfield and K. Kitahara for helpful discussions.
References
2. Barrow JD, Tipler FJ. The Anthropic Cosmological Principle. New York, NY: Oxford University Press (1986). p. 656.
4. Carter B. In: Longair MS, editor. Confrontation of Cosmological Theories with Observational Data. Dordrecht: Reidel (1974), p. 291–8. doi: 10.1007/978-94-010-2220-0_25
5. Carr BJ, Rees MJ. The anthropic principle and the structure of the physical world. Nature (1979) 278:605–12. doi: 10.1038/278605a0
6. National Astronomical Observatory of Japan. Chronological Scientific Tables [in Japanese]. Tokyo: Maruzen Publishing Co. (2013).
7. Lattimer JM Prakash M. The physics of neutron stars. Science (2004) 304:536–42. doi: 10.1126/science.1090720
8. Dienes KR, Dudas E, Gherghetta, T. Grand unification at intermediate mass scales through extra dimensions. Nucl Phys B (1999) 537:47–108. doi: 10.1016/S0550-3213(98)00669-5
9. Bertone G, Hooper D, Silk J. Particle dark matter: evidence, candidates and constraints. Phys Rep. (2005) 405:279–390. doi: 10.1016/j.physrep.2004.08.031
10. Manchester RN, Hobbs GB, Teoh A, Hobb M. The Australia telescope national facility pulsar catalogue. Astron J. (2005) 129:1993–2006. doi: 10.1086/428488
Keywords: self-similarity, symmetry, cosmic microwave background, large numbers hypothesis, large numbers coincidences
Citation: Sonoda T (2016) Self-Similar Symmetry Model and Cosmic Microwave Background. Front. Appl. Math. Stat. 2:5. doi: 10.3389/fams.2016.00005
Received: 01 January 2016; Accepted: 26 April 2016;
Published: 11 May 2016.
Edited by:
Peng Gao, Harvard University, USAReviewed by:
Veselin Filev, Dublin Institute for Advanced Studies, IrelandKazuharu Bamba, Fukushima University, Japan
Copyright © 2016 Sonoda. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tomohide Sonoda, dG9tb0BhbG0uaWN1LmFjLmpw
 Tomohide Sonoda
Tomohide Sonoda