- 1Social Decision-Making Lab, Department of Psychology, University of Cambridge, Cambridge, United Kingdom
- 2Department of Statistics, Yale University, New Haven, CT, United States
The reproducibility of psychological science has become an important topic of debate. In an intriguing recent article, Scheibehenne et al. [1] advocate the use of Bayesian evidence synthesis as a new way to reconcile inconsistent findings in social psychology. As a case in point, they use Goldstein et al.'s [2] “hotel towel” study, a highly cited experiment illustrating the power of social norms in encouraging environmental conservation. Yet, because several recent experiments have failed to reproduce the study's original findings, Scheibehenne et al. [1] make a strong case for the need for better evidence synthesis. In doing so, they reveal an important finding, while none of the individual studies show strong support for the efficacy of social norms in encouraging hotel towel reuse, when combined and reanalyzed using a Bayesian approach, the studies jointly provide strong evidential support for the claim that normative information can encourage positive behavior change. Accordingly, Scheibehenne et al. [1] conclude that Bayesian evidence synthesis is a promising meta-analytic approach (p. 1045).
Although we applaud a Bayesian perspective, it is noteworthy that the approach presented by Scheibehenne et al. [1] is not fully Bayesian because it relies almost exclusively on the use of Bayes Factors. Indeed, although Bayes Factors are now advocated widely in psychology in place of p-values and null hypothesis significance testing (NHST), Bayes factors suffer from some of the same fundamental flaws [3], and much like the “old” statistics, they do not reveal useful information about magnitude and uncertainty [4, 5]. Moreover, although simple rules-of-thumb exist (e.g., see [6]), what constitutes reliable evidence in favor of the null hypothesis is largely unclear and ambiguous. Much like the “p < 0.05” rule of thumb, we are hesitant about the dogmatic use of “automatic” Bayes in psychology—i.e., an uncritical mechanistic interpretation of Bayes factors independent of context [7].
In addition to their ambiguity, Bayes factors provide an incoherent framework for evidential support because of their high sensitivity to the prior and because they penalize hypotheses that contain values with low likelihoods [3, 4, 8]. In short, while there are many “Bayesian” approaches, Bayes factors in particular “have no direct foundational meaning to a Bayesian”, as only posterior probabilities have a proper Bayesian interpretation ([8], p. 56). Although the value of Bayesian inference has been noted before (e.g., [9, 10]), the approach remains underappreciated in psychological science. A formal Bayesian estimation approach finds the entire posterior distribution of a parameter given the data, such as the (pooled) proportions of hotel towel reuse in all control and experiment groups. We show that doing so provides a much simpler and more intuitive Bayesian interpretation of the evidence.
Scheibehenne et al. [1] recorded how many participants reused their towel in the control and experiment groups across all seven experiments. The authors subsequently obtained one-sided Bayes factors for a test of equality of proportions. Using the dataset provided by Scheibehenne et al. [1], we proceed directly to the Bayesian evidence synthesis of the combined total. Assuming a uniform prior distribution (between 0 and 1), we obtain posterior probability distributions for both the control and experiment groups using the JAGS procedure in R [11], which uses a Markov Chain Monte Carlo (MCMC) simulation to generate samples from the posterior distribution. Without the need for Bayes factor hypothesis testing, it is evident that the mean and variance of the posterior distributions differ substantially and only marginally overlap in the tails (Figure 1A). For example, mean hotel towel reuse is about 50% in the control group and 56% in the treatment group (the higher spread in the posterior distribution of the control group reflects greater uncertainty). From the simulation, we visualized the posterior distribution of the difference between the experiment and control group proportions in a histogram (Figure 1B), from which it is also clear that the density centers around an average treatment-effect of 6%. The histogram of the differences visualizes the frequency of each parameter value in the distribution. For example, observed differences in the tails, such as 0 or 15% are extremely unlikely. In fact, we generated a mean-centered credibility interval, which has a clear interpretation: there is a 95% probability that the mean difference between the combined experiment and control groups falls between 2.5 and 9.5%, with an average effect-size of 6%.
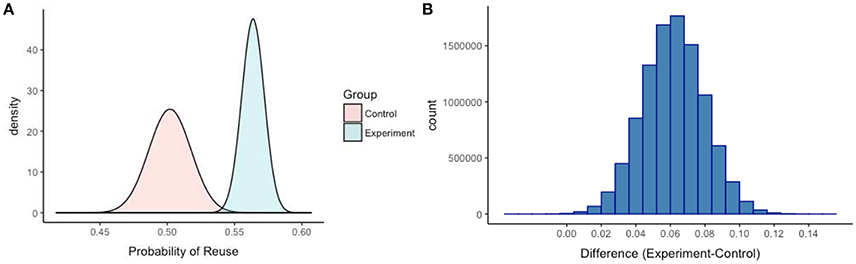
Figure 1. The posterior probability distributions of the combined control and experiment groups are displayed in (A) based on 10 million samples (hotel towel reuse in proportions). (B) Visualizes the posterior distribution of the difference between the control and experiment proportions.
The social norm data serve as a nice illustrative example because the Bayes Factor and Inference procedures happen to converge on a similar result. However, it would be naïve to think that because the two approaches provide a similar conclusion, it matters little what approach researchers use for synthesizing evidence in a Bayesian fashion (see [4] for a similar warning). Accordingly, we provide a free online “Fully Bayesian Evidence Synthesis” application that allows scholars to implement the proposed estimation approach and download the density distributions and simulated data. In sum, while Scheibehenne et al. [1] conclude that the data are “37 times more likely under the alternative than the null hypothesis” (p. 1045), we argue that estimating the full posterior probability distributions of the control and experiment groups (and their differences) is much more intuitive and revealing. For example, it provides more useful information about the parameters (i.e., magnitude and uncertainty) and speaks better to meta-analytic thinking than point estimates. We acknowledge that alternative priors, random rather than fixed-effects pooling, and hierarchical multi-level models could also be explored in this context. In fact, just as social norms can be leveraged to promote sustainability, we hope to change social norms around Bayesian data analysis in psychological science above and beyond the use of Bayes Factors.
Open Practices
All data and materials have been made publicly available via the Open Science Framework and can be accessed at: https://osf.io/vceab/. The Fully Bayesian Evidence Synthesis application is available online at: https://bre-chryst.shinyapps.io/BayesApp/
Author Contributions
All authors contributed equally and approved the final version of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Benjamin Scheibehenne, Sir David Spiegelhalter, and Francis Tuerlinckx for their useful feedback and comments on earlier versions of this manuscript.
References
1. Scheibehenne B, Jamil T, Wagenmakers EJ. Bayesian evidence synthesis can reconcile seemingly inconsistent results: The case of hotel towel reuse. Psychol Sci. (2016) 27:1043–6. doi: 10.1177/0956797616644081
2. Goldstein NJ, Cialdini RB, Griskevicius V. A room with a viewpoint: using social norms to motivate environmental conservation in hotels. J Consum Res. (2008) 35:472–82. doi: 10.1086/586910
3. Lavine M, Schervish MJ. Bayes factors: What they are and what they are not. Am Statist. (1999) 53:119–22. doi: 10.1080/00031305.1999.10474443
4. Kruschke JK, Liddell TM. The Bayesian new statistics: Hypothesis testing, estimation, meta-analysis, and planning from a Bayesian perspective. Psychon Bull Rev. (2017). doi: 10.3758/s13423-016-1221-4. [Epub ahead of print].
7. Gigerenzer G, Marewski JN. Surrogate science: The idol of a universal method for scientific inference. J Manag. (2015) 41:421–40. doi: 10.1177/0149206314547522
8. Bernardo JM. Integrated objective Bayesian estimation and hypothesis testing. In: J. Bernardo M, Bayarri MJ, Berger JO, editors. Bayesian Statistics 9 Oxford, UK: Oxford University Press (2011). p. 1–68.
9. Higgins J, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. J R Stat Soc Ser A (2009) 172:137–59. doi: 10.1111/j.1467-985X.2008.00552.x
11. Plummer M. Rjags: Bayesian Graphical Models using MCMC. R package version 4-6. (2016). Available online at: http://mcmc-jags.sourceforge.net/
Keywords: reproducibility, Bayesian evidence synthesis, social norms, meta-analysis
Citation: van der Linden S and Chryst B (2017) No Need for Bayes Factors: A Fully Bayesian Evidence Synthesis. Front. Appl. Math. Stat. 3:12. doi: 10.3389/fams.2017.00012
Received: 17 April 2017; Accepted: 12 June 2017;
Published: 28 June 2017.
Edited by:
Martin Lages, University of Glasgow, United KingdomReviewed by:
Francis Tuerlinckx, KU Leuven, BelgiumCopyright © 2017 van der Linden and Chryst. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sander van der Linden, c2FuZGVyLnZhbmRlcmxpbmRlbkBwc3ljaG9sLmNhbS5hYy51aw==
 Sander van der Linden
Sander van der Linden Breanne Chryst2
Breanne Chryst2