- 1Department of Mathematical Sciences, Ball State University, Muncie, IN, United States
- 2Department of Mathematics, Central Michigan University, Mount Pleasant, MI, United States
Let ℍ be a separable Hilbert space, let G ⊂ ℍ, and let A be an operator on ℍ. Under appropriate conditions on A and G, it is known that the set of iterations is a frame for ℍ. We call FG(A) a dynamical frame for ℍ, and explore further its properties; in particular, we show that the canonical dual frame of FG(A) also has an iterative set structure. We explore the relations between the operator A, the set G and the number of iterations L which ensure that the system FG(A) is a scalable frame. We give a general statement on frame scalability, and study in detail the case when A is a normal operator, utilizing the unitary diagonalization. In addition, we answer the question of when FG(A) is a scalable frame in several special cases involving block-diagonal and companion operators.
1. Introduction
The problem of generating frames by iterative actions of operators [1–3] has emerged within the research related to the dynamical sampling problem [1, 3–6]. The conditions under which a frame generated by iterative actions of operators exists for a finite-dimensional or a separable Hilbert space have been stated in Aldroubi et al. [1, 3]. If we have a frame, then a linear combination of a dual frame with the dynamically sampled coefficients reproduce the original signal. The natural follow-up questions to ask in this setup are: whether we can obtain a scalable [7–13] frame under iterative actions, and if not, whether we can find a dual frame which preserves the dynamical structure.
Let A be an operator on a separable Hilbert space ℍ. We consider a countable set of vectors G in ℍ, and a function L:G → ℕ0, where ℕ0 = ℕ∪{0}. Related to the iterated system of vectors
we answer the following two questions:
(Q1) For which matrices A, which sets G, and which limits of iterations L is system (Equation 1) a scalable frame for ℍ?
(Q2) Assuming that system (Equation 1) is a frame for ℍ, can we obtain a dual frame for Equation (1), perhaps by iterative actions of some operator?
The motivation for studying systems of type (Equation 1) comes from the dynamical sampling problem (DSP): Let the initial state of a dynamical system be represented by an unknown element f ∈ ℍ. Say the initial state f is evolving under the action of an operator A* to the states , where f0 = f and . Given a set of vectors G ⊂ ℍ, one can find conditions on A, G and L = L(g) which allow the recovery of the initial state f from the set of samples . In short, the problem of signal recovery via dynamical sampling is solvable if the set of vectors (Equation 1) is a frame for ℍ, [1, 3]. In frame theory it is known that every frame has at least one dual frame; if is a frame for ℍ, and its dual frame elements are hg, j, then all f ∈ ℍ are reconstructed as
2. Preliminaries
Throughout this paper ℍ denotes a separable Hilbert space. Given an index set I, a sequence F = {fi}i∈I of nonzero elements of ℍ is a frame for ℍ, if there exist 0 < A ≤ B < ∞ such that
In finite dimensions, we find it useful to express frames as matrices, so we abuse the notation of F as follows: when dim ℍ = n, a frame F = {fi}i∈I for ℍ is often represented by a n × k matrix F, whose column vectors are fi, 1 ≤ i ≤ k (k ≥ n). The frame operator S = FF* is then positive, self-adjoint and invertible.
For each frame F there exists at least one dual frame G = {gi}i∈I, satisfying
The matrix equation FG* = GF* = I is an equivalent expression to the frame representation (Equation 4). The set is called the canonical dual frame.
Finding a dual frame can be computationally challenging; thus it is of interest to work with tight or scalable frames. We say that a frame is A-tight if A = B in Equation (3). When A = 1, we call F a Parseval frame. If a frame F = {fi}i∈I is not tight, but we can find scaling coefficients wi ≥ 0, i ∈ I, such that the scaled frame Fw = {wifi}i∈I is tight, then we call the original frame F a scalable frame. We note that the notion of scalability of a frame is defined for a unit-norm frame in [10], but in this manuscript we do not require a scalable frame to be unit-norm. If the scaling coefficients wi are positive for all i ∈ I, then we call the original frame F a strictly scalable frame.
Let I denote a finite or countable index set, let G = {fs}s ∈ I ⊂ ℍ and let A:ℍ → ℍ be a bounded operator. We call the collection
a dynamical system, where Ls ≥ 0 (Ls may go to ∞) and L = (Ls)s∈I is a sequence of iterations related to the set G. The operator A, involved in generating the set Equation (5), is referred to as a dynamical operator. If A is fixed, then we use the notation , and if G = {f} and L = {L}, then we label (Equation 5) by .
Note that in Aldroubi et al. [1], fs are chosen to be the standard basis vectors, while in this manuscript, we allow the use of any nonzero vector fs ∈ ℍ. If Equation (5) is a frame for ℍ, then we call a dynamical frame, generated by a dynamical operator A, set G and sequence of iterations L.
3. New Results on Dynamical Frames
Theorem 1. Let G = {fs}s∈I ⊂ ℍ, where I is a countable index set, and assume that is a frame for ℍ, with frame operator S. The canonical dual frame of is the dynamical frame , generated by operator B = S−1AS, , and sequence of iterations L.
In addition, every f ∈ ℍ can be reconstructed from the dynamical samples via the frame reconstruction formula
Proof: Let be a frame for ℍ, where G = {fs}s∈I ⊂ ℍ and I is countable, and assume that S is the frame operator for . Then S is an invertible operator, and for any we have that is a canonical dual frame element, where s ∈ I, 0 ≤ j ≤ Ls. If we choose
then for all j ≥ 0 we have
□
Theorem 2. Let ℍ1 and ℍ2 be two separable Hilbert spaces. Let A be a bounded operator on ℍ1 and let B:ℍ1 → ℍ2 be an invertible operator. Let I be a countable index set, and fix G = {fs}s∈I ⊂ ℍ1. Set gs = Bfs ∈ ℍ2, s ∈ I, and C: = BAB−1. For any set of iterations L = (Ls)s∈I, Ls ≥ 0, TFAE:
(i) The set is a frame for ℍ1,
(ii) The set is a frame for ℍ2.
Proof: Let gs = Bfs ∈ ℍ2, s ∈ I, and set C = BAB−1. Note that Cj = BAjB−1, due to B−1B = I. For any , we have
The operator B is invertible, thus BF is a frame if and only if F is a frame, so (i) and (ii) are equivalent.□
If the operator B occurring in Theorem 2 is unitary and ℍ1 = ℍ2, then the property of scalability is preserved. We have:
Corollary 1. Let fs ∈ ℍ, and set for all s ∈ I, where I is a countable index set. Let A, R be two operators on a separable Hilbert space ℍ, and let U be a unitary operator on ℍ. If A = URU*, then TFAE:
(i) is a scalable frame for ℍ,
(ii) is a scalable frame for ℍ.
In the next section, we exploit the simplicity of the unitary diagonalization of normal operators to give more explicit conditions on the normal operator A in order to ensure scalability of a frame of type .
3.1. Normal Operators
Let A be a bounded operator on a separable Hilbert space ℍ, and assume there exists a unitary operator U, and a diagonal operator D such that A = UDU*. Let and set , s ∈ I, where I is countable. Since Aj = UDjU*, it follows that for each j ∈ ℕ0 we have
By Corollary 1, is a scalable frame for ℍ if and only if is a scalable frame for ℍ.
By the spectral theorem, a compact self-adjoint operator on a Hilbert space can be unitarily diagonalized. Thus, we can deliver a more precise statement on dynamical frames scalability when a normal operator is involved; we note that the following result in the finite dimensional case can be generalized when working in a separable Hilbert space with a countable orthonormal basis:
Theorem 3. Let A = UDU* be a normal n × n matrix, where U is unitary, and D is diagonal, with diagonal entries a1, …, an ∈ ℂ. Let fs ∈ ℍ, and set , 1 ≤ s ≤ p.
The set is a scalable frame of ℍ if and only if there exists a positive solution ws,0, ws, 1, …, ws,Ls, 1 ≤ s ≤ p to the system of equations
for all i, j = 1, …, n, i ≠ j.
Proof: Let D be the unitary diagonalization of A, with diagonal entries a1, …, an ∈ ℂ, and let , s ∈ {1, ⋯ , p}, p ≥ 1.
The set is a scalable frame for ℍ if and only if there exist scaling coefficients ws,0, ws, 1, …, ws,Ls, 1 ≤ s ≤ p, which satisfy for all f ∈ ℍ. Restating the last equality in matrix product form illuminates the fact that need to be the positive solutions to the weighted system of Equation (11).
By Corollary 1 the conclusion of the theorem holds true for a finite dimensional Hilbert space ℍ.
□
Theorem 4. If n ≥ 3, then a normal operator on ℝn can not generate a strictly scalable dynamical frame from a single vector in ℝn.
Proof: The Equation (11) implies that for the first three , we always have the relation a1a2, a1a3, and a2a3 are all negative numbers assuming wi ≠ 0, i = 1, 2, 3, which is not possible. Thus any diagonal operator for ℝn can not generate a strictly scalable frame from a single vector in ℝn.
Although a normal operator on ℝn can not generate a strictly scalable dynamical frame from a single vector, there do exist normal operators on ℂn which generate scalable dynamical frames, for example harmonic tight frames.
The problem of finding specific conditions under which the set in item (ii) in Corollary 1 is a scalable frame for ℍ is still open for operators which do not possess a unitary diagonalization. For this reason, we further study several operators with special structures, such as block-diagonal operators (section 4) and companion operators (section 5).
4. Block-Diagonal Operators
In this section, we explore the case when the operator A is of block-diagonal form. Block-diagonal operators give us a chance to offer a partial answer to (Q1) in the case when we don't have a unitary diagonalization.
Let As:ℍs → ℍs be an operator on ℍs, with dim ℍs = ns, 1 ≤ s ≤ p. Let A:ℍ → ℍ be a block-diagonal operator on , constructed as follows:
Let v ∈ ℍs for some 1 ≤ s ≤ p. If ℍ is the direct sum of a family (ℍs)s of Hilbert space, for each index s there exists a canonical inclusion is of ℍs into H. We say that v is well-embeded in f ∈ ℍ with respect to operator (Equation 12) if f = is(v).
Theorem 5. Let As:ℍs → ℍs be an operator on ℍs, with dim ℍs = ns, 1 ≤ s ≤ p. Let A:ℍ → ℍ be a block-diagonal operator on , constructed as in Equation (12). Let vs,1…, vs,ms ∈ ℍs, 1 ≤ s ≤ p be well-embedded in fs,1, …, fs,ms ∈ ℍ, 1 ≤ s ≤ p.
is a (scalable) frame of ℍ if and only if are (scalable) frames of ℍs for all 1 ≤ s ≤ p.
Proof: We assume that all ms = 1, i.e., fs,k = fs, vs,k = vs, and Ls,k = Ls, 1 ≤ s ≤ p, to simplify the presentation of the proof. The matrix representation of with scaling coefficients ws, j, 0 ≤ j ≤ Ls for each s = 1, …, p is of block-diagonal form:
If F is a tight frame, then row vectors of F are orthogonal and have the same norm and so does for each s = 1, …, p. This implies that the system is a scalable frame for ℍs for all 1 ≤ s ≤ p.
Now, suppose that for each 1 ≤ s ≤ p, the system is a scalable frame for ℍs. Then, there exist some scaling coefficients ws, j, 1 ≤ s ≤ p, 0 ≤ j ≤ Ls, such that is a Parseval frame for each s = 1, …p.□
Block operators we can employ in Theorem 5 include:
Example 1. Let a, b, c, d be real numbers.
(a) The operator in ℝ2 generates a tight frame if a ≠ −d,
(b) The operator in ℝ2 generates a tight frame if a > 0 and .
(c) The operator generates a strictly scalable frame if a + b2 < 0.
(d) The operator generates a strictly scalable frame if a > 0 and .
The conditions for Example 1(b) are obtained from the following proposition:
Proposition 1. Let a, b, c, d be real numbers such that a > 0 and abcd ≠ 0. Then the following two statements are equivalent:
(1) .
(2) The system
is a strictly scalable frame for ℝ2.
Proof. We first note that the condition is equivalent to () or ().
(1) ⇒ (2): The conditions imply that
and the conditions imply that
Then
are positive numbers and
is a Parseval frame for ℝ2.
(1) ⇐ (2): If the system F is strictly scalable, then the normalized system
is a unit-norm scalable frame. The Gramian matrix of diagram vectors of F′ has positive scalings in its null space:
Inequality (Equation 15) implies that . Next we show that .
In case b > 0, inequality (Equation 14) implies that
If (c > 0 and ac + bd ≥ 0) or (c < 0 and ac + bd ≤ 0), then a2cd + abd2 > 0, which implies . If c > 0 and ac + bd < 0, then ac < −bd, which implies since ac > 0. Similarly, if c < 0 and ac + bd > 0, then ac > −bd, which implies since ac < 0. This is equivalent to .
In case b < 0, suppose that . Multiply both sides by the positive number −abd2. On one hand we have a2cd ≥ −abd2 and on the other hand, from inequality (14), we have a2cd − abc2 < −abd2 + b2cd. Since a2cd ≥ −abd2, we have −abd2 − abc2 < −abd2 + b2cd, which implies . This contradicts our assumption□
Proposition 2. Let i, j, k, l ∈ ℕ be such that p < k ≤ n, q < l ≤ n, and let N ∈ ℕ. For each m = 1, …, N, we define as
If for each m = 1, …, N, am, bm, cm and dm satisfy the conditions of Proposition 1, and the system
spans ℝn, then Equation (16) is a strictly scalable frame for ℝn.
4.1. Generalization
The problem of generating a frame by iterative actions of a block-diagonal operator (Equation 12) is equivalent to the problem of generating a frame by iterative actions of multiple operators. So, we pose the question: Given operators As, s ∈ ℕ, on a separable Hilbert space ℍ, and fixed vectors v ∈ G ⊂ ℍ, when is the collection {Asv|s ∈ ℕ, v ∈ G} a (scalable) frame for ℍ?
Such frames would naturally arise in applications; for instance, let f ∈ ℍ be the initial state of a physical system that evolves through time, and let the sequence of bounded operators describe the evolution of that physical system i.e., is the sth state of the system at time ts. Assume there are several fixed sampling locations v ∈ G ⊆ ℍ, where samples of the evolved state are taken:
Clearly, f can be recovered from the set of samples if and only if {Asv|v ∈ G, s ∈ ℕ} is a frame for ℍ. Note that this type of a frame is a generalization of frames of iterative actions of operators, when one or more operators are involved.
For a frame generated by actions of a sequence of operators, we find that its canonical dual frame has similar structure:
Theorem 6. Let As, s ∈ I be a sequence of operators on a separable Hilbert space ℍ, and let G ⊂ ℍ. Suppose F(As, I): = {Asv|s ∈ I, v ∈ G} is a frame for ℍ, with frame operator S. Then its canonical dual frame is
Proof: If S denotes the frame operator of the frame F(As, I) for ℍ, then its canonical dual frame elements are , v ∈ G.
Since SS−1 is the identity operator, and , we obtain that the dual frame elements are
□
5. Companion Operators and Generalizations
Let a1, …, an ∈ ℝ which are not all zeros; then
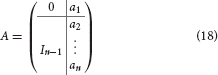
is called a companion operator [14].
Proposition 3. Let the dynamical operator A be a companion operator (18) in ℝn, then we have
(1)
(2) for any orthogonal matrix U, the operator UAU−1 generates an orthonormal basis U.
It is known that the standard orthonormal basis B can not be extended to a scalable frame by adding one vector f ∈ ℍ\B, [8, 11]. Thus, we explore when one can generate a dynamical frame by adding two vectors. Although a companion operator A does not generate a scalable frame , it can generate a scalable frame under certain conditions. Using the companion operator A, we have
where
Proposition 4. [11] Let {e1, …en} be the standard orthonormal basis in ℝn with n ≥ 2. Let f and g be two unit-norm vectors in ℝn.
If either system {e1, …en, f, g} or {e1, …en−1, f, g} is scalable, then f and g have only two nonzero elements in the same entries.
We now assume that is scalable. Then by Proposition 4, am = 0 implies that am−1 = 0 for m ≥ 2. This implies that a1 = … = an−2 = 0. A consequence of this is the following result.
Proposition 5. Let a and b be real numbers such that a > 0 and . Then the companion operator A in ℝn,
generates a strictly scalable frame .
Proof: We have
which is strictly scalable.□
We note that the operator A in Equation (20) is not diagonalizable.
Example 2. Let a and b be real numbers such that and a > 0. Then the operator
generates a strictly scalable frame for ℝn.
Proof: We have
The strict scalability follows by Example 1.□
Example 3. Let 2 sin2(ϕ) − 1 > 0 and let
The set
is a strictly scalable frame of ℝn.
6. Concluding Remarks
We have studied the scalability of dynamical frames in a separable Hilbert space ℍ. Given an operator A on ℍ and a (at most countable) set G ⊂ ℍ, we have explored the relations between A, G and the number of iterations that make the system (1) a scalable frame. In section 3.1 we have fully answered question (Q1) in finite dimensions, when working with a normal operator. We have also studied operators with specialized structures, such as block-diagonal operators (section 4), and companion operators (section 5), which are not necessarily normal; for instance, note that the block-diagonal matrix A in Theorem 5 cannot be normal if one of its blocks is not normal.
In adition, we have established the canonical dual frame for frames of type FG(A); in particular, we showed that the canonical dual frame has, as anticipated, an iterative set structure; in section 4.1, we had generalized the notion of dynamical frames to the notion of frames generated by sequences of operators, and verified that the canonical dual frame result is generalized as well (Theorem 6); this type of result holds true in any separable Hilbert space ℍ.
Author Contributions
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
YK was supported by the Central Michigan University FRCE Research Type A Grant #C48143. RA was supported by the Ball State University Aspire Research Award #I601-16.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest
Acknowledgments
We express our gratitude to Professor S. Narayan for many helpful conversations on this work.
References
1. Aldroubi A, Cabrelli C, Molter U, Tang S. Dynamical sampling. Appl Comput Harmonic Anal. (2017) 42:378–401. doi: 10.1016/j.acha.2015.08.014
2. Aldroubi A, Petrosyan A. Dynamical sampling and systems from iterative actions of operators. In: Pesenson I, Le Gia Q, Mayeli A, Mhaskar H, Zhou DX, editors. Frames and Other Bases in Abstract and Function Spaces: Novel Methods in Harmonic Analysis, Cham: Springer Int. Publishing (2017). pp. 15–26. doi: 10.1007/978-3-319-55550-8_2
3. Aldroubi A, Cabrelli C, Cakmak AF, Molter U, Petrosyan A. Iterative actions of normal operators. J Funct Anal. (2017) 272: 1121–46. doi: 10.1016/j.jfa.2016.10.027
4. Tang S. System identification in dynamical sampling. Adv Comput Math. (2017) 43: 555–80. doi: 10.1007/s10444-016-9497-5
5. Aldroubi A, Davis J, Krishtal, I. Exact reconstruction of signals in evolutionary systems via spatiotemporal trade-off. J Fourier Anal Appl. (2015) 21:11–31. doi: 10.1007/s00041-014-9359-9
6. Aldroubi A, Davis J, Krishtal I. Dynamical sampling: time space trade-Off. Appl Comput Harmon Anal. (2013) 34:495–503. doi: 10.1016/j.acha.2012.09.002
7. Cahill J, Chen X. A note on scalable frames. In: Proceedings of the 10th International Conference on Sampling Theory and Applications, Bremen (2013). p. 93–96.
8. Kutyniok G, Okoudjou K, Philipp F. Scalable frames and convex geometry. Contemp Math. (2013) 626:19–32. doi: 10.1090/conm/626/12507
9. Kutyniok G, Okoudjou KA, Philipp F, Tuley EK. Scalable frames. Linear Algebra Appl. (2013) 438:2225–38. doi: 10.1016/j.laa.2012.10.046
10. Copenhaver M, Kim Y, Logan C, Mayfield K, Narayan SK, Petro MJ, Sheperd J. Diagram vectors and tight frame scaling in finite dimensions. Oper Matrices (2014) 8:78–88. doi: 10.7153/oam-08-02
11. Domagalski R, Kim Y, Narayan SK. On minimal scalings of scalable frames. In: Proceedings of the 11th International Conference on Sampling Theory and Applications, Washington, DC (2015). p. 91–95. doi: 10.1109/SAMPTA.2015.7148857
12. Chen X, Kutyniok G, Okoudjou KA, Philipp F, Wang R. Measures of scalability. IEEE Trans Inf Theory (2015) 61:4410–23. doi: 10.1109/TIT.2015.2441071
13. Benedetto JJ, Fickus M. Finite normalized tight frames. Adv Comput Math. (2003) 18:357–85. doi: 10.1023/A:1021323312367
Keywords: dynamical sampling, frames, scalable frames, iterative actions of operators
Citation: Aceska R and Kim YH (2017) Scalability of Frames Generated by Dynamical Operators. Front. Appl. Math. Stat. 3:22. doi: 10.3389/fams.2017.00022
Received: 31 August 2017; Accepted: 24 October 2017;
Published: 07 November 2017.
Edited by:
Qiyu Sun, University of Central Florida, United StatesReviewed by:
Bei Liu, Tianjin University of Science and Technology, ChinaErnesto De Vito, Università di Genova, Italy
Copyright © 2017 Aceska and Kim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roza Aceska, cmFjZXNrYUBic3UuZWR1
 Roza Aceska
Roza Aceska Yeon H. Kim
Yeon H. Kim