Synchronization, Oscillator Death, and Frequency Modulation in a Class of Biologically Inspired Coupled Oscillators

1. Introduction

The study of circadian rhythms has been a subject of great interest for a long time. The majority of the first studies were mainly based on observations in plants [1–4]. The study of circadian rhythms from a mathematical perspective reached a milestone with the work of Kalmus and Wigglesworth, a biologist and a mathematician, respectively, who associated of circadian rhythms to the existence of a limit cycle, using a hydraulic system as analogy. Kalmus and Wigglesworth presented their work entitled "Shock excited system as models for biological rhythms" along with several mathematical models of circadian rhythms at a Symposium on Biological Rhythms carried out at Cold Spring Harbor in the United States of America in 1960 [5–7]. Lots of other important works on circadian rhythms were presented in this symposium, but the work of Kalmus and Wigglesworth was key in establishing a better mathematical formalism for the study of circadian rhythms. Although many researchers followed the theoretical path proposed by Kalmus and Wigglesworth, the mathematical study of circadian rhythms was finally established by Arthur Winfree (biologist and mathematician), who introduced topology for the description of several aspects of circadian rhythms. An excellent summary of many of the earlier works can be found in Arthur Winfree's master book entitled “The Geometry of Biological Time” [8]. The number of studies about biological rhythms at large has increased greatly in the last two decades, in part due to new technological advances. Particularly related to circadian rhythms, there is now evidence that there is rhythmic patterns of activity at the molecular [9, 10], cellular [11, 12], tissue [13, 14], and systems levels [15–17], and that circadian regulation is involved in jointly regulating activity in all those different levels of biological organization [18–20], and also, taking into account interactions with the environment [21] and perturbations induced by behavior [22, 23].

Mathematical modeling and experimental characterizations of different properties of circadian rhythms have been combined to produce explanations and hypotheses about the rhythmicity in biological phenomena [24–28]. Of particular interest, the ontogeny of circadian rhythm in the crayfish has been studied by Lara-Aparicio et al. [29] combining theoretical and experimental perspectives, building phenomenological mathematical models that capture a series of experimental results involving the synchronization of electro-retinogram activity in crayfish [30–32]. These models couple two van der Pol oscillators [33] represented by state vectors, and include parameters representing the frequency of the oscillators, the radii of the limit cycles, and the first coordinate of the center of the limit cycle. The system is setup such that one oscillator is driving the behavior of the other oscillator, but not vice-versa. One of the main findings with this model is that the driving oscillator induces an Andronov-Hopf bifurcation in the driven oscillator and regulates its frequency.

The model by Aparicio et al. simulates, explains, and has suggested new biological experiments, it is simple enough to allow analytical approaches, and it has provided useful insights about questions referring to the ontogeny of the circadian rhythm in crayfish from the childhood to adult stages. For instance, a hypothesis about the existence of a hormone, which was experimentally detected, was generated from the model. The model also allowed Lara-Aparicio et al. to study synchronization of circadian rhythms with external signals like day and night light cycle [34]. By studying basic principles underlying the generation of oscillations in coupled non-linear systems, these researchers were able to conjecture that circadian rhythms can result from coupling systems of cells, each one oscillating with an ultradian oscillation [35–37]. Synchronization among cells emerges naturally as a motivating theme that has been studied through systems of non-linear Equations [38] representing n oscillators with the classical van der Pol non-linear damping for the terms responsible for the oscillatory dynamics.

In the present paper, we extend the work in Lara-Aparicio et al. [29] and Barriga-Montoya et al. [38] by analyzing two qualitative mathematical models, each capturing a different level of organization in the ontogeny of circadian rhythms. Inspired by gap junction coupling between neurons, or similarly, by chemical coupling in self oscillating networks, we study the bifurcation structure in a deterministic model assuming that the coupling between the oscillators is diffusive. The resulting dynamics resemble neuronal activity at the cellular level. Then, using graph theoretical methods and center manifold theory, we show that synchronous oscillations appear via a Hopf bifurcation in a population of pacemaker oscillators. In this case, the bifurcation parameter is thought of as a representative of the developmental stage of the neurons. We further explore the phenomenon of oscillator death: although the single neurons are endogenously oscillating for sufficiently large values of the bifurcation parameter, the population oscillation dies for sufficiently large coupling, which suggests that the weak coupling hypothesis must be satisfied for robust synchronous oscillations to occur. In the case of all-to-all coupling, we provide necessary conditions for oscillator death to occur and leave the derivation of sufficient conditions to a future report.

Frequency modulation is also an important phenomenon that can be studied with these models. In consideration of the results from the first analysis, we shift our focus to the frequency modulations that emerge as a result of the interconnection of various circadian pacemaker populations. In doing so, we estimate the synchronization frequency as a function of the intrinsic frequencies of the oscillators, their coupling strength, and the topology of the network. To do so, we construct a second model that can be thought of as a stochastic, larger-scale extension of the first model we present. In this case, each population is assumed to be an endogenous oscillator and the coupling is assumed to be linear. Using linear stochastic analysis and under the assumption that the population oscillations are synchronized, we derive a scalar Fokker-Plank equation. The model captures an important feature of circadian rhythm ontogeny: the emergence of low frequency (circadian) oscillations from coupled high frequency (ultradian) oscillators [35–38]. Future work will aim at deriving conditions on the intrinsic frequencies, the coupling strength, and the network topology, that ensure synchronization of the population oscillations.

It is worth noticing that, although the motivation for the present paper is centered around circadian rhythms, the model captures more general phenomena. Our findings include that in diffusively coupled cells resting node dynamics imply global asymptotic stability, oscillating node dynamics imply global synchronization for small coupling, and multistability between oscillator death and global synchronization for large coupling. In stochastic, linearly coupled populations, we describe the dynamical mechanisms through which coupling modulates the frequency of the synchronous oscillation. To the author's knowledge, both phenomena are new from a non-linear collective phenomena perspective. Among other reasons, it is surprising that passive coupling like diffusive coupling could kill an oscillation and create multistability. Similarly, we are not aware of any work providing mechanistic explanations on how coupling can tune a global oscillation frequency.

The paper is organized as follows. In section 2, we present and analyze the model of diffusively coupled oscillators. Two theorems are proved about global asymptotic stability for resting cells and global synchronization for oscillating cells and weak coupling. We then derive sufficient conditions for diffusive coupling-induced oscillator death. In section 3 we present and analyze the model of linearly coupled oscillators. In particular, we derive an explicit formula for the emergent synchronization frequency as a function of the coupling topology and oscillator natural frequencies. Finally we discuss the presented results in section 4.

2. Global Synchronization and Oscillator Death in Diffusively Coupled Oscillators

We regard a network of N coupled oscillators as a directed graph ${G}$ with N vertices, with a network topology codified by a matrix $A={\left[a_{ij}\right]}_{i,j=1}^N$, where a_ij ≥ 0 represent connection weights. If oscillator i receives signals from oscillator j, then the graphical representation of ${G}$ has an arrow from j to i, and a_ij > 0. If a_ij > 0, the signal received by oscillator i from oscillator j is a_ij(x_j − x_i). Assume that the dynamics for each oscillator satisfies the following coupled oscillator dynamics

$\begin{array}{rcll}{ẋ}_i& =& y_i+\mu {\displaystyle \sum _{j=1}^N}{a}_{ij}(x_j-x_i)& (\mathrm{1a})\end{array}$

$\begin{array}{rcll}{ẏ}_i& =& (\lambda -x_i^2-\frac{y_i^2}{{\omega }^2})y_i-{\omega }_i^2{x}_i& (\mathrm{1b})\end{array}$

where μ is the global coupling strength, which uniformly scales the coupling weights a_ij.

In the absence of coupling the oscillator dynamics reduces to the modified van der Pol equation

$\begin{array}{l}{ẍ}_i=(\lambda -x_i^2-\frac{y_i^2}{{\omega }^2})\stackrel{·}{x_i}-{\omega }_i^{2}x.\end{array}$

These equations define a simple dynamical system that can transition between global asymptotic stability and almost global convergence to a hyperbolic limit cycle through variations of the control parameter λ∈ℝ, providing a simple model for various biological systems that exhibit the same transition, in particular neurons and molecular oscillators. For λ < 0 the non-linear dissipation coefficient $-(\lambda -x^2-\frac{y^2}{{\omega }_i^2})$ is always positive, which leads to damped oscillations. For λ > 0 the dissipation coefficient becomes negative close to the origin, which leads to sustained oscillations through a Hopf bifurcation. A generic trajectory belonging to the family of periodic orbits born at the Hopf bifurcation has the form

$\begin{array}{rc}\sqrt{\lambda }(cos({\omega }_{i}t+{\theta }_0),sin({\omega }_{i}t+{\theta }_0)),& (2)\end{array}$

where the θ₀ is the initial phase.

In the presence of coupling, Equations (1a) represent a generic network of diffusively coupled non-linear oscillators. As mentioned earlier, the diffusive form of the coupling can be thought of as gap junction coupling in a neuronal population, or diffusive coupling between non-linear molecular oscillators. In both interpretations, the graph topology is necessarily undirected, that is, a_ij = a_ji. However, the mathematical results presented in this section hold under more general assumptions and we present them in the general form.

2.1. Global Synchronization

We start by recalling some basic graph-theoretical definitions and facts. The graph ${G}$ is said to be strongly connected if for each pair of nodes in ${G}$, there exists a directed path between them. ${G}$ is balanced if $\sum _{j=1}^N{a}_{ij}=\sum _{j=1}^N{a}_{ji}$ for all i.

The Laplacian matrix L = [L_ij:i, j = 1, …, n] for the graph ${G}$ is such that L_ij = −a_ij if i≠j, and $L_{ii}=\sum _{j=1}^N{a}_{ij}$. Note that the vector of ones is always a right null eigenvector of L and zero is always an eigenvalue of L (L1_N = 0). It can be shown that a graph is strongly connected if and only if zero is a simple eigenvalue of the Laplacian matrix [39]. Obviously, symmetric graphs (i.e., satisfying a_ij = a_ji) are balanced, but the converse is not true. Consider, for instance, a directed ring.

The global behavior of the system (1a) for λ < 0 and μ ≥ 0, for a network with connectivity represented by a generic balanced graph is characterized by the next theorem (Figure 1).

FIGURE 1

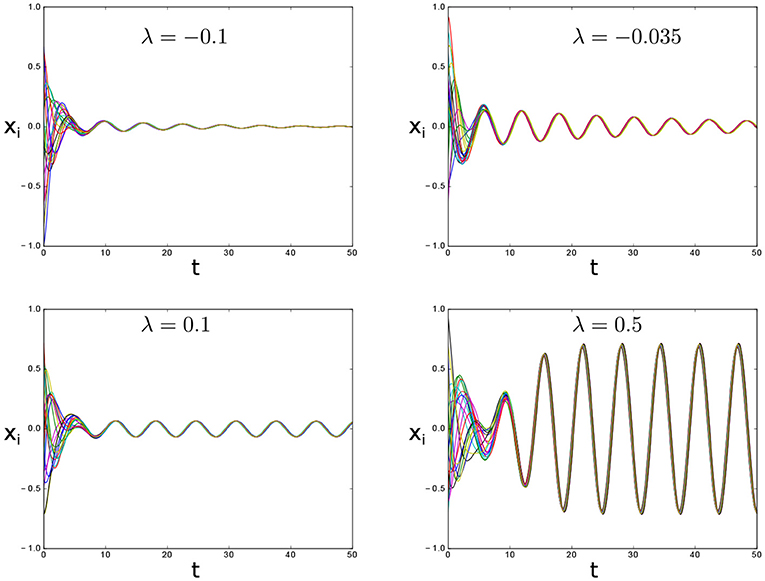
Figure 1. Transition between global asymptotic stability and synchronous oscillation via Hopf bifurcation in system (1a) for μ = 0.05, N = 20, natural frequencies uniformly distributed in the interval [0.9, 1.1] and varying λ. The interconnection topology is all-to-all.

Theorem 2.1. Assume that the graph ${G}$ is balanced and that ω_i = ω_j = ω for all i, j = 1, …, N. If λ < 0, then the origin is globally asymptotically stable and locally exponentially stable for all μ ≥ 0.

Proof. We consider the quadratic Lyapunov function

$V(x,y)={\displaystyle \sum _{i=1}^N}(x_i^2+y_i^2/{\omega }^2).$

The derivative of V along the trajectories of the system (1a) gives

$\begin{array}{rc}\stackrel{·}{V}={\displaystyle \sum _{i=1}^N}(2x_i{ẋ}_i+2y_i{ẏ}_i/{\omega }^2)& (3)\end{array}$

which after substitution of the derivatives ẋ_i and ẏ_i, can be bounded from above as follows

$\begin{array}{l}={\displaystyle \sum _{i=1}^N(2x_i{y}_i-2y_i\frac{{\omega }^2{x}_i}{{\omega }^2}+2\frac{y_i}{{\omega }^2}\left(\lambda -x_i^2-\frac{y_i^2}{{\omega }^2}\right)y_i}\\ -2\mu x_i{\displaystyle \sum _{j=1}^N{a}_{ij}}(x_i-x_j))\\ \le 2\frac{\lambda }{{\omega }^2}{\displaystyle \sum _{i=1}^N{y}_i^2}-2\mu {\displaystyle \sum _{i,j=1}^N{x}_i}{a}_{ij}(x_i-x_j)\\ =2\frac{\lambda }{{\omega }^2}{\displaystyle \sum _{i=1}^N{y}_i^2}-2\mu {\displaystyle \sum _{i,j=1}^N{a}_{ij}}(x_i^2-x_j{x}_i)\\ =2\frac{\lambda }{{\omega }^2}{\displaystyle \sum _{i=1}^N{y}_i^2}-2\mu {\displaystyle \sum _{i,j=1}^N{a}_{ij}}(x_i^2/2-x_j{x}_i+x_i^2/2)\end{array}$

To show that the last term is negative definite, we use the balanced interconnection hypothesis. Let $d_j=\sum _{i=1}^N{a}_{ij}=\sum _{i=1}^N{a}_{ji}$. Then,

${\displaystyle \sum _{i,j=1}^N}{a}_{ij}{x}_j={\displaystyle \sum _{j=1}^N}{d}_j{x}_j={\displaystyle \sum _{i=1}^N}{d}_i{x}_i={\displaystyle \sum _{i,j=1}^N}{a}_{ij}{x}_i.$

As a consequence,

$\begin{array}{lll}\stackrel{·}{V}& \le & \frac{\lambda }{{\omega }^2}{\displaystyle \sum _{i=1}^N}{y}_i^2-\mu {\displaystyle \sum _{i,j=1}^N}{a}_{ij}{(x_i-x_j)}^2\le \frac{\lambda }{{\omega }^2}{\displaystyle \sum _{i=1}^N}{y}_i^2.\end{array}$

Then the global part of statement follows by LaSalle invariance principle [40]. The local part follows by observing that for λ < 0 the linearization of model (1a) at the origin is non-singular and therefore asymptotic stability of the origin implies that all eigenvalues have negative real part. □

Remark. Because exponentially stability implies robustness to small perturbations, Theorem 2.1 remains true for small heterogeneity in the natural frequencies.

Note that, for λ < 0, the system in Equation (1a) exhibits exponentially damped oscillations toward the origin (Figure 1, top panels).

Next we show that, at λ = 0 and identical natural frequencies model (1a) undergoes a supercritical Hopf bifurcation inside the consensus space

${C}=\left\{(x,y)\in {ℝ}^{2N}:x_i=x_j,y_i=y_j,\forall i,j=1,\dots ,N\right\},$

provided the graph is strongly connected. The linearization of the system (1a) is given by

$\begin{array}{rc}J=\left[\begin{array}{cc}-\mu L& I_N\\ -{\omega }^2{I}_N& \lambda I_N\end{array}\right],& (4)\end{array}$

where I_N is the N-dimensional identity matrix and L is the network Laplacian defined in section 2.1. Let 1_N be the N-dimensional vector of ones. Given a (complex) vector ν = (v, w) in the consensus space ${C}$, that is, v = a1_N and w = b1_N for some a, b∈ℂ, the eigenvalue problem for the Jacobian matrix Equation (4), restricted to the consensus space, takes the form

$\begin{array}{l}J\nu =J\left[\begin{array}{c}a{1}_N\\ b{1}_N\end{array}\right]\\ =\left[\begin{array}{c}-\mu La{1}_N+b{1}_N\\ -{\omega }^{2}a+\lambda b{1}_N\end{array}\right]\\ =\left[\begin{array}{c}b{1}_N\\ (-{\omega }^{2}a+\lambda b)1_N\end{array}\right]\\ =\xi \left[\begin{array}{c}a{1}_N\\ b{1}_N\end{array}\right]\end{array}$

where ξ is a (complex) eigenvalue. In the third equality we used the fact that 1_N is a right null eigenvector of L. The last equality shows that $\nu \in {C}$ is an eigenvector of J with eigenvalue ξ if and only if its components a and b satisfy

$\begin{array}{rc}\left[\begin{array}{cc}0& 1\\ -{\omega }^2& \lambda \end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\xi \left[\begin{array}{c}a\\ b\end{array}\right].& (5)\end{array}$

We can now easily solve Equation (5) to obtain the eigenvalues/eigenvectors pairs

$\begin{array}{rc}{\xi }_{\pm }(\lambda )=\frac{\lambda }{2}\pm \frac{1}{2}\sqrt{{\lambda }^2-4{\omega }^2},\left[\begin{array}{c}{a}_{\pm }\\ b_{\pm }\end{array}\right]=\left[\begin{array}{c}\frac{1}{{\omega }^2}(\lambda -{\xi }_{\pm })\\ 1\end{array}\right]& (6)\end{array}$

For λ = 0 we got two purely imaginary eigenvalues which correspond to a supercritical Hopf bifurcation of model (1a) inside the consensus space, as summarized in the following theorem and illustrated in (Figure 1, bottom panels).

Theorem 2.2. For almost all balanced, strongly connected interconnection topologies the following holds. For all μ > 0, the system (1a) undergoes a supercritical Hopf bifurcation at λ = 0 with center manifold given by the consensus space ${C}$. Moreover, the family of periodic solutions born at the Hopf bifurcation are exponentially asymptotically stable and correspond to synchronous oscillations of the oscillator network.

Proof. By Theorem 2.1 the origin is locally exponentially stable for λ < 0. We further observe that, if the interconnection topology is strongly connected, then zero is a simple eigenvalue of L and therefore no either eigenvalue of J satisfies the same eigenvalue problem defined by Equation (5). It then follows by the center manifold theorem [41] and Equation (6), that the system (1a) possesses a two-dimensional center manifold ${{W}}^c$ that is tangent to the consensus space ${C}$, for λ = 0. Moreover, this center manifold is exponentially attractive. By the Hopf bifurcation theorem [42], Equation (6) also implies that the system Equation (1a) undergoes a supercritical Hopf bifurcation inside ${{W}}^c$ when λ crosses zero from negative to positive. By direct substitution inside the model equations, we see that along a generic member of the family of periodic orbits born at the Hopf bifurcation, oscillators are synchronously oscillating with each oscillator orbit given by (2). □

Remark 2.3. Because Hopf bifurcation is codimension-zero (in the sense of [43]), it is persistent under small perturbations, which ensures that Theorem 2.2 remains true for small heterogeneity in the natural frequencies.

2.2. Oscillator Death and Multi-Stability for Stronger Coupling

We now explore the phenomenon of “oscillator death,” induced by strong coupling in model (1a). We restrict our attention to the all-to-all coupling case, i.e., a_ij = 1 for all i≠j. For λ > 0 and μ sufficiently small the synchronous oscillations born at Hopf bifurcation (Theorem 2.2) attract all trajectories. However, the system is multistable, as can be noted from the fact that increasing μ leads to the appearance of a family of steady states that attract some of the trajectories, but the synchronous periodic orbits remain locally exponentially stable (Figure 2). Indeed, depending on the initial conditions, only some trajectories converge to the synchronous oscillations. In the following we will provide geometric insights, without formal proof, about the mechanisms underlying oscillator death and multi-stability in model (1a).

FIGURE 2

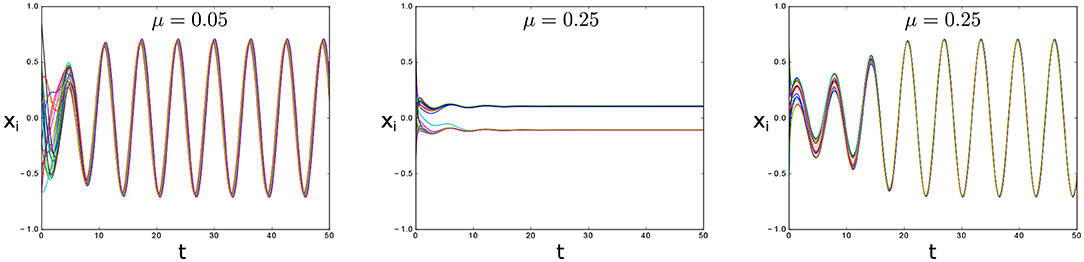
Figure 2. Emergence of oscillator death in model (1a) for λ = 0.5, N = 20, natural frequencies uniformly distributed in the interval [0.9, 1.1] and varying μ. The interconnection topology is all-to-all. Note that for the same value of μ = 0.25 both oscillatory and oscillator death states are possible.

We start by observing that the oscillator death state is characterized by the presence of two dead oscillator clusters. Inside each cluster, oscillators converge to the same steady state. To analyze the appearance of oscillator death steady-states, we can simplify the model by assuming that (x_i, y_i) = (x₁, y₁) for all i = 1, …, N₁ and (x_i, y_i) = (x₂, y₂) for all i = 1, …, N₂, where N₁, N₂ < N, N₁ + N₂ = N, are the cluster sizes. The pairs (x₁, y₁) and (x₂, y₂) define the cluster states.

The cluster state dynamics can be easily derived and read

$\begin{array}{rcll}{ẋ}_1& =& y_1+\mu N_2(x_2-x_1),& (\mathrm{7a})\end{array}$

$\begin{array}{rcll}{ẏ}_1& =& -{\omega }^2{x}_1+(\lambda -x_1^2-\frac{y_1^2}{{\omega }^2})y_1,& (\mathrm{7b})\end{array}$

$\begin{array}{rcll}{ẋ}_2& =& y_2+\mu N_1(x_1-x_2),& (\mathrm{7c})\end{array}$

$\begin{array}{rcll}{ẏ}_2& =& -{\omega }^2{x}_2+(\lambda -x_2^2-\frac{y_2^2}{{\omega }^2})y_2.& (\mathrm{7d})\end{array}$

Each cluster state dynamics has the form

$\begin{array}{rcll}ẋ& =& y+\mu N_j(x_j-x),& (\mathrm{8a})\end{array}$

$\begin{array}{rcll}ẏ& =& -{\omega }^{2}x+(\lambda -x^2-\frac{y^2}{{\omega }^2})y,& (\mathrm{8b})\end{array}$

where N_j is the other cluster size and x_j the other cluster state. A sufficient condition for the appearance of multiple steady states is that there must exist values of x_j for which the model(8a) has multiple steady-states. This condition can easily be verified by analyzing the dependence of the intersection of the nullclines of model (8a) as a function of x_j and the parameters μ and λ (Figure 3).

FIGURE 3

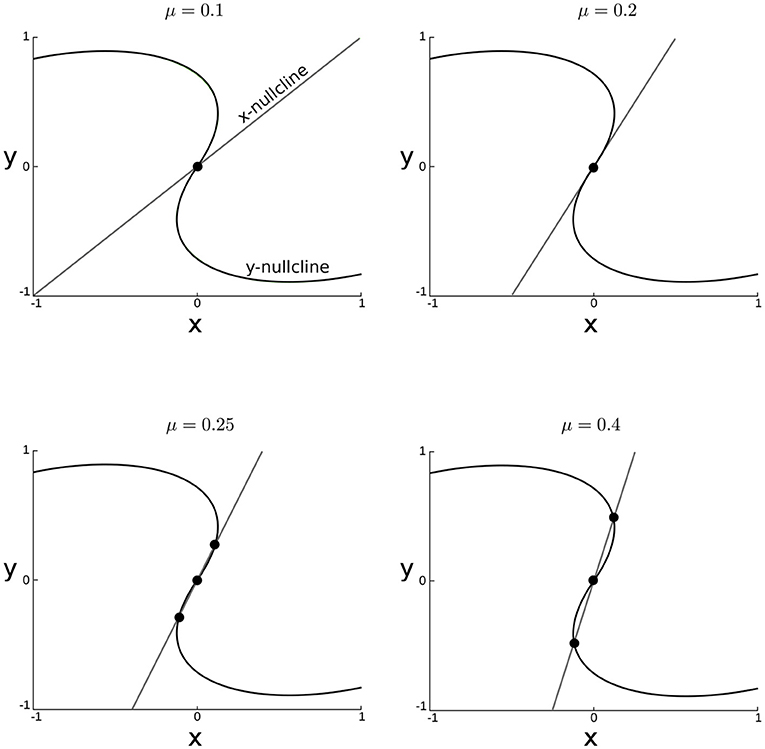
Figure 3. Nullclines of the cluster state dynamics for incresing values of μ for x_j = 0, ω = 1.0, N = 20 and N₁ = N₂ = N/2, λ = 0.5.

If the coupling strength is too small the origin is the only steady state (Figure 3). This steady state is unstable and all trajectories are attracted toward the synchronous periodic orbit. However, new steady states appear for larger values of μ. The critical value of μ for which the new steady-states appear can be found by computing the slope of the nullclines at the origin. The slope of the x-nullcline is evidently μN_j. The slope of the x-nullcline can be computed by implicit differentiation and is given by $\frac{{\omega }^2}{\lambda }$. Multiple steady-states appear if $\mu >\frac{{\omega }^2}{N_j\lambda }$ (Figure 2).

3. Synchronization and Frequency Modulation in Linearly Coupled Oscillators

In this section we present an alternative approach to study synchronization under the influence of noise using the Fokker-Planck equation (FPE). The modeling in this section can be thought of in the context of interacting populations of oscillators. Related work in the context of populations of synchronized neurons can be found in the work by Jiao et al. [44]. Introducing noise in the equation is natural from the biological perspective. However, even in the absence of noise, the introduction of random perturbations allows the extraction of information about the deterministic system. This is done by letting the perturbation amplitudes go to zero. To investigate the dependence of the synchronization frequency on the frequencies of the coupled oscillators, and the different coupling parameters, we assume synchronization, which reduces the FPE equation to an equation in two variables.

We divide this section in two parts. First, we consider a simple deterministic system in which the effect of coupling can be understood. In the second part, we randomly perturb a more general version of the previous model to show that the FP equation provides an approximation for the syncrhonization frequency, and obtain some insights on the effect of noise. Let us then consider a system similar to the one already studied

$\begin{array}{l}{ẍ}_i=-{\omega }^2{x}_i+\nu \left[1-(x_i^2+\frac{{ẋ}_i^2}{{\omega }^2})\right]{ẋ}_i\\ +\mu {\displaystyle \sum _{j=1}^N}{a}_{ij}{x}_j,i=1,\dots ,N,& (9)\end{array}$

Notice that x(t) = sin(ωt) is still a solution for the uncoupled system (μ = 0), independently of the value of ν. This system has the advantage of allowing direct calculations around the limit cycle, which can be written explicitly.

If we linearize the equation and take ν < < 1, we can neglect the contribution of the disipative term. The resulting linear system is

$\begin{array}{l}{ẍ}_i=-({\omega }^2-\mu A_i)x_i,\end{array}$

where $A_i=\sum _{j=1}^N{a}_{ij}{x}_j$, for i = 1, …, N. If all the a_ij = 1, corresponding to a fully connected network of oscillators, the previous system can be reduced to the equation

$\begin{array}{l}ẍ=-({\omega }^2-\mu (N-1))x,\end{array}$

assuming that a synchronized regime is established. This assumption may not always be biologically realistic, but it allows us to obtain the common synchronization frequency in a simple way. Later on we consider the general case and recover this formula as a particular case. This provides an estimate for the synchronization frequency of

${\Omega }_{sync}=\sqrt{{\omega }^2-\mu (N-1)}.$

Moreover, this reduction suggests that synchronized oscillatory behavior takes place for sufficiently small μ. That is, when

${\omega }^2-\mu (N-1)>0,$

Otherwise, exponentially large growth can be expected. Notice that unless the a_ij are equal, the previous reasoning is not consistent and no conclusion can be drawn. We claim that introducing random perturbations and using the FP equation allows us to circumvent this difficulty and analyze the general case. This is the content of what follows. First of all, we write the system in the form

$\begin{array}{l}{ẋ}_i=y_i\\ {ẏ}_i=f_i(x_i,y_i)+\mu {\displaystyle \sum _{j=1}^N}{a}_{ij}{x}_j,i=1,\dots ,N.\end{array}$

Notice that in the linearized regime, anologous to the reasoning for small ν in the previous example, we might naturally assume that

$f_i(x_i,y_i)\approx -{\omega }_i^2.$

Perturbing the equation with Brownian noise we have

$\begin{array}{l}d{x}_i=y_{i}dt+\sqrt{2\epsilon }d{W}_{i1}\\ d{y}_i=\left[-{\omega }_i^2{x}_i+\mu {\displaystyle \sum _{j=1}^N}{a}_{ij}{x}_j\right]dt+\sqrt{2\epsilon }d{W}_{i2},i=1,\dots ,N,\end{array}$

where the W_ij are uncorrelated Brownian motions for i, j∈{1, …, N}. The probability density, u(x₁, …, x_n, y₁, …, y_n, t) of the system being in the state x₁, …, x_n, y₁, …, y_n at time t satisfies the FP Equation

$\begin{array}{rc}\frac{\partial u}{\partial t}=\epsilon \Delta u+\nabla (F(x,y)u),& (10)\end{array}$

where F is the vector field determined by the right hand side of the stochastic system. Looking for stationary solutions, i.e., u_t = 0 and explicitly substituting F in terms of x and y, the equation becomes

$\begin{array}{rc}\epsilon \Delta u+{\displaystyle \sum _i}(y_i{u}_{x_i}+(-{\omega }_i^2{x}_i+\mu {\displaystyle \sum _{j\ne i}}{a}_{ij}{x}_j)u_{y_i})=0.& (11)\end{array}$

If we use the synchronization condition x₁ = … = x_n and y₁ = … = y_n, we obtain the equation

$\begin{array}{l}\epsilon \Delta +ny{u}_x+(-{\displaystyle \sum _i}{\omega }_i^2+\mu {\displaystyle \sum _{i,j}}{a}_{ij})x{u}_y=0.\end{array}$

If we let

$\begin{array}{l}b={\displaystyle \sum _i}{\omega }_i^2-\mu {\displaystyle \sum _{i,j}}{a}_{ij},\end{array}$

we can write the Equation (11) as

$\epsilon \Delta +ny{u}_x-bx{u}_y=0.$

Assuming ε is small, it is reasonable to expect that the probability u will concentrate around the characteristic curves of the first order equation

$ny{u}_x-bx{u}_y=0,$

that are solutions to the system

$\begin{array}{l}ẋ=ny,\\ {ẏ}_i=bx.\end{array}$

By taking the scalar product with the vector (x/n, y/b) we obtain the relation

$ẋ\frac{x}{n}+ẏ\frac{y}{b}=0,$

or equivalently,

$\frac{x^2}{n}+\frac{y^2}{b}=constant,$

which defines the characteristic curves as ellipses. In turn, interpreting these as curves in the phase portrait, the resulting solutions would correspond to periodic trajectories with frequency

$\begin{array}{rc}{\Omega }_{sync}^2=-\frac{b}{n}=\frac{({\displaystyle {\sum }_i}{\omega }_i^2-\mu {\displaystyle {\sum }_{i,j}}{a}_{ij})}{n},& (12)\end{array}$

which provides an estimate for the synchronization frequency in terms of the original frequencies and the coupling parameters. Importantly, it shows that the synchronization frequency decreases with the coupling strength. In particular, formula Equation (12) can be used to study how coupled ultradian oscillations can give rise to circadian oscillations (Figure 4).

FIGURE 4

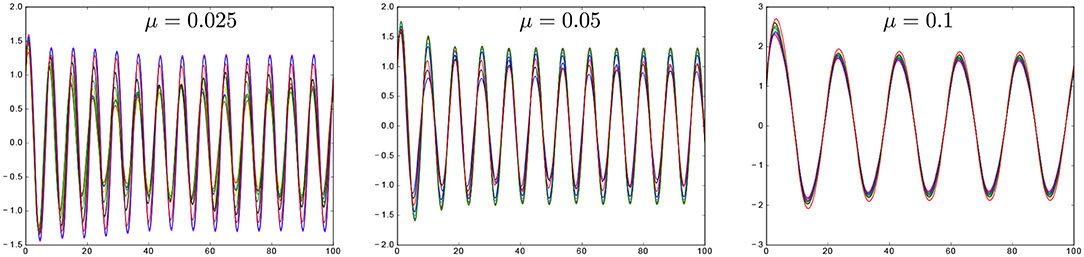
Figure 4. Synchronization and modulation of the synchronization frequency via coupling strength in model (9), for N = 10, natural frequencies uniformly distributed in the interval [0.95, 1.05], all-to-all coupling and varying μ.

4. Discussion and Summary

We have described, through basic geometrical analysis, the relationship between the dissipation coefficient, an intrinsic property of the oscillators we study, and the coupling strength μ in a network of diffusively coupled non-linear oscillators. Our analysis predicts the emergence of sustained oscillations for increasing values of the parameter λ in the system, only for a limited range of coupling strengths. It is reasonable to conjecture from this result, that there is a functional limit in the coupling strength for oscillating tissues in nature above which the tissue oscillations dies. To the best of our knowledge, it is the first time that diffusive coupling has been shown to be able to induce such oscillator death.

We have also derived an estimation for the synchronization frequency of a linearly coupled network of non-linear oscillators in terms of the oscillator natural frequencies and the coupling parameters [Equation (12)]. The presented results are indeed local, that is, the synchronous oscillation is only locally asymptotically stable. The oscillators are not synchronized at the beginning of the simulations, but their spread in state space is very small to ensure convergence to the synchronous oscillation. For a larger spread, a more complex behavior is observed.

We believe that these results constitute predictions that, although possibly difficult to test experimentally, would be worth verifying in light of the existing evidence about the joint frequency modulation of activity between different tissues during the day [23, 45].

The results we have presented thus far emphasize the importance of simple mathematical models in understanding situations where synchronization of multiple oscillating populations appears. The results presented here may help to shed light on both physiological and pathological phenomena involving synchronization of oscillators in different tissues (Parkinson's disease [46, 47], epilepsy [48, 49]). The other way around, it is also of potential importance to unravel mechanisms underlying the disappearance of coordinated oscillatory regimes. In a future publication, we plan to formally justify our estimations, and further, integrate the analysis of oscillations in the cellular and network levels of biological organization, to build up on our understanding of coupling oscillators at the tissue level. Two important extensions of the current models that we are studying are, the full characterization in higher codimension of the bifurcation structures of the system (1a), and also, replacements of the van der Pol dynamics with biophysical models of excitable cells [50]. This last extension may prove useful to explain possible compensatory mechanisms that take place during the beginning of a pathology [51].

Author Contributions

All authors wrote the paper. ML-A proposed the original set of equations, AF and PP-L proposed revised sets of equations and extended models. All authors performed the analysis. AF and MH-V performed simulations.

Funding

This research was supported by DGAPA-PAPIIT (UNAM) grants IA105518 and IA208618

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Beatriz Fuentes-Pardo for her input in discussions about the modeling and its connections with the experimental work she has done. We would also like to thank Carolina Barriga-Montoya for her work on the Fokker-Planck equations and her support with the modeling.

References

1. Bünsow RC. The circadian rhythm of photoperiodic responsiveness in Kalanchoe. In: Stillman B, Stewart D, Grodzicker T, editors. Cold Spring Harbor Symposia on Quantitative Biology. Vol. 25. Cold Spring Harbor Laboratory Press (1960). p. 257–60.

Google Scholar

2. Pol B. Biological rhythms considered as relaxation oscillations. J Intern Med. (1940) 103:76–88.

Google Scholar

3. Sholl D. Regularities in growth curves, including rhythms and allometry. Dyn Growth Process. (1954) 224–241.

Google Scholar

4. Pavlidis T, Zimmerman W, Osborn J. A mathematical model for the temperature effects on circadian rhythms. J Theor Biol. (1968) 18:210–21.

PubMed Abstract | Google Scholar

5. Klotter K. Theoretical analysis of some biological models. In: Stillman B, Stewart D, Grodzicker T, editors. Cold Spring Harbor Symposia on Quantitative Biology. Vol. 25. Cold Spring Harbor Laboratory Press (1960). p. 189–96.

Google Scholar

6. Klotter K. General properties of oscillating systems. In: Stillman B, Stewart D, Grodzicker T, editors. Cold Spring Harbor Symposia on Quantitative Biology. Vol. 25. Cold Spring Harbor Laboratory Press (1960). p. 185–87.

Google Scholar

7. Sweeney BM. The photosynthetic rhythm in single cells of Gonyaulax polyedra. In: Stillman B, Stewart D, Grodzicker T, editors. Cold Spring Harbor Symposia on Quantitative Biology. Vol. 25. Cold Spring Harbor Laboratory Press (1960). p. 145–48.

Google Scholar

8. Winfree AT. The Geometry of Biological Time. Vol. 12. New York, NY: Springer Science & Business Media (2001).

Google Scholar

9. Hirota T, Lee JW, Lewis WG, Zhang EE, Breton G, Liu X, et al. High-throughput chemical screen identifies a novel potent modulator of cellular circadian rhythms and reveals CKIα as a clock regulatory kinase. PLoS Biol. (2010) 8:e1000559. doi: 10.1371/journal.pbio.1000559

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Partch CL, Green CB, Takahashi JS. Molecular architecture of the mammalian circadian clock. Trends Cell Biol. (2014) 24:90–9. doi: 10.1016/j.tcb.2013.07.002.

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Welsh DK, Yoo SH, Liu AC, Takahashi JS, Kay SA. Bioluminescence imaging of individual fibroblasts reveals persistent, independently phased circadian rhythms of clock gene expression. Curr Biol. (2004) 14:2289–95. doi: 10.1016/j.cub.2004.11.057

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hastings MH, Maywood ES, O'Neill JS. Cellular circadian pacemaking and the role of cytosolic rhythms. Curr Biol. (2008) 18:R805–15. doi: 10.1016/j.cub.2008.07.021

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Nader N, Chrousos GP, Kino T. Interactions of the circadian CLOCK system and the HPA axis. Trends Endocrinol Metab. (2010) 21:277–86. doi: 10.1016/j.tem.2009.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Abruzzi KC, Rodriguez J, Menet JS, Desrochers J, Zadina A, Luo W, et al. Drosophila CLOCK target gene characterization: implications for circadian tissue-specific gene expression. Genes Dev. (2011) 25:2374–86. doi: 10.1101/gad.174110.111

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Manoogian EN, Panda S. Circadian rhythms, time-restricted feeding, and healthy aging. Ageing Res Rev. (2017) 39:59–67. doi: 10.1016/j.arr.2016.12.006.

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Tahara Y, Aoyama S, Shibata S. The mammalian circadian clock and its entrainment by stress and exercise. J Physiol Sci. (2017) 67:1–10. doi: 10.1007/s12576-016-0450-7

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Rusak B, Zucker I. Neural regulation of circadian rhythms. Physiol Rev. (1979) 59:449–526.

PubMed Abstract | Google Scholar

18. Guo H, Brewer JM, Lehman MN, Bittman EL. Suprachiasmatic regulation of circadian rhythms of gene expression in hamster peripheral organs: effects of transplanting the pacemaker. J Neurosci. (2006) 26:6406–12. doi: 10.1523/JNEUROSCI.4676-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tahara Y, Shibata S. Circadian rhythms of liver physiology and disease: experimental and clinical evidence. Nat Rev Gastroenterol Hepatol. (2016) 13:217. doi: 10.1038/nrgastro.2016.8

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Oster H, Damerow S, Kiessling S, Jakubcakova V, Abraham D, Tian J, et al. The circadian rhythm of glucocorticoids is regulated by a gating mechanism residing in the adrenal cortical clock. Cell Metab. (2006) 4:163–73. doi: 10.1016/j.cmet.2006.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ishida A, Mutoh T, Ueyama T, Bando H, Masubuchi S, Nakahara D, et al. Light activates the adrenal gland: timing of gene expression and glucocorticoid release. Cell Metab. (2005) 2:297–307. doi: 10.1016/j.cmet.2005.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kiessling S, Eichele G, Oster H. Adrenal glucocorticoids have a key role in circadian resynchronization in a mouse model of jet lag. J clin Invest. (2010) 120:2600–9. doi: 10.1172/JCI41192

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Damiola F, Le Minh N, Preitner N, Kornmann B, Fleury-Olela F, Schibler U. Restricted feeding uncouples circadian oscillators in peripheral tissues from the central pacemaker in the suprachiasmatic nucleus. Genes Dev. (2000) 14:2950–61. doi: 10.1101/gad.183500

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kronauer RE, Czeisler CA, Pilato SF, Moore-Ede MC, Weitzman ED. Mathematical model of the human circadian system with two interacting oscillators. Am J Physiol Regul Integr Comp Physiol. (1982) 242:R3–17.

PubMed Abstract | Google Scholar

25. olde Scheper T, Klinkenberg D, Pennartz C, Van Pelt J. A mathematical model for the intracellular circadian rhythm generator. J Neurosci. (1999) 19:40–47.

Google Scholar

26. Glass L. Synchronization and rhythmic processes in physiology. Nature (2001) 410:277. doi: 10.1038/35065745

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ueda HR, Hagiwara M, Kitano H. Robust oscillations within the interlocked feedback model of Drosophila circadian rhythm. J Theor Biol. (2001) 210:401–6. doi: 10.1006/jtbi.2000.2226

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Jiang J, Liu Q, Niu L. Theoretical investigation on models of circadian rhythms based on dimerization and proteolysis of PER and TIM. Math Biosci Eng. (20170 14:1247–59. doi: 10.3934/mbe.2017064

PubMed Abstract | CrossRef Full Text

29. Lara-Aparicio M, de Medrano SL, Fuentes-Pardo B, Moreno-Sáenz E. A qualitative mathematical model of the ontogeny of a circadian rhythm in crayfish. Bull Math Biol. (1993) 55:97–110.

Google Scholar

30. Fanjul-Moles ML, Moreno-Sáenz E, Villalobos-Hiriart N, Fuentes-Pardo B. ERG circadian rhythm in the course of ontogeny in crayfish. Comp Biochem Physiol A Physiol. (1987) 88:213–9.

Google Scholar

31. Fanjul-Moles ML, Miranda-Anaya M, Fuentes-Pardo B. Effect of monochromatic light upon the erg crcadian rhythm during ontogeny in crayfish (Procambarus clarkii). Comp Biochem Physiol A Physiol. (1992) 102:99–106.

Google Scholar

32. Fuentes-Pardo B, Fanjul-Moles ML, Moreno-Sáenz E. Synchronization by light of the ERG circadian rhythm during ontogeny in the crayfish. Biol Rhythm Res. (1992) 23:81–91.

Google Scholar

33. Van der Pol B. On “relaxation-oscillations.” Lond Edinb Dublin Philos Mag J Sci. (1926) 2:978–92.

Google Scholar

34. Fuentes-Pardo B, Lara-Aparicio M, de Medrano SL. Perturbation of a circadian rhythm by single and periodic signals and its mathematical simulation. Bull Math Biol. (1995) 57:175–89.

Google Scholar

35. Dowse HB, Hall JC, Ringo JM. Circadian and ultradian rhythms in period mutants of Drosophila melanogaster. Behav Genet. (1987) 17:19–35.

PubMed Abstract | Google Scholar

36. Goldbeter A. From Ultradian Biochemical Oscillations to Circadian Rhythms. In: Vanden Driessche T, Guisset JL, Petiau-de Vries GM, editors. Membranes and Circadian Rythms. Springer (1996). p. 67–93.

Google Scholar

37. Lloyd D, Rossi EL. Ultradian Rhythms in Life Processes: An Inquiry Into Fundamental Principles of Chronobiology and Psychobiology.London: Springer Science & Business Media (2012).

Google Scholar

38. Barriga-Montoya C, Padilla-Longoria P, Lara-Aparicio M, Fuentes-Pardo B. Ultradian rhythms underlying the dynamics of the circadian pacemaker. In: Vonend O, editior. Aspects of Pacemakers-Functions and Interactions in Cardiac and Non-Cardiac Indications. InTech (2011).

Google Scholar

39. Agaev R, Chebotarev P. On the spectra of nonsymmetric Laplacian matrices. Linear Algebra Appl. (2005) 399:157–68. doi: 10.1016/j.laa.2004.09.003

CrossRef Full Text | Google Scholar

40. La Salle JP. An invariance principle in the theory of stability, differential equations and dynamical systems. In: Proceedings of the International Symposium, Puerto Rico (1967). p. 277–86.

Google Scholar

41. Guckenheimer J, Holmes P. Local bifurcations. In: Guckenheimer J, Holmes P, editors. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. New York, NY: Springer (1983), p. 117–165. doi: 10.1007/978-1-4612-1140-2_3

CrossRef Full Text | Google Scholar

42. Hassard BD, Kazarinoff ND, Wan YH. Theory and Applications of Hopf Bifurcation. Vol. 41. Cambridge: CUP Archive (1981).

Google Scholar

43. Golubitsky M, Stewart I, Schaeffer DG. Singularities and Groups in Bifurcation Theory. Vol. 1. Verlag: Springer (1985).

Google Scholar

44. Jiao X, Wang R. Synchronous firing patterns of neuronal population with excitatory and inhibitory connections. Int J Non Linear Mech. (2010) 45:647–51. doi: 10.1016/j.ijnonlinmec.2008.11.020

CrossRef Full Text | Google Scholar

45. Le Minh N, Damiola F, Tronche F, Schütz G, Schibler U. Glucocorticoid hormones inhibit food-induced phase-shifting of peripheral circadian oscillators. EMBO J. (2001) 20:7128–36. doi: 10.1093/emboj/20.24.7128

CrossRef Full Text | Google Scholar

46. Hammond C, Bergman H, Brown P. Pathological synchronization in Parkinson's disease: networks, models and treatments. Trends Neurosci. (2007) 30:357–64. doi: 10.1016/j.tins.2007.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Schnitzler A, Gross J. Normal and pathological oscillatory communication in the brain. Nat Revi Neurosci. (2005) 6:285–96. doi: 10.1038/nrn1650

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Engel Jr J, Bragin A, Staba R, Mody I. High-frequency oscillations: what is normal and what is not? Epilepsia (2009) 50:598–604. doi: 10.1111/j.1528-1167.2008.01917.x

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Velazquez JLP, Carlen PL. Gap junctions, synchrony and seizures. Trends Neurosci. (2000) 23:68–74. doi: 10.1016/S0166-2236(99)01497-6

CrossRef Full Text | Google Scholar

50. Herrera-Valdez MA, McKiernan EC, Berger SD, Ryglewski S, Duch C, Crook S. Relating ion channel expression, bifurcation structure, and diverse firing patterns in a model of an identified motor neuron. J comput Neurosci. (2013) 34:211–29. doi: 10.1007/s10827-012-0416-6

PubMed Abstract | CrossRef Full Text | Google Scholar

51. McKiernan EC. A genetic manipulation of motor neuron excitability does not alter locomotor output in Drosophila larvae. PeerJ PrePrints (2015) 3:e469v3. doi: 10.7287/peerj.preprints.469v3

CrossRef Full Text | Google Scholar