Imperfect Amplitude Mediated Chimera States in a Nonlocally Coupled Network

1. Introduction

During the past couple of decades studies on the emerging collective dynamical behavior of a given network of complex nonlinear systems has become an active area of research, due to its capability to mimic various natural phenomena such as clusters, synchronization, chimera, death states, etc. [1–4]. Among the intriguing collective dynamical behaviors exhibited by networks of coupled systems, chimera states have been receiving a wide attention in the recent literature both theoretically and experimentally. In particular, much focus has been paid toward understanding the onset of various types of chimeras. A flurry of research activities on the chimera states have been provoked due to the nonintuitive nature of the associated hybrid dynamical state. Chimera state is characterized by spatially coexisting coherent and incoherent dynamical behaviors arising out of an ensemble of identical systems. So far, chimera states have been found theoretically in limit cycle oscillators [5, 6], time discrete maps [7–9], chaotic models [10, 11], neural systems [10, 12, 13], quantum oscillators [14], population dynamics [15, 16], boolean networks [17] and so on. Chimera states have also been found experimentally in optical [18], electronic [18, 19], optoelectronic [20], chemical [21, 22], electrochemical [23, 24] and mechanical systems [25].

A diverse variety of chimera patterns have been identified depending on the coupling geometry, the strength of the interaction and the values of the parameters of the employed dynamical systems. Specifically, based on the spatial or spatio-temporal distribution of an ensemble of coupled identical systems, chimera states have been classified as amplitude chimera [26–30], globally clustered chimera [31], imperfect traveling chimera [32], breathing chimera [33, 34], spiral wave chimera [35], twisted chimera and multicore spiral chimera states [36]. Among the different types of chimeras, investigations on the onset of the amplitude mediated chimera has received a wide attention in the recent literature. Amplitude-mediated chimera was reported in a nonlocally coupled complex Ginzburg-Landau system in the strong coupling limit which may have potential applications in understanding spatio-temporal patterns in fluid flow experiments and in strongly coupled systems [6]. It is also reported in a system of globally coupled complex Ginzburg-Landau oscillators [37]. The robustness of amplitude mediated chimera state has also been examined in a globally coupled system of active and inactive Ginzburg-Landau oscillators by varying the fraction of active and inactive oscillators [38]. Interestingly, the notion of chimera state is not only restricted to oscillatory dynamics but has also been extended to include so called the death states which have been reported as chimera death [3]. Domains of inhomogeneous death states are termed as cluster oscillation death states whereas coexisting domains of coherent and incoherent death states (of the inhomogeneous death states) constitute the cluster chimera death state. The number of clusters in the death states are found to vary as a function of the coupling range and cluster initial conditions in nonlocally coupled networks [4, 39].

In this report, we unravel the emergence distinct collective dynamical behavior in a network of nonlocally coupled Stuart-Landau oscillators with competing attractive and repulsive couplings. The trade-off between the attractive and repulsive couplings in many natural systems has been revealed as an essential element in determining their functional and evolutionary processes [39, 40]. We find that the competing interaction between them facilitates the emergence of imperfect amplitude mediated chimera, which is characterized by a continuous drift of the oscillators between the homogeneous and the inhomogeneous oscillations as a function of time. Finite-time average of each of the oscillators elucidates the continuous shift between the homogeneous and the inhomogeneous states of the imperfect amplitude mediated chimera. Further, the homogeneous and inhomogeneous states can be distinguished by estimating the strength of inhomogeneous oscillators in each dynamical state. We find that the observed amplitude mediated chimera mediates the transition between the oscillatory and death states. Further, we will demonstrate the emergence of distinct cluster oscillation death and chimera death states as a function of the nonlocal coupling range. We have also found that the number of clusters in the network exponentially decays as a function of the coupling range and obeys a power-law relation.

The structure of the paper is organized as follows. In section 2, we introduce our model of nonlocally coupled Stuart-Landau oscillators with a combination of attractive and repulsive couplings. The emergence of imperfect amplitude mediated chimera state is demonstrated in section 3. The corresponding dynamical transitions are delineated in section 4 and the global dynamical behavior of the coupled systems is depicted in the section 5. Finally, we summarize the obtained results in section 6.

2. The Model

We consider the paradigmatic model of Stuart-Landau limit cycle oscillators, which can be used to model a variety of weakly nonlinear systems near Hopf-bifurcation [41]. In addition, the limit cycle oscillations can be found in many biological and chemical systems such as heart beats, chemical oscillations, vibrations in bridges, etc. [42, 43]. Further, to demonstrate the complex dynamical behaviors in a network of coupled identical Stuart-Landau oscillators, we have employed the nonlocal attractive and repulsive couplings, which can be represented as

$\begin{array}{rcl}{ẋ}_i& =& (\lambda -x_i^2-y_i^2)x_i-\omega y_i+\frac{ϵ}{2P}{\displaystyle \sum _{k=i-P}^{i+P}}(x_k-x_i),\\ {ẏ}_i& =& (\lambda -x_i^2-y_i^2)y_i+\omega x_i-\frac{ϵ}{2P}{\displaystyle \sum _{k=i-P}^{i+P}}(y_k-y_i),i=1,2,\dots ,N,& (1)\end{array}$

where λ is the bifurcation parameter and ω is the natural frequency of the system. x_i and y_i are the state variables of the system. Here, the attractive and repulsive couplings are established via the state variables x_i and y_i (i = 1, 2.., N), respectively, and ϵ is the coupling strength. Throughout the work, the number of oscillators in the network has been chosen as N = 100, except for the cases mentioned specifically in the text, and the values of the parameters are fixed as λ = 1.0, ω = 1.0. The numerical results are obtained through the Runge-Kutta fourth order scheme with a time step 0.01 and the initial states of the oscillators (x_i, y_i) are chosen such that they are independently distributed between -1 to +1 randomly.

3. Amplitude Mediated Chimera

Amplitude chimera is characterized by a partial coherent and a partial incoherent spatio-temporal pattern with amplitude variations in their amplitude dynamics [26]. On the other hand the amplitude mediated chimera state suffers variations in both phase and frequency. Interestingly, we find that the system of nonlocally coupled Stuart-Landau oscillators also exhibit amplitude mediated chimera states, where the synchronized and desynchronized groups are imperfect over time exhibiting quasi-periodic oscillations. In particular, the synchronized group gives rise to inhomogeneous small oscillations populating both the upper and the lower branches of the inhomogeneous state while the desynchronized group oscillates with a larger amplitude. The space-time evolution in Figure 1a clearly illustrates that the oscillators at the boundaries of the upper (yellow/light gray) and the lower (blue/dark gray) branches of the inhomogeneous state exhibit large oscillations. In addition, the oscillators exhibiting large oscillations suffer a drift to either one of the inhomogeneous states with small oscillations and vice versa as a function of time. Further, to elucidate that the oscillators in the network reside in the upper/lower branch of the inhomogeneous state for a finite-time interval and then transits to the homogeneous state for certain other time interval, we have depicted the time evolution of a typical oscillator, indicated along the dotted line in Figures 1a,b. The time evolution of the representative oscillator x₇₂ elucidates that the corresponding oscillator oscillates in the upper branch of the inhomogeneous state for a certain time interval, then it manifests itself as a homogeneous oscillator. After a further finite time interval, the homogeneous oscillations with large amplitude transit to the lower branch of the inhomogeneous state exhibiting small oscillations. The homogeneous large oscillations re-emerge again after a finite time from the lower branch and then populate the upper branch of the inhomogeneous state after a while. These transitions in the dynamical nature of each oscillator takes place continuously as a function of time, thereby manifesting as an imperfect amplitude mediated chimera as a whole. The robust against initial conditions and system size of imperfect amplitude mediated chimera is discussed in the following.

FIGURE 1

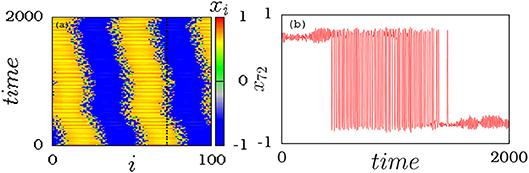
Figure 1. (a) Spatio-temporal evolution of imperfect amplitude mediated chimera (after leaving transients of the order 1 × 10⁴) and (b) time evolution of a representative oscillator x₇₂, a constituent of imperfect amplitude mediated chimera. Parameters: r = 0.4, ω = 1.0, λ = 1.0, ϵ = 0.9 and N = 100.

3.1. Robustness of Imperfect Amplitude Mediated Chimera for Distinct Initial States and System Sizes

In order to show the robustness of the imperfect amplitude mediated chimeras with respect to various initial conditions, we have plotted the space-time evolution and snapshots of such dynamical states for the distribution of different initial states (see Figure 2). The menifestation of amplitude mediated chimeras is evident from the space-time plots, Figures 2a–c, which are plotted for random distribution of initial conditions between 0 to 1, symmetric cluster and asymmetric cluster initial states, respectively. The corresponding snapshots are shown in Figures 2d–f. From Figure 2, it is clear that the observed imperfect amplitude mediated states are robust against random and cluster initial conditions.

FIGURE 2

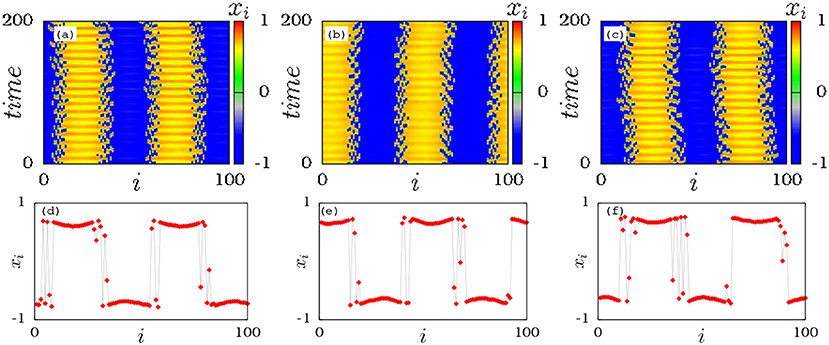
Figure 2. Space-time evolution of amplitude mediated chimera for the distribution of initial states (a) between 0−1 randomly, (b) symmetric cluster, and (c) asymmetric clusters. The corresponding snapshots of (a–c) are shown in (d–f). Parameters are the same as in Figure 1.

Further, it is also found that the observed imperfect amplitude mediated chimeras are robust againt system size (see Figure 3). The space-time plots and snapshots in Figure 3 clearly depict the persistence of amplitude mediated chimera state even while increasing the system size to N = 200, N = 500 and N = 1000, respectively.

FIGURE 3

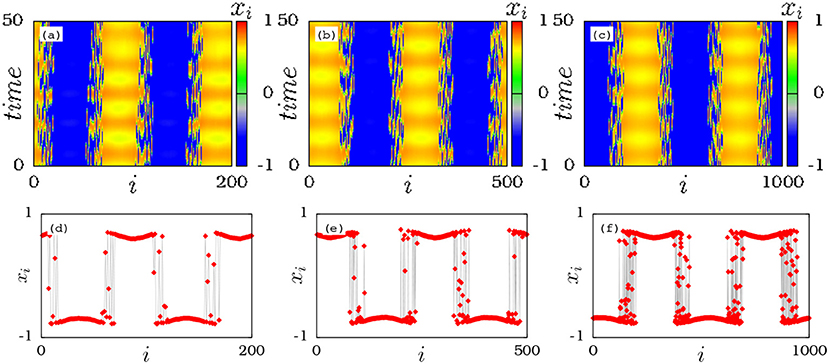
Figure 3. Space-time evolution of amplitude mediated chimera as a function of the size of the network for (a) N = 200, (b) N = 500, and (c) N = 1000. (d–f) Correspond to the snapshots in (a–c). Other parameters are the same as in Figure 1.

The dynamical transitions exhibited by the coupled Stuart-Landau oscillators will be described in the following as a function of the coupling strength.

4. Dynamical Transitions in Coupled Stuart-Landau Oscillators

To start with, the dynamical behavior exhibited by the nonlocally coupled Stuart-Landau oscillators is inspected through the space-time and snapshot plots of the variables x_i, which are shown in Figure 4, for the coupling range r = 0.4. We find that a transition takes place from traveling wave (TW) state to imperfect amplitude mediated chimera (IAMC) state and finally to death states. In case of death states, the coupled Stuart-Landau oscillators exhibit multi-chimera death states (MCDs) through cluster oscillation death (COD) and cluster chimera death (CCD) states. As noted above, the network exhibits traveling wave (TW) state as shown in Figures 4a,f for the coupling strength ϵ = 0.7. It is to be noted that here all the oscillators in the network oscillate homogeneously about the origin with the same frequency and constant velocity. The emergence of the imperfect amplitude mediated chimera (IAMC) state is observed for further increase in the coupling strength as depicted in Figures 4b,g for ϵ = 0.9. In this state the oscillators in the network split into synchronized and desynchronized groups with amplitude variations. The oscillators hop between the synchronized and the desynchronized groups as a function of time, which can be clearly visualized in Figure 1a for sufficiently large time interval, but it resembles stationary amplitude mediated chimera for a short time interval (see Figure 4b). The synchronized group of oscillators oscillates with smaller amplitudes both in the upper and lower branches of the inhomogeneous state whereas the desynchronized group oscillates homogeneously about the origin. On increasing the coupling strength further, the oscillators with homogeneous oscillations populate either the lower or the upper branches of the inhomogeneous steady state, while the oscillators with small inhomogeneous oscillations settle as steady states in the respective branches resulting in a two cluster oscillation death (2COD) state. As a result, all the oscillators in the network occupy either the upper or lower branches of the inhomogeneous steady states as shown in Figures 4c,h for ϵ = 1.0. The emergence of multi-chimera death (MCD) state via two cluster chimera death (2CCD) (see Figures 4d,i for ϵ = 1.12) is observed upon increasing ϵ further as shown in Figures 4e,j for ϵ = 1.2. In the 2CCD state, the oscillators in the cluster edges populate either the upper or the lower branches of the inhomogeneous state randomly and the MCD state is characterized by multiple coherent and incoherent domains of the death states. We may conclude that the imperfect amplitude mediated chimera mediates the transition from traveling wave state to death state.

FIGURE 4

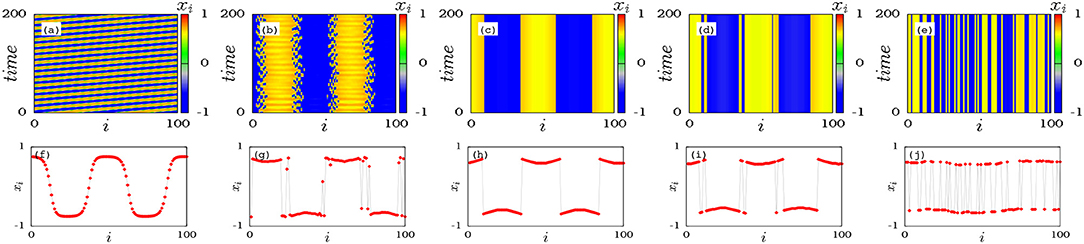
Figure 4. Dynamical behavior of the coupled Stuart-Landau oscillators as a function of coupling strength ϵ for the coupling range r = 0.4. Space-time plots of (a) Traveling wave (TW) state for ϵ = 0.7, (b) imperfect amplitude mediated chimera (IAMC) for ϵ = 0.9, (c) two cluster oscillation death (2COD) for ϵ = 1.0, (d) two cluster chimera death (2CCD) for ϵ = 1.12 and (e) multi-chimera death (MCD) state for ϵ = 1.2. The corresponding snapshots are shown in the lower panel (f–j), respectively. Parameters: r = 0.4, ω = 1.0, λ = 1.0, and N = 100.

We further note that the separation of the homogeneous and inhomogeneous oscillations in the imperfect amplitude mediated chimera state is impossible for a large time interval since these states swing in time alternately in a random fashion. In order to overcome this difficulty, we have considered the evolution of the oscillators constituting the imperfect amplitude mediated chimera in a short time interval as in Figure 5a, which depicts the time evolution of distinct oscillators in the time interval 0 to 500, where the oscillators x₂₀ and x₄₅ are the representative oscillators from the inhomogeneous group whereas x₄ is the representative oscillator from the homogeneous group. The phase space dynamics of the representative oscillators are shown in Figure 5b. It is evident from the figures that the oscillator from the incoherent group x₄ (i = 4) oscillates about the origin quasi-periodically while the oscillators from the coherent group, x₂₀ (i = 20) and x₄₅ (i = 45), oscillate in the upper and lower branches of the inhomogeneous state with smaller amplitudes, respectively. In addition, to distinguish the homogeneous and inhomogeneous states, we have calculated the finite-time average of the variable y_i by dividing the total time (T_tol) into p bins of equal size $q=\frac{T_{tol}}{p}$ (in this case T_tol = 500, which we have divided into 5 bins of equal size q = 100, see Figure 5a). Then the center of mass for the finite-time average of the variable can be estimated by using the formula $<y_{i_{(av)}>}=\underset{{\beta }_1}{\overset{{\beta }_2}{\int }}\frac{y_i(t)dt}{q}$, where β₁ = q(p−1)+1 and β₂ = pq. Here p is the number of bins and q is the finite-time period of the oscillations. The average value of the state variable < y_i(av)> has been calculated for the homogeneous and inhomogeneous oscillations in Figure 5, which takes nonzero value for inhomogeneous oscillations (denoted by squares in Figure 5b) and nearly null value for the homogeneous oscillations (represented by a diamond in Figure 5b).

FIGURE 5

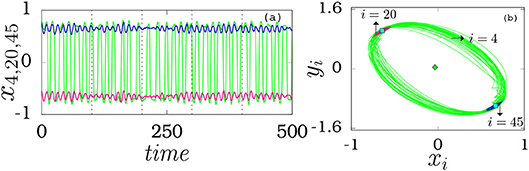
Figure 5. (a) Time series and (b) phase portraits of representative oscillators from the homogeneous and inhomogeneous states constituting the imperfect amplitude mediated chimera. The oscillators x_i, i = 20, 45 are from the upper and lower branches of the inhomogeneous state. The oscillator x_i, i = 4, represents the homogeneous oscillations from the desynchronized group. The corresponding time average of the homogeneous and inhomogeneous oscillations are denoted by diamond and squares in (b). Parameters are the same as in Figure 1.

In addition, the above dynamical transition is also analyzed by estimating the average number of inhomogeneous oscillators. In the traveling wave (TW) state, all the oscillators oscillate homogeneously about the origin whereas some of the oscillators take nonzero center of mass values in the amplitude mediated chimera state constituting the inhomogeneous state. Thus the coherent oscillators in the inhomogeneous state oscillate with small amplitudes with nonzero value of the finite-time average whereas the incoherent oscillators in the homogeneous states oscillate with large amplitudes and null value of the finite-time average. The nonzero value of the finite-time average of the (individual) oscillators indicate that all the oscillators are in the inhomogeneous states, i.e., death states. The strength of inhomogeneous oscillators among the total population in a dynamical state can be found from the following relation,

$\begin{array}{rc}K=1-\frac{{\displaystyle {\sum }_{i=1}^N}{H}_{y_i}}{N},H_{y_i}=\Theta (\delta -<y_{i_{(av)}}>),& (2)\end{array}$

where δ is a predefined threshold value and Θ(.) is the Heaviside step function. The strength of inhomogeneous oscillators (K) shows null value for the traveling wave state and unity for the death state. The value of K lying between 0 < K < 1 corresponds to the amplitude mediated chimera state. To understand the transition among the observed dynamical states, we have plotted the strength of inhomogeneous oscillators (K) in the network as a function of the coupling strength ϵ for two distinct coupling ranges r = 0.2 and r = 0.4 (which have been earlier traced along the lines L₁ and L₂ in Figure 7) in Figures 6A,B, respectively. It is evident from the figures that the transition takes place from traveling wave to cluster oscillation death via amplitude mediated chimera state. Shaded region corresponds to the imperfect amplitude mediated chimera which constitutes the intermediate state between the traveling wave and the coherent death states.

FIGURE 6

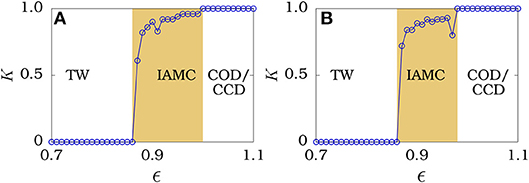
Figure 6. Strength of inhomogeneous oscillators in a network as a function of the coupling strength ϵ for coupling ranges (A) r = 0.2 and (B) r = 0.4 which have been traced along the lines L₁ and L₂ in Figure 7. TW, IAMC, COD/CCD are the traveling wave, imperfect amplitude mediated chimera, cluster oscillation death or cluster chimera death states, respectively. Parameters: ω = 1.0, λ = 1.0, and N = 100.

FIGURE 7

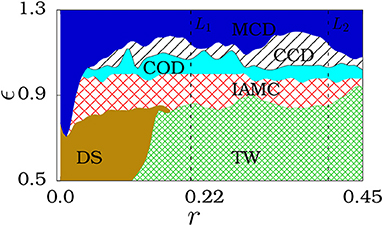
Figure 7. Two parameter plot in (r, ϵ) space. DS, TW, and IAMC represent the desynchronized state, traveling wave state and imperfect amplitude mediated chimera state, respectively. COD, CCD, and MCD denote the cluster oscillation death, cluster chimera death and multi-chimera death states, respectively. Parameters are the same as in Figure 6.

5. Global Dynamical Behavior in Coupled Stuart-Landau Oscillators

The global dynamical behavior of the nonlocally coupled Stuart-Landau oscillators is shown as a two-parameter phase diagram (see Figure 7) in the (r, ϵ) space. For smaller values of the coupling range, there is a transition from desynchronized state to death state via the imperfect amplitude mediated chimera as a function of the coupling strength. On the other hand, for larger values of the coupling range r, the coupled system exhibits transition from the traveling wave state to the death states via imperfect amplitude mediated chimera as a function of the coupling strength. For larger values of the coupling strength, the number of oscillators exhibiting homogeneous large oscillations (constituting incoherent domain of the imperfect amplitude mediated chimera) decreases and finally settles among one of the branches of the inhomogeneous steady state resulting in the coherent oscillation death state in almost the entire coupling range of r. The coherent oscillation death states manifest as a cluster chimera death state and then as a stable multi-chimera death state for further larger values of the coupling strength in the entire coupling range r. We also note here that the structure of the two parameter plot is similar for any other set of initial conditions and that the coexistence of distinct dynamics takes place only near the boundaries due to multistabilities among the dynamical states.

The oscillators in the network segregate into different numbers of clusters as a function of the coupling range r, as shown in Figure 8. The system of coupled Stuart-Landau oscillators exhibit more number of clusters for smaller coupling range than that of larger coupling range. Eleven cluster states are observed for coupling range r = 0.06 as depicted in Figure 8a. Upon increasing the coupling range to r = 0.14 and r = 0.26, it is observed that the number of clusters decreases to five and three, respectively, as illustrated in Figures 8b,c. The number of clusters become two for the coupling range r = 0.4 (see Figure 8d). It is also evident from the figures that the size of the clusters increases while the number of clusters decreases. It is also found that the number of clusters in the amplitude mediated chimera, cluster oscillation death and cluster chimera death states exponentially decreases with increase in the coupling range r. The number of clusters (n₀) as a function of the coupling range r is depicted in Figure 9, which clearly indicates the exponential decrease of the number of clusters. It is also evident from the inset of Figure 9 that the system obeys a power law relation $n_0=r^a$ as a function of the nonlocal coupling range r with best fit a = −0.505. The open circles in the inset denote numerical data, while the corresponding best fit is shown by solid line (red). It is also noticed that the system exhibits symmetric clusters in the oscillation death state as a function of coupling range.

FIGURE 8

Figure 8. Decreasing number of clusters with increasing value of the coupling range r for the coupling strength ϵ = 1.0: (a) 11 clusters for r = 0.06, (b) 5 clusters for r = 0.14, (c) 3 clusters for r = 0.26 (d) 2 clusters for r = 0.4. Other parameters λ = 1.0, ω = 1.0, and N = 100.

FIGURE 9

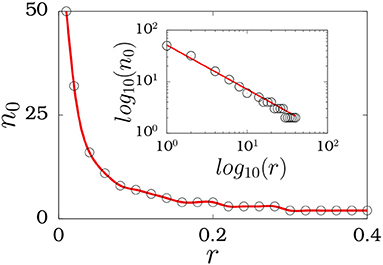
Figure 9. Exponential decay of the number of clusters at ϵ = 1.0 in the inhomogeneous states of cluster oscillation death as a function of the nonlocal coupling range(r). The corresponding power law fit is shown in the inset. The unfilled circles in the inset denote the numerical data and corresponding power law fit is shown by solid line.

For any set of initial conditions, including random, symmetric or asymmetric cluster conditions, the system exhibits only symmetric clusters in the death states which are clearly demonstrated through the transient behavior in Figure 10. The emergence of symmetric clusters in the oscillation death states from the random distribution of (x_i, y_i) between −1 to +1 and 0 to 1 are depicted in Figures 10a,b, respectively. The symmetric initial state distribution ((x_j, y_j) = (+1, −1) for $j=1,2..,\frac{N}{2}$ and (x_j, y_j) = (−1, +1) for $j=\frac{N}{2}+1,..,N$) induced symmetric cluster death states is evident from Figure 10c. Analogously, the asymmetric distribution of initial states also exhibits symmetric cluster death states which is shown in Figure 10d.

FIGURE 10

Figure 10. Transient plots for the emergence of symmetric cluster ocillation death states from distict initial states at r = 0.4 and ϵ = 1.0. The initial states (x_i, y_i) are distributed (a) randomly between -1 to +1, (b) randomly between 0 to 1, (c) in symmetric cluster, and (d) asymmetric cluster conditions. Other parameters are same as in Figure 8.

6. Effect of Noise Intensity on Amplitude Mediated Chimera

The robustness of the imperfect amplitude mediated chimera state is further analyzed in the system (1) by introducing a Gaussian white noise. The system equation with the addition of Gaussian white noise can be expressed as,

$\begin{array}{rcl}{ẋ}_i& =& (\lambda -x_i^2-y_i^2)x_i-\omega y_i+\frac{ϵ}{2P}{\displaystyle \sum _{k=i-P}^{i+P}}(x_k-x_i)+\sqrt{2D}{\zeta }_i(t),\\ {ẏ}_i& =& (\lambda -x_i^2-y_i^2)y_i+\omega x_i-\frac{ϵ}{2P}{\displaystyle \sum _{k=i-P}^{i+P}}(y_k-y_i),i=1,2,\dots ,N,& (3)\end{array}$

where ζ_i(t) ∈ R is the Gaussian white noise and D is the intensity of noise. Here 〈ζ_i(t)〉 = 0, ∀i, and $\langle {\zeta }_i(t){\zeta }_i(t^{\prime })\rangle ={\delta }_{ij}\delta (t-t^{\prime }),$ ∀i, j, where δ_ij and δ(t−t′) are the Kronecker-delta and delta distribution, respectively. Figure 11 is plotted for the regions of imperfect amplitude mediated chimera state in the (r, ϵ) space for three different noise intensities, namely D = 0.0, D = 0.1 and D = 0.5 which are denoted by solid, dot-dashed and dotted lines, respectively. It is evident from the figures that the emergence imperfect amplitude mediated chimera even for increasing larger values of noise intensity which confirms their robustness against noise.

FIGURE 11

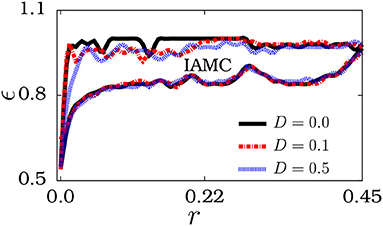
Figure 11. Region of imperfect amplitude mediated chimera (IMAC) states for noise intensities D = 0.0 (solid line), D = 0.1 (dot-dashed line), and D = 0.5 (dotted line).

7. Conclusion

We have investigated the dynamical transitions in a network of nonlocally coupled Stuart-Landau oscillators with combined attractive and repulsive couplings. We found that the competing attractive and repulsive interactions induce imperfect amplitude mediated chimera states. These states are characterized by the oscillators constituting the synchronized and desynchronized groups, which drift randomly between the homogeneous and inhomogeneous states as a function of time. Hence it becomes impossible to determine homogeneous and inhomogeneous groups of oscillators. To overcome this difficulty, we have estimated the finite-time average of each oscillators to distinguish each group. Further, we have distinguished each dynamical state by calculating the strength of the inhomogeneous oscillators in a total population of a network. We found that the observed imperfect amplitude mediated chimera mediates the transition between the oscillatory and oscillation death states and turns out to be the transition route for the cluster oscillation death state. We have also calculated the number of clusters in the oscillation death states as a function of the coupling range. We found that the number of clusters decays exponentially as a function of the coupling range and obeys a power law relation with the nonlocal coupling range.The obtained imperfect amplitude mediated chimera state is robust against various initial states and different sizes of the network. Finally, we also found that the observed imperfect amplitude mediated chimera state is robust against noise by introducing a Gaussian white noise.

Author Contributions

VKC formulated the problem in consultation with the other authors and drafted the manuscript. KS carried out the entire study of the work and completed the manuscript. DVS and ML critically read and revised the manuscript. All the authors discussed the results, drew conclusions and edited the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

KS sincerely thanks the CSIR for a fellowship under SRF Scheme (09/1095(0037)/18-EMR-I). The work of VKC forms part of a research project sponsored by INSA Young Scientist Project under Grant No. SP/YSP/96/2014 and SERB-DST Fast Track scheme for young scientists under Grant No. YSS/2014/000175. DVS is supported by the CSIR EMR Grant No. 03(1400)/17/EMR-II. The work of ML is supported by DST-SERB Distinguished Fellowship.

References

1. Pikovsky A, Rosenblum M, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge, UK: Cambridge University Press (2001).

Google Scholar

2. Kuramoto Y, Battogtokh D. Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlinear Phenom Complex Syst. (2002) 5:380. Available online at: https://arxiv.org/abs/cond-mat/0210694

Google Scholar

3. Schneider I, Kapeller M, Loos S, Zakharova A, Fiedler B, Schöll E. Stable and transient multicluster oscillation death in nonlocally coupled networks. Phys Rev E (2015) 92:052915. doi: 10.1103/PhysRevE.92.052915

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Majhi S, Muruganandam P, Ferreira FF, Ghosh D, Dana SK. Asymmetry in initial cluster size favors symmetry in a network of oscillators. Chaos (2018) 28:081101. doi: 10.1063/1.5043588

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Omelchenko I, Omel'chenko OE, Hövel P, Schöll E. When nonlocal coupling between oscillators becomes stronger: patched synchrony or multichimera states. Phys Rev Lett. (2013) 110:224101. doi: 10.1103/PhysRevLett.110.224101

CrossRef Full Text | Google Scholar

6. Sethia GC, Sen A, Johnston GL. Amplitude-mediated chimera states. Phys Rev E (2013) 88:042917. doi: 10.1103/PhysRevE.88.042917

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Omelchenko I, Maistrenko Y, Hövel P, Schöll E. Loss of coherence in dynamical networks: spatial chaos and chimera states. Phys Rev Lett. (2011) 106:234102. doi: 10.1103/PhysRevLett.106.234102

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Vadivasova TE, Strelkova GI, Bogomolov SA, Anishchenko VS. Correlation analysis of the coherence-incoherence transition in a ring of nonlocally coupled logistic maps. Chaos (2016) 26:093108. doi: 10.1063/1.4962647

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Semenova N, Zakharova A, Schöll E, Anishchenko V. Does hyperbolicity impede emergence of chimera states in networks of nonlocally coupled chaotic oscillators? Europhys. Lett. (2015) 112:40002. doi: 10.1209/0295-5075/112/40002

CrossRef Full Text | Google Scholar

10. Bogomolov SA, Slepnev AV, Strelkova GI, Schöll E, Anishchenko VS. Mechanisms of appearance of amplitude and phase chimera states in ensembles of nonlocally coupled chaotic systems. Commun Nonlin Sci Numer Simulat. (2017) 43:25–36. doi: 10.1016/j.cnsns.2016.06.024

CrossRef Full Text | Google Scholar

11. Gopal R, Chandrasekar VK, Senthilkumar DV, Venkatesan A, Lakshmanan M. Effect of asymmetry parameter on the dynamical states of nonlocally coupled nonlinear oscillators. Phys Rev E (2015) 91:062916. doi: 10.1103/PhysRevE.91.062916

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hizanidis J, Kanas VG, Bezerianos A, Bountis T. Chimera states in networks of nonlocally coupled Hindmarsh–Rose neuron models. Int J Bifurcat Chaos (2014) 24:1450030. doi: 10.1142/S0218127414500308

CrossRef Full Text | Google Scholar

13. Omelchenko I, Provata A, Hizanidis J, Schöll E, Hövel P. Robustness of chimera states for coupled FitzHugh-Nagumo oscillators. Phys Rev E (2015) 91:022917. doi: 10.1103/PhysRevE.91.022917

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bastidas VM, Omelchenko I, Zakharova A, Schöll E, Brandes T. Quantum signatures of chimera states. Phys Rev E (2015) 92:062924. doi: 10.1103/PhysRevE.92.062924

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tsigkri-DeSmedt ND, Hizanidis J, Hövel P, Provata A. Multi-chimera states and transitions in the Leaky Integrate-and-Fire model with nonlocal and hierarchical connectivity. Eur Phys J (2016) 225:1149–64. doi: 10.1140/epjst/e2016-02661-4

CrossRef Full Text | Google Scholar

16. Hizanidis J, Panagakou E, Omelchenko I, Schöll E, Hövel P, Provata A. Chimera states in population dynamics: Networks with fragmented and hierarchical connectivities. Phys Rev E (2015) 92:012915. doi: 10.1103/PhysRevE.92.012915

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Rosin DP, Rontani D, Gauthier DJ. Synchronization of coupled Boolean phase oscillators. Phys Rev E (2014) 89:042907. doi: 10.1103/PhysRevE.89.042907

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hagerstrom AM, Murphy TE, Roy R, Hövel P, Omelchenko I, Schöll E. Experimental observation of chimeras in coupled-map lattices. Nat Phys. (2012) 8:658–61. doi: 10.1038/nphys2372

CrossRef Full Text | Google Scholar

19. Larger L, Penkovsky B, Maistrenko Y. Virtual chimera states for delayed-feedback systems. Phys Rev Lett. (2013) 111:054103. doi: 10.1103/PhysRevLett.111.054103

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Larger L, Penkovsky B, Maistrenko Y. Laser chimeras as a paradigm for multistable patterns in complex systems. Nat Commun. (2015) 6:7752. doi: 10.1038/ncomms8752

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Tinsley MR, Nkomo S, Showalter K. Chimera and phase-cluster states in populations of coupled chemical oscillators. Nat Phys. (2012) 8:662–5. doi: 10.1038/nphys2371

CrossRef Full Text | Google Scholar

22. Nkomo S, Tinsley MR, Showalter K. Chimera states in populations of nonlocally coupled chemical oscillators. Phys Rev Lett. (2013) 110:244102. doi: 10.1103/PhysRevLett.110.244102

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wickramasinghe M, Kiss IZ. Spatially organized dynamical states in chemical oscillator networks: synchronization, dynamical differentiation, and chimera patterns. PLoS ONE (2013) 8:e80586. doi: 10.1371/journal.pone.0080586

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Schmidt L, Schönleber K, Krischer K, García-Morales V. Coexistence of synchrony and incoherence in oscillatory media under nonlinear global coupling. Chaos (2014) 24:013102. doi: 10.1063/1.4858996

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kapitaniak T, Kuzma P, Wojewoda J, Czolczynski K, Maistrenko Y. Imperfect chimera states for coupled pendula. Sci Rep. (2014) 4:6379. doi: 10.1038/srep06379

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zakharova A, Kapeller M, Schöll E. Chimera death: symmetry breaking in dynamical networks. Phys Rev Lett. (2014) 112:154101. doi: 10.1103/PhysRevLett.112.154101

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Loos SAM, Claussen JC, Schöll E, Zakharova A. Chimera patterns under the impact of noise. Phys Rev E (2016) 93:012209. doi: 10.1103/PhysRevE.93.012209

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Tumash L, Zakharova A, Lehnert J, Just W, Schöll E. Stability of amplitude chimeras in oscillator networks. Europhys Lett. (2017) 117:20001. doi: 10.1209/0295-5075/117/20001

CrossRef Full Text | Google Scholar

29. Premalatha K, Chandrasekar VK, Senthilvelan M, Lakshmanan M. Stable amplitude chimera states in a network of locally coupled Stuart-Landau oscillators. Chaos (2018) 28:033110. doi: 10.1063/1.5006454

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sathiyadevi K, Chandrasekar VK, Senthilkumar DV. Stable amplitude chimera in a network of coupled Stuart-Landau oscillators. Phys Rev E (2018) 98:032301. doi: 10.1103/PhysRevE.98.032301

CrossRef Full Text | Google Scholar

31. Sheeba JH, Chandrasekar VK, Lakshmanan M. Chimera and globally clustered chimera: impact of time delay. Phys Rev E (2010) 81:046203. doi: 10.1103/PhysRevE.81.046203

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bera BK, Ghosh D, Banerjee T. Imperfect traveling chimera states induced by local synaptic gradient coupling. Phys Rev E (2016) 94:012215. doi: 10.1103/PhysRevE.94.012215

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Abrams DM, Mirollo R, Strogatz SH, Wiley DA. Solvable model for chimera states of coupled oscillators. Phys Rev Lett. (2008) 101:084103.

PubMed Abstract | Google Scholar

34. Buscarino A, Frasca M, Gambuzza LV, Hövel P. Chimera states in time-varying complex networks. Phys Rev E (2015) 91:022817. doi: 10.1103/PhysRevE.91.022817

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Shima Si, Kuramoto Y. Rotating spiral waves with phase-randomized core in nonlocally coupled oscillators. Phys Rev E (2004) 69:036213. doi: 10.1103/PhysRevE.69.036213

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Xie J, Knobloch E, Kao HC. Twisted chimera states and multicore spiral chimera states on a two-dimensional torus. Phys Rev E (2015) 92:042921. doi: 10.1103/PhysRevE.92.042921

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Sethia GC, Sen A. Chimera states: the existence criteria revisited. Phys Rev Lett. (2014) 112:144101. doi: 10.1103/PhysRevLett.112.144101

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Mukherjee R, Sen A. Amplitude mediated chimera states with active and inactive oscillators. Chaos (2018) 28:053109. doi: 10.1063/1.5031804

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Sathiyadevi K, Chandrasekar VK, Senthilkumar DV, Lakshmanan M. Distinct collective states due to trade-off between attractive and repulsive couplings. Phys Rev E (2018) 97:032207. doi: 10.1103/PhysRevE.97.032207

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Mishra A, Hens C, Bose M, Roy PK, Dana SK. Chimeralike states in a network of oscillators under attractive and repulsive global coupling. Phys Rev E (2015) 92:062920. doi: 10.1103/PhysRevE.92.062920

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Frasca M, Bergner A, Kurths J, Fortuna L. Bifurcations in a star-like network of stuart–landau oscillators. Int J Bifurcat Chaos (2012) 22:1250173. doi: 10.1142/S0218127412501738

CrossRef Full Text | Google Scholar

42. Kawaguchi S. Stability gap between off- and on-firing states in a coupled Ginzburg-Landau oscillator neural network. Prog Theor Phys. (2000) 104:709–721. doi: 10.1143/PTP.104.709

CrossRef Full Text | Google Scholar

43. Uchiyama S. Flow version of statistical neurodynamics for oscillator neural networks. Physica A (2012) 391:2807–17. doi: 10.1016/j.physa.2011.12.026

CrossRef Full Text | Google Scholar