- 1Research Group Numerical Mathematics (Partial Differential Equations), Faculty of Mathematics, Technische Universität Chemnitz, Chemnitz, Germany
- 2ICTEAM Institute, Université Catholique de Louvain, Louvain-la-Neuve, Belgium
We derive a variational model to fit a composite Bézier curve to a set of data points on a Riemannian manifold. The resulting curve is obtained in such a way that its mean squared acceleration is minimal in addition to remaining close the data points. We approximate the acceleration by discretizing the squared second order derivative along the curve. We derive a closed-form, numerically stable and efficient algorithm to compute the gradient of a Bézier curve on manifolds with respect to its control points, expressed as a concatenation of so-called adjoint Jacobi fields. Several examples illustrate the capabilities and validity of this approach both for interpolation and approximation. The examples also illustrate that the approach outperforms previous works tackling this problem.
AMS subject classification (2010). 65K10, 65D10, 65D25, 53C22, 49Q99.
1. Introduction
This papers addresses the problem of fitting a smooth curve to data points d0, …, dn lying on a Riemannian manifold and associated with real-valued parameters t0, …, tn. The curve strikes a balance between a data proximity constraint and a smoothing regularization constraint.
Several applications motivate this problem in engineering and the sciences. For instance, curve fitting is of high interest in projection-based model order reduction of one-dimensional dynamical systems [1]. In that application, the dynamical system depends on the Reynolds number and the model reduction is obtained by computing suitable projectors as points on a Grassmann manifold. Finding a projector is however a time- and memory-consuming task. Based on projectors precomputed for given parameter values, fitting is used to approximate the projector associated with a new parameter value. In Gousenbourger et al. [2], the same strategy is used to approximate wind field orientations represented as points on the manifold of positive semidefinite covariance matrices of size p and rank r. Further applications are involving rigid-body motions on SE(3), like Cosserat rods applications [3], or orientation tracking [4]. Sphere-valued data are also of interest in many applications of data analysis, for storm tracking and prediction, or the study of bird migration [5].
There exists different approaches to tackle the curve fitting problem. Among others, we name here the subdivision schemes approach [6, 7] or the Lie-algebraic methods [8]. However, the most popular approach nowadays is probably to encapsulate the two above-mentioned constraints into an optimization problem
where Γ is an admissible space of curves , t↦γ(t), denotes the (Levi-Civita) second covariant derivative, and ∥·∥γ(t) denotes the Riemannian metric at γ(t) from which we can define a Riemannian distance d(·, ·). Finally, λ∈ℝ is a parameter that strikes the balance between the regularizer and the fitting term . This approach leads to the remarkable property that, when the manifold reduces to the Euclidean space and Γ is the Sobolev space , the solution to (1) is the natural cubic spline [9].
Optimization on manifolds has gained a lot of interest this last decade, starting with the textbook [10] that summarizes several optimization methods on matrix manifolds. Recently, toolboxes have emerged, providing easy access to such optimization methods, e.g., Manopt [11] and MVIRT [12]. The former received a very positive return in many different topics of research, with applications for example in low-rank modeling in image analysis [13], dimensionality reduction [14], phase retrieval [15] or even 5G-like MIMO systems [16]. The latter stems from recent interest in manifold-valued image and data processing, phrased as variational models on the product manifold , where N is the number of pixels. Starting with total variation (TV) regularization of phase-valued data [17, 18], different methods for TV on manifolds [19, 20] have been developed as well as second order methods [21, 22] up to infimal convolution [23] and total generalized variation [23, 24]. Furthermore, different algorithms have been generalized to manifold-valued data, besides the previous works using gradient descent or cyclic proximal point methods, a Douglas–Rachford splitting [25], iteratively reweighted least squares [26] and more general half-quadratic minimization [27] have been introduced.
The curve fitting problem (1), has been tackled differently the past few years. Samir et al. [28] considered the case where Γ is an infinite dimensional Sobolev space of curves, and used the Palais-metric to design a gradient descent algorithm for (1) (see e.g., [29] for an application of this approach). Another method consists in discretizing the curve γ in N points, and therefore considering (see e.g., [30] for a result on SO(3)). Finally, the limit case where λ → 0 is already well studied and known as the geodesic regression [31–33].
A recent topic concerns curve fitting by means of Bézier curves. In that approach, the search space Γ is reduced to as set of composite Bézier curves. Those are a very versatile tool to model smooth curves and surfaces for real- and vector-valued discrete data points (see [34] for a comprehensive textbook), but they can also be used to model smooth curves and surfaces for manifold-valued data [35, 36]. The advantage to work with such objects, compared to classical approaches, are that (i) the search space is drastically reduced to the so-called control points of the Bézier curves (and this leads to better time and memory performances) and (ii) it is very simple to impose differentiability for the optimal curve, which is appreciated in several of the above-mentioned applications. However, while obtaining such an optimal curve reduces directly to solving a linear system of equations for data given on a Euclidean space, there is up to now no known closed form of the optimal Bézier curve for manifold valued data.
In this work, we derive a gradient descent algorithm to compute a differentiable composite Bézier curve that satisfies (1), i.e., such that B(t) has a minimal mean squared acceleration, and fits the set of n+1 manifold-valued data points at their associated time-parameters. We consider the manifold-valued generalization of Bézier curves [36] in the same setting as in Arnould et al. [37], or more recently in Gousenbourger et al. [38]. We employ the (squared) second order absolute difference introduced in Bačák et al. [22] to obtain a discrete approximation of the regularizer from (1). The quality of the approximation depends only on the number of sampling points. We exploit the recursive structure of the De Casteljau algorithm [36] to derive the gradient of the objective function with respect to the control points of B(t). The gradient is built as a recursion of Jacobi fields that, for numerical reasons, are implemented as a concatenation of so-called adjoint Jacobi fields. Furthermore, the corresponding variational model only depends on the number of control points of the composite Bézier curve, and not on the number of sampling points. We finally obtain an approximating model to (1) that we solve with an algorithm only based on three tools on the manifold: the exponential map, the logarithmic map, and a certain Jacobi field along geodesics.
The paper is organized as follows. We introduce the necessary preliminaries—Bézier curves, Riemannian manifolds and Riemannian second order finite differences— in section 2. In section 3 we derive the gradient of the discretized mean squared acceleration of the composite Bézier curve with respect to its control points, and thus of the regularizer of (1). In section 4, we present the corresponding gradient descent algorithm, as well as an efficient gradient evaluation method, to solve (1) for different values of λ. The limit case where λ → ∞ is studied as well. Finally, in section 5, we validate, analyze and illustrate the performance of the algorithm for several numerical examples on the sphere S2 and on the special orthogonal group SO(3). We also compare our solution to existing Bézier fitting methods. A conclusion is given in section 6.
2. Preliminaries
2.1. Bézier Functions and Composite Bézier Spline
Consider the Euclidean space ℝm. A Bézier curve of degree K∈ℕ is a function parametrized by control points and taking the form
where are the Bernstein basis polynomials [34]. For example the linear Bézier curve β1 is just the line segment (1−t)b0+tb1 connecting the two control points b0 and b1. The explicit formulae of the quadratic and cubic Bézier curves read
for given control points and an additional point for the cubic case.
A composite Bézier curve is a function B:[0, n] → ℝm composed of n Bézier curves and defined as
where Ki∈ℕ denotes the degree of the ith Bézier curve βKi of B and , j = 0, …, Ki, are its control points. Furthermore, B(t) is continuous if the last and first control points of two consecutive segments coincide [34]. We introduce pi as the point at the junction of two consecutive Bézier segments, i.e., . Differentiability is obtained if the control points of two consecutive segments are aligned. We introduce further and such that the differentiability condition reads .
Example 1 (C1 conditions for composite cubic Bézier curves). We consider the case where the Bézier segments are all cubic, as represented in Figure 1. The composite Bézier curve B(t) is C1 if , i = 1, …, 4, with , , and .
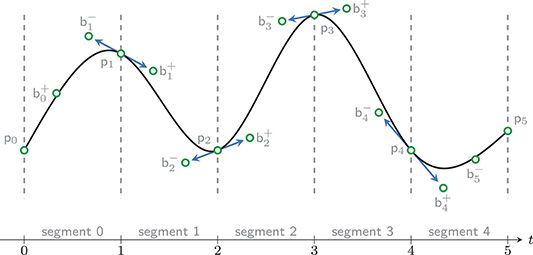
Figure 1. Schematic representation of the composite cubic Bézier curve , for (black), and its control points (green circles). Continuous differentiability is reached at the junction of the segments (the blue arrows draw the first derivative of B).
2.2. Riemannian Manifolds
We consider a complete m-dimensional Riemannian manifold . We refer to O'Neill [39] and do Carmo [40] for an introduction to Riemannian manifolds and to [10] for optimization thereon. We will use the following terminology and notations.
We denote by the (Euclidean) tangent space to at ; is the tangent bundle to ; 〈·, ·〉a denotes the inner product in the tangent space at a and from which we deduce the norm of denoted by . For a (not necessarily unique) shortest geodesic between a and , we write , t↦g(t; a, b), parametrized such that g(0;a, b) = a and g(1;a, b) = b. This choice of parametrization also means that the covariant derivative of g with respect to time satisfies , for all t∈[0, 1], where is the geodesic distance between a and . The Riemannian exponential reads and we denote by ra∈ℝ the maximal radius such that the exponential map is bijective on . Then is called the Riemannian logarithm which is (locally) the inverse of the exponential. A Riemannian manifold is called symmetric in if the geodesic reflection sx at given by the mapping γ(t)↦γ(−t) is an isometry at least locally near x, for all geodesics through γ(0) = x. If is symmetric in every , the manifold is called (Riemannian) symmetric space or symmetric manifold.
In the following we assume, that both the exponential and the logarithmic map are available for the manifold and that they are computationally not too expensive to evaluate. Furthermore, we assume that the manifold is symmetric.
2.3. Composite Bézier Curves on Manifolds
One well-known way to generalize Bézier curves to a Riemannian manifold is via the De Casteljau algorithm [36, section 2]. This algorithm only requires the Riemannian exponential and logarithm and conserves the interpolation property of the first and last control points. Some examples on interpolation and fitting with Bézier curves or Bézier surfaces, i.e., generalizations of tensor product Bézier curves, can be found in Absil et al. [35].
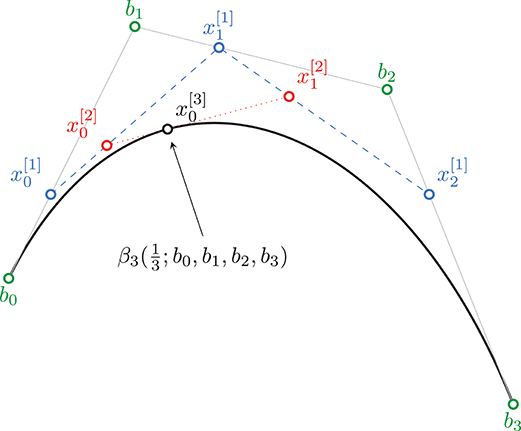
Consider , the manifold-valued Bézier curve of order K driven by K+1 control points . We introduce the points and iterate the construction of further points. For i = 0, …, K−k, k = 1, …, K, we define
as the ith point of the kth step of the De Casteljau algorithm, and obtain .
The De Casteljau algorithm is illustrated on Figure 2 for a Euclidean cubic Bézier curve β3(t; b0, b1, b2, b3). The general cubic Bézier curve can be explicitly expressed on a manifold as
The conditions of continuity and differentiability are generalized to manifolds in Popiel and Noakes [36].
Lemma 2 (Differentiability conditions [36]). Consider the composite Bézier curve consisting of and , i.e.,
The composite Bézier curve B(t) is continuous and continuously differentiable if the two following conditions hold:
The composite Bézier curve is then defined completely analogously to the Euclidean case from Equation (2). The differentiability conditions (4) of Lemma 2 have to be satisfied at each junction point pi, i = 1, …, n − 1.
Example 3 (Composite cubic Bézier curves). The composite cubic Bézier curve is C1 if . See Figure 1 for an example on with n = 5 segments and Figure 3 for an example on with n = 3 segments.
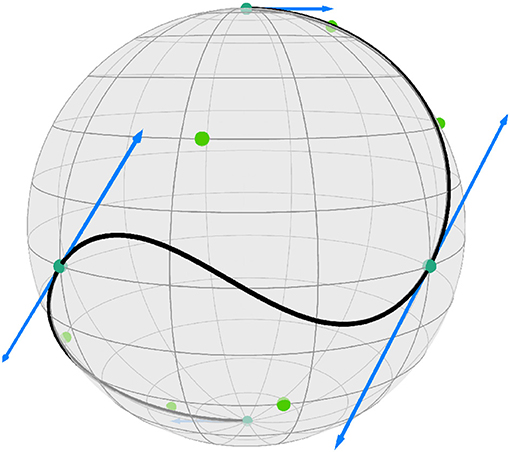
Figure 3. A composite cubic Bézier curve B:[0, 3] → S2. The end points pi, i = 0, …, 3, (cyan) and intermediate points (green) determine its shape; continuous differentiability is illustrated by the logarithmic maps , i∈{1, 2} (blue arrows).
2.4. Discrete Approximation of the Mean Squared Acceleration
We discretize the mean squared acceleration (MSA) of a curve , by discretizing the corresponding integral
i.e., the regularizer from (1). We approximate the squared norm of the second (covariant) derivative by the second order absolute finite difference introduced by Bačák et al. [22]. Consider three points and the set of mid-points of x and z
for all (not necessarily shortest) geodesics g connecting x and z. The manifold-valued second order absolute finite difference is defined by
This definition is equivalent, on the Euclidean space, to .
Using equispaced points t0, …, tN, N∈ℕ, with step size , we approximate , i = 1, …, N−1, and obtain by the trapezoidal rule
For Bézier curves γ(t) = B(t) we obtain for the regularizer in (1) the discretized MSA A(b) that depends on the control points b and reads
3. The Gradient of the Discretized Mean Squared Acceleration
In order to minimize the discretized MSA A(b), we aim to employ a gradient descent algorithm on the product manifold , where M is the number of elements in b. In the following, we derive a closed form of the gradient ∇bA(b) of the discretized MSA (7). This gradient is obtained by means of a recursion and the chain rule. In fact, the derivative of (6) is already known [22], such that it only remains to compute the derivative of the composite Bézier curve.
We first introduce the following notation. We denote by the directional derivative of evaluated at x0, with respect to its argument x and in the direction . We use the short hand Dxf[η] = Dxf[η](x) whenever this directional derivative is evaluated afterwards again at x.
We now state the two following definitions, which are crucial for the rest of this section.
Definition 4 (Gradient [10, Equation (3.31), p. 46]). Let be a real-valued function on a manifold , and .
The gradient of f at x is defined as the tangent vector that fulfills
For multivariate functions f(x, y), we denote the gradient of f with respect to x at (x0, y0) by writing . We shorten this notation as when this gradient is seen as a function of x (and y).
Definition 5 (Chain rule on manifolds [10, p. 195]). Let , be two functions on a manifold and , x↦F(x) = (f ° h)(x) = f(h(x)), their composition. Let and . The directional derivative DxF[η] of F with respect to x in the direction η is given by
where and .
The remainder of this section is organized in four parts. We first recall the theory on Jacobi fields in section 3.1 and their relation to the differential of geodesics (with respect to start and end point). In section 3.2, we apply the chain rule to the composition of two geodesics, which appears within the De Casteljau algorithm. We use this result to build an algorithmic derivation of the differential of a general Bézier curve on manifolds with respect to its control points (section 3.3). We extend the result to composite Bézier curves in section 3.4, including their constraints on junction points pi to enforce the C1 condition (4), and finally gather these results to state the gradient of the discretized MSA (7) with respect to the control points.
3.1. Jacobi Fields as Derivative of a Geodesic
In the following, we introduce a closed form of the differential Dxg(t; ·, y) of a geodesic g(t; x, y), t∈[0, 1], with respect to its start point . The differential with respect to the end point can be obtained by taking the geodesic g(t, y, x) = g(1−t; x, y).
As represented in Figure 4, we denote by γx, ξ, the geodesic starting in γx, ξ(0) = x and with direction . We introduce ζ(s): = logγx, ξ(s)y, the tangential vector in pointing toward y. Then, the geodesic variation Γg, ξ(s, t) of the geodesic g(·;x, y) with respect to the tangential direction is given by
where ε>0. The corresponding Jacobi field Jg, ξ along g is then given by the vector field
that represents the direction of the displacement of g if x is perturbed in a direction ξ.
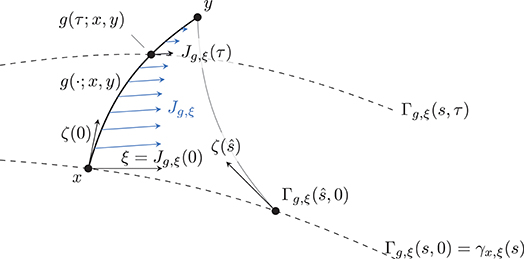
Figure 4. Schematic representation of the variation Γg, ξ(s, t) of a geodesic g w.r.t. the direction . The corresponding Jacobi field along g and in the direction ξ is the vector field .
We directly obtain Jg, ξ(0) = ξ, and Jg, ξ(1) = 0 as well as . Since Γg, ξ(s, t) = g(t; γx, ξ(s), y) we obtain by the chain rule
Remark. This relation between the derivative of geodesics and Jacobi fields is of high interest on symmetric spaces, where Jacobi fields can be computed in closed form, as summarized in the following Lemma.
Lemma 6. [22, Prop. 3.5] Let be a m-dimensional symmetric Riemannian manifold. Let g(t; x, y), t ∈ [0, 1], be a geodesic between , a tangent vector and {ξ1, …ξm} be an orthonormal basis (ONB) of that diagonalizes the curvature operator of with eigenvalues κℓ, ℓ = 1, …, m. For details, see Ch. 4.2 and 5 (Ex. 5) of [40]. Let further denote by {Ξ1(t), …, Ξm(t)} the parallel transported frame of {ξ1, …, ξm} along g. Decomposing , the derivative Dxg[η] becomes
where the Jacobi field along g and in the direction ξℓ is given by
with dg = d(x, y) denoting the length of the geodesic g(t; x, y), t∈[0, 1].
The Jacobi field of the reversed geodesic ḡ(t): = g(t; y, x) = g(1−t; x, y) is obtained using the same orthonormal basis and transported frame but evaluated at s = 1−t. We thus obtain Dyg(t; x, y)[ξℓ] = Dyg(1−t; y, x)[ξℓ] = Jḡ,ξℓ(1−t), where
Note that . Therefore , ℓ = 1, …, m, is an orthonormal basis for this tangent space.
3.2. Derivative of Coupled Geodesics
Let be a symmetric Riemannian manifold. We use the result of Lemma 6 to directly compute the derivative of coupled geodesics, i.e., a function composed of g1(t): = g(t; x, y) and g2(t): = g(t; g1(t), z). By Definition 5, we have
and by (10), we obtain
where the variation direction used in the Jacobi field is now the derivative of g1(t) in direction η. Similarly, we compute the derivative of a reversed coupled geodesic g3(t): = g(t; z, g1(t)) as
Note that the Jacobi field is reversed here, but that its variation direction is the same as the one of the Jacobi field introduced for g2(t). In a computational perspective, it means that we can use the same ONB for the derivatives of both g3 and ḡ3 Furthermore, in this case, the variation direction is also computed by a Jacobi field since Dxg1(t)[η] = Jg1, η(t).
Finally the derivative of g2 (resp. g3) on symmetric spaces is obtained as follows. Let be an ONB of for the inner Jacobi field along g1, and be an ONB of for the outer Jacobi field along g2 (resp. g3). As , and stating , the derivative of g2 (resp. g3) with respect to x in the direction reads
and accordingly for g3.
3.3. Derivative of a Bézier Curve
Sections 3.1 and 3.2 introduced the necessary concepts to compute the derivative of a general Bézier curve βK(t; b0, …, bK), as described in Equation (3), with respect to its control points bj. For readability of the recursive structure investigated in the following, we introduce a slightly simpler notation and the following setting.
Let K be the degree of a Bézier curve βK(t; b0, …, bK) with the control points . We fix k∈{1, …, K}, i∈{0, …, K−k} and t∈[0, 1]. We introduce
for the ith Bézier curve of degree k in the De Casteljau algorithm, and .
Furthermore, given x∈{bi, …, bi+k}, we denote by
its derivative with respect to one of its control points x in the direction .
Remark. Clearly any other derivative of with respect to x = bj, j<i or j>i+k is zero. In addition we have for x = bi and zero otherwise.
Theorem 7 (Derivative of a Bézier curve). Let k ∈ {1, …, K}and i ∈ {0, …, K−k}be given. The derivative of with respect to its control point x: = bj, i ≤ j ≤ i+k, and in the direction is given by
Proof. Let fix t∈[0, 1] and x = bj, i ≤ j ≤ i+k. For readability we set , , and . Note that while f depends on the control points bi, …, bi+k and is a Bézier curve of degree k, both a and b are Bézier curves of degree k−1. The former does not depend on bi+k, and the latter is independent of bi.
We prove the claim by induction. For k = 1 the function is just a geodesic. The case i<j<i+1 does not occur and the remaining first and third cases follow by the notation introduced for k = 0 and Lemma 6.
For k>1 we apply the chain rule (9) to Dxf[η] and obtain
Consider the first term Daf[Dxa[η]] and j<i+k. By (10) and the notation from (14), one directly has
For j = i+k, clearly Dxa[η] = Daf[Dxa[η]] = 0, as a does not depend on bi+k.
We proof the second term similarly. For j>i, by applying the chain rule and using the reversed Jacobi field formulation of Lemma 6 for the derivative of a geodesic with respect to its end point, we obtain
Finally, as Dxb[η] = Dbf[Dxb[η]] = 0 for x = bi, the assumption follows. □
Figure 5 represents one level of the schematic propagation tree to compute the derivative of a Bézier curve.
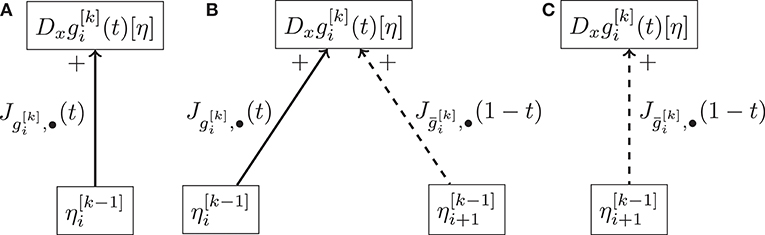
Figure 5. Schematic representation of the cases where elements compose the chained derivative of the ith Bézier curve of order k in the De Casteljau algorithm. The solid line represents a Jacobi field along , while the dashed one represents a reversed Jacobi field. (A) Represents the case x = bi, (B) represents the cases where x∈{bi+1, …, bi+k+1}, and (C) represents the case x = bi+k.
Example 8 (Quadratic Bézier curve). Consider the quadratic Bézier curve defined as
Using the notations (13), we have
The derivative of β2 at t with respect to b0 in the direction , is given by
The derivative of β2 at t with respect to b2 in the direction can be seen as deriving by the first point after inverting the Bezier curve, i.e., looking at , hence we have analogously to the first term
The case Db1β2[η], , involves a chain rule, where b1 appears in both (as its end point) and (as its starting point). Using the two intermediate results (or Jacobi fields of geodesics)
we obtain
Example 9 (Cubic Bézier curve). Consider the cubic Bézier curve defined as
As in Example 8, we use the notations (13) and define
The derivation of β3 with respect to b0 or b3 follows the same structure as in Example 8. The case of Db1β3[η], however, requires two chain rules. The needed Jacobi fields follow the tree structure shown in Figure 6B: given , we define at the first recursion step
and at the second recursion step
Note that both and are actually the derivative of β2(t; b0, b1, b2) and β2(t; b1, b2, b3), respectively, with respect to b1 and direction . Finally we have
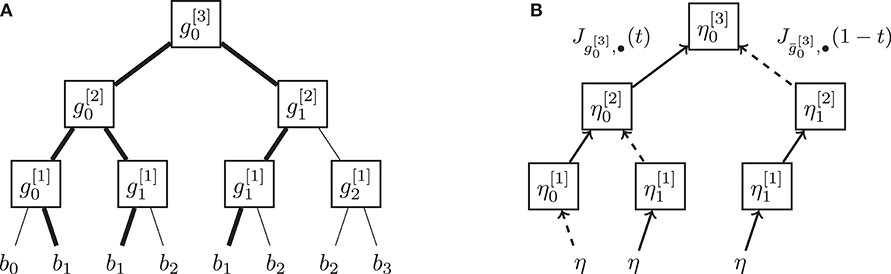
Figure 6. Construction and derivation tree of a Bézier curve β3(t; b0, b1, b2, b3). The derivative with respect to a variable bi is obtained by a recursion of Jacobi fields added at each leaf of the tree. (A) Tree-representation of the construction of a cubic Bezier curve. The thick line tracks the propagation of b1 within the tree. (B) Tree-representation of the construction of . The solid lines are Jacobi fields while dashed lines are reversed Jacobi fields.
The case of Db2β3[η] is obtained symmetrically, with arguments similar to b1.
Note that computing the Jacobi fields involved just follows the same decomposition tree as the De Casteljau algorithm (Figure 6A).
3.4. Joining Segments and Deriving the Gradient
In this subsection we derive the differential of a composite Bézier curve B(t) consisting of n segments and take the C1 conditions into account. We simplify the notations from section 2.1 and set the degree fixed to Ki = K for all segments, e.g., K = 3 for a cubic composite Bézier curve. Then the control points are , j = 0, …, K, i = 0, …, n−1. We further denote by , i = 1, …, n−1 the common junction point of the segments and p0 and pn the start and end points, respectively. For ease of notation we denote by and , i = 1, …, n−1, the two points needed for differentiability (C1) condition investigation, cf. Figure 1 for an illustration of the framework on , with K = 3.
One possibility to enforce the C1 condition (4) is to include it into the composite Bézier curve by replacing with
This way both the directional derivatives of B(t) with respect to and pi change due to a further (most inner) chain rule.
Lemma 10 (Derivative of a composite Bézier curve with C1 condition). Let B be a composite Bézier curve and introduced as above. Replacing eliminates that variable from the composite Bezier curve and keeps the remaining differentials unchanged, except the following which now read
and
In both cases, the first interval includes i−1 = 0, when i = 1.
Proof. Both first cases are from the derivation of a Bézier curve as before, for both second cases replacing yields one (for pi additional) term.
We now derive the gradient of the objective function (7). We introduce the abbreviation , and .
Theorem 11. Let be a m-dimensional manifold, x be one of the control points of a composite Bézier curve B, and {ξ1, …, ξm} be a corresponding orthonormal basis (ONB) of . The gradient of the discretized mean squared acceleration A(b) of B, w.r.t. x, discretized at N+1 equispaced times t0, …, tN is given by
Proof: As , we seek for the coefficients aℓ: = aℓ(x) such that
Therefore, for any tangential vector , we have,
By definition of A and Definition 4 this yields
We compute using the chain rule (Definition 5) as
which, by Definition 4, again becomes
The term on the left of the inner product is given in Bačák et al. [22, section 3] and the right term is given in section 3.3. While the former can be computed using Jacobi fields and a logarithmic map, the latter is the iteratively coupling of Jacobi fields. Furthermore, the differential DxBj[η] can be written as
Hence, we obtain
and by (17), (18), and (19), it follows
which yields the assertion (16).
4. Application to the Fitting Problem
The fitting problem has been tackled different ways this last decades. The approach with Bézier curves is more recent, and we refer to Absil et al. [35], Arnould et al. [37], and Gousenbourger et al. [38] for a detailed overview of these methods.
In this section, we present the numerical framework we use in order to fit a composite Bézier curve B to a set of data points associated with time-parameters t0, …, tn, such that we meet (1). For the sake of simplicity, we limit the study to the case where ti = i, i = 0, …, n. Therefore, the fitting problem (1) becomes
where is the set of the M control points of B. Remark that, compared to (1), the optimization is now done on the product manifold . Furthermore, the fitting term now implies a distance between di and pi, as B(ti) = pi.
The section is divided in three parts: the product manifold is defined in section 4.1, where the contribution of the fitting term in the gradient of E is also presented. Then, we propose an efficient algorithm to compute the gradient of the discretized MSA, based on so-called adjoint Jacobi fields. We finally shortly mention the gradient descent algorithm we use as well as the involved Armijo rule.
4.1. Fitting and Interpolation
Let us clarify the set from (20). We will explicitly present the vector b and state its size M. The set ΓB is the set of the M remaining free control points to optimize, when the continuity constraints are imposed. We distinguish two cases: (i) the fitting case, that corresponds to formulae presented in section 3, and (ii) the interpolation case (λ → ∞) where the constraint di = pi is imposed as well.
For a given composite Bézier curve consisting of a Bézier curve of degree K on each segment, and given the C1 conditions (4), the segments are determined by the points
We investigate the length of M. First, is given by pi and via (4). Second, for the segments i = 2, …, n we can further omit pi−1 since the value also occurs in the segment i−1 as last entry. Finally, the first segment contains the additional value of that is not fixed by C1 constraints. The first segment is thus composed of K+1 control points, while the n−1 remaining segments are determined by K−1 points. In total we obtain M = n(K−1)+2 control points to optimize.
Minimizing A(b) alone leads to the trivial solution, for any set of control points b = (x, …, x), , and this is why the fitting term from (20) is important.
Fitting (0 < λ < ∞). If the segment start and end points are obstructed by noise or allowed to move, we employ a fitting scheme to balance the importance given to the data points d0, …, dn. Equation (20) reads
where λ∈ℝ+ sets the priority to either the data term (large λ) or the mean squared acceleration (small λ) within the minimization. The gradient of the data term is given in Karcher [41], and the gradient of à is given by
Interpolation (λ → ∞). For interpolation we assume that the start point pi−1 and end point pi of the segments i = 1, …, n are fixed to given data di−1 and , respectively. The optimization of the discrete mean squared acceleration A(b) reads
Since the pi are fixed by constraint, they can be omitted from the vector b. We obtain
Since there are n+1 additional constraints, the minimization is hence performed on the product manifold , M′ = M−(n+1) = n(K−2)+1.
4.2. Adjoint Jacobi Fields
In the Euclidean space ℝm, the adjoint operator T* of a linear bounded operator T:ℝm → ℝq is the operator fulfilling
The same can be defined for a linear operator , , on a m-dimensional Riemannian manifold . The adjoint operator satisfies
We are interested in the case where S is the differential operator Dx of a geodesic F(x) = g(t; x, y) for some fixed t∈ℝ and . The differential can be written as
where αℓ are the coefficients of the Jacobi field (11), and ξℓ, Ξℓ(t) are given as in Lemma 6. To derive the adjoint differential we observe that for any we have
Hence the adjoint differential is given by
We introduce the adjoint Jacobi field , as
Note that evaluating the adjoint Jacobi field J* involves the same transported frame {Ξ1(t), …Ξm(t)} and the same coefficients αℓ as the Jacobi field J, which means that the evaluation of the adjoint is in no way inferior to the Jacobi field itself.
The adjoint D* of the differential is useful in particular, when computing the gradient of the composition of with . Setting , we obtain for any that
Especially for the evaluation of the gradient of the composite function h°F we obtain
The main advantage of this technique appears in the case of composite functions, i.e., of the form h°F1°F2 (the generalization to composition with K functions is straightforward). The gradient now reads,
The recursive computation of is then given by the following algorithm
Example 12. For we know by Lemma 3.1 and Lemma 3.2 from Bačák et al. [22]. Let t1, t2, t3∈[0, 1] be time points, and be a given (sub)set of the control points of a (composite) Bézier curve B. We define as the evaluations of B at the three given time points. The composition h°F hence consists of (in order of evaluation) the geodesic evaluations of the De Casteljau algorithm, the mid point function for the first and third time point and a distance function.
The recursive evaluation of the gradient starts with the gradient of the distance function. Then, for the first and third arguments, a mid point Jacobi field is applied. The result is plugged into the last geodesic evaluated within the De Casteljau “tree” of geodesics. At each geodesic, a tangent vector at a point g(tj; a, b) is the input for two adjoint Jacobi fields, one mapping to , the other to . This information is available throughout the recursion steps anyways. After traversing this tree backwards, one obtains the required gradient of h°F.
Note also that even the differentiability constraint (4) yields only two further (most outer) adjoint Jacobi fields, namely and . They correspond to variation of the start point and the end point pi, respectively as stated in (10).
4.3. A Gradient Descent Algorithm
To address (22) or (23), we use a gradient descent algorithm, as described in Absil et al. [10, Ch. 4]. For completeness the algorithm is given in Algorithm 1.
The step sizes are given by the Armijo line search condition presented in Absil et al. [10, Def. 4.2.2]. Let be a Riemannian manifold, be an iterate of the gradient descent, and β, σ∈(0, 1), α>0. Let m be the smallest positive integer such that
We set the step size to in Algorithm 1.
As a stopping criterion we use a maximal number kmax of iterations or a minimal change per iteration . In practice, this last criterion is matched first.
The gradient descent algorithm converges to a critical point if the function F is convex [10, sections 4.3 and 4.4]. The mid-points model (6) posesses two advantages: (i) the complete discretized MSA (7) consists of (chained) evaluations of geodesics and a distance function, and (ii) it reduces to the classical second order differences on the Euclidean space. However, this model is not convex on general manifolds. An example is given in the arXiv preprint (version 3) of Bačák et al. [22]1, Remark 4.6. Another possibility (also reducing to classical second order differences in Euclidean space) is the so-called Log model (see e.g., [42])
The (merely technical) disadvantage of the Log model is that the computation of the gradient involves further Jacobi fields than the one presented above, namely to compute the differentials of the logarithmic map both with respect to its argument Dxlogyx as well as its base point Dylogyx. Still, these can be given in closed form for symmetric Riemannian manifolds [23, Th. 7.2][43, Lem. 2.3]. To the best of our knowledge, the joint convexity of the Log model in x, y and z is still an open question.
5. Examples
In this section, we provide several examples of our algorithm applied to the fitting problem (20).
We validate it first on the Euclidean space and verify that it retrieves the natural cubic smoothing spline. We then present examples on the sphere S2 and the special orthogonal group SO(3). We compare our results with the fast algorithm of Arnould et al. [37], generalized to fitting, and the so-called blended cubic splines from Gousenbourger et al. [38]. The control points of the former are obtained by generalizing the optimal Euclidean conditions of (20) (in ℝm, this is a linear system of equations) to the manifold setting; the curve is afterwards reconstructed by a classical De Casteljau algorithm. In the latter, the curve is obtained as a blending of solutions computed on carefully chosen tangent spaces, i.e., Euclidean spaces.
We will show in this section that the proposed method performs as good as the existing methods when the data is from the Eulidean space (section 5.1). This also means that all methods work equally well whenever the data points on the manifold are local enough. However, we will show by the other examples (sections 5.2 and 5.3) that our proposed method outperforms the others whenever the data points are spread out on the manifold.
The following examples were implemented in MVIRT [12]2, and the comparison implementations from Arnould et al. [37] and Gousenbourger et al. [38] use Manopt [11]3. Note that both toolboxes use a very similar matrix structure and are implemented in Matlab, such that the results can directly be compared.
5.1. Validation on the Euclidean Space
As a first example, we perform a minimization on the Euclidean space . A classical result on ℝm is that the curve γ minimizing (1) is the natural () cubic spline when Γ is a Sobolev space . We compare our approach to the tangential linear system approach derived in Arnould et al. [37] in order to validate our model. We use the following data points
as well as the control points pi = di, and
where the exponential map and geodesic on ℝ3 are actually the addition and line segments, respectively. Note that, by construction, the initial curve is continuously differentiable but (obviously) does not minimize (1). The parameter λ is set to 50. The MSA of this initial curve Ã(b) is approximately 18.8828.
The data points are given to the algorithm of Arnould et al. [37] to reconstruct the optimal Bézier curve B(t), which is the natural cubic spline. The result is shown in Figure 7A together with the first order differences along the curve in Figure 7B as a dotted curve.
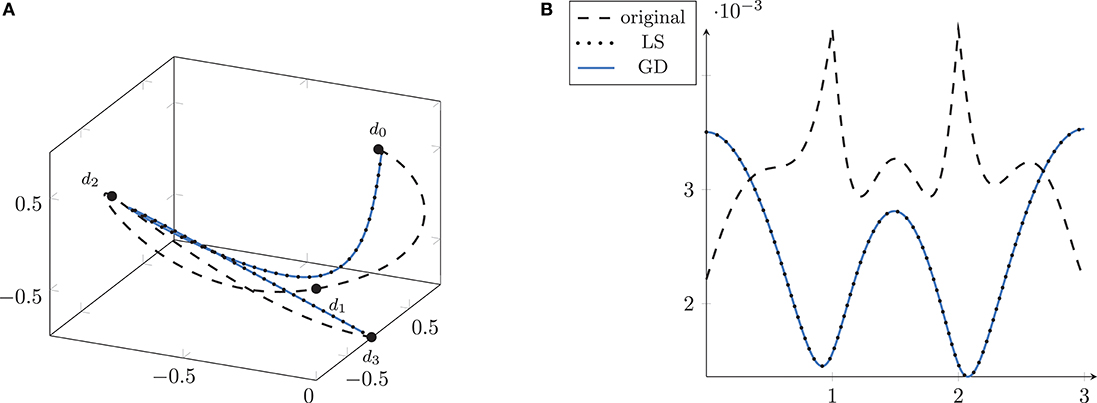
Figure 7. The initial interpolating Bézier curve in ℝ3 (dashed, A) with an MSA of 18.8828 is optimized by the linear system method (LS) from [37] (dotted) and by the proposed gradient descent (GD, solid blue). As expected, both curve coincide, with an MSA of 4.981218. The correspondance is further illustrated with their first order differences in (B).
The set of control points is optimized with our proposed method. We discretize the second order difference using N = 1600 points. The resulting curve and the first order difference plots are also obtained using these sampling values and a first order forward difference. The gradient descent algorithm from Algorithm 1 employs the Armijo rule (24) setting , σ = 10−4, and α = 1. The stopping criteria are or , and the algorithm stops when one of the two is met. For this example, the first criterion stopped the algorithm, while the norm of the gradient was of magnitude 10−6.
Both methods improve the initial functional value of Ã(b)≈18.8828 to a value of Ã(bmin)≈4.981218. Both the linear system approach and the gradient descent perform equally. The difference of objective value is 2.4524 × 10−11 smaller for the gradient descent, and the maximal distance of any sampling point of the resulting curves is of size 4.3 × 10−7. Hence, in the Euclidean space, the proposed gradient descent yields the natural cubic spline, as one would expect.
5.2. Examples on the Sphere S2
Validation on a geodesic. As a second example with a known minimizer, we consider the manifold , i.e., the two-dimensional unit sphere embedded in ℝ3, where geodesics are great arcs. We use the data points
aligned on the geodesic connecting the north pole p0 and the south pole p2, and running through a point p1 on the equator. We define the control points of the cubic Bézier curve as follows:
where x0 and x2 are temporary points and pi = di. We obtain two segments smoothly connected since . The original curve is shown in Figure 8A, where especially the tangent vectors illustrate the different speed at pi.
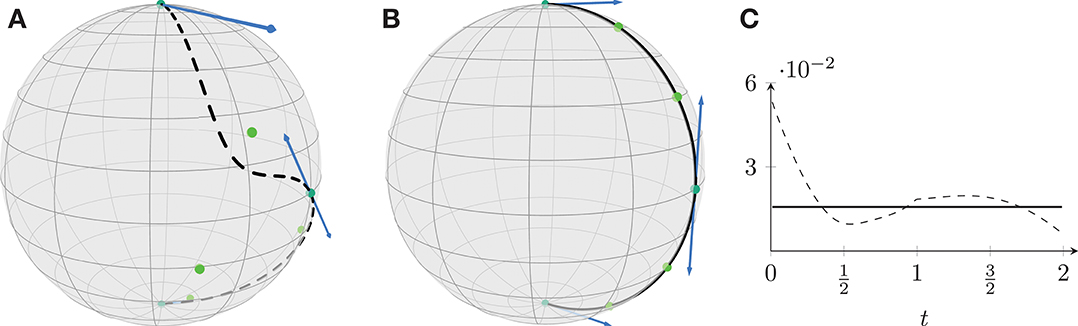
Figure 8. The initial curve (dashed, A) results in a geodesic (solid, B) when minimizing the discrete acceleration. This can also be seen on the first order differences (C).
The control points are optimized with our interpolating model, i.e., we fix the start and end points p0, p1, p2 and minimize A(b).
The curve, as well as the second and first order differences, is sampled with N = 201 equispaced points. The parameters of the Armijo rule are again set to , σ = 10−4, and α = 1. The stopping criteria are slightly relaxed to 10−7 for the distance and 10−5 for the gradient, because of the sines and cosines involved in the exponential map.
The result is shown in Figure 8B. Since the minimizer is the geodesic running from p0 to p2 through p1, we measure the perfomance first by looking at the resulting first order difference, which is constant, as can be seen in Figure 8C. As a second validation, we observe that the maximal distance of the resulting curve to the geodesic is of 2.2357 × 10−6. These evaluations again validate the quality of the gradient descent.
Effect of the data term. As a third example we investigate the effect of λ in the fitting model. We consider the data points
as well as the control points pi = di, and
The remaining control points and are given by the conditions (4). The corresponding curve B(t), t∈[0, 3], is shown in Figure 9 in dashed black. When computing a minimal MSA curve that interpolates B(t) at the points pi, i = 0, …, 3, the acceleration is not that much reduced, see the blue curve in Figure 9A.
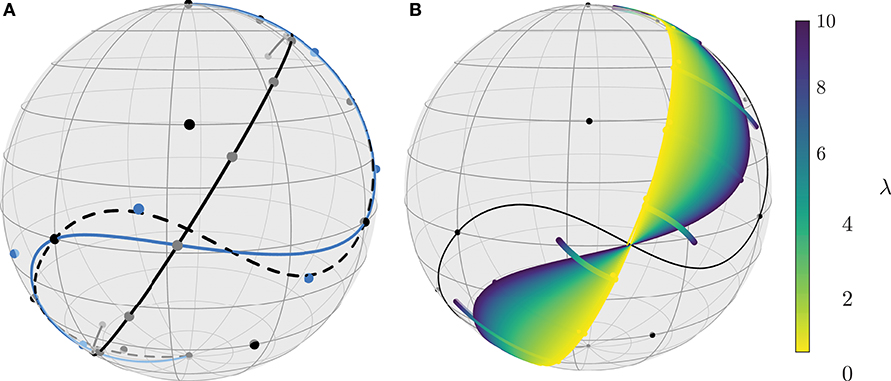
Figure 9. The composite Bézier curves are composed of three segments. The initial curve (dashed, A) is optimized with the interpolating model (solid blue, A) as well as with the fitting model for a continuum of values of λ, from λ = 10 (violet, B) to λ = 0.01 (yellow, B). The limit case where λ = 0 yields an unconstrained geodesic (solid black, A).
For fitting, we consider different values of λ and the same parameters as for the last example. The optimized curve fits the data points closer and closer as λ grows, and the limit λ → ∞ yields the interpolation case. On the other hand smaller values of λ yield less fitting, but also a smaller value of the mean squared acceleration. In the limit case, i.e., λ = 0, the curve (more precisely the control points of the Bézier curve) just follows the gradient flow to a geodesic.
The results are collected in Figure 9. In Figure 9A, the original curve (dashed) is shown together with the solution of the interpolating model (solid blue) and the gradient flow result, i.e., the solution of the fitting model (solid black) with λ = 0. Figure 9B illustrates the effect of λ even further with a continuous variation of λ from a large value of λ = 10 to a small value of λ = 0.01. The image is generated by sampling this range with 1000 equidistant values colored in the colormap viridis. Furthermore, the control points are also shown in the same color.
Several corresponding functional values, see Table 1, further illustrate that with smaller values of λ the discretized MSA also reduces more and more to a geodesic. For λ = 0 there is no coupling to the data points and hence the algorithm does not restrict the position of the geodesic. In other words, any choice for the control points that yields a geodesic, is a solution. Note that the gradient flow still chooses a reasonably near geodesic to the initial data (Figure 9A, solid black).

Table 1. Functional values for the three-segment composite Bézier curve on the sphere and different values of λ.
Comparison with the tangential solution. In the Euclidean space, the method introduced in Arnould et al. [37] and Gousenbourger et al. [38] and the gradient descent proposed here yield the same curve, i.e., the natural cubic spline. On Riemannian manifolds, however, all approaches approximate the optimal solution. Indeed, their method provides a solution by working in different tangent spaces, and ours minimizes a discretization of the objective functional.
In this example we take the same data points di as in (25) now interpreted as points on . Note that the control points constructed in (26) still fit to the sphere since each is built with a vector in and using the corresponding exponential map. The result is shown in Figure 10A. The norm of the first order differences is given in Figure 10B. The initial curve (dashed black) has an objective value of 10.9103. The tangent version (dotted) reduces this value to 7.3293. The proposed method (solid blue) yields a value of 2.7908, regardless of whether the starting curve is the initial one, or the one already computed by Arnould et al. [37]. Note that, when , the tangent version is even not able to compute any result, since the construction is performed in the tangent space of p0 and since logp0p3 is not defined.
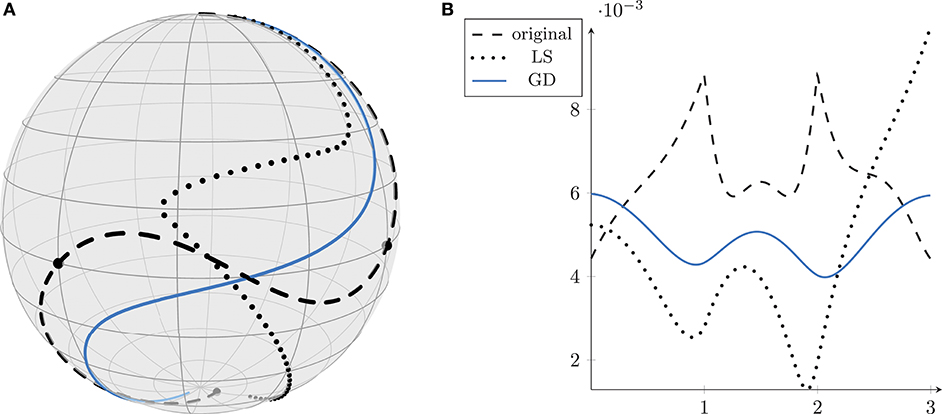
Figure 10. The initial composite Bézier curve on S2 (dashed, A) has an MSA of 10.9103. The curve obtained with the linear system (LS, dotted) of [37] has an MSA of 7.3293. The solution returned by our proposed method (GD, solid blue) outperforms them all with an MSA of 2.7908. This is further illustrated by the first order derivative approximated by first order differences in (B).
5.3. An Example of Orientations
Finally we compare our method with the blended splines introduced in Gousenbourger et al. [38] for orientations, i.e., data given on SO(3). Let
denote the rotation matrices in the x−y, x−z, and y−z planes, respectively. We introduce the three data points
These data points are shown in the first line of Figure 11 in cyan.

Figure 11. From top row to bottom row: (1) the initial data points (cyan), (2) the control points computed by the blended Bézier approach from Gousenbourger et al. [38], (3) 17 points on the corresponding curve, where the height represents the absolute first order difference, and the comparing curve is the first order differences from our model, (4) 17 points along the resulting curve from gradient descent, and (5) the resulting control points of the curve in (4).
We set λ = 10 and discretize (20) with N = 401 equispaced points. This sampling is also used to generate the first order finite differences. The parameters of the gradient descent algorithm are set to the same values as for the examples on the sphere.
We perform the blended spline fitting with two segments and cubic splines. The resulting control points are shown in the second row of Figure 11, in green. The objective value is Ã(b) = 0.6464. We improve this solution with the minimization problem (22) on the product manifold SO(3)6. We obtain the control points shown in the last line of Figure 11 and an objective value of for the resulting minimizer .
We further compare both curves by looking at their absolute first order differences. In the third line of Figure 11, we display 17 orientations along the initial curve with its first order difference as height. The line without samples is the absolute first order differences of the minimizer , scaled to the same magnitude. The line is straightened especially for the first Bézier segment. Nevertheless, the line is still bent a little bit and hence not a geodesic. This can be seen in the fourth line which represents 17 samples of the minimizing curve compared to its control points in the last line, which are drawn on a straight line.
6. Conclusion and Future Work
In this paper, we introduced a method to solve the curve fitting problem to data points on a manifold, using composite Bézier curves. We approximate the mean squared acceleration of the curve by a suitable second order difference and a trapezoidal rule, and derive the corresponding gradient with respect to its control points. The gradient is computed in closed form by exploiting the recursive structure of the De Casteljau algorithm. Therefore, we obtain a formula that reduces to a concatenation of adjoint Jacobi fields.
The evaluation of Jacobi fields is the only additional requirement compared to previous methods, which are solely evaluating exponential and logarithmic maps. For these, closed forms are available on symmetric manifolds.
On the Euclidean space our solution reduces to the natural smoothing spline, the unique acceleration minimizing polynomial curve. The numerical experiments further confirm that the method presented in this paper outperforms the tangent space(s)-based approaches with respect to the functional value.
It is still an open question whether there exists a second order absolute finite difference on a manifold, that is jointly convex. Then convergence would follow by standard arguments of the gradient descent. For such a model, another interesting point for future work is to find out whether only an approximate evaluation of the Jacobi fields suffices for convergence. This would mean that, on manifolds where the Jacobi field can only be evaluated approximately by solving an ODE, the presented approach would still converge.
Author Contributions
Both authors listed have contributed equally to the content of this work and approved the paper for publication.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the following fundings: RB gratefully acknowledges support by DFG grant BE 5888/2–1; P-YG gratefully acknowledges support by the Fonds de la Recherche Scientifique – FNRS and the Fonds Wetenschappelijk Onderzoek – Vlaanderen under EOS Project no 30468160, and Communauté française de Belgique - Actions de Recherche Concertées (contract ARC 14/19-060). Figure 9A is based on an idea of Rozan I. Rosandi.
Footnotes
1. ^See arxiv.org/abs/1506.02409v3
2. ^Open source, available at http://ronnybergmann.net/mvirt/
3. ^Open source, available at http://www.manopt.org
References
1. Pyta L, Abel D. Interpolatory Galerkin models for Navier-Stokes-equations. IFAC-PapersOnLine (2016) 49:204–9. doi: 10.1016/j.ifacol.2016.07.442
2. Gousenbourger PY, Massart E, Musolas A, Absil PA, Jacques L, Hendrickx JM, et al. Piecewise-Bézier C1 smoothing on manifolds with application to wind field estimation. In: ESANN2017. Bruges: Springer (2017). Available online at: https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es2017-77.pdf
3. Sander O. Geodesic finite elements for cosserat rods. Int J Numer Methods Eng. (2010) 82:1645–70. doi: 10.1002/nme.2814
4. Park J. Interpolation and tracking of rigid body orientations. In: ICCAS, Gyeonggi-do (2010). p. 668–73. doi: 10.1109/ICCAS.2010.5670237
5. Su J, Kurtek S, Klassen E, Srivastava A. Statistical analysis of trajectories on Riemannian manifolds: bird migration, Hurricane tracking and video surveillance. Ann Appl Stat. (2014) 8:530–52. doi: 10.1214/13-AOAS701
6. Dyn N. Linear and nonlinear subdivision schemes in geometric modeling. In: Cucker F, Pinkus A, Todd MJ, editors. FoCum. Vol. 363 of London Math. Soc. Lecture Note Ser. Hong Kong: Cambridge University Press (2009). p. 68–92. doi: 10.1017/CBO9781139107068.004
7. Wallner J, Nava Yazdani E, Grohs P. Smoothness properties of Lie group subdivision schemes. Multiscale Model Simulat. (2007) 6:493–505. doi: 10.1137/060668353
8. Shingel T. Interpolation in special orthogonal groups. IMA J Numer Anal. (2008) 29:731–45. doi: 10.1093/imanum/drn033
9. Green PJ, Silverman BW. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach. CRC Press (1993). Available online at: https://www.crcpress.com/Nonparametric-Regression-and-Generalized-Linear-Models-A-roughness-penalty/Green-Silverman/p/book/9780412300400
10. Absil PA, Mahony R, Sepulchre R. Optimization Algorithms on Matrix Manifolds. Princeton, NJ: Princeton University Press (2008). Available online at: https://press.princeton.edu/absil
11. Boumal N, Mishra B, Absil PA, Sepulchre R. Manopt, a matlab toolbox for optimization on manifolds. J Mach Learn Res. (2014) 15:1455–9. Available online at: http://jmlr.org/papers/v15/boumal14a.html
12. Bergmann R. MVIRT a toolbox for manifold-valued image registration. In: IEEE International Conference on Image Processing, IEEE ICIP 2017, Beijing. (2017). Available online at: https://ronnybergmann.net/mvirt/
13. Zhou X, Yang C, Zhao H, Yu W. Low-rank modeling and its applications in image analysis. ACM Comput Surveys (2015) 47:36. doi: 10.1145/2674559
14. Cunningham JP, Ghahramani Z. Linear dimensionality reduction: survey, insights, and generalizations. J Mach Learn Res. (2015) 16:2859–900. Available online at: http://jmlr.org/papers/v16/cunningham15a.html
15. Sun J, Qu Q, Wright J. A geometric analysis of phase retrieval. Found Comput Math. (2017) 8:1131–98. doi: 10.1007/s10208-017-9365-9
16. Yu X, Shen JC, Zhang J, Letaief KB. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems. IEEE J Selected Top Signal Process. (2016) 10:485–500. doi: 10.1109/JSTSP.2016.2523903
17. Strekalovskiy E, Cremers D. Total variation for cyclic structures: convex relaxation and efficient minimization. In: IEEE Conference on Computer Vision and Pattern Recognition (2011). p. 1905–11.
18. Strekalovskiy E, Cremers D. Total cyclic variation and generalizations. J Mat Imaging Vis. (2013) 47:258–77. doi: 10.1007/s10851-012-0396-1
19. Lellmann J, Strekalovskiy E, Koetter S, Cremers D. Total variation regularization for functions with values in a manifold. In: IEEE International Conference on Computer Vision. Sydney, NSW (2013). p. 2944–51. doi: 10.1109/ICCV.2013.366
20. Weinmann A, Demaret L, Storath M. Total variation regularization for manifold-valued data. SIAM J Imaging Sci. (2014) 7:2226–57. doi: 10.1137/130951075
21. Bergmann R, Laus F, Steidl G, Weinmann A. Second order differences of cyclic data and applications in variational denoising. SIAM J Imaging Sci. (2014) 7:2916–53. doi: 10.1137/140969993
22. Bačák M, Bergmann R, Steidl G, Weinmann A. A second order nonsmooth variational model for restoring manifold-valued images. SIAM J Comput. (2016) 38:567–97. doi: 10.1137/15M101988X
23. Bergmann R, Fitschen JH, Persch J, Steidl G. Priors with coupled first and second order differences for manifold-valued image processing. J Math Imaging Vis. (2017) 60:1459–81. doi: 10.1007/s10851-018-0840-y
24. Bredies K, Holler M, Storath M, Weinmann A. Total generalized variation for manifold-valued data. SIAM J Imaging Sci. (2018) 11:1785–48. doi: 10.1137/17M1147597
25. Bergmann R, Persch J, Steidl G. A parallel Douglas–Rachford algorithm for restoring images with values in symmetric Hadamard manifolds. SIAM J Imaging Sci. (2016) 9:901–37. doi: 10.1137/15M1052858
26. Grohs P, Sprecher M. Total variation regularization on Riemannian manifolds by iteratively reweighted minimization. Inform Inference (2016) 5:353–78. doi: 10.1093/imaiai/iaw011
27. Bergmann R, Chan RH, Hielscher R, Persch J, Steidl G. Restoration of manifold-valued images by half-quadratic minimization. Inverse Prob Imaging (2016) 10:281–304. doi: 10.3934/ipi.2016001
28. Samir C, Absil PA, Srivastava A, Klassen E. A gradient-descent method for curve fitting on Riemannian manifolds. Found Comput Math. (2012) 12:49–73. doi: 10.1007/s10208-011-9091-7
29. Su J, Dryden IL, Klassen E, Le H, Srivastava A. Fitting smoothing splines to time-indexed, noisy points on nonlinear manifolds. Image Vis Comput. (2012) 30:428–42. doi: 10.1016/j.imavis.2011.09.006
30. Boumal N, Absil PA. A discrete regression method on manifolds and its application to data on SO(n). In: IFAC Proceedings Volumes (IFAC-PapersOnline). Vol. 18. Milano (2011). p. 2284–89. doi: 10.3182/20110828-6-IT-1002.00542
31. Kim KR, Dryden IL, Le H. Smoothing splines on Riemannian manifolds, with applications to 3D shape space. (2018). arXiv[Preprint]:1801.04978.
32. Fletcher PT. Geodesic regression and the theory of least squares on Riemannian manifolds. Int J Comput Vis. (2013) 105:171–85. doi: 10.1007/s11263-012-0591-y
33. Rentmeesters Q. A gradient method for geodesic data fitting on some symmetric Riemannian manifolds. In: Decision and Control and European Control Conference (CDC-ECC), 2011 50th IEEE Conference on. Orlando, FL (2011). p. 7141–6. doi: 10.1109/CDC.2011.6161280
34. Farin G. Curves Surfaces for CAGD. Morgan Kaufmann (2002). Available online at: https://www.elsevier.com/books/curves-and-surfaces-for-cagd/farin/978-1-55860-737-8
35. Absil PA, Gousenbourger PY, Striewski P, Wirth B. Differentiable Piecewise-Bézier Surfaces on Riemannian Manifolds. SIAM J Imaging Sci. (2016) 9:1788–828. doi: 10.1137/16M1057978
36. Popiel T, Noakes L. Bézier curves and interpolation in Riemannian manifolds. J Approx Theory (2007) 148:111–27. doi: 10.1016/j.jat.2007.03.002
37. Arnould A, Gousenbourger PY, Samir C, Absil PA, Canis M. Fitting smooth paths on Riemannian manifolds: endometrial surface reconstruction and preoperative MRI-based navigation. In: Nielsen F, Barbaresco F, editors. GSI2015. Springer International Publishing (2015). p. 491–8.
38. Gousenbourger PY, Massart E, Absil PA. Data fitting on manifolds with composite Bézier-like curves and blended cubic splines. J Math Imaging Vis. (2018). doi: 10.1007/s10851-018-0865-2
41. Karcher H. Riemannian center of mass and mollifier smoothing. Commun Pure Appl Math. (1977) 30:509–41. doi: 10.1002/cpa.3160300502
42. Boumal N. Interpolation and regression of rotation matrices. In: Nielsen F, Barbaresco F, editors. Geometric Science of Information. Berlin; Heidelberg: Springer. (2013). p. 345–52.
Keywords: Riemannian manifolds, curve fitting, composite Bézier curves, Jacobi fields, variational models
Citation: Bergmann R and Gousenbourger P-Y (2018) A Variational Model for Data Fitting on Manifolds by Minimizing the Acceleration of a Bézier Curve. Front. Appl. Math. Stat. 4:59. doi: 10.3389/fams.2018.00059
Received: 26 July 2018; Accepted: 13 November 2018;
Published: 12 December 2018.
Edited by:
Luca Marchetti, Microsoft Research-University of Trento Centre for Computational and Systems Biology(COSBI), ItalyReviewed by:
Giovanni Mascali, Università della Calabria, ItalyVincenzo Bonnici, Università degli Studi di Verona, Italy
Copyright © 2018 Bergmann and Gousenbourger. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ronny Bergmann, cm9ubnkuYmVyZ21hbm5AbWF0aGVtYXRpay50dS1jaGVtbml0ei5kZQ==
 Ronny Bergmann
Ronny Bergmann Pierre-Yves Gousenbourger
Pierre-Yves Gousenbourger