- 1INRIA Grenoble Rhône-Alpes, Montbonnot-Saint-Martin, France
- 2Laboratoire de Biométrie et Biologie Évolutive, UMR 5558, CNRS, Université de Lyon, Université Lyon 1, Villeurbanne, France
- 3Department of Computer, Automatic and Management Engineering, Sapienza University of Rome, Rome, Italy
Metabolic networks have been used to successfully predict phenotypes based on optimization principles. However, a general framework that would extend to situations not governed by simple optimization, such as multispecies communities, is still lacking. Concepts from evolutionary game theory have been proposed to amend the situation. Alternative metabolic states can be seen as strategies in a “metabolic game,” and phenotypes can be predicted based on the equilibria of this game. In this survey, we review the literature on applying game theory to the study of metabolism, present the general idea of a metabolic game, and discuss open questions and future challenges.
1. Introduction
Metabolic networks have become a standard model in computational biology and high quality genome-scale reconstructions are now available for a wide range of micro-organisms as well as of some eukaryotes. Often the ultimate aim of these models is phenotype prediction, which means predicting from the genome how an organism would behave in a given environment. In this context, constraint-based methods, most prominently Flux Balance Analysis (FBA), have a proven track record in accurately predicting the metabolic behavior of single organisms [1–5].
FBA relies on assumptions about the underlying optimization principles guiding metabolic behavior, and biomass yield relative to nutrient intake is often chosen as the target of maximization. While this assumption is often justified when considering single species systems, it becomes troublesome if one wishes to model several species at the same time [6]. Simple optimization is usually not enough, because competition and interspecies interactions complicate the situation considerably. Formulating a “common goal” for a community of organisms can only be done ad-hoc [7–9]. Moreover, there are situations where even in single species communities, selection can be unfavorable to optimal choices such as maximizing efficiency in nutrient use [10–12].
Game theory is a branch of applied mathematics originally developed to describe and reason about situations where two or more rational agents, the “homo economicus,” are faced with choices and have potentially conflicting goals [13]. All participants want to maximize their own well-being, but are doing so taking into account that everyone else is doing the same. Thus paradoxical, suboptimal, outcomes are possible and even common. Evolutionary game theory was born out of the realization that rational choice can be replaced by natural selection: in the course of evolution the strategy (phenotype) that would “win” the game would prevail by simply proliferating more successfully thanks to its success in the “game” [14, 15].
It turns out that phenotype prediction in the context of metabolic networks is exactly the type of problem that evolutionary game theory was meant to answer: given a set of choices (as defined by a metabolic network reconstruction), what will be the actual metabolism observed? In other words, if we culture a set of organisms together in a given medium, which are the phenotype(s) that emerge as winners?
In this review, we seek to provide a short introduction to both evolutionary game theory and its use in the context of metabolic modeling. We first present the relevant preliminaries and introduce the idea of a metabolic game. We then further expand on the idea by reviewing work done on the topic so far. Finally, we discuss these ideas and contemplate on future prospects.
We wish to call attention to the fact that our focus here is strictly on the idea of using the principles of game theory to reason about metabolic networks. While some papers that address this topic have been included for the sake of completeness, we decided to omit part of the related literature to keep the scope of this review under control. For previous reviews discussing the use of game theory in the context of micro-organisms with slightly different emphases, see [11, 16–18].
Game Theory
The main concepts that compose a game are a set of players, a set of actions for each player, and a payoff function. The players are the participants in the interaction. In the simplest case, they can be interchangeable, meaning they all have the same set of available actions and the same payoff function. A set of actions defines the choice that each player faces and can correspond for example to the expressed phenotype. Finally, the payoff function determines the outcome for each player in each scenario, that is, a combination of actions chosen by the players.
The simplest game is the 2-player, 2-strategy matrix game. If the players are interchangeable, it can be expressed concisely by the payoff matrix:
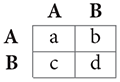
where A and B denote the actions and the entries are payoff values for the row player. For example, if the row player plays A and the column player B, the payoffs for the row and column players are b and c, respectively.
Some of these games have become famous and the actions and payoffs can be given generic interpretations, usually denoted by:
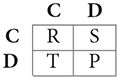
where C stands for “cooperation” and D for “defection,” and the payoffs, denoted by their initials, are known as “Temptation,” “Reward,” “Punishment,” and “Sucker's payoff.” If T > R > P > S, the game is a Prisoner's Dilemma (PD). It corresponds to a situation where the players would both be better off cooperating, but because they will always have the incentive to defect, they end up choosing this inferior outcome, hence the “dilemma.”
A common way to analyse games is using a solution concept. A solution is a state of the game (in other words, a configuration of actions/strategies) that can be reasonably assumed to follow from choices made based on some underlying logic. Arguably the two most well-known examples—as well as the ones most often encountered in the context of evolutionary game theory—are the Nash equilibrium [19, 20] and the Evolutionarily Stable Strategy (ESS) [14]. In a Nash equilibrium, all strategies are chosen in such a way that no player has an incentive to unilaterally change theirs. An ESS is a strategy such that if adopted by every member of a population, a small minority of players using any other strategy cannot invade. In the Prisoner's Dilemma, for both players to choose D is a Nash equilibrium of the game: D dominates the other action in all scenarios (T > R and P > S) [13]. In this case, it is also an ESS.
If the payoffs are switched so that T > R > S > P, the game is called Hawk-Dove or Snowdrift (SD). In contrast to the PD, in this situation it is still better to cooperate even if one's partner fails to do so. Here the Nash equilibrium is to choose an action opposite of one's opponent. If mixed strategies are allowed, meaning a player can choose its action probabilistically, we have a mixed Nash equilibrium where both players follow the same strategy of choosing C with some probability (or a portion of the time). This is also an ESS, and can be interpreted as a population of individuals that comprises a mix of C- and D-players.
The simple matrix game can be readily extended in two ways. First, the number of strategies can be increased, effectively increasing the dimensions of the matrix. This in general leads to no extra complications apart from eventually requiring computational tools for the analysis of the equilibrium structure (see [21–23]). Second, the number of payoff matrices and players can be increased. In other words, players are no longer interchangeable and there can be more than two parties in the interaction. In general, matrix games with more than two players are much harder to analyse than simpler games [24].
The most prominent multiplayer game is the Public Goods. It can be thought of as an extension of the PD to more than two players. In the simplest form, n players each choose whether or not to make a contribution to the common good. The contribution has a cost c for the individual, and yields a benefit r · c that is distributed evenly amongst the group. If r/n < 1, no one will contribute, even though everyone would be better off with all members making the contribution. However, this is true with the kind of linear benefits in the simplest game, but not necessarily in a more general case where the benefit acquired can be a non-linear function of the contributions. In Archetti and Scheuring [25] and Broom and Rychtár [24], it has been argued that in real situations, benefits are usually not linear, but for example saturating.
In principle, any population dynamics model can be used in combination with a game by simply making the growth rate a function of the payoff. Obviously this requires defining with whom and how the game is played. For example, it can be assumed that the population is well-mixed, so that players encounter different types of opponents in a random fashion according to their prevalence. The payoff that an individual is obtaining at a given moment is thus the expectation, calculated over the different possible encounters. The most commonly used formulation is the replicator equation [26, 27]. It describes the dynamics of the frequencies of strategies as:
where ni is the relative density of strategy i in the population, Ei is its expected payoff, and Ē is the average (expected) payoff of the population.
Adaptive dynamics is a framework that combines the ecological and evolutionary time scales to study how strategies will evolve under natural selection [28–30]. Under the assumptions that changes in strategy undergo gradual mutation so that each new genotype changes the phenotype only slightly, and that the mutations occur rarely enough for the ecological and evolutionary dynamics to be separable, adaptive dynamics offers a view beyond simply reasoning about the stable points of evolution such as an ESS. For example, an ESS can be unattainable through gradual mutations. Adaptive dynamics can also explain how evolution toward higher fitness in a homogeneous population can lead to diversity, or so-called branching of the evolutionary tree [30].
Metabolic Games
A metabolic network (see Figure 1) is represented by the so-called stoichiometric matrix S with m rows corresponding to the number of metabolites and n columns to reactions. The standard steady state assumption:
expresses the condition that any flux vector v must render the net production of all internal metabolites zero. However, this still leaves the state of the metabolism largely undetermined. In fact, the steady state condition merely defines the set of possible metabolic strategies available to the organism, comprising all the different pathways at its disposal. The question then is what is the choice made by the organism: which pathways it chooses to activate.
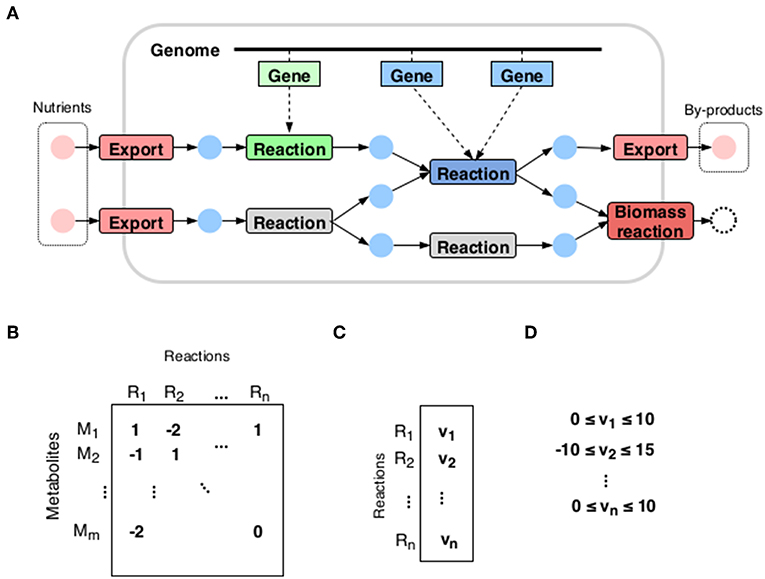
Figure 1. A metabolic reconstruction. (A) A metabolic network is constructed by joining together reactions whose enzymes are recognized in the organism's genome. (B) The most commonly used mathematical representation is the stoichiometric matrix: its rows correspond to the metabolites of the network and columns to reactions. The entries are stoichiometric coefficients: how much of the metabolite is consumed or produced in the reaction. (C) The flux vector expresses the state of the metabolism: its entries correspond to reaction rates. (D) Each reaction rate has a lower and an upper bound.
“Choice” here obviously refers to that made by natural selection. Thus, the question could be put more appropriately as: given the environment, as determined by both abiotic factors as well as the surrounding members of the same and of different species, what is the best response to this environment. Again, “best response” refers to the ability to persist in competition with other members of the community, generally referred to as fitness.
In FBA, the metabolic state is inferred through straightforward optimization (for an illustration of the FBA workflow, see Figure 2). A standard choice is the flux through a biomass reaction. While this is often referred to as growth rate, strictly speaking it corresponds to growth yield [6, 10] (see also section 2). It can be seen as fitness maximization in isolation. As argued throughout this paper, this might not correspond to the strategy of choice if the surrounding community is taken into account. However, if the metabolic state is already sufficiently specified through additional constraints, this growth yield maximization can still be used to determine the fitness given that specific choice. We can thus define a metabolic game: the players are cells, actions are the different metabolic states available to them, and payoffs are calculated using FBA with additional constraints specifying the states chosen in each combination of actions. A schematic representation of this idea is given in Figure 3.
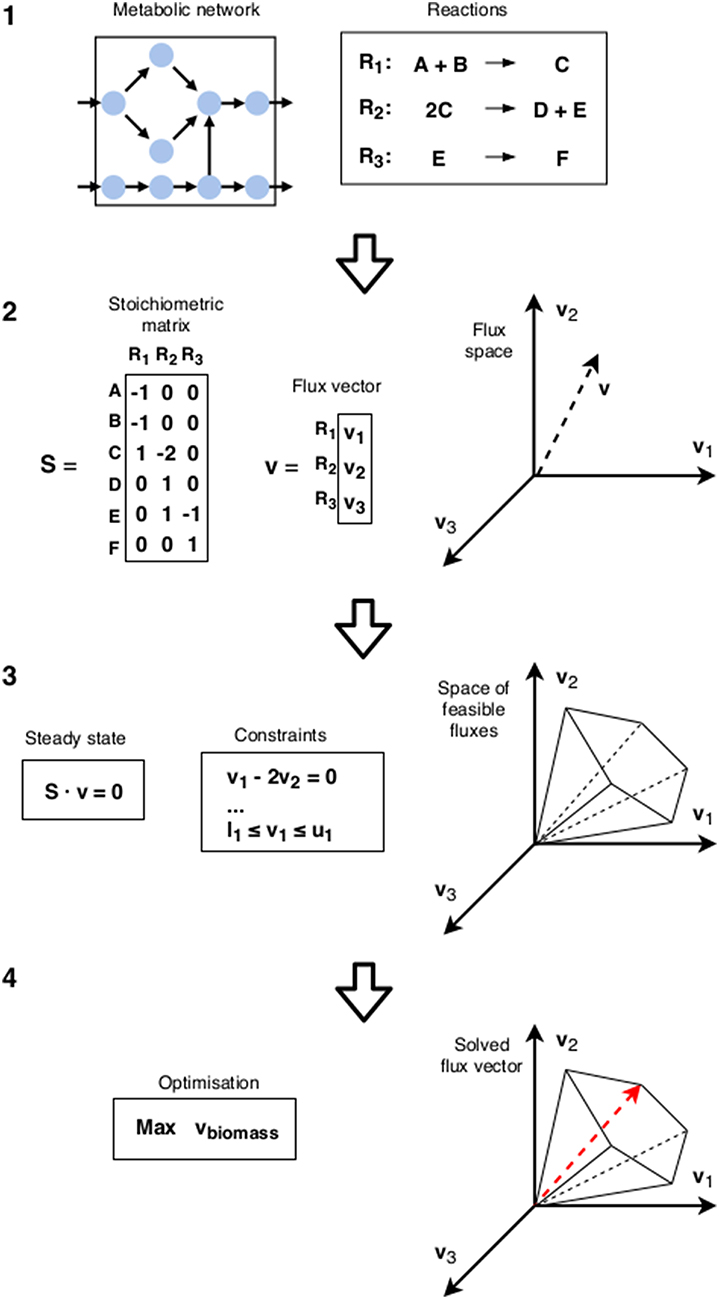
Figure 2. Flux Balance Analysis: (1) The starting point is the metabolic reconstruction. (2) The flux space is a space of possible flux vectors v. (3) Constraints are imposed on the flux space: the steady state condition requires that the net production of all internal metabolites equals zero. This confines the flux vector into a cone-shaped subspace. The upper and lower bounds (li and ui) of the reactions bound the cone, establishing a maximum magnitude. (4) Finally, using linear programming, an objective function (usually a linear combination of certain reaction fluxes that corresponds to a biological objective such as biomass) is maximized to find the predicted flux vector.
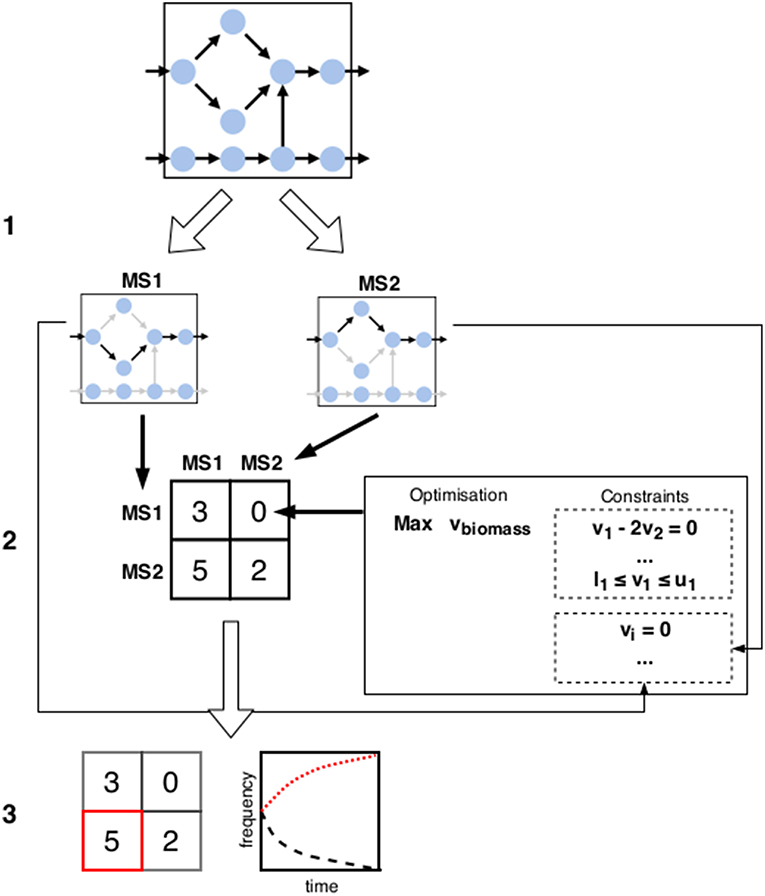
Figure 3. Schematic overview of the tentative framework for metabolic games: (1) Starting from the metabolic network(s) of one or several organisms, possible metabolic phenotypes are subdivided into distinct metabolic strategies (denoted by MS1 and MS2 above). (2) Payoffs for each configuration of strategies are calculated using a method such as FBA. New constraints are added in each scenario to reflect the choice of phenotype implicated by the strategy as well as possible environmental interactions due to the strategy choices of other players (e.g., changes in substrate availability can be enforced by restricting fluxes of import reactions accordingly). (3) Predicted configuration(s) of metabolic strategies is determined by looking for the solutions of the game (e.g., finding the Nash equilibria or studying the dynamics of the strategies).
Consider the toy-model example in Figure 4. The simple network represents a situation where an organism has two options for a primary nutrient: A and B. We assume that in order to efficiently utilize whichever nutrient is chosen, the cell has to specialize. Thus, uptake of both A and B is not feasible. Furthermore, nutrient A is superior, yielding 3 units of the biomass precursor M1 per one unit of A as opposed to a yield of only 2 for B. Thus, following standard FBA, we would conclude that by choosing to uptake A at the maximum rate 1, the cell maximizes its biomass production (vBiom = 3).
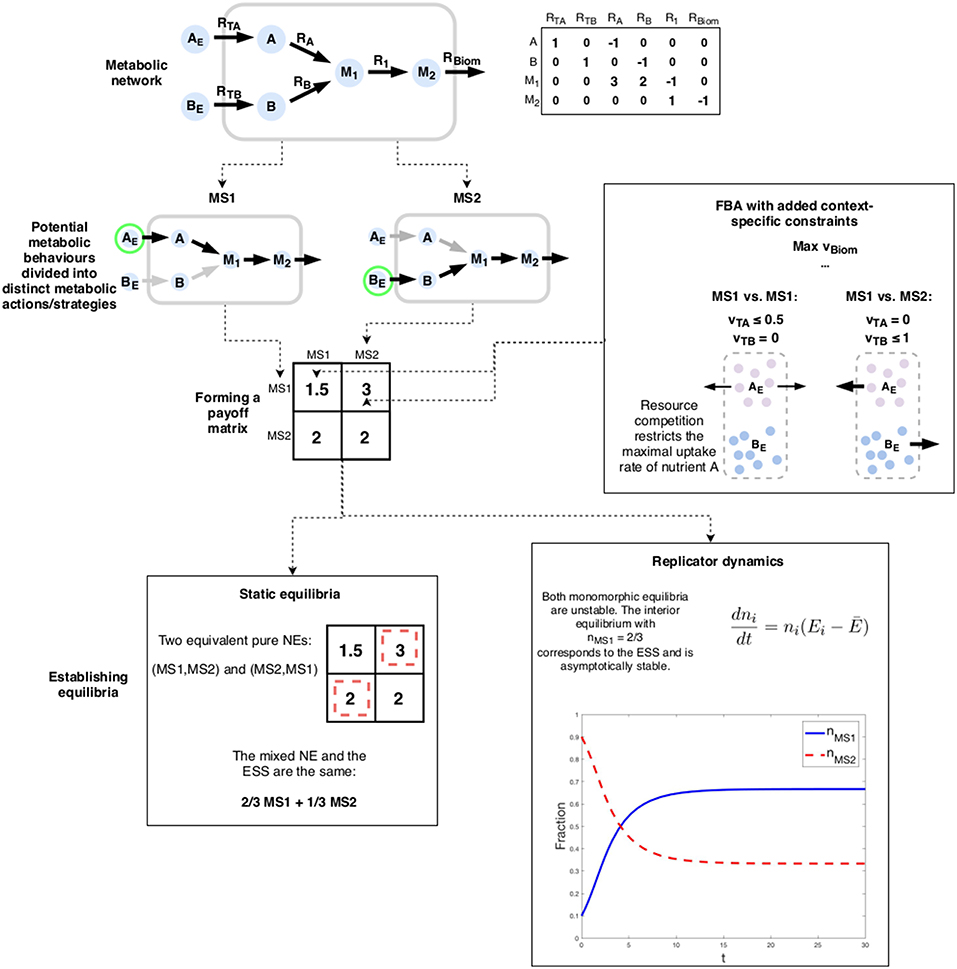
Figure 4. An example of a metabolic game: the choice of nutrient forms the actions of the game. Payoffs are determined using FBA with additional constraints enforcing both the chosen metabolic strategy as well as the impact of the choice of the co-player. The outcome of the game can be analyzed using either static or dynamic solution concepts. In this case, both indicate the same result: expected phenotypic heterogeneity.
We now add a social interaction component by assuming that the presence of A in the environment is limited (for the sake of simplicity we assume that B is abundant). This can be modeled by a simple 2-player matrix game with two actions: to only uptake A and to only uptake B (denoted by “MS1” and “MS2” resp.). Should both players choose A as their nutrient, the maximum uptake rate is halved (vTA ≤ 0.5), reflecting a scarcity of the compound. In this case, maximizing biomass production only yields 1.5 (assuming that vTB = 0).
The pure NE of the game is the “anti-coordination” scenario where the players choose differing strategies. The mixed NE and as well as the ESS is a strategy where both players' choice can be expressed as 2/3MS1 + 1/3MS2, meaning that nutrient A is chosen two-thirds of the time. This can be interpreted as a stochastic strategy where the cell switches from pure MS1 to pure MS2 randomly. The equilibrium of the replicator dynamics (Equation 1) corresponds to the mixed NE and the ESS but with a different interpretation: in a well-mixed population, two-thirds of the cells will use A while the remaining uses B.
The most complete realization to date of this formalism was presented in Zomorrodi and Segre [23]. Indeed, Zomorrodi and Segrè construct different metabolic strategies by setting selected fluxes to zero to simulate knock-outs, and forcing the excretion of “leaky” metabolites that can be taken up by neighboring cells. Payoffs are obtained by maximizing the biomass flux for both genotypes in each pairwise interaction. Together, these define a 2-player matrix game with 2 or more actions (genotypes). To determine which genotype(s) are able to persist, the authors search for Nash equilibria and ESSs using the replicator equation.
As a proof of concept, Zomorrodi and Segrè apply their framework to study invertase production in the yeast Saccharomyces cerevisiae: in order to grow on sucrose, the yeast needs to hydrolyse the sugar molecule. Because invertase is a surface enzyme, much of the resulting monosaccharides leak out. Because producing invertase is costly, it constitutes a public good. This cost is modeled by reducing the ATP production of invertase-producers. It was found that depending on how much of the sugar leaks out and on the cost of producing the enzyme, three different payoff schemes are possible: Prisoner's Dilemma, Snowdrift, and Mutually Beneficial.
The authors also studied amino acid mediated ecological interactions in Escherichia coli. Producer strains leak out amino acids which are costly to produce, and can be taken up by mutants lacking the ability to synthesize them. Several different amino acids were investigated, with up to two at a time spanning four possible strategies (genotypes). Again, both the level of leakiness and the cost of production influence the type of equilibria observed. With low enough levels of leakiness, both an equilibrium with a full producer coexisting with a complete auxotroph, as well as cross-feeding are possible. With increasing leakiness, the full producer becomes non-viable. However, it was also observed that due to interdepencies in amino acid production, in some situations cross-feeding is not possible because losing the ability to produce one amino acid leads to the loss of the ability to produce the other. Zomorrodi and Segrè also studied the evolutionary dynamics of these interactions by performing in silico invasion experiments. They found that cross-feeding can emerge through the progressive loss of amino acid synthesis capabilities, and that this mutually dependent coalition is often stable against invasion by non-producers, consistent with previous experimental findings [31, 32].
2. Yield vs. Rate
One of the questions already extensively explored through applying game theory to metabolism is ATP production. There is a fundamental trade-off between yield and rate of ATP production in heterotrophic organisms: some of the free energy obtained from substrate degradation is needed to drive the reaction. Increasing the portion of free energy that is used for driving the reaction increases the rate of ATP production but lowers the yield. The choice of pathway thus presents a social dilemma. Choosing the efficient strategy would maximize resource usage and benefit the population as a whole. However, if an individual cell chooses to stray from this cooperative path, its faster growth rate will allow it to increase in numbers and eventually overcome the cooperators at the cost of the interest of the community.
In Pfeiffer et al. [33], this question is explored in the context of respiration vs. fermentation. This paper is to our knowledge the first to apply game theory specifically to metabolic pathways. Most organisms can in principle choose to degrade sugar by both the respiration and fermentation pathways. While fermentation provides ATP faster, it has a significantly lower yield. Thus, fermentation can be seen as a wasteful, “selfish” strategy, while respiration is more efficient in terms of nutrient use.
By constructing a simple population model, the authors show that while a population of fermenters will be smaller due to a faster depletion of resources, they can nevertheless take over a population of respirators due to their faster growth rate. This constitutes the famous “tragedy of the commons” [34]. However, if a spatial component is added, respirators can have a chance. This is because at lower nutrient levels, fermenters will deplete their immediate environment of resources and suffer the consequences.
Frick and Schuster [35] explore this question further. They too construct a population model for slow but efficient vs. fast but wasteful resource use. The authors then interpret the steady state population densities of both strategies in each different scenario as payoffs: in this way, the situation is a Prisoner's Dilemma with pure respiration forming the cooperation strategy. This is important because were the growth rates to be taken as the payoffs, one would conclude that fermentation is the optimal choice in all instances. However, from the point of view of sustaining the highest possible population density, cooperation, that is respiration, is the best choice.
Experimental evidence for the results described above was provided in MacLean and Gudelj [36]. The authors used yeast as their model organism and grew pure respirators and respiro-fermenters together in different culture set-ups. They found that while the “cheaters” win in a chemostat, in serial batch and spatially structured populations, the two strategies can coexist.
Schuster et al. [10] critically examined the assumption made in FBA of maximization of biomass yield. They argued that in general there is a trade-off between yield and rate, and that it is not a priori clear which of these conflicting goals would be selected for. Based on the theoretical results previously put forth by Pfeiffer et al. [33] as well as several examples from nature, the authors conclude that maximization of yield cannot be considered a universal principle.
Aledo et al. [37] also studied the yield vs. rate question but this time in glycolysis itself, which can operate under two different regimes: one with a high yield but a slower rate, another with a low yield but a faster rate. Using a simple matrix game model, with payoffs derived as functions of extracellular free energy and in agreement with the Prisoner's Dilemma payoff scheme, the authors showed that in a well-mixed population, cooperation cannot persist. In contrast, if the game is played on a lattice so that players only interact with their neighbors, cooperation is a possible outcome.
Schuster et al. [38] returned to the question of yield vs. rate. They presented a toy model representing a simplified version of ATP production to show that whether maximizing the yield coincides with maximizing the rate depends on the particulars of the system. They also further articulated the idea that alternative pathways can be seen as strategies in the game theoretical sense, and that “choosing” which pathway to use can happen not only through changes in genotype, but also through regulatory changes within the life-span of a cell.
Kareva [39] investigated the yield vs. rate question in the context of cancer cells where the use of the more inefficient glycolysis pathway is observed as one of the hallmarks of cancerous growth and is known as the Warburg effect [40, 41]. However, in contrast to the previous models, the author argued that the use of glycolysis is the cooperative strategy: while recognizing the possibility to increase the rate of glucose uptake, she considered the use of glycolysis to remain detrimental to the individual cell due to its low yield. Meanwhile, the associated lactic acid production can benefit the cancer cell population as a whole, if undertaken in sufficient numbers, because it disproportionately harms non-cancerous cells. Thus, glycolysis can be considered as public goods production. The contradiction with previous studies is clear. However, in the ODE system used to model a population of cells with varying rates of carbon allocated to glycolysis in Kareva [39], it was observed that glycolytic cells do increase in frequency if they have a faster growth rate.
In two successive papers [42, 43], Archetti presented a public goods model of the Warburg effect. He took the same view as Kareva [39] and considered glycolysis as the cooperative strategy amongst cancer cells. The benefit accrued by all participants from glycolysis—increased acidity—is modeled by a double sigmoid function: increased acidity yields a benefit over healthy cells if enough cells are producing lactic acid, but too much will start to hamper the growth of even cancer cells. The dynamics of the frequencies of glycolytic and non-glycolytic cells were modeled using the replicator equation. Because an exact solution of the dynamics for a sigmoid shaped benefit is not available, Bernstein polynomials were used to find an approximate solution. Archetti found that if the cost attached to glycolysis is not too high, glycolytic cooperators can persist at intermediate frequencies.
3. Public Goods
Another possible social dilemma within microbial communities occurs with necessary but costly functions. If a metabolic function is performed at the cell surface or outside the cell, it means that the benefit incurred can be shared by other cells that are possibly not contributing to the undertaking of the said function. Such a situation is best described by a public goods game.
Gore et al. [44] studied the invertase production system of S. cerevisiae described in section 3. Their model is a sort of mix between a public goods game and a matrix game: the authors define payoffs in terms of the fraction of invertase-producers in the population but then go on to compare these payoff values to the well-known 2-player games. If the benefits are linear, cooperation cannot persist unless the benefit derived from sucrose degradation by the invertase-producer exceeds the cost, in which case producing the enzyme is not a public good. On the other hand, with non-linear benefits, frequency-dependent selection allows for a fraction of the cooperators to persist. This result was in line with experimental evidence which confirmed both the coexistence of producers and non-producers as well as the non-linear benefit function.
A similar model was presented in Schuster et al.[45]. In this paper, Schuster et al. studied generic exoenzyme production assuming again that some fraction of the transformed growth product diffuses directly into the producer cell while the rest is available to the surrounding community. This time the benefit from the public good is given by a Monod function modeling the growth rate attained through the available nutrient. The nutrient acquired in turn depends on the fraction of cooperators in the population and cell density, which is a parameter of the model. The authors conclude that depending on the parameters, the fraction of public good that diffuses away, the cost of enzyme production, and the cell density, the model can be seen as a Prisoner's Dilemma, a Snowdrift or a Harmony game.
Archetti [46] studied growth factor production in cancer cells as a public goods game. Growth factor production is costly but the benefits are available to all surrounding cells. The benefit function was assumed to have sigmoid shape and population dynamics were modeled by the replicator equation. As in Archetti [42, 43], Bernstein polynomials were used to circumvent the problem caused by the sigmoid function. Archetti found that depending on how exactly the fraction of producers influences the benefit from growth factor, different types of dynamics are possible: a globally attracting mixed equilibrium where producers and non-producers coexist, the fixation of one type depending on the initial frequencies, or the fixation of producers regardless of the initial conditions.
The model presented in Archetti [46] was expanded on in Archetti [47] by introducing a spatial component. In this model, cells are placed in the nodes of a Voronoi graph. A Voronoi graph has the average connectivity of 6, with very few nodes beyond degree 4–8. Cells receive benefits from growth factors produced by producer-cells within a neighborhood defined by a diffusion parameter, discounted with the distance to the focal cell. The benefit itself is given by a normalized logistic function. In other words, benefits are non-linear. Archetti found that similar to well-mixed populations, cooperation declines as the cost of production increases. Stochasticity in the update rules used to model proliferation and a steeper benefit function also decrease cooperation.
4. Nutrient Choice
Perhaps the best examples showcasing the usefulness of game theoretic thinking are situations where frequency-dependent selection leads to polymorphisms in nutrient use. It is often the case that in a given environment, there is a preferred choice for the main carbon source. However, in any realistic scenario, nutrient availability is limited, and it can be beneficial for the individual to opt for a carbon source that is slightly less optimal, but abundant due to being the “unpopular” choice.
Doebeli [48] considered the evolution of cross-feeding. He constructed a model for a bacterial culture growing in a chemostat, using glucose as its main nutrient. During growth on glucose, acetate is secreted which can also be used as a nutrient, albeit with a lower growth rate. Doebeli assumed that there is a trade-off in using the secondary metabolite: becoming more proficient in using acetate lowers the ability to use glucose efficiently. Furthermore, this trade-off is subject to gradual change through mutations. Bacterial growth and nutrient concentration was modeled using a Michaelis-Menten type model.
Using the theory of adaptive dynamics, Doebeli showed that the frequency-dependent selection following from the trade-off can lead to evolutionary branching and the emergence of a stable polymorphism of glucose and acetate specialists. He also found that if the dynamics are changed to model a serial batch culture instead of a chemostat, evolution of cross-feeding becomes much less likely. In a chemostat culture, the concentration of nutrients is kept constant, while in a batch culture nutrients are allowed to be depleted. These results were further expanded and provided experimental confirmation in Friesen et al. [49].
Kianercy et al. [50] studied the Warburg effect and the reverse Warburg effect. The reverse Warburg effect refers to the phenomenon wherein some cells in a tumor use lactate secreted as a by-product of glycolysis as their energy source. The authors' model is a 2-player matrix game with two types of players: hypoxic and oxygenated cells. Both types have the same available strategies: using either glucose or lactate as their nutrient. Lactate is secreted by hypoxic cells using glucose. Similarly to Kareva [39] and Archetti [42, 43], the authors take yields as payoffs. Thus, using glucose gives a lower payoff for hypoxic cells. The authors found that there exist two stable states and conclude that lactate secretion can induce a transition between high and low levels of glucose consumption.
Healey et al. [51] investigated phenotypic bet-hedging by experiments and a game theory model. Bet-hedging refers to a hypothesis that microbes may increase their survival in fluctuating environments by implementing a stochastic phenotype. In other words, a genetically homogeneous population might display two (or more) distinct phenotypes. In the language of game theory, this would constitute a mixed strategy. The model system in Healey et al.[51] was S. cerevisiae that prefers glucose as its carbon source, but also harbors the GAL network for metabolizing galactose. The game theory model used was a simple foraging game, where a population of players must choose between two resources. One of the resources is the preferred one, and so there is an additional cost associated with using the inferior resource. However, if all members of the population have chosen the preferred resource, it is better for an individual to choose the other. This leads to a stable mixed equilibrium of users of both resources. Experiments performed by Healey et al. corroborated this theoretical result.
5. Discussion
In this paper, we presented the idea of a metabolic game and reviewed the main existing literature on applying evolutionary game theory to the study of metabolism. Most studies so far have evoked game theory as an explanatory device, making use of established knowledge on famous games such as the Prisoner's Dilemma to qualitatively describe specific observed phenomena. We believe that it is possible to go beyond that, and to develop a formalism for the metabolic modeling of multicellular and multispecies communities by combining the ideas behind evolutionary game theory with the existing tools of constraint-based modeling.
The recent paper by Zomorrodi and Segre [23] is a first step in this direction. However, there are significant challenges remaining before the game theoretical perspective can be taken full advantage of. Namely, properly defining the different components of a game must be carefully considered in order to make the models derived as reliable and descriptive as possible.
The first component of a game are the players. They are the participants in the interaction under study. Many of the papers discussed in this survey used some form of a 2-player matrix game to make their arguments. In principle, this type of game represents a situation where two individuals face each other in a single interaction to obtain a single payoff. With this in mind, it seems strange to use this model when talking about microbial populations. However, when the matrix game is embedded in the replicator dynamics or another kind of frequency dependent selection model, it starts to more closely resemble a microbe culture. In a way, payoffs are obtained according to who one's average neighbor is at any given time, as might be imagined to happen in a well-mixed culture.
Yet the question remains if pairwise encounters are sufficient to capture the interaction dynamics of microbes that mainly influence each other through diffusible molecules. The other type of model often used is the public goods game. At first glance it seems to more accurately describe an interaction through diffusible molecules because it considers several players to take part in the game at the same time. For example, in the case of invertase production, it is intuitive to consider the game to comprise those cells that the released glucose can be assumed to reach. However, there are some problems with using the public goods game as a general model. Firstly, the benefit function must be accurately estimated since its form can greatly influence the type of dynamics it gives rise to (see for example [46], see also [44]). This might be difficult to do without experimental evidence. Secondly, public goods games with non-linear benefit functions can be difficult to analyse [46], although some progress has been made in this area recently [52].
Explicit consideration of spatial structure could facilitate properly defining interacting agents. Even if the underlying model is a 2-player game, embedding it into a spatial model so that individuals interact with those around them, and the changes resulting in the environment from these actions (depletion of nutrients etc.) happen locally, will be more faithful to nature. The standard way to represent spatial structure in game theory is to assign players to nodes in a graph as was done in Archetti [47]. This approach might be most applicable to environments such as biofilms. The other option is to use partial differential equations to include spatial dimensions in the population dynamics. The main problem with both approaches is that usually the only analysis possible is through simulations. Furthermore, parameters such as diffusion coefficients might be needed to specify the model.
Considering all of the above, it seems that if the goal is to specify a systematic framework in which a metabolic game can be defined based mainly on the metabolic reconstructions of the organisms, the simple matrix game should be the model of choice. Indeed, in order to have a computational framework anywhere close to the simplicity of the original FBA formalism, it seems that only the high level ideas from game theory, mainly considering the choice available for one individual in conjunction with the choices available to their opponents, can be included. This is already captured by the matrix game. In addition, authors have arrived at similar conclusions modeling the same situation with various more complicated models [44, 45] and the simpler matrix game [23].
With regard to the choice of action/strategy space, the question is mostly a technical one. In principle, a game constructed on the basis of metabolic networks would consider as available actions the range of feasible metabolic behaviors, in other words, the flux cone [53, 54]. However, from a practical standpoint it is evident that some abstraction is needed. Firstly, in order for a matrix game to be defined, the action space needs to be discretized. Secondly, with the number of reactions and thus of flux values to be defined routinely reaching to thousands, the game would surely quickly become intractable.
Several approaches to a decomposition of the flux cone have been proposed. Most notably, three related concepts, elementary flux modes [55, 56], extreme currents [53], and extreme pathways [57] all formulate a mathematical definition of a pathway using concepts from linear algebra and convex analysis. Using such concepts, the space of available metabolic phenotypes can be characterized in terms of which reactions are active, each set corresponding roughly to separate biochemical pathways that are able to operate at a steady state. Unfortunately, the number of elements in such a decomposition grows exponentially with the size of the network [58–60]. It might thus be impossible in practice to define the action space simply using these concepts, at least at the level of genome-scale reconstructions. De Figueiredo et al. [61] have offered a possible amendment by proposing an efficient procedure to compute elementary flux modes in order of increasing number of reactions.
Other concepts worth exploring are the phenotypic phase plane put forth by Edwards et al. [62] and the flux tope by Gerstl et al. [63]. A phenotypic phase plane is defined by the uptake rates of two nutrients. The optimal metabolic behavior is calculated at each point of the plane using a biomass function. It turns out that such a plane is divided into a finite number of distinct regions with qualitatively different metabolic behavior. A flux tope is obtained by specifying a direction for all reversible reactions. It corresponds to a maximal “pathway” (as opposed to a minimal one, such as an elementary flux mode). The authors report that the calculation of all flux topes is possible even at a larger scale.
In Zomorrodi and Segre [23], available metabolic actions were not defined explicitly in terms of flux distributions but rather by excreted compounds. One or several metabolites of interest were first forced to be exported and hence produced (or alternatively to not be produced simulating auxotrophy), after which the metabolic state can be determined using standard optimization principles with the additional constraints. There are compelling arguments for defining actions in metabolic games using extracellular compounds. In general, microbial interactions are often mediated by the exchange of molecules. By focusing on these compounds, the elements of the action space have a clear interpretation in the context of interaction. The set of possible secretions is also much more tractable than the space of all possible metabolic phenotypes.
Interactions based on extracellular metabolites were characterized from a slightly different point of view in Klitgord and Segre [64]. The authors asked whether it is possible to predict species interactions based on culture media. Using genome-scale stoichiometric models they tested whether growth of two organisms was possible in isolation and in tandem in a given medium. This approach showed examples of both mutualistic and commensal relationship induced by growth media.
Wintermute and Silver [65] used a similar model to study the exchange of metabolites. The authors showed how the costs and benefits of extracellular metabolites can be estimated using the concept of shadow prices from constraint-based analysis. The shadow price of a metabolite can be understood as a measure of how much the objective, for example biomass flux, would change if the production of the said metabolite changed. Such an analysis could be very useful for metabolic games since it allows one to compute both the cost of producing a diffusible molecule as well as the benefit derived from it by the organism that is able to receive it.
In a thesis work, Wannagat [66] showed how to compute the minimal sets of compounds two organisms need to exchange in order to be able to grow. Here the approach was qualitative and was used to categorize interactions in terms of their type, but such a procedure could be used also to define the action space in a metabolic game.
Finally, in order to construct a game, one needs to define the payoffs. This is arguably the most crucial step since the payoff values will largely determine the predictions of the model. There is a particular importance to not only qualitatively, but also quantitatively establish accurate payoffs here since the hope is for metabolic game theory to match the predictive ability of FBA. One example from the literature discussed in this paper highlights both the importance and the difficulty in defining payoffs.
In several papers [10, 33, 35, 36], fermentation in the presence of oxygen is seen as a classic “cheater” strategy. From an individual's point of view, the inefficiency of fermentation in terms of yield is not “seen”: what the cell experiences as the consequence of its choice is a growth rate exceeding that of its conspecifics. The result of a wasteful use of resources is only felt at the population level, resulting in a lower sustainable cell density. This is the (in)famous Prisoner's Dilemma. However, when essentially the same situation has been discussed in the context of cancer [39, 42, 47], a completely opposite view has been adopted. Here, fermentation was seen as the cooperation strategy. For example, Archetti [42] described using fermentation as a contribution to a public good, the cost of the action being the loss in yield compared to respiration. While it can be argued that the underlying biology is very different for single-celled microbes and cancerous tissue, the discrepancy is still puzzling.
The problem of properly defining payoffs in the yield vs. rate dilemma is related to that of normalization in FBA [10]. In order to “ground” the flux vector, normalization is needed. A common choice for a numeraire is the uptake of a primary nutrient. The fact that maximization of flux through the biomass reaction in FBA leads to a de facto maximization of biomass yield follows from this operation. Consider now the situation in ATP production. If the value of the objective function in a standard FBA approach is taken as the payoff, respiration is a better strategy than fermentation. However, as already discussed, a fermenter can outgrow its respiring neighbor. From the perspective of evolutionary game theory, it is thus clearly the winner, and its payoff should reflect this fact. However, if we simply switch the payoff from yield to actual rate of biomass production, two fermenters would also obtain the highest payoff together. This is because we have assumed in a simplified way that the external resources are infinite, and hence two fermenters are able to sustain the increased uptake of nutrients they achieve in the presence of respirators. In order to arrive at the Prisoner's Dilemma payoff structure, we need to take into account that if everyone uses fermentation, it can no longer provide the benefit it has over respiration because of a depletion of nutrients.
The above example showcases the difficulty in appropriately quantifying the outcomes in a metabolic game. Optimization of an appropriate objective function can certainly accurately identify “catastrophic” outcomes where growth is not possible, but when conclusions are drawn as to which metabolic strategy would win in intra- or interspecific competition, caution is warranted. One must make sure that the quantity under consideration is apt to decide the winner(s) in an evolutionary sense.
The definition of the action space can also offer a way to quantify the payoffs. For example, if different metabolic phenotypes are characterized by imported and exported metabolites, benefits and costs can be calculated following [65]. This could open the way for a more systematic definition of public goods games using only the knowledge obtained from metabolic models.
To further develop these ideas, finding new suitable model organisms, especially for interspecies interactions, would be of great interest. However, if a generally applicable framework for metabolic games is desired, it is important to avoid over-fitting the model to specific situations. Since for single-species communities the work of Zomorrodi and Segre [23] already offers an excellent starting point, a good goal for future research would be a systematic definition of the action space that does not rely on context-specific biological information. With regard to multispecies interactions, this area of research remains less explored. Thus, even a proof of concept application with metabolic strategies derived based on biological knowledge would be desirable.
Besides games, other models from economics have generated interest in the field of microbiology. The concept of comparative advantage [67] was thus applied to gene circuits in Enyeart et al. [68]. The authors showed that when two bacterial species trade signaling molecules necessary for survival, they both enjoy improved growth, as predicted by the theory of comparative advantage. Tasoff et al. [69] used general equilibrium theory [70] to understand the mutualistic exchange of compounds between micro-organisms. The authors argued that comparative advantage is a necessary condition for the exchange to take place. This theory can be further extended to several organisms exchanging multiple compounds. Other concepts that have been suggested for applications in the microbial context include avoidance of bad trading partners, establishment of local business ties, diversification or specialization, monopolization of a market, and elimination of competitors [71].
Author Contributions
TP, MW, and M-FS conceived the idea. TP and MW performed the literature search. TP wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This study was funded by the Horizon 2020 Program of the European Commission within the Marie Skłodowska-Curie Innovative Training Network MicroWine (grant number 643063).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This is a short text to acknowledge the contributions of specific colleagues, institutions, or agencies that aided the efforts of the authors.
References
1. Varma A, Palsson BO. Metabolic flux balancing: basic concepts, scientific and practical use. Biotechnology. (1994) 12:994–8. doi: 10.1038/nbt1094-994
2. Edwards JS, Palsson BO. Metabolic flux balance analysis and the in silico analysis of Escherichia coli K-12 gene deletions. BMC Bioinformatics. (2000) 1:1. doi: 10.1186/1471-2105-1-1
3. Edwards JS, Ibarra RU, Palsson BO. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat Biotechnol. (2001) 19:125–30. doi: 10.1038/84379
4. Orth JD, Thiele I, Palsson BØ. What is flux balance analysis? Nat Biotechnol. (2010) 28:245–8. doi: 10.1038/nbt.1614
5. O'Brien EJ, Monk JM, Palsson BO. Using genome-scale models to predict biological capabilities. Cell. (2015) 161:971–87. doi: 10.1016/j.cell.2015.05.019
6. Gottstein W, Olivier BG, Bruggeman FJ, Teusink B. Constraint-based stoichiometric modelling from single organisms to microbial communities. J R Soc Interface. (2016) 13:20160627. doi: 10.1098/rsif.2016.0627
7. Stolyar S, Van Dien S, Hillesland KL, Pinel N, Lie TJ, Leigh JA, et al. Metabolic modeling of a mutualistic microbial community. Mol Syst Biol. (2007) 3:92. doi: 10.1038/msb4100131
8. Zomorrodi AR, Maranas CD. OptCom: a multi-level optimization framework for the metabolic modeling and analysis of microbial communities. PLoS Comput Biol. (2012) 8:e1002363. doi: 10.1371/journal.pcbi.1002363
9. Khandelwal RA, Olivier BG, Röling WF, Teusink B, Bruggeman FJ. Community flux balance analysis for microbial consortia at balanced growth. PLoS ONE. (2013) 8:e64567. doi: 10.1371/journal.pone.0064567
10. Schuster S, Pfeiffer T, Fell DA. Is maximization of molar yield in metabolic networks favoured by evolution? J Theor Biol. (2008) 252:497–504. doi: 10.1016/j.jtbi.2007.12.008
11. Schuster S, Kreft JU, Schroeter A, Pfeiffer T. Use of game-theoretical methods in biochemistry and biophysics. J Biol Phys. (2008) 34:1–17. doi: 10.1007/s10867-008-9101-4
12. Lee D, Smallbone K, Dunn WB, Murabito E, Winder CL, Kell DB, et al. Improving metabolic flux predictions using absolute gene expression data. BMC Syst Biol. (2012) 6:73. doi: 10.1186/1752-0509-6-73
13. Von Neumann J, Morgenstern O. Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press (2007).
16. Pfeiffer T, Schuster S. Game-theoretical approaches to studying the evolution of biochemical systems. Trends Biochem Sci. (2005) 30:20–5. doi: 10.1016/j.tibs.2004.11.006
17. Ruppin E, Papin JA, De Figueiredo LF, Schuster S. Metabolic reconstruction, constraint-based analysis and game theory to probe genome-scale metabolic networks. Curr Opin Niotechnol. (2010) 21:502–10. doi: 10.1016/j.copbio.2010.07.002
18. Hummert S, Bohl K, Basanta D, Deutsch A, Werner S, Theißen G, et al. Evolutionary game theory: cells as players. Mol Biosyst. (2014) 10:3044–65. doi: 10.1039/C3MB70602H
19. Nash JF, Jr. Equilibrium points in n-person games. Proc Natl Acad Sci USA. (1950) 36:48–9. doi: 10.1073/pnas.36.1.48
22. Avis D, Rosenberg GD, Savani R, Von Stengel B. Enumeration of Nash equilibria for two-player games. Econ Theor. (2010) 42:9–37. doi: 10.1007/s00199-009-0449-x
23. Zomorrodi AR, Segrè D. Genome-driven evolutionary game theory helps understand the rise of metabolic interdependencies in microbial communities. Nat Commun. (2017) 8:1563. doi: 10.1038/s41467-017-01407-5
25. Archetti M, Scheuring I. Review: game theory of public goods in one-shot social dilemmas without assortment. J Theor Biol. (2012) 299:9–20. doi: 10.1016/j.jtbi.2011.06.018
26. Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge, UK: Cambridge University Press (1998).
27. Page KM, Nowak MA. Unifying evolutionary dynamics. J Theor Biol. (2002) 219:93–8. doi: 10.1016/S0022-5193(02)93112-7
28. Metz JA, Geritz SA, Meszéna G, Jacobs FJ, Van Heerwaarden JS. Adaptive dynamics, a geometrical study of the consequences of nearly faithful reproduction. Stochast Spatial Struct Dynam Syst. (1996) 45:183–231.
29. Dieckmann U, Law R. The dynamical theory of coevolution: a derivation from stochastic ecological processes. J Math Biol. (1996) 34:579–612. doi: 10.1007/BF02409751
30. Geritz SAH, Kisdi E, Meszena G, Metz JAJ. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol Ecol. (1998) 12:35–57. doi: 10.1023/A:1006554906681
31. Pande S, Merker H, Bohl K, Reichelt M, Schuster S, De Figueiredo LF, et al. Fitness and stability of obligate cross-feeding interactions that emerge upon gene loss in bacteria. ISME J. (2014) 8:953. doi: 10.1038/ismej.2013.211
32. Campbell K, Vowinckel J, Mülleder M, Malmsheimer S, Lawrence N, Calvani E, et al. Self-establishing communities enable cooperative metabolite exchange in a eukaryote. Elife. (2015) 4:e09943. doi: 10.7554/eLife.09943
33. Pfeiffer T, Schuster S, Bonhoeffer S. Cooperation and competition in the evolution of ATP-producing pathways. Science. (2001) 292:504–7. doi: 10.1126/science.1058079
34. Lloyd WF. Two Lectures on the Checks to Population: Delivered Before the University of Oxford, in Michaelmas Term 1832. Oxford, UK: JH Parker (1833).
35. Frick T, Schuster S. An example of the prisoner's dilemma in biochemistry. Naturwissenschaften. (2003) 90:327–31. doi: 10.1007/s00114-003-0434-3
36. MacLean RC, Gudelj I. Resource competition and social conflict in experimental populations of yeast. Nature. (2006) 441:498. doi: 10.1038/nature04624
37. Aledo JC, Pérez-Claros JA, Del Valle AE. Switching between cooperation and competition in the use of extracellular glucose. J Mol Evol. (2007) 65:328–39. doi: 10.1007/s00239-007-9014-z
38. Schuster S, de Figueiredo LF, Schroeter A, Kaleta C. Combining metabolic pathway analysis with evolutionary game theory. Explaining the occurrence of low-yield pathways by an analytic optimization approach. Biosystems. (2011) 105:147–53. doi: 10.1016/j.biosystems.2011.05.007
39. Kareva I. Prisoner's dilemma in cancer metabolism. PLoS ONE. (2011) 6:e28576. doi: 10.1371/journal.pone.0028576
40. Warburg O, Wind F, Negelein E. Ueber den stoffwechsel von tumoren im körper. Klinische Wochenschrift. (1926) 5:829–32. doi: 10.1007/BF01726240
41. Warburg O. On the origin of cancer cells. Science. (1956) 123:309–14. doi: 10.1126/science.123.3191.309
42. Archetti M. Evolutionary dynamics of the Warburg effect: glycolysis as a collective action problem among cancer cells. J Theor Biol. (2014) 341:1–8. doi: 10.1016/j.jtbi.2013.09.017
43. Archetti M. Heterogeneity and proliferation of invasive cancer subclones in game theory models of the Warburg effect. Cell Prolif . (2015) 48:259–69. doi: 10.1111/cpr.12169
44. Gore J, Youk H, Van Oudenaarden A. Snowdrift game dynamics and facultative cheating in yeast. Nature. (2009) 459:253–6. doi: 10.1038/nature07921
45. Schuster S, Kreft JU, Brenner N, Wessely F, Theißen G, Ruppin E, et al. Cooperation and cheating in microbial exoenzyme production–theoretical analysis for biotechnological applications. Biotechnol J. (2010) 5:751–8. doi: 10.1002/biot.200900303
46. Archetti M. Evolutionary game theory of growth factor production: implications for tumour heterogeneity and resistance to therapies. Br J Cancer. (2013) 109:1056–62. doi: 10.1038/bjc.2013.336
47. Archetti M. Cooperation among cancer cells as public goods games on Voronoi networks. J Theor Biol. (2016) 396:191–203. doi: 10.1016/j.jtbi.2016.02.027
48. Doebeli M. A model for the evolutionary dynamics of cross-feeding polymorphisms in microorganisms. Popul Ecol. (2002) 44:59–70. doi: 10.1007/s101440200008
49. Friesen ML, Saxer G, Travisano M, Doebeli M. Experimental evidence for sympatric ecological diversification due to frequency-dependent competition in Escherichia coli. Evolution. (2004) 58:245–60. doi: 10.1111/j.0014-3820.2004.tb01642.x
50. Kianercy A, Veltri R, Pienta KJ. Critical transitions in a game theoretic model of tumour metabolism. Interface Focus. (2014) 4:20140014. doi: 10.1098/rsfs.2014.0014
51. Healey D, Axelrod K, Gore J. Negative frequency-dependent interactions can underlie phenotypic heterogeneity in a clonal microbial population. Mol Syst Biol. (2016) 12:877. doi: 10.15252/msb.20167033
52. Archetti M. How to analyze models of nonlinear public goods. Games. (2018) 9:17. doi: 10.3390/g9020017
53. Clarke BL. Stability of complex reaction networks. Adv Chem Phys. (1980) 43: 1–215. doi: 10.1002/9780470142622.ch1
54. Clarke BL. Stoichiometric network analysis. Cell Biophys. (1988) 12:237–53. doi: 10.1007/BF02918360
55. Schuster R, Schuster S. Refined algorithm and computer program for calculating all non–negative fluxes admissible in steady states of biochemical reaction systems with or without some flux rates fixed. Bioinformatics. (1993) 9:79–85. doi: 10.1093/bioinformatics/9.1.79
56. Schuster S, Hilgetag C. On elementary flux modes in biochemical reaction systems at steady state. J Biol Syst. (1994) 2:165–82. doi: 10.1142/S0218339094000131
57. Schilling CH, Edwards JS, Letscher D, Palsson BØ. Combining pathway analysis with flux balance analysis for the comprehensive study of metabolic systems. Biotechnol Bioeng. (2000) 71:286–306. doi: 10.1002/1097-0290(2000)71:4<286::AID-BIT1018>3.0.CO;2-R
58. Klamt S, Stelling J. Combinatorial complexity of pathway analysis in metabolic networks. Mol Biol Rep. (2002) 29:233–6. doi: 10.1023/A:1020390132244
59. Schuster S, Pfeiffer T, Moldenhauer F, Koch I, Dandekar T. Exploring the pathway structure of metabolism: decomposition into subnetworks and application to Mycoplasma pneumoniae. Bioinformatics. (2002) 18:351–61. doi: 10.1093/bioinformatics/18.2.351
60. Acuna V, Chierichetti F, Lacroix V, Marchetti-Spaccamela A, Sagot MF, Stougie L. Modes and cuts in metabolic networks: complexity and algorithms. Biosystems. (2009) 95:51–60. doi: 10.1016/j.biosystems.2008.06.015
61. De Figueiredo LF, Podhorski A, Rubio A, Kaleta C, Beasley JE, Schuster S, et al. Computing the shortest elementary flux modes in genome-scale metabolic networks. Bioinformatics. (2009) 25:3158–65. doi: 10.1093/bioinformatics/btp564
62. Edwards JS, Ramakrishna R, Palsson BO. Characterizing the metabolic phenotype: a phenotype phase plane analysis. Biotechnol Bioeng. (2002) 77:27–36. doi: 10.1002/bit.10047
63. Gerstl MP, Müller S, Regensburger G, Zanghellini J. Flux tope analysis: studying the coordination of reaction directions in metabolic networks. Bioinformatics. (2018) 35:266–73. doi: 10.1093/bioinformatics/bty550
64. Klitgord N, Segrè D. Environments that induce synthetic microbial ecosystems. PLoS Comput Biol. (2010) 6:e1001002. doi: 10.1371/journal.pcbi.1001002
65. Wintermute EH, Silver PA. Emergent cooperation in microbial metabolism. Mol Syst Biol. (2010) 6:407. doi: 10.1038/msb.2010.66
66. Wannagat M. Study of the Evolution of Symbiosis at the Metabolic Level Using Models from Game Theory and Economics. Université de Lyon (2016).
68. Enyeart PJ, Simpson ZB, Ellington AD. A microbial model of economic trading and comparative advantage. J Theor Biol. (2015) 364:326–43. doi: 10.1016/j.jtbi.2014.09.030
69. Tasoff J, Mee MT, Wang HH. An economic framework of microbial trade. PLoS ONE. (2015) 10:e0132907. doi: 10.1371/journal.pone.0132907
70. Varian HR. Intermediate Microeconomics: A Modern Approach (Eighth Edition). 8th ed. W. W. Norton & Company (2009). Available online at: http://www.worldcat.org/isbn/0393934241
Keywords: metabolic modeling, flux balance analysis, evolutionary game theory, microbial interactions, metabolic networks
Citation: Pusa T, Wannagat M and Sagot M-F (2019) Metabolic Games. Front. Appl. Math. Stat. 5:18. doi: 10.3389/fams.2019.00018
Received: 07 December 2018; Accepted: 27 March 2019;
Published: 12 April 2019.
Edited by:
Bud Mishra, New York University, United StatesReviewed by:
Priyanka Baloni, Institute for Systems Biology (ISB), United StatesRanjan K. Dash, Medical College of Wisconsin, United States
Copyright © 2019 Pusa, Wannagat and Sagot. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Taneli Pusa, aGVucmkucHVzYUBpbnJpYS5mcg==
Marie-France Sagot, bWFyaWUtZnJhbmNlLnNhZ290QGlucmlhLmZy
 Taneli Pusa
Taneli Pusa Martin Wannagat1,2
Martin Wannagat1,2 Marie-France Sagot
Marie-France Sagot