Chimera States on a Ring of Strongly Coupled Relaxation Oscillators

1. Introduction

In populations of coupled nonlinear oscillators synchronization [1] and macroscopic non-equilibrium pattern formation [2] are intrinsically linked. In 2002, studying synchronization in a system of nonlocally coupled phase oscillators, Kuramoto and co-workers discovered a symmetry-broken solution comprised of in-phase synchronized and desynchronized oscillatory domains [3, 4]. This state, which was later named chimera state due to its incongruous composition, triggered an increasing number of studies on partial synchronization in populations of coupled nonlinear oscillators [5, 6]. The existence of chimera states on ring topologies has been verified in experiments with chemical and electrochemical oscillators [7, 8], electronic units [9, 10], laser systems [11, 12] and hydrodynamically coupled colloids [13]. They are thought to play an important role in neurological disorders [14] and new metamaterials [15].

Intuitively, chimera states exist due to the nonlocal coupling term, which does not depend on the state of a single local element, but takes into account the spatially extended pattern. Both dynamically distinct domains modulate the coupling term to maintain themselves, respectively. A spatial domain with high coherence results in a large feedback signal that supports high coherence. Conversely a domain with a low coherence leads to a small feedback signal that obstructs high coherence. Together this reinforces the respective coexisting, but incongruous spatiotemporal dynamics [4].

Many studies on coupled oscillators utilize the paradigmatic Kuramoto phase oscillator model due to its simplicity and analytical tractability [16, 17]. Our goal in this paper is to go beyond the weak coupling oscillators and describe chimera patterns on a ring of strongly coupled oscillators, which are based on chemical laboratory experiments. The commonly employed weak-coupling limit in oscillator networks is defined as the lowest order of a systematic perturbation expansion in a smallness parameter ϵ, reducing dynamics of coupled limit-cycle oscillators to pure phase dynamics. This reduction is possible, if the decay of amplitude disturbances, quantified by the transversal Lyapunov exponent, is much faster than the decay of phase disturbances.

A clear definition of a strong coupling limit is not so obvious and the focus of current research on coupled oscillators [18, 19]. A coupling scheme that implies substantial changes in the oscillator frequencies, cannot be viewed as weak. One possibility to differentiate between weak and strong coupling is to measure the phase response curve (PRC) of an oscillator [20]. It quantifies how much the phase ϕ, that parametrizes the oscillation cycle, is advanced or delayed in response to an external perturbation. Small perturbations representative of weak coupling lead to a continuous phase response curve Q(ϕ). Strong coupling perturbations evoke a non-smooth, discontinuous PRC exhibiting a finite jump, for example. Moreover, the PRC under weak-coupling scales linearly with the perturbation amplitude A, while under strong coupling the amplitude scaling turns out to be nonlinear: Q(ϕ; λA) ≠ λ × Q(ϕ; A) with λ ∈ ℝ.

2. Models

The dynamics on an arbitrary finite network of N interacting Kuramoto phase oscillators are described by

$\begin{array}{ll}\frac{d{\varphi }_i}{dt}={\omega }_i+{\displaystyle \sum _{j=1}^N}{W}_{ij}sin({\varphi }_j-{\varphi }_i-\alpha ).& (1)\end{array}$

The state of the i-th oscillator is given by a scalar time-dependent phase variable ϕ_i(t), that repeatedly cycles through values from 0 to 2π. The interaction with other nodes in the network effectively modulates the natural angular frequency ω_i. The modulation strength is encoded in the weighted adjacency matrix W_ij and a 2π-periodic interaction function of the phase difference ϕ_j − ϕ_i.

The weighted adjacency matrix W_ij can encode any network connectivity. Additionally each link can have its own individual weight. In this paper we focus on global coupling given by W_ij = K/N(1 − δ_ij), where δ_ij is the Kronecker delta, and rings with nonlocal coupling given by W_ij = Kexp(‖i − j‖/κ). In both cases K is the coupling strength. For global coupling, the weights are normalized by the number of nodes N. In the nonlocally coupled system, the weights between nonlocal neighbors decay exponentially with a characteristic range of κ according to their distance on the ring network.

The simplest choice for the interaction function is the first Fourier mode. Given a vanishing phase frustration parameter α = 0, if the neighboring node j is ahead in phase, node i will accelerate and conversely if neighbor j lags behind, then node i will decelerate. In the case of identical natural frequencies this interaction eventually leads to exact in-phase alignment. For α ≠ 0, the contribution by the interaction function does not vanish for in-phase alignment, which effectively impedes in-phase synchronization.

Remarkably, all dissipative systems with oscillatory dynamics can be reduced to a Kuramoto phase model with an appropriate interaction function under the assumption that the coupling between oscillators is weak [21]. As discussed above the most important consequence is that the resultant phase change Δϕ due to a perturbation scales linearly with the perturbation amplitude. However, for strongly coupled oscillators this condition can be violated, when the total effect of multiple perturbations is not equal to the linear superposition of the individual effects.

We illustrate one possible realization of this case and its real-world relevance with experimentally well-accessible chemical relaxation oscillators [22–24], that show qualitatively identical behavior to biological nerve and heart cells [25–31]. The oscillators are based on the Belousov-Zhabotinsky reaction and their dynamics are well-captured in the two-component non-dimensionalized Zhabotinsky-Buchholtz-Kiyatkin-Epstein (ZBKE) model [23, 32, 33]:

$\begin{array}{ll}\begin{array}{l}{\dot{u}}_i=\frac{1}{{ϵ}_1}(I_i-u_i(1+u_i)-\frac{u_i-\mu }{u_i+\mu }\left(\beta +q_i\frac{\alpha v_i}{{ϵ}_3+1-v_i}\right)\hfill \\ +\gamma {ϵ}_2{w}_{ss,i}^2+(1-v_i)w_{ss,i}),\hfill \\ {\dot{v}}_i=2I_i+(1-v_i)w_{ss,i}-\frac{\alpha v_i}{{ϵ}_3+1-v_i},\hfill \\ w_{ss,i}(u_i,v_i)=\frac{1}{4\gamma {ϵ}_2}\left(\sqrt{16\gamma u_i{ϵ}_2+v_i^2-2v_i+1}+v_i-1\right),\hfill \\ I_i(t)=I_0+{\displaystyle \sum _{j=1}^N{W}_{ij}\left[v_j(t-\tau )-v_i(t)\right].}\hfill \end{array}& (2)\end{array}$

The oscillation takes place in the dimensionless concentrations of u (bromous acid, HBrO₂) and v (oxidized form of the ruthenium-tris-dimethylene-bipyridine catalyst, ${\text{Ru(dmbpy)}}_3^{3+}$). The latter can be measured spectrophotometrically via fluorescence light in an experiment [23]. The parameters ϵ₁, ϵ₂, ϵ₃, α, β, γ, μ, q depend on reaction rates and initial reagent concentrations. The dimensionless steady-state concentration w_ss (bromous acid radical ${\text{HBrO}}_2^{+}$) adapts adiabatically. The interaction between oscillators is mediated by individual light application I_i via a spatial light modulator that influences the production rates of u and v. For comparability with the Kuramoto model Equation (1), here the interaction is chosen to depend linearly on the difference of the oxidized catalyst concentrations v_j − v_i. To allow for phase frustration in limit cycle oscillators, instead of a phase frustration parameter α Equation (1) we utilize a time delay: v_j(t − τ) − v_i(t) [5]. Only for τ = 0 in-phase synchronization is possible, whereas τ ≠ 0 obstructs it. The weighted adjacency matrix W_ij in the coupling term encodes the network connectivity and can be freely chosen as discussed above. Due to the dissipative nature of both models, we employ the explicit Euler method with a fixed time step Δt for numerical simulation [34].

To get intuition for the dynamics of the ZBKE model (Equation 2), we present the u-v phase plane of a single oscillator in Figure 1A. It features an unstable fixed point inside a stable limit cycle that resulted from a Hopf bifurcation with a consecutive canard explosion [35]. The phase space structure with the cubic shape of the u-nullcline (continuous) and its single intersection with the v-nullcline (dashed) resembles the FitzHugh-Nagumo model for neuronal oscillations [36]. However, the ZBKE phase plane is plotted in logarithmic scale and thus there are only single fast and slow domains on the right and left branch of the limit cycle, respectively. This is further reflected in the consecutive switches between fast rise and slow decay of the v variable (Figure 1B).

FIGURE 1

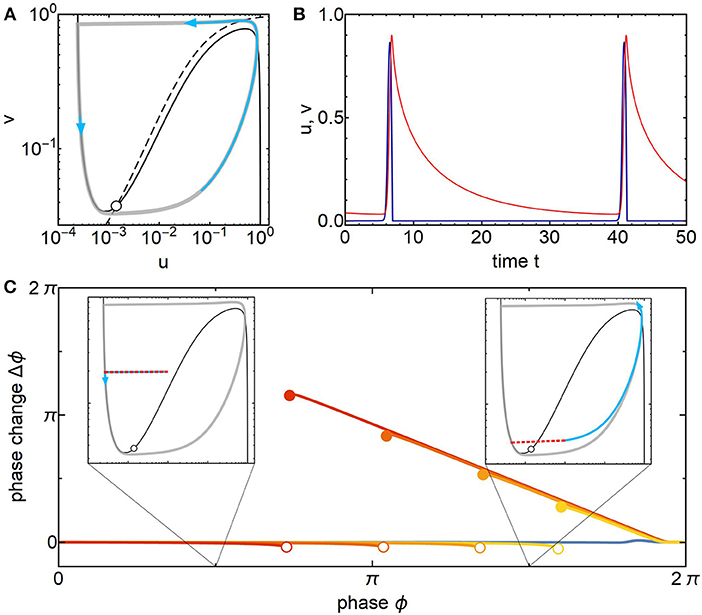
Figure 1. Relaxation oscillator dynamics of the ZBKE model (A) Logarithmically-scaled phase plane consisting of unstable fixed point (empty dot) at the intersection of u- and v-nullclines (continuous, dashed black lines) surrounded by stable limit cycle (gray). Two example trajectories (blue) lasting 3 dimensionless time units illustrate fast and slow dynamics along the limit cycle. (B) Time series of u, v variables (blue, red) exhibit time scale separation that is characteristic for a relaxation oscillation. (C) Phase response curves for different perturbation amplitudes (red to yellow: I_p = {1, 1/2, 1/4, 1/8} × 10⁻³, blue: $I_p=10^{-5}$). Insets show perturbation (red dashed) and perturbed phase plane trajectories (blue) in phase space underlying the measured phase change Δϕ. Parameters: ϵ₁ = 0.11, ${ϵ}_2=1.7\times 10^{-5}$, ${ϵ}_3=1.6\times 10^{-3}$, α = 0.1, β = 1.7 × 10⁻⁵, γ = 1.2, μ = 2.4 × 10⁻⁴, q = 0.7, $I_0=5.25\times 10^{-4}$, natural frequency ω₀ = 0.177, time step Δt = 2 × 10⁻⁴.

To gain insight into the synchronization properties of a set of such oscillators, we measure the corresponding phase response curve Q(ϕ). In Figure 1C we choose an additive perturbation, $(u,v)\mapsto (u+{ϵ}_1^{-1}{I}_p,v+2I_p)$, where I_p is the perturbation strength. This perturbation imitates a short application of light intensity in the experiment.

In contrast to commonly employed smooth phase response curves [20] our PRC exhibits two distinguishing features (Figure 1): First, there is a jump-discontinuity between an initial flat interval, during which the oscillator is insensitive to a perturbation, Δϕ = 0, and a second interval, which is well approximated by Δϕ = 2π − ϕ. Secondly, the perturbation strength does not linearly scale the amplitude of the PRC, but instead changes the position of the jump point ϕ^* and thus the shape, Q(ϕ; λA) ≠ λ × Q(ϕ; A). Overall the PRC is well captured by:

$\begin{array}{ll}Q(\varphi ;I_p)=\{\begin{array}{cc}0\hfill & ,\varphi <{\varphi }^{*}(I_p)\hfill \\ 2\pi -\varphi \hfill & ,\varphi \ge {\varphi }^{*}(I_p)\hfill \end{array}.\hfill & (3)\end{array}$

These features are incompatible with the commonly employed weak coupling approximation. The reason is that the perturbation amplitudes are large and our system exhibits phase-sensitive excitability [37]: During the refractory window at early phases, a perturbation of fixed amplitude fails to push the state across the u-nullcline, but it succeeds during the vulnerable window at later phases and induces a new oscillation cycle immediately (insets Figure 1C). Consequently the position of the jump point ${\varphi }^{*}(I_p)$ in the PRC for a certain perturbation strength I_p can be predicted by the distance between the left branch of the limit cycle and the unstable branch of the u-nullcline. Note that for weak perturbations the PRC qualitatively changes its shape and scales linearly with the perturbation amplitude, as expected.

In Figure 2 we highlight the contrasting synchronization behavior of strongly coupled oscillators (Equation 2) by direct comparison with Kuramoto phase oscillators (Equation 1), which are weakly coupled by definition. It is well known that in an all-to-all coupled network heterogeneous Kuramoto phase oscillators synchronize beyond a critical coupling strength [16]. The Kuramoto order parameter,

$\begin{array}{ll}R=\frac{1}{N}\left|{\displaystyle \sum _{j=1}^N}{e}^{\text{i}{\varphi }_j}\right|,& (4)\end{array}$

quantifies the level of phase synchronization. It ranges from 0 for evenly balanced phase distributions, that include incoherent and cluster states, to 1 for coherent states where all phases narrowly align together. Inclusion of an additive phase frustration parameter in the interaction function of the Kuramoto model, sin(ϕ_j − ϕ_i − α), allows for tuning the interactions between oscillators from attractive to repulsive, leading, respectively to phase alignment for α ∈ [0, π/2[∪]3π/2, 2π[ or conversely to frequency detuning for α ∈ [π/2, 3π/2] (Figure 2A).

FIGURE 2

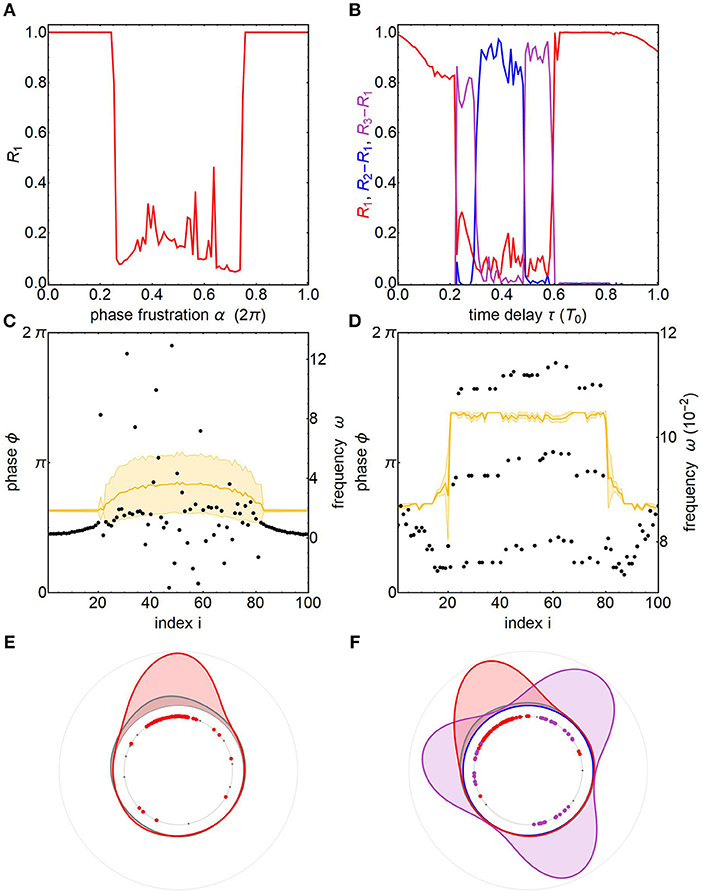
Figure 2. Comparison of chimera states in weakly and strongly coupled oscillators on a ring. Left column: Kuramoto phase oscillators (Equation 1), Right column: ZBKE relaxation oscillators (Equation 2). (A,B) Collective dynamics in a globally coupled network quantified by Kuramoto order parameters as a function of synchronization frustration (α, τ) exhibiting in-phase synchronization, incoherence and d-clusters with d ∈ {2, 3}. Parameters for phase (ZBKE) oscillators: K = 50, Δt = 5 × 10⁻³ (K = 4 × 10⁻⁵, Δt = 2 × 10⁻⁴). (C,D) Collective dynamics on a nonlocally coupled ring network consisting of dynamic modes found in a globally coupled network. Snapshots show phases (black) and frequencies (yellow). Parameters for phase (ZBKE) oscillators: K = 0.1, κ = 35, α = 1.457 (K = 7.93 × 10⁻⁴, κ = 2, τ = 8.67, q ∈ [0.69, 0.71]). (E,F) Smoothed distributions of in-phase (red), 3-cluster (purple) and incoherent (gray) oscillator populations on the phase circle. Parameters: N = 100. Others as in Figure 1.

On a ring topology with nonlocal interactions, it is possible for these two distinct collective states to exist simultaneously in neighboring spatial domains realizing a chimera state (Figure 2C). Oscillators 21-79 are not frequency-locked and their phases are spread out. In contrast, oscillators 1–20 and 80–100 are frequency-locked and their phases align together. They exhibit an average frequency that is smaller than their mean natural frequency, because the phase frustration α for Δϕ = 0 does not get compensated.

This phase pattern is furthermore illustrated with a smoothed polar histogram of the oscillator population (Figure 2E). To differentiate between the populations we employ a localized version of the Kuramoto order parameter that measures the phase coherence in a spatially-bounded interval [i − ℓ, i + ℓ] around oscillator i:

$\begin{array}{ll}{r}_i=\frac{1}{2\ell +1}\left|{\displaystyle \sum _{j=i-\ell }^{i+\ell }}{e}^{\text{i}{\varphi }_j}\right|.& (5)\end{array}$

While oscillators in the coherent population, identified by r_i ≥ 0.7, coalesce to the same phase, incoherent oscillators with r_i < 0.7 are more evenly spread out over the phase circle. The distribution of the incoherent population also exhibits a minor peak that is slightly ahead in phase of the coherent population due to intermittent phase-locking.

In comparison, the strongly coupled oscillators feature coherent and apparently incoherent states in an all-to-all network (Figure 2B). On closer inspection the incoherent state is revealed to be a d-cluster with d ∈ {2, 3} as quantified by R_d − R₁ with the d-cluster Kuramoto order parameter [38]

$\begin{array}{ll}{R}_d=\frac{1}{N}\left|{\displaystyle \sum _{j=1}^N}{e}^{\text{i}d{\varphi }_j}\right|.& (6)\end{array}$

For d = 3 it maps phases of 0, 2π/3, 4π/3 and 2π onto the same value due to the 2π/d-periodicity of the complex exponential. Note that R_d also approaches unity for 1-cluster states, which are also known as coherent in-phase synchronization states. To distinguish d-cluster states from 1-cluster states, we use the difference R_d − R₁.

On the nonlocally coupled ring network we again observe coexistence of the collective states from the all-to-all network. However, for the strongly coupled ZBKE oscillators these are 1-cluster and 3-cluster states (Figure 2D). Apart from the state shown, we also observed coexisting 1 and 2-cluster states as well as 2 and 3-cluster states for other coupling parameters. The polar phase histogram (Figure 2F) clearly highlights the distinct populations as identified by r_d,i, which is a localized version of d-cluster Kuramoto order parameter (Equation 6) similar to Equation (5). The coherent oscillators (r_1,i ≥ 0.7) coalesce around the same phase, while the members of the 3-cluster population (r_3,i − r_1,i > 0.5) are found at three distinct locations on the phase circle. Oscillators at the spatial border between both clusters fail to join either of them due to competing perturbations.

We stress that the mechanism for cluster formation in strongly coupled limit cycle oscillators with delay is qualitatively different from Kuramoto phase oscillators with higher harmonics in the interaction function. The number of clusters for strongly coupled oscillators is not determined by the number of harmonics in the interaction function [21], but instead by the size of the refractory window in relation to the time delay τ in the coupling. The role of time delay is illustrated for a 2-cluster state in Figure 3.

FIGURE 3

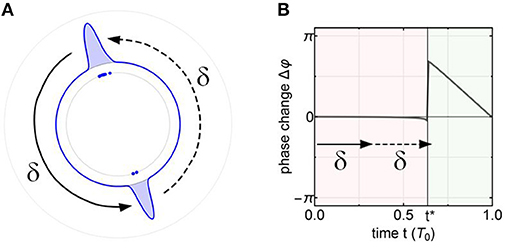
Figure 3. Cluster state mechanism. (A) The smoothed polar histogram shows two antiphasic subpopulations in a globally coupled network. They perturb each other a time δ after they have been perturbed themselves, respectively. Parameters: N = 100, K = 1.4 × 10⁻⁴, τ = 8.67. Other parameters as in Figure 2. (B) The 2-cluster state emerges if the perturbation from the other cluster arrives in the vulnerable window (green) given by the jump point t^* in the PRC.

In a globally coupled network starting from uniformly random phases, oscillators will join either of two clusters, depending on whether they are initially in their refractory window or not. Once the two clusters establish themselves, they stabilize each other via delayed perturbations (Figure 3A) that are sharply localized in time due to the peaked waveform of the v variable (Figure 1B). Even though the network is globally coupled, this perturbation does not affect the population that emits it, because its oscillators are still in their refractory window (Figure 3B). Only the subsequent perturbation from the second cluster induces a new firing event in the first cluster, because it arrives in the vulnerable window. Consequently the period of an oscillator is T₂ = 2δ, where δ = τ + Δt_peak that accounts for the transmission delay and the time required for a peak in v(t) to rise (Δt_peak ≈ 1). Utilizing the PRC, we find that a necessary condition for the appearance of a 2-cluster is that the period T₂ exceeds the refractory window given by the jump discontinuity point $t^{*}={\varphi }^{*}/{\omega }_0$. Note that this can be generalized to d-clusters with d ≥ 1, whose periods follow T_d = δ × d/Δd, where Δd < d is the number of omitted clusters during one spike transmission. It turns out that for weaker coupling strength K, and hence larger refractory windows, cluster states with larger d are possible. This opens the possibility of chimera states, which are comprised of spatial domains exhibiting various d-cluster states [33, 39].

3. Experiments

To demonstrate the real-world viability of the chimera state in strongly coupled relaxation oscillators, we utilize a large reservoir of more than 2,000 chemical micro-oscillators that are coupled via light illumination [23, 33, 39]. From this reservoir we select N = 100 oscillators with a narrow natural frequency distribution (ω₀ = 0.07 ± 0.01Hz). Starting from random initial conditions we observe the development of a two-headed chimera state consisting of two in-phase synchronized domains separated by noisy cluster states (Figures 4A,B). Similar multi-headed chimera states were previously only observed in laser systems [11, 12]. Due to the inherent heterogeneity in periods and phase response behavior [40], the oscillators in the clusters show a larger phase spread than in simulations with homogeneous oscillators. Stronger heterogeneity can furthermore lead to phase switchers [41], which prevent the formation of stationary clusters, resulting in an apparently incoherent domain.

FIGURE 4

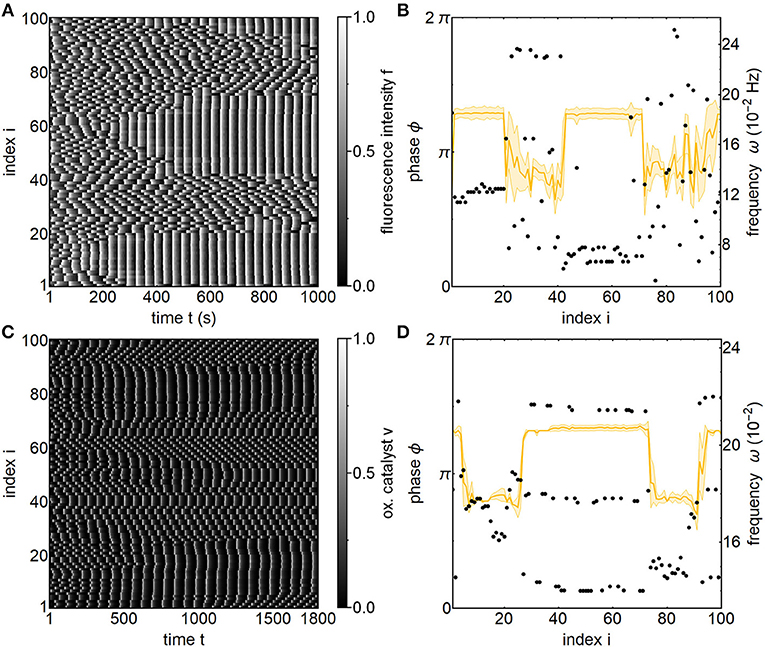
Figure 4. Two-headed chimera state. (A) Experimental space-time plot of the fluorescence intensities of N = 100 nonlocally photo-coupled chemical oscillators exhibiting a two-headed chimera state. (B) Snapshot of instantaneous phases and time-averaged frequencies at time t = 586 s revealing two in-phase synchronized and two noisy cluster domains. Parameters: K = 0.1, κ = 3.3, τ = 32 s, T₀ = 86 ± 12s, [H₂SO₄]₀ = 0.77 M, [NaBrO₃]₀ = 0.51 M, [malonic acid]₀ = 0.16 M, catalyst load: $2.5\times 10^{-5}{\mathrm{\text{mol Rudmbipy}}}_3^3+/\mathrm{\text{g resin}}$. (C) Numerical space-time plot of the oxidized catalyst v. (D) Snapshot of instantaneous phases and time-averaged frequencies at time t = 1, 362 revealing two in-phase synchronized and two noisy cluster domains. Parameters: K = 2.98 × 10⁻⁴, κ = 4, τ = 8.67. Other parameters as in Figure 1.

We stress that the chimera state with strongly coupled oscillators does not require special initial conditions as in the case with phase oscillators [42]. The space-time plot of the observed fluorescence intensities emitted by the oscillators shows the spontaneous formation of the first coherent head (i ∈ [8, 18]) in an environment of incoherent oscillators after only 3 periods. The second head (i ∈ [52, 63]) nucleates at the opposite side of the ring network after 7 periods. After their formation the coherent heads grow over 8 periods until they encompass about 30 oscillators. Upon reaching this extent, their size fluctuates, but their position is fixed on the ring. A snapshot of the phases and frequencies at t = 586 s shows the coherent domains and the clusters with equal phase differences between their constituent subgroups. Even though both coherent heads are respectively in-phase synchronized and move at the same frequency, there is a phase-lag between them. Since in a d-cluster domain, all oscillators are phase-locked they all exhibit the same frequency depending on the number of clusters d. Thus, the frequency distribution of a chimera state consisting of different d-clusters shows distinct noisy flat plateaus for each cluster. This is in contrast to chimera states in Kuramoto phase oscillators, where the frequency distribution exhibits a flat plateau for synchronized oscillators and a large band of frequencies for desynchronized oscillators.

Corresponding numerical simulations (Figures 4C,D) successfully reproduce the two-headed chimera state. In contrast to the experiments, the space-time plot shows a different route to a two-head chimera. At the beginning more than two coherent domains form, but over time they merge together or breakup into a 3-cluster state until only two coherent heads remain. The simulations also highlight that the phase distribution, here consisting of coherent and 3-cluster domains, is not enough to fully characterize the state. The snapshot in Figure 4D shows that the 3-cluster domains have a larger frequency than the coherent domains, whereas the experiments shows the opposite relationship.

Within established classification schemes put forward by Kemeth et al. [43] and Gopal et al. [44], our states can be identified as two-headed static chimera states based on the spatial correlation measure g₀(t) and strength of incoherence SI(t) with a discontinuity measure η = 2.

4. Conclusions

We analyzed the collective behavior of strongly coupled limit cycle oscillators through simulations and experiments. Under strong perturbations the characteristic phase response curve develops a jump-discontinuity, whose position depends on the perturbation amplitude. This behavior is directly rooted in the phase-dependent excitability of the oscillator (Figure 1) and is found commonly in nature [25–31].

We further numerically elucidated the differences between chimera states in Kuramoto phase oscillators and ZBKE relaxation oscillators as exemplary cases for weak and strong coupling. The coherence-incoherence chimera states emerging in the case of weakly coupled Kuramoto phase oscillators are replaced with chimera states consisting of coexisting domains of coherence and d-clusters for strongly coupled relaxation oscillators (Figure 2). The cluster states can be identified using generalized Kuramoto order parameters [38] and their formation can be understood in an all-to-all network with the help of the phase response curve (Figure 3). Ultimately we verified our predictions and their real-world robustness in an experimental setup with photo-coupled chemical oscillators and observed a two-headed chimera state that consisted of two coherent domains and two 3-cluster states (Figure 4). In the future it would be interesting to apply previously developed control schemes[45–47] in the experiment to dictate the position, drift speed and lifetime of the observed multi-headed chimera state as well as investigate the role of noise [48] and multi-layer interaction [49].

Besides resulting in chimera states of different nature, the strongly coupled oscillators also highlight the connection between collective states in global and nonlocal networks. Our results suggest that beyond incoherence-coherence patterns, chimera states can be viewed as time-dependent pattern with distinct spatial domains, whose behavior is inherited from the various dynamical modes during global coupling of the underlying dynamical units.

Author's Note

The simulation codes for oscillators in globally and nonlocally coupled networks are available at: https://github.com/bzjan/Coupled_Oscillators_Solver.

Author Contributions

JT and JR built the set-up and performed experiments. JT and HE designed the study and wrote the paper. The simulations were carried out by JT, JR, and EF. All authors discussed the results and commented on the manuscript.

Funding

This work was supported by the Deutsche Forschungsgemeinschaft (grants GRK 1558 and SFB 910 to JT, JR, EF, and HE).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank J. Six and F. Sielaff from TU Berlin physics department's precision mechanical workshop for preparing the acrylic glass plates with micrometer-sized cavities that hold the micro-oscillators, U. Künkel for assistance in the laboratory.

References

1. Pikovsky A, Rosenblum M, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press (2001). doi: 10.1017/cbo9780511755743

CrossRef Full Text | Google Scholar

2. Cross MC, Hohenberg PC. Pattern formation outside of equilibrium. Rev Mod Phys. (1993) 65:851–1112. doi: 10.1103/RevModPhys.65.851

CrossRef Full Text | Google Scholar

3. Kuramoto Y. Reduction methods applied to non-locally coupled oscillator systems. In: Nonlinear Dynamics and Chaos: Where Do We Go from Here? CRC Press (2002). p. 209–27. Available online at: https://www.taylorfrancis.com/books/9781420033830/chapters/10.1201/9781420033830-11 (accessed January 20, 2019).

Google Scholar

4. Kuramoto Y, Shima S. Rotating spirals without phase singularity in reaction-diffusion systems. Prog Theor Phys Suppl. (2003) 150:115–25. doi: 10.1143/PTPS.150.115

CrossRef Full Text | Google Scholar

5. Panaggio MJ, Abrams DM. Chimera states: coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity. (2015) 28:R67. doi: 10.1088/0951-7715/28/3/R67

CrossRef Full Text | Google Scholar

6. Schöll E. Synchronization patterns and chimera states in complex networks: interplay of topology and dynamics. Eur Phys J Spec Top. (2016) 225:891–919. doi: 10.1140/epjst/e2016-02646-3

CrossRef Full Text | Google Scholar

7. Nkomo S, Tinsley MR, Showalter K. Chimera states in populations of nonlocally coupled chemical oscillators. Phys Rev Lett. (2013) 110:244102. doi: 10.1103/PhysRevLett.110.244102

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wickramasinghe M, Kiss IZ. Spatially organized partial synchronization through the chimera mechanism in a network of electrochemical reactions. Phys Chem Chem Phys. (2014) 16:18360–9. doi: 10.1039/C4CP02249A

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Rosin DP, Rontani D, Haynes ND, Schöll E, Gauthier DJ. Transient scaling and resurgence of chimera states in networks of boolean phase oscillators. Phys Rev E. (2014) 90:030902. doi: 10.1103/PhysRevE.90.030902

PubMed Abstract | CrossRef Full Text | Google Scholar

10. English LQ, Zampetaki A, Kevrekidis PG, Skowronski K, Fritz CB, Abdoulkary S. Analysis and observation of moving domain fronts in a ring of coupled electronic self-oscillators. Chaos. (2017) 27:103125. doi: 10.1063/1.5009088

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hagerstrom AM, Murphy TE, Roy R, Hövel P, Omelchenko I, Schöll E. Experimental observation of chimeras in coupled-map lattices. Nat Phys. (2012) 8:658–61. doi: 10.1038/nphys2372

CrossRef Full Text | Google Scholar

12. Larger L, Penkovsky B, Maistrenko Y. Laser chimeras as a paradigm for multistable patterns in complex systems. Nat Commun. (2015) 6:7752. doi: 10.1038/ncomms8752

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Brumley DR, Bruot N, Kotar J, Goldstein RE, Cicuta P, Polin M. Long-range interactions, wobbles, and phase defects in chains of model cilia. Phys Rev Fluids. (2016) 1:081201. doi: 10.1103/PhysRevFluids.1.081201

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Majhi S, Bera BK, Ghosh D, Perc M. Chimera states in neuronal networks: a review. Phys Life Rev. (2019) 28:100–21. doi: 10.1016/j.plrev.2018.09.003

CrossRef Full Text | Google Scholar

15. Lazarides N, Tsironis GP. Superconducting metamaterials. Phys Rep. (2018) 752:1–67. doi: 10.1016/j.physrep.2018.06.005

CrossRef Full Text | Google Scholar

16. Kuramoto Y. Chemical Oscillations, Waves, and Turbulence. Vol. 19. Springer (1984). Available online at: http://dx.doi.org/10.1007/978-3-642-69689-3.

Google Scholar

17. Acebrón JA, Bonilla LL, Pérez Vicente CJ, Ritort F, Spigler R. The kuramoto model: a simple paradigm for synchronization phenomena. Rev Mod Phys. (2005) 77:137–85. doi: 10.1103/RevModPhys.77.137

CrossRef Full Text | Google Scholar

18. Wilson D, Ermentrout B. Greater accuracy and broadened applicability of phase reduction using isostable coordinates. J Math Biol. (2018) 76:37–66. doi: 10.1007/s00285-017-1141-6

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Rosenblum M, Pikovsky A. Numerical phase reduction beyond the first order approximation. Chaos. (2019) 29:011105. doi: 10.1063/1.5079617

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Winfree AT. The Geometry of Biological Time. 2nd ed. Springer (2001). Available online at: http://dx.doi.org/10.1007/978-1-4757-3484-3.

Google Scholar

21. Kiss IZ. Synchronization engineering. Curr Opin Chem Eng. (2018) 21:1–9. doi: 10.1016/j.coche.2018.02.006

CrossRef Full Text | Google Scholar

22. Totz JF, Snari R, Yengi D, Tinsley MR, Engel H, Showalter K. Phase-lag synchronization in networks of coupled chemical oscillators. Phys Rev E. (2015) 92:022819. doi: 10.1103/PhysRevE.92.022819

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Totz JF, Rode J, Tinsley MR, Showalter K, Engel H. Spiral wave chimera states in large populations of coupled chemical oscillators. Nat Phys. (2018) 14:282–5. doi: 10.1038/s41567-017-0005-8

CrossRef Full Text | Google Scholar

24. Wilson D, Faramarzi S, Moehlis J, Tinsley MR, Showalter K. Synchronization of heterogeneous oscillator populations in response to weak and strong coupling. Chaos. (2018) 28:123114. doi: 10.1063/1.5049475

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Jalife J, Moe GK. Effect of electrotonic potentials on pacemaker activity of canine purkinje fibers in relation to parasystole. Circ Res. (1976) 39:801–8. doi: 10.1161/01.RES.39.6.801

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Johnson CH, Hastings JW. Circadian phototransduction: phase resetting and frequency of the circadian Clock of gonyaulax cells in red light. J Biol Rhythms. (1989) 4:417–37. doi: 10.1177/074873048900400403

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Prinz AA, Thirumalai V, Marder E. The functional consequences of changes in the strength and duration of synaptic inputs to oscillatory neurons. J Neurosci. (2003) 23:943–54. doi: 10.1523/JNEUROSCI.23-03-00943.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Russell DF. Respiratory pattern generation in adult lampreys (lampetra fluviatilis): interneurons and burst resetting. J Comp Physiol. (1986) 158:91–102. doi: 10.1007/BF00614523

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Anumonwo JM, Delmar M, Vinet A, Michaels DC, Jalife J. Phase resetting and entrainment of pacemaker activity in single sinus nodal cells. Circ Res. (1991) 68:1138–53. doi: 10.1161/01.RES.68.4.1138

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wessel R. In vitro study of phase resetting and phase locking in a time-comparison circuit in the electric fish, eigenmannia. Biophys J. (1995) 69:1880–90. doi: 10.1016/S0006-3495(95)80058-5

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Nabi A, Stigen T, Moehlis J, Netoff T. Minimum energy control for in vitro neurons. J Neural Eng. (2013) 10:036005. doi: 10.1088/1741-2560/10/3/036005

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhabotinsky AM, Buchholtz F, Kiyatkin AB, Epstein IR. Oscillations and waves in metal-ion-catalyzed bromate oscillating reactions in highly oxidized states. J Phys Chem. (1993) 97:7578–84. doi: 10.1021/j100131a030

CrossRef Full Text | Google Scholar

33. Totz JF. Synchronization and Waves in Active Media. Springer International Publishing (2019). doi: 10.1007/978-3-030-11057-4

CrossRef Full Text | Google Scholar

34. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes: The Art of Scientific Computing. 3rd ed. Cambridge University Press (2007). Available online at: http://www.cambridge.org/de/academic/subjects/mathematics/numerical-recipes/numerical-recipes-art-scientific-computing-3rd-edition?format=HB&utm_source=shortlink&utm_medium=shortlink&utm_campaign=numericalrecipes (accessed January 20, 2019).

Google Scholar

35. Bertram R, Rubin JE. Multi-timescale systems and fast-slow analysis. Math Biosci. (2017) 287:105–21. doi: 10.1016/j.mbs.2016.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Izhikevich EM. Dynamical Systems in Neuroscience. MIT Press (2007). doi: 10.7551/mitpress/2526.001.0001

CrossRef Full Text | Google Scholar

37. Franović I, Omel'chenko OE, Wolfrum M. Phase-sensitive excitability of a limit cycle. Chaos. (2018) 28:071105. doi: 10.1063/1.5045179

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Daido H. Order function and macroscopic mutual entrainment in uniformly coupled limit-cycle oscillators. Prog Theor Phys. (1992) 88:1213–18. doi: 10.1143/PTP.88.1213

CrossRef Full Text | Google Scholar

39. Rode J. Synchronization in heterogeneous networks-from phase to relaxation oscillators (M.Sc. Thesis). TU Berlin, Berlin, Germany (2016).

Google Scholar

40. Pazó D, Montbrió E, Gallego R. The winfree model with heterogeneous phase-response curves: analytical results. arXiv:arxiv.org/abs/1809.09456 (2018).

Google Scholar

41. Taylor AF, Kapetanopoulos P, Whitaker BJ, Toth R, Bull L, Tinsley MR. Clusters and switchers in globally coupled photochemical oscillators. Phys Rev Lett. (2008) 100:214101. doi: 10.1103/PhysRevLett.100.214101

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Abrams DM, Strogatz SH. Chimera states in a ring of nonlocally coupled oscillators. Int J Bifurcat Chaos. (2006) 16:21–37. doi: 10.1142/S0218127406014551

CrossRef Full Text | Google Scholar

43. Kemeth FP, Haugland SW, Schmidt L, Kevrekidis IG, Krischer K. A classification scheme for chimera states. Chaos. (2016) 26:094815. doi: 10.1063/1.4959804

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Gopal R, Chandrasekar VK, Venkatesan A, Lakshmanan M. Observation and characterization of chimera states in coupled dynamical systems with nonlocal coupling. Phys Rev E. (2014) 89:052914. doi: 10.1103/PhysRevE.89.052914

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Bick C, Martens EA. Controlling chimeras. New J Phys. (2015) 17:033030. doi: 10.1088/1367-2630/17/3/033030

CrossRef Full Text | Google Scholar

46. Omelchenko I, Omel'chenko OE, Zakharova A, Wolfrum M, Schöll E. Tweezers for chimeras in small networks. Phys Rev Lett. (2016) 116:114101. doi: 10.1103/PhysRevLett.116.114101

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Isele T, Hizanidis J, Provata A, Hövel P. Controlling chimera states: the influence of excitable units. Phys Rev E. (2016) 93:022217. doi: 10.1103/PhysRevE.93.022217

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Semenova N, Zakharova A, Anishchenko V, Schöll E. Coherence-resonance chimeras in a network of excitable elements. Phys Rev Lett. (2016) 117:014102. doi: 10.1103/PhysRevLett.117.014102

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Synchronization scenarios of chimeras in multiplex networks. Eur Phys J Spec Top. (2018) 227:1161–71. doi: 10.1140/epjst/e2018-800039-y

CrossRef Full Text | Google Scholar