Volatility Spillover Between Stock Prices and Trading Volume: Evidence From the Pre-, In-, and Post Global Financial Crisis Periods

Introduction

Before investors decide to invest in stocks, they try to obtain information about the factors that affect the value of the stock. As a member of this information body, trading volume plays an important role in forming market information. It also reflects information about changes in the expectations of investors in the market. The high trading volume is evaluated by investors as positive and contributing to the movement in the market. If the relationship between stock price and trading volume can be determined, investors will be able to make more effective decisions with these estimates.

There are many studies in the literature examining the relationship between stock prices and trading volume. Karpoff [1] summarizes the importance of the relationship between price and transaction volume under several headings. The first is that the theory of the relationship between transaction volume and stock returns gives an idea about the structure of financial markets. In other words, according to this theory, the flow of information to the market and the rate of dissemination of information predict the price-value relationship that depends on the size of the market and the existence of short selling restrictions. Second, the relationship between stock return volatility and trading volume has significant implications for event studies using a combination of price-volume data. Finally, this relationship is considered important for the empirical distribution of speculative assets.

There are various hypotheses that deal with the relationship between stock price and trading volume. Of these, the most emphasized ones in the literature are the sequential information hypothesis and the mixture distribution hypothesis. The sequential information hypothesis was developed by Copeland [2] and Jennings et al. [3]. This hypothesis is generally based on the assumption that new information coming to the market does not reach market users at the same time and that the information is disseminated in a sequential process. In other words, according to this hypothesis, the information coming to the market cannot be evaluated by all market participants at the same time and reflected the price and/or trading volume at once. Therefore, it takes some time for information to spread throughout the market and reach a stable final equilibrium point. During this period time, changes in trading volume may lead to changes in prices, and sometimes changes in prices may lead to changes in trading volume. Therefore, according to this hypothesis, there is a two-way and positive causal relationship between trading volume and stock prices. Briefly, according to the sequential information hypothesis, lagged prices have the power to estimate the current trading volume or conversely. Indeed, this approach contradicts the efficient market hypothesis developed by Fama [4]. According to Fama's [4] hypotheses of active markets, the information coming to the market is evaluated by all market participants at the same time, and this information has reflected the prices quickly. Therefore, it is not possible to predict in advance how the price movements in stock markets will develop by looking at past price movements.

The mixed distributions hypothesis was developed by Clark [5] and Epps and Epps [6]. The basic assumption of this hypothesis is that information coming to the market reaches all market participants simultaneously and quickly. Therefore, it is understood that the basic assumptions of this approach are more consistent with the assumptions of Fama's [4] hypotheses of efficient markets as opposed to the sequential information hypothesis. According to the mixed distributions hypothesis, there is a simultaneous positive relationship between stock prices and trading volume. In this case, price and volume change at the same time when new information enters the market. However, according to Clark's [5] models, there is no causality from trading volume to stock price. In contrast, in the Epps and Epps [6] model, trading volume is an indicator of the discrepancy among investors. Revision by investors of their expectations when new information arrives in the market indirectly causes changes in trading volume. Thus, Epps and Epps [6] state that there is a one-way and positive causality relationship from trading volume to prices.

Rather than examining only the factors that determine the stock prices or transaction volume individually, it would be more accurate to examine the relations between the stock price and the trading volume together [7]. Studies testing causality between trading volume and stock prices often use the traditional Granger causality test, which focuses on mean changes based on the assumption of constant variance [8–11]. As a result of the fluctuations caused by the economic crises in the markets, it is seen that the variance does not remain constant in financial market data over time. Therefore, it would be more appropriate to use models that allow change in variance instead of standard time series models based on constant variance acceptance in the analyzes. In the literature, it is seen that there are no studies considering the variances of stock price and trading volume. In this study, it is aimed to contribute to the literature by examining the relationship between the variance of stock price and trading volume with causality test in variance developed by Hafner and Herwartz [12]. The causality test in variance is conducted to investigate the conditional volatility spillover between the stock price and the trading volume.

The aim of this study, considering the variances of stock price and trading volume is to determine whether the mixed distributions hypothesis is valid in the Turkish markets. The causality test in variance is applied to the data covering 02 January 1997–29 December 2017 period. To investigate the impact of the 2008 crisis on the mechanism of volatility spillover between stock price and trading volume, empirical analysis is conducted for three sub-periods (pre-crisis period; 02 January 1997–29 September 2008, crisis period; 3 October 2008–30 September 2009 and post-crisis period; 1 October 2009–29 December 2017).

The rest of the paper is organized as follows: In the second part, studies examining the relationship between variables are given. In the third section, the econometric methodology is explained. In the fourth chapter, data and empirical results are presented. In the last section, the empirical findings are summarized and evaluated.

Literature Review

There are many studies examining the relationship between stock prices and trading volume using different methods. Some studies in the literature have examined the relationship between stock price and trading volume with traditional causality tests [9–11, 13, 14]. In addition to these studies, there are studies examining the relationship between stock prices and trading volume handling different causality tests [8, 11, 15–17].

Chen et al. [9] investigated the relationship between stock returns and trading volume in different markets by the Granger causality test. Analysis findings show that there is a bidirectional causality relationship. Ong [11] found out a bidirectional causality relationship between S&P500 index stock returns and trading volume during the period 1980–2012. Darrat et al. [10] determined a bidirectional causality relationship between stock return volatility and trading volume in the Dow Jones Industrial Average (DJIA) index. These studies support the Sequential Information Hypothesis explaining the relationship between price and volume. Mahajan and Singh [13] investigated the causality relationship between return volatility and trading volume of the Sensitive Index (SENSEX). Granger causality test results show causality relationship from return volatility to trading volume supporting the sequential information arrival hypothesis.

Gunduz and Hatemi [14], in their study, examined the Czech Republic, Hungary, Poland, Russia, and Turkey market. In the analysis, while determining bidirectional causality between stock returns and the trading volume for Poland and Hungary, a unidirectional causal relationship from stock returns to the trading volume has been found for Russia and Turkey. They also stated that there was no causal relationship between the variables in the Czech Republic.

Hiemstra and Jones [8] used the non-linear Granger causality test to investigate the relationship between Dow Jones stock returns and trading volume. A significant bidirectional non-linear causality relationship was found between volume and return. Ong [11] supports the findings of Hiemstra and Jones [8] with its analysis in the S&P500 index. Rashid [15] has concluded that there is a non-linear causality relationship from the trading volume to the index return and a linear causality relationship from the index return to the trading volume in the Pakistan stock market.

In the literature, studies examining the causality relationship between stock prices and trading volume in Turkish markets are available [18–24]. Umutlu [18] has tested whether there is a causal relationship using the ISE National All Index daily closing prices and trading volume data for the period of 2002–2007. In the study, it is concluded that there is a unidirectional causality relationship from stock returns to trading volume. Besides, it is stated that the past 4-day values of price changes may affect future changes in the trading volume and the mixed distributions hypothesis is not valid. Cukur et al. [19], Zor et al. [20], Kayalidere [21], and Nalin [22] determined unidirectional causality relationship from stock prices to trading volume by examining the data in different periods in the Turkey capital markets. These results support the findings of Umutlu [18], Gunduz and Hatemi [14].

A. Boyacioglu et al. [24] found out that there is a bidirectional Granger causality relationship between the ISE 100 index return volatility and trading volume and a negative relationship from the trading volume to return volatility. And they determined that sequential information and mixed distribution hypotheses do not valid in the ISE. Tas [23] investigated whether there is a causality relationship between daily trading volumes and closing prices of the BIST-100 indexes in the period of January 2000–June 2014. According to the Granger causality test, a causality relationship from the stock return to trading volume was determined. However, they found a bidirectional causality relationship between return volatility and volume.

Yilanci and Bozoklu [16] have used asymmetric causality test to see whether the stock prices and trading volume react differently to positive and negative shocks in Turkey's capital markets. As a result of the analysis, it is seen that the relationship between trading volume and stock prices is clearly bidirectional for positive shocks. Buberkoku [17] investigated the relationship between trading volume and stock returns by asymmetric causality tests. Analysis findings, it was determined that there was a unidirectional and positive causality relationship from stock prices to trading volume in eight of the banks examined, and a bidirectional causality relationship was found between the variables of the two banks.

There are studies examining the effect of trading volume on the volatility of stock returns by GARCH models in the literature [9, 25–32]. Ahmed et al. [25] found out that trading volume had a significant effect on return volatility in the Malaysian stock market and mixed distributions hypothesis was not valid. At the same time, it is revealed that the trading volume has no effect on reducing the return volatility. These results support Huang and Yang's [32] studies in the Taiwan stock market. Wang et al. [33] examined the relationship between stock return volatility and the trading volume in the Chinese stock market. According to the GARCH model results, the effect of trading volume on return volatility is positive and statistically significant.

Naka and Oral [30] examined the effect of trading volume on the volatility of stock returns in the Dow Jones Industrial Average index using GARCH and Threshold GARCH (TGARCH) models. In the analysis, it was determined that the trading volume affected the volatility of stock returns. In addition, negative shocks have a greater impact on volatility than positive shocks. Kalu and Chinwe [31] investigated the relationship between the volatility of stock returns and trading volume in Nigeria. Daily data of the All-Share Index were analyzed by GARCH (1,1) and GARCH-X (1,1) models for the period from 3 January 2000 to 21 June 2011. The findings of analyses reveal that the relationship between trading volume and stock returns volatility is positive and statistically significant. But, the findings do not support the mixture distribution hypothesis. Baklaci and Kasman [34] and Çukur [19] tested the mixture distribution hypothesis by employing the GARCH model and they put forward this hypothesis is not valid for Turkey.

Gazel [28] investigated the relationship between trading volume and stock market volatility for countries called Fragile Five Economies (BIITS, Brazil, India, Indonesia, Turkey, and South Africa) for the 2006–2016 period with the EGARCH(1,1) model. In contrast to other studies, Gazel [28] asserts the mixture distribution hypothesis is valid in all BIITS countries under constraints of weekly data.

In the literature review, there is no study examining the causality relationship between the volatility of stock prices and the volatility of trading volume. Analyzing the volatility spillover between the stock prices and trading volume constitutes the originality of this study.

Methodology

In order to evaluate volatility spillover between stock prices and trading volume, in this study, unlike the traditional Granger causality test which focuses on mean changes, the causality test in variance is used, there are two test methods that examine the causality relationship in the variance. The first is the causality test in the variance developed by Cheung and Ng [35] and Hong [36], which is related to the cross-correlation functions (CCF) of the residues obtained from the univariate general autoregressive conditional variable variance (GARCH) estimate. The Portmanteau test, related to the CCF function, faces an important problem of sample size in small and medium-sized samples when the volatility processes are flattened from the sides (leptokurtic). In addition, the causality test in variance based on CCF results take different values according to the degree of lags and leads in the VAR model [12]. The second method, the volatility spillover test of Hafner and Herwartz [12], which is based on the Lagrange multiplier (LM), eliminates the shortcomings of Cheung and Ng's method. In addition, the Monte Carlo experiment, which is in Hafner and Herwartz's [12] test, showed that LM (Lagrange Multiplier) approach is more strong against leptokurtic status in small samples and gives healthier results as the sample grows. Next, we briefly explain the details of the causality test in variance by Hafner and Herwartz [12].

Hafner and Herwartz's [12] causality test in variance is based on GARCH models. The null hypothesis formed to evaluate the dynamic volatility spillover and direction between stock price and trading volume is that there is no causality in the variance between the two variables. The null hypothesis is tested with the following model;

$\begin{array}{l}{\epsilon }_{\text{it}}={\xi }_{\text{it}}\sqrt{{\sigma }_{\text{it}}^{\text{2}}({1+\text{N}\prime }_{\text{j}}\pi )},{\text{N}}_{\text{jt}}=({\epsilon }_{\text{jt}-1}^2,{\sigma }_{\text{jt}-1}^2{)}^{\prime }\end{array}$

Where ξit and ${\sigma }_{it}^2$ are standardized residuals and conditional variance for the series i, respectively. ${\epsilon }_{jt-1}^2$ and ${\sigma }_{jt-1}^2$, j are the square of the error term and the conditional variance for the series j, respectively. H₀: π = 0 means that there is no causality in the variance and H₁: π ≠ 0 indicates that there is causality in the variance. The value of the Gaussian log-likelihood function of ε_it is x_it (${\xi }_{it}^2$-1)/2. x_it is the derivative of the likelihood function in terms of GARCH parameters. Hafner and Herwartz [12] suggested the LM test as follows;

$\begin{array}{l}{\lambda }_{LM}=\frac{1}{4\text{t}}({\displaystyle \sum _{\text{t}=1}^{\text{T}}({\xi }_{\text{it}}^2}-1){\text{N}\prime }_{\text{jt}})\text{V}{({\theta }_{\text{i}})}^{-1}({\displaystyle \sum _{\text{t}=1}^{\text{T}}({\xi }_{\text{it}}^2}-1){\text{N}}_{\text{jt}}\end{array}$

Where,

$\begin{array}{l}V({\theta }_{\text{i}})=\frac{\text{S}}{4T}({\displaystyle \sum _{\text{t}=1}^{\text{T}}{\text{N}}_{\text{jt}}}{\text{N}\prime }_{\text{jt}}-{\displaystyle \sum _{\text{t}=1}^{\text{T}}{\text{N}}_{\text{jt}}}{\text{X}\prime }_{\text{it}}{({\displaystyle \sum _{\text{t}=1}^{\text{T}}{\text{X}}_{\text{jt}}}{\text{X}\prime }_{\text{it}})}^{-1}{\displaystyle \sum _{\text{t}=1}^{\text{T}}{\text{X}}_{\text{jt}}}{\text{N}\prime }_{\text{jt}}),\end{array}$

$\begin{array}{l}\text{S}=\frac{1}{\text{T}}{\displaystyle \sum _{t=1}^T}{({\xi }_{it}^2-1)}^2\end{array}$

In Equation (2), the asymptotic distribution of the test statistic is dependent on misspecification indicators in N_jt. When there are two such indicators in λ_LM equation, the model has an asymptotic chi-square distribution with two degrees of freedom. Rejecting the null hypothesis indicates that there is volatility spillover from series j to series i.

Data and Empirical Results

Data

In this study, the volatility spillover between closing prices of the BIST100 index and trading volume was investigated. The data set covers daily observations from 02 January 1997 to 29 December 2017. To identify the impact of the 2008 global financial crisis, the data are divided into three sub-periods: the pre-crisis period (02 January 1997–29 September 2008), in-crisis period (3 October 2008–30 September 2009) and the post-crisis period (1 October 2009–29 December 2017). The process that emerged in the second half of 2007 in the USA and became a global financial crisis since 2008 has had negative effects on the world economy. Therefore, the period of October 3, 2008 and September 30, 2009 were taken as the crisis period. Data set is procured from the Central Bank Electronic Data Distribution System (EDDS). The percentage change of both series was calculated using the formula Pn/Pn-1. Then, the natural logarithm of the series was taken and analyzed.

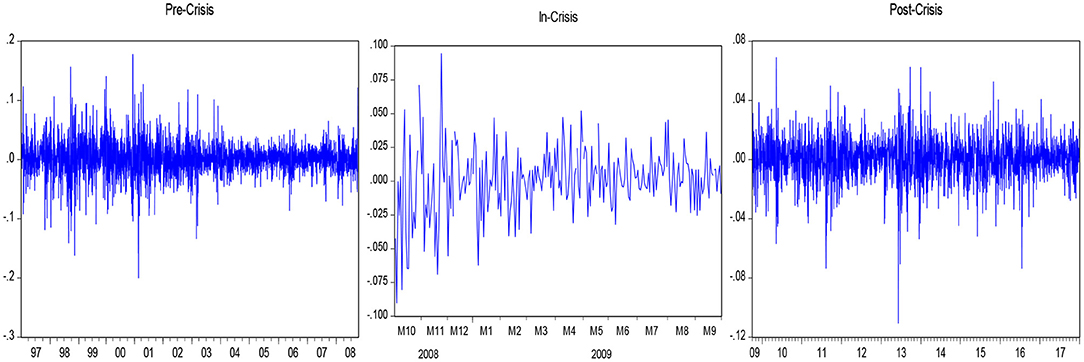
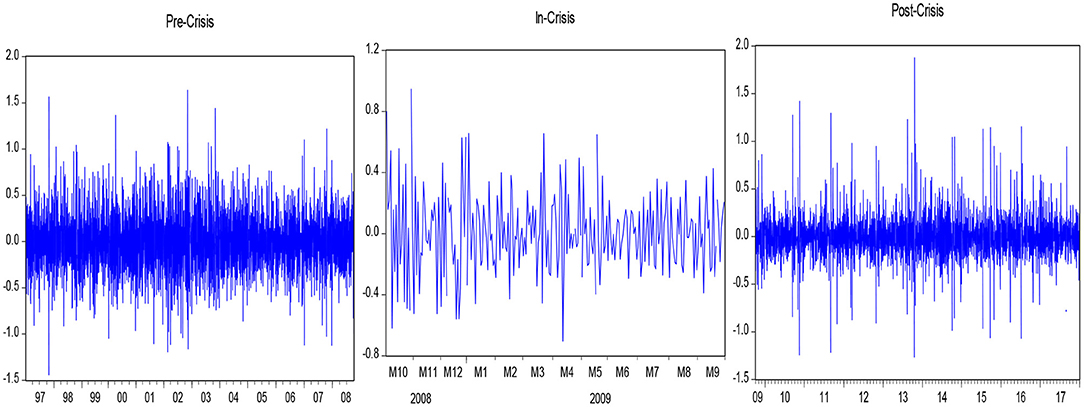
First of all, the movements of stock prices and trading volume are examined in pre-crisis, crisis, and post-crisis periods. When Graphs 1, 2 are examined, it is seen that the series of stock prices and trading volume are extremely volatile in three sub-periods.

GRAPH 1

GRAPH 1. Series of stock prices.

GRAPH 2

GRAPH 2. Series of trading volume.

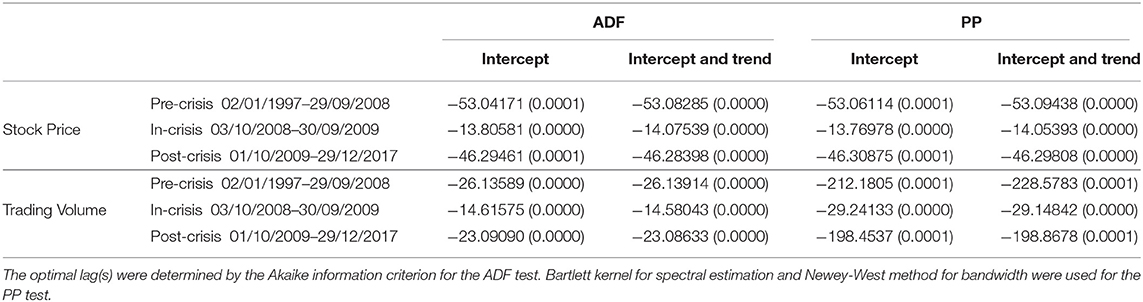
In the next stage of the analysis, the Augmented Dickey-Fuller (ADF) unit root test developed by Dickey and Fuller [37] and Phillips and Perron (PP) unit root test developed by Phillips and Perron [38] were used for stationary analysis. Unit root test results reported in Table 1.

TABLE 1

Table 1. Result for Unit root tests.

According to the results of the unit root test, both ADF and PP tests showed that a series of stock price and trading volume do not have unit root in all sub-periods. The null hypothesis that the unit root exists in the series is rejected. Thus, it is concluded that the level values of the series are stationary I (0).

Empirical Results

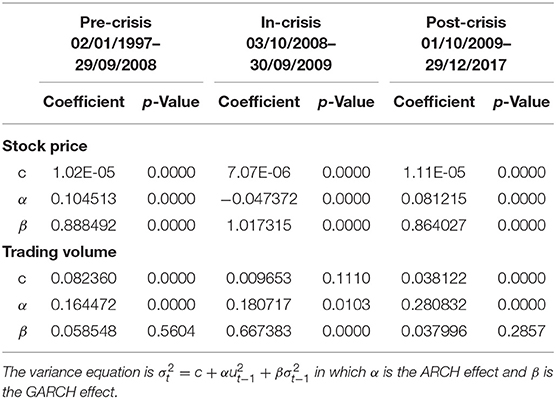
To examine the volatility spillover between stock prices and trading volume, firstly the univariate GARCH (1,1) model was estimated. Table 2 shows the findings for variance equations for the pre-crisis, in-crisis and post-crisis periods. Initially, it should be checked whether the stability conditions of the GARCH model hold which impose the constraints c > 0, 0 ≤ α, 0 ≤ β, α + β <1. α, and β are the ARCH and GARCH parameters, respectively.

TABLE 2

Table 2. Results for variance equations.

The values of the ARCH and GARCH coefficients are interpreted in different ways for conditional volatility. The values of the ARCH and GARCH coefficients are interpreted in different ways for conditional volatility. A higher ARCH coefficient indicates that the effects of a shock are more pronounced in the next period, while a high GARCH coefficient indicates that the effects of a shock are more persistent [39].

GARCH model coefficients of stock price are statistically significant at 1% significance level. GARCH model coefficients of trading volume are statistically significant at 1% significance level, except for the constant term in the pre-crisis and post-crisis period and the GARCH coefficient in the crisis period. The coefficients in the variance equations are positive.

In the GARCH model, the volatility processes of stock prices and trading volume are different between periods. During the crisis, the impact of the ARCH on the stock price is smaller than before and after the crisis. Additionally, the GARCH coefficient is slightly higher in the crisis period than in other periods. The results obtained from the GARCH model show that the effects of the shocks experienced during the crisis period on stock prices are not pronounced but are permanent for a long time. In the pre-crisis and post-crisis periods, price volatility is more pronounced than the crisis period, but the effect remains shorter.

The impact of ARCH on trading volume is lower in the pre- and post-crisis period, but increases in the post-crisis period. Also, while GARCH coefficient is quite high in the crisis period, it is quite low in pre- and post-crisis periods. The effect of the shocks experienced during the crisis period on the trading volume is more pronounced and lasting longer than the pre-crisis period. Moreover, volatility in trading volume after the crisis is higher but short-term.

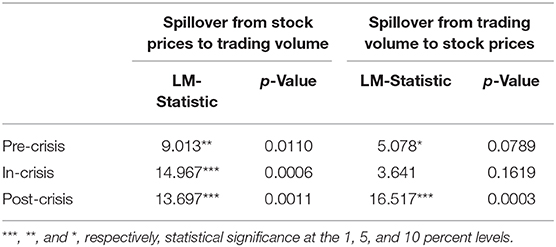
After determining the volatility processes in stock price and trading volume, Hafner and Herwartz's [12] causality test in variance was performed to determine whether there is volatility spillover between stock price and trading volume. The results of the causality test in variance are reported in Table 3.

TABLE 3

Table 3. Result for causality in variance test.

According to the results of the causality test in variance, the null hypothesis is rejected before and after the crisis. The results for the pre-crisis and post-crisis periods show that there is a bidirectional volatility spillover between stock price and trading volume. Additionally, during the crisis, unidirectional volatility spillover from stock price to trading volume is determined.

Conclusion

Stock prices and trading volumes are two important indicators for capital markets. Since these indicators have a volatile structure, it is thought that revealing the relationship between the variances will provide investors with more accurate information. Therefore, the study aims to investigate the volatility spillover between the BIST100 index closing prices and trading volume in the framework of the Mixed Distributions Hypothesis. The data spanning from January 02, 1997 to December 29, 2017are divided into three sub-periods as January 02, 1997–September 29, 2008 (the pre-crisis period), October 03, 2008–September 30, 2009 (the in-crisis period) and October 01, 2009–December 29, 2017 (the post-crisis period) to account for the 2008 global financial crisis.

The results of the analyses show that the stock prices and trading volume series exhibit a volatile structure. Also, the findings from the GARCH model reveal that the stock prices and the trading volume exhibit strong volatility persistence. Using the causality in variance test by Hafner and Herwartz [12], this study examines volatility spillover between stock prices and the trading volume for the pre-crisis, the in-crisis and the post-crisis periods. According to the causality in variance test results, there is a bidirectional volatility spillover between stock prices and trading volume in the pre-crisis and post-crisis periods.

These findings show that the volatility in stock prices and trading volume during the pre-crisis and post-crisis periods affects each other. The study findings, the study of Turkish market data Yilanci and Bozoklu [16], Tas [23] and Boyacioglu et al. [24] coincides with the findings of the studies, while Umutlu [18], Cukur et al. [19], Zor et al. [20], Kayalidere [21], and Nalin [22] do not match the findings of the studies. In this study, while the bidirectional causality relationship is determined between stock price and trading volume, most of the studies in the literature have determined a unidirectional causality relationship from stock prices to trading volume. The reason for this is that other studies examine the causality relationship with the assumption that the variance of the variables included in the analysis is constant. However, it is seen that the financial market data has variance that varies over time. Therefore, it is considered that using the methods that take into account the changing variance in the analysis of financial market data may provide more accurate results. All of these studies have a common finding that there is a relationship between the stock price and transaction volume with lags. So, the mixed distribution hypothesis argues that there is a simultaneous relationship between stock prices and trading volume is not valid in Turkish capital markets. In other words, it appears that the Turkish capital market is not an effective market and the information coming to the market is reflected in market indicators with lags.

During the crisis, unidirectional volatility spillover from stock price to trading volume was determined. In this case, we can say that investors take into account the volatility of stock price when making investment decisions during the crisis. Additionally, it can be stated that investors are insensitive to the volatility of the trading volume and that the volatility of the trading volume does not affect the decisions of the investor.

The volatility spillover between stock prices and trading volume is an important subject for investors. When investors investigate the relationship between stock prices and trading volume, if they look at the relationship between their variances rather than the relationship between their mean changes values, they make more accurate decisions.

The results of this study might contribute to a better understanding of the relationship between stock prices and trading volume. Also, these results can benefit investors who form a portfolio, policymakers and futures work. One of the limitations of this study is the use of single market data in the analysis. For this reason, future studies can be included in different markets and comparative analyzes can be made between markets. Furthermore, once it is determined the volatility spillover, it can be applied in other methods to determine the effect level of the volatility.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Karpoff JM. The relation between price changes and trading volume: a survey. J Financial Quant Anal. (1987) 22:109–25. doi: 10.2307/2330874

CrossRef Full Text | Google Scholar

2. Copeland TE. A model for asset trading under the assumption of sequential information arrival. J Finance. (1976) 31:1149–68. doi: 10.1111/j.1540-6261.1976.tb01966.x

CrossRef Full Text | Google Scholar

3. Jennings RH, Starks LT, Fellingham JC. An equilibrium model of asset trading with sequential information arrival. J Finance. (1981) 36:143–61. doi: 10.1111/j.1540-6261.1981.tb03540.x

CrossRef Full Text | Google Scholar

4. Fama EF. Efficient Capital markets: a review of theory and empirical work. J Finance. (1970) 25:383–417. doi: 10.1111/j.1540-6261.1970.tb00518.x

CrossRef Full Text | Google Scholar

5. Clark P. A subordinated stochastic process model with finite variance for speculative prices. Econometrica. (1973) 31:135–56. doi: 10.2307/1913889

CrossRef Full Text | Google Scholar

6. Epps TW, Epps ML. The stochastic dependence of security price changes and transaction volumes: implication for the mixture of distributions hypothesis. Econometrica. (1976) 44:305–21. doi: 10.2307/1912726

CrossRef Full Text | Google Scholar

7. Gallant AR, Rossi PE, Tauchen G. Stock prices and volume. Rev Financial Stud. (1992) 5:199–242. doi: 10.1093/rfs/5.2.199

CrossRef Full Text | Google Scholar

8. Hiemstra C, Jones DJ. Testing for linear and nonlinear granger causality in the stock price-volume relation. J Finance. (1994) 5:1639–64. doi: 10.1111/j.1540-6261.1994.tb04776.x

CrossRef Full Text | Google Scholar

9. Chen G, Firth M, Rui MO. The dynamic relation between stock returns, trading volume, and volatility. Financial Rev. (2001) 38:153–74. doi: 10.1111/j.1540-6288.2001.tb00024.x

CrossRef Full Text | Google Scholar

10. Darrat AF, Rahman S, Zhong M. Intraday trading volume and return volatility of the DJIA stocks: a note. J Banking Finance. (2003) 27:2035–43. doi: 10.1016/S0378-4266(02)00321-7

CrossRef Full Text | Google Scholar

11. Ong MA. An information theoretic analysis of stock returns, volatility and trading volumes. Appl Econ. (2015) 47:3891–906. doi: 10.1080/00036846.2015.1019040

CrossRef Full Text | Google Scholar

12. Hafner CM, Herwartz H. A Lagrange multiplier test for causality in variance. Econ Lett. (2006) 93:137–41. doi: 10.1016/j.econlet.2006.04.008

CrossRef Full Text | Google Scholar

13. Mahajan S, Singh B. The empirical investigation of relationship between return, volume and volatility dynamics in Indian Stock Market. Eurasian J Bus Econ. (2009) 2:113–37. Available online at: https://www.ejbe.org/EJBE2009Vol02No04p113MAHAJAN-SINGH.pdf

Google Scholar

14. Gunduz L, Hatemi JA. Stock price and volume relation in emerging markets. Emerg Mark Finance Trade. (2005) 41:29–44. doi: 10.1080/1540496X.2005.11052599

CrossRef Full Text | Google Scholar

15. Rashid A. Stock prices and trading volume: an assessment for linear and nonlinear Granger causality. J Asian Econ. (2007) 18:595–612. doi: 10.1016/j.asieco.2007.03.003

CrossRef Full Text | Google Scholar

16. Yilanci V, Bozoklu S. Price and trade volume relationship in Turkish Stock Market: a time-varying asymmetric causality analysis. Ege Acad Rev. (2014) 14:211–20. doi: 10.21121/eab.2014218052

CrossRef Full Text | Google Scholar

17. Buberkoku O. Examining stock returns-trading volume relationship: evidence from Turkish Banks. Mehmet Akif Ersoy Univ J Inst Soc Sci. (2017) 9:457–48. doi: 10.20875/makusobed.324146

CrossRef Full Text | Google Scholar

18. Umutlu G. The causal and dynamic relationship between stock price and trading volume changes: an empirical study in ISE. Gazi Univ J Faculty Econ Admin Sci. (2008) 10:231–46. Available online at: https://dergipark.org.tr/tr/download/article-file/287476

Google Scholar

19. Cukur S, Gumrah U, Ustun Gumrah M. The relationship between stock returns and trading volume in Istanbul Stock Exchange. Nigde Univ J Faculty Econ Admin Sci. (2012) 5:20–35.

Google Scholar

20. Zor I, Bozkurt I, OksUz S. The impact of asymmetric information level on the relationship between price and trading volume: evidence from BIST. Anadolu Univ J Soc Sci. (2016) 16:119–36.

Google Scholar

21. Kayalıdere K, Aktaş H. Causality relationship between price and volume in ISE. Celal Bayar Univ J Inst Soc Sci. (2009) 7:115–24. Available online at: https://dergipark.org.tr/tr/pub/cbayarsos/issue/4072/53791

Google Scholar

22. Nalın TH, Guler S. The relationship between trading volume and stock return in Istanbul Stock Exchange. J Account Finance. (2013) 59:135–47. Available online at: https://dergipark.org.tr/tr/pub/mufad/issue/35644/396430

Google Scholar

23. Tas O, Tokmakcioglu K, Cevikcan G. The relationship between trading volume and returns in Borsa Istanbul. DEU J GSSS. (2016) 18:11–30. doi: 10.16953/deusbed.89624

CrossRef Full Text | Google Scholar

24. Boyacioglu AM, Guvenek B, Alptekin V. The relationship between return volatility and trading volume: an empirical study in the ISE. Mufad J. (2009) 48:200–15. Available online at: https://journal.mufad.org.tr/index.php?option=com_content&view=category&id=904%3Asayi-48-ekim-2010&Itemid=55&layout=default&lang=tr

Google Scholar

25. Ahmed HJA, Hassan A, Nasir AMD. The relationship between trading volume, volatility and stock market returns: a test of Mixed Distribution Hypothesis for a pre- and post crisis on Kuala Lumpur Stock Exchange. Invest Manage Financial Innov. (2005) 3:146–58. Available online at: https://businessperspectives.org/images/pdf/applications/publishing/templates/article/assets/1266/imfi_en_2005_03_Ahmed.pdf

Google Scholar

26. Bose S, Rahman H. Examining the relationship between stock return volatility and trading volume: new evidence from an emerging economy. Appl Econ. (2015) 47:1899–908. doi: 10.1080/00036846.2014.1002885

CrossRef Full Text | Google Scholar

27. Chen CWS, So MKP, Chiang TC. Evidence of stock returns and abnormal trading volume: a threshold quantile regression approach. Jap Econ Rev. (2016) 67:96–124. doi: 10.1111/jere.12074

CrossRef Full Text | Google Scholar

28. Gazel S. The relationship between trading volume and volatility in stock markets: an emprical study in the Fragile Five Economies. Int J Manage Econ Bus. (2017) 13:347–63. doi: 10.17130/ijmeb.2017228688

CrossRef Full Text | Google Scholar

29. Girard E, Biswas R. Trading volume and market volatility: developed versus emerging stock markets. Financial Rev. (2007) 42:429–59. doi: 10.1111/j.1540-6288.2007.00178.x

CrossRef Full Text | Google Scholar

30. Naka A, Oral E. Stock return volatility and trading volume relationships captured with stable paretian GARCH and Threshold GARCH Models. J Bus Econ Res. (2013) 11:47–52. doi: 10.19030/jber.v11i1.7522

CrossRef Full Text | Google Scholar

31. Kalu OE, Chinwe OC. The relationship between stock returns volatility and trading volume in Nigeria. Bus Syst Econ. (2014) 4:115–24. doi: 10.13165/VSE-14-4-2-01

CrossRef Full Text | Google Scholar

32. Huang BN, Yang CW. An empirical investigation of trading volume and return volatility of the Taiwan stock market. Glob Finance J. (2001) 12:55–77. doi: 10.1016/S1044-0283(01)00023-0

CrossRef Full Text | Google Scholar

33. Wang P, Wang P, Liu A. Stock return volatility and trading volume: evidence from the Chinese stock market. J Chin Econ Bus Stud. (2005) 3:39–54. doi: 10.1080/14765280500040518

CrossRef Full Text | Google Scholar

34. Baklaci H, Kasman A. An empirical analysis of trading volume and return volatility relationship in the Turkish Stock Market. Ege Acad Rev. (2006) 6:115–25. Available online at: https://dergipark.org.tr/tr/pub/eab/issue/39839/472388

Google Scholar

35. Cheung YW, Ng LK. A causality in variance test and its application to financial market prices. J Econ. (1996) 72:33–48. doi: 10.1016/0304-4076(94)01714-X

CrossRef Full Text | Google Scholar

36. Hong Y. A test for volatility spillover with application to Exchange rates. J Econ. (2001) 103:183–224. doi: 10.1016/S0304-4076(01)00043-4

CrossRef Full Text | Google Scholar

37. Dickey DA, Fuller WA. Distribution of the estimator for autoregressive time series with a unit root. J Am Stat Assoc. (1979) 74:427–31. doi: 10.1080/01621459.1979.10482531

CrossRef Full Text | Google Scholar

38. Phillips PCB, Perron P. Testing for a unit root in time series regression. Biometrica. (1988) 2:335–46. doi: 10.1093/biomet/75.2.335

CrossRef Full Text | Google Scholar

39. Enders W. Applied Econometric Time Series, 2nd ed. Hoboken, NJ: John Wiley & Sons Inc. (2004).

Google Scholar