- 1Department of Computer Science, Chiba Institute of Technology, Narashino, Japan
- 2Graduate School of Applied Informatics, University of Hyogo, Kobe, Japan
- 3Faculty of Education, Teacher Training Division, Kochi University, Kochi, Japan
- 4Research Center for Child Mental Development, Kanazawa University, Kanazawa, Japan
- 5Department of Neuropsychiatry, University of Fukui, Eiheiji, Japan
- 6Uozu Shinkei Sanatorium, Uozu, Japan
Bipolar disorder (BD), which involves mood swings between mania and depression, is associated with multiple relapses during long-term treatment and high suicide and morbidity rates. In BD, the circadian rhythms, which are measured by daily mood scores and actigraphic records, are disturbed. Chronotherapy has emerged as a potential treatment for BD because it stabilizes the disturbed circadian rhythms and improves BD symptoms. Concrete treatments include light therapy and combination therapy (light therapy and drugs). However, some patients have difficulty adjusting to light therapy; inappropriate light and duration of treatment increase risks for inducing mixed states and the emergence of conditions, such as hypomania and autonomic hyperactivation. Therefore, it is important to devise methods for optimizing chronotherapy for BD. We aimed to develop feedback signals for the frontal cortex, which were based on the delayed feedback method as one of the chaos control methods, to stabilize the disturbed circadian rhythms of BD. Concrete procedures of this study are indicated as follows: first, circadian rhythms of BD are reproduced using the frontal cortex and hypothalamus neural system, which has been previously proposed. Second, the delayed feedback signal is developed by using bifurcation analysis. Third, the effect of delayed feedback signal is evaluated by index for complexity, and power spectrum under the condition with/without stochastic noise in feedback term. We found that application of the delayed feedback signal to the frontal cortical neural activity induces the periodic state of circadian rhythms from the disturbed complex and is feasible for treating BD. However, when increasing the influence of noise in feedback term, the stabilizing effect is diminished. In conclusion, we developed a stabilizing method for disturbed circadian rhythms of BD using the circadian neural systems. The present study highlights the potential usefulness of the chaos control method for treating BD.
1. Introduction
Bipolar disorder (BD), which involves mood swings between mania and depression, is associated with multiple relapses during long-term treatment and high suicide and morbidity rates (Belmaker, 2004). Changes in the glutamatic acid and gamma-aminobutyric acid (GABA) neural pathways and abnormal cortical neural networks have been reported as the neural bases for BD (Sanacora et al., 2012; Schloesser et al., 2012). Moreover, Tobe et al. (2017) showed that abnormal phosphorylation of synaptic connections causes BD. Drugs, such as mood stabilizers (i.e., lithium carbonate and clozapine) and intramuscular neuroleptics are widely utilized for BD. Pharmacological mechanisms of these treatments have been elucidated in previous studies (Hirschfeld et al., 2003; López-Muñoz et al., 2006; Tobe et al., 2017). However, these treatments are also associated with several side effects, such as progressive renal failure and a narrow therapeutic index (Hirschfeld et al., 2003; López-Muñoz et al., 2006). Therefore, previous studies have focused on developing alternative and effective treatment methods for BD (Abreu and Bragança, 2015).
Recently, the clinical efficiency and feasibility of chronotherapy has been studied (Abreu and Bragança, 2015). In mood disorders, including BD, the circadian rhythms, which are measured by daily mood scores and actigraphic records, are disturbed (Yeragani et al., 2003; Glenn et al., 2006; Bonsall et al., 2011; Moore et al., 2014). Chronotherapy stabilizes the disturbed circadian rhythms and improves BD symptoms (Abreu and Bragança, 2015). Concrete treatments include light therapy and combination therapy (light therapy with drugs) (Leibenluft et al., 1995; Terman and Terman, 2005). However, it is difficult for some BD patients to adjust to light therapy; furthermore, inappropriate light and duration of treatment increase the risks of mixed states, hypomania, and autonomic hyperactivation (Terman and Terman, 2005; Sit et al., 2007; Abreu and Bragança, 2015).
The application of nonlinear modeling for drug treatments has also emerged as a potential therapy (Itik et al., 2009; Aihara and Suzuki, 2010; Mhawej et al., 2010; Babaei and Salamci, 2015; Hamdache et al., 2016). Particularly, Tanaka et al. (2010) and Suzuki et al. (2010) proposed the concept of intermittent hormone therapy for preventing the growth of prostate cancer and its divergences; the model was based on the nonlinear control theory and utilized a prostate cancer model. Other control methods, such as optimized cancer immunotherapy and drug treatments involving human immunodeficiency virus have also been developed (Mhawej et al., 2010; Babaei and Salamci, 2015; Hamdache et al., 2016). That is, applying nonlinear control methods has opened a new avenue of medical treatments. Therefore, applying nonlinear control methods to chronotherapy for stabilizing the circadian rhythms of BD is promising for avoiding risks associated with chronotherapy.
Hadaeghi et al. (2016) and Bayani et al. (2017) demonstrated that a mechanism of disturbed circadian rhythms in BD involves aperiodic daily neural activities, which is referred to as chaos-chaos intermittency. In the frontal cortex, chaos-chaos intermittency perturbs the circadian pacemaker of the hypothalamus through model simulation of the neural system (which is comprised of the frontal cortex and hypothalamus). The accuracy of this model is high in comparison with physiological circadian rhythms of BD, and it can explain the relationship between abnormalities in cognitive function and the disturbance of circadian rhythms (Hadaeghi et al., 2013; Hadaeghi et al., 2016; Bayani et al., 2017; Hassanzadeh et al., 2017). Therefore, based on previous findings, it can be inferred that the method for shifting the chaos-chaos intermittency to a periodic state in frontal cortical activity stabilizes the circadian rhythms of BD and optimizes chronotherapy.
To stabilize and adjust chaotic behaviors, various kinds of chaos control methods have been proposed, such as the method established by Ott–Grebogi–Yorke (OGY) Ott et al. (1990), the delayed feedback method (Pyragas, 1992; Nakajima, 1997),
Based on the delayed feedback system, we aimed to develop feedback signals for the frontal cortex that could be used to stabilize disturbed circadian rhythms associated with BD. Concrete procedures used in this study are as follows: first, circadian rhythms of BD were reproduced using bifurcation analysis and the frontal cortex and hypothalamus neural system, as proposed by Hadaeghi et al. (2016). Second, the delayed feedback signal was developed using the bifurcation diagram. Third, the effect of the delayed feedback signal was evaluated by index for complexity and power spectrum analysis under the condition with/without stochastic noise in feedback term.
2. Materials and Methods
2.1. Neural System Composed of the Frontal Cortex and Hypothalamus
The pathology of BD involves multiple complex neural pathways (Sanacora et al., 2012; Schloesser et al., 2012; Tobe et al., 2017). Hadaeghi et al. (2016) focused on the pathological competition between excitatory (glutamatergic) and inhibitory (GABAergic) neurons in the frontal cortex (Tretter et al., 2011; Montague et al., 2012) and impaired connectivity between the frontal cortex and hypothalamus (McKenna and Eyler, 2012; McKenna et al., 2014; Baghdadi et al., 2015) as major factor of BD. They constructed the neural system, which is composed of the frontal cortex and hypothalamus, in order to reproduce healthy and disturbed circadian rhythms, which are associated with BD (Hadaeghi et al., 2016; Bayani et al., 2017). Figure 1 shows an overview of this neural system.
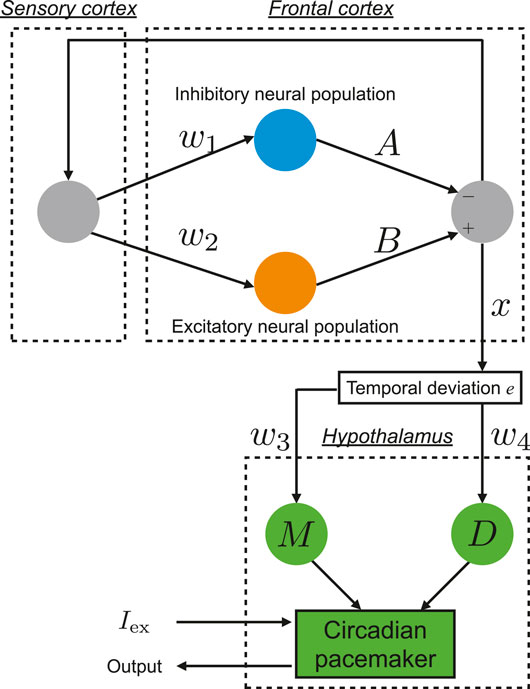
FIGURE 1. Overview of the neural system proposed by Hadaeghi et al. (2016), which is composed of the frontal cortex and hypothalamus to reproduce circadian rhythms.
The daily neural activity of the frontal cortex x(n) (n = 1, 2, …) is controlled by the competition of excitatory and inhibitory neural populations:
Here, w1, w2 the synaptic weights of input to the inhibitory neural population and excitatory neural population are determined, respectively. A, B correspond with the synaptic weights of output from the inhibitory neural population and excitatory neural population, respectively. The output from the frontal cortex to the hypothalamus is defined as the temporal variation from the periodic state with period p:
The dynamics of the circadian pacemaker in the hypothalamus are represented by a two-dimensional map-based model (Pavlov et al., 2011):
where y and z represent the fast and slow variable at time step
where u is given by the external stimulus Iext, and an internal parameter β: u = β + Iext. zs exhibits the peak value of oscillation of z(k). The other parameter, g in Eq. (4) is a parameter for the rising shape of the
Here,
where M is a function of tansig.
The set of parameters used in this study was determined based on previous research by Hadaeghi et al. (2016) and Bayani et al. (2017) as follows:
2.2. Controlling Frontal Cortical Neural Activity by Delayed Feedback Signals
Hadaeghi et al. (2016) demonstrated that healthy periodic circadian rhythms and disturbed circadian rhythms associated with BD are produced by period-p state in the periodic window and chaos–chaos intermittency state, respectively, in the frontal cortical neural activity, as demonstrated by Eq. (1) (Hadaeghi et al., 2016). In this study, we developed the feedback signal to shift the chaos–chaos intermittency of
Here, in the delayed feedback method, the target period is not only the period-p, but also involves p/m(m = 1, 2, …).
In the actual treatment, the estimation of frontal cortical activity and the applying of stimulus involve the measurement error and background noise. To evaluate the influence of stochastic noise in the feedback term, we considered the daily neural activity of the frontal cortex
2.3. Evaluation Indices
2.3.1. Power Spectrum
A power spectrum analysis was performed to evaluate the periodicity of circadian rhythm given by (k). We calculated the power spectrum density (PSD) (dB·day) for output(k) using a fast Fourier transform. A Hanning window was applied to this time-series.
2.3.2. Multiscale Entropy
The approximate entropy was used to evaluate the disturbance of circadian rhythms (Yeragani et al., 2003; Glenn et al., 2006). This approximate entropy was extended to the sample entropy (SampEn) and multiscale entropy (MSE) by modifying the data length dependency and robustness of outliers (Costa et al., 2002). In this study, along with PSD, we used MSE to evaluate the complexity with time scale dependency in the time-series of output(k).
Against stochastic variable
where
In MSE analysis, against coarse-grained series of
SampEn
3. Results
3.1. Circadian Rhythms in the Neural System Are Composed of the Frontal Cortex and Hypothalamus
We have demonstrated that the system behavior in the neural system is composed of the frontal cortex and hypothalamus. Figure 2A shows the bifurcation diagram of the frontal neural activity x(n) as a function of synaptic weight from the inhibitory neural population A. With an increasing A value, x(n) exhibits the period doubling bifurcation and enters a chaotic state
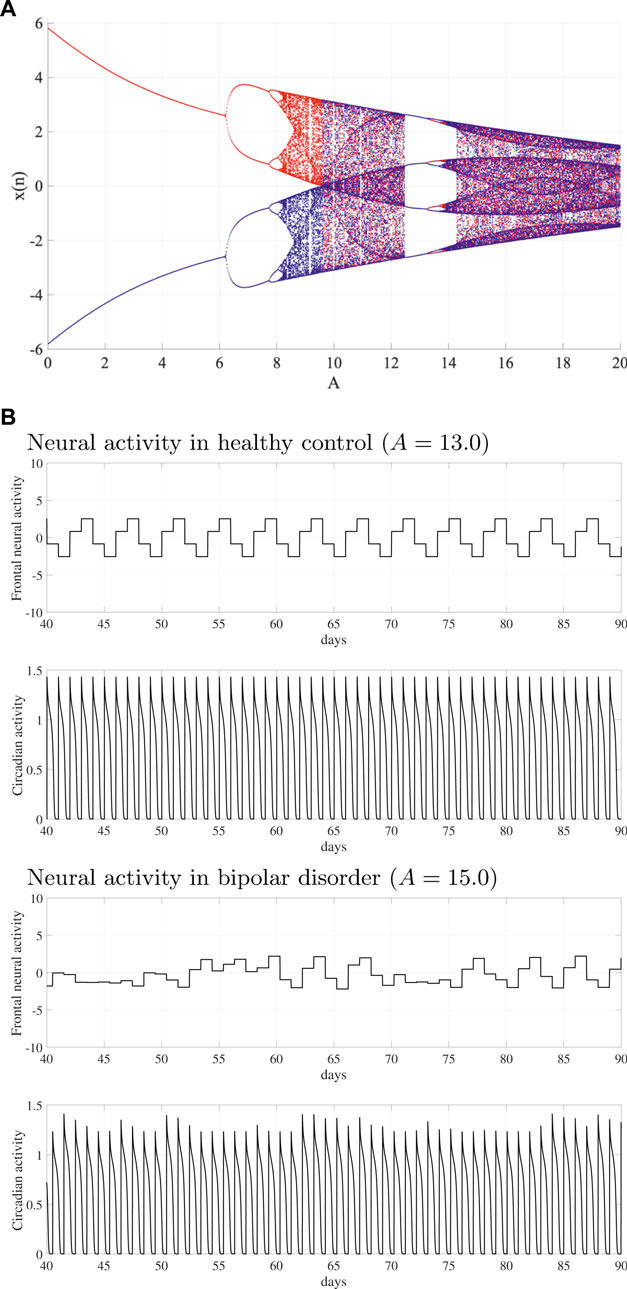
FIGURE 2. System behaviors in the neural system composed of the frontal cortex and hypothalamus as a function of synaptic weight from the inhibitory neural population A. (A) Bifurcation diagram of the frontal neural activity x(n) given by Eq. (1) as a function of A. Blue and red dots indicate the positive and negative initial value x(0) cases, respectively. (B) Time-series of frontal neural activity x(n) and circadian rhythm output(k) are given by Eq. (8) in healthy controls (upper panel) and bipolar disorder (lower panel) patients. In
Figure 2B shows typical examples of the frontal neural activity
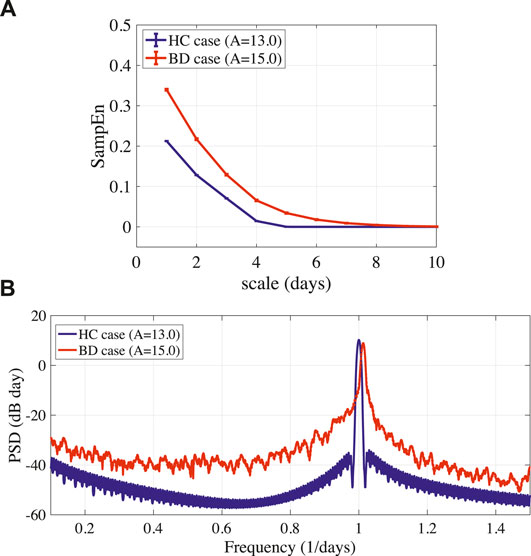
FIGURE 3. (A) Multi-scale entropy analysis of circadian rhythm
3.2. Stabilizing Disturbed Circadian Rhythms Using the Delayed Feedback Method
To stabilize the disturbed circadian rhythms of BD (A = 15.0), the delayed feedback signal was applied to the frontal neural activity using Eq. (10). Figure 4A shows the bifurcation diagram of the frontal neural activity
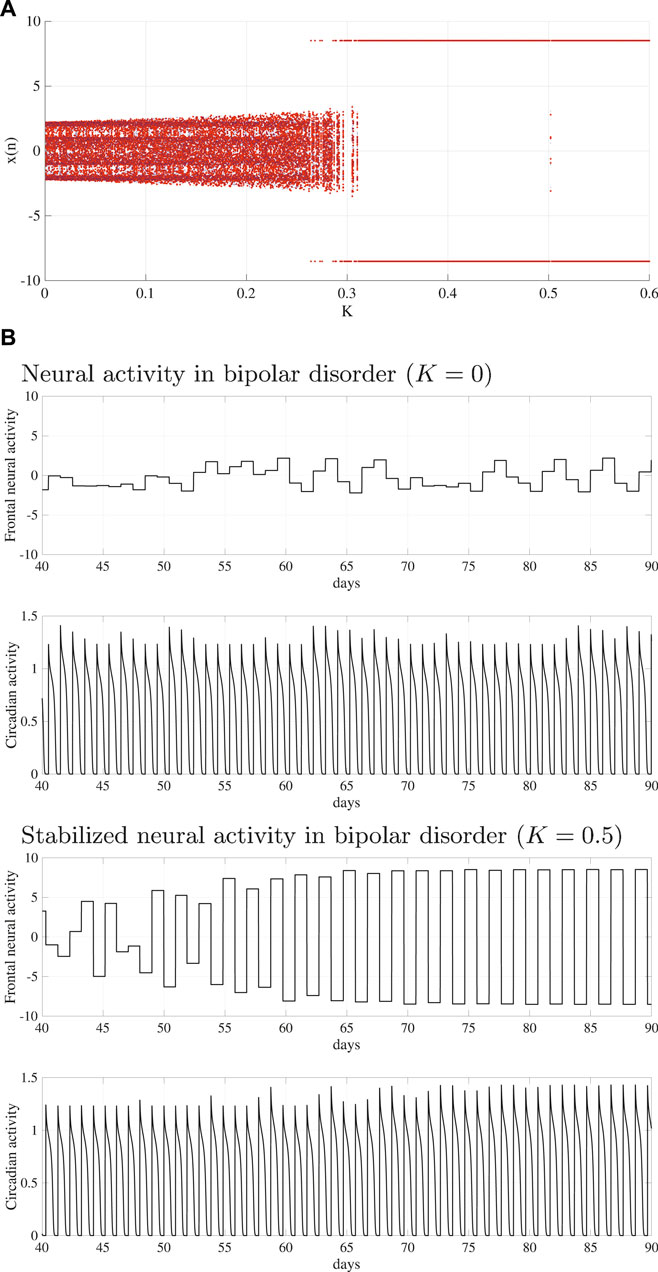
FIGURE 4. System behaviors in the neural system composed of the frontal cortex and hypothalamus as a function of delayed feedback strength K. (A) Bifurcation diagram of the frontal neural activity x(n) given by Eq. (10) as a function of K. Blue and red dots indicate the positive and negative initial value x(0) cases, respectively. (B) Time-series of the frontal neural activity x(n) and circadian rhythm output(k) given by Eq. (8) in the cases without feedback signals (upper panel) and those with feedback signals (lower panel). In
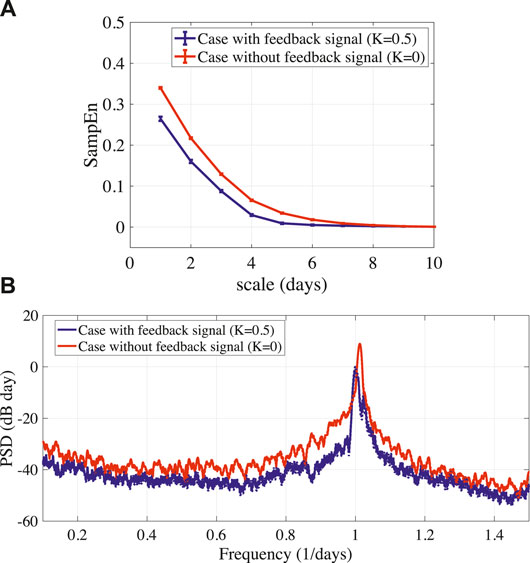
FIGURE 5. (A) MSE analysis of stabilized circadian rhythms output(k) given by Eq. (8) in BD (
3.2. Stabilizing Disturbed Circadian Rhythms in the Case With Delayed Feedback Signals Involving Stochastic Noise
Assuming the estimation of frontal cortical activity and the applying of stimulus involve the measurement error and background noise, we evaluated the influence of stochastic noise in the feedback term given by Eq. (11) to stabilizing disturbed circadian rhythms. Figure 6A showed that the result of MSE analysis in circadian rhythms
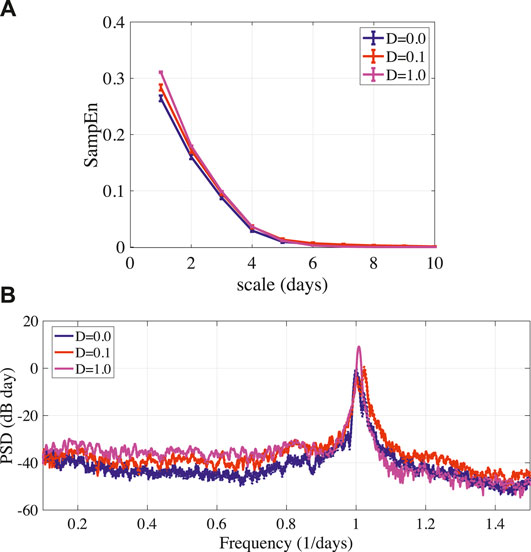
FIGURE 6. (A) MSE analysis of circadian rhythms output(k) given by Eq. (11) in stabilized BD (
4. Discussion and Conclusion
In this study, we reproduced the periodic and disturbed circadian rhythms that corresponded with neural system (frontal cortex and hypothalamus) behaviors of HC and BD patients, which was proposed by Hadaeghi et al. (2016). Furthermore, MSE analysis and power spectrum analysis revealed that the disturbed circadian rhythms of BD exhibited higher complexity than those associated with HC. A disturbed circadian rhythm corresponded with BD; the delayed feedback signal was applied to the frontal cortical neural activity following the delayed feedback method. As a result, the feedback signal induced a periodic circadian rhythm from the disturbed rhythm.
In order to determine the feedback signals in the actual treatment of BD, we must consider the method used to estimate the daily frontal cortical activity. In this estimation, its accuracy strongly affects the ability to stabilize the disturbed circadian rhythm (see Figure 6); therefore, a highly accurate estimation method is needed. As the candidates for the estimation method, Mitsukura and her colleagues developed a method with portable, single-channel electroencephalogram (EEG) devices; the daily variation of these devices was detected via the combination of pattern recognition methods and the obtained EEG time-series (Yamada and Mitsukura, 2016; Ohta et al., 2017). Croce et al. (2018) reported that the daily variation in EEG signals, in regard to circadian rhythms, can be estimated using Higuchi’s fractal dimension of EEG signals as the simple temporal fractal analysis (Croce et al., 2018). Using their method, the daily frontal cortical activity can be estimated and the feedback signals can be determined.
According to the delayed feedback method (Pyragas, 1992; Nakajima, 1997), the feedback signals can also be determined by measuring the observation variables and analyzing their effects on the target dynamics. Therefore, the frontal cortical feedback signals can be developed by physiological and psychological signals, such as actigraphic records, body temperature, and daily mood states, which reflect circadian rhythms. However, based on the construct of the neural systems of the frontal cortex and hypothalamus, as proposed by Hadaeghi et al. (2016), the daily variation of cortical neural activity reflects the disturbance of circadian rhythms. That is, it can be assumed that, in many cases, the observation variable regarding circadian rhythms might include historical frontal cortical activity. In the original delayed feedback methods, the historical effects of observation variables were not considered (Pyragas, 1992; Nakajima, 1997). Therefore, further modifications of the delayed feedback method are necessary for this control.
The actual signals corresponding to the feedback signals in the treatment must be considered. Light therapy and combination therapy (light and drugs) control the melatonin secretion which affects circadian rhythms (Leibenluft et al., 1995; Terman and Terman, 2005). Therefore, the strength and duration of light and the amount of drugs needed to realize the target concentration of melatonin in the blood can correspond with feedback signals. Optimizing chronotherapy based on the delayed feedback method may reduce the risk for inducing mixed states, hypomania and autonomic hyperactivation (Terman and Terman, 2005; Sit et al., 2007; Abreu and Bragança, 2015).
This study has some limitations that should be addressed. Recent studies showed that the network structures, especially topological features, are strongly related with the temporal behavior of neural activity and its functions (Kawai et al., 2019; Nobukawa et al., 2019a; Park et al., 2019; Nobukawa et al., 2020). Many studies regarding neuroimaging modality reported the structural/functional changes of brain network in pathological conditions (Levitt et al., 2017; Takahashi et al., 2017; Takahashi et al., 2018; Ji et al., 2019). However, the frontal cortical network, which was dealt with in this study, is described by the neural population model with only one variable for cortical neural activity. As long as this population model is used, the cortical network structures cannot be implemented. Therefore, future directions for study, should use a neural network model with higher physiological validity, such as a spiking neural network. We plan to construct the frontal cortical neural network including brain network structures; by using the network model with high physiological validity, the effectiveness for our proposed treatment can be further evaluated. Another limitation lies in the delayed feedback method, where the inherent unstable periodic orbit becomes stabilize (Pyragas, 1992; Nakajima, 1997). Therefore, if this inherent unstable periodic orbit is inconsistent with periodic orbit in HC condition, the stabilized orbit is different compared to one in HC condition. Therefore, in our simulation, the frontal cortical activity exhibited the period-2 state and higher amplitude than HC. However, from the viewpoint of actual treatment, the objective is that the pathological disturbed circadian rhythm is changed to a healthy circadian rhythm. Therefore, the target period must be set to healthy period. To realize this purpose, the other chaos control methods that can specify a more detailed target parameter, such as OGY method (Ott et al., 1990), H∞ control (Jiang et al., 2005), and the method utilizing synchronization mechanism (Doho et al., 2020) must be evaluated and compared with the delayed feedback method. We plan to deal with these points in future works. To determine the possible clinical application of this proposed method, the vital reaction regarding the melatonin secretion against light stimulus and drugs must be modeled to determine the strength and duration of light and the amount of drugs needed. Therefore, future studies should implement these vital reactions when modeling for circadian neural systems. Developing feedback signals based on the observation variables of frontal cortical activity is important because actigraphic records and body temperature are easier to obtain, compared to EEG measurements. Furthermore, in addition to BD, abnormal circadian rhythm appears in various chronic-degenerative diseases, caused by the pathological network conditions (Fossion et al., 2017; Fossion et al., 2018). Therefore, focusing on bio-signals that reflect these pathological network conditions’ efficient feedback signals to stabilize it might be designed.
In this study, we developed a method for stabilizing disturbed circadian rhythm in the circadian neural system, which are associated with BD. Although several limitations remain, this method highlights the potential usefulness of the chaos control method for treating BD.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SN, HN, and TT conceived the methods. SN analyzed the results, wrote the main manuscript text, and prepared all the figures. SN and HD conducted the experiments. All authors reviewed the manuscript.
Funding
This work was supported by JSPS KAKENHI for Scientific Research (C) (Grant Number 20K11976) (HN). It was also partially supported by JST CREST (Grant Number JPMJCR17A4).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank Dr. Fatemeh Hadaeghi for useful discussion with numerical simulations.
References
2. Sanacora G, Treccani G, and Popoli M. Towards a glutamate hypothesis of depression. Neuropharmacology. (2012) 62:63–77. doi:10.1016/j.neuropharm.2011.07.036
3. Schloesser RJ, Martinowich K, and Manji HK. Mood-stabilizing drugs: mechanisms of action. Trends Neurosci. (2012) 35:36–46. doi:10.1016/j.tins.2011.11.009
4. Tobe BTD, Crain AM, Winquist AM, Calabrese B, Makihara H, Zhao W-N, et al. Probing the lithium-response pathway in hiPSCs implicates the phosphoregulatory set-point for a cytoskeletal modulator in bipolar pathogenesis. Proc Natl Acad Sci USA. (2017) 114:E4462–71. doi:10.1073/pnas.1700111114
5. Hirschfeld R, Calabrese JR, Weissman MM, Reed M, Davies MA, Frye MA, et al. Screening for bipolar disorder in the community. J Clin Psychiatr. (2003) 64:53–9.
6. López-Muñoz F, Vieta E, Rubio G, García-García P, and Alamo C. Bipolar disorder as an emerging pathology in the scientific literature: a bibliometric approach. J Affect Disord. (2006) 92:161–70. doi:10.1016/j.jad.2006.02.006
7. Abreu T, and Bragança M. The bipolarity of light and dark: a review on bipolar disorder and circadian cycles. J Affect Disord. (2015) 185:219–29. doi:10.1016/j.jad.2015.07.017
8. Yeragani VK, Pohl R, Mallavarapu M, and Balon R. Approximate entropy of symptoms of mood: an effective technique to quantify regularity of mood. Bipolar Disord. (2003) 5:279–86. doi:10.1034/j.1399-5618.2003.00012.x
9. Glenn T, Whybrow PC, Rasgon N, Grof P, Alda M, Baethge C, et al. Approximate entropy of self-reported mood prior to episodes in bipolar disorder. Bipolar Disord. (2006) 8:424–9. doi:10.1111/j.1399-5618.2006.00373.x
10. Bonsall MB, Wallace-Hadrill SMA, Geddes JR, Goodwin GM, and Holmes EA. Nonlinear time-series approaches in characterizing mood stability and mood instability in bipolar disorder. Proc R Soc B. (2011) 279:916–24. doi:10.1098/rspb.2011.1246
11. Moore PJ, Little MA, McSharry PE, Goodwin GM, and Geddes JR. Mood dynamics in bipolar disorder. Int J Bipolar Disord. (2014) 2:11. doi:10.1186/s40345-014-0011-z
12. Leibenluft E, Turner EH, Feldman-Naim S, Schwartz PJ, Wehr TA, and Rosenthal NE. Light therapy in patients with rapid cycling bipolar disorder: preliminary results. Psychopharmacol Bull. (1995) 31:705–10.
13. Terman M, and Terman JS. Light therapy for seasonal and nonseasonal depression: efficacy, protocol, safety, and side effects. CNS Spectrums. (2005) 10:647–63. doi:10.1017/s1092852900019611
14. Sit D, Wisner KL, Hanusa BH, Stull S, and Terman M. Light therapy for bipolar disorder: a case series in women. Bipolar Disord. (2007) 9:918–27. doi:10.1111/j.1399-5618.2007.00451.x
15. Itik M, Salamci MU, and Banks SP. Optimal control of drug therapy in cancer treatment. Nonlinear Anal Theory Methods Appl. (2009) 71:e1473–86. doi:10.1016/j.na.2009.01.214
16. Aihara K, and Suzuki H. Theory of hybrid dynamical systems and its applications to biological and medical systems. Philos Trans R Soc A. (2010) 368:4893–914. doi:10.1098/rsta.2010.0237
17. Mhawej M-J, Moog CH, Biafore F, and Brunet-François C. Control of the HIV infection and drug dosage. Biomed Signal Process Control. (2010) 5:45–52. doi:10.1016/j.bspc.2009.05.001
18. Babaei N, and Salamci MU. Personalized drug administration for cancer treatment using model reference adaptive control. J Theor Biol. (2015) 371:24–44. doi:10.1016/j.jtbi.2015.01.038
19. Hamdache A, Saadi S, and Elmouki I. Nominal and neighboring-optimal control approaches to the adoptive immunotherapy for cancer. Int J Dynam Control. (2016) 4:346–61. doi:10.1007/s40435-015-0205-y
20. Tanaka G, Hirata Y, Goldenberg SL, Bruchovsky N, and Aihara K. Mathematical modelling of prostate cancer growth and its application to hormone therapy. Philos Trans R Soc A. (2010) 368:5029–44. doi:10.1098/rsta.2010.0221
21. Suzuki T, Bruchovsky N, and Aihara K. Piecewise affine systems modelling for optimizing hormone therapy of prostate cancer. Philos Trans R Soc A. (2010) 368:5045–59. doi:10.1098/rsta.2010.0220
22. Hadaeghi F, Hashemi Golpayegani MR, Jafari S, and Murray G. Toward a complex system understanding of bipolar disorder: a chaotic model of abnormal circadian activity rhythms in euthymic bipolar disorder. Aust N Z J Psychiatr. (2016) 50:783–92. doi:10.1177/0004867416642022
23. Bayani A, Hadaeghi F, Jafari S, and Murray G. Critical slowing down as an early warning of transitions in episodes of bipolar disorder: a simulation study based on a computational model of circadian activity rhythms. Chronobiol Int. (2017) 34:235–45. doi:10.1080/07420528.2016.1272608
24. Hadaeghi F, Hashemi Golpayegani MR, and Moradi K. Does “crisis-induced intermittency” explain bipolar disorder dynamics? Front Comput Neurosci. (2013) 7:116. doi:10.3389/fncom.2013.00116
25. Hassanzadeh P, Atyabi F, and Dinarvand R. Application of modelling and nanotechnology-based approaches: the emergence of breakthroughs in theranostics of central nervous system disorders. Life Sci. (2017) 182:93–103. doi:10.1016/j.lfs.2017.06.001
26. Ott E, Grebogi C, and Yorke JA. Controlling chaos. Phys Rev Lett. (1990) 64:1196. doi:10.1103/physrevlett.64.1196
27. Pyragas K. Continuous control of chaos by self-controlling feedback. Phys Lett A. (1992) 170:421–8. doi:10.1016/0375-9601(92)90745-8
28. Nakajima H. On analytical properties of delayed feedback control of chaos. Phys Lett A. (1997) 232:207–10. doi:10.1016/s0375-9601(97)00362-9
29. Jiang W, Guo-Dong Q, and Bin D. H∞ variable universe adaptive fuzzy control for chaotic system. Chaos Solitons Fractals. (2005) 24:1075–86. doi:10.1016/j.chaos.2004.09.056
30. Nobukawa S, Nishimura H, Yamanishi T, and Doho H. Controlling chaotic resonance in systems with chaos-chaos intermittency using external feedback. IEICE Trans Fundam. (2018) E101.A:1900–6. doi:10.1587/transfun.e101.a.1900
31. Nobukawa S, Nishimura H, Yamanishi T, and Doho H. Induced synchronization of chaos-chaos intermittency maintaining asynchronous state of chaotic orbits by external feedback signals. IEICE Trans Fundam. (2019) E102.A:524–31. doi:10.1587/transfun.e102.a.524
32. Li C, Chen L, and Aihara K. Impulsive control of stochastic systems with applications in chaos control, chaos synchronization, and neural networks. Chaos Interdiscipl J Nonlinear Sci. (2008) 18:023132. doi:10.1063/1.2939483
33. Zhou S, Li H, and Zhu Z. Chaos control and synchronization in a fractional neuron network system. Chaos Solitons Fractals. (2008) 36:973–84. doi:10.1016/j.chaos.2006.07.033
34. Nobukawa S, and Shibata N. Controlling chaotic resonance using external feedback signals in neural systems. Sci Rep. (2019) 9:4990. doi:10.1038/s41598-019-41535-0
35. Nobukawa S, Shibata N, Nishimura H, Doho H, Wagatsuma N, and Yamanishi T. Resonance phenomena controlled by external feedback signals and additive noise in neural systems. Sci Rep. (2019) 9:2630. doi:10.1038/s41598-019-48950-3
36. Schöll E, Schuster HG. Handbook of chaos control. Vol. 2. Hoboken, NJ: Wiley Online Library (2008).
37. Tretter F, Rujescu D, Turck CW, and Mewes HW. Pharmacopsychiatry. Editorial. Pharmacopsychiatry. (2011) 44 (Suppl. 1):S1. doi:10.1055/s-0031-1275303
38. Montague PR, Dolan RJ, Friston KJ, and Dayan P. Computational psychiatry. Trends Cognit Sci. (2012) 16:72–80. doi:10.1016/j.tics.2011.11.018
39. McKenna BS, and Eyler LT. Overlapping prefrontal systems involved in cognitive and emotional processing in euthymic bipolar disorder and following sleep deprivation: a review of functional neuroimaging studies. Clin Psychol Rev. (2012) 32:650–63. doi:10.1016/j.cpr.2012.07.003
40. McKenna BS, Drummond SPA, and Eyler LT. Associations between circadian activity rhythms and functional brain abnormalities among euthymic bipolar patients: a preliminary study. J Affect Disord. (2014) 164:101–6. doi:10.1016/j.jad.2014.04.034
41. Baghdadi G, Jafari S, Sprott JC, Towhidkhah F, and Hashemi Golpayegani MR. A chaotic model of sustaining attention problem in attention deficit disorder. Commun Nonlinear Sci Numer Simul. (2015) 20:174–85. doi:10.1016/j.cnsns.2014.05.015
42. Pavlov EA, Osipov GV, Chan CK, and Suykens JAK. Map-based model of the cardiac action potential. Phys Lett A. (2011) 375:2894–902. doi:10.1016/j.physleta.2011.06.014
43. Costa M, Goldberger AL, and Peng C-K. Multiscale entropy analysis of complex physiologic time series. Phys Rev Lett. (2002) 89:68–102. doi:10.1103/physrevlett.89.068102
44. Yamada S, and Mitsukura Y. Detection of circadian rhythms using simple EEG device. In: 2016 11th France-Japan and 9th Europe-Asia Congress on Mechatronics (MECATRONICS)/17th international conference on research and education in mechatronics (REM); 2016 Jun 15–17; Compiegne, France. IEEE (2016) p. 170–3.
45. Ohta E, Ogino M, and Mitsukura Y. Relation extraction for circadian rhythm using the EEG. In: 16th international conference on new trends in intelligent software methodology tools, and techniques, SoMeT 2017; 2017 Sep 26–29; Kitakyushu, Japan. IOS Press (2017) p. 226–32.
46. Croce P, Quercia A, Costa S, and Zappasodi F. Circadian rhythms in fractal features of EEG signals. Front Physiol. (2018) 9:1567. doi:10.3389/fphys.2018.01567
47. Kawai Y, Park J, and Asada M. A small-world topology enhances the echo state property and signal propagation in reservoir computing. Neural Network. (2019) 112:15–23. doi:10.1016/j.neunet.2019.01.002
48. Nobukawa S, Nishimura H, and Yamanishi T. Temporal-specific complexity of spiking patterns in spontaneous activity induced by a dual complex network structure. Sci Rep. (2019) 9:12749. doi:10.1038/s41598-019-49286-8
49. Park J, Ichinose K, Kawai Y, Suzuki J, Asada M, and Mori H. Macroscopic cluster organizations change the complexity of neural activity. Entropy. (2019) 21:214. doi:10.3390/e21020214
50. Nobukawa S, Nishimura H, Wagatsuma N, Ando S, and Yamanishi T. Long-tailed characteristic of spiking pattern alternation induced by log-normal excitatory synaptic distribution. IEEE Trans Neural Networks Learn Syst. (2020) 14:1–13. doi:10.1109/tnnls.2020.3015208
51. Levitt JJ, Nestor PG, Levin L, Pelavin P, Lin P, Kubicki M, et al. Reduced structural connectivity in frontostriatal white matter tracts in the associative loop in schizophrenia. Am J Psychiatry. (2017) 174:1102–11. doi:10.1176/appi.ajp.2017.16091046
52. Takahashi T, Yamanishi T, Nobukawa S, Kasakawa S, Yoshimura Y, Hiraishi H, et al. Band-specific atypical functional connectivity pattern in childhood autism spectrum disorder. Clin Neurophysiol. (2017) 128:1457–65. doi:10.1016/j.clinph.2017.05.010
53. Takahashi T, Goto T, Nobukawa S, Tanaka Y, Kikuchi M, Higashima M, et al. Abnormal functional connectivity of high-frequency rhythms in drug-naïve schizophrenia. Clin Neurophysiol. (2018) 129:222–31. doi:10.1016/j.clinph.2017.11.004
54. Ji E, Guevara P, Guevara M, Grigis A, Labra N, Sarrazin S, et al. Increased and decreased superficial white matter structural connectivity in schizophrenia and bipolar disorder. Schizophr Bull. (2019) 45:1367–78. doi:10.1093/schbul/sbz015
55. Doho H, Nobukawa S, Nishimura H, Wagatsuma N, and Takahashi T. Transition of neural activity from the chaotic bipolar-disorder state to the periodic healthy state using external feedback signals. Front Comput Neurosci. (2020) 14:76. doi:10.3389/fncom.2020.00076
56. Fossion R, Rivera AL, Toledo-Roy JC, Ellis J, and Angelova M. Multiscale adaptive analysis of circadian rhythms and intradaily variability: application to actigraphy time series in acute insomnia subjects. PLoS One. (2017) 12:e0181762. doi:10.1371/journal.pone.0181762
57. Fossion R, Fossion JPJ, Rivera AL, Lecona OA, Toledo-Roy JC, García-Pelagio KP, et al. Homeostasis from a time-series perspective: an intuitive interpretation of the variability of physiological variables. In: Quantitative models for microscopic to macroscopic biological macromolecules and tissues. New York, NY: Springer (2018) p. 87–109.
Keywords: bipolar disorder, circadian rhythms, chaos control, delayed feedback control, chaos–chaos intermittency, chronotherapy
Citation: Nobukawa S, Nishimura H, Doho H and Takahashi T (2020) Stabilizing Circadian Rhythms in Bipolar Disorder by Chaos Control Methods. Front. Appl. Math. Stat. 6:562929. doi: 10.3389/fams.2020.562929
Received: 12 August 2020; Accepted: 15 September 2020;
Published: 08 October 2020.
Edited by:
Plamen Ch. Ivanov, Boston University, United StatesReviewed by:
Ruben Yvan Maarten Fossion, National Autonomous University of Mexico, MexicoHila Dvir, Bar-Ilan University, Israel
Copyright © 2020 Nobukawa, Nishimura, Doho and Takahashi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sou Nobukawa, bm9idWthd2FAY3MuaXQtY2hpYmEuYWMuanA=
 Sou Nobukawa
Sou Nobukawa Haruhiko Nishimura
Haruhiko Nishimura Hirotaka Doho
Hirotaka Doho Tetsuya Takahashi
Tetsuya Takahashi