Estimation and Monitoring of COVID-19's Transmissibility From Publicly Available Data

The 2019 coronavirus disease (COVID-19) pandemic began in the city of Wuhan, China, at the end of 2019 and quickly spread worldwide. The disease is caused by contact with the SARS-CoV-2 virus, which probably jumped from an animal host to humans. SARS-CoV-2 infects various tissues in the body, notably the lungs, and patients usually die from respiratory complications. Mathematical models of the disease have been instrumental to guide the implementation of mitigation strategies aimed at slowing the spread of the disease. One of the key parameters of mathematical models is the basic reproduction ratio R₀, which measures the degree of infectivity of affected individuals. The goal of mitigation is to reduce R₀ as close or below 1 as possible, as it means that new infections are in decline. In this work, we use the recursive least-squares algorithm to establish the stochastic variability of a time-varying R₀(t) from eight different countries: Argentina, Belgium, Brazil, Germany, Italy, New Zealand, Spain, and the United States. The proposed system can be implemented as an online tracking application providing information about the dynamics of the pandemic to health officials and the public at large.

1. Introduction

On March 11, 2020, the World Health Organization (WHO) declared the 2019 coronavirus disease (COVID-19) a global pandemic [1]. COVID-19 is caused by the SARS-CoV-2 coronavirus and was first reported in Wuhan, China, in December 2019 [2]. Since then, COVID-19 has spread globally with millions of laboratory-confirmed cases and hundreds of thousands of deaths [3]. The median incubation period of COVID-19 is 5.1 days, and nearly all infected persons who have symptoms will do so within 12 days of infection [4]. However, an unprecedented characteristic of COVID-19 is its capacity for asymptomatic transmission [5], which contributes to increase the probability of transmission [6]. So far, there is no specific treatment for the disease, and many research teams are currently working on a vaccine that, optimistically, will only be available in 2021. Even then, it will take some time to inoculate a significant share of the population. Meanwhile, hospital structures around the globe (e.g., intensive care units' beds, ventilators, and so on) are becoming overwhelmed with new patients, and the increasing caseload will prove most catastrophic for poor countries, which lack the adequate healthcare capacity to deal with the unparalleled demand posed by COVID-19 [7, 8].

So far, efforts to control the spread of the disease have focused on the adoption of non-pharmaceutical interventions (NPI) based on population behavioral change and social distancing, such as banning large gatherings, enforcing the use of face masks, washing hands, or imposing severe lockdowns [9, 10]. Due to significant uncertainties regarding the transmissibility of SARS-CoV-2 as well as other political, social, and economic considerations, it is necessary to delineate effective social distancing policies that are able to alleviate COVID-19's burden on healthcare structure and borrow time for the development of a vaccine or drug candidates while also simultaneously reducing the socioeconomic strain of living in a locked-down, confined society [11]. The effective monitoring of the epidemic's dynamics plays a crucial role in the ongoing containment efforts but will also continue to do so for some time ahead when social distancing control measures are eventually relaxed, and the first wave of the pandemic is followed some months later by second or third waves of infection that may be more severe than the first [12].

Mathematical models, by providing a quantitative framework for hypothesis evaluation and the estimation of changes in transmission of infectious diseases over time and space, can indicate whether containment measures are having a measurable effect while guiding the design of alternative interventions [13]. Mathematical models vary in many aspects, including complexity in terms of the number of variables and parameters used, spatial and temporal resolution (e.g., discrete vs. continuous time), and design (e.g., deterministic or stochastic) [14]. Mechanistic models of the susceptible–infected–recovered (SIR) type [15, 16] are the standard framework for a wide array of infectious diseases, including COVID-19 (see, for example, [17, 18]). However, parameter estimates for a given model are subject to two major sources of uncertainty: the noise intrinsic to the data and the ad hoc assumptions used for ascertaining parameter estimates [14].

The basic reproduction number [19], R₀, or the average number of new infections caused by an infectious individual [20], is widely used to characterize the dynamics of infectious outbreaks and guide policy planning. For instance, the average R₀ at the start of the SARS pandemic in 2003 was estimated to be around 2.75 and was later reduced to 1 due to intervention strategies, including isolation and quarantine activities [21]. R₀ is an imprecise estimate that is rarely measured directly [it is the product of disease parameters: duration, opportunity, transmission probability, and susceptibility (DOTS)] and rests on particular model structures and assumptions [22]. Modelers face many challenges when trying to provide robust estimations of R₀ in the current pandemics, such as the existence of superspreaders, the fact that SARS-CoV-2 can also be spread by asymptomatic individuals and the scarce availability of testing supplies [17]. Several methods have been proposed to track trends in R₀ during the course of an epidemic [23–27]. The access to reliable estimates of R₀ could provide useful information about the efficacy of containment measures and allow their effective management in order to keep hospitalization rates within a desired approximate range [28].

In the present study, we model the transmission dynamic of COVID-19 in eight countries (Figure 1) using least-squares algorithm (LSA) techniques. The criteria used to select the eight countries were due to their geographical location in either the northern/southern hemisphere or due to specificities regarding their first response to the pandemic threat as reported in the news media. Some (e.g., New Zealand and Argentina) were very effective in responding rapidly to the pandemic by implementing lockdown measures, whereas others (e.g., USA and Brazil) initially downplayed the virus' threat and took longer to initiate containment protocols. Our goal is to contribute to understanding the spread of SARS-CoV-2 and compare R₀ uncertainty arising from noise in the time series data gathered from public online sources. We used machine learning algorithms to optimally estimate a time-varying R₀(t), which allows the monitoring of the ongoing pandemic in almost real time. We compared the daily country reports for R₀ to those we estimated in the present work in order to assess the reliability of official data. Besides, LSA-based techniques were used to reveal clues regarding the dynamics of R₀(t) and its stochasticity in terms of the linear power of the estimation error and provide information on how such stochastic behavior is correlated to the outcome of the ongoing pandemics.

FIGURE 1

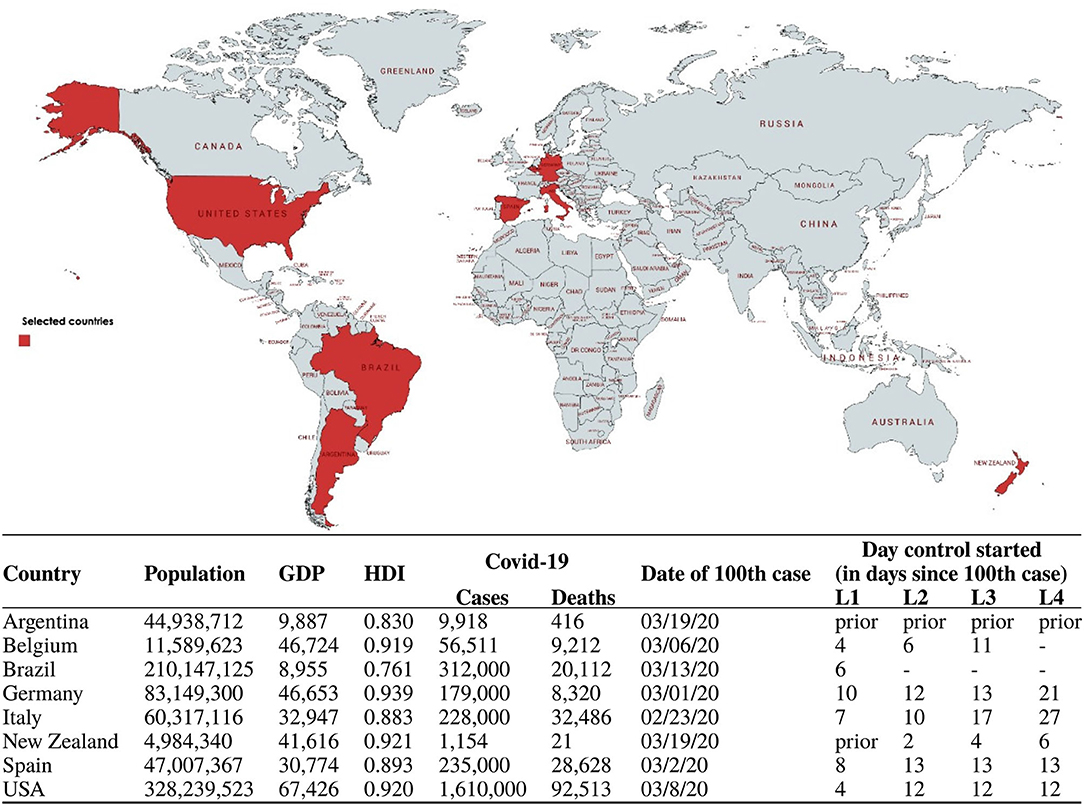
Figure 1. Sociodemographic and COVID-19 data for the eight countries targeted in this study. COVID-19 data accessed on 22/05/2020 on https://coronavirus.jhu.edu/map.html. Intervention data gathered from reference [29]. GDP per capita in US$. Interventions are categorized into Alert Levels 1 to 4 according to the New Zealand framework (L1, Level 1, Prepare; L2, Level 2, Reduce; L3, Level 3, Restrict; L4, Level 4, Eliminate) [29]. Map from mapchart.net.

The LSA is one of the most popular estimation methods in machine learning and has been used in many scientific and engineering applications [30–32], including epidemiology, for calibrating mathematical models' parameters based on time series data while also generating disease forecasts in the near or long terms [14, 33–35]. While it has been used for centuries as a classic curve-fitting technique [31, 32], it is still a basic tool in modern data science because of its least-squares Euclidean ℓ₂-norm minimization that is advantageous over other norms and metrics, such as the ℓ_∞ and ℓ₁ norms, granting reduced sensibility to outliers due to the squared error [32, 36]. Higher-order norms and the use of more generalized cost functions, both linear and non-linear, often require gradient descent solutions, which are the foundation of deep learning algorithms with none, many, or infinite solutions. In comparison, LSA is computationally inexpensive and can even be solved analytically.

LSA estimation is based on the least mean squares (LMS) algorithm, a special case of Bayesian estimation and the foundation of classical optimal estimation theory, where its applicability is commonly attributed to offline batch processing, that is, the whole data set must be a priori available and be processed at once “in one single step into the estimate” [36], involving complex algebraic procedures, such as the inversion of high-order matrices, with dimension equal to the length of the data set. Its offshoot, the recursive least squares (RLS) algorithm, has been used for real-time estimation applications in diverse areas, such as signal and data processing, communications, and control systems [37, 38], since it benefits from the recursive method and avoids matrix inversion by working one sample at a time, both speeding up processing and avoiding a possible ill-conditioned (non-invertible) information matrix formation.

Some of the advantages of RLS algorithm over LMS algorithm, and other more complex gradient descent-based estimation methods, are as follows: its recursive or sequential processing, which requires less memory over a single iteration step; the possibility to capture the dynamics of non-linear and time-varying systems; its native discrete-time synthesis to deal with discrete-time signals; and its dead-beat convergence characteristics, that is, convergence in minimal time [31]. However, one important drawback is the possibility of RLS getting stuck in local minima and becoming unstable when tracking certain classes of signals, as remarked in reference [31]. Thankfully, the exponential functions used in epidemic modeling are within the stable scope of convergence of the RLS method.

In this work, we compare the performance of both the RLS and LMS algorithms on estimating R₀(t), in terms of processing speed and accuracy. While both are LSA-based methods apparently differing just by the sequential-recursive and the batch-processing forms of implementation, we are dealing with a general case problem of estimating a random variable R₀(t) given random variables as well in a maximum-likelihood estimation problem that “implies ignorance of any statistics of the estimated variable” [36], R₀(t). Thus, if the available measurements are independent, RLS and LMS algorithms should achieve the same accuracy performance. Otherwise, the RLS algorithm should perform better.

Our modeling approach is based on a discrete-time multiple-input, multiple-output (MIMO) setup that uses a well-established concept in the design of aerospace navigation systems called sensor fusion, which is summarized by the following statement, “one always gains by adding a new measurement in terms of navigation error, and this no matter how bad the additional measurement is” [39, Remark 4.8]. In this work, we combine data from the number of susceptibles, infections, recoveries, deaths, and individual parameters of three coupled differential equations in order to improve the estimation of R₀(t).

2. Methods

2.1. Data Sources

The COVID-19 data used in this report are publicly available from The Center for Systems Science and Engineering of the Johns Hopkins University (JSU CCSE) [40], which maintains a Repository on Github [41].

2.2. Procedures

The transmission dynamics of the COVID-19 outbreak is usually described by a compartmental model SEIR, where S denotes susceptible, E denotes exposed, I denotes infected, and R denotes removed [42, 43]. In a closed population of P_n individuals, the transitions between the compartments (cf. Figure 2) are described through the following set of differential equations:

$\begin{array}{ll}\frac{d}{dt}s(t)=-\bar{\lambda }s(t)i(t)& (1)\end{array}$

$\begin{array}{ll}\frac{d}{dt}e(t)=\bar{\lambda }s(t)i(t)-\kappa e(t)& (2)\end{array}$

$\begin{array}{ll}\frac{d}{dt}i(t)=\kappa e(t)-\gamma i(t)& (3)\end{array}$

$\begin{array}{ll}\frac{d}{dt}r(t)=\gamma i(t)& (4)\end{array}$

FIGURE 2

Figure 2. SEIR (S denotes susceptible, E denotes exposed, I denotes infected, and R denotes removed) model structure.

where $\bar{\lambda }=\lambda /P_n$, λ is the infection rate, γ is the remove rate, and κ is the incubation rate. From these parameters, it is possible to calculate the basic reproduction ratio, R₀ = λ/γ. Thus, R₀ is not solely dependent on the infection rate but also on the frequency of removals due to death or recoveries.

Assuming that the incubation period of the disease is instantaneous, and the duration of infectivity is the same as the length of the disease, we can consider both groups E and I as contagious and E(t): = I(t). Also, according to the Akaike information criterion (AIC), the simpler SIR model performs much better than an SEIR model in representing the information contained in the confirmed-case data available for COVID-19 [44]. The basic SIR model is described by the set of Kermack–McKendrick equations [45]:

$\begin{array}{ll}\frac{d}{dt}s(t)=-\frac{\lambda }{P_n}s(t)i(t)& (5)\end{array}$

$\begin{array}{ll}\frac{d}{dt}i(t)=\frac{\lambda }{P_n}s(t)i(t)-\gamma i(t)& (6)\end{array}$

$\begin{array}{ll}\frac{d}{dt}r(t)=\gamma i(t)& (7)\end{array}$

2.3. Discrete-Time Susceptible–Infected–Recovered System Parametric Estimation in Real Time

Traditionally, mathematical epidemiology models have been approached with a continuous-time perspective, due in part to the fact that these are more tractable mathematically [46]. However, in order to use machine learning techniques, there is a need for a discrete-time equivalent realization to cope with daily-sampled data [47]. Due to the slow dynamics of the pandemics, a first-order continuous to discrete Euler approximation can be applied to the Kermack–McKendrick equations.

For a general f(t) function, a backward discrete-time derivative approximation is given as:

$\begin{array}{ll}\frac{d}{dt}f(t):=\frac{f(k+1)-f(k)}{T_s}=\Delta f(k+1)/T_s& (8)\end{array}$

where T_s = 1 is the sampling interval in days, and Δ = 1 − q⁻¹ is the discrete difference operator, defined in q⁻¹, the backward shift operator domain. The discrete-time approximations of Equations (5)–(7) are given by the following difference equations, respectively:

$\begin{array}{ll}s(k)=s(k-1)-\lambda (k-1)\frac{s(k-1)i(k-1)}{P_n}& (9)\end{array}$

$\begin{array}{ll}i(k)=i(k-1)+\lambda (k-1)\frac{s(k-1)i(k-1)}{P_n}-\gamma (k-1)i(k-1)& (10)\end{array}$

$\begin{array}{ll}r(k)=r(k-1)+\gamma (k-1)i(k-1)& (11)\end{array}$

The discrete-time SIR system described above considers time-varying parameters in order to continuously adapt the model as new data become available. Using the time series of infections and removals (due to death or recovery), Equations (9)–(11) can be used to estimate the model parameters.

Since Equation (11) has an exclusive dependence with γ(k), this poses a direct estimation problem that can be stated as “for N registered samples, minimize the following quadratic cost function”:

$\begin{array}{ll}{J}_r=\frac{1}{2}{\displaystyle \sum _0^N}{e}_r^2(k)=\frac{1}{2}{\displaystyle \sum _{k=0}^N}{\left[r(k)-\widehat{r}(k)\right]}^2& (12)\end{array}$

Equation (12) is based on the estimation error of r(k). By applying the RLS method to minimize J_r, it is possible to optimally estimate $\widehat{\gamma }(k)$ using the following equation:

$\begin{array}{ll}\widehat{r}(k)=r(k-1)+\widehat{\gamma }(k-1)i(k-1)& (13)\end{array}$

We assume that the estimation error is Gaussian, $e_r(k)~(0,{\sigma }_{e_r}^2)$, with zero mean and variance ${\sigma }_{e_r}^2$, such that $r(k)=\widehat{r}(k)+e_r(k)$. The estimator gain, the parametric estimation, and error covariance minimization are solved recursively as follows:

$\begin{array}{ll}{L}_r(k)=\frac{p_r(k-1)i(k-1)}{1+i(k-1)p_r(k-1)i(k-1)}& (14)\end{array}$

$\begin{array}{ll}\widehat{\gamma }(k)=\widehat{\gamma }(k-1)+L_r(k)\left[r(k)-\widehat{r}(k)\right]& (15)\end{array}$

$\begin{array}{ll}{p}_r(k)=\left[1-L_r(k)i(k-1)\right]p_r(k-1)& (16)\end{array}$

where the error covariance matrix p_r(k) can be reset periodically to prioritize more recent data. Specifically in this work, p_r(k) is a scalar, since only a single parameter is being estimated. Choices to initialize the covariance matrix may vary, depending on prior available covariance information or other positive definite matrix. The higher its magnitude, the higher the estimator gain in the transitory dynamical stage of the estimation procedure.

In regard to Equation (11) and the estimation of $\widehat{\gamma }(k)$, since the infection numbers increase before any removal report is available during the first stages of the pandemic, during this period $\widehat{\gamma }(k)$ tends to zero and eventually makes the time-varying estimated reproduction number tend to infinity:

$\begin{array}{ll}{\widehat{R}}_0(k)=\frac{\widehat{\lambda }(k)}{\widehat{\gamma }(k)\to 0}=\infty & (17)\end{array}$

As a consequence of Equation (17), the estimation method proposed in this work cannot be applied when the number of recovered is not available.

Since Equation (10) depends on both SIR parameters, due to its stronger dependence on $\widehat{\gamma }(k)$ and Equation (11), its estimated value is substituted into Equation (10), and another RLS problem is constructed to estimate $\widehat{\lambda }(k)$, using

$\begin{array}{ll}\widehat{i}(k)=i(k-1)+\widehat{\lambda }(k-1)\frac{ŝ(k-1)i(k-1)}{P_n}-\widehat{\gamma }(k)i(k-1)& (18)\end{array}$

The solution is akin to minimizing the estimation error e_i(k) = i(k) − î(k), using the following equations for estimator gain, parametric estimation update, and error covariance minimization, respectively:

$\begin{array}{ll}{L}_i(k)=\frac{p_i(k-1)\widehat{s}(k-1)i(k-1)/P_n}{1+\left[\widehat{s}(k-1)i(k-1)p_i(k-1)\widehat{s}(k-1)i(k-1)\right]/P_n^2}& (19)\end{array}$

$\begin{array}{ll}\widehat{\lambda }(k)=\widehat{\lambda }(k-1)+L_i(k)\left[i(k)-\widehat{i}(k)\right]& (20)\end{array}$

$\begin{array}{ll}{p}_i(k)=\left\{1-L_i(k)\left[\frac{\widehat{s}(k-1)i(k-1)}{P_n}\right]\right\}{p}_i(k-1)& (21)\end{array}$

Time-series data for Equation (9) is not available, and the evolution of the susceptible compartment in time is in fact estimated based on the known initial condition (i.e., the population P_n) and on the estimated $\widehat{\lambda }(k)$. Thus, it is always estimated and fed back to Equation (18), such that the correct form to represent it, within this time-varying SIR model, is by rewriting Equation (9) based on the estimated susceptible:

$\begin{array}{ll}\widehat{s}(k)=\widehat{s}(k-1)-\widehat{\lambda }(k)\frac{\widehat{s}(k-1)i(k-1)}{P_n}& (22)\end{array}$

The estimation of the time-varying reproduction number, based on the derived discrete-time SIR model, is given by:

$\begin{array}{ll}{\widehat{R}}_0(k)=\frac{\widehat{\lambda }(k)}{\widehat{\gamma }(k)}& (23)\end{array}$

We also adopted two modifications to the nominal ${\widehat{R}}_0(k)$ equation: a moving 4-days average to compensate for the randomness of daily updates on incidence data, as seen in the German Daily Situation Report of the Robert Koch Institute on COVID-19 [48], and the proportion of susceptible individuals in the population, known as the effective reproduction number [14]:

$\begin{array}{ll}{\bar{R}}_0(k)=\frac{\widehat{s}(k)}{P_n}\left[\frac{{\widehat{R}}_0(k)+{\widehat{R}}_0(k-1)+{\widehat{R}}_0(k-2)+{\widehat{R}}_0(k-3)}{4}\right]& (24)\end{array}$

Figure 3 shows a block diagram of the proposed ${\bar{R}}_0(k)$ estimator. This diagram presents a clearer view of the coupled multivariate dynamics and closed-loop characteristics of the proposed estimation approach.

FIGURE 3

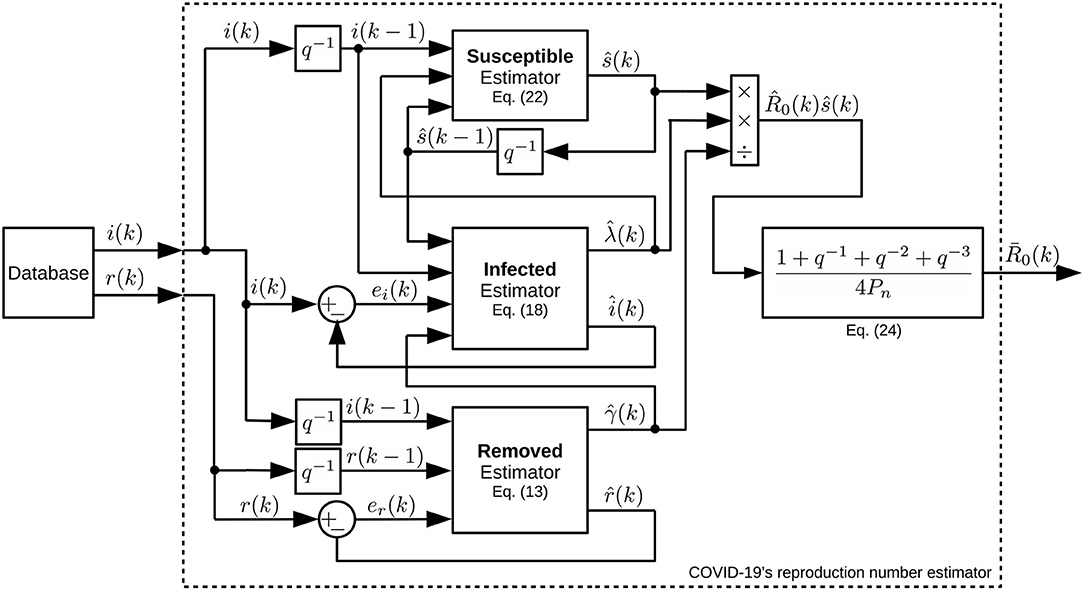
Figure 3. Block diagram of the estimation system. Notice how its subsystems are interconnected using closed-loop strategies and data fusion.

With this formulation, it is possible to analyze the transmission ratio of the pandemics on a daily basis, as with a sensor. Besides, estimations of the transmission ratio produce a dynamic representation from the perspective of the time series of ${\bar{R}}_0(t)$ [henceforth designated simply as ${\widehat{R}}_0(t)$], which allows the modeling of its dynamics and its randomness in order to assess stochastic properties correlated to the time-varying reproduction number, which might reflect how health authorities have been handling the challenges posed by the pandemics in each country considered in this work.

2.4. Modeling of R₀

Henceforth, we assume that we are able to estimate the reproduction number on a daily basis and it is thus possible to consider it as another output of the proposed pandemic model. Thus, by relying on the time series of ${\widehat{R}}_0(k)$ and knowing it is correlated with the number of infected and removed individuals, we deploy machine learning techniques to identify a dynamic system that fits the data.

Different from the real-time monitoring/sensing procedure adopted to estimate ${\widehat{R}}_0(k)$, now, we are interested in obtaining a general model that can describe the dynamics of a system, ${\widehat{R}}_0(q^{-1})$, for a certain period of interest. In order to model such a system, we used the LMS algorithm, which is a non-RLS estimation technique [31, 32], and propose a black-box linearized polynomial model:

$\begin{array}{ll}{\widehat{R}}_0(q^{-1})=\frac{\widehat{B}(q^{-1})I(q^{-1})+\widehat{C}(q^{-1})R(q^{-1})+e_{R_0}(q^{-1})}{\widehat{A}(q^{-1})}& (25)\end{array}$

$\begin{array}{ll}\begin{array}{c}\widehat{A}(q^{-1})=1+{\widehat{a}}_1{q}^{-1}+{\widehat{a}}_2{q}^{-2}\hfill \\ \widehat{B}(q^{-1})={\widehat{b}}_0{q}^{-1}+{\widehat{b}}_1{q}^{-2}\hfill \\ \widehat{C}(q^{-1})={\widehat{c}}_0{q}^{-1}+{\widehat{c}}_1{q}^{-2}\hfill \\ \end{array}\hfill & (26)\end{array}$

where $e_{R_0}(q^{-1})$ is the Gaussian process based on the estimation error e_R0(k) of estimated polynomials shown in Equation (26).

This second-order autoregressive with exogenous input (ARX)-based model structure is assumed considering the fundamental simplicity of the SIR model, in which the infected and removed systems together form a second-order system.

The non-RLS estimator is a batch-processing technique used to optimally estimate the set of parameters that minimizes a quadratic performance index as the one shown in Equation (12), but using a vector–matrix form of error, ${\text{e}}_{R_0}={\widehat{R}}_0-\Phi \widehat{\theta }$. This vector–matrix system is defined as:

$\begin{array}{ll}{\text{e}}_{R_0}={\left[\begin{array}{c}e(0)\cdots e(N)\end{array}\right]}^T& (27)\end{array}$

$\begin{array}{ll}{\widehat{R}}_0={\left[\begin{array}{c}{\widehat{R}}_0(0)\cdots {\widehat{R}}_0(N)\end{array}\right]}^T& (28)\end{array}$

$\begin{array}{ll}{\widehat{\theta }}^{\text{T}}=\left[\begin{array}{cccccc}{\widehat{a}}_1& {\widehat{a}}_2& {\widehat{b}}_0& {\widehat{b}}_1& {\widehat{c}}_0& {\widehat{c}}_1\end{array}\right]& (29)\end{array}$

$\begin{array}{ll}{\Phi }^{\text{T}}=\left[\begin{array}{c}{\varphi }^T(0)\cdots {\varphi }^T(N)\end{array}\right]& (30)\end{array}$

The above equations represent, respectively, the vector of errors, the vector of observed outputs, the estimated parameter vector, and the matrix of regressors. The latter is based on the vectors of regressors formed up to N registered samples, with such vectors defined as:

$\begin{array}{ll}{\varphi }^T(k)=\left[\begin{array}{cccccc}{\widehat{r}}_0(k-1)& {\widehat{r}}_0(k-2)& i(k-1)& i(k-2)& r(k-1)& r(k-2)\end{array}\right]& (31)\end{array}$

The solution to obtain the estimated parameters is straightforward and given by

$\begin{array}{ll}\widehat{\theta }={\left({\Phi }^{\text{T}}\Phi \right)}^{-1}{\Phi }^{\text{T}}{\widehat{R}}_0& (32)\end{array}$

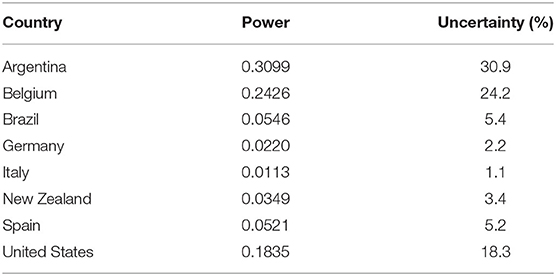
By assuming an ARX linear model, it is possible to evaluate the pandemics from the perspective of linear stochastic systems theory, assessing how the reproduction number decays linearly in time in different countries and how the random nature of events associated with the pandemics affects the model's uncertainties, that is, $e_{R_0}(k)~(0,{\sigma }_{e_{R_0}}^2)$. This calculated uncertainty can give us some clues regarding the effectiveness of pandemic control measures.

We propose that by analyzing the linear power of the ${\widehat{R}}_0(q^{-1})$ estimation error, that is, ${\sigma }_{e_{R_0}}^2$, we can use this stochastic property to generate stochastic ratio curves based on the estimated linearized model of Equation (25). The higher the variability associated with the stochastic ratio, the higher we expect the variance or linear power of the error to be, and consequently, the more uncertain is the official COVID-19 data reported by health authorities.

3. Results

We used publicly available data to validate the algorithms and the estimated time-varying SIR model parameters. This section is organized as follows: we first present the estimated results based on the number of infectious and removals available from different countries. Then, we present time series of daily estimates on R₀(k) based on the RLS-estimated $\widehat{\lambda }(k)$ and $\widehat{\gamma }(k)$ and compare both processing time and accuracy results to the classical LMS method to verify the efficiency of the proposed technique.

These results are followed by the presentation of linearized estimated outputs generated by the ARX-based $\widehat{R}(q^{-1})$ models [shown in Equation (25)] using non-recursive or batch processing of 30-days of R₀(k) estimates. The modeling residuals were assumed to be Gaussian (zero mean). Estimated error variances were used to produce 200 discrete Gaussian sequences as surrogates to additive white noises, depicted by e_R0(k) in Equation (25). These 200 additive noise sequences were used to generate, for every analyzed country, 200 stochastic reproduction ratio trajectories, shown together with the linearized ratio and the real-time estimated ratio. It must be remarked, however, that this value of 200 Monte Carlo simulations were selected heuristically in order to give the necessary visual information in our figures, such that the readers could verify by themselves how the modeling uncertainties of the pandemics could mislead our judgment of the probable effective reproduction number of COVID-19 during the studied period. The number of Monte Carlo simulations thus affects only a post-modeling phase and do not interfere with the estimation of the reproduction number.

3.1. Discrete-Time Susceptible–Infected–Recovered Model Estimation Results

The Achilles' heel of the RLS algorithm for parametric estimation may be the setup of initial conditions and whether they are optimal or not. However, this is a major problem only if the estimated parameters are to be used in a real-time adaptive control system where the closed-loop stability must be guaranteed [31]. This is not the case in the present work, which is interested only in the modeling question itself. Thus, the initial RLS parameters can be either arbitrarily set or set at zero since, theoretically, the RLS estimator is dead-beat and converges in the minimum possible number of iterations [32, 36].

The discrete SIR model proposed in this work is described by three coupled differential equations, each based on a single recursive regression and thus forming a third-order system. Then, theoretically, as a dead-beat estimator, the RLS estimator would take three iterations to converge and estimate optimal parameters. However, we used plenty more iterations than the theoretical requirements by commencing to process data from March 22, 2020 onward but evaluating the results after April 23, 2020, thus giving more than 30 days/iterations for the RLS to converge to an optimal set of parameters by April 23, 2020, when we started our analysis.

The estimators were implemented with arbitrary initial parameters of $\widehat{\gamma }(0)=\widehat{\lambda }(0)=1$ and the initial guess for ${\widehat{R}}_0(0)=1$. The magnitudes of the estimation error covariance matrices were initialized as p_r(0) = p_i(0) = 1, considering that the initial error is large. Both p_r(k) and p_i(k) were reset to 1 every 7 days to prioritize more recent data [49]. The selection of the reset period considered not only the number of days required to wash-out outliers but also to allow weekly changes in the parameters' dynamical behavior, such as due to lockdowns or quarantine relaxation. We also adopted a moving 4-days average for ${\widehat{R}}_0(k)$, shown in Equation (24), to compensate for daily random effects [48]. We only used data from March 22, 2020 onward, when all eight countries already had more than 100 infections reported.

Figures 4, 5 show the dynamics of both infected and removed cases using the SIR model. It must be remarked that the infected curve in the United States was downscaled by a factor of 4 in order to fit in the graph along with the other studied countries. It is evident from Figure 4 that the RLS method provide parametric estimates that fit the reported data. The same goodness of fit cannot be observed in Figure 5, as the number of removals for the United States, for example, poses some difficulties for the RLS estimator, as depicted by the estimated removals (dotted lines) showing a certain dispersion from the real data (continuous lines). However, the inclusion of the removed data set, even with bad measurements, leads to a better estimate of ${\widehat{R}}_0(k)$.

FIGURE 4

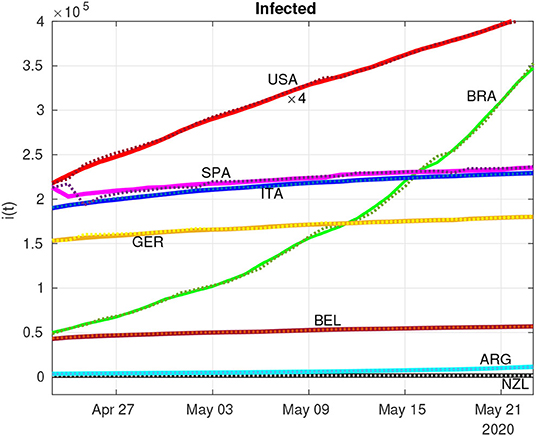
Figure 4. Estimation (dotted lines) of infected individuals (continuous lines) using the recursive least-squares (RLS) technique (the U.S. data was downscaled four times to fit in the graph).

FIGURE 5

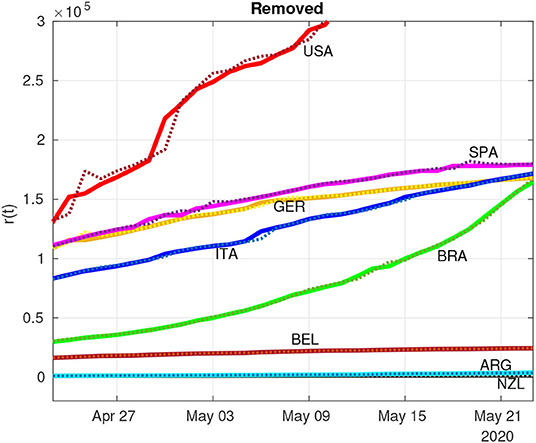
Figure 5. Estimation (dotted lines) of removed individuals (continuous lines) using the RLS technique.

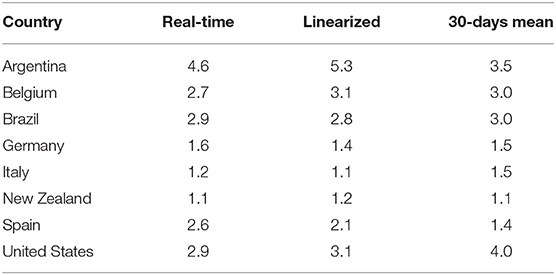
Figure 6 presents the ${\widehat{R}}_0(k)$ of the eight different countries during a period of 2 weeks. Despite the large variability of both Argentina and the United States, there are other countries that are already reducing the number of new infections and where the frequency of removals has increased, such as in Germany, Italy, and New Zealand (see Table 1).

FIGURE 6

Figure 6. Daily monitoring of the COVID-19 pandemic: Dynamic behavior of the estimated reproduction number for 2 weeks in May 2020.

TABLE 1

Table 1. Recoveries (May 21, 2020).

The trajectory of the curves shown in Figure 6 can also be associated with some extraordinary events that occurred during the same period. For example, after May 3, 2020, when some U.S. states had relaxed social distancing guidelines, it is possible to observe a corresponding phasic increase in the basic reproduction ratio of the United States, which was also reported in the Washington Post on May 9, 2020 [50].

One interesting trajectory in Figure 6 regards Argentina. For most of the time, the estimated reproduction ratio of Argentina was one of the highest and comparable only to the United States, despite its low number of infected individuals (cf. Figure 4). This apparent contradiction is related to the low number of removals at the beginning of the pandemic that tends to raise the ${\widehat{R}}_0(k)$ (see Equation 17). Recoveries in Argentina, based on the data of May 16 (cf. Table 1), are ~30.5% of its total infected, close to Belgium with 26.6% and whose transmission ratio is below Argentina's ratio, reinforcing the notion that the transmission ratio is not a static parameter and is best approached by dynamical systems theory.

The results displayed in Figure 4 seem at odds with a recent report that claimed that Brazil's R₀ had recently dropped to 1.4 [51]. However, on the same day a Brazilian newspaper quoted this report, the country had a record number of new infections and deaths [52]. This reinforces the notion that machine learning methods might give better and faster clues regarding the severity of the pandemic in terms of ${\widehat{R}}_0(k)$.

We compared the performance of the proposed RLS estimator with its most common counterpart, the LMS algorithm. In this comparison, we considered the average processing time and the normalized relative estimation error based on the mean-square-based cost function shown in Equation (12). The average processing time results for the RLS and LMS algorithms were, respectively, 14 and 20 ms. We used a computer with a fourth-generation Intel Core i5-4200U CPU at 1.6 GHz, 4 GB of RAM, running Ubuntu 18.04 LTS and Matlab R2018a (Mathworks, Inc., Natick, MA, United States). The accuracy results expressed by normalized relative errors are summarized in Figure 7. Notice that the RLS method outperformed the LMS method in all cases, except for Argentina.

FIGURE 7

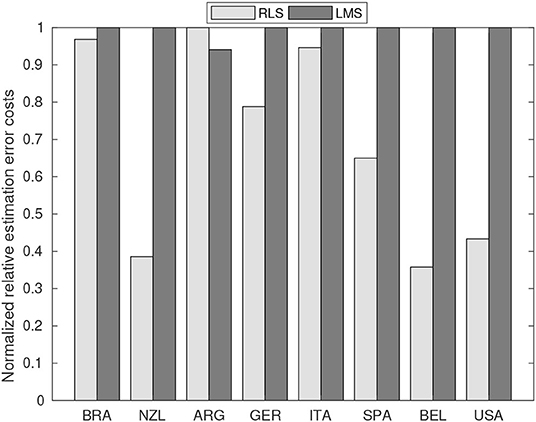
Figure 7. Comparison of normalized relative estimation error costs between the proposed RLS-based technique and the least mean squares (LMS) estimation algorithm. The average processing time of RLS and LMS algorithms was, respectively, 14 and 20 ms.

3.2. Assessing the Pandemics Through R₀ Dynamics

Figures 8–11 show ${\widehat{R}}_0(k)$ for a 30-days period for the eight investigated countries. These figures show linearized R₀ together with the respective real-time estimated data that originated this second-stage estimation. The variance of the estimation error is then used to generate Gaussian sequences that are superimposed on the linearized R₀ estimate, the stochastic ratio, which synthetically reproduces the stochasticity and uncertainties of R₀ estimates. Both Germany and Italy (Figure 8) are through a period of consistently decaying R₀(t). Despite the hard way COVID-19 hit Italy before, its stochastic ratio currently is among the lowest.

FIGURE 8

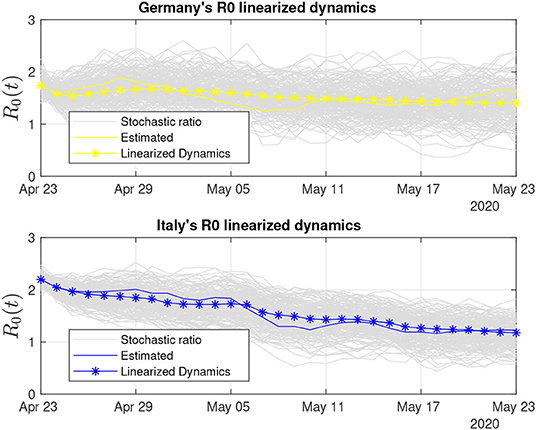
Figure 8. Thirty days of linearized R₀ dynamics for Germany and Italy. Both countries display low variability in the stochastic ratio curve.

Brazil and the United States (Figure 9) are the two most populous countries of our sample and the most hard-hit by COVID-19 among them. Both countries also have been struggling with their uneven response to the pandemics [53]. This outcome is captured by our R₀ sensors, with the Brazilian stochastic ratio being in decrease, as recovered data become more available (see Figure 9).

FIGURE 9

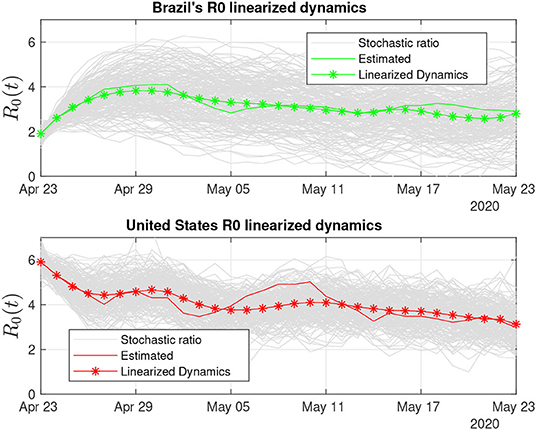
Figure 9. Brazil and the United States display large variability in the stochastic ratio curve, which probably reflects data uncertainty and difficulties to control COVID-19's spread.

In Figure 10, we present linearized R₀ estimates for Spain and Belgium. Spain's estimates have suffered the influence of annotation errors (by subtracting infected individuals on April 24, 2020), which eventually provoked oscillations in the real-time ratio estimate, making it zero-cross on April 27. Such an error was washed out by the linearized estimate and has certainly contributed to its increased degree of uncertainty (see Table 2).

FIGURE 10

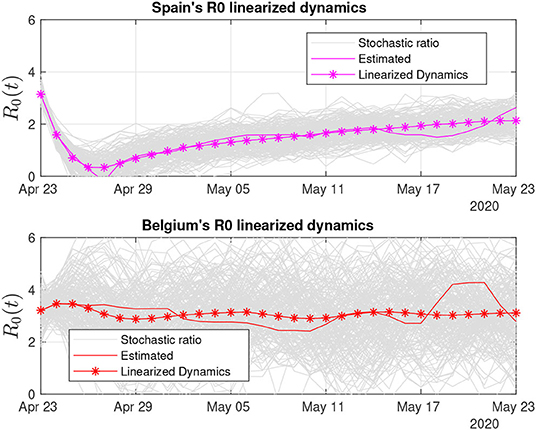
Figure 10. Thirty days of linearized R₀ dynamics for Spain and Belgium. Both countries exhibit high variability of the stochastic ratio, which is suggestive of problems with either data compilation or difficulties to stabilize the pandemic.

TABLE 2

Table 2. Pandemic's uncertainty (up to May 23, 2020).

Belgium's degree of uncertainty was the worst among all the countries, at least during the period we analyzed. One possible clue to understand why Belgium's stochastic ratio became so variable is to consider the impossibility to linearize its dynamics and the associated increase in error. However, our estimation procedure considers the error as Gaussian, and its mean value in fact approaches zero. Thus, the linearized estimate based on 30 days of data has a high probability to be close to the values shown.

Belgium has also shown an increased R₀ during the analyzed period. The low number of recoveries (see Table 1) influenced the frequency of removals and the basic reproduction number, which is the ratio between the frequency of infections and the frequency of removals (see Equation 23). Even though a recent report [54] proposed that Belgium's R₀ at the beginning of May 2020 was 0.8, according to our adaptive SIR-based R₀ estimations, the current situation in Belgium is uncertain with a probable R₀ close to 3.0, which is the mean value of 30 days of linearized dynamics (see Table 3).

TABLE 3

Table 3. R₀ estimates (on/up to May 23, 2020).

Figure 11 shows the trends for Argentina and New Zealand. The R₀ estimates for the two countries, which have the lowest number of infections of the group, suggest that several recent R₀ reports are considering a ratio solely based on the number of infections and population, without estimating and taking into account the frequency of removals, which makes R₀ increase.

FIGURE 11

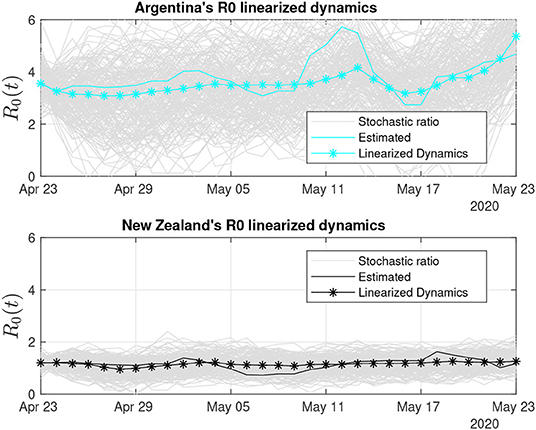
Figure 11. Thirty days of linearized R₀ dynamics for Argentina and New Zealand. New Zealand has been able to control its COVID-19 infection rate, which is reflected on the low variability of the stochastic ratio curve.

We compiled a table of the uncertainty of the estimated stochastic ratios by country (see Table 2), where the percentage of uncertainty is proportional to the linear power of the Gaussian estimation error. Table 3 shows the estimated R₀ estimates by country and demonstrates the usefulness of our approach to provide a real-time picture of the pandemic that can be used to support decision making.

4. Discussion

Almost 2 months after the WHO declared COVID-19 a global pandemic, health complications due to SARS-CoV-2 have caused many deaths and upended the routines of billions of people around the world. Research efforts for the development of a vaccine are being accelerated, but it is still a distant target [55]. At this moment, however, the most effective interventions are NPIs aimed at reducing SARS-CoV-2 transmission rates in order to increase the fraction of severe cases having access to scarce medical resources, such as mechanical ventilation [56].

Mathematical modeling is a valuable instrument to gauge the epidemics' dynamics and evaluate the effects of interventions aimed to control its spread. A crucial parameter is R₀, the basic reproduction number, which is closely followed by health officials and the public alike. As the world hopefully transitions to a gradual release from social distancing measures, many questions still remain about the SARS-CoV-2 virus, and there is all but the inevitability of secondary waves of infection ahead. Thus, the continuing use of mathematical models to track the disease will remain a necessity. However, the utility of models depends on the quality of the data they are fed, and there are many uncertainties regarding publicly available data on COVID-19 cases. For instance, due to the lack of widespread testing and subnotifications on the cause of deaths due to the disease, it is almost impossible to have a definitive picture of transitions between the compartments used to model the disease. Thus, in this work, we provide a system that takes into consideration the degree of uncertainty of the results presented by epidemiological SIR-type models.

The NPIs aimed to control the spread of the COVID-19 pandemic are implemented in a way similar to feedback control systems, with health authorities implementing social restriction measures in response to real-time evaluation of the number of infected and removed cases. Therefore, as in control systems, we are interfering with COVID-19's dynamics, affecting its behavior and parameters, and even discussing the development of real-time monitoring techniques using automation and control systems technologies. However, such closed-loop, control systems still need humans in the loop, and some data annotation mistakes may occur, such as seasonal dynamic changes related to workers shifts, weekend reduced reports, and even possible data manipulation of the data log may compromise the stability of estimators.

We showed that the RLS algorithm performed a better estimation job than the LMS algorithm in the present work, both in speed and accuracy. Real-time parametric estimation techniques, such as RLS, are widely used in the automation and aerospace industries to support adaptive control systems and state estimators. In automation applications, the RLS and LMS estimators are in fact divided into two different technologies, respectively, self-tuning and autotuning [31], where the first refers to real-time online adaptive process and the second involves the following steps: on-demand user request, acquiring the data set with sufficient samples, run offline processing without time constraints, present the results to the user, and decide whether to deploy or not the parametric update. Autotuning is less costlier to implement and thus more common, whereas the self-tuning technology requires online real-time processing with time constraints and is more commonly applied in the aerospace industry [31, 57].

LSA-based estimation is becoming more popular in industrial settings, such as in single-input, single-output (SISO) systems and in MIMO systems; in linear and non-linear system identification; and in polynomial and state-space MIMO system realizations [58, 59]. Such an increase in the use of RLS for real-time applications is justified by the advances of microprocessors to cope with the time constraints of fast dynamical systems, where the sampling interval can go as short as a few nanoseconds. Modern engineering applications with great impact in our society are associated with discrete-time sampled systems and signals, thus requiring adequate and reliable digital estimation algorithms, such as LSA. At least from an engineering viewpoint, the COVID-19's pandemic is also a discrete-time system, since the publicly available data for infections, deaths, and recoveries are updated on a daily basis, thus generating discrete-time sequences with the sampling period of 24 h.

During the COVID-19 pandemic, the scientific community is struggling to study, design, and deploy engineering applications to better assist society with information that could somehow quantify the pandemic's degree of severity based on R₀(t) estimates [60]. Different from traditional modeling approaches, we propose a discrete-time MIMO system realization instead of the continuous-time estimation using ordinary differential equations; the MIMO-based parametric estimation of R₀(t) is obtained through data fusion in a closed-loop estimation arrangement (see Figure 3).

The innovation of our modeling approach is the use of a discrete-time MIMO setup based on sensor fusion, a well-established strategy employed in the design of aerospace navigation systems under the assumption that “one always gains by adding a new measurement in terms of navigation error, and this no matter how bad the additional measurement is” [39, Remark 4.8]. Thus, by fusing data from the number of susceptibles, infections, recoveries, deaths, and individual parameters of the three coupled dynamical equations instead of a single one based solely on infections, the chance of having a better estimate of R₀(t) in the maximum-likelihood sense is higher. Of course, the drawback of our proposed approach is the impossibility to apply it to nations lacking public reports on death and recovery numbers.

Our comparative approach shows that the strict measures adopted by some countries, such as Germany, Italy, Spain, and New Zealand, managed to stabilize the epidemics. In others, such as the United States and Brazil, the delay in adopting such measures and lack of coordination proved decisive to keep the R₀ values high and with a high degree of uncertainty. The real-time estimation of model parameters such as R₀ provides important insight into the underlying epidemic process and provides robustness in the face of imperfect data. This strategy can be eventually implemented as an online tracking application providing information about the dynamics of the pandemic to health officials and the public at large.

Data Availability Statement

The data sets analyzed for this study can be found in the COVID-19 data repository from The Center for Systems Science and Engineering of the Johns Hopkins University (JSU CCSE) [40, 41].

Author Contributions

AS and AP conceived and wrote the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

The fund was Supported by CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico), under Grant No. 408559/2016-0 and Universidade Federal do Pará.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. WHO Announces COVID-19 Outbreak a Pandemic. Available online at: http://www.euro.who.int/en/health-topics/health-emergencies/coronavirus-covid-19/news/news/2020/3/who-announces-covid-19-outbreak-a-pandemic (accessed May 18, 2020).

Google Scholar

2. Zhu N, Zhang D, Wang W, Li X, Yang B, Song J, et al. A novel coronavirus from patients with pneumonia in China 2019. N Engl J Med. (2020) 382:727–33. doi: 10.1056/NEJMoa2001017

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Global Situation Report No. 118. Available online at: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200517-covid-19-sitrep-118.pdf?sfvrsn=21c0dafe_6 (accessed May 18, 2020).

Google Scholar

4. Lauer SA, Grantz KH, Bi Q, Jones FK, Zheng Q, Meredith HR, et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med. (2020) 172:577. doi: 10.7326/M20-0504

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Arons MM, Hatfield KM, Reddy SC, Kimball A, James A, Jacobs JR, et al. Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N Engl J Med. (2020) 382:2081–90. doi: 10.1056/NEJMoa2008457

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Gandhi M, Yokoe DS, Havlir DV. Asymptomatic transmission the Achilles' Heel of current strategies to control Covid-19. N Engl J Med. (2020) 382:2158–60. doi: 10.1056/NEJMe2009758

PubMed Abstract | CrossRef Full Text | Google Scholar

7. El-Sadr WM, Justman J. Africa in the Path of Covid-19. N Engl J Med. (2020) 382:e11. doi: 10.1056/NEJMp2008193

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kirby T. South America prepares for the impact of COVID-19. Lancet Respir Med. (2020) 8:551–2. doi: 10.1016/S2213-2600(20)30218-6

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Anderson RM, Heesterbeek H, Klinkenberg D, Hollingsworth TD. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. (2020) 395:931–4. doi: 10.1016/S0140-6736(20)30567-5

PubMed Abstract | CrossRef Full Text | Google Scholar

10. West R, Michie S, Rubin GJ, Amlôt R. Applying principles of behaviour change to reduce SARS-CoV-2 transmission. Nat Hum Behav. (2020) 4:451–9. doi: 10.1038/s41562-020-0887-9

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Torales J, O'Higgins M, Castaldelli-Maia JM, Ventriglio A. The outbreak of COVID-19 coronavirus and its impact on global mental health. Int J Soc Psychiatry. (2020) 66:317–20. doi: 10.1177/0020764020915212

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Xu S, Li Y. Beware of the second wave of COVID-19. Lancet. (2020) 395:1321–2. doi: 10.1016/S0140-6736(20)30845-X

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ferguson NM, Cummings DAT, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. (2006) 442:448–52. doi: 10.1038/nature04795

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chowell G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: a primer for parameter uncertainty identifiability, and forecasts. Infect Dis Model. (2017) 2:379–98. doi: 10.1016/j.idm.2017.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

15. M'Kendrick AG. Applications of mathematics to medical problems. Proc Edinb Math Soc. (1925) 44:98–130. doi: 10.1017/S0013091500034428

CrossRef Full Text | Google Scholar

16. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond A Math Phys Eng Sci. (1927) 115:700–21. doi: 10.1098/rspa.1927.0118

CrossRef Full Text | Google Scholar

17. Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science. (2020) 368:489–93. doi: 10.1126/science.abb3221

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Weitz JS, Beckett SJ, Coenen AR, Demory D, Dominguez-Mirazo M, Dushoff J, et al. Modeling shield immunity to reduce COVID-19 epidemic spread. Nat Med. (2020) 26:849–54. doi: 10.1038/s41591-020-0895-3

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Viceconte G, Petrosillo N. COVID-19 R0: magic number or conundrum? Infect Dis Rep. (2020) 12:8516. doi: 10.4081/idr.2020.8516

CrossRef Full Text | Google Scholar

20. Ridenhour B, Kowalik JM, Shay DK. Unraveling R0: considerations for public health applications. Am J Publ Health. (2014) 104:e32–41. doi: 10.2105/AJPH.2013.301704

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Riley S. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science. (2003) 300:1961–6. doi: 10.1126/science.1086478

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH. Complexity of the basic reproduction number (R0). Emerg Infect Dis. (2019) 25:1–4. doi: 10.3201/eid2501.171901

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Obadia T, Haneef R, Boëlle PY. The R0 package: a toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med Inform Decis Mak. (2012) 12:147. doi: 10.1186/1472-6947-12-147

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Bettencourt LMA, Ribeiro RM. Real time bayesian estimation of the epidemic potential of emerging infectious diseases. PLoS ONE. (2008) 3:e2185. doi: 10.1371/journal.pone.0002185

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wallinga J. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. (2004) 160:509–16. doi: 10.1093/aje/kwh255

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cauchemez S, Boëlle PY, Donnelly CA, Ferguson NM, Thomas G, Leung GM, et al. Real-time estimates in early detection of SARS. Emerg Infect Dis. (2012) 12:110–3. doi: 10.3201/eid1201.050593

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Cauchemez S, Boëlle P, Thomas G, Valleron A. Estimating in real time the efficacy of measures to control emerging communicable diseases. Am J Epidemiol. (2006) 164:591–7. doi: 10.1093/aje/kwj274

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Moghadas SM, Shoukat A, Fitzpatrick MC, Wells CR, Sah P, Pandey A, et al. Projecting hospital utilization during the COVID-19 outbreaks in the United States. Proc Natl Acad Sci USA. (2020) 117:9122–6. doi: 10.1073/pnas.2004064117

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Binny RN, Hendy SC, James A, Lustig A, Plank MJ, Steyn N. Effect of Alert Level 4 on effective reproduction number: review of international COVID-19 cases. medRxiv. (2020). doi: 10.1101/2020.04.30.20086934

CrossRef Full Text | Google Scholar

30. Nievergelt Y. A tutorial history of least squares with applications to astronomy and geodesy. J Comput Appl Math. (2000) 121:37–72. doi: 10.1016/S0377-0427(00)00343-5

CrossRef Full Text | Google Scholar

31. Astrom KJ, Wittenmark B. Adaptive Control. 2nd ed. Mineola, NY: Dover Publications (2008).

Google Scholar

32. Brunton SL, Kutz JN. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control. Cambridge: Cambridge University Press (2019).

Google Scholar

33. Smirnova A, Chowell G. A primer on stable parameter estimation and forecasting in epidemiology by a problem-oriented regularized least squares algorithm. Infect Dis Model. (2017) 2:268–75. doi: 10.1016/j.idm.2017.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Banks HT, Hu S, Thompson WC. Modeling and Inverse Problems in the Presence of Uncertainty. Boca Raton, FL: CRC Press (2014).

Google Scholar

35. Shen J. A Recursive bifurcation model for predicting the peak of COVID-19 virus spread in United States and Germany. medRxiv [Preprint]. doi: 10.1101/2020.04.09.20059329

CrossRef Full Text | Google Scholar

36. Lewis FL, Xie L, Popa D. Optimal and Robust Estimation. 2nd ed. Boca Raton, FL: CRC Press; Taylor & Francis Group (2008).

Google Scholar

37. Park G, Choi SB. An integrated observer for real-time estimation of vehicle center of gravity height. IEEE Trans Intell Transport Syst. (2020) 1–12. doi: 10.1109/TITS.2020.2988508

CrossRef Full Text | Google Scholar

38. Jaros R, Martinek R, Kahankova R, Koziorek J. Novel hybrid extraction systems for fetal heart rate variability monitoring based on non-invasive fetal electrocardiogram. IEEE Access. (2019) 7:131758–84. doi: 10.1109/ACCESS.2019.2933717

CrossRef Full Text | Google Scholar

39. Kabamba PT, Girard AR. Fundamentals of Aerospace Navigation and Guidance. Cambridge Aerospace Series. Cambridge: Cambridge University Press (2014).

Google Scholar

40. Novel Coronavirus (COVID-19) Cases Data–Humanitarian Data Exchange. Available online at: https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases (accessed May 8, 2020).

Google Scholar

41. CSSEGIS and Data/COVID-19. Available online at: https://github.com/CSSEGISandData/COVID-19 (accessed May 8, 2020).

Google Scholar

42. Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxford University Press (1992).

Google Scholar

43. Brauer F, Castillo-Chavez C. Epidemic models. In: Texts in Applied Mathematics. New York, NY: Springer New York (2011). p. 345–409. doi: 10.1007/978-1-4614-1686-9_9

CrossRef Full Text | Google Scholar

44. Roda WC, Varughese MB, Han D, Li MY. Why is it difficult to accurately predict the COVID-19 epidemic? Infect Dis Model. (2020) 5:271–81. doi: 10.1016/j.idm.2020.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Anderson RM, May RM. Population biology of infectious diseases: part I. Nature. (1979) 280:361–7.

Google Scholar

46. Brauer F, Feng Z, Castillo-Chavez C. Discrete epidemic models. Math Biosci Eng. (2010) 7:1–15. doi: 10.3934/mbe.2010.7.1

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Gómez S, Arenas A, Borge-Holthoefer J, Meloni S, Moreno Y. Discrete-time Markov chain approach to contact-based disease spreading in complex networks. Europhys Lett. (2010) 89:38009. doi: 10.1209/0295-5075/89/38009

CrossRef Full Text | Google Scholar

48. RKI–Coronavirus SARS-CoV-2–Aktueller Lage-/Situationsbericht des RKI zu COVID-19. Available online at: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Gesamt.html (accessed May 6, 2020).

Google Scholar

49. Kevin Systrom. Available online at: http://systrom.com/blog/author/ksys1983/ (accessed May 4, 2020).

Google Scholar

50. Coronavirus Flares as States and Countries Ease Social Distancing Guidelines. Available online at: https://www.washingtonpost.com/national-security/coronavirus-flares-as-states-and-countries-ease-social-distancing-guidelines/2020/05/09/cccb3c0c-9219-11ea-9e23-6914ee410a5f_story.html (accessed May 17, 2020).

Google Scholar

51. Filho RL, Lichtenthaler DG. A dynamic model for Covid-19 in Brazil. medRxiv. (2020). doi: 10.1101/2020.05.10.20097550

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Brazil Registers 888 New Deaths From Coronavirus; Total Number of Deaths Exceeds 18 Thousand. Available online at: https://www1.folha.uol.com.br/internacional/en/scienceandhealth/2020/05/brazil-registers-888-new-deaths-from-coronavirus-total-number-of-deaths-exceeds-18-thousand.shtml (accessed May 21, 2020).

Google Scholar

53. Brazil Once a Leader Struggles to Contain Virus Amid Political Turmoil. Available online at: https://www.nytimes.com/2020/05/16/world/americas/virus-brazil-deaths.html (accessed May 20, 2020).

Google Scholar

54. Basic Reproduction Number of Novel Coronavirus in Belgium Falls to 0.6. Available online at: https://www.vrt.be/vrtnws/en/2020/05/04/basic-reproduction-number-of-novel-coronavirus-in-belgium-falls/ (accessed May 22, 2020).

Google Scholar

55. Graham BS. Rapid COVID-19 vaccine development. Science. (2020) 368:945–6. doi: 10.1126/science.abb8923

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Emanuel EJ, Persad G, Upshur R, Thome B, Parker M, Glickman A, et al. Fair allocation of scarce medical resources in the time of Covid-19. N Engl J Med. (2020) 382:2049–55. doi: 10.1056/NEJMsb2005114

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Administrator N. Simplify, Simplify–Streamlined Adaptive System Works–Capabilities Verified. (2013). Available online at: http://www.nasa.gov/centers/dryden/news/X-Press/mrac.html

Google Scholar

58. Silveira A, Silva A, Coelho A, Real J, Silva O. Design and real-time implementation of a wireless autopilot using multivariable predictive generalized minimum variance control in the state-space. Aerosp Sci Technol. (2020) 105:106053. doi: 10.1016/j.ast.2020.106053

CrossRef Full Text | Google Scholar

59. Vicario F. OKID as a general approach to linear and bilinear system Identification (Ph.D. thesis), New York, NY: Columbia University (2014).

Google Scholar

60. Adam D. A guide to R-the pandemic's misunderstood metric. Nature. (2020) 5883:346–8. doi: 10.1038/d41586-020-02009-w

PubMed Abstract | CrossRef Full Text | Google Scholar