Recent Trends of Controlling Chaotic Resonance and Future Perspectives

1 Introduction

In a wide range of non-linear systems, it is known that additive stochastic noise and internal dynamical fluctuation enhance the ordering of spatio-temporal behaviors, such as the emergence of periodicity and synchronization (as reviewed in [1–6]). Among these phenomena, stochastic resonance is a phenomenon in which the effects of additive noise strengthen the signal response against weak input signals in the non-linear systems with a specific barrier or threshold [7–9] (as reviewed in [1,2,4,10,11]). Recent studies on stochastic resonance have been conducted considering various engineering applications, such as biomedical engineering [12,13], telecommunications [14], and memory storing mechanisms [15–17]. Considering the biological systems in particular, Kurita et al. developed a wearable device that enhances the tactile sensitivity of a surgeon’s hands by applying appropriate vibrations [12,13]. Enders et al. and Seo et al. demonstrated that applying vibrotactile noise in human sensory systems, as a rehabilitation method, improves the haptic sensations in patients with paralysis [18,19]. Van et al. showed that an optimal amount of noise applied using transcranial random noise stimulation as a non-invasive brain stimulation technique to the visual cortex enhances the accuracy of visual-perceptual decisions [20]. In telecommunication systems, Tadokoro et al. proposed a binary phase-shift keying (BPSK) receiver improved using an appropriate additive noise in terms of its bit error rate performance [14]. He et al. showed that in a wireless sensor network, an optimal noise may be used to enhance the sensitivity of a wireless signal for node positioning [21]. In memory storing systems, Ibanez et al. and Stotland et al. demonstrated that the presence of appropriate additive noise enhances the memory functions in memory elements with bi-stable oscillations, even under extremely low power consumption [15,16].

In addition to the additive stochastic noise, deterministic chaos also causes a phenomenon similar to stochastic resonance, which is known as chaotic resonance (as reviewed in [3,4,6]). Chaotic resonance is classified into two types; the first is chaotic resonance in excitable systems, which is typified as spiking neural systems [22–26] (as reviewed in [6]), and the second is systems with chaos-chaos intermittency (CCI), which is the behavior of intermittent transitions of chaotic orbits among separated attractors, such as in a cubic map [27,28], and neural systems [27,29–32]. In this perspective, we focus on the latter type of chaotic resonance. In the latter type, the signal response of chaotic resonance is maximized around the attractor-merging bifurcation for the emergence of CCI [3]. Previous studies have shown that the sensitivity of chaotic resonance is higher than that of stochastic resonance [30,32]. However, the engineering applications of chaotic resonance are limited.

There are two possible reasons for this limitation. First, the stochastic noise required to induce stochastic resonance can be easily controlled from outside of a stochastic resonance system. Conversely, in chaotic resonance, the attractor-merging bifurcation must be induced via the adjustment of internal system parameters [27,29,30]. In many cases, achieving this adjustment from outside of the system is difficult, particularly in biological systems. Second, chaotic resonance degrades owing to noise, which is generally inevitable in real-world systems. Herein, we summarize the recent findings and conceivable approaches to address the aforementioned difficulties, as well as introduce the findings of studies concerning chaotic resonance from the previous decade.

2 Mechanism for Attractor-Merging Bifurcation

Chaotic resonance emerges in systems with CCI behaviors. In this section, the mechanism for the emergence of CCI is reviewed using a cubic map (as reviewed in [3]):

$x\left(t+1\right)=F\left(x\left(t\right)\right),(1)$

$F\left(x\right)=\left(ax-x^3\right)\exp \left(-x^2/b\right),(2)$

where parameter b is set to 10.0 [33]. The top and middle sections of Figure 1 (a) show the dependence of system behaviors on the internal parameter a using the bifurcation diagram and attractor-merging condition F (f_max, min) − x_d [33] as a function of the internal system parameter a. Here, x_d indicates the attractor-separating point of the map function; a cubic map corresponds to x_d = 0. F_max, min exhibits local maximum and minimum values of the map function F at approximately x_d. The attractor-merging bifurcation can be detected by F (f_max, min) − x_d = 0. As a result, at a ≲ 2.84 and under the conditions of F (f_max) − x_d > 0 and F (f_min) − x_d < 0, the chaotic orbit is constrained in either the positive or negative x(t) regions depending on the initial value of x (0). By increasing internal system parameter a to a ≈ 2.84, the attractor-merging bifurcation F (f_max, min) − x_d = 0 emerges. Subsequently, x(t) fluctuates between positive and negative x(t) regions (CCI) under the conditions of F (f_max) − x_d < 0 and F (f_min) − x_d > 0 in a ≳ 2.84. As typical examples of the orbit x(t) and map function F, the bottom section of Figure 1 (a) shows a chaotic orbit constrained in either the positive or negative x(t) region at a = 2.75 for F (f_max) − x_d > 0 and F (f_min) − x_d < 0. Additionally, a chaotic orbit with CCI at a = 2.86 is shown for F (f_max) − x_d < 0 and F (f_min) − x_d > 0, as are the map functions of F. By increasing the value of a, the absolute values of the local maximum/minimum of the map function F increases, and the subsequent attractor-merging conditions are satisfied as F (f_max) − x_d < 0 and F (f_min) − x_d > 0. The mechanism that induces attractor-merging bifurcation is widely observed in chaotic systems [3,34], such as radio-physical oscillators [35], electrical circuits for Shinriki’s circuit [36,37], multilevel DC/DC converters [38], and neural systems for networks composed of excitatory and inhibitory neural populations [39,40], as well as memories embedded in chaotic neural networks [27].

FIGURE 1

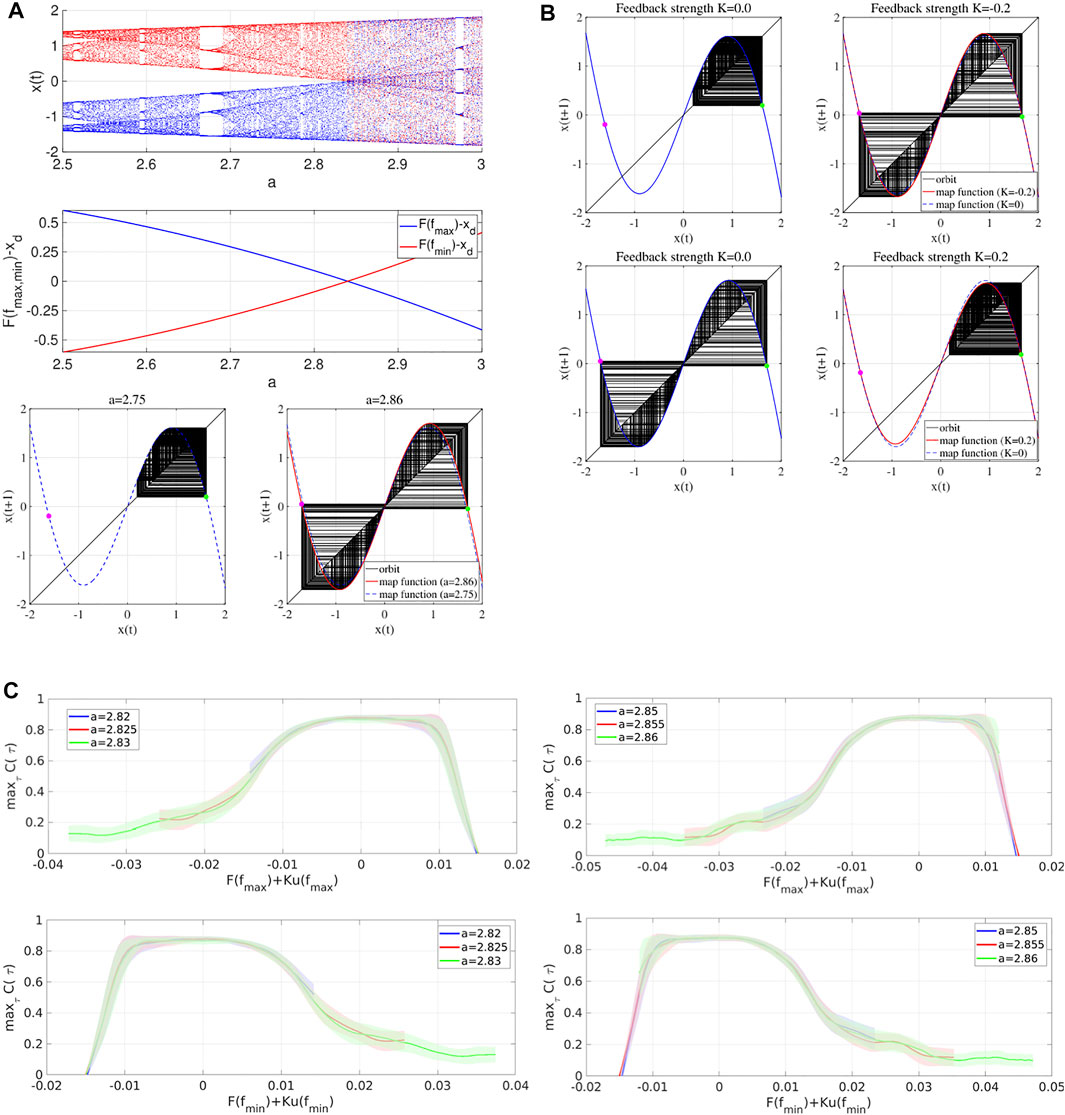
FIGURE 1. (A) Dependence of system behaviors on the internal parameter. The bifurcation diagram is shown as a function of the internal system parameter a. The red and blue dots indicate negative and positive x (0) cases (top part), respectively, and the attractor-merging condition F (f_max, min)− x_d is shown (middle part) (b =10, x_d =0). The orbit, map functions, and attractor-merging condition F (f_max, min)− x_d (indicated by magenta and green dots, respectively) are also shown (bottom part). (B) Attractor-merging and separating achieved by “reduced region of orbit” (RRO) feedback signals in a cubic map (b = 10, σ =0.6). The orbit, map functions, and attractor-merging condition F (f_max, min)+ Ku(f_max, min)− x_d (indicated by the magenta and green dots, respectively) under the attractor-separating condition (a =2.75, K =0) (left-hand side in the upper section) and those under the attractor-merging condition induced by the RRO feedback signal with a negative strength (K = −0.2) (right-hand side in the upper part) are shown. The orbit, map functions, and attractor-merging condition F (f_max, min) + Ku(f_max, min)− x_d under the attractor-merging condition of a = 2.86, K =0 (left-hand side in the bottom part), as well as those under the attractor-separating condition induced by an RRO feedback signal with a positive strength (K = 0.2) (right-hand side in the bottom part) are shown. (C) Ability of the signal response measured by the correlation coefficient max_τC(τ) as a function of the attractor-merging condition F (f_max, min) + Ku(f_max, min)− x_d in the case where attractor-merging is induced by the RRO feedback signal (a = 2.82, 2.825,2.83) (left side), and where attractor-separating is induced by the RRO feedback signal (a =2.85, 2.855,2.86) (right side). Solid line and shaded area represent the mean and standard deviation, respectively, among 10 trials with different initial x (0).

3 Feedback Control for Chaotic Resonance

The frequency of autonomous CCI is very low around the attractor-merging bifurcation, as shown in section 2; therefore, the external signals induce CCI even though the strength of the signals is weak. Consequently, the CCI synchronizes with the external signals, i.e., chaotic resonance appears (see [3,4,6]). Considering the transition of the system state to this bifurcation point, the internal system parameter must be adjusted (reviewed in [3,4,6]). However, in many systems, achieving this adjustment from the outside environment is difficult, particularly in biological systems. To overcome this difficulty, we proposed “reduced region of orbit” (RRO) feedback methods [33]. To demonstrate the effect of RRO feedback signals, the cubic map with an RRO feedback signal u is provided by

$x\left(t+1\right)=F\left(x\left(t\right)\right)+Ku\left(x\left(t\right)\right),(3)$

$u\left(x\right)=-\left(x-x_d\right)\exp \left(-{\left(x-x_d\right)}^2/\left(2{\sigma }^2\right)\right).(4)$

Here, K and σ are the strength of the RRO feedback signals and the parameter used for determining the range of the RRO feedback signal, respectively. In the upper part of Figure 1 (b), the mechanism of the RRO feedback methods is shown. Under the attractor-separating condition F (f_max) − x_d > 0, F (f_min) − x_d < 0, the RRO feedback signals with a negative strength increases the local maximum and minimum values of the map functions. Through this effect, the attractor-merging condition F (f_max) + Ku(f_max) − x_d < 0, F (f_min) + Ku(f_min) − x_d > 0 is induced through the attractor-merging bifurcation, and CCI subsequently emerges. Under the attractor-merging condition F (f_max) − x_d < 0, F (f_min) − x_d > 0, the RRO feedback signals with a positive strength reduce the local maximum and minimum values of the map functions. Due to this phenomenon, the attractor-separating condition F (f_max) + Ku(f_max) − x_d > 0, F (f_min) + Ku(f_min) − x_d < 0 is induced (see the lower section of Figure 1B).

In addition to the RRO feedback signal, the weak external signal S(t) = A sin (Ωt) (A = 0.005, Ω = 0.005) is applied [33]:

$x\left(t+1\right)=F\left(x\left(t\right)\right)+Ku\left(x\left(t\right)\right)+S\left(t\right).(5)$

To quantify this signal response, the correlation between x(t) and S(t), given by max_τC(τ) (τ: delay of signal response of x(t)), is utilized [31,33,41,42]. Figure 1C shows the ability of the signal response measured by max_τC(τ) as a function of the attractor-merging condition F (f_max, min) + Ku(f_max, min) − x_d in the case where attractor-merging is induced by the RRO feedback signal (a = 2.82, 2.825, 2.83) and in the case where attractor-separating is induced by the RRO feedback signal (a = 2.85, 2.855, 2.86). In both the cases, around the attractor-merging condition F (f_max, min) + Ku(f_max, min) − x_d = 0, the ability of signal response exhibits a unimodal maximum peak (the signal-to-noise ratio is widely utilized as the other index for determining the ability of signal response, [3]). This result demonstrates that the RRO feedback signal induces chaotic resonance by controlling the attractor-merging bifurcation. In addition, the RRO feedback signal realizes the induction of chaotic resonance in various types of chaotic systems, including the other cubic maps [33,42], neural systems composed of excitatory and inhibitory neurons [31,41], and continuous [6].

In the previous studies concerning the chaos controlling theory [43], chaotic behaviors, which are considered to degrade system performances, have been removed and transited to a fixed point and periodic state using several types of feedback signals, including the Ott-Grebogi-Yorke method [44], delayed feedback method [45–47], and extended delayed feedback method [48]. By comparison, the RRO feedback method adjusts the chaotic state to an appropriate state, i.e., the attractor-merging bifurcation point, while maintaining the chaotic behaviors. Therefore, this method is significantly different from other conventional chaos controlling methods. As an additional approach for controlling attractor-merging, additive stochastic noise has exhibited effects similar to RRO feedback signals with positive feedback strengths [3]. In our previous studies, the degree of synchronization between a weak input signal and CCI, as well as its sensitivity, were investigated in terms of chaotic resonance under noise [32,49]. The results showed that the degree of synchronization and the sensitivity of chaotic resonance induced by the RRO feedback signals are superior to those achieved using additive stochastic noise. This phenomenon occurred because stochastic noise acts to prevent synchronization via perturbations in addition to providing effects for attractor-merging [32,49]. Additionally, from the perspective of availability, additive stochastic is only utilized under attractor-separating conditions to induce the attractor-merging bifurcation, while RRO feedback signals can be applied to both attractor-separating and merging conditions to induce attractor-merging bifurcation (see Figure 1B) [32,49]. Therefore, the RRO feedback method also exhibits a higher applicability than the method using additive stochastic noise.

4 Influence of Noise for Chaotic Resonance

Considering that both background noise and errors in measurements used to estimate the RRO feedback strength exist in real-world situations, the influences of these factors on chaotic resonance are inevitable. In our recent study [50], two types of noise were assumed for the application of chaotic resonance, namely additive stochastic noise and contaminant noise due to background noise and measurement errors for the estimation of the RRO feedback signal. Here, we assumed that these types of noise are independent of each other. In the map function F for a non-linear system, the additive stochastic noise D_aξ(t) in the map function and the contaminant noise D_cη(t) in the RRO feedback signal u are applied as follows:

$x\left(t+1\right)=F\left(x\left(t\right)\right)+Ku\left(x\left(t\right)+D_c\eta \left(t\right)\right)+D_a\xi \left(t\right),(6)$

$u\left(x\right)=-\left(x-x_d\right)\exp \left(-{\left(x-x_d\right)}^2/\left(2{\sigma }^2\right)\right).(7)$

Here, ξ and η represent Gaussian white noise, while D_a and D_c are the noise strengths for the additive stochastic noise and contaminant noise, respectively. Under the noise-free condition, the frequency of autonomous CCI around the attractor-merging bifurcation where chaotic resonance arises is considerably low [33]. The application of external noise with a relatively weak strength to the system with this low autonomous CCI acts as a perturbation for inducing exogenous CCI. Therefore, both noises increase the CCI frequency. This perturbation that is unrelated to the input signal degrades the degree of synchronization in chaotic resonance [32,41,50,51]. Conversely, under the influence of external noise with greater noise strength, two types of noise result in different CCI tendencies. In the case with additive stochastic noise, the CCI frequency increases with increasing noise strength, as is observed in the case with relatively weak noise strength. In the case with contaminant noise, although low noise strength results in a similar tendency for increasing the CCI, a contaminant noise with greater strength diminishes the profile the RRO feedback function u to induce attractor-merging bifurcation [41,50,51]. Consequently, both noises significantly degrade the occurrence of chaotic resonance induced by the RRO feedback signals. The application of chaotic resonance induced by RRO feedback methods is currently being investigated, especially in the biomedical field, such as a novel approach for neurofeedback to stabilize abnormal circadian rhythms in bipolar disorder [41] and frontal neural activity in attention-deficit hyperactivity disorder [51]. In these applications, the significant difference between the influence of chaotic resonance toward additive and contaminant noise may become important. Additionally, our recent study demonstrated that although the RRO feedback method cannot be applied in strongly noisy conditions [41,51], attractor-merging controlling achieved by additive and contaminant noise may be applied instead of RRO feedback methods [31,50]. Therefore, according to noise strength, choosing an appropriate method for attractor-merging control is crucial for chaotic resonance applications. Additionally, in the case where several types of noise are dependent on each other, the complex characteristic of signal response might depend considerably on the noise strength compared to the case where different types of noise are independent of each other; therefore, this case should be investigated in detail in a future study for efficient application of chaotic resonance and stochastic resonance.

5 Conclusion

In this perspective, based on the recent trends of studies concerning chaotic resonance, we reviewed the RRO feedback method as a new approach to induce chaotic resonance from the outside of a system. Our previously proposed RRO feedback method is currently being investigated for use in biomedical research, and has been typified as neurofeedback-optimized chaotic resonance induced by the RRO feedback method [41,51]. Therefore, although several issues in chaotic resonance remain, we believe that the RRO feedback method provides a novel approach for chaotic resonance applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SN. drafted the main manuscript text and prepared all figures. SN, HN, NW, KI, and TY. discussed the review of chaotic resonance. SN and TT. discussed the clinical applications of chaotic resonance. All authors reviewed and approved the final version of the manuscript.

Funding

This work was supported by the Kayamori Foundation of Informational Science Advancement (grant number, K32-XXV-571) (SN) and by JSPS KAKENHI for the Grant-in-Aid for Scientific Research (C) (grant number, 20K11976) (HN) and (grant number, 18K11450) (TY). It was partially supported by JST CREST (grant number JPMJCR17A4).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Harmer, GP, Davis, BR, and Abbott, D. A Review of Stochastic Resonance: Circuits and Measurement. IEEE Trans Instrum Meas (2002) 51:299–309. doi:10.1109/19.997828

CrossRef Full Text | Google Scholar

2. Pikovsky, A, Rosenblum, M, and Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences, 12. Germany: Cambridge University Press (2003).

Google Scholar

3. Anishchenko, VS, Astakhov, V, Neiman, A, Vadivasova, T, and Schimansky-Geier, L. Nonlinear Dynamics of Chaotic and Stochastic Systems: Tutorial and Modern Developments. Springer Science & Business Media (2007).

Google Scholar

4. Rajasekar, S, and Sanjuán, MAF. Nonlinear Resonances. Cham:Springer (2016).

Google Scholar

5. Strogatz, SH. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology. Chemistry, and Engineering. London; New York: CRC Press (2018).

Google Scholar

6. Nobukawa, S, and Nishimura, H. Synchronization of Chaos in Neural Systems. Front Appl Math Stat (2020) 6:19. doi:10.3389/fams.2020.00019

CrossRef Full Text | Google Scholar

7. Benzi, R, Sutera, A, and Vulpiani, A. The Mechanism of Stochastic Resonance. J Phys A: Math Gen (1981) 14:L453–L457. doi:10.1088/0305-4470/14/11/006

CrossRef Full Text | Google Scholar

8. Nobukawa, S, Hashimoto, R, Nishimura, H, Yamanishi, T, and Chiba, M. Noise-induced Phenomena in the Kaldor Business Cycle Model. Trans ISCIE (2017) 30:459–66. doi:10.5687/iscie.30.459

CrossRef Full Text | Google Scholar

9. Nobukawa, S, and Nishimura, H. Enhancement of Spike-timing-dependent Plasticity in Spiking Neural Systems with Noise. Int J Neur Syst (2016) 26:1550040. doi:10.1142/s0129065715500409

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gammaitoni, L, Hänggi, P, Jung, P, and Marchesoni, F. Stochastic Resonance. Rev Mod Phys (1998) 70:223–87. doi:10.1103/revmodphys.70.223

CrossRef Full Text | Google Scholar

11. Moss, F, Ward, LM, and Sannita, WG. Stochastic Resonance and Sensory Information Processing: a Tutorial and Review of Application. Clin Neurophysiol (2004) 115:267–81. doi:10.1016/j.clinph.2003.09.014

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kurita, Y, Shinohara, M, and Ueda, J. Wearable Sensorimotor Enhancer for Fingertip Based on Stochastic Resonance Effect. IEEE Trans Human-mach Syst (2013) 43:333–7. doi:10.1109/tsmc.2013.2242886

CrossRef Full Text | Google Scholar

13. Kurita, Y, Sueda, Y, Ishikawa, T, Hattori, M, Sawada, H, Egi, H, et al. Surgical Grasping Forceps with Enhanced Sensorimotor Capability via the Stochastic Resonance Effect. Ieee/asme Trans Mechatron (2016) 21:2624–34. doi:10.1109/tmech.2016.2591591

CrossRef Full Text | Google Scholar

14. Tadokoro, Y, Tanaka, H, Nakashima, Y, Yamazato, T, and Arai, S. Enhancing a Bpsk Receiver by Employing a Practical Parallel Network with Stochastic Resonance. Nolta (2019) 10:106–14. doi:10.1587/nolta.10.106

CrossRef Full Text | Google Scholar

15. Ibáñez, S, Fierens, P, Perazzo, R, Patterson, G, and Grosz, D. On the Dynamics of a Single-Bit Stochastic-Resonance Memory Device. The Eur Phys J B (2010) 76:49–55. doi:10.1140/epjb/e2010-00180-8

CrossRef Full Text | Google Scholar

16. Stotland, A, and Di Ventra, M. Stochastic Memory: Memory Enhancement Due to Noise. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:011116. doi:10.1103/PhysRevE.85.011116

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Duan, L, Duan, F, Chapeau-Blondeau, F, and Abbott, D. Stochastic Resonance in Hopfield Neural Networks for Transmitting Binary Signals. Phys Lett A (2020) 384:126143. doi:10.1016/j.physleta.2019.126143

CrossRef Full Text | Google Scholar

18. Enders, LR, Hur, P, Johnson, MJ, and Seo, N. Remote Vibrotactile Noise Improves Light Touch Sensation in Stroke Survivors' Fingertips via Stochastic Resonance. J neuroengineering Rehabil (2013) 10:105. doi:10.1186/1743-0003-10-105

CrossRef Full Text | Google Scholar

19. Seo, NJ, Kosmopoulos, ML, Enders, LR, and Hur, P. Effect of Remote Sensory Noise on Hand Function post Stroke. Front Hum Neurosci (2014) 8:934. doi:10.3389/fnhum.2014.00934

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Van der Groen, O, Tang, MF, Wenderoth, N, and Mattingley, JB. Stochastic Resonance Enhances the Rate of Evidence Accumulation during Combined Brain Stimulation and Perceptual Decision-Making. Plos Comput Biol (2018) 14:e1006301. doi:10.1371/journal.pcbi.1006301

PubMed Abstract | CrossRef Full Text | Google Scholar

21. He, D. A Novel Wireless Sensor Networks Multilateration Positioning Method Based on Quartic Double-Well Bistable Stochastic Resonance Technique. Nolta (2017) 8:49–57. doi:10.1587/nolta.8.49

CrossRef Full Text | Google Scholar

22. Schweighofer, N, Doya, K, Fukai, H, Chiron, JV, Furukawa, T, and Kawato, M. Chaos May Enhance Information Transmission in the Inferior Olive. Proc Natl Acad Sci (2004) 101:4655–60. doi:10.1073/pnas.0305966101

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tokuda, IT, Han, CE, Aihara, K, Kawato, M, and Schweighofer, N. The Role of Chaotic Resonance in Cerebellar Learning. Neural Networks (2010) 23:836–42. doi:10.1016/j.neunet.2010.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Nobukawa, S, Nishimura, H, Yamanishi, T, and Liu, J-Q. Analysis of Chaotic Resonance in Izhikevich Neuron Model. PLoS One (2015) 10:e0138919. doi:10.1371/journal.pone.0138919

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Nobukawa, S, and Nishimura, H. Chaotic Resonance in Coupled Inferior Olive Neurons with the Llinás Approach Neuron Model. Neural Comput (2016) 28:2505–32. doi:10.1162/neco_a_00894

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Nobukawa, S, Nishimura, H, and Yamanishi, T. Chaotic Resonance in Typical Routes to Chaos in the Izhikevich Neuron Model. Sci Rep (2017) 7:1331–9. doi:10.1038/s41598-017-01511-y

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Nobukawa, S, Nishimura, H, and Yamanishi, T. Evaluation of Chaotic Resonance by Lyapunov Exponent in Attractor-Merging Type Systems. In: International Conference on Neural Information Processing. Cham: Springer (2016). p. 430–7. doi:10.1007/978-3-319-46687-3_48

CrossRef Full Text | Google Scholar

28. Nobukawa, S, Doho, H, Shibata, N, Nishimura, H, and Yamanishi, T. Chaos-Chaos Intermittency Synchronization Controlled by External Feedback Signals in Chua's Circuits. IEICE Trans Fundamentals (2020) E103.A:303–12. doi:10.1587/transfun.2019eap1081

CrossRef Full Text | Google Scholar

29. Sinha, S, and Chakrabarti, BK. Deterministic Stochastic Resonance in a Piecewise Linear Chaotic Map. Phys Rev E (1998) 58:8009–12. doi:10.1103/physreve.58.8009

CrossRef Full Text | Google Scholar

30. Nishimura, H, Katada, N, and Aihara, K. Coherent Response in a Chaotic Neural Network. Neural Process Lett (2000) 12:49–58. doi:10.1023/a:1009626028831

CrossRef Full Text | Google Scholar

31. Nobukawa, S, and Shibata, N. Controlling Chaotic Resonance Using External Feedback Signals in Neural Systems. Sci Rep (2019) 9:4990. doi:10.1038/s41598-019-41535-0

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Nobukawa, S, Shibata, N, Nishimura, H, Doho, H, Wagatsuma, N, and Yamanishi, T. Resonance Phenomena Controlled by External Feedback Signals and Additive Noise in Neural Systems. Sci Rep (2019) 9:12630–15. doi:10.1038/s41598-019-48950-3

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Nobukawa, S, Nishimura, H, Yamanishi, T, and Doho, H. Controlling Chaotic Resonance in Systems with Chaos-Chaos Intermittency Using External Feedback. IEICE Trans Fundamentals (2018) E101.A:1900–6. doi:10.1587/transfun.e101.a.1900

CrossRef Full Text | Google Scholar

34. Brezetskyi, S, Dudkowski, D, and Kapitaniak, T. Rare and hidden attractors in van der pol-duffing oscillators. Eur Phys J Spec Top (2015) 224:1459–67. doi:10.1140/epjst/e2015-02471-2

CrossRef Full Text | Google Scholar

35. Kuznetsov, AP, Kuznetsov, SP, Mosekilde, E, and Stankevich, NV. Co-existing Hidden Attractors in a Radio-Physical Oscillator System. J Phys A: Math Theor (2015) 48:125101. doi:10.1088/1751-8113/48/12/125101

CrossRef Full Text | Google Scholar

36. Werner, JP, Stemler, T, and Benner, H. Crisis and Stochastic Resonance in Shinriki's Circuit. Physica D: Nonlinear Phenomena (2008) 237:859–65. doi:10.1016/j.physd.2007.11.009

CrossRef Full Text | Google Scholar

37. Stankevich, NV, Kuznetsov, NV, Leonov, GA, and Chua, LO. Scenario of the Birth of Hidden Attractors in the Chua Circuit. Int J Bifurcation Chaos (2017) 27:1730038. doi:10.1142/s0218127417300385

CrossRef Full Text | Google Scholar

38. Zhusubaliyev, ZT, and Mosekilde, E. Multistability and Hidden Attractors in a Multilevel DC/DC Converter. Mathematics Comput Simulation (2015) 109:32–45. doi:10.1016/j.matcom.2014.08.001

CrossRef Full Text | Google Scholar

39. Sinha, S. Noise-free Stochastic Resonance in Simple Chaotic Systems. Physica A: Stat Mech its Appl (1999) 270:204–14. doi:10.1016/s0378-4371(99)00136-3

CrossRef Full Text | Google Scholar

40. Baghdadi, G, Jafari, S, Sprott, JC, Towhidkhah, F, and Hashemi Golpayegani, MR. A Chaotic Model of Sustaining Attention Problem in Attention Deficit Disorder. Commun Nonlinear Sci Numer Simulation (2015) 20:174–85. doi:10.1016/j.cnsns.2014.05.015

CrossRef Full Text | Google Scholar

41. Doho, H, Nobukawa, S, Nishimura, H, Wagatsuma, N, and Takahashi, T. Transition of Neural Activity from the Chaotic Bipolar-Disorder State to the Periodic Healthy State Using External Feedback Signals. Front Comput Neurosci (2020) 14:76. doi:10.3389/fncom.2020.00076

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Nobukawa, S, Wagatsuma, N, Nishimura, H, Inagaki, K, and Yamanishi, T. Novel Approach for Memory Storage Systems with Chaos-Chaos Intermittency. In: The International Conference On Emerging Techniques In Computational Intelligence. Hyderabad: IEEE (2021). doi:10.1109/icetci51973.2021.9574056

CrossRef Full Text | Google Scholar

43. Schöll, E, and Schuster, HG. Handbook of Chaos Control, 2. Weinheim: Wiley Online Library (2008).

Google Scholar

44. Ott, E, Grebogi, C, and Yorke, JA. Controlling Chaos. Phys Rev Lett (1990) 64:1196–9. doi:10.1103/physrevlett.64.1196

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Pyragas, K. Continuous Control of Chaos by Self-Controlling Feedback. Phys Lett A (1992) 170:421–8. doi:10.1016/0375-9601(92)90745-8

CrossRef Full Text | Google Scholar

46. Nakajima, H. On Analytical Properties of Delayed Feedback Control of Chaos. Phys Lett A (1997) 232:207–10. doi:10.1016/s0375-9601(97)00362-9

CrossRef Full Text | Google Scholar

47. Nobukawa, S, Nishimura, H, Doho, H, and Takahashi, T. Stabilizing Circadian Rhythms in Bipolar Disorder by Chaos Control Methods. Front Appl Math Stat (2020) 6:562929. doi:10.3389/fams.2020.562929

CrossRef Full Text | Google Scholar

48. Pyragas, K. Control of Chaos via an Unstable Delayed Feedback Controller. Phys Rev Lett (2001) 86:2265–8. doi:10.1103/physrevlett.86.2265

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Shibata, N, and Nobukawa, S (2020). Synchronization of Chaos-Chaos Intermittency Controlled by External Feedback and Stochastic Noise, Stochastic Systems Theory and its Applications (SSS). In Proceedings of the ISCIE International Symposium on Stochastic Systems Theory and its Applications (The ISCIE Symposium on Stochastic Systems Theory and Its Applications), Fukushima, November 1–2, 2019, 2020, 17–22. doi:10.5687/sss.2020.17

CrossRef Full Text | Google Scholar

50. Nobukawa, S, Wagatsuma, N, Nishimura, H, Inagaki, K, and Yamanishi, T. Evaluation of Ability of Chaotic Resonance under Noises in Neural Systems Comprising Excitatory-Inhibitory Neurons. In: 2021 IEEE International Conference on Systems, Man, and Cybernetics. Melbourne: IEEE (2021). p. 2189–94.

Google Scholar

51. Nobukawa, S, Wagatsuma, N, Nishimura, H, Doho, H, and Takahashi, T. An Approach for Stabilizing Abnormal Neural Activity in ADHD Using Chaotic Resonance. Front Comput Neurosci (2021) 15:726641. doi:10.3389/fncom.2021.726641

PubMed Abstract | CrossRef Full Text | Google Scholar