- 1School of Mathematics and Statistics, North China University of Water Resources and Electric Power, Zhengzhou, China
- 2School of Information Engineering, North China University of Water Resources and Electric Power, Zhengzhou, China
This study premeditated the synchronization of two fractional-order chaotic systems (FOCSs) with uncertainties and external disturbances. We utilized fuzzy logic systems (FLSs) to estimate unknown nonlinearities, and implemented disturbance observers to estimate unknown bounded external disturbances. Then, a robust control term was devised to compensate for the unavoidable approximation error of the fuzzy system. In addition, a sliding mode surface was devised to construct an adaptive fuzzy sliding mode controller (AFSMC) that can guarantee that the synchronization error converges to a small neighborhood of zero. Finally, the validity of the proposed control strategy was verified via a numerical simulation.
1. Introduction
Fractional calculus has been developing for over three centuries, which is seen as an extension of ordinary calculus. It plays an important role in dealing with non-integer order systems, which have caught the attention of several scholars owing to its fascinating properties and potential application values. Over the past few decades, it has been discovered that, in some actual systems related to time series, compared with integer order systems, fractional order nonlinear systems (FONSs) have better modeling accuracy due to their memory and inheritance, such as financial systems [1], viscoelastic systems [2], dielectric polarization [3], and electrode-electrolyte polarization [4, 5].
Recently, some studies indicated that a considerable number of FONSs behave in chaotic phenomena, which is a nonlinearity with complexity, randomness, unpredictability, and extreme sensitivity to initial values [6–9] and has a great application value in secure communication [10], signal processing, mathematics, biology, machinery [8], etc. Therefore, many scholars conducted extensive and in-depth research on the control and synchronization of fractional order chaotic systems (FOCSs). Zhu et al. [11] proposed a one-way coupling means using a coupling matrix to discuss the synchronous control of the fractional-order Chua's system. Lu [12] adopted a scalar transmission signal to achieve the synchronization of FOCSs that does not depend on Lyapunov exponent conditions. Radwan et al. [13] noticed three switching synchronizations, namely static synchronization, single dynamic synchronization, and double dynamic synchronization, by designing two switches for the slave system to perform active control. The system models utilized in the above literature are widely known. However, in the actual modeling, due to the external environment, parameter uncertainties, and vulnerability to disturbances and other factors, the accurate model of the system is very difficult to be obtained. Thus, it is essential to study the synchronization of FOCSs with uncertain models and disturbances.
It is well known that the uncertainties of FOCSs will affect the synchronization performance. Therefore, researchers attempted to address this issue through various methods, such as fuzzy logic system (FLS) [2, 14–16], adaptive sliding mode control (SMC) [17–20], neural network [21–23]. Among these methods, adaptive fuzzy SMC (AFSMC) is an efficacious and common solution for handling uncertain items that have been proven and recognized by many researchers. It has a relatively quicker dynamic response and cuts down sensitivity to factors such as external disturbances and uncertainties. Boulkroune et al. [24] proposed a novel adaptive fuzzy controller light of the Lyapunov scheme to bring about proper projection synchronization. While Lin et al. [25] proposed an AFSMC method to further reduce the chattering phenomenon in the control by constructing an output feedback control law and an adaptive law to adjust the free parameters online. In addition, Yin et al. [26] put forward a robust controller designed directly in the robot task space by utilizing AFSMC technology, which can guarantee zero steady-state tracking error for a limited time. Based on the AFSMC scheme, Zhu et al. [27] implemented a specific performance of the tracking error by utilizing the conversion function ofan error performance and used the estimation of the weight vector norm in the FLS to cut down the number of estimation parameters so that the designed controller is concise and easy to implement. It is important to note that the AFSMC used in the above literature can handle uncertainties well, but the setup of the controller is very complicated, and the results are not ideal in the presence of disturbances. Therefore, how to devise an ideal controller for uncertain FOCSs with external disturbances deserves further research.
In most FOCSs, external disturbances are unavoidable and have a certain impact on synchronization accuracy. Fortunately, many researchers studied and proposed many effective solutions. Mofid et al. [28] combined a disturbance observation (DOB) with an adaptive SMC scheme to achieve a rapid response for the synchronization of three-dimensional FOCSs. Waghmare et al. [29] adopted a reduced-order extended DOB to estimate unmodeled dynamic and disturbance, which can further improve estimation accuracy, and, at the same time, utilized an SMC technology to design a controller to stabilize the fluctuations in the body, thereby improving the comfort of people riding the vehicle. Guha et al. [30] developed a DOB to estimate disturbance in the endogenous or exogenous system to accelerate dynamic response with minimal flutter, and utilized the Mittag-Leffler stability theorem to ensure the limited time convergence of disturbance error. The above literature provides several outstanding solutions for dealing with disturbances. However, in this study, there have been few results on the synchronization of FOCSs considering disturbances and uncertainties simultaneously.
This study aimed to analyze the synchronization of FOCSs with uncertainties and disturbances based on the AFSMC technology. FLSs are used to estimate uncertain nonlinear terms, while DOBs are designed to estimate external disturbances. The proposed AFSMC strategy ensures that all signals are bounded, and the synchronization errors are asymptotically converged to a small neighborhood of zero. Finally, the effectiveness of the method is demonstrated by Lyapunov's stability theory. The contributions of this article are as follows: (1) taking into account both uncertainties and disturbances, the proposed AFSMC technology can achieve a fast response. (2) a DOB was designed to estimate the disturbance. Compared to traditional fuzzy techniques, a more accurate estimation can be obtained by using the proposed DOB.
The remaining part of the study is laid as follows. Section 2 raises some notations and preliminaries. Section 3 introduces the master-slave systems and the FLSs. Section 4 devises DOBs and adaptive fuzzy controllers, while stability analysis is implemented by using the Lyapunov scheme. Section 5 employs a simulation example to check out and validate this fashion. Furthermore, Section 6 provides the conclusion.
2. Preliminaries
Several fundamental definitions and lemmas with respect to fractional-order integrals and derivatives are useful for stability analysis.
Definition 1. Liu et al. [31] the fractional integral with order ϑ ∈ (0, 1) is defined as
where t ≥ t0, , and (Re(ϑ) > 0) is the familiar Gamma function, where Re(ϑ) is the real part of ϑ.
In this study, we mainly premeditated Caputo's fractional derivative owing to its initial conditions for fractional differential equations possessing an identical physical meaning with the integer-order one.
Definition 2. Abbas and Benchohra [32] Caputo's fractional derivative with order ϑ ∈ (0, 1) is described as
where . Hereafter, represents for convenience.
Lemma 1. Aguila-Camacho et al. [33] if ∂(t) ∈ ℝ is a real-valued continuous differentiable vector function, then we have
Lemma 2. (Yong's Inequality) For ∀a, b ≥ 0, the following inequality holds
Lemma 3. Li and Sun [34] considering the FONS below
there exists a constant t1 > 0 such that, for ∀t ∈ (t1, ∞), the following condition can be fulfilled
where the Ψ(t) is the state variable and η0 and η1 are assumed to be normal numbers.
3. Problem statement
We considered a class of uncertain FOCSs portrayed by the master-slave system below
where and denote the state vector of the master system and the slave system that are assumed to be measurable, respectively and are the smooth unknown nonlinear functions, represents the control input vector, and is the unknown disturbance.
Remark 1. There exist numerous FOCSs in the form described in Equations (7) and (8), such as fractional Chen system, fractional Lu system, and fractional Chua's system; thus, the proposed method is also valid for most of FOCSs.
In particular, to estimate uncertainties, an FLS is required and characterized as below.
Normally, an FLS involves a fuzzifier, a fuzzy inference engine, a defuzzifier, and some fuzzy IF-THEN rules. Fuzzy inference engine is greatly significant and indispensable, which maps the control input vector xT ∈ ℝn to an output through a series of fuzzy rule numbers. The ith rule is portrayed as follows: ℝ(i): if x1 is , …, xn is , then is Λi, where , are fuzzy sets and is the output. By taking advantage of the defuzzification, the output of the FLS can be manifested as follows:
where is the degree of membership of xj to , q is the number of fuzzy rules, is an adjustable parameter vector, and is the fuzzy basis function (FBF), where
Assuming that the picked FBFs have at least one active rule count, i.e., . Thus, FLS (Equation 9) is greatly universally employed in control applications. According to the general approximation outcomes, the FLS (Equation 9) can appraise any nonlinear smooth function f with arbitrary precision in a compact operation space. It should be noted that the construction of the FLS (Equation 9), i.e., membership function parameters and number of rules, can be correctly predesigned by the designer. However, the parameter ρ must be defined by the learning algorithm.
4. Main results
This section discussed about promoting proper synchronization between the systems (Equations 7, 8) by devising a fuzzy adaptive control law ui while guaranteeing that all signals were bounded and the synchronization error asymptotically converged to zero.
To realize the above objects, we first characterized the synchronization errors as
then, we have
For an efficacious layout of the control system and stability analysis, a fractional integral sliding mode surface is presented as
where Si = λiei and , where λi is the positive constant.
From Equation (12), the dynamic of S can be obtained as
If
then, we have
To facilitate the following stability analysis, we made the following assumptions.
Assumption 1. There exists an unknown smooth positive function vector such that , where .
The unknown function can be estimated on a compact operation space Ωy by adopting the FLS (Equation 9), i.e.,
where τi(y) is the FBF vector, which is devised in advance by the projector, and simultaneously, ρi is a parameter vector and .
The optimal estimation of ρi can be described as
Since the vector is only utilized for stability analysis, it is not necessary to calculate its specific values in the implementation process.
Now, and
are the parameter estimation error and the fuzzy estimation error, respectively, where and is a normal number. Additionally, an assumption is given.
Assumption 2. For the fuzzy estimation error, it satisfies , ∀y ∈ Ωy, where is an unknown normal number and .
Then, from Equations (16) and (18), we have
4.1. Design of disturbance observer
We know that unknown external disturbances often appear in real-world systems, which will affect the performance of the system. Therefore, a DOB will be devised immediately to estimate this unknown disturbance of the slave system.
To facilitate the design of the DOB, an auxiliary variable is brought by
The fractional derivative of ξi is
Substituting (Equations 7, 8, 10, and 20 into 21) yields
To enhance the estimation performance of the disturbance, the estimation of the ξi is introduced as
Next, using Equation (20), the DOB can be constructed as
where disturbance estimation error is
Furthermore, based on Equations (20), (24), and (25), we have
Now, by using Equations (22) and (23), the fractional derivative of is obtained as
4.2. Controller design
In this subsection, we devised the synchronous control input by using the adaptive fuzzy method, and further took the Lyapunov method for the stability analysis.
The control input vector is devised to be
where κ0 = Diag(κ01, …, κ0n) and κ1 = Diag(κ11, …, κ1n) are positive definite diagonal matrices.
Next, the adaptive law is designed as
where μρi and βρi are normal numbers.
In light of the preceding foreshadowing, the theorem can be formulated as follows:
Theorem 1. Premeditating the systems (Equations (7), (8)), if a assumptions (Equations 1, 2) are fulfilled, while presuming the sliding mode surface is characterized as Equation (12). Furthermore, the DOB, the controller, and the fuzzy adaptive law are described as Equations (24), (28), and (29), respectively. Then, the system can ensure that the properties hold below.
• All signals remain bounded in a closed-loop system.
• The synchronization error converges asymptotically to a small neighborhood of zero.
First, to accomplish the proof of Theorem 1, an assumption is reasonable to be given.
Assumption 3. The ri(t) and its fractional-order derivative are bounded, i.e., and , where and Mi are unknown positive function and normal number, respectively.
Proof: Selecting the Lyapunov function as
where , , and , from Equations (15), (19), and Lemma 1, the fractional-order derivative of V1 is calculated as
Next, by using Lemma 1, we have
At the same time, according to Lemma 1, Equations (25), and (27), we get
Then, the fractional-order derivative of V can be acquired as
Based on Lemma 2, we have
where is the positive constant.
Then, we got
In line with assumption Lemma 3, Equations (28), and (29), we obtained
where and are positive constants, and .
In accordance with Lemma 3 and Equation (38), we have
and the above inequality (Equation 39) means that
From Equation (40), the e(t) and the S(t) will be finally bounded as t → ∞. Thus, the synchronization of systems (Equations 7 and 8) is realized. This completes the proof process.
■
Remark 2. It could be indicated that, in order to achieve a good synchronization effect, k1i and μρi should be selected as large as probable and to avoid parameter drift problem, if they are chosen too large. At the same time, to get a good control performance, βρi and δ0i should be chosen as small as probable.
5. Simulation results
To certificate the feasibility of the put forward controller for uncertain FOCSs, we premeditated the following systems.
The master system:
The slave system:
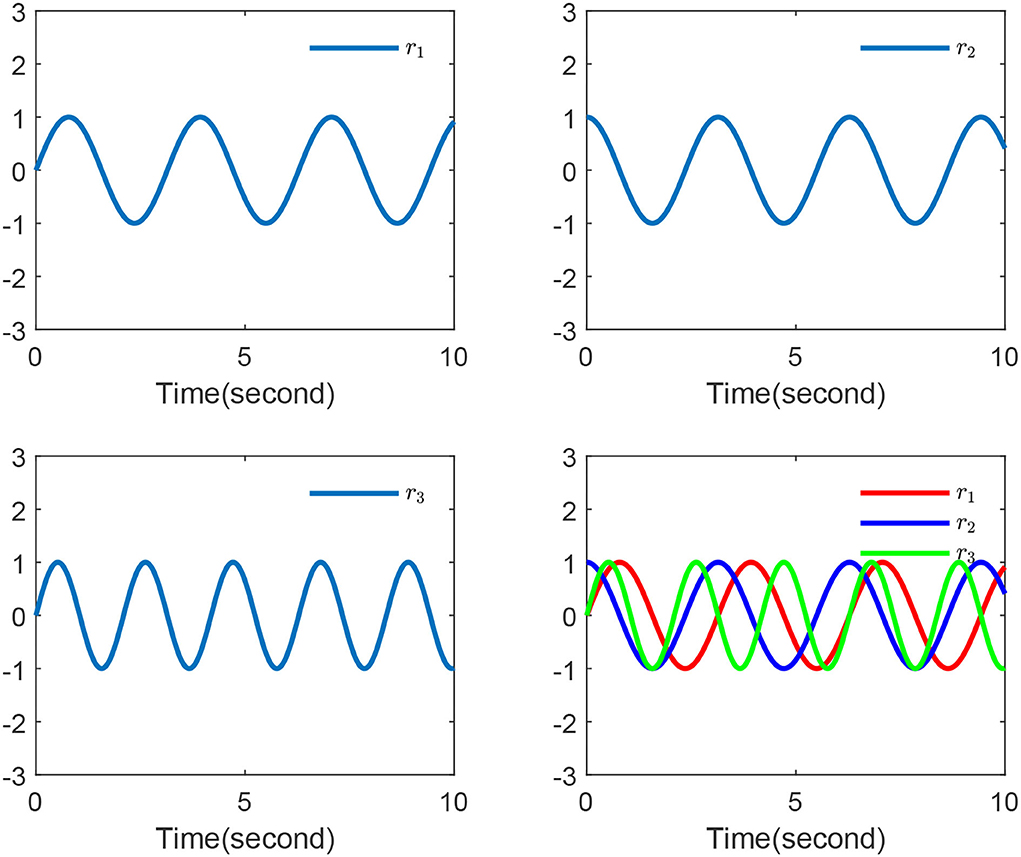
where r1 = sin2t, r2 = cos2t, and r3 = sin3t.
The initial conditions are given as follows: . The opted parameters are revealed as follows: ϑ = 0.85, λ1 = λ2 = λ3 = 2, κ01 = κ02 = κ03 = 0.5, κ11 = κ12 = κ13 = 20, μρ1 = μρ2 = μρ3 = 10, and βρ1 = βρ2 = βρ3 = 0.1.
There is an FLS adopted in the devised controller. The FLS takes x and y as its input and defines six Gaussian membership functions evenly distributed on [−6, 6]. The initial condition is picked as ρ(0) = [1, …, 1]T ∈ ℝ729.
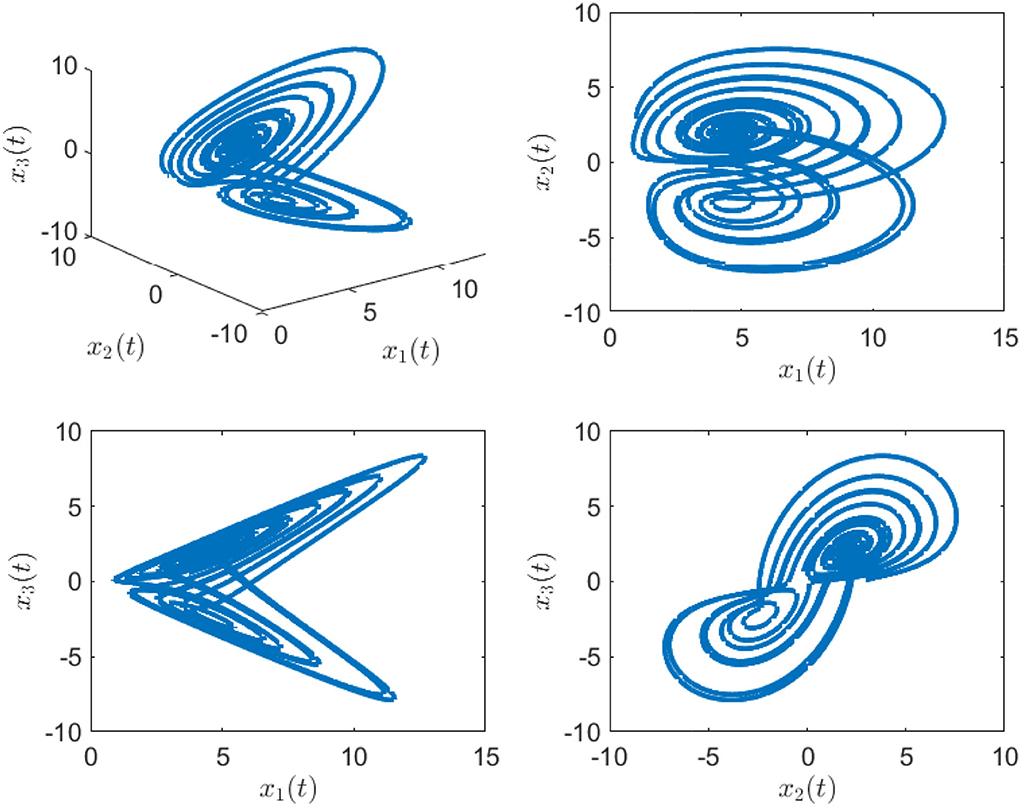
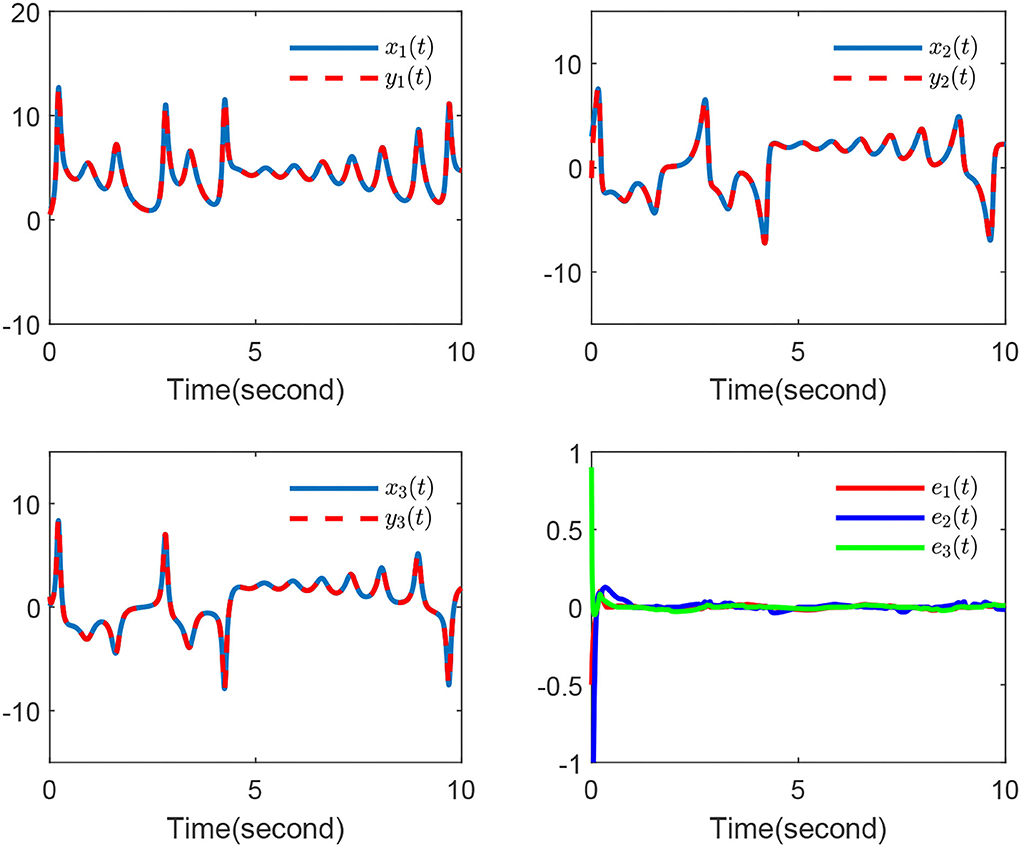
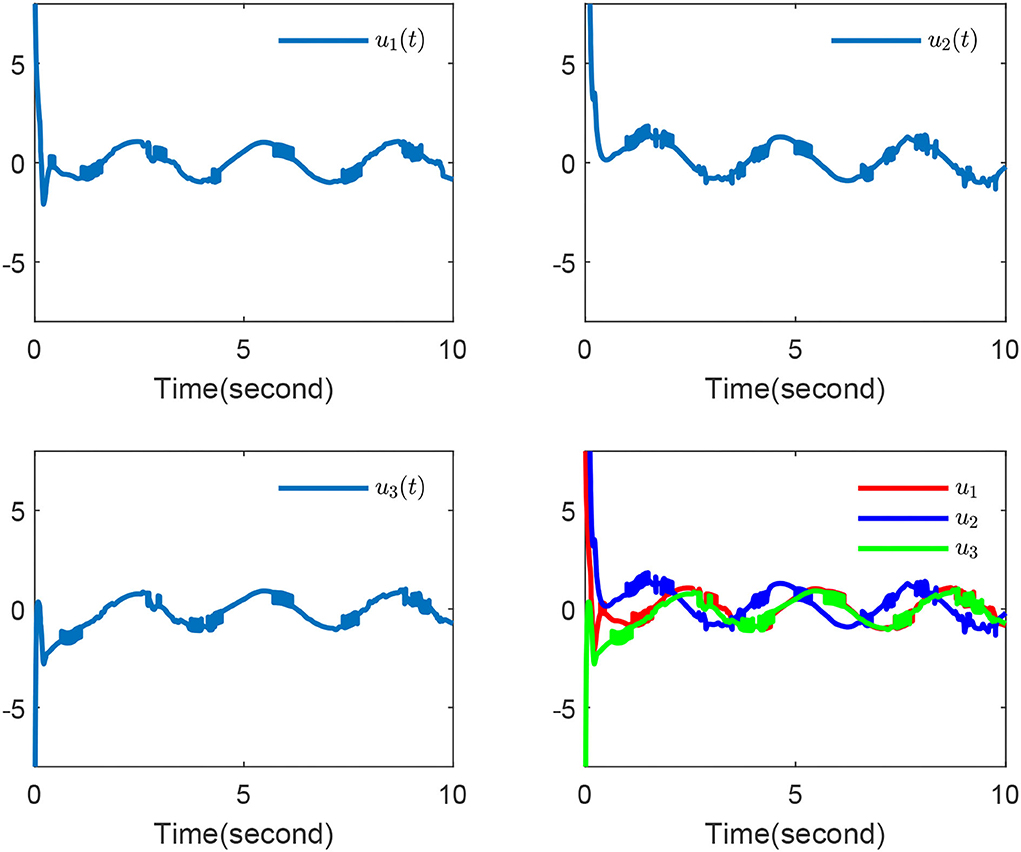
Finally, the simulation outcomes are exhibited in Figures 1–4. Figure 1 displays the chaotic phenomenon of the master system. Figure 2 displays that the master-slave system is practically synchronized. The performances of external disturbance are shown in Figure 3, and the ephemeral actions of the controller are exhibited in Figure 4. This study results showed that the synchronization error has fast convergence, and the controller works well with external disturbances and model uncertainties. Furthermore, we also observed that all signals can remain bounded, so the control objective was achieved.
6. Conclusion
This study investigated the synchronization of two FOCSs with system uncertainties and external disturbances. It is proven that all signals involved are bounded and the synchronization errors asymptotically approached zero by the advanced adaptive fuzzy controller and DOB. In addition, the DOB error and the synchronization error were handled together by using the proposed method. Simultaneously, the simulation results also indicated that the proposed scheme achieved good synchronization. However, the designed controller has the problem of chattering. Future work should focus on addressing this chattering problem.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
YC and FW contributed to the conception and controller design of the proposed method. YC performed the simulation. Both authors contributed to the manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the Key Scientific and Technological Research Project of the Henan Provincial Department of Education (13A520713) and the Henan Provincial Science and Technology Research Project (152102210112).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wang S, He S, Yousefpour A, Jahanshahi H, Repnik R, Perc M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals. (2020) 131:109521. doi: 10.1016/j.chaos.2019.109521
2. Liu H, Li S, Wang H, Sun Y. Adaptive fuzzy control for a class of unknown fractional-order neural networks subject to input nonlinearities and dead-zones. Inf Sci. (2018) 454:30–45. doi: 10.1016/j.ins.2018.04.069
3. Cunha-Filho A, Briend Y, de Lima A, Donadon M. A new and efficient constitutive model based on fractional time derivatives for transient analyses of viscoelastic systems. Mech Syst Signal Process. (2021) 146:107042. doi: 10.1016/j.ymssp.2020.107042
4. He Y, Zhang Y, Sari HMK, Wang Z, Lü Z, Huang X, et al. New insight into Li metal protection: regulating the Li-ion flux via dielectric polarization. Nano Energy. (2021) 89:106334. doi: 10.1016/j.nanoen.2021.106334
5. Liu H, Pan Y, Cao J, Wang H, Zhou Y. Adaptive neural network backstepping control of fractional-order nonlinear systems with actuator faults. IEEE Trans Neural Netw Learn Syst. (2020) 31:5166–77. doi: 10.1109/TNNLS.2020.2964044
6. Wei Z. Dynamical behaviors of a chaotic system with no equilibria. Phys Lett A. (2011) 376:102–8. doi: 10.1016/j.physleta.2011.10.040
7. Qi G, Chen G, Du S, Chen Z, Yuan Z. Analysis of a new chaotic system. Physica A. (2005) 352:295–308. doi: 10.1016/j.physa.2004.12.040
8. Bouzeriba A, Boulkroune A, Bouden T. Projective synchronization of two different fractional-order chaotic systems via adaptive fuzzy control. Neural Comput Appl. (2016) 27:1349–60. doi: 10.1007/s00521-015-1938-4
9. Khan AJahanzaib LS, et al. Synchronization on the adaptive sliding mode controller for fractional order complex chaotic systems with uncertainty and disturbances. Int J Dyn Control. (2019) 7:1419–33. doi: 10.1007/s40435-019-00585-y
10. Fradkov AL, Evans RJ. Control of chaos: methods and applications in engineering. Annu Rev Control. (2005) 29:33–56. doi: 10.1016/j.arcontrol.2005.01.001
11. Zhu H, Zhou S, Zhang J. Chaos and synchronization of the fractional-order Chua¡s system. Chaos Solitons Fractals. (2009) 39:1595–603. doi: 10.1016/j.chaos.2007.06.082
12. Lu JG. Nonlinear observer design to synchronize fractional-order chaotic systems via a scalar transmitted signal. Physica A. (2006) 359:107–18. doi: 10.1016/j.physa.2005.04.040
13. Radwan A, Moaddy K, Salama KN, Momani S, Hashim I. Control and switching synchronization of fractional order chaotic systems using active control technique. J Adv Res. (2014) 5:125–32. doi: 10.1016/j.jare.2013.01.003
14. Ha S, Liu H, Li S, Liu A. Backstepping-based adaptive fuzzy synchronization control for a class of fractional-order chaotic systems with input saturation. Int J Fuzzy Syst. (2019) 21:1571–84. doi: 10.1007/s40815-019-00663-5
15. Mohammadzadeh A, Ghaemi S, Kaynak O, Khanmohammadi S. Observer-based method for synchronization of uncertain fractional order chaotic systems by the use of a general type-2 fuzzy system. Appl Soft Comput. (2016) 49:544–60. doi: 10.1016/j.asoc.2016.08.016
16. Liu H, Pan Y, Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Cybern. (2019) 50:2557–67. doi: 10.1109/TCYB.2019.2938754
17. Yin C, Dadras S, Zhong Sm, Chen Y. Control of a novel class of fractional-order chaotic systems via adaptive sliding mode control approach. Appl Math Model. (2013) 37:2469–83. doi: 10.1016/j.apm.2012.06.002
18. Hosseinnia SH, Ghaderi R, Mahmoudian M, Momani S, et al. Sliding mode synchronization of an uncertain fractional order chaotic system. Comput Math Appl. (2010) 59:1637–43. doi: 10.1016/j.camwa.2009.08.021
19. Deepika D, Kaur S, Narayan S. Uncertainty and disturbance estimator based robust synchronization for a class of uncertain fractional chaotic system via fractional order sliding mode control. Chaos Solitons Fractals. (2018) 115:196–203. doi: 10.1016/j.chaos.2018.07.028
20. Wang P, Wen G, Huang T, Yu W, Lv Y. Asymptotical neuro-adaptive consensus of multi-agent systems with a high dimensional leader and directed switching topology. IEEE Trans Neural Netw Learn Syst. (2022). doi: 10.1109/TNNLS.2022.3156279. [Epub ahead of print].
21. Wang R, Zhang Y, Chen Y, Chen X, Xi L. Fuzzy neural network-based chaos synchronization for a class of fractional-order chaotic systems: an adaptive sliding mode control approach. Nonlinear Dyn. (2020) 100:1275–87. doi: 10.1007/s11071-020-05574-x
22. Li HL, Hu C, Zhang L, Jiang H, Cao J. Complete and finite-time synchronization of fractional-order fuzzy neural networks via nonlinear feedback control. Fuzzy Sets Syst. (2022) 443:50–69. doi: 10.1016/j.fss.2021.11.004
23. Wang P, Wen G, Huang T, Yu W, Ren Y. Observer-based consensus protocol for directed switching networks with a leader of nonzero inputs. IEEE Trans Cybern. (2020) 52:630–40. doi: 10.1109/TCYB.2020.2981518
24. Boulkroune A, Bouzeriba A, Bouden T, Azar AT. Fuzzy adaptive synchronization of uncertain fractional-order chaotic systems. In: Advances in Chaos Theory and Intelligent Control. Berlin: Springer (2016). p. 681–97.
25. Lin TC, Lee TY, Balas VE. Adaptive fuzzy sliding mode control for synchronization of uncertain fractional order chaotic systems. Chaos Solitons Fractals. (2011) 44:791–801. doi: 10.1016/j.chaos.2011.04.005
26. Yin X, Pan L, Cai S. Robust adaptive fuzzy sliding mode trajectory tracking control for serial robotic manipulators. Robot Comput Integr Manuf . (2021) 72:101884. doi: 10.1016/j.rcim.2019.101884
27. Zhu G, Nie L, Lv Z, Sun L, Zhang X, Wang C. Adaptive fuzzy dynamic surface sliding mode control of large-scale power systems with prescribe output tracking performance. ISA Trans. (2020) 99:305–21. doi: 10.1016/j.isatra.2019.08.063
28. Mofid O, Mobayen S, Khooban MH. Sliding mode disturbance observer control based on adaptive synchronization in a class of fractional-order chaotic systems. Int J Adapt Control Signal Process. (2019) 33:462–74. doi: 10.1002/acs.2965
29. Waghmare DB, Asutkar VG, Patre BM. Extended disturbance observer based robust sliding mode control for active suspension system. Int J Dyn Control. (2021) 9:1681–94. doi: 10.1007/s40435-021-00761-z
30. Guha D, Roy PK, Banerjee S. Adaptive fractional-order sliding-mode disturbance observer-based robust theoretical frequency controller applied to hybrid wind-diesel power system. ISA Trans. (2022) doi: 10.1016/j.isatra.2022.06.030. [Epub ahead of print].
31. Liu H, Pan Y, Li S, Chen Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybern Syst. (2017) 47:2209–17. doi: 10.1109/TSMC.2016.2640950
32. Abbas S, Benchohra M. Fractional order partial hyperbolic differential equations involving Caputo¡s derivative. Stud Univ Babes-Bolyai Math. (2012) 57:469–79. doi: 10.1080/17476933.2011.555542
33. Aguila-Camacho N, Duarte-Mermoud MA, Gallegos JA. Lyapunov functions for fractional order systems. Commun Nonlin Sci Num Simulat. (2014) 19:2951–7. doi: 10.1016/j.cnsns.2014.01.022
Keywords: fractional-order chaotic system, adaptive fuzzy control, sliding mode control, disturbance observer, chaos synchronization
Citation: Chen Y and Wang F (2022) Disturbance observer based adaptive fuzzy synchronization controller design for uncertain fractional-order chaotic systems. Front. Appl. Math. Stat. 8:1019047. doi: 10.3389/fams.2022.1019047
Received: 14 August 2022; Accepted: 07 September 2022;
Published: 04 November 2022.
Edited by:
Peijun Wang, Anhui Normal University, ChinaReviewed by:
Zhimin Han, Shaanxi Normal University, ChinaShumin Ha, Shaanxi Normal University, China
Xiulan Zhang, Guangxi Minzu University, China
Copyright © 2022 Chen and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Youjun Chen, Y2hlbnlvdWp1bkBuY3d1LmVkdS5jbg==
 Youjun Chen
Youjun Chen Feng Wang2
Feng Wang2