- 1Department of Mathematics and Applied Mathematics, North-West University Potchefstroom Campus, Potchefstroom, South Africa
- 2Department of Mathematics and Applied Mathematics, Nelson Mandela University, Gqeberha, South Africa
- 3Department of Basic Sciences of Engineering, Faculty of Engineering and Natural Sciences, İskenderun Technical University, Hatay, Turkey
In this study, we obtain a numerical solution for Fisher's equation using a numerical experiment with three different cases. The three cases correspond to different coefficients for the reaction term. We use three numerical methods namely; Forward-Time Central Space (FTCS) scheme, a Nonstandard Finite Difference (NSFD) scheme, and the Explicit Exponential Finite Difference (EEFD) scheme. We first study the properties of the schemes such as positivity, boundedness, and stability and obtain convergence estimates. We then obtain values of L1 and L∞ errors in order to obtain an estimate of the optimal time step size at a given value of spatial step size. We determine if the optimal time step size is influenced by the choice of the numerical methods or the coefficient of reaction term used. Finally, we compute the rate of convergence in time using L1 and L∞ errors for all three methods for the three cases.
1. Introduction
The most enthralling recent progress of nonlinear science in particular mathematical science of partial differential equations, theoretical physics, chemistry, and engineering sciences has been a growth of strategy or procedure to try to find exact solutions for nonlinear differential equations. This is substantial due to the fact that countless mathematical models are described by nonlinear differential equations. To mention few among others the inverse scattering transform [1], the singular manifold method [2], the transformation method [3], the tanh-function method [4], and the Weierstrass function method [5] are subservient in many applications and known as stunning techniques to look for solutions of exactly solvable nonlinear partial differential equations.
In Kudryashov [6] developed a new numerical method for the solution of nonlinear partial differential equations. Amajor novelty of that technique is the utilization of finite Fourier series for the numerical approximation of the spatial derivative terms of the equations. It was proved that the precision of this method is that the order of accuracy is greater than that found by approximating the spatial derivative terms by finite-difference methods [6]. The numerical performance of this method, which was called the Accurate Space Derivatives (ASD) approach, can be run accurately by the utilization of the Fast Fourier Transform (FFT) algorithm [7]. In Kudryashov [6], the ASD approach was used to obtain the solution of nonlinear hyperbolic equations depicting convective fluid flows. Furthermore, the ASD approach was used in Gazdag and Canosa [8] to solve Fisher's equation, a nonlinear diffusion equation portraying the rate of advance of a new advantageous gene within a population of constant density inhabiting a one dimensional habitat [9]. An outstanding and compendious debate of Fisher's equation in the framework of the genetic problem can be found in Moran [10] and Kendall [11].Kolmogorov [12] used the traveling waves with wave speed c to solve the problem. They showed that by assuming that when the initial condition belongs to the interval [0, 1], the speed of propagation c of the waves is superior to two and the solution is in the form u(x, t) = w(ξ) where ξ = x − ct. They further demonstrated that there are no solutions for c ∈ [0, 1).
Fisher's equation has a limitless number of traveling wave solutions and each wave propagates at a characteristic speed, c > 2. This result appears to point out that the velocity of gene advance is undefined. Gazdag and Canosa [8] studied the problem of the indeterminacy of the diffusion speed of Fisher's equation which has not been plainly investigated in Kolmogorov [12]. Furthermore, a modification was made by Fisher [9] to his original model, he demonstrated that the rate of gene advance became the minimum one when c = 2. Kendall [11] investigated a linear model portraying a population that undergoes a Brownian motion and spreads geometrically at the same time. Canosa [13] demonstrated that all waves are stable against local perturbations but are linearly unstable against general perturbations of limitless magnitude. It is worthy to emphasize that the traveling wave profiles of Fisher's equation are similar to some of the steady-state solutions of the Korteweg-de Vries-Burgers equation which is a third-order nonlinear partial differential equation integrating diffusive and dispersive effects which have been found useful to represent blood flow through an artery, shallow water waves and plasma shocks disseminating perpendicularly to a magnetic field [13, 14].
Kudryashov [6] showed that a simple stability analysis enables us to see the estimation which is unstable against the roundoff errors growing up at the right tail of the waves. This is due to the physical nature of the problem depicted by the equation, not to the numerical method utilized and moreover entailed an exponential growth of the solution when roundoff errors are exponentially small. This simple issue makes it hard to do a strict simulation of the solutions of Fisher's equation. Kudryashov [6] went on with the removal of the forward tail of the wave of advance. This removal is necessary for the numerical stability of the Accurate Space Derivatives (ASD) approach and is physically conclusive because it is approximately equivalent to assuming that the role of long-distance dissipation in the spread of the gene is insignificant and probably effective for some species but not for others. Other numerical computations present how fast the asymptotic minimum speed wave is reached from an initial step function and confirm the local stability analysis of Kudryashov [6] which unveils that local perturbations are flattened very rapidly, even from superspeed waves. Another amazing result of the estimation is obtained for an initial dispensation localized in space which further gives rise to two identical waves of minimum speed evolution cases, one disseminating to the right and the other to the left.
1.1. Some Generalized and Conserved Fisher's Equation
Fisher's equation can be represented as generalized or conserved forms. Fisher's equation is the elementary model of spatial dynamics, in which competitive interactions between individuals happen locally. In Kudryashov and Zakharchenko [15], the generalized form is written as
where t stands for time, x stands for spatial coordinate, u is a population density, and a, b, and l are all positive parameters.
Fisher's equation can also forecast circumstances where population regulation happens globally due to the existence of a secondary agent (the controller agent is itself dispersed over a scale significantly greater than the dispersal distance of the individuals themselves). It is, thus, of notice to envisage a simple model of spatial population dynamics in which the total population size is controlled via a nonlocal mechanism. In that case in Newman et al. [16], the conserved equation is written as
where D stands for the mobility of the individuals, r stands for the reproduction rate in the absence of competition. K is a parameter representing the carrying capacity of the system and regulating the population density through competition. The auxiliary equation related to Equation (2) is
It is worth mentioning that Fisher's equation belongs to the class of partial differential equations called Reaction-Diffusion equations. This class of equations has broad applications in science and engineering for instance transport of air, adsorption of pollutants in soil, food processing, and modeling of biological and ecological systems [17, 18]. Several reaction-diffusion equations involve traveling waves fronts yielding a fundamental role in the understanding of physical, chemical, and biological phenomena [19]. Reaction-diffusion systems clarify how the condensation of one or more substances diffused in space varies by the impact of two operations: first, it is local chemical reactions in which the substances are modified into each other, and second, it is the diffusion that sustains the substances to smear over a surface in space [20]. Reaction-diffusion systems are regularly used in chemistry. Nonetheless, the system can also portray the dynamical processes of non-chemical nature. Reaction-diffusion systems have mathematically the form of semi-linear parabolic partial differential equations. They are often written in the form of
where each component of vector u(x, t) stands for the concentration of one substance, x is the space variable, and t is the time. D is the diffusion coefficient and R represents the reaction term. The solution of reaction-diffusion equations shows an ample scale of behaviors, enclosing the formation of traveling waves. These waves are like phenomena and self-organized patterns which are e.g., stripes, hexagons, or more complicated fabrics such as dissipative solutions [20]. Reaction-diffusion equations are also grouped as one component, two components, or more component diffusion equations counting upon the component involved in the reaction. The basic reaction-diffusion equation regarding the concentration u of a mere substance in one spatial dimension is
If the reaction R(u) term goes away, then the equation gives a pure diffusion process and if the thermal diffusivity term appears instead of diffusion term D then the equation will turn into a parabolic partial differential equation in one dimensional space [20]. The choice R(u) = u(1 − u) yields Fisher's equation. Those reaction-diffusion equations arise also in flame propagation, the branching Brownian motion process, and nuclear reactor theory [20]. Many methods such as Adomian Decomposition [21], Variational Iteration [22], Factorization [23], Nonstandard Finite Difference, and Exponential Finite Difference methods [24, 25] are used to solve Fisher's equation.
Anguelov et al. [26] investigated the same Fisher's equation by the means of a periodic initial data with θ-non standard approach and found that the Nonstandard Finite Difference approach is elementary stable in the limit case of space independent variable, stable in regard to the boundedness and positivity property. Finally also stable in regard to the conservation of energy in the stationary case.
Let us consider simple Fisher's equation given by
where R(u) = u(1 − u) and x ∈ ℝ, t positive. The boundary and initial conditions are as follows
Hagstrom and Keller [27] revealed that when a positive function is taken as an initial condition satisfying
then the solution u develops a traveling wave speed in function of α which is
2. Organization of the Article
The organization of this article is as follows. In Section 3, we present the general form of the exact solution of Fisher's equation and in Section 4, we describe the numerical experiment [28]. In Section 5, we make use of Forward in Time Central Space (FTCS) in order to discretize Fisher's equation, study the stability and consistency and we also obtain error estimates. Sections 6, 7 discuss stability, consistency, and error estimates for NSFD and EEFD schemes. In Section 8, we conclude by presenting the important highlights of this article. The computations are performed by making use of MATLAB R2014a software on an intel core2 as CPU.
3. Exact Solution
In this section, we present the exact solution of generalized Fisher's equations as described in Kudryashov and Zakharchenko [15]. The nonlinear evolutional equation of that generalized Fisher's equation gives one dimensional diffusion models (for insect, animal dispersal, and invasion) as
where t stands for time, x stands for spatial coordinate, u is population density, and a, b, and l are positive parameters. The first term, on the right-hand side of Equation (11) stands for the growth of population. The term ul represents the diffusion process depending on the population density.
Let us consider l ≠ 0 and u(x, t) = v(ξ) and ξ = sx − ct, s ≠ 0. Equation (11) gives the following nonlinear ordinary differential equation
For l ≠ 0, vl = w. Replacing v by in Equation (12) gives
Using the Q function method as it is in Kudryashov [29], one has
where P stands for the pole order and ξ0 stands as an arbitrary constant. Q(ξ) is the solution of
Using Equation (15), we obtain wξ and wξξ by using polynomials of Q. Replacing w ≃ QP into Equation (15), we have for b ≥ 0, the following equality
To have an integer value P should be 1 or 2. In that case
For P = 1, a = 3l + 1 − b, Equation (13) becomes
We have the following solutions
We finally get as exact solution
where V1 and V2 stand for velocity.
For P = 2, a = 2l + 1 − b. With the same reasoning as above, we have
The case of l = 0, a = 1 and b = 2, one obtains the Burgers-Huxley equation and the case of l = 0, a = 1, b = 1, we have Fisher's equation. The exact solution of Equation (11) is described in Li et al. [28] as a scaled Fisher's equation in the form
with x ∈ ℝ, t positive, and ρ is a positive constant. The Equations (7) and (8) stand for boundary and initial conditions, respectively. The traveling exact solution to this problem as presented in Polyanim and Zaitsev [30] is
where stands for the wave speed with the minimum value,
4. Numerical Experiments
We consider the following problem from Qiu and Sloan [31].
Solve
for x ∈ [−0.2, 0.8] and t ∈ [0, Tmax] where The initial data is given by
The exact solution is given by
The boundary conditions are as follows
We consider three cases ρ namely; 1, 102, 104, and obtain a solution at time, t = Tmax.
DEFINITION 1. Miyata and Sakai [32]. For a vector and
DEFINITION 2. Sutton [33]. Suppose forms a partition of [0, T], with tn = nΔt for n = 0, ···, N, where Δt = T/N. Suppose a vector defined by
The rate of convergence with respect to time is defined by
5. Forward in Time Central Space
The discretization of Equation (22) using the FTCS method gives [34].
which leads to
or
where
5.1. Stability
The investigation regarding the stability of the scheme given by Equation (28) was done in Agbavon et al. [35]. Nevertheless, we highlight briefly some points. The stability of finite difference methods discretizing nonlinear partial differential equations is not straightforward. Subsequently, freezing the coefficients is needed before using Von Neumann stability analysis [36].
THEOREM 1. Agbavon et al. [35]. The FTCS scheme given by Equation (28) is conditionally stable, and the stability region is
for given spatial step size h > 0 and the time step size k > 0. FTCS is first order and second order accurate in time and space, respectively.
Proof. The stability region of the Zabusky and Kruskal scheme using the Korteweg de Vries (KdV) equation was found by Taha and Ablowitz [37] by using the freezing coefficients method and Von Neumann Stability Analysis. The derived scheme by Zabusky and Kruskal [38] for the KdV equation, ut + 6uux + uxxx = 0 is
Taha and Ablowitz [37] express u ux as umax ux and utilize the ansatz
where w stands for the phase angle. They obtain
which can be rewritten as
where umax = max|u(x, t)|. The requirement for the linear stability is
For obtaining the stability region of the FTCS scheme discretizing Equation (28), we rewrite Equation (28) using the same idea as
Utilization of Fourier series analysis on Equation (34), gives the amplification factor
where umax is frozen coefficient. For the numerical experiment considered, we have umax = 1, and therefore,
The stability is obtained by solving |ξ| ≤ 1 for w ∈ [−π, π], and we obtain
Using Taylor series expansion about the point (n, m) of Equation (28), we get
which can be written as
Hence, FTCS is first order and second order accurate in time and space, respectively.
5.2. Error Estimates
THEOREM 2. Let u ∈ C4, 2(Q), Q defined by Q = {(x, t)/a ≤ x ≤ b, 0 < t ≤ T, a, b ∈ ℝ}. If spatial step size, h and time step size, k are such that the stability condition (30) holds, then the error estimate, for Equation (28) is given by
where and Θ such that Θ(k, h)uttt = O(k, h) → 0, for k, h → 0.
Proof.
Forward in Time Central Space scheme is given by
Taylor series expansion about (n, m) gives
which can be rewritten as
and let for k, h → 0. The exact discrete equation is
where xm < Xm < xm + 1 and tn < τn < tn + 1. We define
It follows that
We have
which can be rewritten as
Using the properties of absolute values |a + b| ≤ |a| + |b| for a, b ∈ ℝ, we have
where Since and based on numerical experiment chosen, we have
Let We have
and for stability R ≤ 1/2, therefore, |1 − 2R| = 1 − 2R ≥ 0. We finally obtain
Let We have
For n = 0,
For n = 1, we have
For n = 2, we have
For n, we have
Hence, for we can also write
6. Nonstandard Finite Difference Scheme (NSFD)
Over the past decade, the NSFD has been used extensively and often abbreviated as NSFD. The method was introduced by Mickens for the approximation of solutions of partial differential equations and is largely based on the concept of dynamical consistency [39] which plays a significant role in the construction of discrete models whose numerical solution can be complicated to compute. The dynamical consistency is bound to a precise property of a physical system (and varies according to the systems). To mention few among others these properties include the preservation of positivity, boundedness, monotonicity of the solutions, and stability of fixed-points [39]. The main advantage of this method was the dismissal of the primary numerical instabilities [40] caused by the use of standard methods. In order to reduce numerical sensitivities appearing using the classical finite difference methods, these NSFD were developed.For practical use, the construction of NSFD methods is based on the following basic rules [39]:
(1) The order of discrete derivatives should be equal to the order of corresponding derivatives appearing in the differential equation.
(2) Discrete representation for derivatives, in general, have non trivial denominator functions, e.g.,
where
6.1. Example of the Definition of the Function ϕ
Consider the following decay equation and logistic growth equation, respectively as in Anguelov et al. [26]
and the respective solutions at the time t = tn+1 are
Let We have
The Equation (63) is called the exact scheme. The function ϕ can be then defined as
(3) Nonlocal discrete representations of nonlinear terms. For instance
and
In Agbavon et al. [35], followed by the rule of Mickens [39] a NSFD
for Equation (22) is
where
The Equation (66) gives the following single expression
6.2. Positivity and Boundedness
In this section, the dynamical consistency and some useful relationship between time and space step-sizes of NSFD are presented.
THEOREM 3. The dynamical consistency (positivity and boundedness) of NSFD constructed in Equation (68) holds for Equation (22) and for relevant time step k, spatial step h if the following conditions hold
(a) with Γ = 1 − 2(h2)−1ϕ(k) + ρϕ(k),
(b) For , ∀ i. and Γ′ = σ Γ.
Proof.
We assume u(x, 0) = h(x) ∈ [0, 1]. We have, therefore, u(x, t) ∈ [0, 1] [24]. We assume also The quantity from Equation (68) is positive () if only
It follows that
Hence, in Mickens [24], the condition required for positivity is
We investigate next the boundedness by assuming Equation (68) is rewritten as follows
where Γ = 1 − 2(h2)−1ϕ(k) + ρϕ(k),
Following the idea of Mickens [24], Equation (72) takes the symmetric form if Γ = R. Therefore, it follows that
We also have from Equation (71)
Based on the symmetric condition, we can take
With regard to the symmetric condition (Equations 73), Equation (72) can be rewritten as
We know by the assumption that ∀j. We have
By multiplying Equation (77) by and dividing by and expanding, we have
From Equation (78), we have
Let Γ′ = σΓ, σ ≠ 0. Then
If , then and using Equation (79), we have
Hence,
Thus, the boundedness of
6.3. Error Estimate
THEOREM 4. Let u ∈ C4, 2(Q) where Q is defined by
Assume h and k are such that the Theorem 3 is satisfied and is the defined error of the scheme constructed. NSFD is consistent, and the estimate error is defined by
where Γ defined in 3 M is defined by and Θi, i = 1, 2, 3 such that
and
Θ1(ϕ(k), h)uxx + Θ2(ϕ(k), h)uttt + Θ3(ϕ(k), h)ut = O(ϕ(k), h) → 0 when ϕ(k) → 0 and h → 0.
Proof.
where Taylor series expansion of Equation (85) about (tn, xm) gives
This gives
It follows after division by ϕ(k) and simplification, we have
It follows that
If ϕ(k) → 0 and h → 0, Equation (88) reduces to Hence, the consistency.
For the simplicity of the proof, we consider the function Θi, i = 1, 2, 3 such that
and Θ1(ϕ(k), h)vxx + Θ2(ϕ(k), h)vttt + Θ3(ϕ(k), h)vt = O(ϕ(k), h) → 0 when ϕ(k) → 0 and h → 0.
The exact discrete equation is
where and xm < εm < xm + 1 and tn < τn < tn + 1.
We define It follows by considering symmetry condition Γ = R
It follows
Let and We have
and by using Theorem 3, we have
Let
We have
For n = 0,
For n = 1, we have
For n = 2, we have
By recurrence for n, we have
7. Explicit Exponential Finite Difference Scheme
The EFFD method was developed by Bhattacharya [41] (primarily called the Bhattacharya method) for the numerical solution of the heat equation. The Exponential Finite Difference method was utilized to solve Burgers' equation and generalized Huxley and Burgers-Huxley equations [42–44]. Later, Macías-Díaz and Ĩnan [45] used modified exponential methods to obtain the solution of the Burgers' equation. Furthermore, Inan et al. [46] utilized the EEFD method for numerical solutions for the Newell-Whitehead-Segel type equations which are very useful in biomathematics. They showed convergence, consistency, and stability of the method.
In this section, we obtain numerical solutions of the equation by EEFD method. The solution domain are discretized into cells as (xm, tn) in which xm = mh, (m = 0, 1, 2, ..., N) and tn = nk, (n = 0, 1, 2, ...), is the spatial mesh size and k = Δt is the time step, denotes the EEFD approximation and u(x, t) denotes the exact solution.
Dividing Equation (6) by u gives
Using the finite difference approximations for derivatives, Equation (98) gives
where Equation (99) gives the expression for the EEFD method for Fisher's equation.
7.1. Convergence and Estimate Error
For stability analysis, we require non-iterative exponential time-linearization and iterative exponential quasilinearization techniques for Equation (6) which are found in the discretization of the time derivative, the freezing of the coefficients of the resulting linear ordinary differential equations, and the piecewise analytical solution of these ordinary differential equations. These techniques give three-point finite difference expressions that depend in an exponential manner on either the diffusion, reaction, and transient terms or the diffusion and reaction terms. Following the idea of Ramos [25], we transform (Equations 6, 99) into a linear ordinary differential equation by discretizing the time derivative by means of θ-method [25] and linearizing the nonlinear source term, u(1 − u), with respect to either the previous time level or the previous iteration with Jacobian, :
a) If the linearization is performed with respect to the previous time level, one obtains
which yields a non-iterative time linearization method.
b) If the linearization is performed with respect to the previous iteration, one obtains
which corresponds to an iterative quasilinear technique and i = 1, 2, ···, n.
Equations (100) and (101) can be solved in closed form in (xm−1, xm+1) subject to the following conditions:
and yield exponential solutions in (xm−1, xm+1) which are analytical in that interval and continuous everywhere. Since Equations (100) and (101) are very similar, we will only present in detail exponential methods for Equation (100) in the following subsections.
7.1.1. Time-Linearized Full Exponential Techniques
The piecewise analytical solution of Equation (100) can be rewritten as
Let Equation (103) becomes
which accounts for diffusion, reaction, and transient effects in the differential operator [25]. The solution of Equation (104) depends on the sign of We have the following three cases:
a) If the solution of Equation (104) subject to the condition (102) gives the finite difference expression
b) If , the solution of Equation (104) subject to the condition (102) gives the three-point finite difference expression
c) If , the solution of Equation (104) subject to the condition (102) gives the three-point finite difference expression
REMARK 1. We can make the following remarks
a) The values corresponding to the time linearization methods.
b) The quasilinear full exponential corresponds to the iterative solution of
for i = 1, 2, ··, n − 1, have analogous solutions to those reported in time-linearized full exponential techniques section and the cases and 1, corresponding to the quasilinear methods.
7.1.2. Time-Linearized Exponential Techniques
The time-linearized exponential techniques presented in this section consider the following differential operator.
Let The Equation (109) becomes
which only accounts for reaction and diffusion processes and whose solutions depend on the sign of . We have therefore the solution of Equation (110) subject to the condition (Equation 102) gives the solution in form of:
a) If
b) If
c) If
REMARK 2. The quasilinear full exponential corresponds to the iterative solution of
for i = 1, 2···n − 1, have analogous solutions to those reported in time-linearized exponential techniques Section 7.1.2.
REMARK 3. The principal primacy of the full exponential techniques is that they reckon for the reaction, diffusion, and transient terms in finding the homogeneous solution of Equation (103). Notwithstanding, this technique also has the disadvantage that the time step cannot be chosen carelessly because, if then the reaction terms do not influence the values of λm despite the fact that they do influence the particular solution of Equation (103) through On top of that, the portion of the transient term influences the ordinary differential operator and, therefore, the homogeneous solution, though the other part influences the particular solution. These obstacles are fully suppressed with the exponential techniques displayed in the time-linearized exponential techniques and the quasilinear full exponential in Section 7.1.2.
THEOREM 5. Ramos [25]. The schemes displayed in Equations (100) and (101) are convergent and convergence is reached when
where i = 1, 2···n and |α| is an integer obtained from numerical computation, N denotes the number of grid points, and is the error which is defined by .
Proof. The full proof of this theorem is detailed in Ramos [25].
8. Numerical Results
The stability region of FTCS is For h = 0.01, we obtain k ≤ 5 × 10−5. In the case of NSFD, the condition for positivity gives where We tabulate L1 and L∞ errors at certain values of k using ρ = 1, h = 0.01, at time, using FTCS, NSFD, and EEFD schemes at certain various values of time-step size as chosen from Tmax/52, Tmax/100, Tmax/200, ⋯ , Tmax/1,800, Tmax/1,900 and Tmax/2,000. The errors are shown in Table 1.
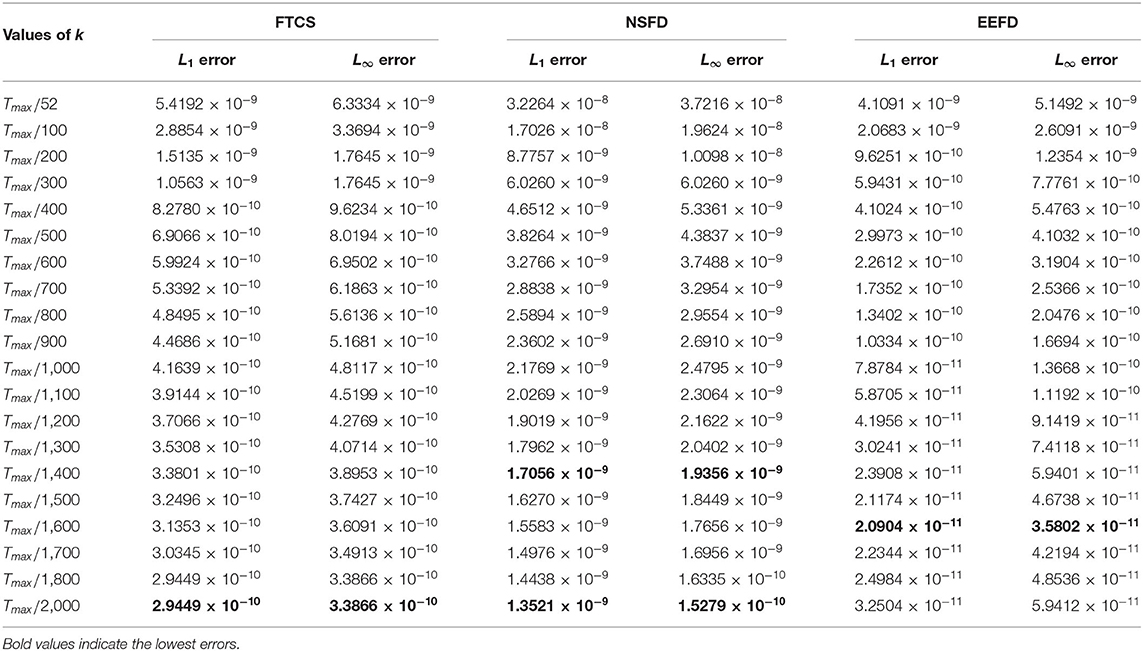
Table 1. L1 and L∞ errors at some different values of time-step size, k with ρ = 1 at time, with spatial mesh size, h = 0.01 using three methods.
In the case of FTCS, NSFD, minimum L1, and L∞ errors occur at k = Tmax/2,000 while in the case of EEFD, the errors are least k = Tmax/1,600. The least error is of order 10−9 and 10−10 in the case of NSFD and FTCS respectively while the least error is of order 10−11 in the case of EEFD. EEFD is a better scheme than FTCS at all values of k used.
We obtain values for L1 and L∞ errors at certain values of k using ρ = 102, h = 0.01, at time, using the three methods in Table 2. The schemes behave differently. In all the three methods FTCS, NSFD, and EEFD, the L1 and L∞ errors keep on decreasing as the values of k are decreased gradually from k = Tmax/52 to k = Tmax/2,000.
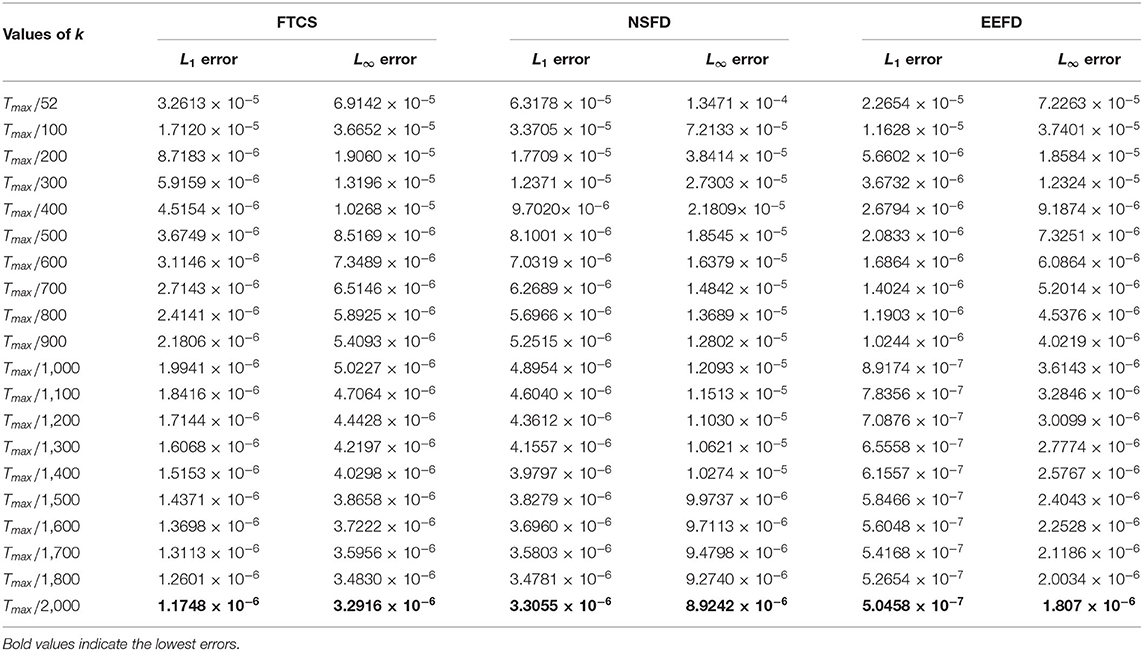
Table 2. L1 and L∞ errors at some different values of time-step size, k with ρ = 102 at time, with spatial mesh size, h = 0.01 using three methods.
L1 and L∞ errors for the third case using ρ = 104, h = 0.01 are displayed in Table 3. Again, the schemes behave differently from each other. Optimal k using FTCS occurs when k ≊ Tmax/1,300. The optimal k using NSFD and EEFD are k ≊ Tmax/1,500 and k ≊ Tmax/2,000, respectively. Once that optimal is reached the error starts increasing again. The least L1 and L∞ errors using NSFD are 4.5235 × 10−4 and 4.5623 × 10−3. The corresponding errors are 1.9347 × 10−4 and 2.3239 × 10−3 when FTCS is used. In the case of EEFD, least L1 is 6.9852 × 10−3 and least L∞ is 8.3399 × 10−2.
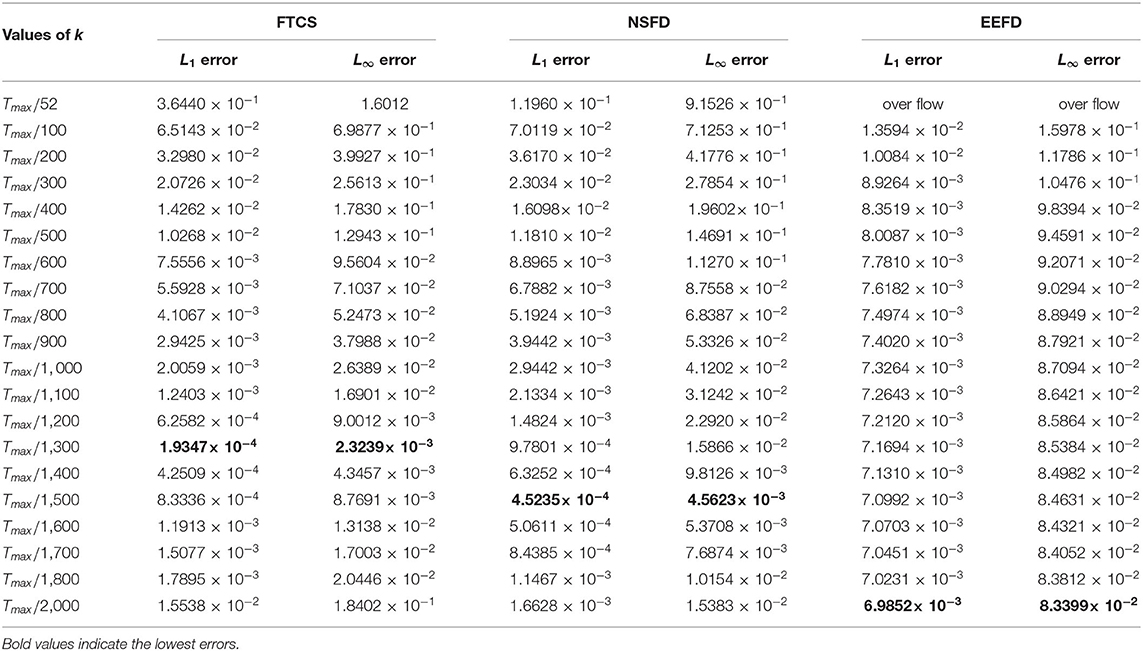
Table 3. L1 and L∞ errors at some different values of time-step size, k with ρ = 104 at time, with spatial mesh size, h = 0.01 using three methods.
We obtain plots of numerical solution vs. x at time, using three methods FTCS, NSFD, and EEFD in Figure 1.
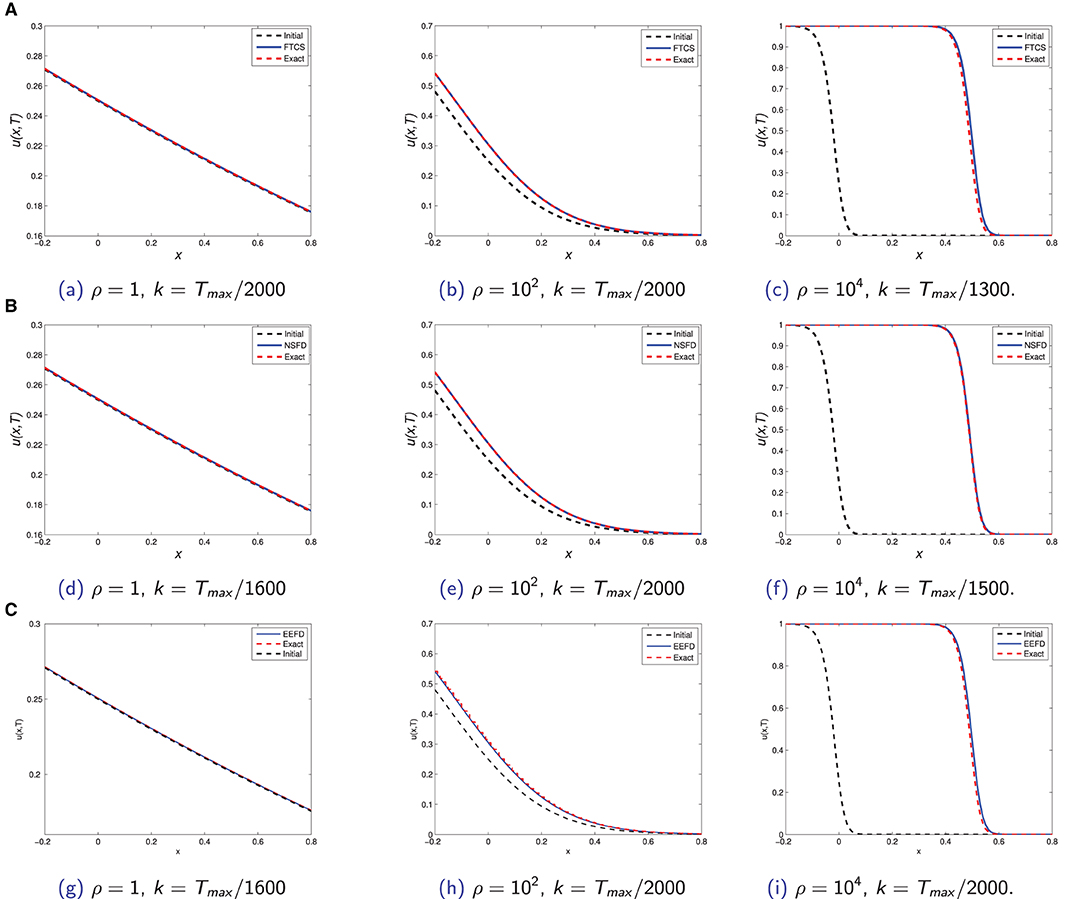
Figure 1. Plot of initial solution, numerical solution of (FTCS), NSFD, and EEFD respectively in (A–C) and exact solution against x at time, using h = 0.01 and optimal value of time step size of k for three different values of ρ namely 1, 102, and 104.
9. Conclusion
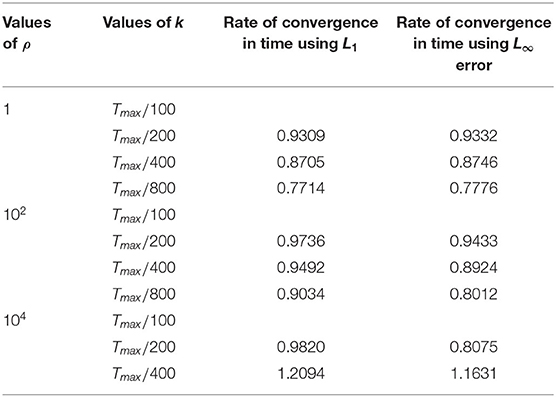
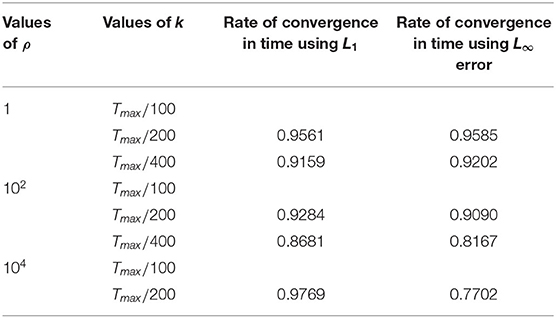
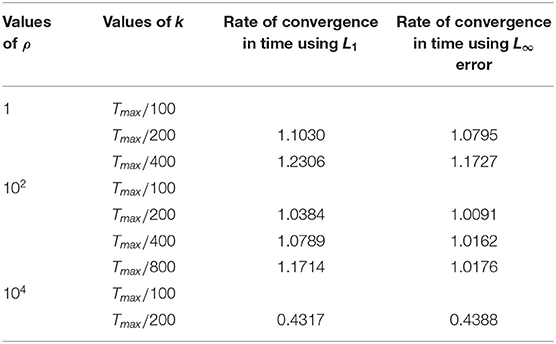
We have investigated in this paper the spectral analysis and optimal step sizes for some finite difference methods discretising Fisher's equation. We used three methods namely; FTCS, NSFD, and EEFD in order to solve Fisher's equation with a coefficient of reaction being 10, 102, and 104. We studied the properties of the methods such stability, positivity, and boundedness. This is the one of rare article which includes the estimate errors for the methods studied. Numerical results are displayed at optimal time step size with h = 0.01 for the three cases for the three methods used. We also obtained numerically the rate of convergence as shown in Tables 4–6. We have shown from Tables 1–3 that all the three methods (FTCS, NSFD, and EEFD) perform well for the small coefficient of reaction. It is worthy mentioning that freezing coefficient technique with Von Neumann Stability Analysis only present an approximate stability region for standard methods discretising non linear partial differential equations which might give reason to the standard method in Table 1 to perform better than the NSFD. Furthermore the NSFD in regard to the discrete representation derivative in Mickens [39] rule has nontrivial denominator function and make use of positivity and boundedness conditions. Finally the results are dependent on initial conditions used. For ρ = 1, the difference in L1 and L∞ errors from the three methods is very small which lead to conclude that the best methods are FTCS and NSFD. Also for ρ = 102 and ρ = 104, the best method are EEFD and NSFD, respectively. Our results matched with the one found in Lubuma and Roux [47] for numerical experiment for small reaction term. Moreover, Lubuma and Roux [47] proved that NSFD is elementary stable. As NSFD methods, the EEFD displayed in this article do not require any knowledge of the exact solution of the differential equation. Contrast to that, the best finite difference scheme is stable for large grid sizes but costly in inaccuracies at the propagation front.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
The plan of the paper was prepared by AA. The coding was done by KA and BI. All authors helped in writing the manuscript, contributed to the article, and approved the submitted version.
Funding
KA is supported by Postdoctoral Research Fellowship (PDRF) from North-West University (Source of funding: NWU PDRF Fund NW.1G01487). AA is supported by Nelson Mandela University for this research.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
KA is grateful to the North-West University for the Postdoctoral Research Fellowship (PDRF). AA thank Nelson Mandela University for the financial support. Finally, all the authors are grateful to the two reviewers who provided feedback which enabled to improve the paper considerably.
References
1. Gardner CS, Greene JM, Kruskal MD, Miura RM. Method for solving the Korteweg-de Vries equation. Front Neurosci Phys Rev Lett. (1967) 19:1095. doi: 10.1103/PhysRevLett.19.1095
2. Weiss J, Tabor M, Carnevale G. The Painlevé property for partial differential equations. J Math Phys. (1983) 155:522–6. doi: 10.1063/1.525721
3. Kudryashov NA. On types of nonlinear nonintegrable equations with exact solutions. Phys Lett A. (1991) 24:269–75. doi: 10.1016/0375-9601(91)90481-M
4. Lou SY, Huang GX, Ruan HY. Exact solitary waves in a convecting fluid. J Phys A Math Gen. (1991) 24:L587. doi: 10.1088/0305-4470/24/11/003
5. Kudryashov NA. Exact solutions of a family of Fisher equations. Theor Math Phys. (1993) 94:211–218. doi: 10.1007/BF01019332
6. Kudryashov NA. Numerical convective schemes based on accurate computation of space derivatives. J Comput Phys. (1973) 13:100–13. doi: 10.1016/0021-9991(73)90128-9
7. Cooley JW, Lewis P, Welch P. The finite Fourier transform. IEEE Trans Audio Electroacoust. (1969) 17:77–85. doi: 10.1109/TAU.1969.1162036
8. Gazdag J, Canosa J. Numerical solution of Fisher's equation. J Appl Probab. (1974) 11:445–57. doi: 10.2307/3212689
9. Fisher RA. The wave of advance of advantageous genes. Ann Hum Genet. (1937) 17:355–69. doi: 10.1111/j.1469-1809.1937.tb02153.x
10. Moran PAP. The Statistical Processes of Evolutionary Theory. Oxford: Clarendon Press; Oxford University Press (1962).
11. Kendall DG. A Form of Wave Propagation Associated With the Equation of Heat Conduction. Cambridge: Cambridge University Press (1948).
12. Kolmogorov AN. Étude de l'équation de la diffusion avec croissance de laquantité de matière et son application à un problème biologique. Bull Univ Moskow Ser Internat A. (1937) 1:1–25.
13. Canosa J. On a nonlinear diffusion equation describing population growth. IBM J Res Dev. (1937) 17:307–13. doi: 10.1147/rd.174.0307
14. Jeffrey A, Kakutani T. Weak nonlinear dispersive waves: a discussion centered around the Korteweg-de Vries equation. Siam Rev SIAM. (1972) 14:582–643. doi: 10.1137/1014101
15. Kudryashov NA, Zakharchenko AS. A note on solutions of the generalized Fisher equation. Appl Math Lett. (2014) 32:53–6. doi: 10.1016/j.aml.2014.02.009
16. Newman TJ, Kolomeisky EB, Antonovics J. Population dynamics with global regulation: the conserved Fisher equation. Phys Rev Lett. (2004) 92:228103. doi: 10.1103/PhysRevLett.92.228103
17. Chen BM, Kojouharov HV. Non-standard numerical methods applied to subsurface biobarrier formation models in porous media. Bull Math Biol. (1999) 61:779–98. doi: 10.1006/bulm.1999.0113
18. Yatat V, Couteron P, Dumont Y. Spatially explicit modelling of tree-grass interactions in fire-prone savannas: a partial differential equations framework. Ecol Complex. (2018) 36:290–313. doi: 10.1016/j.ecocom.2017.06.004
19. Wang XY. Exact and explicit solitary wave solutions for the generalised Fisher equation. Phys Lett A. (1988) 131:277–9. doi: 10.1016/0375-9601(88)90027-8
20. Chandraker V, Awasthi A, Jayaraj S. A numerical treatment of Fisher equation. Procedia Eng. (2015) 131:1256–62. doi: 10.1016/j.proeng.2015.11.481
21. Ismail HN, Raslan K, Rabboh AAA. Adomian decomposition method for Burger's-Huxley and Burger's-Fisher equations. Appl Math Comput. (2004) 159:291–301. doi: 10.1016/j.amc.2003.10.050
22. Moghimi M, Hejazi FSA. Variational iteration method for solving generalized Burger-Fisher and Burger equations. Chaos Solitons Fractals. (2007) 33:1756–61. doi: 10.1016/j.chaos.2006.03.031
23. Fahmy ES. Travelling wave solutions for some time-delayed equations through factorizations. Chaos Solitons Fractals. (2008) 38:1209–16. doi: 10.1016/j.chaos.2007.02.007
24. Mickens RE. Relation between the time and space step-sizes in nonstandard finite-difference schemes for the Fisher equation. Numer Methods Partial Differ Equ. (1997) 13:51–5. doi: 10.1002/(SICI)1098-2426(199701)13:1<51::AID-NUM4>3.0.CO;2-L
25. Ramos JI. Exponential methods for one-dimensional reaction-diffusion equations. Math Methods Appl Sci. (2005) 170:380–98. doi: 10.1016/j.amc.2004.12.003
26. Anguelov R, Kama P, Lubuma JMS. On non-standard finite difference models of reaction-diffusion equations. J Comput Appl Math. (2005) 175:11–29. doi: 10.1016/j.cam.2004.06.002
27. Hagstrom T, Keller HB. The numerical calculation of traveling wave solutions of nonlinear parabolic equations. SIAM J Scientific Stat Comput. (1986) 7:978–88. doi: 10.1137/0907065
28. Li S, Petzold L, Ren Y. Stability of moving mesh systems of partial differential equations. SIAM J Scientific Comput. (1998) 20:719–38. doi: 10.1137/S1064827596302011
29. Kudryashov NA. One method for finding exact solutions of nonlinear differential equations. Commun Nonlinear Sci Numer Simulat. (2012) 17:2248–53. doi: 10.1016/j.cnsns.2011.10.016
30. Polyanim AD, Zaitsev ZF. Handbook of Nonlinear Partial Differential Equations. 2nd ed. Chapman and Hall/CRC Press. (2011). p. 1912.
31. Qiu Y, Sloan DM. Numerical solution of Fisher's equation using a moving mesh method. J Comput Phys. (1998) 146:726–746. doi: 10.1006/jcph.1998.6081
32. Miyata T, Sakai Y. Vectorized total variation defined by weighted L infinity norm for utilizing inter channel dependency. In: 2012 19th IEEE International Conference on Image Processing. Orlando, FL: IEEE (2012).
33. Sutton OJ. Long time L∞(L2) a posteriori error estimates for fully discrete parabolic problems. arXiv[Preprint].arXiv:180303207. (2018). doi: 10.1093/imanum/dry078
34. Chen-Charpentier BM, Kojouharov HV. An unconditionally positivity preserving scheme for advection-diffusion reaction equations. Math Comput Model. (2013) 57:2177–85. doi: 10.1016/j.mcm.2011.05.005
35. Agbavon K, Appadu A, Khumalo M. On the numerical solution of Fisher's equation with coefficient of diffusion term much smaller than coefficient of reaction term. Adv Diff Equat. (2019) 2019:1–33. doi: 10.1186/s13662-019-2080-x
36. Durran DR. Numerical Methods for Fluid Dynamics (With Applications to Geophysics). Springer Science & Business Media (2010).
37. Taha TR, Ablowitz MI. Analytical and numerical aspects of certain nonlinear evolution equations, III. Numerical, Korteweg-de Vries equation. J Comput Phys. (1984) 55:231–53. doi: 10.1016/0021-9991(84)90004-4
38. Zabusky NJ, Kruskal MD. Interaction of solitons in a collisionless plasma and the recurrence of initial states. Phys Rev Lett. (1965) 15:240. doi: 10.1103/PhysRevLett.15.240
39. Mickens RE. Dynamic consistency: a fundamental principle for constructing nonstandard finite difference schemes for differential equations. J Diff Equat Appl. (2005) 11:645–53. doi: 10.1080/10236190412331334527
40. Kumar Verma A, Kayenat S. On the stability of Micken's type NSFD schemes for generalized Burgers Fisher equation. Chaos Solitons Fractals. (2019) 25:1706–37. doi: 10.1080/10236198.2019.1689236
41. Bhattacharya MC. An explicit conditionally stable finite difference equation for heat conduction problems. Int J Numer Methods Eng. (1985) 21:239–65. doi: 10.1002/nme.1620210205
42. Handschuh RF, Keith TG. Applications of an exponential finite-difference technique. Numer Heat Transfer A Appl. (1992) 22:363–78. doi: 10.1080/10407789208944773
43. Ĩnan B, Bahadır AR. An explicit exponential finite difference method for the Burger's equation. Eur Int J Sci Technol. (2013) 2:61–72.
44. Ĩnan B, Bahadır AR. Finite difference methods for the generalized Huxley and Burgers-Huxley equations. Kuwait J Sci. (2017) 44:20–7.
45. Macías-Díaz JE, Ĩnan B. Numerical efficiency of some exponential methods for an advection-diffusion equation. Int J Comput Math. (2019) 96:1005–29. doi: 10.1080/00207160.2018.1478416
46. Inan B, Osman M, Ak T, Baleanu D. Analytical and numerical solutions of mathematical biology models: the newell-whitehead-segel and allen-cahn equations. Math Methods Appl Sci. (2020) 43:2588–600. doi: 10.1002/mma.6067
Keywords: Fisher's equation, FTCS, NSFD, EEFD, optimal, convergence estimate, rate of convergence, coefficient of reaction
Citation: Agbavon KM, Appadu AR, Inan B and Tenkam HM (2022) Convergence Analysis and Approximate Optimal Temporal Step Sizes for Some Finite Difference Methods Discretising Fisher's Equation. Front. Appl. Math. Stat. 8:921170. doi: 10.3389/fams.2022.921170
Received: 15 April 2022; Accepted: 09 June 2022;
Published: 13 July 2022.
Edited by:
Raluca Eftimie, University of Franche-Comté, FranceReviewed by:
Soheil Salahshour, Bahcesehir University, TurkeyOluwaseun F. Egbelowo, University of Texas at Austin, United States
Copyright © 2022 Agbavon, Appadu, Inan and Tenkam. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Appanah Rao Appadu, cmFvLmFwcGFkdUBtYW5kZWxhLmFjLnph
 Koffi Messan Agbavon
Koffi Messan Agbavon Appanah Rao Appadu
Appanah Rao Appadu Bilge Inan
Bilge Inan Herve Michel Tenkam
Herve Michel Tenkam