Computer-assisted modeling of Quorum sensing in bacterial population exposed to antibiotics

A mathematical model for bacterial growth and control by antibiotics treatment, including Quorum sensing as a special kind of communication, is introduced. We aim in setting up a flexible model structure allowing for fast simulations and overview about the general behavior. The deterministic approach can be used for in silico studies of bacterial cooperative behavior in the special case of Quorum sensing. Since antibiotic treatment is the basic and vital way to fight pathogenic bacteria, in the present study, we propose a modification of a reaction-diffusion model of communication processes in a bacterial population exposed to antibiotics. The dynamical biological system is formalized by a system of semilinear parabolic PDEs. The numerical solution of the 2D problem is based on a hybrid computing procedure, which includes a finite difference method combined with a Monte-Carlo simulation of population dynamics. Computational experiments are performed to describe space-time distributions of key chemical compounds characterizing Quorum sensing during the growth of a bacterial population and its decrease resulting from the predetermined strategy of antibiotic treatment.

1. Introduction

Bacteria are not just single cells and acting individually, but have been discovered to form successful communities which have various possibilities to interact, within colonies but also beyond. One such mechanism, detected in more and more bacterial species, is the so-called “Quorum sensing” [1]. It is based on an intracellular gene regulation system and uses signal molecules, the so-called, which are produced inside the cells and can be transported and diffuse in the extracellular space.

Quorum sensing systems are known to control many important phenotypic changes of the bacteria. Historically first luminescence of the marine bacterial species Vibrio fischeri was found in the light organ of the squid Euprymna scolopes. Later, more and more species were found to use similar systems for different purposes, like pathogenicity and biofilm production [2]. Furthermore, Quorum sensing may even influence the resistance against several stressors like antibiotics to some extent, as considered e.g., in [3].

More concretely, we consider the Gram-negative bacterial species Pseudomonas putida IsoF, whose Quorum sensing system is quite well-known and has been used in many previous publications as a model organism for this purpose. Even though, this sounds very specific, P. putida uses a type of Quorum sensing system as many other Gram-negative bacteria also do, with slight differences in the molecule structure, but analogous architecture of the gene regulation system [4]. Usually, they use so-called Acyl-homoserine lactones (short: AHL) as autoinducer molecules. Thus, the ppu system of P. putida can be taken as prototype system, and the mathematical modeling can easily be transferred also to other species and their Quorum sensing systems. As a special property, P. putida also produces an enzyme which can degrade autoinducers, the so-called Lactonase [5]. Corresponding models have been considered in previous publications and can be taken as standard [6, 7].

However, as a main treatment of bacterial infections in patients since many decades, antibiotics are used, fight against bacterial infections and to kill or at least reduce growth of the bacteria. We aim in setting up a simple and fast to calculate model. This means, we focus on the most essential parts: growth of whole colonies, decrease during the presence of antibiotics. To keep it as simple as possible, we neglect any refined structures of the colony growth, as they may play a minor role for our purposes. Based on this, we want to keep the basic Quorum sensing model in, including the Lactonase in the model setup. By that we can always check, if (and when) the Quorum sensing system, including the behavioral changes controlled by it, is active or not, given a certain antibiotics treatment.

For our in silico study, we focus on the situation of bacterial colonies, e.g., on surfaces of medical devices or on laboratory equipment. They can be easier ”treated” than bacterial infections in a living host, where many side aspects may play a role. We want to set up a prototype model which is easy to handle, but already provides the structure to be adapted to more concrete situations. The hybrid structure contains a time-dependent colony growth including an explicit saturation and the effect of the antibiotics treatment on the one hand side, as well as a classic reaction-diffusion model to describe the spread of AHL and Lactonase molecules on a surface layer. For the antibiotics treatment we assume for simplification that it can be applied on the whole surface at once, e.g., by putting a water-based layer above which contains the antibiotics in a homogeneous concentration. Thus, it is sufficient to use one homogeneous time-dependent variable for the antibiotics for the whole system.

The model approach allows to easily make simulations, to place the bacterial colonies, also to handle many of them at once. It provides a simplified structure, which can also be easily used to control such systems, e.g., how a treatment should look like to keep a bacterial population under control, such that it doesn't activate it's Quorum sensing system and by that doesn't become pathogenic.

The present study aims in the development of the mathematical model of Quorum sensing in a Gram-negative bacterial population under the inhibitory action of antibiotics. The overall goal is to design a hybrid model that provides a quick approach by combining the continuous deterministic approach (expressed by the reaction-diffusion model of bacterial communication) and the discrete stochastic simulation of vital activity of bacteria exposed to antibiotics. By that, we keep the model as simple as possible to focus on the essential behavior. The paper is organized as follows. The mathematical statement of the reaction-diffusion problem, the applied numerical method, and the computational setup are presented in Section 2. Section 3 focuses on the computer simulations of space-time distributions of key characteristics of Quorum sensing for P. putida bacterial species. We will perform a full cycle of mathematical modeling and computer simulation to explore the changes in chemical compounds characterizing bacterial communication at varying strategies of antibiotic treatment.

2. Mathematical problem statement and computational details

2.1. Governing equations for modeling of bacterial Quorum sensing

The basic model of the bacterial communication process describes the dynamics of changes in concentrations of key chemical compounds such as AHL and Lactonase, which characterize the “quorum level” in a bacterial population and the “level” of its degradation, respectively [8]. The bacterial Quorum sensing model can be referred to as a reaction-diffusion dynamical system. In the two-dimensional case, the mathematical model is expressed by an initial-boundary value problem for a system of partial differential equations:

$\begin{array}{ll}\frac{\partial U}{\partial t}=D_U\Delta U-{\gamma }_{U}U-{\gamma }_{L\to U}LU+F_1\left(x,y,t,U\right),& (1)\end{array}$

$\begin{array}{l}\frac{\partial L}{\partial t}=D_L\Delta U-{\gamma }_{L}L+F_2\left(x,y,t,U\right),\\ 0<x<l,0<y<l,0<t\le t_{ob},& (2)\end{array}$

$\begin{array}{ll}U\left(x,y,0\right)=0,L\left(x,y,0\right)=0,0\le x\le l,0\le y\le l,& (3)\end{array}$

$U\left(0,y,t\right)=0,U\left(l,y,t\right)=0,L\left(0,y,t\right)=0,L\left(l,y,t\right)=0,$

$\begin{array}{l}U\left(x,0,t\right)=0,U\left(x,l,t\right)=0,L\left(x,0,t\right)=0,\end{array}$

$\begin{array}{ll}L\left(x,l,t\right)=0,0<t\le t_{ob},& (4)\end{array}$

where U(x, y, t) is the AHL concentration and L(x, y, t) is the Lactonase concentration produced by bacteria, both given in mol/l; l is the linear size of the solution domain in μm; t_ob is the observation time in h; γ_U, γ_L→U, γ_L, D_U, D_L are model parameters (detailed description below) associated with the processes of diffusion and degradation of main chemical compounds.

The governing Equations (1)–(2) describe the dynamics and diffusion of AHL and Lactonase concentrations, the natural degradation of AHL and Lactonase, degradation of AHL by Lactonase due to the negative feedback, the production of AHL and the reaction of Lactonase resulting from the positive feedback. The generation terms F₁(x, y, t, U) and F₂(x, y, t, U) are defined by the assumed normal distribution of bacterial population density and the Hill function taking into account the possible changes in bacterial concentration:

$\begin{array}{l}{F}_m\left(x,y,t,U\right)=N\left(t\right){\displaystyle \sum _{v=1}^V}{f}_{m}exp\left(-\frac{{\left(x-x_c^v\right)}^2+{\left(y-y_c^v\right)}^2}{{\sigma }^2}\right),\\ m=1,2,& (5)\end{array}$

$\begin{array}{l}{f}_1\left(U\right)={\alpha }_U+{\beta }_U\frac{U^n}{\left({\left(U_{th}\right)}^n+U^n\right)},\\ f_2\left(U\right)={\beta }_L\frac{U^n}{\left({\left(U_{th}+\epsilon \right)}^n+U^n\right)},& (6)\end{array}$

where $\left(x_c^v,y_c^v\right)$ is the position of the bacterial colony with the number v; N(t) is the normalized function defined the dynamics of a bacterial population density; σ = σ(t), ε, α_U, β_U, β_L, U_th, n are model parameters, which specify the principles underlying the time dependence of the bacterial population density and its spatial distribution in the solution domain.

Therefore, the mathematical model is formalized by an initial-boundary value problem for the system of semilinear reaction-diffusion PDEs. Some remarks devoted to the existence and uniqueness of solutions can be found in [8] supported by theoretical reviews [9, 10]. Obviously, the construction of analytical solutions for the considered problem meets essential difficulties. Thus, we focus in our present study on the application of numerical methods, namely a finite difference method combined with a stochastic procedure for the simulation of the bacterial population dynamics, to obtain solutions of the problem (1)–(6).

2.2. Numerical scheme for solving the problem

The equations of the system (1)–(2) could be written in the following general form:

$\begin{array}{ll}\frac{\partial u}{\partial t}=D\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)-qu+F,& (7)\end{array}$

where u = U, q = γ_U + γ_L→UL, D = D_U, F = F₁ for Equation (1) and u = L, q = γ_L, D = D_L, F = F₂ for Equation (2).

To solve the problem numerically, we apply a splitting finite-difference method [11]. For instance, we use the concept of the Peaceman-Rachford alternating direction method. Notice that the main advantage of the method is a fairly good correlation between accuracy and computational costs. This method is quite simple in programming, at the same time, for standard problems it is absolutely stable and has the second order of accuracy with respect to space and time variables. For small Courant numbers, this method is used even to test other schemes. The disadvantages of this scheme include conditional convergence when the number of spatial variables is more than two. In addition, this method is conditionally stable when solving problems with the Neumann and Robin boundary conditions [11, 12]. Since our particular problem does not have such limitations, the alternating direction method turned out to be a promising candidate for constructing a numerical algorithm.

Here, let us introduce ${\Omega }_{h_1,h_2}^{\tau }$ as a space-time grid covering the solution domain:

$\begin{array}{l}{\Omega }_{h_1,h_2}^{\tau }=\{x_i=(i-1)h_1,i=\overline{1,N+1},y_j=(j-1)h_2,\\ j=\overline{1,M+1},t^k=(k-1)\tau ,k=\overline{1,K+1}\}.\end{array}$

To deal properly with functions, we introduce the discrete function space of grid functions, which is isomorphic to finite dimensional Euclidean spaces. Further, the space of grid functions is equipped with an appropriate discrete norm (for instance, l₂ norm is further used).

Therefore, we have the following finite difference approximation on the first temporal semi-step k + 1/2 for i = 2, 3, ..., N, j = 2, 3, ..., M, k = 1, 2, ..., K:

$\begin{array}{l}\left[-\frac{D\tau }{2h_1^2}\right]u_{i-1,j}^{\left(s+1\right)}+\left[1+\frac{D\tau }{2h_1^2}+\frac{\tau q_{i,j}^{k+1/2}}{2}\right]u_{i,j}^{\left(s+1\right)}\\ +\left[-\frac{D\tau }{2h_1^2}\right]u_{i+1,j}^{\left(s+1\right)}=u_{i,j}^k+\frac{D\tau }{2h_2^2}\left[u_{i,j-1}^k-2u_{i,j}^k+u_{i,j+1}^k\right]\\ +\frac{\tau }{2}\tilde{F},& (8)\end{array}$

where the iterative sequence $u_{i,j}^{\left(s\right)}$, s = 1, 2, ..., converges to the $u_{i,j}^{k+1/2}$, starting with $u_{i,j}^{\left(1\right)}=u_{i,j}^k$; $q_{i,j}^{k+1/2}={\gamma }_U+{\gamma }_{L\to U}{L}_{i,j}^{k+1/2}$ for the Equation (1) and $q_{i,j}^{k+1/2}={\gamma }_L$ for the Equation (2).

In this case, we supplement the computational scheme by the iterative procedure due to the presence of nonlinear terms in the generation parts of equations. In order to calculate the Lactonase concentration, we set $\tilde{F}=F\left(x_i,y_j,t^k,U_{i,j}^k\right)$ for the Equation (2). Further, we suppose that $\tilde{F}=F\left(x_i,y_j,t^k,U_{i,j}^{\left(s\right)}\right)$ to calculate the AHL concentration with the Equation (1). And then, we again solve Equation (2) with $\tilde{F}=F\left(x_i,y_j,t^k,U_{i,j}^{\left(k+1/2\right)}\right)$ to obtain the update distribution of the Lactonase concentration.

In a similar way, we can derive the computational scheme for the second time semi-step k + 1:

$\begin{array}{l}\left[-\frac{D\tau }{2h_2^2}\right]u_{i,j-1}^{\left(s+1\right)}+\left[1+\frac{D\tau }{2h_2^2}+\frac{\tau q_{i,j}^{k+1}}{2}\right]u_{i,j}^{\left(s+1\right)}+\left[-\frac{D\tau }{2h_2^2}\right]u_{i,j+1}^{\left(s+1\right)}\\ =u_{i,j}^{k+1/2}+\frac{D\tau }{2h_1^2}\left[u_{i-1,j}^{k+1/2}-2u_{i,j}^{k+1/2}+u_{i+1,j}^{k+1/2}\right]+\frac{\tau }{2}\tilde{F},& (9)\end{array}$

where the iterative sequence $u_{i,j}^{\left(s\right)}$, s = 1, 2, ..., converges to the $u_{i,j}^{k+1}$, starting with $u_{i,j}^{\left(1\right)}=u_{i,j}^{k+1/2}$; $q_{i,j}^{k+1}={\gamma }_U+{\gamma }_{L\to U}{L}_{i,j}^{k+1}$ for the Equation (1); $q_{i,j}^{k+1}={\gamma }_L$ for the Equation (2); $\tilde{F}=F\left(x_i,y_j,t^{k+1},U_{i,j}^{\left(k+1\right)}\right)$ for (2) and $\tilde{F}=F\left(x_i,y_j,t^k,U_{i,j}^{\left(s\right)}\right)$ for (1). The systems defined by (8)–(9) are supplemented by discrete initial and boundary conditions:

$\begin{array}{ll}{u}_{i,j}^1=0,i=1,2,...,N+1,j=1,2,...,M+1,& (10)\end{array}$

$u_{i,1}^k=0,u_{i,M+1}^k=0,i=1,2,...,N+1,k=2,3,...K+1,$

$\begin{array}{ll}{u}_{1,j}^k=0,u_{N+1,j}^k=0,j=1,2,...,M+1,k=2,3,...K+1,& (11)\end{array}$

To solve the systems of linear equations on each time layer, we apply the Thomas algorithm.

2.3. Computational algorithm for simulation of bacterial population dynamics

The mathematical problem statement allows us to calculate the space-time distributions of chemical compounds regulating Quorum sensing for bacterial colonies, which are located at a priori defined positions in the computational domain. At the same time, we can provide simulations in a more realistic manner by including the algorithm of modeling bacterial population dynamics into the general computation scheme. In the present study, we use the ideas of a stochastic generation and the logistic growth of a bacterial population. The approach to constructing a hybrid scheme combining a deterministic model and stochastic modeling of bacterial evolution has been proposed before and successfully tested in our previous studies [7, 13, 14].

The computational algorithm is based on the following assumptions. During the observation process, bacteria colonies of circular shapes are growing stochastically on the plane OXY according to the logistic law. First, up to three bacterial colonies start to grow simultaneously from randomly chosen points $\left(x_c^v,y_c^v\right)$, and besides, with different probabilities, i.e. the probability of appearance of one colony is essentially greater than for two and three (for example, for one colony p¹ = 0.6, for two colonies p² = 0.3, and for three colonies p³ = 0.1). According to the Monte-Carlo method, a new bacterial colony can appear at a random time, but with a small probability on each time layer (for instance, p^v = 0.1). The linear size (radius) of each bacterial colony is denoted by $R\left(x_c^v,y_c^v,t\right)$. The time-dependent value of R is calculated by the logistic law of growth:

$\begin{array}{ll}{R}^v\left(t\right)=\frac{I{R}_{0}exp\left(rt\right)}{I+R_0\left(exp\left(rt\right)-1\right)},v=1,2,...V,& (12)\end{array}$

where R₀ is the initial linear size of a bacterial colony, which can grow up by assumption to a limiting linear size of I, in μm, and r is the parameter related to the rate of bacterial growth in 1/h.

Here, we suppose that all bacterial colonies grow with a similar velocity. If the colonies are overlapping, the source functions F₁ and F₂ are determined by a superposition of corresponding contributions. Note also that the parameter σ in (5) is approximately estimated according to the “3-Sigma rule,” specifically, as R^v(t)/3.

Further, we start the degradation of a bacterial population by simulating the action of antibiotics at a defined time, when the total bacterial concentration reaches 4.6·10¹¹ cells/l. This value corresponds to the normalized value of N(t) equaled to the unit. At the same time, we stop “generating” new bacterial colonies.

In addition, we need to formalize the relation between the linear size of bacterial colonies and the antibiotic action. In the present study, we apply a simplified approach. We suppose that the concentration of antibiotics does not depend on spatial coordinates, but is homogeneous on the whole surface, and it can be specified as a time-dependent function. To be precise, let us consider the antibiotics of ciprofloxacin as an example [15]. An approximation of concentration dynamics for ciprofloxacin can be plotted with the use of empirical data: the maximum value reaches at time moment 4–8 h and approximately after 12–24 h the concentration falls to a certain level. We use the Rayleigh distribution for the approximation:

$\begin{array}{ll}A\left(t\right)=A_{0}texp\left(\frac{-t^2}{A_1}\right).& (13)\end{array}$

Hence, we can assume for simplicity that the linear size of each bacterial colony reduced due to antibiotic action can be expressed as follows:

$\begin{array}{ll}{R}^v\left(t\right)={\tilde{R}}^v\left(t\right)\left(1-\theta \frac{A^2\left(t\right)}{A^2\left(t\right)+m}\right),v=1,2,...V,& (14)\end{array}$

where ${\tilde{R}}^v\left(t\right)$ is the current value of the linear size of v colony; θ is the empirical constant provided the certain density of alive population; the parameter m corresponds to the maximum value of antibiotic concentration.

Further, to determine the time-dependent bacterial density N(t) (the normalized value) we assume here for simplicity that this function can be described by the formula for the growth range:

$\begin{array}{ll}N\left(t\right)={\left(1+exp\left(-\mu \left(t-b_1\right)\right)\right)}^{-1},t\le t_d,& (15)\end{array}$

and we use the following expression to approximate decreasing in the bacterial population density as a result of the degradation due to a single antibiotic treatment:

$\begin{array}{ll}N\left(t\right)=a+b{\left(1+exp\left(\mu \left(t-b_2\right)\right)\right)}^{-1},t>t_d,& (16)\end{array}$

where a, b₁, b₂, μ are approximation parameters, which, in particular, provide a smooth behavior of N(t) at time moment t_d.

Notice that the Equations (15)–(16) provide a model description of time-dependent behavior of the bacterial concentration (namely, the periods of bacterial growth and degradation to equilibrium values, the velocity of changes in concentration, the relative level of degradation). The ”height” of the bacterial concentration is influenced by the parameters α_U, β_U, α_L, and the corresponding dimensions are correspondent to the basic Equations (5)–(6).

Therefore, the space distribution of a bacterial population is stochastically simulated on each time layer, taking into account the mechanisms of growth and degradation. At the same time, for all bacterial colonies, we calculate the corresponding bacterial concentration in view of the growth or degradation phase.

3. Computational experiments results and discussions

3.1. General algorithm, specification of the model object, and computational setup

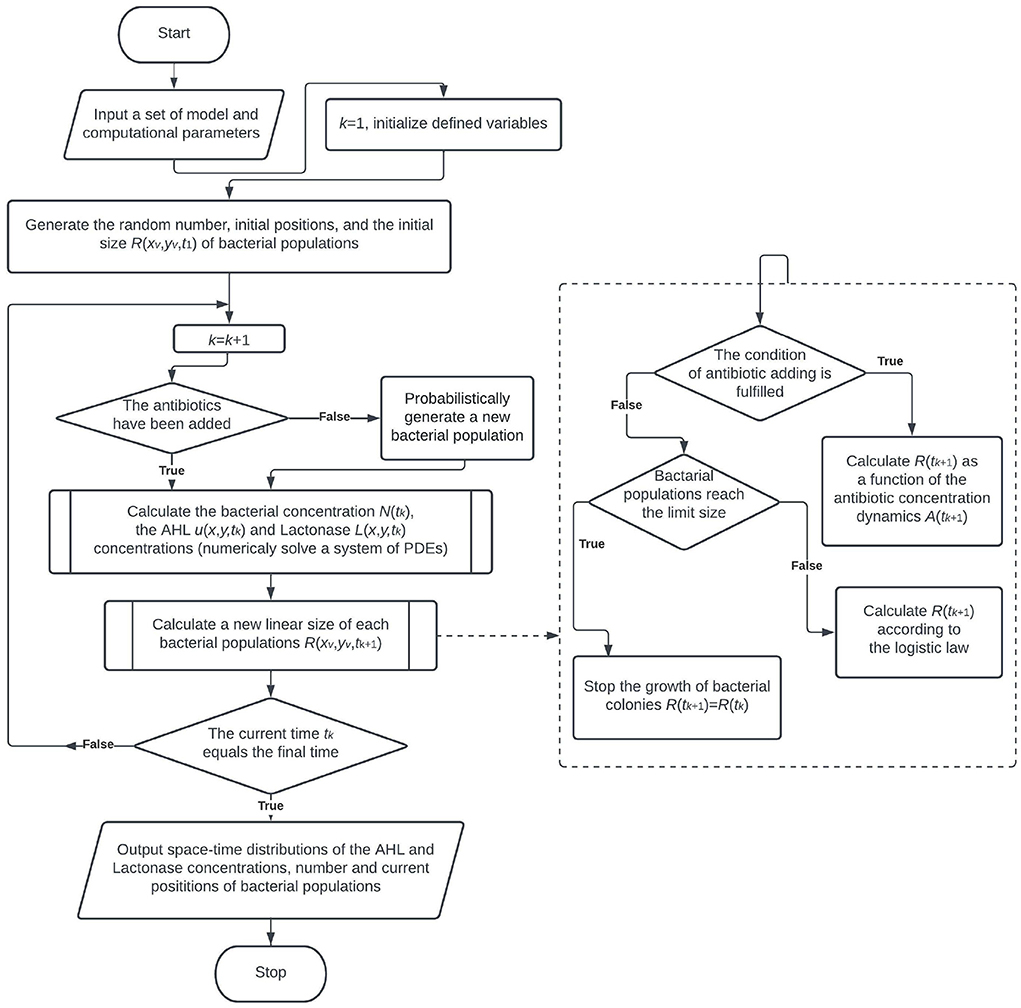
By construction, the procedure of model implementation includes the Monte-Carlo simulation of bacterial population growth, the finite difference iterative scheme to solve PDEs and calculate the chemical compounds, the algorithm for simulation of the degradation of a bacterial population due to antibiotic action, and the functional dependence for bacterial concentration, taking into account the time-dependent decrease of the bacterial amount. The flowchart of the general computational algorithm is shown in Figure 1.

FIGURE 1

Figure 1. The flowchart of the general algorithm.

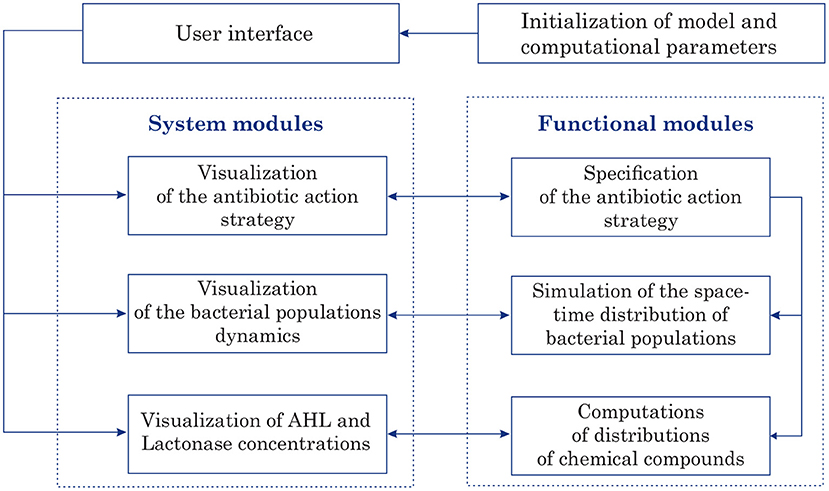
The program implementation of 2D model of bacterial Quorum sensing was performed in Matlab. The designed software is intended for computer simulations of space-time distributions of chemical compounds such as AHL and Lactonase concentrations at given parameters. Figure 2 illustrates the program application architecture diagram. In these terms, conducting simulations requires initialization of the model as well as computational parameters. The graphical user interface (GUI) permits to submit all parameters and options that are necessary to accomplish a quorum sensing simulation. The GUI provides options to access the core system and modules that compute and visualize the antibiotic strategy (as time-dependent function of an antibiotic concentration), characteristics of bacterial populations (location at each moment, summarized linear size, total amount, etc.), and space-time distributions of main characteristics of quorum sensing, namely AHL and Lactonase concentrations during the observation process.

FIGURE 2

Figure 2. The program application architecture diagram.

For instance, we will consider Pseudomonas putida IsoF as an object of mathematical modeling [16].

Pseudomonas putida is a Gram-negative rod-shaped bacterium of Pseudomonas genus, that lives in soils, waters, and plants. Generally, P. putida is defined as a nonpathogenic bacterium due to the lack of virulence-related genes [17]. P. putida IsoF is considered as an object due to its versatility and ease of handling to examine Quorum sensing. Note also that recent research suggests that P. putida can be a human pathogen causing nosocomial infections in patients with a weakened immune system like cancer patients and newborns [18]. P. putida can provide the exchange platform for more virulent and antibiotic resistant microorganisms such as deadly Pseudomonas aeruginosa [19]. Most infections caused by P. genus demonstrate resistance to certain antibiotics and their combinations. Therefore, P. putida represents an important model organism to perform simulations of Quorum sensing characteristics in a bacterial population under antibiotic action.

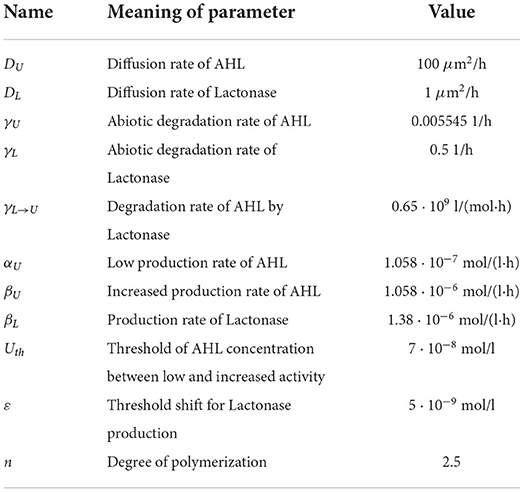
Let us assume that we have a two-dimensional domain limited by 0 ≤ x ≤ 100 μm and 0 ≤ y ≤ 100 μm. The time of observation is up to 50–100 h. We choose the model parameter values as listed in Table 1 using previously estimated values [8]. The empirical parameter θ in (14) is fixed to be 0.2. The time of start of antibiotic action is estimated as t_d = 10 − 16 h.

TABLE 1

Table 1. Parameter values estimated for the bacterium P. putida.

The values of the parameters for bacterial density approximation (15)–(16) are established empirically from microbiological experiments for Pseudomonas bacterial species [20, 21]. We specify a following set of approximation parameters for the bacterial dynamics: b₁ = 6 h, b₂ = 18 h, μ = 1.4 1/h. Figure 3 illustrates the time-dependent behavior of bacterial density for the species P. putida. In this case, we suppose 30% decreasing in the bacterial population density within 10 h due to a single antibiotic action.

FIGURE 3

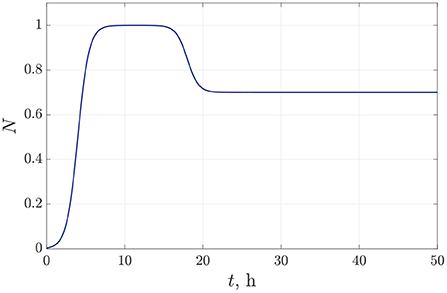
Figure 3. The time dependence of the normalized bacterial density under single antibiotic treatment.

In addition, we conducted a numerical study of the stability of a constructed computational scheme. As far as the initial and boundary conditions are strictly defined for the corresponding chemical substances, here we examine the stability of the computational scheme by variation of the “amplitude part” of the generating terms defined by F_m. In more detail, we vary the parameters of α_U, β_U, and β_L. Here we assume that the parameters of α_U, β_U, and β_L alternately increase by 20, 30, 40, 50% while the others remain the same (with respect to the initial values as listed in Table 1). In order to estimate the perturbations of grid functions under the “amplitude parameters” variation, we use the following estimations: ${\xi }_m=\Vert {Ū}_m-U_{m-1}{\Vert }_2/\Vert U_{m-1}{\Vert }_2,{\phi }_m=\Vert {\bar{L}}_m-L_{m-1}{\Vert }_2/\Vert L_{m-1}{\Vert }_2,m=2,3,4,5$, where m = 1 corresponds to the AHL and Lactonase concentrations calculated for the last time moment at h₁ = h₂ = 1 μm and τ = 0.01 h at initial parameters listed in Table 1. For these computations we suppose that there is only one bacterial colony located at the central position of the computational domain with a linear size of 10 μm.

Figure 4 shows the estimation of the perturbation of corresponding grid functions. These data suggest an appearance of slight perturbations of the AHL and Lactonase concentrations under the variation of the “source functions.” The almost linear growth of the estimations indicates the numerical stability of the computational algorithm.

FIGURE 4

Figure 4. The estimation of the perturbations of grid functions for AHL concentration (A), and the Lactonase concentration (B) under the variation of the parameters of generating terms α_U (1), β_U (2), and β_L (3).

3.2. Time-dependent simulations of Quorum sensing characteristics in bacterial population of P. putida under antibiotics action

We conducted numerical experiments for the 2D reaction-diffusion model combined with the procedure of the Monte-Carlo simulation of bacterial growth and further degradation of the population due to antibiotic action. According to the above algorithm, one, two or three bacterial colonies with a circular shape can start to grow at an initial time. The initial radius R₀ of each bacterial colony is set to be 1 μm. The parameter of the rate of logistics population growth is assumed to be r = 0.4 1/h, the limiting value of linear size is I = 20 μm. During the bacterial evolution process, a new bacterial colony appears with a small probability specified as 0.1 per time step of the simulation, chosen to be 0.5h. Concretely, for the first simulation, we had two bacterial colonies at the start moment and the total amount V, equaled to 4.

In the first case, we suppose that we do a single antibiotic treatment when the bacteria reach the critical value of population density. The time-dependent function (13) defining the dynamics of antibiotic concentration during the observation time is shown in Figure 5A. The parameters of the approximation (13) are set to be A₀ = 1.65 and A₁ = 32. Here we can claim that antibiotics reach an acting maximum concentration after 3.5–4 h after adding and acting during 10–13 h. Figure 5B illustrates the dynamics of the total value of linear size $R\left(t\right)={\sum }_{v=1}^V{R}^v\left(t\right)$ of bacterial colonies. We see that the bacterial population has time to reach the equilibrium value before we start the degradation by antibiotics at t = 12 h. After that, the R(t) leveled off at 2.017 μm.

FIGURE 5

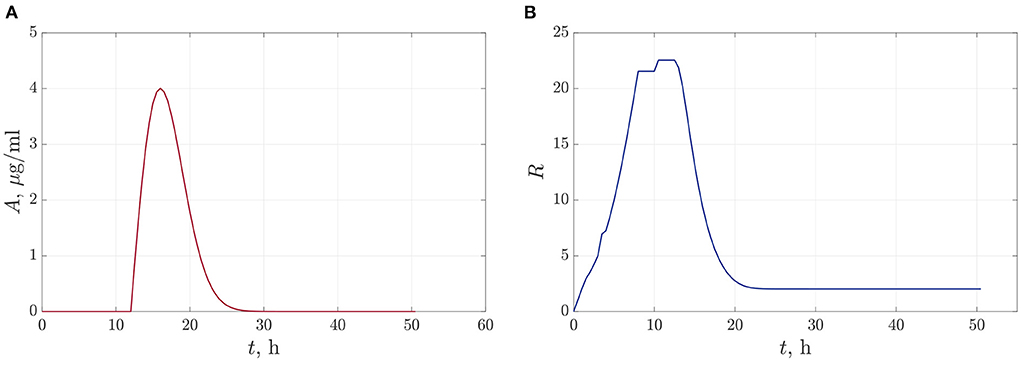
Figure 5. The dynamics of changes in antibiotic concentration (A), and the total linear size of bacterial colonies at single antibiotic treatment (B).

The following figures (Figures 6A,B) present the space distributions of key chemical compounds characterizing Quorum sensing in the bacterial community, namely the AHL and Lactonase concentrations calculated at a fixed time 12 h. In addition, graphs in Figure 7 visualize the maximum values of the AHL and Lactonase concentrations as time dependencies. These data indicate that the Lactonase concentration reached a maximum value before adding antibiotics, whereas the AHL concentration declined slightly due to the interaction between these players. The results suggest that the AHL concentration fell gradually, followed by a stabilization to the level of 4.89·10⁻¹⁰ mol/l, at the same time, the Lactonase concentration decreases more essential and leveled to the value of 6.76·10⁻¹³ mol/l. The average value of the AHL concentration equals 1.36·10⁻¹⁰ mol/l at the final time point.

FIGURE 6

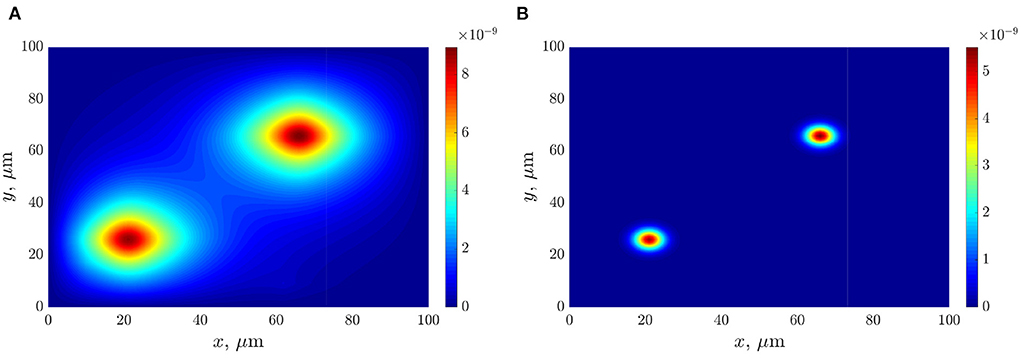
Figure 6. The distributions of chemical compounds calculated at time 12 h: (A)—the AHL concentration; (B)—the Lactonase concentration.

FIGURE 7

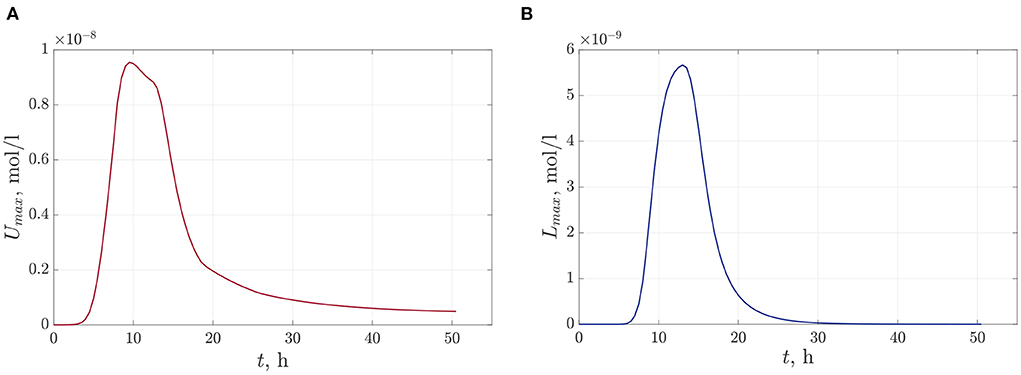
Figure 7. The time-dependent profiles of maximum values of chemical compounds during the observation time 50 h: (A)—the AHL concentration and (B)—the Lactonase concentration at single antibiotic treatment.

This means that antibiotic action affects the enzyme, preventing the bacterial quorum to a greater extent than the signaling substance that provides the quorum itself. We can observe that a small bacterial population that has been reduced by a factor of ten is still producing signaling molecules. This effect can be referred to as the emergence of increasing the resistance of reduced bacterial population. Hence, we can conclude that a single antibiotic treatment leads to a reduction in the bacterial population under the assumed conditions of computational experiments. However, the Quorum sensing level in a reduced population remains very high compared to a saturated population, and a bacterial population will be able to quickly restore their numbers in the presence of a nutrient medium. Therefore, the obvious strategies for suppressing Quorum sensing are to use a multiple antibiotic treatments strategy, an increasing antibiotic doze, a combination of different antibiotics, or even combining application of antibiotics and natural degrading enzymes.

3.3. A multiple antibiotic treatment strategy: Numerical experiments

Note that due to the stochasticity underlying the simulation of population generation and growth an exact reproduction of the computational experiments is not possible. Let us consider a computational experiment in which we apply a multiple antibiotic treatment strategy. For instance, we assume that antibiotic treatment was done three times, specifically at 12, 24, and 36 h (Figure 8A). In these terms, the function of bacterial density dynamics N(t) includes three degradation phases as presented in Figure 8B. Figure 9A shows the changes in the total bacterial linear size R(t) during the observation time. The graph is characterized by a sharp decline to the value of 4.8·10⁻⁵ μm. The simulations suggest a more significant decrease in the AHL concentration as presented in Figure 9B, where the maximum value corresponds to 1.78·10⁻¹⁰ mol/l at the final time t = 50 h. Nevertheless, the quorum level remains considerable even for a negligible population size. Concretely, the average value of AHL concentration is equal to 4.26·10⁻¹¹ mol/l at the last moment. This effect is caused by the diffusion processes and long relaxation time of the AHL concentration. Moreover, as we mentioned above, antibiotic adding has a strong effect on the Lactonase concentration, resulting in the suppression of this enzyme, which in turn does not essentially inhibit the AHL concentration.

FIGURE 8

Figure 8. The dynamics of changes in the antibiotic concentration—(A) and the normalized bacterial concentration dynamics—(B) under multiple exposure to antibiotics.

FIGURE 9

Figure 9. The time dependence of total linear size of bacterial colonies—(A) and the dynamics of the maximum values of the AHL concentration—(B) at the multiple antibiotic treatment.

We conducted a series of computational experiments, varying the interval between antibiotic treatment: 4, 8, 12, 16 h with a triple sequential addition of the same concentration. The findings allow us to conclude that all applied strategies lead to significant degradation of the bacterial population and a decrease in the AHL concentration. The total linear size of the population varies in the range of 2·10⁻⁵ − 4·10⁻⁴ μm and the average value of the AHL concentration changes from 2·10⁻¹¹ to 8·10⁻¹¹ mol/l at t = t_ob. It follows that the frequent use (within the considered range) of antibiotics does not confer treatment benefits.

It should be pointed out that we simulate the effect of a powerful antibiotic action in a simplified situation, excluding the growth of the population after treatment. However, as known, pathogenic species of the P. genus exhibit resistant behavior [22], i.e., capable of continuing their vital activity under antibiotic treatment. Obviously, the intervals of antibiotic exposure should not exceed the duration of the antibiotic action (in our case, it is about 16 h), otherwise the surviving population will strive to restore equilibrium amount.

Figures 10A–C show frames of evolution of a typical bacterial population growing in colonies under triple antibiotic treatment 12 h apart (12, 24, 36 h, respectively). In this computational experiment, we assume that the bacterial population can continue to grow after antibiotic action (for example, after 55 h), but more slowly than in the initial case (the parameter of the logistic growth r = 0.1). Also, new bacterial colonies can appear during simulations. The space distributions of the AHL concentration are presented in Figures 10D–F computed at fixed moments: at the beginning of bacterial evolution—5 h, at the beginning of antibiotic action—12 h, and at the final time 100 h. Figure 11 gives a detailed visualization of time-dependence of the total linear size of the population and the average value of the AHL concentration. Our data indicate that after 17 h, the population restored its numbers. At the same time, the “communication level” of the bacterial population is only 20% of the equilibrium value in the absence of inhibition due to antibiotics. This effect is caused by a long relaxation time of the AHL concentration and an additional increase in the Lactonase concentration.

FIGURE 10

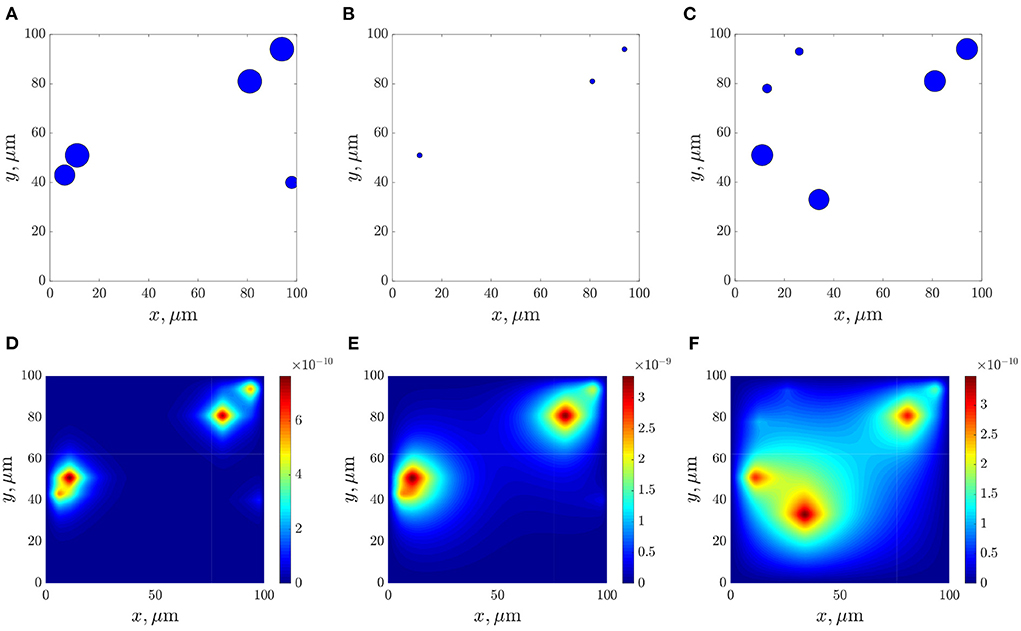
Figure 10. The dynamics of bacterial population (A–C), and the space distributions of the AHL concentration—(D–F), calculated at the corresponding moments 5, 12, and 100 h.

FIGURE 11

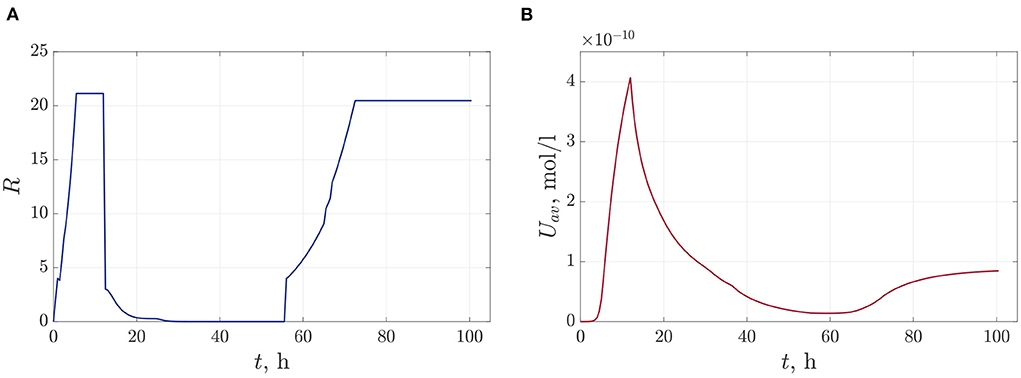
Figure 11. The time dependence of the total linear size of bacterial colonies—(A) and the dynamics of the average value of the AHL concentration—(B).

4. Conclusions

In summary, we have shown that the developed hybrid mathematical model allows to examine the behavior of key chemical compounds characterizing bacterial communication during antibiotic treatment. We have proposed suitable computational techniques to conduct time-dependent simulations of bacterial quorum sensing. The computational procedure for the model implementation includes the following points: First, we performed the Monte-Carlo simulation of bacterial maturation and population growth. Then, to estimate chemical compounds, the system of PDEs was numerically solved with the finite difference iterative scheme. Finally, we conducted simulations of the degradation of a bacterial population due to antibiotic action, taking into account the time-dependent decrease in the number of bacteria.

The continued insilico studies of bacterial cooperative behavior hold great promise in microbiology. Computational experiments based on the mathematical model of Quorum sensing in pathogenic bacteria provide a set of tools for building a new level of understanding of the mechanisms of response formation to external influences. The obtained data suggest that even a small bacterial population maintains an essential quorum, which will be able to restore the equilibrium population size provided the nutrient medium and in the absence of further external inhibitors (or, for example, a weak immune system). The big advantage of the presented approach is that it allows for a quick overview and estimate of the system behavior, what was our purpose here. Additional studies are required to modify the mathematical model, e.g., by introducing space-time distributions of bacterial biomass and antibiotic concentration, providing more details and accuracy, but requiring more computational effort and more detailed knowledge about the biological system. This general approach can be useful for further studies of optimal modes of antibiotic and other treatments.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author contributions

CK and AM designed the conceptualization, performed the numerical simulations, validation, analysis of results, and wrote the original manuscript. AM derived computational scheme and designed the computer program. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by TUM Publishing Fund and also partially supported by the Ministry of Science and Higher Education of the Russian Federation (project no. 122082400001-8, AM).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fuqua C, Greenberg EP. Listening on bacteria: acyl-homoserine lactone signalling. Nat Rev Mol Cell Biol. (2002) 3:685–95. doi: 10.1038/nrm907

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Williams P, Winzer K, Chan W, Camara M. Look who's talking: communication and quorum sensing in the bacterial world. Philos Trans R Soc B. (2007) 362:1119–34. doi: 10.1098/rstb.2007.2039

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lin LH, Wang JH, Yo JL, Li YY, Liu GX. Effects of Allicin on the formation of Pseudomonas aeruginosa biofilm and the production of Quorum-sensing controlled virulence factors. Pol J Microbiol. (2013) 62:243–51. doi: 10.33073/pjm-2013-032

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Whitehead NA, Barnard AML, Slater H, Simpson NJL, Salmond GPC. Quorum-sensing in Gram-negative bacteria. FEMS Microbiol Rev. (2001) 25:365–404. doi: 10.1111/j.1574-6976.2001.tb00583.x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Fekete A, Kuttler C, Rothballer M, Hense BA, Fischer D, Buddrus-Schiemann K, et al. Dynamic regulation of N-acyl-homoserine lactone production and degradation in Pseudomonas putida IsoF. FEMS Microbiol Ecol. (2010) 72:22–34. doi: 10.1111/j.1574-6941.2009.00828.x

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Buddrus-Schiemann K, Rieger M, Muhlbauer M, Barbarossa MV, Kuttler C, Hense BA, et al. Analysis of N-acylhomoserine lactone dynamics in continuous cultures of Pseudomonas putida IsoF by use of ELISA and UHPLC/qTOF-MS-derived measurements and mathematical models. Anal Bioanal Chem. (2014) 406:6373–83. doi: 10.1007/s00216-014-8063-6

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kuttler C, Maslovskaya A. Computer simulation of communication in bacterial populations under external impact of signal-degrading enzymes. Proc CEUR Worksh Proc. (2020) 2783:163–79.

8. Kuttler C. Reaction-diffusion equations and their application on bacterial communication. In: Rao ASRS, Pyne S, Rao CR, editors. Handbook of Statistics. Amsterdam: Elsevier (2017). p. 55–91. doi: 10.1016/bs.host.2017.07.003

CrossRef Full Text | Google Scholar

9. Lions JL, Magenes E. Non-Homogeneous Boundary Value Problems and Applications. Berlin; Heidelberg; New York, NY: Springer-Verlag (1972). doi: 10.1007/978-3-642-65161-8

CrossRef Full Text | Google Scholar

10. Evans LC. Partial Differential Equations. Providence, RI: American Mathematical Society (2010).

11. Samarskii AA. The Theory of Difference Schemes. Boca Raton, FL: CRC Press (2001). doi: 10.1201/9780203908518

CrossRef Full Text | Google Scholar

12. Glowinski R, Osher SJ, Yin W. Splitting Methods in Communication, Imaging, Science, and Engineering. Cham: Springer International Publishing (2016). doi: 10.1007/978-3-319-41589-5

CrossRef Full Text | Google Scholar

13. Kuttler C, Maslovskaya A. Hybrid stochastic fractional-based approach to modeling bacterial quorum sensing. Appl Math Model. (2021) 93:360–75. doi: 10.1016/j.apm.2020.12.019

CrossRef Full Text | Google Scholar

14. Kuttler C, Maslovskaya A, Moroz L. Numerical simulation of time-fractional diffusion-wave processes applied to communication in bacterial populations. In: Proceedings of the IEEE Days on Diffraction. St. Petersburg: IEEE (2021) p. 114–9. doi: 10.1109/DD52349.2021.9598648

CrossRef Full Text | Google Scholar

15. Rakhmawatie DD, Mustofa M, Sholikhah EN. Effects of ciprofloxacin concentrations on the resistance of uropathogen Escherichia coli: in vitro kinetics and dynamics simulation model. J Med Sci. (2020) 52:191–204. doi: 10.19106/JMedSci005203202001

CrossRef Full Text | Google Scholar

16. Cárcamo-Oyarce G, Lumjiaktase P, Kümmerli R, Eberl L. Quorum sensing triggers the stochastic escape of individual cells from Pseudomonas putida biofilms. Nat Commun. (2015) 6:5945. doi: 10.1038/ncomms6945

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Weimer A, Kohlstedt M, Volke DC, Nikel PI, Wittmann C. Industrial biotechnology of Pseudomonas putida: advances and prospects. Appl Microbiol Biotechnol. (2020) 104:7745–66. doi: 10.1007/s00253-020-10811-9

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Fernández M, Porcel M, de la Torre J, Molina-Henares MA, Daddaoua A, Llamas MA, et al. Analysis of the pathogenic potential of nosocomial Pseudomonas putida strains. Front Microbiol. (2015) 6:871. doi: 10.3389/fmicb.2015.00871

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Peter S, Oberhettinger P, Schuele L, Dinkelacker A, Vogel W, Dörfel D, et al. Genomic characterization of clinical and environmental Pseudomonas putida group strains and determination of their role in the transfer of antimicrobial resistance genes to Pseudomonas aeruginosa. BMC Genomics. (2017) 18:859. doi: 10.1186/s12864-017-4216-2

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Shen N, Jiang M, Wei P. The kinetic study on the production of hydantoinase and n-carbamoylase by Pseudomonas JS-01. J Nanjing Univ Chem Technol. (2001) 23:36–9.

21. Ditmarsch D, Xavier JB. High-resolution time series of Pseudomonas aeruginosa gene expression and rhamnolipid secretion through growth curve synchronization. BMC Microbiol. (2011) 11:1409. doi: 10.1186/1471-2180-11-140

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Žiemytė M, Carda-Diéguez M, Rodríguez-Díaz JC, Ventero MP, Mira A, Ferrer MD. Real-time monitoring of Pseudomonas aeruginosa biofilm growth dynamics and persister cells' eradication. Emerg Microbes Infect. (2021) 10:2062–75. doi: 10.1080/22221751.2021.1994355

PubMed Abstract | CrossRef Full Text | Google Scholar