- 1Department of Mathematics, College of Science & Arts, King Abdulaziz University, Rabigh, Saudi Arabia
- 2Department of Mathematics, University of Swabi, Swabi, Pakistan
- 3Department of Mathematical Sciences, University of Lakki Marwat, Lakki Marwat, Pakistan
- 4Department of Industrial Machines and Equipments, Faculty of Engineering, “Lucian Blaga” University of Sibiu, Sibiu, Romania
- 5Department of Civil Engineering, College of Engineering, Institute of Energy Infrastructure, Universiti Tenaga Nasional, Kajang, Selangor, Malaysia
Social media addiction (SMA) is the excessive use of social media platforms, resulting in negative consequences for individuals. It is characterized by an uncontrollable urge to use social media, leading to negative effects in human's life. This study aims to construct a mathematical model to conceptualize the transmission dynamics of SMA and explore the underlying mechanisms of this harmful addiction in the framework of fractional derivative. The fundamentals of fractional calculus are listed for examining the model. Equilibrium points are identified, and the reproduction parameter R0 is computed to understand the dynamics of SMA spread. Stability analysis of the equilibria is performed, and the impact of various input parameters is numerically investigated. The existence and uniqueness of the proposed SMA model are demonstrated through simulations, which also study the intricate dynamics with respect to different input factors. To develop effective control strategies, the system's dynamical behavior is examined, and the influence of fractional derivative order on fluctuations is explored. This research offers a range of suggestions aimed at reducing the occurrence of social media addiction.
1. Introduction
Social media and fractional calculus, social media addiction, mathematical model, Caputo-Fabrizio operator, numerical scheme, dynamical behavior internet are specific platforms and websites that facilitate social interactions, content sharing, and networking among users. These platforms typically have features that allow individuals to create profiles, connect with friends, share updates, photos, videos, and engage in conversations and communities [1–3]. Social media, when utilized properly, can help people develop essential abilities such as information access [4], self-directed learning [5], problem-solving [6], and business, but those who misuse it have a detrimental impact on them [7, 8]. The most important negative impact is social media addiction [8]. In the beginning, social media addiction appears to be safe, similar to addiction to gambling, alcohol, and narcotics, but it is a serious trend that has to be addressed [9]. The individuals who are spending much time on social media such as YouTube, Facebook, Twitter, Instagram, and other such platforms are called social media addicted individuals [6]. Despite the myriad benefits social media offers, it is crucial to exercise responsible usage and remain aware of potential downsides, including privacy issues, information overload, cyberbullying, and the risk of addiction. Signs and symptoms of social media addiction may include compulsive checking, neglecting responsibilities, tolerance, neglecting relationship, disturbance in sleeping, and impact on mental health.
Numerous methods have been presented in academic literature to comprehend various real-world situations [10–12]. Social media addiction has emerged as a prominent and pressing problem, garnering significant attention and concern within the academic and scientific community [13]. As a result of this, substantial research on this topic has been done in multiple nations [8, 13] and attracted many researchers. Affinity-based information diffusion in social networks can be analyzed using tools from Lie algebra, particularly through the concept of graph representations. In [14], the authors proposed a dynamical information diffusion model that incorporates the concept of affinity among individuals toward the information being disseminated in social networks. The activities associated with addiction can cause serious issues at home, work, and school which can have a negative impact on society as a whole [3, 4]. Before it has any more negative impacts than what we can now see, this issue needs to be addressed [9, 13]. The easiest approach to do this is to think about how social media addiction will affect your life. Advertising and informational campaigns regarding the harmful consequences of social media are seen as a form of control. The alternative strategy involves employing therapeutic techniques such as disabling notifications [6], setting time limits for social media use [7], deleting apps [15], disconnecting from technology [16], never using a smartphone in bed, and others. It has been acknowledged that there is a high negative impact of social media addiction; moreover, protective policies are required to reduce and manage its influence. Hence, we propose a mathematical model to comprehend the dynamics of social media dissemination, aiming to conceptualize the comprehensive phenomena and forecast potential control strategies that hold the capacity to ameliorate the adverse repercussions arising from social media addiction and foster more conducive usage patterns.
Fractional calculus offers a valuable mathematical framework for modeling complex phenomena, analyzing intricate systems, and providing more accurate descriptions of various natural and engineered systems [17–19]. It enables a deeper understanding and improved control of processes with fractional-order dynamics that go beyond the capabilities of traditional integer-order calculus. In literature [20, 21], novel fractional operators were developed that were successfully applied to the simulation of numerous real-world scenarios. Ordinary differential systems are widely recognized as suitable for local systems that are not influenced by external factors. However, conventional differential operators are unable to handle the complexity and crossover behavior of natural phenomena. Fractional calculus have numerous applications in control theory, finance, image processing, electrochemistry, and many other branches of science and engineering. Its ability to describe and analyze systems with non-local, non-linear, and memory-dependent behavior makes it a valuable tool in many scientific, engineering, and mathematical fields. In this study, we will utilize the concept of full memory to interrogate and understand the intricate phenomena of social media addiction. We opt to find out the most sensitive factors of the system and suggest to the concerned officials.
We have decided to propose a mathematical model for SMA using Caputo-Fabrizio of order ϖ∈(0, 1] as a consequence of the study mentioned above. The remaining article is structured as follows: Section 2 includes the fundamental results and claims of the fractional-calculus. In Section 3, we construct a fractional Caputo-Fabrizio (CF) derivative-based model of social media addiction (SMA). We examined the equilibriums and ascertained the reproduction number for the recommended system in Section 4. Existence and uniqueness of the solution of our system are examined with the use of fixed-point theory in Section 5. We also established a numerical framework in Section 5 to examine how various input factors affect the system's dynamics. The study's conclusion is provided in Section 6.
2. Fractional concepts
In this study, the rudimentary results of Caputo-Fabrizio (CF) fractional derivative will be presented for the analysis of the recommended model. The basic concepts are given below.
Definition 2.1. Let a function then its CF fractional derivative [21] is given as
where c2 > c1 and 𝔘(τ) represents the normality [21] such that 0 ≤ ϖ ≥ 1. If , then we can write
Remark 2.1. If and , then Equation (2) states that
Moreover, we can write
Definition 2.2. [22]. The integral in fractional framework for is stated below as
in which the order of fractional derivative is represented by ϖ with the restriction that 0 < ϖ < 1.
Remark 2.2. On the basis of Definition 2.2, we can write
which states that , 0 < ϖ < 1. By utilizing (6) through the study [22], we obtained the following result:
where fractional order is ϖ with 0 < ϖ < 1.
3. Formulation of the non-integer model
In this formulation, we classified the humans population into five subclasses symbolized in the following manner; 𝔖 represents the susceptible individuals, exposed individuals are represented by 𝔈, addicted individuals are indicated by 𝔄, recovered class of individuals are denoted by ℜ while the individuals not permanently addicted with SMA are represented by 𝔔.
The susceptible class grows due to the recruitment of individuals at the rate of α. Moreover, the term ωξℜ increases the population, while the terms ϕθ𝔄𝔖 and (μ+ρ)𝔖 lowers the population where ω is the proportion of recovered individuals that were susceptible to SMA, ξ is the transmission rate from the recovered class, ϕ is the rate at which addiction is transmitted to individuals, θ is the rate at which susceptible individuals came in contact with addicted individuals, μ represents the susceptible individuals that were not addicted to social media, and ρ is the natural fatality rate. Therefore, the susceptible individuals class can be stated as
The exposed class increases due to ϕθ𝔄𝔖, while the term (τ + ρ)𝔈 decreases the population, where τ is the treatment rate of addicted individuals. Thus, the exposed class is mathematically represented as
The term υτ𝔈 increases the addicted class population, while (ρ + ζ + ψ)ℜ lowers the population, where ζ is the progression rate from the addicted to the recovered class and ψ is the fatality rate due to SMA. Hence, the addicted class is mathematically given as
The recovered class grows due to τ𝔈 and ζ𝔄, while it decreases due to υτ𝔈 and (ρ+ξ)ℜ. Thus, the recovered class is represented by
The class of not permanently addicted individuals increases by μ𝔖 and ξℜ, while it decreases due to ωξℜ and ρθ. Therefore, the class of individuals permanently not addicted with social media is stated as
Thus, the above-stated assumptions lead us to derive an ODE model for SMA, which is stated below as
having state-variables
The total population is stated by
In particular, the realistic problem can benefit greatly from the use of fractional calculus. It has been demonstrated that fractional frameworks can more precisely depict the dynamics of real-world problems than traditional integer-order derivatives. The fractional framework equivalent to the aforementioned SMA model is stated below:
where CF fractional operator order is ϖ. The parameters of the model are described in Table 1 in detail. The following result provides the SMA fractional system positive invariant region stated as follows.
Theorem 3.1. The set Γ will be a positive invariant for system (9) of SMA if .
Proof Let us consider any solution of the system (9) for the set (𝔖, 𝔈, 𝔄, ℜ, 𝔔). Since we know that
Then adding the equations of system (9), we get that
If no death occurs due to SMA, then Equation (10) can be rewritten as
Then, is the solution of Equation (11), as t → ∞, then Therefore, the set is a positive invariant of system (9).
4. Analysis of fractional dynamics
Now, we will examine the steady-state and stability of the recommended fractional model (9) of SMA. First, we investigate the system's addiction-free equilibrium, represented by 𝔈0. Consider the fractional model of SMA described above in steady states without addiction. Thus, we get the SMA addiction-free equilibrium as follows:
For a reproduction parameter, we proceed as follows:
Evaluating Jacobian of matrix and at 𝔈0, we get the following:
Hence, we get that , which gives the reproduction number as
Theorem 4.1. If R0 < 1, then the system (9) addiction-free equilibrium is locally asymptotically stable and unstable otherwise.
Proof To get the required results, first we will evaluate the Jacobian matrix of the system (9) at 𝔈0 as follows:
The eigenvalues of the matrix are
and the remaining two eigenvalues will be obtained by solving the below stated quadratic equation:
where and
To check that the roots of the quadratic equation are negative, we utilize the Routh-Hurwitz criteria which state that the Equation (14) has negative real roots if . Obviously, , we may write in the following form:
which shows that if 𝔈0 < 1. Therefore, we proved that if 𝔈0 < 1, then the SMA addiction-free equilibrium is locally asymptotically stable.
The equilibrium point with addiction can be obtained by supposing Equation (9) equal to zero as follows:
and on further simplification, we get that
,
where
ℵ2 = υτωξ(ψ+ρ)−τωξ(ζ+ξ+ρ) + (ζ+ψ+ρ)(τ+ρ)(ξ+ρ).
Theorem 4.2. If R0 > 1, then the fractional system (9) has locally asymptotically stable endemic steady-state.
To analyze the local asymptotic stability of the endemic equilibrium in a dynamical system, we typically perform linear stability analysis. This involves linearizing the system's equations around the endemic equilibrium point and examining the eigenvalues of the resulting Jacobian matrix. The local asymptotic stability is determined by the signs of the real parts of the eigenvalues. If all eigenvalues have negative real parts, then the endemic equilibrium is locally asymptotically stable. This means that small perturbations around the equilibrium point will decay over time, and the system will ultimately return to the endemic equilibrium after experiencing minor disturbances.
5. Analysis of the solutions
In this study, we concentrate on the examination of the recommended SMA fractional system solutions. The presence of a solution of system (9) will be investigated using the fixed-point theory. We move forward in the following manner:
Utilizing the similar approach listed in [22], we get the following result
Moreover, we can write
Theorem 5.1. If the condition holds then the kernels 𝔏1, 𝔏2, 𝔏3, 𝔏4, and 𝔏5 satisfies the condition of Lipschitz and contraction.
Proof 5.1 To obtain the required result, we proceed in the following way:
Taking norm on Equation (19) and further evaluating, we get
Let , where due to boundedness, we achieve the following result
Hence, the Lipschitz condition is obtained for 𝔏1, from the condition , we can also get the contraction. Similarly, the Lipschitz condition for 𝔏2, 𝔏3, 𝔏4, and 𝔏5 can be derived as
After simplifying Equation (17), we get
moreover, we obtain that
initial values are given as
We get the difference terms in the following manner:
Observing that
Similarly, we obtain
Equation (27) states that
which gives the following equation
Additionally,
In similar manner, we get the following results
Theorem 5.2. If we can find t0 such that it satisfies the following condition
then, the proposed fractional system (9) have an exact coupled-solutions.
Proof 5.2 Since the Lipschitz condition holds and 𝔖(t), 𝔈(t), 𝔄(t), ℜ(t), and 𝔔(t) are bounded. Then, Equations (30) and (31) implies
Hence, the continuity and existence of the solution are proved. In order to prove that the above mentioned is a solution of system (9), we take the following steps:
Now consider
Moreover, we have
At time t0, we have
Proceeding in the same manner and utilizing (36), we obtain
Moving in the same manner as stated above, we get that and approaches to 0 as q approaches ∞.
Theorem 5.3. If the below stated condition holds
then the solution of system (9) will be unique.
Proof 5.3 To prove the required result, let the above (37) holds true and (𝔖1(t), 𝔈1(t), 𝔄1(t), ℜ1(t), 𝔔1(t)) is any other solution of system (9), then
Taking norm on (38), we obtain
Hence, by using Lipschitz condition, we get the following result:
This shows that
Moreover, we have
and the above inequality 41 implies that
which gives
Similarly, we get the following results
Hence, the fractional system (9) of social media addiction has a unique solution.
In the upcoming subsection, we will present a numerical scheme to visualize the solution pathways of the proposed model. We will perform different numerical simulations to show the variation in the system with different values of input factors.
5.1. Numerical scheme for the system
In this study, our objective is to evaluate the significance of input factors on the output of the proposed fractional system through various simulations. The primary goal is to gain insights into the critical parameters driving the recommended dynamics. First, we provide the numerical solution for the Caputo-Fabrizio model (6) using the scheme introduced in reference [23]. The numerical scheme consists of the following steps:
For t = tn+1, n = 0, 1, 2, ..., we have
The expression for the difference between successive terms is
The function is approximated in the time interval [tm, t(m+1)] through the interpolation polynomial as follows:
in which h = tm−tm−1. Using the above approximation, the integral in (45) can be calculated as
Thus, we obtained the following:
Similarly, we can extend the approach to calculate for other compartments within the system. The numerical scheme described above is employed to obtain the numerical results. Additionally, we make assumptions for the initial values of state-variables and input parameters to facilitate the computations. The outcome of the most sensitive scenario will be proposed to relevant authorities as a preventive measure against social media addiction.
In the first scenario presented in Figures 1–3, we illustrated the time series of the exposed, addicted, and recovered class with different values of fractional parameter. We assumed the value of the fractional order to be 1.0, 0.9, and 0.8 in the first simulation shown in Figure 1, 0.6, 0.7, and 0.8 in the second simulation represented in Figure 2, and 0.4, 0.5, and 0.6 in the third simulation demonstrated in Figure 3. It has been observed that the fractional order significantly contribute to the proposed dynamics and can lower exposed and addicted individuals in the society by lowering the fractional parameter. In these figures, the arrows indicate that decreasing the fractional parameter leads to a reduction in the number of exposed and addicted individuals within the society. Second, we checked the influence of the contact rate of addicted to the susceptible individuals presented in Figure 4. In this simulation, the contact rate ϕ is taken to be 0.255, 0.355, and 0.455. Finally, we presented the influence of the input parameters ρ and ξ in Figures 5, 6, respectively. The value of ρ is assumed to be 0.221, 0.321, and 0.421, while the value of ξ is considered to be 0.046, 0.056, and 0.066. The role of these parameters has been visualized on the time series of exposed, addicted, and recovered individuals of the system. Our analysis predicts that how the input factors influence the output of the system of social media addiction.
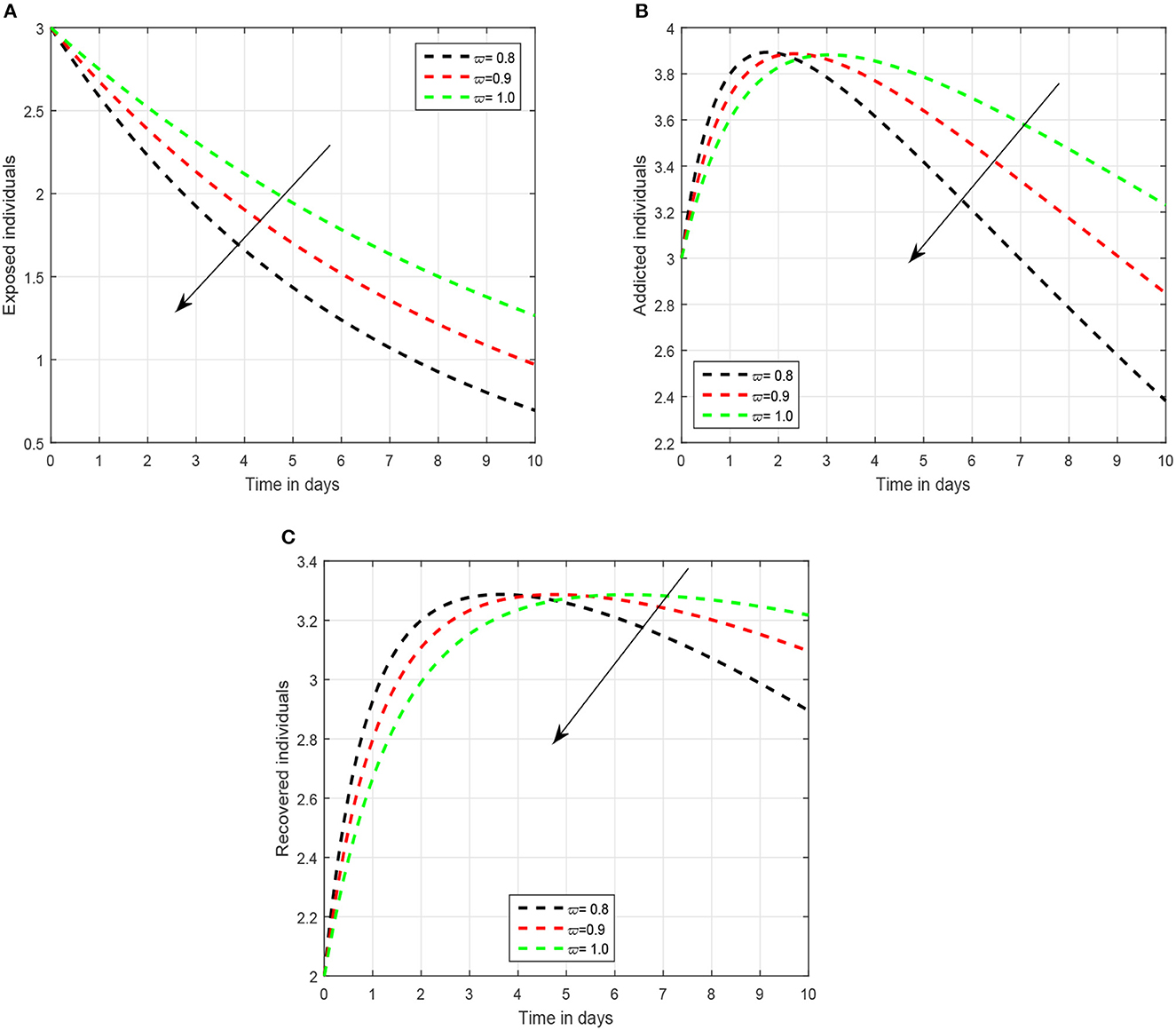
Figure 1. Illustration of the solution pathways of (A) exposed individuals, (B) addicted individuals, and (C) recovered individuals of the recommended system with fractional order 1.0, 0.9, 0.8, where the arrow shows a decrease in the addiction level with the decrease in fractional parameter.
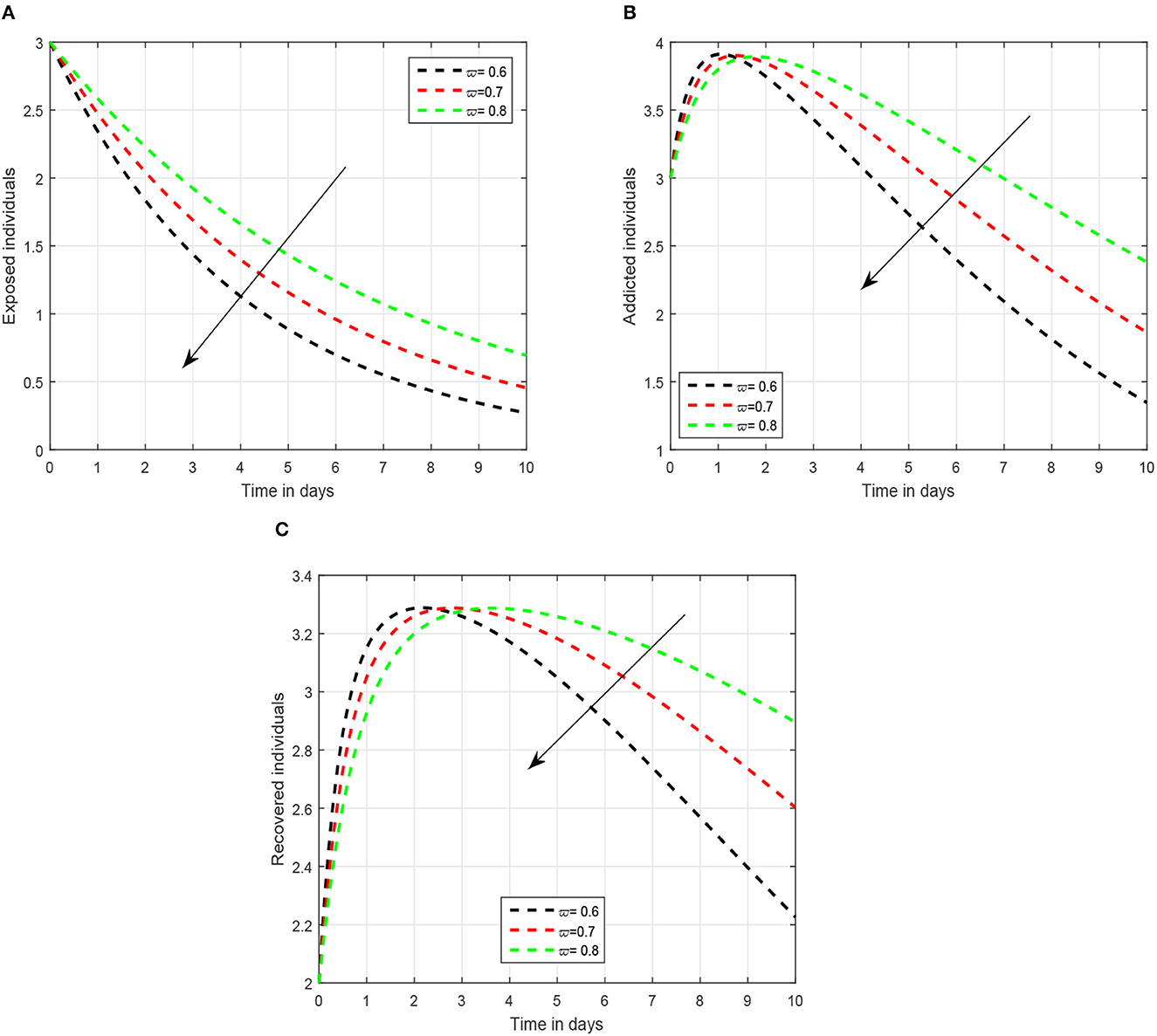
Figure 2. Illustration of the solution pathways of (A) exposed individuals, (B) addicted individuals, and (C) recovered individuals of the recommended system with fractional order 0.8, 0.7, 0.6 where the arrow shows a decrease in the addiction level with the decrease in fractional parameter.
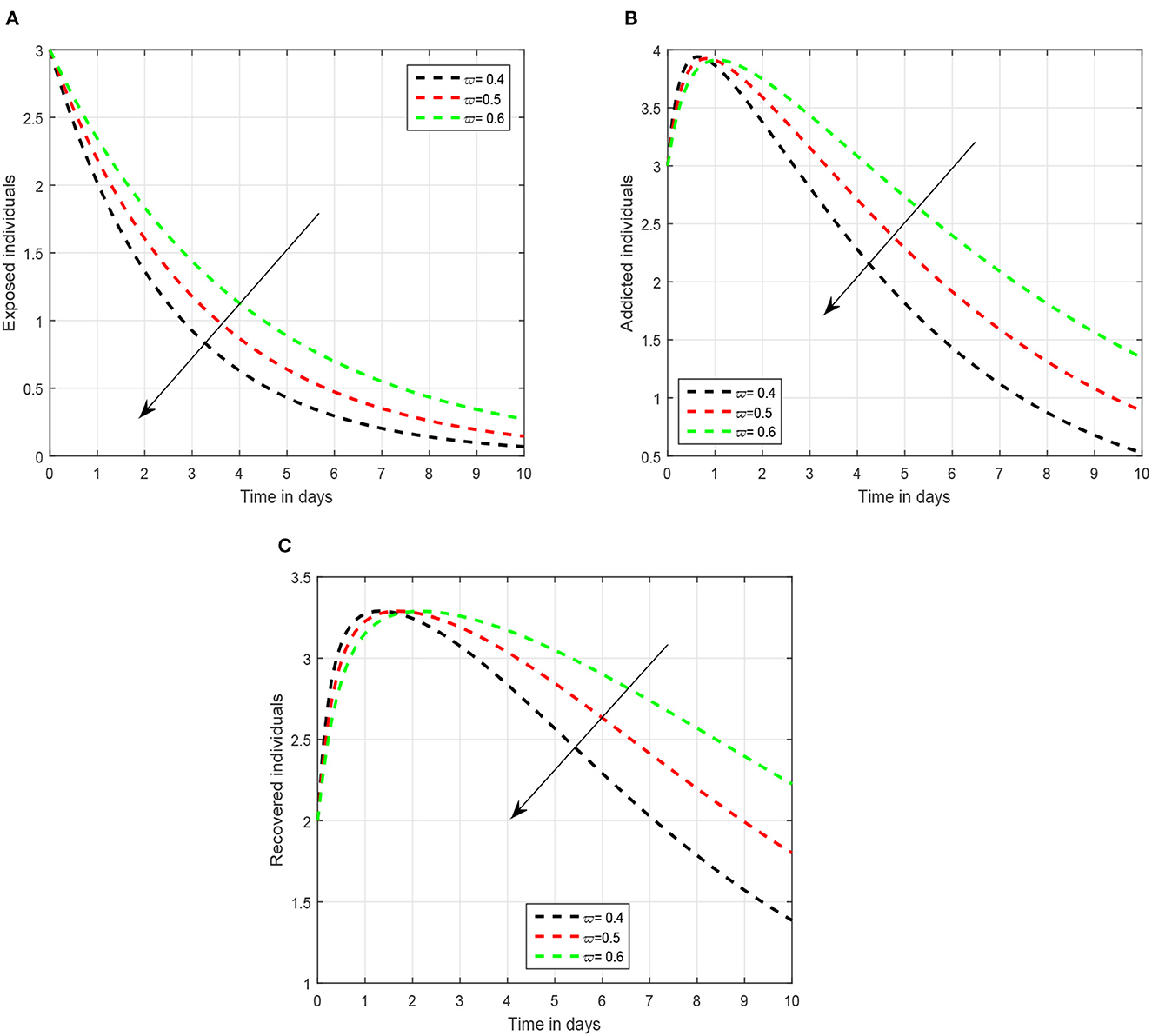
Figure 3. Illustration of the solution pathways (A) exposed individuals, (B) addicted individuals, and (C) recovered individuals of the recommended system with fractional order 0.6, 0.5, and 0.4 where the arrow shows a decrease in the addiction level with the decrease in fractional parameter.
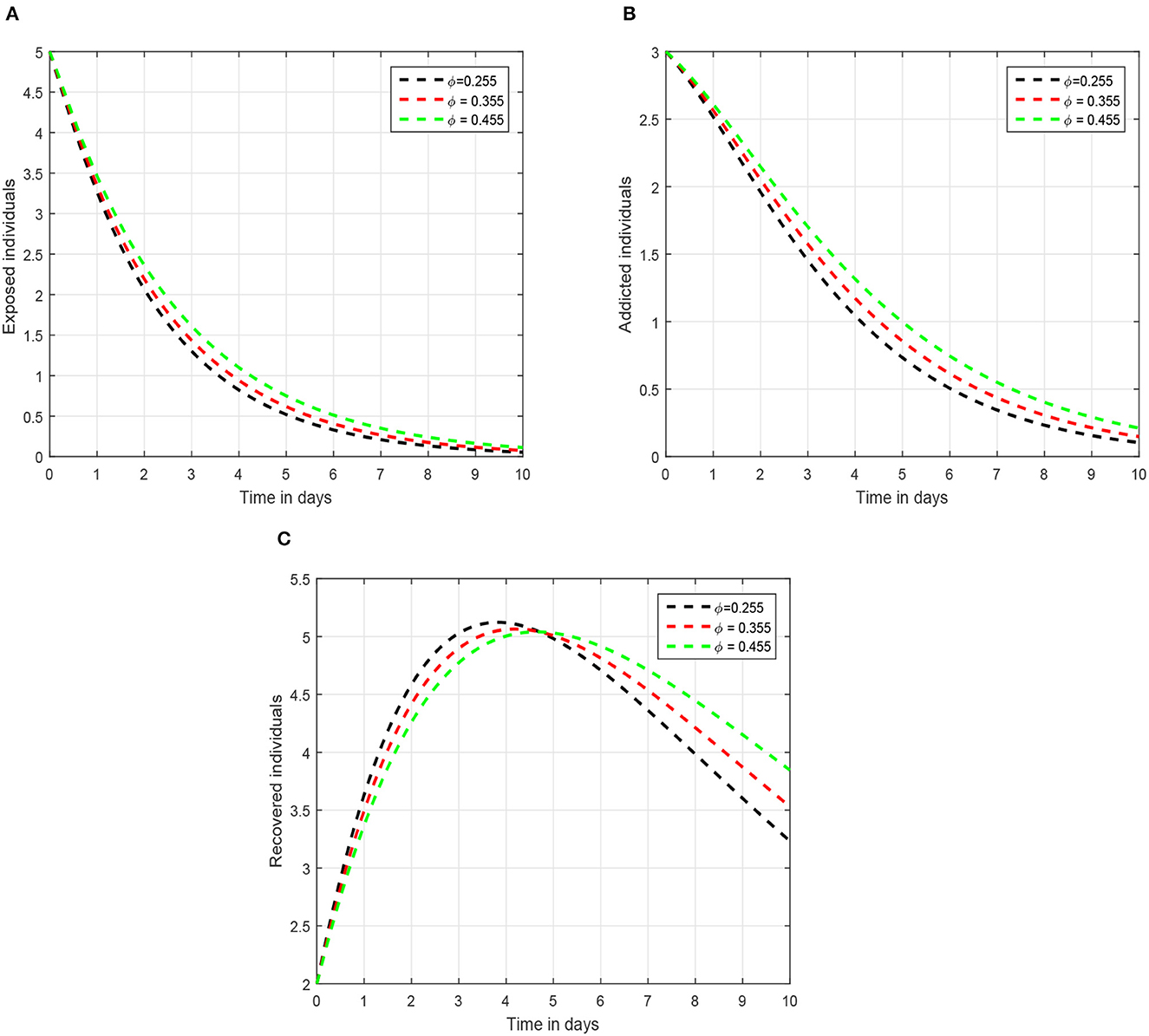
Figure 4. Graphical view analysis of the solution pathways of (A) exposed individuals, (B) addicted individuals, and (C) recovered individuals of the recommended system with contact rate 0.255, 0.355, and 0.455.
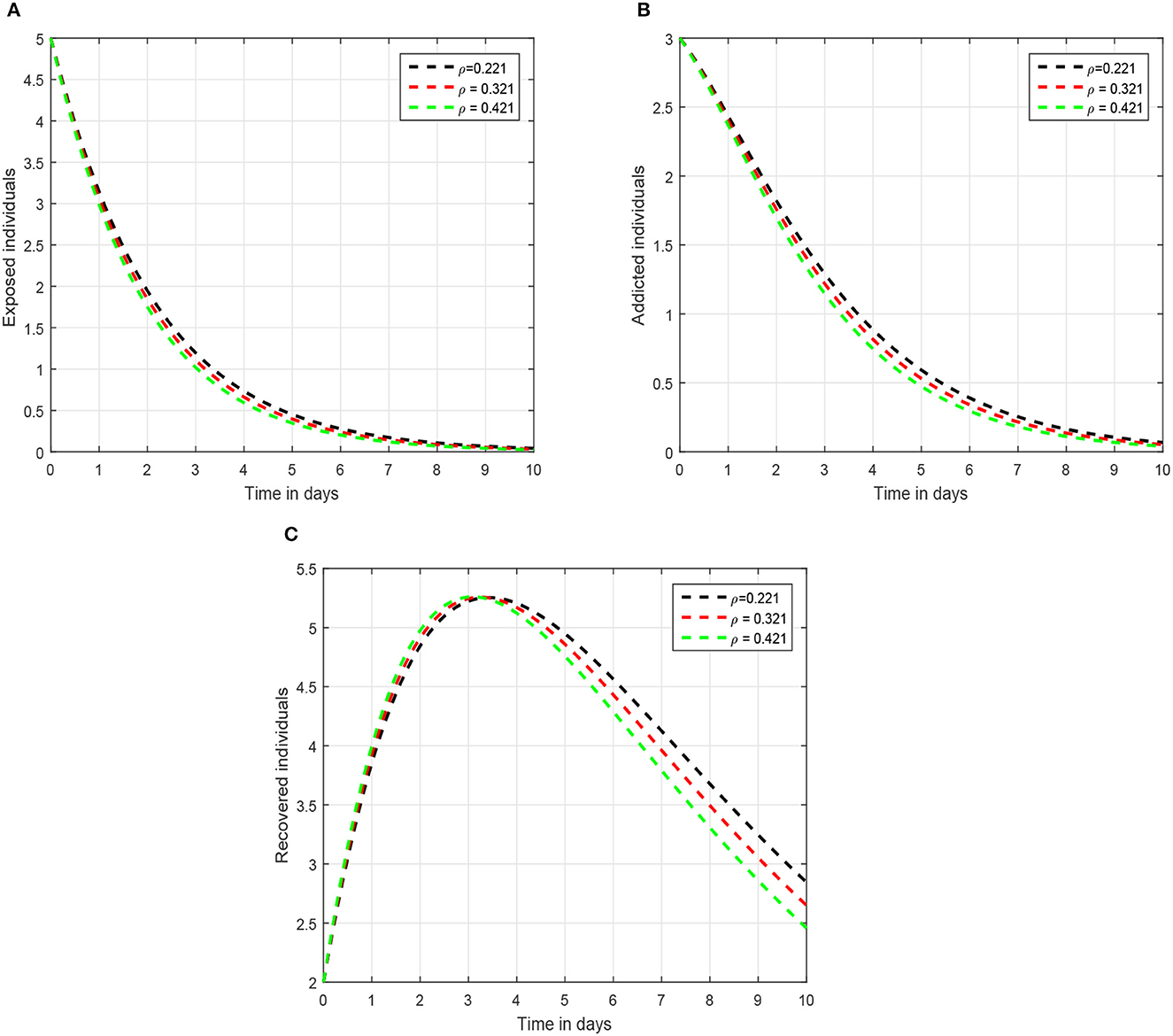
Figure 5. Graphical view analysis of the solution pathways of (A) exposed individuals, (B) addicted individuals, and (C) recovered individuals of the recommended system with input parameter ρ = 0.221, 0.321, 0.421.
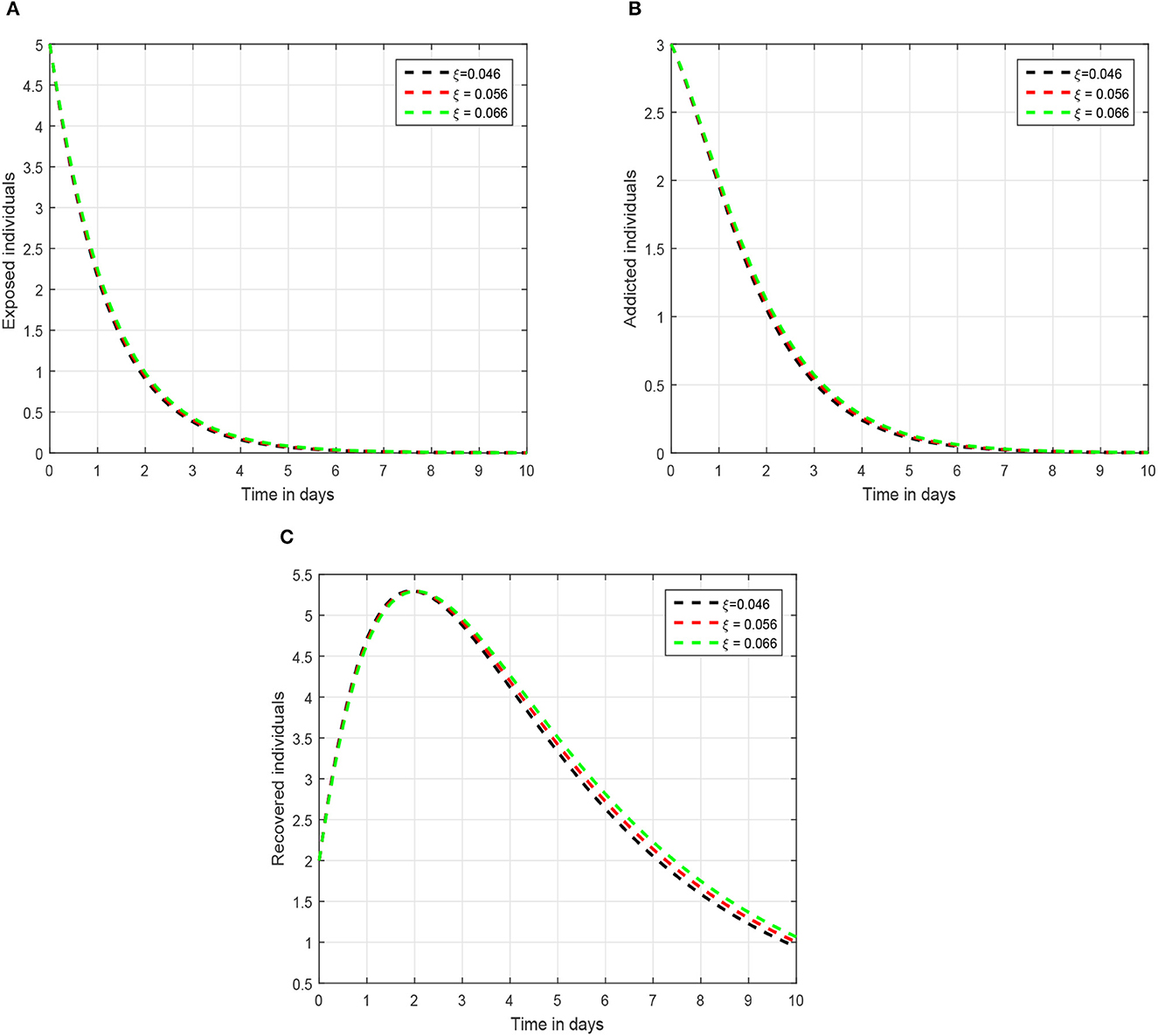
Figure 6. Dynamical behavior of (A) exposed individuals, (B) addicted individuals, and (C) recovered individuals of the recommended system with input parameter ξ = 0.046, 0.056, 0.066.
It is essential to recognize that while social media can offer many benefits, excessive and uncontrolled use can lead to addiction and negative effects. Individuals should be aware of their social media habits and take necessary steps to maintain a healthy balance between their online and offline lives. If someone suspects they or someone they know is struggling with social media addiction, seeking support from mental health professionals or support groups can be beneficial.
6. Conclusion
The addiction to social media is a significant concern due to its potential adverse effects on various aspects of individuals' lives, such as their social interactions, daily activities, and overall health. Therefore, it is imperative to investigate the influence of different factors on social media addiction. In this study, we constructed a mathematical model for social media addiction using the Caputo-Fabrizio derivative, a fractional calculus approach. To examine the dynamics of the proposed model, we utilized basic results from fractional theory. The model's equilibrium points were analyzed, and the reproduction parameter was determined, denoted as R0. We demonstrated that the equilibrium point representing an addiction-free state is locally asymptotically stable when R0 < 1 and unstable under other conditions. We have shown the existence and uniqueness of the solution of the recommended model of social media addiction. For analyzing the system's time series behavior, we employed a numerical scheme. Through numerical analysis, we illustrated the dynamical behavior of the social media addiction model under various parameter settings. This allowed us to conceptualize how various input parameters can influence the dynamics of social media addiction. In particular, we observed how different factors contribute to the development and progression of social media addiction. The research outcomes provide valuable insights for public health interventions aimed at preventing social media addiction. We predicted crucial scenarios that could lead to severe addiction and recommended key factors that can be targeted to mitigate the risk of addiction. By understanding the dynamics of social media addiction through our model, policymaker professionals can devise effective strategies to promote healthy social media usage and safeguard individuals from the detrimental effects of excessive social media engagement.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This project was financed by Lucian Blaga University of Sibiu through the research grant LBUS-IRG-2023.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wu AM, Cheung VI, Ku L, Hung EP. Psychological risk factors of addiction to social networking sites among Chinese smartphone users. J Behav Addict. (2013) 2:160–6. doi: 10.1556/JBA.2.2013.006
2. Tayo SS, Adebola ST, Yahya DO. Social media: usage and influence on undergraduate studies in Nigerian universities. Int J Educ Dev Inform Commun Technol. (2019) 15:53–62.
3. Guedes E, Nardi AE, Guimarães FMCL, Machado S, King ALS. Social networking, a new online addiction: a review of Facebook and other addiction disorders. MedicalExpress. (2016) 3:1–6. doi: 10.5935/MedicalExpress.2016.01.01
4. Siddiqui S, Singh T. Social media its impact with positive and negative aspects. Int J Comput Appl Technol Res. (2016) 5:71–75. doi: 10.7753/IJCATR0502.1006
5. Simsek A, Elciyar K, Kizilhan T. A comparative study on social media addiction of high school and university students. Contemp Educ Technol. (2019) 10:106–19. doi: 10.30935/cet.554452
6. Hou Y, Xiong D, Jiang T, Song L, Wang Q. Social media addiction: its impact, mediation, and intervention. Cyberpsychology. (2019) 13. doi: 10.5817/CP2019-1-4
7. Shek DT, Tang VM, Lo CY. Internet addiction in Chinese adolescents in Hong Kong: assessment, profiles, and psychosocial correlates. The Scientific World Journal. (2008) 8:776–87. doi: 10.1100/tsw.2008.104
8. Monacis L, De Palo V, Griffiths MD, Sinatra M. Social networking addiction, attachment style, and validation of the Italian version of the Bergen Social Media Addiction Scale. J Behav Addict. (2017) 6:178–86. doi: 10.1556/2006.6.2017.023
9. Chakraborty K, Basu D, Kumar KV. Internet addiction: consensus, controversies, and the way ahead. East Asian Arch Psychiatry. (2010) 20:123–32.
10. Hamad AA, Abdulridha MM, Kadhim NM, Pushparaj S, Meenakshi R, Ibrahim AM. Learning methods of business intelligence and group related diagnostics on patient management by using artificial dynamic system. J Nanomater. (2022) 2022:4891601. doi: 10.1155/2022/4891601
11. Jan R, Shah Z, Deebani W, Alzahrani E. Analysis and dynamical behavior of a novel dengue model via fractional calculus. Int J Biomath. (2022) 15:2250036. doi: 10.1142/S179352452250036X
12. Al-Rahawe BA, Hamad AA, Al-Zuhairy MH, Khalaf HH, Abebaw S. The commitment of Nineveh governorate residents to the precautionary measures against global 2019 pandemic and dermatological affection of precautions. Appl Bionics Biomech. (2021) 2021:1526931. doi: 10.1155/2021/1526931
13. Bernard KJ, Dzandza PE. Effect of Social Media on Academic Performance of Students in Ghanaian Universities: A Case Study of University of Ghana. Legon (2018).
14. Shang Y. Lie algebraic discussion for affinity based information diffusion in social networks. Open Phys. (2017) 15:705–11. doi: 10.1515/phys-2017-0083
15. Al Rushaidan A, Al Hugail N, Al Fahhad A, Talaue A, Alsaad GM. The impact of social media on academic performance of selected college students. Int J Adv Inform Technol. (2018) 8:27–35. doi: 10.5121/ijait.2018.8503
16. Brevers D, Turel O. Strategies for self-controlling social media use: Classification and role in preventing social media addiction symptoms. J Behav Addict. (2019) 8:554–63. doi: 10.1556/2006.8.2019.49
17. Shah Z, Bonyah E, Alzahrani E, Jan R, Aedh Alreshidi N. Chaotic phenomena and oscillations in dynamical behaviour of financial system via fractional calculus. Complexity. (2022) 2022:8113760. doi: 10.1155/2022/8113760
18. Sierociuk D, Skovranek T, Macias M, Podlubny I, Petras I, Dzielinski A, et al. Diffusion process modeling by using fractional-order models. Appl Math Comput. (2015) 257:2–11. doi: 10.1016/j.amc.2014.11.028
19. Moaddy K, Radwan AG, Salama KN, Momani S, Hashim I. The fractional-order modeling and synchronization of electrically coupled neuron systems. Comput Math Appl. (2012) 64:3329–39. doi: 10.1016/j.camwa.2012.01.005
20. Samko SG, Kilbas AA, Marichev OI. Fractional integrals and derivatives. vol. 1. Yverdon-les-Bains: Gordon and Breach Science Publishers (1993).
21. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Prog Fract Different Appl. (2015) 1:73–85.
22. Losada J, Nieto JJ. Properties of a new fractional derivative without singular kernel. Prog Fract Different Appl. (2015) 1:87–92.
Keywords: fractional calculus, social media addiction, mathematical model, Caputo-Fabrizio operator, numerical scheme, dynamical behavior
Citation: Shutaywi M, Rehman ZU, Shah Z, Vrinceanu N, Jan R, Deebani W and Dumitrascu O (2023) Modeling and analysis of the addiction of social media through fractional calculus. Front. Appl. Math. Stat. 9:1210404. doi: 10.3389/fams.2023.1210404
Received: 22 April 2023; Accepted: 24 July 2023;
Published: 09 August 2023.
Edited by:
Christos Volos, Aristotle University of Thessaloniki, GreeceReviewed by:
Omar Abu Arqub, Al-Balqa Applied University, JordanGuoyong Yuan, Hebei Normal University, China
Yilun Shang, Northumbria University, United Kingdom
Copyright © 2023 Shutaywi, Rehman, Shah, Vrinceanu, Jan, Deebani and Dumitrascu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Narcisa Vrinceanu, dnJpbmNlYW51Lm5hcmNpc2FpQHVsYnNpYml1LnJv
 Meshal Shutaywi
Meshal Shutaywi Ziad Ur Rehman2
Ziad Ur Rehman2 Zahir Shah
Zahir Shah Narcisa Vrinceanu
Narcisa Vrinceanu Rashid Jan
Rashid Jan