- 1Department of Applied Mathematics, Adama Science and Technology University, Adama, Ethiopia
- 2Department of Mathematics and Applied Mathematics, University of the Western Cape, Cape Town, South Africa
In this article, a class of singularly perturbed time-delay two-parameter second-order parabolic problems are considered. The presence of the two small parameters attached to the derivatives causes the solution of the given problem to exhibit boundary layer(s). We have developed a uniformly convergent nonstandard fitted operator finite difference method (NSFOFDM) to solve the considered problems. The Crank-Nicolson scheme with a uniform mesh is used for the discretization of the time derivative, while for the spatial discretization, we have applied a fitted operator finite difference method following the nonstandard methodology of Mickens. Moreover, the solution bounds of the governing equation are shown by asymptotic analysis. The convergence of the proposed numerical scheme is investigated using truncation error and the barrier function approach. The study shows that our proposed scheme is uniformly convergent independent of the perturbation parameters, quadratically in time, and linearly in space. Numerical experiments are carried out, and the results are presented in tables and graphically.
1. Introduction
Singular perturbation problems (SPPs) were first established as a research domain in the early 1990's [1] with the development of the boundary-layer idea in viscous flow [2] and has flourished over the last few years. Despite the large amount of studies that have already been done in this thematic area, more relevant and timely research is still ongoing.
Differential equations whose highest order derivative terms are attached with small positive number(s) are called singularly perturbed problems (SPPs). Singularly perturbation problems appearing with two small parameters are said to be two-parameter singularly perturbed problems. A singularly perturbed delay differential equation (SPDDE) is a differential equation in which the highest derivative is multiplied by a small parameter and containing at least one delay term either at the space variable, time variable, or both.
A lot of real-life physical problems are represented by linear or nonlinear differential models or by SPPs whose solution depends on the magnitude of the perturbation parameter. Singularly perturbed problems (SPPs) occur in the modeling of fluid dynamics, elasticity theory, quantum mechanics, reaction diffusion process, chemical reactor theory, plasma dynamics, meteorology, diffraction theory, aerodynamics, modeling of semi-conductors, hydrodynamics, and in several other applied fields [3–6].
Two-parameter singularly perturbed parabolic differential equations with time delay have many applications in different fields, for example, in engineering such as drift diffusion equation of semi conductor modeling [7] and chemical reactor model [8] in fluid dynamics [9].
Friedrichs and Wasow [10] were the first to use the term singular perturbation problems in their seminar at New York. In such problems, there are often narrow transition regions called boundary layers. In these regions, the solution changes rapidly or jumps abruptly and behaves regularly and slowly away from the layers.
For the solution of singular perturbation problems, one may apply the numerical approach or the asymptotic approach. The asymptotic approach provides the qualitative behavior of the problem and gives only a semi-quantitative information. However, the numerical approach provides quantitative information.
To solve singularly perturbed problems numerically (when analytical solutions are not available or more complicated), one can use finite difference methods, finite elements methods, spline approximation methods, and others, but, unless very fine grids are used, standard finite difference methods can not resolve the layers(s) and may not provide a uniformly convergent solution throughout the given domain.
The two non classical finite difference methods (FDMs) used for solving SPPs are fitted mesh methods (FMFDMs) and fitted operator methods (FOFDMs). In this article, we develop a uniformly convergent and accurate non-standard fitted operator finite difference method (NSFOFDM) based on the methodology of Mickens [11].
As the parameters ε and μ in the problem (1) of section (2) tend to zero, the solution will produce boundary layer(s) at x = 0 and x = 1. When μ = 1, problem (1) is convection- diffusion problem [12–14], and in this case, a boundary layer(s) of width O(ε) will occur around the edge x = 0. Again, when μ = 0, we have a parabolic reaction-diffusion problem [15] and thin boundary layers of width appear near x = 0 and x = 1. O'Malley [16] introduced singularly perturbed two-parameter problems and examined asymptotic expansion for their solutions. O'Malley [16, 17] identified that the nature of these problems is quite affected by the choice of ratio of μ2 to ε.
O'Malley et al. developed numerical methods to improve the accuracy of the asymptotic methods [16]. The class of time-dependent SPPs of convection-diffusion types with two parameter were studied in Munyakazi [18] using the classical finite difference method. Recently, the numerical solution of second-order two-parametric singularly perturbed ordinary differential equations (ODEs) with smooth data [19–32] and non-smooth data [33, 34] were considered.
Some uniformly convergent numerical methods for singularly perturbed time dependent delay differential equations have been developed in Bashier and Patidar, Kaushik et al., Kumar and Kumar, Erdogan and Cen, Cen, Singh et al., Ansari et al., and Kumar and Kumar [35–42].
In Govindarao et al. [43], a first-order uniformly convergent method was developed for two-parameter time dependent SPPs using an upwind finite difference scheme on Shishkin type meshes.
Solving two-parameter SPPs analytically is either more difficult task or the analytical solution does not exist. This is because of the small parameters attached to the highest order terms of the given problem. These attached small parameters exhibit a layer behavior in the solutions. The classical finite difference methods give unstable solution in the layer region. Moreover, the convergence and stability of the solution in numerical part varies according to the small parameters. From the existing literature we have seen, developing a parameter uniformly convergent numerical method for two-parameter singularly perturbed problems is still a challenging task.
The objective of this study is to analyze the solution when the delay is non-zero and the effect of the delay on the boundary layer solution, as well as investigate problems (1)–(2) with smooth data. We are inspired to develop a parameter uniformly convergent numerical scheme to treat a class of second-order two-parameter singularly perturbed time dependent problem (1)–(2). A non-standard fitted operator finite difference method based on the Crank-Nicolson discretization for time variable comprising a non-standard fitted operator finite difference on uniform mesh for spatial variable. The developed scheme is of second order in time and first order in space but has been improved to second order in both variables by using temporal mesh refinement in Section (5) in Tables 4, 5. Moreover, the comparison of the developed scheme with the existing scheme in Kumar and Kumar [44] is investigated in Section (5) in Table 6. The comparison shows that the maximum point-wise error of our scheme is less than the scheme in Kumar and Kumar [44].
This article is organized as follows. We first discuss the qualitative properties such as the bounds of the analytical solution u(x, t) of problem (1–2) and its derivative bounds in Section (2). The numerical scheme of the continuous problem is presented in Section (3). In this section, we also discuss the time discretization, the space discretization, the continuous problem discretization, and bounds of the discrete solution. The stability and convergence analysis of the scheme is presented in Section (4). In Section (5), we provide numerical example to show uniformly convergence of solution and its accuracy. We present the result and conclusions in Section (6).
2. The continuous problem
We consider the following two families of two-parameter singularly perturbed time-delay problem. Our domain = D∪∂D, where D = (0, 1) × (0, T] and ∂D = Ll ∪ Ld ∪ Lr with Ld = [0, 1] × [−γ, 0](delay interval), Ll = {0} × (0, T](left side boundary) and Lr = {1} × (0, T](right side boundary). The governing equation is as follows:
where Lu(x, t) = εuxx(x, t) + μa(x, t)ux(x, t) − b(x, t)u(x, t), 0 < ε ≤ 1 and 0 ≤ μ ≤ 1 are perturbation parameters and γ is a delay parameter. In problem (1–2), we suppose that a(x, t), b(x, t), c(x, t), f(x, t), Φl(t), Φr(t), and Φd(x, t) for are sufficiently smooth functions such that a(x, t) ≥ α > 0, b(x, t) ≥ β > 0, and c(x, t) ≥ ϒ > 0, independent of the perturbation parameters. At the corners, the regularity and compatibility conditions are
for D = (0, 1) × (0, T], and so that Φd (x, t) (initial-boundary data) satisfies appropriate compatibility criteria at the two corners, (0, 0) and (1, 0). Based on the above assumptions, the given problem in (1) possesses a unique solution in the considered domain.
2.1. Some qualitative properties of the continuous problem
In this section, we present some analytical properties of the governing problem (1–2) in one space dimension and defined domain .
First, we will state and prove minimum principle and describe derivative bounds for the solution.
Lemma 2.1. The minimum principle for the continuous SPP [44]. Let . If φ|∂D ≥ 0 and , then .
Proof. Let (x⋆, t⋆) be an arbitrary point in a plane, D = (0, 1) × (0, T) such that and again suppose that φ(x⋆, t⋆) < 0. Clearly, (x⋆, t⋆) ∉ {0, 1} × {0, T} and from the definition of (x⋆, t⋆), we have (applying first and second derivative test for multi-variable functions). Now, we have
This is a contradiction. So that our initial assumption φ(x⋆, t⋆) < 0 is wrong. Therefore, . Since (x⋆, t⋆) is arbitrary point, we have φ(x, t) ≥ 0 for all . □
Lemma 2.2. Bound of the continuous SPP and its derivatives. Let u be the solution of problem (1)–(2) such that u = v + wL + wR, where v is the regular component and wL and wR are the left and right singular components, respectively [44], and let C be sufficiently large constant which is independent of the perturbation parameters. Then,
b. For all non- negative integers i and j (0 ≤ i + 2j ≤ 4), the derivatives of the solution u of problem (1)–(2) satisfy
where
Proof. One can get the proof in Kumar and Kumar and O'Riordan et al. [44, 45].
The singular component and the regular component derivative bounds are justified by the following theorem.
Theorem 2.1. For i, j ∈ 𝕎 = {0, 1, 2, 3, ...}, satisfying 0 ≤ i + 2j ≤ 4, derivative bounds for u are given by
Proof. The detail of the proof is in Kumar and Kumar and O'Riordan et al. [44, 45].
3. The numerical scheme
Here, we develop the numerical scheme by discretizing the temporal domain, the spatial domain, and the given singularly perturbed problem in (1)–(2).
3.1. Semi-discrete scheme using temporal discretization
For the discretization of the temporal domain, we divide the given time domain [0, T] using a uniform mesh. We have chosen γ in such a way that T = kγ for some positive integer k > 1. Moreover, if the set DM is the collection of all mesh points in [0, T] and if is all mesh points in [−γ, 0], then and , respectively, where M is the number of mesh points in time interval [0, T] and m is the number of mesh points in [−γ, 0]. The continuous problem is semi-discretized using the Crank-Nicolson finite difference method in the temporal direction. The derivation of Crank Niconson scheme for Ut(x, tj) at (x, j + 1/2) time step is by using Taylor's series expansion for Uj+1 and Uj.
Now, if we subtract (4) from (3), then the term Uj+1/2(x) is eliminated and we obtain
and the local truncation error (Tj+1/2(x)) is
Rearranging the problem in (1) using the above discritizations, we can write the semi-discretized scheme as
where
Lemma 3.1. Semi-discrete minimum principle. Assume that is the discrete operator given in (5) and φj+1(x) is any mesh function satisfying and for 0 ≤ j ≤ M, then .
Proof. Let s⋆ ∈ D be any arbitrary point, such that . Again, suppose φj+1(x) < 0. It is clear that the set . By using the concept of first test and second derivative test for multi-variable functions of calculus, we have . This gives LMφ(s⋆)j+1 > 0 which contradict to the fact that LMφ(x)j+1 ≤ 0. Therefore, is our desire result. □ □
Lemma 3.2. Estimate of local error. Suppose that The error estimate in temporal direction for sufficiently large constant C is
Proof. From the Crank-Nicholson finite difference method of temporal discritization, the fourth order Taylor's series expansion, we have
Using Equation 6 into (1)–(2), we get
Again, we apply the semi-discrete minimum operator for ek+1, and then we have
Then, by lemma (3.1) the local error is bounded and given as
□
Lemma 3.3. Estimate of global error. The global error, of the time discretization satisfies
where C is a constant independent of ε, μ, and Δt.
Proof. By using the estimation of local errors, the global error at j + 1 nodal points is given as
Thus, the semi-discrete scheme is convergent of order two in time.
Lemma 3.4. Let Uj(x) be the semi-discrete solution of (1)–(2). For a certain order of derivative q that depends on the smoothness of data, Uj(x) satisfies the following bound following bound:
where p is any real constant such that 0 < p < 1.
Proof. This lemma was proved in Kadalbajoo and Yadaw [46]. □
□
3.2. Full-discrete scheme using spatial discretization
To discritize the spatial domain, we consider that denotes the interval [0, 1] and then divide it into N sub-intervals such that
Then, the discretization of the rectangular domain is , and also the discretization of the boundary data and boundary conditions is , where and . denotes the uniform temporal meshes in [−γ, 0]. Again, using the space discretization and the semi-discrete in (5), we can write the full-discrete scheme as
Next, the resulting discretized equation in (7) can be rearranged using a non-standard fitted operator finite difference method following the steps in Mickens [11].
where
and
Again, from Munyakazi [18], the denominator function is given by
Equation 8 can be written in compact form as
where
4. Discrete stability and uniform convergence analysis
In this section, we investigate the stability and uniform convergence of the developed scheme.
Lemma 4.1. Discrete minimum principle.
Assume that is the discrete operator given in (10) and is any mesh function satisfying and for 0 ≤ i ≤ N, 0 ≤ j ≤ M and then .
Proof. Let s and l be indices such that for . Again, assume that . It is clear to see that (s, l) ∉ {0, N} × {0, M} because . It follows that and .
which is a contradiction to the fact that . Therefore, . The indices s and l being arbitrary, we obtain in . □ □
The immediate consequence of the above lemma is the following lemma which is about a uniform stability estimate.
Lemma 4.2. Uniform stability estimate.
At any time level tj, if is any mesh function such that , then
Proof. To prove this lemma, we use the concept of barrier functions and the above discrete minimum principle. Therefore, we define the two barrier functions as
where
. Therefore, by lemma (4.1) above, we obtain
. □
This lemma shows the uniform stability of the operator LN, M. In the following two lemmas, we analyze the convergence of scheme in (8) using bounds of the truncation error in both variables.
Theorem 4.1. Error estimate in the spatial discretization.Let and are the solution Equations 5, 8, respectively. If N and C are mesh number and sufficiently large constant, then the following error bound holds.
Proof. To prove this theorem, we use the differential and difference equation, and then define the error as follows:
Now, the Taylor's series expansion of , and are
Using these substitutions in (12) and applying some simplification gives
Again, using the bounds of the derivatives in lemma (2.2), we can describe the bound of the error below:
Combining lemma (3.3) and theorem (4.1), we can state the following theorem as main results.
Theorem 4.2. The main result.
Let u(x, t) be the exact solution of (1)–(2) and is its numerical approximation obtained using (8). Then, there exists a constant C independent of ε, μ, h, and Δt such that
Proof. To prove this theorem, we take the left side of (15), then applying triangular inequality by using the semi-discrete solution, as follows:
Using the error bounds of lemma (3.3) and Theorem (4.1) for the result in 16, we get
Hence,
5. Numerical results and discussion
The following example is implemented to demonstrate the applicability of the proposed scheme in (8). Here, maximum absolute errors (point-wise error) and numerical rate of convergence are calculated on the considered meshes (Shishkin mesh type, [47]) using the double mesh principle given in Doolan et al. [48] as follows.
Example 5.1. Consider the following time-delay problem [44]:
In Tables 1, 2, we computed the maximum pointwise errors and the corresponding rates of convergence for the developed numerical scheme for example (5.1). Thus, the results are presented using μ = 10−3 and different values of ε as shown in Table 1, and using ε = 10−3 and different values of μ as shown in Table 2 with the discretization parameters N and M varying with the same ratio (N and M both multiplied by 2). Here, we see that the rate of convergence of the developed fitted operator finite difference scheme is very close to one(confirm the spatial order). Again, the result in Table 3 is computed using μ = 10−3 and different values of ε with the discretization parameters N and M varying with the ratios of 4 and 2, respectively, and the rate of convergence is still the first order.
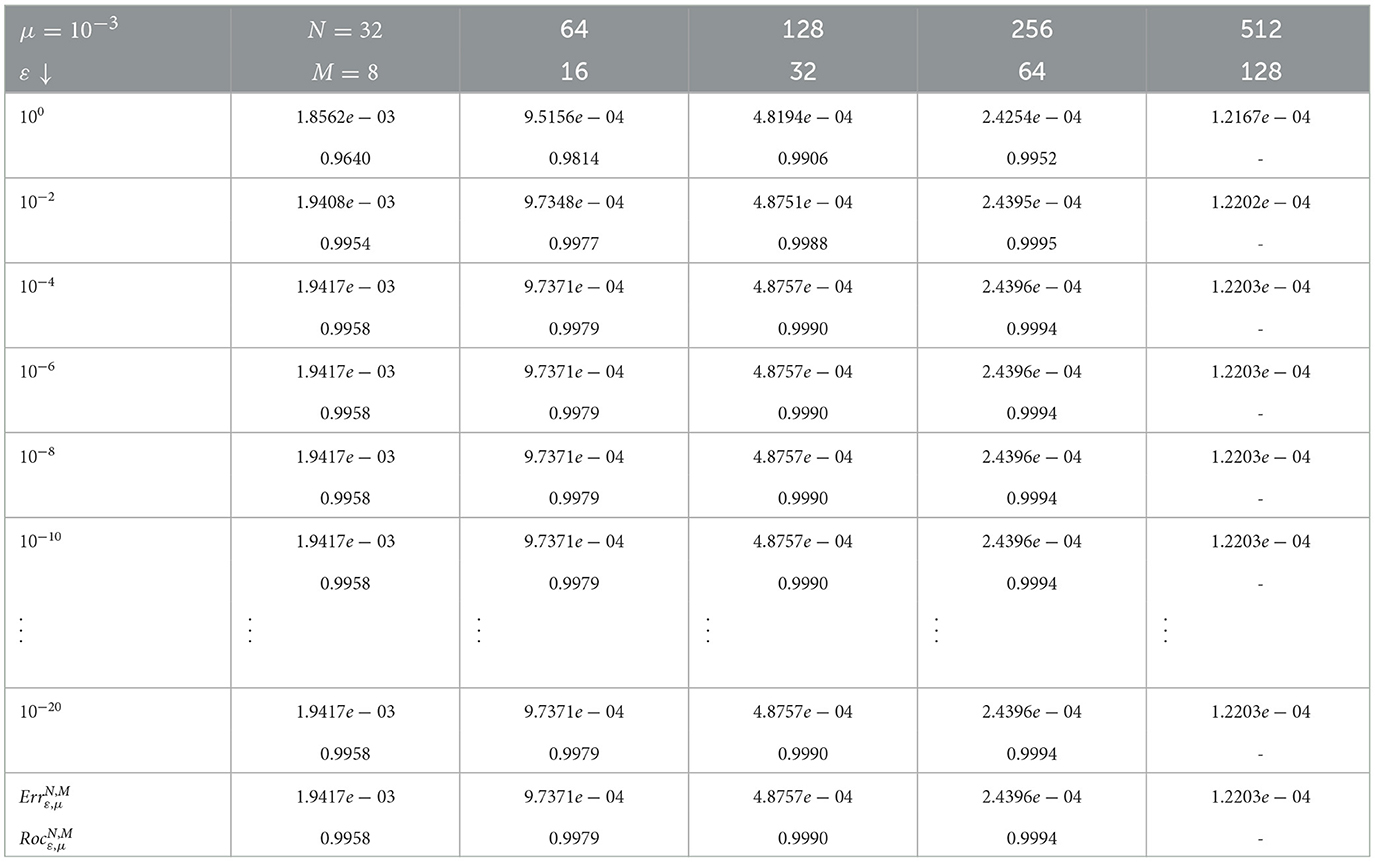
Table 1. Maximum errors and rates of convergence using scheme (8) for example (5.1) with μ = 10−3 and different values of ε.
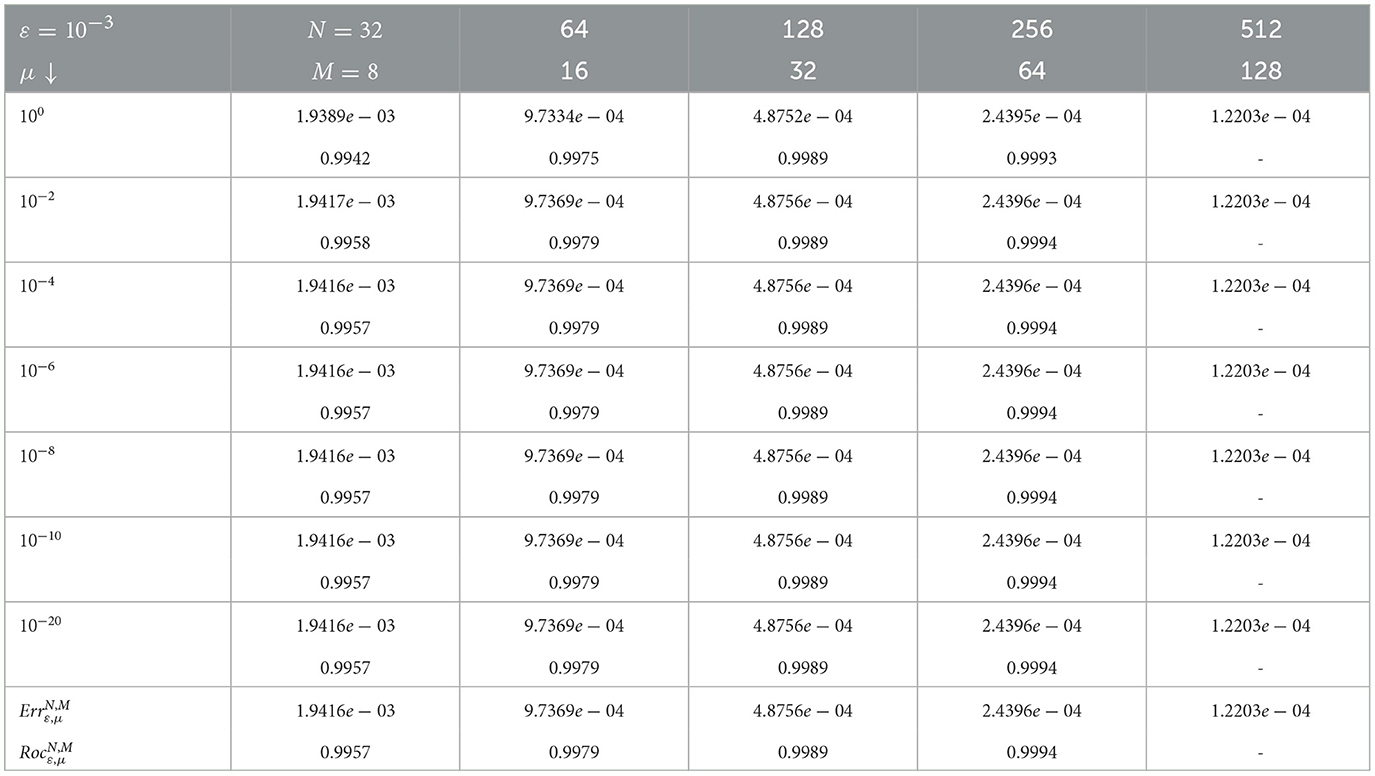
Table 2. Maximum errors and rates of convergence using scheme (8) for example (5.1) with ε = 10−3 and different values of μ.
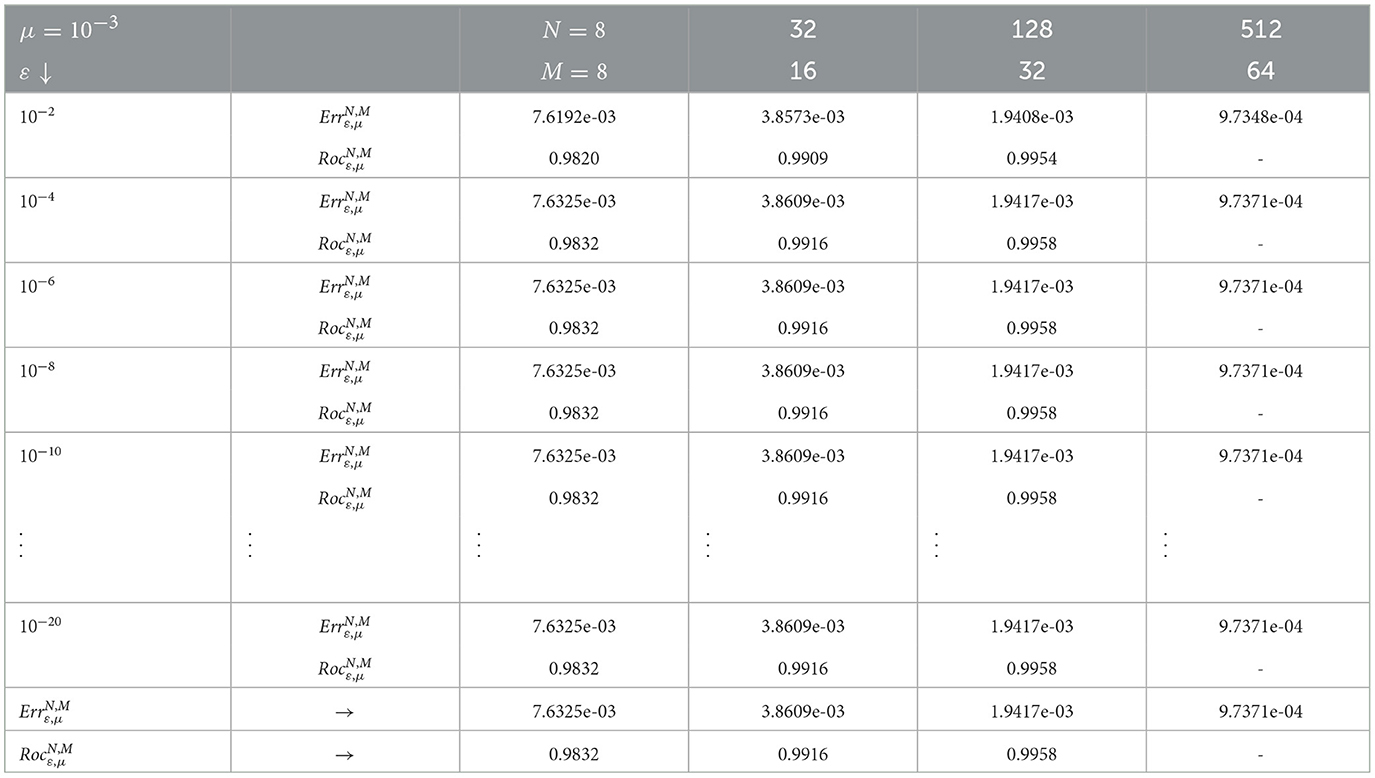
Table 3. Maximum errors and rates of convergence using scheme (8) for example (5.1) with μ = 10−3 and different values of ε.
In Tables 4, 5, we computed the maximum pointwise errors and the corresponding rates of convergence for the numerical solution of example (5.1) using scheme (8). Thus, the results are presented by taking the values of μ and and ε as we have done for Tables 1, 2 and also using the discretization parameters N and M varying with the ratios of 2 and 4, respectively. Here, we show that the rate of convergence of the developed fitted operator finite difference scheme is almost two(confirm temporal order).
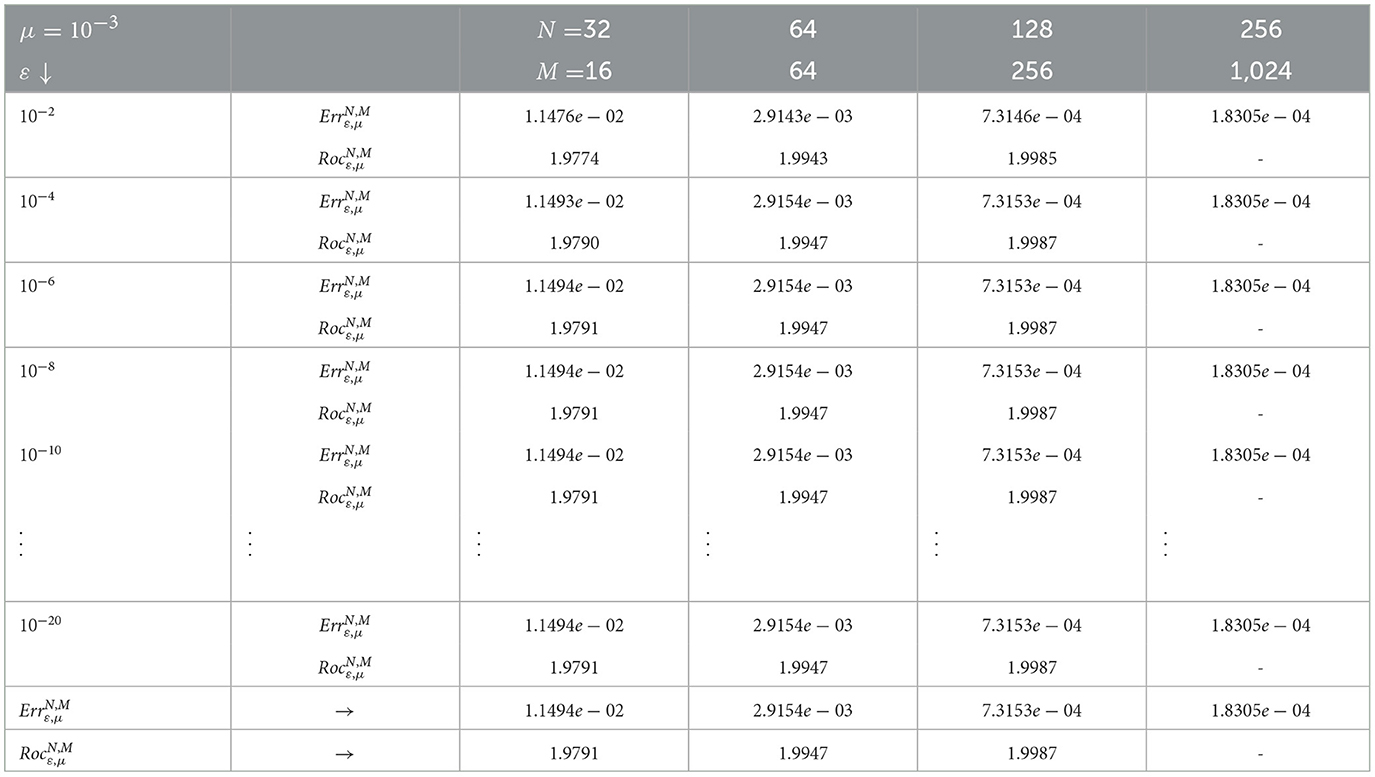
Table 4. Maximum errors and rates of convergence using scheme (8) for example (5.1) with μ = 10−3 and different values of ε.
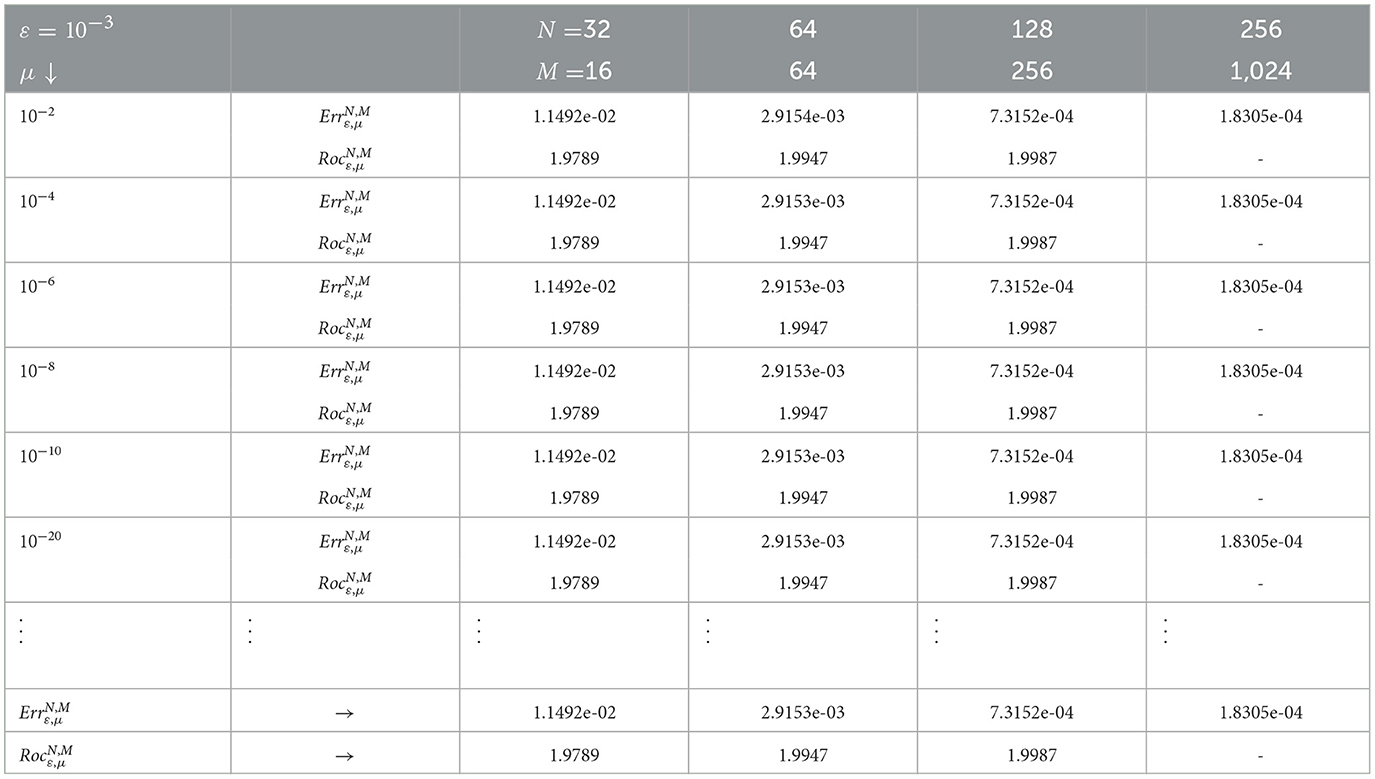
Table 5. Maximum errors and rates of convergence using scheme (8) for example (5.1) with ε = 10−3 and different values of μ.
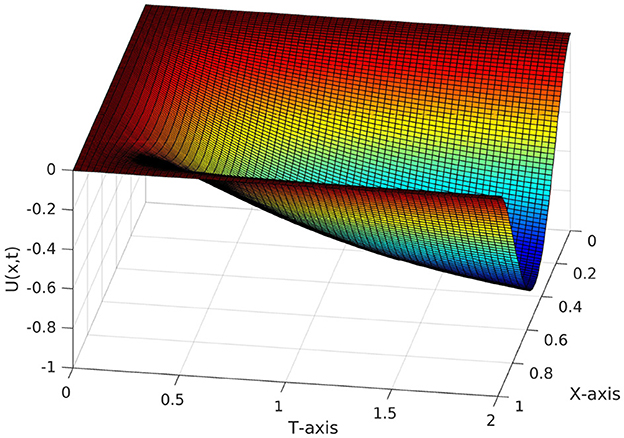
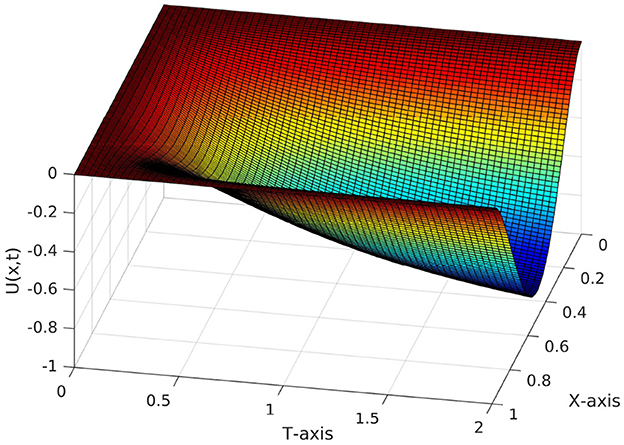
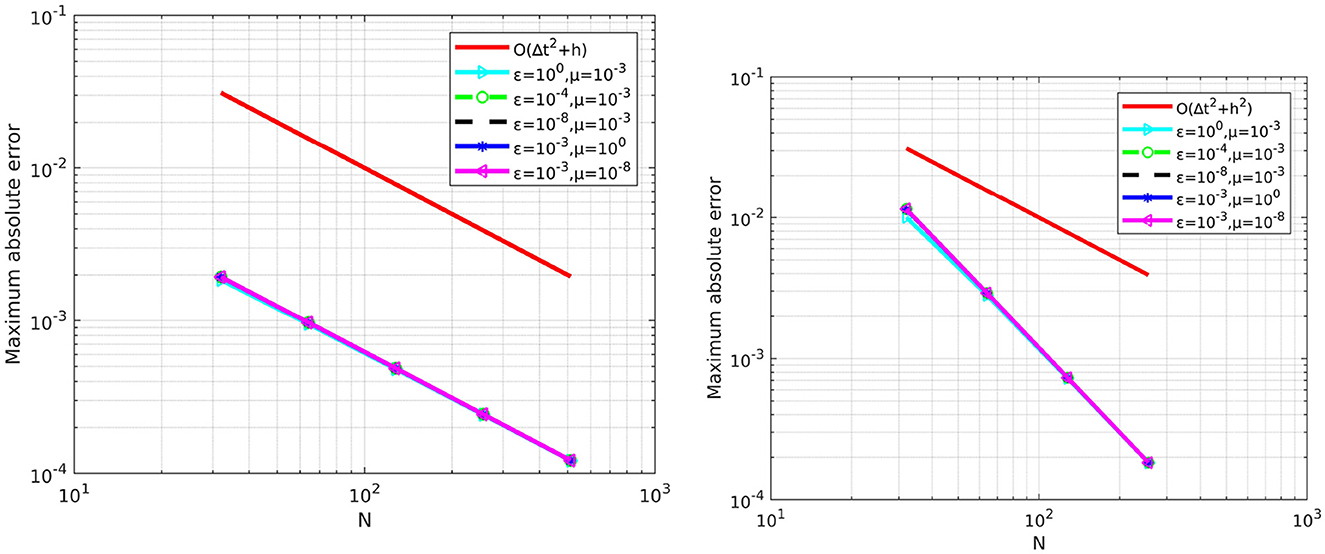
Table 6 shows the comparison of our scheme with the reference cited in Kumar and Kumar [44]. The comparison confirms that the maximum point-wise error, obtained by our scheme is less than the error obtained by the scheme in Kumar and Kumar [44]. For the given example (5.1) the plotted Figures 1, 2 exhibit that the boundary layer behavior in the solution of the given problem. Again, the log-log plot in Figure 3 supports our theoretical error estimates.
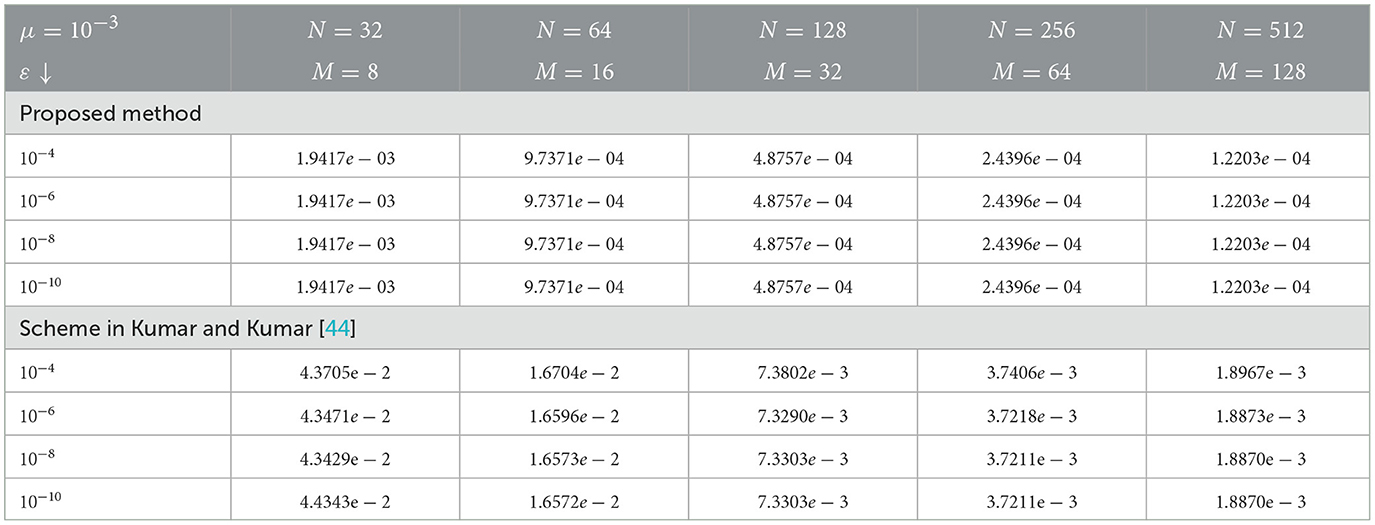
Table 6. Comparison of of our scheme in (8) with an existing schemes in Kumar and Kumar [44] using example (5.1).
6. Conclusion
We have developed a non-standard fitted operator finite difference method (NSFOFDM) for solving singularly perturbed time-delay partial differential equation with two perturbation parameters. In this study, uniform meshes have been considered in both space and time directions. The discretization was by using the implicit Crank-Nicolson finite difference method for time variable and a non-standard fitted operator finite difference(NSFOFDM) for space variable. The proposed numerical method is uniformly convergent independent of both the perturbation parameters, ε and μ. The scheme is shown to be first order in space and second order in time theoretically, but, we improved the order of convergence to the second order in both variables using temporal mesh refinement as shown in Tables 4, 5. To confirm the theoretical convergence results and to demonstrate the applicability of the proposed method, an example has been provided and results are presented in tables and graphs using Matlab software. The numerical example confirms the theoretical analyses. In our study, we considered two-parameter time-delay problem in one space dimensional. Future researches can be done in two space dimension.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors contributed significantly, directly, and academically to the work and agreed to its publication.
Acknowledgments
The authors wish to acknowledge the referees for their constructive suggestions and comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Van Dyke M. Nineteenth-century roots of the boundary-layer idea. Siam Rev. (1994) 36:415–24. doi: 10.1137/1036097
2. Prandtl L. Über Flussigkeitsbewegung bei sehr kleiner Reibung. Heidelberg: Verhandl III, Internat Math-Kong; Leipzig: Teubner (1904). p. 484–91.
3. Chandru M, Das P, Ramos H. Numerical treatment of two-parameter singularly perturbed parabolic convection diffusion problems with non-smooth data. Math Methods Appl Sci. (2018) 41:5359–87. doi: 10.1002/mma.5067
4. Zahra W, El Mhlawy AM. Numerical solution of two-parameter singularly perturbed boundary value problems via exponential spline. J King Saud Univ Sci. (2013) 25:201–8. doi: 10.1016/j.jksus.2013.01.003
5. Abdelhakem M, Youssri Y. Two spectral Legendre's derivative algorithms for Lane-Emden, Bratu equations, and singular perturbed problems. Appl Num Math. (2021) 169:243–55. doi: 10.1016/j.apnum.2021.07.006
6. Abd-Elhameed W, Youssri Y, Doha E. A novel operational matrix method based on shifted Legendre polynomials for solving second-order boundary value problems involving singular, singularly perturbed and Bratu-type equations. Math Sci. (2015) 9:93–102. doi: 10.1007/s40096-015-0155-8
7. Polak S, Den Heijer C, Schilders W, Markowich P. Semiconductor device modelling from the numerical point of view. Int J Num Methods Eng. (1987) 24:763–838.
8. Chen J, O'Malley RE. Jr. On the asymptotic solution of a two-parameter boundary value problem of chemical reactor theory. SIAM J Appl Math. (1974) 26:717–29.
10. Friedrichs KO, Wasow WR. Singular perturbations of non-linear oscillations. Duke Math J. (1946) 13:367–81.
11. Mickens RE. Nonstandard Finite Difference Models of Differential Equations. Singapore: World Scientific (1994).
12. Kopteva N. Uniform pointwise convergence of difference schemes for convection-diffusion problems on layer-adapted meshes. Computing. (2001) 66:179–97. doi: 10.1007/s006070170034
13. Roos HG, Uzelac Z. The SDFEM for a convection-diffusion problem with two small parameters. Comput Methods Appl Math. (2003) 3:443–58. doi: 10.2478/cmam-2003-0029
14. Yüzbaşı Ş, Şahin N. Numerical solutions of singularly perturbed one-dimensional parabolic convection–diffusion problems by the Bessel collocation method. Appl Math Comput. Elsevier (2013) 220:305–15. doi: 10.1016/j.amc.2013.06.027
15. Miller J, O'Riordan E, Shishkin G, Shishkina L. Fitted mesh methods for problems with parabolic boundary layers. In: Mathematical Proceedings of the Royal Irish Academy. JSTOR (1998). p. 173–90.
16. O'Malley. Two-parameter singular perturbation problems for second-order equations. J Math Mech. (1967) 16:1143–64.
17. O'Malley. Boundary value problems for linear systems of ordinary differential equations involving many small parameters. J Math Mech. (1969) 18:835–55.
18. Munyakazi JB. A robust finite difference method for two-parameter parabolic convection-diffusion problems. Appl Math Inform Sci. (2015) 9:2877. doi: 10.12785/amis/090614
19. Das P, Natesan S. Numerical solution of a system of singularly perturbed convection diffusion boundary value problems using mesh equidistribution technique. Aust J Math Anal Appl. (2013) 10:1–17.
20. Das P. Comparison of a priori and a posteriori meshes for singularly perturbed nonlinear parameterized problems. J Comput Appl Math. (2015) 290:16–25. doi: 10.1016/j.cam.2015.04.034
21. Das P, Natesan S. Higher-order parameter uniform convergent schemes for Robin type reaction-diffusion problems using adaptively generated grid. Int J Comput Methods. (2012) 9:1250052. doi: 10.1142/S0219876212500521
22. Das P, Natesan S. Richardson extrapolation method for singularly perturbed convection-diffusion problems on adaptively generated mesh. Comput Model Eng Sci. (2013) 90:463–85.
23. Das P, Natesan S. Adaptive mesh generation for singularly perturbed fourth-order ordinary differential equations. Int J Comput Math. (2015) 92:562–78. doi: 10.1080/00207160.2014.902054
24. Dehghan M. Numerical solution of the three-dimensional advection–diffusion equation. Appl Math Comput. (2004) 150:5–19. doi: 10.1016/S0096-3003(03)00193-0
25. Gracia J, O'Riordan E, Pickett M. A parameter robust second order numerical method for a singularly perturbed two-parameter problem. Appl Num Math. (2006) 56:962–80. doi: 10.1016/j.apnum.2005.08.002
26. Kadalbajoo MK, Jha A. Exponentially fitted cubic spline for two-parameter singularly perturbed boundary value problems. Int J Comput Math. (2012) 89:836–50. doi: 10.1080/00207160.2012.663492
27. Kaushik A. Singular perturbation analysis of bistable differential equation arising in the nerve pulse propagation. Nonlin Anal. (2008) 9:2106–27. doi: 10.1016/j.nonrwa.2007.06.014
28. Kellogg RB, Tsan A. Analysis of some difference approximations for a singular perturbation problem without turning points. Math Comput. (1978) 32:1025–39.
29. Linss T. A posteriori error estimation for a singularly perturbed problem with two small parameters. Int J Num Anal Model. (2010) 7:491–506.
30. O'Riordan E, Pickett ML, Shishkin GI. Singularly perturbed problems modeling reaction-convection-diffusion processes. Comput Methods Appl Math. (2003) 3:424–42. doi: 10.2478/cmam-2003-0028
31. Patidar KC. A robust fitted operator finite difference method for a two-parameter singular perturbation problem. J Diff Eq Appl. (2008) 14:1197–214. doi: 10.1080/10236190701817383
32. Vulanović R. A higher-order scheme for quasilinear boundary value problems with two small parameters. Computing. (2001) 67:287–303. doi: 10.1007/s006070170002
33. Chandru M, Prabha T, Shanthi V. A parameter robust higher order numerical method for singularly perturbed two parameter problems with non-smooth data. J Comput Appl Math. (2017) 309:11–27. doi: 10.1016/j.cam.2016.06.009
34. Shanthi V, Ramanujam N, Natesan S. Fitted mesh method for singularly perturbed reaction-convection-diffusion problems with boundary and interior layers. J Appl Math Comput. (2006) 22:49–65. doi: 10.1007/BF02896460
35. Bashier EB, Patidar KC. A novel fitted operator finite difference method for a singularly perturbed delay parabolic partial differential equation. Appl Math Comput. (2011) 217:4728–39. doi: 10.1016/j.amc.2010.11.028
36. Kaushik A, Sharma K, Sharma M. A parameter uniform difference scheme for parabolic partial differential equation with a retarded argument. Appl Math Model. (2010) 34:4232–42. doi: 10.1016/j.apm.2010.04.020
37. Kumar S, Kumar M. High order parameter-uniform discretization for singularly perturbed parabolic partial differential equations with time delay. Comput Math Appl. (2014) 68:1355–67. doi: 10.1016/j.camwa.2014.09.004
38. Erdogan F, Cen Z. A uniformly almost second order convergent numerical method for singularly perturbed delay differential equations. J Comput Appl Math. (2018) 333:382–94. doi: 10.1016/j.cam.2017.11.017
39. Cen Z. A second-order finite difference scheme for a class of singularly perturbed delay differential equations. Int J Comput Math. (2010) 87:173–85. doi: 10.1080/00207160801989875
40. Singh J, Kumar S, Kumar M. A domain decomposition method for solving singularly perturbed parabolic reaction-diffusion problems with time delay. Num Methods Part Diff Eq. (2018) 34:1849–66. doi: 10.1002/num.22256
41. Ansari A, Bakr S, Shishkin G. A parameter-robust finite difference method for singularly perturbed delay parabolic partial differential equations. J Comput Appl Math. (2007) 205:552–66. doi: 10.1016/j.cam.2006.05.032
42. Kumar S, Kumar M. A second order uniformly convergent numerical scheme for parameterized singularly perturbed delay differential problems. Num Algorit. (2017) 76:349–60. doi: 10.1007/s11075-016-0258-9
43. Govindarao L, Sahu SR, Mohapatra J. Uniformly convergent numerical method for singularly perturbed time delay parabolic problem with two small parameters. Iran J Sci Technol Trans A. (2019) 43:2373–83. doi: 10.1007/s40995-019-00697-2
44. Kumar S, Kumar M. A robust numerical method for a two-parameter singularly perturbed time delay parabolic problem. Comput Appl Math. (2020) 39:1–25. doi: 10.1007/s40314-020-01236-1
45. O'Riordan E, Pickett M, Shishkin G. Parameter-uniform finite difference schemes for singularly perturbed parabolic diffusion-convection-reaction problems. Math Comput. (2006) 75:1135–54. doi: 10.1090/S0025-5718-06-01846-1
46. Kadalbajoo M, Yadaw AS. Parameter-uniform finite element method for two-parameter singularly perturbed parabolic reaction-diffusion problems. Int J Comput Methods. (2012) 9:1250047. doi: 10.1142/S0219876212500478
47. Miller JJ, O'riordan E, Shishkin GI. Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions. Singapore: World Scientific (1996).
Keywords: singular perturbation, delay differential equation, non-standard finite difference method, uniformly convergent scheme, boundary layers
Citation: Mohye MA, Munyakazi JB and Dinka TG (2023) A nonstandard fitted operator finite difference method for two-parameter singularly perturbed time-delay parabolic problems. Front. Appl. Math. Stat. 9:1222162. doi: 10.3389/fams.2023.1222162
Received: 13 May 2023; Accepted: 15 August 2023;
Published: 05 September 2023.
Edited by:
Eric Chung, The Chinese University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Youssri Hassan Youssri, Cairo University, EgyptNdolane Sene, Cheikh Anta Diop University, Senegal
Copyright © 2023 Mohye, Munyakazi and Dinka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tekle Gemechu Dinka, dGVrZ2VtQHlhaG9vLmNvbQ==
 Mekashaw Ali Mohye
Mekashaw Ali Mohye Justin B. Munyakazi
Justin B. Munyakazi Tekle Gemechu Dinka
Tekle Gemechu Dinka