- Department of Mathematics, Dilla University, Dilla, Ethiopia
This study deals with a fitted third-degree B-spline collocation method for two parametric singularly perturbed parabolic problems with a time lag. The proposed method comprises the Cranck-Nicolson method for time discretization and the third-degree B-spline method spatial variable discretization. Rigorous numerical experimentations were carried out on some test examples. The obtained numerical results depict that the proposed scheme is more accurate than some methods existing in the literature. Parameter convergence analysis of the scheme is carried out and shows the present scheme is (ε−μ)−uniform convergent with the order of convergence ((Δt)2 + ℓ2).
1 Introduction
We consider the following two-parametric singularly perturbed parabolic problem with the time lag of the form:
where , T is fixed time, ε, γ(0 < ε, γ ≪ 1) are two small perturbation parameters and τ > 0 is delay parameter. For the existence and uniqueness of the solution, the functions a(s, t), b(s, t), c(s, t), f(s, t) q0(t), q1(t) and θ(s, t) are sufficiently smooth and bounded with a(s, t) ≥ α > 0, b(s, t) ≥ ϖ > 0, b(s, t)+c(s, t) ≥ β > 0. The mathematical models related to two-parameter singularly perturbed problem of type (1) arises in transport phenomena in chemistry, biology, chemical reactor theory [1], lubrication theory [2], and dc motor theory [3] and flow through unsaturated porous media [4].
Due to the dual presence of singular parameters and time delay in the problem finding oscillation-free solution of Equation (1) using contemporary computational methods are very tough task. To overcome such limitations, some scholars developed parameter uniform numerical methods. For instance, Sumit et al. [5] presented a robust numerical scheme using a hybrid monotone finite difference scheme on uniform mesh in time and a piecewise uniform Shishkin mesh in space for Equation (1). Govindarao et al. [6] developed a uniformly convergent computational method using the implicit Euler scheme for temporal discretization on a uniform mesh and the upwind difference scheme for the spatial discretization on the Shishkin type meshes for Equation (1). The authors in the study mentioned in the references [7] and [8] constructed a parameter uniform numerical method based on a uniform mesh for Equation (1). The schemes in the study mentioned in the references [5] and [6] need apriori knowledge about the location and the width of the boundary layer(s) which might be difficult to understand for beginner researchers. Exponentially fitted difference (EFD) schemes have gained popularity as a powerful technique to singularly perturbed problems. For instance, the authors in the study mentioned in the references [9–11] suggested different EFD schemes for singularly perturbed two-point boundary-value problems. The aforementioned studies above motivate us, to propose and analyze the fitted third-degree B-spline collocation scheme for Equation (1). Analytical aspects of the problem, the description of the proposed scheme, and its corresponding analysis are preserved in the subsequent sections.
1.1 Apriori estimates for the solution of the continuous problem
When τ < ε, the use of Taylor's series expansion for the term containing shift argument is valid [12]. On applying Taylor's series expansion on u(s, t − τ), we have:
Now taking Equation (2) into Equation (1), we have:
where, η(s, t) = b(s, t)−c(s, t), dτ(s, t) = 1 + τc(s, t).
Lemma 1. (Continuous minimum principle). If , u|∂Ω ≥ 0 and . Then, .
Proof. Assume that the arbitrary function u attains its minimum value at the point such that and suppose that u(s*, t*) < 0. Clearly, (s*, t*)∉∂Ω. Therefore, , and . Moreover, for (s*, t*) ∈ Ω, we have
which is illogicality to the supposition that . It follows that .
Lemma 2. (Uniform stability estimate) Let u(s, t) be the solution of Equation (3), then we have:
where is used to denote maximum norm given by
Proof. Let Θ± be the barrier functions given as
Then at the initial and boundary conditions, we have
Applying the differential operator in (3) on Θ±(s, t), we have
Since η(s, t) ≥ β > 0 we have η(s, t)β−1 > 1, and the fact ‖f‖ ≥ f(s, t) implies that . Hence, Lemma (1) confirms , which yields the desired result.
The above Lemma (1) and Lemma (2) are guarantees for the existence and uniqueness solution of Equation (3), respectively.
2 Formulation of the numerical method
2.1 Temporal semi-discretization
We describe the uniform mesh for the domain Ωt as
Applying the Crank-Nicholson method on t−direction of Equation (3) yields
where
and
The local truncation error (LTE) of the temporal semi-discretization of Equation (6) is defined as ej+1 = u(s, tj+1) − U(s, tj+1), where U(s, tj+1) is the solution of the following BVP
Now, we state the bounds for the errors in the local and global as follows.
Lemma 3. (LTE) If
the LTE of Equation (6) is given by
Proof. See [6].
Lemma 4. Underneath Lemma (3), the global error estimate (GEE)at tj is given by
Proof. From Lemma 3, we have
where C(C > 0) is constant independent of ε, μ, and Δt.
2.2 Spatial discretization
To approximate Equation (6), we employ the third-degree B-spline collocation method. We divide the space domain as with si = iℓ, where ℓ = 1/N. The third-degree B-Spline (Bi(s)) can be defined as [13]
where form a basis over . Let be the set of all third-degree B-spline functions over the subintervals . Let λ = {B−1, B0, B1, ⋯ , BN+1} and be the set of all linear components of . The function are linearly independent, thus is dimensional space of [14].
In the third-degree B-spline collocation method, we approximate the exact solution U(s, tj+1) by S(s) in the form:
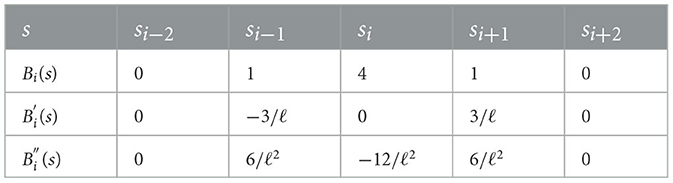
where αi(t)'s are time-dependent parameters to be determined from the collocation method together with using the boundary and initial conditions. The values of Bi(s) and its derivatives are presented in Table 1.
From Equation (10) and Table 1, we have
At s = si undertaking the notation U(si, tj+1) = Û(si) Equation (6) and introducing a fitting factor σ(si) in the resulting equation to handle the influence of perturbation parameter on solution profile, we have
In the corresponding time level, plugging Equation (11) at the knots into Equation (12) and simplifying, we obtain
where
The fitting factor σi is given as [15, 16]
where ρ = ℓ/ε.
At each (j + 1)th time level, this gives (N + 1) equations with (N + 3) unknowns . Using boundary conditions in Equation (11) and the first and last equation, of Equation (13), we get
where
which is a diagonally dominant and non-singular matrix. Consequently, we get a exclusively solvable system of equations. So, we can solve the system in the study mentioned in the reference [15] for α′s, substituting these values into Equation (10), and we obtain the required approximate solution.
3 Convergence analysis
Lemma 5. [15] The B-Splines B−1, B0, B1, ..., BN+1, satisfy the inequality
Proof. See [15]
Lemma 6. Let S(s) be the collocation approximation from the space of third-degree splines to the solution Û(s) of Equation (15) at the (j + 1)th time step. If g ∈ C2[0, 1], the parameter uniform error estimate is given by:
where C is a positive constant independent of ε, μ, and N.
Proof. Let R(s) be the unique spline interpolate from to the solution Û(si) of the Equation (12) given by
If , , and adopting the Hall error estimates [17] for this case, we get
where the c0, c1, and c2 are the constants independent of ℓ and N. Therefore, from the estimates of the above equations and the collocating conditions , it follows
Since ε ≪ 1 and as ℓ → 0, we obtain the following estimate
From the power series expansion of hyperbolic cotangent function, we have and then |scoths − 1| ≤ Cs2. This and Equation (14) indicate
Substituting Equation (19) in Equation (18), we get
Using relationship in Equation (15), yields,
where ,
Using Equation (20), we get
It is observed that the coefficient matrix A is diagonally dominant as they gratify the subsequent relations::
In addition, from the first and last rows of Y, we have
The above diagonal dominant property for smaller values of ℓ [18] gives
From (20)-(22), we get
Now to estimate and , using the boundary conditions, we get
Therefore
The above inequality allows us to estimate: ‖S(s)−R(s)‖∞, so ‖Û(s)−S(s)‖∞. In specific,
Thus, substituting Equation (24) and Lemma 5 in (25), we get
This gives
Using the triangle inequality rule, we obtain
Using first term of Equation (17) and Equation (26) into Equation (27), we have
Theorem 1. Let u(si, tj) and S(si, tj) be the solution of the problem (3) and the collocation approximation from the space ξ3(Ωs) to the solution u(si, tj), respectively. If ,
4 Test examples, numerical computations, and discussions
Some numerical experiments have been presented using the following examples.
Example 1. Consider the following problem of the form (1) [5, 6]
Example 2. Consider the following problem of the form (1) [5, 6]
Since the exact solution for Examples (1) and (2) is not exist, we use the double mesh principle to compute the maximum absolute errors, for each ε and μ, using the following formula [15, 19]:
where is the numerical solution with (N, M) mesh points, and is the numerical solution at the finer mesh with (2N, 2M) mesh points. The (ε, γ)-uniform absolute errors are calculated using the following formula:
The numerical rate of convergence and the (ε, γ)-uniform rate of convergence are computed by using the following formulas, respectively.
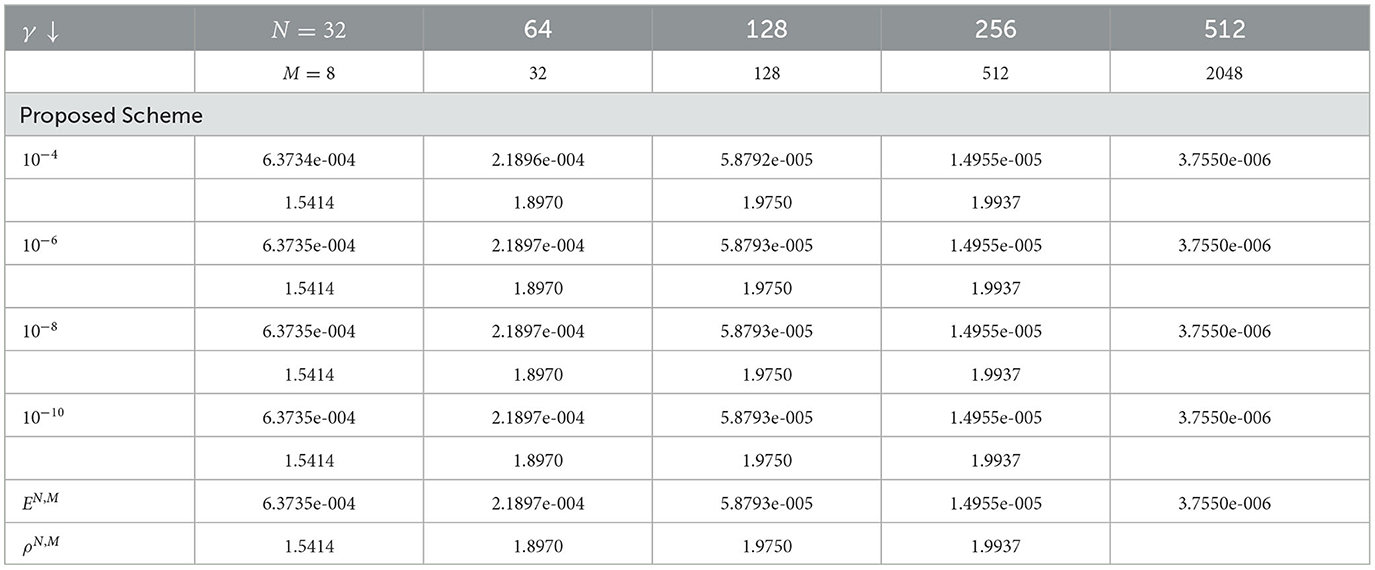
The computed results by the proposed scheme and comparison with previous schemes for the considered problems are presented in Tables 2–5. From these tables, we observed that the presented method provides more accurate results than results in the study mentioned in the references [5] and [6]. 3-D view numerical simulation for Examples (1) and (2) is presented in Figures 1, 2, respectively. These figures show that as (ε, γ) goes very small, twin boundary layers formed at s = 0 and s = 1. We have plotted a log-log plot of the verses N in Figures 3A, B for (1)-(2), respectively. This figure shows that the scheme is stable and (ε, γ)−uniformly convergent.
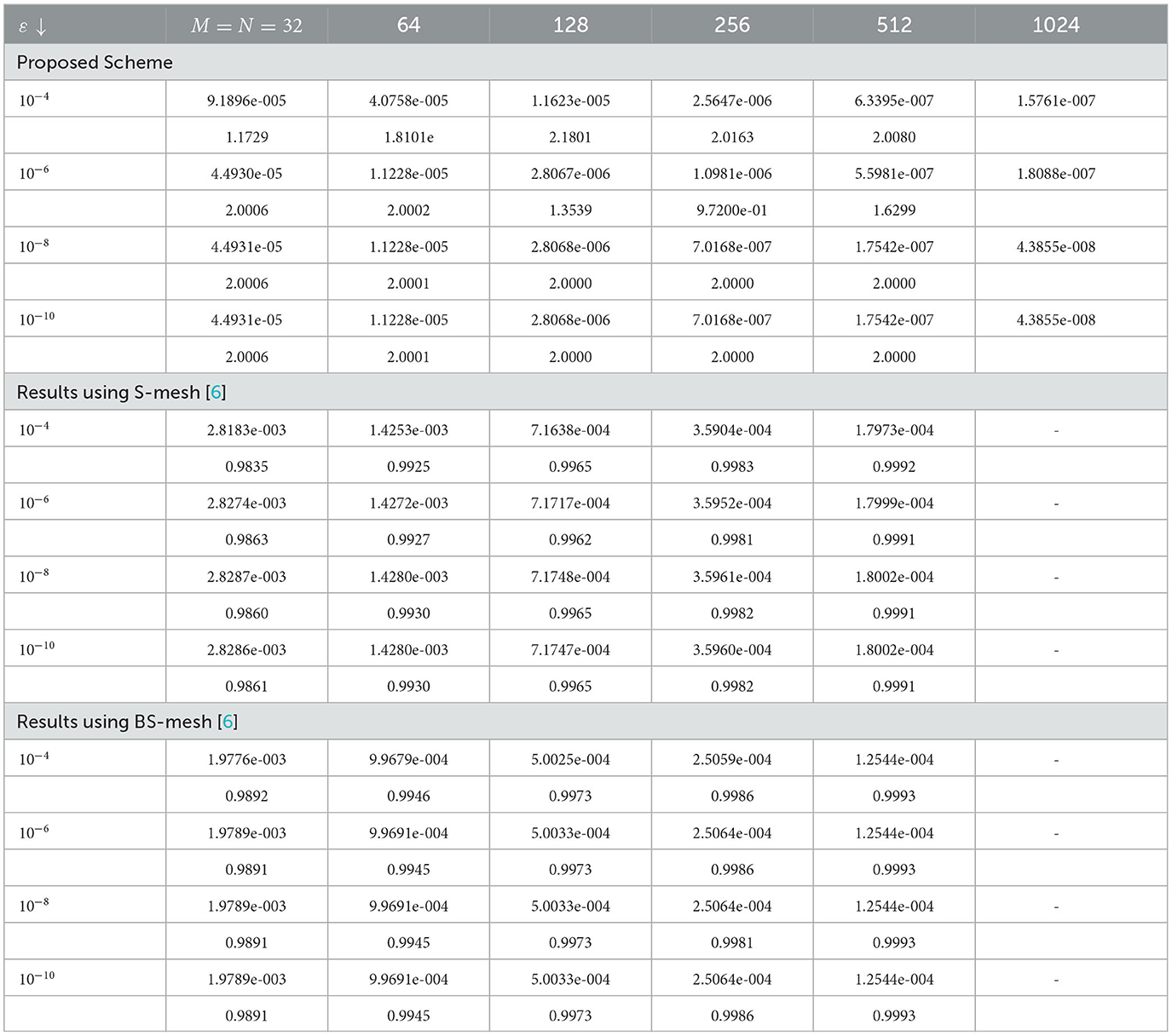
Table 2. Comparison of and for fixed γ = 10−4 and varying ε for Example (1) with the study mentioned in the reference [6] using Shishkin (S-) mesh and Bakhvalov-Shishkin (BS-) mesh.
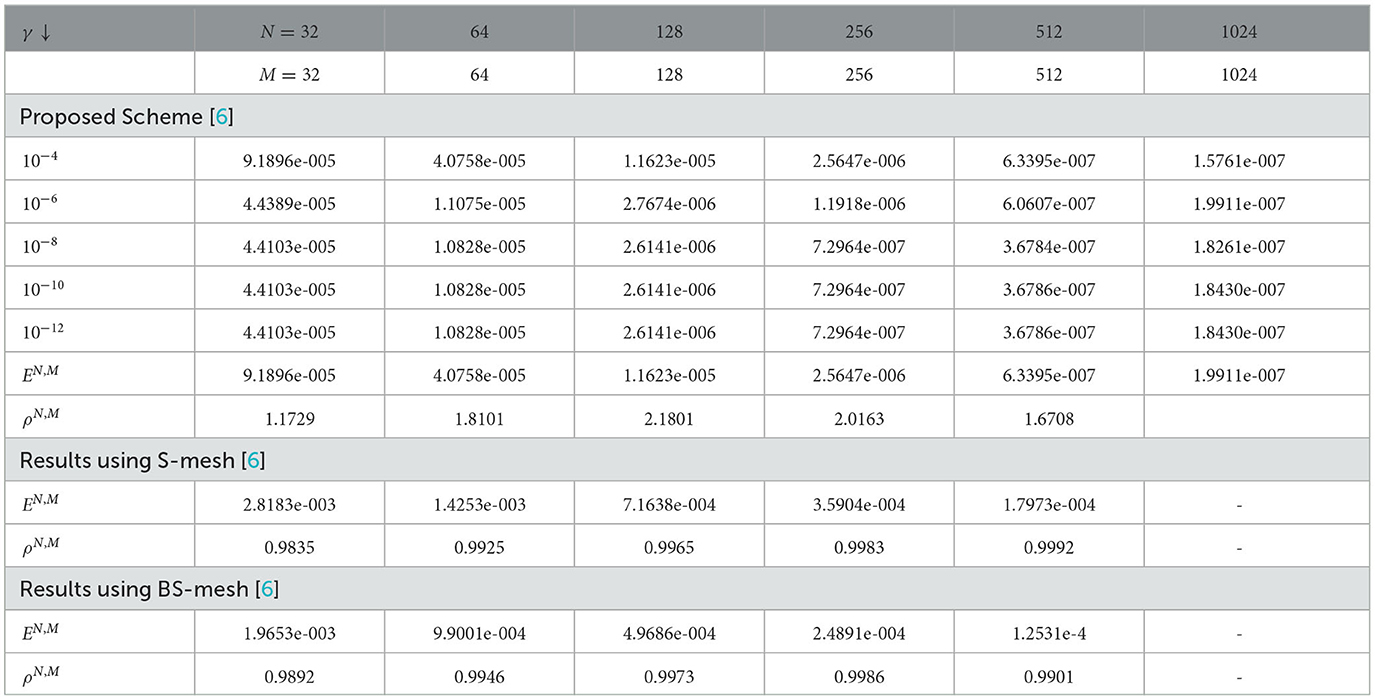
Table 3. Comparison of , EN,M, and ρN,M for ϵ = 10−4 and varying γ for Example (1) with the study mentioned in the reference [6] using S- mesh and BS- mesh.
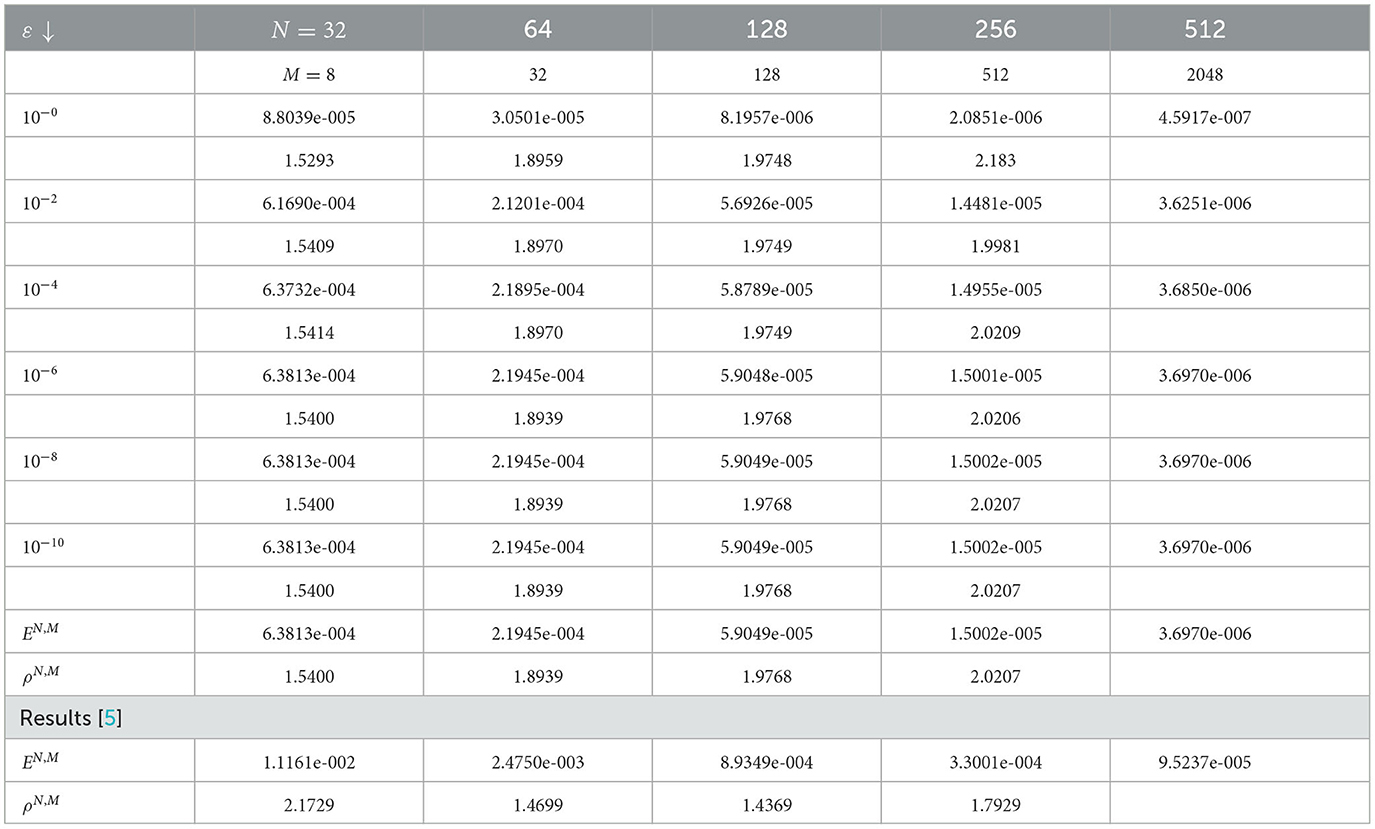
Table 4. Comparison of and for γ = 10−3 and varying ε for Example (2) with the results mentioned in the reference [5].
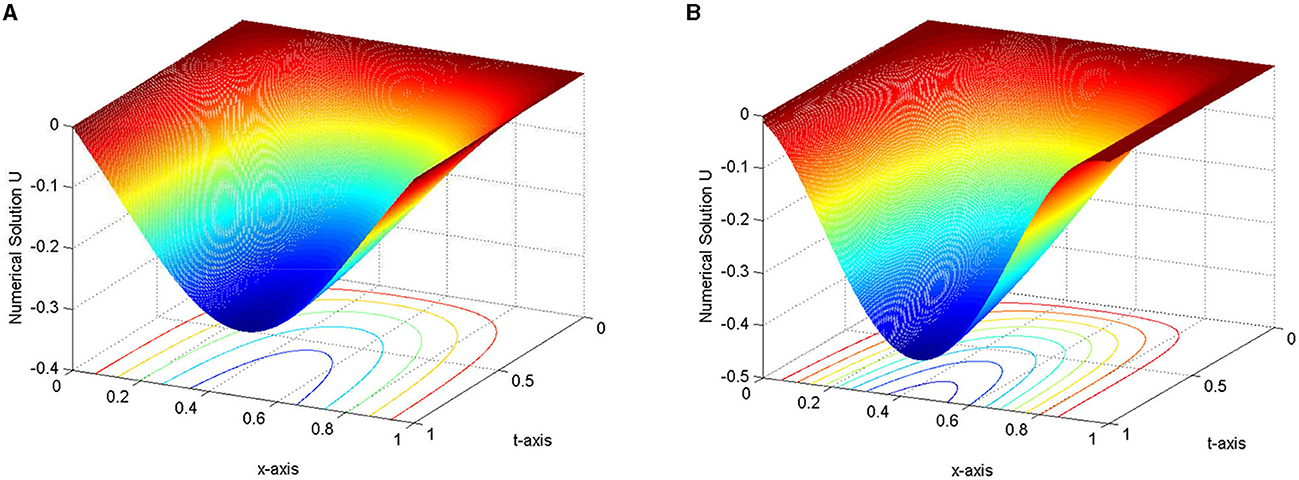
Figure 1. 3-D view numerical solution profile for Example 1 at N = 512 = M. (A) γ = 10−6, ε = 10−1. (B) γ = 10−1, ε = 10−6.
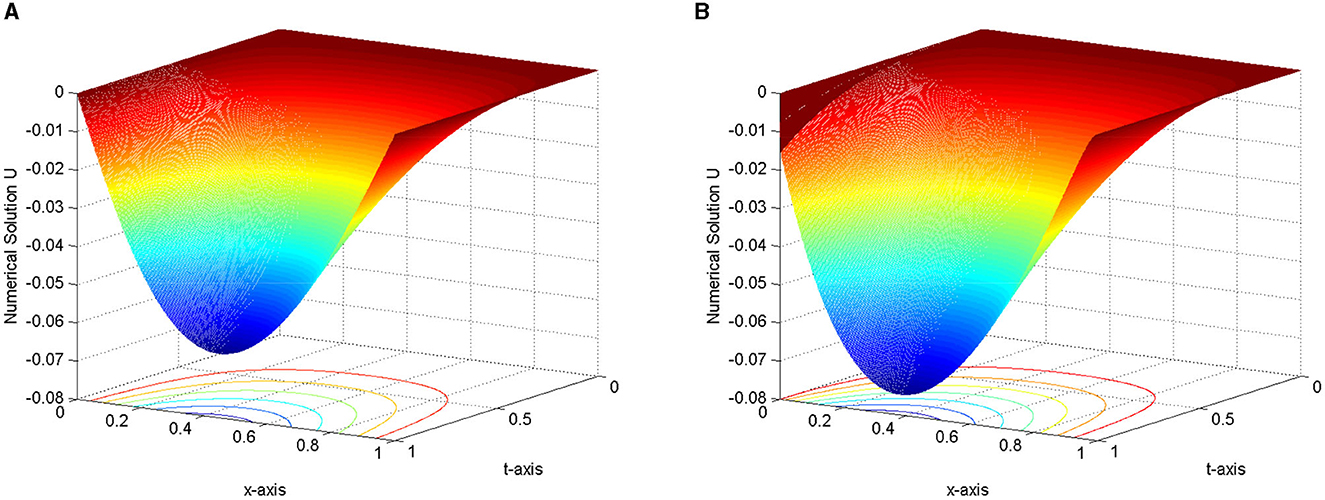
Figure 2. 3-D view numerical solution profile for Example 2 at N = 512 = M. (A) γ = 10−6, ε = 10−1. (B) γ = 10−1, ε = 10−6.
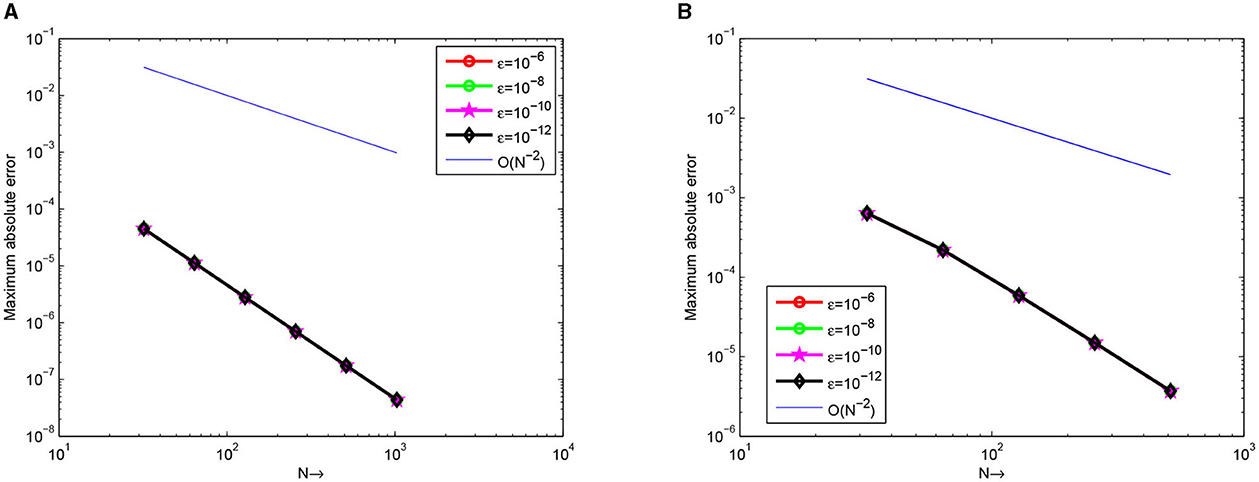
Figure 3. Loglog plot of the maximum point-wise errors for Examples 1 and 2 at different values of ε. (A) Example 1 with γ = 10−4. (B) Example 2 with γ = 10−3.
5 Conclusion
In this study, second order numerical method for the two-parametric singularly perturbed time delay parabolic problem on a uniform mesh is presented. The problem is discretized by the Crank-Nicolson method in time and the third-degree B-spline method in space variable. The presented scheme is proven to be an (ε, γ)−uniformly convergent accuracy of order O((Δt)2 + ℓ2). To validate the theoretical findings, some test examples are considered. The computed results are in agreement with the theoretical investigations. Furthermore, the numerical results show that the presented scheme gives better results than available schemes in the literature.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
ITD: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review and editing. WGM: Conceptualization, Investigation, Methodology, Validation, Writing - review and editing. GDK: Investigation, Methodology, Validation, Writing - review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors would like to thank the editor and referees for careful reading and giving prolific comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Chen J, O'Malley RE Jr. On the asymptotic solution of a two-parameter boundary value problem of chemical reactor theory. SIAM J Appl Math. (1974) 26:717–29. doi: 10.1137/0126064
2. DiPrima RC. Asymptotic methods for an infinitely long slider squeeze-film bearing. J Lubricat Technol. (1968) 90:173–83. doi: 10.1115/1.3601534
3. Vasil'eva AB. Asymptotic methods in the theory of ordinary differential equations containing small parameters in front of the highest derivatives. USSR Comput Math Phys. (1963) 3:823–63. doi: 10.1016/0041-5553(63)90381-1
4. Bhathawala PH, Verma AP. A two-parameter singular perturbation solution of one dimension flow through unsaturated porous media. Proc Indian Natl Sci Acad. (1975) 43:380–4.
5. Saini S, Kumar S, Kuldeep K, Kumar M. A robust numerical method for a two-parameter singularly perturbed time delay parabolic problem. Comput Appl Math. (2020) 39. doi: 10.1007/s40314-020-01236-1
6. Govindarao L, Sahu SR, Mohapatra J. Uniformly convergent numerical method for singularly perturbed time delay parabolic problem with two small parameters. Iran J Sci Technol Trans A Sci. (2019) 43:2373–83. doi: 10.1007/s40995-019-00697-2
7. Negero NT. A uniformly convergent numerical scheme for two parameters singularly perturbed parabolic convection-diffusion problems with a large temporal lag. Results Appl Math. (2022) 16:100338. doi: 10.1016/j.rinam.2022.100338
8. Negero NT. A parameter-uniform efficient numerical scheme for singularly perturbed time-delay parabolic problems with two small parameters. Partial Diff Equat Appl Math. (2023) 7:100518. doi: 10.1016/j.padiff.2023.100518
9. Vigo-Aguiara J, Natesan S. An efficient numerical method for singular perturbation problems. J Comput Appl Math. (2006) 192:132–41. doi: 10.1016/j.cam.2005.04.042
10. Natesan S, Vico-Acuiar J, Ramanujam N. A numerical algorithm for singular perturbation problems exhibiting weak boundary layers. Comput Math Appl. (2003) 45:469–79. doi: 10.1016/S0898-1221(03)80031-7
11. Vico-Acuiar J, Natesan S. A parallel boundary value technique for singularly perturbed two-point boundary value problems. J Supercomput. (2004) 27:195–206. doi: 10.1023/B:SUPE.0000009322.23950.53
12. Tian H. The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag. J Math Anal Appl. (2002) 270:143–9. doi: 10.1016/S0022-247X(02)00056-2
15. Daba IT, Duressa GF. Collocation method using artificial viscosity for time dependent singularly perturbed differential–difference equations. Math Comput Simulat. (2022) 192:201–20. doi: 10.1016/j.matcom.2021.09.005
16. O'Malley RE. Singular Perturbation Methods for Ordinary Differential Equations. Berlin: Springer (1991). doi: 10.1007/978-1-4612-0977-5
17. Hall C. On error bounds for spline interpolation. J Approx Theory. (1968) 1:209–18. doi: 10.1016/0021-9045(68)90025-7
18. Varah JM. A lower bound for the smallest singular value of a matrix. Linear Algebra Appl. (1975) 11:3–5. doi: 10.1016/0024-3795(75)90112-3
Keywords: third degree B-spline collocation method, Crank-Nicholson method, time delay, two-parametric, parameter uniform numerical method
Citation: Daba IT, Melesse WG and Kebede GD (2024) Third-degree B-spline collocation method for singularly perturbed time delay parabolic problem with two parameters. Front. Appl. Math. Stat. 9:1260651. doi: 10.3389/fams.2023.1260651
Received: 18 July 2023; Accepted: 13 December 2023;
Published: 08 January 2024.
Edited by:
Justin B. Munyakazi, University of the Western Cape, South AfricaReviewed by:
Youssri Hassan Youssri, Cairo University, EgyptAhmed Atta, Ain Shams University, Egypt
Copyright © 2024 Daba, Melesse and Kebede. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Imiru Takele Daba, aW1pcnV0YWtlbGVAZ21haWwuY29t
 Imiru Takele Daba
Imiru Takele Daba Wondwosen Gebeyaw Melesse
Wondwosen Gebeyaw Melesse Guta Demisu Kebede
Guta Demisu Kebede