Fractional-order projection of a chaotic system with hidden attractors and its passivity-based synchronization

This paper presents the fractional-order projection of a chaotic system, which delivers a collection of self-excited and hidden chaotic attractors as a function of a single system parameter. Based on an integer-order chaotic system and the proposed transformation, the fractional-order chaotic system obtains when the divergence of integer and fractional vector fields flows in the same direction. Phase portraits, bifurcation diagrams, and Lyapunov exponents validate the chaos generation. Apart from these results, two passivity-based fractional control laws are designed effectively for the integer and fractional-order chaotic systems. In both cases, the synchronization schemes depend on suitable storage functions given by the fractional Lyapunov theory. Several numerical experiments confirm the proposed approach and agree well with the mathematical deductions.

1. Introduction

Because chaos phenomenon is ubiquitous in diverse fields of science, such as electronics, mechanics, physics, optics, quantum, etc., it is imperative to continue discovering and analyzing chaotic systems. As well known, the chaotic attractors of dynamical systems can be classified as self-excited and hidden, which may contain one-scroll, two-scrolls, multi-wing, and multi-scrolls. In literature, the scientific community has been working hard to propose novel chaotic systems in discrete (maps) or continuous (flows) domains since they could mean a step forward in understanding physical phenomena with significant engineering applications [1–8]. However, there is still a need for new chaotic systems encompassing recent approaches, like quantum chaos, hidden attractors, multi-stability, and fractional-order calculus, among others.

In particular, several works have demonstrated that the fractional-order derivatives with long-term memory, such as Caputo, Riemann-Liouville, and Grünwald-Letnikov, improve the accuracy of the mathematical models in real-world situations [9–13]. However, most of those papers have only changed the integer-order derivative for a fractional-order one, a procedure known as fractionalization. For example, Han et al. explained the co-existence of a fractional-order chaotic attractor along with its implementation in a Digital Signal Processor (DSP) [14]. Then, Akgül et al. achieved the synchronization between two fractional-order chaotic systems based on memristor and memcapacitor, respectively [15]. Next, Alassafi et al. presented a finite time command filter for obtaining a fuzzy synchronization between two fractional-order multi-wing chaotic systems [16]. Dutta et al. introduced a new memductance-based fractional-order chaotic system and a fixed time synchronization method [17]. Finally, Fiaz et al. showed the synchronization among integer and fractional-order chaotic systems using the inactive control methodology [18].

To the authors' best knowledge, no study has been conducted on the projection/transformation from an integer-order chaotic system to the fractional-order domain based on the inner product of both vector fields, i.e., when the vectors point in the direction of maximal increase of the function. In this manner, we propose a novel approach to determine a projection of the gradient vector field of an integer-order chaotic system onto the vector field of a fractional-order chaotic system. Projections have proven to be a valuable mathematical tool for studying dynamical systems. For instance, Sheu and Capoferri et al. demonstrated quantum projections and pseudo-differential projections, respectively [19, 20]. Lau et al. and Dorrek et al. revealed projections in Banach algebras and projection functions of the Alesker-Fourier transform, respectively [21, 22]. Next, Basso reported both maximal projection constants and maximal projections in a three-dimensional subspace [23]. Finally, Baillon et al. and Angelos et al. documented the conditions for periodic projections and limit cycles of successive projections in ℝⁿ [24, 25]. In fact, the presented projection/transformation may be helpful to improve the security of encryption schemes based on chaos since achieving the gradient vectors evolve in the same direction increases the computational complexity compared to the traditional fractionalization technique.

Additionally, the second goal of this work is to find hidden attractors in the proposed integer-order chaotic system. A hidden attractor presents a domain of attraction far from any unstable equilibrium point. Therefore, exploring hidden attractors is essential to understanding unexpected and disastrous responses in engineering applications [26–28]. To this end, various numerical and analytical strategies can be used, such as numerical continuation algorithms, homotopy methods, etc. In particular, Munoz-Pacheco et al. [29] introduced an approach to find hidden attractors using the Bendixson theorem. A similar strategy is implemented in this work, where the main difference is that the presented system possesses only a single parameter. Other procedures to locate hidden attractors are detailed in Gong et al. [30], Danca and Lampart [31], Wang et al. [32], Liu et al. [33], Pulido-Luna et al. [34], and Yue et al. [35]. Certainly, the hidden attractor of the integer-order system can be projected to the fractional-order domain under the proposed transformation.

After completing the fractional-order projection, we introduce a passivity-based control approach to get synchronized responses between the integer-order system and its fractional-order projection. Such control strategies take advantage of the energy dissipation of dynamical systems by considering input and output variables and a storage function [36–38]. Accordingly, accurate responses and decreased control efforts can be achieved by using the dissipation properties of integer-order and fractional-order-projection systems, which is valuable in engineering applications as was shown in Shen et al. [39], Wu et al. [40], and Gandarilla et al. [41]. Nevertheless, most passivity-based synchronization schemes have been implemented for integer-order systems, such as Yao et al. [42], Syed and Yogambigai [43], Kaviarasan et al. [44], Stoorvogel et al. [45], Ihle et al. [46], and Mathiyalagan et al. [47], which studied the synchronization in complex and neural networks, respectively. On the other hand, a collection of passivity-based control for the case of fractional-order systems is shown in Zambrano-Serrano et al. [48], Qi et al. [49], Xiao et al. [50], Rajchakit et al. [51], Shafiya and Nagamani [52], and Padmaja and Balasubramaniam [53]. Based on the previous discussion, conducting research on fractional-order projection in dynamical systems is crucial to fully understanding this fascinating and less-explored topic. The contributions of this work are:

• One of the first times introducing a projection/transformation of an integer-order chaotic system into the fractional-order domain based on the inner product of the vector fields under the condition that both gradients evolve in the same direction.

• The hidden attractor of the novel integer-order chaotic system is also projected into the fractional-order domain by applying the proposed approach.

• Based on the fractional-order Lyapunov theory and appropriate storage functions, a passivity-based fractional controller is introduced to synchronize the integer-order chaotic systems with its fractional-order projection.

• The hidden attractor in the integer-order system was located by determining the divergence of the vector field and the Bendixson theorem.

The outline of the manuscript is as follows: Section 2 shows the mathematical foundations of fractional-order calculus. Section 3 presents the novel integer-order chaotic system and the fractional-order projection system. Phase portraits, bifurcation diagrams, and Lyapunov exponents are used to validate the chaotic behavior. Section 4 introduces the passivity-based control strategy, whereas Section 5 delivers various numerical experiments to demonstrate the synchronization between identical chaotic systems. Finally, the discussion and conclusion are given in Sections 6 and 7, respectively.

2. Theoretical background

In this section, the mathematical foundations of fractional-order calculus are given. More specifically, we define Caputo derivatives and Riemann-Liouville integrals and derivatives.

Definition 1. [54]. The Riemann-Liouville derivative of order α is given by:

$\begin{array}{ll}\frac{d^{\alpha }}{d{t}^{\alpha }}f(t)=\frac{1}{\Gamma (n-\alpha )}\frac{d^n}{d{t}^n}{\displaystyle {\int }_0^t\frac{f^{(n)}(\tau )}{{(t-\tau )}^{\alpha +1-n}}}d\tau & (1)\end{array}$

Definition 2. [55]. The Caputo derivative is given by:

$\begin{array}{ll}\frac{d^{\alpha }}{d{t}^{\alpha }}f(t)=\frac{1}{\Gamma (n-\alpha )}{\displaystyle {\int }_0^t\frac{f^{(n)}(\tau )}{{(t-\tau )}^{\alpha +1-n}}}d\tau & (2)\end{array}$

Definition 3. [56]. The left-side Riemann-Liouville integral of order α_i is given by:

$\begin{array}{ll}{}_0{I}_t^{{\alpha }_i}{f}_i(t)=\frac{1}{\Gamma ({\alpha }_i)}{\displaystyle {\int }_0^t\frac{f_i(\tau )}{{(t-\tau )}^{1-{\alpha }_i}}}d\tau & (3)\end{array}$

Definition 4. [57, 58]. The Caputo time-fractional derivative operator of order α > 1 is defined as:

$\begin{array}{ll}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}f(x,t)=\frac{1}{\Gamma (n-\alpha )}{\displaystyle {\int }_0^t\frac{\frac{{\partial }^n}{\partial {\tau }^n}f(x,\tau )}{{(t-\tau )}^{\alpha +1-n}}}d\tau .& (4)\end{array}$

with n − 1 < α ≤ n for Definition 1, Definition 2, and Definition 4. For α = n, the classical calculus definitions are recovered.

3. Problem formulation

Let us introduce a novel integer-order chaotic system composed of six terms (three linear, two nonlinear, and one constant) and a single system parameter, given by:

$\begin{array}{l}{\dot{x}}_1=-a\text{ sign}(x_2)+x_3^3,\\ {\dot{x}}_2=-x_3-1,\\ {\dot{x}}_3=-x_1-x_3,& (5)\end{array}$

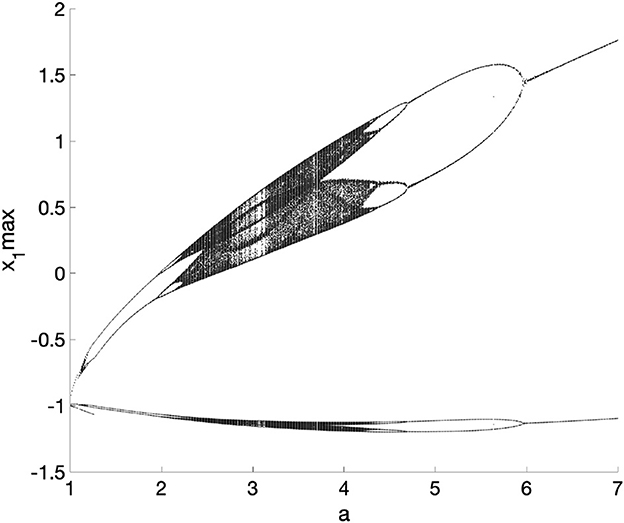
with a ∈ ℝ and x_i, i = 1, 2, 3 being state-variables. For f(x) = 0, it is straightforward to deduce that system (5) has no equilibrium points when a ≠ ±1. To demonstrate that the proposed system generates chaotic behavior, we compute the Lyapunov exponents by Wolf algorithm [59, 60]: λ₁ = 0.984, λ₂ = 0.000, and λ₃ = −2.623. Due to λ₁ is positive, the chaotic behavior is confirmed. Figure 1 shows the hidden attractors of the chaotic system. As a remark, the hidden attractor is found using the approach given in Munoz-Pacheco et al. [29] but adapted to the real-valued chaotic system (5). By applying the Bendixson theorem, the domain of attraction changes when a = 3.1, i.e., the hidden attractor is discovered. We observe that the hidden attractor localization is a function only of the system parameter a, becoming a simple system in the Sprott sense but with abundant complex behaviors. Figure 2 presents the bifurcation diagram for variable x₁ and x₁. From these diagrams, it is noticed that the mechanism of chaos generation is via period-doubling bifurcations. Even though a single system parameter controls the dynamical behaviors, continuous and dense chaos regions suggest the proposed system is robust against external perturbations. After the numerical analysis of the integer-order chaotic system, the next step is obtaining a fractional-order system.

FIGURE 1

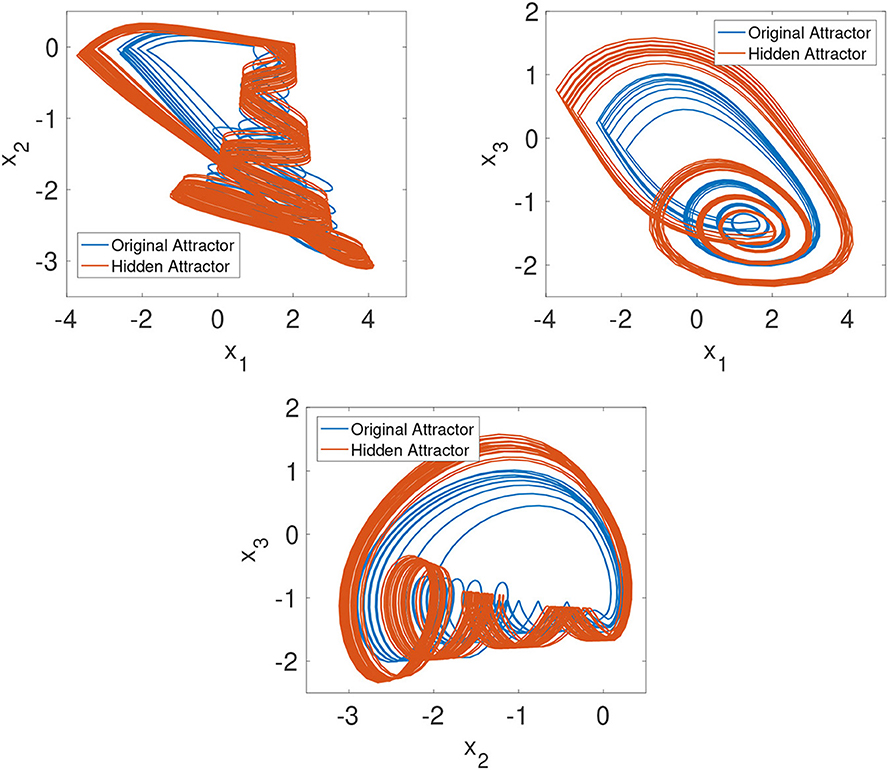
Figure 1. Original and hidden chaotic attractors generated by system (5): (A) x₁ − x₂, (B) x₂ − x₃, and (C) x₁ − x₂ − x₃.

FIGURE 2

Figure 2. Bifurcation diagram for the proposed chaotic system (5).

3.1. Fractional-order projection of the chaotic system with hidden attractor

The main idea of the proposed approach involves a projection of an integer-order chaotic system onto a fractional-order domain. It's important to note that we are not converting the integer-order system into a fractional-order system, also known as fractionalization, which involves replacing the integer-order derivative with a fractional-order operator. This theory has been thoroughly studied in the literature. On the contrary, we search for a projection of the gradient of the vector field from the integer-order chaotic system onto the vector field of the fractional-order chaotic system, i.e., the gradient vector field of both systems should point in the same direction. Under this transformation, the hidden attractor of the integer-order system is also projected to the fractional-order domain. Let us state Theorem 1 to obtain the fractional-order projection.

Theorem 1. Consider an integer order chaotic system given by $\frac{d{X}_1}{dt}=f(X_1,t)$ and a fractional-order chaotic system given by $D^{\alpha }{X}_1=g(X_1,t)$ where $X_1\in {ℝ}^n$ is the state vector, $f(X_1,t)\in {ℝ}^n$, $g(X_1,t)\in {ℝ}^n$ are the respective vector fields, and n − 1 ≤ α < n is the fractional-order. By considering that $f(X_1,t)={\left[f_1(X_1,t),f_2(X_1,t),f_3(X_1,t)\right]}^T$ and $g(X_1,t)={\left[g_1(X_1,t),g_2(X_1,t),g_3(X_1,t)\right]}^T$, then the transformation $\mathcal{T}(f(X_1,t))=g(X_1,t)$ : ℝⁿ → ℝⁿ occurs only iff:

$\begin{array}{r}\mathcal{T}(f(X_1,t))=\{g(X_1,t)\in {ℝ}^n:\langle {\nabla }_t^T\left(X_1(0)+{\displaystyle {\int }_0^{t}f}(X_1,\tau )d\tau \right),\\ \frac{{\partial }^{\alpha +1}}{\partial t^{\alpha +1}}{X}_1\rangle =1\},& (6)\end{array}$

with ${\nabla }_t={\left[\frac{\partial }{\partial t},\frac{\partial }{\partial t},...,\frac{\partial }{\partial t}\right]}^T$, to guarantee the vector fields of the integer-order system and fractional-order projected chaotic system (6) are collinear, i.e., the projection of the vector field f (X₁, t) into $\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}{X}_1$ must be equal to 1 ∀t ∈ [0, t_f], in which t_f is the final time.

Proof. Consider the definition of the inner product for two vector fields f(t) ∈ ℝⁿ and g(t) ∈ ℝⁿ:

$\begin{array}{ll}\langle f(t),g(t)\rangle ={\displaystyle {\int }_0^{t}f}{(\tau )}^{T}g(\tau )d\tau .& (7)\end{array}$

Then, the inner product for the vector field $f(X_1,\tau )\in {ℝ}^n$ with the state variable $X_1\in {ℝ}^n$ is given by:

$\begin{array}{l}\langle {\nabla }_t^T\left(X_1(0)+{\displaystyle {\int }_0^{t}f}(X_1,\tau )d\tau \right),\frac{{\partial }^{\alpha +1}}{\partial t^{\alpha +1}}{X}_1\rangle \\ ={\displaystyle {\int }_0^t{\left[{\nabla }_t^T{\displaystyle {\int }_0^{t}f}(X_1,\tau )d\tau \right]}^T}\frac{{\partial }^{\alpha +1}}{\partial t^{\alpha +1}}{X}_1({\tau }_1)d{\tau }_1.& (8)\end{array}$

By Leibniz's theorem of multivariable calculus, we have:

$\begin{array}{ll}={\nabla }_t^T{\displaystyle {\int }_0^t\frac{\partial }{\partial t}}{\left[{\displaystyle {\int }_0^{t}f}(X_1,\tau )d\tau \right]}^T\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}{X}_1({\tau }_1)d{\tau }_1,& (9)\end{array}$

$\begin{array}{ll}={\nabla }_t^T{\displaystyle {\int }_0^{t}f}{(X_1,{\tau }_1)}^T\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}{X}_1({\tau }_1)d{\tau }_1,& (10)\end{array}$

$\begin{array}{ll}=f{(X_1,t)}^T\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}{X}_1(t).& (11)\end{array}$

To obtain a collinear projection, the inner product of the two vector fields must be in the same direction ∀t ∈ [0, t_f], as given by:

$\begin{array}{ll}{f}_1(X_1,t)\frac{{\partial }^{\alpha }{x}_1}{\partial t^{\alpha }}+f_2(X_1,t)\frac{{\partial }^{\alpha }{x}_2}{\partial t^{\alpha }}+f_3(X_1,t)\frac{{\partial }^{\alpha }{x}_3}{\partial t^{\alpha }}=1,& (12)\end{array}$

where

$\begin{array}{ll}\{\begin{array}{l}\frac{{\partial }^{\alpha }{x}_1}{\partial t^{\alpha }}=\frac{1}{f_1(X_1,t)},\\ \frac{{\partial }^{\alpha }{x}_2}{\partial t^{\alpha }}=-f_3(X_1,t),\\ \frac{{\partial }^{\alpha }{x}_3}{\partial t^{\alpha }}=f_2(X_1,t).\end{array}& (13)\end{array}$

The proof is completed. □

Using Theorem 1, we can obtain the projection of f(X₁, t) into $\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}{X}_1$. In this manner, system (5) is transformed into a fractional-order dynamical system with the form of Equation (13) under the following set of components.

$\begin{array}{ll}\{\begin{array}{l}{f}_1(X_1,t)=-a\text{sign}(x_2)+x_3^3,\\ f_2(X_1,t)=-x_3-1,\\ f_3(X_1,t)=-x_1-x_3.\end{array}& (14)\end{array}$

Figure 3 illustrates the resulting attractors of the fractional-order projection system (13)-(14). This figure shows that the trajectories of the integer-order system are mapped onto a fractional-order domain, evidencing the usefulness of the proposed projection. Additionally, It is important to note that not only the original attractor is projected but also the hidden attractor. As well known, projections on different vector spaces are common in quantum mechanics, fluid mechanics, particle systems, optics, and so forth. So, the results obtained may be useful for such areas. For the aim of a physical circuit implementation, we refer the reader to the references [61, 62] as guidelines for designing fractional-order chaotic systems.

FIGURE 3

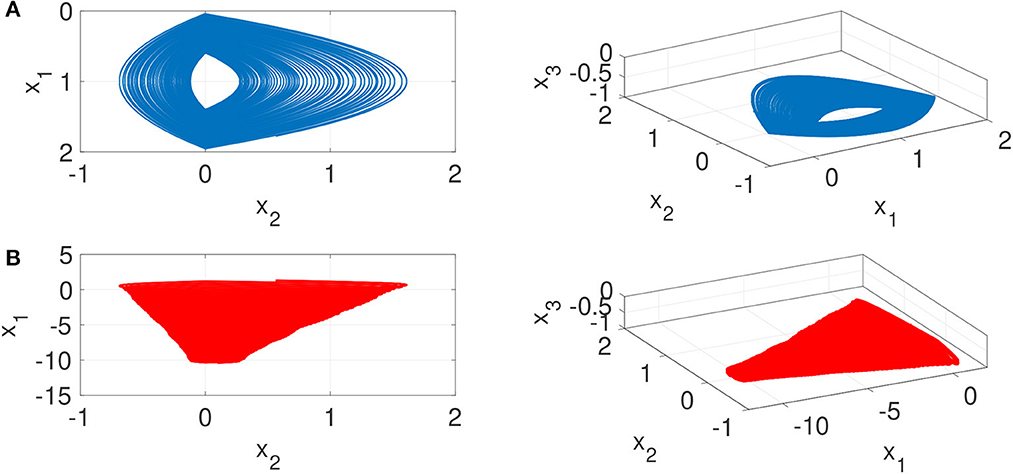
Figure 3. Phase portraits of the fractional-order projection Equation (13): (A) Original attractor x₁ − x₂ (blue color), (B) Hidden attractor x₁ − x₂ (orange color).

4. Passivity-based synchronization for identical chaotic systems

In this section, we introduce two control laws based on passivity to synchronize the integer-order chaotic system with its fractional-order projection. In the case of the integer-order system, the passivity-based controller is designed by taking into consideration the energy and dissipation properties. Therefore, the controller provides an accurate synchronization between drive and response systems while the passivity-based control law attains anti-oscillation properties. It means the control effort does not possess any oscillation, essential to prevent any harmful events in physical implementations. Similarly, the dissipative properties of the fractional-order projection system are considered for designing an appropriate fractional-order controller. In both cases, the passivity-based control laws are obtained by the Lyapunov theory.

For synchronization purposes, let us consider system (5) as the drive system, whereas the response system is given by:

$\begin{array}{l}{\dot{\widehat{x}}}_1=-a\text{ sign}({\widehat{x}}_2)+{\widehat{x}}_3^3+u_1,\\ {\dot{\widehat{x}}}_2=-{\widehat{x}}_3-1+u_2,\\ {\dot{\widehat{x}}}_3=-{\widehat{x}}_1-{\widehat{x}}_3+u_3,& (15)\end{array}$

By assuming that:

$\begin{array}{ll}{X}_1=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right],X_2=\left[\begin{array}{c}{\widehat{x}}_1\\ {\widehat{x}}_2\\ {\widehat{x}}_3\end{array}\right],U=\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right],& (16)\end{array}$

with $X_1\in {ℝ}^3$, $X_2\in {ℝ}^3$ and U ∈ ℝ³, systems (Equation 5) and (Equation 15) can be recast as:

$\begin{array}{ll}\begin{array}{llll}{\dot{X}}_1\hfill & =f(X_1)\hfill & {\dot{X}}_2\hfill & =f(X_2)+U,\hfill \end{array}& (17)\end{array}$

where the error variable is defined by:

$\begin{array}{l}e=X_1-X_2,\\ \dot{e}={\dot{X}}_1-{\dot{X}}_2=f(X_1)-f(X_2)-U,& (18)\end{array}$

4.1. Passivity-based synchronization for the integer-order chaotic system

For the passivity-based synchronization, we design a controller that uses the passivity Property 1 [63–67]. As a consequence, we establish Theorem 2 to find the required passivity-based control law.

Property 1. A dynamical system in the form of ė = f(e, v, t), where e is the error variable, v is the dynamic input variable, and t is the time parameter with output y = e(t), is passive iff the derivative of the storage function V_s(x) satisfies:

$\begin{array}{ll}{\dot{V}}_s\le y^{T}v.& (19)\end{array}$

Theorem 2. For drive and response systems given by Equation (5) and (15), respectively, the passivity-based condition is fulfilled by using Property 1 and the control synchronization law:

$\begin{array}{ll}U=f(X_1)-f(X_2)+Kv+\frac{e}{\parallel e{\parallel }^2}{v}^T{K}^C{D}^{\alpha }v-v,& (20)\end{array}$

under the storage function V_s(X), in which v is the dynamic input controller with the form of:

$\begin{array}{ll}\dot{v}=Ke+K{}^C{D}^{\alpha }v,& (21)\end{array}$

with K ∈ ℝ^3×3 being a positive definite gain matrix and ^CD^α the Caputo derivative of order α with 0 < α < 1.

Proof. To find the passivity-based control law, let us consider the storage function:

$\begin{array}{ll}{V}_s=\frac{1}{2}{e}^{T}e+\frac{1}{2}{v}^{T}v.& (22)\end{array}$

By taking the derivative of Equation (22), we have:

$\begin{array}{ll}{\dot{V}}_s\le e^T\left[{\dot{X}}_1-{\dot{X}}_2\right]+v^T\left[Ke+K{}^C{D}^{\alpha }v\right],& (23)\end{array}$

resulting in the synchronization controller input (20). Then Equation (23) becomes:

$\begin{array}{ll}{\dot{V}}_s\le e^{T}v\le y^{T}v.& (24)\end{array}$

To obtain the optimal gain K_min for the state feedback component of the dynamic input v, the next outcomes should be considered:

$\begin{array}{l}\Lambda =\left\{K\in {ℝ}^{n\times n}:\nabla ·f(X_1)-\nabla ·f(X_2)-\nabla ·U<0)\right\},\\ {\Lambda }_m\subseteq \Lambda ,\\ K_{min}=\underset{K}{\text{inf}}{\Lambda }_m(X_1,X_2,K).& (25)\end{array}$

This completes the proof. □

In Section 5.3, we demonstrate the performance of the set (25) for variations in gain matrix K and sensitivity to the constant parameter a. In both scenarios, the synchronization becomes unstable if the gain does not meet the conditions defined in Equation 25.

4.2. Passivity-based synchronization for the fractional-order chaotic system

In this scenario, we present Theorem 3. This Theorem relies on the passivity Property 2 outlined in Zambrano-Serrano et al. [48] and allows us to derive the synchronization law for the fractional-order projection system.

Property 2. A dynamical system is passive iff:

$\begin{array}{ll}2{\displaystyle {\int }_0^t{y}^T}(s)v(s)ds\ge -\gamma {\displaystyle {\int }_0^t{v}^T}(s)v(s)ds& (26)\end{array}$

for γ > 0 and the state feedback input v = Ke, in which K is a gain matrix of appropriate dimensions.

Theorem 3. Let us consider the error variable between the drive and response system as e = X₁ − X₂, and system outputs y₁ = X₁ and y₂ = X₂ with y = y₁ − y₂ = e. By assuming a storage function V(e, v) and using Property 2, the synchronization between the drive and response systems is achieved if and only if the following control law is obtained:

$\begin{array}{ll}u=g(X_1)-g(X_2)-v.& (27)\end{array}$

where the auxiliary input variable is given as v = Ke with the gain matrix K ∈ ℝ^3×3.

Proof. Let us consider the following storage function in order that the passivity condition of Property 2 can be satisfied.

$\begin{array}{ll}V=e^{T}e+{}^C{D}^{-\alpha }{v}^{T}v.& (28)\end{array}$

Next, the fractional-order derivative of Equation (28) yields:

$\begin{array}{ll}{}^C{D}^{\alpha }V\le 2e^T{}^C{D}^{\alpha }e+2v^{T}v.& (29)\end{array}$

By considering the error variable e = X₁ − X₂ and system outputs y₁ and y₂, Equation (29) becomes

$\begin{array}{ll}{}^C{D}^{\alpha }V\le 2e^T\left[g(X_1)-g(X_2)-u\right]+2v^{T}v.& (30)\end{array}$

and substituting the control law Equation (27) in Equation (30), we have:

$\begin{array}{l}{}^C{D}^{\alpha }V\le 2e^{T}v+2v^{T}v,\\ {}^C{D}^{\alpha }V\le 2y^{T}v+2v^{T}v.& (31)\end{array}$

Then, we obtain the following expression by integrating both sides of Equation (31),

$\begin{array}{ll}{D}^{-1}{}^C{D}^{\alpha }V\le 2{\displaystyle {\int }_0^t{y}^T}(s)v(s)ds+2{\displaystyle {\int }_0^t{v}^T}(s)v(s)ds.& (32)\end{array}$

Assuming ^CD^−(1−α)V ≥ 0 [68], Equation (32) becomes:

$\begin{array}{ll}2{\displaystyle {\int }_0^{t}y}(s)v(s)ds\ge -2{\displaystyle {\int }_0^t{v}^T}(s)v(s)ds.& (33)\end{array}$

Therefore, the passivity condition is fulfilled, and the proof is completed. □

5. Numerical experiments

In the following sections, we present several numerical experiments for chaos synchronization. First, the synchronization between integer-order chaotic systems is given. Next, we analyze the synchronization scheme for the proposed fractional-order projection. To gain a better understanding of the performance of the presented passivity-based controllers, we test various scenarios, including different initial conditions and fractional orders. In addition, we also demonstrate the performance of the set (25) for variations in gain matrix K and sensitivity to the constant parameter a. All simulations are computed on a PC with an Intel Centrino processor running the GNU software Octave 4.2.2.

5.1. Experiment 1: integer-order scenario

By setting a derivative order α = 0.95 for the fractional-order controller and the constant parameter a = 2.5, the numerical results for the passivity-based synchronization using Theorem (2) are shown in Figures 4–6. In this case, the simulations are computed with initial conditions $X_2(0)={\left[0.1,0.1,0.1\right]}^T$ and $X_1(0)={\left[0.09,0.1005,0.095\right]}^T$ for the response and drive systems, respectively, and a gain matrix K as follows:

$\begin{array}{ll}K=\left[\begin{array}{ccc}0.0018& 0& 0\\ 0& 0.0018& 0\\ 0& 0& 0.0018\end{array}\right].& (34)\end{array}$

Figure 4 illustrates how the response system variables ${\widehat{x}}_1$, ${\widehat{x}}_2$, and ${\widehat{x}}_3$ track the evolution of the drive chaotic system. From these results, we observe that the error is minimal when the passivity-based controller proposed in Section 4.1 is applied, as corroborated in Figure 5. Despite the piecewise continuous function in system (5), the passivity-based controller drives the error variable to zero. In Figure 7, the control effort of input variables U₁, U₂ and U₃ is displayed. It is evident that synchronization has been successfully achieved with low control efforts. This is particularly significant when the synchronization scheme is intended for a hardware implementation. In this manner, the novel integer-order chaotic system (5) can be synchronized efficiently by using Theorem 2, which considers the dissipation properties of the closed-loop system. It is important to mention that dissipation plays a critical role in synchronizing the drive and response variables with low control efforts.

FIGURE 4

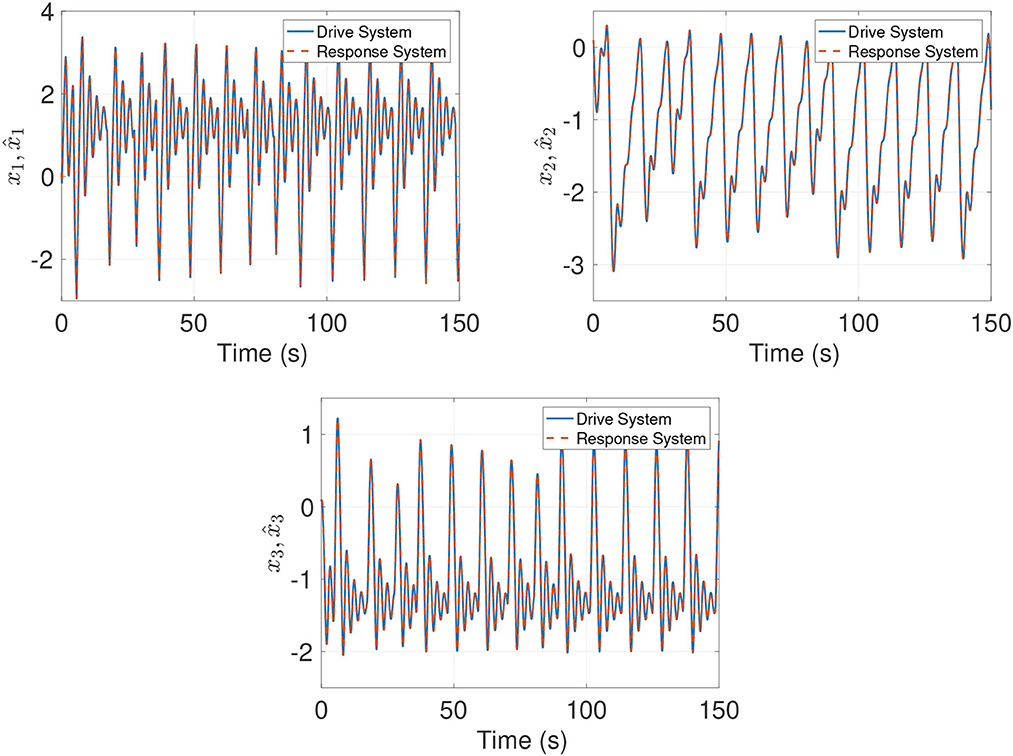
Figure 4. Synchronization results between identical integer-order chaotic systems expressed by Equation (5) under the passivity-based synchronization in Section 4.1.

FIGURE 5

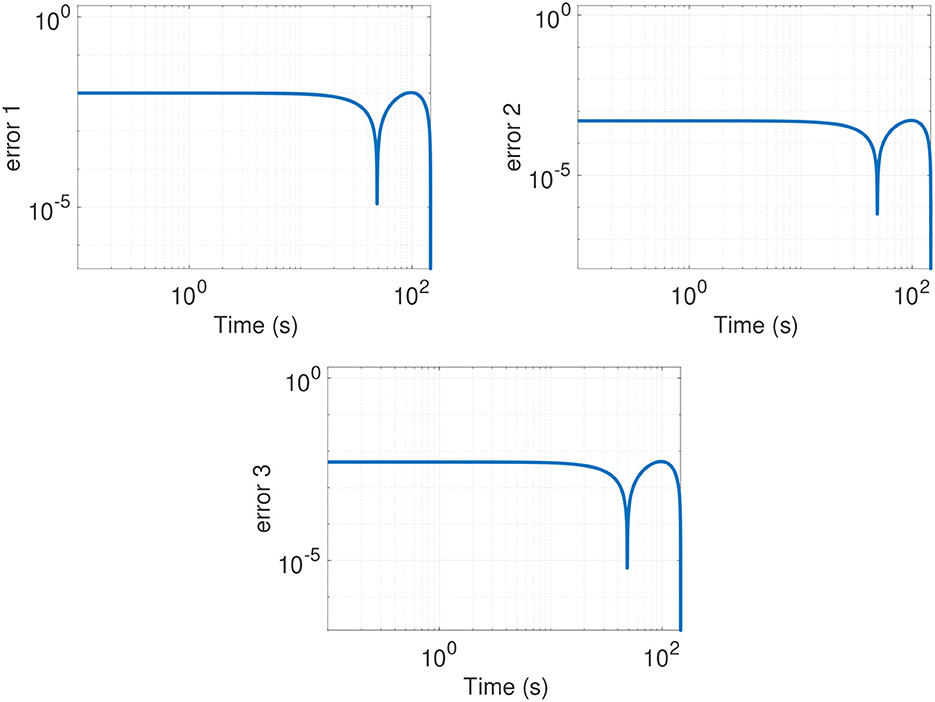
Figure 5. Synchronization error between drive and response variables for the integer-order case in this figure.

FIGURE 6

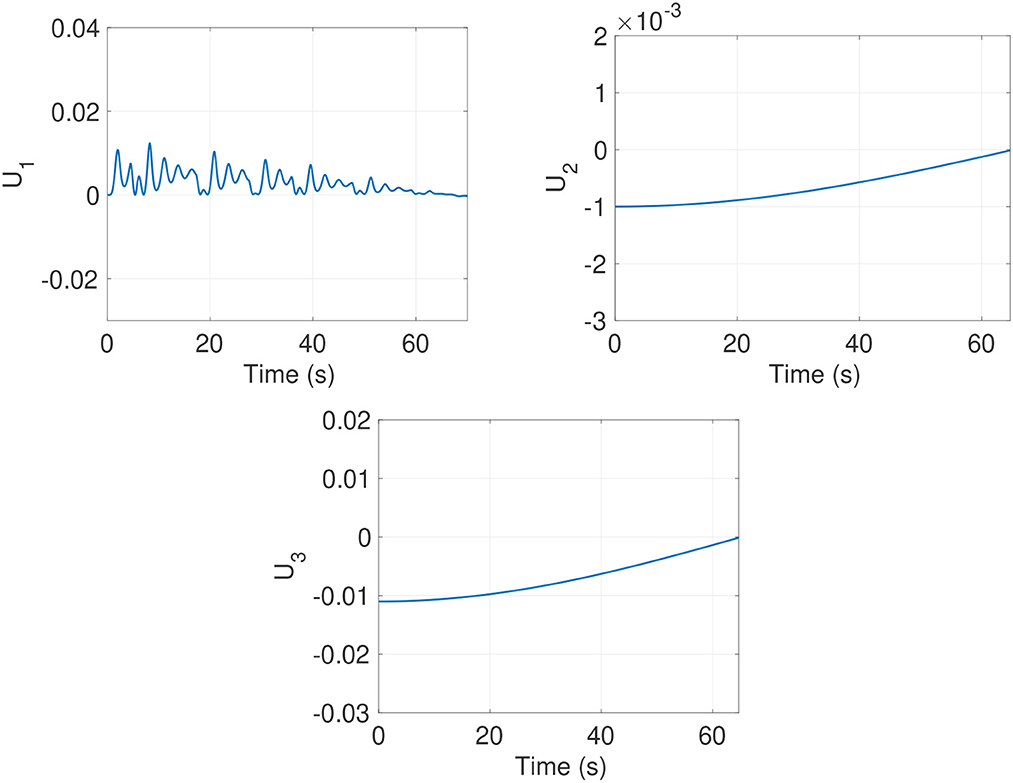
Figure 6. Control effort of the input variables u1, u2, u3 for the integer-order case in Figure 4.

FIGURE 7

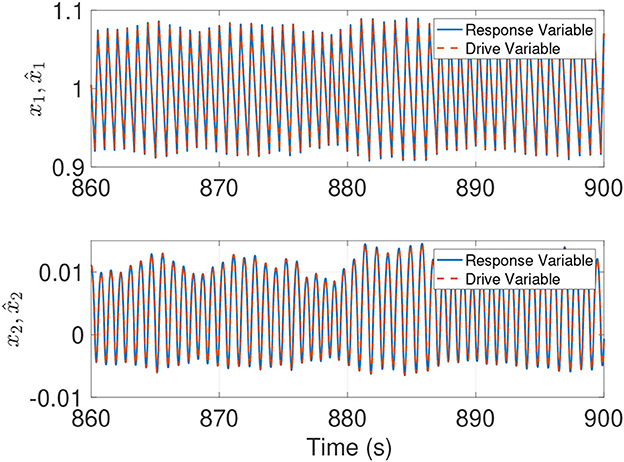
Figure 7. Evolution in time of the drive and response system variables for the fractional-order projection.

5.2. Experiment 2: fractional-order scenario

In this subsection, we conduct a numerical experiment to demonstrate the synchronization of the transformed/projected fractional-order chaotic system. In this case, we have chosen initial conditions $X_1(0)={\left[2,1,-3\right]}^T$ for drive system and $X_2(0)={\left[0.1,0.1,0.1\right]}^T$ for response system with a = 2.5. It is worth noting that the fractional order of the projection system (13)–(13) is set as α = 0.998, whereas the fractional order of the controller given in Theorem 3 is selected as α = 0.95. In addition, the gain matrix K in Equation (27) is given by:

$\begin{array}{ll}K=\left[\begin{array}{ccc}100& 0& 0\\ 0& 100& 0\\ 0& 0& 100\end{array}\right].& (35)\end{array}$

Figure 7 shows the synchronization between system variables ($x_1,{\widehat{x}}_1$), ($x_2,{\widehat{x}}_2$), and ($x_3,{\widehat{x}}_3$), respectively. Figure 8 displays the error variables along with the control effort of the input variables U₁, U₂ and U₃ to obtain synchronized behaviors. In this numerical experiment, we confirm that the fractional-order passivity-based controller can stabilize the fractional-order chaotic projection system, no matter the type of attractor, i.e., hidden or self-excited attractor. From Figure 8, we also note that the error variables converge to zero in a finite time. In this manner, the proposed passivity-based controller leads the system variables to be synchronized efficiently. An important outcome is that having an appropriate gain matrix K in Equation (27) can avoid undesired oscillations in control inputs. This can be advantageous in various engineering applications. In conclusion, the proposed passivity-based controller synchronizes the drive and response systems by the Caputo derivative of the Lyapunov function, similar to the results observed in the integer order scenario.

FIGURE 8

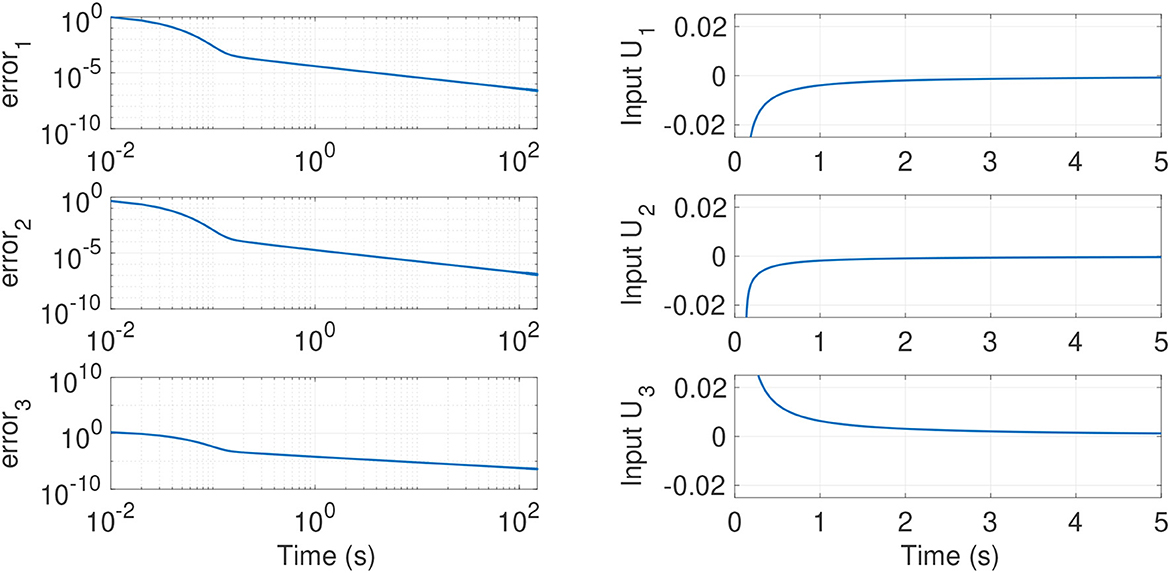
Figure 8. Evolution in time of the error and input variables, respectively, for the fractional-order projection.

5.3. Experiment 3: gain sensitivity analysis

Since the matrix gain K and the system parameter a can be altered by perturbations, we perform a sensitivity analysis for both parameters. The idea consists of selecting different values for both parameters and computing the resulting error between response and drive systems. It is essential to mention that the sensitivity analysis is based on the set Λ in Equation (25) to demonstrate the optimal gain region for the state feedback component of the dynamic input, i.e., the range where the controller is stable or unstable. Thus, we study the following cases:

• The gain K is varied for the controller in Section 4.1, implemented in Experiment-1.

• The parameter a is varied for the controller in Section 4.1, implemented in Experiment-1.

• The gain K is varied for the controller in Section 4.2, implemented in Experiment-2.

• The parameter a is varied for the controller in Section 4.2, implemented in Experiment-2.

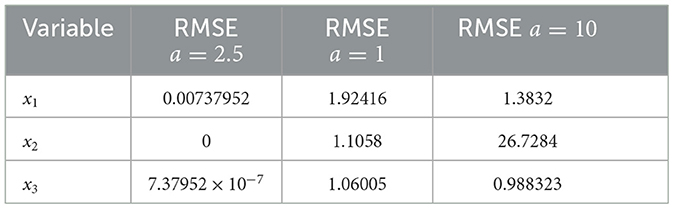
Figure 9 and Table 1 present the synchronized state variables, error variables, and Root Mean Square Error (RMSE), respectively. We discovered that the RMSE is at its lowest level when K is set to 0.0018. As K increases, the RMSE increases as well, but when the gain K approaches zero, there are only minor fluctuations in the RMSE. It is important to remark that the RMSE is zero for the variable x₂ because we have used positive definite diagonal matrices in Experiment-1. Once the optimal gain K has been determined, the next step is varying the system parameter a. Figure 10 and Table 2 give the RMSE for distinct values of a. It can be noticed that the variations in the system parameter provoke higher errors. In conclusion, the parameter a significantly affects the passivity-based controller given in Experimen-1.

FIGURE 9

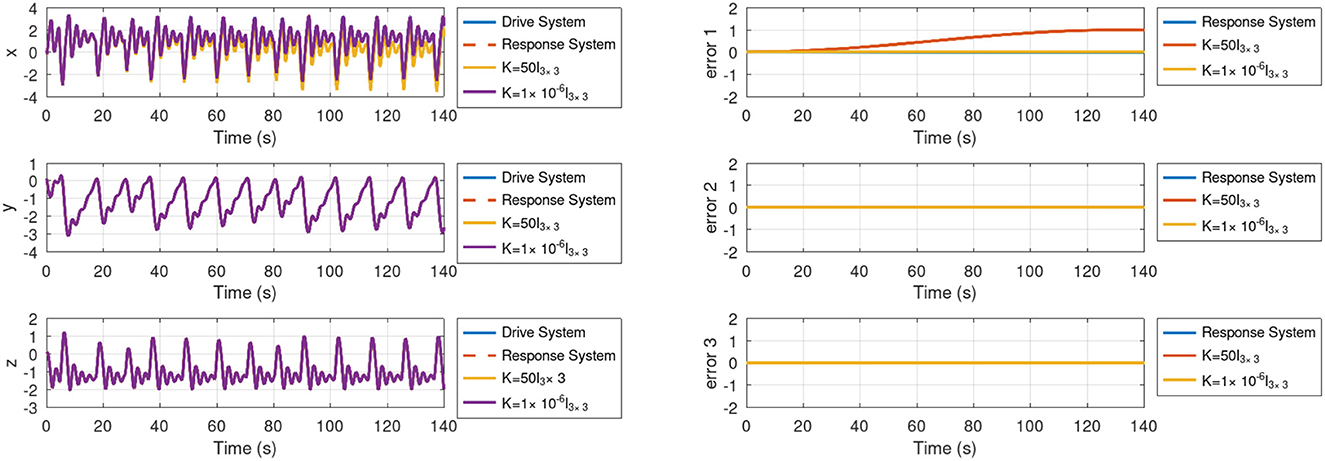
Figure 9. Time response of system variables x, y, z with their respective errors for Experiment-1 for gain K variations.

TABLE 1

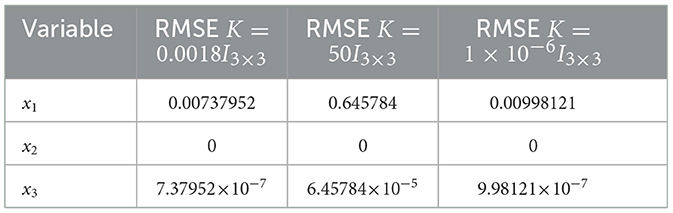
Table 1. Root mean square error of the system variables by varying gain K with a = 2.5 in Experiment 1.

FIGURE 10

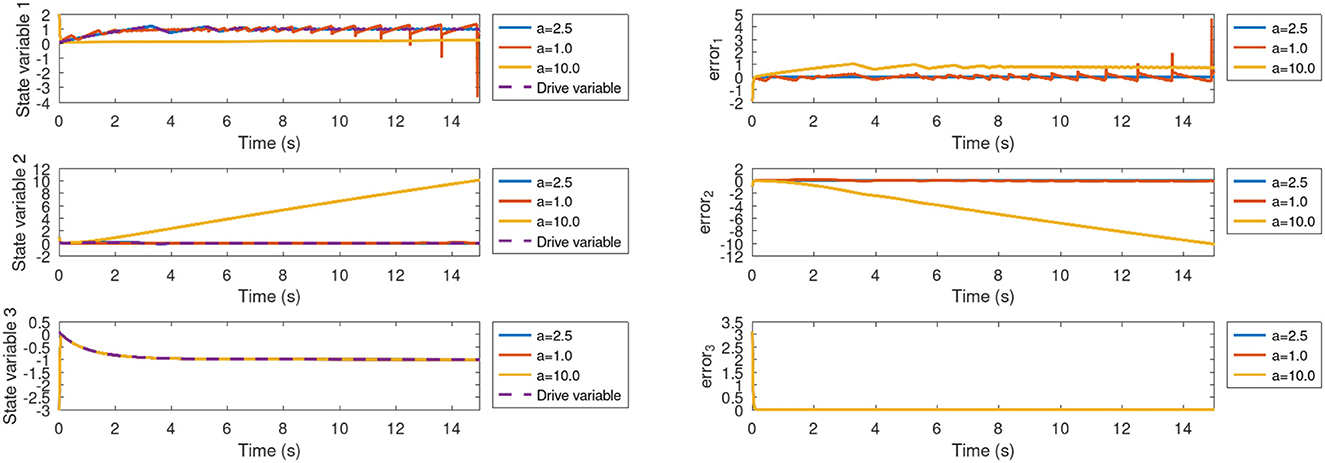
Figure 10. Time response of system variables x, y, z with their respective errors for Experiment-1 for parameter a variations.

TABLE 2

Table 2. Root mean square error of the system variables by varying parameter a in Experiment-1.

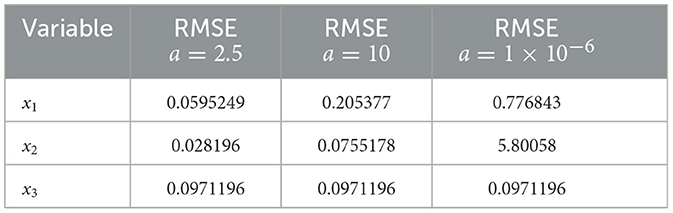
For the sensitivity analysis in Experiment-2, Figure 11 and Table 3 summarizes the findings. Analogous to the previous experiment, an optimal value of gain K reduces RMSE. For instance, the smallest RMSE is obtained for K = 100I_3×3 with a = 2.5 as shown in Table 3. However, when K is set to I_3×3, the settling time is shorter, while the error continues to be bounded to some extent (Figure 11). Finally, Figure 12 shows the synchronization and error results, whereas Table 4 presents the RMSE for variations of the system parameter a in Experiment-2. By using the optimal gain K = 100I_3×3 determined previously, the constant parameter is specified to different values as given in Table 4. We found that the smallest RMSE is obtained for the typical value, i.e., a = 2.5. Otherwise, the RMSE remains lower if a increases. But when a tends to zero, the error rises as shown in Figure 12.

FIGURE 11

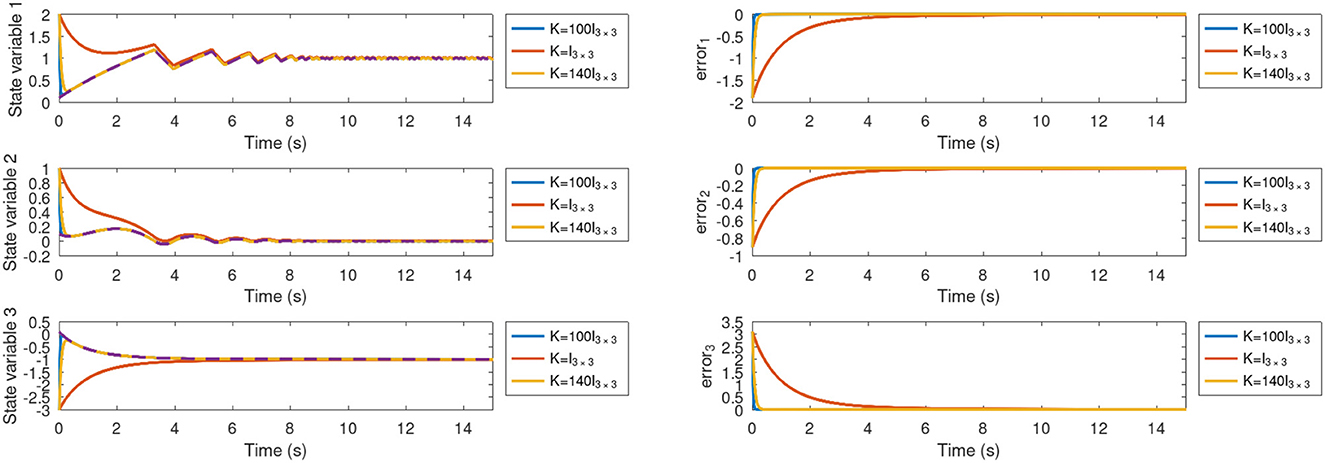
Figure 11. Time response of system variables x, y, z with their respective errors for Experiment-2 for gain K variations.

TABLE 3

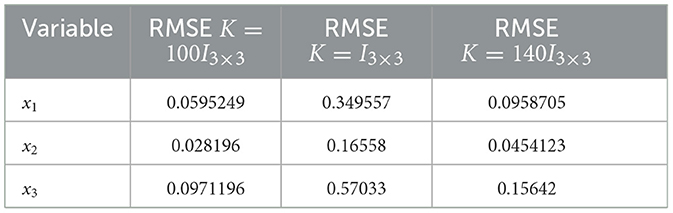
Table 3. Root mean square error of the system variables by varying gain K with a = 2.5 in Experiment 2.

FIGURE 12

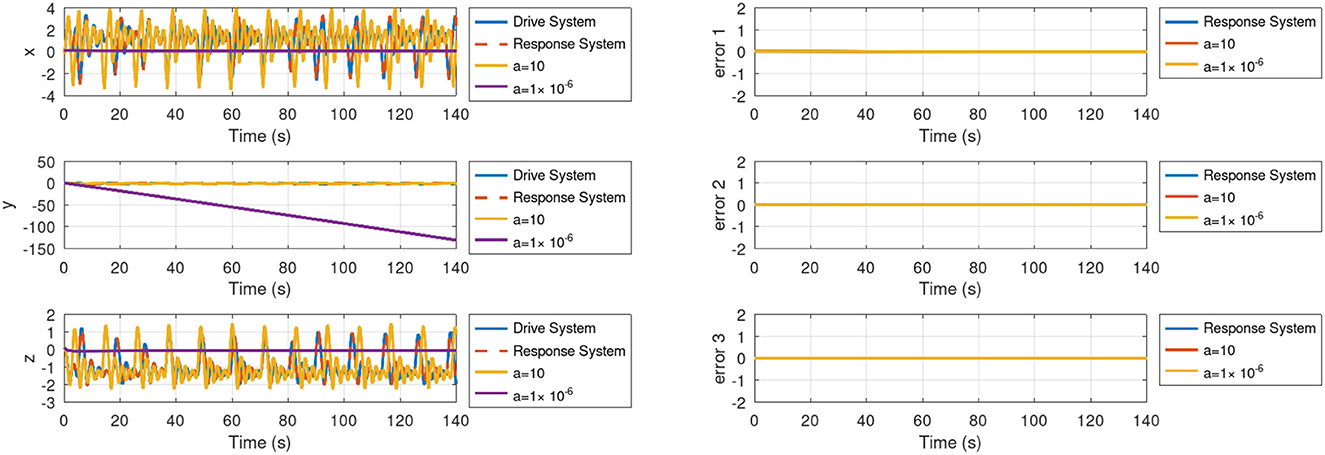
Figure 12. Time response of system variables x, y, z with their respective errors for Experiment-2 for parameter a variations.

TABLE 4

Table 4. Root mean square error of the system variables by varying parameter a in Experiment-2.

6. Discussion

Based on theoretical and experimental results from the previous sections, it is clear that a novel chaotic system has been discovered. Since the system equations contain no unnecessary terms and the system parameter has a minimum of digits; it can be considered elegant in the sense of Sprott [69, 70]. In particular, the bifurcation diagrams present dense regions where chaos arises, even if the system possesses just one parameter. By Bendixson theorem, the hidden attractor is located for a certain value of parameter a. One of the most important contributions is that the integer-order chaotic system is projected into the fractional-order domain. As was demonstrated in Section 3.1, the proposed approach is not a conversion from an integer-order to a fractional-order dynamical system. We aim to project an integer-order dynamical system into a fractional-order dynamical system via $\mathcal{T}(f(X_1))=g(X_1)$: ℝⁿ → ℝⁿ. This projection consists of the inner product between the integer-order and fractional-order dynamical systems, i.e., the projection drives the gradient vector field of the integer-order system to flow in the same direction as the vector field of the fractional-order system. In fact, the hidden chaotic attractor, obtained in the original integer-order chaotic system, is also projected into the fractional-order chaotic system.

On the other hand, the passivity-based control for the integer order chaotic system is done by considering the energy dissipation properties of the error dynamics between the drive and response state variables as given in Section 4.1. Simulation results confirm that this approach achieves accurate synchronization. One noteworthy aspect of this passivity-based controller is the inclusion of a fractional-order term that effectively reduces oscillations in input variables, making it a valuable tool in practical implementations. In addition, a passivity-based control law is also proposed for the fractional-order chaotic system in Section 4.2. Based on Property 2, a fractional-order controller is implemented to obtain synchronized behaviors in the fractional-order projection system.

7. Conclusion

In this paper, a novel integer-order chaotic system and its projection into the fractional-order domain have been reported. We have demonstrated that a successful projection of an integer-order chaotic system into a fractional-order system depends on the inner product of both vector fields, i.e., the gradient vector fields should point in the direction of maximal increase. Additionally, two suitable passivity-based controllers were derived using the energy dissipation properties of the error dynamics. Several experimental simulations proved that synchronization is achieved satisfactorily for integer-order and fractional-order chaotic systems, respectively.

A potential application of the proposed projection is in modeling the chaotic behavior in physical systems such as optical and quantum systems. On the other hand, the two passivity-based control strategies are suitable for hardware implementation, for instance, using electronic circuits, because they may require low-count components. Thus, both control strategies can be helpful for chaotic synchronization in secure communications. The passivity-based controllers will be extended for the underactuated case in future works. This means the synchronization will be analyzed when only one or two control inputs are considered.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FS: Conceptualization, Methodology, Software, Validation, Writing—original draft, Writing—review and editing. JM-P: Conceptualization, Methodology, Software, Validation, Writing—original draft, Writing—review and editing. MF: Conceptualization, Methodology, Software, Validation, Writing—original draft, Writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by VIEP-BUAP Grant No. VIEP-2023 and LNS-2023; project no. 202302051C.

Acknowledgments

JM-P thankfully acknowledges computer resources, technical advice, and support provided by Laboratorio Nacional de Supercómputo del Sureste de México (LNS), a member of the CONACYT national laboratories, with project: 202302051C.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Serrano FE, Ghosh D. Robust stabilization and synchronization in a network of chaotic systems with time-varying delays. Chaos, Solitons Fract. (2022) 159:112134. doi: 10.1016/j.chaos.2022.112134

CrossRef Full Text | Google Scholar

2. Dai JY, Ma Y, Zhou NR. Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4D hyper-chaotic Henon map. Quant Inf Proc. (2021) 20:1–24. doi: 10.1007/s11128-021-03187-w

CrossRef Full Text | Google Scholar

3. Xu L, Zhang J, A. Novel four - Wing chaotic system with multiple attractors based on hyperbolic sine: Application to image encryption*. Integration. (2022) 87:313–31. doi: 10.1016/j.vlsi.2022.07.012

CrossRef Full Text | Google Scholar

4. Zhu D, Tong X, Wang Z, Zhang M. A novel lightweight block encryption algorithm based on combined chaotic system. J Inf Secur Applic. (2022) 69:103289. doi: 10.1016/j.jisa.2022.103289

CrossRef Full Text | Google Scholar

5. Sahoo S, Roy BK. Generalisation of a class of multi-wing chaotic systems and control of a new multi-wing chaotic system. IFAC-PapersOnLine. (2022) 55:927–933. doi: 10.1016/j.ifacol.2022.04.152

CrossRef Full Text | Google Scholar

6. Azam A, Aqeel M, Sunny DA. Segmented disc dynamo with symmetric multidirectional patterns of multiscroll chaotic attractors. Math Comput Simul. (2022) 200:108–27. doi: 10.1016/j.matcom.2022.04.005

CrossRef Full Text | Google Scholar

7. Peixe T, Rodrigues AA. Persistent strange attractors in 3D polymatrix replicators. Phys D Nonl Phenom. (2022) 438:133346. doi: 10.1016/j.physd.2022.133346

CrossRef Full Text | Google Scholar

8. Bashkirtseva I, Ryashko L. Stochastic generation and shifts of phantom attractors in the 2D Rulkov model. Chaos, Solitons Fract. (2022) 159:112111. doi: 10.1016/j.chaos.2022.112111

CrossRef Full Text | Google Scholar

9. Ionescu C, Lopes A, Copot D, Machado JT, Bates JH. The role of fractional calculus in modeling biological phenomena: a review. Communic Nonl Sci Numer Simul. (2017) 51:141–59. doi: 10.1016/j.cnsns.2017.04.001

CrossRef Full Text | Google Scholar

10. Bçžleanu D, Lopes AM. Applications in Engineering, Life and Social Sciences, Part B. Berlin: Walter de Gruyter GmbH & Co KG. (2019). doi: 10.1515/9783110571929

CrossRef Full Text | Google Scholar

11. Diethelm K, Kiryakova V, Luchko Y, Machado JT, Tarasov VE. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. (2022) 107:3245–70. doi: 10.1007/s11071-021-07158-9

CrossRef Full Text | Google Scholar

12. Tavazoei MS, Tavakoli-Kakhki M, Bizzarri F. Nonlinear fractional-order circuits and systems: Motivation, a brief overview, and some future directions. IEEE Open J Circ Syst. (2020) 1:220–32. doi: 10.1109/OJCAS.2020.3029254

CrossRef Full Text | Google Scholar

13. Machado JAT. The evolution of fractional calculus. Chaos Theory Applic. (2022) 4:59–63. Available online at: https://dergipark.org.tr/en/pub/chaos/issue/64884/993129

Google Scholar

14. Han X, Mou J, Xiong L, Ma C, Liu T, Cao Y. Coexistence of infinite attractors in a fractional-order chaotic system with two nonlinear functions and its DSP implementation. Integration. (2021) 81:43–55. doi: 10.1016/j.vlsi.2021.05.010

CrossRef Full Text | Google Scholar

15. Akgül A, Rajagopal K, Durdu A, Pala MA, Boyraz OF, Yildiz MZ. A simple fractional-order chaotic system based on memristor and memcapacitor and its synchronization application. Chaos, Solitons Fract. (2021) 152:111306. doi: 10.1016/j.chaos.2021.111306

CrossRef Full Text | Google Scholar

16. Alassafi MO, Ha S, Alsaadi FE, Ahmad AM, Cao J. Fuzzy synchronization of fractional-order chaotic systems using finite-time command filter. Inf Sci. (2021) 579:325–46. doi: 10.1016/j.ins.2021.08.005

CrossRef Full Text | Google Scholar

17. Dutta M, Roy BK, A. new memductance-based fractional-order chaotic system and its fixed-time synchronisation. Chaos Soliton Fract. (2021) 145:110782. doi: 10.1016/j.chaos.2021.110782

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Fiaz M, Aqeel M, Marwan M, Sabir M. Integer and fractional order analysis of a 3D system and generalization of synchronization for a class of chaotic systems. Chaos Soliton Fract. (2022) 155:111743. doi: 10.1016/j.chaos.2021.111743

CrossRef Full Text | Google Scholar

19. Sheu AJL. Projections over quantum homogeneous odd-dimensional spheres. J Funct Analy. (2019) 277:3491–512. doi: 10.1016/j.jfa.2019.05.006

CrossRef Full Text | Google Scholar

20. Capoferri M, Vassiliev D. Invariant subspaces of elliptic systems I: Pseudodifferential projections. J Funct Analy. (2022) 282:109402. doi: 10.1016/j.jfa.2022.109402

CrossRef Full Text | Google Scholar

21. Lau ATM, Loy RJ. Contractive projections on Banach algebras. J Funct Analy. (2008) 254:2513–33. doi: 10.1016/j.jfa.2008.02.008

CrossRef Full Text | Google Scholar

22. Dorrek F, Schuster FE. Projection functions, area measures and the Alesker Fourier transform. J Funct Analy. (2017) 273:2026–69. doi: 10.1016/j.jfa.2017.06.003

CrossRef Full Text | Google Scholar

23. Basso G. Computation of maximal projection constants. J Funct Analy. (2019) 277:3560–85. doi: 10.1016/j.jfa.2019.05.011

CrossRef Full Text | Google Scholar

24. Angelos J, Grossman G, Kaufman E, Lenker T, Rakesh L. Limit cycles for successive projections onto hyperplanes in Rn. Linear Algebra Appl. (1998) 285:201–28. doi: 10.1016/S0024-3795(98)10116-7

CrossRef Full Text | Google Scholar

25. Baillon JB, Combettes PL, Cominetti R. There is no variational characterization of the cycles in the method of periodic projections. J Funct Analy. (2012) 262:400–8. doi: 10.1016/j.jfa.2011.09.002

CrossRef Full Text | Google Scholar

26. Leonov G, Kuznetsov N, Vagaitsev V. Localization of hidden Chua's attractors. Phys Lett A. (2011) 375:2230–3. doi: 10.1016/j.physleta.2011.04.037

CrossRef Full Text | Google Scholar

27. Leonov GA, Kuznetsov NV. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int J Bifurc Chaos. (2013) 23:1330002. doi: 10.1142/S0218127413300024

CrossRef Full Text | Google Scholar

28. Munoz-Pacheco JM, Zambrano-Serrano E, Volos C, Jafari S, Kengne J, Rajagopal K, et al. new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy. (2018) 20:564. doi: 10.3390/e20080564

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Munoz-Pacheco JM, Volos C, Serrano FE, Jafari S, Kengne J, Rajagopal K. Stabilization and synchronization of a complex hidden attractor chaotic system by backstepping technique. Entropy. (2021) 23:921. doi: 10.3390/e23070921

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Gong LH, Luo HX, Wu RQ, Zhou NR. New 4D chaotic system with hidden attractors and self-excited attractors and its application in image encryption based on RNG. Phys A. (2022) 591:126793. doi: 10.1016/j.physa.2021.126793

CrossRef Full Text | Google Scholar

31. Danca MF, Lampart M. Hidden and self-excited attractors in a heterogeneous Cournot oligopoly model. Chaos Soliton Fract. (2021) 142:110371. doi: 10.1016/j.chaos.2020.110371

CrossRef Full Text | Google Scholar

32. Wang X, Gao M, Iu HHC, Wang C. Tri-valued memristor-based hyper-chaotic system with hidden and coexistent attractors. Chaos Soliton Fract. (2022) 159:112177. doi: 10.1016/j.chaos.2022.112177

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Liu T, Yan H, Banerjee S, Mou J, A. fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Soliton Fract. (2021) 145:110791. doi: 10.1016/j.chaos.2021.110791

CrossRef Full Text | Google Scholar

34. Pulido-Luna JR, López-Rentería JA, Cazarez-Castro NR, Campos E, A. two-directional grid multiscroll hidden attractor based on piecewise linear system and its application in pseudo-random bit generator. Integration. (2021) 81:34–42. doi: 10.1016/j.vlsi.2021.04.011

CrossRef Full Text | Google Scholar

35. Yue X, Lv G, Zhang Y. Rare and hidden attractors in a periodically forced Duffing system with absolute nonlinearity. Chaos Soliton Fract. (2021) 150:111108. doi: 10.1016/j.chaos.2021.111108

CrossRef Full Text | Google Scholar

36. Sakata N, Fujimoto K, Maruta I. On trajectory tracking control of simple port-Hamiltonian systems based on passivity based sliding mode control. IFAC-PapersOnLine. (2021) 54:38–43. doi: 10.1016/j.ifacol.2021.11.052

CrossRef Full Text | Google Scholar

37. Belkhier Y, Achour A, Bures M, Ullah N, Bajaj M, Zawbaa HM, et al. Interconnection and damping assignment passivity-based non-linear observer control for efficiency maximization of permanent magnet synchronous motor. Energy Rep. (2022) 8:1350–61. doi: 10.1016/j.egyr.2021.12.057

CrossRef Full Text | Google Scholar

38. Han Y, Yang M, Yang P, Xu L, Blaabjerg F. Passivity-based stability analysis of parallel single-phase inverters with hybrid reference frame control considering PLL effect. Int J Electr Power Energy Syst. (2022) 135:107473. doi: 10.1016/j.ijepes.2021.107473

CrossRef Full Text | Google Scholar

39. Shen PY, Schatz J, Caverly RJ. Passivity-based adaptive trajectory control of an underactuated 3-DOF overhead crane. Control Eng Pract. (2021) 112:104834. doi: 10.1016/j.conengprac.2021.104834

CrossRef Full Text | Google Scholar

40. Wu KN, Zhou WJ, Liu XZ. Passivity-based boundary control for delay reaction-diffusion systems. J Franklin Inst. (2022). doi: 10.1016/j.jfranklin.2022.04.011

CrossRef Full Text | Google Scholar

41. Gandarilla I, Santibáñez V, Sandoval J, Romero JG, PID. passivity-based control laws for joint position regulation of a self-balancing robot. Control Eng Pract. (2021) 116:104927. doi: 10.1016/j.conengprac.2021.104927

CrossRef Full Text | Google Scholar

42. Yao J, Guan ZH, Hill DJ. Passivity-based control and synchronization of general complex dynamical networks. Automatica. (2009) 45:2107–13. doi: 10.1016/j.automatica.2009.05.006

CrossRef Full Text | Google Scholar

43. Syed Ali M, Yogambigai J. Passivity-based synchronization of stochastic switched complex dynamical networks with additive time-varying delays via impulsive control. Neurocomputing. (2018) 273:209–21. doi: 10.1016/j.neucom.2017.07.053

CrossRef Full Text | Google Scholar

44. Kaviarasan B, Sakthivel R, Lim Y. Synchronization of complex dynamical networks with uncertain inner coupling and successive delays based on passivity theory. Neurocomputing. (2016) 186:127–38. doi: 10.1016/j.neucom.2015.12.071

CrossRef Full Text | Google Scholar

45. Stoorvogel AA, Nojavanzadeh D, Liu Z, Saberi A. Squared-down passivity-based H-infinity and H2 almost synchronization of homogeneous continuous-time multi-agent systems with partial-state coupling via static protocol. Eur J Control. (2020) 54:73–86. doi: 10.1016/j.ejcon.2019.11.008

CrossRef Full Text | Google Scholar

46. Ihle IAF, Arcak M, Fossen TI. Passivity-based designs for synchronized path-following. Automatica. (2007) 43:1508–18. doi: 10.1016/j.automatica.2007.02.018

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Mathiyalagan K, Anbuvithya R, Sakthivel R, Park JH, Prakash P. Non-fragile H-infinity synchronization of memristor-based neural networks using passivity theory. Neur Netw. (2016) 74:85–100. doi: 10.1016/j.neunet.2015.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Zambrano-Serrano E, Munoz-Pacheco JM, Serrano FE, Sánchez-Gaspariano LA, Volos C. Experimental verification of the multi-scroll chaotic attractors synchronization in PWL arbitrary-order systems using direct coupling and passivity-based control. Integration. (2021) 81:56–70. doi: 10.1016/j.vlsi.2021.05.012

CrossRef Full Text | Google Scholar

49. Qi F, Chai Y, Chen L, Chen Y, Wu R. Passivity-based non-fragile control of a class of uncertain fractional-order nonlinear systems. Integration. (2021) 81:25–33. doi: 10.1016/j.vlsi.2021.05.009

CrossRef Full Text | Google Scholar

50. Xiao S, Wang Z, Wang C. Passivity analysis of fractional-order neural networks with interval parameter uncertainties via an interval matrix polytope approach. Neurocomputing. (2022) 477:96–103. doi: 10.1016/j.neucom.2021.12.106

CrossRef Full Text | Google Scholar

51. Rajchakit G, Chanthorn P, Niezabitowski M, Raja R, Baleanu D, Pratap A. Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks. Neurocomputing. (2020) 417:290–301. doi: 10.1016/j.neucom.2020.07.036

CrossRef Full Text | Google Scholar

52. Shafiya M, Nagamani G. New finite-time passivity criteria for delayed fractional-order neural networks based on Lyapunov function approach. Chaos Soliton Fract. (2022) 158:112005. doi: 10.1016/j.chaos.2022.112005

CrossRef Full Text | Google Scholar

53. Padmaja N, Balasubramaniam P. Mixed H-infinity/passivity based stability analysis of fractional order gene regulatory networks with variable delays. Math Comput Simul. (2022) 192:167–81. doi: 10.1016/j.matcom.2021.08.023

CrossRef Full Text | Google Scholar

54. Podlubny I. Fractional Differential Equations. San Diego, CA, USA: Mathematics in Science and Engineering Academic Press. (1999).

Google Scholar

55. Diethelm K. The analysis of fractional differential equations: An application-oriented exposition using differential operators of Caputo type. In: Lecture Notes in Mathematics; Berlin: Springer Science & Business Media (2010). doi: 10.1007/978-3-642-14574-2

CrossRef Full Text | Google Scholar

56. Gorenflo R, Mainardi F. Fractional calculus. In: Fractals and Fractional Calculus in Continuum Mechanics; Springer (1997). p. 223–276. doi: 10.1007/978-3-7091-2664-6_5

CrossRef Full Text | Google Scholar

57. Akinlar MA, Kurulay M. A novel method for analytical solutions of fractional partial differential equations. Mathem Probl Eng. (2013) 2013:195708. doi: 10.1155/2013/195708

CrossRef Full Text | Google Scholar

58. Mockary S, Babolian E, Vahidi AR. A fast numerical method for fractional partial differential equations. Adv Differ Equat. (2019) 161:525–539. doi: 10.1016/j.apnum.2020.12.007

CrossRef Full Text | Google Scholar

59. Wolf A, Swift JB, Swinney HL, Vastano JA. Determining Lyapunov exponents from a time series. Phys D. (1985) 16:285–317. doi: 10.1016/0167-2789(85)90011-9

CrossRef Full Text | Google Scholar

60. Danca MF, Kuznetsov N. Matlab code for Lyapunov exponents of fractional-order systems. Int J Bifurc Chaos. (2018) 28:1850067. doi: 10.1142/S0218127418500670

CrossRef Full Text | Google Scholar

61. Clemente-López D, Munoz-Pacheco JM, Rangel-Magdaleno JdJ. A review of the digital implementation of continuous-time fractional-order chaotic systems using FPGAs and embedded hardware. Arch Comput Method Eng. (2022) 30:951–83. doi: 10.1007/s11831-022-09824-6

CrossRef Full Text | Google Scholar

62. Munoz-Pacheco JM, Lujano-Hernández LC, Mu niz-Montero C, Akgül A, Sánchez-Gaspariano LA, Li CB, et al. Active realization of fractional-order integrators and their application in multiscroll chaotic systems. Complexity. (2021) 2021:1–16. doi: 10.1155/2021/6623855

CrossRef Full Text | Google Scholar

63. Meissen C, Klausen K, Arcak M, Fossen TI, Packard A. Passivity-based formation control for UAVs with a suspended load. IFAC-PapersOnLine. (2017) 50:13150–5. doi: 10.1016/j.ifacol.2017.08.2169

CrossRef Full Text | Google Scholar

64. Reyes-Baez R, van der Schaft A, Jayawardhana B. Passivity based distributed tracking control of networked Euler-Lagrange systems. IFAC-PapersOnLine. (2018) 51:136–41. doi: 10.1016/j.ifacol.2018.12.024

CrossRef Full Text | Google Scholar

65. Wang C, Zhang H, Fan W, Ma P. Adaptive control method for chaotic power systems based on finite-time stability theory and passivity-based control approach. Chaos Soliton Fract. (2018) 112:159–67. doi: 10.1016/j.chaos.2018.05.005

CrossRef Full Text | Google Scholar

66. Zenfari S, Laabissi M, Achhab ME. Passivity based control method for the diffusion process. IFAC-PapersOnLine. (2019) 52:80–4. doi: 10.1016/j.ifacol.2019.07.014

CrossRef Full Text | Google Scholar

67. Takhi H, Kemih K, Moysis L, Volos C. Passivity based sliding mode control and synchronization of a perturbed uncertain unified chaotic system. Math Comput Simul. (2021) 181:150–69. doi: 10.1016/j.matcom.2020.09.020

CrossRef Full Text | Google Scholar

68. Ding Z, Zeng Z, Zhang H, Wang L, Wang L. New results on passivity of fractional-order uncertain neural networks. Neurocomputing. (2019) 351:51–9. doi: 10.1016/j.neucom.2019.03.042

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Sprott JC. Elegant Chaos: Algebraically Simple Chaotic Flows. Singapore: World Scientific. (2010). doi: 10.1142/7183

CrossRef Full Text | Google Scholar

70. Sprott JC, A. proposed standard for the publication of new chaotic systems. Int J Bifurc Chaos. (2011) 21:2391–4. doi: 10.1142/S021812741103009X

CrossRef Full Text | Google Scholar