A cell-level dynamical model for malaria parasite infection with antimalarial drug treatment

1 Introduction

Malaria still poses a danger to global health as well as affects economic growth and progress in high-burden areas. Nearly half of the world population is at risk for malaria infection, with approximately half a million deaths per year [1, 2], mainly in African countries, among children under 5 years of age [3]. Malaria is caused by intracellular parasites of the genus Plasmodium; of these, Plasmodium falciparum is the most virulent form among the five species (P. vivax, P. ovale, P. malaria, P. falciparum, and P. knowlesi) that infect humans [4]. Malaria is a life-threatening disease that is transmitted between humans via vectors (during the blood meal of female Anglophile mosquitoes).

Malaria infection begins when malaria parasites in the form of sporozoites are deposited by female Anopheles mosquitoes into the host's skin during a blood meal. After a short period of time, the sporozoites travel to the liver. The liver-stage of Plasmodium infection is required and occurs when mosquito-transmitted Plasmodium sporozoites infiltrate hepatocytes [5]. This stage is clinically silent and untreatable, and affected individuals are asymptomatic. Inside the hepatocyte, a parasite divides into thousands of merozoites through a process called schizogony, where they differentiate into pre-erythrocytic forms (PEFs) [6]. The matured infected liver (schizont) ruptures and releases thousands of merozoites into the bloodstream, invading red-blood cells (RBCs) [7].

The infected red-blood cells developed through the ring, trophozoites, and schizont phases [8]. The parasite remains in its ring form, which has low morphological change and limited metabolic activity. The parasite then progresses to the mature trophozoite (feeding) stage, where it develops quickly and becomes more metabolically active. The parasite eventually transforms into a schizont with the commencement of nuclear division [9], and the resulting mature schizont contains 16–32 daughter merozoites. These schizonts ruptured, releasing daughter merozoites to invade new RBCs. This cycle of erythrocytic development depends on the parasite species [8, 9], and it is during this stage that an individual will start to experience malaria-related symptoms such as periodic fever upon each bursting phase of the infected red-blood cells to release the merozoites. The fever decreases during the parasite replicating phase inside the RBCs, and the patient appears to be improving [10].

A certain amount of merozoites develop into sexual gametocytes within the host in the form of male (microgametes) and female (macrogametes) gametocytes in the infected red-blood cells. The mosquito ingested these gametocytes while feeding on blood. In the mosquito's gut, the male and female gametocytes join to produce a zygote [11], which grows into an ookinete and migrates through the midgut epithelium of the mosquito to become an oocyst between 24 and 36h later. The oocyst then develops into sporozoites through asexual sporogenic replication [12–16]. The WHO suggests using combination therapy against parasites in the asexual hepatocytic, and erythrocytic stages that has been associated with clinical symptoms and the accompanying mortality. The development of vaccinations, vector control, chemotherapy with antimalarial medications, chemoprophylaxis, and other methods are the primary ways that malaria is eliminated or reduced in prevalence. Most antimalarials act by targeting two or more phases of the parasite's life cycle in order to prevent it [17].

The antimalarial therapies have been developed and classified as primary tissue schizontocides act on the pre-erythrocytic forms (primary tissue phases) of the malaria parasite. Administration of medications that destroy sporozoites or the primary tissue forms entirely avoids erythrocytic infection. The primaquine and pamaquine are active in the primary tissue schizonts. Additionally, metformin therapy inhibits Plasmodium falciparum development in human hepatocytes, which may result in pretreatment-induced defects in parasite invasion or effective clearance of liver-stage Plasmodium parasites [18]. Blood schizontocides act on the asexual erythrocytic forms of all malaria parasites. Quinine, mepacrine, 4-aminoquinolines, and chloroquine are used to treat and effectively reduce blood schizonts due to their powerful and quick actions [19]. Gametocytocidal drugs (gametocytocides) prevent the transmission of parasites into mosquitoes and reduce the human reservoir of the disease. The 8-aminoquinolines, pamaquine, plasmocide, primaquine, and quinocide are most active in the sexual forms of all species of malaria parasites [20].

Although most of the time, artemisinin-based combination therapies (ACT) are recommended by the WHO to treat malaria with Plasmodium, such as artemether plus lumefantrine, artesunate plus amodiaquine, artesunate plus mefloquine, dihydroartemisinin plus piperaquine, artesunate plus sulfadoxine–pyrimethamine (SP), artesunate plus tetracycline or doxycycline or clindamycin, and quinine plus tetracycline or doxycycline or clindamycin [21], which are recommended for uncomplicated malaria infection [22].

Several mathematical malaria models have been developed and studied at in-host levels, with important results toward the evolution of malaria, Plasmodium. Anderson et al. [23] developed a within-host model. The authors analyzed non-linear dynamical phenomena in host-parasite interactions with reference to a series of different problems ranging from the impact on the transmission of control measures based on vaccination and chemotherapy to the effects of immunologic responses targeted at different stages in a parasite's life cycle. Hetzel and Anderson [24] discovered the blood-stage malaria parasite in the absence of a human immune response. They consider the densities of three cell populations: healthy red-blood cells, infected red-blood cells, and free merozoites. Elaiw and Agha [25] studied a reaction-diffusion model for the blood-stage dynamics of malaria infection with CTL and antibody immune responses. The model explores the interactions between uninfected red-blood cells (erythrocytes), three types of infected red-blood cells, free merozoites, CTLs, and antibodies. They introduced some parameters to measure the effect of antimalarial drugs and isoleucine starvation on the blood cycle of malaria infection.

In the study by Li et al. [26], the blood-stage dynamics of malaria in an infected human host including susceptible red-blood cells, infected red-blood cells, malaria parasitemia, and immune effectors, a mathematical model was discovered. The authors generalized from Anderson [27] and Anderson et al. [23] using non-linear bounded Michaelis-Menten-Monod functions to describe how the immune system interacts with the infected red-blood cells and merozoites. The model displayed that periodic oscillations occur as a result of Hopf bifurcation at the positive equilibrium, illuminating the fact that the immune response and malaria infections are always linked. Song et al. [28] investigated the two inside-the host mathematical models (with and without immune responses) for replicating the dynamics of the malaria parasites. The researchers also incorporate competition (between parasites that are drug-sensitive and those that are drug-resistant), drug treatment, and immunologic response whenever examining the evolution of drug resistance inside an infected host. The studies [29–33] are projected for the blood stage malaria parasites with immune response.

In a study by Tabo et al. [34], the interaction of the malaria parasite in sexual and asexualual stages during its life cycle, i.e., a combination of hepatocyte stage, erythrocyte stage, and mosquito-stage malaria parasite into one mathematical model is studied. The authors also include blood-stage treatment as a control strategy and investigate the effect of the treatment for malaria control within the host. The model that represents the dynamics of healthy hepatocytes, infected hepatocytes, sporozoites in the infected liver, healthy erythrocytes, infected erythrocytes, merozoites in the blood, and gametocytes in the mosquito, and oocysts in the mosquito. The study [35] proposed the within-host dynamics of malaria infection with the immune system and treatment. The researchers considered the interactions of the hepatocyte cells, erythrocyte cells, malaria parasites, and immune cells. The findings indicated the progression of malaria and control of the disease with a treatment strategy that combines very efficient medications against malaria parasites with effective immune responses. The studies [34, 36, 37] are proposed the in-host dynamics of malaria infection by considering both erythrocyte stage and hepatocyte stage malaria infection. However, to the best of our knowledge, no study has considered the within-host dynamics of malaria parasites with stage-specific antimalarial drug treatment.

In this study, we investigated the within-host dynamics of malaria infection with primary liver-stage antimalarial drug treatment (tissue schizontocides), blood-stage antimalarial drug treatment (blood schizontocides), and gametocytocidal drug treatment (gametocytocides). We present the local and global stability of the parasite-free equilibrium point. It shows that the parasite-free equilibrium point is both local and global stable if basic reproduction is less than one. The existence and local stability analysis of the parasite-persistence equilibrium is shown. In addition, in order to supplement the theoretical and analytical results, we instantiate different numerical simulations. The rest of the study is organized as follows: In Section 2, the mathematical model is formulated. In Section 3, qualitative analysis of the model is investigated. Numerical simulation is performed in Section 4. The conclusion of the study is conferred in Section 5.

2 Model formulation

In this study, we provide a deterministic model that describes the inside-human-host dynamics of malaria Plasmodium. Our model contains seven compartments, as follows: uninfected hepatocyte H(t), infected hepatocyte H_I(t), uninfected RBCs R(t), infected red-blood cell (iRBCs) R_I(t), malaria parasite in the form of sporozoite S(t), malaria parasite in the form of merozoite M(t), and gametocyte G(t) at time t.

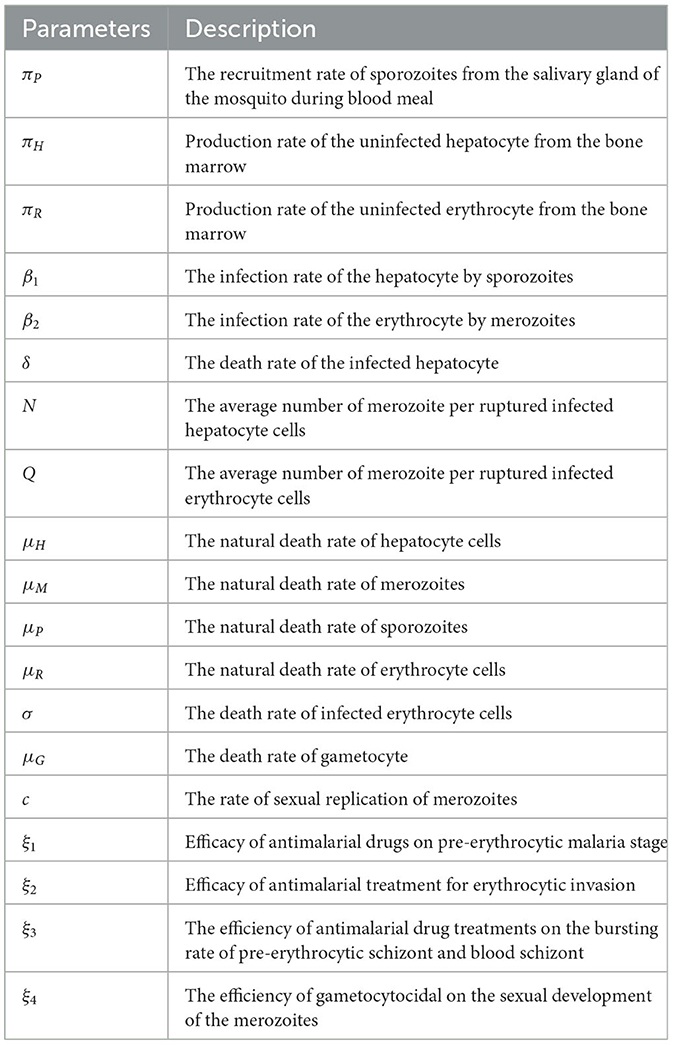
The malaria parasite in the form of sporozoites is recruited from the salivary gland of the female Anopheles mosquito, with the blood meals at a constant rate π_S and die naturally at a rate μ_S. The hepatocyte cells are supplied from the bone marrow at a rate π_H. The hepatocytes are invaded by sporozoites that are injected into the human body during mosquito blood feeding at a constant rate β₁. This invasion is reduced due to tissue schizontocides (liver-stage antimalarial drug treatment) which is administrated pre-erythrocytic stage of malaria infection at a rate (1 − ξ₁)β₁, where ξ₁ (0 < ξ₁ ≤ 1) is the efficacy of antimalarial drug on pre-erythrocytic malaria stage. The hepatocytes suffered natural death at a constant rate μ_H. The population of infected hepatocytes increases as the healthy hepatocytes get infection at a rate (1 − ξ₁)β₁ and decreases owing to ruptured and die at a rate δ. The healthy erythrocytes (RBCs) are recruited from the bone marrow at a constant rate π_R. They acquire infection due to the invasion of merozoites that are released from the liver schizont at a rate β₂. The invasion rate is attenuated when blood-stage antimalarial drug treatment (blood-schizontocides) is administrated at the rate (1 − ξ₂)β₂, where ξ₂(0 < ξ₂ ≤ 1) is the efficacy of antimalarial treatment on erythrocytic invasion, and the RBCs die naturally at a constant rate μ_R. The iRBCs burst and die at a constant rate σ. The merozoite population is produced when the infected hepatocyte ruptures and releases thousands of merozoites into the blood system at a rate δN, where N is the average number of merozoite released per ruptured infected hepatocytic cells, and during the iRBCs ruptured and release 16–32 merozoites per ruptured iRBC into the bloodstream at a constant rate σQ to invade fresh erythrocytes (RBCs), where Q is the average number of merozoites per ruptured iRBCs.

The production of the merozoite is reduced when antimalarial drug treatments; primary tissue(pre-erythrocytic) schizontocides and blood schizontocides are administrated at the rate of (1 − ξ₃)N and (1 − ξ₃)Q, respectively, where ξ₃(0 < ξ₃ ≤ 1) is the efficacy of antimalarial drug treatments on the average number of merozoites rupturing rate of pre-erythrocytic schizont and blood schizont. The population of merozoite will reduce due to the natural death rate μ_M. After the invasion of the red-blood cells, some number of merozoites develop into male (microgametes) and female (macrogametes) gametocytes that arise within-host at a rate c. The sexual form (gametocytes) are destroyed due to the administration of gametocytocide [19] at a rate ξ₄ (0 < ξ₄ ≤ 1). The gametocytes die naturally at a rate μ_G. Note that, ξ_i = 0, i = 1, …, 4 implies that the antimalarial drug treatments are not effective at all, and ξ_i = 1 means that they are 100% effective. Assume that an uninfected erythrocyte's observation of merozoites and an uninfected hepatocyte's observation of sporozoites are ignored. The state variables and all the model biological parameters are listed in Tables 1, 2, respectively. Based on the above descriptions and the model schematic diagram (Figure 1), the formulated model equation is given by

$\begin{array}{ll}\begin{array}{l}\frac{dH}{dt}={\pi }_H-(1-{\xi }_1){\beta }_{1}HS-{\mu }_{H}H,\\ \frac{d{H}_I}{dt}=(1-{\xi }_1){\beta }_{1}HS-\delta H_I,\\ \frac{dR}{dt}={\pi }_R-(1-{\xi }_2){\beta }_{2}RM-{\mu }_{R}R,\\ \frac{d{R}_I}{dt}=(1-{\xi }_2){\beta }_{2}RM-\sigma R_I,\\ \frac{dS}{dt}={\pi }_S-{\mu }_{S}S,\\ \frac{dM}{dt}=(1-{\xi }_3)N\delta H_I+(1-{\xi }_3)Q\sigma R_I-{\mu }_{M}M,\\ \frac{dG}{dt}=c{R}_I-{\xi }_{4}G-{\mu }_{G}G,\end{array}& (1)\end{array}$

with non-negative initial condition

$\begin{array}{l}H(0)=H_0,H_I(0)=H_{I0},M(0)=M_0,S(0)=S_0,R(0)=R_0,\end{array}$

$\begin{array}{ll}{R}_I(0)=R_{I0},G(0)=G_0.& (2)\end{array}$

TABLE 1

Table 1. State variables and their description.

TABLE 2

Table 2. Model parameters and their description.

FIGURE 1

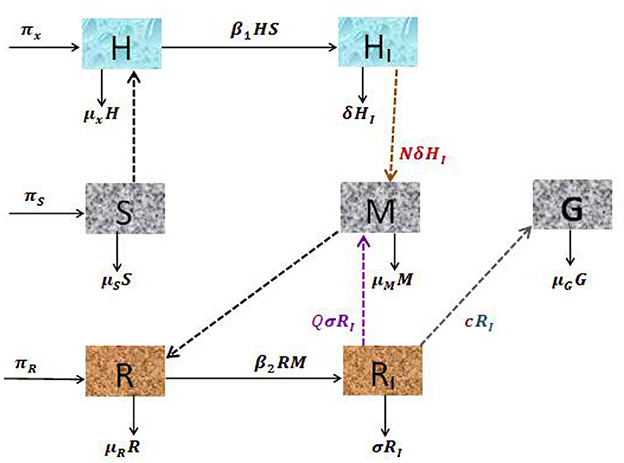
Figure 1. Schematic diagram of the dynamical system of hepatocytic-erythrocytic stage malaria parasite.

3 Qualitative analysis of the model

In this section, we investigate the positivity and boundedness of the developed model, equilibria, stability analysis of the equilibria, and sensitivity analysis of basic reproduction number.

3.1 Positivity and boundedness of the solution

Theorem 1. The solutions of system (Equation 1) with non-negative initial conditions, H₀, H_I0, R₀, R_I0, M₀, S₀, and G₀, remain non-negative for all time t ≥ 0.

Proof 1. The first equation of dynamical system (Equation 1) gives rise to

$\begin{array}{l}\frac{dH}{dt}={\pi }_H-(1-{\xi }_1){\beta }_{1}HS-{\mu }_{H}H\ge -((1-{\xi }_1){\beta }_{1}S+{\mu }_H)H,\\ \frac{dH}{H}\ge -((1-{\xi }_1){\beta }_{1}S+{\mu }_H)dt,\\ {\displaystyle {\int }_0^t}\frac{dH}{H}\ge -{\displaystyle {\int }_0^t}((1-{\xi }_1){\beta }_{1}S+{\mu }_H)dt,\\ H(t)\ge H_0{e}^{-{\int }_0^t((1-{\xi }_1){\beta }_{1}S+{\mu }_H)dt}>0.\end{array}$

The second equation of dynamical system (Equation 1) gives rise to

$\begin{array}{l}\frac{d{H}_I}{dt}=(1-{\xi }_1){\beta }_{1}HS-\delta H_I\ge -\delta H_I,\\ \frac{d{H}_I}{H_I}\ge -\delta dt,{\displaystyle {\int }_0^t}\frac{d{H}_I}{H_I}\ge -{\displaystyle {\int }_0^t}\delta dt,\\ H_I(t)\ge H_{I0}{e}^{-\delta t}\ge 0.\end{array}$

In the same procedure, it can be shown that the state variables R(t), R_I(t), S(t), M(t), and G(t) are non-negative for all t ≥ 0. Therefore, the solution of the dynamical system (Equation 1) is non-negative for all t ≥ 0.

Theorem 2. The biologically feasible region

$\begin{array}{l}\Omega =\left\{(H,H_I,R,R_I,S,M,G)\in R_{+}^7:N_H\le \frac{{\pi }_H}{d_1},N_R\le \frac{{\pi }_R}{d_2}and{N}_S\le \frac{{\pi }_S}{d_3}\right\}\end{array}$

is positively invariant to the dynamical system (Equation 1).

Proof 2. The total hepatocyte population at a time t is denoted by N_H(t) and defined as

$\begin{array}{ll}{N}_H(t)=H(t)+H_I(t).& (3)\end{array}$

By differentiating (Equation 2) with respect to time t, we obtain

$\begin{array}{ll}\begin{array}{l}\frac{d{N}_H}{dt}={\pi }_H-(1-{\xi }_1){\beta }_{1}HS-{\mu }_{H}H+(1-{\xi }_1){\beta }_{1}HS-\delta H_I\\ ={\pi }_H-{\mu }_{H}H-\delta H_I,\\ \le {\pi }_H-d_1{N}_H,where{d}_1=min\left\{{\mu }_H,\delta \right\},\\ N_H(t)\le \frac{{\pi }_H}{d_1}+\left(N_{H0}-\frac{{\pi }_H}{d_1}\right)e^{-d_{1}t}.\end{array}& (4)\end{array}$

Similarly, we can apply this procedure to red-blood cells N_R(t) = R(t)+R_I(t).

$\begin{array}{ll}\begin{array}{l}\frac{d{N}_R}{dt}={\pi }_R-(1-{\xi }_2){\beta }_{2}RM-{\mu }_{R}R+(1-{\xi }_2){\beta }_{2}RM-\sigma R_I-c{R}_I,\\ ={\pi }_R-{\mu }_{R}R-\sigma R_I\le {\pi }_R-d_2{N}_R,where{d}_2=min\left\{{\mu }_R,\sigma \right\},\\ N_R(t)\le \frac{{\pi }_R}{d_2}+\left(N_{R0}-\frac{{\pi }_R}{{\mu }_{R^{\prime }}}\right)e^{-d_{2}t}.\end{array}& (5)\end{array}$

Lastly, the total malaria parasite population in the form of sporozoites, merozoites, and gametocytes at a time t is given as N_S(t) = S(t)+M(t)+G(t),

$\begin{array}{ll}\begin{array}{l}\frac{d{N}_S}{dt}=(1-{\xi }_3)N\delta H_I+(1-{\xi }_3)Q\sigma R_I-{\mu }_{M}M+{\pi }_S-{\mu }_{S}S\\ +c{R}_I-{\mu }_{G}G-{\xi }_{4}G,\\ \le (1-{\xi }_3)N\delta H_I+(1-{\xi }_3)Q\sigma R_I+c{R}_I+{\pi }_S-d_3{N}_S,\\ where{d}_3=min\left\{{\mu }_M,{\mu }_G,{\mu }_S\right\}\\ N_S(t)\le \frac{{\pi }_S}{d_3}\\ +\left(N_{S0}-\frac{{\pi }_S}{d_3}+{\displaystyle {\int }_0^t}(1-{\xi }_3)N\delta H_I+(1-{\xi }_3)Q\sigma R_I+c{R}_{I}dt\right)e^{-d_{3}t}.\end{array}& (6)\end{array}$

Taking the limit as t → ∞ for the Equations (4), (5), and (6), we obtained $N_H(t)\le \frac{{\pi }_H}{d_1}$, $N_R(t)\le \frac{{\pi }_R}{d_2}$, and $N_S(t)\le \frac{{\pi }_S}{d_3}$. Therefore, the biologically feasible region Ω is positive invariant to the in-host malaria model (Equation 1).

3.2 Parasite-free equilibrium point

The parasite-free equilibrium point is the steady-state solution where there is no parasite in the host cell. It is obtained by setting the right-hand side of the dynamical system (1) to zero. Thus, $E_0=(H^0,H{I}^0,R^0,R{I}^0,S^0,M^0,G^0)=(\frac{{\pi }_H}{{\mu }_H},0,\frac{{\pi }_R}{{\mu }_R},0,0,0,0)$.

3.3 The basic reproduction number

The in-host basic reproduction number is the average number of secondary infections due to the introduction of sporozoites in human host cells. It is computed using the technique of the next-generation matrix approach described by Van den Driessche and Watmough [38]. We consider only the infected compartments H_I, R_I, M and G. Let F_i be the rate of new appearance and V_i be the rate of transfer from one compartment to another by any means and given as

$\begin{array}{ll}{F}_i=\left(\begin{array}{c}(1-{\xi }_1){\beta }_{1}HS\\ (1-{\xi }_2){\beta }_{2}RM\\ 0\\ 0\\ 0\end{array}\right),& (7)\end{array}$

$\begin{array}{l}{V}_i=\left(\begin{array}{c}\delta H_I\\ \sigma R_I\\ -{\pi }_S+{\mu }_{S}S\\ -(1-{\xi }_3)N\delta H_I-(1-{\xi }_3)Q\sigma R_I+{\mu }_{M}M\\ -c{R}_I+{\xi }_{4}G+{\mu }_{G}G\end{array}\right).\end{array}$

The Jacobian matrix of vectors F and V are obtained via the differentiating F_i and V_i of the Equation (7) with respect to the infected compartments at the parasite-free equilibrium point $E_0=(\frac{{\pi }_H}{{\mu }_H},0,\frac{{\pi }_R}{{\mu }_R},0,0,0,0)$ and give as

$\begin{array}{ll}F=\left(\begin{array}{ccccc}0& 0& (1-{\xi }_1){\beta }_1{H}_0& 0& 0\\ 0& 0& 0& (1-{\xi }_2){\beta }_2{R}_0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right),& (8)\end{array}$

$\begin{array}{ll}V=\left(\begin{array}{ccccc}\delta & 0& 0& 0& 0\\ 0& \sigma & 0& 0& 0\\ 0& 0& {\mu }_S& 0& 0\\ -(1-{\xi }_3)N\delta & -(1-{\xi }_3)Q\sigma & 0& {\mu }_M& 0\\ 0& -c& 0& 0& {\xi }_4+{\mu }_G\end{array}\right).& (9)\end{array}$

Hence, the inverse of the matrix V is

$\begin{array}{ll}{V}^{-1}=\left(\begin{array}{ccccc}\frac{1}{\delta }& 0& 0& 0& 0\\ 0& \frac{1}{\sigma }& 0& 0& 0\\ 0& 0& \frac{1}{{\mu }_S}& 0& 0\\ \frac{(1-{\xi }_3)N\delta }{\delta {\mu }_m}& \frac{(1-{\xi }_3)Q\sigma }{{\mu }_m\sigma }& 0& \frac{1}{{\mu }_M}& 0\\ 0& \frac{c}{\sigma ({\mu }_g+{\xi }_4)}& 0& 0& \frac{1}{{\xi }_4+{\mu }_G}\end{array}\right).& (10)\end{array}$

The basic reproduction number ${\mathcal{R}}_0$ is the spectral radius of ρ(FV⁻¹). Thus,

$\begin{array}{ll}{\mathcal{R}}_0=\rho (F{V}^{-1})=\frac{(1-{\xi }_2)(1-{\xi }_3){\beta }_2{\pi }_{R}Q}{{\mu }_R{\mu }_M}.& (11)\end{array}$

3.4 Local stability analysis of parasite-free equilibrium point

In this section, we present the local stability analysis of the parasite-free equilibrium (PFE) point, by linearizing the dynamical system (Equation 1) at E₀. The Jacobian matrix at any point is given as

$\begin{array}{l}J(E)=\\ \left(\begin{array}{ccccccc}-A_1-{\mu }_H& 0& 0& 0& -(1-{\xi }_1){\beta }_{1}H& 0& 0\\ A_1& -\delta & 0& 0& (1-{\xi }_1){\beta }_{1}H& 0& 0\\ 0& 0& -A_2-{\mu }_R& 0& 0& -(1-{\xi }_2){\beta }_{2}R& 0\\ 0& 0& A_2& -\sigma & 0& (1-{\xi }_2){\beta }_{2}R& 0\\ 0& 0& 0& 0& -{\mu }_S& 0& 0\\ 0& (1-{\xi }_3)N\delta & 0& (1-{\xi }_3)Q\sigma & 0& -{\mu }_M& 0\\ 0& 0& 0& c& 0& 0& -({\xi }_4+{\mu }_G)\end{array}\right),& (12)\end{array}$

where A₁ = (1 − ξ₁)β₁S and A₂ = (1 − ξ₂)β₂M.

Theorem 3. The parasite-free equilibrium E₀ is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

Proof 3. The Jacobian matrix at parasite-free equilibrium point E₀ is given by

$\begin{array}{ll}\begin{array}{l}J(E_0)=\left(\begin{array}{ccccccc}-{\mu }_H& 0& 0& 0& \frac{-(1-{\xi }_1){\beta }_1{\pi }_H}{{\mu }_H}& 0& 0\\ 0& -\delta & 0& 0& (\frac{-(1-{\xi }_1){\beta }_1{\pi }_H}{{\mu }_H}& 0& 0\\ 0& 0& -{\mu }_R& 0& 0& \frac{-(1-{\xi }_2){\beta }_2{\pi }_R}{{\mu }_R}& 0\\ 0& 0& 0& -\sigma & 0& \frac{(1-{\xi }_2){\beta }_2{\pi }_R}{{\mu }_R}& 0\\ 0& 0& 0& 0& -{\mu }_S& 0& 0\\ 0& (1-{\xi }_3)N\delta & 0& (1-{\xi }_3)Q\sigma & 0& -{\mu }_M& 0\\ 0& 0& 0& c& 0& 0& -({\xi }_4+{\mu }_G)\end{array}\right).\end{array}& (13)\end{array}$

The eigenvalues of the Jacobian matrix, J(E⁰) are obtained from the corresponding characteristic polynomial equation |J(E⁰)−λI| = 0. Clearly, the first, third, and seventh column of the Jacobian matrix (Equation 13) has only diagonal entries. Thus, the eigenvalues λ₁ = −μ_H, λ₃ = −μ_R and λ₇ = −(ξ₄ + μ_G). The remaining eigenvalues are obtained from the sub-matrix

$\begin{array}{ll}{J}^1(E_0)=\left(\begin{array}{cccc}-\delta & 0& (\frac{-(1-{\xi }_1){\beta }_1{\pi }_H}{{\mu }_H}& 0\\ 0& -\sigma & 0& \frac{(1-{\xi }_2){\beta }_2{\pi }_R}{{\mu }_R}\\ 0& 0& -{\mu }_S& 0\\ (1-{\xi }_3)N\delta & (1-{\xi }_3)Q\sigma & 0& -{\mu }_M\end{array}\right).& (14)\end{array}$

The associated characteristic equation of the Jacobian matrix Equation (14) is $|J^1(E_0)-\lambda I|=0$, which means

$\begin{array}{ll}(\delta +\lambda )({\mu }_S+\lambda )\left((\sigma +\lambda )({\mu }_M+\lambda )-\frac{(1-{\xi }_3)(1-{\xi }_2){\beta }_2{\pi }_R\sigma Q}{{\mu }_R}\right)=0.& (15)\end{array}$

Simply, we have λ₂ = −δ, λ₅ = −μ_S, and the remaining eigenvalues are obtained from the equation

$\begin{array}{ll}{\lambda }^2+B_1\lambda +B_0=0,& (16)\end{array}$

where

$\begin{array}{l}{B}_0=\sigma +{\mu }_M,and{B}_1={\mu }_M\sigma -\frac{(1-{\xi }_3)(1-{\xi }_2){\beta }_2{\pi }_R\sigma Q}{{\mu }_R}.\end{array}$

Applying Routh–Hurwitz stability criterion, the characteristic Equation (16) has roots with a negative real part if B₀ > 0 and B₁ > 0. Obviously, B₀ > 0. We now need to show B₁ > 0. Now,

$\begin{array}{l}{B}_1={\mu }_M\sigma -\frac{(1-{\xi }_3)(1-{\xi }_2){\beta }_2{\pi }_R\sigma Q}{{\mu }_R},\\ ={\mu }_M\sigma \left(1-\frac{(1-{\xi }_3)(1-{\xi }_2){\beta }_2{\pi }_{R}Q}{{\mu }_R{\mu }_M}\right),\\ ={\mu }_M\sigma (1-{\mathcal{R}}_0).\end{array}$

We observe that B₁ > 0 if ${\mathcal{R}}_0<1$. Therefore, the parasite-free equilibrium point is locally asymptotically if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

3.5 Global stability analysis of parasite-free equilibrium point

Here, we provide the global stability analysis of a parasite-free equilibrium point using a suitable Lypounove function.

Theorem 4. If ${\mathcal{R}}_0\le 1$, then the parasite-free equilibrium E₀ is globally asymptotically stable.

Proof 4. A suitable Lyapunov functional defined as

$\begin{array}{l}L=N(H-H^0-H^{0}ln\frac{H}{H^0})+N{H}_I+Q(R-R^0-ln\frac{R}{R^0})\\ +N{R}_I+Q{R}_I+S+\frac{1}{1-{\xi }_3}M+QG.\end{array}$

A Lyapunov functional L is non-negative and strictly minimized to the parasite-free equilibrium point. We now compute the derivative of L as follows:

$\begin{array}{l}\frac{dL}{dt}=N\left(1-\frac{H^0}{H}\right)\frac{dH}{dt}+N\frac{d{H}_I}{dt}+Q\left(1-\frac{R^0}{R}\right)\frac{dR}{dt}+Q\frac{d{R}_I}{dt}\\ +\frac{dS}{dt}+\frac{1}{1-{\xi }_3}\frac{dM}{dt}+Q\frac{dG}{dt}\end{array}$

$\begin{array}{l}=N\left(1-\frac{H^0}{H}\right)({\pi }_H-(1-{\xi }_1){\beta }_{1}HS-{\mu }_{H}H)\\ +N((1-{\xi }_1){\beta }_{1}HS-\delta H_I)\\ +Q\left(1-\frac{R^0}{R}\right)({\pi }_R-(1-{\xi }_2){\beta }_{2}RM-{\mu }_{R}R)\\ +Q((1-{\xi }_2){\beta }_{2}RM-\sigma R_I)\\ +{\pi }_S-{\mu }_{H}S+\frac{1}{1-{\xi }_3}((1-{\xi }_3)N\delta H_I\\ +(1-{\xi }_3)Q\sigma R_I-{\mu }_{M}M)+c{R}_I-{\xi }_{4}G-{\mu }_{G}G\\ =N\left(1-\frac{H^0}{H}\right)({\mu }_H{H}^0-(1-{\xi }_1){\beta }_{1}HS-{\mu }_{H}H)\\ +N((1-{\xi }_1){\beta }_{1}HS-\delta H_I)\\ +Q\left(1-\frac{R^0}{R}\right)({\mu }_R{R}^0-(1-{\xi }_2){\beta }_{2}RM-{\mu }_{R}R)\\ +Q((1-{\xi }_2){\beta }_{2}RM-\sigma R_I)+{\mu }_S{S}^0-{\mu }_{S}S\\ \frac{1}{1-{\xi }_3}((1-{\xi }_3)N\delta H_I+(1-{\xi }_3)Q\sigma R_I-{\mu }_{M}M)+c{R}_I\\ -{\xi }_{4}G-{\mu }_{G}G\\ =-{\mu }_{H}N\frac{{(H-H^0)}^2}{H}-N(1-{\xi }_1){\beta }_{1}HS+N(1-{\xi }_1){\beta }_{1}HS\\ +\frac{H^0}{H}(1-{\xi }_1){\beta }_{1}HS\\ -{\mu }_{R}Q\frac{{(R-R^0)}^2}{R}-Q(1-{\xi }_2){\beta }_{2}MR+Q(1-{\xi }_2){\beta }_{2}MR\\ +\frac{R^0}{R}Q(1-{\xi }_2){\beta }_{2}MR-\frac{{\mu }_{M}M}{1-{\xi }_3}\\ +{\mu }_S{S}^0-{\mu }_{S}S-Qc{R}_I+Qc{R}_I-({\xi }_4+{\mu }_G)G\\ =-{\mu }_{H}N\frac{{(H-H^0)}^2}{H}+\frac{{\pi }_H}{{\mu }_H}(1-{\xi }_1){\beta }_{1}S-{\mu }_{R}Q\frac{{(R-R^0)}^2}{R}\\ +\frac{{\pi }_R}{{\mu }_R}Q(1-{\xi }_2){\beta }_{2}M-{\mu }_{S}S-\frac{{\mu }_{M}M}{1-{\xi }_3}-({\xi }_4+{\mu }_G)G\\ =-{\mu }_{H}N\frac{{(H-H^0)}^2}{H}-{\mu }_{R}Q\frac{{(R-R^0)}^2}{R}\\ +\frac{{\mu }_M}{(1-{\xi }_3)}\left(ℛ0-1\right)M-{\mu }_S\left(1-\frac{S^0}{S}-\frac{{\pi }_H(1-{\xi }_1){\beta }_1}{{\mu }_H{\mu }_S}\right)S\\ -({\xi }_4+{\mu }_G)G.\end{array}$

The expression $\frac{dL}{dt}\le 0$ if R₀ < 1 and $\frac{S^0}{S}+\frac{{\pi }_H(1+{\xi }_1){\beta }_1}{{\mu }_H{\mu }_S}\le 1$ for any positive H, H_I, R, R_I, S, M, G. The equality $\frac{dL}{dt}=0$, holds if and only if for $H=H^0,R=R^0,G=G^0,{\mathcal{R}}_0=1$, and ${\pi }_H(1-{\xi }_1){\beta }_1/{\mu }_H{\mu }_S+S^0/S=1$. Therefore, by LaSalle's Invariance Principle [39], the parasite-free equilibrium E₀ is global asymptotically stable for ${\mathcal{R}}_0<1$.

3.6 Parasite persistence equilibrium point

The parasite persistence equilibrium point is the steady-state solution at which the malaria parasite persists in the host cells. It is computed by setting the right hand side of the system Equation (1) to zero. The parasite persistence equilibrium point E^* is investigated and given as

$\begin{array}{l}{E}^{*}(H^{*},H_I^{*},R^{*},R_I^{*},S^{*},M^{*},G^{*})=\{\begin{array}{l}{H}^{*}=\frac{{\pi }_H}{(1-{\xi }_1){\beta }_1\frac{{\pi }_S}{{\mu }_S}+{\mu }_H},\\ H_I^{*}=\frac{(1-{\xi }_1){\beta }_1{\pi }_S{\pi }_H}{\delta ({\mu }_S(1-{\xi }_1)\frac{{\pi }_S}{{\mu }_S}+{\mu }_H)},\\ R^{*}=\frac{{\pi }_R}{(1-{\xi }_2){\beta }_2{M}^{*}+{\mu }_R},\\ R_I^{*}=\frac{(1-{\xi }_2){\pi }_R{\beta }_2{M}^{*}}{((1-{\xi }_2){\beta }_2{M}^{*}+{\mu }_R)\sigma }\\ S^{*}=\frac{{\pi }_S}{{\mu }_S},\\ G^{*}=\frac{c(1-{\xi }_2){\pi }_R{\beta }_2{M}^{*}}{((1-{\xi }_2){\beta }_2{M}^{*}+{\mu }_R)\sigma ({\xi }_4+{\mu }_G)},\end{array}\end{array}$

where M^* is the positive roots of

$\begin{array}{ll}P(M^{*})=d_0{M^{*}}^2+d_1{M}^{*}+d_2=0,& (17)\end{array}$

and the coefficients d₂, d₁, and d₀ are given as

$\begin{array}{ll}\begin{array}{l}{d}_0={\mu }_S(1-{\xi }_1)\frac{{\pi }_S}{{\mu }_S}+{\mu }_H{\mu }_M(1-{\xi }_2){\beta }_2\sigma ,\\ d_1=({\mu }_S(1-{\xi }_1)\frac{{\pi }_S}{{\mu }_S}+{\mu }_H){\mu }_M{\mu }_R\sigma (1-{\mathcal{R}}_0)\\ -(1-{\xi }_3)N(1-{\xi }_1){\beta }_1{\pi }_S{\pi }_H(1-{\xi }_2){\beta }_2\sigma ,\\ d_2=-(1-{\xi }_3)N(1-{\xi }_1){\beta }_1{\pi }_S{\pi }_H{\mu }_R(\sigma +c).\end{array}& (18)\end{array}$

By Descarts' rule of sign, the system Equation (1) has a parasite persistence equilibrium, if d₁ < 0 implies that R₀ > 1 and/or if d₁ < 0 implies that R₀ > 1, and if the discriminant Δ = 0, where

$\begin{array}{l}*\Delta =d_1^2-4d_2{d}_0\\ =(({\mu }_S(1-{\xi }_1)\frac{{\pi }_S}{{\mu }_S}+{\mu }_H){\mu }_M{\mu }_R(\sigma +c)\left(1-{ℛ}_0\right)\\ {-(1-{\xi }_3)N(1-{\xi }_1){\beta }_1{\pi }_S{\pi }_H(1-{\xi }_2){\beta }_2\sigma )}^2,\\ +4({\mu }_S(1-{\xi }_1)\frac{{\pi }_S}{{\mu }_S}+{\mu }_H)({\mu }_M(1-{\xi }_2){\beta }_2\sigma )(1-{\xi }_3)N(1\\ -{\xi }_1){\beta }_1{\pi }_S{\pi }_H{\mu }_R(\sigma +c).\end{array}$

From Equation (18), it is not difficult to see that d₀ is always positive and d₂ is negative. Thus, by Descarts' rule of sign and/or discriminant, a parasite persistence equilibrium point exists if R₀ > 1.

3.7 Local stability analysis of parasite persistence equilibrium point

In this section, we examine the local stability analysis of parasite persistence equilibrium via linearzing the system Equation (1) at E^*.

Theorem 5. The parasite persistence equilibrium point is locally asymptotically stable if R₀ > 1 and unstable if R₀ < 1.

Proof 5. The Jacobian matrix at parasite persistence equilibrium, E^* is given as

$\begin{array}{ll}\begin{array}{l}J(E^{*})=\\ \left(\begin{array}{ccccccc}-A_1-{\mu }_H& 0& 0& 0& -(1-{\xi }_1){\beta }_{1}H& 0& 0\\ A_1& -\delta & 0& 0& (1-{\xi }_1){\beta }_{1}H& 0& 0\\ 0& 0& -A_2-{\mu }_R& 0& 0& -(1-{\xi }_2){\beta }_2{R}^{*}& 0\\ 0& 0& A_2& -\sigma & 0& (1-{\xi }_2){\beta }_2{R}^{*}& 0\\ 0& 0& 0& 0& -{\mu }_S& 0& 0\\ 0& (1-{\xi }_3)N\delta & 0& (1-{\xi }_3)Q\sigma & 0& -{\mu }_M& 0\\ 0& 0& 0& c& 0& 0& -({\xi }_4+{\mu }_G)\end{array}\right),\end{array}& (19)\end{array}$

where $A_1=(1-{\xi }_1){\beta }_1{S}^{*}$ and $A_2=(1-{\xi }_2){\beta }_2{M}^{*}$.

The associated characteristic equation is given as det(J(E^*)−λI) = 0. To simplify the steps now, the last column of the Jacobian matrix (19) has only diagonal entry; thus, we have λ₇ = −(ξ₄ + μ_G). The fifth row of the Jacobian matrix has only a diagonal entry, and we can easily obtain the λ₅ = −μ_S. The remaining eigenvalues are obtained from the submatrix

$\begin{array}{l}{J}_1(E^{*})\\ =\left(\begin{array}{ccccc}-A_1-{\mu }_H& 0& 0& 0& 0\\ A_1& -\delta & 0& 0& 0\\ 0& 0& -A_2-{\mu }_R& 0& -(1-{\xi }_2){\beta }_2{R}^{*}\\ 0& 0& A_2& -\delta & (1-{\xi }_2){\beta }_2{R}^{*}\\ 0& (1-{\xi }_3)N\delta & 0& (1-{\xi }_3)Q\sigma & -{\mu }_M\end{array}\right).& (20)\end{array}$

The associated characteristic equation is given as $det(J_1(E^{*})-\lambda I)=0$. Thus,

$\begin{array}{ll}(A_1+{\mu }_H+\lambda )(\delta +\lambda )({\lambda }^3+B_0{\lambda }^2+B_1\lambda +B_0)=0,& (21)\end{array}$

where

$\begin{array}{l}{B}_0=\delta +{\mu }_M+A_2+{\mu }_R,\\ B_1=\delta {\mu }_M+(A_2+{\mu }_R)(\delta +{\mu }_M),\end{array}$

$\begin{array}{l}{B}_2=\delta {\mu }_M(A_2+{\mu }_R)-(1-{\xi }_2)(1-{\xi }_3)Q\delta {\beta }_2{R}^{*}\\ +(1-{\xi }_2)(1-{\xi }_3){\beta }_2{A}_{2}Q\delta R^{*}.\end{array}$

From characteristic polynomial Equation (21), we have λ₁ = −A₁ − μ_H, λ₂ = −δ or

$\begin{array}{ll}{\lambda }^3+B_0{\lambda }^2+B_1\lambda +B_0=0.& (22)\end{array}$

Applying the Routh-Hurwitz stability criteria, the polynomial Equation (22) has roots with negative real part if B₀ > 0, B₁ > 0, B₂ > 0, and B₂ − B₀B₁ > 0. Therefore, the parasite persistence equilibrium point is locally asymptotically stable if R₀ > 1. This completes the proof.

3.8 Sensitivity analysis

In this section, we present the sensitivity analysis for the basic reproduction number ${\mathcal{R}}_0$ to identify the parameters that have a high impact on disease elaboration within the host. The normalized forward sensitivity index of a variable to a parameter is the ratio of the relative change in the variable to the relative change in the parameter. If the variable is a differentiable function of the parameter, the sensitivity index is then defined using partial derivatives.

Definition: The normalized forward sensitivity index of a variable M that depends differentiability on a parameter u is defined as

$\begin{array}{l}{\Theta }_u^M=\frac{\partial M}{\partial u}\times \frac{u}{M}\end{array}$

As we have an explicit formula for R₀ given in Equation (11), we derive an analytical expression for the sensitivity of R₀

${\Theta }_{\vartheta }^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial \vartheta }\times \frac{\vartheta }{{\mathcal{R}}_0},$

where ϑ is represented the model parameters which belongs to basic reproduction number ${\mathcal{R}}_0$. Now,

$\begin{array}{l}{\Theta }_{{\beta }_2}^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial {\beta }_2}\times \frac{{\beta }_2}{{\mathcal{R}}_0}=+1,{\Theta }_{{\pi }_R}^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial {\pi }_R}\times \frac{{\pi }_R}{{\mathcal{R}}_0}=+1,\\ {\Theta }_Q^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial Q}\times \frac{Q}{{\mathcal{R}}_0}=+1,{\Theta }_{{\mu }_M}^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial {\mu }_M}\times \frac{{\mu }_M}{{\mathcal{R}}_0}=-1\\ {\Theta }_{{\mu }_R}^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial {\mu }_R}\times \frac{{\mu }_R}{{\mathcal{R}}_0}=-1.\end{array}$

From Table 3, we see that the infection rate of the erythrocyte by merozoites β₂, average number of merozoites per ruptured infected erythrocyte cells Q, the production rate of the uninfected erythrocyte π_R, natural death rate merozoites μ_M, and natural death rate of red-blood cells μ_R are the most sensitive parameters. A 10% increase (or decrease) in β₂, Q, and π_R is a 10% increase (or decrease) in ℜ₀. A 10% increase (decrease) in μ_M and μ_R is a 10% decrease (or increase) in ℜ₀.

TABLE 3

Table 3. Sensitivity index of within-host basic reproduction number ${\mathcal{R}}_0$.

4 Numerical simulations

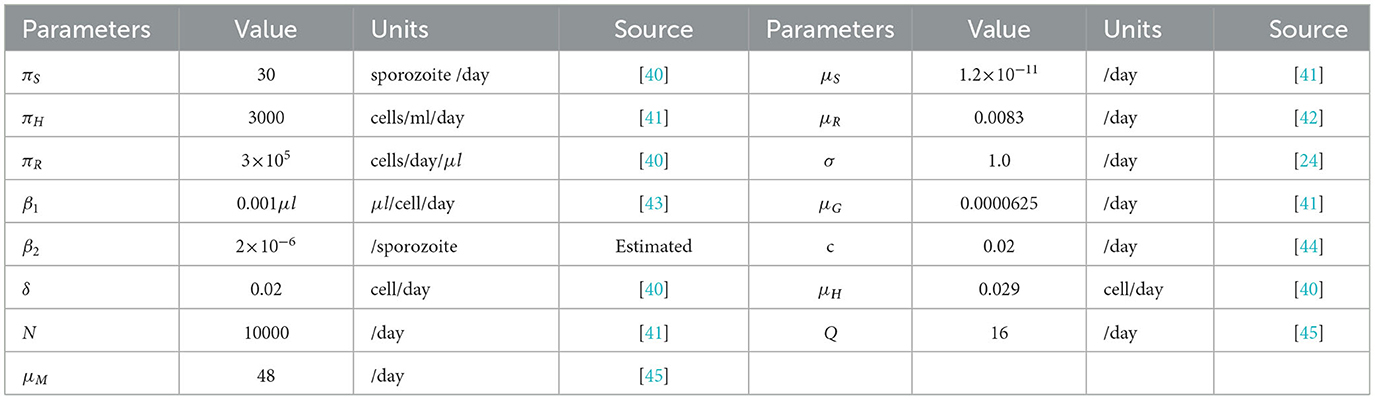
In this section, we present the numerical simulation of model (Equation 1) in order to supplement the analytical results. The initial condition we used in this simulation is H(0) = 3000, H_I(0) = 10, R(0) = 500000, R_I(0) = 200, S(0) = 200, M(0) = 40, 000, and G(0) = 20, and the model parameters are given in Table 4. Using the model parameter values, we have within host basic reproduction number ${\mathcal{R}}_0=24.0964$ without antimalarial drug treatment (ξ₁ = 0, ξ₂ = 0) and ${\mathcal{R}}_0=6.0241$ with antimalarial drug treatment 50% effective (ξ₁ = 50%, ξ₂ = 50% effective). The simulation of the system equations are integrated using the ode45 solver in MATLAB.

TABLE 4

Table 4. Model parameter values.

Figure 2 reveals the dynamical behavior of model (Equation 1) in the absence of antimalarial drug treatments, i.e., all-stage antimalarial drug treatment is not administered (ξ₁ = 0, ξ₂ = 0, ξ₃ = 0, and ξ₄ = 0). The vulnerable hepatocytes and red blood cells decrease over time, whereas the other state variables are rise. All the system solutions converge to an endemic equilibrium point. The effect of primary tissue schizontocides on healthy and infected hepatocytes is shown in Figure 3. As metformin's antimalarial effectiveness rises, the number of healthy hepatocytes also rises (see Figure 3A). Figure 3B reveals that when the effectiveness of metformin antimalarial treatment rises, the number of infected hepatocytes declines. Figure 4A shows the iRBCs decrease as the efficiency of blood schizontocides increases. Figure 4B indicates the impact of blood schizontocide and primary tissue schizontocide on merozoites. The merozoite population decreases as the blood schizontocides and primary tissue schizontocides efficiency increases. The impact of blood schizontocides (blood-stage antimalarial medication treatment) on red blood cells is depicted in Figure 5. As blood schizontocides (blood-stage antimalarial drug therapy) increases, the number of uninfected red blood cells rises (see Figure 5A). As indicated in Figure 5B, the infected red blood cells gradually declines as the blood schizontocides (antimalarial drug treatment at the blood-stage) increases. Figure 6 demonstrates that as the average number of merozoites per ruptured infected erythrocyte grows, both the population of merozoites and the infected RBCs increases.

FIGURE 2

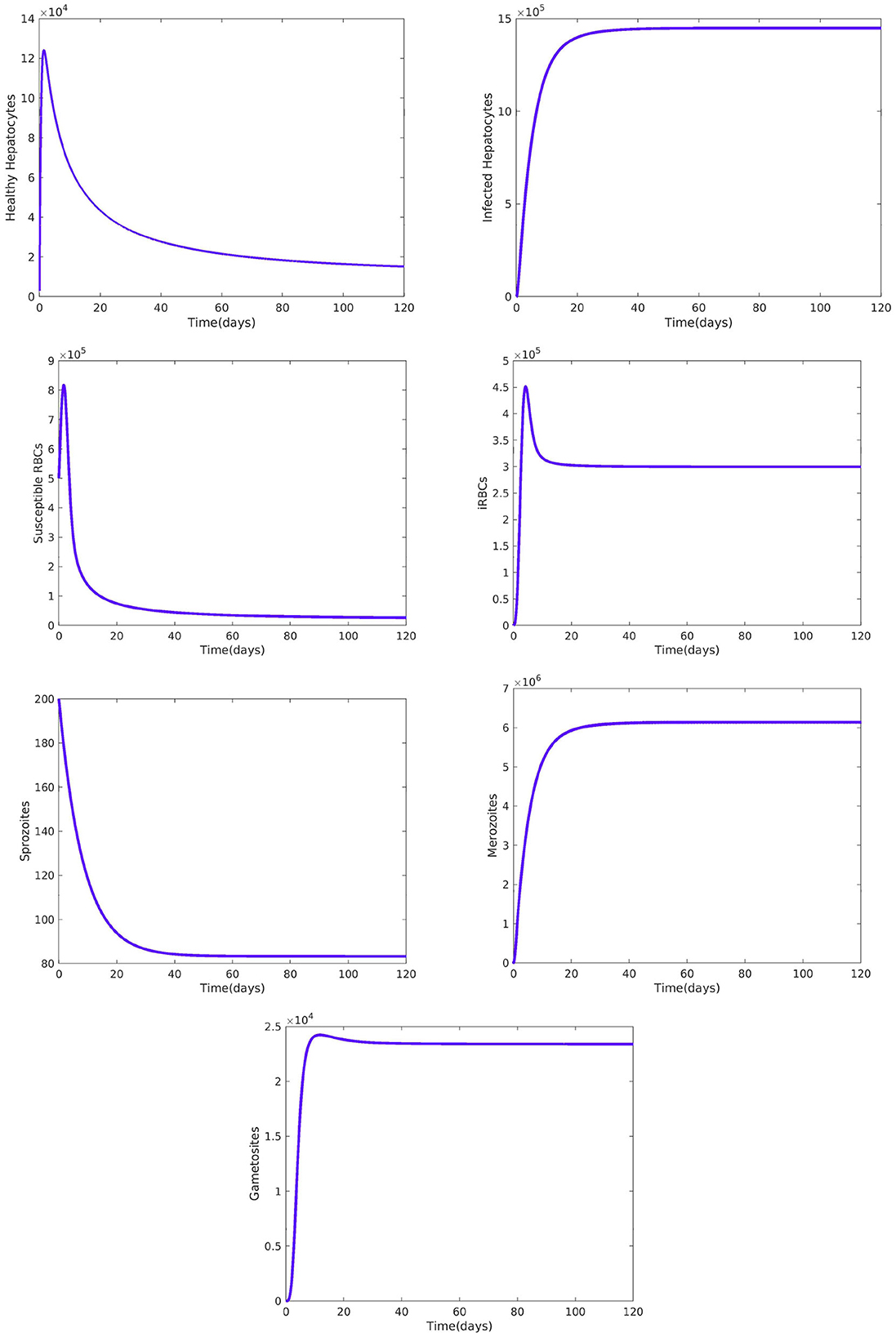
Figure 2. Dynamical behavior of the system Equation (1) without malaria drug treatments, i.e., ${\xi }_1=0,$ ${\xi }_2=0,$ ${\xi }_3=0,$ ${\xi }_4=0,$ ${\mathcal{R}}_0=24.695$ and all the other parameters are fixed as in Table 4.

FIGURE 3

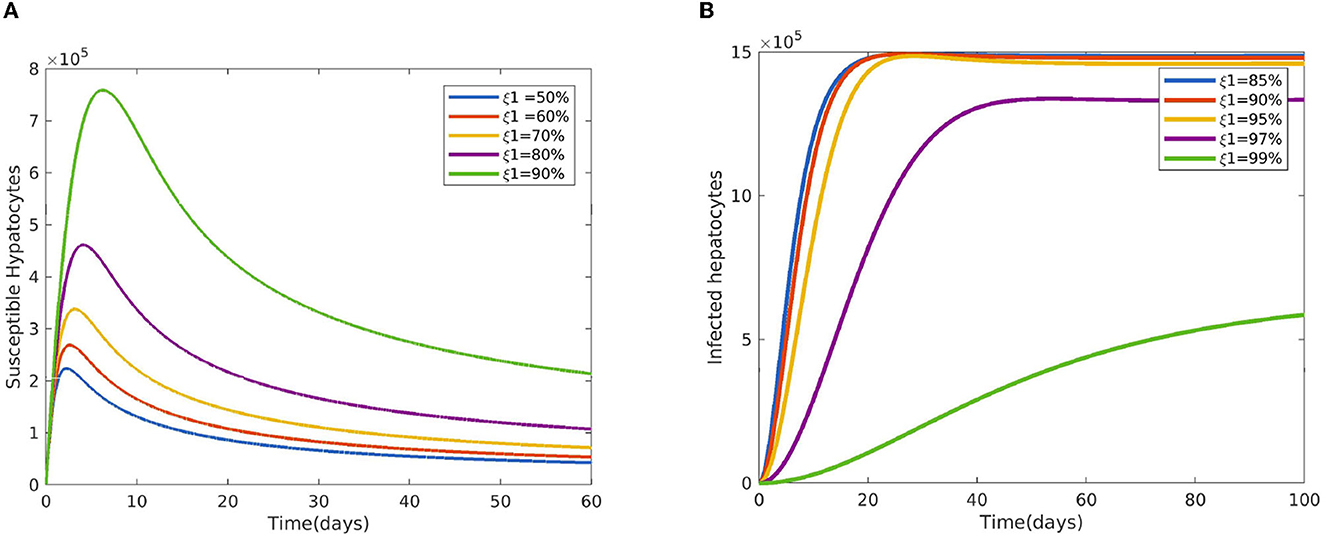
Figure 3. Impact of primary tissue schizontocides (pre-erythrocytic treatment) ξ₁ (A) on susceptible hepatocytes (B) on infected hepatocytes using the following parameter values: ${\pi }_S=30,$ ${\pi }_H=3000,$ ${\pi }_R=3\times 10^5,$ ${\beta }_1=0.001,$ ${\beta }_2=2\times 10^{-6},$ $\delta =0.02,$ $N=10000,$ ${\mu }_M=48,$ ${\mu }_S=1.2\times 10^{-11},$ ${\mu }_R=0.0083,$ $\sigma =1.0,$ ${\mu }_G=0.0000625,$ $c=0.02,$ ${\mu }_H=0.029,$ $Q=16$ and all the other parameters are fixed as in Table 4.

FIGURE 4

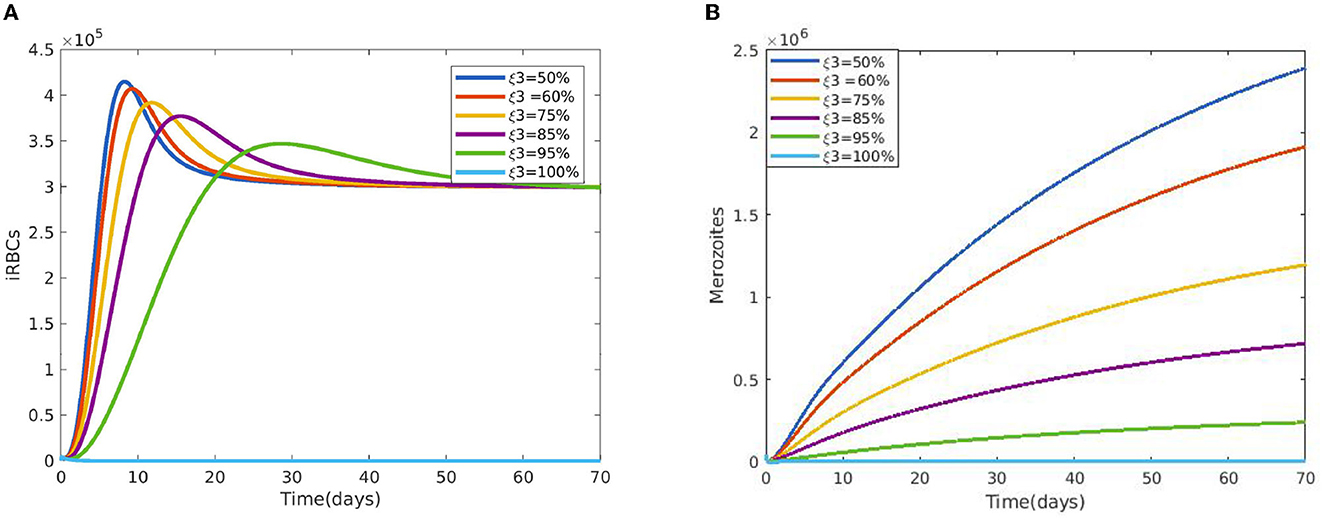
Figure 4. (A) Impact of blood schizontocides ξ₃ on iRBCs. (B) Impact of blood schizontocides ξ₃ on merozoites using the following parameter values: ${\pi }_S=30,$ ${\pi }_H=3,000,$ ${\pi }_R=3\times 10^5,$ ${\beta }_1=0.001,$ ${\beta }_2=2\times 10^{-6},$ $\delta =0.02,$ $N=10,000,$ ${\mu }_M=48,$ ${\mu }_S=1.2\times 10^{-11},$ ${\mu }_R=0.0083,$ $\sigma =1.0,$ ${\mu }_G=0.0000625,$ $c=0.02,$ ${\mu }_H=0.029,$ $Q=16$ and all the other parameters are fixed as in Table 4.

FIGURE 5

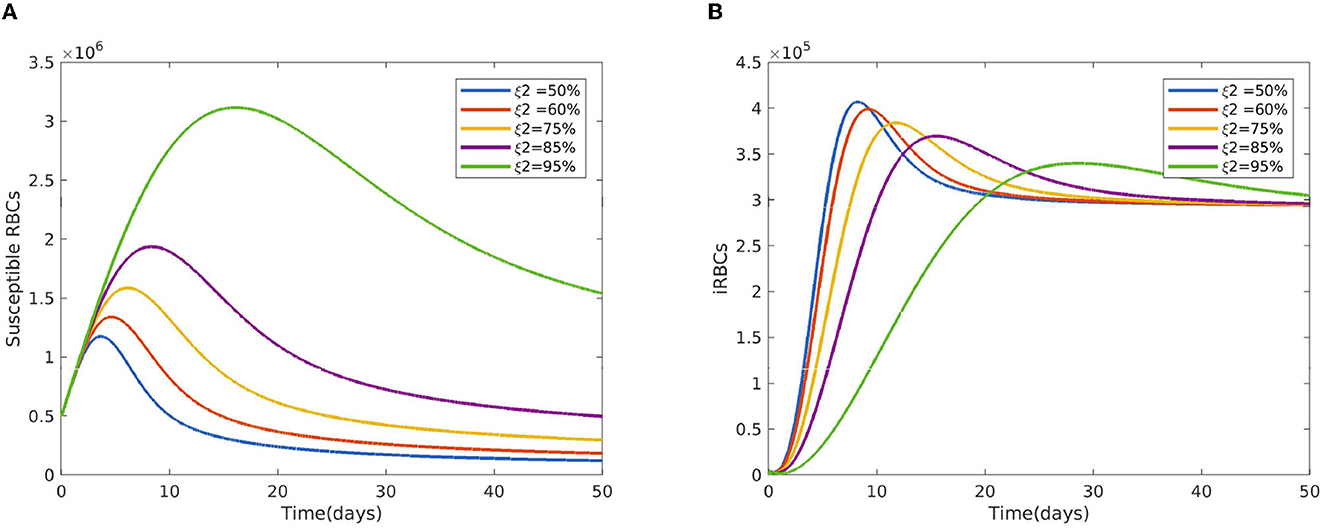
Figure 5. Impact of the blood schizontocides ξ₂ (A) on healthy RBCs (B) on iRBCs using the following parameter values: ${\pi }_S=30,$ ${\pi }_H=3000,$ ${\pi }_R=3\times 10^5,$ ${\beta }_1=0.001,$ ${\beta }_2=2\times 10^{-6},$ $\delta =0.02,$ $N=10,000,$ ${\mu }_M=48,$ ${\mu }_S=1.2\times 10^{-11},$ ${\mu }_R=0.0083,$ $\sigma =1.0,$ ${\mu }_G=0.0000625,$ $c=0.02,$ ${\mu }_H=0.029,$ $Q=16$ and all the other parameters are fixed as in Table 4.

FIGURE 6

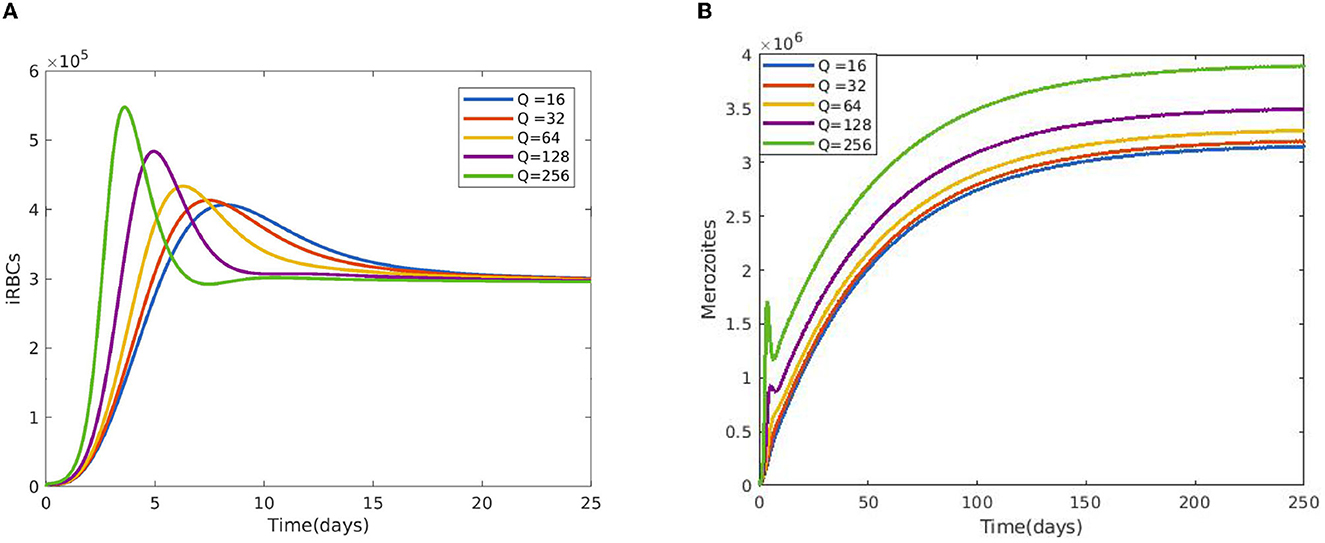
Figure 6. Impact of average number of merozoites per ruptured infected erythrocyte cells Q (A) on iRBCs and (B) on merozoites using the following parameter values: ${\pi }_S=30,$ ${\pi }_H=3,000,$ ${\pi }_R=3\times 10^5,$ ${\beta }_1=0.001,$ ${\beta }_2=2\times 10^{-6},$ $\delta =0.02,$ $N=10,000,$ ${\mu }_M=48,$ ${\mu }_S=1.2\times 10^{-11},$ ${\mu }_R=0.0083,$ $\sigma =1.0,$ ${\mu }_G=0.0000625,$ $c=0.02,$ ${\mu }_H=0.029,$ $Q=16$ and all the other parameters are fixed as in Table 4.

Figure 7A displays the gametocyte population declines as the effectiveness of gametocytocidal medication therapy (gametocytocidal) increases. Figure 7B exhibits the effect of the average number of merozoites discharged per ruptured infected hepatocytic cell on merozoites. As the average number of merozoites discharged per ruptured infected hepatocytic cell increases, the merozoite population increases. Figure 8A depicts the impact of the infection rate of erythrocyte β₂ and the antimalarial treatment on erythrocytic invasion (blood schizontocides efficacy) ξ₂ on the basic reproduction number R₀. Figure 8B displays the impact of the infection rate of the erythrocyte β₂ and blood schizontocides drug treatment ξ₃ on the basic reproduction number R₀. As imagined, to reduce the R₀ value below unity, the infection rate of the erythrocyte must be very low, almost irrespective of the blood schizontocides. That is, despite the availability of antimalarial treatment, inconsiderate mixing needs to be observed to prevent an excessive number of parasites inside the host cell. Figure 9A indicates the influence of the average number of merozoite per ruptured infected erythrocyte cell Q and blood-stage antimalarial drug treatment (efficacy of antimalarial treatment on erythrocytic invasion) ξ₂ on the basic reproduction number R₀. Figure 9B shows the impact of the average number of merozoite per ruptured infected erythrocyte cells Q and efficiency of antimalarial drug treatments on the bursting rate of pre-erythrocytic schizont and blood schizont ξ₃. The figures illustrates decreasing the average number of merozoites per ruptured infected erythrocyte cell Q and raising blood-stage antimalarial drug treatment ξ₂ and blood schizontocide ξ₃ decreases the in-host basic reproduction number R₀, which, in turn, decreases the in-host malaria parasite. Figure 10A exhibits the impact of the infection rate of erythrocyte β₂ and the average number of merozoite per ruptured infected erythrocyte cells Q on the basic reproduction number, R₀. The within-host basic reproduction number is rises as both the infection rate of the erythrocyte and the average number of merozoite per ruptured infected erythrocyte cells increases. Figure 10B demonstrates the within-host reproduction number increases as the infection rate of the erythrocyte increases; however, the average number of merozoites per ruptured infected hepatocyte cell N has no impact on the reproduction number.

FIGURE 7

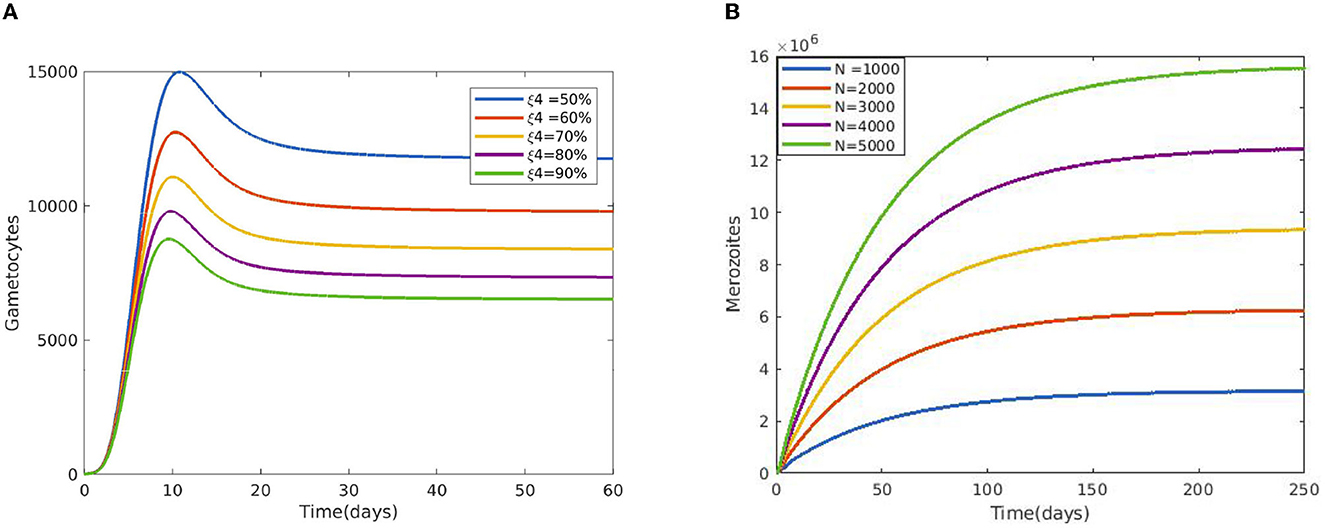
Figure 7. (A) Impact of gametocytocidal drugs (gametocytocides) on sexual replication of malaria parasites. (B) Effect of the average number of merozoite released per ruptured infected hepatocytic cells using the following parameter values: ${\pi }_S=30,$ ${\pi }_H=3,000,$ ${\pi }_R=3\times 10^5,$ ${\beta }_1=0.001,$ ${\beta }_2=2\times 10^{-6},$ $\delta =0.02,$ ${\mu }_M=48,$ ${\mu }_S=1.2\times 10^{-11},$ ${\mu }_R=0.0083,$ $\sigma =1.0,$ ${\mu }_G=0.0000625,$ $c=0.02,{\mu }_H=0.029,$ $Q=16$ and all the other parameters are fixed as in Table 4.

FIGURE 8

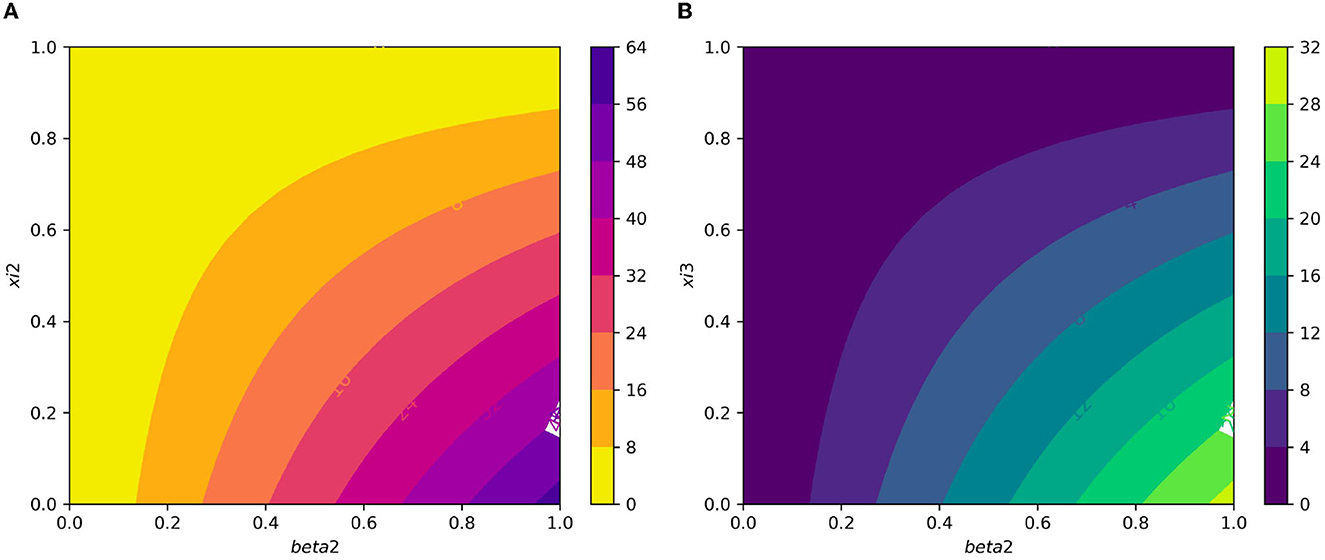
Figure 8. (A) Contour plot of ${\mathcal{R}}_0$ with respect to infection rate of the erythrocyte β₂ and efficacy of antimalarial treatment on erythrocytic invasion (blood schizontocides efficacy) ξ₂. (B) Contour plot of ${\mathcal{R}}_0$ with respect to the infection rate of the erythrocyte β₂ and efficiency of antimalarial drug treatments on the bursting rate of erythrocytic (blood schizontocides efficacy) ξ₃.

FIGURE 9

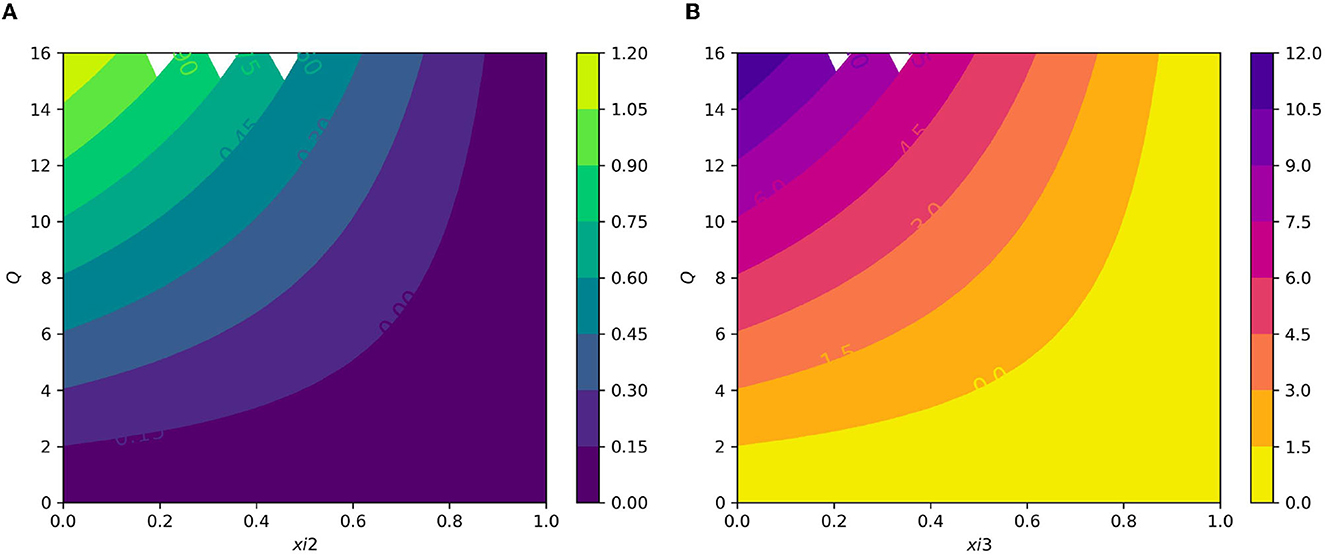
Figure 9. (A) Contour plot of ${\mathcal{R}}_0$ with respect to the average number of merozoite per ruptured infected erythrocyte cells Q and blood stage antimalarial drug treatment (efficacy of antimalarial treatment on erythrocytic invasion) ξ₂. (B) Contour plot of ${\mathcal{R}}_0$ average number of merozoite per ruptured infected erythrocyte cells Q and efficiency of antimalarial drug treatments on the bursting rate of pre-erythrocytic schizont and blood schizont ξ₃.

FIGURE 10

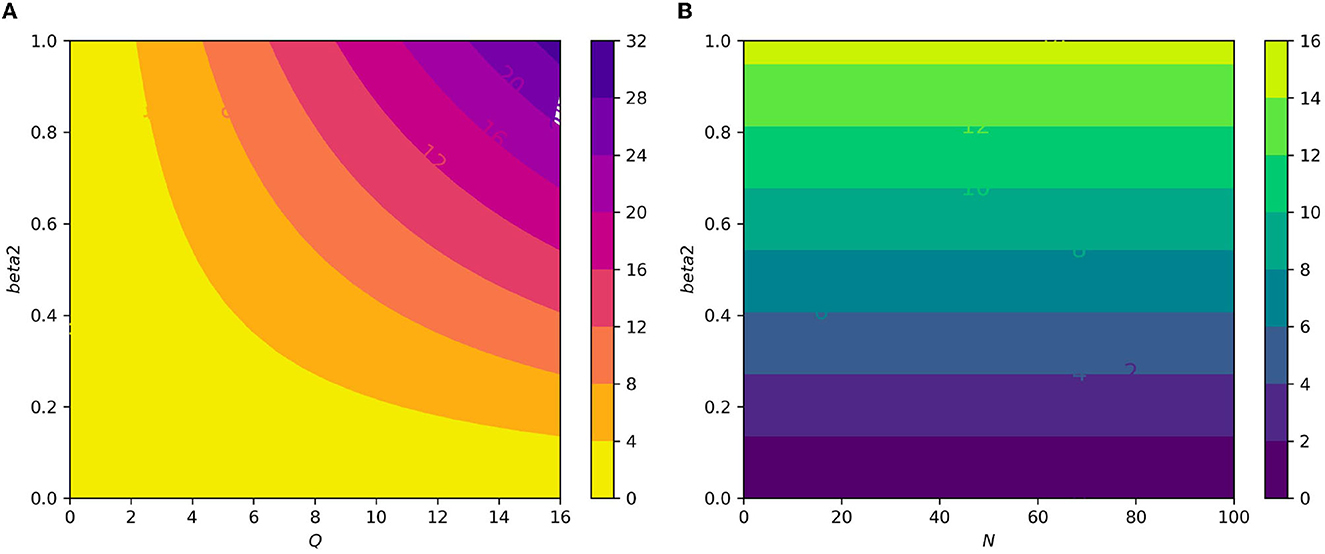
Figure 10. (A) Contour plot of ${\mathcal{R}}_0$ with respect to the infection rate of the erythrocyte β₂ and an average number of merozoite per ruptured infected erythrocyte cells Q. (B) Contour plot of ${\mathcal{R}}_0$ with respect to an infection rate of the erythrocyte β₂ and an average number of merozoite per ruptured infected hepatocyte cells N.

5 Conclusion

In this study, we investigated a cell-level mathematical model for malaria parasite infection with antimalarial drug treatment. The model includes the interactions of hepatocyte cells, red blood cells, and malaria parasites. The qualitative analysis of the developed model, such as the positivity, and boundedness of the solution is discussed. The equilibria and their stability analysis are investigated, where the parasite-free equilibrium point is both local and global stable if the basic reproduction number ${\mathcal{R}}_0$ is less than unity. The global stability analysis of the parasite-free equilibrium point is investigated using a suitable Lyponove function. The existence of parasite persistence equilibrium points is reached using Descarts' rule of sign and its local stability is investigated by applying Routh-Hurwitz stability criterion. We computed a sensitivity analysis of the in-host basic reproduction number to investigate most influential parameters in the within-host malaria parasites using the normalized forward sensitivity index. As a result, the infection rate of the erythrocyte by merozoites, the average number of merozoites per ruptured infected erythrocyte, the natural death rate of merozoites, and the requirement rate of the uninfected erythrocytes are the most influential ones. Different numerical simulations are performed to supplement our analytical findings and it is observed to be in good agreement. Furthermore, the simulation result reveals that the administration of antimalarial drug treatment, such as primary tissue schizontocides, blood schizontocides, and gametocytocides, are used to the eliminate the malaria parasites from the human host cells. This study's findings offer guidance for antimalarial medication therapy and malaria control. By lowering the average number of merozoites per ruptured infected infected erythrocyte and hepatocyte, we can restrict the generation of malaria parasites within the host and prevent them from being infected. Primary tissue schizontocide and blood-stage schizontocides will be administered in order to achieve this. In this study, we consider the constant antimalarial treatment and single strains of malaria infection. In future, we will extend it to optimal control problems using time-dependent antimalarial drug treatment, fractional order differential equations in order to investigate the memory effect, and different strains of malaria infection.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the patients/participants was not required to participate in this study in accordance with the national legislation and the institutional requirements.

Author contributions

JA: Conceptualization, Formal analysis, Investigation, Methodology, Software, Writing – original draft, Writing – review & editing. GT: Supervision, Visualization, Writing – original draft, Writing – review & editing. SD: Investigation, Supervision, Visualization, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors acknowledge Adama Science and Technology University for its support during this research work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jagannathan P, Kakuru A. Malaria in 2022: increasing challenges, cautious optimism. Nat Commun. (2022) 13:2678. doi: 10.1038/s41467-022-30133-w

PubMed Abstract | CrossRef Full Text | Google Scholar

2. WHO. World malaria report 2022. Geneva: World Health Organization (2022).

Google Scholar

3. Rosenthal PJ. Malaria in 2022: challenges and progress. Am J Trop Med Hyg. (2022) 106:1565. doi: 10.4269/ajtmh.22-0128

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Agnandji ST, Fernandes JF, Bache EB, Ramharter MP. Clinical development of RTS, S/AS malaria vaccine: a systematic review of clinical Phase I-III trials. Future Microbiol. (2015) 10:1553–78. doi: 10.2217/fmb.15.90

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dhangadamajhi G, Kar SK, Ranjit MR. The survival strategies of malaria parasite in the red blood cell and host cell polymorphisms. Malaria Res Treat. (2010) 2010:973094. doi: 10.4061/2010/973094

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Risco-Castillo V, Topçu SH, Carine MP, Manzoni G, Bigorgne AE, Briquet S, et al. Malaria sporozoites traverse host cells within transient vacuoles. Cell Host Microbe. (2015) 18:593–603. doi: 10.1016/j.chom.2015.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Su Xz, Zhang C, Joy DA. Host-malaria parasite interactions and impacts on mutual evolution. Front Cell Infect Microbiol. (2020) 10:587933. doi: 10.3389/fcimb.2020.587933

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yang X, Su Y, Li H, Zhuo X. Optimal control of a cell-to-cell fractional-order model with periodic immune response for HCV. Symmetry. (2021) 13:2121. doi: 10.3390/sym13112121

CrossRef Full Text | Google Scholar

9. Sherling ES, van Ooij C. Host cell remodeling by pathogens: the exomembrane system in Plasmodium-infected erythrocytes. FEMS Microbiol Rev. (2016) 40:701–21. doi: 10.1093/femsre/fuw016

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mandala WL, Harawa V, Dzinjalamala F, Tembo D. The role of different components of the immune system against Plasmodium falciparum malaria: possible contribution towards malaria vaccine development. Mol Biochem Parasitol. (2021) 246:111425. doi: 10.1016/j.molbiopara.2021.111425

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Engwerda CR, Good MF. Interactions between malaria parasites and the host immune system. Curr Opin Immunol. (2005) 17:381–7. doi: 10.1016/j.coi.2005.05.010

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Greenwood BN, Marsh KS, Snow RW. Why do some African children develop severe malaria? Parasitol Today. (1991) 7:277–81. doi: 10.1016/0169-4758(91)90096-7

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Baker DA. Malaria gametocytogenesis. Mol Biochem Parasitol. (2010) 172:57–65. doi: 10.1016/j.molbiopara.2010.03.019

CrossRef Full Text | Google Scholar

14. McQueen PG, Williamson KC, McKenzie FE. Host immune constraints on malaria transmission: insights from population biology of within-host parasites. Malar J. (2013) 12:1–18. doi: 10.1186/1475-2875-12-206

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sreenivasamurthy SK, Dey G, Ramu M, Kumar M, Gupta MK, Mohanty AK, et al. A compendium of molecules involved in vector-pathogen interactions pertaining to malaria. Malar J. (2013) 12:1–7. doi: 10.1186/1475-2875-12-216

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Acharya P, Garg M, Kumar P, Munjal A, Raja K. Host-parasite interactions in human malaria: clinical implications of basic research. Front Microbiol. (2017) 8:889. doi: 10.3389/fmicb.2017.00889

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Pinheiro L, Feitosa LM, Silveira FF, Boechat N. Current antimalarial therapies and advances in the development of semi-synthetic artemisinin derivatives. Anais Acad Brasil Ciências. (2018) 90:1251–71. doi: 10.1590/0001-3765201820170830

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Vera IM, Ruivo MTG, Rocha LFL, Marques S, Bhatia SN, Mota MM, et al. Targeting liver stage malaria with metformin. JCI Insight. (2019) 4:e127441. doi: 10.1172/jci.insight.127441

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bruce-Chwatt LJ. Classification of antimalarial drugs in relation to different stages in the life-cycle of the parasite: commentary on a diagram. Bull World Health Organ. (1962) 27:287.

PubMed Abstract | Google Scholar

20. Munro BA, McMorran BJ. Antimalarial drug strategies to target plasmodium gametocytes. Parasitologia. (2022) 2:101–24. doi: 10.3390/parasitologia2020011

CrossRef Full Text | Google Scholar

21. Anvikar AR, Arora UR, Chattopadhya D, Das BC, Dash AP, Dhariwal A, et al. Guidelines for diagnosis and treatment of malaria in India. Natl Inst Malaria Res. (2011).

Google Scholar

22. Organization WH. Guidelines for the Treatment of Malaria. Geneva: World Health Organization. (2015).

Google Scholar

23. Anderson RM, May RM, Gupta CS. Non-linear phenomena in host-parasite interactions. Parasitology. (1989) 99:S59–79. doi: 10.1017/S0031182000083426

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Hetzel CJ, Anderson RM. The within-host cellular dynamics of bloodstage malaria: theoretical and experimental studies. Parasitology. (1996) 113:25–38. doi: 10.1017/S0031182000066245

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Elaiw A, Al Agha A. Global analysis of a reaction-diffusion within-host malaria infection model with adaptive immune response. Mathematics. (2020) 8:563. doi: 10.3390/math8040563

CrossRef Full Text | Google Scholar

26. Li Y, Ruan S, Xiao D. The within-host dynamics of malaria infection with immune response. Mathem Biosci Eng. (2011) 8:999–1018. doi: 10.3934/mbe.2011.8.999

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Anderson RM. Complex dynamic behaviours in the interaction between parasite populations and the host's immune system. Int J Parasitol. (1998) 28:551–66. doi: 10.1016/S0020-7519(97)00207-5

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Song T, Wang C, Tian B. Mathematical models for within-host competition of malaria parasites. Mathem Biosci Eng. (2019) 16:6623–53. doi: 10.3934/mbe.2019330

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Iggidr A, Kamgang JC, Sallet G, Tewa JJ. Global analysis of new malaria intrahost models with a competitive exclusion principle. SIAM J Appl Math. (2006) 67:260–78. doi: 10.1137/050643271

CrossRef Full Text | Google Scholar

30. Tewa JJ, Fokouop R, Mewoli B, Bowong S. Mathematical analysis of a general class of ordinary differential equations coming from within-hosts models of malaria with immune effectors. Appl Math Comput. (2012) 218:7347–61. doi: 10.1016/j.amc.2011.10.085

CrossRef Full Text | Google Scholar

31. Kamangira B, Nyamugure P, Magombedze G. A theoretical mathematical assessment of the effectiveness of coartemether in the treatment of Plasmodium falciparum malaria infection. Math Biosci. (2014) 256:28–41. doi: 10.1016/j.mbs.2014.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Chen H, Wang W, Fu R, Luo J. Global analysis of a mathematical model on malaria with competitive strains and immune responses. Appl Math Comput. (2015) 259:132–52. doi: 10.1016/j.amc.2015.02.073

CrossRef Full Text | Google Scholar

33. Khoury DS, Aogo R, Randriafanomezantsoa-Radohery G, McCaw JM, Simpson JA, McCarthy JS, et al. Within-host modeling of blood-stage malaria. Immunol Rev. (2018) 285:168–93. doi: 10.1111/imr.12697

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Tabo Z, Luboobi LS, Ssebuliba J. Mathematical modelling of the in-host dynamics of malaria and the effects of treatment. Parasitology. (2000) 121:227–35. doi: 10.22436/jmcs.017.01.01

CrossRef Full Text | Google Scholar

35. Chinebu TI, Ezennorom EO, Okwor JU. Simulation of an intracellular differential equation model of the dynamics of malaria with immune control and treatment. Int J Trend Sci Res Dev. (2018) 2:1–21. doi: 10.31142/ijtsrd18476

CrossRef Full Text | Google Scholar

36. Orwa TO, Mbogo RW, Luboobi LS. Multiple-strain malaria infection and its impacts on plasmodium falciparum resistance to antimalarial therapy: a mathematical modelling perspective. Comput Mathem Method Med. (2019) 2019:9783986. doi: 10.1155/2019/9783986

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Annan K. In-host analysis of malaria dynamics in humans. Open J Appl Sci. (2020) 10:191–209. doi: 10.4236/ojapps.2020.105015

CrossRef Full Text | Google Scholar

38. Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. (2002) 180:29–48. doi: 10.1016/S0025-5564(02)00108-6

PubMed Abstract | CrossRef Full Text | Google Scholar

39. La Salle JP. The Stability of Dynamical Systems. Philadelphia, PA: SIAM. (1976). doi: 10.1137/1.9781611970432

CrossRef Full Text | Google Scholar

40. Orwa T, Mbogo R, Luboobi L. Mathematical model for the in-host malaria dynamics subject to malaria vaccines. Lett Biomathem. (2018) 5:222–51. doi: 10.1080/23737867.2018.1526132

CrossRef Full Text | Google Scholar

41. Selemani MA, Luboobi LS, Nkansah-Gyekye Y. On stability of the in-human host and in-mosquito dynamics of malaria parasite. Asian J Mathem Appl. (2016) 2016:1–23.

Google Scholar

42. Anderson RM, May RM. Infectious Diseases of Humans. Oxford UK: Oxford University Press. (1991). doi: 10.1093/oso/9780198545996.001.0001

CrossRef Full Text | Google Scholar

43. Selemani MA, Luboobi LS, Nkansah-Gyekye Y. The in-human host and in-mosquito dynamics of malaria parasites with immune responses. New Trends Mathem Sci. (2017) 5:182–207. doi: 10.20852/ntmsci.2017.196

CrossRef Full Text | Google Scholar

44. Hellriegel B. Modelling the immune response to malaria with ecological concepts: short-term behaviour against long-term equilibrium. Proc R Soc London B. (1992) 250:249–56. doi: 10.1098/rspb.1992.0156

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Chiyaka C, Garira W, Dube S. Modelling immune response and drug therapy in human malaria infection. Comput Math Methods Med. (2008) 9:143–63. doi: 10.1080/17486700701865661

CrossRef Full Text | Google Scholar