- Leibniz Centre General Linguistics, Berlin, Germany
There is a controversial debate about which implicatures are triggered by logically complex sentences. This article introduces a novel experimental paradigm based on a game-theoretic design to test these implicatures. In particular, we investigated two cases adjudicating between different accounts of implicature (“Each girl found some of her marbles” and “Some of the girls found some of their marbles”). The advantage of our paradigm is that we can provide an explicit game-theoretical model of the experimental situation so that participants’ interpretation of test sentences can be read off from their choices between various actions (rather than requiring metalinguistic judgments). The study shows that, in our scenario, strong (embedded) implicatures are drawn reliably. We evaluate the predictions of several structural and game-theoretic accounts for the data and discuss the broader relevance of the findings for theories of implicature and the framework they belong to.
1. Introduction
In this article, we present a novel experimental paradigm to test logically complex sentences containing the implicature trigger “some.” The main contribution is an action-based paradigm which allows us to reason backwards from participant’s action choices to their underlying interpretation of test sentences. Our paradigm is connected to a game-theoretic model as a linking model between pragmatic theory and participants’ behavior in the experiment. Our novel approach avoids many problems of previously used paradigms which require metalinguistic judgments (see Section 3). The second contribution of this article is a novel test case adjudicating between different theories of implicature: embedding of “some” under “some” itself (e.g., “Some of the girls found some of their marbles”). There has been a controversial debate about sentences with multiple scalar terms, and different theories make different predictions about available implicatures. From among the many theories that exist, we focus on those that provide specific enough predictions to be testable in an experimental situation.
All theories agree about the implicatures of “some” in logically simple sentences, as in (1). In this example, it is uncontroversial that the quantifier “some” may give rise to the “some but not all” implicature:
(1) Some of the girls found their marbles.
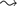 Some but not all found them.
Some but not all found them.
The implicature can be explained from a choice that the speaker made between the quantifiers “some” and “all.” If the speaker had believed that all found their marbles, then he would have said so. This means that the speaker had to make a choice between (1) and the stronger alternative (2):
(2) All of the girls found their marbles.
If it can be assumed that he is honest, cooperative, and knows whether some or all of the girls found their marbles, then the only reason for choosing “some” must be that he believes that not all passed. Hence, it follows from an utterance of (1) that the stronger alternative (2) is false. The inference from some to not all is called a scalar implicature, as the pair ⟨all, some⟩ can be considered a lexicalised scale which is activated by the use of “some” (Horn, 1972; Gazdar, 1979).
In this paper, we are concerned with implicatures triggered by “some” embedded under “all” or “some” itself, as in (3). In contrast to (1), it is much more controversial whether or not they can have an interpretation in which the embedded some has a “some but not all” reading.
(3) a. All of the girls found some of their marbles.
b. Some of the girls found some of their marbles.
If the same reasoning is applied to (3a) as to (1), then it only follows that it is not the case that all of the girls found all of their marbles. One could, however, also assume that (3a) communicates that all found some but not all of their marbles. In the first case, the negation takes scope over the whole “all all” alternative. It is therefore called a global implicature. In the second case, the negation of the stronger “all” alternative applies locally where the implicature trigger “some” occurred.1 It is therefore called a local or embedded implicature. The implicatures corresponding to global and local negation of relevant alternatives are the following:
(4) All of the girls found some of their marbles.
a. Local: All of the girls found some but not all of their marbles.
b. Global: Not all of the girls found all of their marbles.
In the case of (3b), there are more alternative sentences which result from replacing “some” by “all.” The corresponding local and global implicatures are:
(5) Some of the girls found some of their marbles.
a. Local: Some of the girls found some but not all of their marbles.
b. Global: None of the girls found all of their marbles.
The two sentences in (3) show an interesting contrast: for the “all some” sentence the local implicature is stronger than the global implicature, whereas for the “some some” sentence the global implicature (5b) is stronger. As we will see, theories of implicature make different predictions about which interpretation arises in the two sentences.
In this study, the two test sentences in (3) are embedded in a scenario that makes the contrast between different readings relevant. In particular, participants need to choose a set of rewards depending on how many marbles the girls find. To preview our results, in this scenario sentences in which “some” is embedded under “all” receive the strong interpretation in (4a), and sentences in which “some” is embedded under “some” itself the strong interpretation in (5b). Interestingly, the observations neither fit traditional globalist nor localist accounts. Apart from these structural accounts, we will also discuss the predictions of two game-theoretic models by Franke (2009) and Benz (2012b) 2 as well as more recent versions of grammatical accounts. This article is organized as follows. First, we present the theoretical background concerning implicatures of complex sentences. Second, we discuss previous experimental research on embedded implicatures. Then, we present a game-theoretic model for our novel experimental paradigm and the experiment we conducted. Finally, we evaluate the fit of the data to different theories of implicature and discuss the relevance of the findings.
2. Theoretical Approaches to Implicature in Complex Sentences
2.1. Neo-Gricean Reasoning
All theories addressing implicatures of complex sentences in one or the other way generalize or modify the neo-Gricean model of scalar implicature developed by Horn (1972, 1989), Gazdar (1979), and others (see Levinson, 1983 Ch. 3 and Levinson, 2000 for a summary Ch. 2). The two sentences in (3) are two alternative utterances which are generated by replacing “some” and “all” by each other. They are equally complex, and the alternative with “some” is logically weaker than the one with “all.” If the speaker chooses the weaker alternative, then normally the addressee is entitled to infer that the stronger alternative is false. In the neo-Gricean tradition, implicatures are part of communicated meaning but not part of semantic meaning. An argument for them being pragmatic in nature is their cancellability, this means, they can be explicitly negated by the speaker as in “Some, in fact, all of the girls found their marbles.”
For the critical sentences in (3), the neo-Gricean reasoning can be applied without modification. The only difference to (1) is that the scalar terms occur in several positions, and not only in one. The alternatives are again generated by replacing “some” and “all” for each other:
(6) a. ∃-∃: Some of the girls found some of their marbles.
b. ∃-∀: Some of the girls found all of their marbles.
c. ∀-∃: All of the girls found some of their marbles.
d. ∀-∀: All of the girls found all of their marbles.
2.2. Localism vs. Globalism
According to neo-Gricean reasoning, all stronger alternatives are negated. For the sentence “All girls found some of their marbles” the only stronger alternative utterance is that “All girls found all of their marbles” ∀-∀. The negation of this alternative utterance yields the global reading as the only predicted implicature. Hence, for the sentences in (6), the neo-Gricean reasoning is identical to the reasoning in the so-called globalist accounts (Sauerland, 2004; Russell, 2006; Geurts, 2009, 2010).
In localist approaches, alternatives may be alternatives to embedded phrases, and the negation of stronger alternatives is applied locally where alternatives are activated. In Chierchia’s (Chierchia, 2004) recursive version, alternatives are activated lexically whenever the compositional interpretation reached a phrase containing a scalar element, and stronger alternatives were negated by default.
In newer versions of localism (e.g., Fox, 2007; Chierchia et al., 2012; Chierchia, 2013), the embedded implicatures are generated by silent only operators (henceforth O) which can be inserted at phrasal nodes. For example, the interpretation (8) of ∀-∃ is the result of silent only inserted over the quantifier phrase:
(7) All of the girls found O [some of their marbles].
The effect of the operator is to locally negate the stronger alternative “all of their marbles,” and to add it to the compositional meaning. This produces the following local reading:
(8) All of the girls found some but not all of their marbles.
In the localist framework, the global reading is produced by inserting silent only at sentence level. In these accounts, O operators are constituents of the underlying syntax tree, such that the surface form has at least three different interpretations (the local, the global, and the literal reading). As implicatures are fully integrated in syntax and semantics, this kind of approach is called grammatical account.
2.3. Representation of Predicted Readings
In the following, we represent the different readings predicted for our critical sentences. To represent the meaning of sentences, we need a set of possible worlds. The set of worlds that can be distinguished by these sentences can be constructed by the help of the following propositions, where represents “none,” ∃, “some,” ∃! “some but not all,” and ∀ “all”:
(9) a. : Some of the X Ved none of the Y.
b. ∃-∃!: Some of the X Ved some but not all of the Y.
c. ∃-∀: Some of the X Ved all of the Y.
Thereby, our scenario distinguishes between the following seven possible worlds:
| (10) | 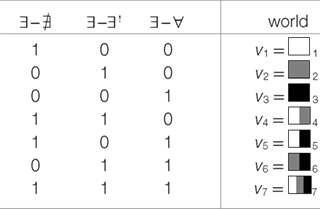 |
The following table shows the predicted readings of ∀-∃ and ∃-∃ according to two traditional structural accounts, Chierchia’s recursive version of localism,3 and Sauerland’s globalist model. We have chosen these two theories as examples of traditional structural accounts since they are the best worked out theories that make precise predictions for our scenario.
| (11) | 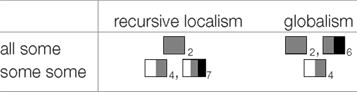 |
The next table shows the different readings of ∀-∃ as predicted by recent grammaticalist versions of localism (Chierchia et al., 2012). The first reading is the literal, the second the local, and the third the global reading of ∀-∃.
| (12) |  |
The next table shows the readings predicted by the grammaticalist version of localism for sentence ∃-∃.4 Every occurrence of O introduces the negation of all stronger alternatives in its scope. As in the case of ∀-∃ in (12), the first line (a) shows the literal reading of ∃-∃, and the last line (e) the global reading. The other readings are local readings predicted by inserting silent O below sentence level. As can be seen, recent grammatical theories predict various different readings.
| (13) | 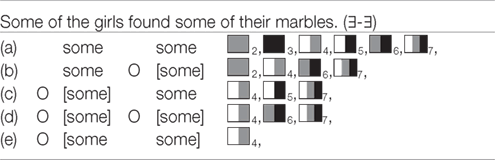 |
The local and global accounts are structural accounts in so far as implicatures are derived from purely structural properties of sentences. The global accounts provide a unique pragmatic interpretation. Newer grammatical accounts, in contrast, predict a wide range of possible readings, as can be seen from (13). A problem that remains unsolved by grammatical accounts is how interpretation in specific utterance situations can be predicted. The reason for this problem can be sought in the lack of an explicit representation of contextual relevance in grammatical accounts.
2.4. Game-Theoretic Accounts
Interactional accounts based on game-theoretic models of communication address this problem, explicitly representing contextual relevance (Franke, 2009; Benz, 2012b). That is, these accounts allow the representation of relevance in terms of speaker and hearer preferences over subsequent acts. Implicature is explained from an optimization of both the speaker’s utterance selection strategy and the hearer’s interpretation strategy. The speaker’s strategy maps semantic messages to utterances, and the hearer’s interpretation strategy utterances to messages. Interactional models, therefore, have to distinguish alternative messages from alternative utterances. Here, we consider two types of approaches, one defines alternative messages from alternative utterances (Franke, 2009), and the other defines alternative utterances from alternative messages (Benz, 2012b).
Iterated Best Response (IBR) models derive implicatures by an iterated learning process involving several rounds of interaction and improvement until speaker and hearer arrive at optimal strategies. It starts with a speaker S0 who arbitrarily chooses true sentences from a set of alternatives to communicate messages. For example, if he wants to communicate { }, he will produce ∀-∃ and ∃-∃ with equal probability. The hearer chooses the interpretation which has the highest likelihood of being the message the speaker intended to convey. For example, when receiving ∀-∃, it is more likely that the speaker meant {
}, he will produce ∀-∃ and ∃-∃ with equal probability. The hearer chooses the interpretation which has the highest likelihood of being the message the speaker intended to convey. For example, when receiving ∀-∃, it is more likely that the speaker meant { } than {
} than { } or {
} or {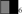 }. Hence, hearer H1 chooses {
}. Hence, hearer H1 chooses {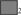 }. In game-theoretic terms, this is the best response to the speaker’s strategy S0 when receiving ∀-∃. Therefore, ∀-∃ implicates that the speaker meant {
}. In game-theoretic terms, this is the best response to the speaker’s strategy S0 when receiving ∀-∃. Therefore, ∀-∃ implicates that the speaker meant {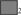 }, and ∃-∃ implicates that he meant {
}, and ∃-∃ implicates that he meant {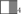 }.
}.
The model in Benz (2012b) explored what can be inferred from an utterance of ∀-∃ or ∃-∃ as constituents of possibly more complex utterances. It assumes a scenario in which the set of possible messages is identical to the set of possible worlds in (10). The alternative utterances are the utterances represented in (9) together with their conjunctions.
Hence, for every message, i.e., possible world, there is an utterance that literally describes it. For example, the message {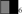 } can be described by ∀–∃ ∧ ∃!–∀ “All girls found some and some but not all girls found all marbles.” The model adds rules which allow the elimination of redundant linguistic material. For example, ∀–∃ ∧ ∃!–∀ may be simplified to ∀–∃ ∧ ∃–∀ by elimination of “but not all.” The restriction “but not all” is redundant because the speaker’s message {
} can be described by ∀–∃ ∧ ∃!–∀ “All girls found some and some but not all girls found all marbles.” The model adds rules which allow the elimination of redundant linguistic material. For example, ∀–∃ ∧ ∃!–∀ may be simplified to ∀–∃ ∧ ∃–∀ by elimination of “but not all.” The restriction “but not all” is redundant because the speaker’s message {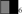 } can still be uniquely recovered from ∀–∃ ∧ ∃–∀. The elimination rules and recoverability constraints are described in more detail in Appendix D. In this model, a sentence implicates a proposition p if p holds true of every speaker message that can be uniquely recovered from an utterance U of which the sentence is a sub-string. For example, ∀–∃ can occur as a conjunct in ∀–∃ ∧ ∃–∀ and in . The recoverable speaker messages are
} can still be uniquely recovered from ∀–∃ ∧ ∃–∀. The elimination rules and recoverability constraints are described in more detail in Appendix D. In this model, a sentence implicates a proposition p if p holds true of every speaker message that can be uniquely recovered from an utterance U of which the sentence is a sub-string. For example, ∀–∃ can occur as a conjunct in ∀–∃ ∧ ∃–∀ and in . The recoverable speaker messages are 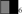 and
and 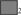 , respectively. Hence, from an occurrence of ∀-∃ as constituent of a larger utterance it can only be inferred that the actual state is an element of {
, respectively. Hence, from an occurrence of ∀-∃ as constituent of a larger utterance it can only be inferred that the actual state is an element of {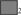 ,
, 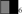 }. The model, therefore, predicts rather weak implicatures for the different alternative utterances.
}. The model, therefore, predicts rather weak implicatures for the different alternative utterances.
The following table in (14) summarizes the implicatures predicted by the two interactional models for ∀-∃ and ∃-∃.
| (14) |  |
3. Previous Experimental Research
Structural theories, as presented in the previous section, do not immediately tell us how to test for implicature in complex sentences. For Griceans, implicature are subject to a number of constraints, for example, they have to be relevant to be drawn. Game-theoretic accounts, in turn, allow the representation of relevance in terms of speaker and hearer preferences over subsequent acts, the choice of which depends on the interpretation of speaker utterances. This will play an essential role in the experimental design proposed in the next section. In this section, we discuss previous experiments on implicatures of complex sentences, and, in particular, the methodological issues raised by them. As we will see, the issue of context dependence also plays a central role for the interpretation of these experiments. Of the two critical sentences of our study, previous experiments only considered the “all–some” sentence (∀-∃). In our overview, we will concentrate on this condition.
Among the first experiments testing embedded implicatures were Geurts and Pouscoulous (2009) and Chemla (2009). These experiments tried to prove or disprove that embedded implicatures exist, i.e., that there is a significant proportion of subjects that infer embedded local implicatures. Geurts and Pouscoulous (2009) used a picture-verification task in conjunction with sentences like “All squares are connected with some of the circles.”5 Specifically, participants had to judge whether the sentence was true or false in the scenario represented by the picture, which contradicted the local implicature. In this setup, none of the participants rejected the sentence with the embedded implicature trigger. Following up on this paradigm, Benz and Gotzner (2014) found that there was a general bias for participants to interpret sentences literally. Hence, the absence of local readings in the picture-verification paradigm by Geurts and Pouscoulous (2009) may be a floor effect.
The study by Chemla (2009) employed an inferential task, for example, subjects had to indicate whether they can infer from the utterance “Everyone remembered some of the dates that No one remembered all the dates.” Chemla provided participants with general contexts, for instance, that students had 20 historical dates to remember in a surprise exam and the teacher utters the sentence after having corrected the copies. The proportion of subjects inferring the embedded implicature for the everyone–some sentence was about 40% (Chemla, 2009). Although it can be argued that Chemla’s study showed that some subjects infer embedded implicature, it does not show that they can be reliably communicated. Furthermore, there is a worry about the general context provided by Chemla that may have contributed to a reduction of inferred local implicature. In the given example, it remains open whether the teacher’s utterance was intended to tell each individual student how he performed, or whether it was intended as a summary statement. In the former case, the performance of every single student is relevant, and, hence, also whether every student remembered some and not all of the historical dates. In the latter case, it may be enough to provide a lower bound on their performance. As it remains open what kind of context obtains, a rational subject should answer that it is not possible to infer from “Everyone remembered most of the dates” that no student remembered all dates.
Clifton (2010) followed up on the study by Geurts and Pouscoulous (2009) with a picture matching task. They found that when participants were presented with a choice between a picture satisfying the local or the global reading, they showed a preference for the former. They conclude that the picture-verification paradigm by Geurts and Pouscoulous underestimates embedded implicatures. Finally, Chemla and Spector (2011) modified the picture-verification task by Geurts and Pouscoulous (2009) by introducing gradient judgments. Critically, they compared truth value judgments for four picture conditions representing (a) the local reading, (b) the global reading, (c) the literal reading, and (d) a false control. The finding was a gradient response pattern among these four conditions such that subjects rated the sentence best if the picture satisfied the local reading, which is also consistent with the global and literal readings. Chemla and Spector took this gradient pattern as evidence that embedded implicatures exist.
The studies by Clifton (2010) and Chemla and Spector (2011) have been heavily criticized in Geurts and van Tiel (2013) who argued that the effects measured are not due to local implicatures but to typicality effects. That typicality plays a role in such pictorial setups was also shown experimentally by van Tiel (2014). It is not the place here to discuss the arguments further as they are of no consequence to our own experiment. It suffices to say that the methodological issues raised against Clifton (2010) and Chemla and Spector (2011) render it unclear how to evaluate their results. Nevertheless, it should be noted that the gradient response pattern found by Chemla and Spector (2011) has recently been replicated by Potts et al. (2016) with more natural stimuli as well as by Gotzner and Romoli (2017) with an inferential task, which is less prone to typicality effects. Most importantly, all of the studies carried out so far only show that local readings exist to a certain degree or are drawn by a subset of the population. No study to date has shown that embedded implicatures are reliably communicated in a context that makes different readings contextually relevant.
4. The Best Response Approach: Model of Experimental Situation
4.1. Core Assumptions
Grice considered conversational implicatures to be part of communicated meaning. This means, in particular, that it becomes part of the common ground that the speaker meant to communicate them. Implicatures follow from (a) the fact that the speaker chose a certain utterance and (b) the assumption that he followed certain conversational maxims and the cooperative principle. Scalar implicatures, in particular, are based on the quantity maxim. The quantity maxim is only one maxim among others, and all the maxims are subordinated to Grice’s cooperative principle “Make your conversational contribution such as is required, at the stage at which it occurs, by the accepted purpose or direction of the talk exchange in which you are engaged” (Grice, 1989). Following Grice, one should, therefore, expect that an implicature can only arise if there is a recognizable purpose or direction to which the speaker’s utterance is subordinated, and to which the implicature is relevant.
To encourage the computation of embedded implicatures, we devised a scenario in which Grice’s purpose or direction of the talk exchange is provided by an explicit decision problem. In our experimental scenario, there are four sisters who each own a set of four special edition marbles. The marbles get lost during play, and in the end they have to find them again. Their mother promises them a reward depending on how many marbles they find. A girl gets (i) chocolate if she finds all 4 of her marbles, (ii) candy if she finds fewer than 4 of her marbles, and (iii) a gummy bear when she finds none of her 4 marbles (as a consolation prize). Participants receive a statement by the mother about how many of the marbles the girls have found. Then, their task is to buy the sweets for the girls. For example, if the mother says “No girl found any of her marbles,” then subjects should only buy gummy bears. In our scenario, the subjects’ decision problem is to decide which sweets to buy.
The mother knows the actual world and provides information to the addressee, i.e., the test subjects. It can also be assumed that subjects take the mother to be truthful and cooperative. The subjects can choose between 23 = 8 actions, namely buying one, several, or none of the following sweets:
(15) a.  : Gummy bear b.
: Gummy bear b.  : Candy c.
: Candy c.  : Chocolate
: Chocolate
We use stylized bar charts as representation of possible combinations. Each of the combinations is one action, for example:
(16) a.  : gummy bears and chocolate, no candies
: gummy bears and chocolate, no candies
b.  : candies and chocolate, no gummy bears
: candies and chocolate, no gummy bears
c.  : candies, no gummy bears or chocolate.
: candies, no gummy bears or chocolate.
With respect to participants’ task, two concrete situations v and w can be considered equivalent, if each action is equally useful in both situations. There are seven possible worlds which we need to distinguish, depending on the proportions of girls which have found none, some, or all of their marbles. They are the same worlds as those introduced in (10). The reward system guarantees that meaning differences distinguishing between individual worlds are all relevant. For convenience, we repeat the definition of the seven possible worlds from (10):
| (17) | 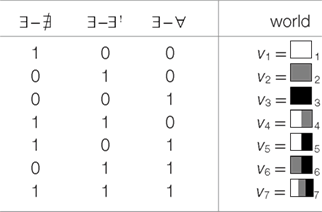 |
The communicative situation of the scenario has the structure of a signaling game (Lewis, 1969). The design is therefore based on a game-theoretic model. It is not necessary to introduce game theory in this section. It is, however, necessary to understand how the subjects’ interpretation of an utterance can be inferred from their choice of actions. Let us consider the sentence “Each of the girls found some of her marbles.” Literally this sentence means that the actual world is an element of {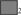 ,
,  ,
,  }. Hence, to be certain that the mother can give each of the girls the right reward, candies and chocolate have to be bought, but no gummy bears. If, however, the addressee interprets the sentence with an embedded implicature, then she must assume that the actual world is
}. Hence, to be certain that the mother can give each of the girls the right reward, candies and chocolate have to be bought, but no gummy bears. If, however, the addressee interprets the sentence with an embedded implicature, then she must assume that the actual world is  . Hence, she should only buy candy.
. Hence, she should only buy candy.
We first show which action combinations are optimal in the different possible worlds. Fortunately, this is easy to see, as the following table shows:
| (18) | 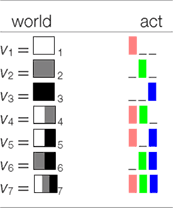 |
To know what is best in the various possible worlds is, however, not enough. We also have to know what the best choice is given an information state in which it is uncertain what the actual world is. This can also be inferred easily from the color coding that we used. For the following information states it is optimal to choose two kinds of sweets:
| (19) | 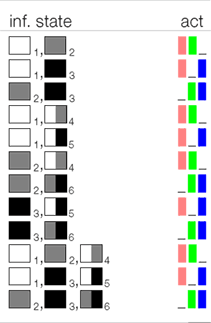 |
For all other information states, the best choice is  , that is buying all types of sweets. Note that the optimal behavior is to buy sweets if they might be needed, that is buying too few sweets is disadvantageous (see the Supplementary Material for a discussion of this point).
, that is buying all types of sweets. Note that the optimal behavior is to buy sweets if they might be needed, that is buying too few sweets is disadvantageous (see the Supplementary Material for a discussion of this point).
The addressee makes his or her choice after hearing the mother’s utterance. The interpretation of this utterance is the same as the information state. In the context of signaling games, the optimal choice in response to a previously received message is called a “best response.” For that reason, we call our paradigm best response paradigm.
If a certain choice of action is observed, it can be read off from the tables in (18) and (19) how the hearer could have interpreted the mother’s utterance. If she uttered “All girls found some of their marbles,” then observing choice  , it follows that the hearer must believe that the mother meant
, it follows that the hearer must believe that the mother meant 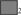 . If we observe the choice of
. If we observe the choice of  , then the hearer may be in one of five different information states. In the case of our second test sentence “Some of the girls found some of their marbles,” there remain two possible information states that are consistent with its semantic meaning: {
, then the hearer may be in one of five different information states. In the case of our second test sentence “Some of the girls found some of their marbles,” there remain two possible information states that are consistent with its semantic meaning: {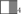 } and {
} and {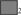 ,
, 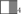 }.
}.
4.2. Action Choice Predicted by Different Theories
From the tables in (18) and (19), we can also read off which actions the addressee should choose according to the theoretical models. The predicted interpretation and the associated best choices are shown in (20).
| (20) | 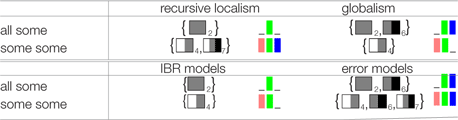 |
We can also see that, although a choice of  is a best response to the “some some” sentence for two information states, only one of them is predicted by any of the theories. This means that the two test sentences can single out one of the theories as fitting best to the data.
is a best response to the “some some” sentence for two information states, only one of them is predicted by any of the theories. This means that the two test sentences can single out one of the theories as fitting best to the data.
The grammatical version of localism (e.g., Fox, 2007; Chierchia et al., 2012; Chierchia, 2013) has two main problems with our scenario. As we have seen in Section 2, grammatical theories predict at least five different readings for ∃-∃: (a) some some, (b) some O [some], (c) O [some] some, (d) O [some] O [some], and (e) O [some some]. From (13), we can see that the best response to (a) to (d) is the choice of  , and that to (e) is
, and that to (e) is  . Since the theory confines itself to describing possible meanings in pure compositional grammar, it is not obvious how to apply it to our scenario. One reasonable assumption is that each test subject chooses one of the grammatical readings (a) to (e), and then makes her decision about the sweets.6 Let a be the proportion of subjects choosing interpretation (a), b the proportion choosing (b), etc. If α is the proportion of subjects choosing
. Since the theory confines itself to describing possible meanings in pure compositional grammar, it is not obvious how to apply it to our scenario. One reasonable assumption is that each test subject chooses one of the grammatical readings (a) to (e), and then makes her decision about the sweets.6 Let a be the proportion of subjects choosing interpretation (a), b the proportion choosing (b), etc. If α is the proportion of subjects choosing  , β the proportion choosing
, β the proportion choosing  , and γ the proportion choosing
, and γ the proportion choosing  , then, as each subject has to choose one interpretation of (a) to (e), it follows that α = a + b + c + d + e = 1 = β, and that γ = 1 − e. All theories agree that ∃-∃ implicates that some girls found none and that not all found all of their marbles. Hence, according to all theories, subjects should choose gummy bears and candy, and hence predict that α = β = 1. Therefore, the only value relevant to a comparison is the value of γ. However, any value of γ is consistent with the grammatical account. This means that the account cannot make any testable prediction about the outcome of our experiment. We return to this point in the general discussion.7
, then, as each subject has to choose one interpretation of (a) to (e), it follows that α = a + b + c + d + e = 1 = β, and that γ = 1 − e. All theories agree that ∃-∃ implicates that some girls found none and that not all found all of their marbles. Hence, according to all theories, subjects should choose gummy bears and candy, and hence predict that α = β = 1. Therefore, the only value relevant to a comparison is the value of γ. However, any value of γ is consistent with the grammatical account. This means that the account cannot make any testable prediction about the outcome of our experiment. We return to this point in the general discussion.7
5. The Best Response Experiment
5.1. Methods
5.1.1. Participants
Participants were recruited on Amazon’s Mturk platform in two survey versions with different orders. Only participants with US IP addresses were allowed to take part in the experiment and participants were further screened for native language. In total, 40 native English speakers (mean age: 33.77, 21 females, 19 males) took part in the experiment. All participants answered the control questions correctly and gave consistent responses in the filler items. Hence, we included all 40 participants in the analysis of the data.
The experiments were conducted in accordance with the ethics policy of the Deutsche Forschungsgemeinschaft (DFG) under approval of grant Nr. 01UG1411. Since the study involved a healthy adult population no ethics consent was required according to institution’s guidelines and national regulations. Participant’s consent was obtained by virtue of survey completion and their data were fully anonymized.
5.1.2. Scenario and Task
Participants in our experiment were presented with a scenario involving four sisters who each own a set of four special edition marbles (a scenario introduced by Degen and Goodman (2014) which we extend with an action-based task). While the girls are playing the marbles get lost and they have to find them again. Participants in our experiment were told that the mother of the girls wants to reward her girls depending on how many marbles they find. In particular, participants were presented with the following reward system in the instructions (all instructions are found in Appendix A):
A girl gets:
• chocolate if she finds all 4 of her marbles
• candy if she finds fewer than 4 of her marbles
• a gummy bear when she finds none of her 4 marbles (as a consolation prize).
Participants’ task is to buy sweets for the four girls depending on the statement the mother utters. In the instructions, we gave participants an example statement, telling them that if the mother says “No girl found any of her marbles” they should only buy gummy bears. After participants had read the instructions, they were asked control questions about the number of marbles each girl owns and which reward type a girl gets depending on how many marbles she found.
5.1.3. Experimental Items
In the main part of the experiment, participants were asked to give binary responses (YES/NO) for each of the three types of sweets: chocolate, candy, and gummy bears. In our critical test sentences, some was embedded under each and under some itself, repeated below. Our two critical conditions were shown twice in the experiment.
(21) a. Each of the girls found some of her marbles.
b. Some of the girls found some of their marbles.
An example experimental trial with each-some and a possible response choice is presented in (22). Participants had to check one of two radio buttons for each type of sweets.
| (22) |  |
We further included a control item with the sentence “Each girl found some and possibly all of her marbles” in the middle of the experiment. In this control item, participants should choose both candy and chocolate since the statement makes the upper bound relevant. In addition, we included seven other filler items (for example, the sentence “Each girl found all marbles”). Hence, each participant saw 12 items in total. We created two different lists randomizing the order of presentation of items. Appendix B presents a list of all experimental items.
5.2. Results
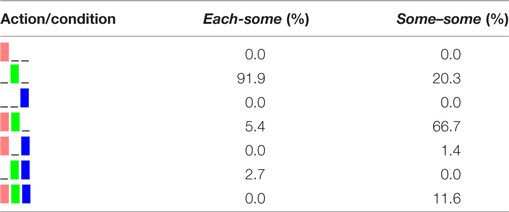
Figure 1 shows the mean percentage of YES responses across critical conditions for each reward type. If participants did not buy chocolate, they have computed the strong inference that no girl found all of her marbles. In the condition with “each-some” 4% of the participants bought chocolate and 12% in the case of some-some. Table 1 details the percentages of each combination of action choices per condition.
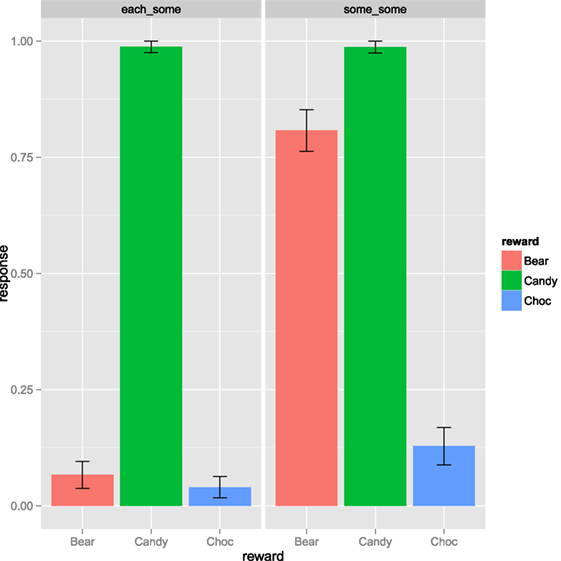
Figure 1. Experiment 1: % YES responses for sentence (25)-a (each-some, left column) and (25)-b (some-some, right column). The colors mark different reward types (gummy bears “none” = red, candy “some” = green, chocolate “all” = blue). Error bars represent SEM.
We computed a Fisher’s exact test on the contingency table presented in 1 which showed a significant difference across conditions (p < 0.0001). In Table A1 in Appendix, we present an additional analysis of the data comparing the individual choice of each sweet type across conditions.
In the control item with the sentence “Each girl found some and possibly all of her marbles” 92% of the participants bought both candy and chocolate (which differed significantly from the choice of sweets in the each-some condition, p < 0.0001). This indicates that when participants are uncertain whether a girl found some or possibly all marbles, they choose both types of candy to be on the safe side. In turn, in the critical items with some the majority of participants did not buy chocolate. Hence, participants ruled out the possibility that a girl found all marbles in these utterances.
5.3. Discussion
In our experiment, we wanted to find out whether strong implicatures triggered by embedded “some” are reliably drawn if the pragmatic conditions are appropriate. The results shown in Figure 1 and Table 1 indicate that participants infer the strong implicature that no girl found all marbles both when “some” is embedded under each as well as when it is embedded under “some” itself. In the first case, it results from an embedded local implicature (each some but not all), in the second from a global implicature (not some all).
A potential concern with the methodology we used here is that participants refuse to buy chocolate because they are uncertain whether they indeed need this type of sweet.8 However, according to this logic participants should also show inconsistent responses in their other actions (e.g., in the filler items). Moreover, our control item “Each girl found some and possibly all of her marbles” indicated that participants bought both chocolate and candy when it was unclear whether a girl may have found all marbles. This control condition strengthens the conjecture that in the critical sentences participants refused the reward type chocolate because they computed the inference that no girl found all of her marbles.
Another potential concern is the remaining variation in the response patterns. The predictions of the theories that we consider are categorical, yet, as we can see, participant’s overall responses were not always at 100 or 0%. Part of this is certainly due to noise typically observed in experimental setups. However, in the case of “some-some” sentences, there was a substantial number of participants not choosing gummy bears (20%), that is these participants did not infer that there was a group of girls which found none of their marbles (not all some). This observation about some-some sentences is, however, in conflict with all theories, as all of them predict that the unembedded some implicates that not all found some marbles. The utterance may seem under-informative to subjects, such that they may want to react with a clarification request. However, this is not possible in our experimental set up. Whether the observed deviation from 100% for gummy bears has a deeper meaning for pragmatic theory is an issue that has to be left to future research. In the comparison of theories presented in the next section, this deviation can be disregarded since all theories made the same prediction that gummy bears are required.
In summary, our new best response paradigm yields a high rate of embedded implicatures in a scenario where the different readings of sentences are relevant to a subsequent action selection task. It achieves this in a setting that mirrors natural language comprehension, without requiring any metalinguistic judgments from participants.
6. Evaluation of Results
As mentioned earlier, the two test sentences (23a) and (23b) can differentiate between all four theories which we are about to compare.
(23) a. Each of the girls found some of her marbles.
b. Some of the girls found some of their marbles.
The results shown in Figure 1 are: for (23a) subjects chose  , i.e., candy and neither gummy bears nor chocolate, and for (23b) subjects overwhelmingly chose
, i.e., candy and neither gummy bears nor chocolate, and for (23b) subjects overwhelmingly chose  , i.e., candy and gummy bears but no chocolate. We first note that the possibility that subjects interpret literally can be excluded, as the following table shows:
, i.e., candy and gummy bears but no chocolate. We first note that the possibility that subjects interpret literally can be excluded, as the following table shows:
| (24) |  |
The predictions of the recursive localist model of Chierchia (2004), the globalist model of Sauerland (2004), and the game-theoretic interactional models of Franke (2009) and Benz (2012b) were shown in (20). We repeat this table together with the observed distributions of action choices in (25).
| (25) | 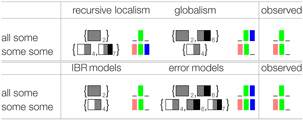 |
As we can see, Franke’s IBR model fits best to the data qualitatively. Chierchia’s recursive version of localism makes a too weak prediction for (23b), and the globalist model of Sauerland a too weak prediction for (23a). The predictions of Benz’s model are too weak for both test sentences.9 Chierchia’s and Sauerland’s theories of implicatures also allow for the cancelation of implicatures. However, cancelation can only lead to weaker interpretations, and therefore does not improve their fit to the observed data.
In Section 4, we have already shown why grammatical versions of localism do not make specific enough predictions for our scenario since, essentially, they predict the sentences to be highly ambiguous. One way to go about this problem is to amend grammatical theories with the Strongest Meaning Hypothesis such that participants adopt the strongest reading for both test sentences (see especially Chierchia et al. (2012) for such an argument). However, other experiments have shown that participants do not always compute a strong implicature (e.g., Geurts and Pouscoulous, 2009), as would be predicted by the Strongest Meaning Hypothesis. Hence, this hypothesis cannot be valid independently of contexts and, thereby, constitutes just another degree of freedom in grammatical accounts. Therefore, even with the Strongest Meaning Hypothesis, an additional linking model to predict participants’ action choices in our experimental scenario is needed.
Game-theoretic models, in turn, explicitly represent contextual relevance and predict utterance interpretation to be dependent on the interaction between hearer and speaker. Crucially, the interpretation of an utterance in a given context will also depend on which utterances can be produced in that context. In the following, we have a closer look at IBR and error models. As we have seen, Franke’s IBR model correctly predicts the subjects’ choice of sweets for both test sentences. There is, however, a problem if we go beyond the two test sentences and consider the test scenario as a whole. In a game-theoretic model, one has to define not only alternative utterance between which the speaker can choose but also alternative messages that he may want to communicate. Franke, in his (Franke, 2009) model, first constructs alternative utterances on the basis of the actual utterance using Horn scales as in structural theories, and then, on the basis of these alternative utterances, he constructs the alternative messages. This construction provides a set of alternative messages consisting of { }, {
}, { }, {
}, {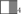 }, {
}, {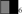 } and {
} and { ,
, 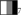 }. However, the real set of alternative messages consists of {
}. However, the real set of alternative messages consists of { } to {
} to {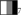 }, as defined in (10). Hence, the IBR model, as set up in Franke (2009), does not provide an exact representation of the experimental situation. As it explains implicature from the assumption that interlocutors converge on an efficient mapping between alternative messages and alternative utterances, the size and content of these sets matters.
}, as defined in (10). Hence, the IBR model, as set up in Franke (2009), does not provide an exact representation of the experimental situation. As it explains implicature from the assumption that interlocutors converge on an efficient mapping between alternative messages and alternative utterances, the size and content of these sets matters.
An important question is how significant these results are to the general frameworks to which the models belong. Although the model of Benz (2012b) fares worst among those compared, it can be modified easily to fit the data, as explained in Appendix D. Franke’s (Franke, 2009) model is already consistent with the results but could be improved with respect to fit to the experimental situation. However, even if it had been found to be inconsistent with the data, this would have hardly counted as a disprove of the general principle of equilibrium selection by iterated best responses. Furthermore, there are newer players in the field, namely Bayesian accounts (Frank and Goodman, 2012; Bergen et al., 2016; Potts et al., 2016), that share the basic ideas of IBR approaches developed by Franke and Jäger (2014), but promise even more fine-grained representations of probabilistic decision making. It has yet to be shown how easily these approaches can be adapted to the specific scenario that we have tested here. In this respect, our experiment provides an interesting test for refinements of interactional models. For structural accounts of implicature, it may be considerably harder to adapt them to our scenario. These accounts have obvious problems making context-specific predictions about implicature. A comparison of the scenario of this study, which reliably produced embedded implicatures, with the experiments by Geurts and Pouscoulous (2009), which produced no embedded implicature, shows that context-specific models are needed.
7. Conclusion
Our study demonstrated that contexts exist in which strong implicature of the type “all some” 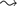 “all some but not all” are part of communicated meaning, thereby verifying one of Grice’s core requirements for being an implicature. We introduced an experimental scenario in which the utterance interpretation is relevant to subsequent actions. The scenario has the structure of a signaling game starting with one of the seven possible worlds
“all some but not all” are part of communicated meaning, thereby verifying one of Grice’s core requirements for being an implicature. We introduced an experimental scenario in which the utterance interpretation is relevant to subsequent actions. The scenario has the structure of a signaling game starting with one of the seven possible worlds to
to 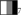 , then the mother choosing an utterance, and finally the subject choosing the kinds of sweets which are needed as rewards. An underlying assumption is that the test subject’s choice is always a best response, i.e., the best action given her information state after interpreting the mother’s utterance. What this model leaves open is how the utterances are interpreted. As we have seen, our experimental data allowed us to read off this information from the participants’ choice of sweets. Finally, we could use this information to test the predictions of four models: Chierchia’s early recursive version of localism (Chierchia, 2004), Sauerland’s globalist theory (Sauerland, 2004), Franke’s iterated best response model (Franke, 2009, 2011), and Benz’s error model (Benz, 2012b). Of these theories, Franke’s model is the only one that is consistent with the experimental results. Furthermore, we have discussed the issues newer grammatical accounts face with our experimental scenario.
, then the mother choosing an utterance, and finally the subject choosing the kinds of sweets which are needed as rewards. An underlying assumption is that the test subject’s choice is always a best response, i.e., the best action given her information state after interpreting the mother’s utterance. What this model leaves open is how the utterances are interpreted. As we have seen, our experimental data allowed us to read off this information from the participants’ choice of sweets. Finally, we could use this information to test the predictions of four models: Chierchia’s early recursive version of localism (Chierchia, 2004), Sauerland’s globalist theory (Sauerland, 2004), Franke’s iterated best response model (Franke, 2009, 2011), and Benz’s error model (Benz, 2012b). Of these theories, Franke’s model is the only one that is consistent with the experimental results. Furthermore, we have discussed the issues newer grammatical accounts face with our experimental scenario.
Previous experimental studies (Geurts and Pouscoulous, 2009; Clifton, 2010; Chemla and Spector, 2011), motivated by grammatical accounts tried to find evidence for local implicatures generated by the sentences alone without contextual support. They therefore tried to create neutral contexts which are not influenced by extra-linguistic factors. It has been argued that the evidence for local implicature claimed by some of the studies may be explained as a typicality effect (van Tiel, 2014), and hence not as evidence for implicature. Furthermore, the idea of a neutral context may itself be problematic, as the discussion of Geurts and Pouscoulous (2009) study in Benz and Gotzner (2014) shows. It seems better to have control over the context by providing it explicitly in the experimental scenario since participants can always construct a context on the fly. However, the point we make here is not about which paradigm should be preferred. This depends on the nature of the research question and we pursued a different question than previous studies: we did not ask whether the pure linguistic material of complex sentences triggers local readings in some subjects but whether there are contexts in which they occur as part of communicated meaning, i.e., whether there are contexts in which they are reliably drawn.
There are two obvious questions raised by our study which we have to leave to future research. First, what are the exact parameters on which the reliable drawing of strong implicature depends? The neo-Gricean literature knows several constraints that must be satisfied for implicatures to be drawn: the speaker must know the actual state of the world, speaker and hearer must be cooperative, all additionally implicated information must be contextually relevant, and all these conditions must be common knowledge. In our scenario, we created a context in which these conditions are satisfied. So, a natural question is whether they are indeed all necessary. Another further question is second, what are the utterances and implicatures that would be generated in the other five possible worlds besides 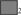 and
and 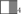 ?
?
We hope that our article also demonstrated the advantage of having an explicit model of the experimental situation. A common issue in psycholinguistic research is the linking of theory to the experimental task. This linking is much facilitated by the availability of a model. This also generates stronger requirements for the theories which have been put forward. As we have seen, the newer grammatical approach, which dominates much of the theoretical debate, is not able to make any prediction in a concrete scenario as the one used in our experiments. We therefore recommend theories which explicitly model contextual factors and thereby make specific predictions for utterance interpretation in a given context. Game-theoretic approaches, as we have seen, fare pretty well in this respect. What is more, they make their predictions on the basis of models of the utterance situation, and not only say how utterances should be interpreted but also which utterances should be produced.
Ethics Statement
At the time of commencement of the study, ethical approval was not required for this study design according to the local legislation.
Author Contributions
NG prepared the final revision of the paper. AB developed the game-theoretic model of the experimental situation and evaluated the fit of the data to different theories. The first draft of the paper, except for Section 5, was written by AB. Both authors edited the paper and share responsibility for all parts.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This work was supported by the Bundesministerium für Bildung und Forschung (BMBF) (Grant Nr. 01UG1411) and the Deutsche Forschungsgemeinschaft (DFG) as part of the Priority Program SPP 1727 “Xprag.de: New pragmatic theories based on experimental evidence” (Grant Nr. BE 4348/4-1).
Supplementary Material
The Supplementary Material for this article can be found online at https://www.frontiersin.org/articles/10.3389/fcomm.2017.00021/full#supplementary-material.
Footnotes
- ^If one gives up the restriction that global negation can only be applied to logically stronger alternatives, the local reading (4a) can be derived by global negation of Some of the girls found all of their marbles (Chemla and Spector, 2011). However, this generalization is hardly acceptable from a Gricean perspective.
- ^At the time of writing this article, the Bayesian accounts of Bergen et al. (2016) and Potts et al. (2016) had not been published and are therefore not included in this discussion.
- ^For the sentence ∃-∃, Chierchia (2004) predicts two local implicatures. The lower “some” produces an embedded “some but not all.” The higher “some” embeds the strong meaning and, in addition, negates the stronger alternative which is built relative to the weak semantic meaning (see Chierchia, 2004) for details and a similar example involving “or.”
- ^In principle, there are also O [some O [some]], O [O [some] some], and O [O [some] O [some]]. However, they do not produce truth-conditionally different readings.
- ^Geurts and Pouscoulous (2009) also did an experiment with an inferential task in which about half of the participants adopted the local reading. However, they argued that the inferential task produced an inflated number of implicatures.
- ^If one assumes that addressees do not choose a unique interpretation but only assign probabilities to (a)–(e), the argument does not change significantly.
- ^Finally, we should also mention the discourse structural account of Asher (2013), who derives embedded implicature from coherence relations. We leave this account out of consideration as the experimental situation that we consider lacks the rhetorical structure that would allow us to derive implicatures from this theory.
- ^In general, it would be desirable to test multiple scenarios in future experiments to exclude that observed response patterns are based on idiosyncratic properties of the scenario.
- ^See, however, Appendix D for a suggestion of how to revise it to fit the data as well as the experimental scenario.
References
Asher, N. (2013). Implicatures and discourse structure. Lingua. 132, 13–28. doi: 10.1016/j.lingua.2012.10.001
Benz, A. (2012a). Errors in pragmatics. J. Logic Lang. Info. 21, 97–116. doi:10.1007/s10849-011-9149-6
Benz, A. (2012b). “Implicatures of complex sentences in error models,” in Practical Theories and Empirical Practice, ed. A. Schalley (Amsterdam: John Benjamins), 273–306.
Benz, A., and Gotzner, N. (2014). “Embedded implicatures revisited: issues with the truth-value judgment paradigm,” in Proceedings of the Formal & Experimental Pragmatics Workshop, eds J. Degen, M. Franke, and N. D. Goodman (Tübingen), 1–6.
Bergen, L., Levy, R., and Goodman, N. D. (2016). Pragmatic reasoning through semantic inference. Semant. Pragmat. 9, 20. doi:10.3765/sp.9.20
Chemla, E. (2009). Universal implicatures and free choice effects: experimental data. Semant. Pragmat. 2, 1–33. doi:10.3765/sp.2.2
Chemla, E., and Spector, B. (2011). Experimental evidence for embedded scalar implicatures. J. Semant. 28, 359–400. doi:10.1093/jos/ffq023
Chierchia, G. (2004). “Scalar implicatures, polarity phenomena, and the syntax/pragmatics interface,” in Structures and Beyond, ed. A. Belletti (Oxford: Oxford University Press), 39–103.
Chierchia, G. (2013). Logic in Grammar: Polarity, Free Choice, and Intervention. Oxford: Oxford University Press.
Chierchia, G., Fox, D., and Spector, B. (2012). “Scalar implicature as a grammatical phenomenon,” in Semantics: An International Handbook of Natural Language Meaning, Vol. 3, eds C. Maienborn, K. von Heusinger, and P. Portner (Berlin: De Gruyter Mouton), 2297–2331.
Clifton, C. Jr., and Dube, C. (2010). Embedded implicatures observed: a comment on Geurts and Pouscoulous (2009). Semantics and Pragmatics 3, 1–13. doi:10.3765/sp.3.7
Degen, J., and Goodman, N. D. (2014). “Lost your marbles? The puzzle of dependent measures in experimental pragmatics,” in Proceedings of the 36th Annual Conference of the Cognitive Science Society, eds P. Bello, M. Guarini, M. McShane, and B. Scassellati 397–402.
Fox, D. (2007). “Free choice and the theory of scalar implicatures,” in Presupposition and Implicature in Compositions Lsemantics, eds U. Sauerland, and P. Stateva (Basingstoke: Palgrave Mcmillan), 71–120.
Frank, M. C., and Goodman, N. D. (2012). Predicting pragmatic reasoning in language games. Science 336, 998. doi:10.1126/science.1218633
Franke, M. (2009). Signal to Act: Game Theory in Pragmatics. PhD thesis, Amsterdam: Universiteit van Amsterdam. ILLC Dissertation Series DS-2009-11.
Franke, M. (2011). Quantity implicatures, exhaustive interpretation, and rational conversation. Semant. Pragmat. 4, 1–82. doi:10.3765/sp.4.1
Franke, M., and Jäger, G. (2016). Probabilistic pragmatics, or why Bayes’ rule is probably important for pragmatics. Zeitschrift für Sprachwissenschaft. 35, 3–44. doi:10.1515/zfs-2016-0002
Gazdar, G. (1979). Pragmatics: Implicature, Presupposition, and Logical Form. New York: Academic Press.
Geurts, B. (2009). Scalar implicatures and local pragmatics. Mind Lang. 24, 51–79. doi:10.1111/j.1468-0017.2008.01353.x
Geurts, B., and Pouscoulous, N. (2009). Embedded implicatures? Semant. Pragmat. 2, 1–34. doi:10.3765/sp.2.4
Gotzner, N., and Romoli, J. (2017). The scalar inferences of strong scalar terms under negative quantifiers and constraints on the theory of alternatives. J. Semantics. doi:10.1093/jos/ffx016
Horn, L. R. (1972). On the Semantic Properties of the Logical Operators in English. PhD thesis, Bloomington: Indiana University.
Levinson, S. C. (2000). Presumptive Meanings: The Theory of Generalized Conversational Implicatures. Cambridge, MA: MIT Press.
Potts, C., Lassiter, D., Levy, R., and Frank, M. C. (2016). Embedded implicatures as pragmatic inferences under compositional lexical uncertainty. J. Semant. 33, 755–802. doi:10.1093/jos/ffv012
Russell, B. (2006). Against grammatical computation of scalar implicatures. J. Semant. 23, 361–382. doi:10.1093/jos/ffl008
Sauerland, U. (2004). Scalar implicatures in complex sentences. Linguist. Philos. 27, 367–391. doi:10.1023/B:LING.0000023378.71748.db
van Tiel, B. (2014). Quantity Matters: Implicatures, Typicality and Truth. PhD thesis, Nijmegen: Radboud Universiteit Nijmegen.
Appendix
A. Instructions
Ann, Kate, Sue, Mary are sisters. They are really into collecting marbles. Each of the sisters has a set of 4 special edition marbles. While the girls are playing, their rooms often get messy and they lose their marbles. As their mother really wants her girls to tidy their rooms she has decided to reward them if they find their marbles. A girl will get
• chocolate if she finds all 4 of her marbles
• candy if she finds fewer than 4 of her marbles
• a gummy bear if she finds none of her 4 marbles as a consolation prize.
In this experiment you will read sentences that were uttered by the mother after she checked the marble bags. The mother sends you to buy sweets for her girls. For example, she may tell you that none of the girls found any of her marbles, in which case you should only buy gummy bears. Please keep in mind that one girl can only get one reward.
Before you begin the experiment, please answer the following question: How many special edition marbles does each sister own? ___
What reward will a girl get when she has found….
all 4 of her marbles? ___
fewer than 4 of her marbles? ___
none of her 4 marbles? ___
B. List of Experimental Items
i. Some of the girls found some of their marbles
ii. No girl found any of her marbles
iii. Each girl found some of her marbles
iv. Only Sue found some of her marbles
v. Sue and Mary did not find any of their marbles
vi. No girl found all of her marbles
vii. Kate found some of her marbles
viii. Each girl found some and possibly all of her marbles
ix. Each girl found some of her marbles
x. Each girl found all of her marbles
xi. Some of the girls found some of their marbles
xii. Exactly one girl found some of her marbles.
C. Additional Analyses
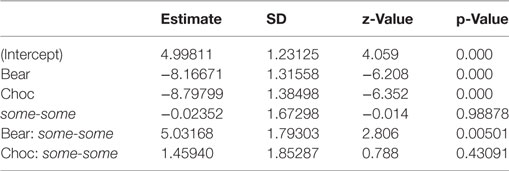
Our dependent variable was binary (choice of sweet: 1 or 0). We therefore computed a logit mixed effects model including the fixed factors quantifier condition (each-some vs. some-some), reward type (bear, candy, chocolate), and their interaction (reference level: each-some, candy) and the random factors participants and items. The model showed a significant difference across reward type: Participants chose candy (“some”) more often than chocolate (“all,” z = −6.35, p < 0.001) and than bears (“none,” z = −6.2, p < 0.001), corresponding to the reading that each girl found some but not all of her marbles. There was no difference between the two quantifier conditions at the baseline level (each-some vs. some-some: p > 0.9). However, the model revealed an interaction between quantifier condition and reward type, indicating that participants chose bears more often in the condition with some-some (bear vs. candy across quantifier condition: z = 2.8, p < 0.01). This response pattern is consistent with the reading that no girl found all marbles and some did not find any marbles in the some-some condition. Table A1 shows a summary of the mixed model.
D. Error Models
As all interactional models, error models (Benz, 2012a,b) distinguish alternative utterances and alternative messages. The utterances are conjunctions of elements of 𝒰, the smallest set that contains all formulae Q − Q′ = “Q of theX Ved Q′ of the Y” with Q, Q′ in {}. The alternative messages are the seven possible worlds in (10). The conjunctive utterances which literally describe one of the possible worlds contain the following sentences:
| (26) |  |
The core idea in Benz (2012b) was that speakers are allowed to eliminate linguistic material from their utterances as long as this elimination does not lead to uncertainty about the world referred to, or to violations of the maxim of quality. In Benz (2012b), two elimination rules were assumed:
(27) Elimination rules
a. : reduction of “some but not all” to “some”
b. Uα ∧ Uβ → Uβ: unrestricted elimination of conjuncts.
If the rules are applied without further restrictions, then uncertainty about the world referred to can arise and the maxim of quality can be violated. For example, a reduction may violate quality. To provide a precise definition of the elimination constraints, we recursively define the notion of a licensed description of a world v, where v is one of the seven possible worlds from (10). First, the sentences listed in (26) are licensed description of their respective possible worlds. Then, an elimination produces a licensed description of world v, if U is a licensed description of v and the following two constraints are satisfied:
(28) Elimination constraints
a. (quality)
b. There is no v′ ≠ v, and no licensed description U″ of v′ and no elimination rule β such that (recoverability).
If U is a licensed description of world v, then an utterance of U implicates that the speaker intended to communicate that the actual world is v.1
The elimination rules in (27) together with the elimination constraints in (28) lead to the weak implicatures reported in (14). The experimental results can, however, be explained by the following more restricted elimination rules:
(29) Elimination rules
a. : reduction of “some but not all” to “some”
b. : elimination of conjuncts with empty subjects
c. : elimination of conjuncts with empty objects
d. with order of application: and before .
These modified rules do not allow for the arbitrary elimination of conjuncts, but only for the elimination of in the subject or the object phrase . For example, ∀-∃ = “All found some” is a licensed utterance for 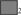 that can be derived via . Hence, the modified model predicts that ∀-∃ implicates that “all found some but not all.” The strong implicature of ∃-∃ can be derived for
that can be derived via . Hence, the modified model predicts that ∀-∃ implicates that “all found some but not all.” The strong implicature of ∃-∃ can be derived for 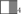 via
via
Footnote
- ^From this description, it is not clear why this framework is an interactional theory. In Benz (2012b), based on Benz (2012a), the recoverability constraint is justified by a detailed game theoretic model. It can be shown that equilibrium strategies in signalling games with efficient clarification requests and elimination rules which are constrained by (quality) must also satisfy the (recoverability) constraint. The model was formulated not with elimination rules but in terms of sub-signal relations. The set of licensed descriptions were called errors, as we can think of eliminations as omissions by a lazy speaker. The resulting models were therefore called error models.
Keywords: embedded implicatures, experimental pragmatics, game-theoretic pragmatics, localism, globalism
Citation: Gotzner N and Benz A (2018) The Best Response Paradigm: A New Approach to Test Implicatures of Complex Sentences. Front. Commun. 2:21. doi: 10.3389/fcomm.2017.00021
Received: 12 April 2017; Accepted: 23 November 2017;
Published: 12 January 2018
Edited by:
Andrea Moro, Istituto Universitario di Studi Superiori di Pavia (IUSS), ItalyReviewed by:
Francesca Foppolo, Università degli studi di Milano Bicocca, ItalyBrian Dillon, University of Massachusetts Amherst, United States
Copyright: © 2018 Gotzner and Benz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicole Gotzner, Z290em5lckBsZWlibml6LXphcy5kZQ==;
Anton Benz, YmVuekBsZWlibml6LXphcy5kZQ==
 Nicole Gotzner
Nicole Gotzner Anton Benz
Anton Benz