1. Exhaustification
1.1 Scientific theories are formulated based on experiments and our hunch about what must be right, i.e., “conceptual necessities” or “truisms.” For the study of language, these truisms include the thesis that linguistic communication is cooperative: speakers stick to the point and tell “the truth, the whole truth, and nothing but the truth” (Fox, 2016). Here is one way to spell this out1.
(1) Cooperative Speaker (CS)
Given a question under discussion Q, a speaker x will, by default, assert a proposition ϕ such that
(i) ϕ ∈ RQ “ϕ is relevant with respect to Q”
(ii) K(ϕ) “x believes ϕ”
(iii) ∀ψ((ψ ∈ RQ ∧ K(ψ)) → ϕ ⊆ ψ) “ϕ entails every relevant proposition that x believes”
CS turns out to be at odds with some of the most common observations. Here is one, for example. Suppose Q is who John talked to, with “who” ranging over Mary and Sue. Thus, M = [John talked to Mary] and S = [John talked to Sue] are both relevant. Assuming that relevance with respect to some question under discussion is closed under Boolean operations (cf. Groenendijk and Stokhof, 1984; Lewis, 1988),
(2) Closure conditions on relevance
(i) If ϕ is relevant, ¬ϕ is relevant
(ii) If ϕ and ψ are relevant, ϕ∧ψ is relevant
the set RQ of relevant sentences with respect to Q will be BC({M, S}), i.e., the Boolean closure of {M, S}2. Now let us say that the strongest proposition in this set entailed by the speaker's belief is M∧¬S. From CS it follows that the speaker will assert not M, not ¬S, but M∧¬S, the strongest of the three, which means she will utter not (3a), not (3b), but (3c).
(3) a. John talked to Mary
b. John didn't talk to Sue
c. John talked to Mary but not Sue
The fact, however, is that the speaker can freely choose between (3a) and (3c). The discrepancy between prediction and observation is shown in (4).
(4) Speaker's belief: M∧¬S
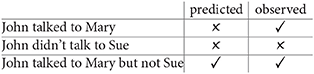
Thus, two sentences which are predicted to have different meanings behave as if they have the same meaning under the assumption that CS is true.
Here is another example. Suppose the strongest relevant proposition entailed by the speaker's belief is M. Given CS, she will assert M. Since M and M∨(M∧S) are equivalent, we predict that the speaker can freely choose between (5a) and (5b).
(5) a. John talked to Mary
b. John talked to Mary, or both Mary and Sue
The fact, however, is that she will say (5b), not (5a). The discrepancy between prediction and observation is shown in (6).
(6) Speaker's belief: M

Thus, two sentences which are predicted to have the same meaning behave as if they have different meanings under the assumption that CS is true.
1.2 Paul Grice sketches a way to derive such facts from CS itself plus other assumptions about how people think when they speak (Grice, 1967). The goal is to not tinker with the grammar3. Here is his account of the first example. Suppose the speaker asserts M and nothing else. It follows, from CS, that K(M), and given that S is relevant and not entailed by M, it follows, again from CS, that ¬ K(S). Assuming that the speaker is opinionated about S, i.e., that K(S) ∨ K(¬S), it follows that K(¬S). And from K(M) and K(¬S) it follows that K(M∧¬S)4. Thus, by asserting M, the speaker conveys K(M ∧ ¬S), which would also be conveyed by her asserting M∧¬S. This is why she can freely choose between (3a) and (3c): these sentences convey the same belief, namely M∧¬S. To introduce some terminology at this point, M is the “assertion,” S the “alternative,” ¬S the “scalar implicature,” and M∧¬S the “strengthened meaning.”
This account is appealing. It accords with our intuition that messages can be conveyed by what is said plus reasoning about what could have been said. All we must do is change “assert” to “convey” in the definition of CS, which we are, of course, willing to do. As it turns out, however, Grice's account is flawed. The crack is RQ. Recall that this set is assumed to be closed under Boolean operations. Thus, it contains both S and ¬S, which means the same reasoning as presented above could be applied with ¬S in place of S, and the speaker would convey, by asserting M, not K(M∧¬S), but K(M∧S). The reasoning would go like this. Suppose the speaker asserts M and nothing else. It follows, from CS, that K(M), and given that ¬S is relevant and is not entailed by M, it follows, again from CS, that ¬K(¬S). Assuming that the speaker is opinionated about ¬S, i.e., that K(¬S) ∨ K(¬¬S), it follows that K(¬¬S), i.e., that K(S). And from K(M) and K(S) it follows that K(M∧ S).
Grice's attempt at explaining the first example failed. The reason is that there are too many alternatives in RQ. Specifically, there are those which give rise to incompatible strengthened meanings. These are called “symmetric alternatives,” and the problem they pose is called the “symmetry problem5”. An obvious fix, therefore, is to tamper with RQ, specifically to “break” the symmetry in this set by keeping S in it and pruning ¬S from it. But this amounts, practically, to being incoherent: how can a proposition be relevant while its negation is not6?
In addition, Grice has no explanation for the second example: even if ¬S could be pruned from RQ, both (5a) and (5b) should still express the proposition M, which means asserting either of them should license the same implicature ¬S, clearly not what is observed7.
1.3 The “grammatical approach to implicatures” provides a way to square CS with the facts (cf. Krifka, 1995; Fox, 2007; Chierchia et al., 2012). The idea is that we have to tinker with the grammar after all. The core of the proposal is the postulation of a covert lexical item, EXHC, which composes with a sentence ϕ, its “prejacent,” to affirm ϕ and negate a selection of ϕ's alternatives8.
(7) Interpretation of EXHC
[EXHC ϕ] ⇔ ϕ ∧ ⋀
Procedurally, the calculation of [EXHC ϕ] consists of the following steps: (i) pick a set C of “contextually salient” alternatives; (ii) restrict C by intersecting it with the set F(ϕ) of “formal” alternatives; (iii) select from F(ϕ) ∩ C the set Eϕ(F(ϕ) ∩ C) of “innocently excludable” alternatives; (iv) conjoin ϕ with the negation of every innocently excludable alternative.
The value of C is discourse dependent. A natural candidate for C is RQ, the set of relevant sentences given the question under discussion Q. The functions F and Eϕ are defined in syntactic and semantic terms, respectively9.
(8) Definition of formal and innocently excludable alternatives10.
a. F(ϕ) = {ψ ∣ ψ is no more complex than ϕ }
b. Eϕ(X): = ⋂{X′ | X′ is a maximal subset of X such that {ϕ} ∪ {¬ψ | ψ ∈ X ′} is consistent}
Katzir (2007), and later Fox and Katzir (2011), propose to explicate the relation “is no more complex than” in (8a) as follows: ψ is no more complex than ϕ iff ψ is derivable from ϕ by successively replacing constituents of sentences, beginning with ϕ itself, with elements of the “substitution source” (SS), defined as in (9).
(9) Substitution source (SS)
SS = {x ∣ x is a lexical item} ∪ {x ∣
x is a constituent of an expression uttered in the context}
As for (8b), the idea is this: (i) try to build maximal subsets of X which contain sentences that can be consistently negated together with ϕ, then intersect these subsets: in this intersection are the innocently excludable alternatives.
To illustrate how the system works, suppose a disjunction of M and S was uttered, with (10) as its parse.
(10) EXHC [ϕM ∨ S]
Given that ϕ, M and S have all been uttered, from the prejacent ϕ we can derive ϕ by replacing ϕ with itself, M by replacing ϕ with M, S by replacing ϕ with S, and [M ∧ S] by replacing ∨ with ∧. Assuming C = BC({M, S}), we have F(ϕ) ∩ C = {ϕ, M, S, M ∧ S}. Call this set A1. Let us now try to build maximal subsets of A1 which contain sentences that can be consistently negated together with ϕ. One such set is A2 = {M, M ∧ S}, since {ϕ, ¬M, ¬[M ∧ S]} is consistent. Another is A3 = {S, M ∧ S}, since {ϕ, ¬S, ¬[M ∧ S]} is consistent. Now intersect A2 and A3. The result is A4 = A2 ∩ A3 = {M ∧ S}. This is the set of innocently excludable alternatives. We derive (11).
(11) EXHC [ϕM ∨ S] ⇔ ϕ∧¬[M ∧ S]
This explains the availability of the “exclusive” reading of plain disjunctions. For example, the string in (12a) will now have (12b) as parse, which is interpreted as (M∨S)∧¬(M∧S), i.e., as “John talked to Mary or Sue but not both.”
(12) a. John talked to Mary or Sue
b. EXHBC({M, S}) [John talked to Mary or Sue]
In the above example, the individual disjuncts derived by F from the disjunction end up being excluded from the domain of exhaustification by Eϕ. The situation changes when the disjunction is embedded under a universal quantifier, such as the modal necessity operator, as in (13) (Sauerland, 2004)11.
(13) EXHC[ϕ□[ψM ∨ S]]
Applying F to the prejacent ϕ, we derive, again, ϕ by replacing ϕ with itself, □M by replacing ψ with M, □S by replacing ψ with S, and □[M ∧ S] by replacing ∨ with ∧. Assuming C = BC({□M, □S}), this means F(ϕ) ∩ C = {ϕ, □M, □S, □[M ∧ S]}, which means Eϕ(F(ϕ) ∩ C) = {□M, □S, □[M ∧ S]}. We derive (14).
(14) EXHC [ϕ □[ψ M ∨ S]] ⇔ ϕ ∧ ¬□M ∧ ¬□S ⇔ ϕ ∧ ◇M ∧ ◇ S
This explains the availability of the “distributive” reading of disjunctions embedded under universal quantifiers. For example, the string in (15a) will now have (15b) as parse, which is interpreted as “John is required to talk to Mary or Sue and he is allowed to talk to Mary and he is allowed to talk to Sue,” exactly what is observed.
(15) a. John is required to talk to Mary or Sue
b. EXHBC({□M,□S}) □[John talked to Mary or Sue]
Note that F can also derive alternatives by replacing constituents of the prejacent with linguistic materials which have been used in the discourse context but which are not part of the prejacent itself. This makes it possible to analyze “particularized implicatures” as cases of exhaustification. As an example, consider the inference licensed by A's response to B's question below (cf. Matsumoto, 1995; Katzir, 2007).
(16) A: Yesterday it was warm and sunny with gusts of wind.
B: What about today?
A: Today it was warm.
A's response to B's question licenses the implicature that today it was not warm and sunny with gusts of wind. The alternative needed for this implicature is derived from the prejacent by replacing [warm] with [warm and sunny with gusts of wind], which is a constituent that has been uttered in the context but is not part of the prejacent itself12.
Coming back to the two apparent counter examples to CS discussed 1.1, here is what the grammatical approach to implicatures can say. Let us start with the first one. The puzzle posed by this example can be formulated in terms of this question: how can (17a) and (17b) be equivalent?
(17) a. John talked to Mary
b. John talked to Mary but not Sue
The introduction of EXHC into the lexicon makes it possible to understand this question not as rhetorical, but technical. It now has a straightforward answer: (17a) can be parsed as (18).
(18) EXHC [ϕ John talked to Mary]
where C = BC({John talked to Mary, John talked to Sue})
As it turns out, among the members of C, only (19a), besides ϕ itself, is no more complex than the prejacent: (19a) is derivable from ϕ by replacing [Mary] with [Sue], but no other member of C, besides ϕ itself, is derivable from ϕ by successively replacing constituents of ϕ with salient linguistic materials or items stored in the lexicon. Crucially, (19b) is not derivable from ϕ in that way.
(19) a. John talked to Sue
b. John did not talk to Sue
Given C = BC({M, S}), we have F(ϕ) ∩ C = {ϕ, (19a)}, which means Eϕ(F(ϕ) ∩ C) = {(19a)}, which means [EXHC [ϕ John talked to Mary]] ⇔ ϕ ∧ ¬[John talked to Sue]. This is how (17a) and (17b) can be equivalent. Note, however, that explaining how (17a) and (17b) can be equivalent actually falls short of accounting for the facts. In reality, these sentences not only can, but must be equivalent: if (17a) is uttered where RQ = BC({M, S}), it will have to be understood as M∧¬S. This means, in effect, that a parse with EXHC is the default (cf. Krifka, 1995; Fox, 2007; Magri, 2009). The generalization is stated in (20).
(20) Mandatory Exhaustification
Every matrix sentence is parsed with EXHC by default
Let us now consider the second example. The problem posed by this example can be formulated in terms of the following question: how can (21a) and (21b) not be equivalent?
(21) a. John talked to Mary
b. John talked to Mary, or both Mary and Sue
Just as for the first example, the answer is now straightforward. Keeping to C = BC({M, S}), the following two parses will deliver the right result. Note that the outer EXHC in (22b) is merged to satisfy (20). Semantically, it is vacuous.
(22) a. EXHC [John talked to Mary]
b. EXHC [[EXHC John talked to Mary] or [John talked to Mary and Sue]]
We already know that (22a) means M ∧ ¬S. The reader is invited to verify for herself that (22b) means M∨(M ∧ S), which is equivalent to M. Note that there are two instances of EXHC in (22b), one of which is embedded. If EXHC is merged at only the matrix level, as in (23), the resulting meaning will be M∧¬S, as can also be verified by the reader.
(23) EXHC [[John talked to Mary] or [John talked to Mary and Sue]]
The embeddability of EXHC corroborates the claim that it is a lexical item which can be syntactically integrated, not a notational device which models pragmatic reasoning performed at the speech act level (cf. Fox, 2007; Magri, 2009; Chierchia et al., 2012; Crnič, 2012).
But we again fall short of explaining the phenomenon: it is not that (21b) can be interpreted as M, but that it must be. Specifically, (21b) cannot be interpreted as M∧¬S. This means that (21b) must be parsed as (22b) and cannot be parsed as (23). Obviously, (20) does not explain this fact, as this principle only requires EXHC at the matrix level. Note, also, that (23) is stronger than (22b). What can force a sentence to be weakened by an instance of embedded EXHC? The answer has to do with the fact that (21b) is not deviant in the same way (24) is.
(24) #John saw a dog or an animal
This sentence violates the following principle, which for present purposes we take to be a primitive of grammar (Hurford, 1974).
(25) Hurford's Constraint (HC)
A disjunction is deviant if one disjunct entails the other
It is HC which forces (21b) to be parsed as (22b): because the first disjunct is exhaustified, it is incompatible with the second disjunct. The parse in (23), on the other hand, violates HC, since the second disjunct of the prejacent entails the first13.
1.4. At this point, an irony is perhaps worth noting: CS was originally motivated by the wish to derive implicatures from extra-grammatical principles, but it turns out that in order to keep CS, implicatures have to be derived in the grammar. The question to ask is what role CS plays in the interpretation of utterances. The answer is that CS derives “ignorance inferences.” A simple consequence of CS is (26).
(26) Ignorance inference
A speaker who asserts ϕ is ignorant about every relevant
ψ which is not settled by ϕ
We say that the speaker is “ignorant” about ϕ iff ¬K(ϕ) ∧ ¬K(¬ϕ), and say that ϕ “settles” ψ iff ϕ entails ψ or ϕ entails ¬ψ. Here, then, is how (26) follows from CS. Given CS, the speaker's assertion should entail every relevant proposition which she believes to be true. Suppose ψ is relevant. Then, ¬ψ is relevant also. If the speaker's assertion entails neither ψ nor ¬ψ, then it must be that she believes neither ψ nor ¬ψ, i.e., that she is ignorant about ψ.
The theorem in (26) is easy to illustrate. Consider, again (21b), which is repeated in (27a). As we have argued, this sentence is parsed as (27b).
(27) a. John talked to Mary, or both Mary and Sue
b. EXHC [[EXHC John talked to Mary] or [John talked to Mary and Sue]]
Observationally, (27a) conveys the message that the speaker is ignorant about the proposition that John talked to Sue: if asked whether John talked to Sue, she will not be able to say yes or say no truthfully. In other words, (27a) conveys the message that ¬K(S) ∧ ¬K(¬S). This is predicted, since it follows from (27b) neither that John talked to Sue, nor that John did not talk to Sue.
2. Contextual Restriction
2.1 Recall Grice's problem: there are too many alternatives in RQ. Specifically, for every alternative in RQ which could give rise to the attested strengthened meaning, there is a “symmetric” counterpart in the same set which could give rise to a non-attested strengthened meaning inconsistent with the attested one. Let us state the sense of “symmetric alternatives” which has underlied our usage of this notion so far.
(28) Symmetric alternatives
ψ and ψ′ are symmetric alternatives of ϕ in X iff
(i) ψ, ψ′ ∈ X
(ii) {ϕ, ¬ψ} and {ϕ, ¬ψ′} are consistent
(iii) {ϕ, ¬ψ, ¬ψ′} is inconsistent
Thus, S and ¬S are symmetric alternatives of M in BC({M, S}). From the assertion of M, pragmatic reasoning based on CS will derive K(S ∧ ¬S) under the assumption that the speaker is opinionated about S, and derive ¬K(S) ∧ ¬K(¬S) under the assumption that the speaker is not opinionated about S. The first inference means the speaker is incoherent, the second means she is ignorant about S, i.e., that she has no idea whether S is true or not. Neither accords with intuition, as an assertion of M is observed to license the inference that K(¬S), i.e., that the speaker believes that S is false. This discrepancy between prediction and observation which results from the existence of symmetric alternatives is the “symmetry problem.” As we saw in the last section, the grammatical approach to implicatures solves this problem, or more precisely this instance of it, by denying the premise that M is the assertion. Instead, it claims that what was asserted is really [EXHC M], which is, by virtue of compositional semantics, synonymous with [M ∧ ¬S]. In this case, symmetry is broken by F: one of the symmetric alternatives, ¬S, is more complex than the prejacent, while the other, S, is not.
2.2 Let us now turn to a discussion of salience. We have identified the set of salient sentences with the set of sentences relevant to the question under discussion. We can ask whether salience is just relevance. Since the only condition on relevance, by assumption, is closure under Boolean operations, the question amounts to whether salience is the same as closure under Boolean operations, and if not, how these notions are related. One way to frame the issue is to ask what the relationship is between the sets REL and SAL, defined in (29).
(29) a. REL: = {X ∣ X is closed under Boolean operations}
b. SAL: = {X ∣ X is contextually salient}
To be contextually salient, or in short, salient, is to be the value of C such that [EXHC ϕ] licenses the attested inference in the given context. I will argue that there is no systematic relationship between REL and SAL. Specifically, I will argue that these sets partially overlap, i.e., that REL − SAL, REL∩SAL and SAL − REL are all non-empty.
Let us show that REL ∩ SAL ⧧ { }. Consider the discourse below, where A's response to B's utterance is parsed as indicated.
(30) A: What do you want to know?
B: I want to know who John talked to.
A: EXHC [John talked to Mary]. ↝ M∧ ¬S
The last sentence, with the indicated parse, licenses the inference that John talked to Mary only. This inference can be derived by identifying C with the set BC({M, S}). This set, being closed under Boolean operations, is also a member of REL, which means it is both in SAL and in REL, which means REL ∩ SAL ⧧ { }.
Let us show that REL − SAL ⧧ { }. Consider the discourse below14.
(31) A: What do you want to know?
B: I want to know whether John talked to Mary, and in case he didn't, whether he talked to Sue.
A: EXHC [John talked to Mary or Sue]. ¬M ∧ S
The question under discussion—“whether John talked to Mary, and in case he didn't, whether he talked to Sue”—partitions logical space into the cells M, ¬M ∧ S, ¬M ∧ ¬S. This partition corresponds to the set BC({M ∨ S, M}), which is an element of REL. However, it is not salient: if it were, the last sentence in (31), parsed as indicated, would license the inference that John talked to only Sue. But we observe that sentence does not license this inference. Therefore, REL − SAL ⧧ { }.
To see that SAL − REL ⧧ { }, consider the discourse in (32).
(32) A: What do you want to know?
B: I want to know how the students did on the exam.
A: EXHC [Not all of them passed the exam].↝ some of them did
The last sentence in (32), with the indicated parse, licenses the inference that some of the students passed the exam. This must result from Eϕ(F(ϕ) ∩ C) containing (33a) but not (33b).
(33) a. [not [some of the students passed the exam]]
b. [some of the students passed the exam]
As F(ϕ), by definition, contains both (33a) and (33b) and Eϕ, also by definition, cannot prune one to the exclusion of the other, C must contain (33a) but not (33b), i.e., C must be the set {(33a)}. This set is not closed under Boolean operations, so it is not in REL. Given that it is in SAL, because it is the value of C, it is in SAL − REL, which means SAL − REL ⧧ { }.
2.3 We have just seen that there is no systematic relationship between relevance and salience: there are relevance sets which are salience sets (REL ∩ SAL ⧧ { }), relevance sets which are not salience sets (REL − SAL ⧧ { }), and salience sets which are not relevance sets (SAL − REL ⧧ { }). We will now consider another possible criterion for salience: utterance. Let us define the set UTT as containing sets of sentences which are derived by using linguistic materials that have been uttered in the context15.
(34) UTT: = {X ∣ X ⊆ {Y ∣ Y is derived by using linguistic materials that have been uttered in the context}}
What is the relationship between UTT and SAL? Again, I will argue that there is no systematic relationship between UTT and SAL, specifically that UTT ∩ SAL, UTT − SAL, and SAL − UTT are all non-empty.
To see both that UTT ∩ SAL ⧧ { } and that UTT − SAL ⧧ { }, consider the discourse in (35).
(35) A: John went for a run. He didn't smoke.
B: What about Bill?
A: Bill went for a run.
↝ Bill smoked
A's response to B's question, parsed as (36), clearly has a reading which implies that Bill is not like John, i.e., that he smoked. In this case, F(ϕ) contains both (36a), derived from ϕ by replacing [VP go for a run] with [VP smoke], and (36b), derived from ϕ by replacing [ went for a run] with [ didn't smoke].
(36) EXHC [ϕ Bill went for a run]
a. [ψ Bill smoked]
b. [ψ′ Bill didn't smoke]
As both [ didn't smoke] and [VP smoke] are constituents that have been uttered, UTT contains {(36a)}, {(36b)}, and {(36a),(36b)}. However, the attested inference of (36), namely that Bill smoked, requires that C contain (36b) but not (36a), i.e., that C = {(36b)}. This means both that SAL contains something which is in UTT and that UTT contains something which is not in SAL, i.e., both that UTT ∩ SAL ⧧ { } and that UTT − SAL ⧧ { }.
It remains to show that SAL−UTT⧧ { }. This we have actually done with the discourse in (30), where the last sentence, repeated here in (37a), is observed to license the inference that (37b) is false. This inference requires (37b) to be a formal alternative of (37a), i.e., to be derivable from (37a) by replacing [Mary] with [Sue].
(37) a. John talked to Mary
b. John talked to Sue
The context we constructed is such that [Sue] has not been uttered. The attested inference, thus, shows that (37b) is in SAL but not in UTT, i.e., that SAL − UTT ⧧ { }.
2.4 Relevance and utterance can be defined with sufficient precision to make concrete predictions. However, C cannot be defined in terms of these notions, and it is, at this point, not clear what other notion can be resorted to in establishing an understanding of salience. This poses a threat to the predictive power of the grammatical approach to implicatures. Katzir (2014) suggests a way to circumvent this threat: to change the definition of EXHC from (7), repeated in (38a) to (38b). The new definition amounts to stipulating that salience, whatever it is, cannot break symmetry: it allows Eϕ to weed out any symmetry in F(ϕ) before C has a chance.
(38) a. [EXHC ϕ] ⇔ ϕ ∧ ⋀ old definition
b. [EXHC ϕ] ⇔ ϕ ∧ ⋀ new definition
Katzir's proposal solves the problem posed by (31). What we want to rule out is the possibility of M∨S having M but not S as alternative. This is achieved by (38-b): although both M and S are in F(M ∨ S), they will both be eliminated from Eϕ(F(ϕ)) by the definition of Eϕ. Thus, the unattested implicature can never arise, no matter what C is.
Katzir's solution, however, fails to account for the other cases of unpredicted symmetry breaking, namely (32) and (35). Trinh and Haida (2015) propose to deal with (32) by revising the definition of F. They suggest to impose the following condition on F, specifically on the replacement operation which derives alternatives from the prejacent.
(39) Atomicity (first part)
[u/v]([x/y](z)) is undefined if u is a subconstituent of y
where [x/y](z) stands for the result of replacing x in z with y, i.e., the result of applying the replacement of x with y to z. Call z the “input,” x the “target,” and y the “substitute.” What atomicity says is that no target may be a subconstituent of a substitute. The condition prevents (33b) to be derived from 2. This derivation would involve two steps: (i) replacing ϕ with ψ and (ii) replacing [all], a subconstituent of ψ, with [some]. The second step is ruled out by Atomicity: [all/some]([ϕ/ψ](ϕ)) is undefined, because [all] is a subconstituent of ψ16.
(40) [ϕ not [ψ all of the students passed the exam]]
Trinh (2018) proposes to add another clause to Atomicity to deal with the case in (35). This clause constrains what can be a substitution source.
(41) Atomicity (second part)
If x, y ∈ SS and neither x nor y is a lexical item, x is not a subconstituent of y
This condition would prevent [VP smoke] and [ didn't smoke] from both being elements of SS, thus preventing [ψ Bill smoked] and [ψ′ Bill didn't smoke] from both being alternatives of [ϕ Bill went for a run]. It would, however, allow ψ′ Bill didn't smoke] as an alternative, making it possible to derive the attested implicature17.
Apart from being a partial solution which necessitates the complication of F, the new definition of EXHC also raises a “why” question: why does language opt for (38b) instead of (38a)? There is a certain conceptual naturalness to the presence of C, F, and Eϕ in the definition of exhaustification, since these mean pragmatic, syntactic, and semantic factors are all involved, a common feature of linguistic interpretation. However, it is much harder, if possible at all, to say why the order of operations in (38b) is more natural than that in (38a)18.
3. Conclusion
The grammatical approach to implicatures derives what was traditionally considered “pragmatic” inferences in the grammar by way of compositional semantics. It succeeds in accounting for inference patterns exhibited by a large number of cases while keeping to an overwhelmingly intuitive understanding of language use. But the proposal has a black box: the predictions it makes depend on which sentences are salient. It turns out, on closer inspection, that there is no systematic relationship between salience and relevance, nor is there one between salience and utterance. One way to resolve this problem is to stipulate that salience cannot break symmetry, and on that stipulation, calibrate other components of exhaustification to account for the facts. This strategy necessitates the complication of F, the function which maps sentences to their structurally simpler alternatives. Also, it brings into clear relief the need for a deeper explanation for the way pragmatics, semantics, and syntax interact in the process of exhaustification.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was funded by the ERC Advanced Grant Speech Acts in Grammar and Discourse (SPAGAD), ERC-2017-ADG 787929. The publication of this article was funded by the Open Access Fund of the Leibniz Association.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^Clauses (i), (ii) and (iii) of CS derive from the Gricean maxims of Relation, Quality, and Quantity, respectively (Grice, 1967). There is a fourth maxim, Manner, which is orthogonal to what we will be discussing.
2. ^This means being relevant with respect to Q is not the same as being a congruent answer of Q. For example, “John did not talk to Mary” is relevant to but not a congruent answer of “who did John talk to.” I thank one of the reviewers for drawing my attention to this distinction.
3. ^As correctly pointed out by one of the reviewers, the “Gricean account” presented here is not literally Grice (1967)—that work did not formulate CS or impose closure conditions on relevance, for example—but an exegesis thereof which has become more or less established among those who work in this area. The reformulation of the maxims of conversation as CS in (1) (see note 1) and the explication of relevance as subject to the closure conditions in (2) can be considered amendments which are compatible with what Grice says and at the same time sharpen it into a proposal that can be more concretely evaluated and critiqued.
4. ^The assumption of an “opinionated speaker” was not made explicit in Grice (1967). That it must be added to strengthen ¬K(S) to the more observationally adequate K(¬S) was noted by others (cf. Soames, 1982; Horn, 1989; Sauerland, 2004). See note 3.
5. ^Instances of the symmetry problem were first pointed out in Kroch (1972).
6. ^We can think of a relevant proposition as one whose truth value we are interested in finding out. Obviously, we cannot want to know whether p is true without wanting to know whether ¬p is true.
7. ^The problem of semantically equivalent sentences licensing different implicatures is sometimes called the “functionality problem” (Van Rooij and Schulz, 2004).
8. ^The definition in (7) was proposed in Fox (2007). I write “∧X” for the conjunction of all elements of X.
9. ^Thus, EXHC shares with pronominal elements in having an indexical component in addition to syntactic and semantic features. Take the pronoun [him7], for example. It carries an index which is assigned a value by the context. Semantically, it refers to male entities. Syntactically, it cannot be bound within the smallest clause, etc.
10. ^Notationally, ⋂X is the intersection of all elements of X.
11. ^Following standard practice, I use □ to represent universal modals, such as [must], [have to], [be required], etc., and ◇ to represent existential modals, such as [may], [can], [be allowed], etc.
12. ^In text object language expressions are put inside square brackets.
13. ^See Meyer (2013, 2014) for an explanation as to why exhaustification cannot rescue (24).
14. ^I assume that in general, any set of propositions which is closed under Boolean operations corresponds to a possible question under discussion. I thank one of the reviewers for suggesting that this assumption needs to be stated, and also, for suggesting the discourse context in (31) which makes the set BC({M, M∨S}) relevant.
15. ^Naturally, “having been uttered” cannot be taken to mean “consisting of morphemes that have been pronounced.” So much of language is silent that a collection of overt morphemes will rarely yield any interpretation. To “utter X” has to be understood as to “give some hints about X by way of making sound.” In that sense, elliptical sentences, copies of movement, null pronouns, etc., are all part of the utterance.
16. ^Note that (33b) cannot be derived from 2 by first replacing [all] in 2 with [some], generating [α not [β some of the students passed the exam]], followed by replacing α with β. The second step of this derivation is by definition not legitimate, since β is not an element of SS: it is not a lexical item, and it is not a constituent of any expression uttered in the context.
17. ^See Trinh (2018) for arguments as to why [smoke] should be considered a VP and not a lexical item. Also, note that (41) will not prevent the derivation of the bipartite conjunction [B and C] from the tripartite disjunction [A or [B or C]], and thus, will not prevent us from deriving the “only one” interpretation of tripartite disjunctions. This is because [B and C] is equivalent to [B and [C or C]], etc. In other words, the only non-lexical members which SS must contain are the individual disjuncts A, B, and C, none of which is a subconstituent of any other. I thank one of the reviewers for raising this point.
18. ^One is reminded of the issue raised by Mats Rooth about Irene Heim's definition of the context change potentials of logical connectives: there are several definitions of, say, [if A, B] which gets the truth conditions right, but only one which gets the projection of presuppositions right, and there is no clear reason why one definition is more natural than the others (cf. Heim, 1990; Schlenker, 2008).
References
Chierchia, G., Fox, D., and Spector, B. (2012). “The grammatical view of scalar implicatures and the relationship between semantics and pragmatics,” in Semantics: An International Handbook of Natural Language Meaning, eds P. Portner, C. Maienborn, and K. von Heusinger (Berlin: De Gruyter), 2297–2232.
Crnič, L. (2012). Focus particles and embedded exhaustification. J. Semant. 30, 533–558. doi: 10.1093/jos/ffs018
Fox, D. (2007). “Free choice disjunction and the theory of scalar implicatures,” in Presupposition and Implicature in Compositional Semantics, eds U. Sauerland, and P. Stateva (New York, NY: Palgrave-Macmillan), 71–120.
Fox, D. (2016). Topics in Exhaustification. Minicourse taught at the Hebrew University of Jerusalem, Jerusalem.
Fox, D., and Katzir, R. (2011). On the characterization of alternatives. Nat. Lang. Semant. 19, 87–107. doi: 10.1007/s11050-010-9065-3
Grice, P. (1967). Logic and Conversation. William James Lectures. Cambridge: Harvard University Press.
Groenendijk, J., and Stokhof, M. (1984). Studies on the semantics of questions and the pragmatics of answers (PhD thesis), University of Amsterdam, Amsterdam, Netherlands.
Heim, I. (1990). “Presupposition projection,” in Presupposition, Lexical Meaning and Discourse Processes: Workshop Reader, ed R. van der Sandt (Nijmegen: University of Nijmegen).
Katzir, R. (2007). Structurally-defined alternatives. Linguist. Philos. 30, 669–690. doi: 10.1007/s10988-008-9029-y
Katzir, R. (2014). “On the roles of markedness and contradiction in the use of alternatives,” in Semantics, Pragmatics and the Case of Scalar Implicatures, ed S. Pistoia-Reda (London: Palgrave), 40–71.
Krifka, M. (1995). The semantics and pragmatics of polarity items. Linguist. Anal. 25, 209–257. doi: 10.3765/salt.v4i0.2462
Kroch, A. (1972). Lexical and inferred meanings for some time adverbials. Q. Progr. Rep. Res. Lab. Electron. 104, 260–267.
Lewis, D. (1988). Relevant implication. Theoria 54, 161–174. doi: 10.1111/j.1755-2567.1988.tb00716.x
Magri, G. (2009). A theory of individual-level predicates based on blind mandatory scalar implicatures. Nat. Lang. Semant. 17, 245–297. doi: 10.1007/s11050-009-9042-x
Matsumoto, Y. (1995). The conversational condition on horn scales. Linguist. Philos. 18, 21–60. doi: 10.1007/BF00984960
Meyer, M.-C. (2013). Ignorance and grammar (PhD thesis), Massachusetts Institute of Technology, Cambridge, MA, United States.
Meyer, M. C. (2014). “Deriving Hurford's constraint,” in Proceedings of SALT 24 (New York, NY), 577–596.
Sauerland, U. (2004). Scalar implicatures in complex sentences. Linguist. Philos. 27, 367–391. doi: 10.1023/B:LING.0000023378.71748.db
Schlenker, P. (2008). Be articulate: a pragmatic theory of presupposition projection. Theor. Linguist. 34, 157–212. doi: 10.1515/THLI.2008.013
Soames, S. (1982). How presuppositions are inherited: a solution to the projection problem. Linguist. Inq. 13, 483–545.
Trinh, T., and Haida, A. (2015). Constraining the derivation of alternatives. Nat. Lang. Semant. 23, 249–270. doi: 10.1007/s11050-015-9115-y
Keywords: implicatures, alternatives, exhaustification, salience, atomicity
Citation: Trinh T (2019) Exhaustification and Contextual Restriction. Front. Commun. 4:47. doi: 10.3389/fcomm.2019.00047
Received: 11 March 2019; Accepted: 15 August 2019;
Published: 03 September 2019.
Edited by:
Sophie Repp, University of Cologne, GermanyReviewed by:
Alexandre Cremers, University of Amsterdam, NetherlandsEdgar Onea Onea, University of Graz, Austria
Copyright © 2019 Trinh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tue Trinh, dHVldHJpbmhAYWx1bS5taXQuZWR1
 Tue Trinh
Tue Trinh