- Leibniz-Centre General Linguistics, Berlin, Germany
Searle (Speech Acts, 1969) introduced his famous distinction between constitutive and regulative rules that together define felicity conditions of speech acts. Regulative rules are normative rules, whereas constitutive rules define what counts as a performance of a speech act. In this paper we demonstrate with the example of assertions and referential uses of definite description that simple regulative rules can be given to speech acts that hold only on a core of well-behaved utterance situations. From this core, extended uses can be derived based on epistemic paths that are defined by the epistemic perspectives of speaker and hearer. As the use of speech acts get extended to a wider class of utterance situations, conflicts with the constitutive rules can emerge. We show that the extended uses are nevertheless felicitous. We represent epistemic relations in a possible worlds framework, and take an interactional approach that considers speech acts as part of joint communicative acts.
1 Introduction
Pragmatics is often defined as the study of language in context (see Korta and Perry, 2020, Sec. 4), and, in particular, the study of the relation of signs to interpreters (Morris, 1938, p. 6). Context is a multifaceted concept that includes, among other things, the physical environment, social relations, the dialogue history, and epistemic states of the interlocutors. In this article, we address the dependencies between felicity conditions of communicative acts and the epistemic relations between interlocutors, i.e., their knowledge about each other and the facts of the world. Central to our approach will be the assumption that communicative acts are organized as action–response pairs (joint projects,Clark, 1996) that need to be coordinated between speaker and hearer.
Suppose one undertakes it to define felicity conditions of, for example, the speech act of asserting, then the question arises whether the requirement that speakers know that p, if they assert p, is part of the definition of the speech act, or merely a normative rule imposed by general requirements about cooperative communication (Grice, 1975). Searle (1969) introduced the famous distinction between regulative and constitutive rules that govern the use of speech acts. Constitutive rules are defining rules that say which linguistic utterances count as performances of a certain speech act type. Regulative rules are normative rules that say how a speech act should be performed. In Searle’s classification, regulative rules include constraints on the speaker’s or hearer’s information state. For example, the act of asserting is subject to the regulative rule that speakers must believe what they assert to be true (Searle, 1969, p. 66). As constitutive rules state requirements particular of certain speech acts, and regulative rules general requirements of rational behavior, one would like constitutive requirements to be weak, and regulative rules to be powerful and applicable to as wide a range of speech acts as possible. In this article, we concentrate on two communicative acts that seem, at first, little related to each other: the illocutionary act of asserting and the locutionary act of referring to a specific object with a definite description. We assume that they are constituted by the following minimal rules:
1) Assertion. The utterance of a sentence expressing proposition φ is a legitimate communicative act given the state of affairs represented by a model m if, and only if φ is true in m.
2) Referential definite description. The utterance of a definite description ‘the φ’ with the aim of referring to a referent r is a legitimate communicative act given the state of affairs represented by a model m if, and only if
Clearly, these rules on their own cannot guarantee the felicity of their communicative acts. Clark and Marshall (1981) argued that successful referential uses of definite descriptions require that
3) Leo told me that it is snowing in the Alps, but I knew that the snowing had stopped.
4) Leo told me that it is snowing in the Alps, but I knew that she is lying.
If (1) is correct, then no utterance of a sentence with propositional content φ should count as an assertion if φ is false. However, in (3) it seems fine to report that someone (Leo) asserted a proposition φ (snowing in the Alps) although the person reporting this act knows that φ is false. Example (4) shows that an utterance with meaning φ can be reported as an assertion even if the person uttering it is known to disbelieve φ. This shows that constitutive rules cannot be understood as semantic meaning components of reported assertions such that ‘A told B that φ.’ would mean that there is an event e which is an utterance event with speaker A and addressee B and propositional content φ for which rule (1) holds. Nevertheless, the constituting rules must play some role in reported utterance events.
With Searle, we assume that constitutive and regulative rules define speech acts as social institutions. They are a form of conventional linguistic behavior. We postulate that this behavior is defined for a core of perfect communicative situations in which interlocutors can entertain only true beliefs and are assumed to be fully cooperative. The constitutive rules only apply here. From this core, communicative acts are extended to more complex and possibly non-cooperative utterance situations via epistemic paths that involve changing perspectives between interlocutors. For example, in (3) the speaker S who reports Leo’s utterance believes that from Leo’s perspective constitutive rule (1) is satisfied, and, hence, that the utterance can be called an assertion from Leo’s perspective. We assume that the path from S’s to Leo’s perspective allows S to call Leo’s utterance an ‘assertion’, although the constitutive rule (1) is violated from S’s own perspective. In (4), the constitutive rule (1) is violated from both the speaker S’s perspective and from Leo’s perspective. However, Leo must think that from S’s perspective it is satisfied. Hence, it is the path from S to Leo to S that allows S, or us as readers of (4), to classify Leo’s utterance as assertion. However, paths can be more convoluted than suggested by (3) and (4) alone. Suspicions may introduce circular paths and mutual mistrust in the validity of constitutive rules. We show also for these situations how epistemic paths can justify the classification of utterances as assertions.
We present a theory that explains how epistemic paths can give rise to felicitous joint communicative acts that extend beyond the epistemic core of perfect utterance situations. In contrast to Searle, we take an interactional perspective on speech acts (see Clark, 1996) where speaker and hearer have each to perform their own required act: the speaker performs an utterance act that is followed by an appropriate response of the hearer. We introduce two epistemic felicity constraints that decide whether a joint communicative act is consistent with the interlocutor’s beliefs: a licensing constraint and a uniqueness constraint. Licensing requires that the joint act is possible from the interlocutor’s perspectives, and uniqueness that the hearer’s response is uniquely determined by the speaker’s utterance act. We will see how the constraints eliminate infelicitous communicative acts when joint acts are extended to new epistemic situations.
In the next section, we present a general format for the representation of constitutive rules for speech acts. We then consider referential uses of definite descriptions in more detail and demonstrate how epistemic paths allow extended uses outside the communicative core situations. In particular, we consider the examples discussed by Clark and Marshall (1981) that are supposed to show that felicitous references to an object r with the φ require that
2 Representing Constitutive Rules as Joint Projects
Searle (1969, Sec. 2.5) illustrates the difference between constitutive and regulative rules with the rules of Chess. The rules of Chess are a paradigmatic example of constitutive rules, the main purpose of which it is to define what counts as a move of the game. In addition to constitutive rules there may also be regulative rules, for example, that the players should not smoke and abstain from distracting behavior. However, these rules do not define chess. As an example of a constitutive rule, Searle (1969, p. 34) cites the rules for checkmate. In general, these rules take into account only the position of pieces on the chess board. Some rules may also take into account the game history, for example, the rule of castling. For example, moving the White King from his start position1 two squares to the right and the Rook from its start position to the left of the King counts as legal chess move called castling kingside if King and Rook had not moved before, none of the squares between them are occupied, and the King does not move out of, through, or into check. If this rule that defines the legal move of kingside castling in chess were given to a program that checks the moves of players, then any violation of its conditions would mean that the program would reject the move as a move of chess. Nevertheless, we can, without contradiction, make statements as in (5) and (6), which are analogous to (3) and (4).
5) Leo castled kingside, but I knew that the King had moved before.
6) Leo castled kingside, but I knew that she is cheating.
As in the case of speech acts, exploiting the different perspectives of people involved can explain why one can call a move ‘castling’ although it violates its defining rules. In (5), the move may seem legal from Leo’s perspective, or from the perspective of an observer who does not know the history of the game. In (6), the move may seem legal from an outside observer’s perspective, or the violation may go unnoticed from the opponent’s perspective. Also in (7), the speaker can describe what he did as castling kingside.
7) I castled kingside. Luckily, my opponent didn’t remember that the King had moved before.
The speaker could not say ‘I moved the pieces as if I castled kingside,’ or ‘I pretended to castle kingside.’ He has to say that he castled kingside, although one could say that he pretended to perform a legal move.
There seem to be the same pragmatic mechanisms at work that widen the meaning of ‘castling’ and the meaning of ‘asserting’. However, playing chess differs in important respects from conversation. Chess is a game with strictly opposed players, whereas we assume with Grice (1975) that an unmarked conversational situation is one where speakers and hearers are cooperative. Chess is a game without private information, i.e., whatever happens in the game as well as the positions of the pieces on the board are shared knowledge between players. In a typical dialogue situation the knowledge of speaker and hearer differ. And performing a certain speech act, for example, asserting, requires the speaker to have more knowledge than the hearer. A further difference is that chess games can be described as sequences of moves by the White and Black players. It has been argued forcibly by, for example, Clark (1996) that conversation is a sequence of joint coordinated actions, i.e., that each communicative act performed by the speaker needs a corresponding communicative act on the hearer side to be completed. These pairs of communicative acts have been called ‘joint projects’ Clark (1996).2 We follow this line of research and represent communicative acts as triples consisting of a model m, a communicative act a performed by the speaker, and a response act r by the hearer. Hence, each joint project is a set of triples
8) Assertion. Let
Note that each sentence s defines its own joint project. Hence, the classification into joint projects is more fine-grained than the classification into speech acts. This is also true of the following representation of referential uses of definite descriptions. We assume that each pair consisting of a description the φ and a referent r define their own joint project.
9) Referential definite description. Let
The constitutive rules have to be accompanied by regulative rules. Together they define the felicity conditions of a speech act. Here, we only consider felicity conditions that pertain to the epistemic perspectives of speaker and hearer. As mentioned before, we consider two constraints called licensing and uniqueness.
10) Licensing. Let p be a given joint project. An utterance act a is epistemically licensed for the speaker, if from the speaker’s perspective doing a can initiate the joint project p in all possible state of affairs m and for all possible belief states of the hearer. An utterance act a is epistemically licensed for the hearer, if from the hearer’s perspective doing a can initiate the joint project p in at least one possible state of affairs m and for at least one belief states of the speaker.
11) Uniqueness. Let p be a given joint project. An utterance act a satisfies the uniqueness condition for p from the speaker’s or hearer’s perspective, if it holds for all their possible states of affairs m for which doing a can initiate any joint project that a leads to the same hearer response r such that the joint communicative act
If we ask for a deeper reason for these constraints, then the answer is the requirement that interlocutors should not gamble. If licensing is violated, then the speaker believes that the attempted speech act may fail. For the hearer, a violation of licensing means that the speaker’s utterance act is inconsistent with the hearer’s beliefs. If uniqueness is violated, then it is unclear how to respond to the utterance act. This complete ban on gambling may be too strict a requirement for realistic utterance situations, but, as a logical idealization, it is appropriate for our purposes.3
3 The Referential use of Definite Descriptions
In this section we consider referential uses of definite descriptions. As mentioned before, there are two closely related problems about the interpretation of communicative acts: the classification problem and the meaning problem. The classification problem stems from the fact that utterances and uses of definite descriptions can be classified as assertions or referential uses although their constitutive conditions are not satisfied. Referential uses of definite descriptions provide examples that are particularly suitable for studying the role of epistemic paths in the classification problem.
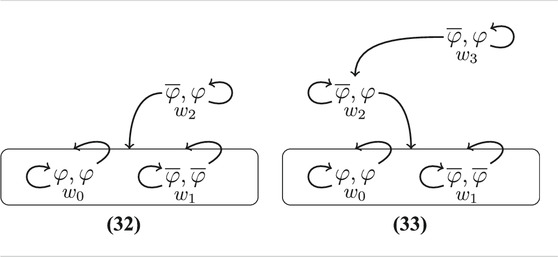
In their influential study, Clark and Marshall (1981, C&M) discuss a series of examples that show that reference to an object r with definite description the φ can fail although any finite sequence of conditions the speaker beliefs that
On Wednesday morning Ann and Bob read the early edition of the newspaper and discuss the fact that it says that A Day at the Races is playing that night at the Roxy. Later, Ann sees the late edition, notes that the movie has been corrected to Monkey Business, and marks it with her blue pencil. Still later, as Ann watches without Bob knowing it, he picks up the late edition and sees Ann’s pencil mark. That afternoon, Ann sees Bob and asks, “Have you ever seen the movie showing at the Roxy tonight?” (Clark and Marshall, 1981, p. 13, Version 4)
Here, Bob must reason as follows: Ann knows that Monkey Business is playing tonight. But she thinks I believe that we both are mutually convinced that A Day at the Races is showing. So she must think that I think she refers to A Day at the Races. Hence, knowing that Monkey Business is showing, and knowing that the speaker knows that Monkey Business is showing is not enough to ensure successful reference to Monkey Business.
More and more complicated examples can be constructed that show that any finite sequence of sentences ‘Ann knows that Bob knows that … that Monkey Business is showing that night’ is not enough to ensure reference to Monkey Business. Clark & Marshall arrive at the conclusion that both participants need to know that all sentences of the form (12) have to be true in order to secure reference to Monkey Business.
12)
Here, the
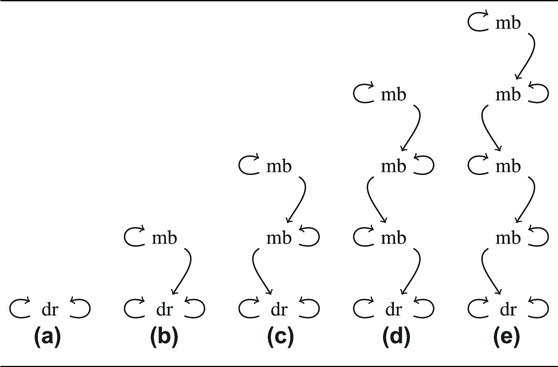
TABLE 1. Different information states considered by Clark and Marshall (1981, C&M, pp. 11–14). Abbreviations: dr: A Day at the Races is showing, mb: Monkey Business is showing. Each node represents a possible world. Arrows w → v say that v is an epistemic possibility in world w; arrows to the left point to possible worlds of the speaker’s information state (‘Ann’), arrows to the right to possible worlds of the hearer’s information state (‘Bob’). b) is Version 2 of C&M; c) is C&M’s Version 3; d) is their Version 4; and e) is their Version 5.
We are interested in the question: What does the definite description the φ = ‘The movie showing at the Roxy tonight?’ actually refer to? Each of C&M’s scenarios starts with Ann and Bob reading together that A Day at the Races is showing. This initial epistemic state is represented by a) in Table 1. We can distinguish a reading that is based on public information, and one that is based on private information. In the a) and the b) situation, where Bob thinks to be in situation a), the φ obviously refers to A Day at the Races, which is based on shared public belief. In situation c), the answer is not as clear cut. Bob may answer ‘No, I’ve never seen A Day at the Races. But, you know, the program has been corrected. Monkey Business is showing.’, because he thinks that Ann thinks that it is public knowledge that A Day at the Races is showing. Bob may also answer ‘Yes, I have. You know, the program has been corrected and Monkey Business is showing. I saw the movie last year on TV.’ This interpretation of the definite description is based on Bob’s private beliefs about which movie is showing. This reading involves a repair, as Bob must think that Ann will, at first, interpret the Yes-answer as a confirmation of the proposition that Bob has seen A Day at the Races. We are only interested in the interpretation based on public information, that does not involve a repair. In C&M’s more complex scenarios, the two readings seem both to be available. We, therefore, modify C&M’s examples in a way that favors the public reading. The modified examples show that the public reading is available although the conditions about beliefs in (12) may be violated for arbitrarily large n.
In the following scenarios, the question is always what is the referent of the φ = the movie showing at the Roxy tonight? Version 1 in (13) is the basic scenario in which
13) Version 1. On Wednesday morning Ann and Bob read the newsletter on Ann’s computer and discuss the fact that it says that Monkey Business is playing at the Roxy that night. Later Ann decides that she wants to stay at home. She calls Bob and asks, ‘Do you want to watch the movie showing at the Roxy tonight on Netflix with me?’
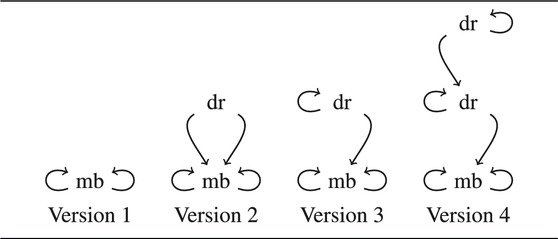
TABLE 2. Different information states considered in (13)–(16). Abbreviations: dr: A Day at the Races is showing, mb: Monkey Business is showing. Each node represents a possible world. Arrows w → v say that v is an epistemic possibility in world w; arrows to the left point to possible worlds of the speaker’s information state, arrows to the right to possible worlds of the hearer’s information state.
In the next version, the beliefs of Ann and Bob have not changed, but the truth of
14) Version 2. On Wednesday morning Ann and Bob read the newsletter on Ann’s computer and discuss the fact that it says that Monkey Business is playing at the Roxy that night. Later, a correction was sent saying that, in fact, A Day at the races is playing. Neither Ann nor Bob notice the correction. Later Ann decides that she wants to stay at home. She calls Bob and asks, ‘Do you want to watch the movie showing at the Roxy tonight on Netflix with me?’
In Version 3, Ann learns that
15) Version 3. On Wednesday morning Ann and Bob read the newsletter on Ann’s computer and discuss the fact that it says that Monkey Business is playing at the Roxy that night. Later, a correction was sent saying that, in fact, A Day at the races is playing. Only Ann notices the correction. She doesn’t like A Day at the races. She knows that Bob would love to see it, but that he couldn’t have noticed the correction. She calls Bob and asks, ‘Do you want to watch the movie showing at the Roxy tonight on Netflix with me?’
In Version 4, both Ann and Bob learn that
16) Version 4. On Wednesday morning Ann and Bob read the newsletter on Ann’s computer and discuss the fact that it says that Monkey Business is playing at the Roxy that night. Later, a correction was sent saying that, in fact, A Day at the races is playing. Ann notices the correction. Later, Bob reads her email and notices the correction, and notices also that Ann has read it. Bob would love to see A Day at the races but he knows that Ann doesn’t like it at all. He wants to please her, but doesn’t want her to know that he reads her mail without her knowing it, he calls Ann and asks, ‘Do you want to watch the movie showing at the Roxy tonight on Netflix with me?’
In this manner, more and more complex epistemic states can be created in which it holds that
The graphs in Tables 1 and 2 point to a solution. The complex states constructed by C&M and by us embed a basic situation in which common knowledge of
4 Assertions
In this section, we consider assertions in situations that show epistemic relations between speaker and hearer similar to those seen with the modified Clark & Marshall scenarios. The examples are taken from (Benz, 2008) and slightly modified for the present discussion. There are two possible states of affairs, either it snows in the Alps (φ), or it does not snow in the Alps (
17)Version 1. Helga calls up her son Stephan who lives in a small town in the Alps and asks him whether he wants to visit her in Munich. Stephan answers: ‘It is snowing in the mountains. So I don’t want to drive now.’
Version 2. Helga calls up her son Stephan and asks him whether he wants to visit her in Munich. Stephan answers: ‘It is snowing in the mountains. So I don’t want to drive now.’ But he has not checked the weather for some time, and it is now raining and the streets are clear.
Version 3. Helga calls up her son Stephan and asks him whether he wants to visit her in Munich. Stephan has a new girl-friend and prefers to stay at home this weekend. He answers: ‘It is snowing in the mountains. So I don’t want to drive now.’ However, he knows that it is not snowing and that the streets are clear.
Version 4. Helga calls up her son Stephan and asks him whether he wants to visit her in Munich. Stephan answers: ‘It is snowing in the mountains.’ Helga has just talked to her daughter, who lives next to Stephan, and learned from her that it is not snowing and that the streets are clear. She also learned that Stephan has a new girl-friend and prefers to stay at home this weekend.
The epistemic relations in the basic situation is shown in (18). There are two states of the world: one in which it snows in the Alps (φ), and in which the speaker knows that it snows and says so, and another in which it does not snow (
18) The epistemic relations in Version 1 of (17):
In (8), the joint project of asserting a sentence s with meaning φ has been defined as the set of all triples

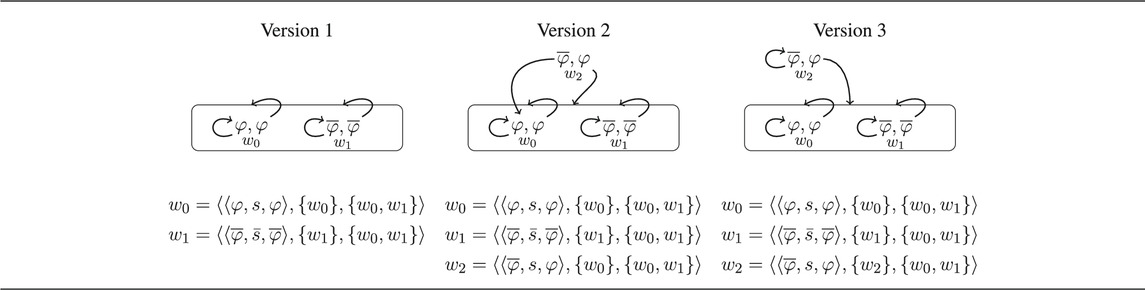
TABLE 3. Information states in versions 2 to 4 of (17). The nodes of the graph are pairs of formulas, where the first formula says whether φ or
A comparison between Tables 2 and 3 shows that the graphs are structurally identical except for their respective basic versions. The same reasoning that explains why the use of a definite description the φ can count as a referential act with target Monkey Business in the situations represented by the top nodes of Versions 2–4 in Table 2 explains why the utterance of ‘It is snowing in the mountains.’ can count as an assertoric act with propositional content φ in the situations represented by the top nodes of Versions 2–4 in Table 3. The classification as assertoric act travels along the epistemic path leading from the top node down to the basic situation that properly licenses the assertion.
We will introduce the mathematical framework which allows us to handle these examples precisely in Section 5. Before we turn to formal representations, we have a closer look at the structure of the epistemic graphs. They can be divided into a base and a hierarchical structure building up on it. The hierarchical part shows descending paths. The bases can differ in their internal structure. As we have seen, the bases for assertions in (18) and that for referential uses of definite descriptions shown in Table 2 have different structure. Table 4 shows three further possibilities for the base of the assertoric speech act. The first a) is a copy of the base for the referential use of definite descriptions. As a plausible base for Version 1 of (17) it is ruled out by an additional pragmatic constraint that says that the speaker should not say what is already common belief. However, we do not formalize this constraint so that a) remains a theoretical possibility. In setting up the epistemic graph in (18), we made the assumption that it is known that the speaker knows whether it is snowing, or not. This assumption does not follow, however, from Version 1 of (17). Table 4b and c show two possibilities where the hearer thinks it possible that the speaker does not know whether it snows. There are even more possibilities. For example, by bending the hearer’s edge going out from the rightmost
Our task is to explain why a certain utterance can be classified as an assertion in a given node in an epistemic graph. We adopt the following strategy: once it is explained why this classification is justified in a base situation, the classification can travel upward through the hierarchical part of the graph. This means, we can divide our considerations into that of the basic level and that of the higher hierarchical levels. Once the classification problem is solved for the base, the solution for the hierarchical part follows. One characteristic of the bases is the absence of descending paths. This means that all nodes in the bases are connected with each other. This leads to circular structures. We therefore consider circular structures separated from hierarchical ones.
5 The Model
As explained in Section 2, we adopt a Clark (1996) perspective and represent communicative acts not as isolated acts but as coordinated joint projects consisting of a linguistic act by the speaker and a response by the hearer. A joint project consists of triples
5.1 Possible Worlds and Epistemic Relations
The joint projects do not represent epistemic relations between interlocutors and interlocutors and the world. We adopt a possible worlds representation in which beliefs are modeled as sets of epistemically possible worlds. A world has the form:5
19) Possible world: A possible world w is a triple
We write
In standard set theory, there is no
The update that we just described can be represented by a formal update operator *. It models the effect of mutual learning some information Y.6 In Eq. 1,
The graph of Version 1 of Table 6 represents
We are now in a position to explain an important modeling decision. Why do possible worlds represent joint communicative acts
20)
If we replace
21)
Every solution that solves (21) also provides a solution for (20). As every system of equations has only one solution, it follows that the solutions for
Possible worlds defined by systems of equations can represent utterance situations one at a time. It would be desirable to have definitions of whole classes of utterance situations that share certain characteristics. To avoid the necessary apparatus, we continue on a case by case basis.7
We need some additional concepts. First, we introduce the notion of an epistemic path. An epistemic path from
The transitive hull of a world w is the set of worlds that includes w itself and all worlds that can be reached from w via a connecting epistemic path. Let w be a possible world. We first construct sets of worlds that are reachable in
The transitive hull of w is then defined as the union of all
It can be verified that
Finally, we introduce two formal properties of possible worlds w:
The first property entails that interlocutors know what they know, and know what they do not know. This is sometimes considered too strong an assumption about beliefs. We assume it here for convenience. The other property says that it is common knowledge that interlocutors have only true beliefs. If truthfulness holds for w, then every path in
We always assume introspection, and for elements of the base of an epistemic graph, we also assume truthfulness.
5.2 The Base Level of an Epistemic Graph
In Table 4 we have seen various examples of basic epistemic graphs. They have in common that all worlds are connected with each other. This is entailed by the truthfulness condition that we assume to hold for all well-behaved communicative situations. The idea is that we can first solve the simpler task of classifying communicative acts in well-behaved situations, and then generalize the classification to the ill-behaved ones.
The epistemic relations in an utterance situation is represented by an epistemic graph. The goal of this section is to show how a sub-graph can be constructed that satisfies all epistemic felicity conditions. This construction will be a fixed-point construction. We first introduce formal variants of the licensing and uniqueness conditions.
Let us consider licensing from the speaker’s perspective. If the speaker wants to start a joint project p he has be to sure that it can be performed in all epistemically possible worlds. The speaker can only perform a single act. Hence, there must be an act a such that for all epistemically possible states of affairs m there is a response r and a world
For convenience, we also introduce notation for the set
With these preparations, we can introduce the formal constraints for licensing and uniqueness. They are formulated as conditions on information states, i.e., sets of possible worlds X, that depend on a project p and an act a:
The uniqueness condition says that for every state of affairs in which act a can initiate a joint communicative act it will lead to the same response. Uniqueness is downward entailing, i.e.,
We can now show how to construct a maximal sub–set of a given set X in which the epistemic felicity conditions licensing and uniqueness are mutually guaranteed to hold. Let there be a given set
This is the set of all
The hearer, in contrast to the speaker, does not need to believe that act a initiates project p in all possible worlds. It suffices that he believes that it is consistent with his information. Hence, licensing can be restricted to a non-empty sub-set of his belief state:
We can construct the set of possible worlds in which the epistemic felicity conditions are mutual knowledge by an iterative process of eliminating worlds that do not satisfy them. The construction proceeds in parallel for all acts a and joint projects
In the next step, this is repeated for the hearer’s epistemic felicity conditions:
This construction continues such that in each odd step the speaker’s epistemic felicity conditions are checked, and in the even steps the hearer’s:
Fortunately, it is not necessary to repeat this infinitely often. We can show that:
Why should the construction stabilize after three steps? After the first step, it is common knowledge that licensing and uniqueness hold from the speaker’s perspective. As belief states can only become smaller by updating, the speaker’s uniqueness condition is guaranteed to hold for all following construction steps. As for each remaining world w, it holds that
22) Fixed-point. Given a set of joint projects
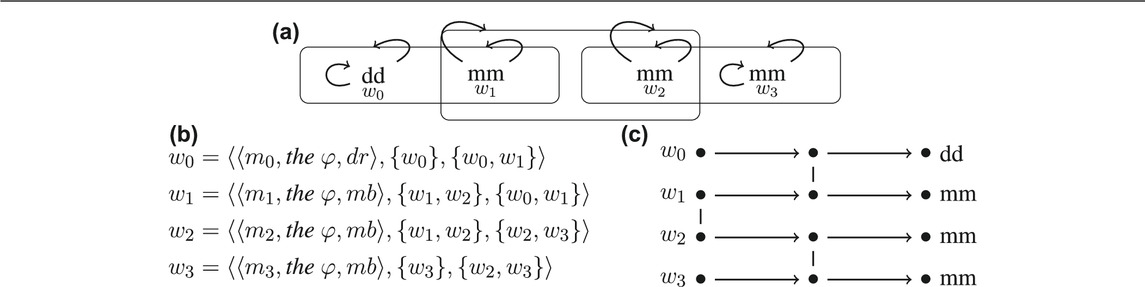
We next consider some examples. The first (23) demonstrates several points: first, basic cases can become more complex than the ones considered before; second, there are additional modeling assumptions that have to be made; third, for visualization there is a different type of graph that is better suited for base situations; and fourth, it shows how the construction is applied for finding fixed–points for epistemically felicitous referential uses of definite descriptions.
23) Scenario. The following is common knowledge. Either (
In which situation is it mutually felicitous to refer to Monkey Business with
There are two competing joint projects starting with the φ: The project
24)
Clearly, licensing is satisfied for the speaker’s information state in both
25)
The update in Step 2 again eliminates
26)
Now, if we consider
27)
Now, the prediction is that Ann can use the φ for referring to Monkey Business only in situation
The definition of possible worlds becomes more complicated when adding project l. As project l is defined for all state of affairs, it does not need to be shown in graphs, except some state of affairs would otherwise be eliminated. The simplified graphs in Table 8 represent the possible worlds defined in construction steps (25)–(27) with joint project l only showing when necessary.
5.3 Hierarchical Epistemic Graphs
The base level of a graph consist of worlds that satisfy truthfulness and introspection. Now, we turn to examples where the truthfulness condition is violated. All the examples that we have seen are represented by graphs that have a base in
The first condition says that worlds at the base have order type 0. The second, that for other worlds w the order type is the smallest ordinal that is larger than all order types of worlds from which w cannot be reached by an epistemic path.8 The last condition introduces the order type of a set of possible worlds which is the smallest ordinal that is at least as large as the order types of all the worlds in the set. For example, in Table 7, the worlds
Let us first consider Versions 2 and 3 in Table 5 with the corresponding examples in (17). The joint project of asserting sentence s with meaning φ was defined as the set of all triples
This means, the joint communicative acts
The conditions are unchanged, except that basic projects have been replaced by extended projects. The licensing condition says that the joint communicative act can be performed in all epistemically possible state of affairs, and uniqueness that performing it leads to a unique response for each state. The operators selecting worlds satisfying the epistemic felicity constraints stay the same, except that the basic projects are replaced by extended projects. For convenience, they are shown in Eq. 26 and Eq. 27.
Apart from checking whether licensing and uniqueness hold for the speaker and hearer’s perspective, the operators check whether the joint communicative act represented by a possible world is an instantiation of a given extended joint project
With these operators, a fixed–point can be constructed as in 17, the only difference being that the construction is applied bottom up, level by level. We eschew the technical details and demonstrate their workings with some examples. Let us consider the graphs in Table 9. In graphs a), c), and d), the belief states of participants are subsets of the base level. In

TABLE 9. Epistemic graphs: (a), (b) for assertions in scenarios similar to (17); (a): false belief case, (b): lying; (c), (d) for reference in scenarios similar to (13)–(16); (c): failed joint reference on higher level, (d): successful joint reference on higher level. Abbreviations: φ a proposition,
We next turn to b) in Table 9. From the hearer’s perspective, the situation is identical to that of a) or that of Version 1 in (17) with graph (18). Hence, we only need to consider the speaker’s perspective in
With c) and d), we switch to referential uses of definite descriptions. Clearly, in c) the interpretation of the φ = ‘The movie showing at the Roxy tonight’ cannot agree between speaker and hearer, neither in
In all examples of Table 9, the belief states of interlocutors are subsets of the base level or singleton sets. We can also find natural situations with belief states with uncertainty at higher levels. Examples are shown in Table 10. In a) The speaker does not know whether φ or
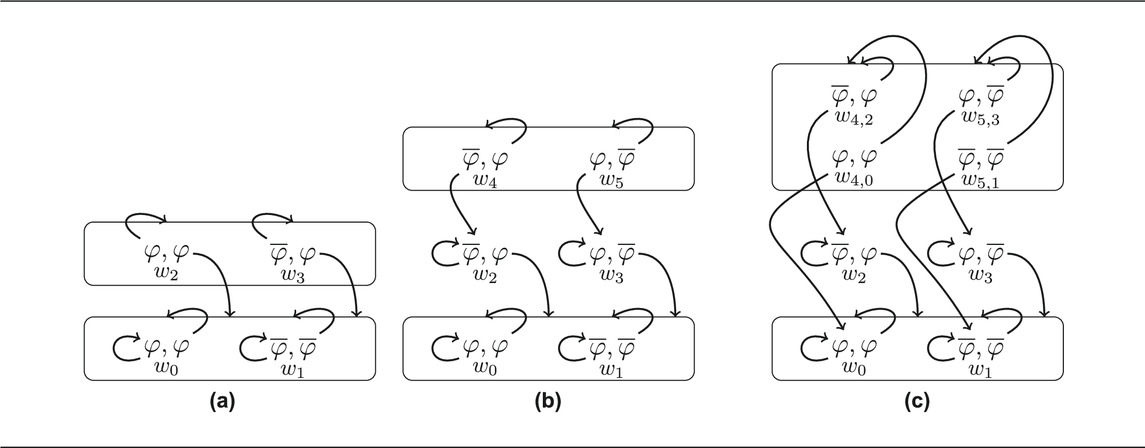
TABLE 10. Epistemic graphs with uncertainty on higher levels. (a), (b) for assertions in scenarios similar to (17); (a): case of insufficient information, (b): detected lying, (c): hearer uncertainty: is speaker honest or lying. Abbreviations: φ a proposition,
In b) of Table 10, a case is shown in which the hearer knows that the speaker is lying but does not know whether φ or
The examples that we have considered so far show strictly hierarchical belief states. This means, in every possible world that is not in the base level, there is one agent whose belief set has an order type that is smaller than the world’s order type. Graphically, this means that the belief set of one agent is a subset of the levels that are below the actual world. More precisely, they are defined as follows:
28) A possible world is strictly hierarchical, if for all v in the transitive hull
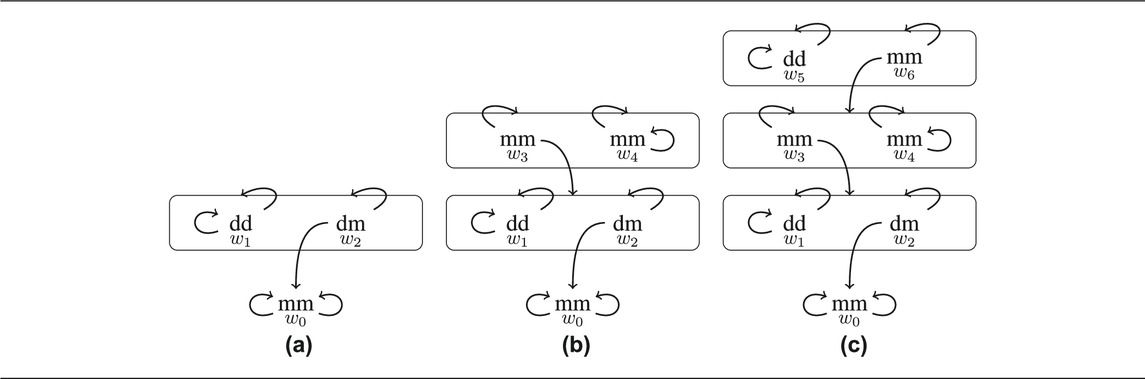
If belief states are not strictly hierarchical, they must show circular relations on higher levels. We consider some examples. Table 11 shows three epistemic graphs with possible worlds that can be reached from each other via epistemic paths.
We consdier an example:
29) Ann and Bob attend a course on film studies. Together they listen as the lecturer tells the class that, this evening, the course will watch Monkey Business at the cinema. Later, in the library, Bob meets the lecturer as she talks to another film student. However, Bob cannot see who the student is. He thinks it is Clara, another student, or Ann. The lecturer notices him and says: “Oh, Bob! Good to see you. I made a mistake. The movie showing this evening is A Day at the Races, and not Monkey Business.” Bob leaves without asking who the other student is. He knows that Ann cannot have learned about the correction if she was not in the library. Later, he receives a mail from Ann telling him that she doesn’t like the movie showing at the cinema tonight.
What is Ann referring to? The situation is represented by Graph a) in Table 11. If Ann was not the other student in the library, then, clearly, she refers to Monkey Business. If she was there, then she knows that Bob knows that A Day at the Races is showing and that Bob knows that the other student knows it too. She also knows that he does not know that the other student was she herself. Hence, if she was the other student then she knows that Bob cannot know what
At this point, we should recall that the iterative application of the felicity operators corresponds to the iterative reasoning about each other and the ensuing step by step elimination of epistemic possibilities that are not consistent with uniqueness and licensing. The problem with world
If a world w is rooted in the lower level with respect to an act a and a project p, and if
The next example is one that shows two levels with circular belief states. It uses the same type of communicative situation with uncertain bystander as Example (29).
30) Ann and Bob attend a course on film studies. Together they listen as the lecturer tells the class that, this evening, the course will watch Monkey Business at the cinema together. Later, in the library, Bob meets the lecturer as she talks to another film student. However, Bob cannot see who the student is. He thinks it is Clara, another student, or Ann. The lecturer notices him and says: “Oh, Bob! Good to see you. I made a mistake. The movie showing this evening is A Day at the Races, and not Monkey Business. Bob leaves without asking who the other student is. Still later, he meets the lecturer again in the cafeteria. She tells him that the program has changed again. Then Ann comes in. The lecturer tells her: “Hallo Ann, I have just told this student here that the program changed again. It is Monkey Business that is showing tonight.” Bob noticed that Ann could not see him, that she must think that it could be him but that she could not be certain. He also knew that she must think that he could not learn about the change of program if he was not the student in the cafeteria. Bob also noticed that Ann must have been the other student in the library. Later, he receives a mail from Ann, telling him that she doesn’t like the movie showing at the cinema tonight.
The situation is represented by b) in Table 11. It can be easily checked that the fixed–point on the second level is identical to the level consisting of
In principle, we can add more and more levels with circular structure. Graph c) in Table 11 shows an example with four levels. As world
As final example in this section, we present a situation that resembles (29) but is not about reference but about assertions.
31) Helga calls up her son Stephan and asks him whether he wants to visit her in Munich. Stephan tells her that he will watch the weather forecast this evening and call her in the morning. Helga knows the channel where Stephan watches the late news and learns that it is snowing in the Alps the next day. Next morning a mutual friend video calls her and mentions that the forecast has changed and that the streets are free of snow. In the background, Helga can see someone who resembles her son Stephan, but she cannot be sure. Shortly afterward, she receives a text message from Stephan saying that he cannot visit her because snow is forecasted and he doesn’t want to drive then. He also wrote that he will not have his smartphone with him and cannot read text messages that day. She knows that Stephan has a new girl-friend and prefers to stay at home.
Is Stephan lying about snow in the Alps, or not? The situation is represented by the graph in Table 12a.
World
What is the difference between the graphs in Tables 11a and 12a? The answer is that we chose a minimal representation of (29) in Table 11a. We saw in (18) and Table 4 that the basic utterance situation for assertions can come in different varieties. The textual description of the utterance situation in (17) leaves the exact epistemic relations between speaker and hearer underspecified. The same underspecification is encountered with Example (29). An alternative to the graph in Table 11a is shown in Table 12b.9 Here, world
6 Comparison and Outlook
We developed a theory of epistemic felicity conditions and speech acts that followed a path charted by the works of J. Searle, H.P. Grice, and H.H. Clark. For both assertions and definite descriptions there is a large body of literature, so large that we can only hint at how our model fits into the general landscape of semantic and pragmatic theories. For both referential uses of definite descriptions and assertions we make minimal assumption about dialogue context. In our model, familiarity (Heim, 1982) and uniqueness (Russell, 1905, 1919) of referents are not semantic properties of definite descriptions but follow from pragmatic felicity conditions that hold in very basic epistemic graphs only. If the felicity conditions are not met, then the referent remains undefined (see Strawson, 1950). Our model also accounts for situation in which the decription of a definite does, or may not apply to the referent as in Donnellan’s (1966) famous Martini-glass example (an example is shown in Table 11, Graph a)). For assertions, our constitutive rules only require that the asserted proposition is true (Weiner, 2005), from which the requirement that the speaker believes it (Williamson, 1996; Turri, 2016) follows as a felicity requirement of basic utterance situations, but it may be violated at higher order belief states. In particular, our model shows how the existence of non–cooperative language use and un-truthfulness can be reconciled with the constitutive requirement of truthfulness (see Pagin 2016 for an overview of the related philosophical discussion).
Our model is about epistemic felicity conditions of speech acts. Which speech acts can be performed in a dialogue situation is pragmatically dependent on the interlocutors’ beliefs about the world and about each other. There are theories that try to predict possible speech acts without reference to private beliefs. Prominent examples are commitment theories, discourse structural approaches, or approaches based on the idea of common scoreboards. In a commitment approach, if a speaker asserts a sentence then s/he takes on the (social) obligation of defending its truth; s/he does, however, not necessarily express a belief in it.10 Discourse structural approaches explain the possible sequences of speech acts by discourse relations that must hold between dialogue moves. Example are the Segmented Discourse Representation Theory (Asher and Lascarides, 2003) and the Rhetorical Structure Theory (Mann and Thompson, 1988). Relevant is here, for example, the account of strategic conversation in non–cooperative discourse by Asher and Lascarides (2013). The idea that information update in dialogue can be modeled with public scoreboards can be traced back to Lewis (1979). The scoreboard represents the public information of interlocutors. Each communicative act updates the scoreboard in specific ways. In ideal cases, the update only depends on the old scoreboard and the sentence uttered. Hence, the update after an honest assertion and a lie would be the same. A comparison of our model to any one of these approaches would go beyond the scope of this article. A common motivation for all of them are the problems that epistemic accounts of speech acts face when confronted with non-cooperative discourse or utterance situations with higher–order belief states. Our model shows how these problems can be overcome.
In the previous sections we have seen how the interlocutors’ limited perspectives can give rise to extended uses of communicative acts. On the base level, where interlocutors follow constitutive rules and have only truthful beliefs, the joint communicative acts that mutually satisfy the epistemic felicity conditions of licensing and uniqueness can be found by a fixed-point construction. The fixed-point construction depends only on a given set of joint projects, hence, it generalizes to any type of communicative act, the constitutive uses of which can be represented by joint communicative acts of the form
The elements of
We said before that constitutive rules define a form of social institution consisting in a conventionalized regularity of linguistic behavior. In the following, we tied this behavior to a class of well–behaved utterance situations at the base of the epistemic graphs that we have seen. From there, the behavior is extended to a wider class of hierarchical epistemic states. We have seen that, in extending the behavior, indistinguishability between utterance situations play a crucial role. The extended use of a communicative act can travel up the hierarchy along epistemic paths because the situation on the higher level is for one, or sometimes both interlocutors indistinguishable from one at a lower level.
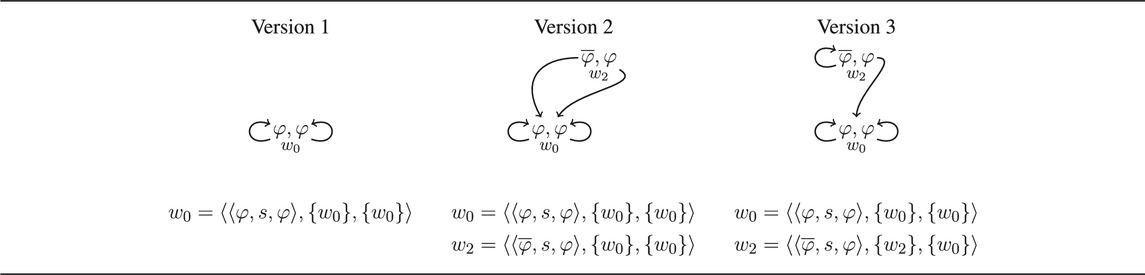
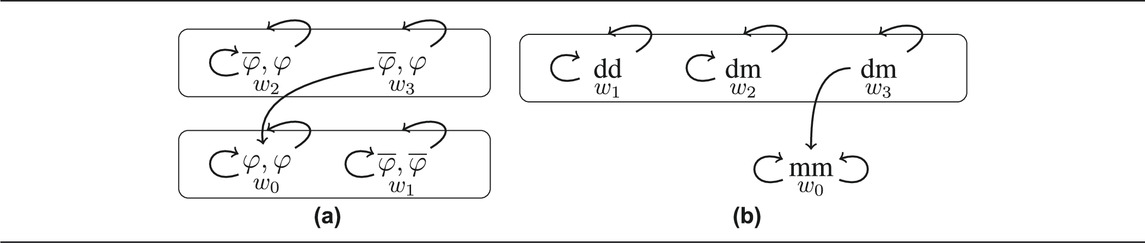
If a communicative act is defined for a constitutive core, then our theory also predicts that extended uses that violate the constitutive rules exist. Hence, if honest, truthful assertions exist, then also assertions based on false beliefs must exist, as well as outright lies. This also means that the definitions of speech acts can be simplified considerably, as only constitutive rules for uses in the well–behaved core have to be considered.12 A non-trivial observation is that extended uses can still be classified with the same name as the uses in the constitutive core. In the introduction we mentioned the following examples in (32) and (33):
32) Leo told me that it is snowing in the Alps, but I knew that the snowing had stopped. (false belief).
33) Leo told me that it is snowing in the Alps, but I knew that she is lying. (lying).
Assuming that tell reports an assertion event, then the examples show that classifying an utterance as assertion is consistent with false beliefs and lying. This raises a question about the semantics of tell. If the constitutive rules were part of the semantic meaning of assertions, then, given how we have defined the constitutive joint project of asserting, the sentence ‘Leo told me that φ’ should mean that Leo uttered a sentence with meaning φ and she uttered it in a situation in which this sentence is true. Clearly, the examples in (3′) and (4′) are not consistent with such a semantic rule. Table 13 shows two graphs for the examples.
In our model, we distinguished between the project as defined by its constitutive rules and the extended project that is defined by the action–response pairs alone. This means, if p is a joint project, then the extended project
This solution assumes that lexical meaning is flexible and allows for contextual adjustment taking the interlocutors perspectives and the resulting indistinguishability between utterance situations into account. There are other paths for seeking a solution that come to mind. For example, one could assume that the lexical meaning of tell has a meaning that is weak enough to be consistent with all epistemic graphs that we have considered in this article. Commitment approaches belong here. We must, however, leave the comparison and further pursuit of the semantic issues to future research.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
AB is the sole author of this article.
Funding
European Research Council, award number(s): ERC 787929 SPAGAD: Speech Acts in Grammar and Discourse. The publication of this article was funded by the Open Access Fund of the Leibniz Association.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1The chess board is an
2‘Joint projects’ can be seen as a generalization of the notion of adjacency pairs (Schegloff and Sacks, 1973).
3This does not mean that we consider ambiguity and lack of understanding to be minor dialogue problems. The uniqueness constraint is a regulatory, i.e., normative constraint. Normative rules can be violated with or without intend. Crucial for us is that their logical consequences can be studied without considering repair strategies that apply in case of violations.
4The representation of the hearer’s response by a formula φ is not essential here. We could have represented the same joint project as
5For the relation between possible worlds as defined in (19) and Kripke–frames for modal logics see Appendix A.2.
6The notation with
7For example, the class of all possible worlds could be introduced as the maximal fixed–point of the set continuous operator
8Set theoretically the supremum of a set of ordinals is just the union of these ordinals. The definition is maximally general and extends into the transfinite. However, in this article, we only consider worlds with finite order type.
9There are, in fact, an infinitude of alternatives. We leave the clarification of this issue to future research.
10There are, however, various meanings that have been given to the term commitment. For an older overview, see (Brabanter and Dendale, 2008). For recent discussions, see e.g., (Krifka, 2012; Geurts, 2019; Krifka, 2019).
11In line with H.H. Clark’s propositions 3 and 6, (1996, p. 23/24).
12However, we have to concede that extending the account to cover intricate problems that motivate, for example, dynamic syntactic theories like DS-TTR (see Gregoromichelaki et al., 2011) needs further work (e.g., on the problem of split turn taking; see Gregoromichelaki and Kempson, 2016 for an overview; I thank the reviewers for bringing this important phenomenon to my attention).
References
Aczel, P. (1988). Non-well-founded Sets. Stanford, CA: Center for the Study of Language and Information.
Asher, N., and Lascarides, A. (2003). Logics of Conversation. Cambridge: Cambridge University Press.
Asher, N., and Lascarides, A. (2013). Strategic Conversation. Semantics and Pragmatics 6, 1–62. doi:10.3765/sp.6.2
Baltag, A., and Renne, B. (2016). “Dynamic Epistemic Logic,” in The Stanford Encyclopedia of Philosophy. Editor E. N. Zalta (Winter: Metaphysics Research Lab, Stanford University).
Baltag, A., van Ditmarsch, H. P., and Moss, L. S. (2008). “Epistemic Logic and Information Update,” in Handbook on the Philosophy of Information. (Amsterdam: Elsevier Science Publishers), 361–455. doi:10.1016/b978-0-444-51726-5.50015-7
Barwise, J., and Etchemendy, J. (1989). The Liar: An Essay on Truth and Circularity. Oxford: Oxford University Press.
Barwise, J., and Moss, L. (1996). Vicious Circles. Stanford, CA: Center for the Study of Language and Information.
Barwise, J. (1989). “On the Model Theory of Common Knowledge,” in The Situation in Logic. Editor J. Barwise (Stanford, CA: CSLI Lecture Notes), 201–220.
Benz, A. (2008). “Assertions in AFA Set Theory,” in New Approaches to Classes and Concepts. Editor K. Robering (London: College Publications), 143–176.
Benz, A. (2012). On a Super Large Fixed-point of Common Information in Multi-Agent Signalling Games. Logic J. IGPL 20, 94–120. doi:10.1093/jigpal/jzr027
Clark, H. H., and Marshall, C. R. (1981). “Definite Reference and Mutual Knowledge,” in Elements of Discourse Understanding. Editors A. K. Joshi, B. Webber, and I. Sag (Cambridge: Cambridge University Press), 10–63.
De Brabanter, P., and Dendale, P. (2008). Commitment: the Term and the Notions. Belgian J. Linguistics 22, 1–14. doi:10.1075/bjl.22.01de
Donnellan, K. S. (1966). Reference and Definite Descriptions. Phil. Rev. 75, 281–304. doi:10.2307/2183143
Fagin, R., Halpern, J. Y., Moses, Y., and Moshe, Y. V. (1995). Reasoning about Knowledge. Cambridge MA: MIT Press.
Gerbrandy, J. (1998). Bisimulations on Planet Kripke. Ph.D. Thesis, Institute for Logic, Language and Computation. Amsterdam: Universiteit van Amsterdam.
Gerbrandy, J., and Groeneveld, W. (1997). Reasoning about Information Change. J. logic, Lang. Inf. 6, 147–169. doi:10.1023/a:1008222603071
Geurts, B. (2019). Communication as Commitment Sharing: Speech Acts, Implicatures, Common Ground. Theor. Linguistics 45, 1–30. doi:10.1515/tl-2019-0001
Ginzburg, J. (2012). The Interactive Stance: Meaning for Conversation. Oxford: Oxford University Press.
Gregoromichelaki, E., and Kempson, R. (2016). “Joint Utterances and the (Split-)Turn Taking Puzzle,” in Interdisciplinary Studies in Pragmatics, Culture and Society. Perspectives in Pragmatics, Philosophy & Psychology. Editors A. Capone, and J. L. Mey (Switzerland: Springer International Publishing), 703–743. doi:10.1007/978-3-319-12616-6_28
Gregoromichelaki, E., Kempson, R., Purver, M., Mills, G. J., Cann, R., Meyer-Viol, W., et al. (2011). Incrementality and Intention-Recognition in Utterance Processing. Dialogue and Discourse 2, 199–233. doi:10.5087/dad.2011.109
Grice, H. P. (1975). “Logic and Conversation,” in Syntax and Semantics. Editors P. Cole, and J. L. Morgan (New York: Academic Press), 41–58. doi:10.1163/9789004368811_003
Heim, I. (1982). The Semantics of Definite and Indefinite Noun Phrases. Amherst: The University of Massachusetts. Ph.D. thesis.
Korta, K., and Perry, J. (2020). “Pragmatics,” in The Stanford Encyclopedia of Philosophy. Editor E. N. Zalta (Stanford: Metaphysics Research Lab, Stanford University).
Krifka, M. (2012). “Commitment Space Semantics: Declarative Questions, Negated Questions, and Question Tags,” in Proceedings of the 25th Semantics and Linguistic Theory Conference (SALT). Editors S. D’Antonio, M. Moroney, and C. R. Little.
Mann, W. C., and Thompson, S. A. (1988). Rhetorical Structure Theory: Toward a Functional Theory of Text Organization. Text 8, 243–281. doi:10.1515/text.1.1988.8.3.243
Morris, C. W. (1938). “Foundations of the Theory of Signs,” in International Encyclopedia of Unified Science. Editors O. Neurath, R. Carnap, and C. W. Morris (Chicago: The University of Chicago Press), 1–59.
Pagin, P. (2016). “Assertion,” in The Stanford Encyclopedia of Philosophy. Editor E. N. Zalta (Winter: Metaphysics Research Lab, Stanford University).
Schegloff, E. A., and Sacks, H. (1973). Opening up Closings. Semiotica 8, 289–327. doi:10.1515/semi.1973.8.4.289
Turri, J. (2016). Knowledge and the Norm of Assertion: An Essay in Philosophical Science. Cambridge: Open Book Publishers. doi:10.11647/OBP.0083
van Benthem, J. (2011). Logical Dynamics of Information and Interaction. Cambridge: Cambridge University Press.
Weiner, M. (2005). Must We Know what We Say? Phil. Rev. 114, 227–251. doi:10.1215/00318108-114-2-227
7 Appendix
7.1 How to read epistemic graphs
Table 14 shows how to read epistemic graphs. We assume that there is a speaker A and an addressee B. Arrows to the left of a world point to A’s information state, and arrows to the right to B’s information state. An information state is a set of possible worlds. If an arrow points to a single world w, then the respective information state is a set with w as single element. If an information state has more than one element, it is represented by a box encircling its elements. For convenience, basic building units of graphs are shown in the Table 14.

TABLE 14. Reading epistemic graphs. The comments to the right explain new features of the respective graphs.
7.2 Epistemic Graphs and Kripke Frames
We address the question how epistemic graphs are related to Kripke frames for epistemic modal logic. Epistemic modal logic can be traced back to (Hintikka, 1962). For a newer introduction and an overview see e.g., (van Benthem, 2011) and (Baltag et al., 2008; Baltag and Renne, 2016). In epistemic modal logics, epistemic possibility is modeled by accessibility relations between worlds. For each agent i there is a relations
In reverse, if a system of equations is given that defines an epistemic graph, and
Keywords: speech acts, common knowledge, epistemic perspective, referential acts, assertions
Citation: Benz A (2021) Epistemic Perspectives and Communicative Acts. Front. Commun. 6:612733. doi: 10.3389/fcomm.2021.612733
Received: 30 September 2020; Accepted: 18 June 2021;
Published: 18 August 2021.
Edited by:
Petra Hendriks, University of Groningen, NetherlandsReviewed by:
Jonathan Ginzburg, Université Paris Diderot, FranceRobert Van Rooij, University of Amsterdam, Netherlands
Copyright © 2021 Benz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anton Benz, YmVuekBsZWlibml6LXphcy5kZQ==
 Anton Benz
Anton Benz